Enhancing Sensitivity of Double-Walled Carbon Nanotubes with Longitudinal Magnetic Field
Abstract
1. Introduction
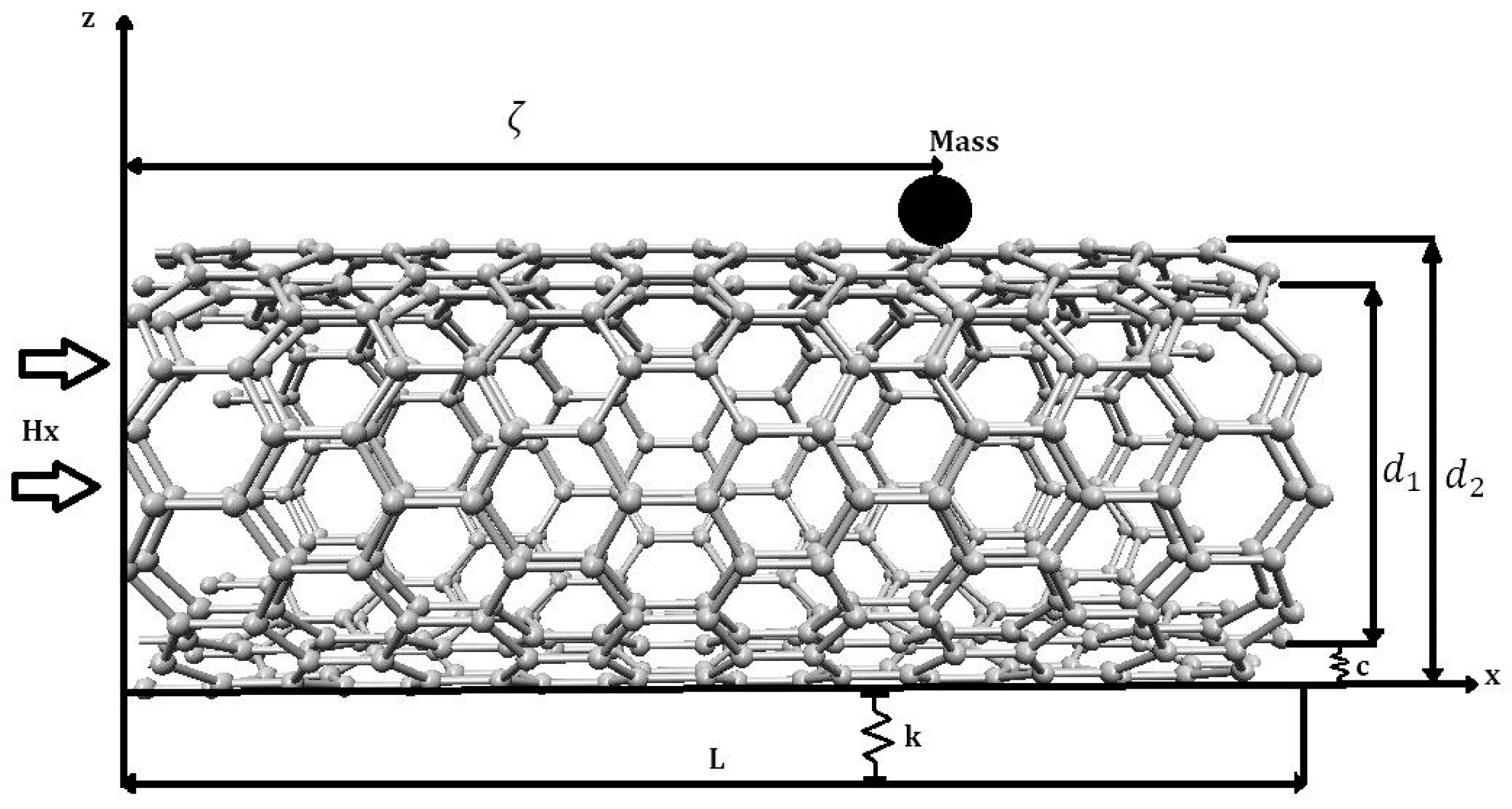
2. Theoretical Basis
Maxwell’s Relations
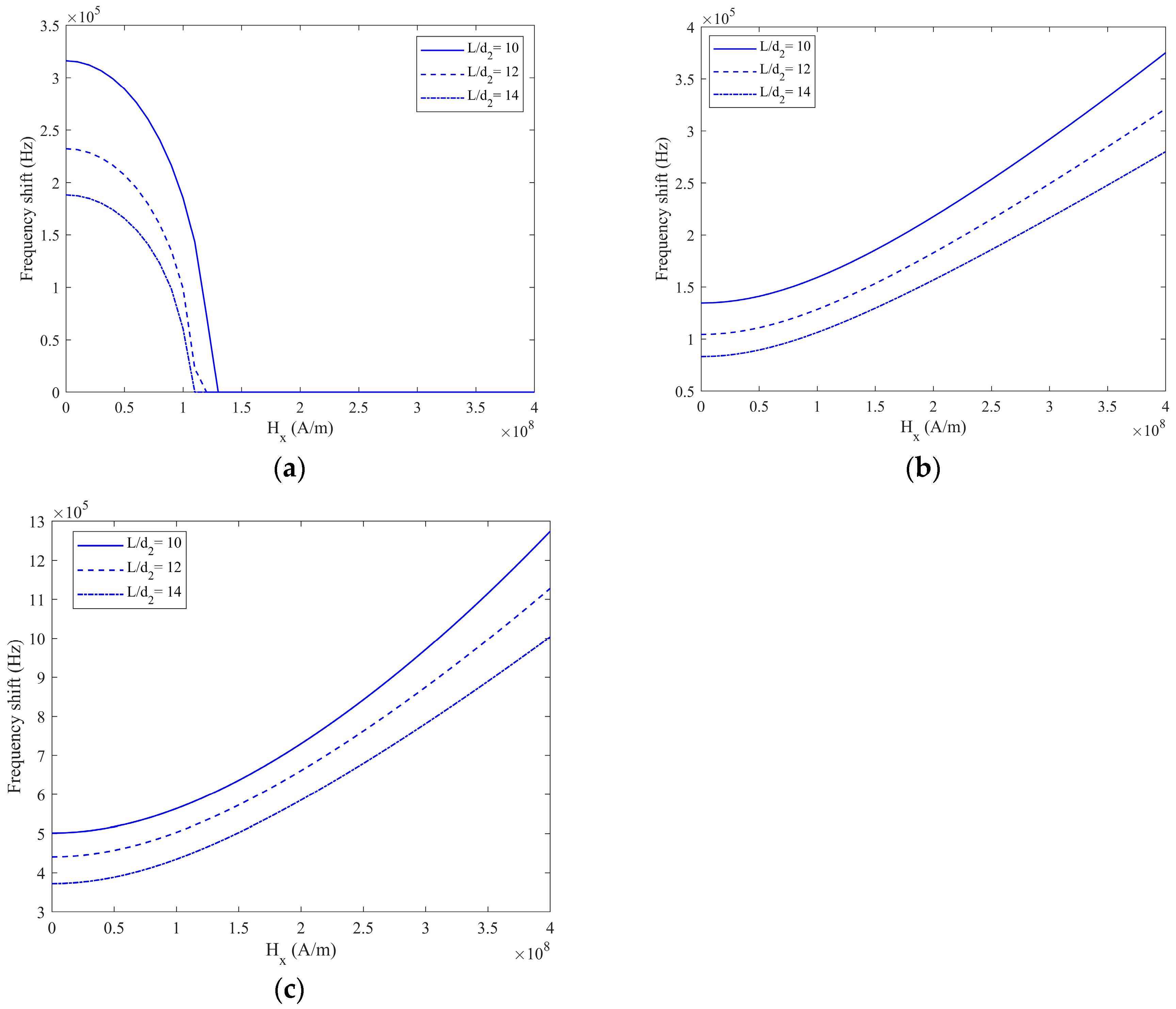
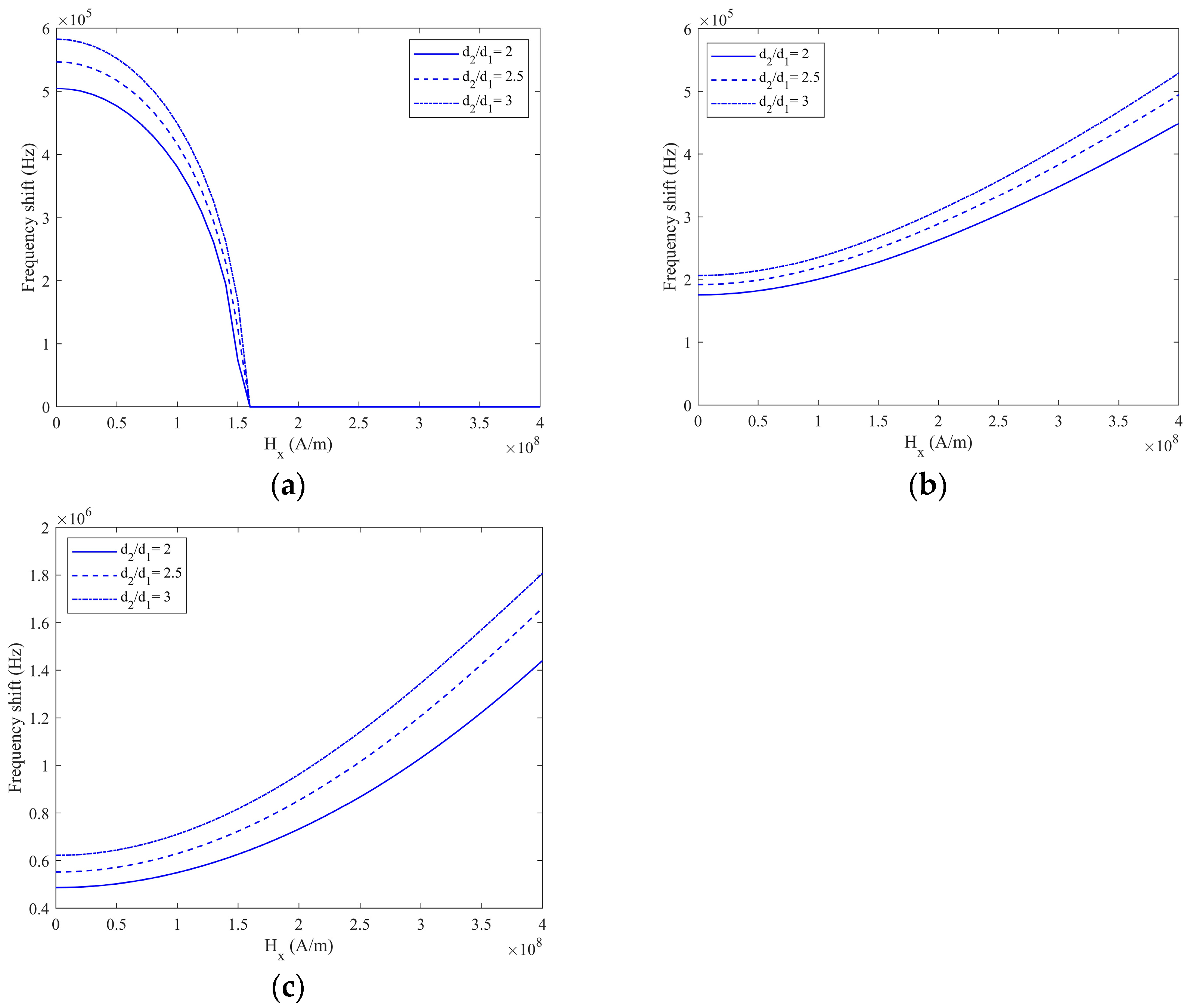
3. Results and Discussions
This Study’s Limitations and Potential Future Research Areas
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Guo, Q.; Cui, D.J.S. Recent advances in nanotechnology applied to biosensors. Sensors 2009, 9, 1033–1053. [Google Scholar] [CrossRef]
- Kim, W.; Oh, H.; Kwak, Y.; Park, K.; Ju, B.-K.; Kim, K. Development of a carbon nanotube-based touchscreen capable of multi-touch and multi-force sensing. Sensors 2015, 15, 28732–28741. [Google Scholar] [CrossRef] [PubMed]
- Chien, W.T.; Chen, C.S.; Chen, H.H. Resonant frequency analysis of fixed-free single-walled carbon nanotube-based mass sensor. Sens. Actuators A Phys. 2006, 126, 117–121. [Google Scholar]
- Schroeder, V.; Savagatrup, S.; He, M.; Lin, S.; Swager, T.M. Carbon nanotube chemical sensors. Chem. Rev. 2018, 119, 599–663. [Google Scholar] [CrossRef] [PubMed]
- Kruss, S.; Hilmer, A.J.; Zhang, J.; Reuel, N.F.; Mu, B.; Strano, M.S. Carbon nanotubes as optical biomedical sensors. Adv. Drug Deliv. Rev. 2013, 65, 1933–1950. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, R.; Adhikari, S.; Mitchell, J. Vibrating carbon nanotube based bio-sensors. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 42, 104–109. [Google Scholar] [CrossRef]
- Trivedi, S.; Kumar, S.; Sharma, S.C.; Harsha, S.P. Biosensing application of multiwall boron nitride nanotube-based nanoresonator for detecting various viruses. IET Nanobiotechnol. 2015, 9, 259–263. [Google Scholar] [CrossRef]
- Mortimer, M.; Petersen, E.J.; Buchholz, B.A.; Orias, E.; Holden, P.A. Bioaccumulation of multiwall carbon nanotubes in Tetrahymena thermophila by direct feeding or trophic transfer. Environ. Sci. Technol. 2016, 50, 8876–8885. [Google Scholar] [CrossRef] [PubMed]
- Khater, M.E.; Abdel-Rahman, E.M.; Nayfeh, A.H. A mass sensing technique for electrostatically-actuated mems. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; pp. 655–661. [Google Scholar]
- Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using double-layered graphene sheets resonators. J. Appl. Phys. 2013, 114, 094307. [Google Scholar] [CrossRef]
- Ardali, J.R.; Ghaderi, R.; Raeiszadeh, F. Effect of microbeam geometry on the nano-mass sensor performance. Mech. Ind. 2019, 20, 304. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ramos, D.; Martínez, J.; Fernández-Regúlez, M.; García, R.; San Paulo, Á.; Calleja, M.; Tamayo, J. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotechnol. 2010, 5, 641–645. [Google Scholar] [CrossRef] [PubMed]
- Abadal, G.; Davis, Z.J.; Helbo, B.; Borrise, X.; Ruiz, R.; Boisen, A.; Campabadal, F.; Esteve, J.; Figueras, E.; Perez-Murano, F. Electromechanical model of a resonating nano-cantilever-based sensor for high-resolution and high-sensitivity mass detection. Nanotechnology 2001, 12, 100. [Google Scholar] [CrossRef]
- Jiang, Y.; Tan, C.Y.; Tan, S.Y.; Wong, M.S.F.; Chen, Y.F.; Zhang, L.; Yao, K.; Gan, S.K.E.; Verma, C.; Tan, Y.-J. SAW sensor for Influenza A virus detection enabled with efficient surface functionalization. Sens. Actuators B Chem. 2015, 209, 78–84. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Airborne engineered nanoparticle mass sensor based on a silicon resonant cantilever. Sens. Actuators B Chem. 2013, 180, 77–89. [Google Scholar] [CrossRef]
- Zarepour, M.; Hosseini, S.A.; Ghadiri, M. Free vibration investigation of nano mass sensor using differential transformation method. Appl. Phys. A 2017, 123, 181. [Google Scholar] [CrossRef]
- Bouchaala, A.; Nayfeh, A.H.; Younis, M.I. Frequency shifts of micro and nano cantilever beam resonators due to added masses. J. Dyn. Syst. Meas. Control 2016, 138, 091002. [Google Scholar] [CrossRef]
- Habibi, S.; Nematollahi, M. Position and mass identification in nanotube mass sensor using neural networks. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5377–5387. [Google Scholar] [CrossRef]
- Soltani, P.; Pashaei, O.; Taherian, M.M.; Farshidianfar, A. Free vibration of a carbon nanotube-based mass sensor. Adv. Mater. Res. 2012, 403, 1163–1167. [Google Scholar] [CrossRef]
- Patel, A.M.; Joshi, A.Y. Detection of biological objects using dynamic characteristics of double-walled carbon nanotubes. Appl. Nanosci. 2015, 5, 681–695. [Google Scholar] [CrossRef]
- Pacholarz, K.J.; Garlish, R.A.; Taylor, R.J.; Barran, P.E. Mass spectrometry based tools to investigate protein–ligand interactions for drug discovery. Chem. Soc. Rev. 2012, 41, 4335–4355. [Google Scholar] [CrossRef]
- Ghatkesar, M.K.; Barwich, V.; Braun, T.; Ramseyer, J.-P.; Gerber, C.; Hegner, M.; Lang, H.P.; Drechsler, U.; Despont, M. Higher modes of vibration increase mass sensitivity in nanomechanical microcantilevers. Nanotechnology 2007, 18, 445502. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, G.-J.; Zhang, L.; Li, X.-F. Vibration of double-walled carbon nanotube based nanomechanical sensor with initial axial stress. Comput. Mater. Sci. 2012, 58, 51–58. [Google Scholar] [CrossRef]
- Herrera-May, A.L.; Soler-Balcazar, J.C.; Vázquez-Leal, H.; Martínez-Castillo, J.; Vigueras-Zuñiga, M.O.; Aguilera-Cortés, L.A. Recent advances of MEMS resonators for Lorentz force based magnetic field sensors: Design, applications and challenges. Sensors 2016, 16, 1359. [Google Scholar] [CrossRef]
- Kumar, A.; Kaur, D. Magnetic field tunable piezoelectric resonator for MEMS applications. Sens. Actuators A Phys. 2023, 364, 114803. [Google Scholar] [CrossRef]
- White, C.; Piazza, G.; Stephanou, P.; Pisano, A. Design of nano-gap piezoelectric resonators for mechanical RF magnetic field modulation. Sens. Actuators A Phys. 2007, 134, 239–244. [Google Scholar] [CrossRef]
- Lucklum, F.; Jakoby, B. Novel magnetic–acoustic resonator sensors for remote liquid phase measurement and mass detection. Sens. Actuators A Phys. 2008, 145, 44–51. [Google Scholar] [CrossRef]
- Murmu, T.; McCarthy, M.; Adhikari, S. Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: A nonlocal elasticity approach. J. Sound Vib. 2012, 331, 5069–5086. [Google Scholar] [CrossRef]
- Sobamowo, M.; Akanmu, J.; Adeleye, O.; Akingbade, S.; Yinusa, A. Coupled effects of magnetic field, number of walls, geometric imperfection, temperature change, and boundary conditions on nonlocal nonlinear vibration of carbon nanotubes resting on elastic foundations. Forces Mech. 2021, 3, 100010. [Google Scholar] [CrossRef]
- Zhen, Y.-X.; Wen, S.-L.; Tang, Y. Free vibration analysis of viscoelastic nanotubes under longitudinal magnetic field based on nonlocal strain gradient Timoshenko beam model. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 105, 116–124. [Google Scholar] [CrossRef]
- Sadeghi-Goughari, M.; Jeon, S.; Kwon, H.-J. Effects of magnetic-fluid flow on structural instability of a carbon nanotube conveying nanoflow under a longitudinal magnetic field. Phys. Lett. A 2017, 381, 2898–2905. [Google Scholar] [CrossRef]
- Zhang, D.; Lei, Y.; Shen, Z. Effect of longitudinal magnetic field on vibration characteristics of single-walled carbon nanotubes in a viscoelastic medium. Braz. J. Phys. 2017, 47, 640–656. [Google Scholar] [CrossRef]
- Yinusa, A.; Sobamowo, M.; Adelaja, A. Nonlinear vibration analysis of an embedded branched nanofluid-conveying carbon nanotube: Influence of downstream angle, temperature change and two dimensional external magnetic field. Nano Mater. Sci. 2020, 2, 323–332. [Google Scholar] [CrossRef]
- Arda, M.; Aydogdu, M. Vibration analysis of carbon nanotube mass sensors considering both inertia and stiffness of the detected mass. Mech. Based Des. Struct. Mach. 2022, 50, 841–857. [Google Scholar] [CrossRef]
- Ceballes, S.; Saunders, B.; Abdelkefi, A. Nonlocal Timoshenko modeling effectiveness for carbon nanotube-based mass sensors. Eur. J. Mech.-A/Solids 2022, 92, 104462. [Google Scholar] [CrossRef]
- Ekinci, K.; Yang, Y.T.; Roukes, M. Ultimate limits to inertial mass sensing based upon nanoelectromechanical systems. J. Appl. Phys. 2004, 95, 2682–2689. [Google Scholar] [CrossRef]
- Borm, P.; Klaessig, F.C.; Landry, T.D.; Moudgil, B.; Pauluhn, J.; Thomas, K.; Trottier, R.; Wood, S. Research strategies for safety evaluation of nanomaterials, part V: Role of dissolution in biological fate and effects of nanoscale particles. Toxicol. Sci. 2006, 90, 23–32. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Mohammadi, F.S.; Rahimi, Z.; Sumelka, W.; Yang, X.-J. Investigation of free vibration and buckling of Timoshenko nano-beam based on a general form of Eringen theory using conformable fractional derivative and Galerkin method. Eng. Trans. 2019, 67, 347–367. [Google Scholar]
- Rahimi, Z.; Sumelka, W.; Baleanu, D. A mechanical model based on conformal strain energy and its application to bending and buckling of nanobeam structures. J. Comput. Nonlinear Dyn. 2019, 14, 061004. [Google Scholar] [CrossRef]
- Rahimi, Z.; Rezazadeh, G.; Sumelka, W. A non-local fractional stress–strain gradient theory. Int. J. Mech. Mater. Des. 2020, 16, 265–278. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. In Modeling of Carbon Nanotubes, Graphene and Their Composites; Springer: Berlin/Heidelberg, Germany, 2014; pp. 57–82. [Google Scholar]
- Ahmadi, H.R.; Rahimi, Z.; Sumelka, W. Thermoelastic damping in orthotropic and isotropic NEMS resonators accounting for double nonlocal thermoelastic effects. J. Therm. Stress. 2020, 44, 342–358. [Google Scholar] [CrossRef]
- Rashidi, H.; Rahimi, Z.; Sumelka, W. Effects of the slip boundary condition on dynamics and pull-in instability of carbon nanotubes conveying fluid. Microfluid. Nanofluidics 2018, 22, 131. [Google Scholar] [CrossRef]
- Rahimi, Z.; Yazdani, J.; Hatami, H.; Sumelka, W.; Baleanu, D.; Najafi, S. Determination of hazardous metal ions in the water with resonant MEMS biosensor frequency shift–concept and preliminary theoretical analysis. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 529–537. [Google Scholar] [CrossRef]
- Rahimi, Z.; Sumelka, W.; Ahmadi, S.R.; Baleanu, D. Study and control of thermoelastic damping of in-plane vibration of the functionally graded nano-plate. J. Vib. Control 2019, 25, 2850–2862. [Google Scholar] [CrossRef]
- Hutchison, J.; Kiselev, N.; Krinichnaya, E.; Krestinin, A.; Loutfy, R.; Morawsky, A.; Muradyan, V.; Obraztsova, E.; Sloan, J.; Terekhov, S. Double-walled carbon nanotubes fabricated by a hydrogen arc discharge method. Carbon 2001, 39, 761–770. [Google Scholar] [CrossRef]
- Saito, Y.; Nakahira, T.; Uemura, S. Growth conditions of double-walled carbon nanotubes in arc discharge. J. Phys. Chem. B 2003, 107, 931–934. [Google Scholar] [CrossRef]
- Huang, H.; Kajiura, H.; Tsutsui, S.; Murakami, Y.; Ata, M. High-quality double-walled carbon nanotube super bundles grown in a hydrogen-free atmosphere. J. Phys. Chem. B 2003, 107, 8794–8798. [Google Scholar] [CrossRef]
- Qiu, H.; Shi, Z.; Guan, L.; You, L.; Gao, M.; Zhang, S.; Qiu, J.; Gu, Z. High-efficient synthesis of double-walled carbon nanotubes by arc discharge method using chloride as a promoter. Carbon 2006, 44, 516–521. [Google Scholar] [CrossRef]
- Mateiu, R.; Davis, Z.J.; Madsen, D.N.; Mølhave, K.; Bøggild, P.; Rassmusen, A.-M.; Brorson, M.; Jacobsen, C.J.; Boisen, A. An approach to a multi-walled carbon nanotube based mass sensor. Microelectron. Eng. 2004, 73, 670–674. [Google Scholar] [CrossRef]
- Amara, K.; Tounsi, A.; Mechab, I. Nonlocal elasticity effect on column buckling of multiwalled carbon nanotubes under temperature field. Appl. Math. Model. 2010, 34, 3933–3942. [Google Scholar] [CrossRef]
- Pirmoradian, M.; Torkan, E.; Toghraie, D. Study on size-dependent vibration and stability of DWCNTs subjected to moving nanoparticles and embedded on two-parameter foundations. Mech. Mater. 2020, 142, 103279. [Google Scholar] [CrossRef]
- Xu, K.; Guo, X.; Ru, C. Vibration of a double-walled carbon nanotube aroused by nonlinear intertube van der Waals forces. J. Appl. Phys. 2006, 99, 064303. [Google Scholar] [CrossRef]
- Elishakoff, I.; Pentaras, D. Fundamental natural frequencies of double-walled carbon nanotubes. J. Sound Vib. 2009, 322, 652–664. [Google Scholar] [CrossRef]
- Khosrozadeh, A.; Hajabasi, M. Free vibration of embedded double-walled carbon nanotubes considering nonlinear interlayer van der Waals forces. Appl. Math. Model. 2012, 36, 997–1007. [Google Scholar] [CrossRef]
- Murmu, T.; McCarthy, M.; Adhikari, S. Nonlocal elasticity based magnetic field affected vibration response of double single-walled carbon nanotube systems. J. Appl. Phys. 2012, 111, 113511. [Google Scholar] [CrossRef]
- Xu, K.-Y.; Aifantis, E.C.; Yan, Y.-H. Vibrations of double-walled carbon nanotubes with different boundary conditions between inner and outer tubes. J. Appl. Mech. Mar. 2008, 75, 021013. [Google Scholar] [CrossRef]
- Lassagne, B.; Garcia-Sanchez, D.; Aguasca, A.; Bachtold, A. Ultrasensitive mass sensing with a nanotube electromechanical resonator. Nano Lett. 2008, 8, 3735–3738. [Google Scholar] [CrossRef]
- Li, H.; Wang, X. Nonlinear frequency shift behavior of graphene–elastic–piezoelectric laminated films as a nano-mass detector. Int. J. Solids Struct. 2016, 84, 17–26. [Google Scholar] [CrossRef]
- Şimşek, M. Large amplitude free vibration of nanobeams with various boundary conditions based on the nonlocal elasticity theory. Compos. Part B Eng. 2014, 56, 621–628. [Google Scholar] [CrossRef]
- Cho, S.-H.; Choi, M.-S.; Kang, D.-K.; Lee, J.H.; Kim, C.-W. Analysis on mass sensing characteristics of SWCNT-based nano-mechanical resonators using continuum mechanics based finite element analysis. J. Mech. Sci. Technol. 2015, 29, 4801–4806. [Google Scholar] [CrossRef]
- Lee, H.-L.; Hsu, J.-C.; Chang, W.-J. Frequency shift of carbon-nanotube-based mass sensor using nonlocal elasticity theory. Nanoscale Res. Lett. 2010, 5, 1774–1778. [Google Scholar] [CrossRef] [PubMed]
- Chaste, J.; Eichler, A.; Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.-L.; Yang, Y.C.; Chang, W.J. Mass detection using a graphene-based nanomechanical resonator. Jpn. J. Appl. Phys. 2013, 52, 025101. [Google Scholar] [CrossRef]



| Elishakoff et al. [55] | Xu et al. [54] | Present Study | |
|---|---|---|---|
| simply supported | 0.46830 | 0.46 | 0.47 |
| cantilevered | 0.202 | 0.17 | 0.17 |
| bridged | 1.0515 | 1.06 | 1.085 |
| Mode | ||||
|---|---|---|---|---|
| Khosrozadeh et al. [56] | Present Study | Khosrozadeh et al. [56] | Present Study | |
| 1 | 0.5113 | 0.4997 | 0.6665 | 0.6539 |
| 2 | 1.9328 | 1.9127 | - | 1.9571 |
| 3 | 4.1670 | 4.1817 | - | 4.2040 |
| c () | (nm) | Marmu et al. [57] | Present Study |
|---|---|---|---|
| 0 | 0 | 1.6625 | 1.6625 |
| 0.5 | 1.6592 | 1.6592 | |
| 1 | 1.6496 | 1.6496 | |
| 0.0694 | 0 | 4.4304 | 4.4304 |
| 0.5 | 4.4305 | 4.4305 | |
| 1 | 4.4846 | 4.4846 |
| Symbol | Description | Numerical Value |
|---|---|---|
| Length (nm) | 5.55 | |
| Density (kg/m3) | 2300 | |
| Young’s modulus (N/m2) | 1 × 1012 | |
| Outside diameter (nm) | 1.4 | |
| Inside diameter (nm) | 0.7 | |
| Thickness (nm) | 0.34 | |
| Outside area (nm2) | 1.4954 | |
| Inside area (nm2) | 0.7477 | |
| Moments of inertia (nm4) | 0.0566, 0.3879 | |
| Magnetic intensity (A/m) | 1 × 108 | |
| Elastic foundation modulus (N/m2) | 5 × 108 | |
| Position of attached mass (nm) | - | |
| Attached mass (g) | - | |
| Aspect ratio | - | |
| Non-local parameter (nm) | 0–1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, H.R.; Rahimi, Z.; Sumelka, W. Enhancing Sensitivity of Double-Walled Carbon Nanotubes with Longitudinal Magnetic Field. Appl. Sci. 2024, 14, 3010. https://doi.org/10.3390/app14073010
Ahmadi HR, Rahimi Z, Sumelka W. Enhancing Sensitivity of Double-Walled Carbon Nanotubes with Longitudinal Magnetic Field. Applied Sciences. 2024; 14(7):3010. https://doi.org/10.3390/app14073010
Chicago/Turabian StyleAhmadi, Hamid Reza, Zaher Rahimi, and Wojciech Sumelka. 2024. "Enhancing Sensitivity of Double-Walled Carbon Nanotubes with Longitudinal Magnetic Field" Applied Sciences 14, no. 7: 3010. https://doi.org/10.3390/app14073010
APA StyleAhmadi, H. R., Rahimi, Z., & Sumelka, W. (2024). Enhancing Sensitivity of Double-Walled Carbon Nanotubes with Longitudinal Magnetic Field. Applied Sciences, 14(7), 3010. https://doi.org/10.3390/app14073010








