A Multi-Objective Optimal Control Method for Navigating Connected and Automated Vehicles at Signalized Intersections Based on Reinforcement Learning
Abstract
:1. Introduction
- The CAV is recognized as an agent that collects information on its status and surroundings, such as Signal Phase and Timing (SPaT) data and vehicle motion parameters, via roadside and onboard devices. It then interacts with the environment, utilizing RL algorithms to support decision-making and control;
- A general Markov decision process (MDP) framework for vehicle control is established, with a carefully designed reward function that considers energy consumption, traffic efficiency, driving comfort, and safety;
- Compared with traditional optimization model-based control approaches, our method employs a model-free reinforcement learning algorithm to generate the CAV’s trajectory in real time. This significantly reduces computational complexity and enhances the ability to handle complex real-world scenarios.
2. Problem Statement and Modeling
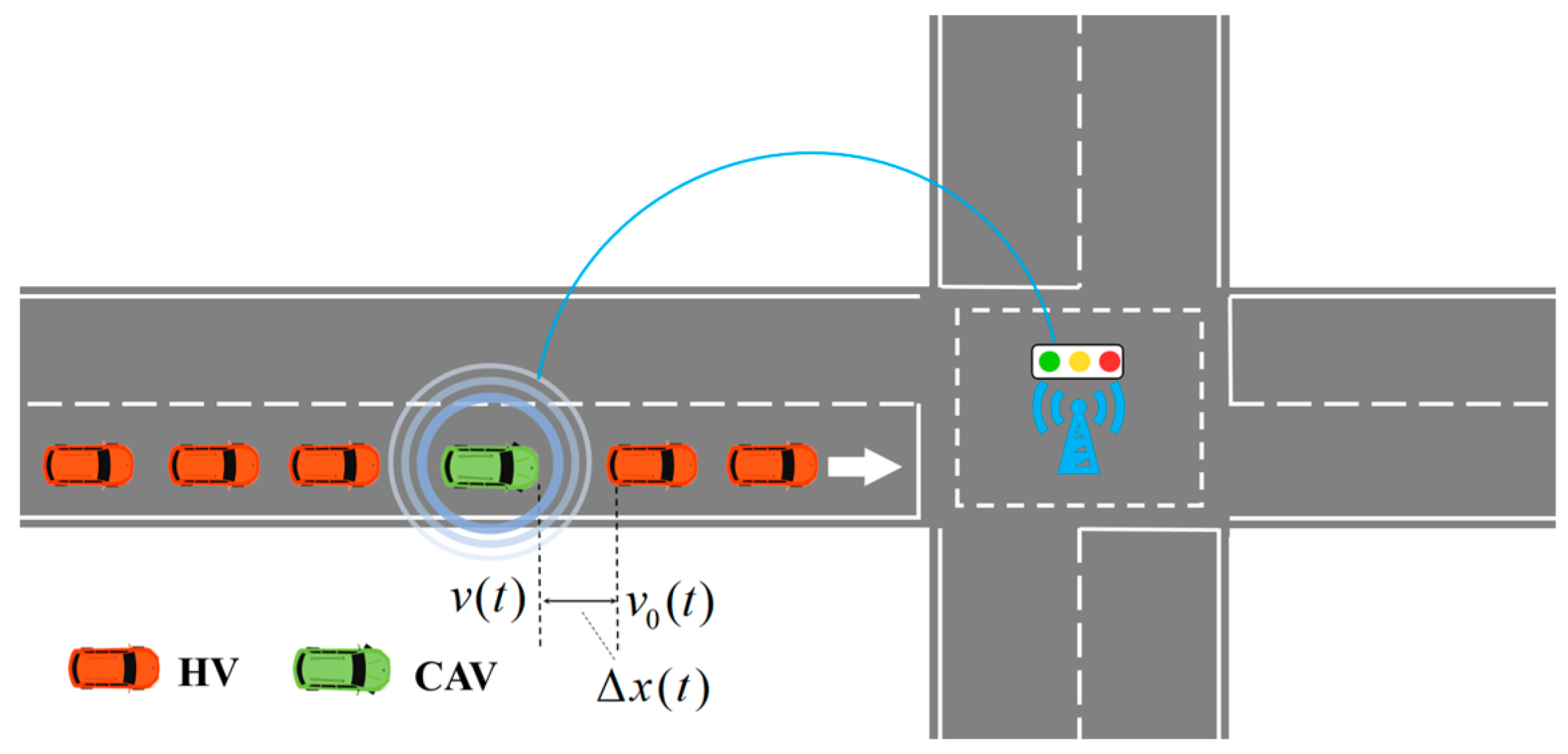
2.1. Research Scenario
2.2. Description of MDP
- (1)
- The road is solely used by motor vehicles in prime driving condition, adhering to established regulations and free from unforeseen incidents like malfunctions or erratic intrusions;
- (2)
- Real-time information regarding the vehicle’s position, speed, and acceleration is accessible. Simultaneously, real-time communication between onboard devices and roadside equipment is assured, without any delays.
2.2.1. State
2.2.2. Action
2.2.3. Reward
3. Design and Analysis of Algorithm
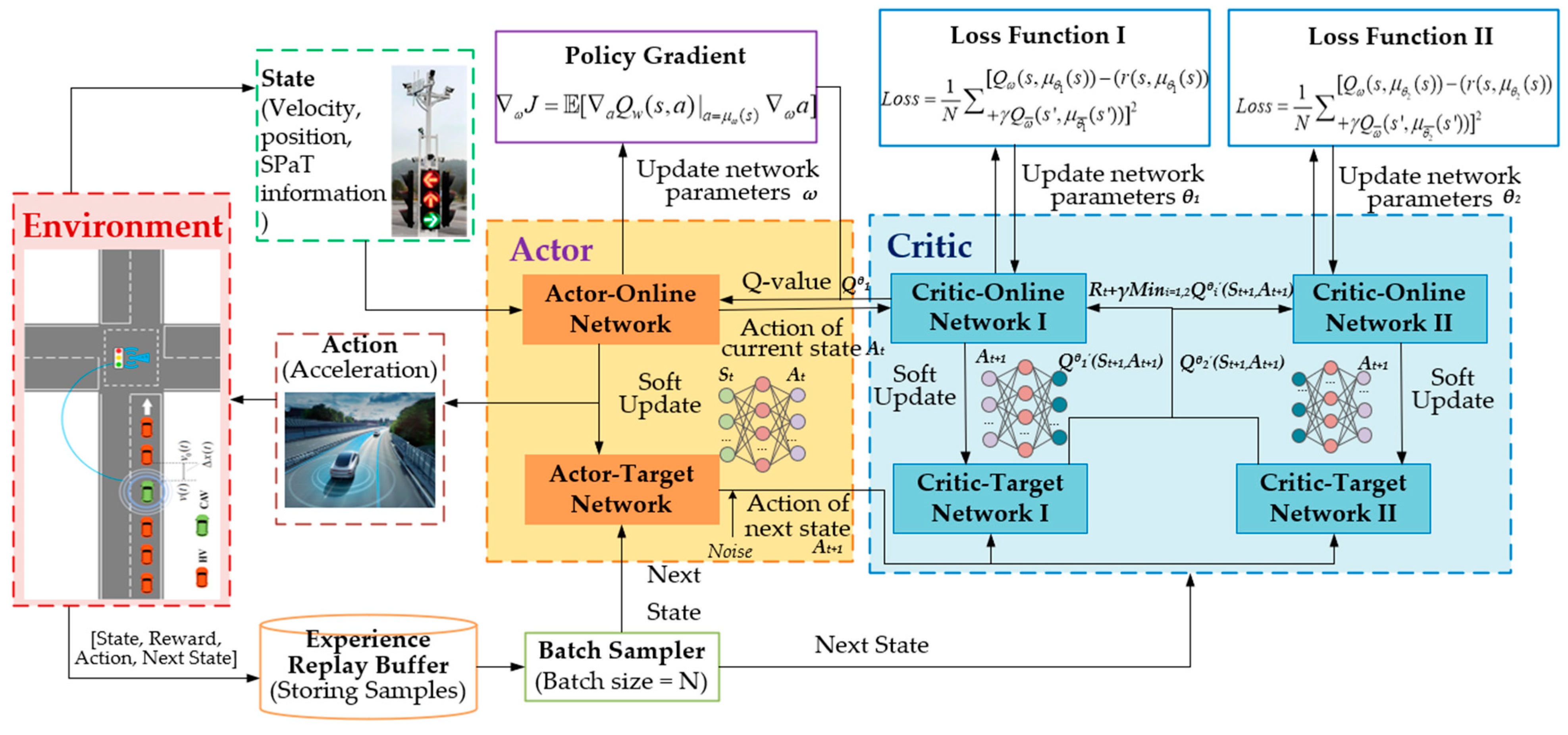
3.1. TD3 Algorithm
3.2. Vehicle Control Algorithm
- Step1.
- Initialization: Upon initiation, the environment state () is reset, and essential road and traffic demand data are transmitted to the vehicle controller. The TD3 algorithm receives state information, including speed, position, and SPaT. It initializes action () and provides a predicted sequence of actions to the environment.
- Step2.
- Interaction with the environment: After receiving the action sequence, the environment calculates the reward () of the vehicle until it approaches the road boundary. Subsequently, the calculated state and reward are transmitted back to the controller. The TD3 algorithm stores these tuples in the experience pool, accumulating valuable training samples.
- Step3.
- Training: Training begins once the replay buffer reaches its capacity, utilizing the stored samples to refine decision-making for vehicle actions. The algorithm continues training until the maximum exploration step is reached, signifying the conclusion of the current episode of training. Upon reaching the maximum number of iterations, the algorithm indicates the attainment of the terminal state.
- Step4.
- Output: The algorithm outputs a control strategy () for driving actions, including uniform speed, acceleration, and deceleration. This strategy is meticulously designed to maximize cumulative rewards (), reflecting the algorithm’s learned optimal behavior in response to the dynamic road environment and traffic conditions.
4. Examples and Discussion
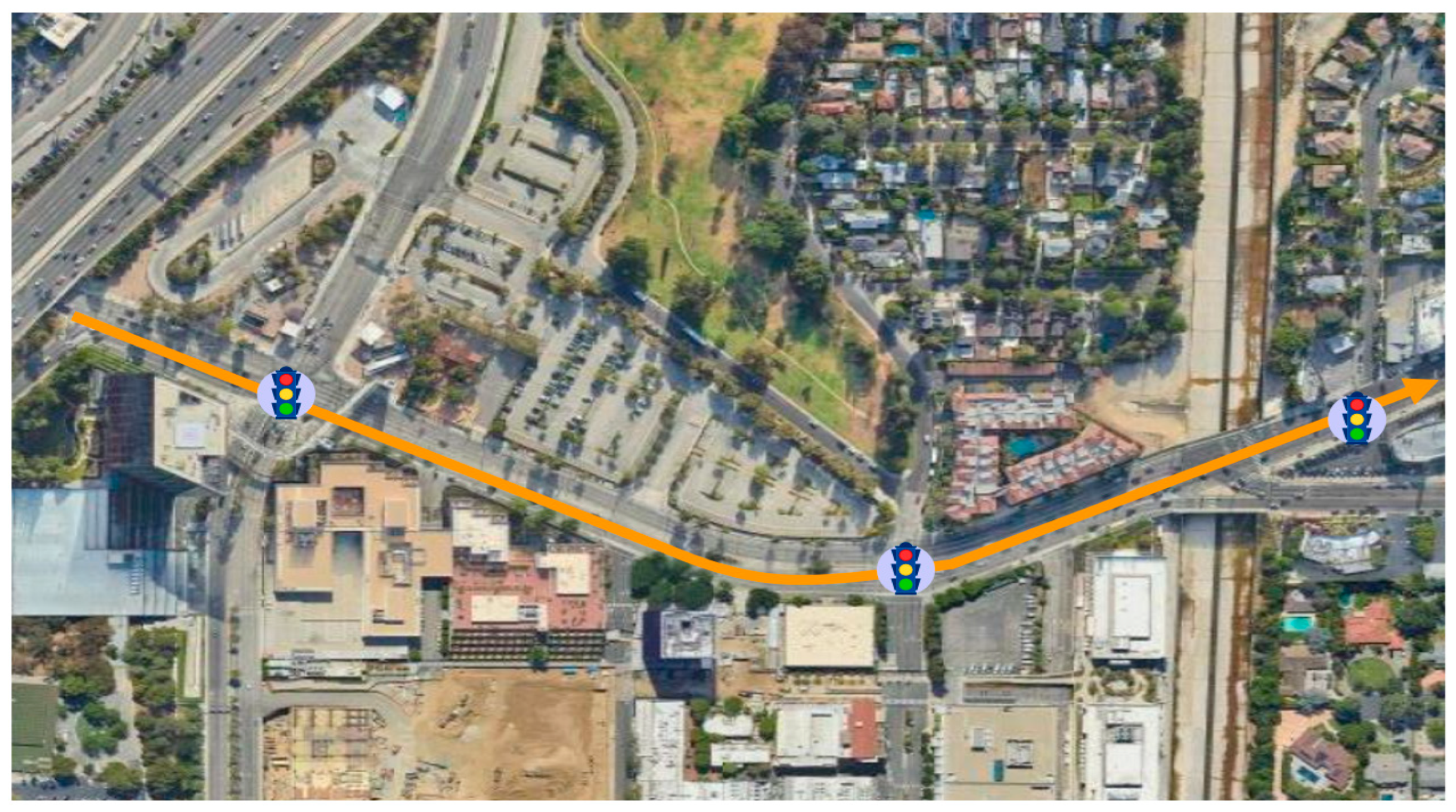
4.1. Simulation Platform and Scenarios
4.2. Experimental Design and Parameters Settings
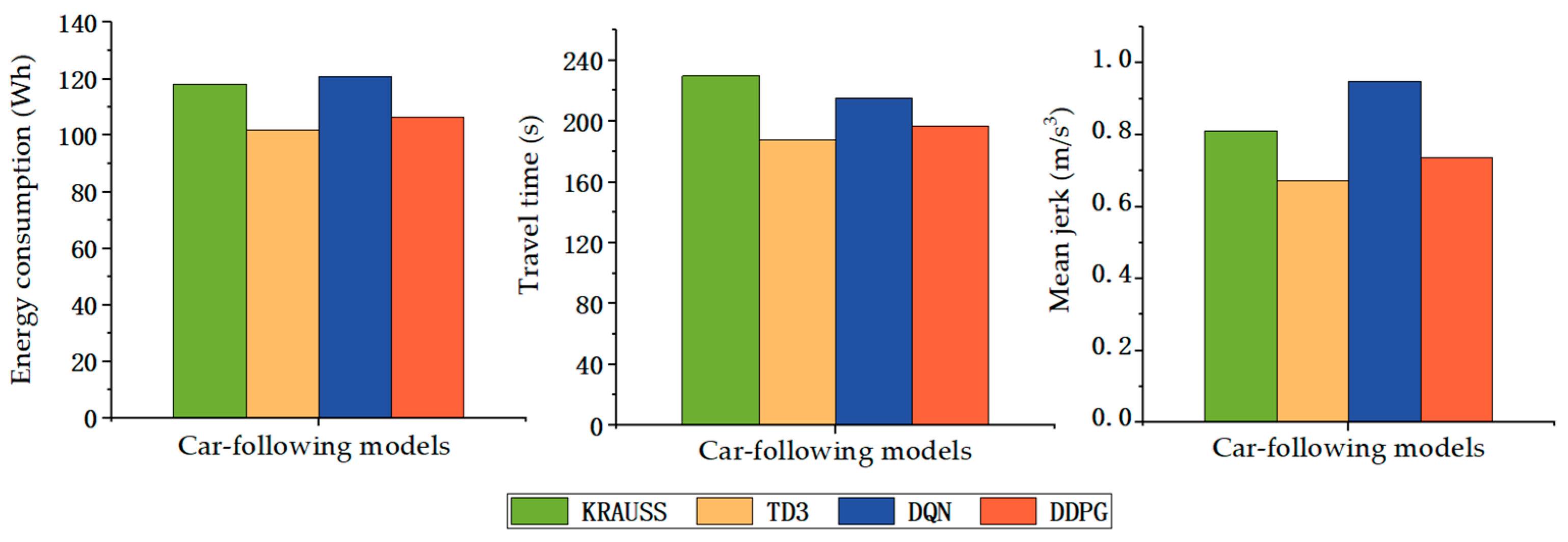
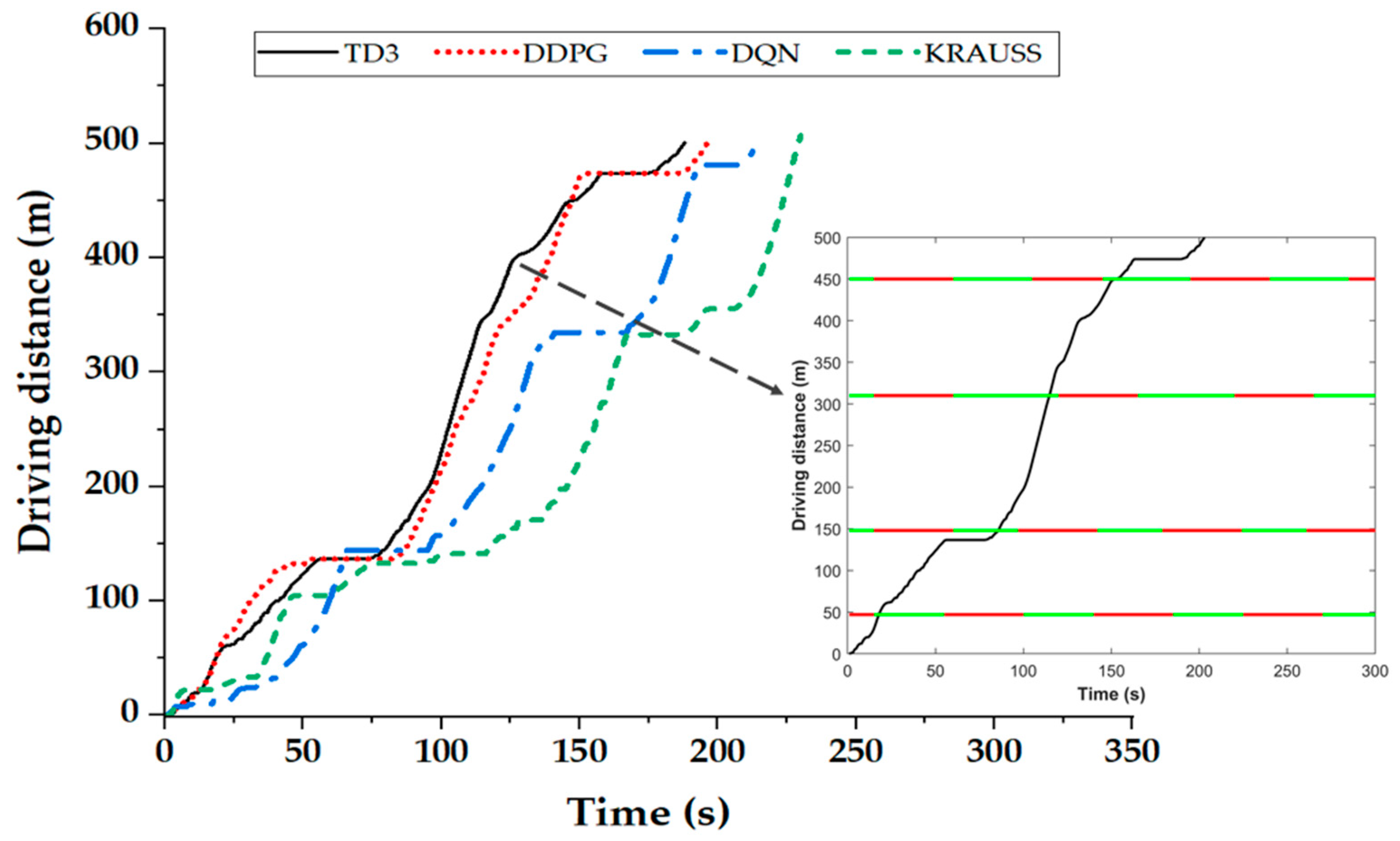
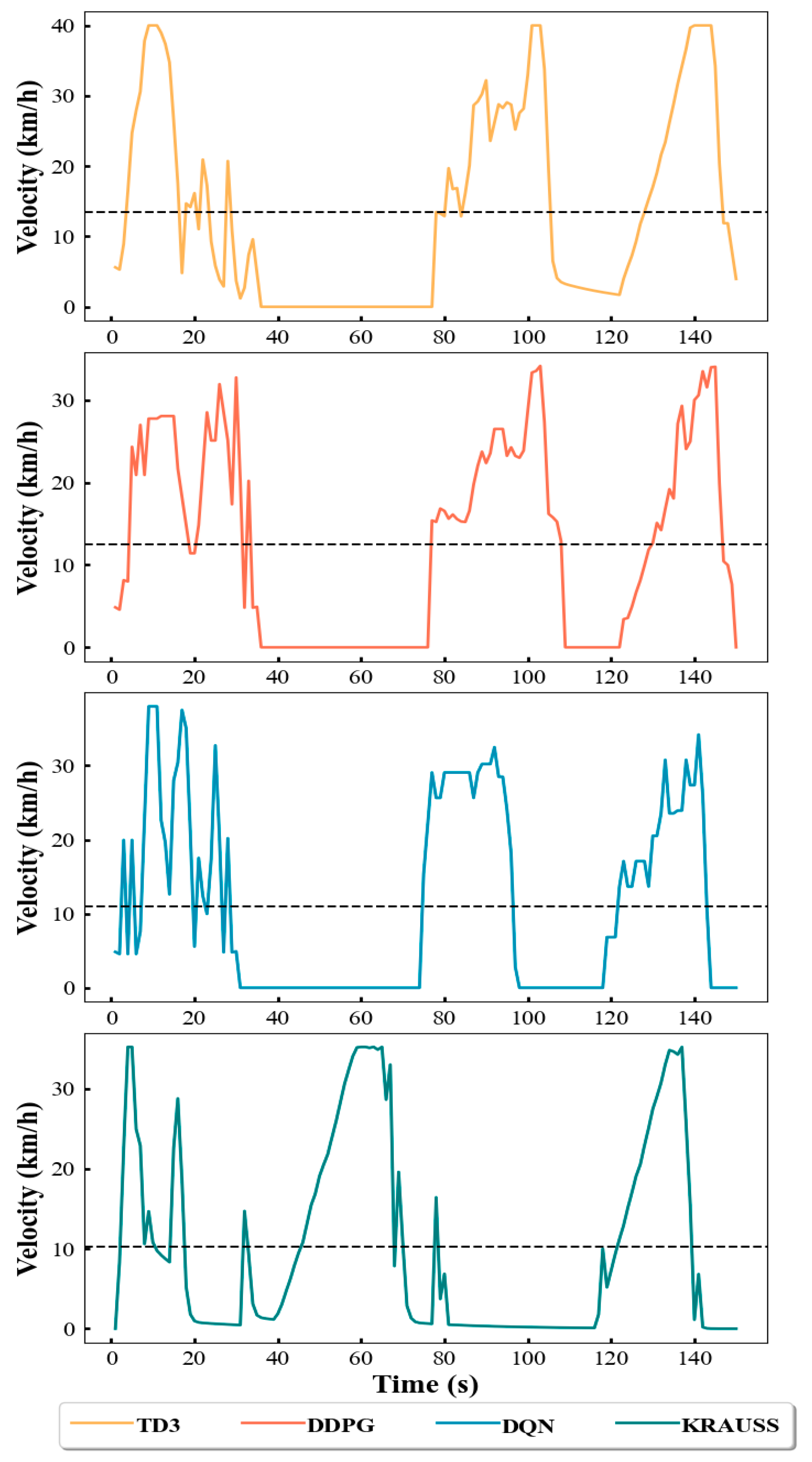
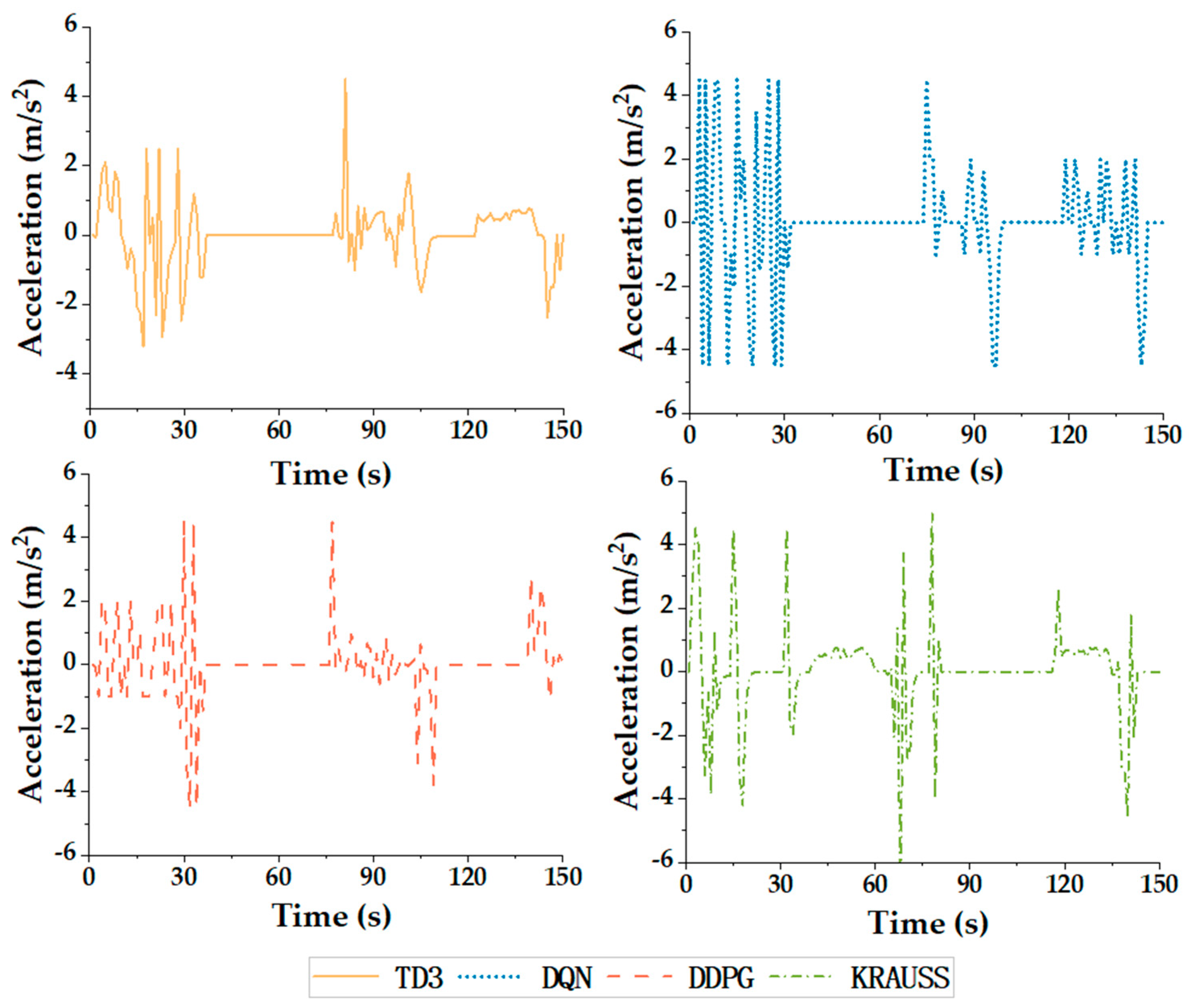
4.3. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Description |
| CAVs | Connected and Automated Vehicle |
| EVs | Electric Vehicles |
| HEVs | Hybrid Electric Vehicles |
| e-CAVs | Electric, Connected, and Autonomous Vehicles |
| HVs | Human-driven Vehicle |
| RL | Reinforcement Learning |
| DRL | Deep Reinforcement Learning |
| MDP | Markov Decision Process |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient |
| TTC | Time to Collision |
| DQN | Deep Q-Network |
| DDPG | Deep Deterministic Policy Gradient |
| SPaT | Signal Phase and Timing |
References
- De Campos, G.R.; Falcone, P.; Hult, R.; Wymeersch, H.; Sjöberg, J. Traffic coordination at road intersections: Autonomous decision-making algorithms using model-based heuristics. IEEE Intell. Transp. Syst. Mag. 2017, 9, 8–21. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Zhao, H.; Peeta, S.; Hu, S.; Wang, Y.; Zheng, Z.D. A car-following model for connected and automated vehicles with heterogeneous time delays under fixed and switching communication topologies. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14846–14858. [Google Scholar] [CrossRef]
- Deng, Z.; Shi, Y.; Han, Q.; Lv, L.; Shen, W.M. A conflict duration graph-based coordination method for connected and automated vehicles at signal-free intersections. Appl. Sci. 2020, 10, 6223. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, Y.; He, S.; Ran, B. Improving method of real-time offset tuning for arterial signal coordination using probe trajectory data. Adv. Mech. Eng. 2017, 9, 1687814016683355. [Google Scholar] [CrossRef]
- Saboohi, Y.; Farzaneh, H. Model for developing an eco-driving strategy of a passenger vehicle based on the least fuel consumption. Appl. Energy 2008, 86, 1925–1932. [Google Scholar] [CrossRef]
- Shao, Y.; Sun, Z. Eco-approach with traffic prediction and experimental validation for connected and autonomous vehicle. IEEE Trans. Intell. Transp. Syst. 2021, 22, 1562–1572. [Google Scholar] [CrossRef]
- Yu, C.; Feng, Y.; Liu, H.; Ma, W.; Yang, X. Integrated Optimization of Traffic Signals and Vehicle Trajectories at Isolated Urban Intersections. Transp. Res. B-Meth. 2018, 112, 89–112. [Google Scholar] [CrossRef]
- Jiang, H.; Jia, H.; Shi, A.; Meng, W.; Byungkyu, B. Eco Approaching at an Isolated Signalized Intersection under Partially Connected and Automated Vehicles Environment. Transp. Res. C-Emerg. Technol. 2017, 79, 290–307. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, D.; Jiang, J.; Lan, J.; Mason, B.; Tian, D.; Li, L. A less-disturbed ecological driving strategy for connected and automated vehicles. IEEE Trans. Intell. Veh. 2023, 8, 413–424. [Google Scholar] [CrossRef]
- Kargar, M.; Zhang, C.; Song, X. Integrated optimization of power management and vehicle motion control for autonomous hybrid electric vehicles. IEEE Trans. Veh. Technol. 2023, 72, 11147–11155. [Google Scholar] [CrossRef]
- Wu, X.; He, X.; Yu, G. Energy-optimal speed control for electric vehicles on signalized arterials. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2786–2796. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; He, X.; Yu, G.; Wang, Y. An eco-driving system for electric vehicles with signal control under v2x environment. Transp. Res. C-Emerg. Technol. 2018, 93, 335–350. [Google Scholar] [CrossRef]
- Lu, C.; Dong, J.; Hu, L. Energy-efficient adaptive cruise control for electric connected and autonomous vehicles. IEEE Intell. Transp. Syst. Mag. 2019, 11, 42–55. [Google Scholar] [CrossRef]
- Xia, H.; Boriboonsomsin, K.; Barth, M. Dynamic eco-driving for signalized arterial corridors and its indirect network-wide energy/emissions benefits. J. Intell. Transp. Syst. 2013, 17, 31–41. [Google Scholar] [CrossRef]
- Lan, Y.; Han, M.; Fang, S.; Wu, G.; Sheng, H.; Wei, H.; Zhao, X. Differentiated speed planning for connected and automated electric vehicles at signalized intersections considering dynamic wireless power transfer. J. Adv. Transp. 2022, 2022, 5879568. [Google Scholar]
- Du, Y.; Shang, G.; Chai, L.; Chen, J. Eco-driving method for signalized intersection based on departure time prediction. China J. Highw. Transp. 2022, 35, 277–288. [Google Scholar]
- Li, Y.; Zhao, H.; Zhang, L.; Zhang, C. An extended car-following model incorporating the effects of lateral gap and gradient. Physica A 2018, 503, 177–189. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, J.; Wang, B. Energy-efficient driving for adaptive traffic signal control environment via explainable reinforcement learning. Appl. Sci. 2022, 12, 5380. [Google Scholar] [CrossRef]
- Liu, C.; Sheng, Z.; Chen, S.; Shi, H.; Ran, B. Longitudinal control of connected and automated vehicles among signalized intersections in mixed traffic flow with deep reinforcement learning approach. Phys. A 2023, 629, 129189. [Google Scholar] [CrossRef]
- Mousa, S.R.; Ishak, S.; Mousa, R.M.; Codjoe, J. Developing an eco-driving application for semi-actuated signalized intersections and modeling the market penetration rates of eco-driving. Transp. Res. Record 2019, 2673, 466–477. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, J.; Li, D. Eco-driving at signalized intersections: A parameterized reinforcement learning approach. Transp. B 2022, 11, 1406–1431. [Google Scholar] [CrossRef]
- Bin Al Islam, S.M.A.; Abdul Aziz, H.M.; Wang, H.; Young, S.E. Minimizing energy consumption from connected signalized intersections by reinforcement learning. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 7 December 2018. [Google Scholar]
- Guo, Q.; Ohay, A.; Liu, Z.; Ban, X. Hybrid Deep Reinforcement Learning based Eco-Driving for Low-Level Connected and Automated Vehicles along Signalized Corridors. Transp. Res. C-Emerg. Technol. 2021, 124, 2–18. [Google Scholar]
- Qu, X.; Yu, Y.; Zhou, M.; Lin, C.; Wang, X. Jointly dampening traffic oscillations and improving energy consumption with electric, connected and automated vehicles: A reinforcement learning based approach. Appl. Energy 2020, 257, 114030. [Google Scholar] [CrossRef]
- Chen, Y.; Jiao, P.; Bai, R.; Li, R. Modeling car following behavior of autonomous driving vehicles based on deep reinforcement learning. J. Transp. Inf. Saf. 2023, 41, 67–75. [Google Scholar]
- Zhang, J.; Jiang, X.; Liu, Z.; Zheng, L.; Ran, B. A study on autonomous intersection management: Planning-based strategy improved by convolutional neural network. KSCE J. Civ. Eng. 2021, 25, 3995–4004. [Google Scholar] [CrossRef]
- Tran, Q.-D.; Bae, S.-H. An Efficiency Enhancing Methodology for Multiple Autonomous Vehicles in an Urban Network Adopting Deep Reinforcement Learning. Appl. Sci. 2021, 11, 1514. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Fan, J. Speed planning for connected and automated vehicles in urban scenarios using deep reinforcement learning. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022. [Google Scholar]
- Wu, T.; Zhou, P.; Liu, K.; Yuan, Y.; Wang, X.; Huang, H.; Wu, D. Multi-agent deep reinforcement learning for urban traffic light control in vehicular networks. IEEE Trans. Veh. Technol. 2020, 69, 8243–8256. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, X.; Ma, D.; Qiu, H. A survey of application of deep reinforcement learning in urban traffic signal control methods. Mod. Transp. Metall. Mater. 2022, 2, 84–93. [Google Scholar]
- Zhou, M.; Yang, Y.; Qu, X. Development of an Efficient driving strategy for connected and automated vehicles at signalized intersections: A reinforcement learning approach. IEEE Trans. Intell. Transp. Syst. 2020, 21, 433–443. [Google Scholar] [CrossRef]
- Zhuang, H.; Lei, C.; Chen, Y.; Tan, X. Cooperative Decision-Making for Mixed Traffic at an Unsignalized Intersection Based on Multi-Agent Reinforcement Learning. Appl. Sci. 2023, 13, 5018. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, X.; Chen, K.; Yu, X.; Luo, Y. Online longitudinal trajectory planning for connected and autonomous vehicles in mixed traffic flow with deep reinforcement learning approach. J. Intell. Transp. Syst. 2022, 27, 396–410. [Google Scholar] [CrossRef]
- Kurczveil, T.; López, P.Á.; Schnieder, E. Implementation of an energy model and a charging infrastructure in SUMO. In Proceedings of the 1st International Conference on Simulation of Urban Mobility, Berlin, Germany, 15–17 May 2013. [Google Scholar]
- Zhang, J.; Wu, K.; Cheng, M.; Yang, M.; Cheng, Y.; Li, S. Safety evaluation for connected and autonomous vehicles’ exclusive lanes considering penetrate ratios and impact of trucks using surrogate safety measures. J. Adv. Transp. 2020, 2020, 5847814. [Google Scholar] [CrossRef]
- Zhao, W.; Ngoduy, D.; Shepherd, S.; Liu, R.; Papageorgiou, M. A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalized intersection. Transp. Res. C-Emerg. Technol. 2018, 95, 802–821. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Hu, H.; Wang, Y.; Tong, W.; Zhao, J.; Gu, Y. Path planning for autonomous vehicles in unknown dynamic environment based on deep reinforcement learning. Appl. Sci. 2023, 13, 10056. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Erdmann, J. Lane-changing model in SUMO. In Proceedings of the SUMO 2014, Berlin, Germany, 15 May 2014. [Google Scholar]
- Garcia, A.G.; Tria, L.A.R.; Talampas, M.C.R. Development of an energy-efficient routing algorithm for electric vehicles. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019. [Google Scholar]



| Functional Module | Description |
|---|---|
| Environmental construction | This module is responsible for creating and editing the road network, with specific functions such as determining the starting and ending points, adding traffic demands, dividing the lanes, and configuring signal timing. |
| Simulation operation | This module is responsible for running the simulation program, with specific functions including setting the simulation duration, calculating the state space and reward function, and outputting the action strategy, as well as resetting the environment when the algorithm training termination conditions are met. |
| Data collection | This module is responsible for data acquisition and saving, with specific functions including acquiring vehicle trajectory data through the Traci interface, saving the simulation results in a numerical matrix, and outputting the data in *.csv file format for later organization and analysis. |
| Parameter | Value |
|---|---|
| Design hour volume of HVs (veh/h) | 1600 |
| Total driving distance (m) | 525 |
| The speed limit (km/h) | 40 |
| Vehicle acceleration (m/s2) | (−4.500, 4.500) |
| Minimum safety distance between front and rear vehicles (m) | 30 |
| Green time (s) | [41, 37, 64, 46] |
| Yellow time (s) | [3.50, 3.90, 3.50, 3.50] |
| All-red time (s) | [0.50, 1.50, 1.00, 1.00] |
| Maximum training steps | 105 |
| Batch size | 256 |
| Learning rate | 10−4 |
| Discount factor | 0.98 |
| Car-Following Mode | Evaluation Indicators | ||
|---|---|---|---|
| Electricity Consumption (Wh) | Travel Time (s) | Mean Jerk (m/s3) | |
| TD3 | 101.845 | 188 | 0.674 |
| DDPG | 106.463 | 197 | 0.736 |
| DQN | 120.943 | 215 | 0.949 |
| KRAUSS | 118.102 | 230 | 0.811 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhang, H.; Feng, Z.; Zhang, J.; Qian, Y.; Wang, B. A Multi-Objective Optimal Control Method for Navigating Connected and Automated Vehicles at Signalized Intersections Based on Reinforcement Learning. Appl. Sci. 2024, 14, 3124. https://doi.org/10.3390/app14073124
Jiang H, Zhang H, Feng Z, Zhang J, Qian Y, Wang B. A Multi-Objective Optimal Control Method for Navigating Connected and Automated Vehicles at Signalized Intersections Based on Reinforcement Learning. Applied Sciences. 2024; 14(7):3124. https://doi.org/10.3390/app14073124
Chicago/Turabian StyleJiang, Han, Hongbin Zhang, Zhanyu Feng, Jian Zhang, Yu Qian, and Bo Wang. 2024. "A Multi-Objective Optimal Control Method for Navigating Connected and Automated Vehicles at Signalized Intersections Based on Reinforcement Learning" Applied Sciences 14, no. 7: 3124. https://doi.org/10.3390/app14073124
APA StyleJiang, H., Zhang, H., Feng, Z., Zhang, J., Qian, Y., & Wang, B. (2024). A Multi-Objective Optimal Control Method for Navigating Connected and Automated Vehicles at Signalized Intersections Based on Reinforcement Learning. Applied Sciences, 14(7), 3124. https://doi.org/10.3390/app14073124







