Research on Out-of-Plane Bending Test of PVB Laminated Glass Plate with Different Number of Layers
Abstract
1. Introduction
2. Materials and Methods
2.1. Mechanical Properties of PVB
2.1.1. PVB Sample Design
2.1.2. Test Setup
2.1.3. Elastic Modulus of PVB
2.2. Bending Experiment on PVB Laminated Glass
2.2.1. LG Sample Design
2.2.2. Displacement Measurement Technology (DIC Technology)
2.2.3. Test Setup
3. Results and Discussion
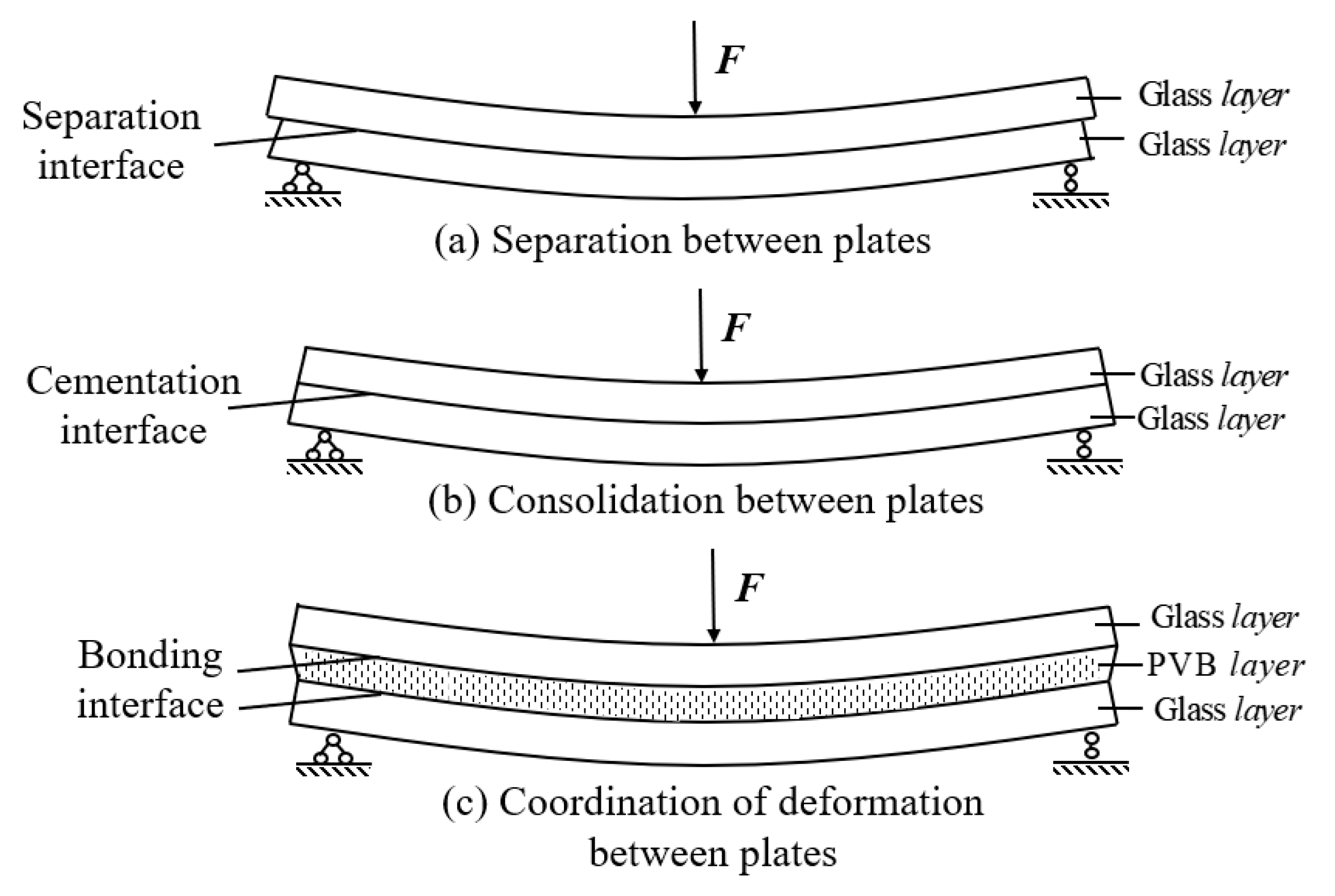
3.1. Destruction Mode of PVB LG
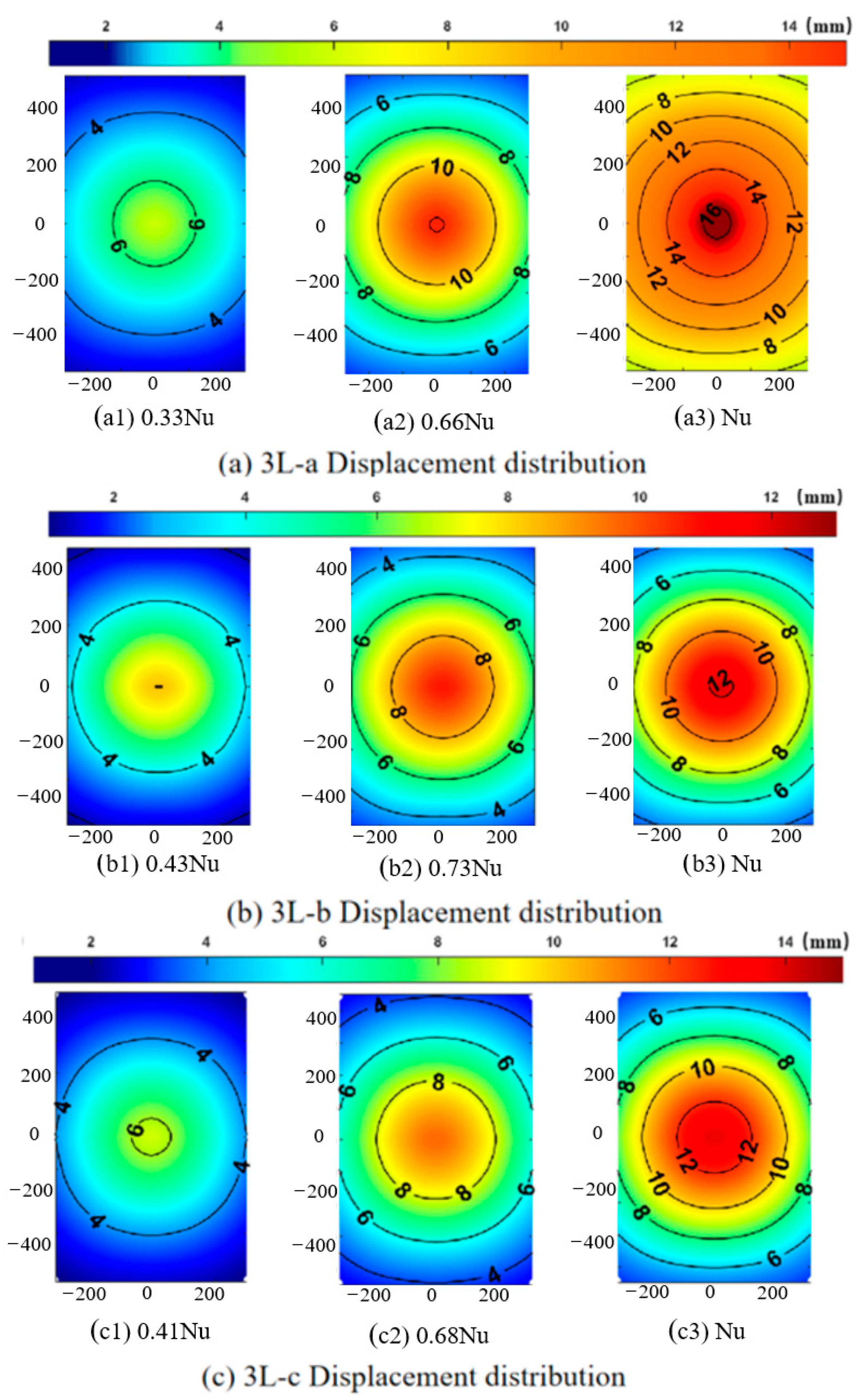
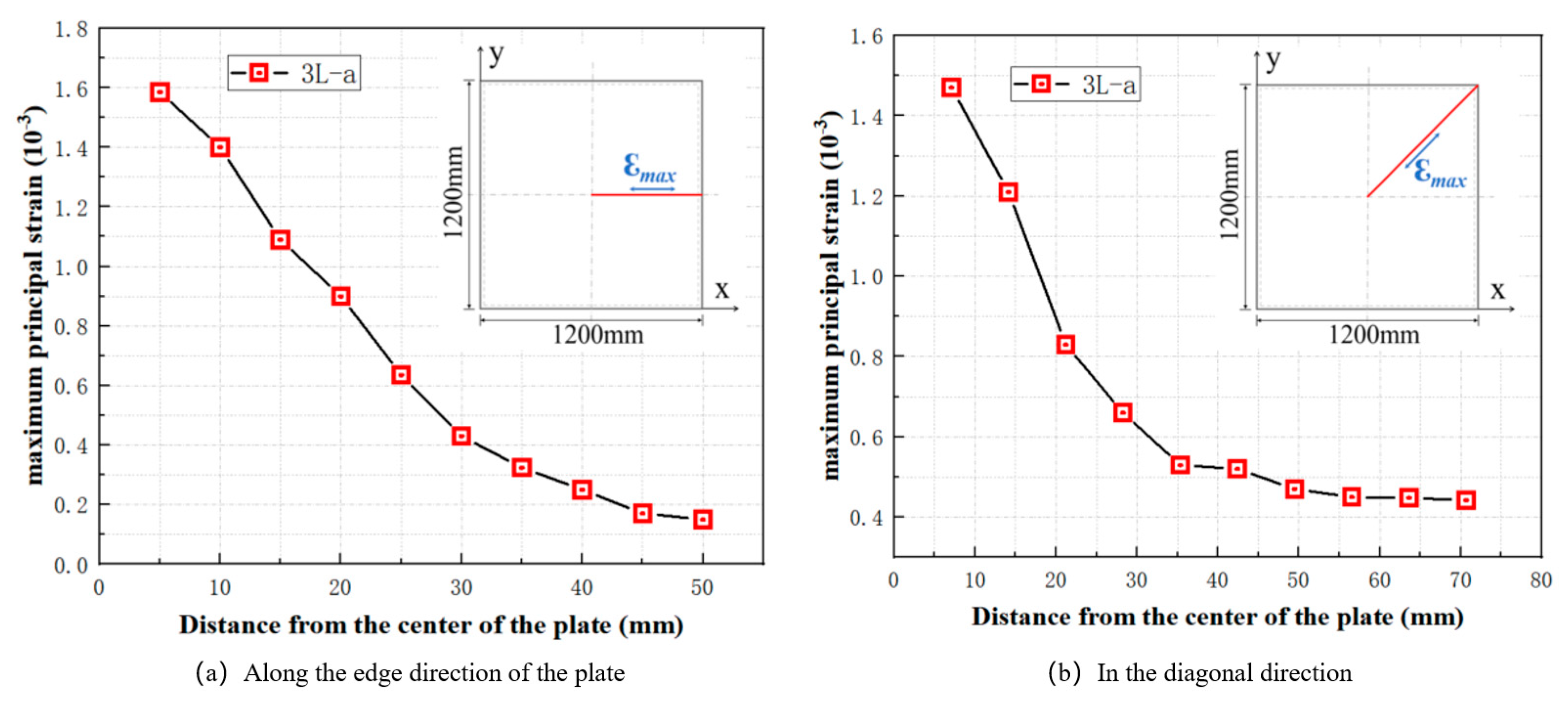
3.2. In-Plane Distribution of Deflection and Maximum Principal Strain
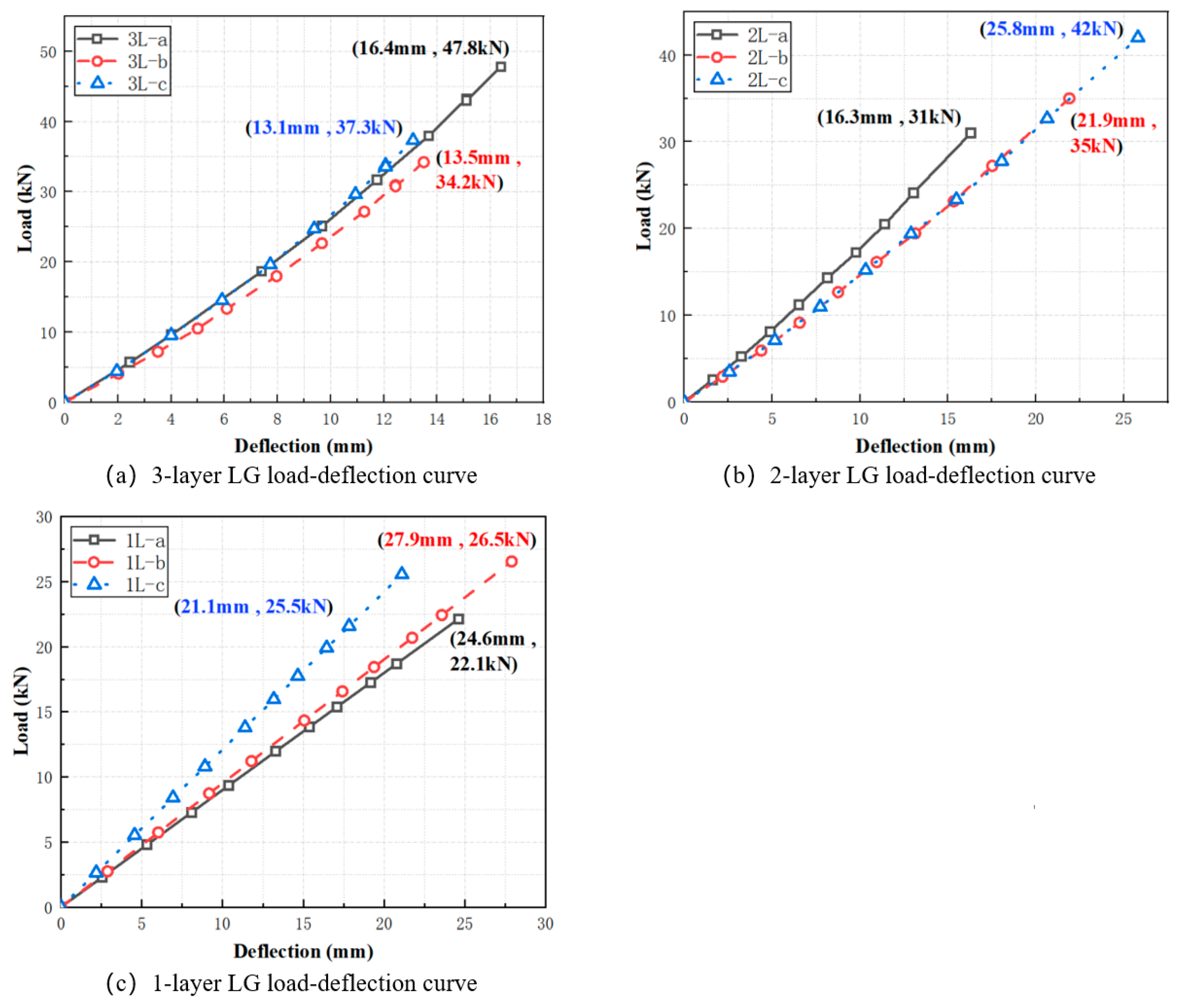
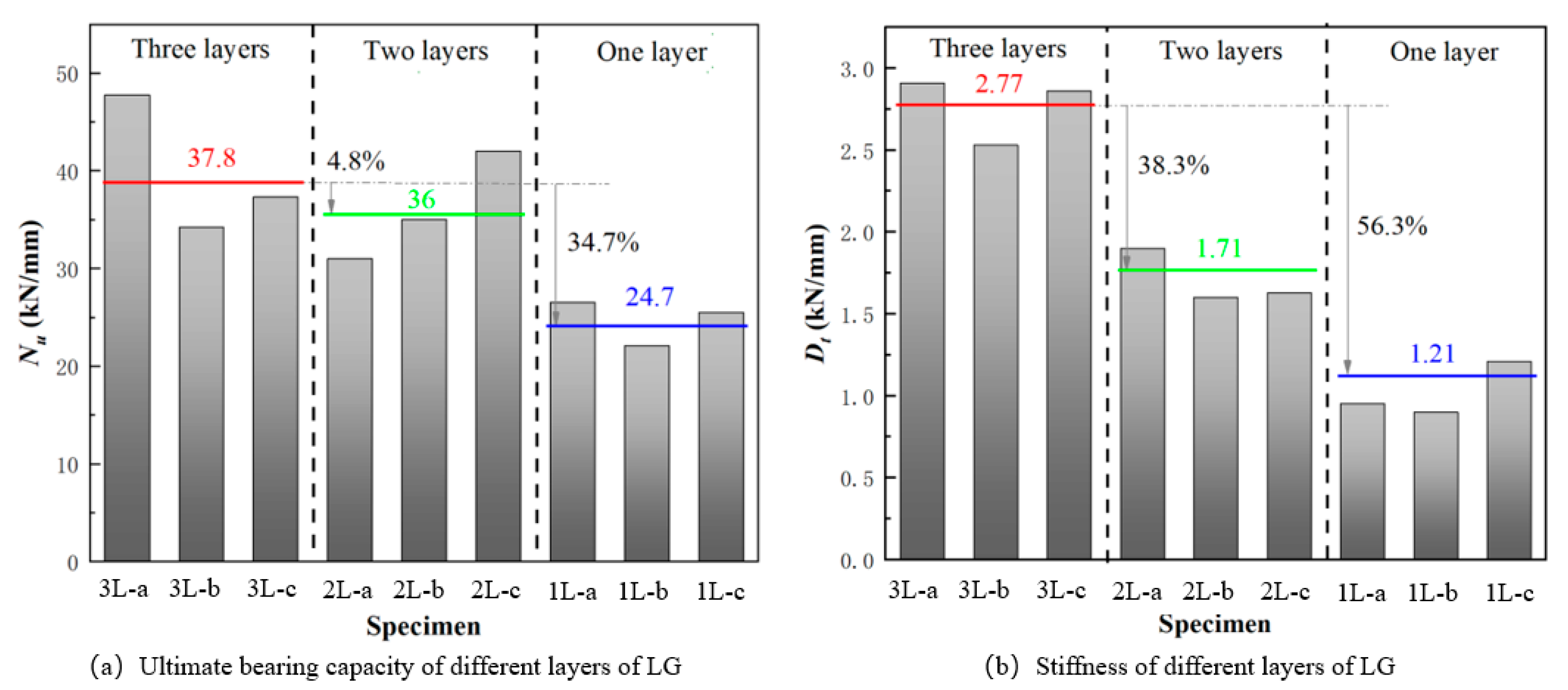
3.3. The Influence of the Number of Layers of Glass on Ultimate Load
3.4. The Influence of the Number of Layers of Glass on Stiffness
3.5. Selection of PVB Modulus for the Calculation of PVB LG
4. Conclusions
- The load–displacement curve remains approximately linear prior to damage in the LG. Displacement manifests a circular distribution within the plane, with the first principal strain value increasing towards the center of the plate. The direction of the first principal strain radiates from the center of the plate.
- The average ultimate load capacity for three-layer, two-layer, and single-layer PVB laminated glass is 37.8 kN, 36 kN, and 24.7 kN, respectively, corresponding to a ratio of 1:0.95:0.65. The bending stiffness values for the same are 2.77 kN/mm, 1.71 kN/mm, and 1.21 kN/mm, respectively, with a ratio of 1:0.62:0.44. The ultimate bearing capacity of PVB LG increases with the number of layers; however, this increase diminishes with additional layers, leading to material waste. For economic efficiency, it is advisable to utilize LG with fewer layers in practical applications. The stiffness of LG increases nonlinearly with the addition of layers, an effect attributable to the characteristics of PVB. For engineering structures with strict deformation limits, selecting PVB LG with more layers is necessary.
- The mechanical property testing presented in this paper reveals that the constitutive model of PVB laminate transitions from tensile deformation to fracture with a bilinear relationship to strain rate. Elastic modulus is found to be lower at reduced strain rates. Linearity is maintained when axial strain is below 0.6. Beyond an axial strain of 1.6, the elastic modulus significantly increases, the differential being more than tenfold. Considering the overall bending deformation of laminated glass plates, the maximum principal strain on the surface is two orders of magnitude less than 0.6. Therefore, this study concludes that the PVB layer involved in deformation coordination is within the low strain rate stage. For calculating the out-of-plane bending of laminated glass, it may be treated as a material with small-scale linear elasticity. The recommended elastic modulus is 1.34 MPa.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ivanov, I.V. Analysis, modelling, and optimization of laminated glasses as plane beam. Int. J. Solids Struct. 2006, 43, 6887–6907. [Google Scholar] [CrossRef]
- Vallabhan, C.G.; Minor, J.E.; Nagalla, S.R. Stresses in layered glass units and monolithic glass plates. J. Struct. Eng. 1987, 113, 36–43. [Google Scholar] [CrossRef]
- Bennison, S.J.; Jagota, A.; Smith, C.A. Fracture of glass/poly (vinyl_butyral)_laminates. in biaxial flexure. Am. Ceram. Soc. 1999, 82, 1762–1770. [Google Scholar] [CrossRef]
- Nawar, M.; Salim, H.; Lafta, M.; Elshihy, A. Quasi-Static Performance of Interlayer Systems for Laminated Glass. J. Mater. Civ. Eng. 2015, 28, 04015084. [Google Scholar] [CrossRef]
- Edel, M.T. The Effect of Temperature on the Bending of laminated Glass Beams. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1997. [Google Scholar]
- Hooper, J.A. On the bending of architectural laminated glass. Int. J. Mech. Sci. 1973, 15, 309–323. [Google Scholar] [CrossRef]
- Aşık, M.Z.; Tezcan, S. A mathematical model for the behavior of laminated glass beams. Comput. Struct. 2005, 83, 1742–1753. [Google Scholar] [CrossRef]
- Aşık, M.Z. Laminated glass plates: Revealing of nonlinear behavior. Comput. Struct. 2003, 81, 2659–2671. [Google Scholar] [CrossRef]
- Vallabhan, C.G.; Wang, B.Y.-T.; Chou, G.D.; Minor, J.E. Thin glass plates on elastic supports. J. Struct. Eng. 1985, 111, 2416–2426. [Google Scholar] [CrossRef]
- AS 1288-2006; Glass in Buildings-Selection and Installation. Australian Standard: Sydney, Australia, 2006.
- Siebert, G. Comparison of IGU-design according to German and European Standards. ce/papers 2018, 2, 81–92. [Google Scholar] [CrossRef]
- JGJ 113-2015; Technical Specification for Application of Architectural Glass. Human Resources and Social Security Ministry of the People’s Republic of China: Beijing, China, 2015.
- ASTME1300-16; Standard Practice for Determining Load Resistance of Glass in Buildings. ASTM International: West Conshohocken, PA, USA, 2007.
- Behr, R.A. Design of architectural glazing to resist earthquakes. J. Archit. Eng. 2006, 12, 122–128. [Google Scholar] [CrossRef]
- Kaiser, N.D.; Behr, R.A.; Minor, J.E.; Dharani, L.R.; Ji, F.; Kremer, P.A. Impact resistance of laminated glass using “sacrificial ply” design concept. J. Archit. Eng. 2000, 6, 24–34. [Google Scholar] [CrossRef]
- Weggel, D.C.; Zapata, B.J. Laminated glass curtain walls and laminated glass lites subjected to low-level blast loading. J. Struct. Eng. 2008, 134, 466–477. [Google Scholar] [CrossRef]
- Saxe, T.J.; Behr, R.A.; Minor, J.E.; Kremer, P.A.; Dharani, L.R. Effects of missile size and glass type on impact resistance of “sacrificial ply” laminated glass. J. Archit. Eng. 2002, 8, 24–39. [Google Scholar] [CrossRef]
- Biolzi, L.; Simoncelli, M. Overall response of 2-ply laminated glass plates under out-of-plane loading. Eng. Struct. 2022, 256, 113967. [Google Scholar] [CrossRef]
- Galić, M.; Grozdanić, G.; Divić, V.; Marović, P. Parametric Analyses of the Influence of Temperature, Load Duration, and Interlayer Thickness on a Laminated Glass Structure Exposed to Out-of-Plane Loading. Crystals 2022, 12, 838. [Google Scholar] [CrossRef]
- Ali, H.; Gianni, C.R. A simple model for inflexed multi-layered laminated glass beams based on refined zig-zag theory. J. Appl. Mech. -Trans. Asme 2022, 90, 011002. [Google Scholar]
- Jaśkowiec, J.; Pluciński, P.; Stankiewicz, A.; Cichoń, C. Three-dimensional modelling of laminated glass bending on two-dimensional in-plane mesh. Compos. Part B 2017, 120, 63–82. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Bedon, C.; Youssef, M.A.; Chaturvedi, S. Effect of non-uniform temperature exposure on the out-of-plane bending performance of ordinary laminated glass plate. Compos. Struct. 2021, 275, 114517. [Google Scholar] [CrossRef]
- Yongjiu, S.; Ying, M.; Yuanqing, W. Finite element analysis of bending performance of point-supported laminated glass plate. Archit. Sci. 2009, 25, 1–3+8. [Google Scholar]
- Wen, W.; Lipu, R.; Jiading, P. Study on the deformation performance of point-supported laminated glass panels. Sichuan Archit. 2008, 5, 139–140. [Google Scholar]
- Galuppi, L.; Royer-Carfagni, G. Enhanced effective thickness of multi-layered laminated glass. Compos. Part B Eng. 2014, 64, 202–213. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Meng, Z. Mechanical behaviour of frame-supported insulating glass during cold bending. J. Build. Eng. 2023, 65, 105722. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Pawar, J.S. Experimental and simulation studies on bending behavior of laminated glass with polyvinyl butyral and ethyl vinyl acetate inter-layers of different critical thicknesses. J. Sandw. Struct. Mater. 2019, 21, 2219–2238. [Google Scholar] [CrossRef]
- Mohagheghian, I.; Wang, Y.; Jiang, L.; Zhang, X.; Guo, X.; Yan, Y.; Kinloch, A.J.; Dear, J.P. Quasi-static bending and low velocity impact performance of monolithic and laminated glass windows employing chemically strengthened glass. Eur. J. Mech./A Solids 2017, 63, 165–186. [Google Scholar] [CrossRef]
- Huang, X.; Liu, G.; Liu, Q.; Bennison, S.J. Influence of Interlayers on the Flexural Performance of Four-Side Supported Laminated Glass at Room Temperature. Adv. Struct. Eng. 2015, 18, 33–43. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Du Bois, P.A.; Kolling, S.; Fassnacht, W. Modelling of safety glass for crash simulation. Comput. Mater. Sci. 2003, 28, 675–683. [Google Scholar] [CrossRef]
- Du Bois, P.A.; Kolling, S.; Koesters, M.; Frank, T. Material behaviour of polymers under impact loading. Int. J. Impact Eng. 2006, 32, 725–740. [Google Scholar] [CrossRef]
- ISO 3537; Road Vehicles-Safety Glazing Materials-Mechanical Tests. ISO: Geneva, Switzerland, 1993.
- Kluppel, M.; Schramm, J.A. Generalized tube model of rubber elasticity andstress softening of filler reinforced elastomer systems. Macromol. React. Eng. 2000, 9, 742–754. [Google Scholar]
- Xu, J.; Li, Y.; Ge, D.; Liu, B.; Zhu, M. Experimental investigation on constitutive behavior of PVB under impact loading. Int. J. Impact Eng. 2010, 38, 106–114. [Google Scholar] [CrossRef]
- Rong, W.; Chen, S. Research on the properties of PVB at home and abroad. Polym. Bull. 2012, 5, 82–88. [Google Scholar]
- Duan, Q.; Gong, W.; Guo, B.; Wu, L.; Yu, X.; Xie, H. Techniques of speckle fabrication and image processing for high temperature digital image correlation. J. Tsinghua Univ. (Sci. Technol.) 2019, 59, 425–431. [Google Scholar]
- Wang, X.; Zhang, Q.; Tao, Z.; Chen, J.; Chen, J. Theoretical and experimental study on the load-bearing performance of four-sided simply supported laminated glass. Build. Struct. 2012, 42, 173–175. [Google Scholar]
- Cong, D. Study on the bending resistance of point-supported laminated glass 2003. Natl. Conf. Struct. Eng. 2003, 1, 499–504. [Google Scholar]


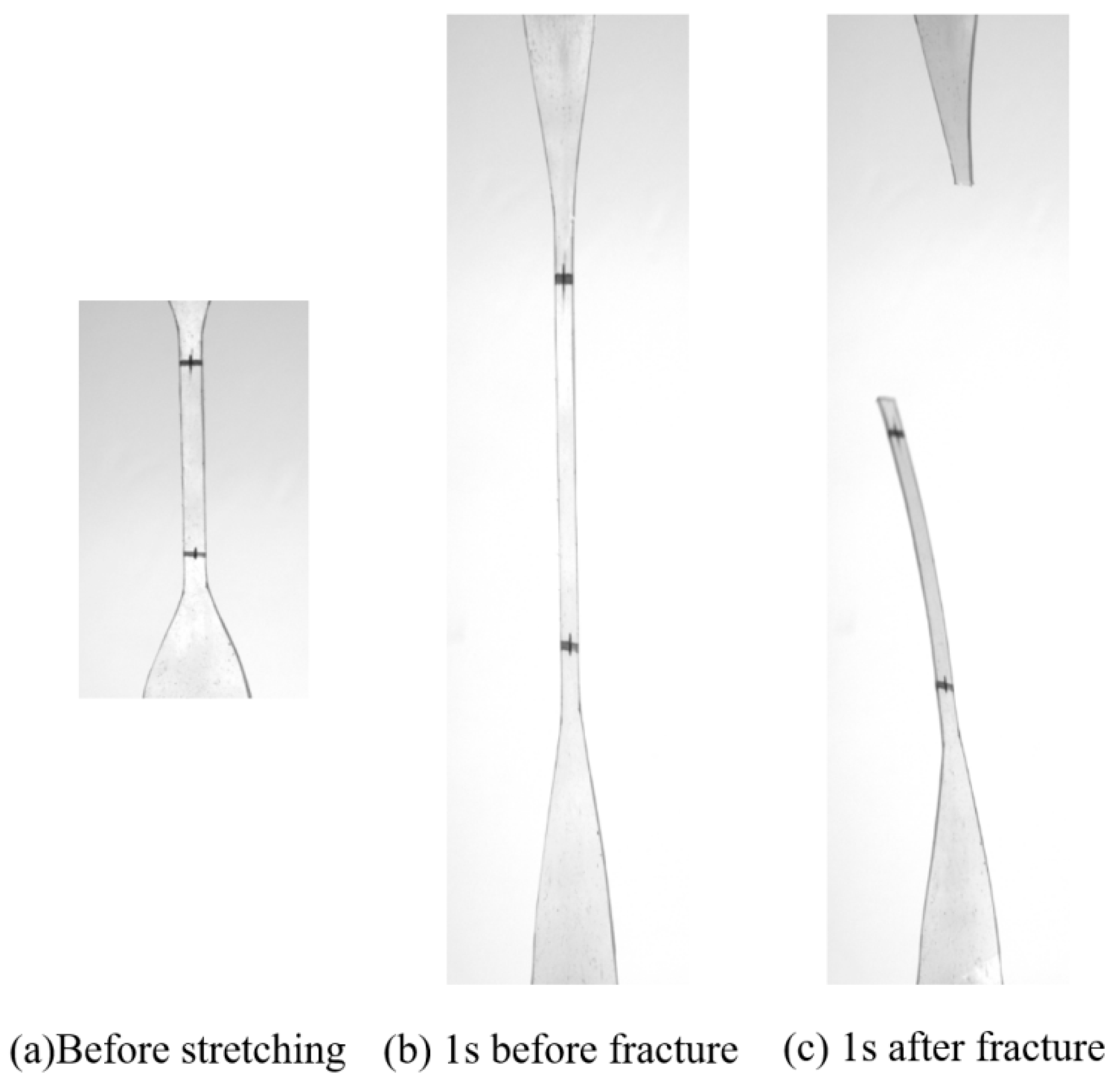
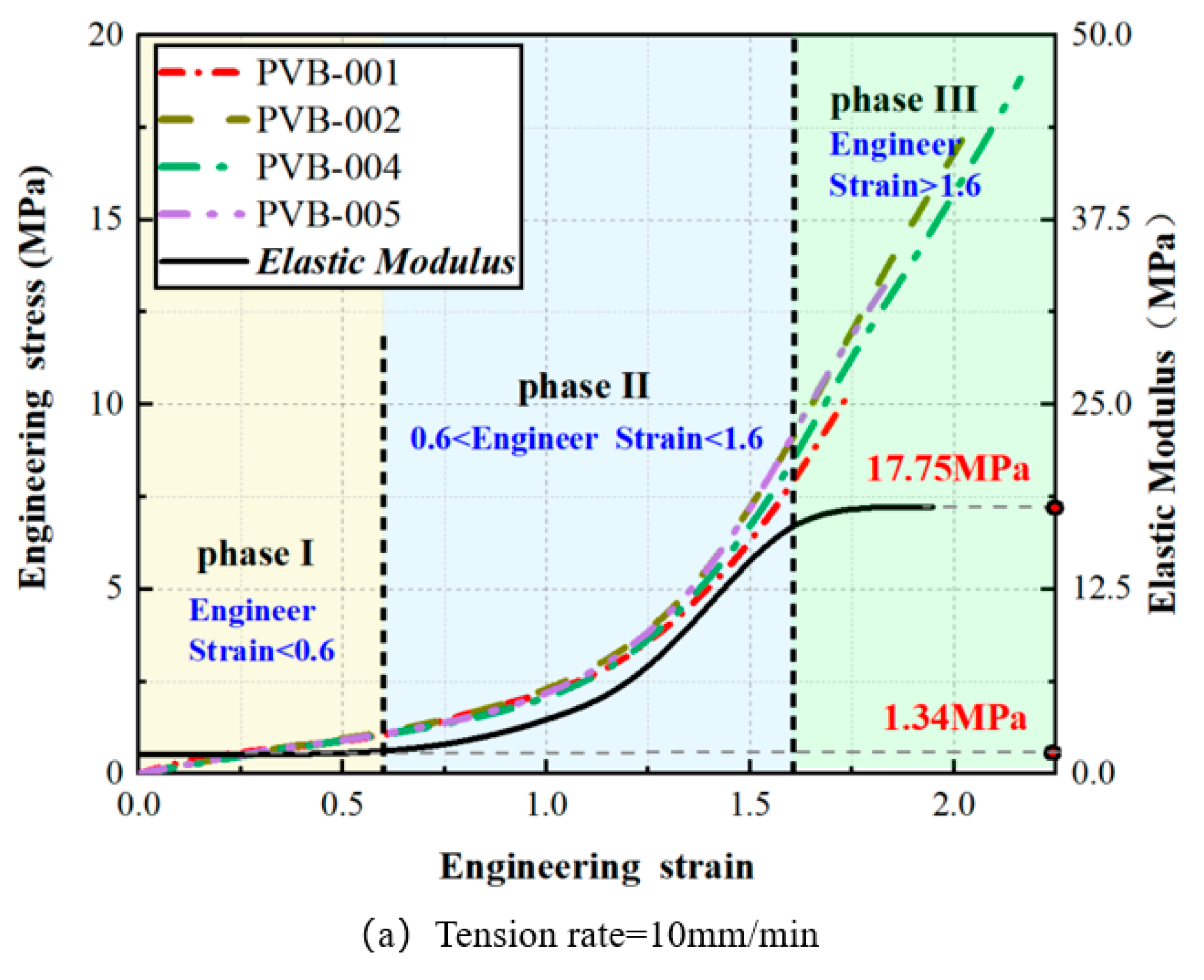
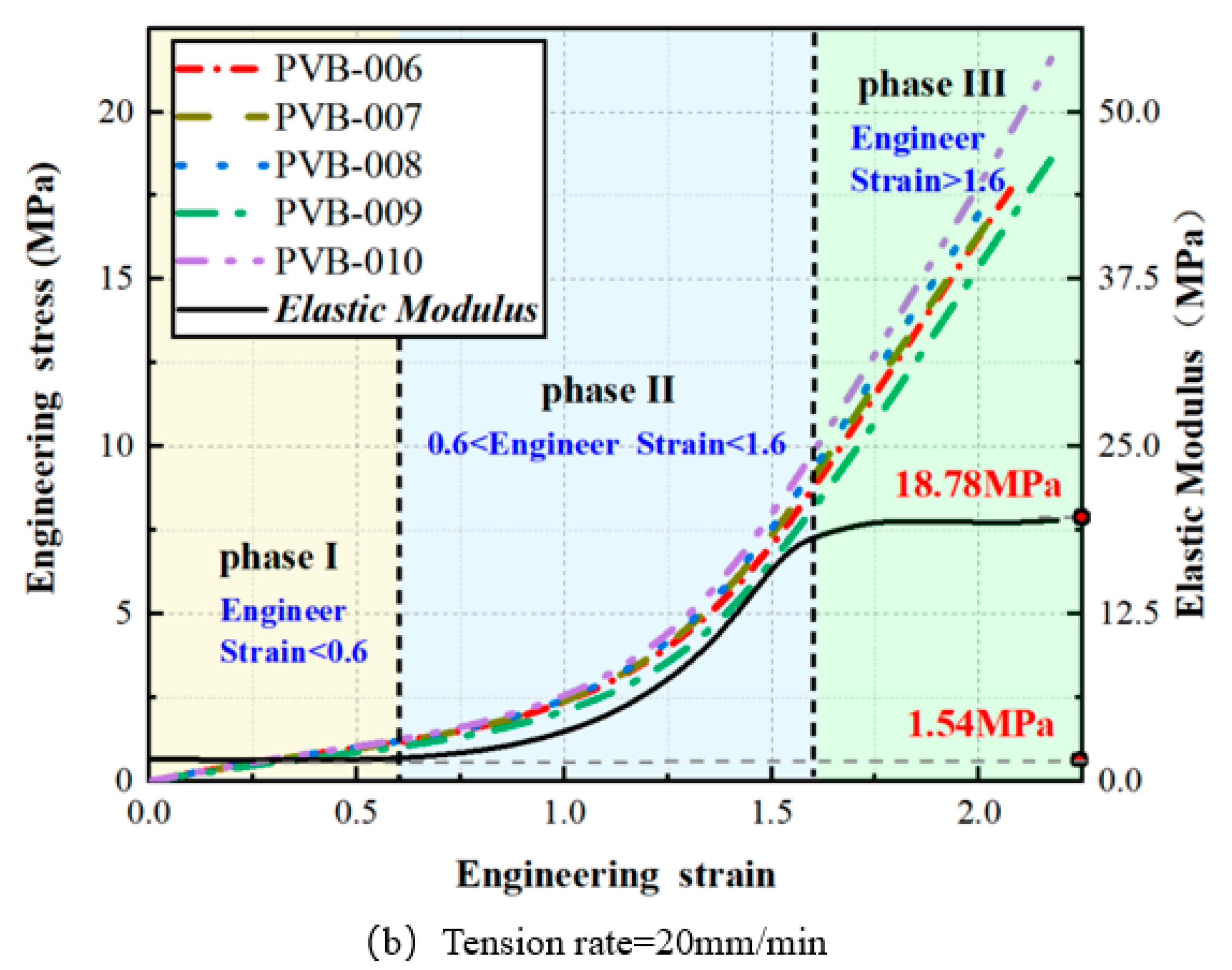
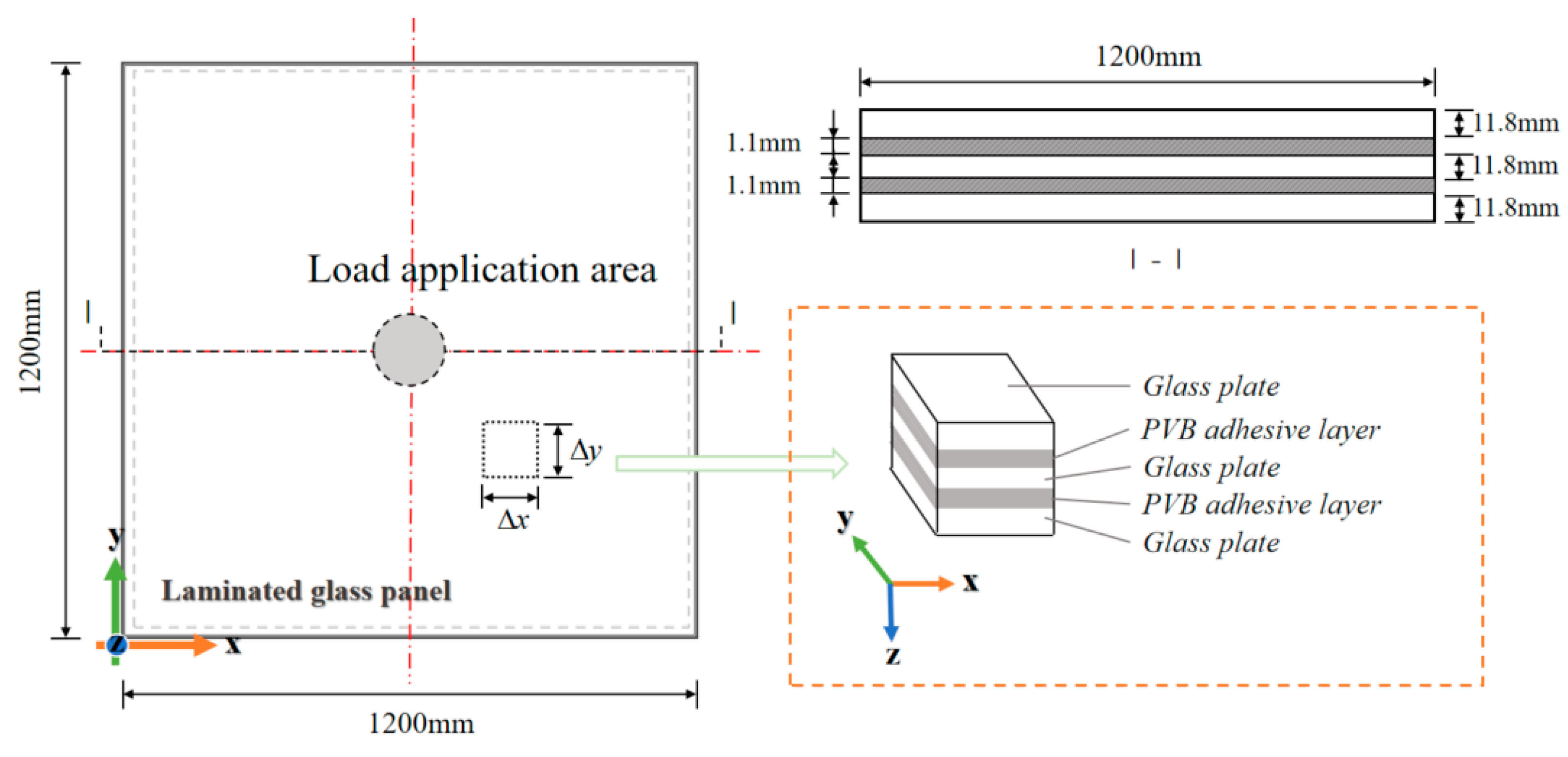
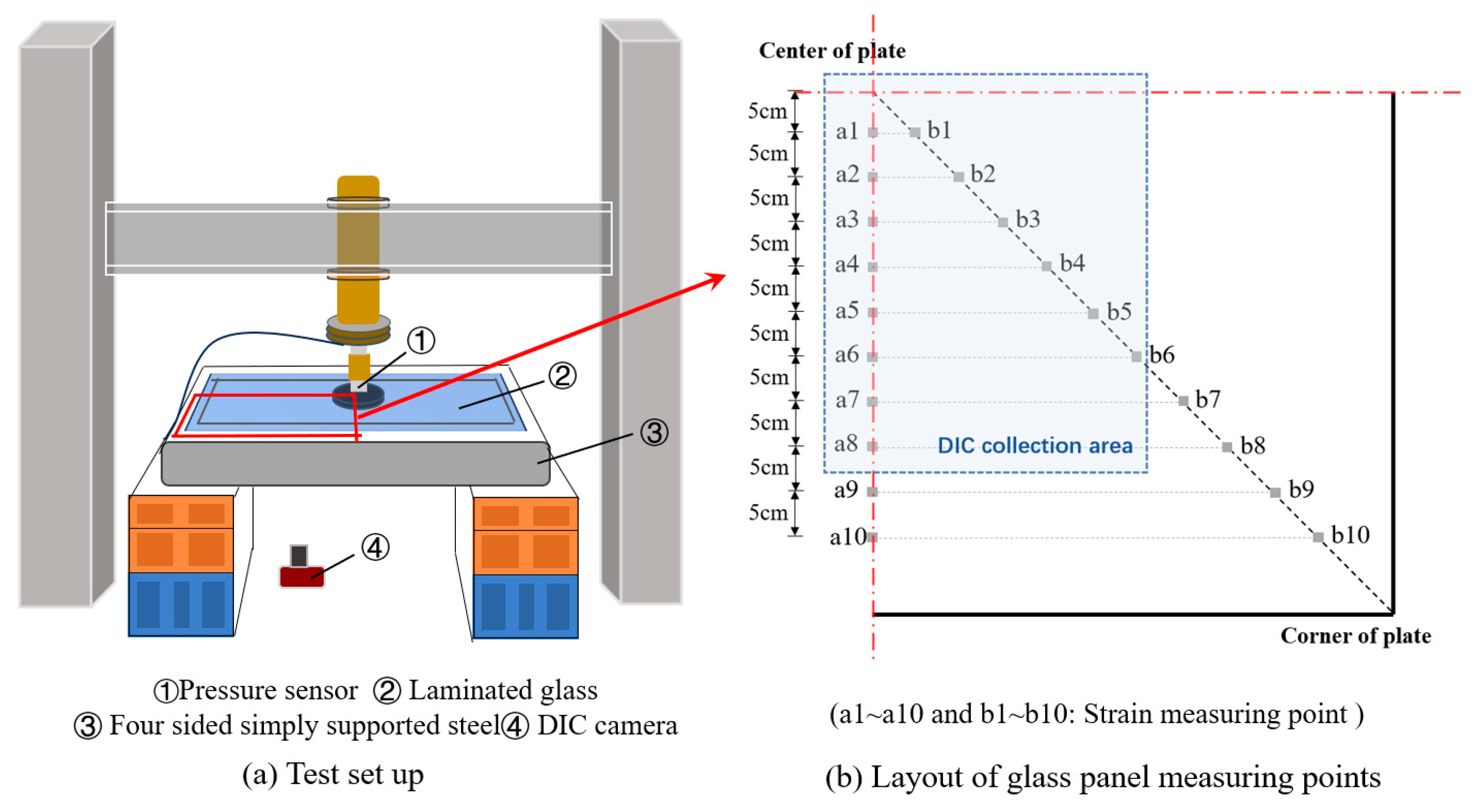




| No. | Symbol | Physical Parameter | Size (mm) |
|---|---|---|---|
| 1 | L | Total length | 115 |
| 2 | d | Thickness | 1.1 |
| 3 | b | Small radius | 14 |
| 4 | G0 | Gauge length | 25 |
| 5 | W | End width | 25 |
| 6 | H | Distance between fixtures | 80 |
| 7 | C | Middle section width | 6 |
| 8 | R0 | Middle section length | 33 |
| 9 | R1 | Large radius | 25 |
| No. | Parameter | Value |
|---|---|---|
| 1 | Sensor | 1.1″ IMX304 Global shutter CMOS (FRAMOS, Ottawa, ON, Canada) |
| 2 | Resolving power | 4112 (H) × 3008 (V) |
| 3 | Pixel depth | 8 bit |
| 4 | Image data format | Mono8, Mono12, Mono12p |
| 5 | Pixel size | 3.45 μm |
| 6 | Mechanical dimensions (W × H × L) | 44 mm × 29 mm × 86.3 mm |
| Number | Sample | (mm/min) | (%) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|
| 1 | PVB-001 | 10 | 1.74 | 10.27 | 1.04 | 17.78 |
| 2 | PVB-002 | 10 | 2.03 | 17.37 | 1.43 | 18.42 |
| 3 | PVB-003 | 10 | / | / | / | / |
| 4 | PVB-004 | 10 | 2.16 | 18.82 | 1.47 | 18.32 |
| 5 | PVB-005 | 10 | 1.85 | 13.67 | 1.41 | 16.48 |
| 6 | PVB-006 | 20 | 2.08 | 17.85 | 1.57 | 18.54 |
| 7 | PVB-007 | 20 | 2.06 | 17.32 | 1.51 | 18.65 |
| 8 | PVB-008 | 20 | 2.02 | 17.24 | 1.57 | 18.32 |
| 9 | PVB-009 | 20 | 2.19 | 18.87 | 1.37 | 18.72 |
| 10 | PVB-010 | 20 | 2.19 | 21.98 | 1.70 | 19.67 |
| No. | Specimen Label | (kN) | (mm) | (kN/mm) | |
|---|---|---|---|---|---|
| 1 | 3L-a | 3 | 47.8 | 16.4 | 2.91 |
| 2 | 3L-b | 34.2 | 13.5 | 2.53 | |
| 3 | 3L-c | 37.3 | 13.1 | 2.86 | |
| 4 | 2L-a | 2 | 31 | 16.3 | 1.9 |
| 5 | 2L-b | 35 | 21.9 | 1.6 | |
| 6 | 2L-c | 42 | 25.8 | 1.63 | |
| 7 | 1L-a | 1 | 22.1 | 24.6 | 0.9 |
| 8 | 1L-b | 26.5 | 27.9 | 0.95 | |
| 9 | 1L-c | 25.5 | 21.1 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, L.; Li, H.; Zhang, N.; Shi, W.; Haider, R. Research on Out-of-Plane Bending Test of PVB Laminated Glass Plate with Different Number of Layers. Appl. Sci. 2024, 14, 3416. https://doi.org/10.3390/app14083416
Yun L, Li H, Zhang N, Shi W, Haider R. Research on Out-of-Plane Bending Test of PVB Laminated Glass Plate with Different Number of Layers. Applied Sciences. 2024; 14(8):3416. https://doi.org/10.3390/app14083416
Chicago/Turabian StyleYun, Lu, Hui Li, Ning Zhang, Wei Shi, and Rizwan Haider. 2024. "Research on Out-of-Plane Bending Test of PVB Laminated Glass Plate with Different Number of Layers" Applied Sciences 14, no. 8: 3416. https://doi.org/10.3390/app14083416
APA StyleYun, L., Li, H., Zhang, N., Shi, W., & Haider, R. (2024). Research on Out-of-Plane Bending Test of PVB Laminated Glass Plate with Different Number of Layers. Applied Sciences, 14(8), 3416. https://doi.org/10.3390/app14083416






