Research on the Autonomous Control Technology Used in the Slurry Mixing System of Cementing Units
Abstract
:1. Introduction
2. Working Principle and Model Establishment of the Slurry Mixing System
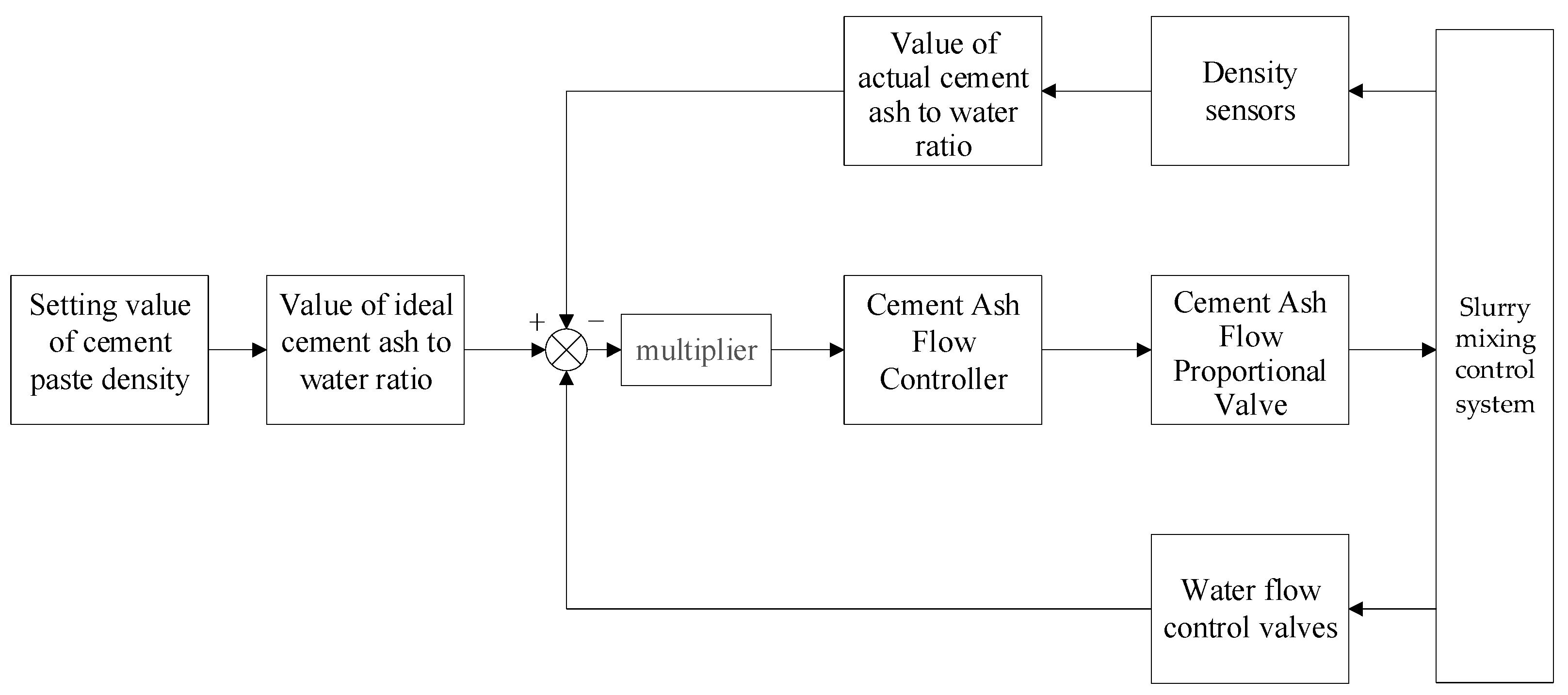
2.1. Working Principle of the Slurry Mixing System
2.2. Establishment of the Slurry Mixing System Model
- (1)
- Proportional amplifier
- (2)
- Solenoid proportional valve
3. Design of the Slurry Mixing System Controller
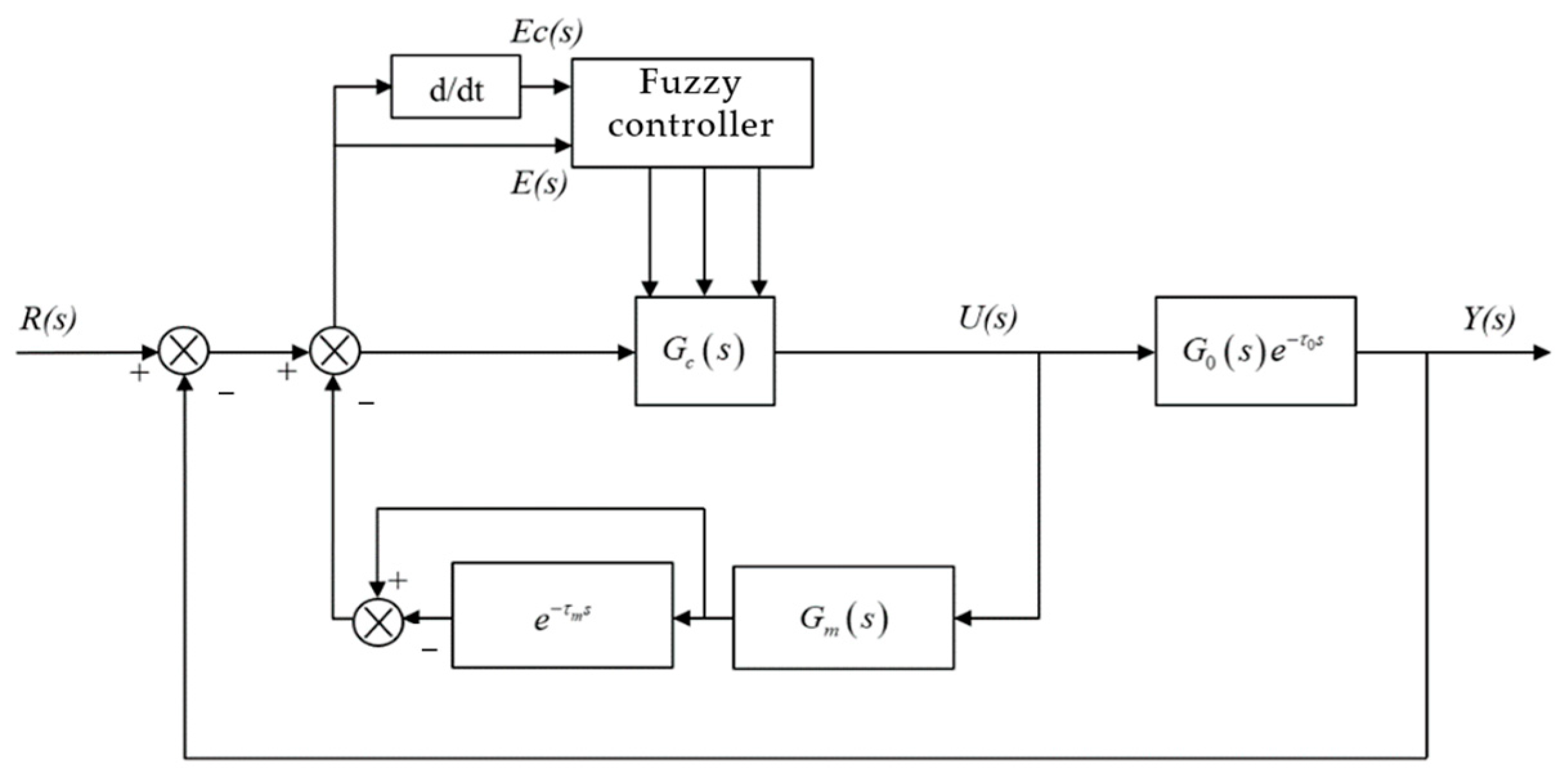
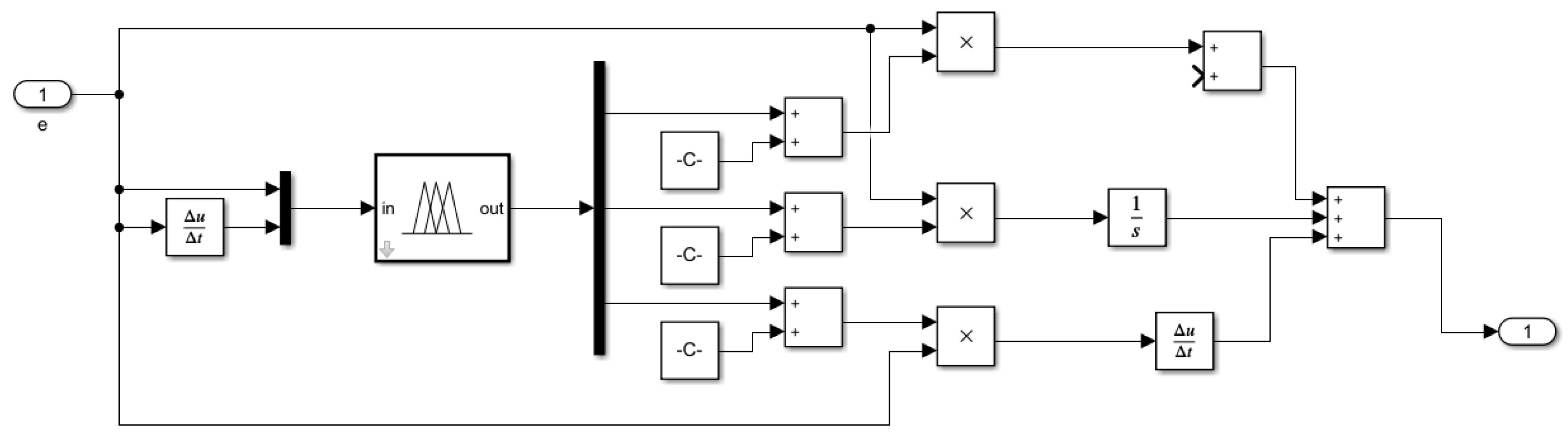
3.1. Design of the Smith Fuzzy PID Controller
- (1)
- Fuzzification
- (2)
- Fuzzy Inference
- (3)
- Defuzzification
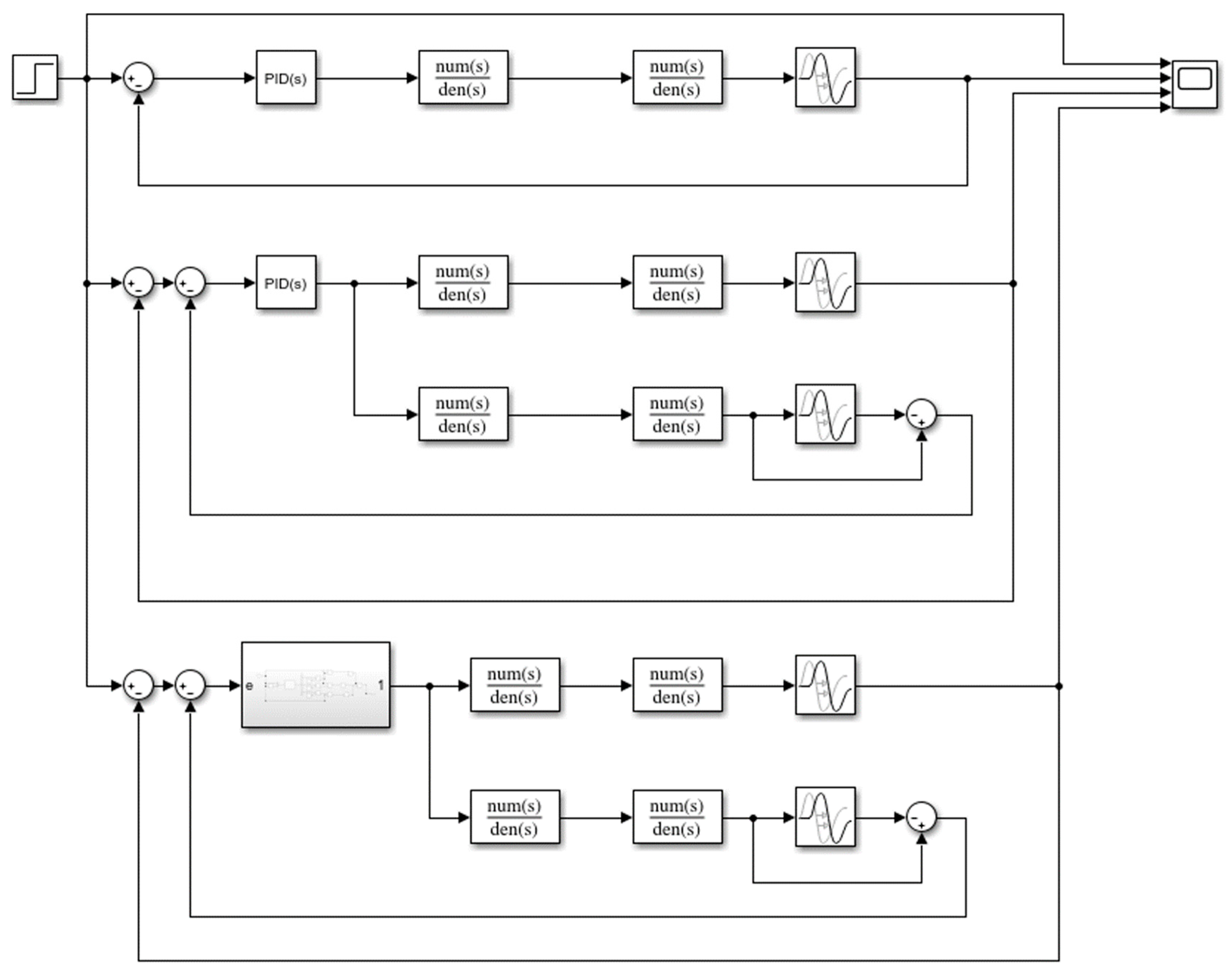
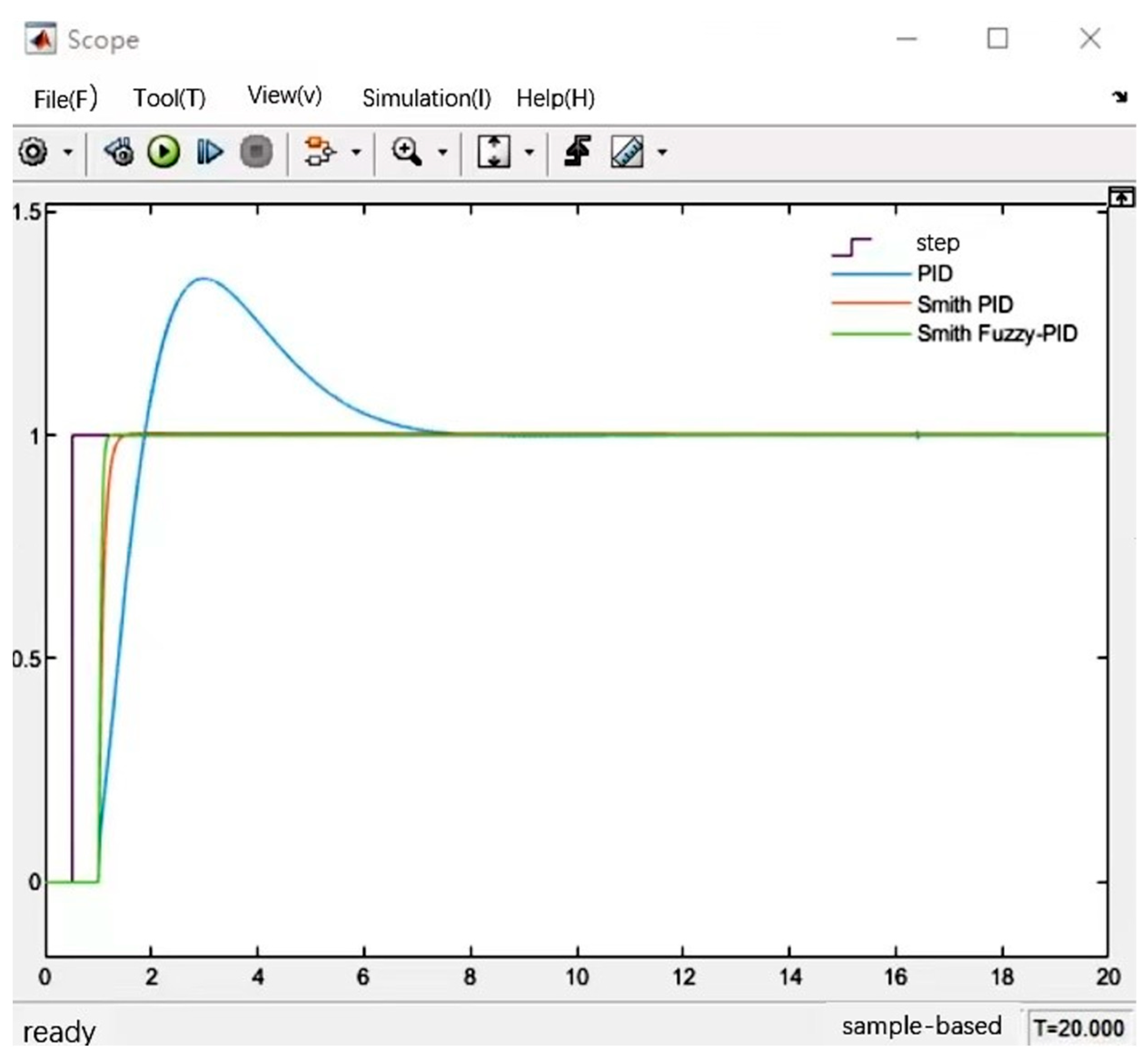
3.2. Control Algorithm Simulation
- (1)
- The conventional PID controller has a large overshoot and a long adjustment time.
- (2)
- Compared with the conventional PID control, Smith predictive compensation control does not have any overshoot, and the stability of the system is greatly improved. In addition, the rise time is shorter, and it can reach a stable state faster.
- (3)
- By adding fuzzy control on the basis of Smith prediction compensation, the system response time is shortened, the response speed is significantly improved, and the response capacity of the control system is stronger.
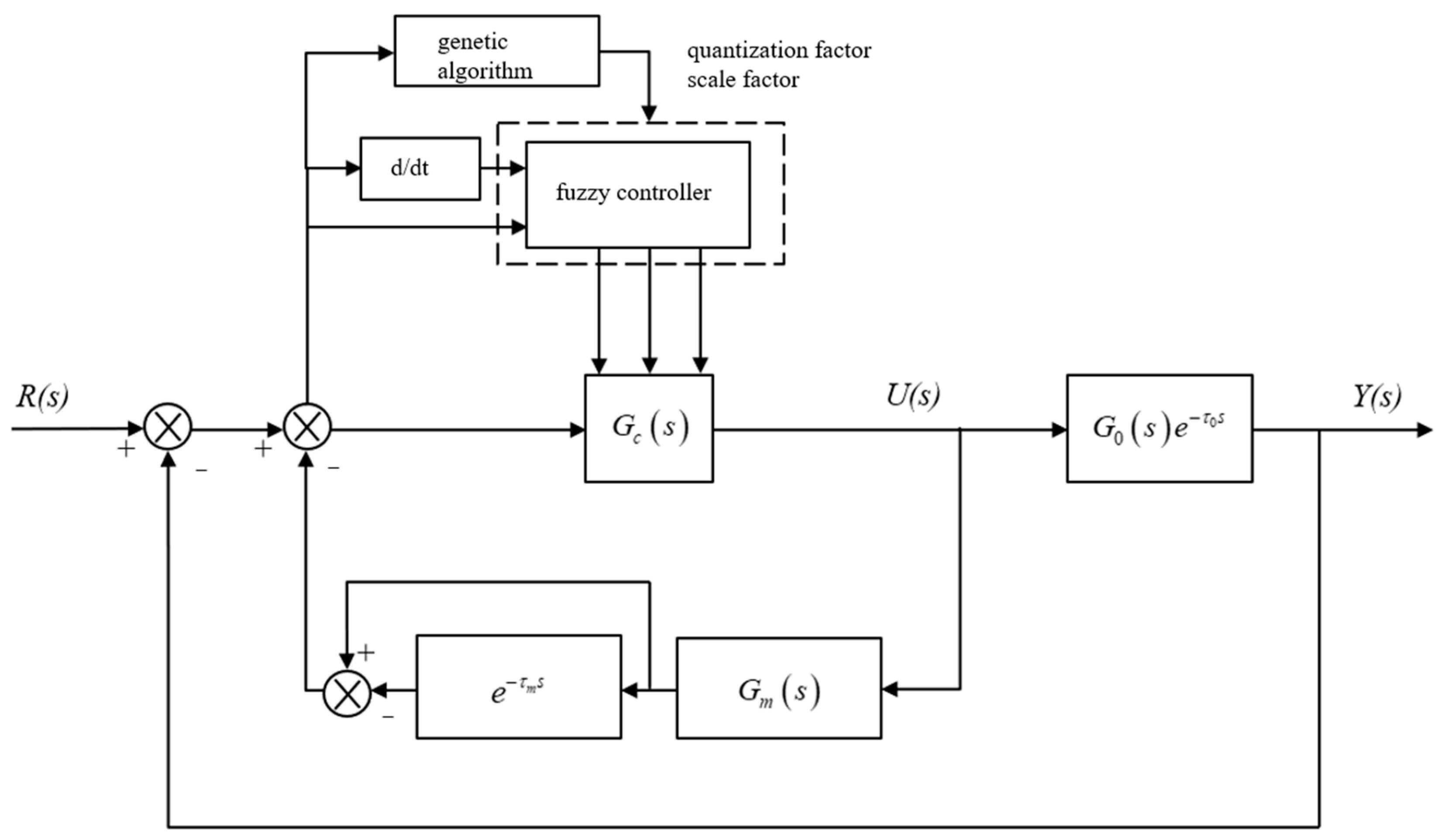
4. Optimization of the Slurry Mixing System Control Scheme
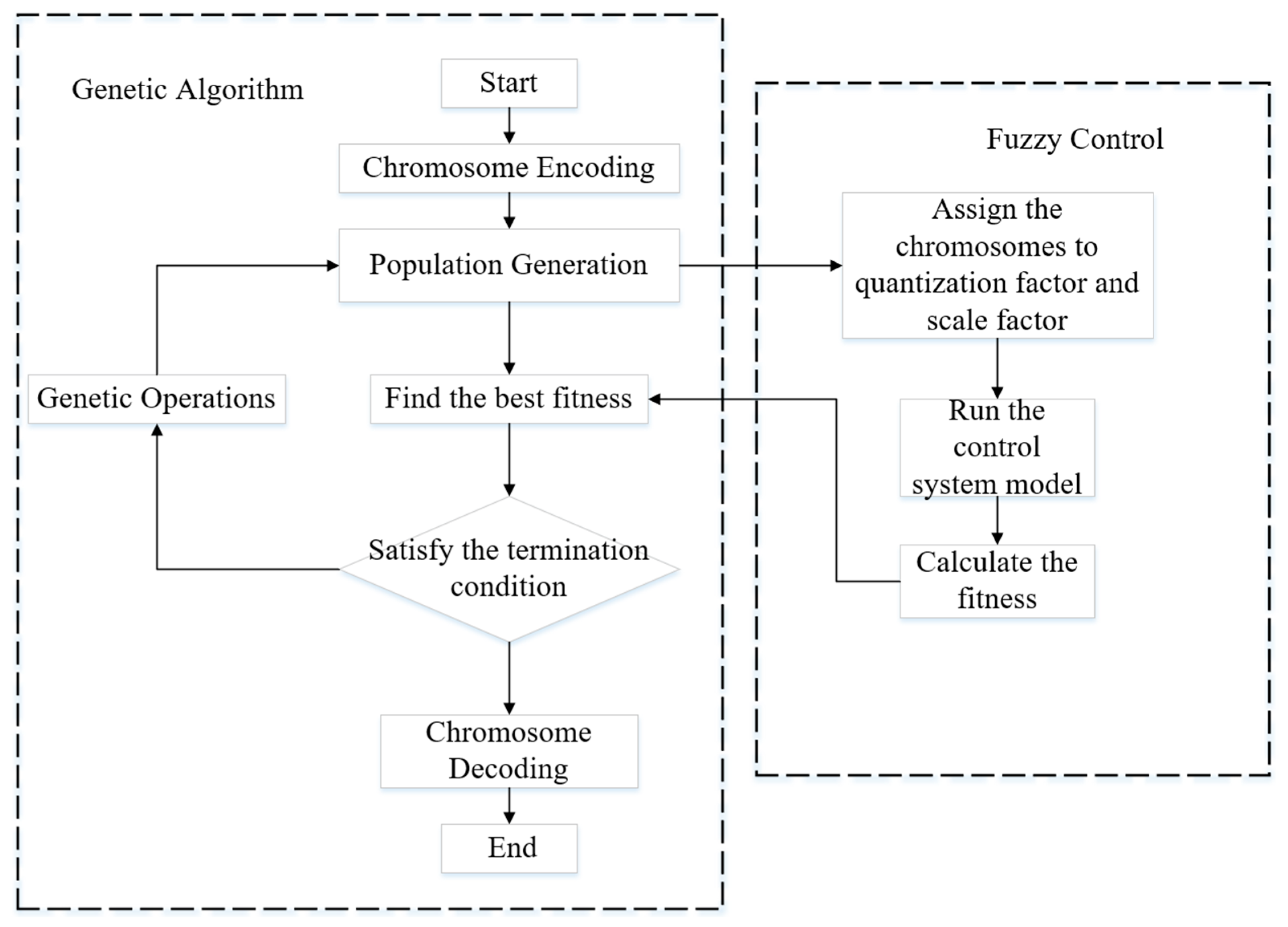
4.1. The Genetic Algorithm Used to Optimize the Slurry Mixing System
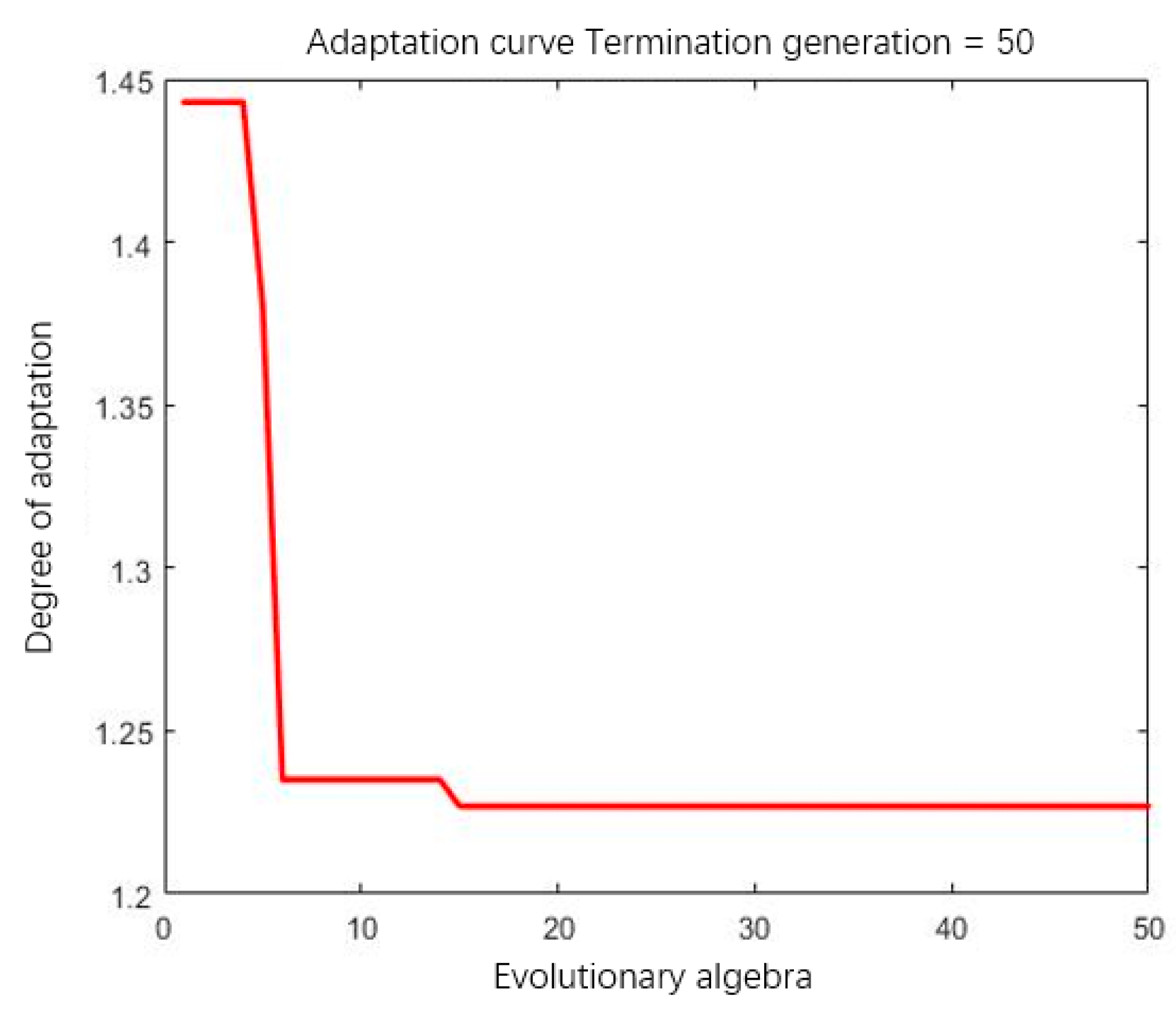
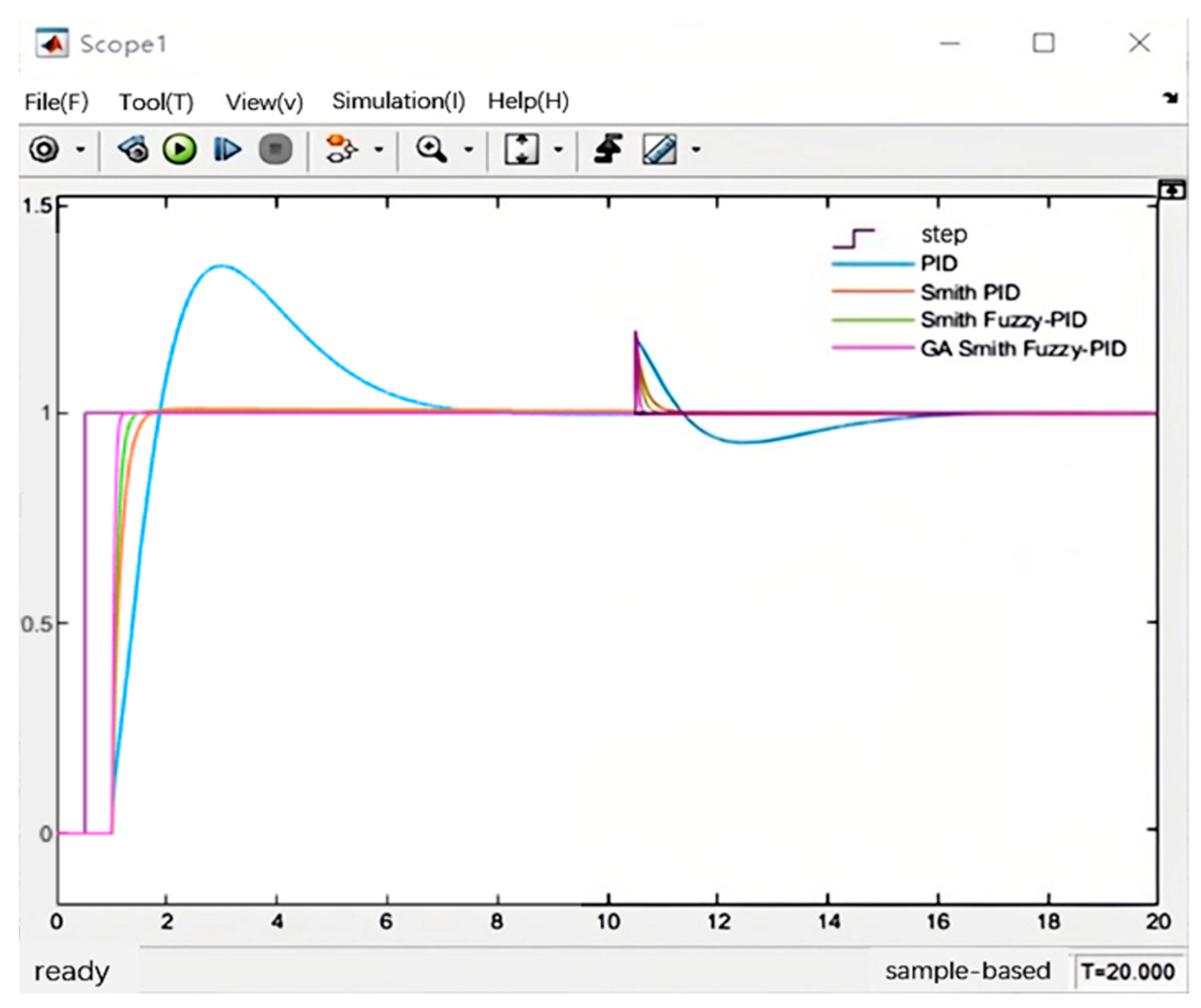
4.2. Simulation of the Control Algorithm
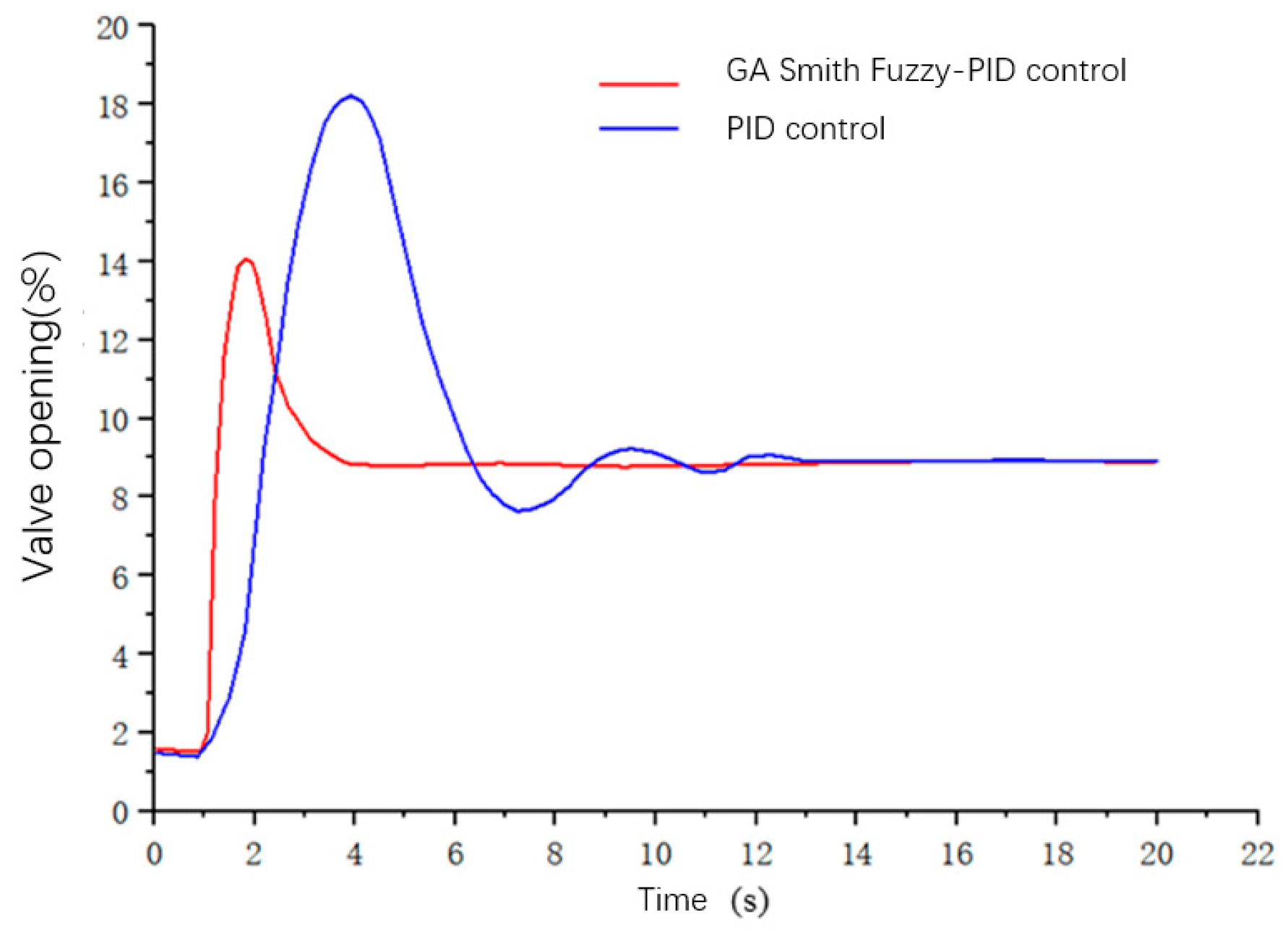
- (1)
- The conventional PID controller has a large overshoot, poor system stability, a long adjustment time, and poor anti-interference ability.
- (2)
- The Smith predictive compensation control has a smoother curve, and it shows almost no obvious fluctuations and oscillations. Concurrently, it has a shorter rise time and can reach a stable state relatively faster; however, the response time is long.
- (3)
- Regarding the Smith fuzzy PID control, the rise time is about 0.7 s, which means that it can reach the steady state quickly, and the overshoot is very small, measuring at around 0.32%, and the anti-interference ability is improved compared with the previous two methods.
- (4)
- Regarding the GA Smith fuzzy PID control, the rise time is the shortest, around 0.3 s, the response speed is extremely fast, and its anti-interference ability is strong. Concurrently, the overshoot of the system is small and there is no steady-state error; therefore, the stability and dynamic performance of the system are better.
5. Experimental Verification
5.1. Experimental Principle
5.2. Experimental Procedures
- (1)
- We checked to ensure that all components were normal and then started the water pump to add water to the slurry mixing tank.
- (2)
- We started the recirculating pump, turned on the densitometer, and supplied cement to the slurry mixing tank via gravity.
- (3)
- We confirmed that the density of the cement slurry rose slowly after the cement entered the slurry mixing tank. When the density approached the set density, we adjusted the proportional valve to control the water flow rate.
- (4)
- We continued the mixing process, transferred the densitometer data to the PLC, and adjusted the proportional valve through the slurry mixing autonomous control system to finally adjust the slurry density to the design value.
- (5)
- We observed the controller output in real time during the experimental process. Thereafter, we checked the valve openness indicator dial and recorded the valve openness.
- (6)
- We performed the experiment twice, using one controller for slurry mixing density control each time, and compared and analyzed the experimental results.
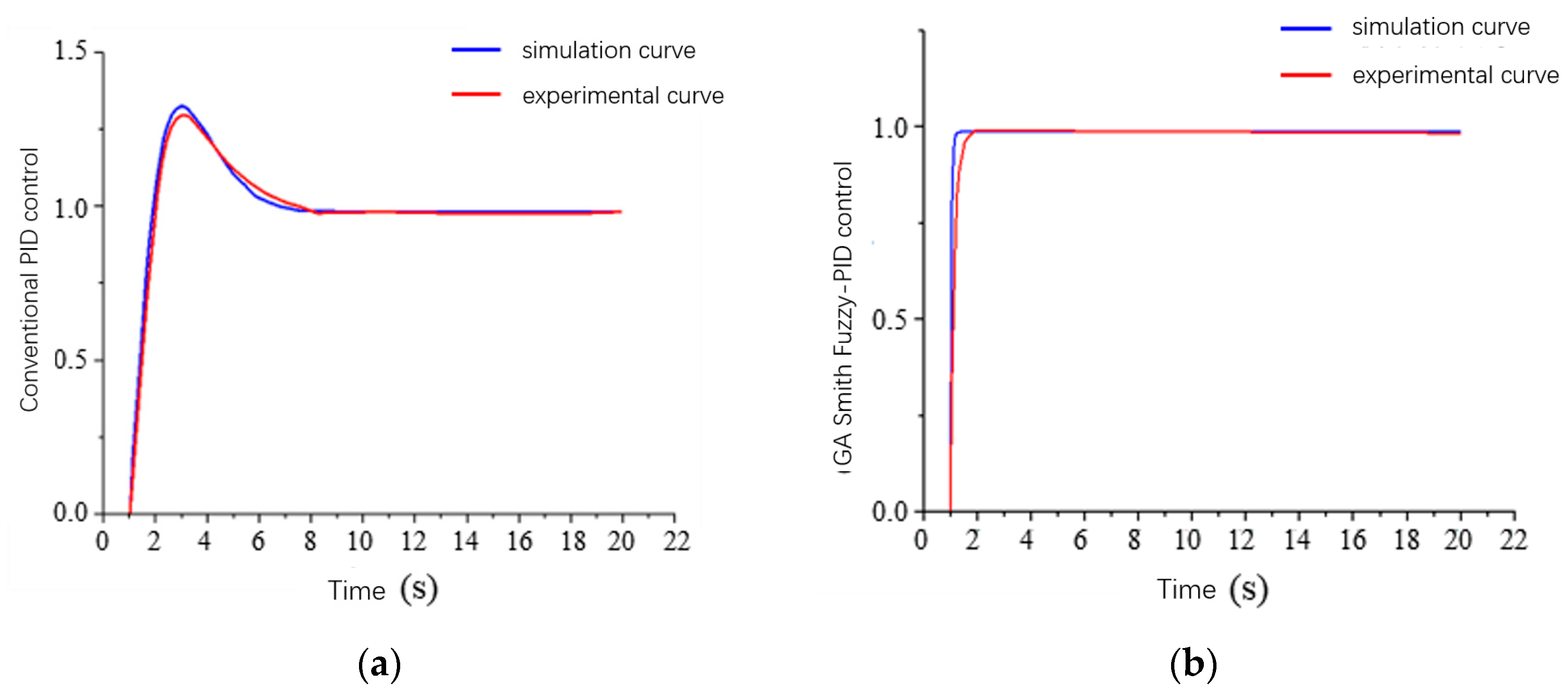
5.3. Experimental Data Recording and Analysis
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, Q. Research on the New Problems and Development Direction Faced by Domestic Cementing at Present. Mod. Bus. Tra. Ind. 2018, 39, 180–181. [Google Scholar]
- Blanchini, F.; Casagrande, D.; Miani, S. Stable LPV Realization of the Smith Predictor. Int. J. Syst. Sci. 2016, 47, 2393–2401. [Google Scholar] [CrossRef]
- Bai, J.B. Research on Adaptive Control of Test Room Air Conditioning System. Master’s Thesis, Southeast University, Nanjing, China, 2006. [Google Scholar]
- Mohamed, A.R.S.; Doaa, K.I.; Mostafa, B. Application of PSO Tuned Fuzzy Logic Controller for LFC of Two-area Power System with Redox Flow Battery and PV Solar Park. Ain. Shams. Eng. J. 2022, 13, 101710. [Google Scholar]
- Gao, J.; Zhang, J.; Feng, X. Main Steam Pressure Control Technology Based on Mismatch Compensated Smith-RBF Neural Network. J. Chongqing Univ. 2019, 42, 105–113. [Google Scholar]
- Ning, X.; Wang, Z.; Wang, C.; Wu, B. Adaptive Feedforward and Feedback Compensation Method for Real-time Hybrid Simulation Based on a Discrete Physical Testing System Model. J. Earthq. Eng. 2020, 26, 3841–3863. [Google Scholar] [CrossRef]
- Wang, J.S. Research on Precise Train Stopping Algorithm Based on Particle Swarm PID-Smith Controller. Sci. Tech. Inno. 2023, 15–19. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Zuo, K.; Khan, M.J. An Improved Genetic Algorithm Optimization Fuzzy Controller Applied to the Wellhead Back Pressure Control System. Mech. Syst. Signal PR 2020, 142, 106708. [Google Scholar] [CrossRef]
- Wang, Y.T.; Liu, J.; Li, J.C.; Chen, B.; Li, Q. Using the Smith PSO-Fuzzy PID Model to Control Electrical Conductivity of Nutrient Solution of Precision Fertilization. J. Irrig. Drain 2022, 41, 37–44. [Google Scholar]
- Moura, J.P.; Fonseca Neto, J.V.; Rego, P.H.M. A neuro-fuzzy model for online optimal tuning of pid controllers in industrial system applications to the mining sector. IEEE Trans. Fuzzy Syst. 2019, 28, 1864–1877. [Google Scholar] [CrossRef]
- Park, D.; Le, T.L.; Quynh, N.V.; Long, N.K.; Hong, S.K. Online tuning of pid controller using a multilayer fuzzy neural network design for quadcopter attitude tracking control. Front. Neurorobotics 2021, 14, 619350. [Google Scholar] [CrossRef] [PubMed]
- Han, H.G.; Wu, X.L.; Liu, Z.; Qiao, J.F. Design of self-organizing intelligent controller using fuzzy neural network. IEEE Trans. Fuzzy Syst. 2018, 26, 3037–3111. [Google Scholar] [CrossRef]
- Liu, J.W.; Tao, X.; Ma, X.Y.; Feng, K.G.; Chen, J.M. Fuzzy controllers with neural network predictor for second-order linear systems with time delay. IEEE Access 2020, 8, 206049–206062. [Google Scholar] [CrossRef]
- Fang, Y.K.; Cheng, C.Y.; Dong, Z.; Min, H.G.; Zhao, X.M. A fault diagnosis framework for autonomous vehicles based on hybrid data analysis methods combined with fuzzy PID control. In Proceedings of the International Conference on Unmanned Systems, Harbin, China, 27–28 November 2020. [Google Scholar]
- Lei, Y.; Wu, Y.Q.; Yuan, Y.Q.; Chen, C. Intelligent neural network controller optimization and simulation using GA. In Proceedings of the International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019. [Google Scholar]
- Feng, Y.; Wu, M.; Chen, X.; Chen, L.; Du, S. A fuzzy pid controller with nonlinear compensation term for mold level of continuous casting process. Inf. Sci. 2020, 539, 487–503. [Google Scholar] [CrossRef]
- Zhang, R.M.; Zeng, D.Q.; Ju, H.P.; Lam, H.K.; Xie, X.P. Fuzzy sampled-data control for synchronization of t-s fuzzy reaction-diffusion neural networks with additive time-varying delays. IEEE Trans. Cybern. 2021, 51, 2384–2397. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Lam, H.K.; Xuan, C.B.; Chen, M. Adaptive neuro-fuzzy pid controller based on twin delayed deep deterministic policy gradient algorithm. Neurocomputing 2020, 402, 183–194. [Google Scholar] [CrossRef]
- Fathollahi, A.; Andresen, B. Multi-Machine Power System Transient Stability Enhancement Utilizing a Fractional Order-Based Nonlinear Stabilizer. Fractal Fract. 2023, 7, 808. [Google Scholar] [CrossRef]
- Fathollahi, A.; Gheisarnejad, M. Robust Artificial intelligence Controller for Stabilization of Full-Bridge Converters Feeding Constant Power Loads. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3504–3508. [Google Scholar] [CrossRef]
- Mpalaskas, A.C.; Matikas, T.E.; Aggelis, D.G. Acoustic monitoring for the evaluation of concrete structures and materials. In Acoustic Emission and Related Non-Destructive Evaluation Techniques in the Fracture Mechanics of Concrete; Woodhead Publishing: Sawston, UK, 2015; pp. 269–286. [Google Scholar]
- Panagiotis, G.A.; Paulo, B.L.; Panayiotis, C.R. Revealing the nature of metakaolin-based concrete materials using artificial intelligence techniques. Constr. Build. Mater. 2022, 322, 126500. [Google Scholar]
- Liu, Y.H. Research on Speed Tracking Control of Permanent Magnet Maglev Train Based on Predictive Fuzzy PID Control Algorithm. Master’s Thesis, Jiangxi University of Science and Technology, Nanchang, China, 2022; pp. 5–16. [Google Scholar]
- Hong, Z.Q.; Xu, W.B.; Lv, C.; Ouyang, Q.; Wang, Z.S. Deep Reinforcement Learning-PI Air Rudder Servo System Control Strategy Based on Genetic Algorithm Optimization. J. Mech. Elec. Eng. 2023, 40, 1071–1078. [Google Scholar]
- Yu, Z.; Fu, Y.G.; Zhang, J. Simulation of Stellar Spectrum Controlled by Fuzzy PID. Opt. Precision Eng. 2023, 31, 1619–1630. [Google Scholar]

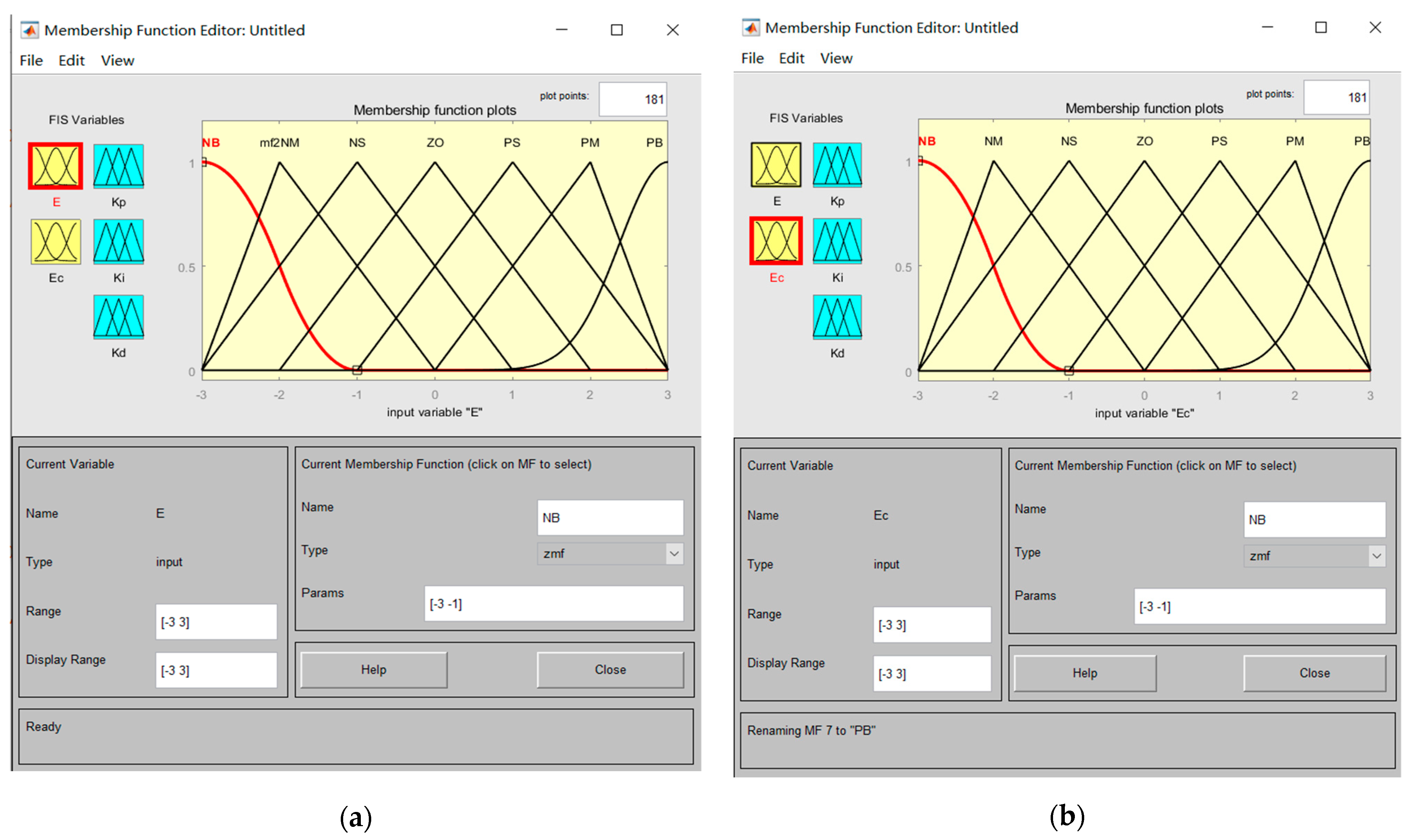
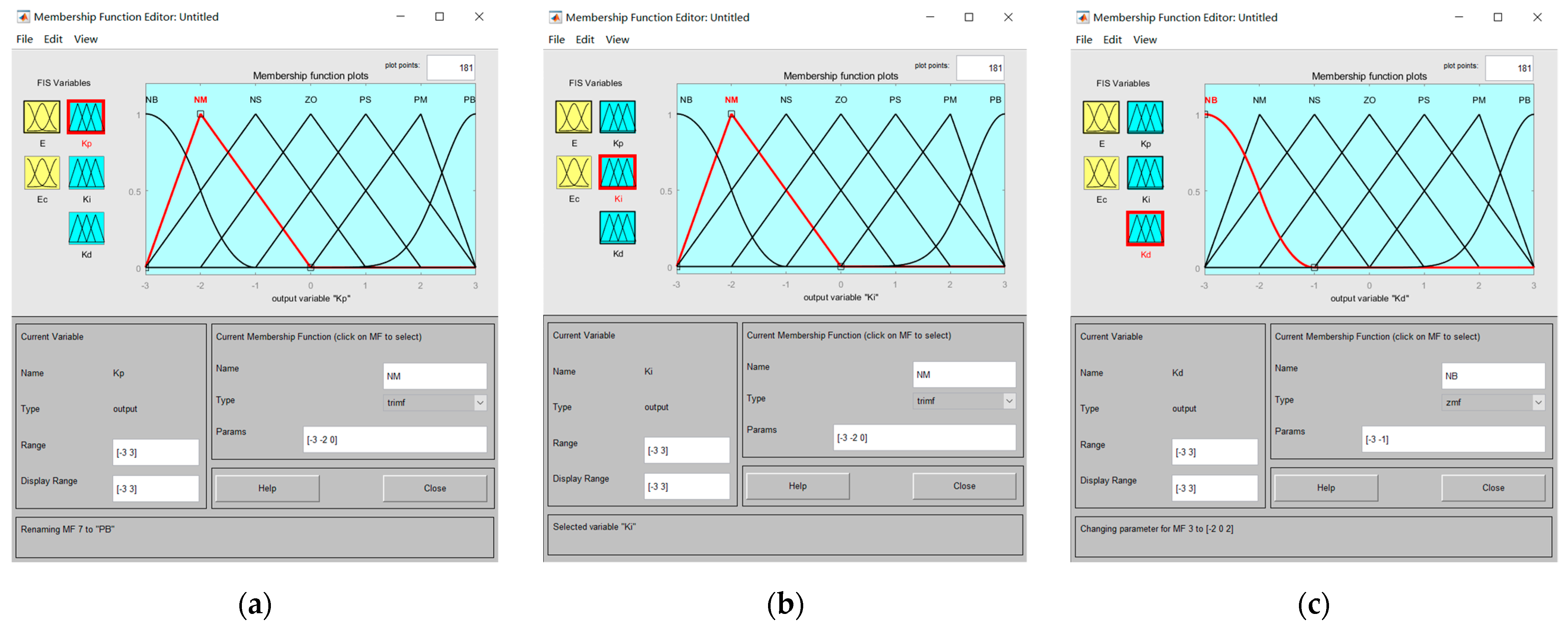



| Variable | Range |
|---|---|
| e | [−3, 3] |
| ec | [−3, 3] |
| Kp | [−0.3, 0.3] |
| Ki | [−0.06, 0.06] |
| Kd | [−0.3, 0.3] |
| e | ec | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/NM |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NM | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NM/PM/NS | NM/PM/ZO |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO |
| PM | PS/ZO/PB | ZO/ZO/NS | NS/PS/PS | NM/PS/PS | NM/PM/PS | NM/PB/PS | NB/PB/PB |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | NB/PB/PB |
| Operating Parameter | Rise Time (s) | Peak Value | Overshoot | Stabilization Time (s) |
|---|---|---|---|---|
| Conventional PID Control | 1.875 | 1.36 | 35.6% | 6.985 |
| Smith Predictive Control | 1.071 | 1.02 | 2. 1% | 1.165 |
| Smith Fuzzy PID Control | 0.702 | 1.01 | 1. 3% | 0.732 |
| GA Smith Fuzzy PID Control | 0.450 | 1.01 | 0. 9% | 0.464 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Hou, G.; Yang, H.; Hu, C.; Cui, J.; Xiao, W. Research on the Autonomous Control Technology Used in the Slurry Mixing System of Cementing Units. Appl. Sci. 2024, 14, 3568. https://doi.org/10.3390/app14093568
Gao X, Hou G, Yang H, Hu C, Cui J, Xiao W. Research on the Autonomous Control Technology Used in the Slurry Mixing System of Cementing Units. Applied Sciences. 2024; 14(9):3568. https://doi.org/10.3390/app14093568
Chicago/Turabian StyleGao, Xiang, Guojian Hou, Huiwen Yang, Changmiao Hu, Junguo Cui, and Wensheng Xiao. 2024. "Research on the Autonomous Control Technology Used in the Slurry Mixing System of Cementing Units" Applied Sciences 14, no. 9: 3568. https://doi.org/10.3390/app14093568
APA StyleGao, X., Hou, G., Yang, H., Hu, C., Cui, J., & Xiao, W. (2024). Research on the Autonomous Control Technology Used in the Slurry Mixing System of Cementing Units. Applied Sciences, 14(9), 3568. https://doi.org/10.3390/app14093568






