Adaptive Whale Optimization Algorithm–DBiLSTM for Autonomous Underwater Vehicle (AUV) Trajectory Prediction
Abstract
1. Introduction
2. Model Introduction
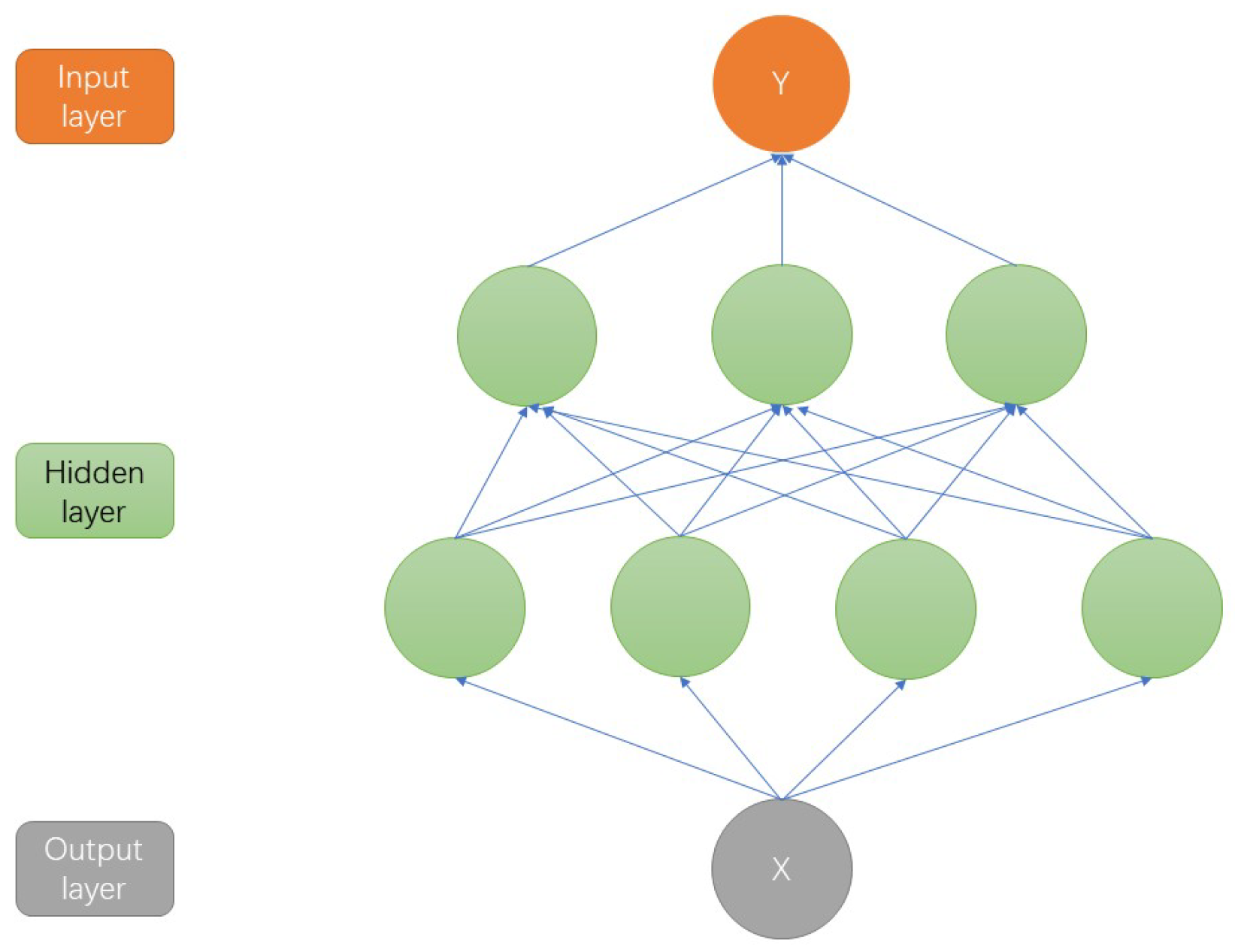
2.1. RNN Neural Network
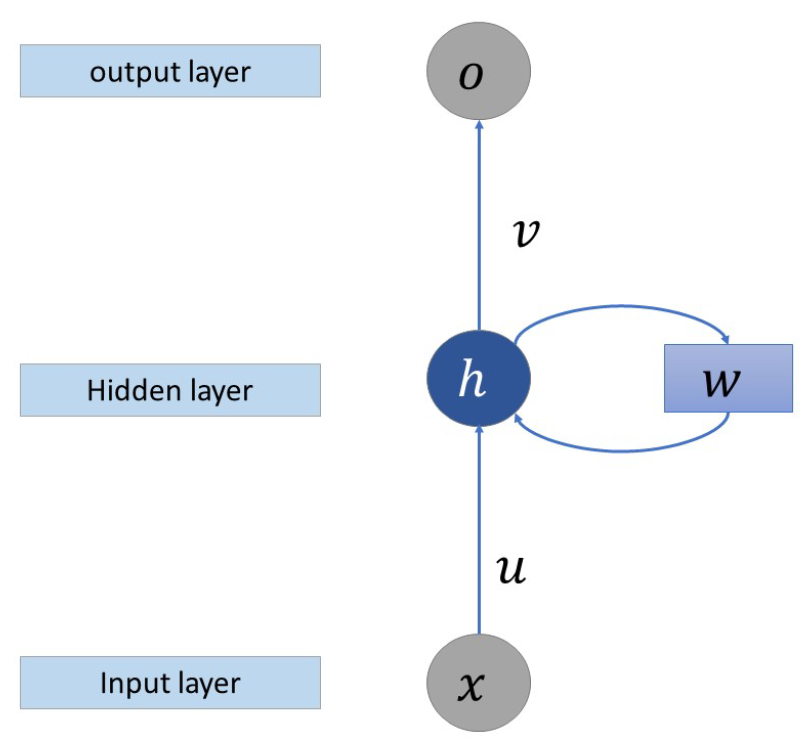
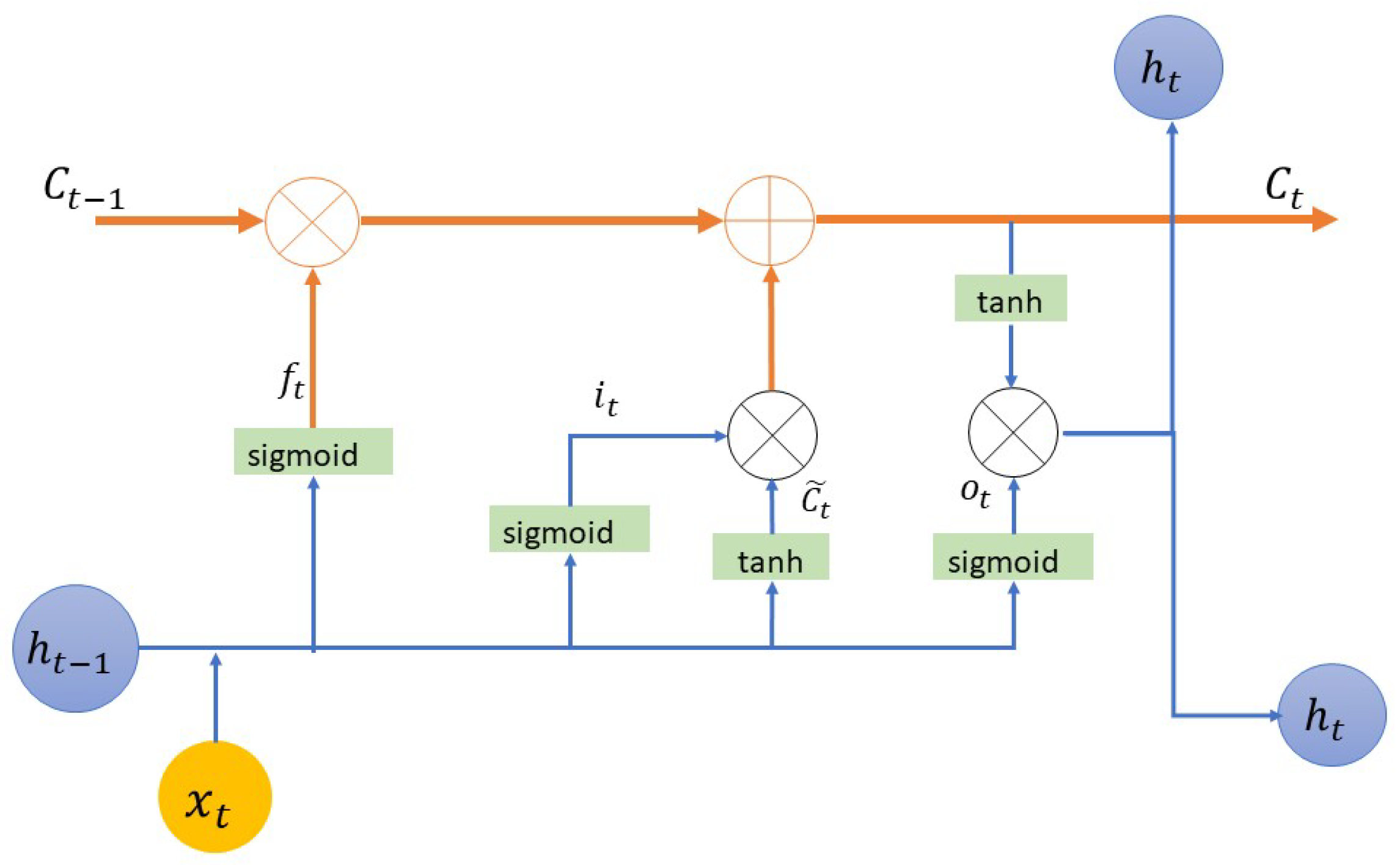
2.2. LSTM Neural Network
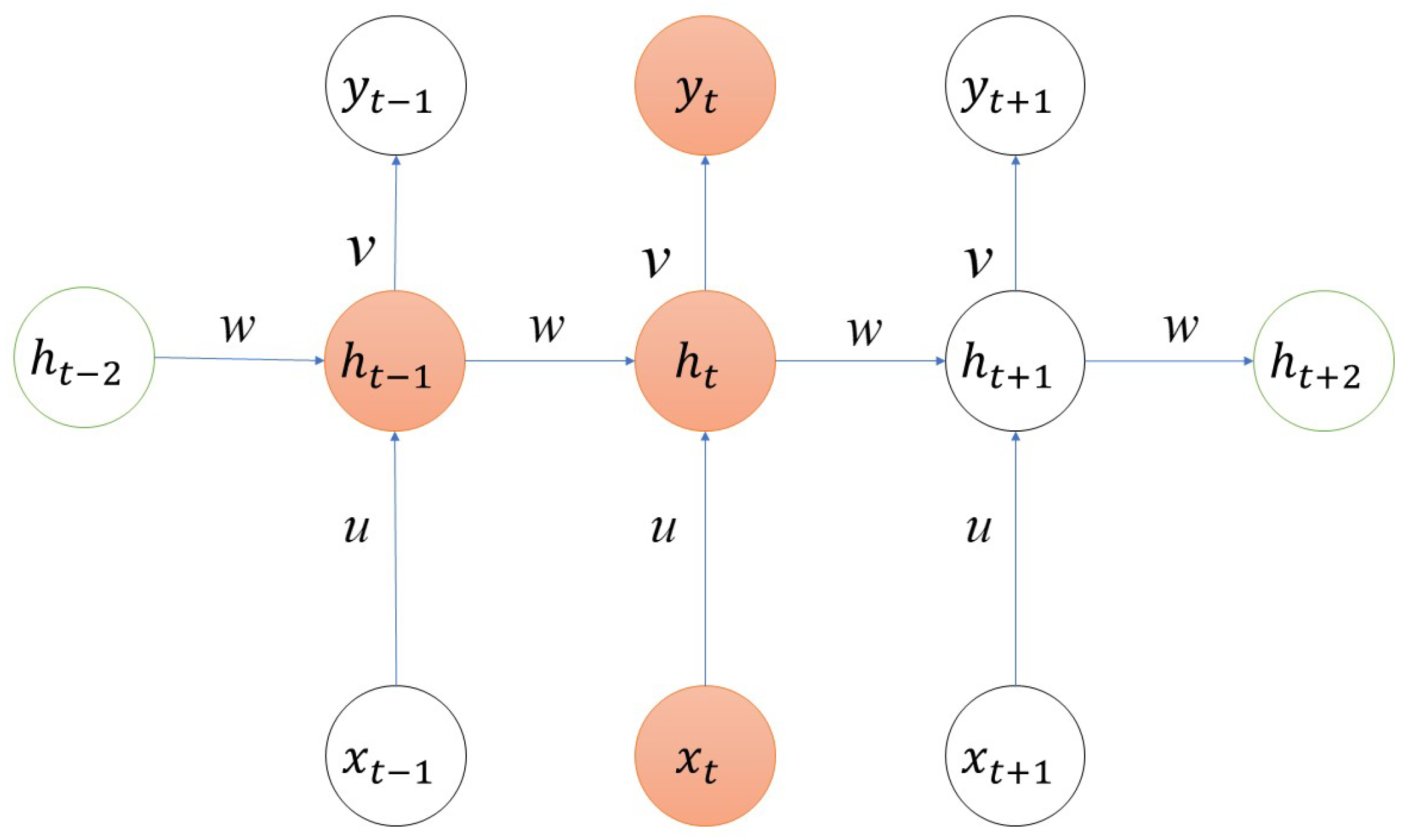
2.3. BiLSTM Neural Network
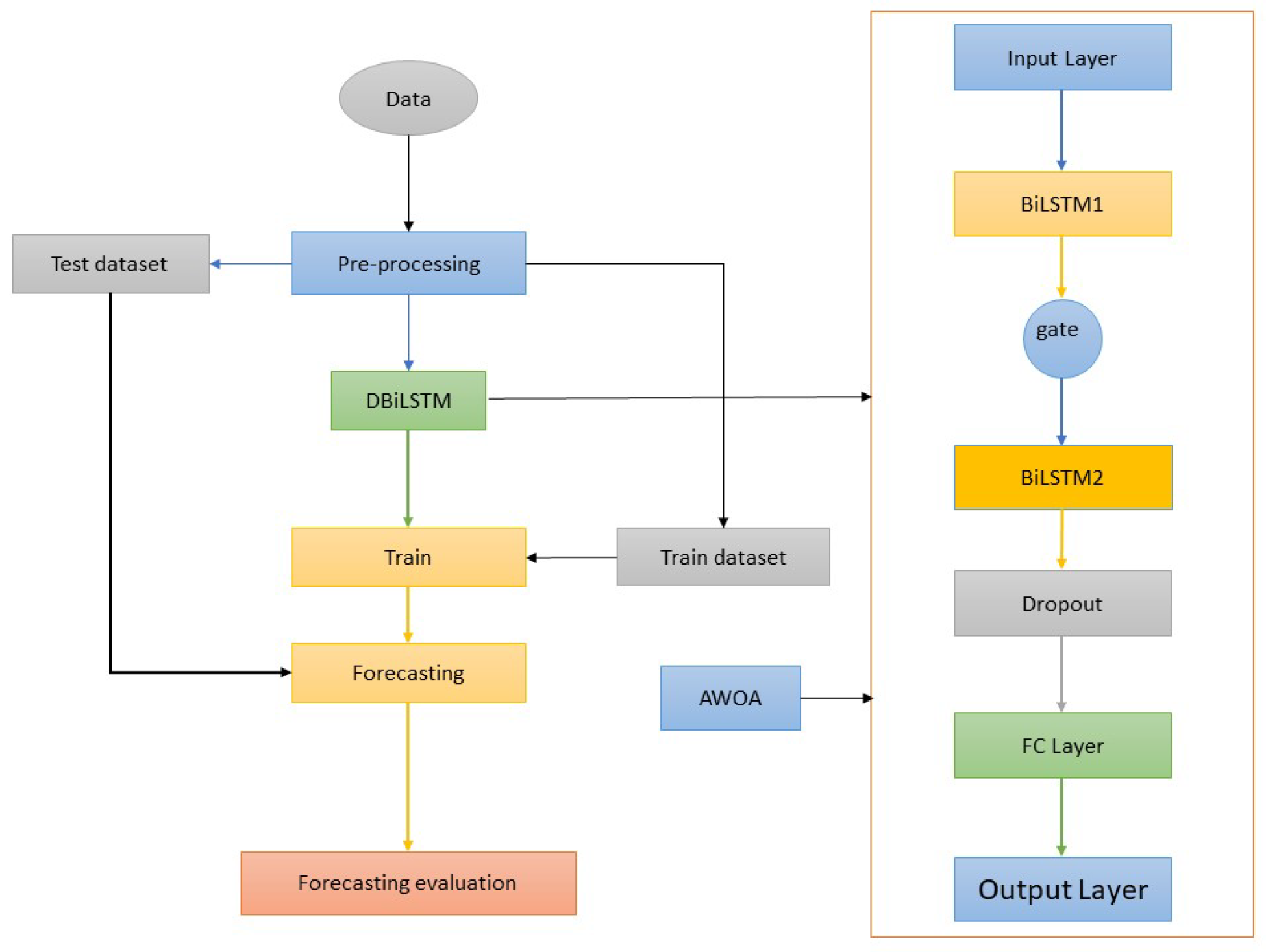
2.4. AWOA-DBiLSTM Neural Network Modeling
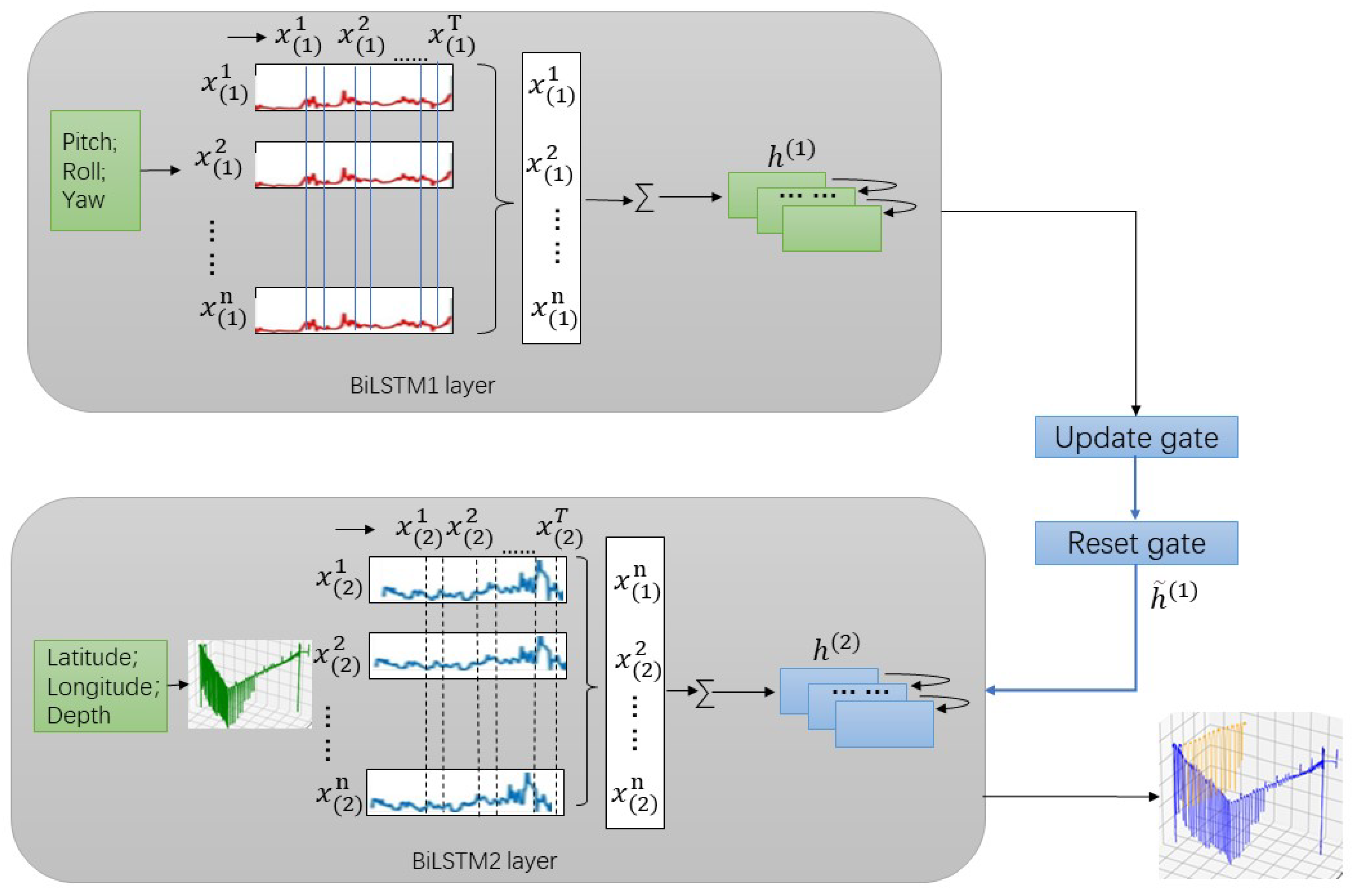
2.4.1. DBiLSTM Neural Network
2.4.2. Adaptive Whale Optimization Algorithm (AWOA)
- Searching behavior:The algorithm is configured to randomly select a search agent when and update the positions of other whales based on the randomly selected whale position, forcing the whale to stray from the prey in order to find more suitable prey. This can strengthen the algorithm’s exploration ability and, thus, allow it to conduct a global search. is the position vector of a randomly selected whale.
- Encircling behavior:The search range of the whale is the global solution space, and it needs to determine the position of the prey first in order to encircle the prey and update its own position by encircling the prey; Equation (17) shows the process of the whale encircling the prey. A and C represent the coefficients, and t is the current number of iterations. The whale’s current position is represented by , while its best position to date is shown by . The following equations can be used to find A and C:Here, t indicates the current iteration number and indicates the maximum number of iterations. and represent random values within the range (0, 1), where the value of a drops linearly from 2 to 0 over the duration of iterations.
- Hunting behavior:When a whale engages in hunting, it swims in a spiral motion towards its prey. This hunting behavior can be represented by the following model:The distance between the whale and its prey is shown above as , where is the position vector with the best current position. The spiral’s form is determined by the maturity parameter, b, which is a constant. b can take any positive real value, and this constant controls the shape and degree of expansion of the logarithmic spiral, with larger values leading to tighter spiral shapes and smaller values leading to looser spiral shapes. The random number l falls between −1 and 1. A whale executing spiral encirclement moves towards its prey in a spiral trajectory while simultaneously constricting the encirclement. By probabilistically selecting the contraction envelopment mechanism for and the spiral model for to update the whale’s position, the mathematical model is represented as follows:When attacking the prey, the mathematical model is set close to the prey to decrease the value of a. The position of A changes with the change in a. During iteration, when the value decreases from 2 to 0, A is a random value within [−a, a]; when A is in [−1, 1], the next position of the whale is any position between the present position and the position of the prey. The algorithm is set so that the whale launches an attack when A < 1.
2.4.3. AWOA-DBiLSTM Model Deployment
3. Experiments and Result Analysis
3.1. Materials and Methods
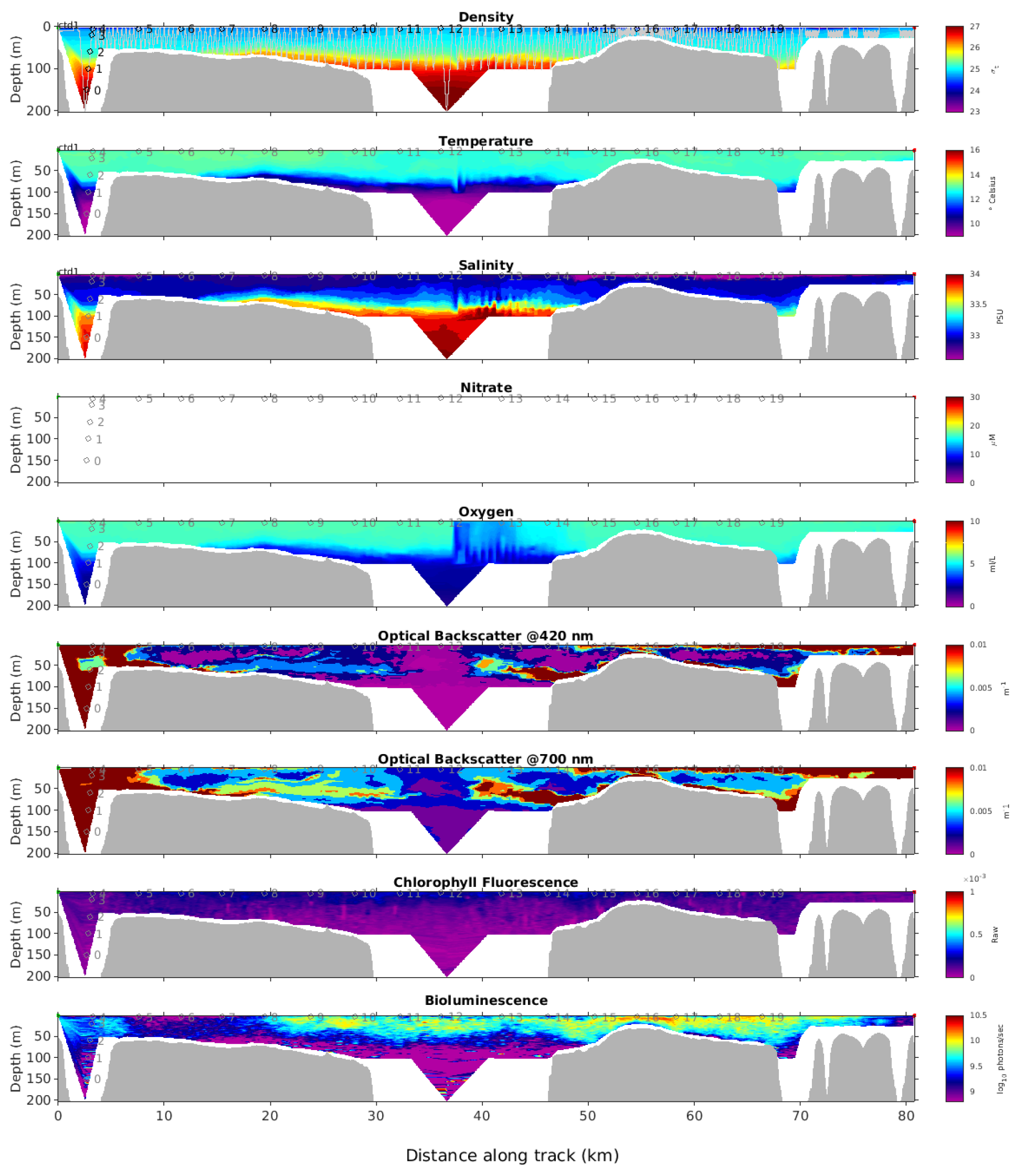
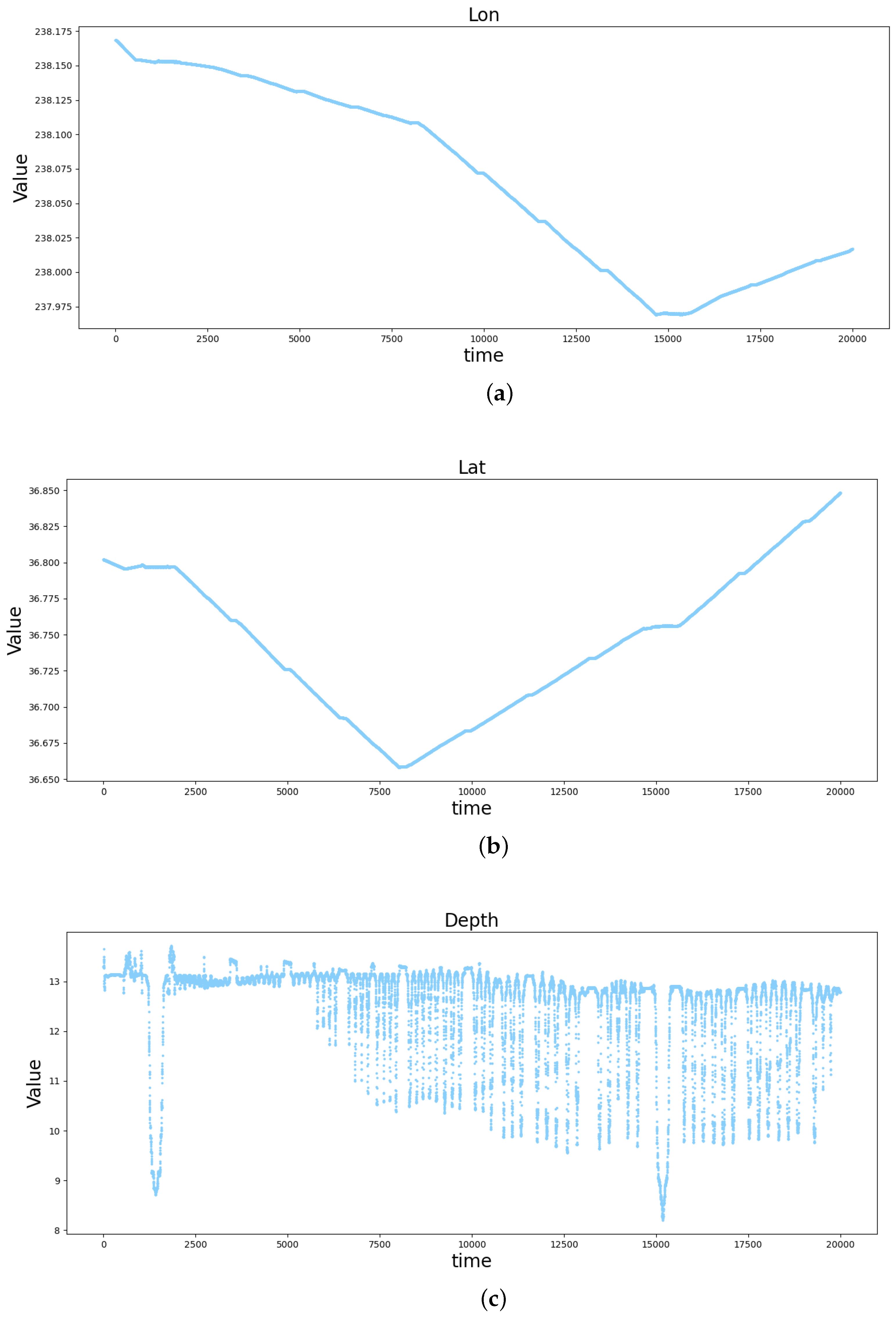
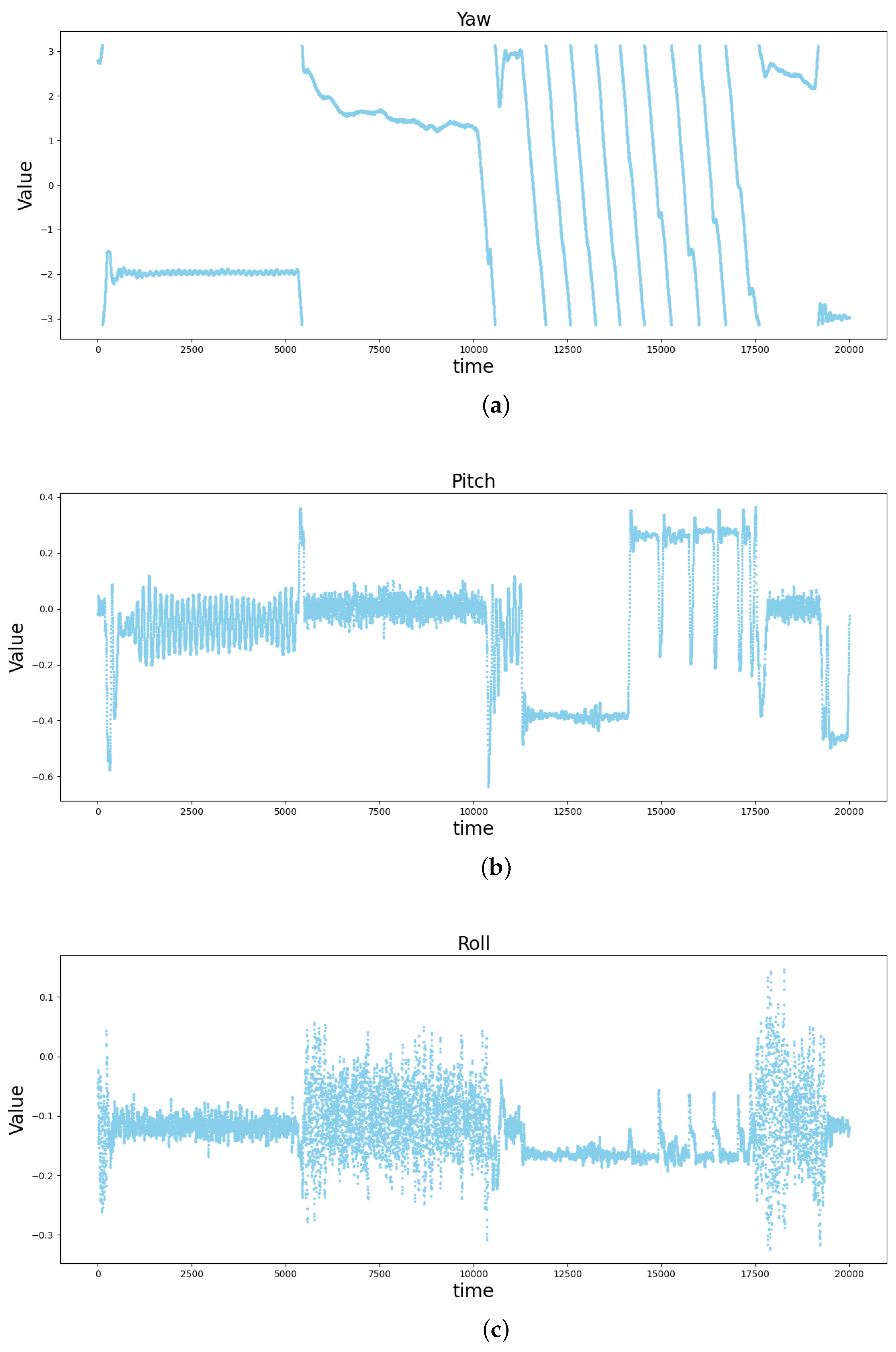
3.1.1. Data Preprocessing
3.1.2. Experimental Test Standard
3.1.3. Experimental Configuration and Experimental Procedures
3.2. Analysis of Experimental Results
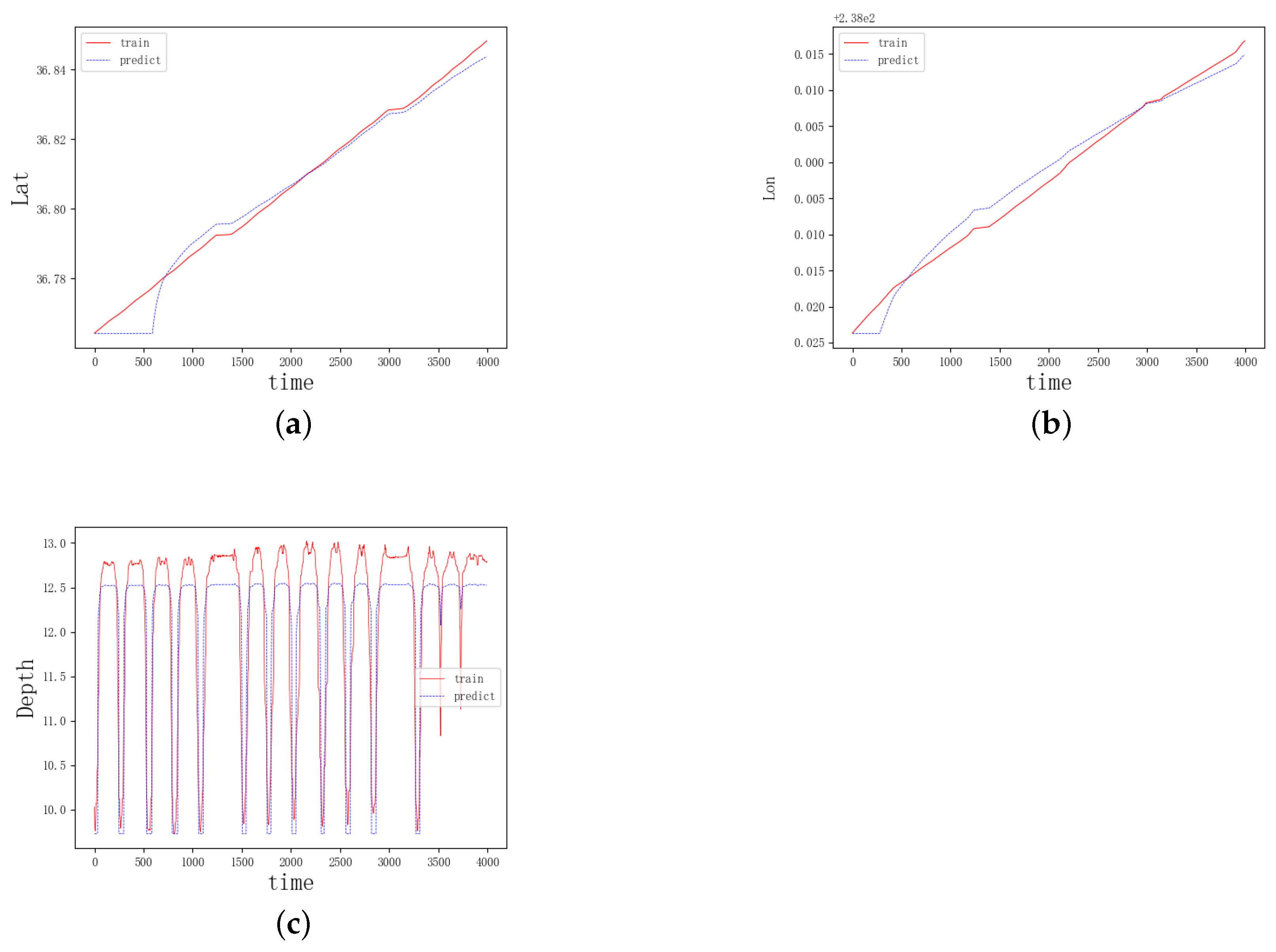
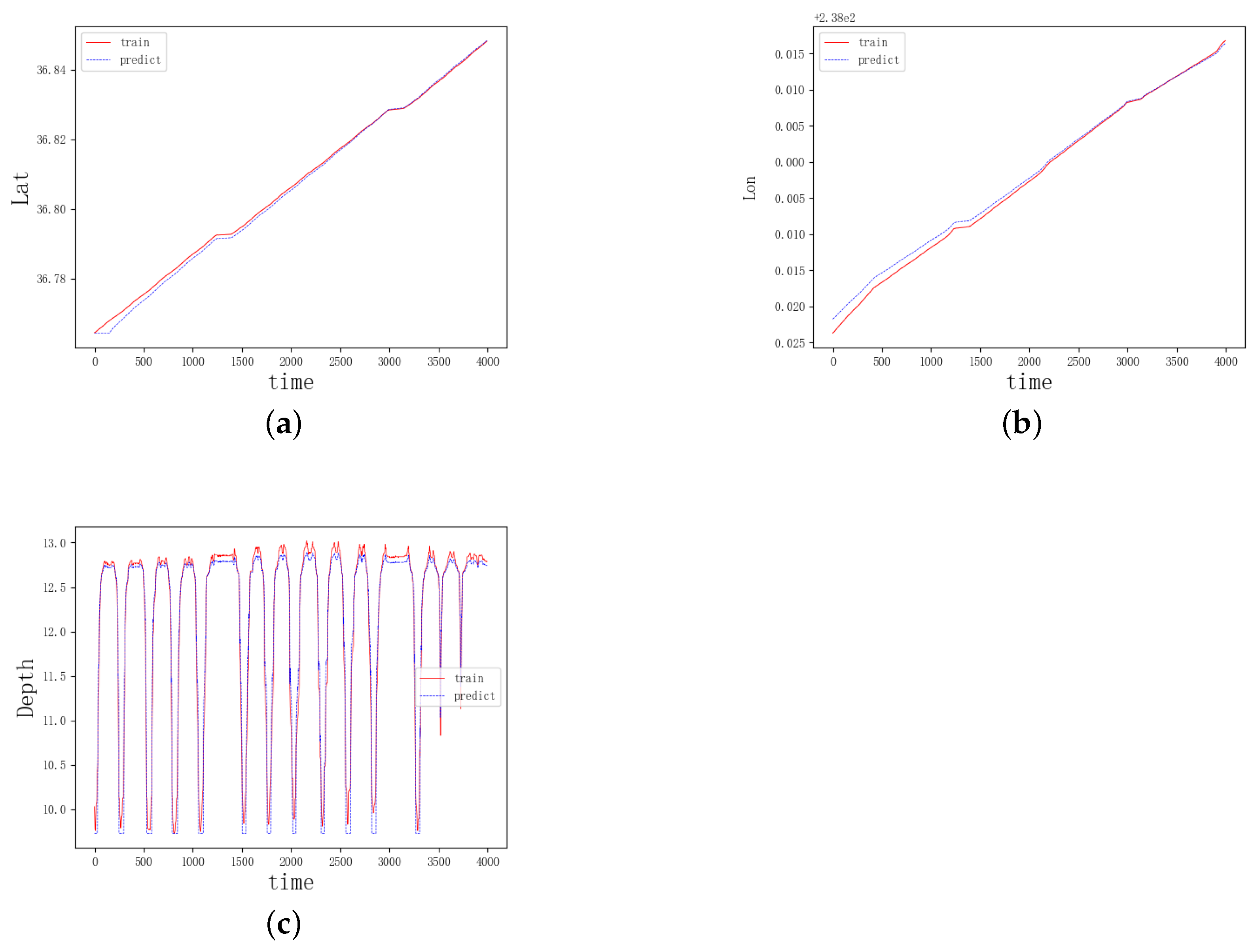
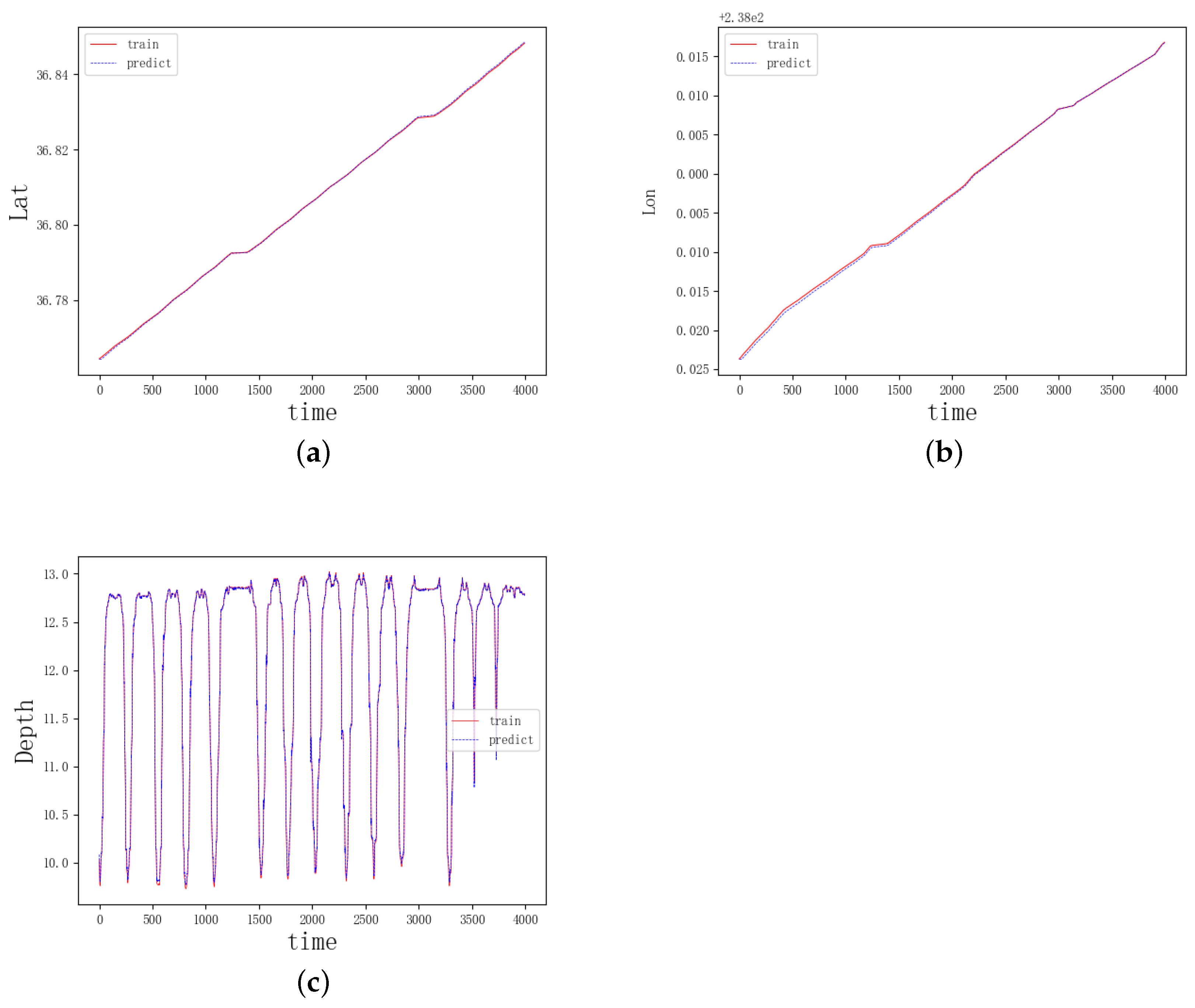
3.2.1. Model Evaluation
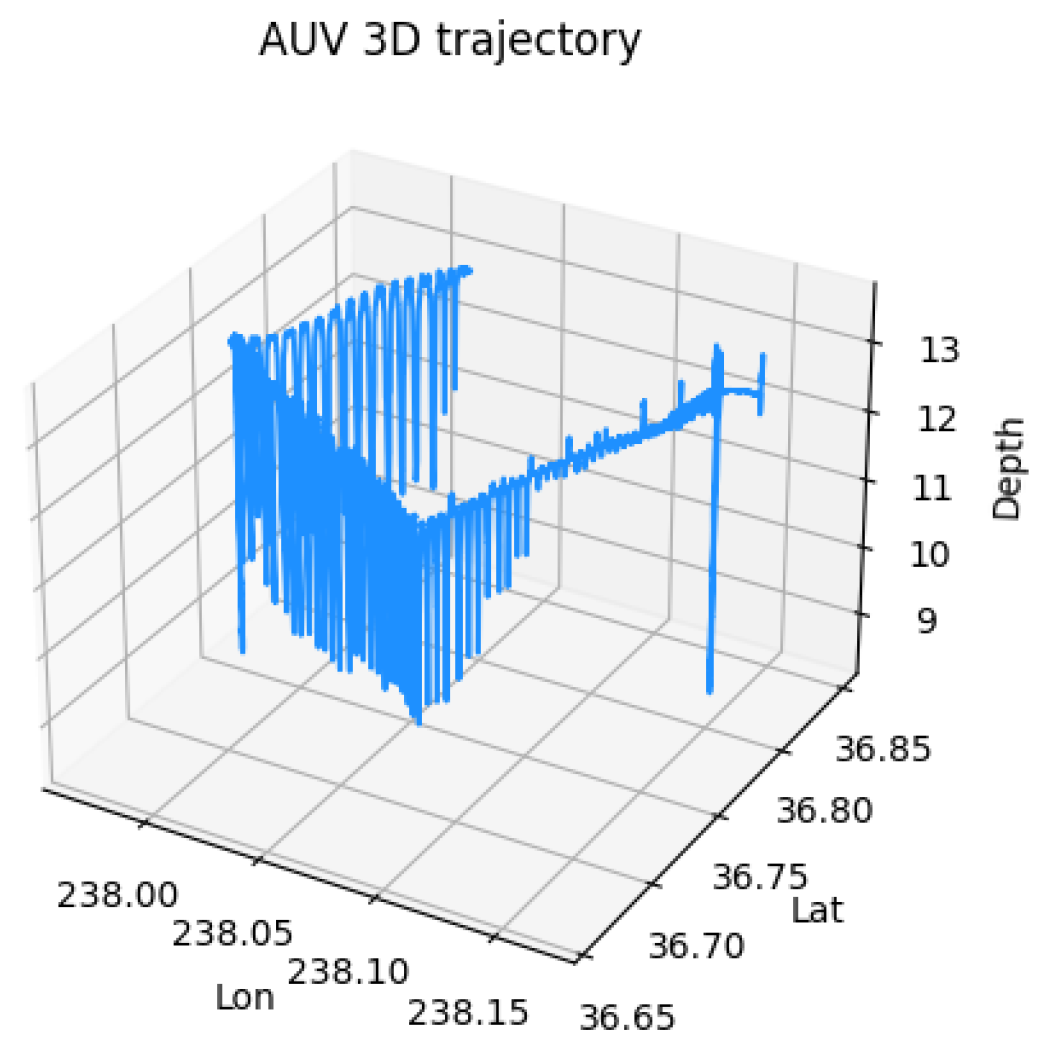
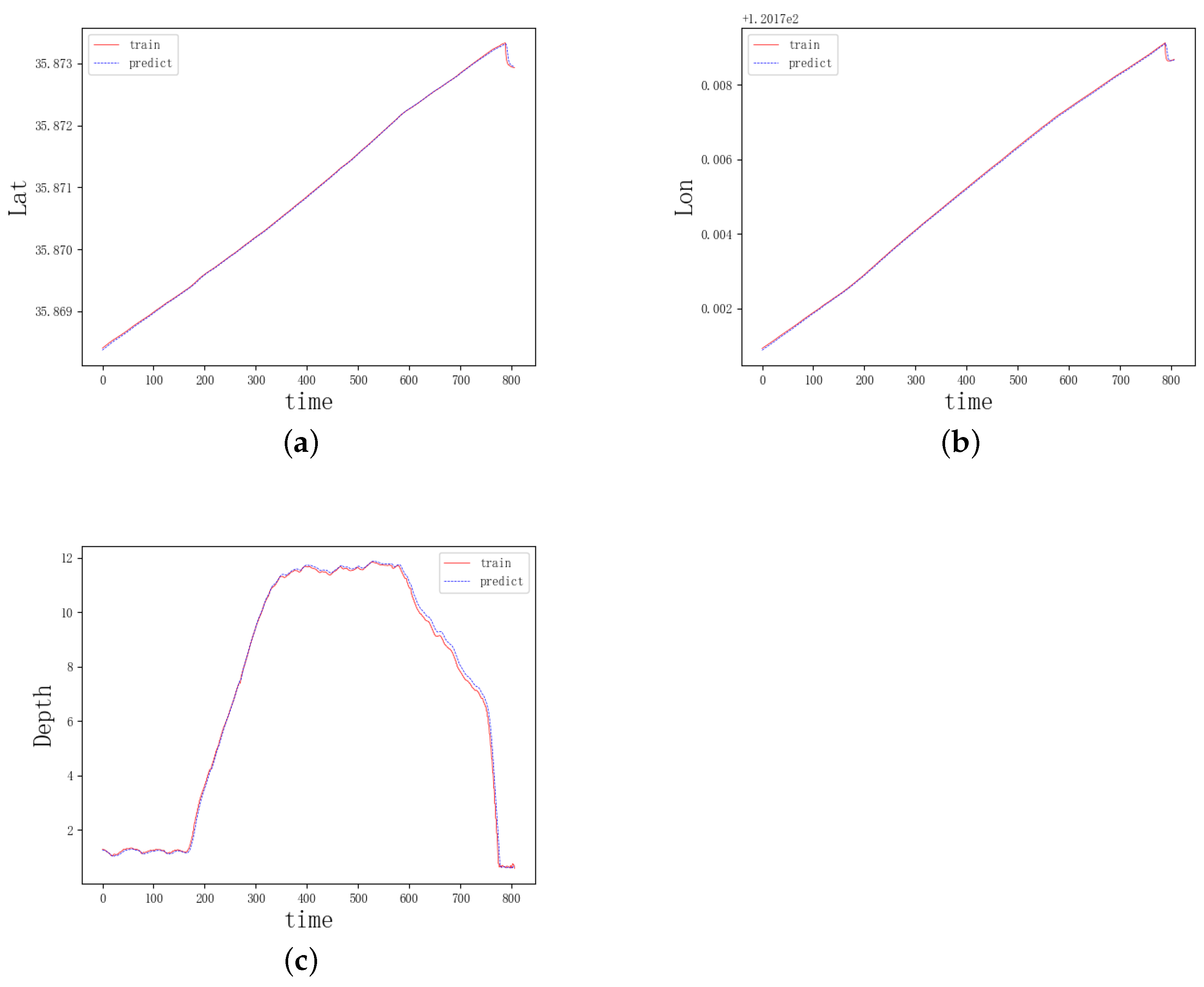
3.2.2. Model Generalizability Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Du, L. Auv trajectory tracking models and control strategies: A review. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- Li, M.; Zhang, R.; Chen, X.; Liu, K. Assessment of underwater navigation safety based on dynamic Bayesian network facing uncertain knowledge and various information. Front. Mar. Sci. 2022, 9, 1069841. [Google Scholar] [CrossRef]
- Cao, Q.; Yu, G.; Qiao, Z. Application and recent progress of inland water monitoring using remote sensing techniques. Environ. Monit. Assess 2023, 195, 125. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Ye, D.; Zhao, J.; He, D. Three-dimensional trajectory tracking for underactuated AUVs with bio-inspired velocity regulation. Int. J. Nav. Archit. Ocean Eng. 2023, 10, 282–293. [Google Scholar] [CrossRef]
- Honaryar, A.; Ghiasi, M. Design of a Bio-inspired Hull Shape for an AUV from Hydrodynamic Stability Point of View through Experiment and Numerical Analysis. Bionic Eng. 2018, 10, 950–959. [Google Scholar] [CrossRef]
- Liang, X.; Dong, Z.; Hou, Y.; Mu, X. Energy-saving optimization for spacing configurations of a pair of self-propelled AUV based on hull form uncertainty design. Ocean Eng. 2020, 218, 108235. [Google Scholar] [CrossRef]
- Xiang, X.; Lapierre, L.; Jouvencel, B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration. Robot. Auton. Syst. 2015, 67, 14–22. [Google Scholar] [CrossRef]
- Ji, D.; Wang, R.; Zhai, Y.; Gu, H. Dynamic modeling of quadrotor AUV using a novel CFD simulation. Ocean Eng. 2021, 237, 109651. [Google Scholar] [CrossRef]
- Cardenas, P.; de Barros, E.A. Estimation of AUV hydrodynamic coefficients using analytical and system identification approaches. IEEE J. Ocean Eng. 2019, 45, 1157–1176. [Google Scholar] [CrossRef]
- Go, G.; Ahn, H.T. Hydrodynamic derivative determination based on CFD and motion simulation for a tow-fish. Appl. Ocean Res. 2019, 82, 191–209. [Google Scholar] [CrossRef]
- Sun, F.J.; Zhu, Z.H.; LaRosa, M. Dynamic modeling of cable towed body using nodal position finite element method. Appl. Ocean Res. 2011, 38, 529–540. [Google Scholar] [CrossRef]
- Tan, K.M.; Anvar, A.; Lu, T.F. Autonomous underwater vehicle (AUV) dynamics modeling and performance evaluation. World Acad. Sci. Eng. Technol. 2012, 6, 2012-10-28. [Google Scholar]
- Lapierre, L.; Soetanto, D. Nonlinear path-following control of an AUV. Ocean Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Chen, C.L.P. Reinforcement learning based model-free optimized trajectory tracking strategy design for an AUV. Ocean Eng. 2022, 469, 289–297. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Pascoal, A.M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents. Int. J. Control 2007, 80, 1092–1108. [Google Scholar] [CrossRef]
- Simha, A.; Kotta, Ü. A geometric approach to position tracking control of a nonholonomic planar rigid body: Case study of an underwater vehicle. Proc. Est. Acad. Sci. 2007, 80, 1092–1108. [Google Scholar] [CrossRef]
- Meng, L.; Lin, Y.; Gu, H.; Su, T.-C. Study on the mechanics characteristics of an underwater towing system for recycling an Autonomous Underwater Vehicle (AUV). Appl. Ocean Res. 2018, 79, 123–133. [Google Scholar] [CrossRef]
- Ferreira, B.M.; Matos, A.C.; Cruz, N.A. Modeling and control of trimares auv. In Proceedings of the 12th International Conference on Autonomous Robot Systems and Competitions, Guimarães, Portugal, 11 April 2012; pp. 57–62. [Google Scholar]
- Tanabe, R.; Matsui, T.; Tanaka, T.S.T. Winter wheat yield prediction using convolutional neural networks and UAV-based multispectral imagery. Field Crop. Res. 2023, 281, 108786. [Google Scholar] [CrossRef]
- Alharbi, A.; Petrunin, I.; Panagiotakopoulos, D. Deep Learning Architecture for UAV Traffic-Density Prediction. Drones 2023, 7, 78. [Google Scholar] [CrossRef]
- Chen, S.; Chen, B.; Shu, P.; Wang, Z.; Chen, C. Real-time unmanned aerial vehicle flight path prediction using a bi-directional long short-term memory network with error compensation. J. Comput. Des. Eng. 2023, 10, 16–35. [Google Scholar] [CrossRef]
- Lee, D.-H.; Liu, J.-L. End-to-end deep learning of lane detection and path prediction for real-time autonomous driving. Signal Image Video Process. 2023, 17, 199–205. [Google Scholar] [CrossRef]
- Qiao, Y.; Yin, J.; Wang, W.; Duarte, F.; Yang, J.; Ratti, C. Survey of deep learning for autonomous surface vehicles in marine environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3678–3701. [Google Scholar] [CrossRef]
- Katariya, V.; Baharani, M.; Morris, N.; Shoghli, O.; Tabkhi, H. Deeptrack: Lightweight deep learning for vehicle trajectory prediction in highways. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18927–18936. [Google Scholar] [CrossRef]
- Li, H.; Jiao, H.; Yang, Z. Ship trajectory prediction based on machine learning and deep learning: A systematic review and methods analysis. Eng. Appl. Artif. Intell. 2023, 126, 107062. [Google Scholar] [CrossRef]
- Tang, H.; Yin, Y.; Shen, H. A model for vessel trajectory prediction based on long short-term memory neural network. J. Mar. Eng. Technol. 2022, 21, 136–145. [Google Scholar] [CrossRef]
- Schimpf, N.; Wang, Z.; Li, S.; Knoblock, E.J.; Li, H.; Apaza, R.D. A Generalized Approach to Aircraft Trajectory Prediction via Supervised Deep Learning. J. Mar. Eng. Technol. 2023, 11, 116183–116195. [Google Scholar] [CrossRef]
- Wu, H.; Liang, Y.; Zhou, B.; Sun, H. A Bi-LSTM and AutoEncoder Based Framework for Multi-step Flight Trajectory Prediction. In Proceedings of the 12th International Conference on Autonomous Robot Systems and Competitions, Niigata, Japan, 21–23 April 2023; pp. 44–50. [Google Scholar]
- Huang, J.; Ding, W. Aircraft Trajectory Prediction Based on Bayesian Optimised Temporal Convolutional Network–Bidirectional Gated Recurrent Unit Hybrid Neural Network. Int. J. Aerosp. Eng. 2022, 2022, 2086904. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Kim, J.; Moon, N. BiLSTM model based on multivariate time series data in multiple field for forecasting trading area. J. Ambient. Intell. Humaniz. Comput. 2019, 2019, 1–10. [Google Scholar]
- Zhang, X.; Zhong, C.; Zhang, J.; Wang, T.; Ng, W.W. Robust recurrent neural networks for time series forecasting. Neurocomputing 2023, 526, 143–157. [Google Scholar] [CrossRef]
- Scholin, C.; Ryan, J.P.; Nahorniak, J.; Nahorniak, J. Robust Recurrent Neural Networks for Time Series Forecasting. In Autonomous Underwater Vehicle Monterey Bay Time Series—AUV Dorado from AUV Dorado in Monterey Bay from, 2003–2099; (C-MORE Project, Prochlorococcus Project); Biological and Chemical Oceanography Data Management Office (BCO-DMO): Woods Hole, MA, USA, 2011. [Google Scholar]


| Models | Metric | Lat | Lon | Depth |
|---|---|---|---|---|
| BiLSTM | MSE | 0.22721 | ||
| RMSE | 0.00286 | 0.00185 | 0.47666 | |
| MAE | 0.00228 | 0.00167 | 0.39565 | |
| DBiLSTM | MSE | 0.04509 | ||
| RMSE | 0.00182 | 0.00081 | 0.21234 | |
| MAE | 0.00151 | 0.00065 | 0.15015 | |
| AWOA-DBiLSTM | MSE | 0.00159 | ||
| RMSE | 0.00026 | 0.00037 | 0.03992 | |
| MAE | 0.00021 | 0.00027 | 0.01974 |
| Metric | Lat | Lon | Depth |
|---|---|---|---|
| MSE | 0.01936 | ||
| RMSE | 0.13915 | ||
| MAE | 0.10997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Zhang, J.; Zhang, T. Adaptive Whale Optimization Algorithm–DBiLSTM for Autonomous Underwater Vehicle (AUV) Trajectory Prediction. Appl. Sci. 2024, 14, 3646. https://doi.org/10.3390/app14093646
Guo S, Zhang J, Zhang T. Adaptive Whale Optimization Algorithm–DBiLSTM for Autonomous Underwater Vehicle (AUV) Trajectory Prediction. Applied Sciences. 2024; 14(9):3646. https://doi.org/10.3390/app14093646
Chicago/Turabian StyleGuo, Shufang, Jing Zhang, and Tianchi Zhang. 2024. "Adaptive Whale Optimization Algorithm–DBiLSTM for Autonomous Underwater Vehicle (AUV) Trajectory Prediction" Applied Sciences 14, no. 9: 3646. https://doi.org/10.3390/app14093646
APA StyleGuo, S., Zhang, J., & Zhang, T. (2024). Adaptive Whale Optimization Algorithm–DBiLSTM for Autonomous Underwater Vehicle (AUV) Trajectory Prediction. Applied Sciences, 14(9), 3646. https://doi.org/10.3390/app14093646






