Numerical Simulation on the Leakage-Induced Collapse of Segmental Tunnels

Abstract

Sudden leakage during tunnel construction poses a great threat to the safety of the tunnel. There are relatively few studies on the mechanism of structural collapse induced by tunnel leakage, so it is difficult to propose effective control measures. To solve this problem, a coupled fluid–solid strata analysis model and a nonlinear FEM tunnel model were established based on model test results to analyze the mechanism of tunnel collapse. The following conclusions were drawn: (1) A DEM-based coupled fluid–solid model combined with a nonlinear FEM tunnel model can effectively simulate the physical process of tunnel collapse. (2) The mechanism of tunnel leakage-induced strata response is the continuous destabilization and reappearance of the soil arching effect, which restricts the erosion of the soil and results in macroscopic soil caves, and finally leads to the impact load of the destabilized soil. (3) The process of the tunnel structure collapse is as follows: firstly, a large deformation of the tunnel structure is caused by the redistribution of external loads generated by the earth arching effect; then, due to the multiple impact loads from the destabilization of the soil, plastic hinges are generated at the tunnel joints, and the tunnel collapses.

1. Introduction

When leakage occurs in underground structures during the construction process, it often leads to structural damage and ground surface settlement, and in severe cases, it may even induce large-scale ground subsidence, resulting in great economic losses [1]. Among the various construction methods, shield tunnels are mostly used to pass through urban areas, which are densely populated with buildings, and in the event of a leakage accident, this may be extremely hazardous [2,3,4,5]. For example, water leakage caused structural damage to the tunnel of Line 1 of the St. Petersburg Metro in Russia [6]. In 2003, the Shanghai Metro Line 4 project was faced with water and sand inrush during construction, which ultimately led to the collapse of the tunnel [7]. In 2018, leakage accidents happened in Foshan Subway Line 2, which led to the collapse of the tunnel [2]. Therefore, it is necessary to carry out research on the mechanism of structural collapse accidents induced by tunnel leakage.

Since accidents of tunnel leakage-induced structural collapse are unpredictable and destructive, it is difficult to obtain accident information using on-site measurements or full-scale model tests [8,9]. Therefore, studies for this type of accident are often carried out using reduced-scale model tests. To investigate the problem of shield tail leakage during construction, leading to structural collapse, Yu, Zhou, Chen, Arulrajah, and Suksun Horpibulsuk [2] conducted an experimental study on the failure mode of the shield tail sealing system based on the Foshan tunnel collapse accident. Shen et al. [10] discussed the sealing performance of the shield tail in that accident under different environmental conditions by means of model tests. To investigate the tunnel collapse accidents caused by leakage in connecting passages, Zheng et al. [11] simulated the occurrence of water and sand inrush by removing a segment at the waist of a model tunnel in a reduced-scale model test and then investigated the change in the external load in the process, and pointed out that the tunnel collapse was due to the redistribution of the external loads.

Due to the limitation of the scale, reduced-scale model tests are mostly used to obtain a qualitative process and observe phenomena during tunnel accidents, which makes it difficult to study the tunnel collapse mechanism, so it is necessary to carry out numerical simulations for the tunnel collapse process. From the physical phenomena of the tunnel collapse process, it can be seen that the response of the strata contains seepage erosion at the microscopic level [12] as well as discontinuous large deformation of the soil at the macroscopic level, while the tunnel structure exhibits large deformation and structural collapse, which is a relatively complex physical process.

Among the simulation methods for soil, it is difficult to reproduce the physical process of large deformation in soil by continuous medium methods (e.g., FEM), so researchers mostly use discontinuous medium analysis methods such as SPH, DEM, and MPM to carry out the simulation. Among them, the DEM method is the most widely used method for the simulation of soil. For the soil seepage erosion problem, the DEM-based fluid–solid coupling model has been chosen by many researchers to carry out micro-mechanism studies, and to discuss the influence of different factors on the erosion process, such as particle shape [13,14], particle size distribution [15,16,17], soil stress [18,19,20], clogging effect [21], and so on. For the problem of discontinuous large deformation induced by seepage erosion of soil, the DEM-based coupled fluid–solid analysis method also has relevant applications. For example, Zhang et al. [22] simulated tunnel leakage in a saturated sandy soil using the CFD-DEM method. The process of seepage erosion development after tunnel leakage was discussed and parameters such as particle size distribution were analyzed. Qian et al. [23] conducted a numerical simulation to analyze the complete process of seepage erosion after tunnel joint leakage using a coupled CFD-DEM method. The influence of burial depth and soil size distribution on seepage erosion was investigated. Tang et al. [24] investigated the ground subsidence due to pipeline leakage. In that model, the strata were simulated by DEM and the fluids were investigated by the Darcy flow formulas. From the above discussion, it can be seen that the DEM-based coupled fluid–solid analysis method is suitable for solving the seepage erosion problem and the subsequent soil deformation problem caused by it. Therefore, it can be applied to the simulation of the stratum in this research.

In the process of structural collapse induced by leakage in shield tunnels, the deformation of tunnels is relatively small compared to the deformation of the strata in terms of scale. The main role of the tunnel is to provide an outlet for the soil, while the deformation of the structure itself has a small effect on the seepage erosion of the soil due to the stiffness. Therefore, when simulating the stratum response during a tunnel collapse, the details of the tunnel structure can be simplified without considering the effect of its deformation. For the tunnel, the response of the shield tunnel can be accurately analyzed by building an FEM tunnel model and applying the loads extracted from the strata model to analyze the tunnel collapse mechanism. In conclusion, decoupling the large deformation of strata and tunnel collapse is a more feasible simulation idea under the consideration of the strata–tunnel interaction.

Based on the above discussion, a coupled fluid–solid strata model and a nonlinear FEM tunnel model were established for simulating the tunnel collapse process based on model test results [25]. After experimental validation, the strata response during tunnel collapse and the process of tunnel collapse were analyzed.

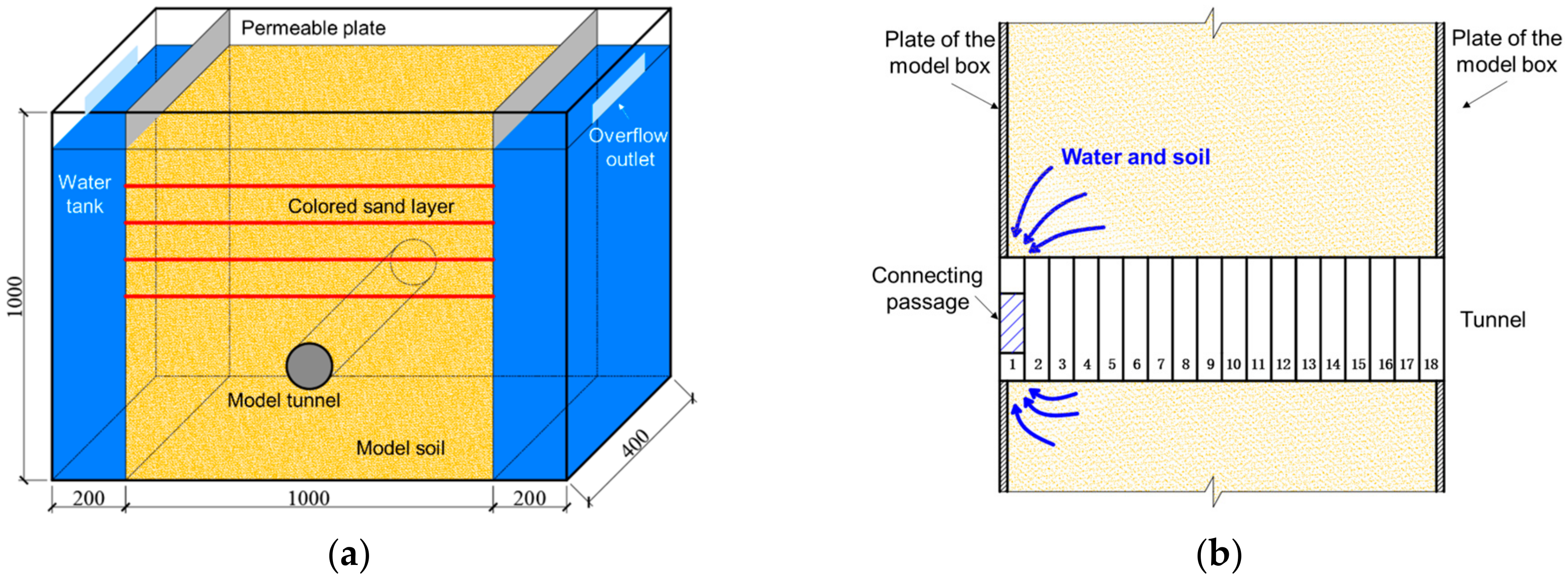
2. Model Tests

2.1. Test Design

The accident at Shanghai Metro Line 4 was selected as the background for the reduced-scale model tests [7]. At 6:00 a.m. on 1 July 2003, when the excavation of the connecting passage was still 0.8 m away from penetration, the freezing system broke down, resulting in the melting of the frozen soil, and a large amount of soil and water rushed from the excavated surface of the connecting passage through the openings of the connecting passage and into the tunnel. This eventually caused the collapse of part of the tunnel and ground subsidence in the surrounding area, resulting in severe tilting of surrounding buildings.

The tests were carried out in a model box at a reduced scale with a geometrical similarity ratio of 50. The model box is shown in Figure 1a, and has dimensions of 1400 mm × 400 mm × 1000 mm. The model box consists of a soil box in the center and water tanks on both sides. The colored sand layers were used to visualize the displacement of the strata. The tunnel is buried in the soil box, which is separated from the water tanks on both sides by a permeable plate to provide water sources for the tunnel leakage and to control the water level at the same time. To ensure constant water levels throughout the tests, overflow outlets were set on both sides of the water tanks. Throughout the test, continuous water was refilled into the water tanks. The presence of overflow outlets ensured that the water level remained stable, as any excess water would flow out once it surpassed the height of these outlets.

When leakage accidents occur at the location of the connecting passage, a longitudinal symmetry condition is assumed to be satisfied along the direction of the tunnel, so the tunnel and the soil can be taken as a semi-structure to carry out the tests. Before the tests, an opening (20 mm × 20 mm) was made in the tunnel-connecting passage and sealed with a rubber plug. Then, the plug was removed at the beginning of the tests to trigger the water and sand inrush, as shown in Figure 1b, which illustrates a side view of the test setup. A total of 18-ring model tunnels were employed, with the leakage point located at the first ring.

In the model tests, different proportions of sand and clay were mixed to obtain model soil with obvious differences in key parameters, from which the soil that had the parameters close to the background case was selected for the tests. The raw material of sand is quartz sand. The clay material was selected from natural clay. Percentages of 0%, 5%, 10%, and 20% content of clay were added into sand. The soil parameters were then compared with the key parameters in the background case in

Table 1. Physical and mechanical parameters of soils.

Soil Type		Content of Clay (%)	Cohesion (kPa)	Friction Angle (°)	Permeability Coefficient (m/s)
Model soil	A	0	0.34	40.17	2.21 × 10−3
	B	5	1.81	35.56	1.33 × 10−4
	C	10	2.88	35.87	8.04 × 10−5
	D	20	4.28	34.16	6.45 × 10−5
Background case		/	3.0	32.0	5.34 × 10−4

. It can be seen that, when the clay content is 5%, the parameters of the soil are the closest to that of the background case. Therefore, the soil mixture with 5% clay addition was chosen as the model soil for the tests.

Gypsum was used as the material for the reduced-scale model tunnel. The dimensions of the model tunnel meet the geometric similarity ratio of 50 when compared with the prototype. Also, the compressive strength of gypsum material in the model tunnel is 1.1 MPa, which meets the similarity ratio for compressive strength, which is 55 MPa in the actual tunnel. The model tunnel is shown in Figure 2.

2.2. Test Results

It was observed in the tests that the process of soil erosion had visible stages, which is shown in Figure 3 [25]. In the figure, the green arrows indicate the direction of soil displacement. The internal phenomena in the tunnel during the process are shown in Figure 4. Based on the different physical phenomena, the process of soil development and tunnel response after tunnel leakage can be divided into four stages as follows:

(1)

Stage 1: After the start of water and soil rushing from the waist to the interior of the tunnel, a visible soil cave appeared on the exterior of the tunnel, and the displacement of the soil was mainly concentrated in the interior of the soil cave. The initial soil cave was temporarily stabilized, as shown in Figure 3a. At the same time, the top of the tunnel slowly deformed inward, as shown in Figure 4a.

(2)

Stage 2: The initial soil cave destabilized, soil erosion developed again, and the erosion area rapidly developed upward. Subsequently, a secondary soil cave formed and temporarily stabilized again, as shown in Figure 3b. For the tunnel, it was observed that the top of the tunnel showed large deformations and dislocation, as shown in Figure 4b.

(3)

Stage 3: After a brief period of stabilization, the secondary soil cave destabilized again and the erosion area developed upward, followed by the formation of a third soil cave. The third soil cave again entered the temporary stabilization state, as shown in Figure 3c. At the end of this stage, the top of the tunnel was impacted by falling soil, and several segments collapsed, as shown in Figure 4c.

(4)

Stage 4: The third soil cave destabilized, the ground subsided, and the destabilized soil fell on the top and shoulder of the tunnel, as shown in Figure 3d. Several rings of the tunnel collapsed, as shown in Figure 4d.

3. Numerical Model

The stratum was analyzed by a coupled fluid–solid model, while the tunnel was simulated by a nonlinear FEA model. The interaction between the strata and the tunnel was taken into consideration by extracting the loads in the strata model and applying them to the structure. In addition, considering the complexity and feasibility of the computational model, a two-dimensional model was used for analysis.

3.1. Soil Model

3.1.1. Description of the Coupled Fluid–Solid Model

In this numerical model, the finite difference method (FDM) and the discrete element method (DEM) were integrated, where the DEM simulates the behavior of the soil particles while FDM simulates the fluid behavior. The soil is represented by rigid particles in DEM simulation, with their movements being independent of each other. The transmission of force between particles occurs through contacts. Newton’s second law governs the relationship between force (or moment) and particle motion, where motion results from contact forces and other physical forces acting on the particles. Contact forces between particles adhere to the force-displacement law, which updates contact forces based on relative motion at contact points. Specifically, the interparticle forces can be determined according to the distance between particles and the contact law. Next, the resultant force on each DEM particle will be determined. Then, the movement of each particle will be calculated using Newton’s second law, and the position of the particle will be updated after each calculation step. This approach ensures the accurate simulation of mechanical behaviors among particles, supported by previous studies demonstrating the effectiveness of DEM models in capturing soil deformation behavior [26,27]

The forces exerted on the soil particles within the flow field follow Equation (1):

$$\frac{\partial \overrightarrow{u}}{\partial t}=\frac{{\overrightarrow{f}}_{mech}+{\overrightarrow{f}}_{fluid}}{m}+\overrightarrow{\mathrm{g}}$$

(1)

where $\overrightarrow{u}$ is the particle velocity, $m$ is the particle mass, ${\overrightarrow{f}}_{fluid}$ is the hydraulic force applied on the particle, ${\overrightarrow{f}}_{mech}$ is the sum of the external forces acting on the particle (externally exerted force and contact force between the particles), and $\overrightarrow{\mathrm{g}}$ is the acceleration of gravity.

The force ${\overrightarrow{f}}_{fluid}$ applied on the particles is mainly composed of the drag force generated by the fluid [28], which can be calculated according to the following equation:

$${\overrightarrow{f}}_{drag}=V_i{\gamma }_{w}i$$

(2)

where $V_i$ is the particle volume, ${\gamma }_w$ is the unit weight of water, and $i$ is the hydraulic gradient.

To achieve bidirectional coupling between the fluid and soil, the soil’s influence on the flow field was accounted for by adjusting the permeability coefficient. In granular materials, the permeability coefficient can be determined by converting the porosity. The Kozeny–Carman equation was adopted in the model [29]:

$$k=\frac{1}{C_s{S}_s^2{T}^2}\frac{{\gamma }_w}{\mu }\frac{e^3}{1+e}$$

(3)

Here, $C_s$ is the shape factor of the granular material, S_s is the surface area per unit volume of the soil, $T$ is the tortuosity factor, $\mu$ is the dynamic viscosity, and $e$ is the void ratio.

The DEM and FDM joint calculation process can be described as follows. First, the strata model and fluid model are established, respectively, in DEM and FDM. Then, the fluid mesh and node information are transferred to the DEM program. Subsequently, the FDM software computes the flow field, transmitting the resulting pressure distribution and velocity to the DEM software. Next, the DEM software reads the fluid field, applies hydraulic forces to particles, and conducts DEM calculations. After completing the calculations, the DEM software reads the porosity of each fluid unit and converts it into an updated permeability coefficient. This coefficient is then returned to the FDM software to update the flow field parameters. In this coupling process, the coupling time was set to 0.01 s, and it was assumed that the fluid field remained unchanged during this brief period [24]. The condition of termination in this model is the number of calculation steps [24,30]. These steps are iterated until the calculation steps reach the required number. The DEM analysis was performed with the commercial DEM software PFC 5.0 [31]. The FDM calculation was performed with the commercial FDM software FLAC 5.01 [32].

3.1.2. Numerical Model Based on the Tests

Observations from the tests revealed that the area of soil erosion resulting from tunnel leakage was smaller than the dimensions of the model test box (1000 mm × 1000 mm). Consequently, to optimize computational resources, the size of the simulated soil model was determined according to the region of strata displacement observed in the tests. The dimensions of the model were set at 800 mm in width and 660 mm in height. With these considerations, both the DEM model and the FDM model were established.

The FDM model elements were uniformly divided, with each element side measuring 20 mm. Additionally, adjustments were made to the surrounding area of the tunnel based on its shape. In total, 1320 FDM elements were generated. The water pressure boundary conditions were established in accordance with the model tests: the pressure at the strata top and at the tunnel opening were set to 0, while the pressure at the sides and bottom was determined based on the actual water pressure distribution. The pressure distribution is shown in Figure 5a.

In the DEM soil model, the particle size was enlarged by a factor of 2.5 compared to actual soil particles to enhance computational efficiency. Deisman et al. [33] proposed the following equation to describe the particle size effect:

$$RES=\left(\frac{L}{R_{min}}\right)\left(\frac{1}{1+\frac{R_{max}}{R_{min}}}\right)$$

(4)

where $L$ is the length of the shortest side of the model, and $R_{max}$ and $R_{min}$ are the maximum and minimum particle diameters, respectively. When RES ≥ 10, the size and number of particles in the model have only a small influence on the mechanical properties of the soil. Considering the model size and computational ability, the soil particles in the model were enlarged by a factor of 2.5. The shortest side of the model was taken as the diameter of the shield tunnel R = 124 mm, the maximum particle diameter of the enlarged model particles was 2.5 mm, and the minimum particle diameter was 0.25 mm. Then, the RES in this model is 45, which meets the above requirements and the enlarged particles should not influence the mechanical behavior of the soil. A rigid circular wall was employed to simulate the tunnel. Consistent with the model tests, water and sand inrush were triggered by removing a section of the wall at the corresponding position. Due to the enlarged particle size, the tunnel opening was also enlarged. While the tunnel opening size in the model tests was 2 cm, it was enlarged to 5 cm in the numerical simulation. The strata model is shown in Figure 5b.

Within the DEM model, the contact among soil particles was defined by the linear contact bond model. Once the particle-to-particle bond reaches its strength limit, it transitions to the linear contact model. Calibration of parameters was conducted through shear tests, and the specific parameters are outlined in

Table 2. Parameters in the discrete element model.

Parameters	Values
Particle density (kg/m3)	2700
Damping	0.7
Friction coefficient of particles	0.8
Tensile strength of particle contacts (Pa)	36
Shear strength of particle contacts (Pa)	36
Normal stiffness of particle contacts (N/m)	$1.0\times {10}^8$
Shear stiffness of particle contacts (N/m)	$5.0\times {10}^7$
Porosity of soils	0.4
Normal stiffness of contacts between wall and particles (N/m)	$1.0\times {10}^8$
Shear stiffness of contacts between wall and particles (N/m)	$1.0\times {10}^8$
Friction coefficient between wall and particles	0.6

.

To reflect the response of the tunnel when subjected to the load redistribution induced by the external strata change, the loads at critical moments calculated by the strata model were selected and applied to the tunnel. The contact force of the soil particles to the tunnel was monitored during the strata calculations. Considering the tunnel size and external particle size, the monitoring range of each monitoring point was taken as the average contact force on the tunnel wall over circle segments with a 30° center angle. In this case, the wall size of the monitoring point range (31.4 mm) was 12.6 times the maximum particle size (2.5 mm), which could reduce the error caused by the particle size effect. Based on this idea, a total of 12 measurement points were arranged outside the tunnel in the strata model, as shown in Figure 6.

3.2. Numerical Tunnel Model

The tunnel model was analyzed using a single-ring tunnel. Since the bearing capacity of the tunnel is greatly reduced due to the opening on the waist, it is unable to reflect the process in which leakage occurs and eventually induces the collapse of the whole structure. In the coupled fluid–solid strata model, although the loads were extracted from the tunnel with an opening, the loads can also be assumed to be identical to the loads of the adjacent intact tunnel. The reason is that the dimensions of the destabilized falling soil (maximum of about 600 mm in the model tests) were much larger than the width of the model tunnel (24 mm), so the impact loads applied to the opened tunnel ring and the adjacent ring are close to each other, which has been proven in the model tests [25]. In summary, the tunnel was analyzed using a complete single-ring model without opening. The earth pressure was applied to the tunnel, thus reflecting the mechanism of structural collapse without weakening the lining bearing capacity.

The geometric nonlinearity of the tunnel structure needs to be considered in the analysis because the tunnel is subjected to large deformations and eventually collapses. In addition, the material nonlinearity problem also needs to be considered in the analysis because the material of some sections and joints enters the elastic–plastic state when the structure collapses. Therefore, a nonlinear analysis model of the shield tunnel was established.

The tunnel model was constructed using LS-DYNA 971 [34], a versatile finite element software package known for its proficiency in simulating dynamic phenomena. Hughes–Liu beam elements [34] with cross-section integration were employed to represent segment behavior. The segment section was discretized into eight layers, comprising six layers of concrete and two layers of reinforcing bars. The thickness and positioning of the steel bar layers were determined based on the actual segment’s steel bar positions and areas. Longitudinal joints were modeled using a combination of nonlinear springs and rigid beams. The joint surfaces were treated as rigid beams, with lengths matching the segment thickness. Multiple compressive springs and one tensile spring were utilized between the two rigid beams to simulate compression between the segment concrete and bolt tensile behavior. Liu et al. [35] verified the validity of the model by full-scale model tests, so the verification of the tunnel model will not be repeated here. The dimensions and joint angles are consistent with the model tests, as shown in Figure 7.

In the strata analysis model, the tunnel was simulated with a rigid wall at a fixed position. Therefore, the external loads of the tunnel captured in the simulation were from the active loads generated by the soil, and there were no passive soil resistance forces due to the deformation or settlement of the tunnel. In the simulation of the tunnel structure, to consider the passive resistance of the strata, a series of soil springs, which are only subjected to compression, were established around the tunnel.

It has to be noted that dynamic effects have been taken into consideration during both the DEM extraction of forces acting on tunnel structures and the FEA simulation of tunnel structures. During the DEM simulation, the extracted impact load act on the tunnel structure was influenced by dynamic effects. This means that the forces extracted through DEM were not solely static but also accounted for in dynamic interactions. Subsequently, in the FEM simulation of tunnel structures, dynamic effects were also accounted for. This ensured that the simulation accurately represented the dynamic behavior and response of the tunnel structure under various loading conditions, including those derived from the DEM analysis.

3.3. Model Validation

The strata response obtained from the numerical simulation is shown in Figure 8. The comparison of Figure 3 and Figure 8 shows that the numerical simulation reproduces the key phenomena observed in the model tests. After the tunnel leakage, seepage erosion occurred to the surrounding soil, and unstable soil caves appeared several times. The strata erosion continuously developed to the strata surface in the form of soil cave formation—soil cave destabilization—and soil cave reappearance, and the strata surface remained stable in the process of erosion development. The phenomena comparison proves that the coupled fluid–solid model used in the analysis can effectively reproduce the model test process, which is suitable for subsequent in-depth analysis.

4. Tunnel Collapse Process Analysis

4.1. Strata Response

4.1.1. Seepage Erosion

To analyze the characteristics of seepage erosion in the external strata, the distribution of soil porosity after the tunnel leakage was analyzed, and the distribution of porosity in the external strata was plotted in Figure 9. From the figure, with the process of seepage erosion, the porosity changes correspondingly.

(1)

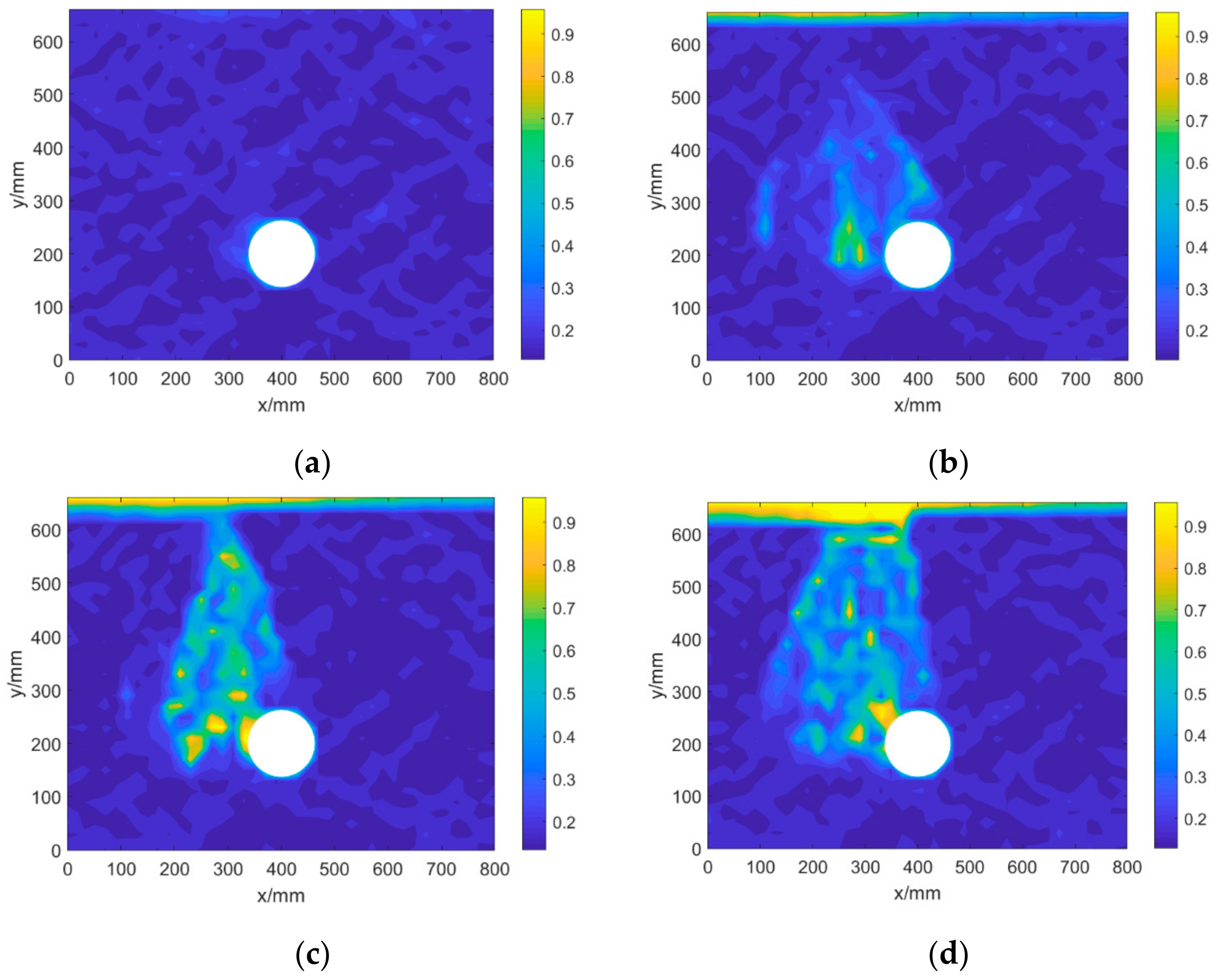
After the tunnel leakage started, the porosity near the leakage point increased rapidly, which led to an increase in the permeability coefficient near the leakage point, and the seepage rate increased, further accelerating the erosion process, as shown in Figure 9a.

(2)

After the formation of the soil caves, the porosity inside the cave increased rapidly due to the loss of particles, as shown in Figure 9b,c.

(3)

When the strata surface subsidence occurred, a region of sharp increase in porosity was formed from the surface to the leakage point, as shown in Figure 9d.

The analysis revealed that the change in porosity after tunnel leakage was confined to the interior of the soil cave, and the porosity of the strata outside the soil cave was almost unchanged. This suggests that the soil cave hinders the loss of particles, resulting in seepage erosion being confined to the interior of the soil cave.

4.1.2. Soil Arching Effect

To analyze the change in the soil arching effect, the change in contact force chain between soil particles during tunnel leakage was analyzed, as shown in Figure 10, where the width of the contact force chain indicates the magnitude of the contact force. It can be seen from the figure that, along with the development of seepage erosion, the distribution of soil contact force chain shows obvious stage changes:

(1)

Before the start of leakage, the distribution of the contact force showed a trend of large contact force at the bottom and smaller contact force as it went upward, as shown in Figure 10a. The reason is that the soil stress at the bottom is larger due to gravity.

(2)

After the leakage, a visible soil arch first appeared near the leakage point, and the soil arch feet fell at the top as well as the bottom of the tunnel, which generated an initial soil cave in the external strata, as shown in Figure 10b.

(3)

The initial soil arch was destabilized with the development of seepage erosion, and then a secondary soil arch was formed. The width and height of the secondary soil arch increased relative to the initial soil arch, and the position of the soil arch’s feet shifted toward the shoulder and bottom of the tunnel, as shown in Figure 10. At the same time, there was almost no contact force chain inside the soil arch, indicating that the particles inside the soil arch were in a state of dispersion.

(4)

After the destabilization of the secondary soil arch, the third soil arch appeared at a higher position, with no visible change in the width of the soil arch, the foot of the arch stopped moving, but the height of the soil arch increased, as shown in Figure 10d. At this time, a contact force chain was observed inside the soil arch, indicating that the soil destabilized and fell in the form of a whole piece, rather than scattered in the form of loose particles.

(5)

When the third soil arch reached the critical height, the soil arch destabilized completely. At this time, there was no complete contact force chain from the strata surface to the tunnel leakage point, as shown in Figure 10e.

In summary, the microscopic mechanism that induces the development of strata erosion after tunnel leakage is the continuous destabilization and reappearance of the soil arching effect formed by soil particles. In the process of soil arch development, the height and width of the soil arch increase continuously, which leads to a decrease in its stability and eventually triggers surface subsidence.

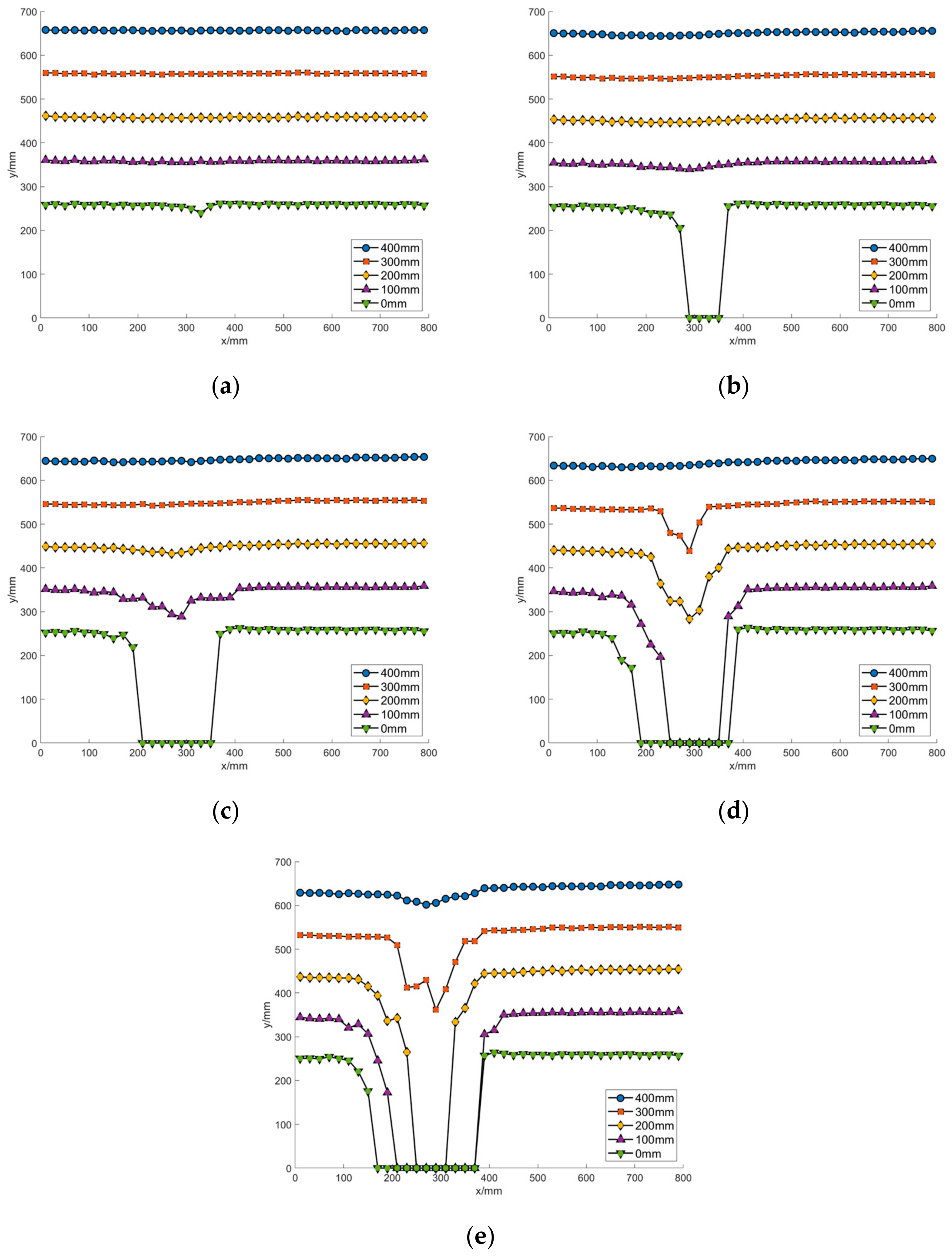
4.1.3. Strata Displacement

To analyze the displacement of the strata after the leakage at the tunnel waist, four layers of monitoring points were arranged every 100 mm above the tunnel at a burial depth of 0 mm (top of the tunnel) to 400 mm (strata surface). The distribution of the displacement in different stages of seepage erosion is shown in Figure 11, in which the monitoring points falling to height 0 indicate that the points rushed into the tunnel. The following can be seen from the figure:

(1)

After the leakage, the layer at a height of 0 mm (i.e., the top of the tunnel) started to subside. The layers at other heights above the tunnel remained stable, as shown in Figure 11a.

(2)

After the formation of the initial soil cave, the particles at 0 mm above the tunnel were lost, and the stratum at the height of 100 mm subsided slightly, while the stratum above 100 mm remained stable, as shown in Figure 11b.

(3)

After the formation of the secondary soil cave, the subsidence range of the stratum expanded. The stratum at the height of 300 mm started to subside, and the stratum at the height of 400 mm remained stable, as shown in Figure 11c.

(4)

After the formation of the third soil cave, the strata above the tunnel at the height of 0 mm~300 mm all settled downward visibly, but there was only a slight settlement on the strata surface, as shown in Figure 11d.

(5)

After the destabilization of the third soil arch, the strata at a height of 400 mm, i.e., the strata surface, started to subside downwards, as shown in Figure 11e.

It can be seen from the displacement patterns of the strata at different depths above the tunnel that, although soil loss occurred after the tunnel leakage, the strata above the soil cave remained temporarily stable. When the soil cave loses stability, the upper soil will fall suddenly and generate impact loads to the tunnel.

4.2. Structural Response

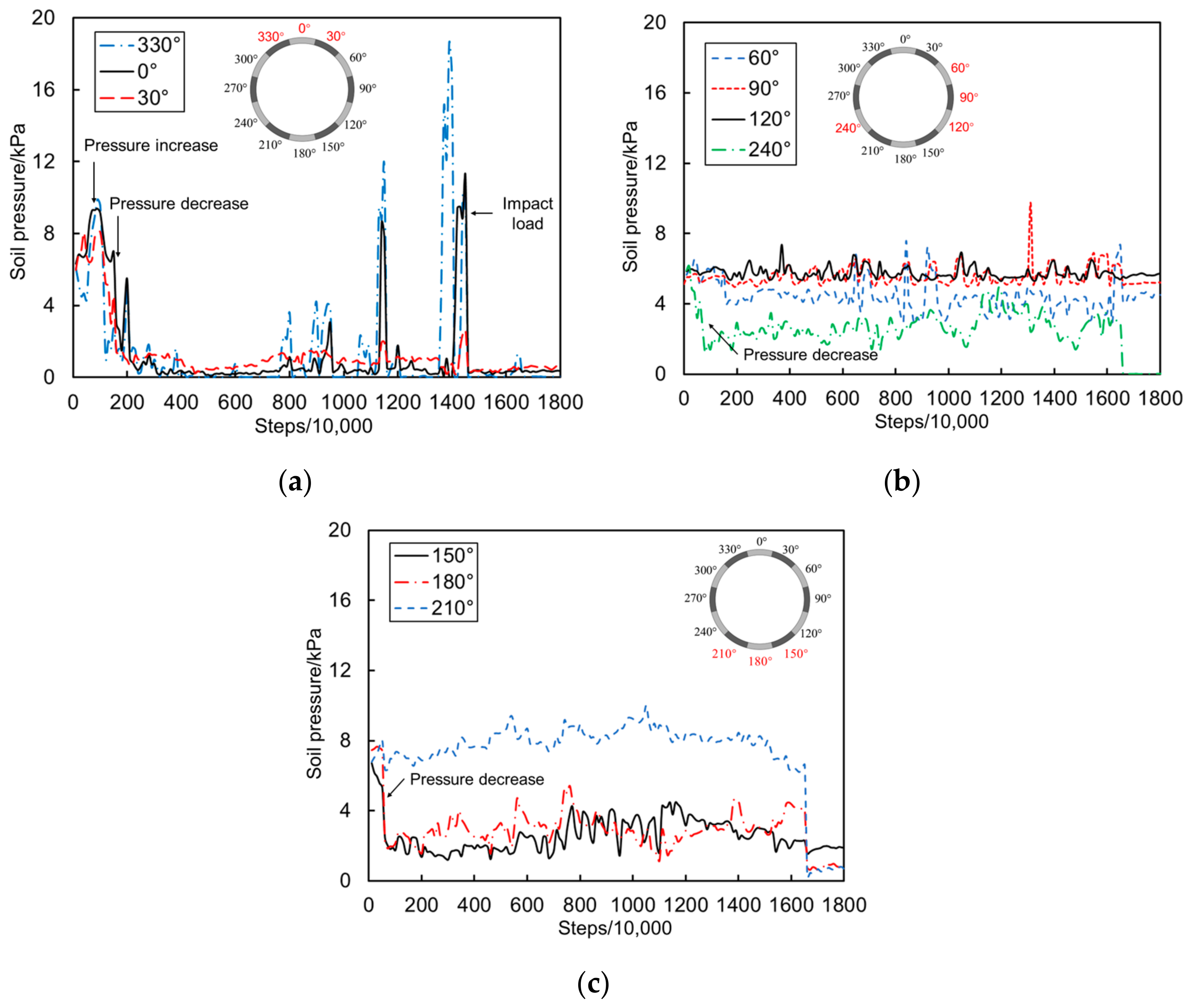
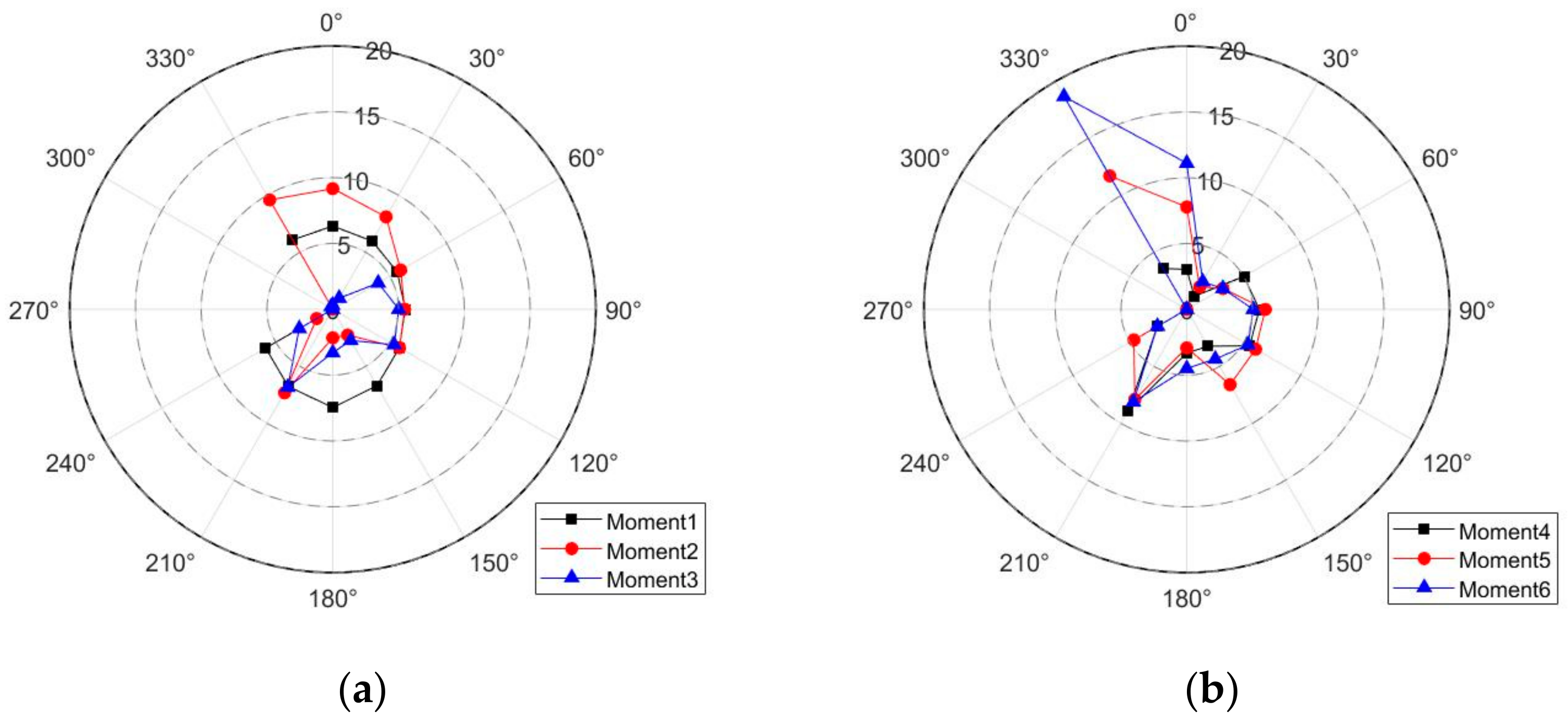
4.2.1. Distribution of Earth Pressure

Based on the results of the strata analysis, the contact forces applied to the tunnel were extracted. The loads applied to the tunnel are shown in Figure 12. The opening is located at the angles of 270° and 300°, so the loads of these two monitoring points are zero due to the opening.

The loads applied to the top of the tunnel (0°, 30°, and 330°) are shown in Figure 12a. The load at the top of the tunnel first shows an increase after the leakage. Then, the load decreases rapidly. After that, several sudden increases in load occur due to impact loads. Three main impact loads were observed in the numerical simulation, and the magnitude of the three impact loads increases with the increase in the height of the destabilized soil, and the third impact load reaches 18.68 kPa.

The loads applied to the tunnel waist (60°, 90°, 120°, and 240°) are plotted in Figure 12b. Two different load trends can be observed. The measurement points at 60°, 90°, and 120° are located at the backside compared to the opening of the tunnel, are less affected by the leakage, and show a more stable trend of the load in the simulation. The measurement point at 240° is located at the lower side of the tunnel opening, and the load decreases rapidly due to soil loss and then stabilizes.

The loads applied to the bottom of the tunnel (150°, 180°, and 210°) are shown in Figure 12a. The loads applied at the angle of 150° and 180° show a sharp decrease after the leakage, while the loads at 210° show a relatively stable trend. The reason for this is that, with the supports of the soil arch located at the angle of 210°, the loads remain stable even with some of the surrounding soil loss.

Based on the aforementioned loads calculated from the strata model, the loads at key moments were extracted and applied to the FEM tunnel model to investigate the response of the tunnel structure and the cause of the tunnel collapse.

The external load distributions at the tunnel at the six critical moments were extracted, and their distributions are shown in Figure 13. The load characteristics of the six key moments were analyzed as follows:

(1)

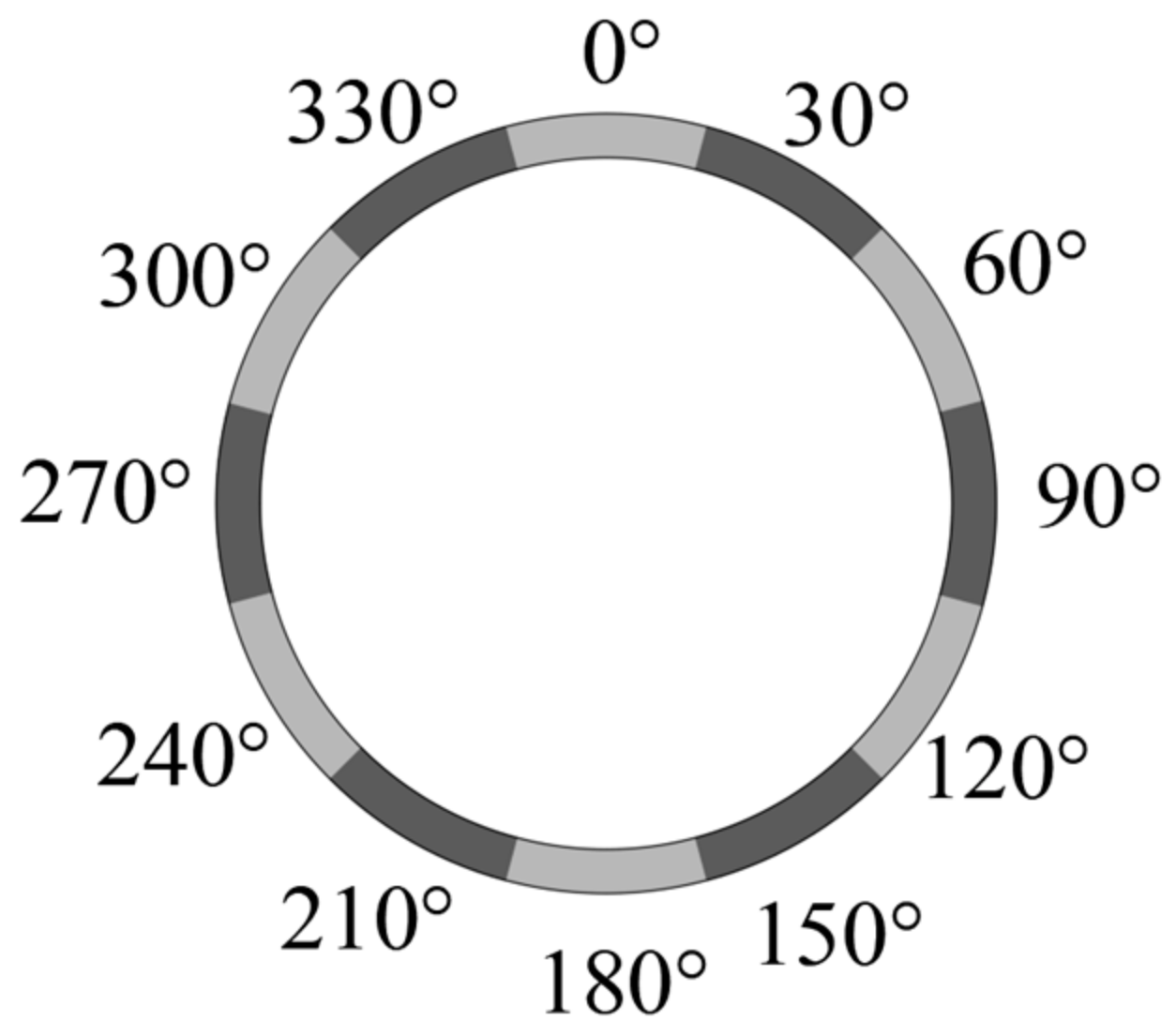
Moment 1: The moment when the leakage started was chosen as the moment 1. The initial pressure is shown in Figure 13a. From the load distribution, it can be seen that the external load distribution of the tunnel at moment 1 was relatively uniform, with larger loads at the top and bottom of the tunnel and smaller loads at the waist.

(2)

Moment 2: the moment when the initial soil arch formed was chosen as moment 2. The load at the top and bottom of the tunnel increased significantly due to the soil arching effect, as shown in Figure 13a.

(3)

Moment 3: the moment when the initial soil arch was destabilized was chosen as moment 3. At this moment, the top of the tunnel was completely within the soil cave, and the loads were decreased to the lowest value. Since the soil erosion had not yet progressed to other locations of the tunnel, the loads at other locations of the tunnel were relatively stable. The supports of the arch were at the 210° location, and the loads were larger than those at other locations, as shown in Figure 13a.

(4)

Moment 4: at this moment, the top of the tunnel was subjected to the first impact load, while the bottom pressure reached its peak due to the soil arch feet, but the back side of the tunnel opening was relatively stable, as shown in Figure 13b.

(5)

Moment 5: the moment of the second impact load was chosen as moment 5. The load at the top 0° and 330° increased significantly, as shown in Figure 13b.

(6)

Moment 6: at this moment, the third impact load was applied to the tunnel. The loads at the top 0° and 330° reached the peak, while the loads at other locations remained relatively stable, as shown in Figure 13b.

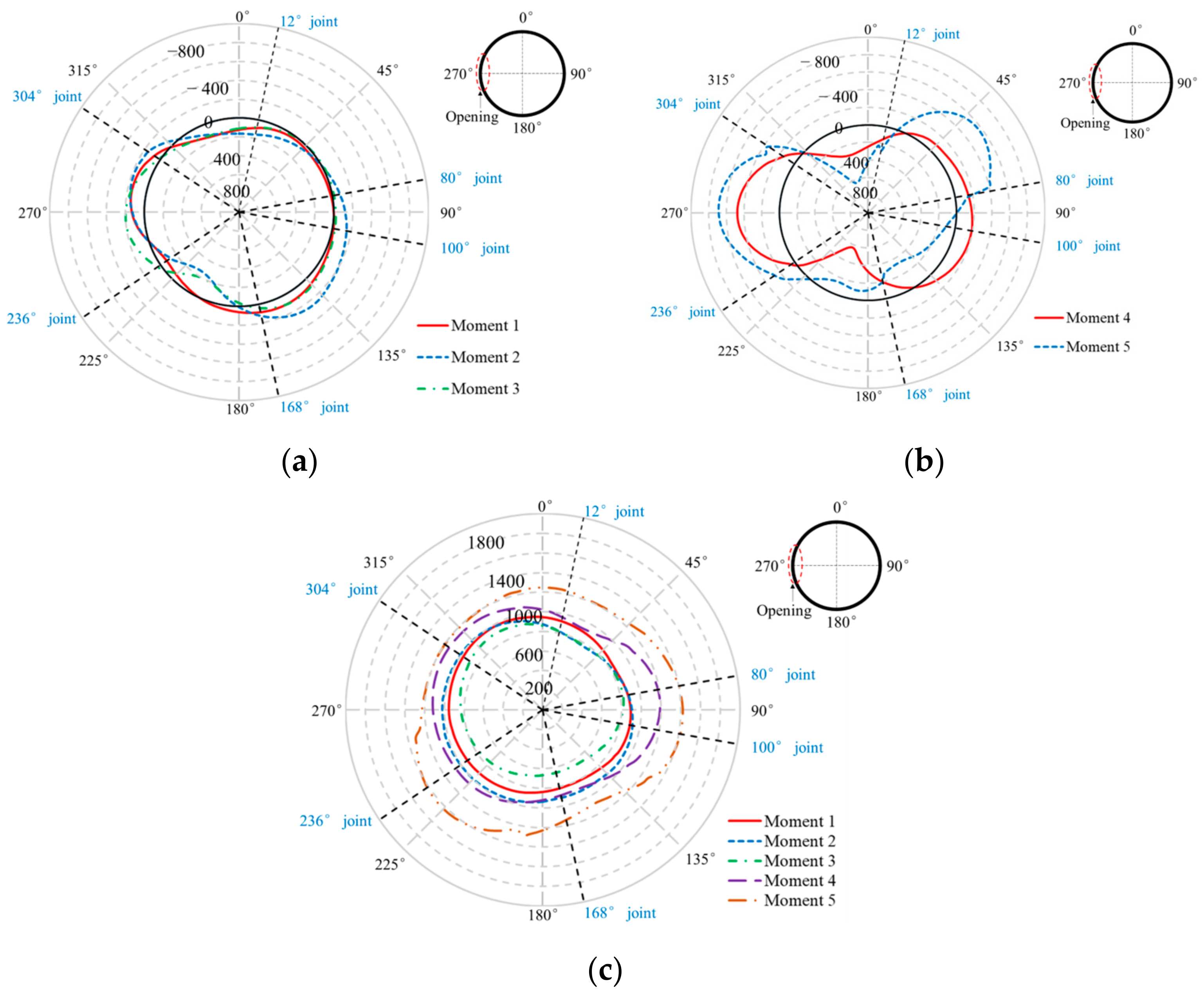
4.2.2. Tunnel Collapse Process

In the simulation of tunnel collapse, the external loads were applied one by one according to the six key loads extracted from the stratigraphic analysis, which corresponded to the moments from 1 to 6. The internal forces at the six moments are shown in Figure 14, where the bending moments are positive in tension at the inner side of the tunnel and the axial forces are positive in compression. Taking the loading moment as the vertical axis coordinate and the relative displacement between the top and bottom of the tunnel as the horizontal axis coordinate, the damage development process of the tunnel structure is plotted in Figure 15. To facilitate the analysis and comparison, the results of the numerical simulation were transformed into the data of the prototype according to the similarity relationship. The structural damage development process was analyzed as follows:

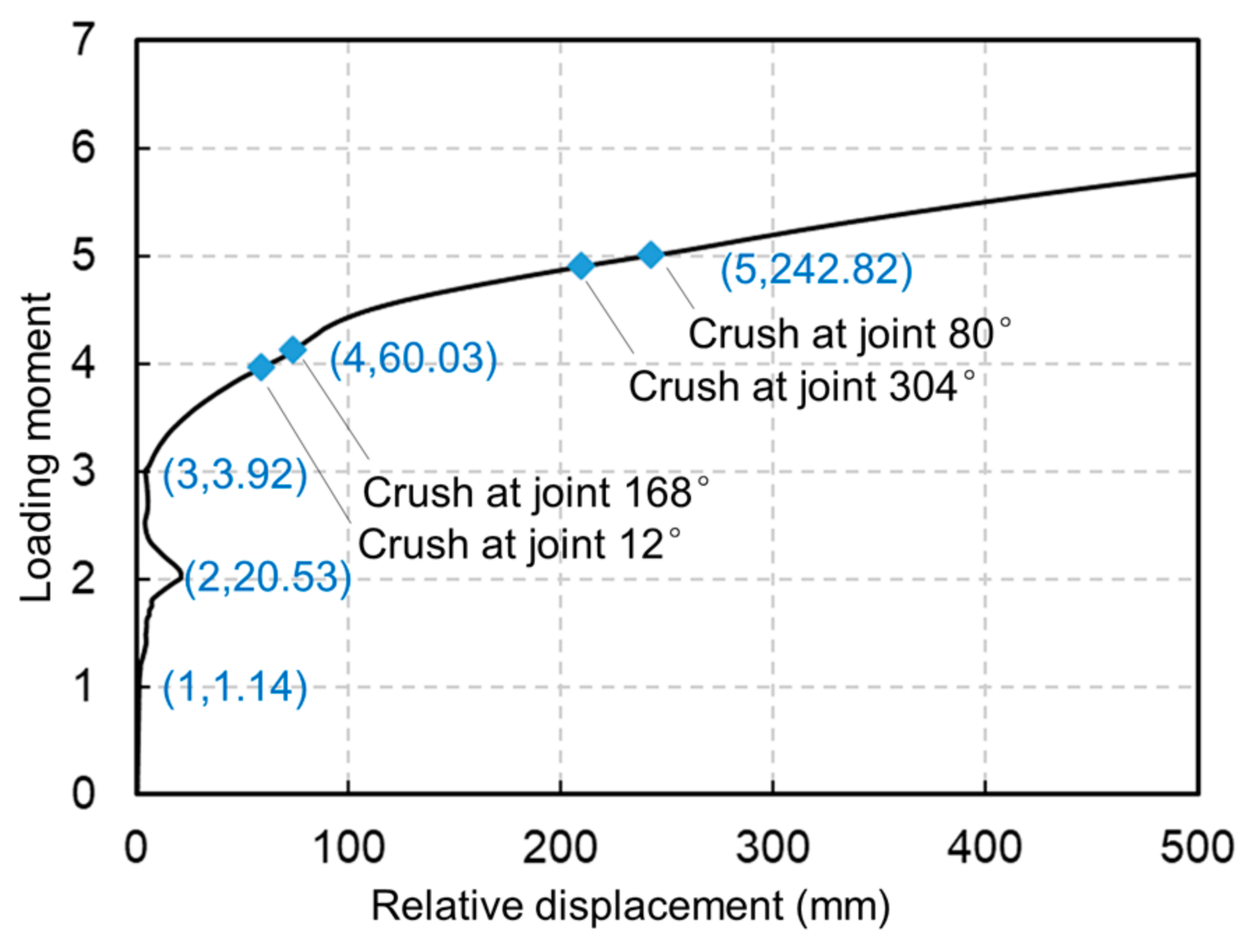
(1)

Moment 1: at this time, the tunnel was subjected to normally distributed external soil and water pressure, which resulted in a 1.14 mm top–bottom convergence, and no structural damage had occurred yet.

(2)

Moment 2: with the formation of the initial soil arch, the load at the top and bottom of the tunnel increased significantly. Under the dual effects of waist load decrease and top and bottom loads increase, the bending moment generated at moment 2 increased significantly, thus leading to large top and bottom convergence deformation of 20.53 mm.

(3)

Moment 3: after the initial soil arch destabilization, the pressure at the top of the tunnel decreased. Therefore, the bending moment decreased, resulting in the relative displacement between the top and bottom of the tunnel decreasing to 3.92 mm.

(4)

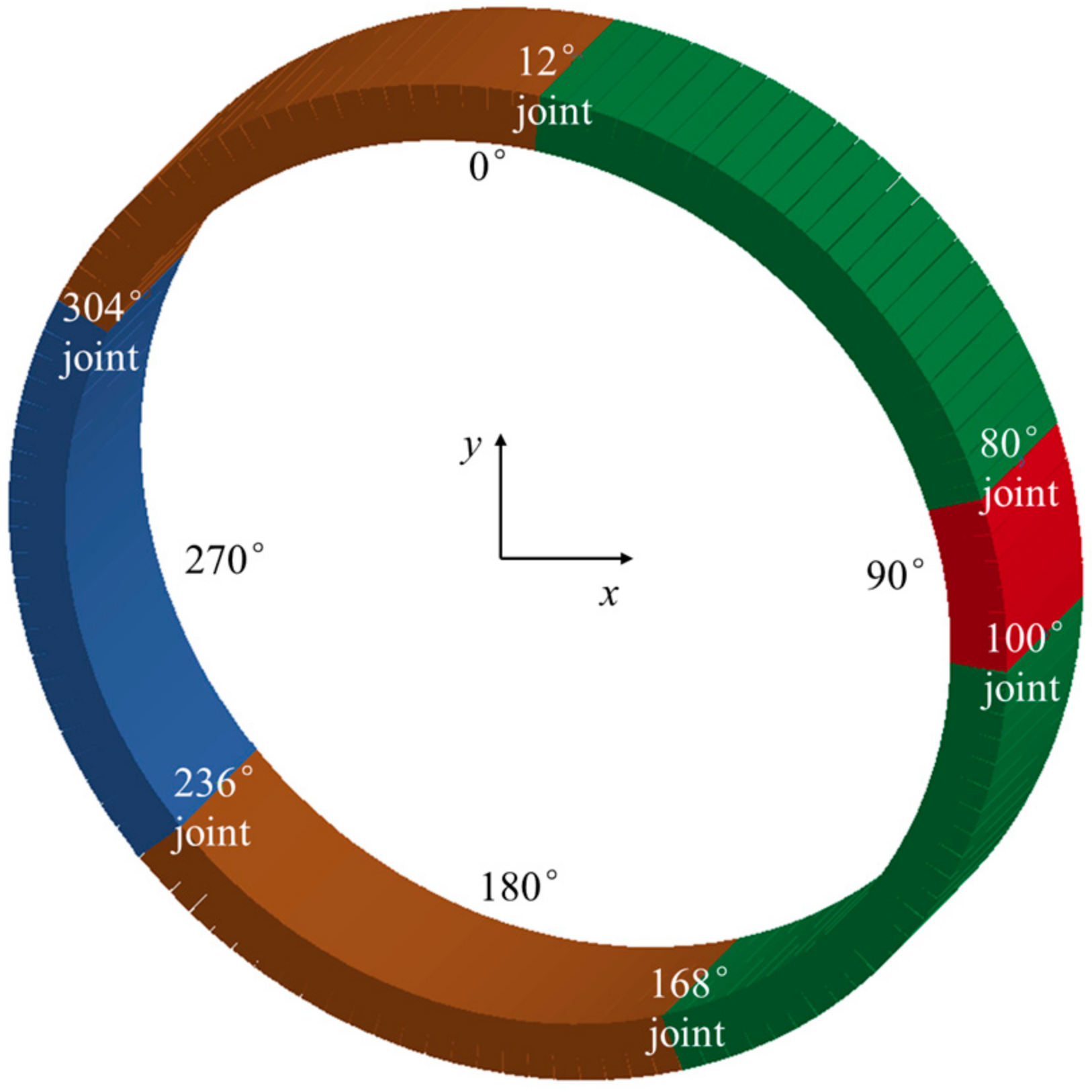
Moment 4: after the first impact load was applied to the top of the tunnel, the load on the top of the tunnel increased suddenly, and the bending moments of the top and bottom of the tunnel and the waist of the tunnel increased significantly, resulting in the crushing of the gypsum at the 12° and 168° joints.

(5)

Moment 5: after the second impact load was applied to the top of the tunnel, the gypsum of the 80° and 304° joints at the waist of the tunnel was crushed. Up to now, four plastic hinges appeared in the tunnel and the tunnel was destabilized. At this time, the convergent deformation at the top and bottom of the tunnel had reached 242.82 mm.

A comparison of the collapse phenomena of the tunnel calculated by numerical simulation and in the model tests is shown in Figure 16. As can be seen from the comparison, the damage phenomena of the tunnel obtained from numerical simulation and the test results have a high degree of compatibility. Both are manifested in the overall destabilization of the upper part of the tunnel. Plastic hinges were formed at the joints, and the top two segments were destabilized and rotated, while the bottom deformation of the tunnels was relatively small. This proves the reliability of the numerical simulation results.

5. Conclusions

In this paper, a coupled fluid–solid strata model and a nonlinear FEM tunnel model were established to simulate the tunnel collapse process based on test results. After experimental validation, the strata response and the process of the tunnel collapse were analyzed. The following conclusions were drawn from the study:

(1)

A DEM-based coupled fluid–solid strata model combined with a nonlinear FEM tunnel model can be used to effectively simulate the complete process of tunnel leakage-induced collapse. By comparing with the tests, it was proved that the coupled fluid–solid model can be used to reproduce the phenomena of seepage erosion. By extracting the external loads of the tunnel obtained from the strata model and applying them to the FEM tunnel model, the tunnel collapse process can be simulated in a refined way, and the collapse mechanism of the tunnel structure can be obtained.

(2)

Based on the coupled fluid–solid analysis, it was pointed out that the microscopic mechanism of tunnel seepage-induced strata response was the continuous destabilization and reproduction of the soil arching effect formed by the soil particles. During the development of the soil arch, the height and width of the soil arch increased continuously, which led to the degradation of its stability and ultimately triggered the subsidence of the strata surface. On the one hand, the soil arching effect hinders the development of seepage erosion, so the erosion of the soil is limited to the interior of the soil arch, which is manifested as the generation of soil caves in the macroscopic phenomena; on the other hand, the soil arching effect temporarily supports the soil above, and there is no obvious subsidence of the strata surface in the process of erosion, which results in a sudden destabilization of the strata and impact loads on the tunnel.

(3)

The collapse process of the tunnel is as follows: firstly, due to the soil arching effect, the load outside the tunnel structure is redistributed, the loads at the feet of the arch rise significantly, the loads inside the soil arch dissipate, and the tunnel undergoes large deformation as a result; subsequently, due to the impact loads from the destabilization of the soil, the tunnel is damaged at several joints and generates plastic hinges, and ultimately the tunnel is destabilized and collapses.

Given the unpredictability of tunnel collapse accidents, acquiring insights from engineering accidents is difficult. In this study, the strata response and tunnel collapse mechanism were investigated through numerical simulation. The conclusions drawn from the study can deepen the understanding of the mechanism of tunnel leakage accidents so that effective prevention measures can be put forward in the future.