Research on Mechanical Properties of Steel-Polypropylene Fiber-Reinforced Concrete after High-Temperature Treatments
Abstract
1. Introduction
2. Test Overview
2.1. Mixing Proportion of Raw Materials
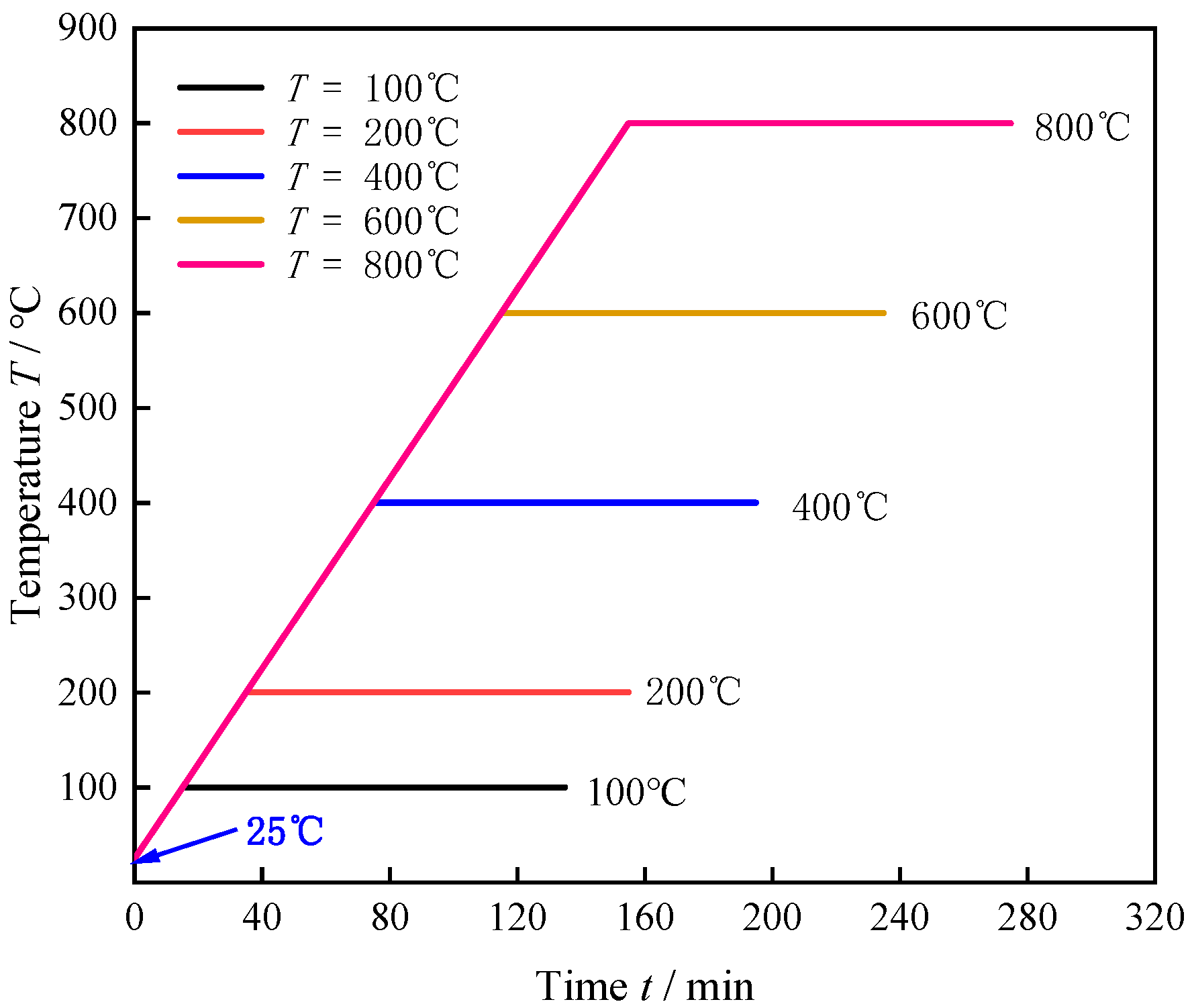
2.2. Specimen Preparation
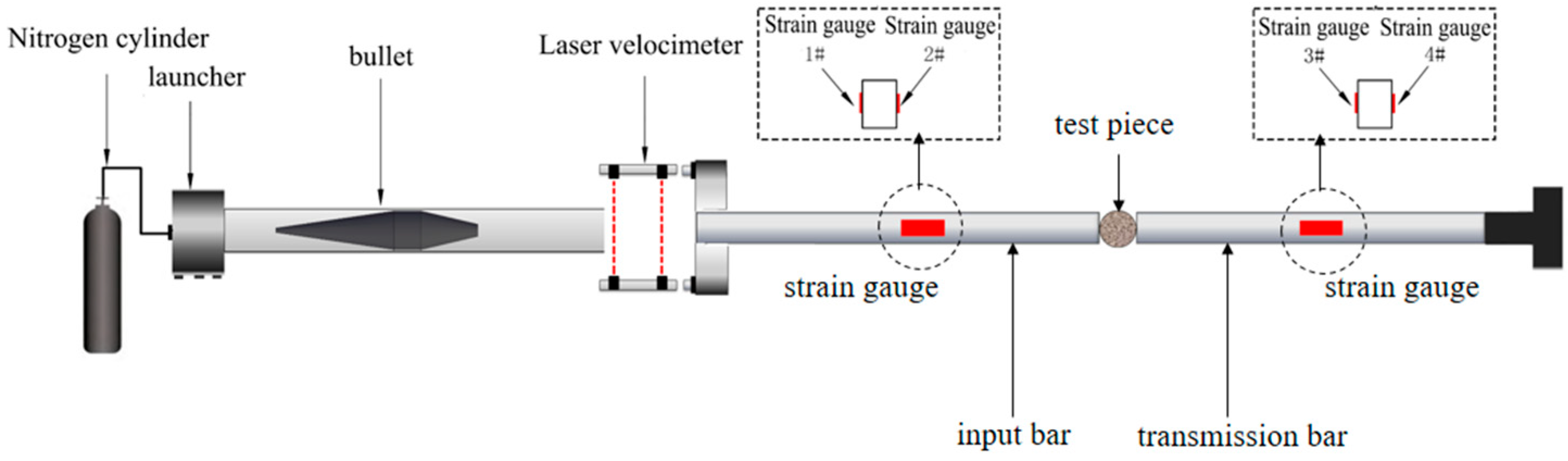
2.3. Test Device and Principle
3. Test Scheme and Result Analysis
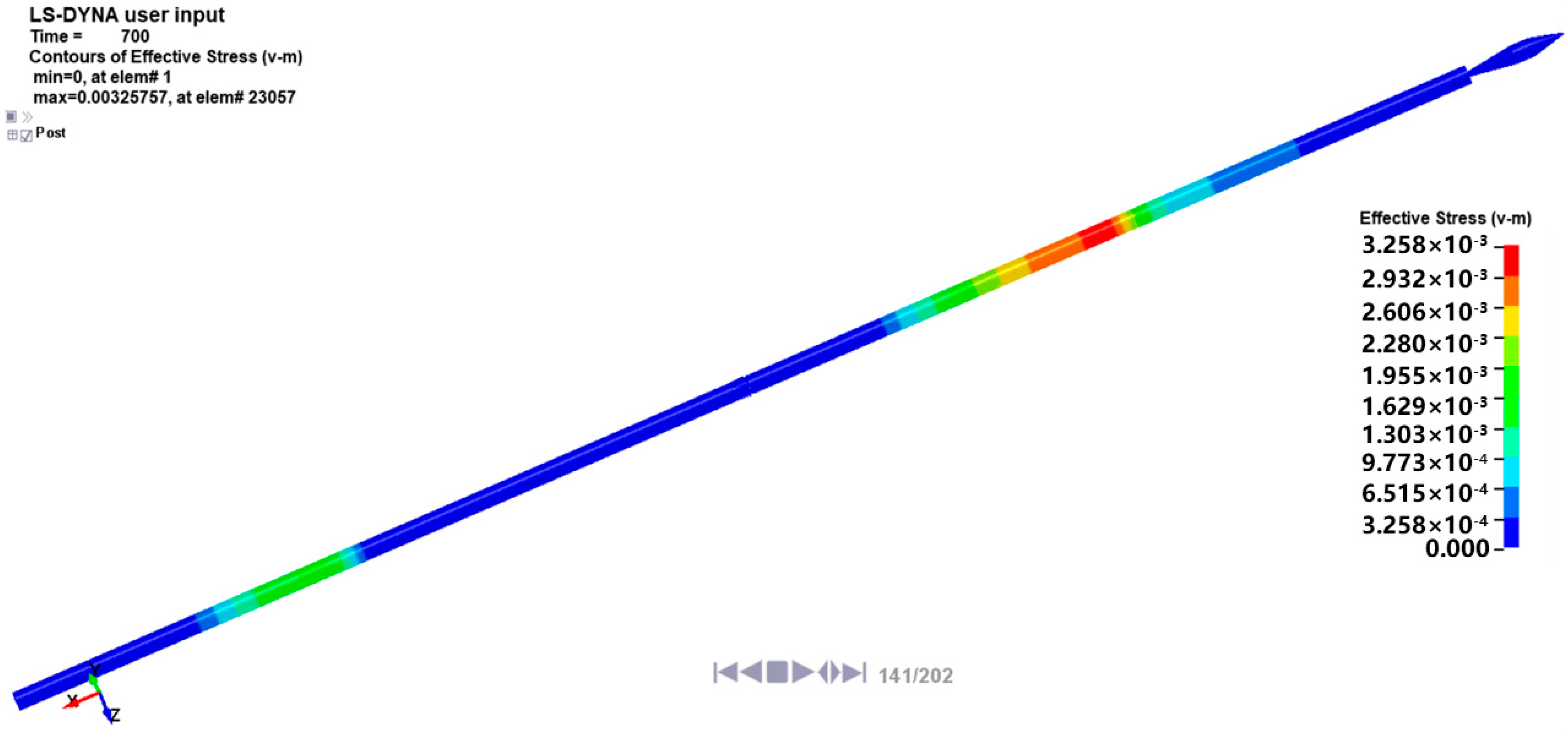
3.1. Stress Uniformity Verification
3.2. Uniaxial Dynamic Impact Compression Test
3.2.1. Test Results
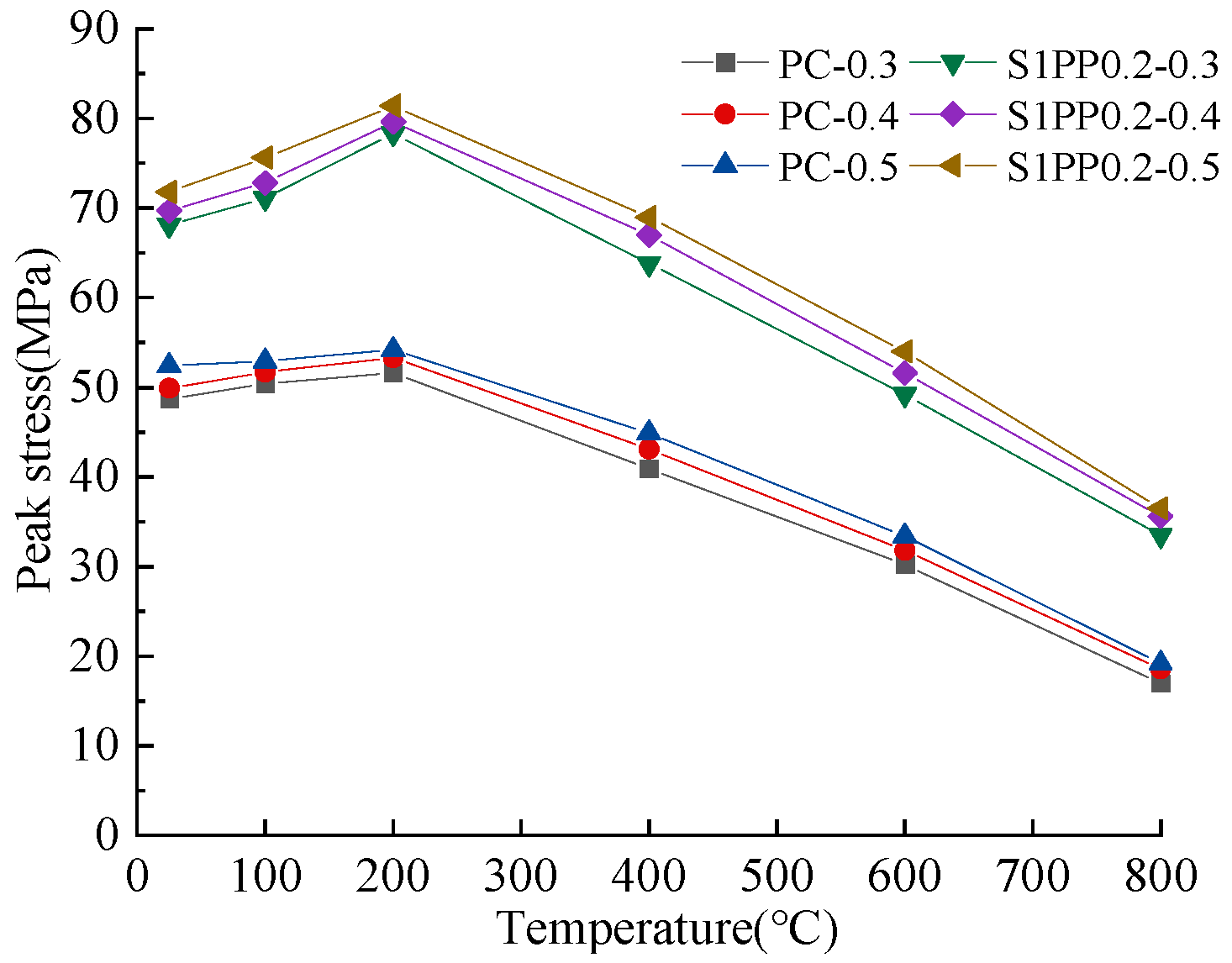
3.2.2. Dynamic Peak Intensity
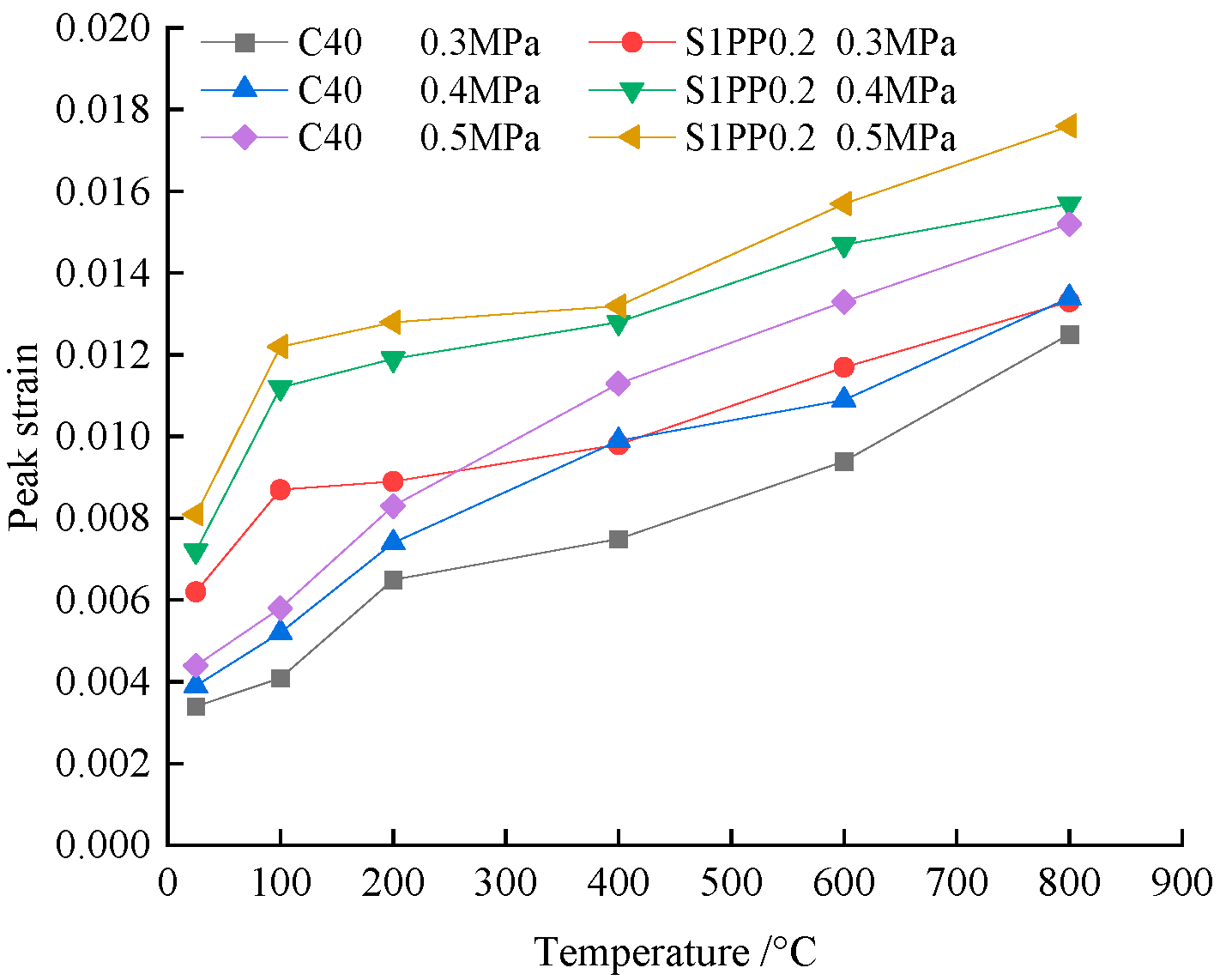
3.2.3. Dynamic Peak Strain
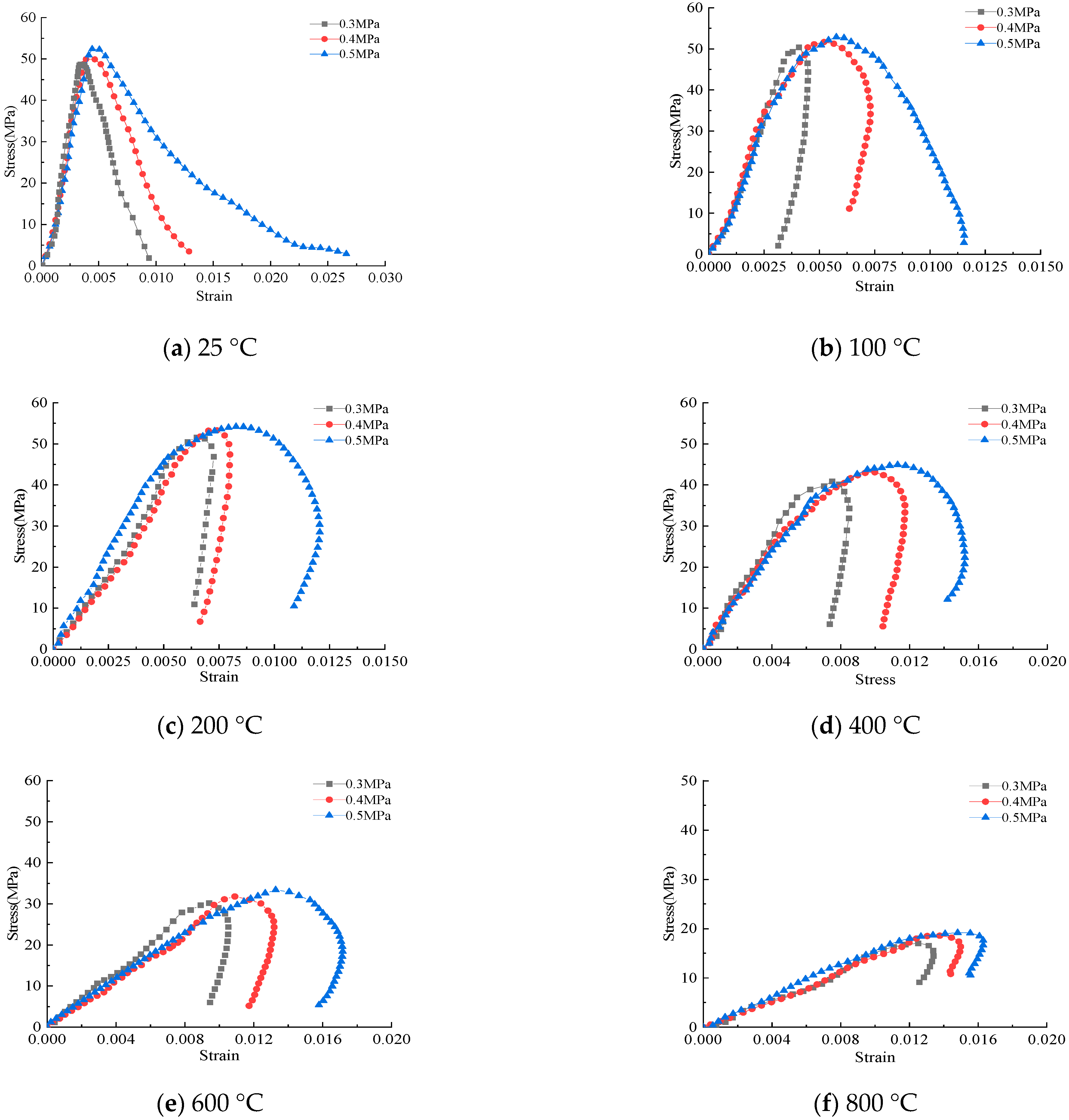
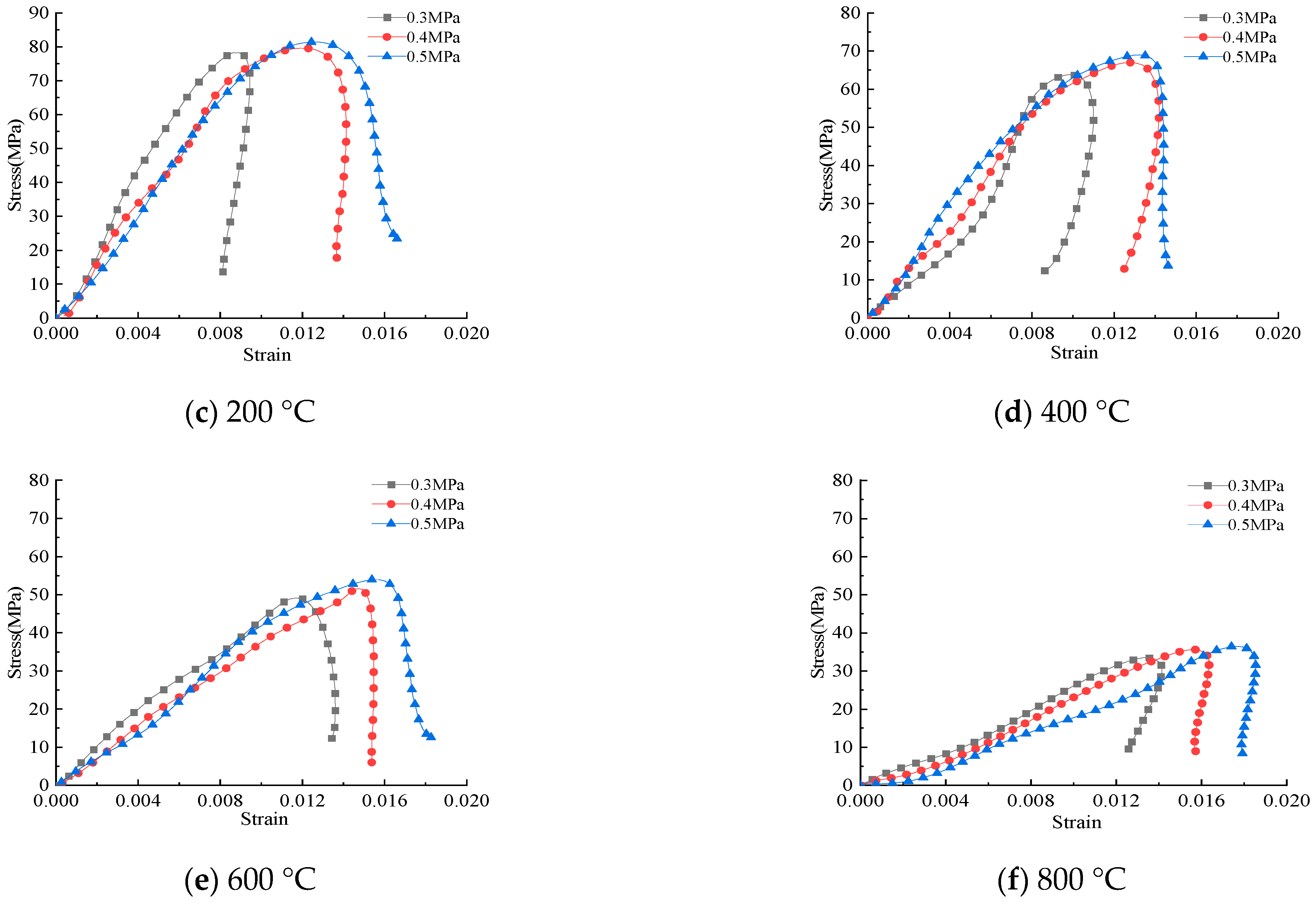
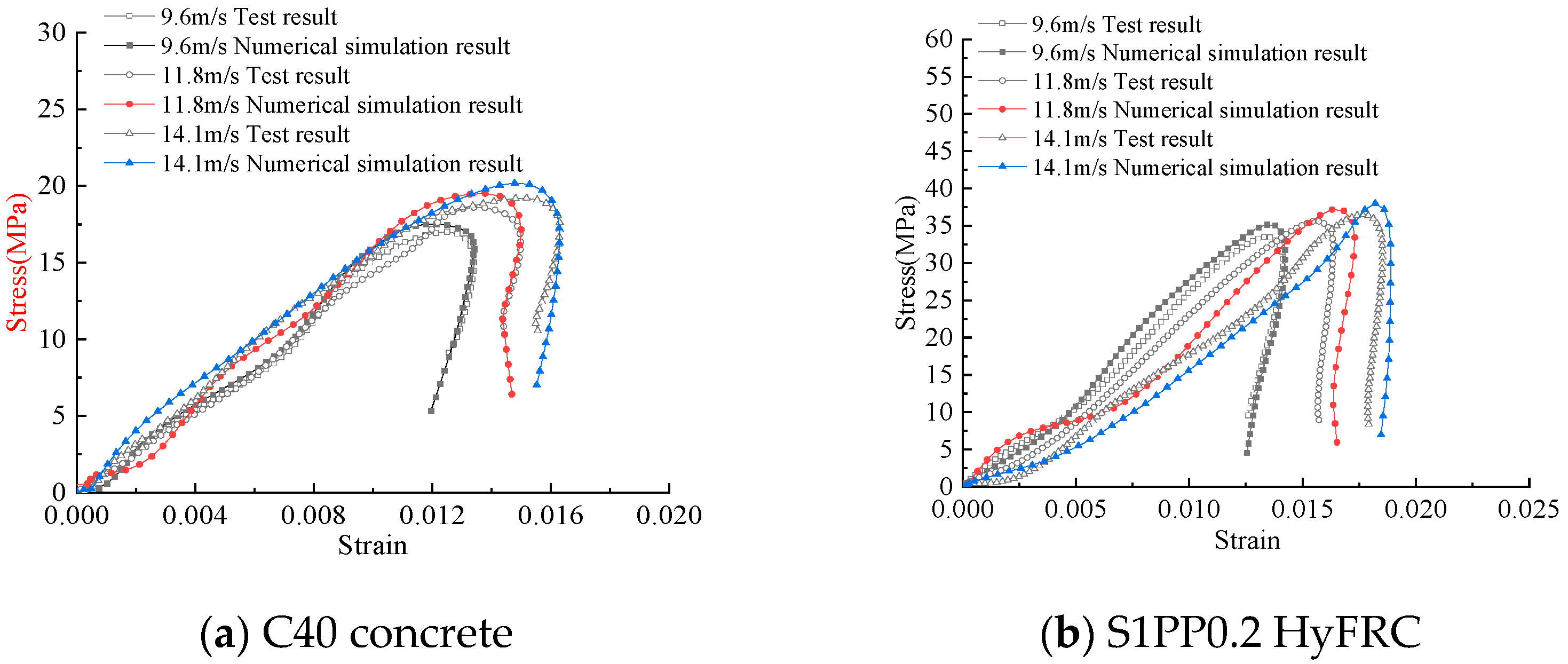
3.2.4. Stress-Strain Curves
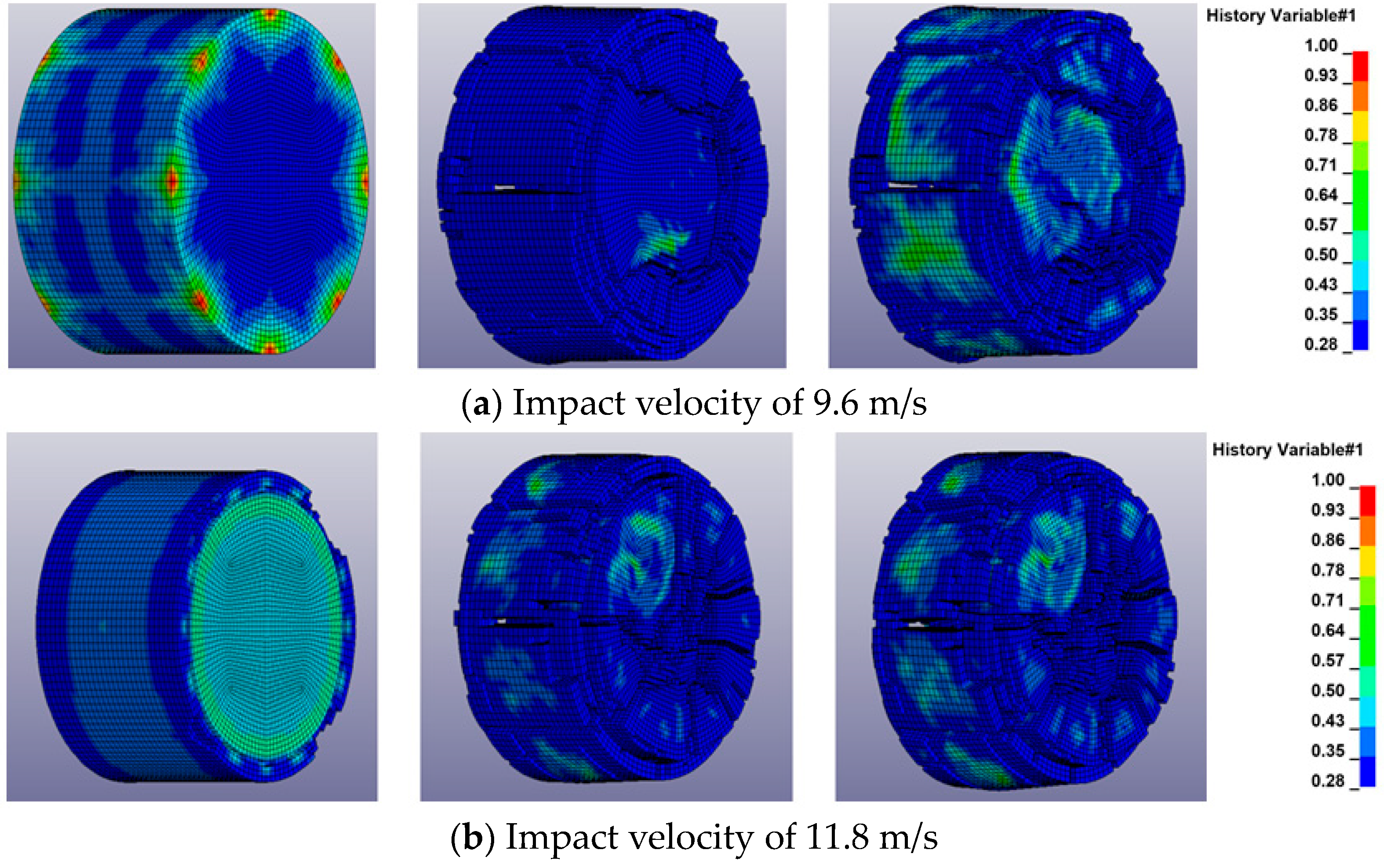
3.2.5. Analysis of Failure Modes
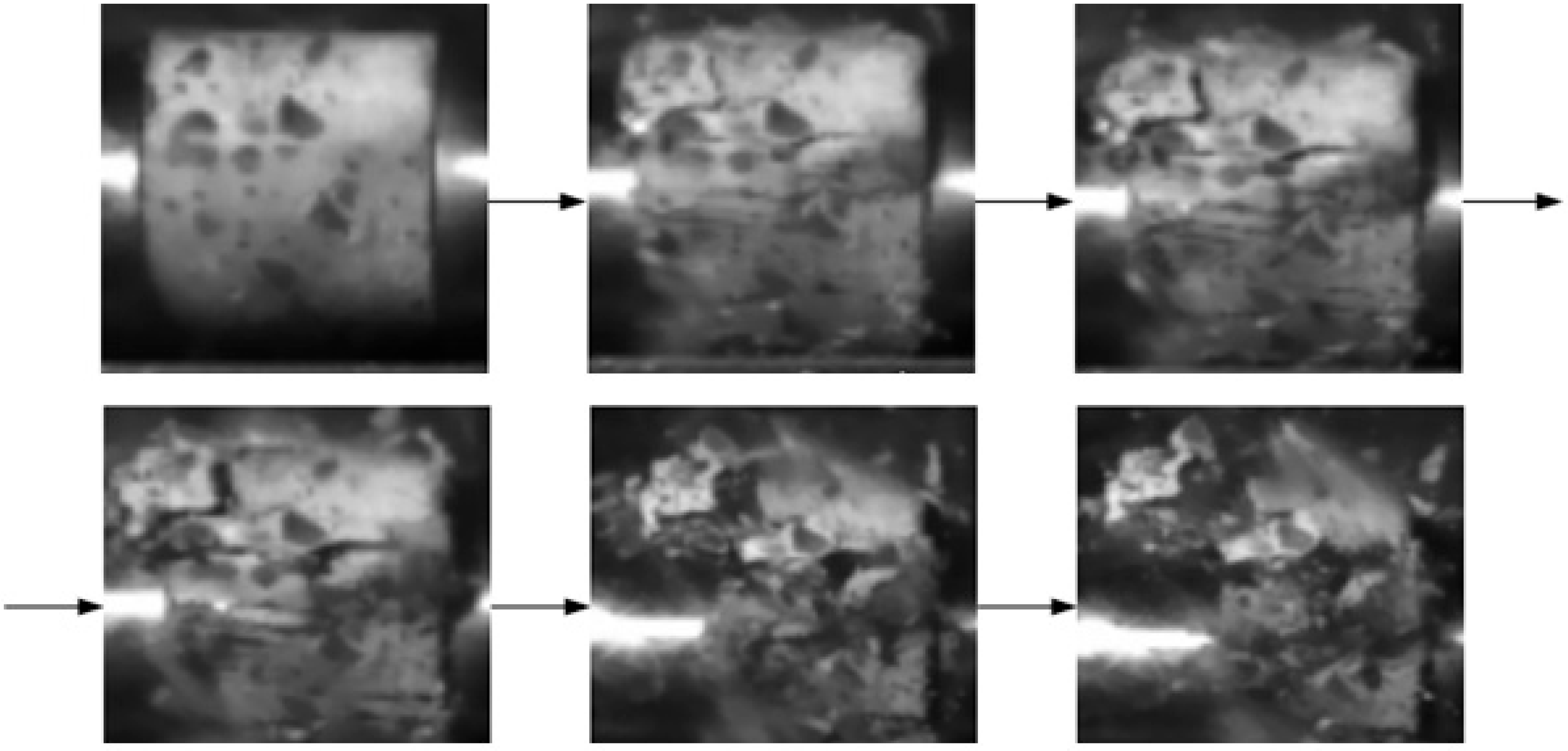
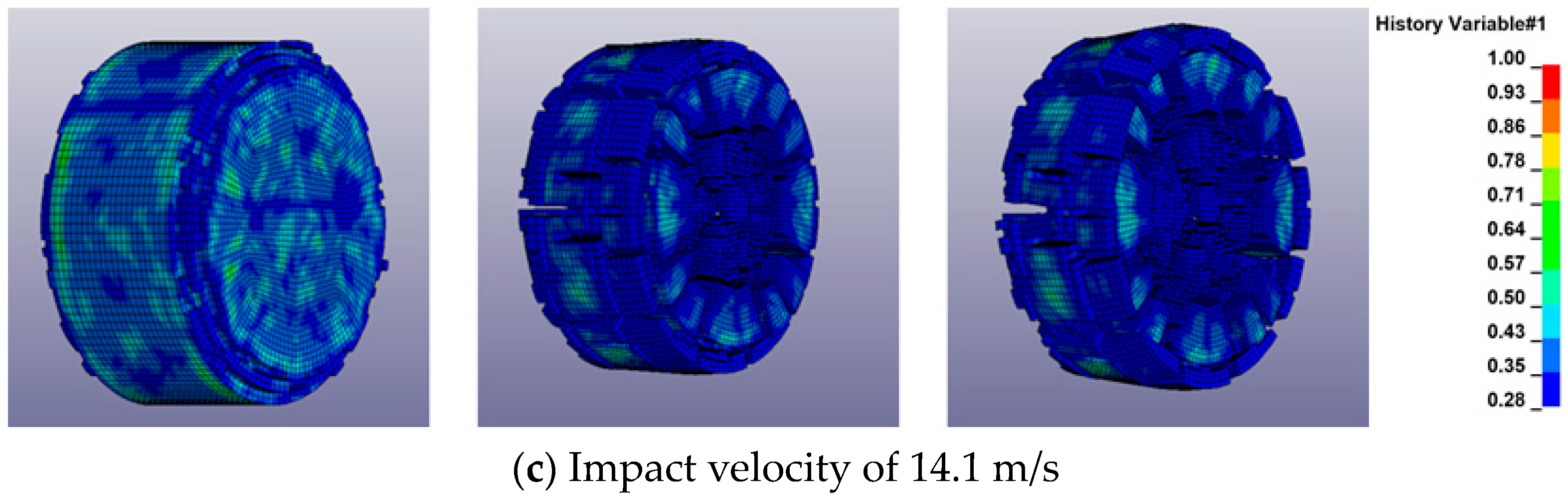
3.3. Analysis of High-Speed Camera Results
4. Numerical Simulation
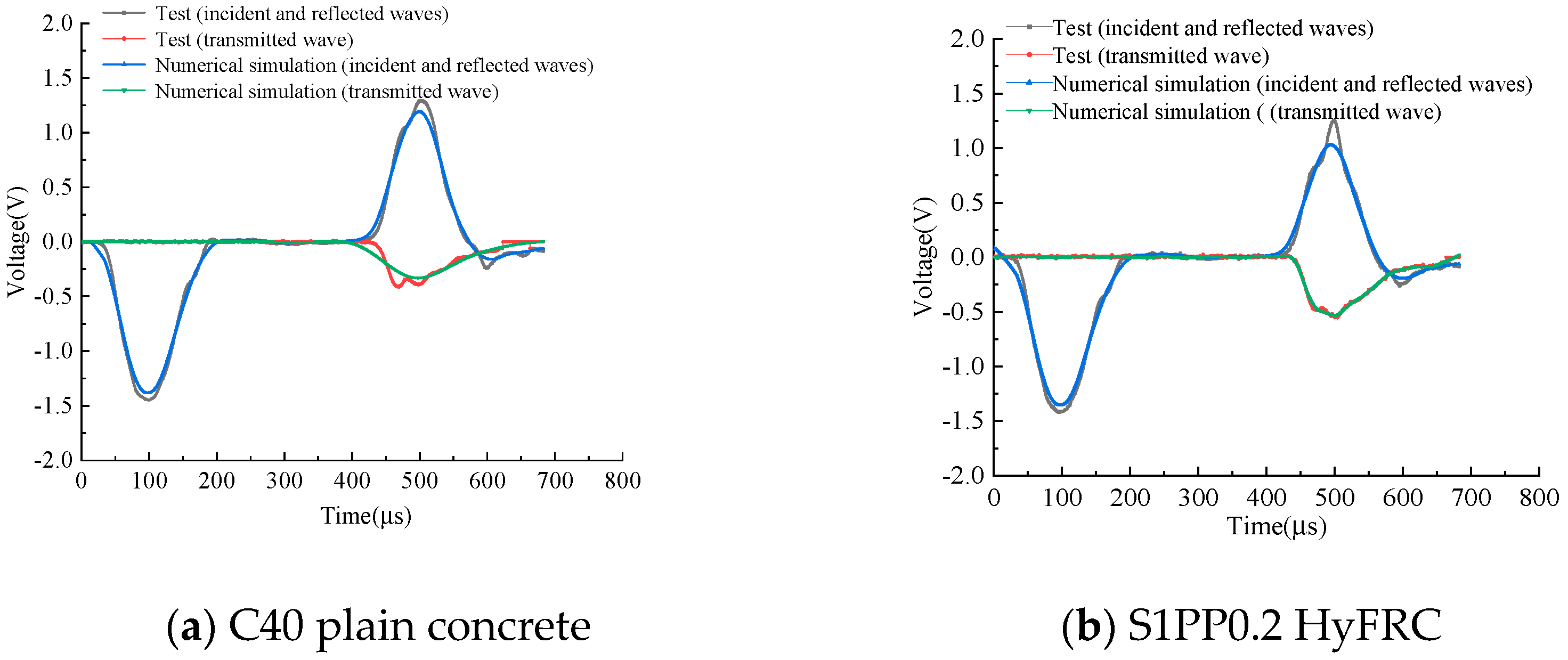
4.1. Establishment of the SHPB Finite Element Model
4.2. Determination of Concrete Material Parameters
- (1)
- Yield surface equation
- (2)
- Damage evolution equation
- (3)
- State equation
4.3. Numerical Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, X.; Shen, A.Q.; Guo, Y.C. Experimental study on road performance of basalt fiber reinforced bitumen mastics. J. Build. Mater. 2016, 19, 659–664. [Google Scholar]
- Xin, M.; Wang, X.Z.; Dong, H. Summary of research on durability of fiber concrete. J. Liaoning Univ. Technol. (Nat. Sci. Ed.) 2020, 40, 35–39. [Google Scholar]
- Kumari, G.J.; Ojarestaghi, S.S.M.; Bhojaraju, C. Influence of thermal cycles and high-temperature exposures on the residual strength of hybrid steel/glass fiber-reinforced self-consolidating concrete. Structures 2023, 55, 1532–1541. [Google Scholar] [CrossRef]
- Jiang, X.G. Research on the durability of basalt fiber reinforced concrete. Anhui Archit. 2021, 28, 117–118. [Google Scholar]
- Peng, S.; Li, L.; Wu, J.; Jiang, X.Q.; Du, X.L. lmpact tests on dynamic compressive behaviors of steel fiber reinforced concrete at elevated temperature. Vib. Shock 2019, 38, 149–154. [Google Scholar]
- Wang, L. Experimental Study on the Mechanical Properties and Damage Evolution of Basalt Fiber Reinforced Concrete after High Temperature. Master’s Thesis, Inner Mongolia University of Technology, Huhehaote, China, 2017. [Google Scholar]
- Hou, L.N.; He, M.D.; Huang, W.; Zhou, X.F. Research status and prospect of mechanical properties of fiber-reinforced recycled concrete. J. Xi’an Univ. Technol. 2021, 37, 403–413. [Google Scholar]
- Zhao, L.P. Mechanical Behavior and Calculation Methods of Fiber & Nanosized Materials Reinforced Concrete at High Temperature. Ph.D. Thesis, Zhengzhou University, Zhengzhou, China, 2017. [Google Scholar]
- Zhao, Y.R.; Liu, D.K.; Wang, L.; Liu, F.F. Experimental study on mechanical properties of basalt fiber concrete after high temperature. Concrete 2019, 20, 72–75. [Google Scholar]
- Jiang, W.; Jiang, J.S.; Teng, C.L. Research status of hybrid fiber reinforced concrete. Build. Mater. Dev. Orientat. 2019, 17, 13–16. [Google Scholar] [CrossRef]
- Liu, X.; Liang, D.Y.; Luo, J.J.; Tang, Y.Q.; Wang, T.Q. Experimental study on compressive strength of steel fiber reinforced concrete at high temperature. Concrete 2018, 1, 31–34. [Google Scholar]
- Yang, J. Experimental Research on Mechanical Properties, Explosive Spalling Behavior and Its Improvements of Ultra-High-Performance Concrete with Coarse Aggregate Exposed to High Temperature. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Huang, J.S. Research of the Properties of Polyvinyl Alcohol Fiber Concrete. Master’s Thesis, Yangzhou University, Yangzhou, China, 2018. [Google Scholar]
- Varona, B.; Baeza, J.; Bru, D. Influence of high temperature on the mechanical properties of hybrid fibre reinforced normal and high strength concrete. Constr. Build. Mater. 2018, 159, 73–82. [Google Scholar] [CrossRef]
- Kodur, V.; Khaliq, W. Effect of temperature on thermal properties of different types of high-strength concrete. J. Mater. Civ. Eng. 2011, 23, 793–801. [Google Scholar] [CrossRef]
- Sanchayan, S.; Foster, S.J. High temperature behaviour of hybrid steel-PVA fibre reinforced reactive powder concrete. Mater. Struct. 2016, 49, 769–782. [Google Scholar] [CrossRef]
- GB175-2007; Common Portland Cement. Standards Press of China: Beijing, China, 2007.
- GB/T1596-2017; Fly Ash Used for Cement and Concrete. Standards Press of China: Beijing, China, 2017.
- JGJ5 5-2011; Concrete Mixing Ratio Design Regulations. China Building Industry Press: Beijing, China, 2011.
- CECS13:2009; FRC Experimental Method Standard. China Plan Publishing House: Beijing, China, 2009.
- Li, T.; Zhang, X.G.; Liu, H.X.; Fang, J.Z.; Chen, C. Experimental research on mechanical properties of hybrid fiber concrete after high temperature. J. Railw. Sci. Eng. 2020, 17, 1171–1177. [Google Scholar]
- Liu, Y.W.; Liu, L.; Meng, X. Study on the mechanical properties of basalt fiber concrete under different temperature and with different dosage. Chem. Miner. Process. 2022, 51, 26–31. [Google Scholar]
- Gong, F.Q. Experimental Study of Rock Mechanical Properties under Coupled Static-Dynamic Loads and Dynamic Strength Criterion. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Mao, Z.H.; Zhang, J.C.; Li, Y.Q.; Du, G.F.; Yang, X. Performance Degradation and Microscopic Structure of Reactive Powder Concrete after Exposure to High Temperature. J. Build. Mater. 2020, 25, 1225–1232. [Google Scholar]
- Ni, X. Effect of Polypropylene Fiber on Mechanical Properties of Concrete under Cyclic Loading. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2021. [Google Scholar]
- Xu, J.Y.; Zhao, D.H.; Fan, F.L. Dynamic Characteristics of Fiber Reinforced Concrete; Northwest University of Technology Press: Xi’an, China, 2013. [Google Scholar]
- Luo, H.L.; Yang, D.Y.; Zhou, X.Y.; Shan, C.C.; Liu, X.; Zhao, F.L. Mechanical properties of polypropylene fiber reinforced concrete with different aspect ratios. Acta Mater. Compos. Sin. 2019, 36, 1935–1948. [Google Scholar]
- Ren, S.Y. An experimental study of high strain-rate properties of clay under high consolidation stress. Soil Dyn. Earthq. Eng. 2017, 92, 46–51. [Google Scholar]
- Liu, P. SHPB Tests for Cement Mortar Materials and Their Parameter Sensitivity and Uncertainty Analysis. Ph.D. Thesis, Hunan University, Changsha, China, 2018. [Google Scholar]
- Liu, P.; Zhou, X.; Qian, Q. Dynamic splitting tensile properties of concrete and cement mortar. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 757–770. [Google Scholar] [CrossRef]
- Sun, H. Study on Impact Splitting Tensile Properties of High Strength Concretewith Steel Polypropylene Hybrid Fiber. Ph.D. Thesis, Southwest University of Science and Technology, Mianyang, China, 2018. [Google Scholar]
- Chen, B.F.; Qiu, X.; Chen, J.Y. Numerical simulation of concrete impact test using split Hopkinson pressure bundled bars device. J. Appl. Mech. 2017, 34, 125–130. [Google Scholar]
- Wang, C.; Song, R.; Wang, G. Modifications of the HJC (Holmquist-Johnson-Cook) Model for an Improved Numerical Simulation of Roller Compacted Concrete (RCC) Structures Subjected to Impact Loadings. Materials 2020, 13, 1361. [Google Scholar] [CrossRef]
- Sun, Y.X.; Wang, J.; Wu, H.J.; Zhou, J.Q.; Li, J.Z.; Pi, A.G.; Huang, F.L. Experiment and simulation on high-pressure equation of state for concrete. Explos. Shock 2020, 40, 4–13. [Google Scholar]
- Yuan, L.Z.; Miao, C.H.; Shan, J.F.; Wang, P.F.; Xu, S.L. On strain-rate and inertia effects of concrete samples under impact. Explos. Shock 2022, 42, 18–30. [Google Scholar]
- Xie, L. Comparative study the mechanical properties of HJC and K&C concrete models under explosion. J. Yanbian Univ. (Nat. Sci. Ed.) 2020, 46, 164–168. [Google Scholar]
- Wu, S.; Zhao, J.H.; Wang, J.; Li, N.; Li, Y. Study on parameters of HJC constitutive model based on numerical simulation of concrete SHPB test. J. Comput. Mech. 2015, 32, 789–795. [Google Scholar]
- Zhang, S.R.; Song, R.; Wang, C.; Shang, C.; Wei, P.Y. Modification of a dynamic constitutive model-HC model for roller-compacted concrete and numerical verification. Vib. Shock 2019, 38, 25–31. [Google Scholar]
- Li, R.; Liu, L.; Zhang, Z.H.; Wang, Y. Numerical simulation of marble damaged by high temperature in SHPB experiment based on HC model. Eng. Blasting 2022, 28, 37–44. [Google Scholar]
- Wang, Y.Y. Numerical Simulation of Dynamic Mechanical Behavior of Desert Sand Concrete. Master’s Thesis, Ningxia University, Yingchuang, China, 2016. [Google Scholar]





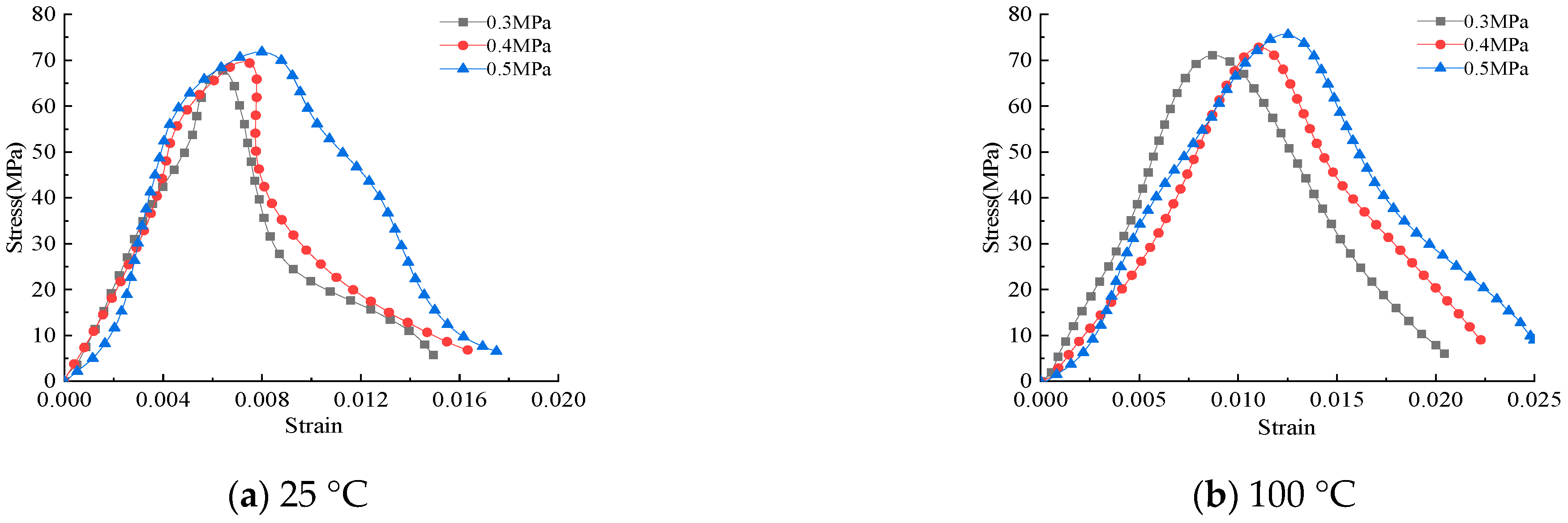








| Filament Diameter (mm) | Cut Length (mm) | Density (kg/m3) | Elastic Modulus (GPa) | Tensile Strength (MPa) | Ultimate Elongation (%) |
|---|---|---|---|---|---|
| 1 | 35 | 7850 | 202 | 1000 | 2.6 |
| Filament Diameter (μm) | Length (mm) | Relative Density (-) | Elastic Modulus (GPa) | Tensile Strength (MPa) | Elongation at Break (%) |
|---|---|---|---|---|---|
| 48 | 12 | 0.91 | 4.8 | 500 | 15 |
| Cement (kg/m3) | Water (kg/m3) | Sand (kg/m3) | Gravel (kg/m3) | Fly Ash (kg/m3) | Water-Reducing Admixture (kg/m3) |
|---|---|---|---|---|---|
| 463 | 185 | 541 | 1261 | 93 | 2.25 |
| Specimen Types | Static Compressive Strength/MPa | |||||
|---|---|---|---|---|---|---|
| 25° | 100° | 200° | 400° | 600° | 800° | |
| PC | 41.6 | 42.7 | 43.7 | 36.2 | 26.5 | 14.8 |
| S1PP0.2 | 53.2 | 56.0 | 61.2 | 51.9 | 40.0 | 27.0 |
| Temperature/°C | Specimen Code | Impact Air Pressure/MPa | Peak Stress/MPa | Peak Strain |
|---|---|---|---|---|
| 25 | PC-25-1 | 0.3 | 48.7 | 0.0034 |
| PC-25-2 | 0.4 | 49.9 | 0.0039 | |
| PC-25-3 | 0.5 | 52.4 | 0.0044 | |
| S1PP0.2-25-1 | 0.3 | 71.1 | 0.0062 | |
| S1PP0.2-25-2 | 0.4 | 69.7 | 0.0072 | |
| S1PP0.2-25-3 | 0.5 | 71.8 | 0.0081 | |
| 100 | PC-100-1 | 0.3 | 50.4 | 0.0041 |
| PC-100-2 | 0.4 | 51.7 | 0.0052 | |
| PC-100-3 | 0.5 | 52.9 | 0.0058 | |
| S1PP0.2-100-1 | 0.3 | 71.1 | 0.0087 | |
| S1PP0.2-100-2 | 0.4 | 72.8 | 0.0112 | |
| S1PP0.2-100-3 | 0.5 | 75.6 | 0.0122 | |
| 200 | PC-200-1 | 0.3 | 51.6 | 0.0065 |
| PC-200-2 | 0.4 | 53.3 | 0.0074 | |
| PC-200-3 | 0.5 | 54.2 | 0.0083 | |
| S1PP0.2-200-1 | 0.3 | 79.6 | 0.0089 | |
| S1PP0.2-200-2 | 0.4 | 78.3 | 0.0119 | |
| S1PP0.2-200-3 | 0.5 | 81.4 | 0.0128 | |
| 400 | PC-400-1 | 0.3 | 40.9 | 0.0075 |
| PC-400-2 | 0.4 | 43.1 | 0.0099 | |
| PC-400-3 | 0.5 | 44.9 | 0.0113 | |
| S1PP0.2-400-1 | 0.3 | 63.8 | 0.0098 | |
| S1PP0.2-400-2 | 0.4 | 67.0 | 0.0128 | |
| S1PP0.2-400-3 | 0.5 | 69.0 | 0.0132 | |
| 600 | PC-600-1 | 0.3 | 30.2 | 0.0094 |
| PC-600-2 | 0.4 | 31.8 | 0.0109 | |
| PC-600-3 | 0.5 | 33.4 | 0.0133 | |
| S1PP0.2-600-1 | 0.3 | 49.2 | 0.0117 | |
| S1PP0.2-600-2 | 0.4 | 51.6 | 0.0147 | |
| S1PP0.2-600-3 | 0.5 | 54.0 | 0.0157 | |
| 800 | PC-800-1 | 0.3 | 17.0 | 0.0125 |
| PC-800-2 | 0.4 | 18.6 | 0.0134 | |
| PC-800-3 | 0.5 | 19.2 | 0.0152 | |
| S1PP0.2-800-1 | 0.3 | 33.5 | 0.0133 | |
| S1PP0.2-800-2 | 0.4 | 35.6 | 0.0157 | |
| S1PP0.2-800-3 | 0.5 | 36.5 | 0.0176 |
| Density (kg/m3) | 2181 | Pressure at the crushing point (MPa) | 4.9 |
| Shear modulus (GPa) | 2.75 | Volumetric strain at the collapsing point | 0.000675 |
| Normalized viscous strength | 0.45 | Pressure at the compaction point (MPa) | 810 |
| Normalized pressure hardening coefficient | 1.28 | Volumetric strain at the compaction point | 0.1 |
| Strain rate influence coefficient | 0.006 | Damage factor | 0.04 |
| Normalized pressure hardening coefficient | 0.61 | Damage factor | 1.0 |
| Static uniaxial compressive strength (MPa) | 14.8 | Pressure parameter (GPa) | 85 |
| Static tensile strength (MPa) | 2.38 | Pressure parameter (GPa) | −171 |
| Reference strain rate (ms−1) | 0.001 | Pressure parameter (GPa) | 208 |
| Total plastic strain before damage EFmin | 0.01 | Failure mode FS | 0.004 |
| Normalized maximum strength SFmax | 7 |
| Density (kg/m3) | 2317 | Pressure at the crushing point (MPa) | 9.0 |
| Shear modulus (GPa) | 4.28 | Volumetric strain at the collapsing point | 0.000675 |
| Normalized viscous strength | 0.51 | Pressure at the compaction point (MPa) | 810 |
| Normalized pressure hardening coefficient | 1.42 | Volumetric strain at the compaction point | 0.1 |
| Strain rate influence coefficient | 0.007 | Damage factor | 0.04 |
| Normalized pressure hardening coefficient | 0.63 | Damage factor | 1.0 |
| Static uniaxial compressive strength (MPa) | 27.0 | Pressure parameter (GPa) | 85 |
| Static tensile strength (MPa) | 3.22 | Pressure parameter (GPa) | −171 |
| Reference strain rate (ms−1) | 0.001 | Pressure parameter (GPa) | 208 |
| Total plastic strain before damage EFmin | 0.001 | Failure mode FS | 0.004 |
| Normalized maximum strength SFmax | 7 |
| Type of Concrete | Impact Velocity | Test Method | Peak Stress Error | Peak Strain | Peak Stress Error | Peak Strain Error |
|---|---|---|---|---|---|---|
| C40 concrete | 9.6 m/s | Test | 17.0 | 0.0125 | 2.94% | 3.20% |
| Numerical simulation | 17.5 | 0.0121 | ||||
| 11.8 m/s | Test | 18.6 | 0.0134 | 4.84% | 2.99% | |
| Numerical simulation | 19.5 | 0.0138 | ||||
| 14.1 m/s | Test | 19.2 | 0.0152 | 5.21% | 2.63% | |
| Numerical simulation | 20.2 | 0.0148 | ||||
| S1PP0.2 HyFRC | 9.6 m/s | Test | 33.5 | 0.0133 | 4.78% | 0.75% |
| Numerical simulation | 35.1 | 0.0134 | ||||
| 11.8 m/s | Test | 35.6 | 0.0157 | 4.49% | 3.82% | |
| Numerical simulation | 37.2 | 0.0163 | ||||
| 14.1 m/s | Test | 36.5 | 0.0176 | 4.11% | 3.41% | |
| Numerical simulation | 38.0 | 0.0182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Li, X.; Liu, L.; Chen, X.; Du, J. Research on Mechanical Properties of Steel-Polypropylene Fiber-Reinforced Concrete after High-Temperature Treatments. Appl. Sci. 2024, 14, 3861. https://doi.org/10.3390/app14093861
Shen X, Li X, Liu L, Chen X, Du J. Research on Mechanical Properties of Steel-Polypropylene Fiber-Reinforced Concrete after High-Temperature Treatments. Applied Sciences. 2024; 14(9):3861. https://doi.org/10.3390/app14093861
Chicago/Turabian StyleShen, Xinggang, Xia Li, Lei Liu, Xinzuo Chen, and Jun Du. 2024. "Research on Mechanical Properties of Steel-Polypropylene Fiber-Reinforced Concrete after High-Temperature Treatments" Applied Sciences 14, no. 9: 3861. https://doi.org/10.3390/app14093861
APA StyleShen, X., Li, X., Liu, L., Chen, X., & Du, J. (2024). Research on Mechanical Properties of Steel-Polypropylene Fiber-Reinforced Concrete after High-Temperature Treatments. Applied Sciences, 14(9), 3861. https://doi.org/10.3390/app14093861






