Efficient Crowd Anomaly Detection Using Sparse Feature Tracking and Neural Network
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
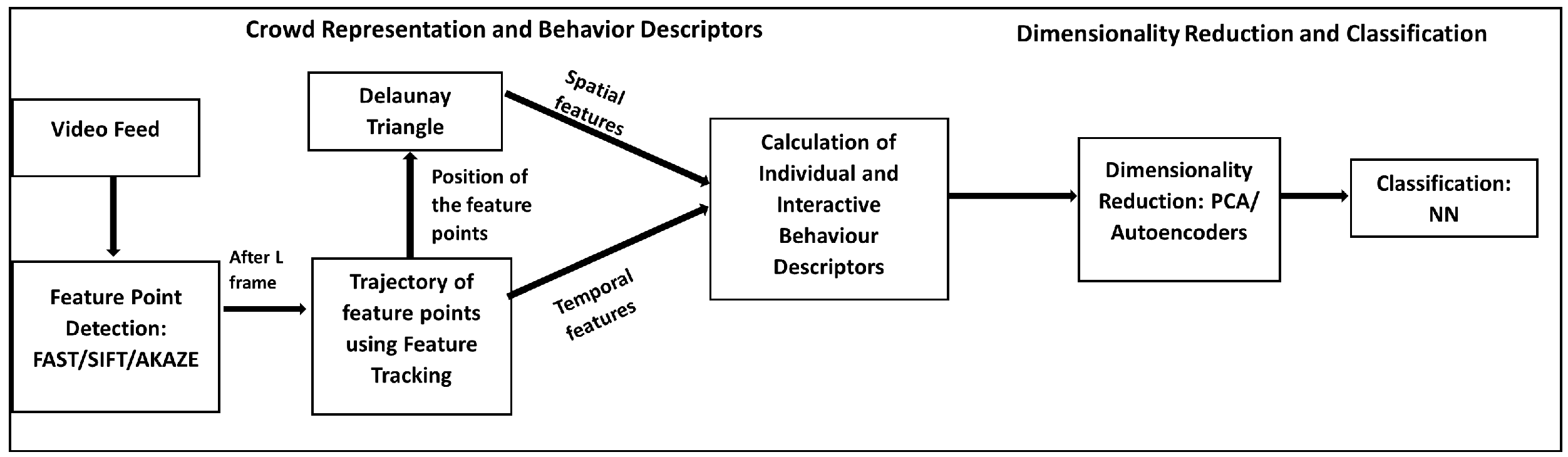
3.1. Crowd Representation and Behaviour Descriptors
3.1.1. Local Feature Extraction
- Features from Accelerated Segment Test (FAST)The FAST algorithm was initially proposed by Rosten and Drummond [32] and has been used to identify interest points in an image. Interest points are pixels with well-defined positions that can be reliably detected. These points contain significant local information and should be consistently detected across different images. It scans the image using a circular neighbourhood around each pixel and identifies potential key points based on intensity differences. The algorithm employs acceleration techniques, such as a corner criterion using predetermined sample points, to reduce the computational overhead. Non-maximum suppression is applied to select the most salient key points, discarding redundant ones. Interest point detection finds application in image matching, object recognition, and tracking and can also be utilised for crowd anomaly detection. While there are established algorithms for corner detection, such as Harris and SUSAN, the FAST algorithm was developed to address the need for a computationally efficient interest point detector suitable for real-time applications with limited computational resources, like SLAM on a mobile robot [33].
- Scale Invariant Feature Transform (SIFT)The SIFT algorithm, which was first introduced in [34], is one of the most widely known feature detection–description algorithms. It approximates the Laplacian-of-Gaussian (LoG) by utilising the Difference-of-Gaussians (DoG) operator. The DoG operator is employed to search for local maxima in images at various zoom levels, enabling the identification of feature points. To extract a robust descriptor, SIFT computes 128 bin values by considering a 16 × 16 neighbourhood around each detected feature and segmenting it into sub-blocks. Although SIFT exhibits robust invariance to image rotations, scales, and limited affine variations, its major drawback is its high computational cost. In Equation (1), the Difference-of-Gaussians (DoG) response at a given scale in the Scale Invariant Feature Transform (SIFT) algorithm is obtained by convolving the image I(x, y) with the difference of two Gaussian filters calculated at different scales. The result of this convolution represents the DoG response, which is used to detect feature points in the image.
- Accelerated-KAZE (AKAZE)The Accelerated-KAZE (AKAZE) algorithm, introduced in [11], is an extension of the KAZE algorithm that utilises a computationally efficient framework called Fast Explicit Diffusion (FED) to construct its non-linear scale spaces. AKAZE is based on non-linear diffusion filtering and employs the determinant of the Hessian matrix for feature detection. To enhance the rotation invariance, AKAZE utilises Scharr filters. The maximum responses obtained from the detectors indicate specific feature point locations. These feature points serve as the foundation for AKAZE’s robust and distinctive feature detection. The AKAZE descriptor relies on the Modified Local Difference Binary (MLDB) algorithm, which is both powerful and efficient. AKAZE’s scale spaces have a non-linear nature, resulting in invariance to scale, rotation, and limited affine transformations. Moreover, AKAZE’s features become increasingly distinctive as they are scaled up or down.
3.1.2. Sparse Feature Tracking
3.1.3. Spatial Representation Using Delaunay Triangulation
3.1.4. Visual Descriptors
- Individual BehavioursIn order to scrutinise individual actions within the crowd, we utilise two descriptors that are specifically tailored towards capturing dynamics at the individual level. Descriptors like flow directions and velocity offer insights into various aspects of individual behaviour, thereby enabling the greater comprehension of crowd interactions and movement.
- Flow DirectionThis descriptor characterises individual behaviours in terms of the motion direction, distinguishing between smooth and chaotic motions by capturing variations in tracklets’ directions [37]. This is achieved by utilising the complete history of each trajectory, which is divided into F segments , enabling a detailed analysis of directional changes over time. Following this, the variation in flow direction is determined by calculating the average of the angular differences across all trajectory segments, as given in Equation (7). This calculation provides insights into the changes in the flow direction throughout the trajectory.where , and ., and is defined for vectors and as in Equation (8),with representing the angle between the vector a and the x-axis,
- VelocityThe velocity of individuals is computed using the motion vectors as defined in Equation (4). To ensure accuracy, the motion vectors from the most recent frame history are considered, specifically those that exceed a predefined threshold for acceleration and velocity. By identifying these informative motion vectors, the velocity can be determined by dividing the vector norm by the total number of frames, as given in Equation (9).To optimise the computational efficiency, the Euclidean distance is calculated between each motion vector’s origin and current position, rather than summing the distances across fragments [37]. Empirical evidence indicates that both methods yield equivalent results, validating our decision to use the more computationally efficient method. It is worth noting that the descriptor parameter is adapted based on the video’s frame rate. This adaptation effectively compensates for perspective distortions within and between videos by incorporating perspective map weights into the motion vector’s norm. The velocity descriptor plays a vital role in capturing individuals’ speed, proving particularly valuable in scenarios where individuals exhibit variations in their speed due to factors such as danger or urgency.
- Interactive BehavioursBesides individual behaviour descriptors, we highlight the significance of integrating interactive descriptors for a comprehensive analysis. In this study, we employ a set of five interactive descriptors, three of which capture spatiotemporal information, while the remaining two specifically target spatial properties. These descriptors draw inspiration from [14] but have unique formulations as they incorporate the local crowd representation as a fundamental element in their computation. The descriptors used in this analysis include stability, collectiveness, conflict, local density, and uniformity. They are computed locally, enabling a detailed examination of the crowd characteristics and offering valuable insights for crowd analysis.
- StabilityThe concept of stability, as defined in [14], captures the degree of consistency in the topological structure of a crowd over time. It measures the tendency of individuals in a crowd to maintain their proximity to the same set of neighbours as time progresses. By assessing the stability property, valuable insights can be gained into the persistent patterns and relationships within the crowd, providing a deeper understanding of its dynamics and behaviour. This characteristic is established by drawing a parallel between a Delaunay graph’s topological structure and a crowd’s evolving structure. To be more precise, the stability of a graph at time k is calculated [37] via its graphical distance to the corresponding graph at time , where represents the interval used to fragment the trajectory for the computation of the descriptor, as defined in Equation (7). In order to establish temporal matching between cliques, the proposed graphical distance utilises the temporal aspect of the model of the tracklets and is locally computed for each vertex. The stability of a given vertex is calculated as the strain between the two adjacent cliques and , computed as in the following Equation (10):Each clique is represented by a set of clockwise-oriented triangles, and this is used to define the graphical distance between two cliques and , represented by Equation (11):The term pertains to the quantity of neighbours within the clique. The computation is carried out in two steps, as currently formulated. Initially, we determine the dissimilarity between the triangles that are matched and indexed as and . For the remaining triangles on both sides, where no matching is achieved through tracklets, we estimate the distance by selecting the most similar triangle as a potential corresponding candidate. The function denotes the measure of the distance between triangles, which is mathematically defined as the discrepancy in the cross ratio, taking into account the relative size of each triangle.where and in Equation (12) are the area and the cross ratio of a triangle indexed by . To calculate the cross ratio, we use Equation (13):The cross ratio is used to measure the shape difference since it is invariant to a projective transform. For a triangle , it is computed using the two ends of the boundary edges and , and the projections and of the midpoints of two sides ([ and ) on the boundary line. Since the cross ratio is not affected by a projective transformation, it can be used to quantify the degree of shape dissimilarity between two figures. This ratio is calculated for a triangle , by locating the endpoints of the boundary edges and and the projections of the midpoints of the two sides ([ and ) onto the boundary line and .
- CollectivenessThe collectiveness property in crowd analysis refers to how pedestrians move together as a group. In [14], this property is quantified by computing each individual’s directional deviation from the group’s global motion. Traditionally, coherent motion has been determined using predefined collective transitions. However, an alternative approach is used in this work by utilising cliques for the local computation of this descriptor [37]. Specifically, the collectiveness of a set of seed points is defined based on the degree of motion deviation from the global motion exhibited by their neighbouring points, all moving cohesively towards a common goal, as defined by the clique. By considering the local interactions within the clique, we can capture the collectiveness of the pedestrians, providing valuable insights into their coordinated movement patterns and group dynamics. The collectiveness can be computed using the following Equation (14):where
- ConflictConflict is an important property that captures human interactions in crowded environments, particularly when individuals are near each other. Like the approach used to compute the collectiveness descriptor, the conflict property is also computed locally [37]. A neighbour point from the corresponding clique is considered as a potential conflict point candidate for each seed point only if both of their motion vectors converge, indicating movement towards their origins. Consequently, the set of conflict points, denoted as , forms a subset of the neighbours. Once the set of conflict points is determined, the conflict level of the central point is calculated by considering the angular difference and distance from the other points. The calculation of the conflict level is represented by Equation (15), in which the angular difference and distance from the other points are used to determine the conflict level of the central point. This helps to gain insights into the level of interpersonal interaction and potential congestion in crowded scenes, enabling a more comprehensive understanding of the dynamics and social behaviours within the crowd.
- Local DensityThe local density descriptor focuses solely on the spatial aspect of the model, distinguishing it from the previous interactive descriptors. It captures a critical characteristic of crowd behaviour, specifically how individuals are distributed within the scene. An approximate measure of the local density can be obtained by assessing the proximity of nearby features, as defined in [15]. This is based on the observation that when nearby features move closer together, it indicates a higher likelihood of a larger crowd gathering in that area. After removing static tracklets, the remaining raw tracklets are utilised for this purpose. Each vertex’s local density, denoted as , is estimated by applying a kernel density function to the relative positions of the vertices within their respective neighbourhood sets. Instead of using a clique as in [15], a clique from the Delaunay graph is employed to define the neighbourhood set [37]. The calculation of the local density descriptor is shown in Equation (16) as follows:The contribution of each neighbouring point to the density calculation is determined by the bandwidth of the 2D Gaussian kernel, represented as . It is crucial to select an appropriate value for to ensure that feature points in close proximity to are adequately considered in the density estimation. A larger is required for objects that are closer together due to the influence of perspective distortions on the detected feature points. A normalisation process is applied to the perspective map to address this issue, and the Euclidean distances between vertices are adjusted accordingly. This normalisation guarantees that the computation of the local density remains consistent regardless of the scale or resolution used, providing reliable and comparable results.
- UniformityThe uniformity descriptor is employed to assess the coherence of the spatial distribution of regional features. It indicates whether a group exhibits a tendency to cluster together (uniform) or to fragment into smaller subgroups (nonuniform), as described in [14]. This descriptor operates at a semi-local level, focusing on the characteristics of groups rather than individual points. To achieve this, a clustering algorithm is applied to visually distinguish different types of people. Distance-based clustering, which identifies clusters based on the proximity of points, is a suitable approach as it does not require prior knowledge of the number of clusters [37]. Subsequently, for a set of clusters denoted as clusters , the modularity function is computed for each cluster to quantify its consistency. This evaluation considers both internal and external relationships within the clusters, providing insights into the level of coherence exhibited by the group. It is calculated as in Equation (17) given below:The computation of the uniformity descriptor involves graph-based calculations. After applying the clustering procedure, each vertex is assigned to a specific cluster. The distances between connected points are considered to determine the inter-cluster and intra-cluster relationships. If a connected point belongs to the same cluster as the seed point, the distance is used to enhance the intra-cluster weight. Conversely, if the connected point belongs to a different cluster, the distance contributes to the inter-cluster weight. This analysis is performed using a first-order clique , which facilitates the assessment of the spatial relationships between vertices within and across clusters [37].Shorter within-class distances and longer between-class distances are indicative of a high level of spatial uniformity within each grouping.The proposed visual and local descriptors capture both interactive and individual properties, offering valuable insights into crowds’ spatial distributions and movements. These descriptors are particularly relevant for high-level analysis as they closely align with the crowd behaviour and semantic information. Each descriptor is encoded using a 1D histogram with 16 bins, enabling statistical computations at both local patch and global frame levels. The histogram effectively represents the distribution of the descriptor values within specific regions, making it a suitable choice for our analysis. After scaling, the histograms can be concatenated to form a feature vector. The current methodology serves as a robust foundation for the detection of crowd anomalies across diverse scenarios.
3.2. Dimensionality Reduction and Classification
4. Results
4.1. Datasets
4.2. Crowd Representation
4.3. Classification Results
4.4. Result Comparison
5. Conclusions and Future Study
- Transitioning from conventional neural networks to advanced deep learning architectures promises enhanced performance;
- Incorporating cutting-edge feature extraction methods can provide more comprehensive insights into crowd behaviour patterns;
- To enable real-world applicability, rigorous testing on real-time datasets that encompass distortions and complexities is necessary;
- The fusion of multimodal data and the extension of the methodology to detect various types of anomalies hold substantial potential.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAD | Crowd Anomaly Detection |
| PCA | Principle Component Analysis |
| FAST | Features from the Accelerated Segment Test |
| SIFT | Scale-Invariant Feature Transform |
| AKAZE | Accelerated-KAZE |
| NN | Neural Network |
| ACC | Accuracy |
| AUC | Area Under the Curve |
References
- Aldayri, A.; Albattah, W. Taxonomy of Anomaly Detection Techniques in Crowd Scenes. Sensors 2022, 22, 6080. [Google Scholar] [CrossRef] [PubMed]
- Altowairqi, S.; Luo, S.; Greer, P. A Review of the Recent Progress on Crowd Anomaly Detection. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 3448–3470. [Google Scholar] [CrossRef]
- Kaltsa, V.; Briassouli, A.; Kompatsiaris, I.; Hadjileontiadis, L.J.; Strintzis, M.G. Swarm intelligence for detecting interesting events in crowded environments. IEEE Trans. Image Process. 2015, 24, 2153–2166. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, P.C.; Audigier, R.; Pham, Q.C. RIMOC, a feature to discriminate unstructured motions: Application to violence detection for video-surveillance. Comput. Vis. Image Underst. 2016, 144, 121–143. [Google Scholar] [CrossRef]
- Li, T.; Chang, H.; Wang, M.; Ni, B.; Hong, R.; Yan, S. Crowded scene analysis: A survey. IEEE Trans. Circuits Syst. Video Technol. 2014, 25, 367–386. [Google Scholar] [CrossRef]
- Loy, C.C.; Xiang, T.; Gong, S. Detecting and discriminating behavioural anomalies. Pattern Recognit. 2011, 44, 117–132. [Google Scholar] [CrossRef]
- Choi, W.; Savarese, S. A unified framework for multi-target tracking and collective activity recognition. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part IV 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 215–230. [Google Scholar]
- Real-Time Crowd Simulation: A Review. Available online: http://www.leggettnet.org.uk/docs/crowdsimulation.pdf (accessed on 31 December 2023).
- Krausz, B.; Bauckhage, C. Loveparade 2010: Automatic video analysis of a crowd disaster. Comput. Vis. Image Underst. 2012, 116, 307–319. [Google Scholar] [CrossRef]
- Benabbas, Y.; Ihaddadene, N.; Djeraba, C. Motion pattern extraction and event detection for automatic visual surveillance. EURASIP J. Image Video Process. 2010, 2011, 163682. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Solutions, T. Fast explicit diffusion for accelerated features in nonlinear scale spaces. IEEE Trans. Patt. Anal. Mach. Intell 2011, 34, 1281–1298. [Google Scholar]
- Rao, A.S.; Gubbi, J.; Marusic, S.; Palaniswami, M. Crowd event detection on optical flow manifolds. IEEE Trans. Cybern. 2015, 46, 1524–1537. [Google Scholar] [CrossRef]
- Mousavi, H.; Mohammadi, S.; Perina, A.; Chellali, R.; Murino, V. Analyzing tracklets for the detection of abnormal crowd behavior. In Proceedings of the 2015 IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 148–155. [Google Scholar]
- Shao, J.; Change Loy, C.; Wang, X. Scene-independent group profiling in crowd. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2219–2226. [Google Scholar]
- Fradi, H.; Dugelay, J.L. Spatial and temporal variations of feature tracks for crowd behavior analysis. J. Multimodal User Interfaces 2016, 10, 307–317. [Google Scholar] [CrossRef]
- Mehran, R.; Oyama, A.; Shah, M. Abnormal crowd behavior detection using social force model. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 935–942. [Google Scholar]
- Wu, S.; Moore, B.E.; Shah, M. Chaotic invariants of lagrangian particle trajectories for anomaly detection in crowded scenes. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2054–2060. [Google Scholar]
- Mehran, R.; Moore, B.E.; Shah, M. A Streakline Representation of Flow in Crowded Scenes. In Computer Vision–ECCV 2010: 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; Proceedings, Part III 11; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6313, pp. 439–452. [Google Scholar]
- Bendali-Braham, M.; Weber, J.; Forestier, G.; Idoumghar, L.; Muller, P.A. Recent trends in crowd analysis: A review. Mach. Learn. Appl. 2021, 4, 100023. [Google Scholar] [CrossRef]
- Feng, J.; Wang, D.; Zhang, L. Crowd Anomaly Detection via Spatial Constraints and Meaningful Perturbation. ISPRS Int. J. Geo-Inf. 2022, 11, 205. [Google Scholar] [CrossRef]
- Singh, K.; Rajora, S.; Vishwakarma, D.K.; Tripathi, G.; Kumar, S.; Walia, G.S. Crowd anomaly detection using Aggregation of Ensembles of fine-tuned ConvNets. Neurocomputing 2020, 371, 188–198. [Google Scholar] [CrossRef]
- Alhothali, A.; Balabid, A.; Alharthi, R.; Alzahrani, B.; Alotaibi, R.; Barnawi, A. Anomalous event detection and localization in dense crowd scenes. Multimed. Tools Appl. 2023, 82, 15673–15694. [Google Scholar] [CrossRef]
- Alafif, T.; Hadi, A.; Allahyani, M.; Alzahrani, B.; Alhothali, A.; Alotaibi, R.; Barnawi, A. Hybrid classifiers for spatio-temporal real-time abnormal behaviors detection, tracking, and recognition in massive hajj crowds. arXiv 2022, arXiv:2207.11931. [Google Scholar]
- Hao, Y.; Li, J.; Wang, N.; Wang, X.; Gao, X. Spatiotemporal consistency-enhanced network for video anomaly detection. Pattern Recognit. 2022, 121, 108232. [Google Scholar] [CrossRef]
- Traoré, A.; Akhloufi, M.A. Violence detection in videos using deep recurrent and convolutional neural networks. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 154–159. [Google Scholar]
- Doshi, K.; Yilmaz, Y. A modular and unified framework for detecting and localizing video anomalies. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2022; pp. 3982–3991. [Google Scholar]
- Alafif, T.; Alzahrani, B.; Cao, Y.; Alotaibi, R.; Barnawi, A.; Chen, M. Generative adversarial network based abnormal behavior detection in massive crowd videos: A Hajj case study. J. Ambient Intell. Humaniz. Comput. 2021, 13, 4077–4088. [Google Scholar] [CrossRef]
- Ullah, W.; Ullah, A.; Hussain, T.; Khan, Z.A.; Baik, S.W. An efficient anomaly recognition framework using an attention residual LSTM in surveillance videos. Sensors 2021, 21, 2811. [Google Scholar] [CrossRef]
- Bhuiyan, M.R.; Abdullah, J.; Hashim, N.; Al Farid, F.; Samsudin, M.A.; Abdullah, N.; Uddin, J. Hajj pilgrimage video analytics using CNN. Bull. Electr. Eng. Inform. 2021, 10, 2598–2606. [Google Scholar] [CrossRef]
- Sikdar, A.; Chowdhury, A.S. An adaptive training-less framework for anomaly detection in crowd scenes. Neurocomputing 2020, 415, 317–331. [Google Scholar] [CrossRef]
- Xiao, X. Abnormal Event Detection and Localization Based on Crowd Analysis in Video Surveillance. J. Artif. Intell. Pract. 2023, 6, 58–65. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and better: A machine learning approach to corner detection. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Rosten, E.; Drummond, T. Fusing points and lines for high performance tracking. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 2, pp. 1508–1515. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sharmin, N.; Brad, R. Optimal filter estimation for Lucas-Kanade optical flow. Sensors 2012, 12, 12694–12709. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, IJCAI’81, San Francisco, CA, USA, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Fradi, H.; Luvison, B.; Pham, Q.C. Crowd behavior analysis using local mid-level visual descriptors. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 589–602. [Google Scholar] [CrossRef]
- Shin, D.; Tjahjadi, T. Similarity invariant delaunay graph matching. In Proceedings of the Structural, Syntactic, and Statistical Pattern Recognition: Joint IAPR International Workshop, SSPR & SPR 2008, Orlando, FL, USA, 4–6 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 25–34. [Google Scholar]
- Partridge, M.; Calvo, R.A. Fast dimensionality reduction and simple PCA. Intell. Data Anal. 1998, 2, 203–214. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Aljuaid, H.; Akhter, I.; Alsufyani, N.; Shorfuzzaman, M.; Alarfaj, M.; Alnowaiser, K.; Jalal, A.; Park, J. Postures anomaly tracking and prediction learning model over crowd data analytics. PeerJ Comput. Sci. 2023, 9, e1355. [Google Scholar] [CrossRef]
- Hassner, T.; Itcher, Y.; Kliper-Gross, O. Violent flows: Real-time detection of violent crowd behavior. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Cong, Y.; Yuan, J.; Liu, J. Sparse reconstruction cost for abnormal event detection. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3449–3456. [Google Scholar]
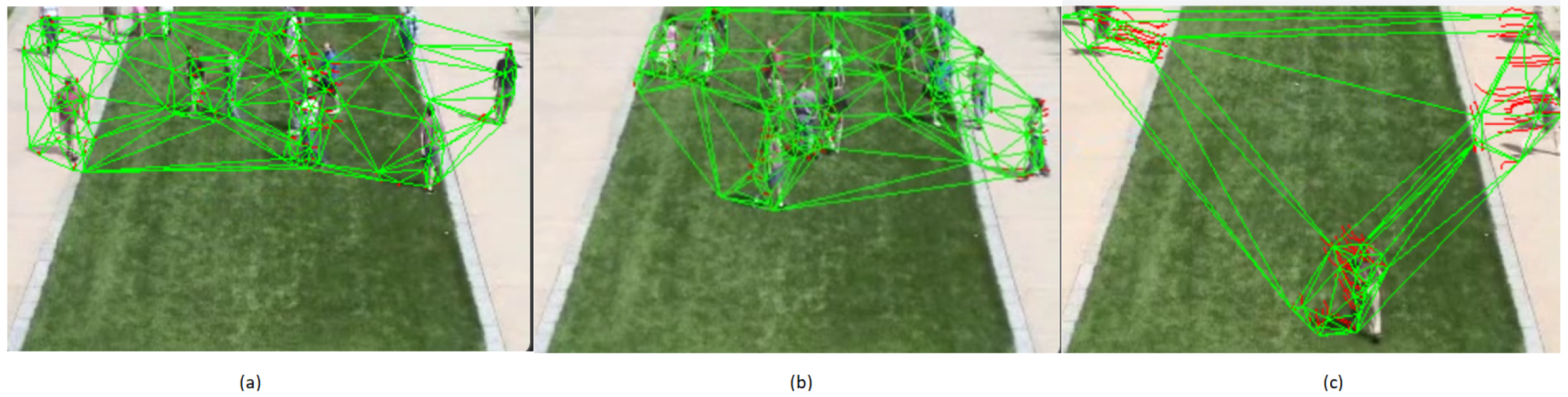
| Methods | Datasets Used | Performance Metrics |
|---|---|---|
| GAN [24] | ShanghaiTech | 73.8% AUC |
| RNN, 2D CNN [25] | Violent-Flow | 93.53% Accuracy |
| CNN, RNN KNN, Optical Flow [26] | ShanghaiTech | 73.62% Accuracy |
| Optical Flow GAN [27] | Hajj datasets UMN | 79.63% Accuracy 98.1% AUC |
| CNN Residual LSTM [28] | UCF-Crime | 70.4% AUC |
| CNN [29] | ShanghaiTech | 240.0 MAE, 260.5 MSE |
| CNN, Random Forest [23] | HajjV2 | 76.08% AUC |
| Optical Flow [30] | ShanghaiTech | 89.29% AUC |
| CNN, Histogram of Optical Flow, SVM [22] | HajjV2 | 88.96% AUC |
| gKLT + Collectiveness Energy Index (CEI) [31] | UMN | Scene 1: 92.32%, Scene 3: 94.2% |
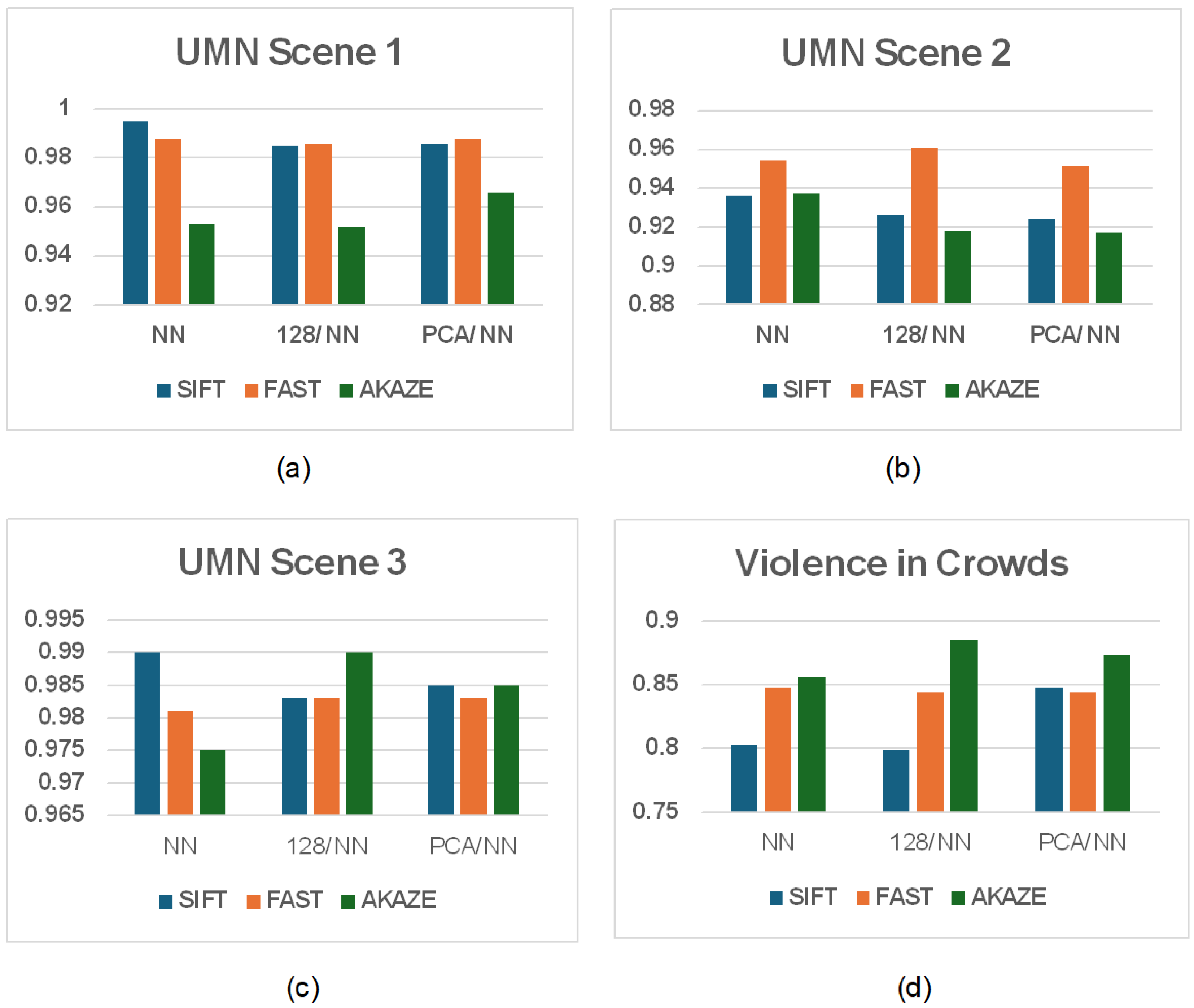
| Scene 1 | NN | 128/NN | PCA/NN |
| SIFT | ACC: 0.995 AUC: 0.990 | ACC: 0.985 AUC: 0.979 | ACC: 0.986 AUC: 0.983 |
| FAST | ACC: 0.988 AUC: 0.977 | ACC: 0.986 AUC: 0.973 | ACC: 0.988 AUC: 0.978 |
| AKAZE | ACC: 0.953 AUC: 0.904 | ACC: 0.952 AUC: 0.943 | ACC: 0.966 AUC: 0.955 |
| Scene 2 | NN | 128/NN | PCA/NN |
| SIFT | ACC: 0.936 AUC: 0.901 | ACC: 0.926 AUC: 0.893 | ACC: 0.924 AUC: 0.885 |
| FAST | ACC: 0.954 AUC: 0.937 | ACC: 0.961 AUC: 0.943 | ACC: 0.951 AUC: 0.931 |
| AKAZE | ACC: 0.937 AUC: 0.892 | ACC: 0.918 AUC: 0.892 | ACC: 0.917 AUC: 0.872 |
| Scene 3 | NN | 128/NN | PCA/NN |
| SIFT | ACC: 0.990 AUC: 0.976 | ACC: 0.983 AUC: 0.980 | ACC: 0.985 AUC: 0.968 |
| FAST | ACC: 0.981 AUC: 0.956 | ACC: 0.983 AUC: 0.973 | ACC: 0.983 AUC: 0.959 |
| AKAZE | ACC: 0.975 AUC: 0.914 | ACC: 0.990 AUC: 0.988 | ACC: 0.985 AUC: 0.968 |
| Methods | NN | 128/NN | PCA/NN |
|---|---|---|---|
| SIFT | ACC: 0.803 AUC: 0.805 | ACC: 0.799 AUC: 0.804 | ACC: 0.848 AUC: 0.846 |
| FAST | ACC: 0.848 AUC: 0.851 | ACC: 0.844 AUC: 0.847 | ACC: 0.844 AUC: 0.851 |
| AKAZE | ACC: 0.856 AUC: 0.862 | ACC: 0.885 AUC: 0.895 | ACC: 0.873 AUC: 0.878 |
| Methods | AUC % | Accuracy % |
|---|---|---|
| Optical Flow [16] | 84.0 | / |
| SFM [16] | 96.0 | / |
| Sparse Reconstruction [43] | 97.0 | / |
| Visual Descriptors [37] | Scene 1: 0.98.72, Scene 2: 95.21, Scene 3: 97.50 | / |
| Optical Flow, GAN [27] | 98.1 | / |
| Our Approach | Scene 1: 99.0, Scene 2: 94.3, Scene 3: 98.8 | Scene 1: 99.5, Scene 2: 96.1, Scene 3: 99.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altowairqi, S.; Luo, S.; Greer, P.; Chen, S. Efficient Crowd Anomaly Detection Using Sparse Feature Tracking and Neural Network. Appl. Sci. 2024, 14, 3928. https://doi.org/10.3390/app14093928
Altowairqi S, Luo S, Greer P, Chen S. Efficient Crowd Anomaly Detection Using Sparse Feature Tracking and Neural Network. Applied Sciences. 2024; 14(9):3928. https://doi.org/10.3390/app14093928
Chicago/Turabian StyleAltowairqi, Sarah, Suhuai Luo, Peter Greer, and Shan Chen. 2024. "Efficient Crowd Anomaly Detection Using Sparse Feature Tracking and Neural Network" Applied Sciences 14, no. 9: 3928. https://doi.org/10.3390/app14093928
APA StyleAltowairqi, S., Luo, S., Greer, P., & Chen, S. (2024). Efficient Crowd Anomaly Detection Using Sparse Feature Tracking and Neural Network. Applied Sciences, 14(9), 3928. https://doi.org/10.3390/app14093928







