Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact
Abstract
1. Introduction
2. Methodology
2.1. Projection Matrix
2.2. Static Modal Derivatives
2.2.1. Dominant Mode Selection
2.2.2. Static Modal Derivative Selection
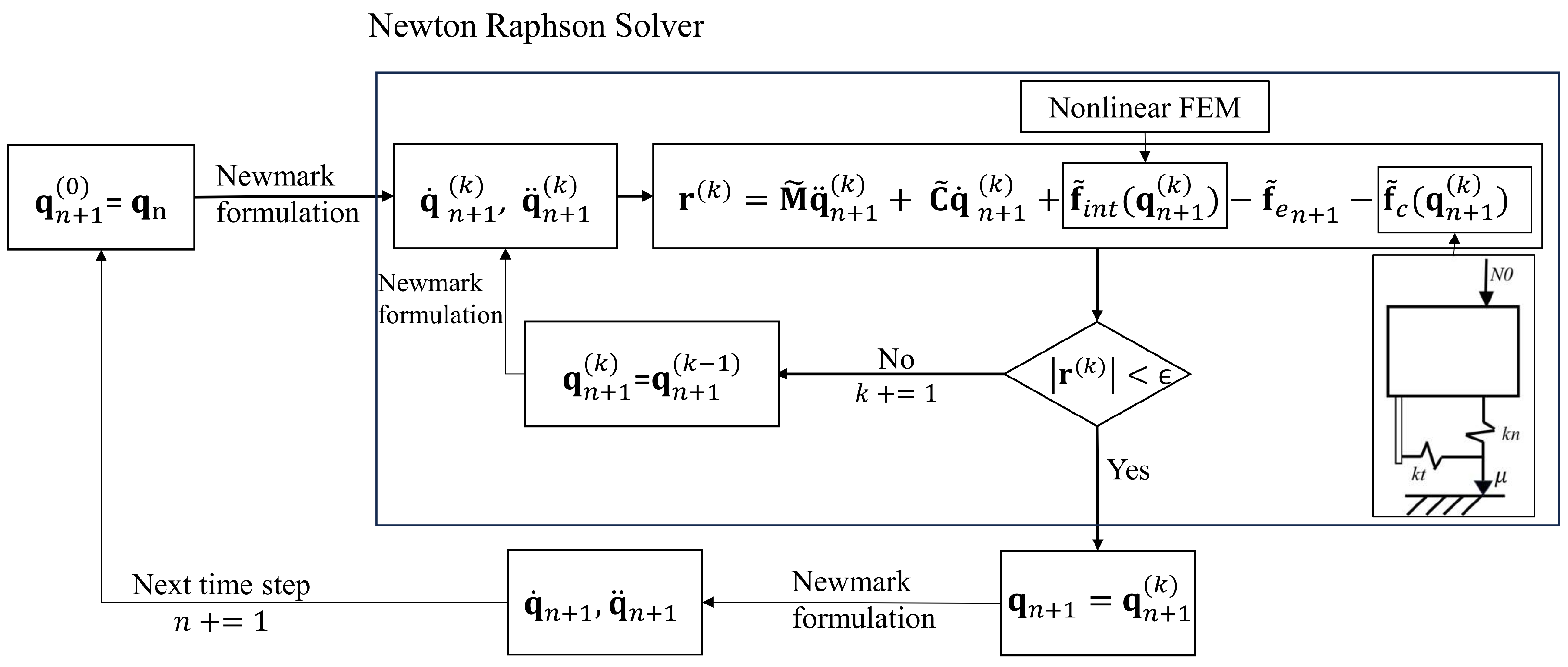
2.3. Time Domain Analysis
3. Numerical Analysis
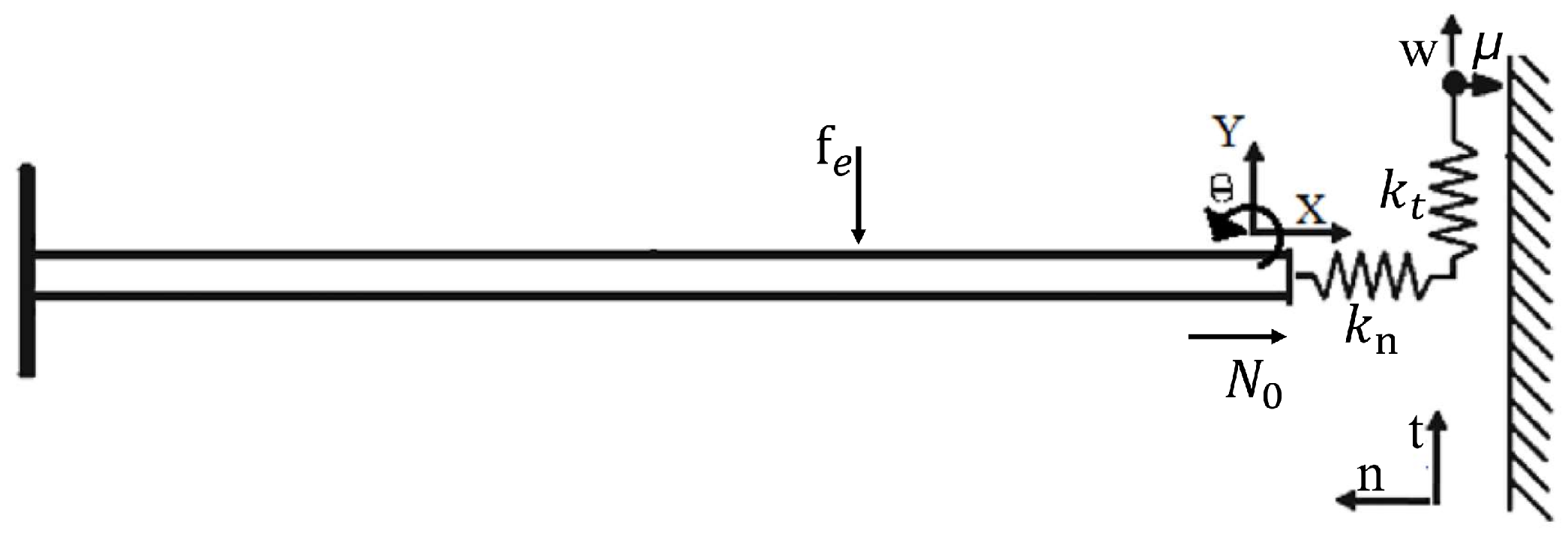
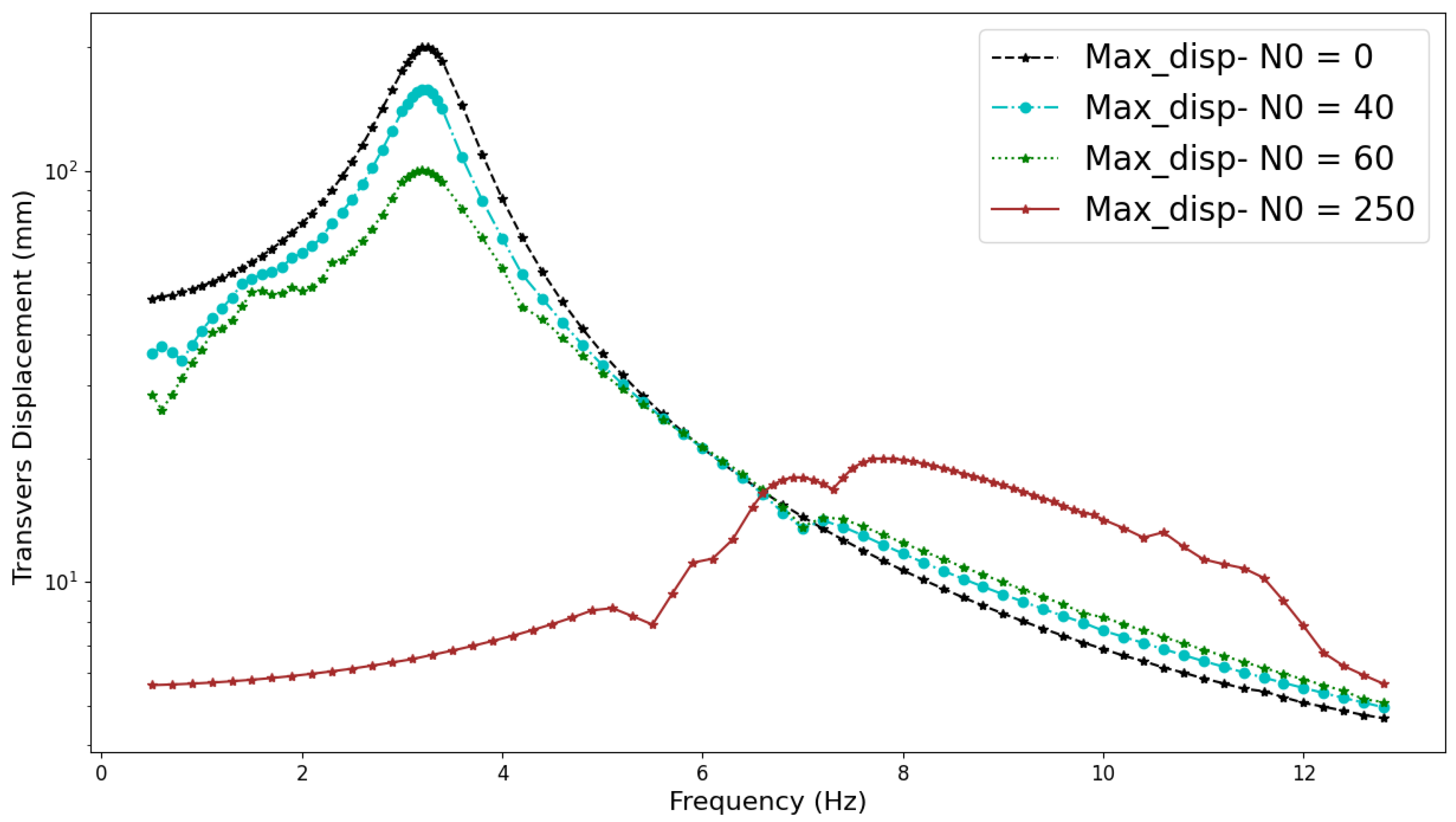
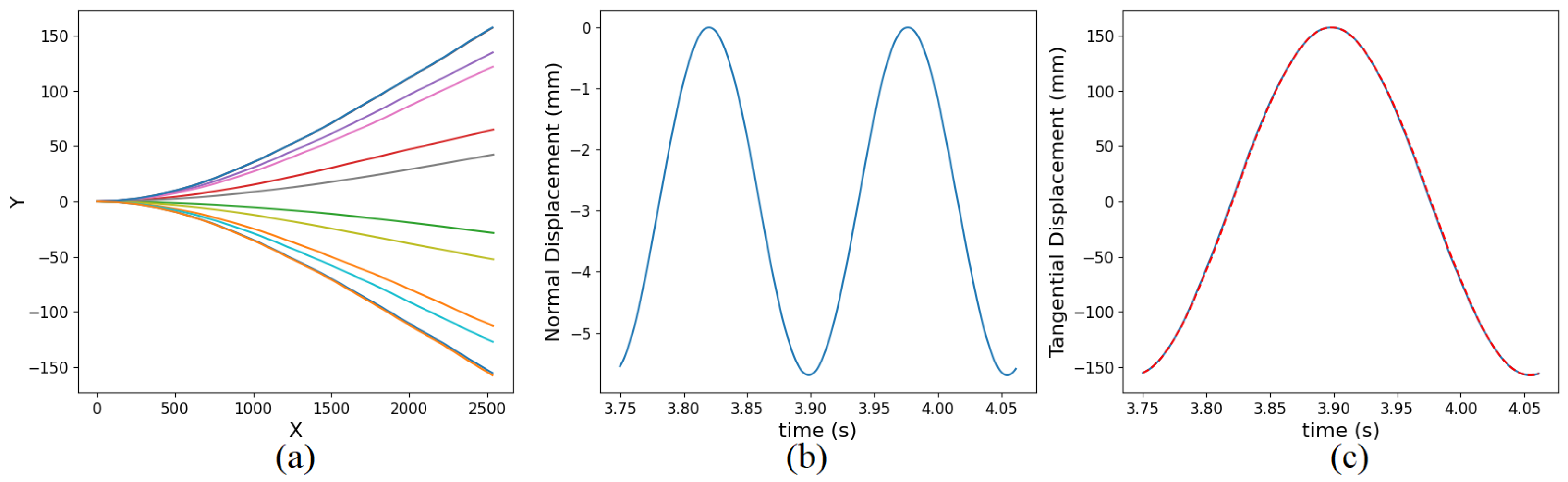
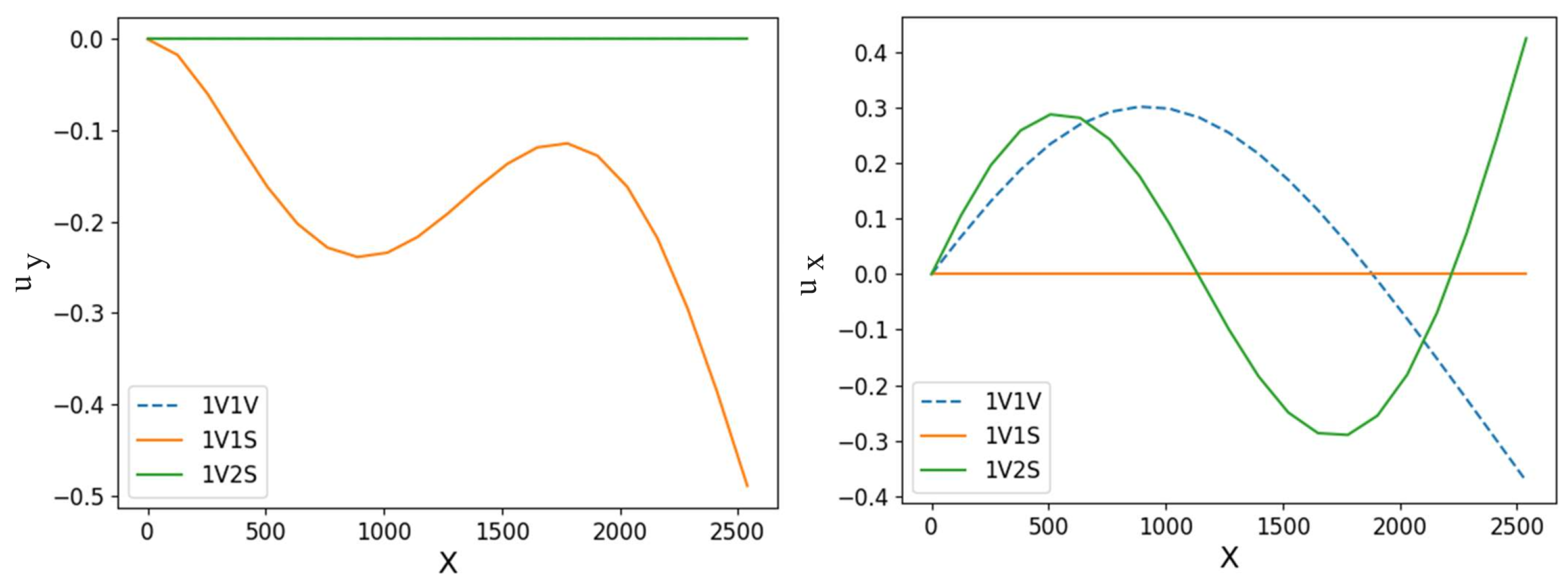
3.1. Slip–Liftoff Configuration
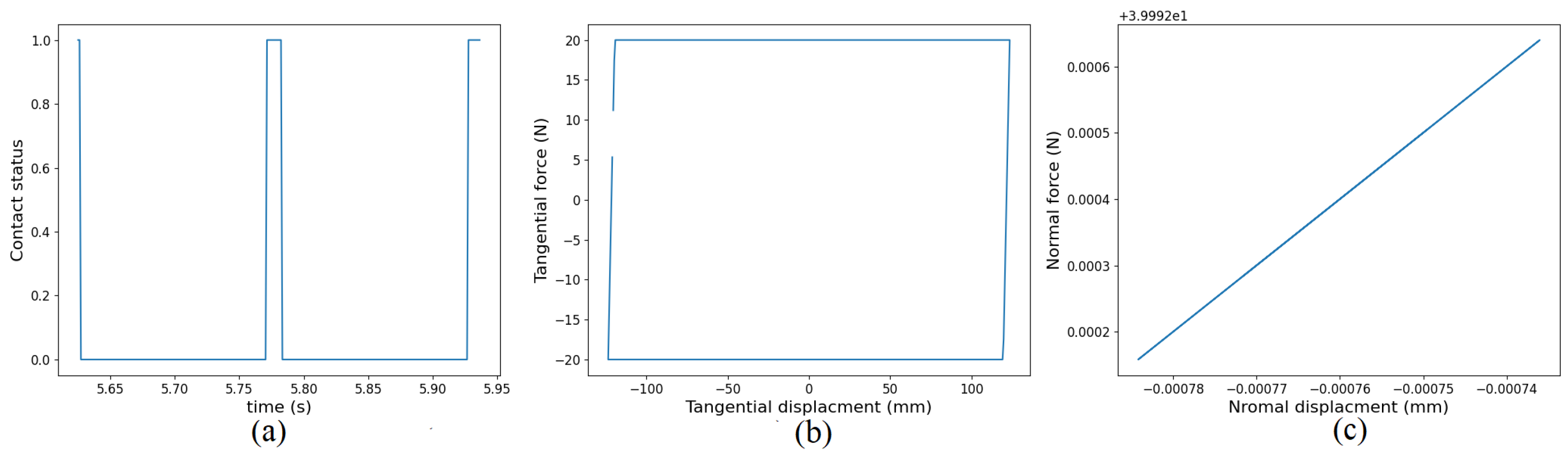
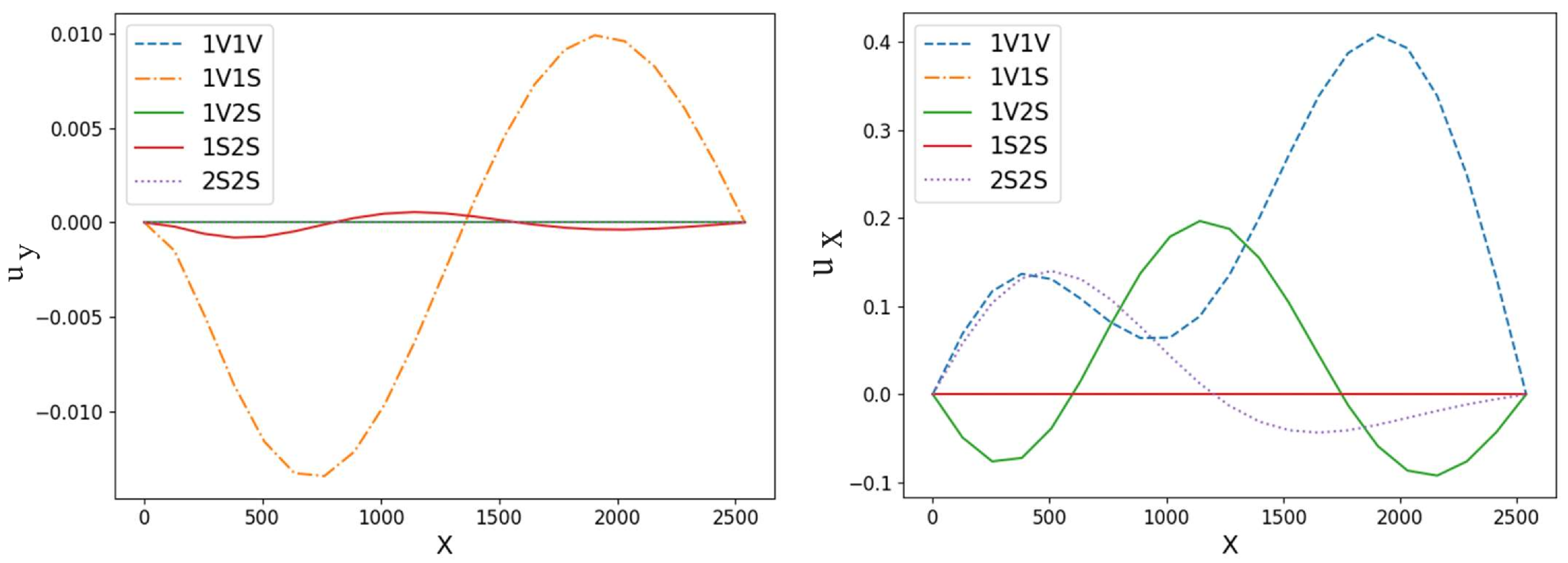
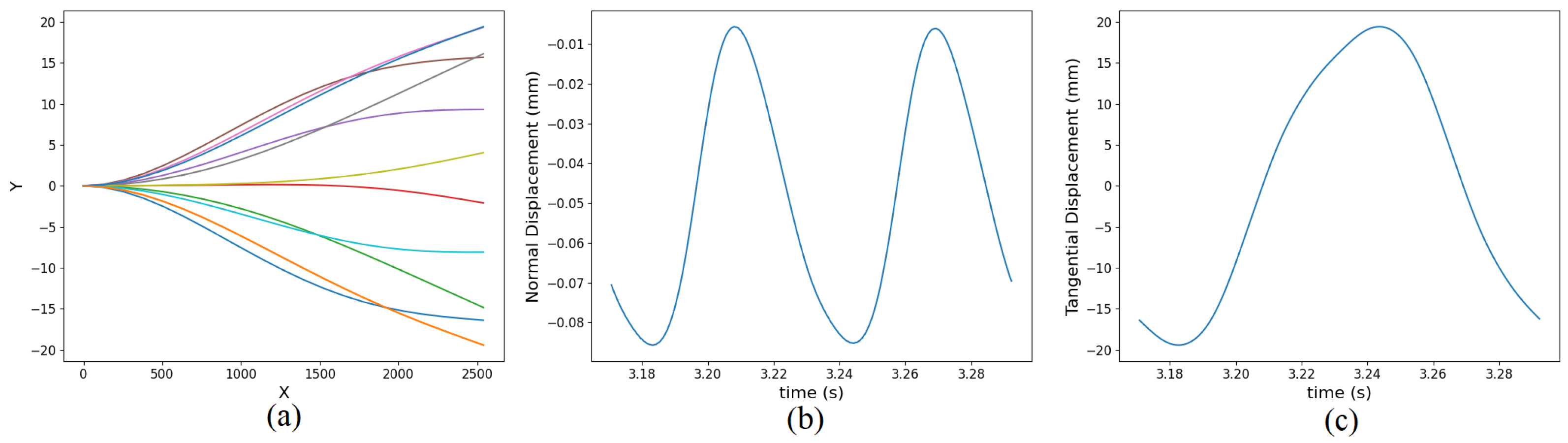
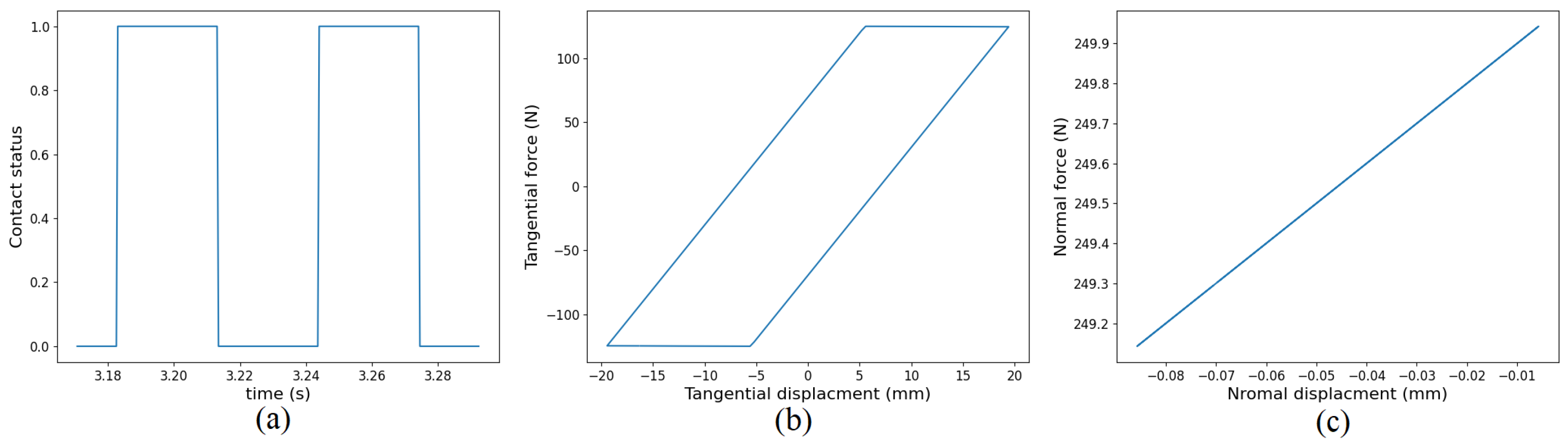
3.2. Stick–Slip Configuration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DoF | Degree of Freedom. |
| CMS | Component Mode Synthesis. |
| ROM | Reduced Order Model. |
| EQM | Equations of Motion. |
| GL | Geometrically Linear. |
| GNL | Geometrically Nonlinear. |
| MAC | Modal Assurance Criterion. |
| MMI | Maximum Modal Interaction. |
| SMD | Static Modal Derivative. |
| 1V | 1st normal mode. |
| 1S | 1st static mode. |
| Rubin-MD | Rubin reduced model enhanced with modal derivatives. |
| CB-MD | Craig–Bampton reduced model enhanced with modal derivatives. |
References
- Balmaseda, M.; Jacquet-Richardet, G.; Placzek, A.; Tran, D.M. Reduced order models for nonlinear dynamic analysis with application to a fan blade. J. Eng. Gas Turbines Power 2020, 142, 041002. [Google Scholar] [CrossRef]
- Larsen, J.W.; Nielsen, S.R. Non-linear dynamics of wind turbine wings. Int. J. Non-Linear Mech. 2006, 41, 629–643. [Google Scholar] [CrossRef]
- Capiez-Lernout, E.; Soize, C.; Mbaye, M. Geometric nonlinear dynamic analysis of uncertain structures with cyclic symmetry-Application to a mistuned industrial bladed disk. In Proceedings of the International Conference on Uncertainty in Structural Dynamics, USD2014, Leuven, Belgium, 15–17 September 2014; pp. 1–14. [Google Scholar]
- Delhez, E.; Nyssen, F.; Golinval, J.C.; Batailly, A. Comparative study of blades reduced order models with geometrical nonlinearities and contact interfaces. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: London, UK, 2020; Volume 84232, p. V011T30A017. [Google Scholar]
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Jain, S.; Tiso, P. Hyper-reduction over nonlinear manifolds for large nonlinear mechanical systems. J. Comput. Nonlinear Dyn. 2019, 14, 081008. [Google Scholar] [CrossRef]
- Bui, T.A.; Kim, J.S.; Park, J. Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics 2023, 11, 1572. [Google Scholar] [CrossRef]
- Yuan, J.; El-Haddad, F.; Salles, L.; Wong, C. Numerical Assessment of Reduced Order Modeling Techniques for Dynamic Analysis of Jointed Structures With Contact Nonlinearities. J. Eng. Gas Turbines Power 2019, 141, 031027. [Google Scholar] [CrossRef]
- Haenle, U.; Dinkler, D.; Kroeplin, B. Interaction of local and global nonlinearities of elastic rotating structures. AIAA J. 1995, 33, 933–937. [Google Scholar] [CrossRef]
- Charleux, D.; Gibert, C.; Thouverez, F.; Dupeux, J. Numerical and experimental study of friction damping blade attachments of rotating bladed disks. Int. J. Rotating Mach. 2006, 2006, 071302. [Google Scholar] [CrossRef]
- Petrov, E.; Ewins, D. Effects of damping and varying contact area at blade-disk joints in forced response analysis of bladed disk assemblies. J. Turbomach. 2006, 128, 403–410. [Google Scholar] [CrossRef]
- Craig, R.; Bampton, M. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- MacNeal, R.H. A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef]
- Rubin, S. Improved component-mode representation for structural dynamic analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- Martinez, D.; Marne, T.; Gregory, D.; Miller, A. Combined experimental/analytical modeling using component mode synthesis. In Proceedings of the 25th Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, USA, 22–25 October 1984; p. 941. [Google Scholar]
- Rixen, D.J. A dual Craig–Bampton method for dynamic substructuring. J. Comput. Appl. Math. 2004, 168, 383–391. [Google Scholar] [CrossRef]
- Kuether, R.J.; Allen, M.S.; Hollkamp, J.J. Modal substructuring of geometrically nonlinear finite-element models. AIAA J. 2016, 54, 691–702. [Google Scholar] [CrossRef]
- Martin, A.; Thouverez, F. Dynamic analysis and reduction of a cyclic symmetric system subjected to geometric nonlinearities. J. Eng. Gas Turbines Power 2019, 141, 041027. [Google Scholar] [CrossRef]
- Wenneker, F. Component Mode Synthesis for Geometrically Nonlinear Structures. Doctoral Dissertation, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Wenneker, F.; Tiso, P. A substructuring method for geometrically nonlinear structures. In Dynamics of Coupled Structures, Volume 1: Proceedings of the 32nd IMAC, A Conference and Exposition on Structural Dynamics, 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 157–165. [Google Scholar]
- Wu, L.; Tiso, P.; Van Keulen, F. A modal derivatives enhanced Craig-Bampton method for geometrically nonlinear structural dynamics. In Proceedings of the 27th International Conference on Noise and Vibration Engineering and International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 19–21 September 2016; pp. 3615–3624. [Google Scholar]
- Mahdiabadi, M.K.; Bartl, A.; Xu, D.; Tiso, P.; Rixen, D.J. An augmented free-interface-based modal substructuring for nonlinear structural dynamics including interface reduction. J. Sound Vib. 2019, 462, 114915. [Google Scholar] [CrossRef]
- Wu, L.; Tiso, P.; Tatsis, K.; Chatzi, E.; van Keulen, F. A modal derivatives enhanced Rubin substructuring method for geometrically nonlinear multibody systems. Multibody Syst. Dyn. 2019, 45, 57–85. [Google Scholar] [CrossRef]
- Delhez, E.; Nyssen, F.; Golinval, J.C.; Batailly, A. Numerical study of bladed structures with geometric and contact nonlinearities. J. Sound Vib. 2023, 544, 117382. [Google Scholar] [CrossRef]
- Shetty, D.; Allen, M.; Park, K. A new approach to model a system with both friction and geometric nonlinearity. J. Sound Vib. 2023, 552, 117631. [Google Scholar] [CrossRef]
- Tiso, P. Optimal second order reduction basis selection for nonlinear transient analysis. In Modal Analysis Topics, Volume 3: Proceedings of the 29th IMAC, A Conference on Structural Dynamics, 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 27–39. [Google Scholar]
- Bui, T.A.; Park, J.; Kim, J.S. A reduced-order model for geometrically nonlinear curved beam structures with substructuring techniques. Int. J. -Non-Linear Mech. 2024, 162, 104724. [Google Scholar] [CrossRef]
- Allen, M.S.; Rixen, D.; van der Seijs, M.; Tiso, P.; Abrahamsson, T.; Mayes, R.L.; Allen, M.S.; Rixen, D.; van der Seijs, M.; Tiso, P.; et al. Model reduction concepts and substructuring approaches for nonlinear systems. In Substructuring in Engineering Dynamics: Emerging Numerical and Experimental Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 233–267. [Google Scholar]
- Thomas, O.; Sénéchal, A.; Deü, J.F. Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams. Nonlinear Dyn. 2016, 86, 1293–1318. [Google Scholar] [CrossRef]
- Weeger, O.; Wever, U.; Simeon, B. On the use of modal derivatives for nonlinear model order reduction. Int. J. Numer. Methods Eng. 2016, 108, 1579–1602. [Google Scholar] [CrossRef]
- Mashayekhi, F.; Zucca, S.; Nobari, A.S. Evaluation of free interface-based reduction techniques for nonlinear forced response analysis of shrouded blades. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7459–7475. [Google Scholar] [CrossRef]
- Rutzmoser, J.B.; Rixen, D.J.; Tiso, P.; Jain, S. Generalization of quadratic manifolds for reduced order modeling of nonlinear structural dynamics. Comput. Struct. 2017, 192, 196–209. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Gastaldi, C.; Berruti, T.M. Competitive time marching solution methods for systems with friction-induced nonlinearities. Appl. Sci. 2018, 8, 291. [Google Scholar] [CrossRef]
- Yang, B.; Menq, C. Characterization of 3D contact kinematics and prediction of resonant response of structures having 3D frictional constraint. J. Sound Vib. 1998, 217, 909–925. [Google Scholar]
- Felippa, C.A.; Crivelli, L.A.; Haugen, B. A survey of the core-congruential formulation for geometrically nonlinear TL finite elements. Arch. Comput. Methods Eng. 1994, 1, 1–48. [Google Scholar] [CrossRef]
- Firrone, C.M.; Zucca, S. Modelling friction contacts in structural dynamics and its application to turbine bladed disks. Numer.-Anal.-Theory Appl. 2011, 14, 301–334. [Google Scholar]

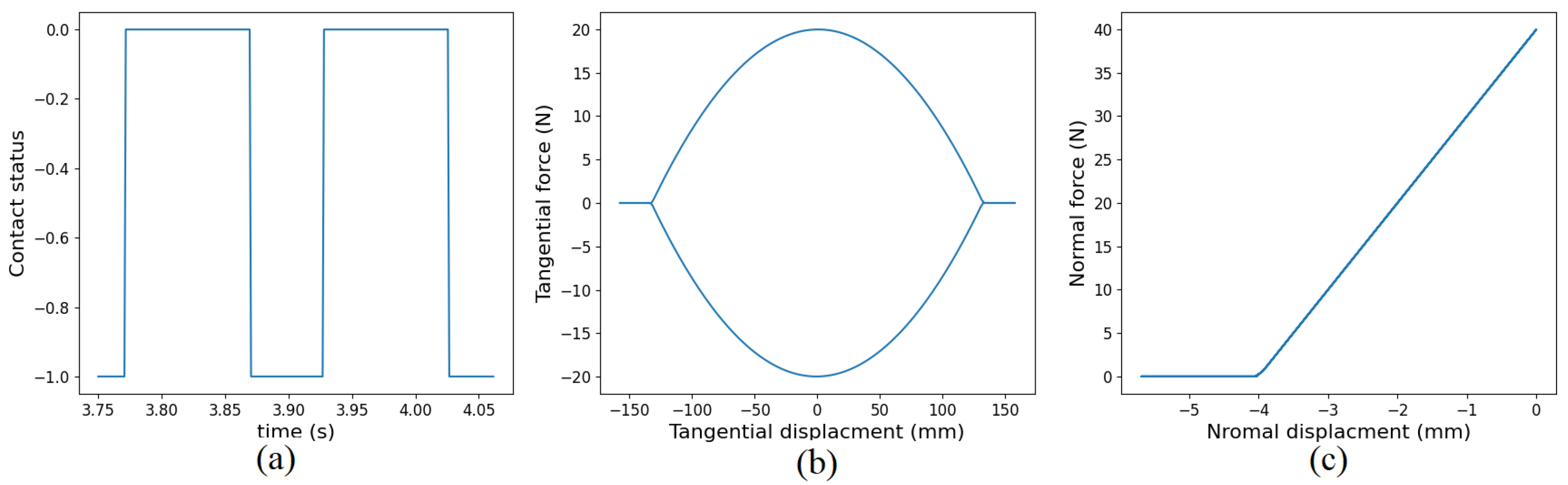
| Slip–Liftoff | Open Contact | |||
|---|---|---|---|---|
| Uy (mm) | Ux (mm) | Uy (mm) | Ux (mm) | |
| Geometrically linear model | 123.5 | 0.00039 | 200.8 | 0.0 |
| Geometrically nonlinear model | 157.6 | 2.835 | 200.5 | 4.6 |
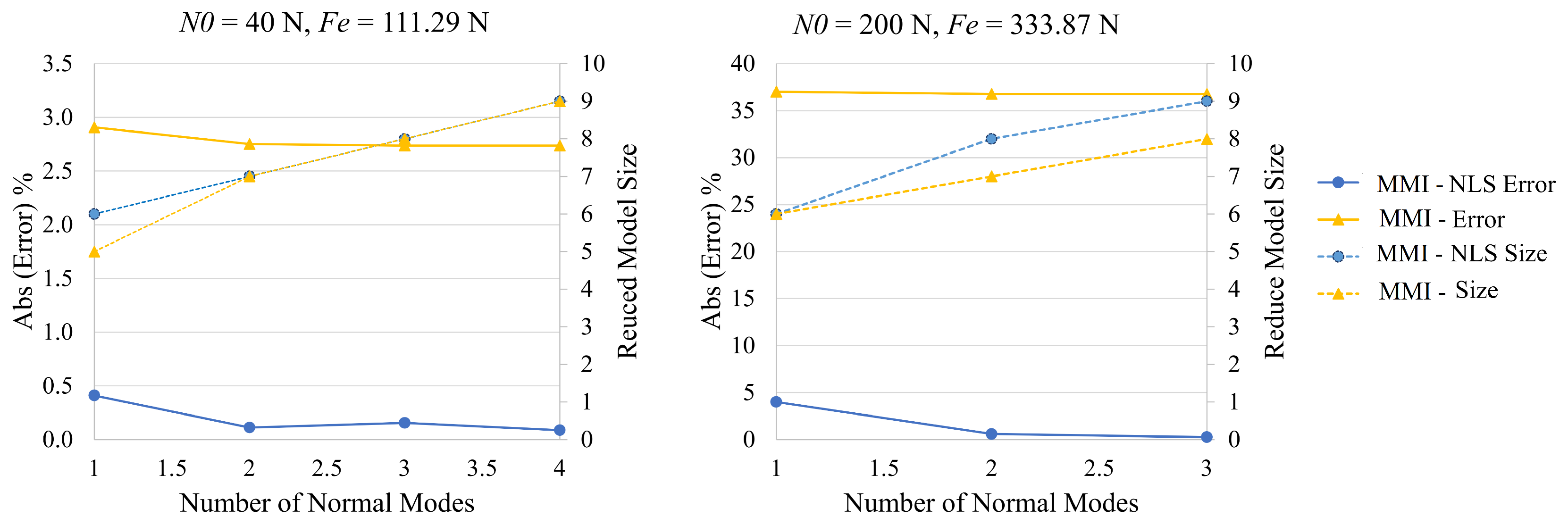
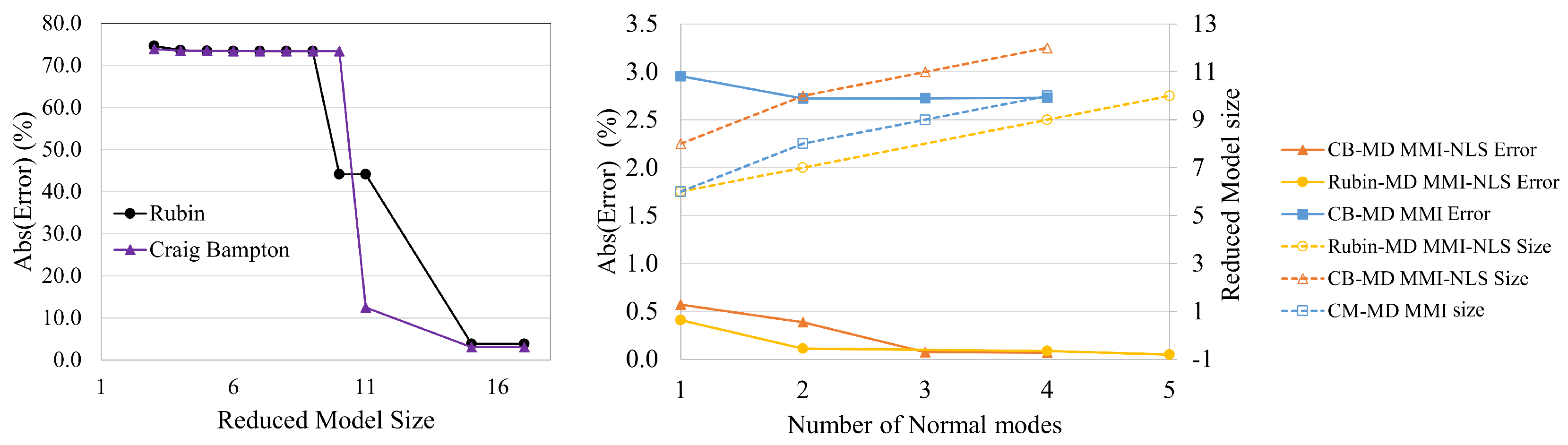
| Normal Modes | Static Modal Derivatives | Error % = 111.29 N | Error % = 333.87 N | |
|---|---|---|---|---|
| Rubin with SMD | 1V | 1V1V | 4.03 | 42 |
| Rubin with SMD | 1V | 1V1V, 1V1S, 1V2S | 0.41 | 4.2 |
| CB with SMD | 1V | 1V1V | 7.18 | 49 |
| CB with SMD | 1V | 1V1V, 1V1S, 1V2S | 0.57 | 26.3 |
| 1S2S, 2S2S |
| (mm) | (mm) | |
|---|---|---|
| Geometrically linear model | 19.73 | 0.00248 |
| Geometrically nonlinear model | 19.618 | 0.044 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashayekhi, F.; Zucca, S. Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact. Appl. Sci. 2024, 14, 3936. https://doi.org/10.3390/app14093936
Mashayekhi F, Zucca S. Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact. Applied Sciences. 2024; 14(9):3936. https://doi.org/10.3390/app14093936
Chicago/Turabian StyleMashayekhi, Fahimeh, and Stefano Zucca. 2024. "Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact" Applied Sciences 14, no. 9: 3936. https://doi.org/10.3390/app14093936
APA StyleMashayekhi, F., & Zucca, S. (2024). Modal Derivatives for Efficient Vibration Prediction of Geometrically Nonlinear Structures with Friction Contact. Applied Sciences, 14(9), 3936. https://doi.org/10.3390/app14093936






