Effects of Arm Swing in Lower Limb Muscle Activation and Coordination During Treadmill Walking
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Speed and Cadence
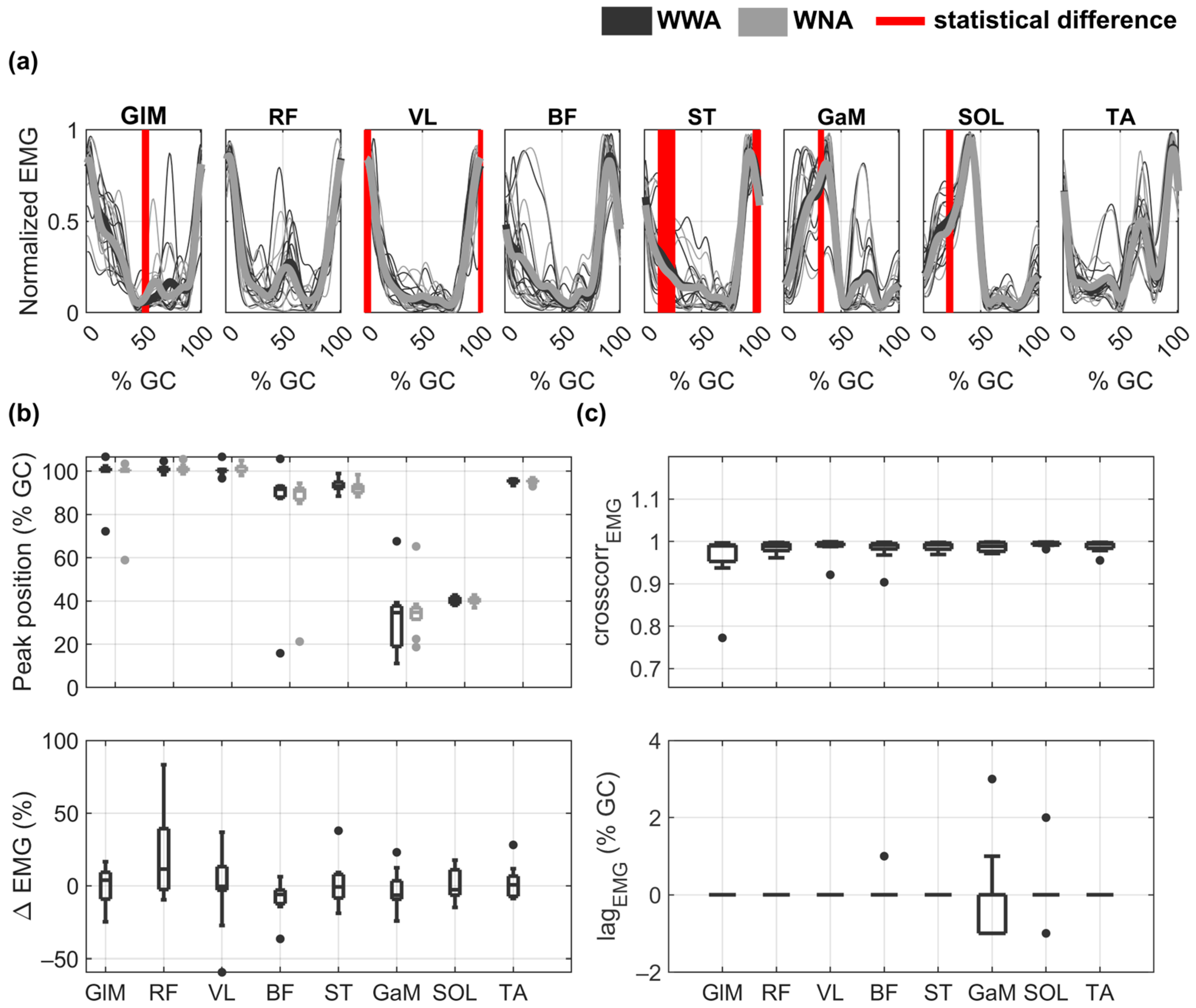
3.2. EMG Envelopes and Performance Indicators
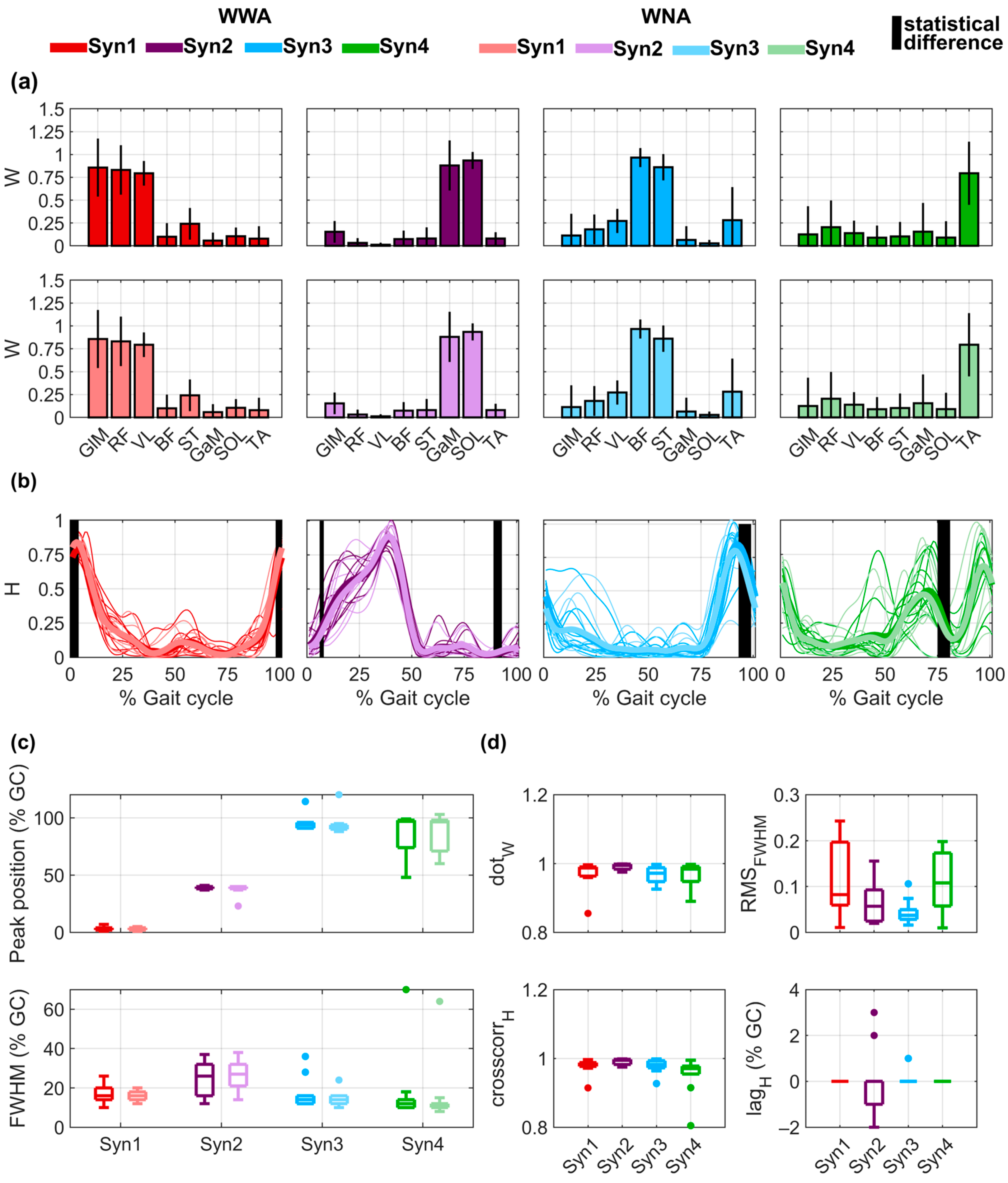
3.3. Muscle Synergy Components
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Takakusaki, K. Neurophysiology of gait: From the spinal cord to the frontal lobe. Mov. Disord. 2013, 28, 1483–1491. [Google Scholar] [CrossRef]
- Zehr, E.P.; Carroll, T.J.; Chua, R.; Collins, D.F.; Frigon, A.; Haridas, C.; Hundza, S.R.; Thompson, A.K. Possible contributions of CPG activity to the control of rhythmic human arm movement. Can. J. Physiol. Pharmacol. 2004, 82, 556–568. [Google Scholar] [CrossRef]
- Clark, D.J.; Ting, L.H.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J. Neurophysiol. 2010, 103, 844–857. [Google Scholar] [CrossRef] [PubMed]
- Moreira, L.; Figueiredo, J.; Fonseca, P.; Vilas-Boas, J.P.; Santos, C.P. Lower limb kinematic, kinetic, and EMG data from young healthy humans during walking at controlled speeds. Sci. Data 2021, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, H.; Leng, Y.; Lei, D.; Yu, Q.; Li, K.; Ding, M.; Lo, W.L.A. A protocol to analyze the global literature on the clinical benefit of interlimb-coordinated intervention in gait recovery and the associated neurophysiological changes in patients with stroke. Front. Neurol. 2022, 13, 959917. [Google Scholar] [CrossRef] [PubMed]
- Zehr, E.P.; Barss, T.S.; Dragert, K.; Frigon, A.; Vasudevan, E.V.; Haridas, C.; Hundza, S.; Kaupp, C.; Klarner, T.; Klimstra, M.; et al. Neuromechanical interactions between the limbs during human locomotion: An evolutionary perspective with translation to rehabilitation. Exp. Brain Res. 2016, 234, 3059–3081. [Google Scholar] [CrossRef] [PubMed]
- Massaad, F.; Levin, O.; Meyns, P.; Drijkoningen, D.; Swinnen, S.P.; Duysens, J. Arm sway holds sway: Locomotor-like modulation of leg reflexes when arms swing in alternation. Neuroscience 2014, 258, 34–46. [Google Scholar] [CrossRef]
- Meyns, P.; Bruijn, S.M.; Duysens, J. The how and why of arm swing during human walking. Gait Posture 2013, 38, 555–562. [Google Scholar] [CrossRef] [PubMed]
- Pijnappels, M.; Kingma, I.; Wezenberg, D.; Reurink, G.; van Dieën, J.H. Armed against falls: The contribution of arm movements to balance recovery after tripping. Exp. Brain Res. 2010, 201, 689–699. [Google Scholar] [CrossRef] [PubMed]
- Ortega, J.D.; Fehlman, L.A.; Farley, C.T. Effects of aging and arm swing on the metabolic cost of stability in human walking. J. Biomech. 2008, 41, 3303–3308. [Google Scholar] [CrossRef] [PubMed]
- Umberger, B.R. Effects of suppressing arm swing on kinematics, kinetics, and energetics of human walking. J. Biomech. 2008, 41, 2575–2580. [Google Scholar] [CrossRef]
- Yizhar, Z.; Boulos, S.; Inbar, O.; Carmeli, E. The effect of restricted arm swing on energy expenditure in healthy men. Int. J. Rehabil. Res. 2009, 32, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Lang, C.; Schleichardt, A.; Warschun, F.; Walter, N.; Fleckenstein, D.; Berkel, F.; Ueberschär, O. Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners. Sports 2023, 11, 204. [Google Scholar] [CrossRef]
- Ballesteros, M.L.F.; Buchthal, F.; Rosenfalck, P. The pattern of muscular activity during the arm swing of natural walking. Acta Physiol. Scand. 1965, 63, 296–310. [Google Scholar] [CrossRef] [PubMed]
- Goudriaan, M.; Jonkers, I.; van Dieen, J.H.; Bruijn, S.M. Arm swing in human walking: What is their drive? Gait Posture 2014, 40, 321–326. [Google Scholar] [CrossRef]
- Weersink, J.B.; de Jong, B.M.; Halliday, D.M.; Maurits, N.M. Intermuscular coherence analysis in older adults reveals that gait-related arm swing drives lower limb muscles via subcortical and cortical pathways. J. Physiol. 2021, 599, 2283–2298. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P.; Huang, H.J.; Kao, P.C. Moving the arms to activate the legs. Exerc. Sport Sci. Rev. 2006, 34, 113–120. [Google Scholar] [CrossRef]
- Stephenson, J.L.; De Serres, S.J.; Lamontagne, A. The effect of arm movements on the lower limb during gait after a stroke. Gait Posture 2010, 31, 109–115. [Google Scholar] [CrossRef]
- Kang, T.W.; Oh, D.W.; Lee, J.H.; Cynn, H.S. Effects of integrating rhythmic arm swing into robot-assisted walking in patients with subacute stroke: A randomized controlled pilot study. Int. J. Rehabil. Res. 2018, 41, 57–62. [Google Scholar] [CrossRef]
- Aoyagi, D.; Ichinose, W.E.; Harkema, S.J.; Reinkensmeyer, D.J.; Bobrow, J.E. A robot and control algorithm that can synchronously assist in naturalistic motion during body-weight-supported gait training following neurologic injury. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 387–400. [Google Scholar] [CrossRef]
- Bishop, L.; Omofuma, I.; Stein, J.; Agrawal, S.; Quinn, L. Treadmill-Based Locomotor Training With Robotic Pelvic Assist and Visual Feedback: A Feasibility Study. J. Neurol. Phys. Ther. 2020, 44, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Hunt, K.J. Mechanical Design and Control System Development of a Rehabilitation Robotic System for Walking With Arm Swing. Front. Rehabil. Sci. 2021, 2, 720182. [Google Scholar] [CrossRef] [PubMed]
- Swinnen, E.; Baeyens, J.P.; Knaepen, K.; Michielsend, M.; Clijsene, R.; Beckwéea, D.; Kerckhofs, E. Robot-assisted walking with the Lokomat: The influence of different levels of guidance force on thorax and pelvis kinematics. Clin. Biomech. 2015, 30, 254–259. [Google Scholar] [CrossRef]
- Barroso, F.O.; Torricelli, D.; Moreno, J.C.; Taylor, J.; Gomez-Soriano, J.; Bravo-Esteban, E.; Piazza, S.; Santos, C.; Pons, J.L. Shared muscle synergies in human walking and cycling. J. Neurophysiol. 2014, 112, 1984–1998. [Google Scholar] [CrossRef]
- Bernstein, N. The Co-Ordination and Regulation of Movements; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- d’Avella, A.; Saltiel, P.; Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 2003, 6, 300–308. [Google Scholar] [CrossRef]
- Dominici, N.; Ivanenko, Y.P.; Cappellini, G.; d’Avella, A.; Mondì, V.; Cicchese, M.; Fabiano, A.; Silei, T.; Di Paolo, A.; Giannini, C.; et al. Locomotor primitives in newborn babies and their development. Science 2011, 334, 997–999. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Cappellini, G.; Dominici, N.; Poppele, R.E.; Lacquaniti, F. Modular control of limb movements during human locomotion. J. Neurosci. 2007, 27, 11149–11161. [Google Scholar] [CrossRef] [PubMed]
- Taborri, J.; Agostini, V.; Artemiadis, P.K.; Ghislieri, M.; Jacobs, D.A.; Roh, J.; Rossi, S. Feasibility of Muscle Synergy Outcomes in Clinics, Robotics, and Sports: A Systematic Review. Appl. Bionics Biomech. 2018, 2018, 3934698. [Google Scholar] [CrossRef]
- Torricelli, D.; Barroso, F.; Coscia, M.; Alessandro, C.; Lunardini, F.; Esteban, E.B.; d’Avella, A. Muscle synergies in clinical practice: Theoretical and practical implications. In Biosystems and Biorobotics; Pons, J., Raya, R., González, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 10, pp. 251–272. [Google Scholar] [CrossRef]
- Ferreira, C.L.; Oliveira Barroso, F.; Torricelli, D.; Pons, J.L.; Politti, F.; Lucareli, P.R.G. Muscle synergies analysis shows altered neural strategies in women with patellofemoral pain during walking. PLoS ONE 2023, 18, e0292464. [Google Scholar] [CrossRef]
- Magrath, W.J.; Qiu, C.S.; Hanwright, P.J.; Tuffaha, S.H.; Khavanin, N. A Systematic Review of Muscle Synergies during a Walking Gait to Define Optimal Donor-Recipient Pairings for Lower Extremity Functional Reconstruction. Plast. Reconstr. Surg. -Glob. Open 2022, 10, e4438. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, A.S.; Gizzi, L.; Ketabi, S.; Farina, D.; Kersting, U.G. Modular Control of Treadmill vs Overground Running. PLoS ONE 2016, 11, e0153307. [Google Scholar] [CrossRef] [PubMed]
- Barroso, F.O.; Torricelli, D.; Bravo-Esteban, E.; Taylor, J.; Gómez-Soriano, J.; Santos, C.; Moreno, J.C.; Pons, J.L. Muscle Synergies in Cycling after Incomplete Spinal Cord Injury: Correlation with Clinical Measures of Motor Function and Spasticity. Front. Hum. Neurosci. 2016, 9, 706. [Google Scholar] [CrossRef] [PubMed]
- Cartier, T.; Vigouroux, L.; Viehweger, E.; Rao, G. Subject specific muscle synergies and mechanical output during cycling with arms or legs. PeerJ 2022, 10, e13155. [Google Scholar] [CrossRef] [PubMed]
- Hug, F.; Turpin, N.A.; Couturier, A.; Dorel, S. Consistency of muscle synergies during pedaling across different mechanical constraints. J. Neurophysiol. 2011, 106, 91–103. [Google Scholar] [CrossRef]
- Boccia, G.; Zoppirolli, C.; Bortolan, L.; Schena, F.; Pellegrini, B. Shared and task-specific muscle synergies of Nordic walking and conventional walking. Scand. J. Med. Sci. Sports 2018, 28, 905–918. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, H.; Kato, T.; Kaneko, N.; Kobayashi, H.; Hoshino, M.; Kokubun, T.; Nakazawa, K. Basic locomotor muscle synergies used in land walking are finely tuned during underwater walking. Sci. Rep. 2021, 11, 18480. [Google Scholar] [CrossRef]
- Hagedoorn, L.; Zadravec, M.; Olenšek, A.; van Asseldonk, E.; Matjačić, Z. The Existence of Shared Muscle Synergies Underlying Perturbed and Unperturbed Gait Depends on Walking Speed. Appl. Sci. 2022, 12, 2135. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2004, 556 Pt 1, 267–282. [Google Scholar] [CrossRef]
- Coscia, M.; Monaco, V.; Martelloni, C.; Rossi, B.; Chisari, C.; Micera, S. Muscle synergies and spinal maps are sensitive to the asymmetry induced by a unilateral stroke. J. Neuroeng. Rehabil. 2015, 12, 39. [Google Scholar] [CrossRef]
- Stephenson, J.L.; Lamontagne, A.; De Serres, S.J. The coordination of upper and lower limb movements during gait in healthy and stroke individuals. Gait Posture 2009, 29, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Olenšek, A.; Zadravec, M.; Matjačić, Z. Feasibility of Using Visual Cues for Evoking Self-induced Perturbations for Assessing Dynamic Balance During Walking. Biosyst. Biorobotics 2022, 28, 841–844. [Google Scholar] [CrossRef]
- Stegeman, D.; Hermens, H. Standards for surface electromyography: The European project Surface EMG for non-invasive assessment of muscles (SENIAM). Enschede Roessingh Res. Dev. 2007, 10, 108–112. [Google Scholar]
- Kerkman, J.N.; Bekius, A.; Boonstra, T.W.; Daffertshofer, A.; Dominici, N. Muscle Synergies and Coherence Networks Reflect Different Modes of Coordination During Walking. Front. Physiol. 2020, 11, 751. [Google Scholar] [CrossRef] [PubMed]
- Turpin, N.A.; Uriac, S.; Dalleau, G. How to improve the muscle synergy analysis methodology? Eur. J. Appl. Physiol. 2021, 121, 1009–1025. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Baker, J.S.; Gu, Y. Adaptive neuro-fuzzy inference system model driven by the non-negative matrix factorization-extracted muscle synergy patterns to estimate lower limb joint movements. Comput. Methods Programs Biomed. 2023, 242, 107848. [Google Scholar] [CrossRef] [PubMed]
- Hug, F.; Turpin, N.A.; Guével, A.; Dorel, S. Is interindividual variability of EMG patterns in trained cyclists related to different muscle synergies? J. Appl. Physiol. 2010, 108, 1727–1736. [Google Scholar] [CrossRef]
- Hug, F. Can muscle coordination be precisely studied by surface electromyography? J. Electromyogr. Kinesiol. 2011, 21, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Lunardini, F.; Casellato, C.; Bertucco, M.; Sanger, T.D.; Pedrocchi, A. Children With and Without Dystonia Share Common Muscle Synergies While Performing Writing Tasks. Ann. Biomed. Eng. 2017, 45, 1949–1962. [Google Scholar] [CrossRef] [PubMed]
- Cappellini, G.; Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Motor patterns in human walking and running. J. Neurophysiol. 2006, 95, 3426–3437. [Google Scholar] [CrossRef] [PubMed]
- d’avella, A.; Bizzi, E. Shared and specific muscle synergies in natural motor behaviors. Proc. Natl. Acad. Sci. USA. 2005, 102, 3076–3081. [Google Scholar] [CrossRef]
- Pellegrino, L.; Coscia, M.; Casadio, M. Muscle activities in similar arms performing identical tasks reveal the neural basis of muscle synergies. Exp. Brain Res. 2020, 238, 121–138. [Google Scholar] [CrossRef] [PubMed]
- Semaan, M.B.; Wallard, L.; Ruiz, V.; Gillet, C.; Leteneur, S.; Simoneau-Buessinger, E. Is treadmill walking biomechanically comparable to overground walking? A systematic review. Gait Posture 2022, 92, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Kautz, S.A.; Bowden, M.G.; Clark, D.J.; Neptune, R.R. Comparison of motor control deficits during treadmill and overground walking poststroke. Neurorehabil. Neural Repair 2011, 25, 756–765. [Google Scholar] [CrossRef]
- Kim, M.H.; Yoo, W.G. Effect of minimizing arm swing while walking on the trunk and gluteal muscles. J. Phys. Ther. Sci. 2017, 29, 79–80. [Google Scholar] [CrossRef] [PubMed]
- Molina Rueda, F.; Carratalá Tejada, M. La Marcha: Biomecánica, Evaluación y Patología; Editorial Médica Panamericana S.A.: Ciudad de Mexico, Mexico, 2020. [Google Scholar]
- Kim, T.Y.; Yoo, W.G.; An, D.H.; Oh, J.S.; Shin, S.J. The effects of different gait speeds and lower arm weight on the activities of the latissimus dorsi, gluteus medius, and gluteus maximus muscles. J. Phys. Ther. Sci. 2013, 25, 1483–1484. [Google Scholar] [CrossRef] [PubMed]
- Donker, S.F.; Mulder, T.; Nienhuis, B.; Duysens, J. Adaptations in arm movements for added mass to wrist or ankle during walking. Exp. Brain Res. 2002, 146, 26–31. [Google Scholar] [CrossRef]
- Hill, A.; Nantel, J. The effects of arm swing amplitude and lower-limb asymmetry on gait stability. PLoS ONE 2019, 14, e0218644. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Pizzolato, C.; Lloyd, D.G.; Carty, C.P.; Devaprakash, D.; Diamond, L.E. Non-negative matrix factorisation is the most appropriate method for extraction of muscle synergies in walking and running. Sci. Rep. 2020, 10, 8266. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, K.L.; Roemmich, R.T.; Cam, B.; Fregly, B.J.; Hass, C.J. Persons with Parkinson’s disease exhibit decreased neuromuscular complexity during gait. Clin. Neurophysiol. 2013, 124, 1390–1397. [Google Scholar] [CrossRef]
- Routson, R.L.; Clark, D.J.; Bowden, M.G.; Kautz, S.A.; Neptune, R.R. The influence of locomotor rehabilitation on module quality and post-stroke hemiparetic walking performance. Gait Posture 2013, 38, 511–517. [Google Scholar] [CrossRef] [PubMed]
- Gizzi, L.; Nielsen, J.F.; Felici, F.; Ivanenko, Y.P.; Farina, D. Impulses of activation but not motor modules are preserved in the locomotion of subacute stroke patients. J. Neurophysiol. 2011, 106, 202–210. [Google Scholar] [CrossRef] [PubMed]
- van Kammen, K.; Boonstra, A.M.; van der Woude, L.H.V.; Reinders-Messelink, H.A.; den Otter, R. Differences in muscle activity and temporal step parameters between Lokomat guided walking and treadmill walking in post-stroke hemiparetic patients and healthy walkers. J. Neuroeng. Rehabil. 2017, 14, 32. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Millán, T.; Sanz-Morère, C.B.; Cherubini, A.; Urrutia, R.; Oliveira Barroso, F.; Pons, J.L.; Tornero, J. Effects of Arm Swing in Lower Limb Muscle Activation and Coordination During Treadmill Walking. Appl. Sci. 2025, 15, 192. https://doi.org/10.3390/app15010192
Rodríguez-Millán T, Sanz-Morère CB, Cherubini A, Urrutia R, Oliveira Barroso F, Pons JL, Tornero J. Effects of Arm Swing in Lower Limb Muscle Activation and Coordination During Treadmill Walking. Applied Sciences. 2025; 15(1):192. https://doi.org/10.3390/app15010192
Chicago/Turabian StyleRodríguez-Millán, Teresa, Clara B. Sanz-Morère, Agnese Cherubini, Rocío Urrutia, Filipe Oliveira Barroso, José L. Pons, and Jesús Tornero. 2025. "Effects of Arm Swing in Lower Limb Muscle Activation and Coordination During Treadmill Walking" Applied Sciences 15, no. 1: 192. https://doi.org/10.3390/app15010192
APA StyleRodríguez-Millán, T., Sanz-Morère, C. B., Cherubini, A., Urrutia, R., Oliveira Barroso, F., Pons, J. L., & Tornero, J. (2025). Effects of Arm Swing in Lower Limb Muscle Activation and Coordination During Treadmill Walking. Applied Sciences, 15(1), 192. https://doi.org/10.3390/app15010192





