High-Impedance Fault Detection in DC Microgrid Lines Using Open-Set Recognition
Abstract
1. Introduction
- Modeling high-impedance fault detection as an open-set recognition problem;
- Development of a novel high-impedance fault detection method in DC microgrids based on neural network with open-set recognition capabilities;
- Simulation and detailed analysis of high-impedance faults in DC microgrid lines connecting passive loads.
2. Faults in DC Microgrids
2.1. Low-Impedance Faults
2.2. High-Impedance Faults
3. Fault Detection
3.1. Classification with Neural Networks
3.2. Open-Set Recognition
3.2.1. Open-Set Recognition Problem
3.2.2. Open-Set Recognition Using NNs
3.3. Proposed Fault Detection Method
4. Case Study
4.1. System Description
4.2. Dataset
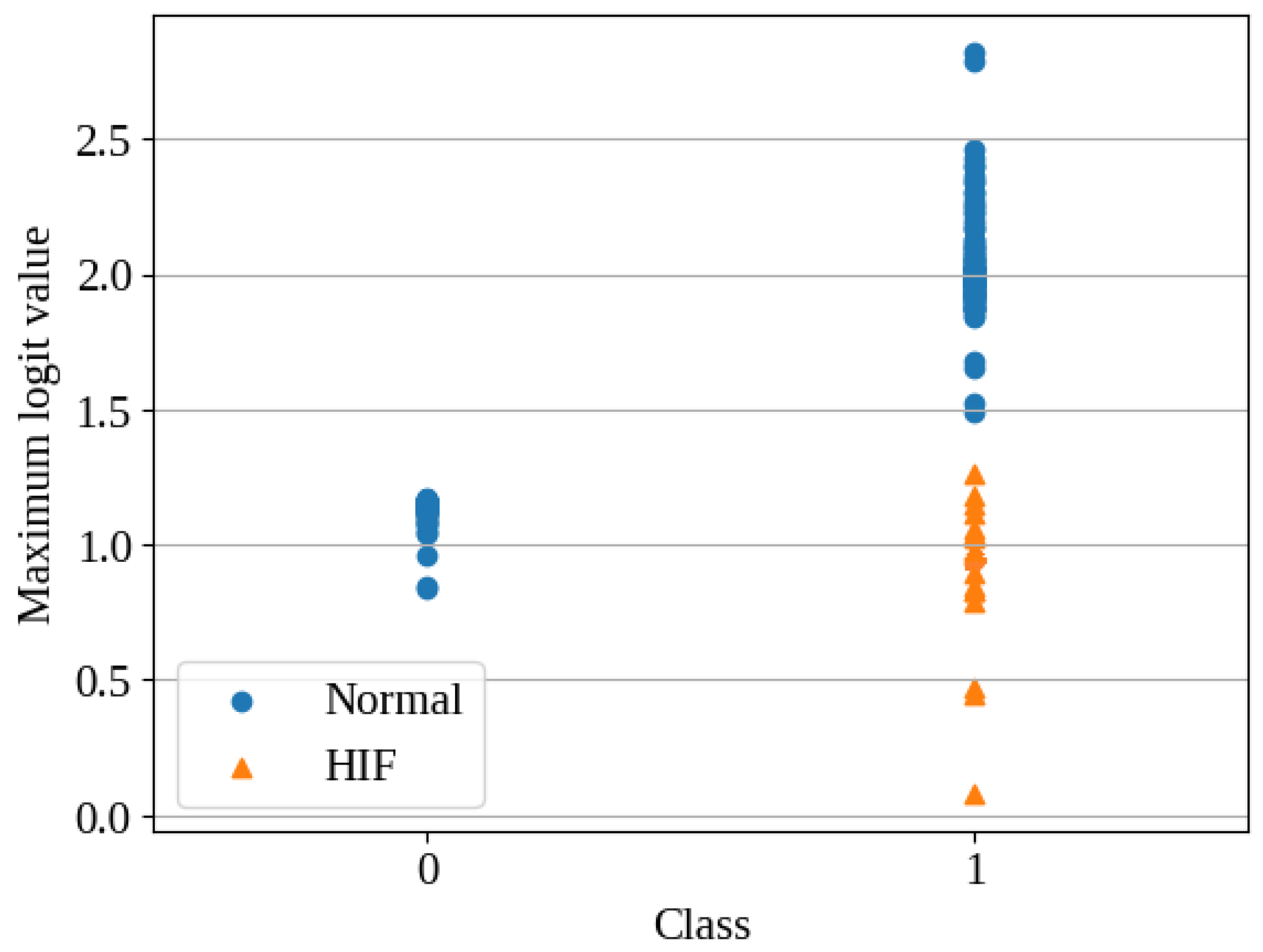
4.3. Results
4.4. Comparison with Existing NN-Based Methods
4.5. Fault Detection Algorithm
| Algorithm 1 High-impedance fault detection |
OFFLINE
|
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| BESS | Battery energy storage system |
| BPNN | Back-propagation neural network |
| CNN | Convolutional neural network |
| DC | Direct current |
| DER | Distributed energy sources |
| DWT | Discrete wavelet transform |
| FFNN | Feed-forward neural network |
| FFT | Fast Fourier transform |
| GAN | Generative adversarial network |
| HIF | High-impedance fault |
| kNN | k-Nearest neighbors |
| LIF | Low-impedance fault |
| MLS | Maximum logit score |
| MPPT | Maximum power point tracking |
| NN | Neural network |
| OSR | Open-set recognition |
| PV | Photo-voltaic |
| ReLU | Rectified linear unit |
| RNN | Recurrent neural network |
| RES | Renewable energy sources |
| SVM | Support vector machine |
| VSC | Voltage source converter |
References
- Muhtadi, A.; Pandit, D.; Nguyen, N.; Mitra, J. Distributed Energy Resources Based Microgrid: Review of Architecture, Control, and Reliability. IEEE Trans. Ind. Appl. 2021, 57, 2223–2235. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Papadimitriou, C.N.; Zountouridou, E.I.; Hatziargyriou, N.D. Review of hierarchical control in DC microgrids. Electr. Power Syst. Res. 2015, 122, 159–167. [Google Scholar] [CrossRef]
- Ansari, S.; Chandel, A.; Tariq, M. A Comprehensive Review on Power Converters Control and Control Strategies of AC/DC Microgrid. IEEE Access 2021, 9, 17998–18015. [Google Scholar] [CrossRef]
- Grcić, I.; Pandžić, H.; Novosel, D. Fault Detection in DC Microgrids Using Short-Time Fourier Transform. Energies 2021, 14, 277. [Google Scholar] [CrossRef]
- Čuljak, M.; Pandžić, H.; Havelka, J. Mathematical Morphology-Based Fault Detection in Radial DC Microgrids Considering Fault Current from VSC. IEEE Trans. Smart Grid 2023, 14, 2545–2557. [Google Scholar] [CrossRef]
- Grcić, I.; Pandžixcx, H. Fault Detection in DC Microgrids using Recurrent Neural Networks. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–6. [Google Scholar]
- Ali, Z.; Terriche, Y.; Abbas, S.Z.; Hassan, M.A.; Sadiq, M.; Su, C.L.; Guerrero, J.M. Fault Management in DC Microgrids: A Review of Challenges, Countermeasures, and Future Research Trends. IEEE Access 2021, 9, 128032–128054. [Google Scholar] [CrossRef]
- Yao, X.; Wang, J.; Schweickart, D.L. Review and recent developments in DC arc fault detection. In Proceedings of the 2016 IEEE International Power Modulator and High Voltage Conference (IPMHVC), San Francisco, CA, USA, 6–9 July 2016; pp. 467–472. [Google Scholar]
- Dhar, S.; Patnaik, R.K.; Dash, P.K. Fault Detection and Location of Photovoltaic Based DC Microgrid Using Differential Protection Strategy. IEEE Trans. Smart Grid 2018, 9, 4303–4312. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Paul, K.C.; Ban, Y.; Chen, C.; Zhao, T. ArcNet: Series AC Arc Fault Detection Based on Raw Current and Convolutional Neural Network. IEEE Trans. Ind. Inform. 2022, 18, 77–86. [Google Scholar] [CrossRef]
- Paz, F.; Ordonez, M. High-Impedance Fault Detection Method for DC Microgrids. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 787–792. [Google Scholar]
- Taheri, B.; Hosseini, S.A. Detection of High Impedance Fault in DC Microgrid Using Impedance Prediction Technique. In Proceedings of the 2020 15th International Conference on Protection and Automation of Power Systems (IPAPS), Shiraz, Iran, 30–31 December 2020; pp. 68–73. [Google Scholar]
- Sheikh, A.A.; Wakode, S.A.; Deshmukh, R.R.; Ballal, M.S. Detection of High Impedance Fault in DC Microgrid. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–4. [Google Scholar]
- Rao, G.K.; Jena, P. Fault Detection in DC Microgrid Based on the Resistance Estimation. IEEE Syst. J. 2022, 16, 1009–1020. [Google Scholar] [CrossRef]
- Stanescu, D.; Digulescu, A.; Ioana, C.; Serbanescu, A.; Zhang, Y.D.; Senjyu, T.; So-In, C.; Joshi, A. On the Existing and New Potential Methods for Partial Discharge Source Monitoring in Electrical Power Grids. In Smart Trends in Computing and Communications; Lecture Notes in Networks and Systems; Springer: Singapore, 2022; Volume 286. [Google Scholar]
- Stanescu, D.; Digulescu, A.; Ioana, C.; Serbanescu, A. Entropy-Based Characterization of the Transient Phenomena—Systemic Approach. Mathematics 2021, 9, 648. [Google Scholar] [CrossRef]
- Srivastava, C.; Tripathy, M. Novel Grounding and Protection Strategy for DC Microgrid Restraining Fault Current. IEEE Trans. Power Deliv. 2024, 39, 2182–2193. [Google Scholar] [CrossRef]
- Miao, W.; Wang, Z.; Wang, F.; Lam, K.H.; Pong, P.W.T. Multicharacteristics Arc Model and Autocorrelation-Algorithm Based Arc Fault Detector for DC Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 4875–4886. [Google Scholar] [CrossRef]
- Valero, A. High Impedance Fault Detection Method in Multi-Grounded Distribution Networks. Ph.D. Dissertation, École polytechnique de Bruxelles Université Libre de Bruxelles, Brussels, Belgium, 2012. [Google Scholar]
- Masa, A.V.; Werben, S.; Maun, J.C. Incorporation of data-mining in protection technology for high impedance fault detection. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Subramaniam, K.; Illindala, M.S. High Impedance Fault Detection and Isolation in DC Microgrids. In Proceedings of the 2019 IEEE/IAS 55th Industrial and Commercial Power Systems Technical Conference (I&CPS), Calgary, AB, Canada, 5–8 May 2019; pp. 1–8. [Google Scholar]
- Wakode, S.A.; Kumar, S.; Ballal, M.S. A Flexible Protection Approach for DC Microgrid Using Wavelet based Machine Learning Technique. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, Chhattisgarh, India, 19–22 December 2021; pp. 1–5. [Google Scholar]
- Bramareswara Rao, S.N.V.; Kumar, Y.V.P.; Amir, M.; Muyeen, S.M. Fault detection and classification in hybrid energy-based multi-area grid-connected microgrid clusters using discrete wavelet transform with deep neural networks. Electr. Eng. 2024. [Google Scholar] [CrossRef]
- Taheri, B.; Hosseini, S.A.; Salehimehr, S.; Razavi, F. A Novel Approach for Detection High Impedance Fault in DC Microgrid. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 287–292. [Google Scholar]
- Grcić, I.; Pandžić, H. Artificial Neural Network for High-Impedance-Fault Detection in DC Microgrids. In Proceedings of the 2023 IEEE PES Conference on Innovative Smart Grid Technologies—Middle East (ISGT Middle East), Abu Dhabi, United Arab Emirates, 12–15 March 2023; pp. 1–5. [Google Scholar]
- Aziz, F.; Haq, A.U.; Ahmad, S.; Mahmoud, Y.; Jalal, M.; Ali, U. A Novel Convolutional Neural Network-Based Approach for Fault Classification in Photovoltaic Arrays. IEEE Access 2020, 8, 41889–41904. [Google Scholar] [CrossRef]
- Lu, S.; Sirojan, T.; Phung, B.T.; Zhang, D.; Ambikairajah, E. DA-DCGAN: An Effective Methodology for DC Series Arc Fault Diagnosis in Photovoltaic Systems. IEEE Access 2019, 7, 45831–45840. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Othman, M.L.; Padmanaban, S.; Sekar, K.; Ramachandran, R.; Hizam, H.; Vinayagam, A.; Islam, M.Z. LSTM Recurrent Neural Network Classifier for High Impedance Fault Detection in Solar PV Integrated Power System. IEEE Access 2021, 9, 32672–32687. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y. Identification and Detection of DC Arc Fault in Photovoltaic Power Generation System. In Proceedings of the 2020 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Vientiane, Laos, 11–12 January 2020; pp. 440–444. [Google Scholar]
- Omran, A.H.; Said, D.M.; Hussin, S.M.; Mirsaeidi, S.; Abid, Y.M. An Intelligent Classification Method of Series Arc Fault Models Using Deep Learning Algorithm. In Proceedings of the 2020 IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 21–24 July 2020; pp. 44–48. [Google Scholar]
- Patil, D.D.; Bindu, S.; SushilThale. Arc Fault Detection in DC Microgrid Using Deep Neural Network. In Proceedings of the 2021 4th Biennial International Conference on Nascent Technologies in Engineering (ICNTE), NaviMumbai, India, 15–16 January 2021; pp. 1–6. [Google Scholar]
- Cai, X.; Wai, R.-J. Intelligent DC Arc-Fault Detection of Solar PV Power Generation System via Optimized VMD-Based Signal Processing and PSO–SVM Classifier. IEEE J. Photovolt. 2022, 12, 1058–1077. [Google Scholar] [CrossRef]
- Lu, S.; Sahoo, A.; Ma, R.; Phung, B.T. DC Series Arc Fault Detection Using Machine Learning in Photovoltaic Systems: Recent Developments and Challenges. In Proceedings of the 2020 8th International Conference on Condition Monitoring and Diagnosis (CMD), Phuket, Thailand, 25–28 October 2020; pp. 416–421. [Google Scholar]
- Mansouri, M.; Trabelsi, M.; Nounou, H.; Nounou, M. Deep Learning-Based Fault Diagnosis of Photovoltaic Systems: A Comprehensive Review and Enhancement Prospects. IEEE Access 2021, 9, 126286–126306. [Google Scholar] [CrossRef]
- Scheirer, W.J.; de Rezende Rocha, A.; Sapkota, A.; Boult, T.E. Toward Open Set Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1757–1772. [Google Scholar] [CrossRef]
- Bendale, A.; Boult, T.E. Towards Open Set Deep Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1563–1572. [Google Scholar]
- Geng, C.; Huang, S.-J.; Chen, S. Recent Advances in Open Set Recognition: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3614–3631. [Google Scholar] [CrossRef] [PubMed]
- Beheshtaein, S.; Cuzner, R.M.; Forouzesh, M.; Savaghebi, M.; Guerrero, J.M. DC Microgrid Protection: A Comprehensive Review. IEEE J. Emerg. Sel. Top. Power Electron. 2019; early access. [Google Scholar]
- Bayati, N. Fault Detection and Location of DC Microgrids. Ph.D. Dissertation, Faculty of Engineering and Science, Aalborg University, Aalborg, Denmark, 2020. [Google Scholar]
- Li, J.; Kohler, J.L. New insight into the detection of high-impedance arcing faults on DC trolley systems. IEEE Trans. Ind. Appl. 1999, 35, 1169–1173. [Google Scholar]
- Bayati, N.; Savaghebi, M. A high-impedance fault detection scheme for DC aircrafts based on comb filter and second derivative of voltage. Green Energy Intell. Transp. 2023, 2, 100073. [Google Scholar] [CrossRef]
- Oh, Y.; Kim, C.; Gwon, G.; Noh, C.; Bukhari, S.; Haider, R.; Gush, T. Fault detection scheme based on mathematical morphology in last mile radial low voltage DC distribution networks. Int. J. Electr. Power Energy Syst. 2019, 106, 520–527. [Google Scholar] [CrossRef]
- Andrea, J.; Schweitzer, P.; Tisserand, E. A New DC and AC Arc Fault Electrical Model. In Proceedings of the 2010 56th IEEE Holm Conference on Electrical Contacts, Charleston, SC, USA, 4–7 October 2010; pp. 1–6. [Google Scholar]
- Yadav, N.; Tummuru, N.R. Short-Circuit Fault Detection and Isolation Using Filter Capacitor Current Signature in Low-Voltage DC Microgrid Applications. IEEE Trans. Ind. Electron. 2022, 69, 8491–8500. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognition 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Hüsken, M.; Stagge, P. Recurrent neural networks for time series classification. Neurocomputing 2003, 50, 223–235. [Google Scholar] [CrossRef]
- Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 427–436. [Google Scholar]
- Vaze, S.; Han, K.; Vedaldi, A.; Zisserman, A. Open-Set Recognition: A Good Closed-Set Classifier is All You Need. In Proceedings of the Tenth International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022; pp. 1–26. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of Tricks for Image Classification with Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 558–567. [Google Scholar]
- Ghaderi, A.; Ginn, H.L.; Mohammadpour, H.A. High impedance fault detection: A review. Electr. Power Syst. Res. 2017, 143, 376–388. [Google Scholar] [CrossRef]
- Saribulut, L.; Teke, A.; Tumay, M. Fundamentals and literature review of Fourier transform in power quality issues. J. Electr. Electron. Eng. Res. 2013, 5, 9–22. [Google Scholar]
- Saleh, M.; Esa, Y.; Mhandi, Y.; Brandauer, W.; Mohamed, A. Design and implementation of CCNY DC microgrid testbed. In Proceedings of the 2016 IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–7. [Google Scholar]
- Grcić, I. Dataset HIF Detection [Data Set]. Available online: https://github.com/ivangrcic/dataset-hif-detection (accessed on 15 November 2024.).
- Putzke, J.L.; Michels, L.; Bellinaso, L.V. Electric Arcs in Photovoltaic Systems: A Comparative Analysis of IEC 63027, UL 1699B, and GB-t 39750 Standards. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP), Florianopolis, Brazil, 26–29 November 2023; pp. 1–5. [Google Scholar]
- Wang, Y.; Zhou, J.; Paul, K.C.; Zhao, T.; Sheng, D. Explainability Approach-Based Series Arc Fault Detection Method for Photovoltaic Systems. IEEE Access 2024, 12, 45530–45542. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J. A Review of Artificial Intelligence in Embedded Systems. Micromachines 2023, 14, 897. [Google Scholar] [CrossRef] [PubMed]
- Capra, M.; Bussolino, B.; Marchisio, A.; Shafique, M.; Masera, G.; Martina, M. An Updated Survey of Efficient Hardware Architectures for Accelerating Deep Convolutional Neural Networks. Future Internet 2020, 12, 113. [Google Scholar] [CrossRef]
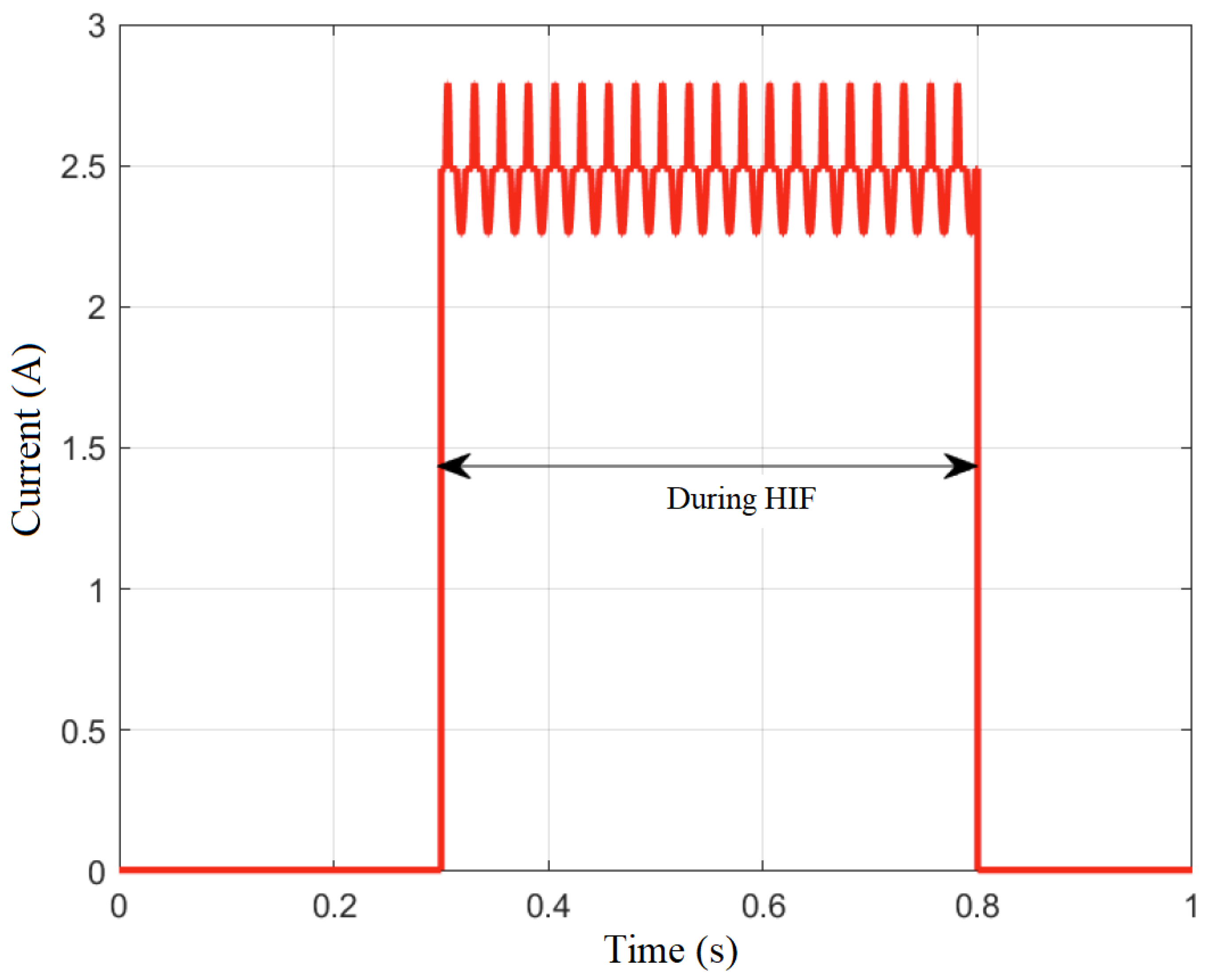

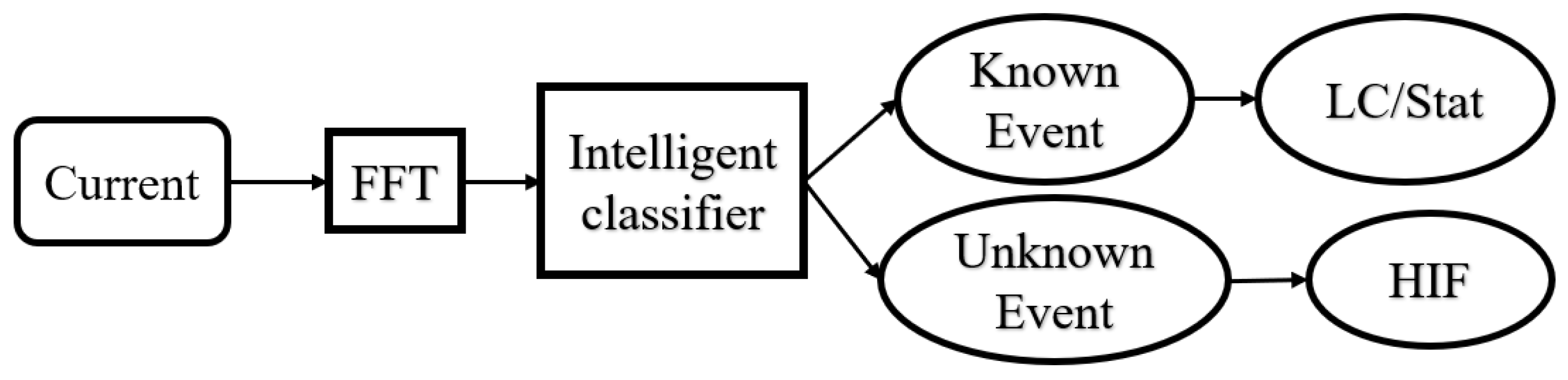
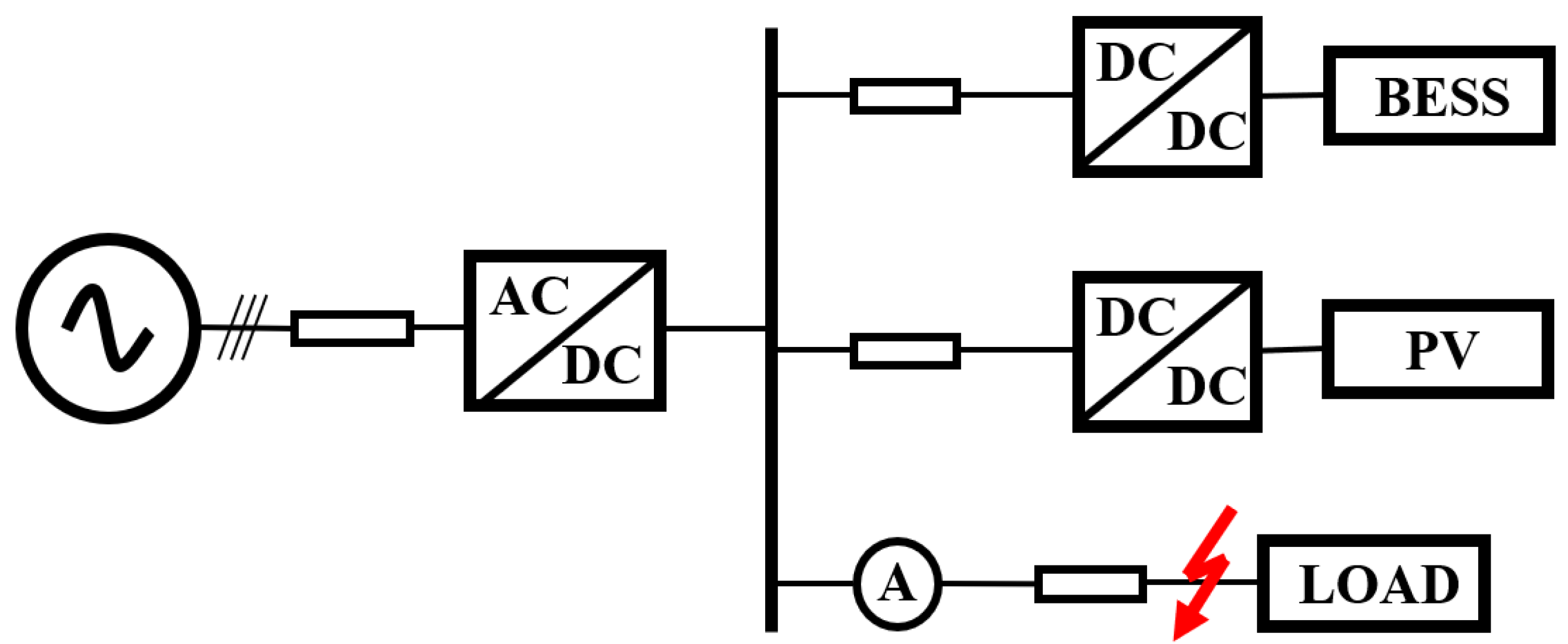

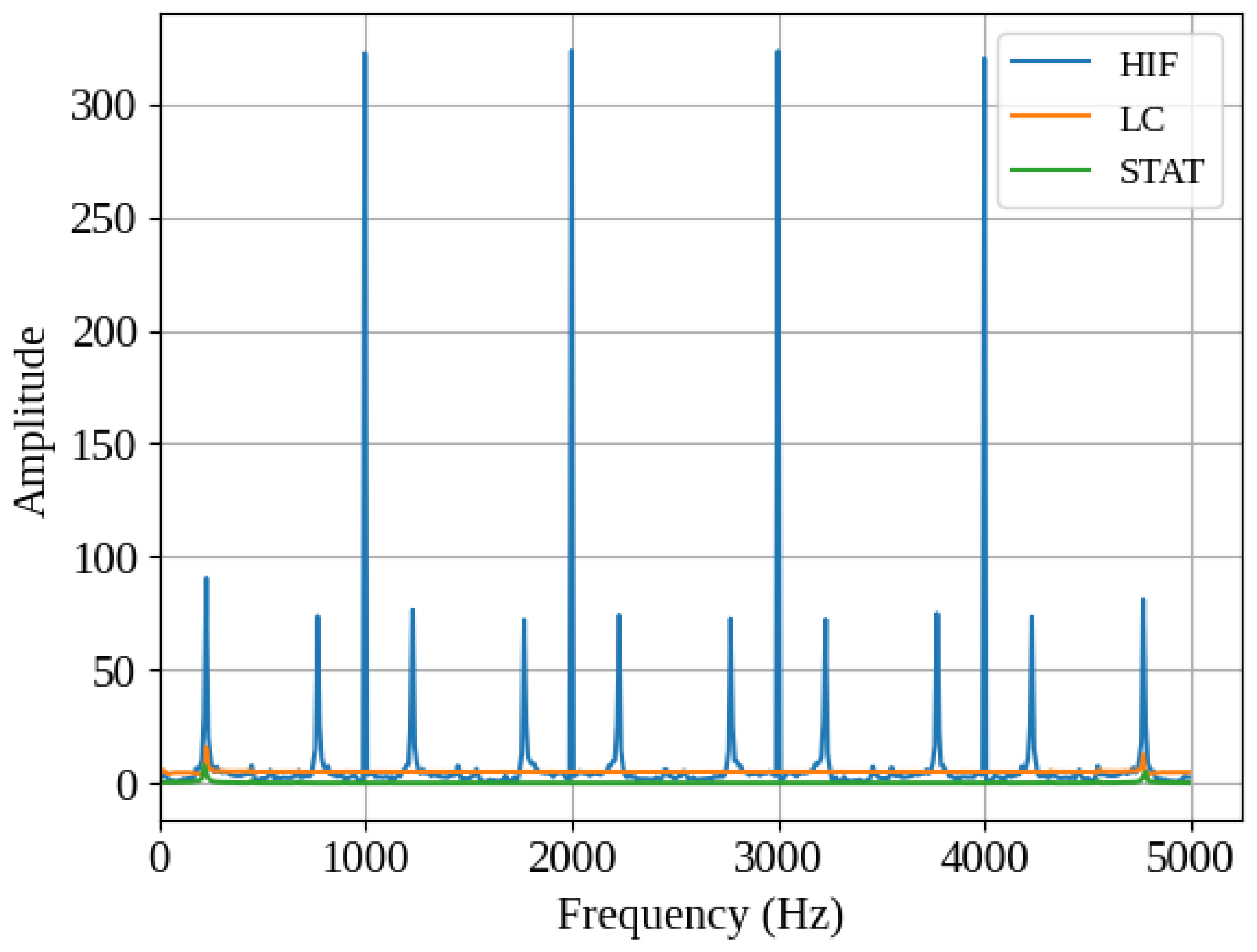


| Parameter | Rated Value |
|---|---|
| Bus voltage | 500 V |
| VSC rated power | 15 kW |
| BESS capacity | 12 kWh |
| PV peak power | 6 kW @ 25 °C |
| Load | 5 kW |
| Line parameters | 20 mΩ, 62 μH |
| FFNN | FFNN + OSR | |
|---|---|---|
| No. hidden layers | 3 | 3 |
| Nodes per layer | [500, 2000, 2000, 400, 2] | [500, 2000, 2000, 400, 2] |
| Nonlinearity | ReLU | ReLU |
| Batch size | 32 | 32 |
| Optimizer | RMSprop | RMSprop |
| Learning rate | 1 × 10−4 | Cosine (1 × 10−3 to 1 × 10−4) |
| Learning rate warmup | - | 10% of epochs (init. 1 × 10−4) |
| Epochs | 50 | 50 |
| Label smoothing | - | 0.1 |
| Accuracy | 99.99% | 99.99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grcić, I.; Pandžić, H. High-Impedance Fault Detection in DC Microgrid Lines Using Open-Set Recognition. Appl. Sci. 2025, 15, 193. https://doi.org/10.3390/app15010193
Grcić I, Pandžić H. High-Impedance Fault Detection in DC Microgrid Lines Using Open-Set Recognition. Applied Sciences. 2025; 15(1):193. https://doi.org/10.3390/app15010193
Chicago/Turabian StyleGrcić, Ivan, and Hrvoje Pandžić. 2025. "High-Impedance Fault Detection in DC Microgrid Lines Using Open-Set Recognition" Applied Sciences 15, no. 1: 193. https://doi.org/10.3390/app15010193
APA StyleGrcić, I., & Pandžić, H. (2025). High-Impedance Fault Detection in DC Microgrid Lines Using Open-Set Recognition. Applied Sciences, 15(1), 193. https://doi.org/10.3390/app15010193








