Dynamically Triggered Damage Around Rock Tunnels: An Experimental and Theoretical Investigation
Abstract
1. Introduction
2. Experimental Setup
2.1. Sample Preparation and Material Characteristics
2.2. Test System
3. Experimental Results and Analysis
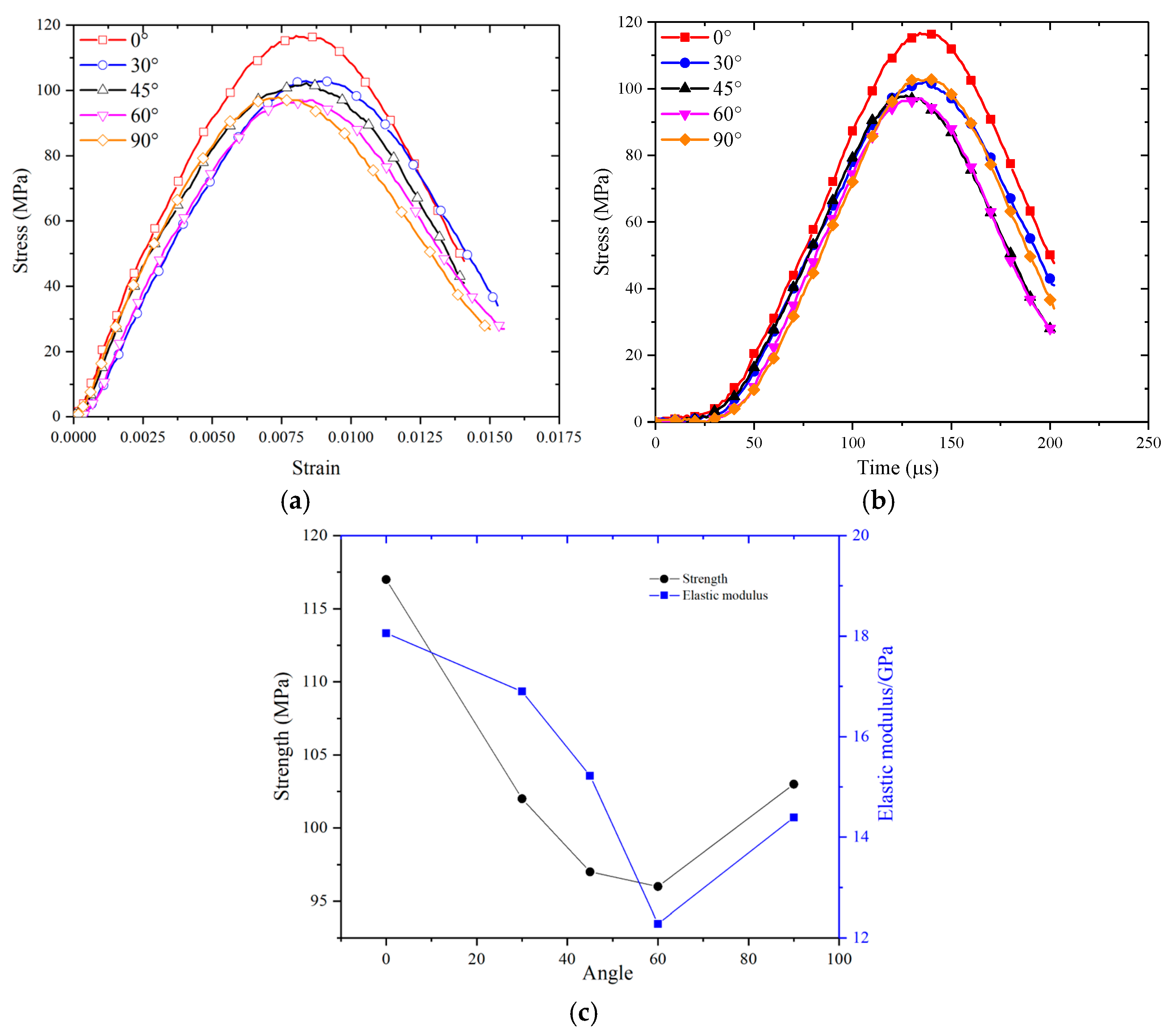
3.1. Dynamic Mechanical Properties
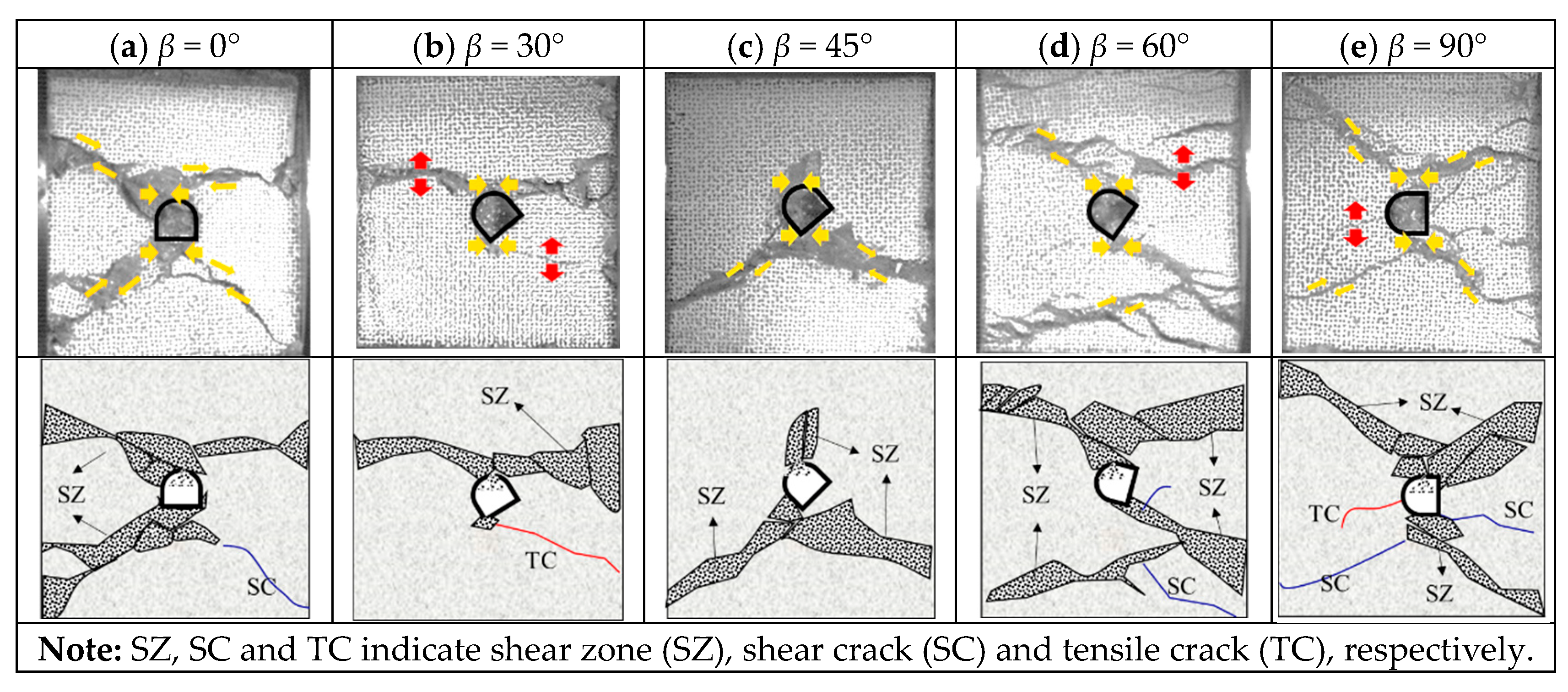
3.2. Fracture Process of the Sample
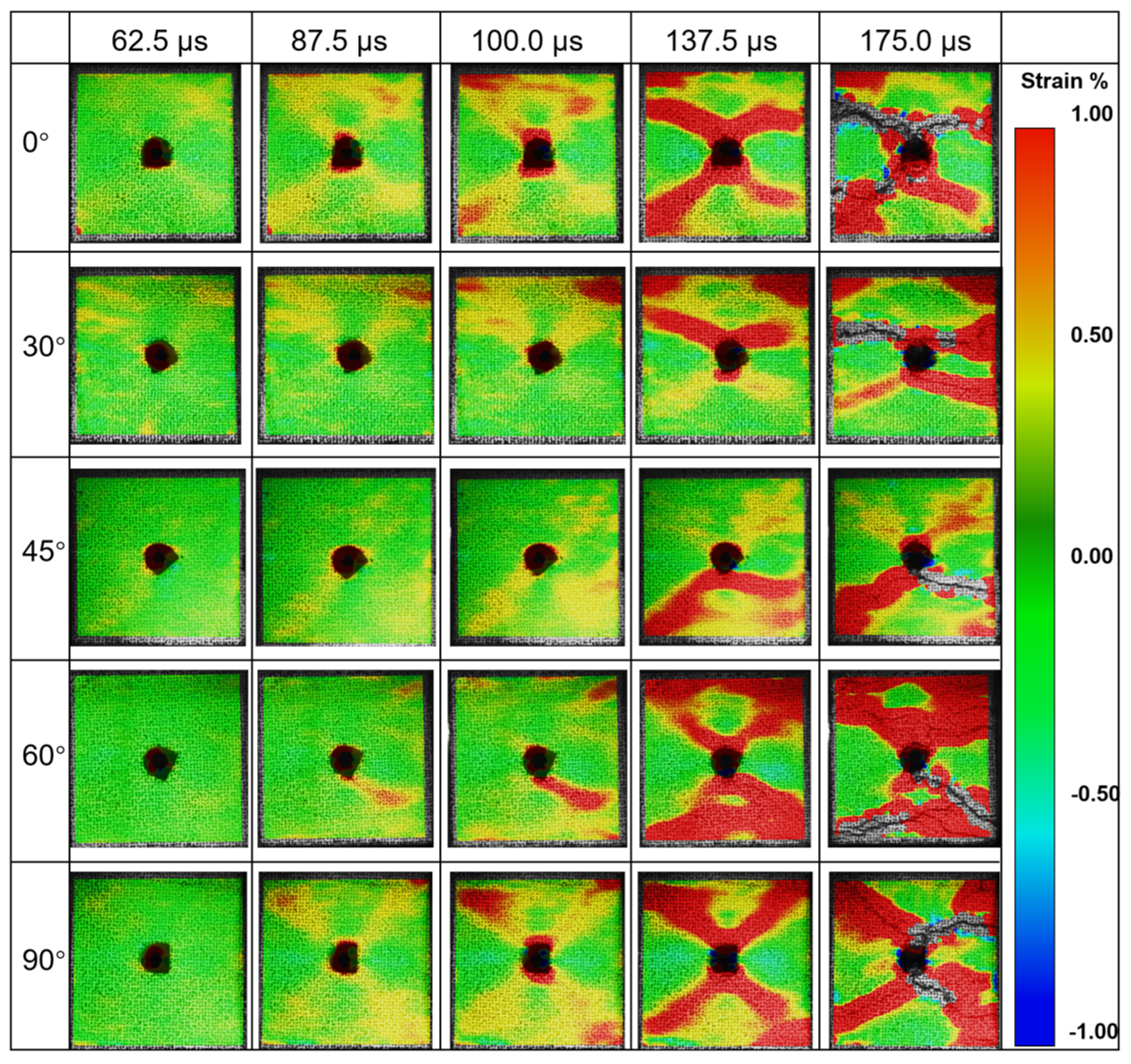
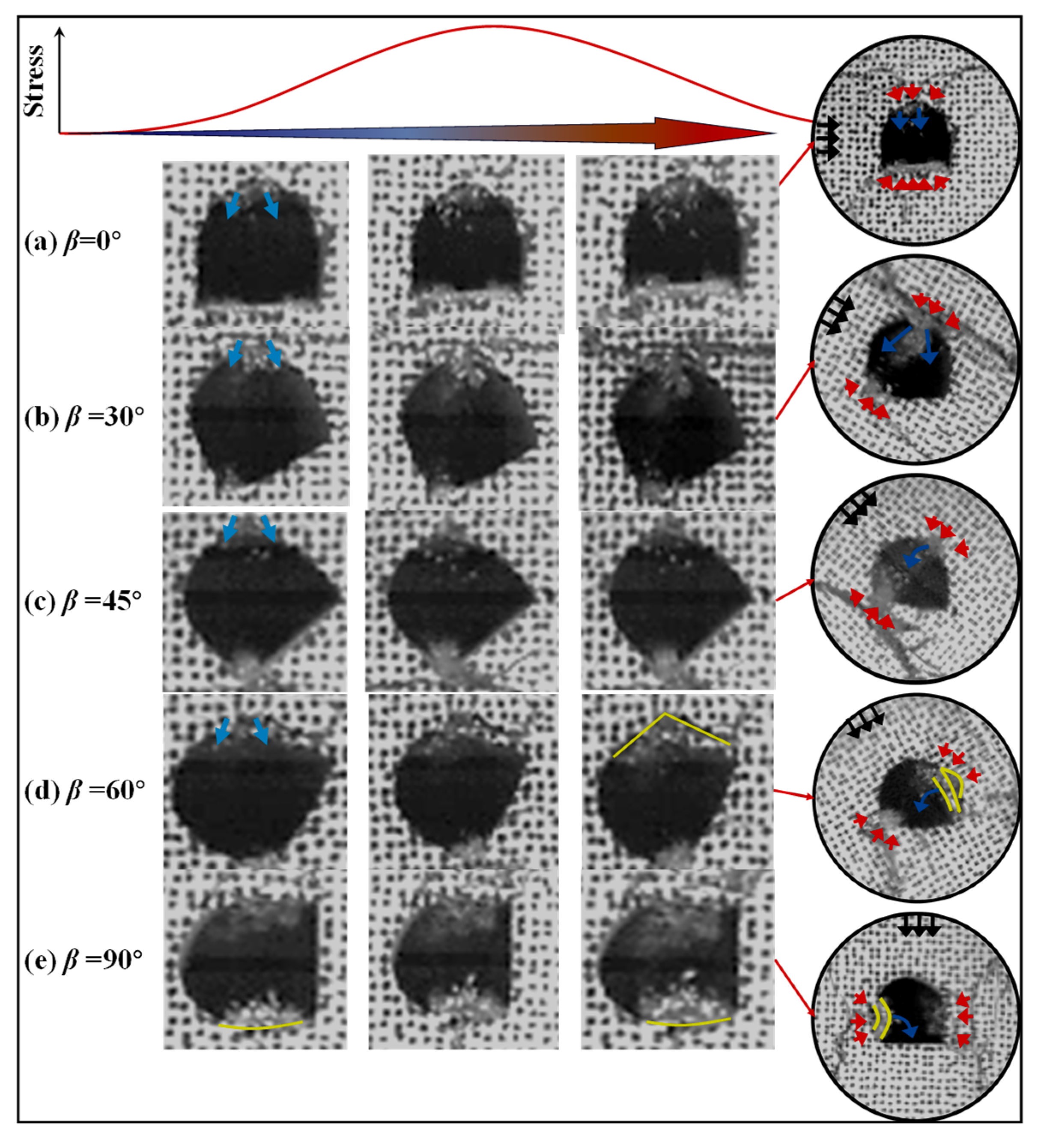
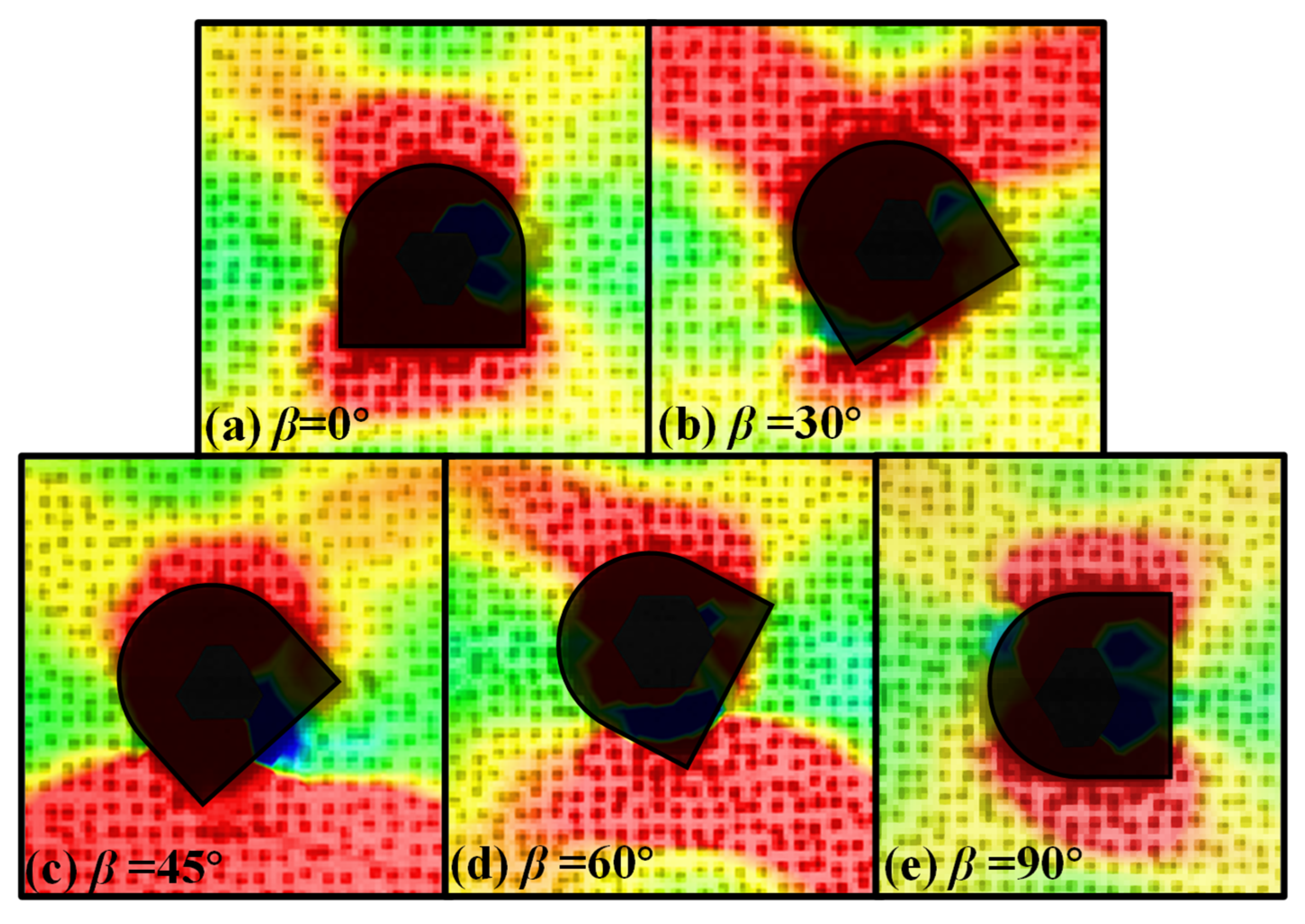
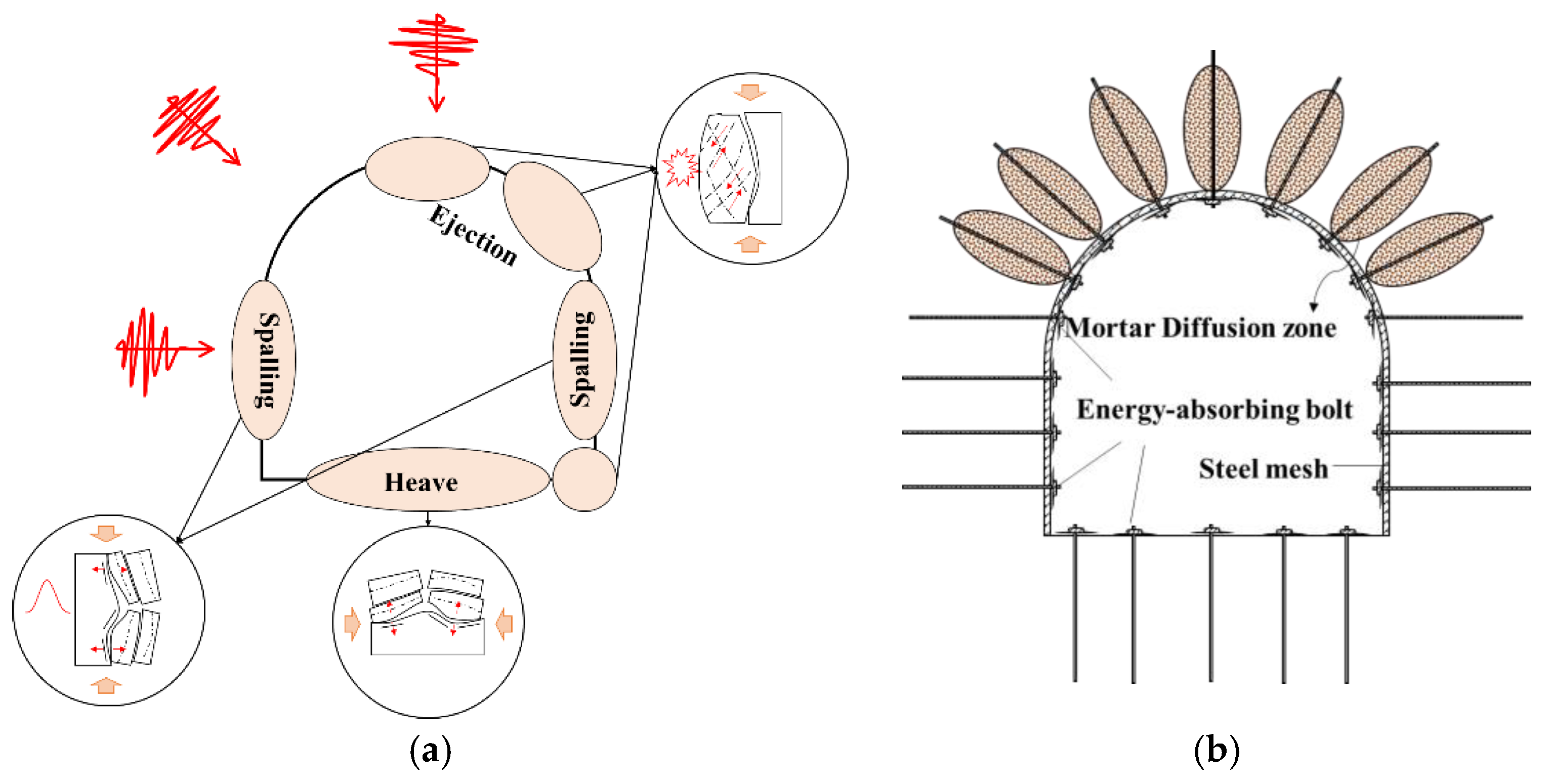
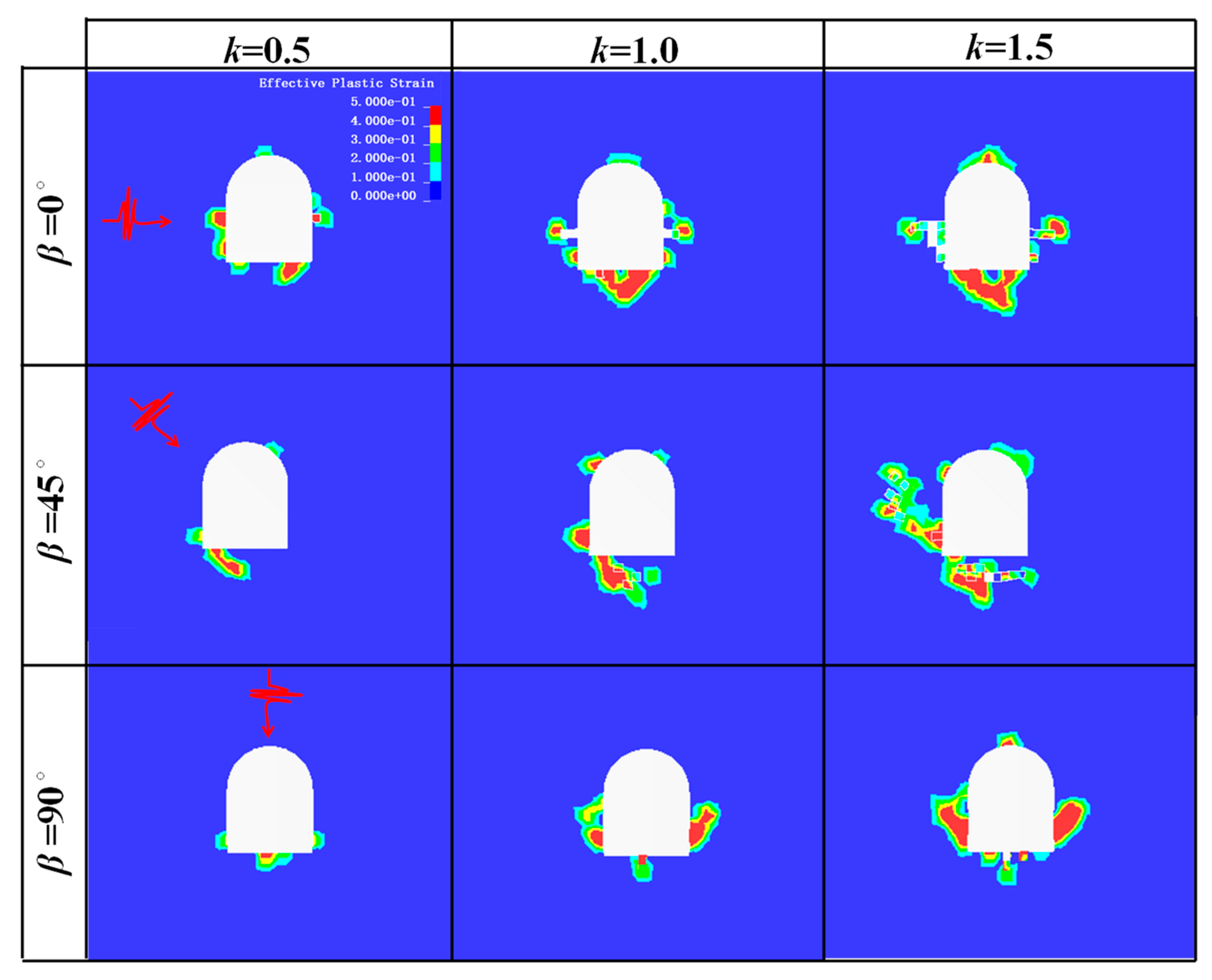
3.3. Damage Around the Arched Hole Under Impact
- (I)
- Heaving, which is manifested when the top and bottom of the specimen experience significant compressive stress at a 0° incident angle. Under this condition, the bottom is compressed and protrudes toward the center free surface, resulting in the formation of a heave.
- (II)
- Rock ejection, which is observed in almost all cases, primarily at the top of the arch, the arch shoulder, and the foot of the arch. This rock ejection is a result of the progressive accumulation and subsequent release of strain energy around the circumference of the arched hole during dynamic impacts. A portion of this energy is converted into kinetic energy, resulting in the ejection of rock debris [30].
- (III)
- Spalling, which occurs in the side walls, is induced by the same mechanism as (I). This is a consequence of an elevation in the circumferential compressive stress [31] during dynamic disturbances. A stress gradient is formed within a localized area, causing deviations in the direction of principal stresses. This ultimately leads to the spalling of surrounding rock from areas experiencing higher stress levels.
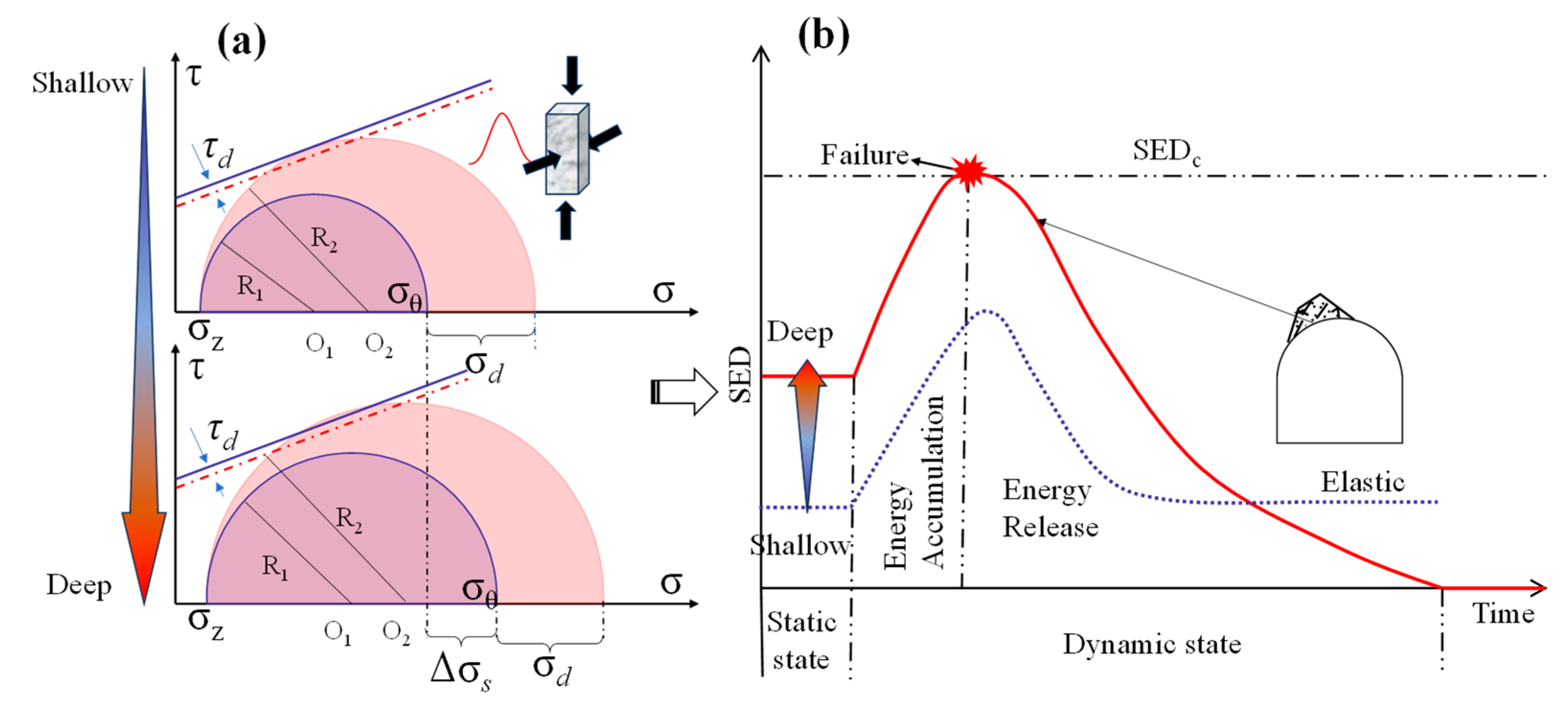
4. Stress State Around the Arched Hole Under Dynamic Impact
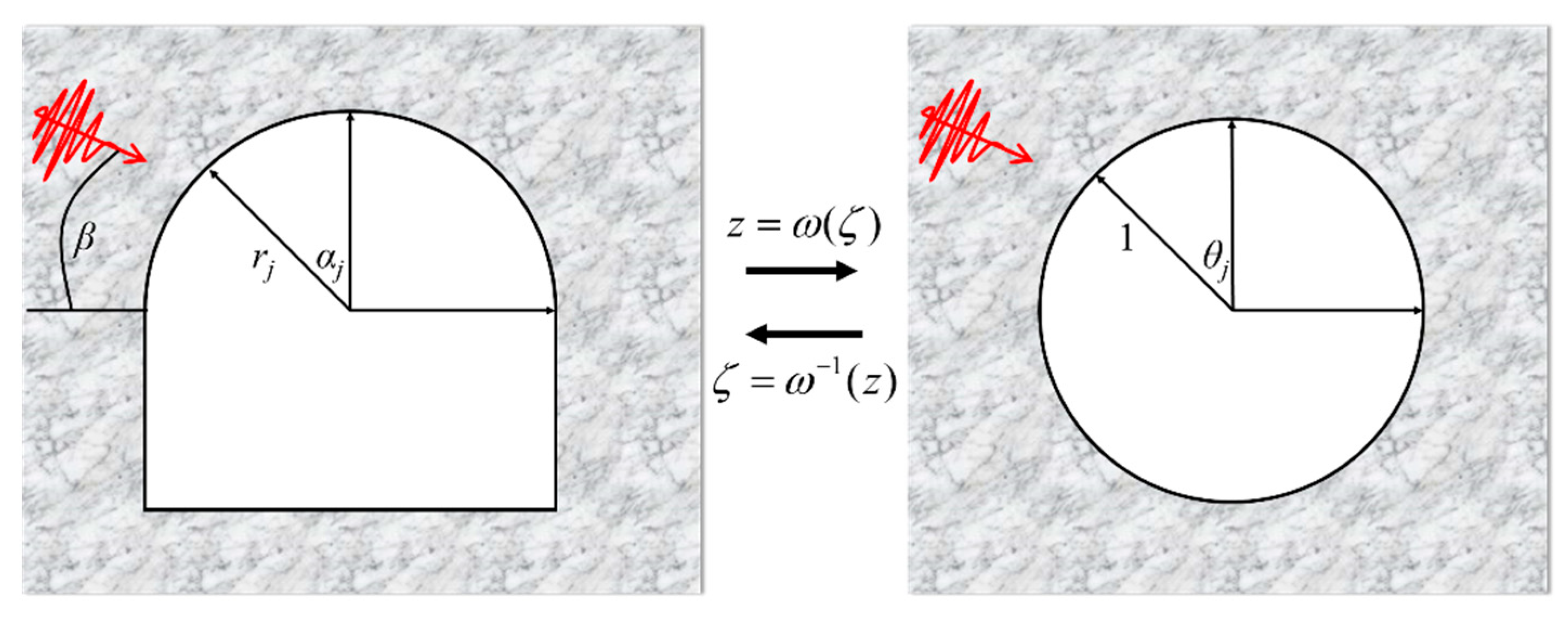
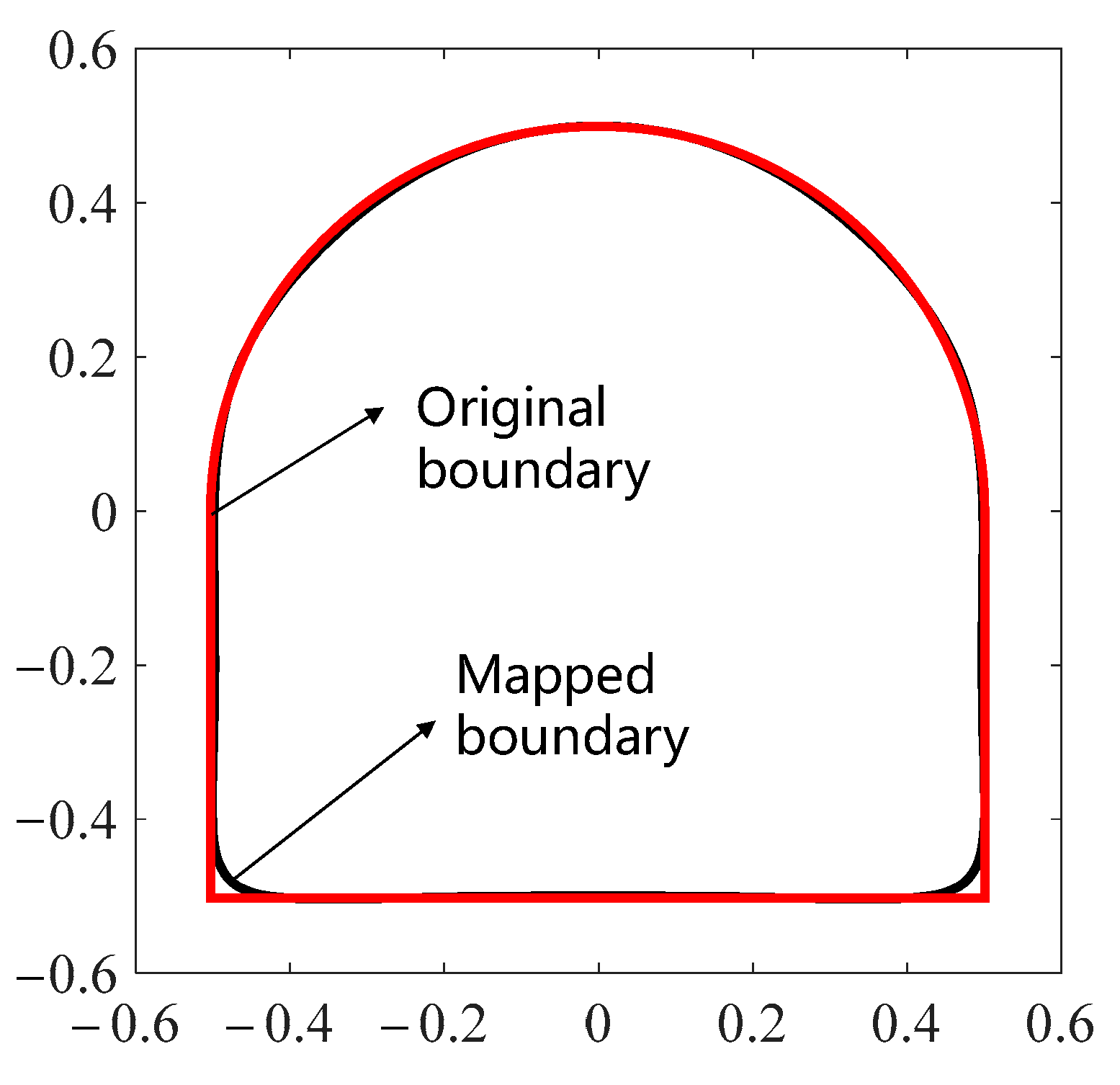
4.1. Conformal Mapping of Arched Hole
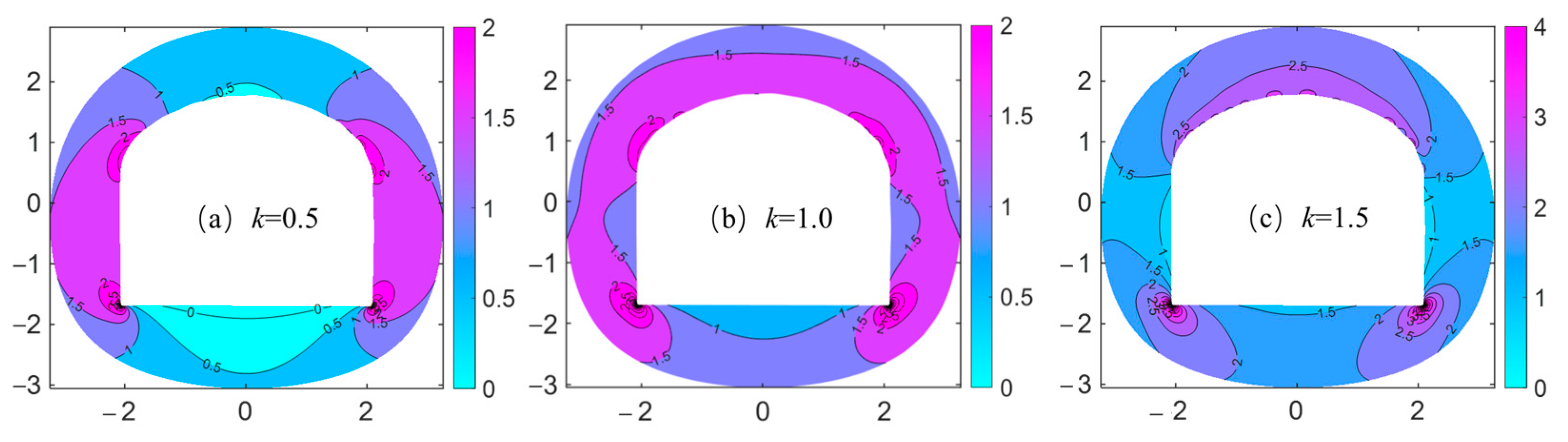
4.2. Dynamic Stress Distribution Around an Arched Hole
5. Discussion
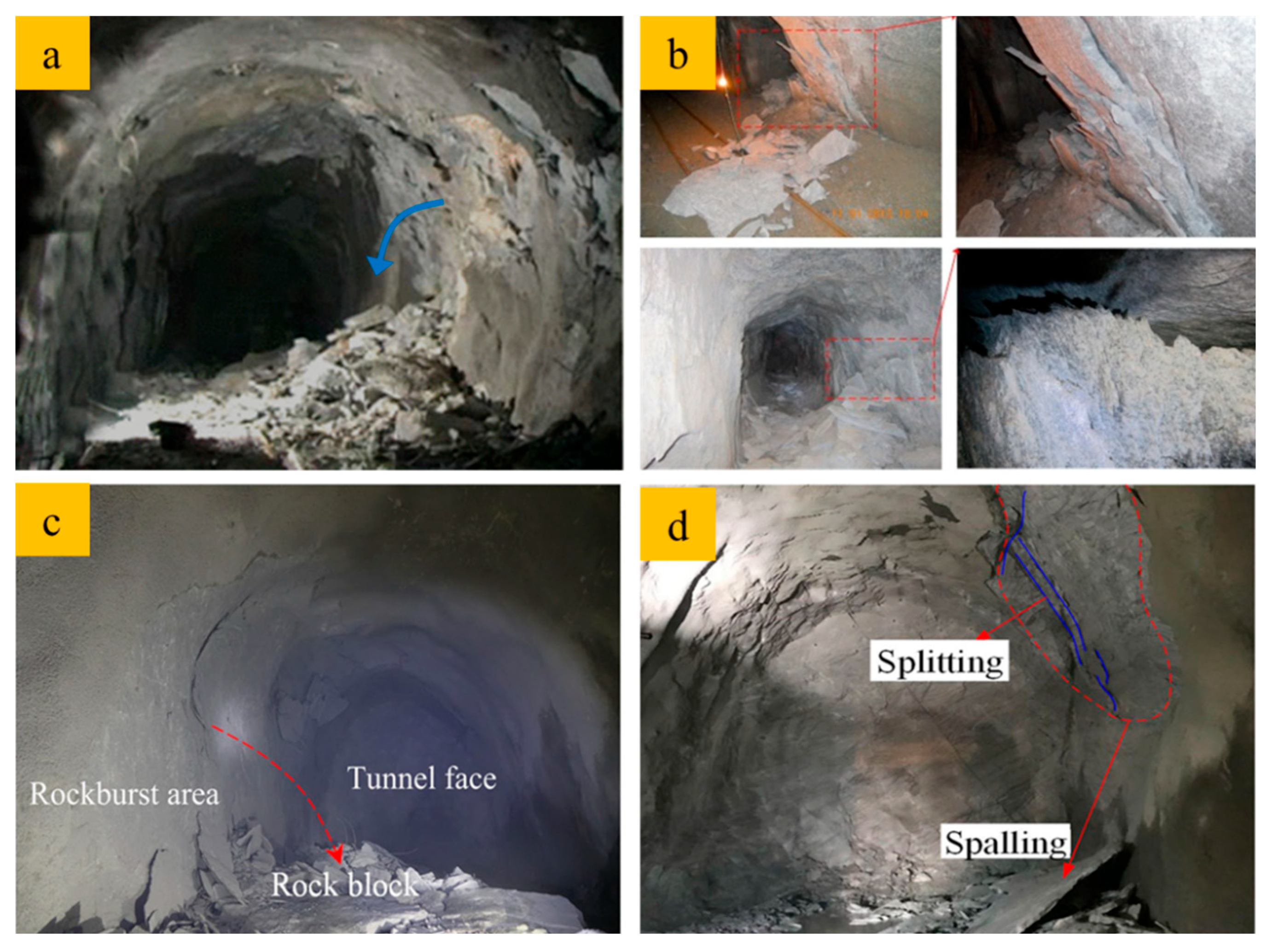
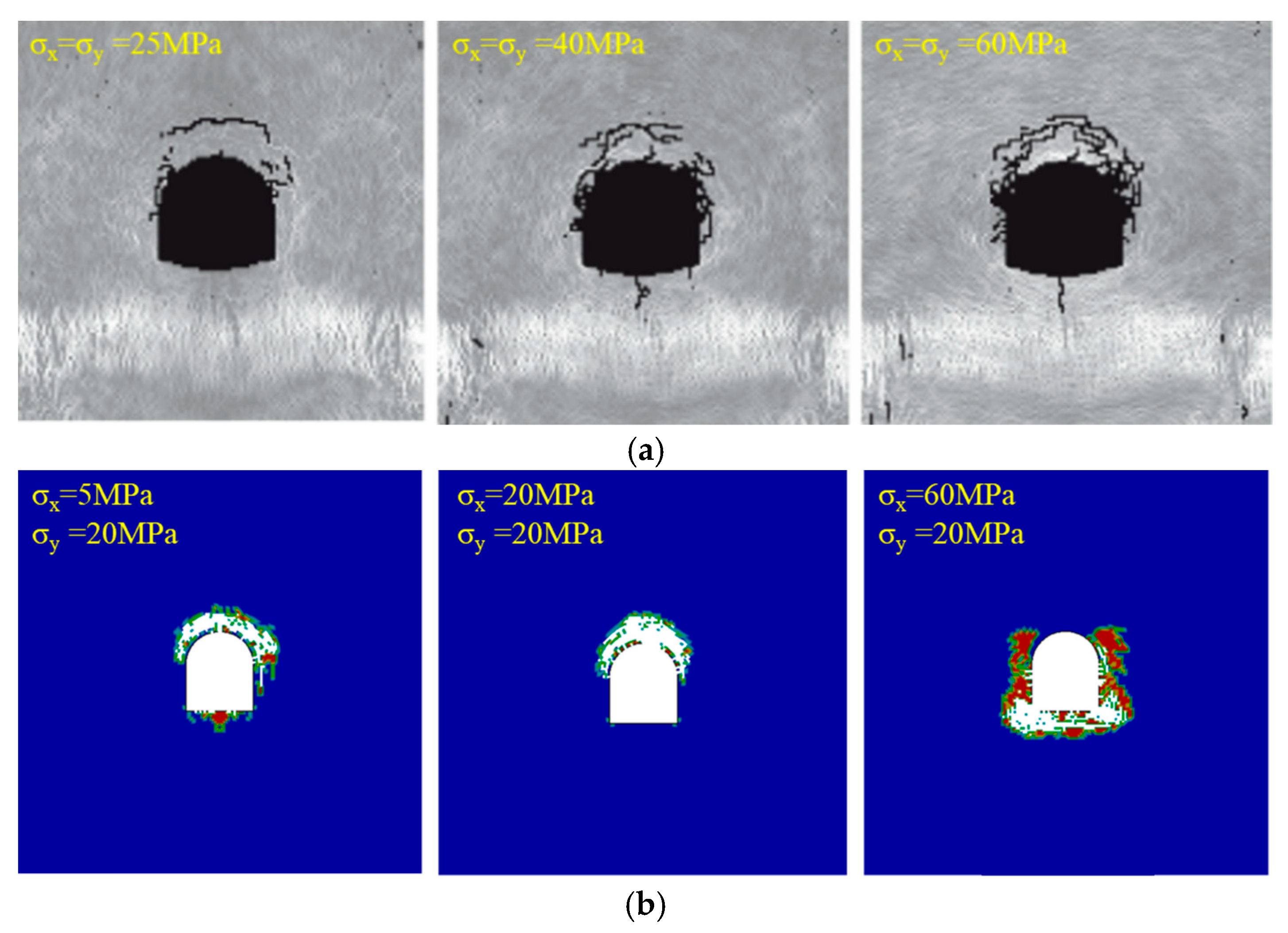
5.1. Insights from Experimental Results for In Situ Observations
5.2. Influence of Dynamic Disturbance Direction on Damage Distribution and Potential Support Systems
5.3. The Role of Geo-Stress and Dynamic Disturbances in Tunnel Failure
6. Conclusions
- (1)
- The initial damage in the vicinity of the arched hole occurs in areas where there is a concentration of circumferential stress, leading to a strain concentration. As the loading continues, macroscopic cracks develop, resulting in overall specimen damage. The early destruction of the specimen is accompanied by the ejection of rock fragments, which serves as an indication of the dynamic destruction of the rock mass.
- (2)
- The complex function and conformal mapping method are capable of handling the transient dynamic stress distribution around the arched hole or tunnel, and the theoretical results are consistent with the experimental results. Under transient dynamic loading, the stress distribution around the arched hole/tunnel is highly influenced by the angle of incidence, and both the overall strength and the elastic modulus of the specimen are at their lowest at an incident angle of 60°. In the direction of perpendicular incidence, a significant concentration of compressive stress is generated, which is the primary cause of tunnel damage under dynamic disturbance, and the tensile stress concentration occurs in the direction of incidence.
- (3)
- When there is initial stress, dynamic disturbance introduces additional stress and energy, altering the original stress and energy state of the surrounding rock. As the initial stress increases, the surrounding rock becomes more susceptible to damage under dynamic disturbance. The intensity of the damage becomes more dramatic, accompanied by a considerable strain energy release.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siren, T.; Kantia, P.; Rinne, M. Considerations and observations of stress-induced and construction-induced excavation damage zone in crystalline rock. Int. J. Rock Mech. Min. Sci. 2015, 73, 165–174. [Google Scholar] [CrossRef]
- Pao, Y.H.; Mow, C.C.; Achenbach, J.D. The Diffraction of Elastic Waves and Dynamic Stress Concentration. J. Appl. Mech. 1973, 40, 213–219. [Google Scholar] [CrossRef]
- Lu, S.W.; Zhou, C.B.; Zhang, Z.; Jiang, N. Particle velocity response of surrounding rock of a circular tunnel subjected to cylindrical P-waves. Tunn. Undergr. Space Technol. 2019, 83, 393–400. [Google Scholar] [CrossRef]
- Penzien, J. Seismically induced racking of tunnel linings. Earthq. Eng. Struct. Dyn. 2000, 29, 683–691. [Google Scholar] [CrossRef]
- Sun, B.B.; Zhang, S.R.; Cui, W.; Deng, M.J.; Wang, C. Nonlinear dynamic response and damage analysis of hydraulic arched tunnels subjected to P waves with arbitrary incoming angles. Comput. Geotech. 2020, 118, 103358. [Google Scholar] [CrossRef]
- Zhao, R.; Tao, M.; Zhao, H.; Cao, W.; Li, X.; Wang, S. Dynamics fracture characteristics of cylindrically-bored granodiorite rocks under different hole size and initial stress state. Theor. Appl. Fract. Mech. 2020, 109, 102702. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, Y.; Yao, W.; Xia, K.; Junxi, T.; Zhan, Z. Dynamic failure characteristics of surrounding rocks under different lateral pressure coefficients in deep tunnel transient excavation. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 17. [Google Scholar] [CrossRef]
- Zou, C.; Li, J.; Zhao, X.; Zhao, J. Why are tensile cracks suppressed under dynamic loading?—Transition strain rate for failure mode. Extrem. Mech. Lett. 2021, 49, 101506. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Gao, Y.F.; Dai, D.H.; Huang, C.X. Effect of imperfect interfaces on dynamic response of a composite lining tunnel with an isolation layer under plane P and SV waves. Soil Dyn. Earthq. Eng. 2021, 142, 106586. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Yang, R.S.; Li, J.; Chen, S.L.; Li, D. Study on dynamic mechanical characteristics of specimens with cavity under prestressing conditions. Eng. Fract. Mech. 2024, 312, 110602. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.; Gong, H.; Jiang, J.; Zhou, A.; Pingkuang, L. Subcritical crack growth and fracture behavior of three rocks containing quartz under wet and dry conditions. Theor. Appl. Fract. Mech. 2023, 126, 103948. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.; Pingkuang, L.; Zhang, C.; Gao, F. Dynamic Damage and Failure of Layered Sandstone with Pre-cracked Hole Under Combined Cyclic Impact and Static Loads. Rock Mech. Rock Eng. 2022, 56, 2271–2291. [Google Scholar] [CrossRef]
- Weng, L.; Li, X.; Taheri, A.; Wu, Q.; Xie, X. Fracture Evolution Around a Cavity in Brittle Rock Under Uniaxial Compression and Coupled Static–Dynamic Loads. Rock Mech. Rock Eng. 2018, 51, 531–545. [Google Scholar] [CrossRef]
- Qiu, J.; Xie, H.; Zhu, J.; Wang, J.; Deng, J. Dynamic response and rockburst characteristics of underground cavern with unexposed joint. Int. J. Rock Mech. Min. Sci. 2023, 169, 105442. [Google Scholar] [CrossRef]
- Li, D.; Xiao, P.; Han, Z.; Zhu, Q. Mechanical and failure properties of rocks with a cavity under coupled static and dynamic loads. Eng. Fract. Mech. 2020, 225, 106195. [Google Scholar] [CrossRef]
- Zhao, H.; Tao, M.; Li, X.; Hong, Z.; Zhao, R.; Cao, W. Experimental investigation on dynamic mechanical properties and fracture evolution behavior of the underground openings with excavation damaged zones. Int. J. Damage Mech. 2022, 31, 1533–1561. [Google Scholar] [CrossRef]
- Lisjak, A.; Garitte, B.; Grasselli, G.; Müller, H.R.; Vietor, T. The excavation of a circular tunnel in a bedded argillaceous rock (Opalinus Clay): Short-term rock mass response and FDEM numerical analysis. Tunn. Undergr. Space Technol. 2015, 45, 227–248. [Google Scholar] [CrossRef]
- Li, M.; Mei, W.; Pan, P.-Z.; Yan, F.; Wu, Z.; Feng, X.-T. Modeling transient excavation-induced dynamic responses in rock mass using an elasto-plastic cellular automaton. Tunn. Undergr. Space Technol. 2020, 96, 103183. [Google Scholar] [CrossRef]
- Feng, F.; Li, X.; Rostami, J.; Li, D. Modeling hard rock failure induced by structural planes around deep circular tunnels. Eng. Fract. Mech. 2019, 205, 152–174. [Google Scholar] [CrossRef]
- Li, X.; Weng, L. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance. Tunn. Undergr. Space Technol. 2016, 54, 61–72. [Google Scholar] [CrossRef]
- Brown, E.T. Rock Characterization, Testing & Monitoring: ISRM Suggested Methods; Pergamon Press: Oxford, UK, 1981. [Google Scholar]
- Ai, D.; Zhao, Y.; Wang, Q.; Li, C. Experimental and numerical investigation of crack propagation and dynamic properties of rock in SHPB indirect tension test. Int. J. Impact Eng. 2019, 126, 135–146. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Lok, T.-S.; Hong, L.; Yin, T. Innovative testing technique of rock subjected to coupled static and dynamic loads. Int. J. Rock Mech. Min. Sci. 2008, 45, 739–748. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Xia, K.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.L.; Dai, F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar] [CrossRef]
- Li, D.; Gao, F.; Han, Z.; Zhu, Q. Experimental evaluation on rock failure mechanism with combined flaws in a connected geometry under coupled static-dynamic loads. Soil Dyn. Earthq. Eng. 2020, 132, 106088. [Google Scholar] [CrossRef]
- Mohr, D.; Gary, G.; Lundberg, B. Evaluation of stress–strain curve estimates in dynamic experiments. Int. J. Impact Eng. 2010, 37, 161–169. [Google Scholar] [CrossRef]
- Liu, X.-R.; Yang, S.-Q.; Huang, Y.-H.; Cheng, J.-L. Experimental study on the strength and fracture mechanism of sandstone containing elliptical holes and fissures under uniaxial compression. Eng. Fract. Mech. 2019, 205, 205–217. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, D.; Han, Z.; Xiao, P.; Li, B. Failure characteristics of brittle rock containing two rectangular holes under uniaxial compression and coupled static-dynamic loads. Acta Geotech. 2022, 17, 131–152. [Google Scholar] [CrossRef]
- Wu, H.; Dai, B.; Cheng, L.; Lu, R.; Zhao, G.Y.; Liang, W.Z. Experimental study of dynamic mechanical response and energy dissipation of rock having a circular opening under impact loading. Min. Metall. Explor. 2021, 38, 1111–1124. [Google Scholar] [CrossRef]
- Su, G.; Chen, Y.; Jiang, Q.; Li, C.; Cai, W. Spalling failure of deep hard rock caverns. J. Rock Mech. Geotech. Eng. 2023, 15, 2083–2104. [Google Scholar] [CrossRef]
- Li, C.; Li, X. Influence of wavelength-to-tunnel-diameter ratio on dynamic response of underground tunnels subjected to blasting loads. Int. J. Rock Mech. Min. Sci. 2018, 112, 323–338. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Brown, E. Rock Mechanics for Underground Mining; Chapman Hall: Boca Raton, FL, USA, 2006; Volume 1993. [Google Scholar]
- Wu, H.; Zhao, G.; Liang, W. Mechanical properties and fracture characteristics of pre-holed rocks subjected to uniaxial loading: A comparative analysis of five hole shapes. Theor. Appl. Fract. Mech. 2020, 105, 102433. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Liang, W. Investigation of cracking behavior and mechanism of sandstone specimens with a hole under compression. Int. J. Mech. Sci. 2019, 163, 105084. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X. Dynamic stress concentration of a non-circular cavern in a viscoelastic medium subjected to a plane P-wave. Acta Mech. 2022, 233, 1455–1466. [Google Scholar] [CrossRef]
- Liu, D.; Gai, B.; Tao, G. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Xiang, G.; Tao, M.; Zhao, R.; Zhao, H.; Burhan Memon, M.; Wu, C. Dynamic response of water-rich tunnel subjected to plane P wave considering excavation induced damage zone. Undergr. Space 2023, 15, 113–130. [Google Scholar] [CrossRef]
- Lu, W.; Yang, J.; Yan, P.; Chen, M.; Zhou, C.; Luo, Y.; Jin, L. Dynamic response of rock mass induced by the transient release of in-situ stress. Int. J. Rock Mech. Min. Sci. 2012, 53, 129–141. [Google Scholar] [CrossRef]
- Hong, Z.; Tao, M.; Wu, C.; Zhou, J.; Wang, D. The spatial distribution of excavation damaged zone around underground roadways during blasting excavation. Bull. Eng. Geol. Environ. 2023, 82, 155. [Google Scholar] [CrossRef]
- Tsinidis, G.; de Silva, F.; Anastasopoulos, I.; Bilotta, E.; Bobet, A.; Hashash, Y.; He, C.; Kampas, G.; Knappett, J.; Madabhushi, G.; et al. Seismic behaviour of tunnels: From experiments to analysis. Tunn. Undergr. Space Technol. 2020, 99, 103334. [Google Scholar] [CrossRef]
- Zhu, W.C.; Li, Z.H.; Zhu, L.; Tang, C.A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance. Tunn. Undergr. Space Technol. 2010, 25, 587–599. [Google Scholar] [CrossRef]
- He, M.; Xia, H.; Jia, X.; Gong, W.; Zhao, F.; Liang, K. Studies on classification, criteria and control of rockbursts. J. Rock Mech. Geotech. Eng. 2012, 2012, 97–114. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, X.-T.; Yang, C.; Su, G. Experimental Study on the Failure Characteristics of Granite Subjected to Weak Dynamic Disturbance Under Different σ3 Conditions. Rock Mech. Rock Eng. 2021, 54, 5577–5590. [Google Scholar] [CrossRef]
- Mitelman, A.; Elmo, D. Analysis of tunnel support design to withstand spalling induced by blasting. Tunn. Undergr. Space Technol. 2016, 51, 354–361. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, C.; Kang, J.; Li, Y.; Wang, M. Study on the mechanism of zonal disintegration around an excavation. Int. J. Rock Mech. Min. Sci. 2014, 67, 88–95. [Google Scholar] [CrossRef]
- He, M.; Gong, W.; Wang, J.; Qi, P.; Tao, Z.; Du, S.; Peng, Y. Development of a novel energy-absorbing bolt with extraordinarily large elongation and constant resistance. Int. J. Rock Mech. Min. Sci. 2014, 67, 29–42. [Google Scholar] [CrossRef]
- Li, C. A new energy-absorbing bolt for rock support in high stress rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 396–404. [Google Scholar] [CrossRef]
- Hu, L.; Li, Y.; Liang, X.; Tang, C.a.; Yan, L. Rock Damage and Energy Balance of Strainbursts Induced by Low Frequency Seismic Disturbance at High Static Stress. Rock Mech. Rock Eng. 2020, 53, 4857–4872. [Google Scholar] [CrossRef]
- Gu, L.J.; Feng, X.T.; Kong, R.; Yang, C.X.; Han, Q.; Xia, Y.L. Excavation stress path induced fracturing mechanism of hard rock in deep tunnel. Rock Mech. Rock Eng. 2023, 56, 1779–1806. [Google Scholar] [CrossRef]
- Zhao, R.; Tao, M.; Xiang, G.-L.; Wang, S.-F.; Zhao, H.-T. Blasting induced dynamic stress concentration and failure characteristics of deep-buried rock tunnel. J. Cent. S. Univ. 2024, 31, 2321–2340. [Google Scholar] [CrossRef]
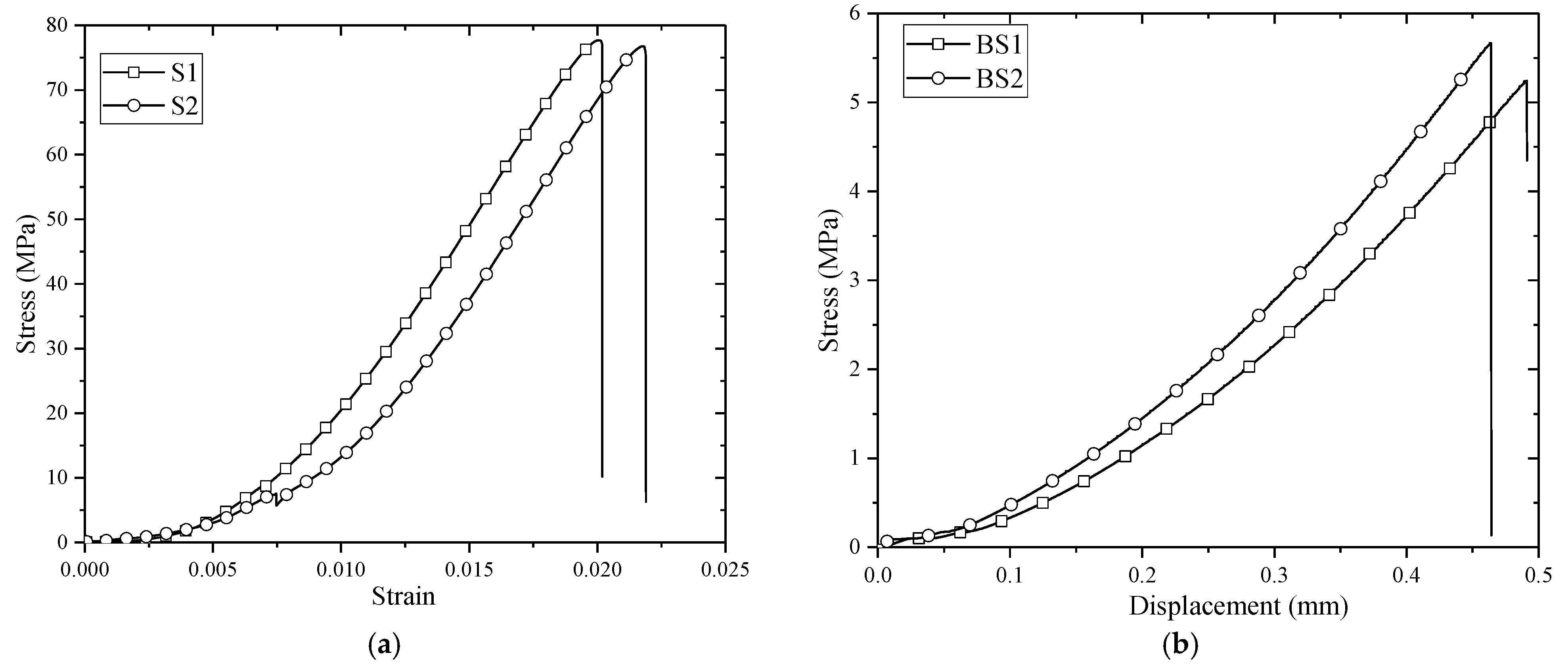
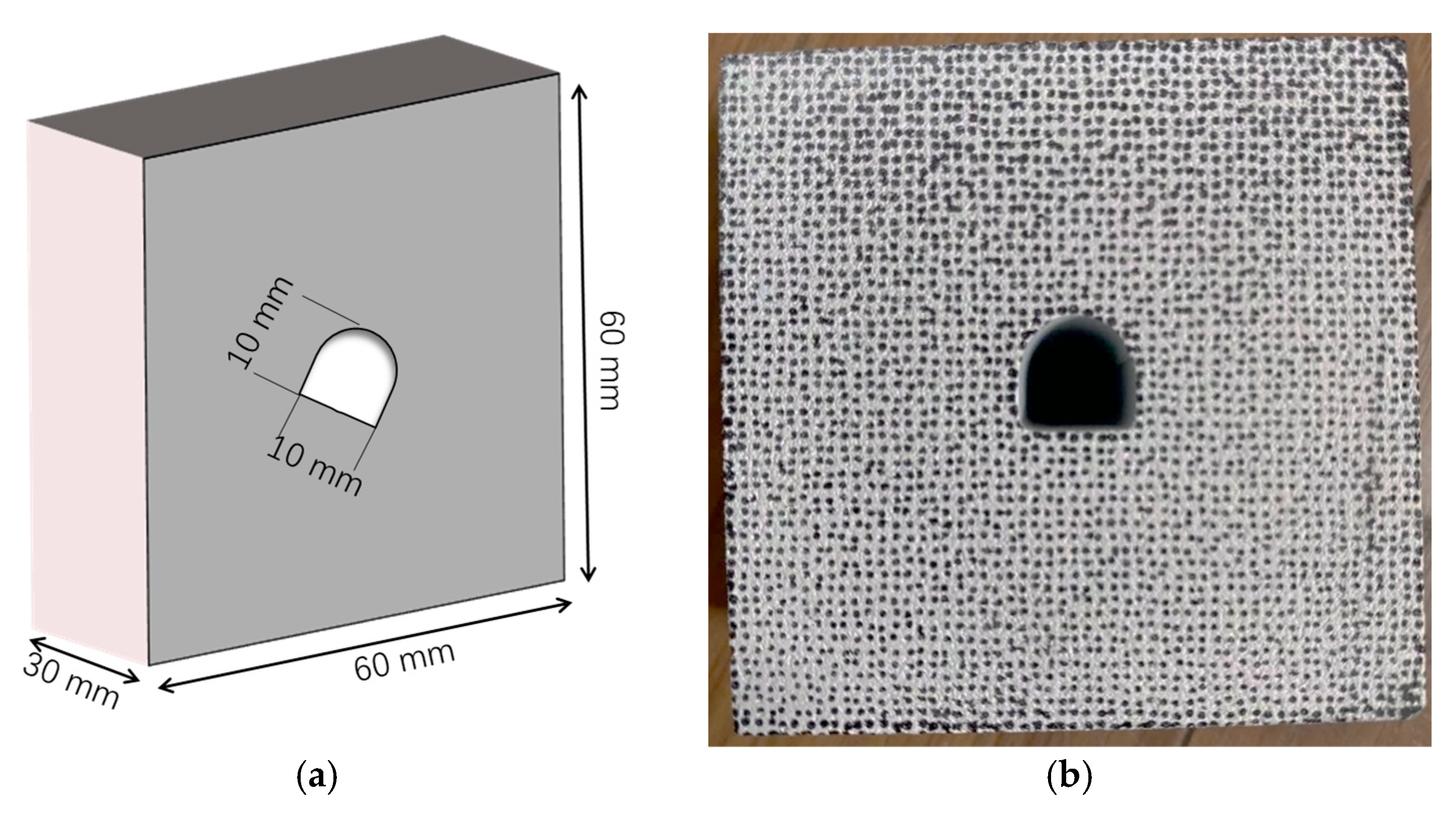


| Density (kg/m3) | Elastic Modulus (GPa) | P-Wave Velocity (m/s) | UCS (MPa) | UTS (MPa) |
|---|---|---|---|---|
| 2357 | 11.65 | 2760 | 77.5 | 5.4 |
| No. | Equipment | Parameters | Quantity |
|---|---|---|---|
| 1 | SHPB: Incident bar, transmitted bar, absorption bar | Made of high-strength 40Cr alloy steel. The diameter, elastic modulus, P-wave velocity and density of the bars are 50 mm, 233 GPa, 5458 m/s and 7817 kg/m3 | 1 |
| 2 | High-speed camera (Phantom V711; Vision Research Inc., Wayne, NJ, USA) | With the lens of Nikon AF Zoom-Nikkor 80–200 mm f/2.8D ED (Nikon, Tokyo, Japan). Resolution was set as 256 × 256 pixels at a frame rate of 79,161 fps. | 1 |
| 3 | LED lights (ZF-3000; Zifon, Shanzhen, China) | Brightness of 2800 lumens | 2 |
| 4 | SDY2107A super dynamic strain meter (Rongjida, Shanghai, China) | \ | 1 |
| 5 | DL850E digital oscilloscope (Yokogawa, Tokyo, Japan) | \ | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tao, M.; Ding, W.; Zhao, R. Dynamically Triggered Damage Around Rock Tunnels: An Experimental and Theoretical Investigation. Appl. Sci. 2025, 15, 7716. https://doi.org/10.3390/app15147716
Wang W, Tao M, Ding W, Zhao R. Dynamically Triggered Damage Around Rock Tunnels: An Experimental and Theoretical Investigation. Applied Sciences. 2025; 15(14):7716. https://doi.org/10.3390/app15147716
Chicago/Turabian StyleWang, Wanlu, Ming Tao, Wenjun Ding, and Rui Zhao. 2025. "Dynamically Triggered Damage Around Rock Tunnels: An Experimental and Theoretical Investigation" Applied Sciences 15, no. 14: 7716. https://doi.org/10.3390/app15147716
APA StyleWang, W., Tao, M., Ding, W., & Zhao, R. (2025). Dynamically Triggered Damage Around Rock Tunnels: An Experimental and Theoretical Investigation. Applied Sciences, 15(14), 7716. https://doi.org/10.3390/app15147716





