Abstract
Microwave-assisted rock fragmentation has been considered as one of the most promising technologies in rock excavation, but due to the fact that excavation is usually carried out in water-rich environments, understanding the dynamic fracture properties of rocks with different water contents after microwave irradiation is thus desirable. This study employed an enhanced split Hopkinson pressure bar (SHPB) system to perform dynamic fracture tests on pre-cracked semi-circular bending (SCB) specimens. It systematically explores the changes in the mechanical properties of sandstone under both dry and saturated conditions after exposure to 700 W of microwave radiation for 10 min. Infrared thermal imaging was utilized to capture the temperature distribution across the specimens, while digital image correlation (DIC) and high-speed photography were used to simultaneously record the crack propagation process. Based on the principle of energy conservation, the analysis of energy dissipation during fracture was performed, and the micro-damage evolution mechanism of the material was revealed through scanning electron microscopy (SEM). The results demonstrated that saturated sandstone exhibited a more rapid heating response and significantly lower dynamic fracture toughness and fracture energy compared to dry samples after microwave irradiation. These findings indicate that water saturation amplifies the weakening effect induced by microwaves, making the rock more susceptible to low-stress fractures. The underlying damage mechanisms of microwave radiation on water-bearing sandstone were interpreted with the theory of pore water pressure and structural thermal stresses.
1. Introduction
With the rapid growth of the world population and the increasing demand for mineral resources from industrialization, mining companies have been forced to improve production efficiency to meet the growing demand for mineral resources. Given the continuous depletion of high-grade mineral deposits on or near the surface, the high demand for mineral resources is forcing advances in mining and exploration technologies to achieve more sustainable, automated, continuous, and deep mining rock breaking techniques [,]. Continuous mining technology has been identified as a key factor in improving mining production efficiency [,,].
The efficient fragmentation of hard rock and maintaining the long-term stability of the surrounding rock are significant challenges encountered during underground mineral resource exploitation. The traditional drilling and blasting method is unable to meet the requirements of green continuous mining in deep hard rock mines due to its intermittency and risk during mining operations, low energy utilization rate, and the potential for rock damage and water inrush disasters [,,]. Relevant scholars have proposed rock breaking methods such as mechanical cutting, high-pressure water jets, microwave or laser beams, and high-temperature plasma jets [,,,,,] and conducted extensive theoretical research and laboratory experiments. Among them, mechanical cutting has the advantages of continuous operation, high construction quality, minimal excavation-induced damage, high safety, and economical operation. It underwent significant development in the latter half of the last century. Notably, the successful development and application of full-section tunnel boring machines (TBMs) along with coal mining machinery have significantly advanced comprehensive mechanized coal resource extraction, greatly enhancing both operational efficiency and safety. However, in metal mines, the extreme wear and tear on cutterheads is a significant issue due to the high strength and abrasiveness of the ore, rendering the mechanical crushing of rocks an exceptionally challenging task [,]. To solve this challenge, researchers have proposed a variety of assisted rock breaking methods. Microwave-assisted rock breaking has a good application prospect [,] and can effectively improve mechanical wear. Microwave action on hard rock will produce thermal effects, resulting in heating damage to the rock [,,].
Fracture toughness is a key parameter in the fracture mechanics of rocks, and the current research on rock fracture toughness under microwave radiation mainly focuses on static conditions [,,,]. Zhou et al. [] used crack extension strain gauges to measure the dynamic fracture crack extension rate of rocks and found that the crack extension rate initially increased due to the fracture process zone (FPZ) and then gradually leveled off. Lu et al. [] and Dai et al. [,] observed that the uniaxial tensile and compressive strengths and point load strength of rocks decreased significantly with increasing microwave power and radiation time. Hartlieb et al. [], through a combination of indoor experiments and numerical simulations, conclude that the microwave heating effect depends on the depth of microwave penetration and rock size, in addition to the non-homogeneity of the rock material. Qin et al. [] studied the effects of different microwave radiation durations at a power density of 8 × 106 W/m3 on granite samples. Xia et al. [] conducted three-point bending impact loading tests on Laurentian granite NSCB samples using the SHPB system to determine their mode I dynamic fracture parameters, including dynamic initiation toughness, fracture energy, dynamic extension toughness, and crack extension rate. The fracture toughness of interfaces between different rocks or minerals is also crucial for assessing rock mass stability in mining operations [].
The above studies have focused on the effect of microwaves on the fracture toughness of dry rock [], but in practice, rock blasting is often carried out in water-rich environments. The presence of water significantly affects the physical and mechanical properties of rock [,,]. During microwave heating, the presence of pore water enhances the microwave heating capacity of sandstone, exposing the rock to high-temperature thermal shock. Additionally, the volume expansion of water can significantly damage the rock. Dai et al. [] found that water is a key factor in the deterioration of the rock. Microwave radiation after cooling in water can produce greater damage to the rock. Peinsitt et al. [] irradiated sandstone, granite, and basalt under both dry and water-saturated conditions in a 2.45 GHz, 3 kW multimode cavity microwave oven and measured the uniaxial compressive strength and ultrasonic velocity of the rocks. Their results indicated that water saturation enhanced the weakening effect of microwaves on rocks, particularly on sandstone, while having minimal impact on granite and a negligible effect on basalt. Deng et al. [] investigated the effect of water saturation on the kinetic behavior of sandstones under different porosity conditions and its mechanism and found that the porosity of sandstones increased and the kinetic strength and total energy dissipation decreased with the increase in the number of cycles. Li et al. [] concluded from experiments that as the water content decreases, the long-term strength of the rock sample increases, and the damage becomes more severe. The presence of pore water intensifies the damage caused by microwave radiation, laying a solid foundation for the broader application of microwave-assisted rock breaking technology.
This paper aims to investigate the dynamic fracture mechanical properties of dry and saturated rocks under the action of microwave radiation. The mode I fracture toughness of NSCB samples was measured in dry and water-saturated states under the modified SHPB test system, respectively. The thermal imager was employed to analyze the changes in the heating rate and temperature distribution uniformity of the sample surface. The fracture failure process of the NSCB sample was recorded by a high-speed camera, the deformation field of the sample was analyzed and calculated by digital image correlation (DIC) technology, and the variation of the crack propagation rate and rotational angular velocity of sandstone with the loading rate was obtained. In addition, the study explores the internal mechanisms and differences in fracture toughness between dry and saturated sandstones under microwave radiation by examining the evolution of the microstructure around the tip of the prefabricated crack and changes in the size of the FPZ. This research provides insights that are more aligned with the complex geological environments and stress conditions encountered during microwave-assisted rock breaking, particularly under dynamic disturbance loads.
2. Materials and Methods
2.1. Sample Preparation
The sandstone samples used in this study were sourced from an underground metal mine in Changsha City, Hunan Province, China. These samples are characterized by high porosity and water absorption. The intact sandstone fragments exhibit a brownish-red color and a relatively uniform texture, with no visible surface cracks. X-ray diffraction analysis was used to obtain specific mass fractions of the mineral components, the main components being quartz (41.23%), feldspar (28.41%), calcite (13.04%), and muscovite (9.27%), as well as minor amounts of hematite (5.63%) and chlorite (2.42%). The grain size of the minerals ranges from 0.03 to 0.5 mm, with some larger particles reaching up to 0.6 mm, classifying the sandstone as a fine- to medium-grained sedimentary rock. The basic physical and mechanical properties of the sandstone are presented in Table 1.

Table 1.
Essential physical and mechanical property parameters of sandstone (mean values and standard deviation).
To investigate the dynamic fracture behavior of the selected sandstone, cores were extracted from the same sandstone rock mass using a diamond drill bit with an internal diameter of 50 mm. During the coring process, the direction of the drill bit was maintained consistently to avoid the influence of rock material anisotropy on the test results. Cylindrical cores were cut into 20 mm thick discs using a rock cutter, and then each disc was sawn in half. Because of the saw tooth thickness, only one standard half-disc sample was obtained for one disc sample. An edge notch of 5 mm in length and 1 mm in width was machined on the half-disc sample. In order to make the notch crack tip sharp enough, a diamond circular saw was used to further sharpen and form the crack tip. The schematic diagrams of the NSCB sample and the machined sample are shown in Figure 1.
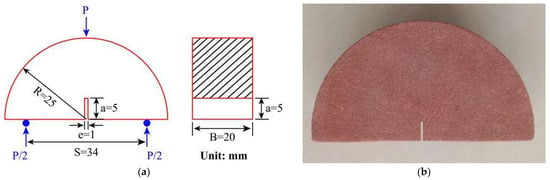
Figure 1.
(a) Schematic diagram of the NSCB sample; (b) processed red sandstone NSCB sample.
A total of 36 NSCB samples were prepared and dried in a vacuum oven at 105 °C for 48 h. The dried samples were then divided into two groups: dry and water-saturated. The water saturation process followed the free absorption method, where the samples were fully submerged in pure water with a pH of 7 and a temperature of 25 °C for 48 h to achieve a saturated state, as shown in Figure 2a. During the soaking process, the sample was taken out every 1 h interval and then dried the surface of the sandstone. The water on the surface of the sandstone was weighed until the weight of the sample remained constant. By changing the weight of sandstone, the moisture content of the sample under different soaking time conditions can be calculated.
where represents the moisture content of the sample, while and denote the dry weight and wet weight of the sample after soaking for a certain period, respectively. Figure 2b illustrates the variation curve of the water content of sandstone samples with immersion time. During the initial stage of immersion, the water content of the sandstone increases rapidly. However, as immersion time progresses, the growth rate of the water content gradually slows. After approximately 28 h of immersion, the weight of the sandstone no longer increases, indicating that the rock has reached a fully water-saturated state. Through regression analysis, the water content of sandstone and soaking time conform to the following functional relationship:
where is the saturated water content of the sample, is the sample soaking time, and is the fitting parameter.
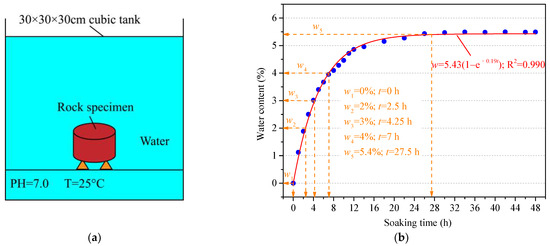
Figure 2.
(a) Schematic diagram of the water immersion treatment method; (b) variation of water content vs. soaking time.
For each group of samples, three samples were used for static fracture strength tests, and fifteen samples were used for dynamic fracture tests with different loading rates.
2.2. Experimental Devices and Techniques
2.2.1. Microwave Heating System
The microwave heating equipment is a multimode cavity industrial microwave oven produced by Hunan Huaye Microwave Technology Co., Ltd., Changsha, China. Figure 3 shows its internal structure and temperature measurement method. The system mainly includes four parts: microwave heating components, control panel, temperature measurement equipment, and cooling system. The microwave generator is composed of four magnetrons with a maximum output power of 1.5 kW. The working voltage of the equipment is 380 V, the microwave frequency is 2.45 GHz, and the maximum output power is 6 kW. The microwave oven has built-in thermocouples and infrared temperature measurement equipment to monitor the surface temperature of the sample in real time.

Figure 3.
Multimode industrial microwave oven equipment.
In order to study the damage caused by radiation time on dry and saturated sandstone. The prepared dry and saturated sandstone samples were heated in a 700 W multimode cavity microwave oven for 10 min, and the surface temperature of the samples was measured by a full-color infrared camera with 320 × 240 pixels at intervals of 30 s. At the same time, the weight change in the samples was recorded, and the whole measurement process was completed within seconds after the end of the microwave radiation and the opening of the furnace door, so the surface temperature changes of the samples could be ignored.
2.2.2. Split Hopkinson Pressure Bar System
The SHPB test system is used to test the dynamic mechanical properties of rock. It is mainly composed of a stress wave loading device, a signal acquisition system, and a high-speed camera. The loading device drives the spindle-shaped bullet to hit the incident rod through the compression cylinder, generating a slowly rising half-sinusoidal incident stress wave, eliminating the effect of P-C oscillations, and ensuring the stress balance at both ends of the sample. The sample is clamped between the incident rod and the transmission rod and kept in a straight line with the elastic rod. After the bullet hits the incident rod, the incident wave propagates to the sample, the reflected wave and transmitted wave are generated due to the difference in wave impedance, and the residual energy is absorbed by the absorber rod. The bullet, incident rod, and transmission rod are made of high-strength 40 Cr alloy steel, with a density of 7810 kg/m3, a Poisson’s ratio of 0.28, and a longitudinal wave velocity of 5400 M/s. The signal was collected by pasting strain gauges on the incident rod and transmission rod 750 mm away from the sample. The strain signals are displayed as voltage signals on an oscilloscope, after the Wheatstone bridge and super dynamic strain gauge are amplified and filtered. The high-speed camera is triggered by the incident wave signal and synchronized with the oscilloscope to record the dynamic rock fragmentation process completely. The schematic diagram of the installation and loading method of the NSCB sample during the dynamic fracture process is shown in Figure 4. Finally, the voltage signal recorded by the strain gauge is converted into the stress signal, and the strength, strain, and strain rate of rock dynamic failure can be calculated by the following formula []:
where ,, and are the modulus of elasticity of the elastic bar, the longitudinal wave speed, and the cross-sectional area, and are the sample length and the cross-sectional area, and , , and are the incident stress, the reflected stress, and the transmitted stress, respectively.
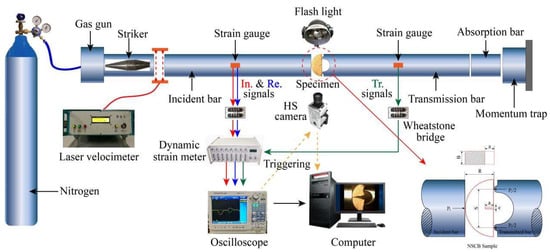
Figure 4.
Schematic diagram of the NSCB sample loading method in the dynamic fracture test.
2.2.3. Verify the Stress Balance
The stress balance between the two ends of the sample is the basic premise of the validity of the SHPB test. According to the one-dimensional stress wave propagation theory of the SHPB test, the load at both ends of the sample is as follows:
where and are the modulus of elasticity and cross-sectional area of the elastic bar and , , and , are the incident strain, reflected strain, and transmitted strain, respectively.
Figure 5a shows the force balance curve of a typical NSCB sandstone sample during dynamic testing. It can be observed that during the application of impact load, the superimposed stress curve and the transmitted stress curve basically coincide, that is, , indicating that the loading force at both ends of the sample is almost the same. Therefore, the inertia effect during dynamic loading can be ignored, and the quasi-static theory can be used to analyze the stress on the sample. The formula for calculating the mode I dynamic stress intensity factor of the NSCB sample is as follows [,]:
where is the mode I dynamic fracture stress intensity factor (SIF); is the length of the precast crack; and are the radius and thickness of the sample, respectively; and is the dimensionless parameter related to the sample geometry as follows [,]:
where is the distance between the two loading points of the transmission; , , and .
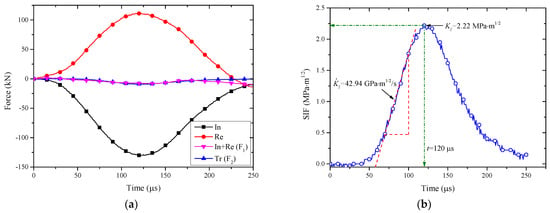
Figure 5.
(a) Verification of dynamic stress balance at both ends of the NSCB sample; (b) determination method of test loading rate.
During the test, the dynamic stress equilibrium was verified for each sample. Two test data sets from the dry group and one from the water-saturated group did not reach dynamic equilibrium, and thus, these three data sets were excluded from the analysis. On the other hand, Figure 5b shows a typical relationship curve of the stress strength factor with loading time, defining the slope of the approximate linear segment during the rise of the curve as the loading rate. In Figure 5b, the loading rate and fracture toughness of the sample are and , respectively.
2.2.4. Digital Image Correlation Technology
This test uses a Hikvision, Hangzhou, China FASTCAM AS1.1 high-speed camera to capture the dynamic fracture process of a sandstone sample and a DIC technique to analyze and calculate the deformation field of the sample. In order to achieve synchronous recording between the high-speed camera and stress waves, the camera is connected to a super dynamic strain gauge. Once the voltage signal recorded in the incident rod rises to −34 mV, the high-speed camera starts shooting. The camera resolution was set to 256 × 244 pixels, and the capture rate was 80,000 frames per second, taking a picture every 12.5 microseconds.
The basic principle of the DIC technique relies on the assumption that the grayscale value of the image remains constant during the loading process. Therefore, strain and displacement fields are obtained using image correlation by tracking the motion of pixels in the reference and deformed images []. For a detailed explanation of the DIC technique, refer to the introduction by Sutton et al. []. To accurately capture pixels, it is necessary to prepare a speckle field with high resolution on the surface of sandstone samples. Firstly, clean the sandstone sample surface with a degreasing agent and then spray the sample surface with white matt paint to form a thin and uniform white background. After the white paint dried, select a speckle-making plate with suitable density bumps and press it on the surface of the white paint to produce randomly distributed black spots. Taking the photos taken by a high-speed camera before the deformation of the sample as the reference, and a series of deformation images during the loading process as the target, the deformation and failure process of the sample during the whole loading process is analyzed.
VIC-2D 6.0 software is used to analyze and calculate the deformation field on the specimen surface, which mainly includes the following steps: (1) import a series of speckle photos into the VIC-2D data processing software and then select the region of interest (ROI) on the surface of the sample; (2) divide the ROI into several subsets of a specified size and step size and calibrate the images based on the actual size of the sample; (3) calculate the initial displacement of these subsets and search for corresponding subsets in the target image based on the correlation algorithm; (4) calculate displacement and engineering strain based on the different positions of the subset in the reference image and the target image; and (5) obtain the strain field through differential treatment of the displacement. The working principle and process of calculating the sample deformation field using the DIC technique are illustrated in Figure 6.
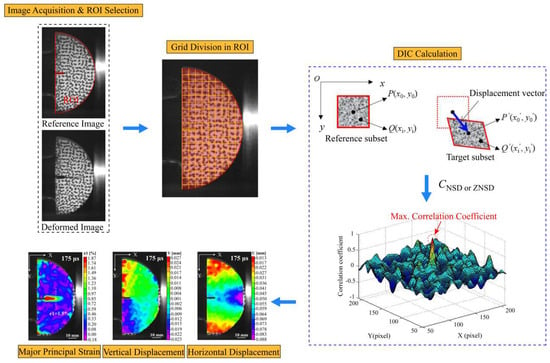
Figure 6.
Schematic diagram of the working principle of the sample deformation field calculated by DIC technology.
3. Results
3.1. Temperature Distribution Characteristics
The surface temperature distribution characteristics of the water-saturated sandstone samples recorded by the thermal imager during microwave radiation are given in Figure 7. Due to the small size of the half-disc samples, the thermographic differences between dry and water-saturated sandstone samples are not particularly pronounced. However, as the duration of microwave radiation increases, the samples exhibit a pattern of higher temperatures at the center and lower temperatures at the edges. The center of the sample appears bright white, with the heat extending outward. Eventually, the highest temperature stabilizes at the center and remains unchanged. This phenomenon occurs primarily due to the differing heat dissipation conditions from the interior to the exterior of the rock, resulting in a higher temperature at the center of the rock, which gradually decreases in a circular pattern toward the edge of the sample.
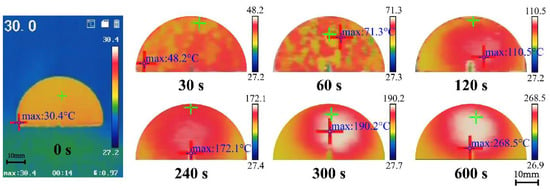
Figure 7.
Thermal imaging of the temperature distribution of water-saturated sandstone samples during microwave heating.
As the mode I fracture of NSCB samples propagates along the prefabricated cracks, it can be observed from Figure 7 that when the microwave heating time reaches 120 s, the highest temperature begins to concentrate around the prefabricated cracks. This indicates that microwave radiation has a significant impact on the FPZ of the sandstone.
Due to the uneven temperature distribution on the surface of the sample, thermal imaging analysis software IVMS-4800 2.1.0.3 was used to quantitatively analyze the surface temperature of the sandstone sample. Figure 8 shows the maximum temperature, average temperature, and the ratio of maximum temperature to average temperature on the surface of dry and saturated sandstone samples during microwave radiation, respectively, to quantitatively analyze the effect of pore water on the microwave heating effect of sandstone semi-circular samples.
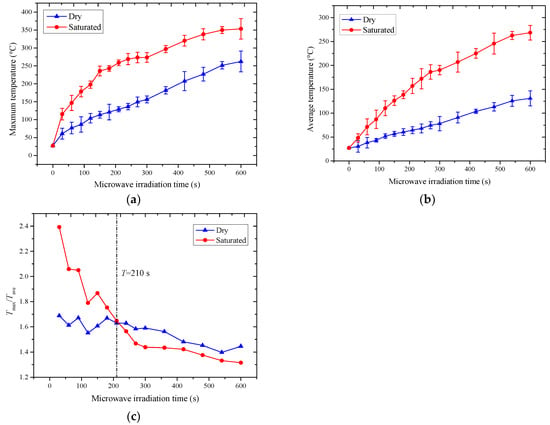
Figure 8.
Variation of the maximum surface temperature: (a) average temperature, (b) variation with microwave radiation time, (c) maximum surface temperature of the sample and the ratio of the average temperature (Tmax/Tave) variation with microwave radiation time.
Firstly, for dry sandstone samples, both the maximum and average temperatures show an approximately linear increase in temperature with the increase in microwave radiation time. This also indicates that the dielectric heat generation capacity of dry sandstone samples does not undergo significant changes during microwave heating. In contrast, the temperature rise in the water-saturated sandstone samples can be divided into two distinct stages; the turning point of microwave radiation time appears at 300 s. In the first stage, 0–300 s, the presence of pore water leads to an increase in the dielectric properties of the sandstone, in which the water molecules are the first to absorb microwave energy and convert it into heat energy for transfer to the rock matrix, resulting in a higher heating rate of the water-saturated sandstone. In the second stage, when the microwave radiation time exceeds 300 s, the average surface temperature of the sample has approached 200 °C. At this time, the water inside the rock has been completely dried, and the main microwave absorption medium at this stage is the rock matrix, rather than the water molecules inside the sample. Since the dielectric loss factor of sandstone minerals is relatively low, the efficiency of microwave energy absorption decreases, leading to a slower rate of surface temperature rise beyond 300 s.
In addition, the ratio of the highest temperature to the average temperature on the surface of the sample (Tmax/Tave) can, to some extent, reflect the uniformity of temperature distribution. The larger the ratio between the two, the more uneven the temperature distribution on the rock surface. Figure 8c shows the variation of this ratio for both dry and water-saturated sandstone with microwave radiation time. It can be observed that both curves exhibit a rapid decline followed by stabilization as the microwave radiation time increases, which also indicates that with the extension of microwave radiation time. The heat convection and conduction within the sample in high high-temperature environment will lead to a more uniform rock temperature distribution. Another important phenomenon is that the temperature non-uniformity of saturated sandstone is higher than that of dry sandstone before 210 s, which may be due to the dielectric heat generated by the pore water inside the rock, causing the heating rate of the sample to be greater than its own thermal conduction or diffusion rate, resulting in a significant “hot spot effect” on its surface. After 210 s, the unevenness of temperature distribution on the surface of saturated sandstone tends to stabilize and is lower than that of dry sandstone samples. This may be because saturated sandstone has reached a higher temperature state at this time, and its internal heat conduction and convection are intense. On the other hand, the loss of moisture also leads to a slower heating rate of the rock, during which the heat conduction rate is greater than the microwave heating rate, resulting in a more uniform temperature distribution on the surface of the sample.
3.2. Static Physico-Mechanical Property Changes
The changes in static physical and mechanical parameters of dry and water-saturated sandstone after exposure to microwave radiation are shown in Figure 9. (1) The density of the sandstone showed little to no change after microwave radiation, whether in the dry or water-saturated state. This is likely because the temperatures during the experiment were not high enough to cause mineral decomposition. (2) Under the effect of microwave radiation, the presence of pore water has a significant pore expansion and fracturing effect on the rock, as shown by the increase in porosity of water-saturated sandstones by about 35% after experiencing microwave radiation. (3) Due to the low sensitivity of dry sandstone to microwave radiation, the damage to these samples was minimal, as evidenced by a decrease in longitudinal wave velocity and static fracture toughness of less than 5%. (4) The presence of pore water significantly aggravated the damage caused by microwave radiation. Compared to dry samples, the longitudinal wave velocity and fracture toughness of water-saturated sandstone decreased by 26% and 45%, respectively, after microwave exposure.
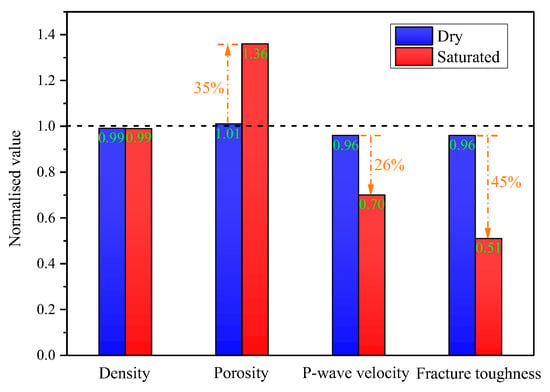
Figure 9.
Normalized values of static physical and mechanical parameters of dry and water-saturated sandstone after microwave radiation action.
3.3. Correlation of Dynamic Cracking Toughness Rate
The initiation toughness measured by the NSCB method is actually the peak value of the stress intensity factor historical curve at the beginning of crack propagation, which can reflect the rock’s ability to resist initiation. Therefore, fracture toughness is an important parameter for evaluating the weakening effect of microwave radiation on fractured rock masses. The dynamic fracture initiation toughness of both dry and water-saturated sandstones after microwave radiation is presented in Figure 10. It can be found that the fracture toughness of sandstone in both dry and water-saturated states shows a significant and similar loading rate dependence, and the fracture toughness of water-saturated sandstone is significantly lower than that of dry samples after microwave radiation. At a loading rate of 200 GPa·m1/2/s, the fracture toughness of the water-saturated samples decreased by approximately 33.4% compared to the dry samples, indicating that pore water plays a positive role in microwave weakening of rock fracture toughness. In Figure 10, lowercase subscripts d and s are used to distinguish between the fracture initiation toughness of dry sandstone and water-saturated sandstone, represented as and , respectively. The fitted relationship between fracture toughness and loading rate of sandstone can be expressed as follows:
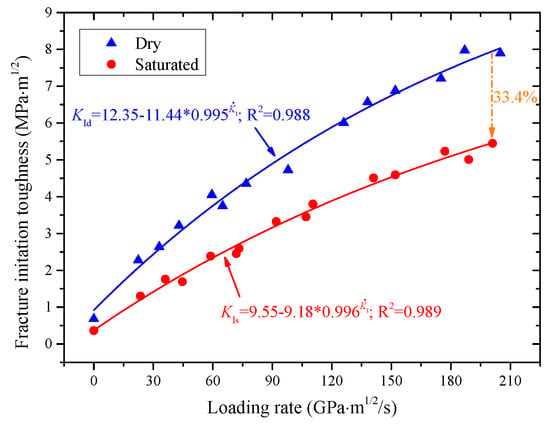
Figure 10.
Relationship between sandstone cracking toughness and loading rate.
The fracture initiation, propagation, and debris movement trajectories of the NSCB samples, as captured by the high-speed camera, are shown in Figure 11. The photos taken by the high-speed camera indicate that the rock started to crack at a loading time of 162.5 μs, and the crack propagation began at the tip of the pre-existing crack and propagated along the potential failure path. However, the initial fracture shape was so small that it could only be detected through repeated comparison of the images before and after fracture initiation. The fracture propagation path of the NSCB samples became visible to the naked eye at 175 μs. As the loading time progressed, the fracture continued to propagate along the potential failure path toward the incident bar, gradually splitting the sample into two intact fragments, each resembling a fan (one-quarter of a circle). These two fragments rotated around the incident bar’s loading point in opposite directions—upward and downward—using the fracture line as the central axis. The rotation angles between the two fragments were measured at different time intervals: 8.5° at 287.5 μs, 11° at 325 μs, and 17.5° at 400 μs. This indicates that the angular velocity of rotation of the fragment increased gradually during this period, reaching 581.7 rad/s and 756.3 rad/s, respectively. It should be noted that the calculation method of the angular velocity of rotation is based on the artificial measurement of the photographs taken by the high-speed camera, and there is inevitably some error in the calculation process.
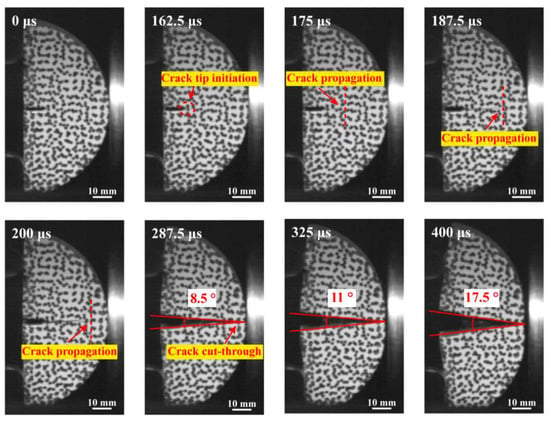
Figure 11.
Photograph of the dynamic fracture process of dry sandstone taken by a high-speed camera.
3.4. Quantification of Crack Growth Rate Based on DIC
The DIC technique enables the calculation of the maximum principal strain on the surface of the NSCB sample throughout the entire loading process, providing a visualization of the evolution of horizontal and vertical displacements. As shown in Figure 12, at 162.5 μs, microcracks start to appear from the pre-existing crack tip. Horizontal strain is observed at the loading end of the incident rod after the stress wave reaches the sample, and vertical strain begins to form in the area around the notch tip. This is consistent with the crack initiation time determined by our high-speed camera.
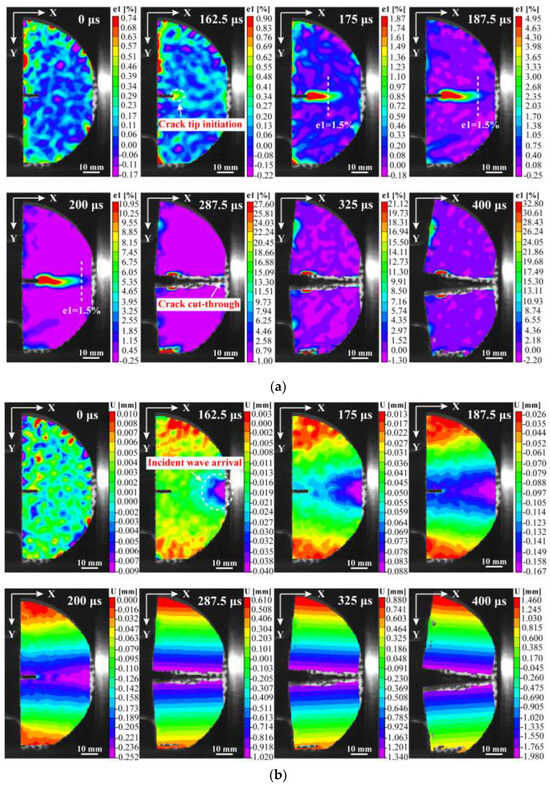
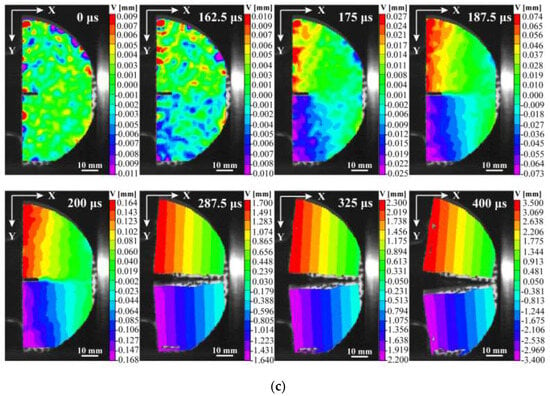
Figure 12.
Under DIC technology, the maximum principal strain (a), horizontal displacement strain (b), and vertical displacement strain (c) on the surface of NSCB are shown.
Microcracks develop rapidly over time and expand along the potential fracture path toward the incident bar, eventually splitting the sample into two equal fragments. As shown in Figure 12c, all values of the vertical strain at the crack tip are positive, which also indicates that the fracture is caused by tensile stress. In addition, the crack visible to the naked eye as observed by the high-speed camera was compared with the crack extension process as indicated by the maximum principal strain obtained from the DIC processing, and the results showed that the maximum principal strain corresponding to the crack tip extension that could be identified by the high-speed camera was .
The crack extension velocity is an essential parameter for characterizing the dynamic fracture process of rocks. Based on the DIC technique, the crack extension velocity is determined from the variation of the vertical displacement field of the sample during the dynamic loading process. The DIC post-processing software VIC-2D 6.0 includes a virtual displacement extensometer measurement tool. As shown in Figure 13a, two displacement pins, E0 and E1, are placed perpendicular to the crack extension trajectory, with a distance of 15 mm between them. Additionally, Zhou et al. [], while measuring the crack extension velocity in dynamic fracture of rocks using crack extension strain gauges, found that the velocity initially increases due to the influence of the FPZ before gradually leveling off. To minimize the impact of the FPZ on measurement results, E0 was placed 1 mm from the prefabricated crack tip.
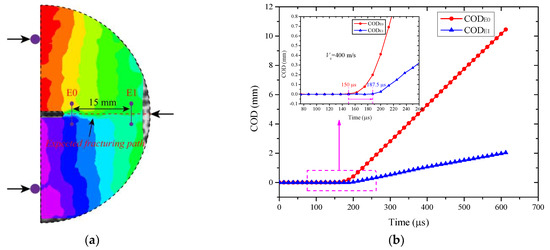
Figure 13.
(a) Schematic diagram of the displacement extensometer arrangement; (b) COD history of the two extensometers measured by DIC.
As shown in Figure 13b, the displacement extensometer values remain at 0 at the beginning of loading. As the loading time progressed, the crack passes through the displacement meter elongation meters E0 and E1 at 150 μs and 187.5 μs, respectively, and the two elongation meter values continue to increase. For a given loading time, the values of E0 and E1 are the crack opening displacement (COD) at the given position of the sample. The moment of a sudden increase in E0 and E1 data can be regarded as the fracture time at the corresponding position, and the distance between the two extensometers is 15 mm. From this, it can be calculated that the average speed of crack propagation in the sample within this propagation distance range is 400 m/s.
The variation in crack propagation speed of microwave-radiated sandstone for the loading rate was obtained, as shown in Figure 14. It can be observed that the crack propagation rate of sandstone increases with the loading rate after microwave radiation. In the loading rate range of 22.4~205 GPa·m1/2/s, the crack expansion rates of dry and water-saturated sandstone samples after microwave radiation were 259.5~610.9 m/s and 362.6~760.4 m/s, respectively. Under the same loading rate conditions, the crack propagation speed of the saturated sample is significantly higher than that of the dry sample, and the sensitivity of the loading rate to the crack propagation speed of the saturated sample is also higher. This is because the steam water pressure generated by the saturated sample inside the rock under microwave radiation will reduce the bonding strength between particles, ultimately leading to a significant decrease in its ability to resist load and crack propagation.
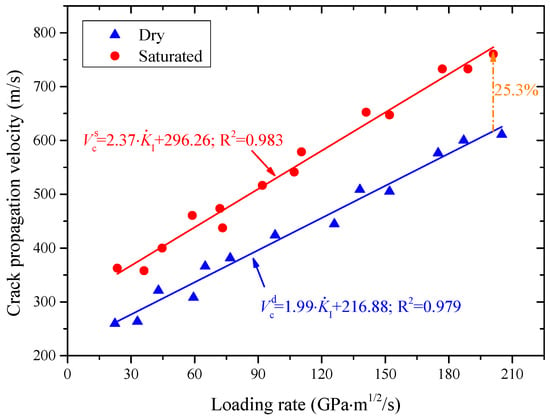
Figure 14.
Crack expansion rate versus loading rate.
3.5. Energy Dissipation Characteristics of Dynamic Fracture
Under impact loading, energy is transferred in the form of stress waves. Based on elastic wave theory, the energy carried by each waveform in the SHPB system can be calculated according to the following formula [,,,,]:
where , , and represent the energy carried by the incident, reflected, and transmitted waves, respectively; is the P-wave velocity of the elastic bar, and is the moment when the sample is completely fractured. According to the Law of Conservation of Energy, if the energy lost due to friction between the elastic bar and the sample is negligible, the energy absorbed by the sample can be expressed as the following equation:
Generally, in the NSCB dynamic fracture test, the energy absorbed by the rock sample consists of three main components [,,]: (1) the total energy dissipated by fracture (Ω), which is used to generate new fracture surfaces and microcracks; (2) the residual kinetic energy (T) trapped in the fragments, manifested as two fragments rotating around the loading orbit during mode I fracture; and (3) the energy dissipated in other forms, including heat, electromagnetic energy, and acoustic energy. Due to the small proportion of other energies in conventional SHPB testing, they can be ignored. Thus, the total fracture dissipation energy can be approximated as follows []:
The residual kinetic energy of the fragment is used primarily for the translational and rotational motion of the two fractured fragments, as calculated by the following formula []:
where is the mass of each flight fragment; represents the inertia of rotation around the axis; is the rotational angular velocity; and denotes the displacement caused by the barycenter of the fragment, and it can be obtained from the product of the distance between the center of mass and the loading point and the angular velocity of rotation.
In this study, the DIC method was employed to efficiently and accurately measure the angular velocity of rotation of fractured fragments . The fracture fragment rotation process during the crack failure is schematically illustrated in Figure 15a. Two symmetric reference points, P1 and P2, located on either side of the prefabricated fracture, were selected from the horizontal and vertical displacement fields using VIC-2D software. The distances L from P1 and P2 to the mounting point are equivalent, and the angular velocity of fragment rotation can be calculated using the formula , where is the displacement of the selected reference point in this study and . Based on the displacement trajectories of P1 and P2, the variations of the angular velocity of rotation can be deduced from the DIC analysis, as shown in Figure 15b.
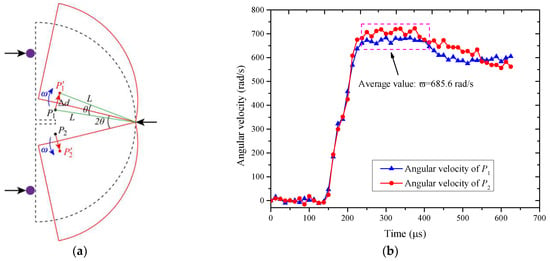
Figure 15.
(a) Schematic diagram of the rotation of sample NSCB; (b) variation of rotational angular velocity with loading time.
It can be observed that after the initiation of the rock crack, the angular velocity of rotation increases rapidly with loading time and then stabilizes. Moreover, the angular velocities of the two fragments are nearly equal, indicating that the rotation of the two fragments is almost symmetrical at the onset of crack initiation. As loading time continues, the rotational angular velocity experiences a slight decrease after 400 μs, eventually reaching and maintaining a relatively stable value. This minor decrease is likely due to the sliding of the sample between the elastic bars. Therefore, the average value of the first stable phase of angular velocity is selected as the average rotational angular velocity of the fragments, which is obtained by averaging the angular velocity values in the dashed rectangle in Figure 15b. In Figure 15b, the average of the rotation angle with sandstone fragments is 685.6 rad/s.
Furthermore, the average dynamic fracture energy of the NSCB sample , which is the energy consumed per unit fracture area (), can be expressed as follows []:
In calculating the average dynamic fracture energy , the newly created fracture surface is calculated by . The roughness of the fracture surface and the area of the newly formed microcracks are not evaluated. Therefore, the obtained in this study represents the upper limit of the average fracture energy.
The correlation between energy distribution and loading rate of sandstone samples in dynamic NSCB tests is shown in Figure 16a. At the same loading rate, the residual kinetic energy of the water-saturated samples is greater than that of the dry samples. This indicates that the ability of water-saturated sandstone to resist loading and crack propagation is reduced after microwave radiation, manifested by a higher rotational angular velocity of fragments, resulting in a higher residual kinetic energy of the calculated sample.
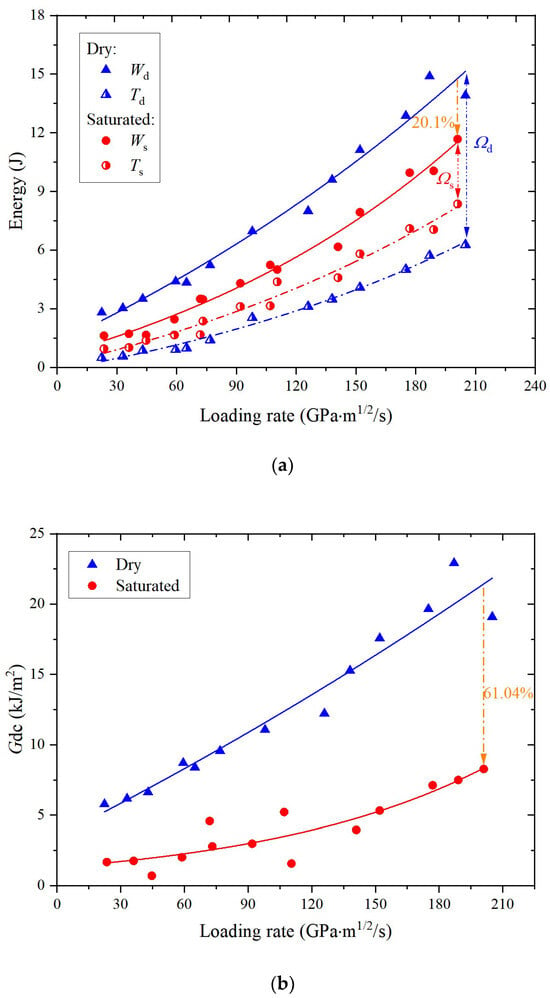
Figure 16.
Energy distribution in relation to loading rate: (a) absorbed energy and residual kinetic energy of the sample; (b) dynamic rupture energy.
The energy absorbed by the saturated sample is less than that of the dry sample. At a loading rate of 200 GPa·m1/2/s, the disparity between them is 20.1%. From the energy absorption values alone, it can be inferred that microwave radiation has a more pronounced damaging and fracturing effect on water-saturated sandstone, resulting in fracture damage at lower energy absorption levels.
The residual kinetic energy of the water-saturated sandstone samples is greater than that of the dry samples. This results in a significantly larger difference in the dynamic fracture energy consumed to generate new fracture surfaces and microcracks between the two states. It also indicates that the presence of pore water has a significant effect on the magnitude of the residual kinetic energy during the calculation of the dynamic fracture energy of microwave-radiated sandstones.
Based on the principle of energy conservation, the dynamic fracture energy consumed per unit fracture area is shown in Figure 16b. It can be observed that the dynamic fracture energy increases with the rise in loading rate, and the dynamic fracture energy of the water-saturated sandstone sample is significantly lower than that of the dry sandstone sample after microwave radiation. At a loading rate of 200 GPa·m1/2/s, the difference in fracture energy between the dry and water-saturated sandstone samples reaches 61.04%. This also indicates that when sandstone is in a fully saturated state, microwave radiation can have a significant weakening effect on sandstone, leading to a significant decrease in the fracture energy of the rock. In the engineering application of rock excavation, the reduction in rock fracture energy indicates that only a small amount of mechanical energy is required to break the rock during mechanical excavation so as to obtain more efficient rock breaking.
3.6. Dynamic Fracture Propagation Toughness
Dynamic fracture propagation toughness is a parameter that reflects the resistance of materials to crack propagation. When cracking occurs in an engineering rock, it is crucial to implement measures to prevent further crack expansion, ensuring the safety of the rock structure and avoiding further damage. Dynamic fracture propagation toughness represents the critical dynamic stress intensity at a given crack propagation speed. Under high-strain-rate loading conditions, the effect of the crack expansion rate on the dynamic stress intensity factor cannot be ignored. Ravi-Chandar [] has given a formula to calculate a particular crack expansion rate accounting for as follows:
The relevant physical and mechanical parameters of the sandstone involved above are summarized in Table 1.
Figure 17 illustrates the relationship between dynamic fracture propagation toughness and the crack propagation speed of sandstone, showing a positive correlation between the two. Moreover, under the same crack propagation speed conditions, the expansion toughness of dry sandstone samples is higher. In other words, the dry sandstone must overcome a higher fracture extensional toughness if the rock is to produce the same damage rate. This observation also indicates that water-saturated sandstone sustains more significant internal damage after microwave radiation, making it more prone to low-stress fractures or rapid failure when subjected to external loads. For assisted rock breaking, a lower fracture propagation toughness means that the breaking tool can more easily penetrate the rock, leading to the formation of longer fractures. Additionally, a rock with lower propagation toughness will exhibit a faster crack expansion rate under the same cutting force, significantly improving the efficiency of rock breaking operations.
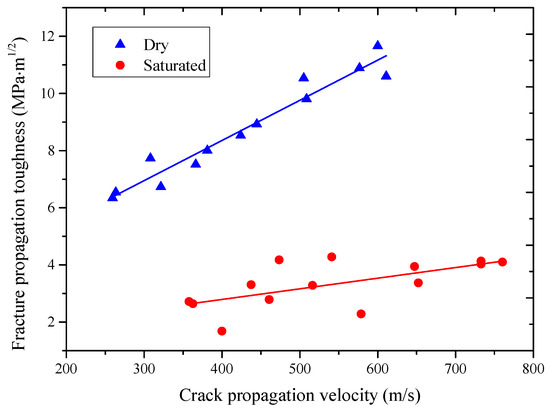
Figure 17.
Relationship between dynamic fracture propagation toughness and crack extension rate.
4. Discussion
4.1. Water-Weakening Mechanisms in Microwave-Assisted Rock Breaking
Microwave heating is the process of converting microwave energy into thermal energy by utilizing the dielectric properties of materials. Based on the varying sensitivity of different materials to microwaves, they can be categorized into three distinct types: microwave transparent, microwave insulator, and microwave absorber. The sandstone material selected for this study exhibits relatively low dielectric properties typical of rock-forming minerals, classifying it as a low microwave absorber. During the drying process of sandstone via microwave radiation, most of the microwave energy passes through the sandstone specimen; only a small fraction is absorbed and converted into thermal energy within the material. Consequently, under conditions of microwave radiation, the heating rate of dry sandstone specimens remains relatively low.
Numerous studies have demonstrated that water, being a strong polar molecule, serves as an effective microwave-absorbing material. The presence of water alters the dielectric properties of rock minerals significantly. In a microwaved environment, water molecules undergo rotational orientation due to electromagnetic fields; this interaction leads to friction and collisions among neighboring molecules, resulting in pronounced heating phenomena. The heat absorbed by water subsequently propagates to surrounding rock matrices through conduction and convection processes, thereby increasing the heating rate in water-bearing sandstones.
However, as temperature rises during this process, moisture undergoes phase change, generating water vapor, which exerts pressure on inner pore walls—this contributes to crack formation and development within the rock structure, as evidenced by micromorphological characteristics observed in sandstone samples. Therefore, during microwave treatment of sandstone, pore water functions dually as both a microwave absorber and fracturing fluid; its fundamental principles and processes are illustrated in Figure 18.
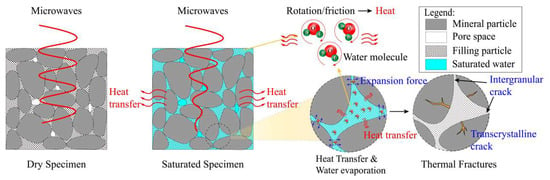
Figure 18.
Schematic diagram of the microwave heating process and the weakening mechanism of water-bearing sandstone.
4.2. Microcrack Extension in Sandstone Microwave Damage
Analysis of the test results reveals that microwave radiation caused a significant decrease in the dynamic fracture toughness of sandstone. The dynamic fracture initiation and propagation toughness of water-saturated samples were notably lower than those of dry samples. The dynamic fracture energy and extensional toughness of the water-saturated sandstone samples were also lower under the same loading rate or crack extension rate. In addition, the crack propagation speed of the saturated sandstone samples also increased significantly after the microwave radiation. These experimental findings demonstrate that the presence of pore water within the rock exacerbates the damage caused by microwave radiation, making the rock more susceptible to low-stress fractures or rapid failure when subjected to external loads. This series of phenomena can be attributed to the evolution of the microstructure around the prefabricated crack tip following microwave radiation.
A rectangular area measuring 15 mm in length and 10 mm in width, situated above the precast crack tip, was selected for Scanning Electron Microscope (SEM) analysis. The microstructural changes in both dry and saturated sandstone samples after microwave radiation were observed, and the results are shown in Figure 19. The SEM images reveal that, prior to microwave treatment, the sandstone samples were internally compact, with only a few initial pores visible and no significant microcrack development, as shown in Figure 19a.

Figure 19.
SEM images of the NSCB sample around the crack tip before and after microwave irradiation.
The internal microstructure of both dry and water-saturated sandstone samples changed to some extent after exposure to the same microwave power and irradiation time. For the dry sandstone sample, a small number of cracks developed along the crystal boundaries inside the rock following microwave radiation, but these cracks were relatively small, and the overall structure remained fairly dense, as shown in Figure 19b. This is because microwave-sensitive minerals within the sandstone are the first to heat up under microwave radiation, leading to significant volume expansion and a non-uniform temperature distribution inside the rock. The localized inhomogeneous deformation generated within the rock and the temperature gradients lead to its structural thermal stresses at the microscopic level. With structural thermal stresses, along-crystal cracks are generated between sandstone mineral grains. The generation of cracks will lead to an increase in the FPZ of the rock and the reduction in its ability to resist external loading and crack expansion, which is reflected in the decrease in its dynamic fracture toughness. Figure 20 illustrates the increase in sandstone crack density and the enlargement of the FPZ due to microwave radiation.
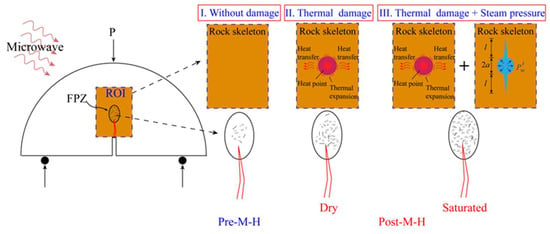
Figure 20.
Schematic diagram of the increase in the FPZ size of sandstone due to increased density of cracks by microwave radiation.
In the SEM images of the water-saturated sandstone samples after microwave radiation, numerous cracks and pores can be observed along the crystals. Additionally, there are many loose particles within the rock, resulting in a rougher microstructural surface, as illustrated in Figure 19c. Compared to the dry sandstone samples with the action of microwave radiation, the size and number of microcracks inside the water-saturated sandstone are significantly increased, resulting in this difference for two main reasons as follows:
- (1)
- The presence of pore water within sandstone enhances the rock’s dielectric properties, resulting in a higher heating rate under microwave radiation. Moreover, under the same microwave radiation conditions, sandstone can reach higher temperatures. The combination of high temperature and thermal shock leads to significant thermal damage within the sandstone.
- (2)
- Under microwave rapid heating conditions, pore water undergoes a phase transition and quickly transforms into steam, forming a binary gas mixture consisting of water vapor and air within the pores. Due to the constraint imposed by the pore size on the volumetric expansion of water molecules, expansion pressure is generated and exerted on the inner surfaces of the pores. This pressure leads to the development of additional pores within the rock structure and causes existing microcracks to expand and coalesce. Since the size of the FPZ in rocks is proportional to the density of microcracks, microwave irradiation results in a significant increase in FPZ size in saturated sandstone. This increase is more pronounced compared to that observed in dry sandstone samples. Consequently, the dynamic fracture toughness of saturated sandstone after microwave treatment is considerably lower than that of its dry counterpart.
In summary, during microwave heating of sandstone samples, the presence of pore water not only enhances the microwave absorption capacity of the sandstone, subjecting the rock to high temperatures and thermal shock, but also generates vapor pressure that promotes the expansion of internal pores and the propagation of microcracks. This creates a dual weakening effect, contributing to the reduction in fracture toughness of sandstone under microwave radiation. The resulting formation and agglomeration of microcracks near the crack tip will lead to an increase in the FPZ of the rock, and the anti-load capacity of the pre-cracking will be lowered. Thus, after microwave radiation, the dynamic crack initiation toughness, extensional toughness, and dynamic fracture energy of water-saturated sandstone samples decrease, while the crack propagation rate increases.
4.3. Limitations and Future Research Perspectives
Considerable efforts have been devoted to investigating the alterations in the physical and mechanical properties of rocks subjected to microwave irradiation. Nevertheless, the factors influencing the extent of microwave-induced weakening in rocks remain insufficiently explored, and relatively few studies have integrated microwave heating technology into engineering applications. Based on existing research, the following recommendations for future investigations are proposed:
- (1)
- The NSCB semi-circular sandstone specimens used in the experiment were small in size, which facilitated laboratory control and observation. However, their thermal conductivity and crack propagation behavior differed in scale from those of large rock masses in the field. Therefore, caution should be exercised when extrapolating the conclusions to the engineering scale.
- (2)
- Most of the studies on the response of rocks to microwave radiation have been carried out using multimode cavity microwave ovens. Compared with single-mode-cavity microwave ovens, multimode-cavity microwave ovens have the advantages of uniform heating, high energy utilization, and no risk of microwave leakage, but they have relatively low power densities and are only suitable for laboratory studies. Therefore, after fully understanding the destructive behavior of microwave irradiation on small-sized rock samples, it is necessary to use high-power single-mode-cavity microwave equipment to conduct surface radiation tests on large-sized rock bodies, thus shifting the laboratory research to field tests.
- (3)
- In engineering practice, it is sometimes necessary to simultaneously employ mechanical cutting and microwave irradiation to achieve continuous excavation in underground engineering and tunneling operations. Consequently, further research on the dynamic mechanical properties of rocks under real-time microwave heating conditions remains essential. Additionally, addressing the issue of preventing microwave leakage during shock loading is a critical problem that must be resolved first.
- (4)
- Microwave radiation is a multi-field coupled heating process influenced by electromagnetic, temperature, stress, and mass transfer fields. It is necessary to analyze the mechanical behavior of rocks under microwave radiation by the finite element or discrete element method to determine the relationship between the microwave-induced temperature distribution, thermal stress, and fracture density.
5. Conclusions
This study systematically elucidates the dominant role of water in the dynamic fracture behavior of sandstones under microwave radiation, where the presence of pore water leads to a dual weakening effect of high temperature and thermal shock on sandstones. For such microwave-insensitive sandstones tested in this paper, the initial water content is the decisive factor controlling the microwave fracturing effect. As long as the initial water content of the sample exceeds a specific value, microwave radiation can cause significant damage to the rock. When excavating microwave-insensitive rocks, water can be injected into the rock to increase the dielectric properties, providing an effective solution for the application of microwave fracturing technology in microwave-insensitive rocks. Therefore, we further investigated the coupled effects of water content and loading rate on the mechanical behavior of rocks under microwave radiation. Based on the SHPB test system, we investigated the dynamic mechanical behavior of water-bearing sandstone after microwave radiation, which provides key theoretical support for the application of microwave-assisted rock breaking technology in water-rich formations. The main conclusions are as follows:
- (1)
- The heating rate of saturated sandstone samples under microwave radiation is significantly higher than that of dry sandstone. And, with the passage of microwave radiation time, the heating process of dry sandstone samples increases approximately linearly, while the heating rate of saturated sandstone samples slows down after 300 s of irradiation time.
- (2)
- The initiation toughness of sandstone exhibits significant loading rate dependence. The fracture toughness of saturated sandstone after microwave radiation is significantly lower than that of dry samples. This indicates that pore water plays a positive role in microwave weakening of rock fracture toughness.
- (3)
- The crack propagation speed of the saturated samples was significantly higher than that of the dry samples under the same loading rate condition, and the loading rate sensitivity of the crack propagation speed of the saturated samples was also higher. When the loading rate was 200 GPa·m1/2/s, the crack extension rate of microwave-irradiated saturated sandstone samples increased by 25.3% relative to that of dry samples.
- (4)
- The dynamic fracture extension toughness and fracture energy of the saturated sandstone specimens were smaller than those of the dry specimens after microwave radiation, which indicated that the saturated sandstone’s ability to resist crack extension was reduced after microwave radiation, and the rock was more susceptible to low stress fracture and rapid failure.
Author Contributions
P.W.: methodology, data curation, validation, resources, and writing—review editing. Y.L. and D.C.: data curation, investigation, and writing—original draft. T.Y.: supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by the National Natural Science Foundation of China (No. 52504079 and No. 41972283); the Guangxi Natural Science Foundation of China (No. 2024GXNSFBA010427 and No. 2025GXNSFAA069611); and Guangxi Emergency Management Joint Innovation Science and Technology Project (No. 2025GXYJ009 and No. 2025GXYJ024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We are grateful for the support provided by these funds, which laid the foundation for our experiments. We also express our gratitude to the Multi-disciplinary Integrated Innovation Experimental Teaching Center for Resource, Environment and Materials of Guangxi University for providing us with such a research environment.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| NSCB | notched semi-circular bend |
| SHPB | split Hopkinson pressure bar |
| TBM | tunnel boring machine |
| FPZ | fracture process zone |
| DIC | digital image correlation |
| ROI | region of interest |
| COD | crack opening displacement |
| SEM | scanning electron microscope |
References
- Gu, D.S.; Li, X.B. Modern Science and Technology for Metal Deposit Mining; Metallurgical Industry Press: Beijing, China, 2006. [Google Scholar]
- Wang, Y.M. Opportunities and challenges to metal mine mining industry and the technical countermeasures. Mod. Min. 2011, 27, 1–14. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.B.; Cao, Z.W.; Zhou, J.; Huang, L.Q.; Wang, S.F.; Yao, J.R.; He, Z.G.; Ma, C.D.; Dong, L.J.; Zhao, G.Y. Innovation of hard rock mining methods and construction of intelligent green mines: A case study of kai yang phosphate mine. Chin. J. Nonferrous Met. 2019, 29, 2364–2380. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.B.; Huang, L.Q.; Zhou, J.; Wang, S.F.; Ma, C.D.; Chen, J.Z.; Liu, Z.X.; Li, Q.Y.; Zhao, G.Y. Review and prospect of mining technology in hard rock mines. Chin. J. Nonferrous Met. 2019, 29, 1828–1847. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.B.; Yao, J.R.; Du, K. Innovation of mining models and construction of intelligent green mine in hard rock mine: In Kai yang Phosphate Mine as an example. Chin. J. Rock Mech. En. 2013, 32, 1101–1111. (In Chinese) [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. En. 2015, 34, 2161–2178. (In Chinese) [Google Scholar] [CrossRef]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Research on deep mining rock mechanics and engineering disaster control. Coal Mine Support 2007, 3, 1–14. (In Chinese) [Google Scholar]
- Yao, J.R.; Li, X.B.; Sun, L.C.; Wang, M.; Yao, H.; Wang, Q.P.; Li, W.P.; Wang, S.F. Non-explosive mechanized mining of deep hard ore by using high-frequency crushing hammer. Met. Mine 2021, 50, 27–33. (In Chinese) [Google Scholar] [CrossRef]
- Xia, Y.M.; Zhang, K.; Liu, J.S. Design optimization of TBM disc cutters for different geological conditions. World J. Text Eng. Technol. 2015, 3, 218–231. [Google Scholar] [CrossRef]
- Rostami, J. Performance prediction of hard rock Tunnel Boring Machines (TBMs) in difficult ground. Tunn. Undergr. Sp. Tech. 2016, 57, 173–182. [Google Scholar] [CrossRef]
- Ciccu, R.; Grosso, B. Improvement of disc cutter performance by water jet assistance. Rock Mech. Rock Eng. 2014, 47, 733–744. [Google Scholar] [CrossRef]
- Kocis, I.; Kristofic, T.; Gajdos, M.; Horvath, G.; Jankovic, S. Utilization of electrical plasma for hard rock drilling and casing milling. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, London, UK, 17–19 March 2015. [Google Scholar] [CrossRef]
- Shi, X.M.; Duan, Y.L.; Han, B.; Zhao, J. Enhanced rock breakage by pulsed laser induced cavitation bubbles: Preliminary experimental observations and conclusion. Geomech. Geophys. Geo Energ. Geo Res. 2020, 6, 25. [Google Scholar] [CrossRef]
- Kahraman, S.; Canpolat, A.N.; Fener, M. The influence of microwave treatment on the compressive and tensile strength of igneous rocks. Int. J. Rock Mec. Min. Sci. 2020, 129, 104303. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Zhang, Q.B.; Zhao, J. Challenges and opportunities of using tunnel boring machines in mining. Tunn. Undergr. Sp. Tech. 2016, 57, 287–299. [Google Scholar] [CrossRef]
- Aydin, G.; Karakurt, I.; Aydiner, K. Wear performance of saw blades in processing of granitic rocks and development of models for wear estimation. Rock Mech. Rock Eng. 2013, 46, 1559–1575. [Google Scholar] [CrossRef]
- Lu, G.M.; Zhou, J.J.; Li, Y.H.; Zhang, X.W.; Gao, W.Y. The influence of minerals on the mechanism of microwave-induced fracturing of rocks. J. Appl. Geophys. 2020, 180, 104123. [Google Scholar] [CrossRef]
- Zhao, Q.H.; Zhao, X.B.; Zheng, Y.L.; Li, J.C.; He, J.L.; Zou, C.J. Heating characteristics of igneous rock-forming minerals under microwave irradiation. Int. J. Rock Mech. Min. 2020, 135, 104519. [Google Scholar] [CrossRef]
- Hu, J.J.; Xie, H.P.; Sun, Q.; Li, C.B.; Liu, G.K. Changes in the thermodynamic properties of alkaline granite after cyclic quenching following high temperature action. Int. J. Min. Sci. Technol. 2021, 31, 843–852. [Google Scholar] [CrossRef]
- Hu, J.J.; Xie, H.P.; Gao, M.Z.; Li, C.B.; Sun, Q. Damage mechanism and heat transfer characteristics of limestone after thermal shock cycle treatments based on geothermal development. Int. J. Rock Mech. Min. Sci. 2022, 160, 105269. [Google Scholar] [CrossRef]
- Hartlieb, P.; Leindl, M.; Kuchar, F.; Antretter, T.; Moser, P. Damage of basalt induced by microwave irradiation. Miner. Eng. 2012, 31, 82–89. [Google Scholar] [CrossRef]
- Ge, Z.L.; Sun, Q.; Hu, J.J.; Guan, Y.H.; Liu, W.; Wang, S.F.; Geng, J.S. Fracture characteristics and thermal damage mechanism of shale under microwave radiation. J. Therm. Anal. Calorim. 2024, 149, 13147–13160. [Google Scholar] [CrossRef]
- Ge, Z.L.; Sun, Q.; Xue, L.; Yang, T. The influence of microwave treatment on the mode I fracture toughness of granite. Eng. Fract. Mech. 2021, 249, 107768. [Google Scholar] [CrossRef]
- Bai, G.G.; Sun, Q.; Jia, H.L.; Ge, Z.L.; Li, P.F. Variations in fracture toughness of SCB granite influenced by microwave heating. Eng. Fract. Mech. 2021, 258, 108048. [Google Scholar] [CrossRef]
- Hassani, F.; Nekoovaght, P.M.; Gharib, N. The influence of microwave irradiation on rocks for microwave-assisted underground excavation. J. Rock Mech. Geotech. Eng. 2016, 8, 1–15. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Cao, W.Z.; Chen, L.; Zhou, J. Effects of water content on fracture and mechanical behavior of sandstone with a low clay mineral content. Eng. Fract. Mech. 2018, 193, 47–65. [Google Scholar] [CrossRef]
- Lu, G.M.; Feng, X.T.; Li, Y.H.; Hassani, F.; Zhang, X.W. Experimental investigation on the effects of microwave treatment on basalt heating, mechanical strength, and fragmentation. Rock Mech. Rock Eng. 2019, 52, 2535–2549. [Google Scholar] [CrossRef]
- Dai, J.; Du, W.P.; Wu, T. Experimental study of rock fracture after microwave irradiation and impact load. J. Henan Polytech. Univ. Nat. Sci. 2016, 35, 420–423. (In Chinese) [Google Scholar] [CrossRef]
- Dai, J.; Pan, Y.B.; Meng, Z. Experimental study on influential factors of rock strength weakening under microwave irradiation. J. Xi’an Univ. Sci. Technol. 2016, 36, 364–368. (In Chinese) [Google Scholar] [CrossRef]
- Hartlieb, P.; Toifl, M.; Kuchar, F.; Meisels, R.; Antretter, T. Thermo-physical properties of selected hard rocks and their relation to microwave-assisted comminution. Miner. Eng. 2015, 91, 34–41. [Google Scholar] [CrossRef]
- Qin, L.; Dai, J.; Teng, P. Study on the effect of microwave irradiation on rock strength. J. Eng. Sci. Technol. Rev. 2015, 8, 91–96. [Google Scholar] [CrossRef]
- Xia, K.W.; Wang, Z.; Wu, B.B.; Xu, Y.; Yue, T.L. Research progress on dynamic response of deep rocks under coupled hydraulic-mechanical loading. J. China Coal Soc. 2024, 49, 454–478. (In Chinese) [Google Scholar] [CrossRef]
- Satish, H.; Ouellet, J.; Raghavan, V.; Radziszewski, P. Investigating microwave assisted rock breakage for possible space mining applications. Min. Technol. 2006, 115, 34–40. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Xu, Y.; Yao, W.; Xia, K.W.; Lu, G.M. Effect of microwave irradiation on dynamic mode-I fracture parameters of Barre granite. Eng. Fract. Mech. 2020, 224, 106748. [Google Scholar] [CrossRef]
- Jia, H.L.; Wang, T.; Xiang, W.; Tan, L.; Shen, Y.J.; Yang, G.S. Influence of water content on the physical and mechanical behaviour of argillac-eous siltstone and some microscopic explanations. Chin. J. Rock Mech. En. 2018, 37, 1618–1628. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, E.F.; Yang, G.S.; Tang, L.Y.; Yang, Q.; Xie, Z.W. Study on influence of water content to damage and degradation laws of argillaceous siltstone. Coal Sci. Technol. 2019, 47, 14–20. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, K.; Ran, S.H.; Zeng, P.; Yang, D.X.; Teng, T.Y. Effect of moisture content on characteristic stress and acoustic emission characteristics of red sandstone. Rock Soil Mech. 2021, 42, 899–908. (In Chinese) [Google Scholar] [CrossRef]
- Dai, J.; Wang, Y.L.; Huang, B.B.; Wang, Y.P.; Li, H. Experimental study on the effect of water on the degradation of hard rock under microwave irradiation. Chin. J. Undergr. Sp. Eng. 2020, 16, 691–696. (In Chinese) [Google Scholar]
- Peinsitt, T.; Kuchar, F.; Hartlieb, P.; Moser, P.; Kargl, H.; Restner, U.; Sifferlinger, N. Microwave heating of dry and water saturated basalt, granite and sandstone. Int. J. Min. Miner. Eng. 2010, 2, 18–29. [Google Scholar] [CrossRef]
- Deng, H.F.; Li, J.L.; Wang, K.W.; Liu, J.; Zhu, M.; Lu, T. Research on secondary porosity changing law of sandstone under saturation-air dry cycles. Rock Soil Mech. 2012, 33, 483–488. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.G.; Li, H.M.; Xu, G.S. Influence of water content on mechanical characteristics of weakly cemented sandstone. J. Min. Strata Control Eng. J. 2021, 3, 043029. (In Chinese) [Google Scholar] [CrossRef]
- Wang, L. Fundamentals of Stress Wave; National Defense Industry Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Zhang, Q.B.; Zhao, J. Quasi-static and dynamic fracture behaviour of rock materials: Phenomena and mechanisms. Int. J. Fract. 2014, 189, 1–32. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Du, X.M.; Chen, L.; Wang, H.Q.; Zang, H.Z. Water saturation effects on dynamic fracture behavior of sandstone. Int. J. Rock Mech. Min. Sci. 2019, 114, 46–61. [Google Scholar] [CrossRef]
- Chen, R.; Xia, K.; Dai, F.; Lu, F.; Luo, S.N. Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing. Eng. Fract. Mech. 2009, 76, 1268–1276. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Obara, Y.; Ayatollahi, M.R.; Chong, K.P.; Funatsu, T. ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock Mech. Rock Eng. 2014, 47, 267–274. [Google Scholar] [CrossRef]
- Zhu, Q.Q.; Ma, C.; Li, X.B.; Li, D.Y. Effect of filling on failure characteristics of diorite with double rectangular holes under coupled static-dynamic loads. Rock Mech. Rock Eng. 2021, 54, 2741–2761. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Ping, Q.; Luo, X.; Ma, Q.Y.; Yuan, P. Broken energy dissipation characteristics of sandstone specimens under impact loads. Chin. J. Rock Mech. Eng. 2015, 34 (Suppl. S2), 4197. (In Chinese) [Google Scholar] [CrossRef]
- Wen, S.; Zhao, X.W.; Chang, Y.L.; Li, B. Energy dissipation of dynamic failure of mixed rock specimens subject to SHPB compression. J. Basic Sci. Eng. 2021, 29, 483–492. (In Chinese) [Google Scholar] [CrossRef]
- Chen, P.Y.; Zhao, F.J.; Chen, B.; Tian, X.Y. Energy dissipation characteristics of prefabricated fractured rock under impact load. Miner. Eng. Res. 2021, 36, 17–23. (In Chinese) [Google Scholar] [CrossRef]
- Hu, J.; Gong, F.Q.; Jia, H.Y. Research on mechanical and energy dissipation characteristics of red sandstone in SHPB compression test. Gold Sci. Technol. 2020, 28, 411–420. (In Chinese) [Google Scholar] [CrossRef]
- Wang, M.X.; Wang, H.B.; Zong, Q. Experimental study on energy dissipation of mudstone in coal mine under impact loading. J. China Coal Soc. 2019, 44, 1716–1725. (In Chinese) [Google Scholar] [CrossRef]
- Gao, F.; Yang, G.; Xiong, X.; Zhou, K.P.; Cong, L.; Li, J.L. Experimental study on the dynamic mechanical characteristics of slope rock under low-temperature conditions. Chin. J. Eng. 2023, 45, 171–181. (In Chinese) [Google Scholar] [CrossRef]
- Ping, Q.; Ma, Q.Y.; Yuan, P. Energy dissipation analysis of stone specimens in SHPB tensile test. J. Min. Saf. Eng. 2013, 30, 401–407. (In Chinese) [Google Scholar]
- Sun, Y.J.; Qi, C.Z.; Zhu, H.T.; Guo, Y.P.; Wang, Y.Q. Energy analysis on rock dynamic fracture process. Chin. J. Undergr. Sp. Eng. 2020, 16, 43–49. (In Chinese) [Google Scholar]
- Ravi-Chandar, K. Dynamic Fracture; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).