Contextual Real-Time Optimization on FPGA by Dynamic Selection of Chaotic Maps and Adaptive Metaheuristics
Abstract
1. Introduction
- (1)
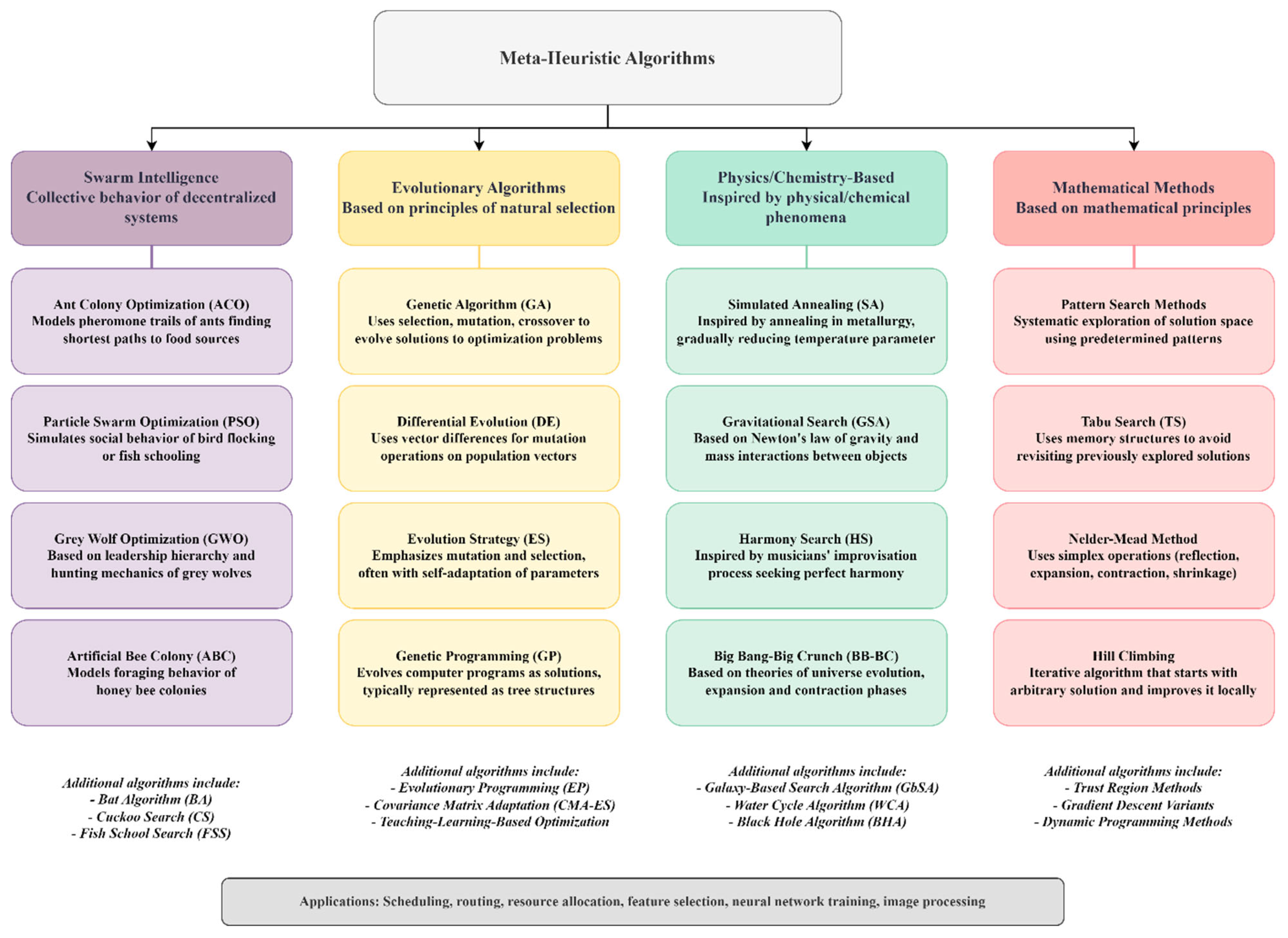
- Swarm Intelligence (collective behavior): This type is based on simple agents (ants, bees, birds, and wolves) that interact in a distributed manner to produce global solutions [11]. Examples of this type include Ant Colony Optimization (ACO), which uses pheromone traces to guide the exploration of graphs; Particle Swarm Optimization (PSO), which adjusts the speed of each particle according to its best history and that of the group; Gray Wolf Optimization (GWO), which models the hierarchy and hunting mechanisms of gray wolves; and Artificial Bee Colony (ABC), which is inspired by the sharing of information between foragers and scouts to direct the search.
- (2)
- Evolutionary Algorithms (natural selection): This type includes, for example, GA (genetic algorithm), which uses classic selection and recombination operators. DE (differential evolution) uses vector mutations based on the differences between individuals. ES (Evolution Strategy) focuses on self-adaptation of mutation parameters. GP (genetic programming) uses the evolution of program trees to solve a problem [1,12,13,14].
- (3)
- Physics/Chemistry-Based Algorithms (physical or chemical phenomena): These are based on the analogue of natural processes (cooling, gravitation, musical harmony, and cosmic expansion). Examples of this type include SA (simulated annealing), which relies on simulated annealing and temperature decay to escape local minima. GSA (Gravitational Search Algorithm) is based on attractive interactions inspired by gravity. HS (Harmony Search) is based on musical improvisation to generate and memorize ‘chords’ of variables. BB-BC (big bang-big brunch) is based on alternating dispersion (big bang) and contraction (big crunch) [15,16,17].
- (4)
- Mathematical Methods: These have their origins in derived operations or pure heuristics without biological inspiration, often deterministic. Examples of this type include Pattern Search, which is based on systematic explorations following predefined patterns. TS (Tabu Search) depends on memory structures to avoid revisiting recent solutions. Nelder–Mead is based on the simplex method for gradient-free minimization. Hill climbing is based on iterative local improvement [18,19].
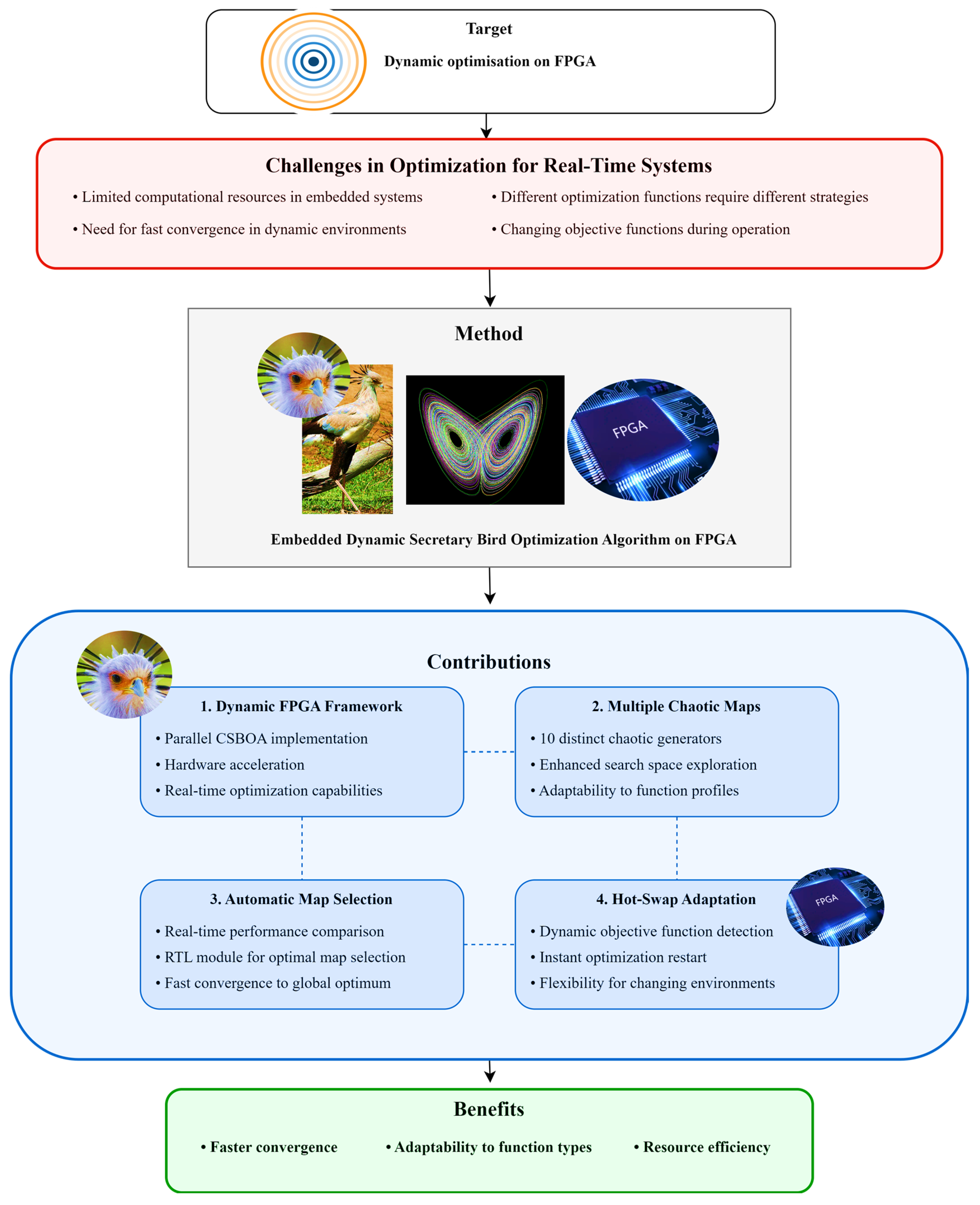
- Dynamic FPGA architecture
- Multiple chaotic maps
- Automatic card selection
- Adaptation hot-swap
2. Preliminary Foundations
2.1. Chaotic Maps
2.2. Basic Algorithm for Optimising the Secretary Bird
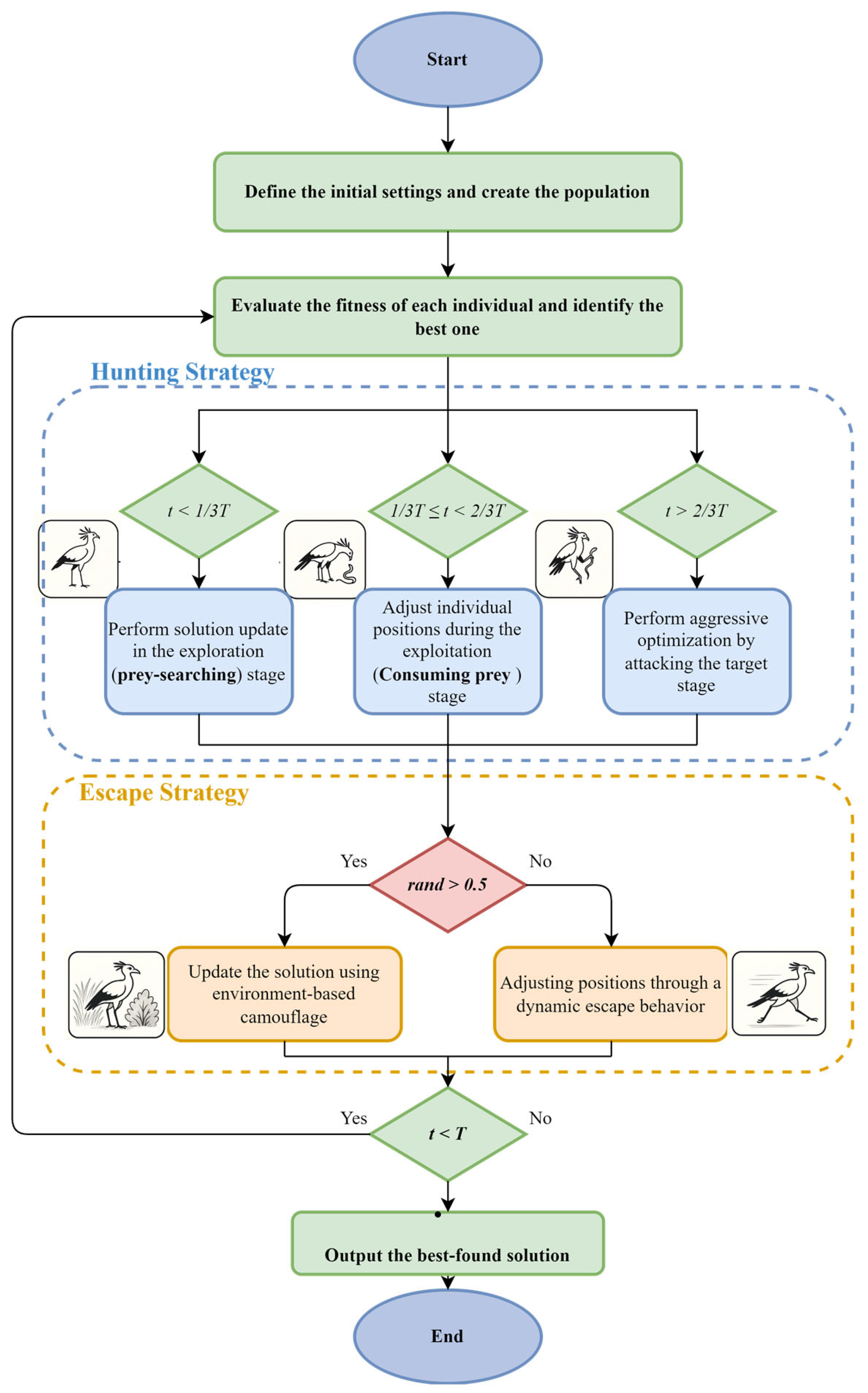
2.2.1. Initial Preparation Phase
- lb and ub represent, respectively, the vectors of the lower and upper bounds of the decision variables.
- rand is a random vector of the same dimension M, each component of which follows a uniform distribution on the interval [0,1].
- M is the dimension of the problem, i.e., the total number of variables to be optimized.
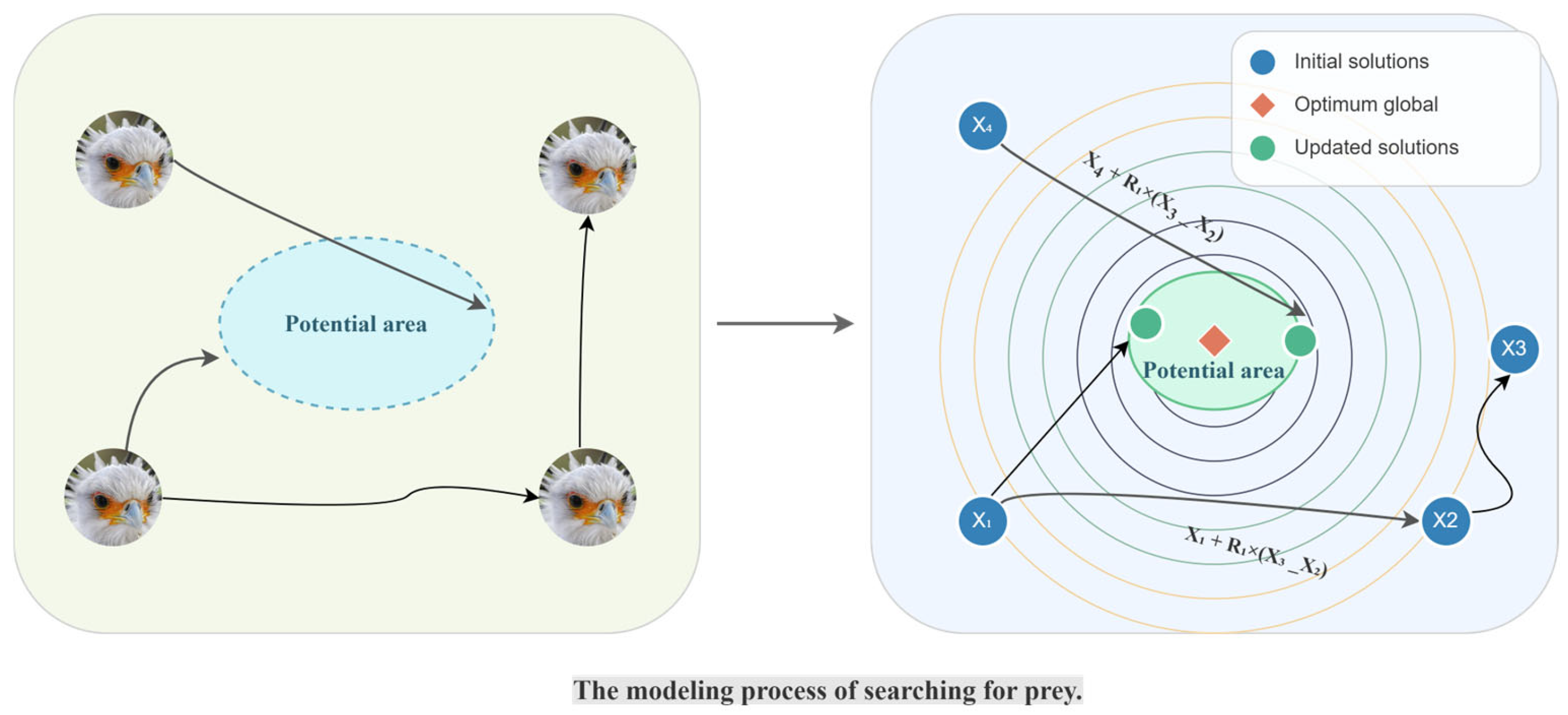
2.2.2. Hunting Strategy for Secretary Birds
- Searching for prey (exploration);
- Consuming of prey (intermediate exploitation);
- Attacking prey (final exploitation).
- Xr1(t) and Xr2(t) are two solutions randomly selected from the current population (with r1 ≠ r2 ≠ i).
- R1 is a random vector of size 1 × M, whose components follow a uniform distribution on the interval [0, 1].
- Fi is the fitness value associated with individual Xi.
- Finew is the fitness value corresponding to the new position generated.
- Consuming of prey—intermediate exploitation
- Attacking prey—final exploitation
- calculated by:
2.2.3. Escape Strategy for Secretary Birds
- RB = randn (1, M) is a random vector following a standard normal distribution (mean 0, standard deviation 1).
- T is the maximum number of iterations.
- M is the dimension of the problem.
- R2 is a random vector whose components are uniformly distributed in [0, 1].
- K is a control coefficient (often taken to be 1).
- Xrand (t) is the position of a randomly selected individual in the population at iteration t.
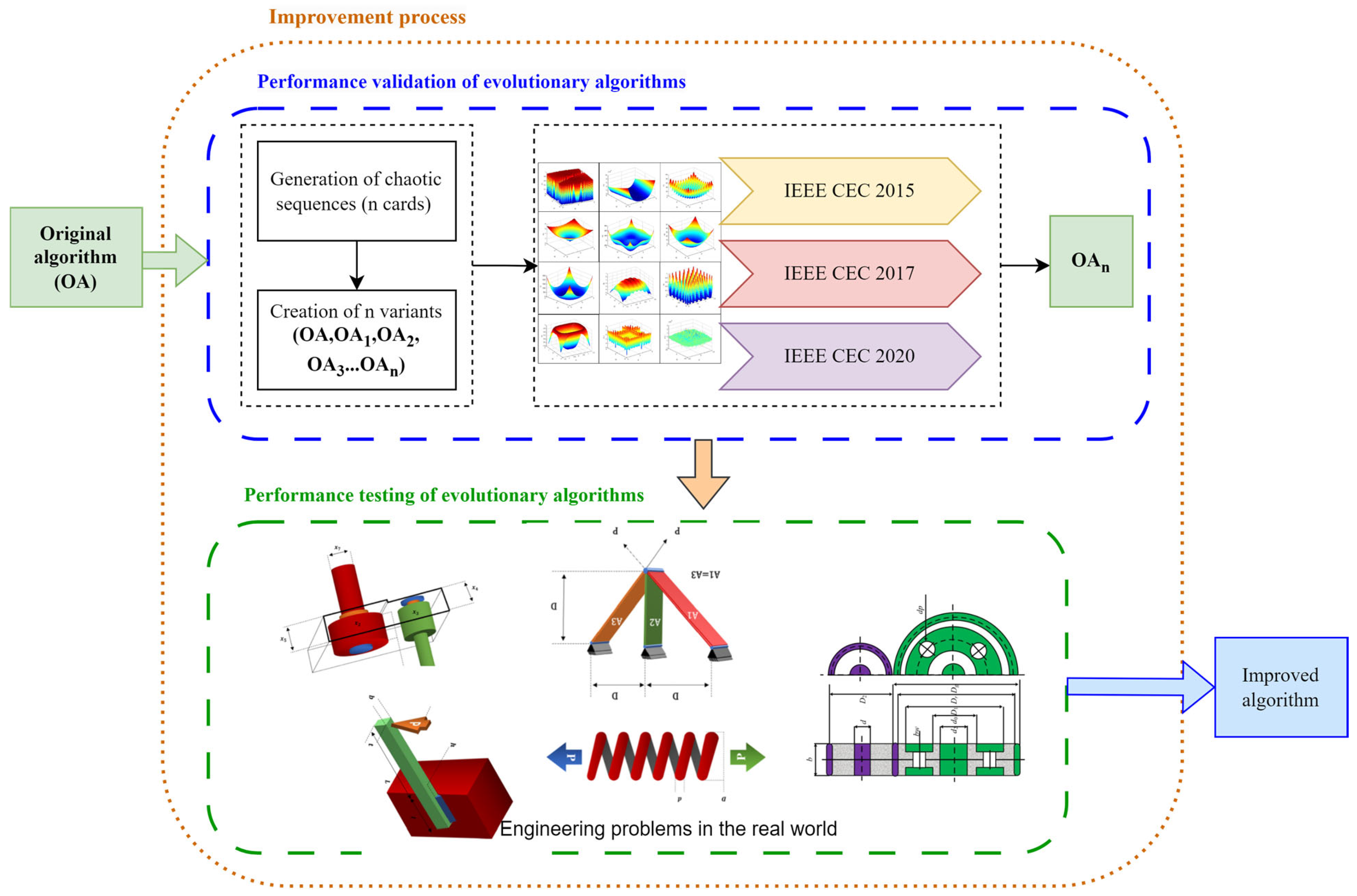
3. Proposed Method
4. Results and Simulations
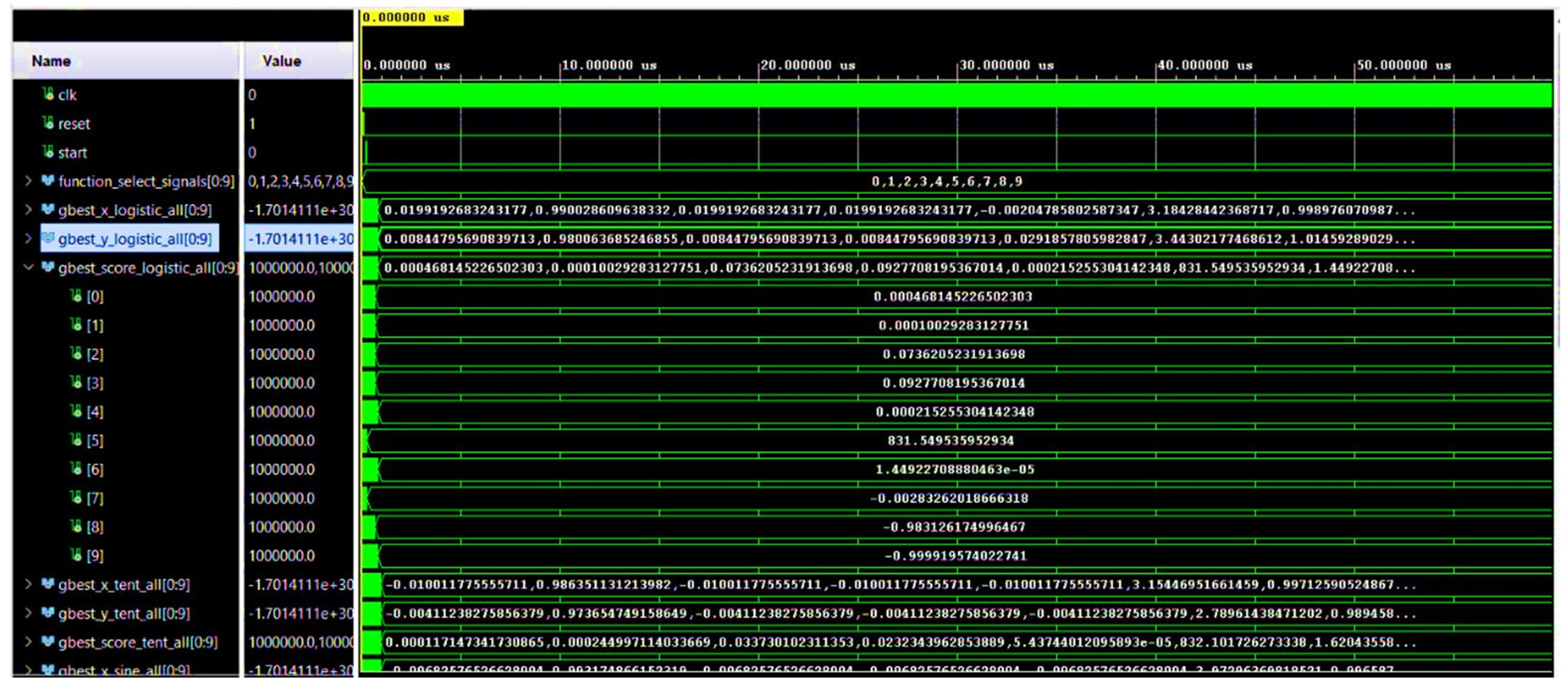
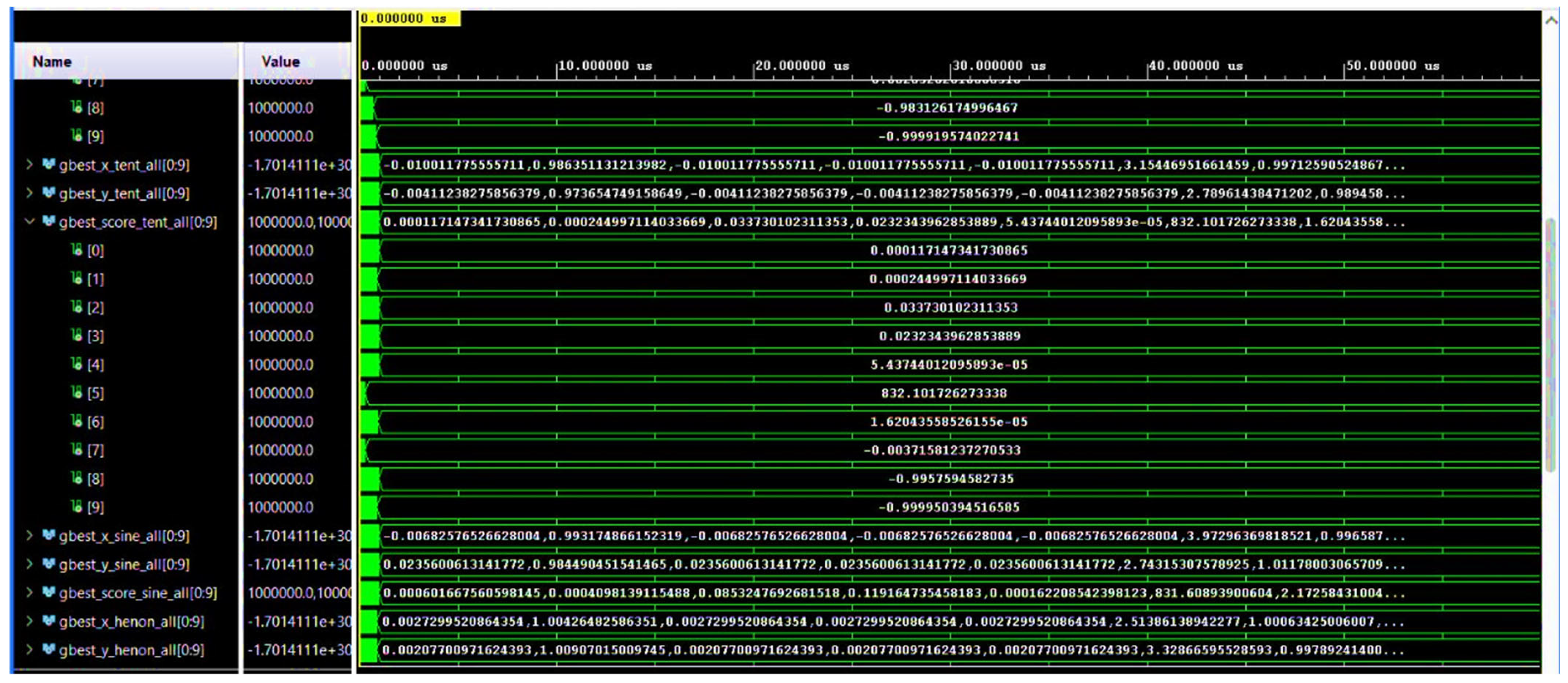
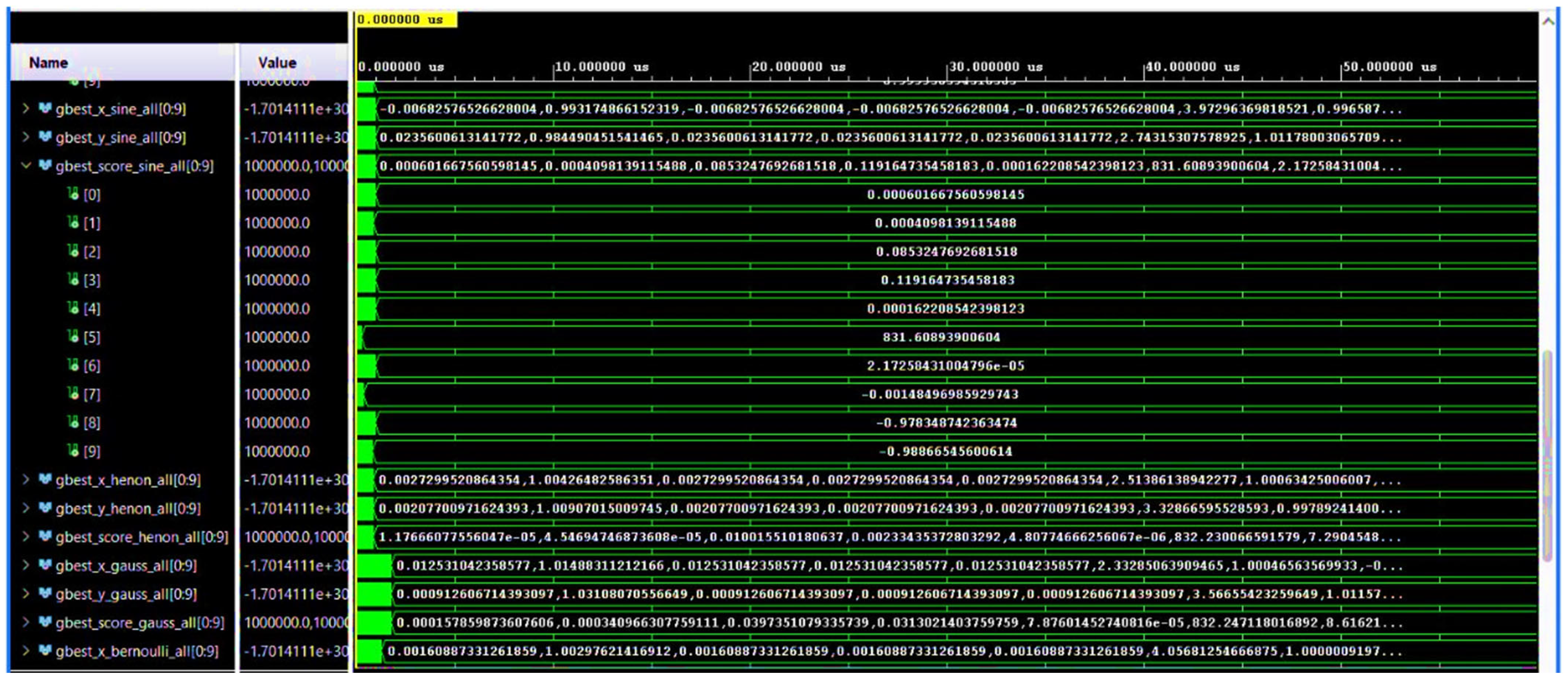
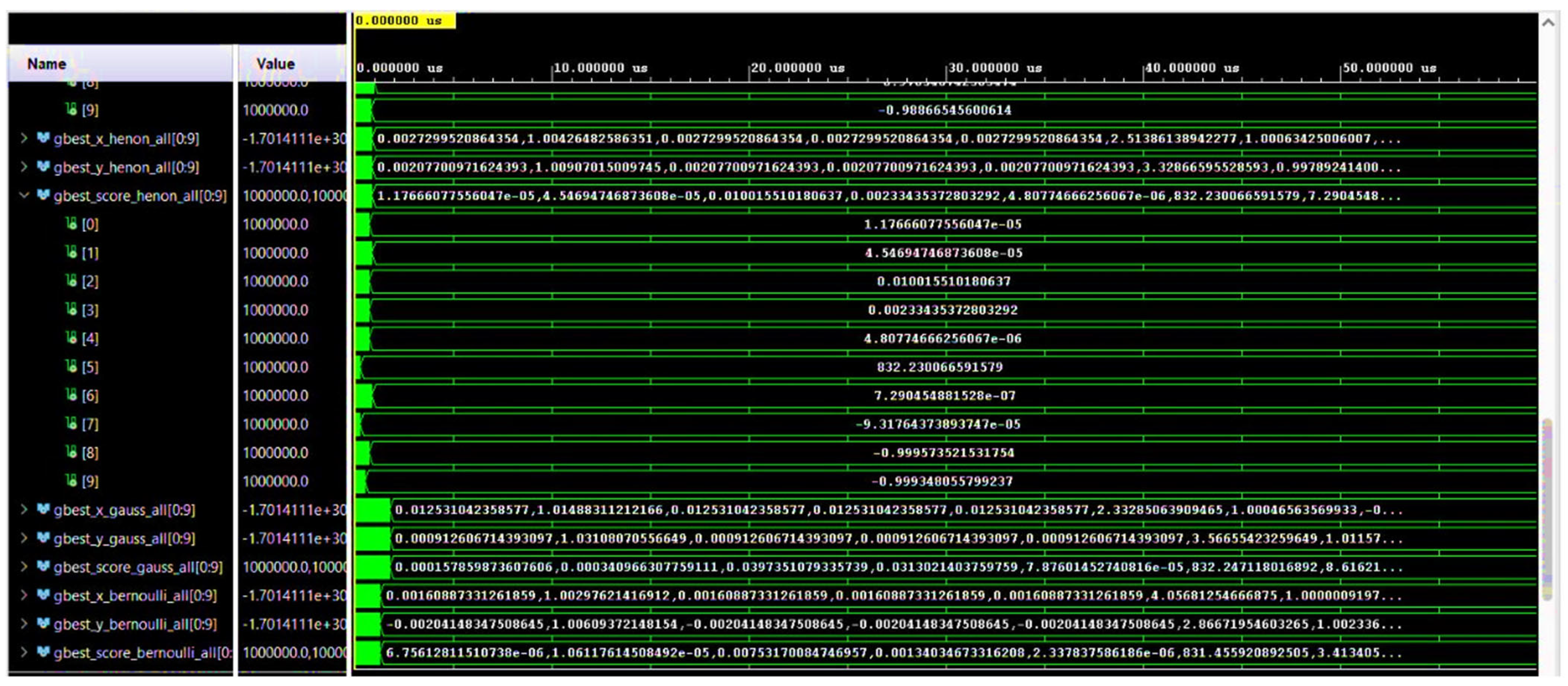
4.1. Analysis of Internal Convergence Signals (Vivado)
- The voted solution vectors (gbest_x/y_voted_all) contain the best final positions retained after 500 iterations per function.
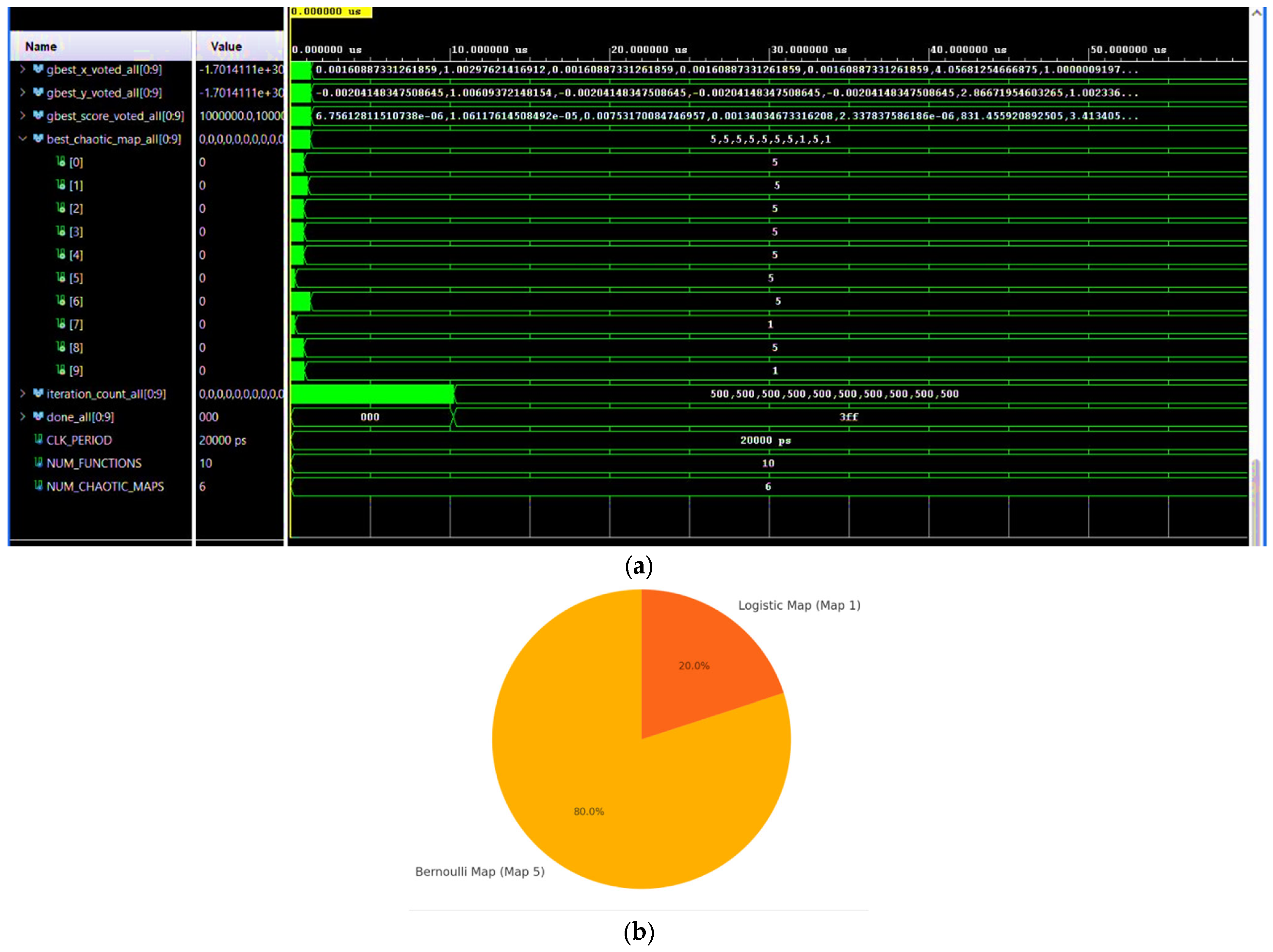
- The best_chaotic_map_all vector displays the identifiers of the chaotic maps selected as a result of the adaptive vote. In this example, the algorithm selected Map 5 (Bernoulli map) for 8 out of 10 functions, and Map 1 (Logistic map) for the other 2, reflecting their respective performance in the given context (Figure 17b).
- The system correctly identifies the best-performing cards.
- It applies them to the right functions.
- Produces optimum results in a completely autonomous and material manner.
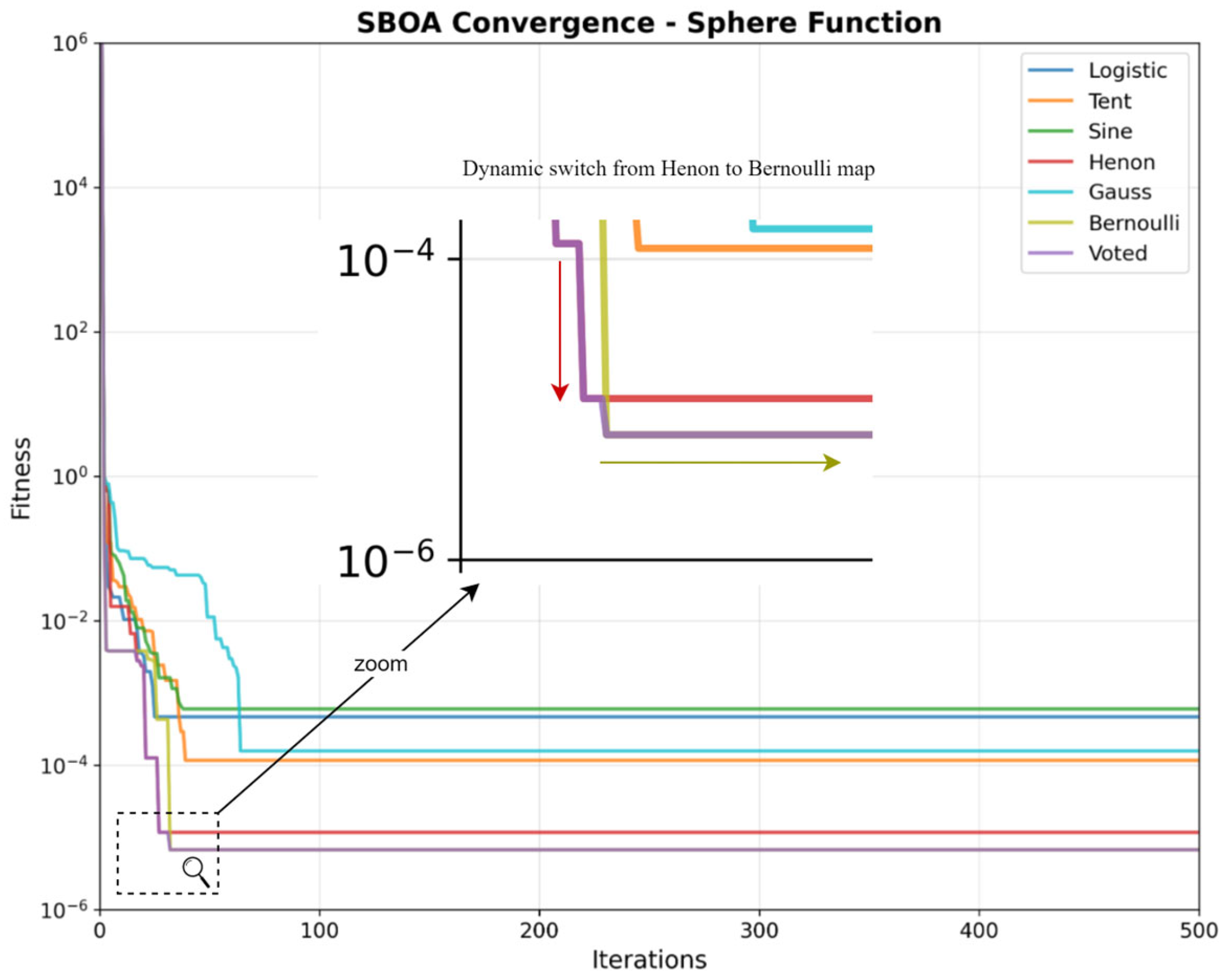
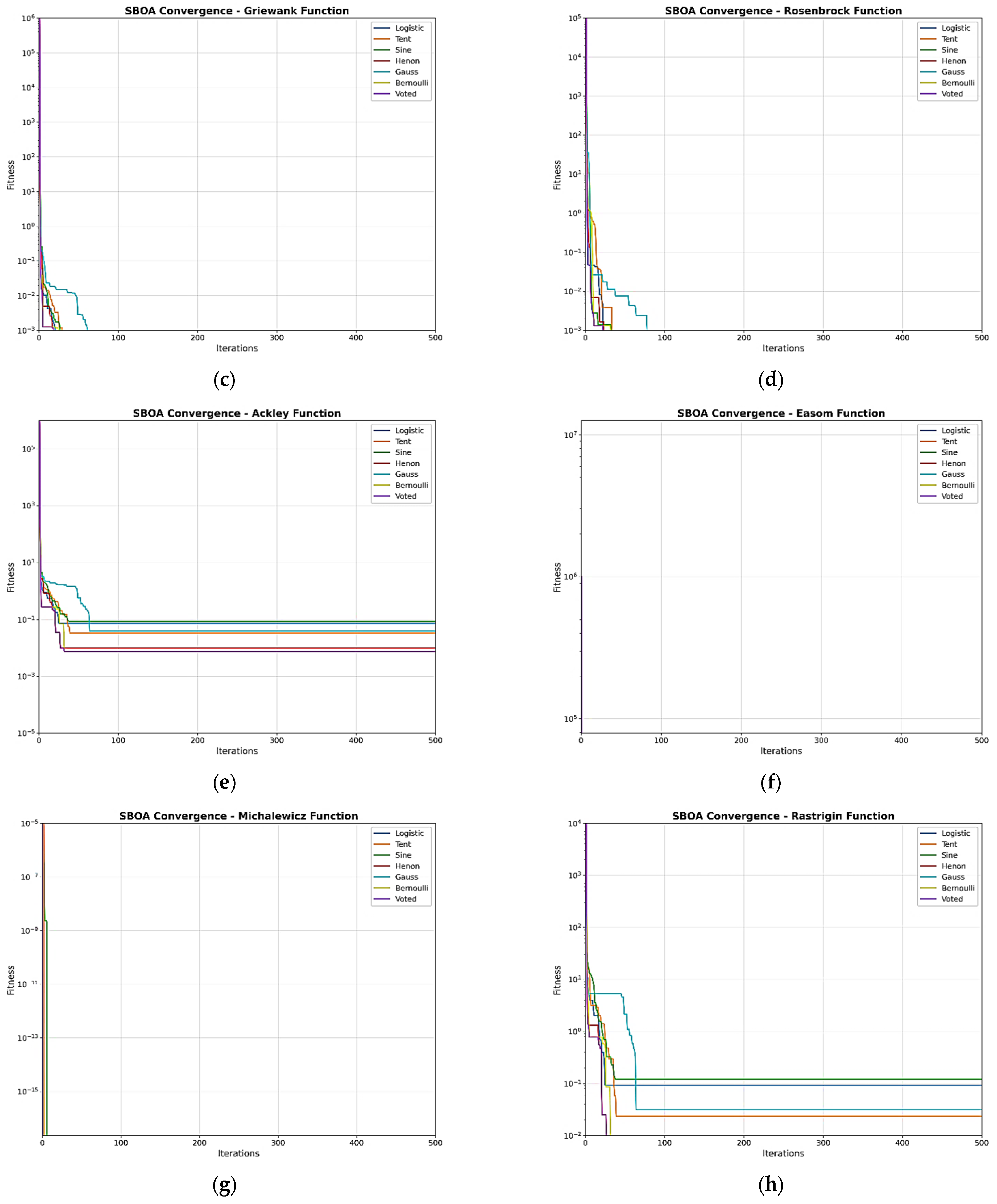
4.2. Convergence Analysis on Benchmark Functions
4.3. Analysis of the Use of Material Resources
4.4. Multi-Instance RTL Architecture and Voted Strategy
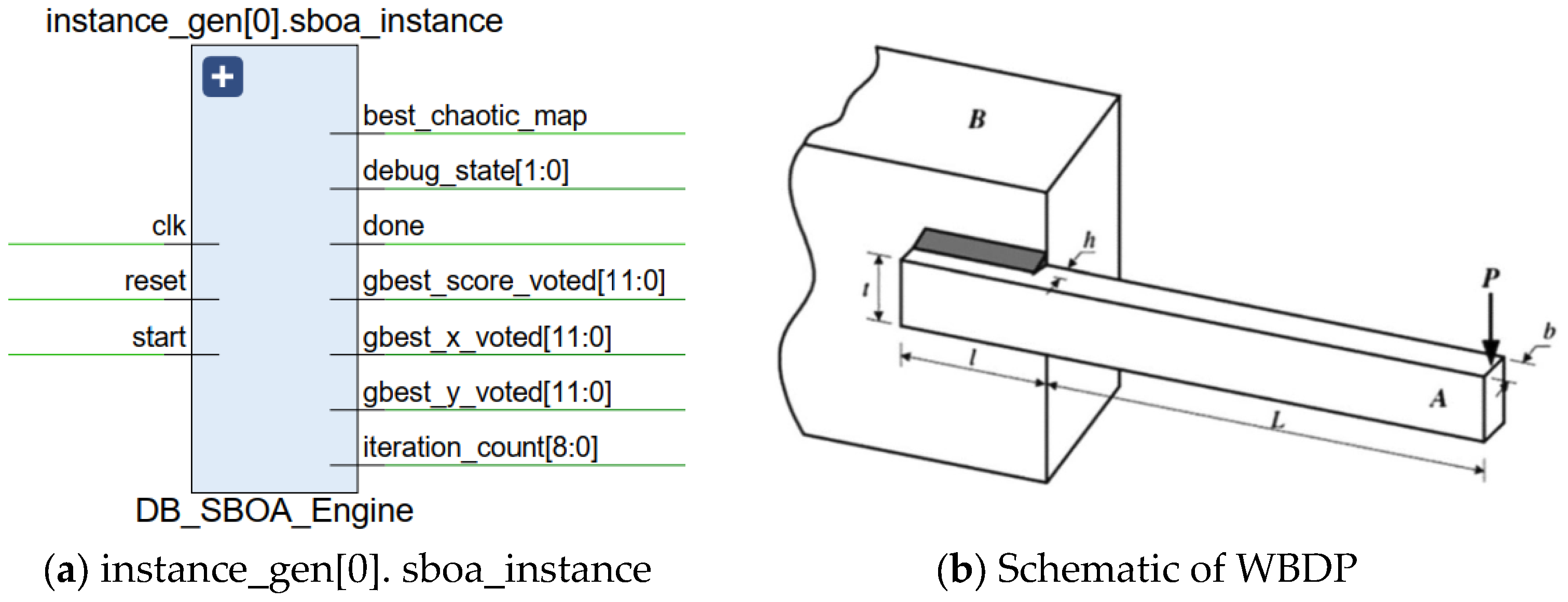
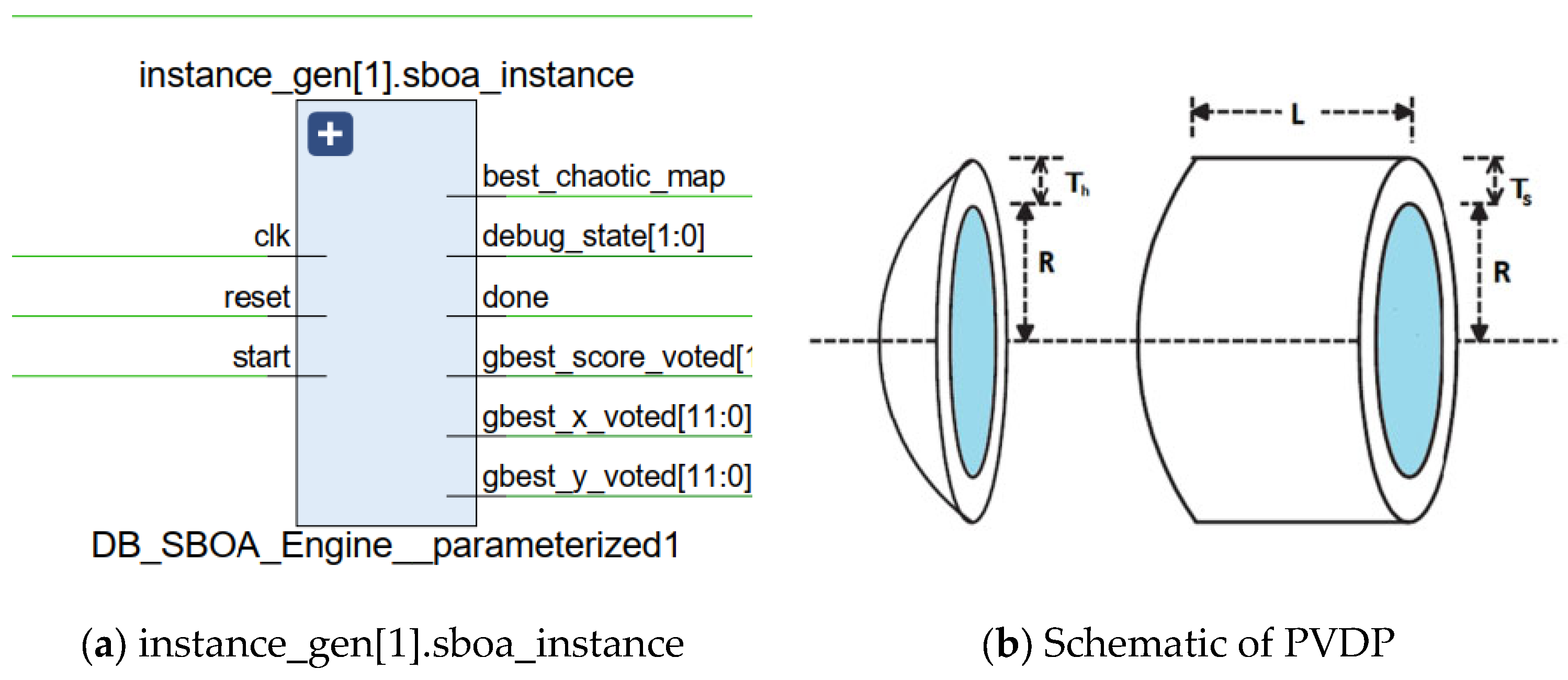
4.4.1. General View of the RTL Circuit
- Energy Consumption
4.4.2. Details of the Optimization Engines (Sub-Blocks)
- gbest_score_voted [11:0]: Best simulated bird score for the WBDP problem.
- best_chaotic_map: Chaotic map that produced this solution.
5. Discussion, Limitations, and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pooja; Sood, S.K. Scientometric analysis of quantum-inspired metaheuristic algorithms. Artif. Intell. Rev. 2024, 57, 22. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Djenouri, Y.; Hu, G.; Ali, A.A.; Shaban, H. Metaheuristic Algorithms and Their Applications in Wireless Sensor Networks: Review, Open Issues, and Challenges; Springer: Greer, SC, USA, 2024; Volume 27, ISBN 1058602404619. [Google Scholar]
- Seyyedabbasi, A.; Tareq Tareq, W.Z.; Bacanin, N. An effective hybrid metaheuristic algorithm for solving global optimization algorithms. Multimed. Tools Appl. 2024, 83, 85103–85138. [Google Scholar] [CrossRef]
- Khalvati, B.; Kavousi, K.; Keyhanipour, A.H.; Arabfard, M. Identifying candidate biomarkers for detecting bronchogenic carcinoma stages using metaheuristic algorithms based on information fusion theory. Discov. Oncol. 2025, 16, 632. [Google Scholar] [CrossRef] [PubMed]
- Razavi-Termeh, S.V.; Sadeghi-Niaraki, A.; Abba, S.I.; Ali, F.; Choi, S.M. Enhancing spatial prediction of groundwater-prone areas through optimization of a boosting algorithm with bio-inspired metaheuristic algorithms. Appl. Water Sci. 2024, 14, 244. [Google Scholar] [CrossRef]
- Cui, E.H.; Zhang, Z.; Chen, C.J.; Wong, W.K. Applications of nature-inspired metaheuristic algorithms for tackling optimization problems across disciplines. Sci. Rep. 2024, 14, 9403. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Abdelhamid, A.M.; Sultan, H.M. Comprehensive analysis of optimal power flow using recent metaheuristic algorithms. Sci. Rep. 2024, 14, 13422. [Google Scholar] [CrossRef]
- Van Thieu, N.; Nguyen, N.H.; Sherif, M.; El-Shafie, A.; Ahmed, A.N. Integrated metaheuristic algorithms with extreme learning machine models for river streamflow prediction. Sci. Rep. 2024, 14, 13597. [Google Scholar] [CrossRef]
- Cuevas, E.; Ascencio-Piña, C.R.; Pérez, M.; Morales-Castañeda, B. Considering radial basis function neural network for effective solution generation in metaheuristic algorithms. Sci. Rep. 2024, 14, 16806. [Google Scholar] [CrossRef]
- Nayak, G.H.H.; Alam, M.W.; Naik, B.S.; Varshini, B.S.; Avinash, G.; Kumar, R.R.; Ray, M.; Singh, K.N. Meta-transformer: Leveraging metaheuristic algorithms for agricultural commodity price forecasting. J. Big Data 2025, 12, 138. [Google Scholar] [CrossRef]
- Rath, M.; Darwish, A.; Pati, B.; Pattanayak, B.K.; Panigrahi, C.R. 2—Swarm intelligence as a solution for technological problems associated with Internet of Things. In Intelligent Data-Centric Systems; Hassanien, A.E., Darwish, A., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 21–45. ISBN 978-0-12-818287-1. [Google Scholar]
- Chekira, C.; Marzouq, M.; El Fadili, H.; Lakhliai, Z.; da Graça Ruano, M. Join security and block watermarking-based evolutionary algorithm and Racah moments for medical imaging. Biomed. Signal Process. Control 2024, 96, 106554. [Google Scholar] [CrossRef]
- Azam, N.A.; Haider, T.; Hayat, U. An optimized watermarking scheme based on genetic algorithm and elliptic curve. Swarm Evol. Comput. 2024, 91, 101723. [Google Scholar] [CrossRef]
- Starzec, M.; Starzec, G.; Byrski, A.; Turek, W. Distributed ant colony optimization based on actor model. Parallel Comput. 2019, 90, 102573. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Almuqren, L.; Aljameel, S.S.; Alqahtani, H.; Alotaibi, S.S.; Hamza, M.A.; Salama, A.S. A White Shark Equilibrium Optimizer with a Hybrid Deep-Learning-Based Cybersecurity Solution for a Smart City Environment. Sensors 2023, 23, 7370. [Google Scholar] [CrossRef]
- Naserbegi, A.; Aghaie, M.; Zolfaghari, A. Implementation of Grey Wolf Optimization (GWO) algorithm to multi-objective loading pattern optimization of a PWR reactor. Ann. Nucl. Energy 2020, 148, 107703. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Rahman, M.A.; Sokkalingam, R.; Othman, M.; Biswas, K.; Abdullah, L.; Kadir, E.A. Nature-inspired metaheuristic techniques for combinatorial optimization problems: Overview and recent advances. Mathematics 2021, 9, 633. [Google Scholar] [CrossRef]
- Mansouri, H.; Elkhanchouli, K.; Elghouate, N.; Bencherqui, A.; Tahiri, M.A.; Karmouni, H.; Sayyouri, M.; Moustabchir, H.; Askar, S.S.; Abouhawwash, M. A modified black-winged kite optimizer based on chaotic maps for global optimization of real-world applications. Knowl.-Based Syst. 2025, 318, 113558. [Google Scholar] [CrossRef]
- El maloufy, A.; Bencherqui, A.; Tahiri, M.A.; El Ghouate, N.; Karmouni, H.; Sayyouri, M.; Askar, S.S.; Abouhawwash, M. Chaos-enhanced white shark optimization algorithms CWSO for global optimization. Alexandria Eng. J. 2025, 122, 465–483. [Google Scholar] [CrossRef]
- El Ghouate, N.; Bencherqui, A.; Mansouri, H.; Maloufy, A.E.; Tahiri, M.A.; Karmouni, H.; Sayyouri, M.; Askar, S.S.; Abouhawwash, M. Improving the Kepler optimization algorithm with chaotic maps: Comprehensive performance evaluation and engineering applications. Artif. Intell. Rev. 2024, 57, 313. [Google Scholar] [CrossRef]
- Bencherqui, A.; Tahiri, M.A.; Karmouni, H.; Alfidi, M.; El Afou, Y.; Qjidaa, H.; Sayyouri, M. Chaos-Enhanced Archimede Algorithm for Global Optimization of Real-World Engineering Problems and Signal Feature Extraction. Processes 2024, 12, 406. [Google Scholar] [CrossRef]
- Wienand, J.F.; Karch, S.; Impertro, A.; Schweizer, C.; McCulloch, E.; Vasseur, R.; Gopalakrishnan, S.; Aidelsburger, M.; Bloch, I. Emergence of fluctuating hydrodynamics in chaotic quantum systems. Nat. Phys. 2024, 20, 1732–1737. [Google Scholar] [CrossRef]
- Kesgin, B.U.; Teğin, U. Implementing the analogous neural network using chaotic strange attractors. Commun. Eng. 2024, 3, 99. [Google Scholar] [CrossRef]
- Cao, W.; Huang, Y.; Zhang, H. Screen chaotic motion by Shannon entropy in curved spacetimes. Eur. Phys. J. C 2025, 85, 568. [Google Scholar] [CrossRef]
- Rudnicki, R. Ergodic and Chaotic Properties of the Heat Equation. J. Dyn. Differ. Equ. 2024, 2024, 1–12. [Google Scholar] [CrossRef]
- Kobiolka, J.; Habermann, J.; Yamakou, M.E. Reduced-order adaptive synchronization in a chaotic neural network with parameter mismatch: A dynamical system versus machine learning approach. Nonlinear Dyn. 2025, 113, 10989–11008. [Google Scholar] [CrossRef]
- Calgan, H.; Gokyildirim, A.; Ilten, E.; Demirtas, M. Classification of fractional-order chaotic systems using deep learning methods. Eur. Phys. J. Spec. Top. 2025, 123, 1–19. [Google Scholar] [CrossRef]
- Li, R.; Liu, T.; Yin, J. An encryption algorithm for color images based on an improved dual-chaotic system combined with DNA encoding. Sci. Rep. 2024, 14, 20733. [Google Scholar] [CrossRef]
- Wang, Q.; Sang, H.; Wang, P.; Yu, X.; Yang, Z. A novel 4D chaotic system coupling with dual-memristors and application in image encryption. Sci. Rep. 2024, 14, 29615. [Google Scholar] [CrossRef]
- Yang, J.; Li, C.; Zhang, Q.; Wu, Z.; Zhang, X.; Liu, P.; Liu, Z.; Tao, C.; Zheng, G.; Yang, Y.; et al. Chaos-enhanced manganese electrolysis: Nodule suppression and improved efficiency using controllable chaotic electrical signals. Sci. Rep. 2025, 15, 59. [Google Scholar] [CrossRef]
- Sambas, A.; Zhang, X.; Moghrabi, I.A.R.; Vaidyanathan, S.; Benkouider, K.; Alçın, M.; Koyuncu, İ.; Tuna, M.; Sulaiman, I.M.; Mohamed, M.A.; et al. ANN-based chaotic PRNG in the novel jerk chaotic system and its application for the image encryption via 2-D Hilbert curve. Sci. Rep. 2024, 14, 29602. [Google Scholar] [CrossRef]
- Du, J.; Zhang, J.; Li, S.; Yang, Z. Enhanced artificial hummingbird algorithm with chaotic traversal flight. Sci. Rep. 2024, 14, 25892. [Google Scholar] [CrossRef]
- Özalp, E.; Magri, L. Stability analysis of chaotic systems in latent spaces. Nonlinear Dyn. 2025, 113, 13791–13806. [Google Scholar] [CrossRef] [PubMed]
- Mekala, S.; Phani Kumar, S. Enhancing pancreatic cancer detection in CT images through secretary wolf bird optimization and deep learning. Sci. Rep. 2025, 15, 19787. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wei, P.; Li, Y. Enhanced secretary bird optimization algorithm with multi-strategy fusion and Cauchy—Gaussian crossover. Sci. Rep. 2025, 15, 23163. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhang, M.; Huang, Q.; Wu, X.; Wan, L.; Huang, J. Secretary bird optimization algorithm based on quantum computing and multiple strategies improvement for KELM diabetes classification. Sci. Rep. 2025, 15, 3774. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Elsayed, G.; Abass, E.S. FPGA design and implementation for montgomery multiplication algorithm using MATLAB HDL coder. Bull. Natl. Res. Cent. 2024, 48, 129. [Google Scholar] [CrossRef]
- Purraji, M.; Zamiri, E.; Sanchez, A.; de Castro, A. Rapid Prototyping for Design and Test of FPGA-Based Model Predictive Controllers for Power Converters. J. Electr. Eng. Technol. 2025, 20, 2419–2438. [Google Scholar] [CrossRef]
- Alhammami, M. FPGA hardware kit for remote training platforms. Discov. Educ. 2024, 3, 102. [Google Scholar] [CrossRef]
- İnce, E.; Karakaya, B.; Türk, M. Designing hardware for a robust high-speed cryptographic key generator based on multiple chaotic systems and its FPGA implementation for real-time video encryption. Multimed. Tools Appl. 2024, 83, 64499–64532. [Google Scholar] [CrossRef]
- Tian, S.; Song, Q.; He, J.; Wang, Y.; Nie, K.; Du, G.; Bu, L. Implementation of JPEG XS entropy encoding and decoding on FPGA. J. Real-Time Image Process. 2024, 21, 34. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Z.; Gudukbay Akbulut, G.; Narayanan, V.; Kandemir, M.T.; Das, C.R. FPGA-based accelerator for adaptive banded event alignment in nanopore sequencing data analysis. BMC Bioinform. 2025, 26, 83. [Google Scholar] [CrossRef] [PubMed]
- Estudillo-Valdez, M.A.; Adeyemi, V.A.; Tlelo-Cuautle, E.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.C. FPGA realization of four chaotic interference cases in a terrestrial trajectory model and application in image transmission. Sci. Rep. 2023, 13, 12969. [Google Scholar] [CrossRef]
- Yalcin, O.B.; Hematpour, N.; Faruk Birgul, O. Design of the new classic and quantum chaotic maps and implementation on FPGA. Arab. J. Sci. Eng. 2025, 1–47. [Google Scholar] [CrossRef]
- Khanzadi, H.; Eshghi, M.; Borujeni, S.E. Image Encryption Using Random Bit Sequence Based on Chaotic Maps. Arab. J. Sci. Eng. 2014, 39, 1039–1047. [Google Scholar] [CrossRef]
- Akçay, L.; Yalçın, B.Ö. Lightweight ASIP Design for Lattice-Based Post-quantum Cryptography Algorithms. Arab. J. Sci. Eng. 2025, 50, 835–849. [Google Scholar] [CrossRef]
- Özbay, H.; Özer, İ.; Dalcali, A.; Çetin, O.; Temurtaş, F. Sensorless Position Estimation in Electromagnetic Launchers Using Recurrent Neural Networks with Repeated k-Fold Cross-Validation. Arab. J. Sci. Eng. 2025, 1–19. [Google Scholar] [CrossRef]
- Sadeeq, H.; Abdulazeez, A.M. Hardware Implementation of Firefly Optimization Algorithm Using FPGAS. In Proceedings of the 2018 International Conference on Advanced Science and Engineering (ICOASE), Duhok, Iraq, 9–11 October 2018; pp. 30–35. [Google Scholar] [CrossRef]
- Firmansyah, I.; Setiadi, B.; Subekti, A.; Nugraha, H.; Kurniawan, E.; Yamaguchi, Y. Enhancing IoT data acquisition efficiency via FPGA-based implementation with OpenCL framework. Comput. Electr. Eng. 2024, 120, 109830. [Google Scholar] [CrossRef]
- Bessalah, H.; Alim-Ferhat, F.; Salhi, H.; Seddiki, S.; Issad, M.; Kerdjidj, O. On line wavelets transform on a xilinx FPGA circuit to medical images compression. In Proceedings of the 2009 International Conference on Digital Image Processing, Bangkok, Thailand, 7–9 March 2009; IEEE: New York, NY, USA; pp. 8–12. [Google Scholar]
- Park, J.; Lee, H.; Kwon, H.H.; Hwang, Y.; Choi, W. Parallelized particle swarm optimization on FPGA for realtime ballistic target tracking. Sensors 2023, 23, 8456. [Google Scholar] [CrossRef]
- Lee, H.; Kim, K.; Kwon, Y.; Hong, E. Real-time particle swarm optimization on FPGA for the optimal message-chain structure. Electronics 2018, 7, 274. [Google Scholar] [CrossRef]
- Zermani, M.A.; Manita, G.; Chhabra, A.; Feki, E.; Mami, A. FPGA-based hardware implementation of chaotic opposition-based arithmetic optimization algorithm. Appl. Soft Comput. 2024, 154, 111352. [Google Scholar] [CrossRef]
- Hassanein, A.; El-Abd, M.; Damaj, I.; Rehman, H.U. Parallel hardware implementation of the brain storm optimization algorithm using FPGAs. Microprocess. Microsyst. 2020, 74, 103005. [Google Scholar] [CrossRef]
- Ortiz, A.; Mendez, E.; Balderas, D.; Ponce, P.; Macias, I.; Molina, A. Hardware implementation of metaheuristics through LabVIEW FPGA. Appl. Soft Comput. 2021, 113, 107908. [Google Scholar] [CrossRef]











| Map’s Name | Map of Chebyshev | Map’s Name | Circular Map | Map’s Name | Gauss Map |
|---|---|---|---|---|---|
| Function | Function | Function | |||
| Range | Range | Range | |||
 |  |  | |||
| Map’s Name | Iterative map | Map’s Name | Logistic map | Map’s Name | Piecewise map |
| Function | Function | Function | |||
| Range | Range | Range | |||
 |  |  | |||
| Map’s Name | Sine map | Map’s Name | Tent map | Map’s Name | Sinusoidal map |
| Function | Function | Function | |||
| Range | Range | Range | |||
 |  |  | |||
| Resource | Estimation | Available | Resource Utilization Rate (%) with the Q(16.16) Format |
|---|---|---|---|
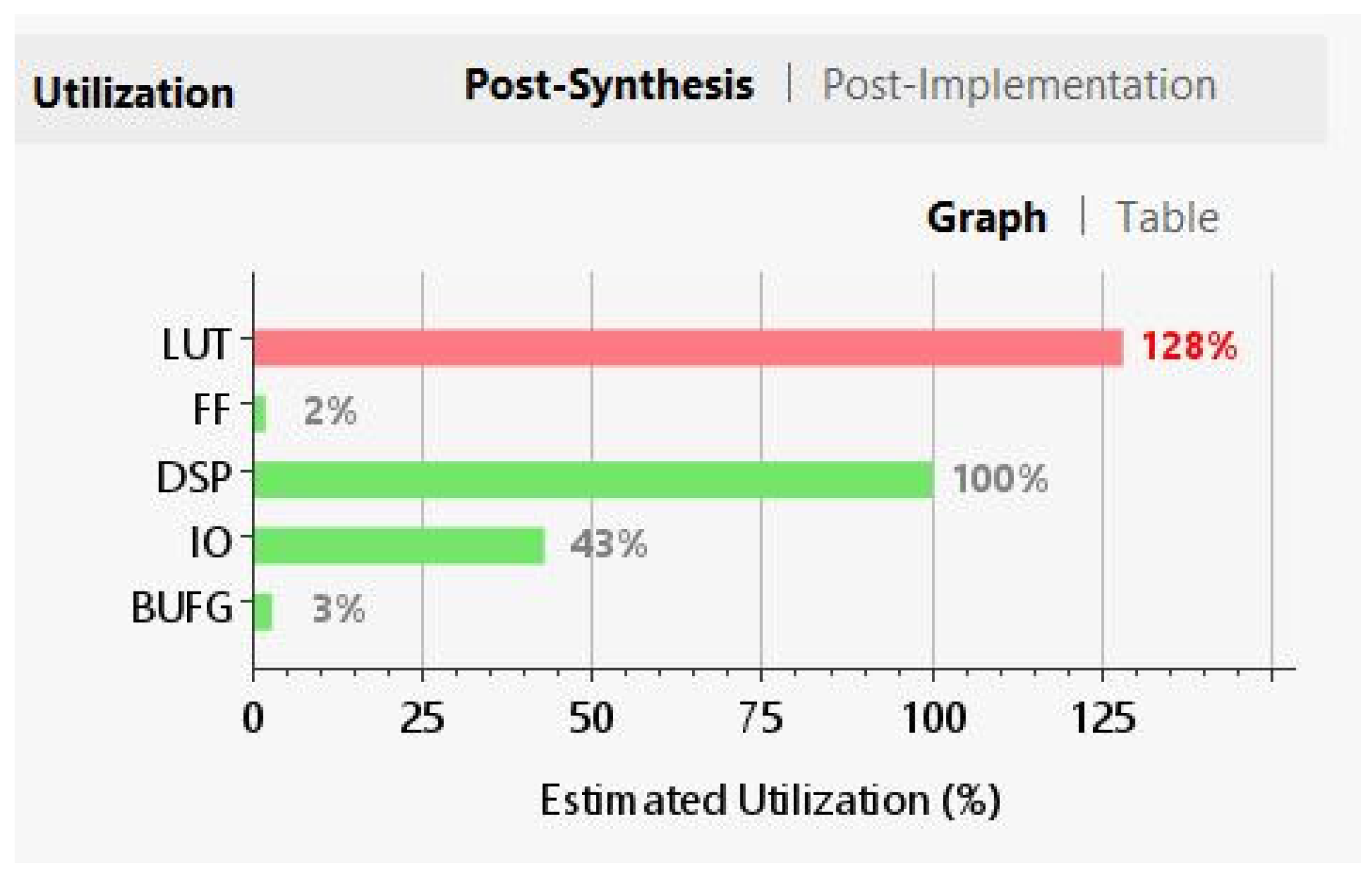
| LUT | 81,192 | 63,400 | 128.06 |
| FF | 2830 | 126,800 | 2.23 |
| DSP | 240 | 240 | 100.00 |
| IO | 91 | 210 | 43.33 |
| BUFG | 1 | 32 | 3.13 |
| Criterion | Q(16.16) (32 Bits) | Q(4.8) (12 Bits) | Observations |
|---|---|---|---|
| LUT utilization | 128% | 80% | Q4.8 makes the design feasible on XC7A100T |
| DSP utilization | 100% (saturation) | 72% | Reduced pressure on DSP resources |
| FF utilization | 2.23% | 3.10% | Slight increase due to simplified registers |
| Hardware feasibility | No (exceeds resources) | Yes (within constraints) | Q4.8 adopted for the final implementation |
| Q(16.16) (500 Iteration) | Q(4.8) (100 Iteration) | Q(4.8) (200 Iteration) | Q(4.8) (400 Iteration) | Q(4.8) (500 Iteration) | Observations | |
|---|---|---|---|---|---|---|
| LUT | 128% (exceeds capacity) | 74% | 76% | 78% | 80% | LUT usage grows moderately with iterations, Q4.8 remains feasible |
| DSP | 100% (saturation) | 70% | 71% | 72% | 72% | DSP usage stabilizes after 200 iterations |
| FF | 2.23% | 2.6% | 2.8% | 3.0% | 3.1% | Slight linear increase with iterations |
| Hardware feasibility | No (exceeds resources) | Yes | Yes | Yes | Yes | Q4.8 feasible across all tested iterations |
| Component | Consumption | Percentage |
|---|---|---|
| Total On-Chip Power | 0.672 W | 100% |
| Dynamic Power | 0.573 W | 85% |
| Signals | 0.269 W | 40% |
| Logic | 0.240 W | 36% |
| DSP | 0.057 W | 8% |
| Clocks | 0.006 W | 1% |
| Algorithms | The Optimal Values of the Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| Tent map | 0.204381 | 3.522334 | 9.034708 | 0.205602 | 1.728744 |
| Sine map | 0.201018 | 4.686782 | 9.612454 | 0.211338 | 2.129173 |
| Henon map | 0.216840 | 3.335610 | 8.803418 | 0.216370 | 1.764686 |
| Gauss map | 0.208568 | 3.492564 | 9.033946 | 0.206490 | 1.730838 |
| Bernoulli map | 0.204591 | 3.586618 | 9.297796 | 0.209565 | 2.445557 |
| Logistic map | 0.202103 | 3.451066 | 9.011632 | 0.202332 | 1.723378 |
| Algorithms | Our Method | Ref. [23] | Ref. [22] | Ref. [21] | Ref. [20] |
|---|---|---|---|---|---|
| Optimal cost | 1.723378 | 1.7810 | 1.7248 | 1.725388 | 1.72550 |
| Algorithms | The Optimal Values of the Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| Ts | Th | R | L | ||
| Logistic Map | 0.778582 | 0.387650 | 39.75602 | 193.6284 | 5.85955 × 103 |
| Sine map | 1.226265 | 14.23855 | 51.61191 | 199.0000 | 8.04700 × 104 |
| Henon map | 1.253378 | 0.616931 | 64.64376 | 12.56498 | 8.30154 × 103 |
| Gauss map | 0.793030 | 0.404503 | 42.00121 | 191.1295 | 6.85206 × 103 |
| Bernoulli map | 0.863308 | 0.652729 | 41.57705 | 172.9799 | 6.40800 × 103 |
| Tent map | 1.600845 | 0.268473 | 41.51013 | 150.3559 | 5.880360 × 103 |
| Algorithms | Our Method | Ref. [21] | Ref. [22] | Ref. [23] | Ref. [20] |
|---|---|---|---|---|---|
| Optimal cost | 5.880360 × 103 | 5.8820851 × 103 | 5.8853 × 103 | 5.89166 × 103 | 5.92846 × 103 |
| Algorithms | The Optimal Values of the Variables | Optimal Weight | ||
|---|---|---|---|---|
| d | D | N | ||
| Tent map | 0.054395 | 0.354290 | 8.276532 | 0.024838 |
| Sine map | 0.086496 | 1.476000 | 2.476000 | 0.020506 |
| Henon map | 0.050384 | 0.563342 | 14.12413 | 0.023438 |
| Gauss map | 0.050495 | 0.358552 | 12.45398 | 0.023134 |
| Logistic map | 0.053251 | 0.385056 | 10.6976860 | 0.016763 |
| Bernoulli map | 0.052227 | 0.342264 | 12.00704 | 0.012521 |
| Algorithms | Our Method | Ref. [21] | Ref. [22] | Ref. [23] | Ref. [20] |
|---|---|---|---|---|---|
| Optimal weight | 0.012521 | 0.012670 | 0.0126 | 0.012671 | 0.0126670 |
| Reference | Method Used | Chaotic Map | FPGA Board | Energy Consumption | Resources (LUT/Registers) |
|---|---|---|---|---|---|
| [56] | Chaotic-Opposition-Based Arithmetic Optimization Algorithm (COAOA) with OBL | Logistic map (chaotic randomizer) | Xilinx Virtex-7 VC707 | Reported as significantly reduced vs. software (exact values not provided) | 8924 LUTs (16% of total resources) |
| [54] | Parallelized Particle Swarm Optimization (PSO) | None (pure PSO) | AMD Zynq 7000 SoC ZC706 | Focused on real-time throughput; energy metrics not reported | ≈40.51% of total FPGA capacity |
| [57] | Random Grouping Brain Storm Optimization (RGBSO) with hardware parallelization | None (LFSR used as random generator) | Altera Stratix IV | No direct value; reported energy gain vs. GPU | 583 Logic Elements; 232 Registers; Fmax = 250 MHz; |
| [58] | FPGA implementation of PSO, BA, GWO, EA, Nelder–Mead via LabVIEW | None (native FPGA random generator) | Xilinx Kintex-7 | Energy not detailed; strong acceleration (~50× vs. PC) | LUTs 78% |
| Proposed Method | Secretary Bird Optimization Algorithm (SBOA) with dynamic-voting-based chaotic map selection | Logistic, Tent, Sine, Henon, Gauss, Bernoulli (6 generators, adaptive selection) | Xilinx Artix-7 (Nexys 4 DDR, XC7A100T) | 0.672 W (85% dynamic = 0.573 W) | LUTs: 74–80% (Q4.8, feasible); DSP: 70–72%; Registers: ≈2.6–3.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouchker, R.; Tahiri, H.; Mchichou, I.; Tahiri, M.A.; Amakdouf, H.; Sayyouri, M. Contextual Real-Time Optimization on FPGA by Dynamic Selection of Chaotic Maps and Adaptive Metaheuristics. Appl. Sci. 2025, 15, 10695. https://doi.org/10.3390/app151910695
Ouchker R, Tahiri H, Mchichou I, Tahiri MA, Amakdouf H, Sayyouri M. Contextual Real-Time Optimization on FPGA by Dynamic Selection of Chaotic Maps and Adaptive Metaheuristics. Applied Sciences. 2025; 15(19):10695. https://doi.org/10.3390/app151910695
Chicago/Turabian StyleOuchker, Rabab, Hamza Tahiri, Ismail Mchichou, Mohamed Amine Tahiri, Hicham Amakdouf, and Mhamed Sayyouri. 2025. "Contextual Real-Time Optimization on FPGA by Dynamic Selection of Chaotic Maps and Adaptive Metaheuristics" Applied Sciences 15, no. 19: 10695. https://doi.org/10.3390/app151910695
APA StyleOuchker, R., Tahiri, H., Mchichou, I., Tahiri, M. A., Amakdouf, H., & Sayyouri, M. (2025). Contextual Real-Time Optimization on FPGA by Dynamic Selection of Chaotic Maps and Adaptive Metaheuristics. Applied Sciences, 15(19), 10695. https://doi.org/10.3390/app151910695








