The Effects of Changing the Support Point in a Given Cross Section on Structural Stability
Abstract
1. Introduction
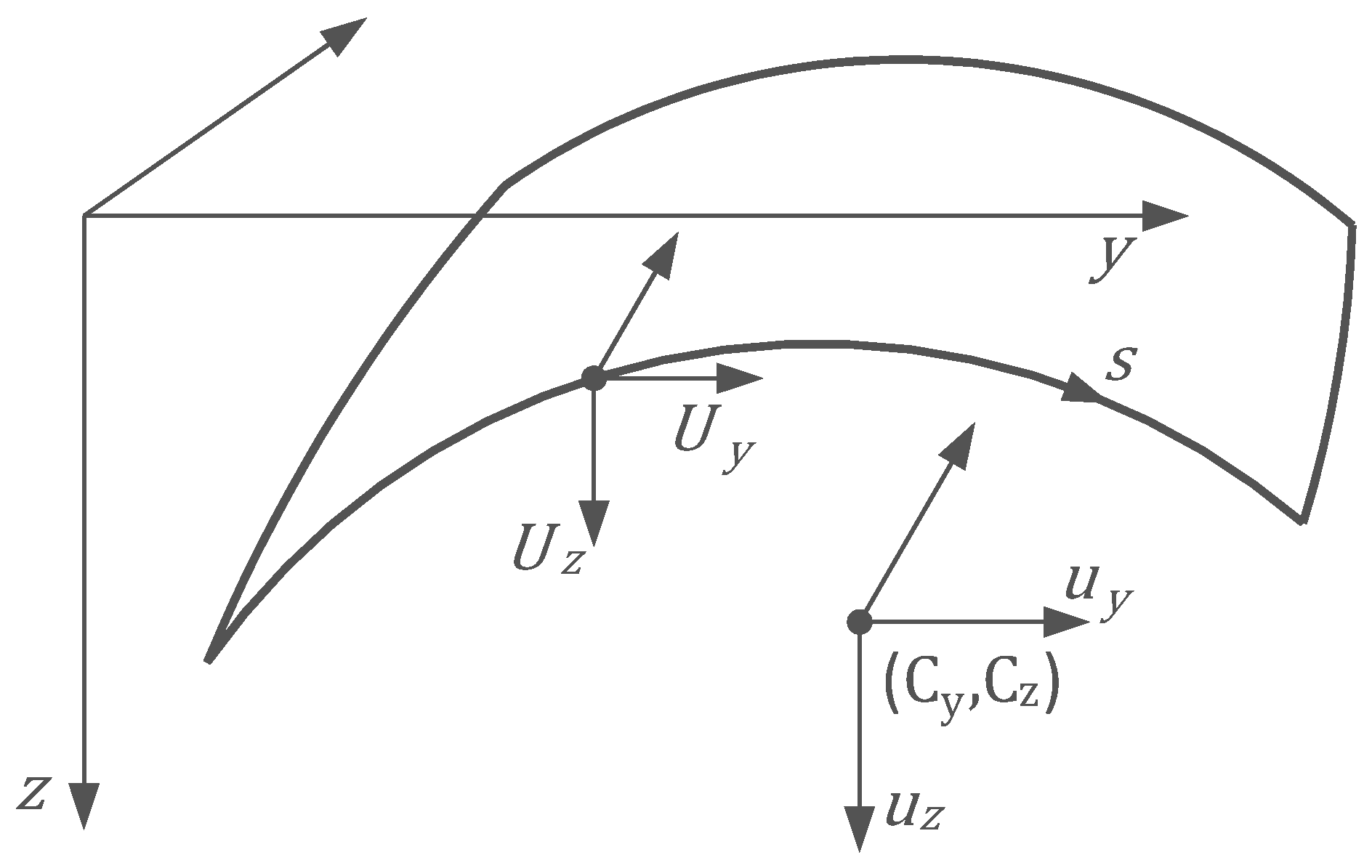
2. Mathematical Description of Rod Model
3. Derivation of Displacement Equations for Stability Loss
4. Solution of Displacement Equations
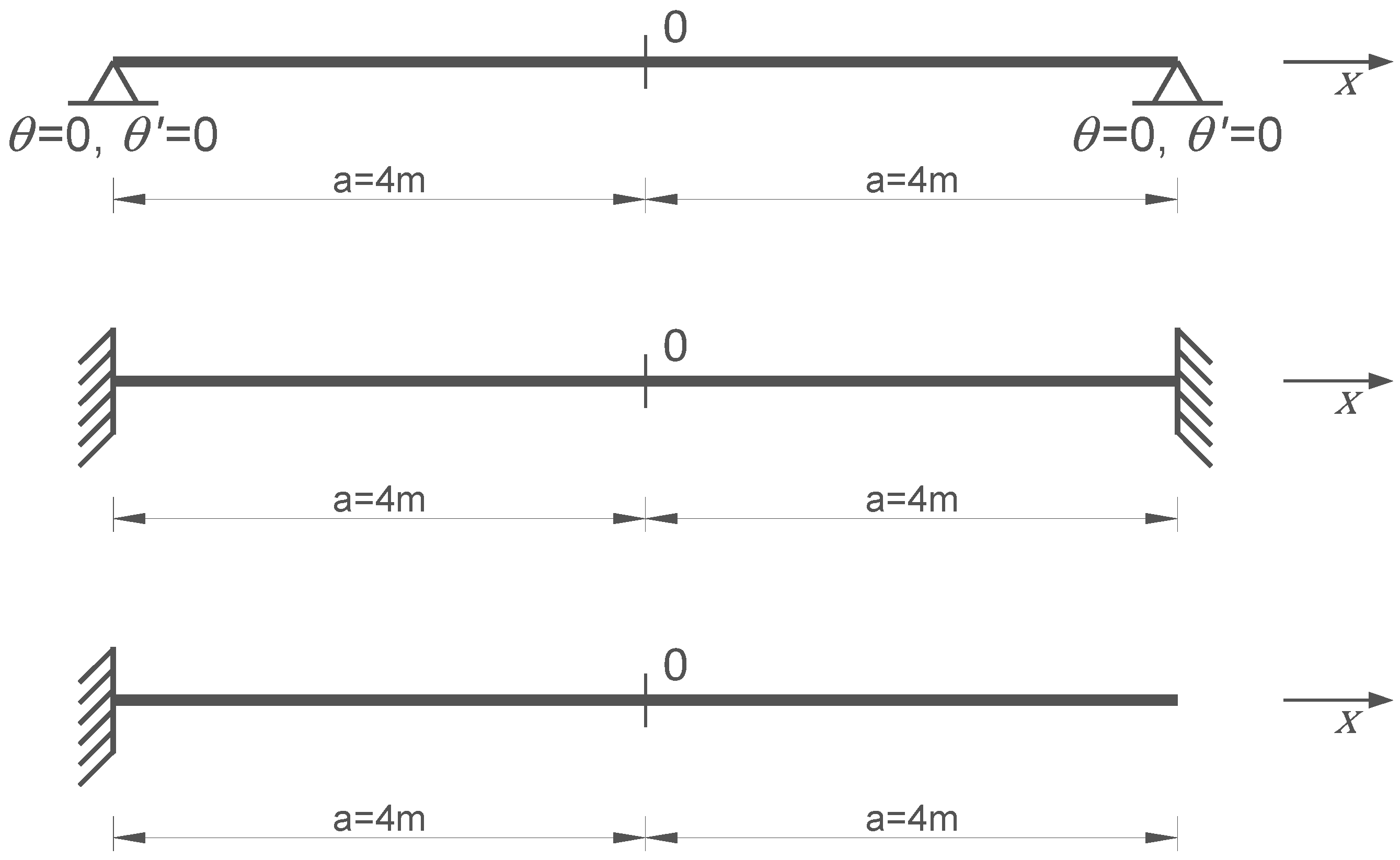
5. Problem Formulation
- -
- Pinned—P:
- -
- Clamped—C:
- -
- Free—F:
6. Analysis of Results
- For beams with a bisymmetric cross section:
- ○
- 7.24–7.87 times greater when the load acts on the bottom flange;
- ○
- 4.26–4.55 times greater when the load acts in the centre of the web;
- ○
- 2.46–2.56 times greater when the load acts on the top flange.
- For beams with the “⏊”cross section:
- ○
- 5.36–5.51 times greater when the load acts on the bottom flange;
- ○
- 3.09–3.39 times greater when the load acts in the centre of the web;
- ○
- 2.06–2.20 times greater when the load acts on the top flange.
- For beams with the “⏉” cross section:
- ○
- 7.62–9.24 times greater than when the load acts on the bottom flange;
- ○
- 4.71–5.51 greater when the load acts in the centre of the web;
- ○
- 2.40–2.62 greater when the load acts on the top flange.
- For beams with a bisymmetric cross section:
- ○
- 0.56–0.95 when the load acts on the bottom flange;
- ○
- 0.39–0.78 when the load acts in the centre of the web;
- ○
- 0.16–0.51 when the load acts on the top flange.
- For beams with the “⏊” cross section:
- ○
- 0.95–1.61 when the load acts on the bottom flange;
- ○
- 0.59–1.48 when the load acts in the centre of the web;
- ○
- 0.26–0.94 when the load acts on the top flange.
- For beams with the “⏉” cross section:
- ○
- 0.34–0.56 when the load acts on the bottom flange;
- ○
- 0.28–0.44 when the loads acts in the centre of the web;
- ○
- 0.15–0.32 when the load acts on the top flange.
- is the critical load value when the load is applied to the bottom flange;
- is the critical load value when the load is applied to the centre of the web;
- is the critical load value when the load is applied to the top flange.
- When the top flange is the support point, the rate of critical load increment increases as the load application point is lowered;
- When the centre of the web is the support point, the critical load increment is close to a linear increment (the rate of increment is almost constant) as the load application point is lowered;
- When the bottom flange is the support point, the rate of critical load increment slightly decreases as the load application point is lowered.
- When the top flange is the support point, the rate of critical load increment increases as the load application point is lowered (as for beams with a bisymmetric cross section and the “⏉” cross section);
- When the centre of the web is the support point, the rate of critical load increment slightly increases when the load application point is lowered;
- When the bottom flange is the support point, the critical load increment is close to a linear increment (the rate of increment is almost constant) as the load application point is lowered.
- is the critical load value when the beam is supported in the centre of the bottom flange;
- is the critical load value when the beam is supported in the centre of the web;
- is the critical load value when the beam is supported in the centre of the top of the top flange.
- 1.162–1.523 times for the beam with a bisymmetric cross section;
- 1.177–1.539 times for the beam with the “⏊” cross section;
- 1.027–1.323 times for the beam with the “⏉” cross section.
- 3.004–25.946 times for the beam with a bisymmetric cross section;
- 2.712–16.840 times for the beam with the “⏊” cross section;
- 2.779–39.170 times for the beam with the “⏉” cross section.
7. Conclusions
- The model presented in this paper accurately describes the geometry of the rod and its displacements and, even with a small approximation base, yields accurate results (agreeing with FEM results). The FEM computer programs for the analysis of thin-walled rod structures known to the authors do not contain thin-walled nonprismatic elements. The FEM model is a certain simplification as prismatic finite elements are used to model a nonprismatic system.
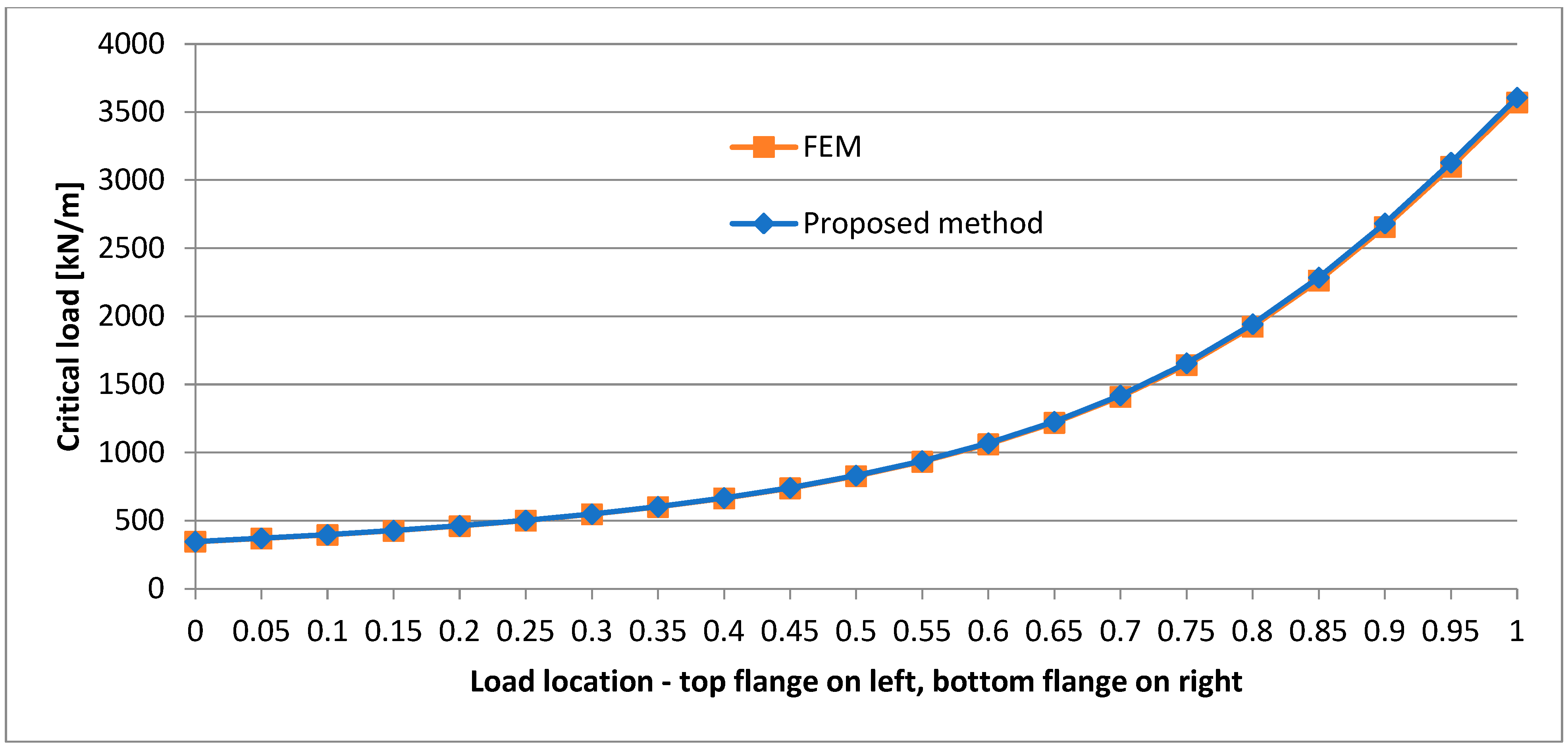
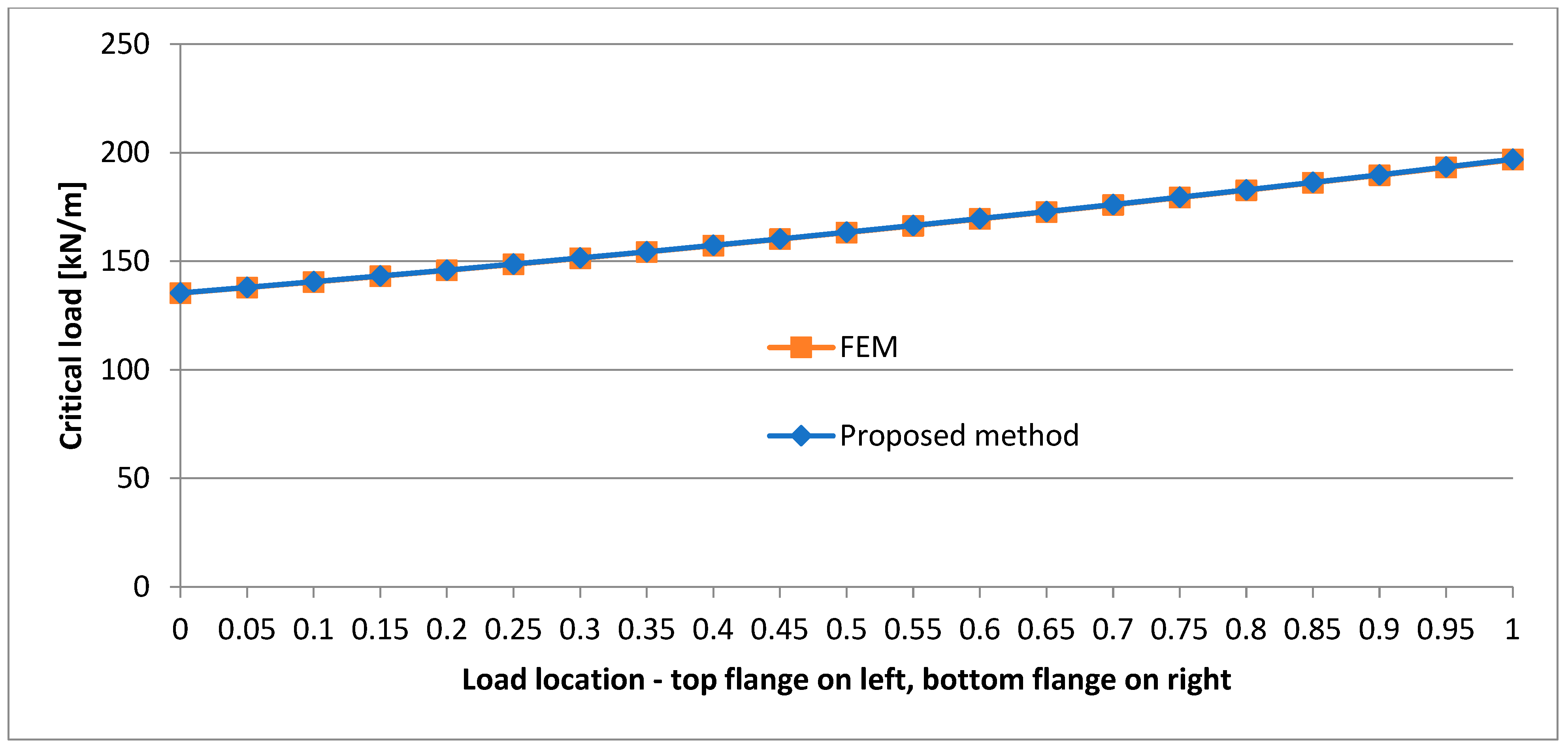
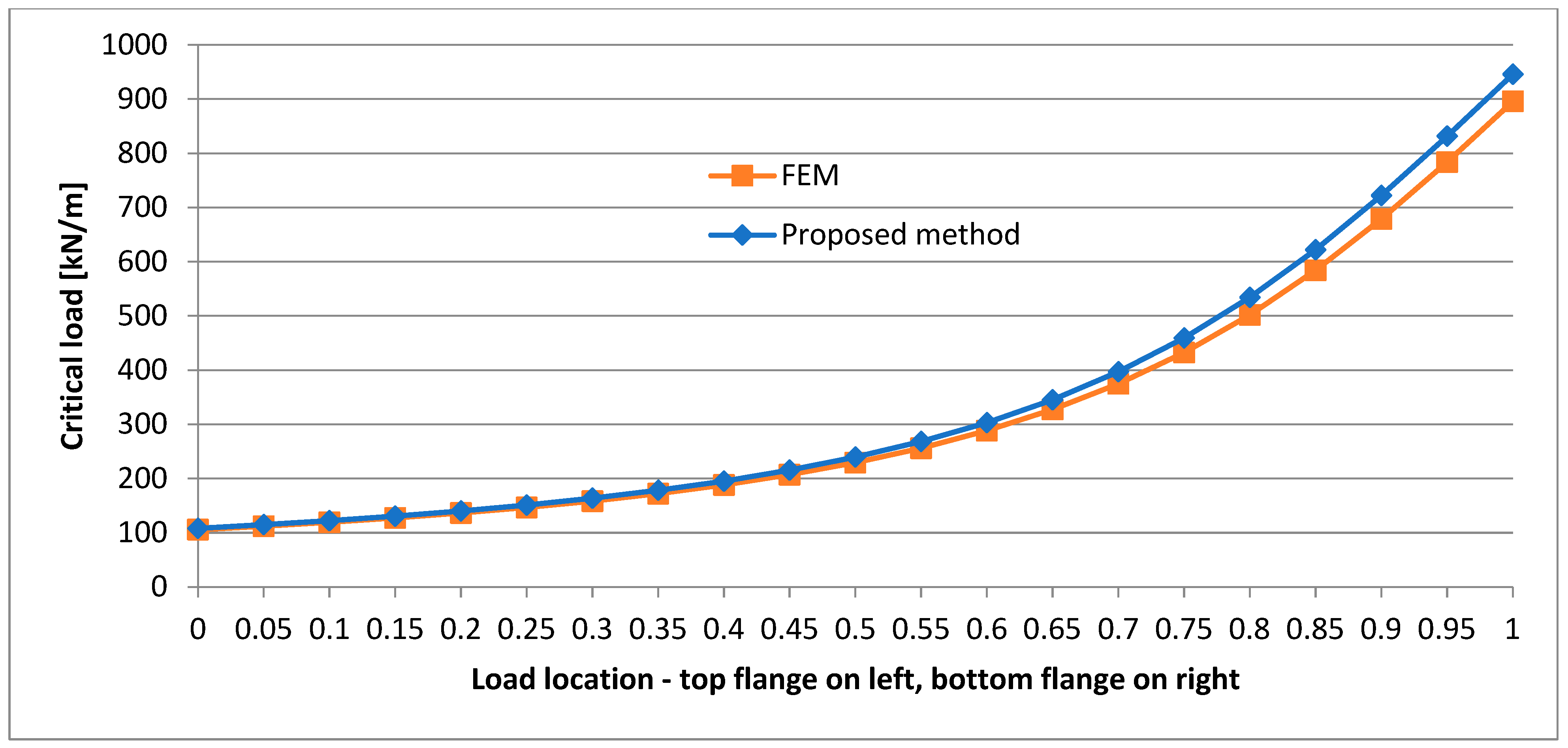
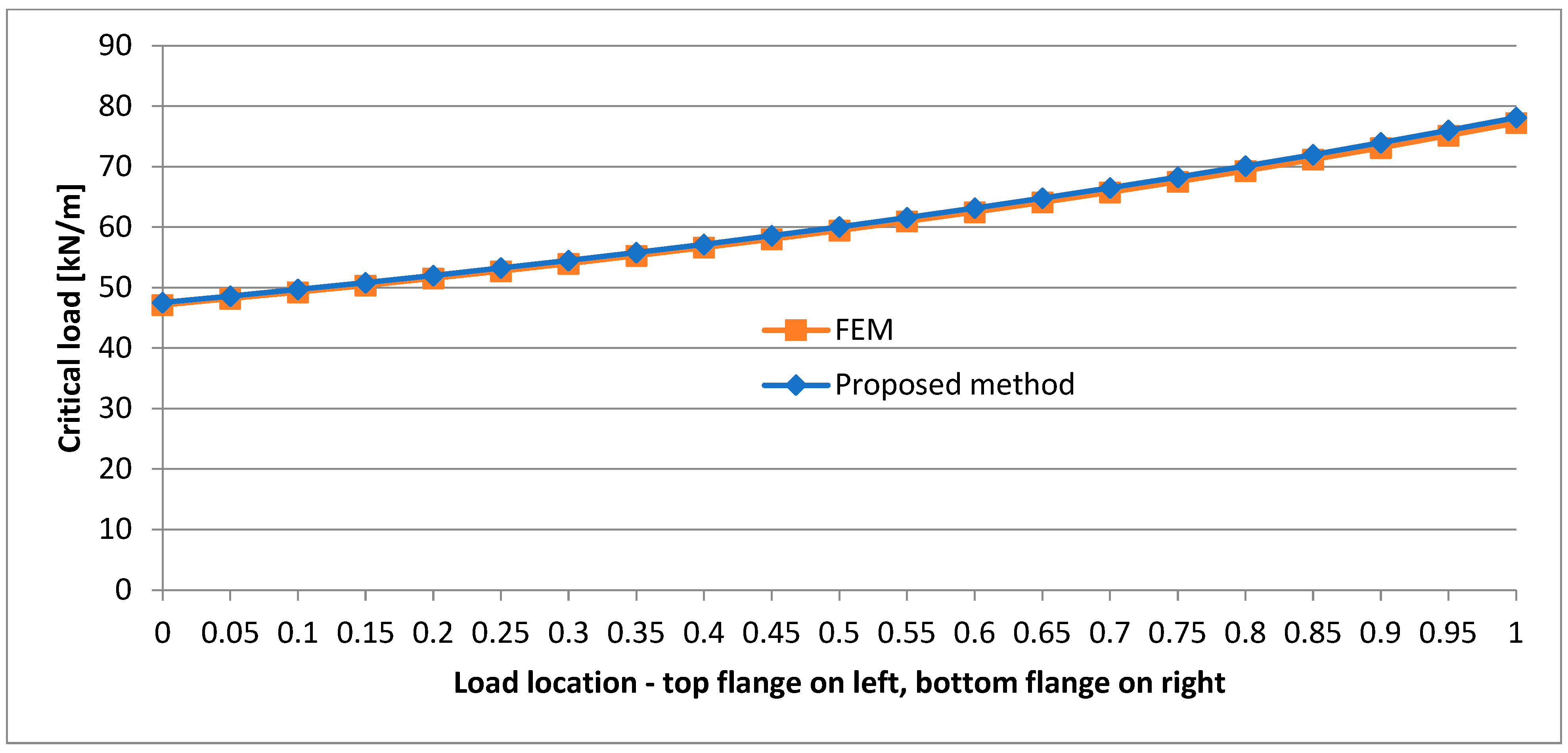
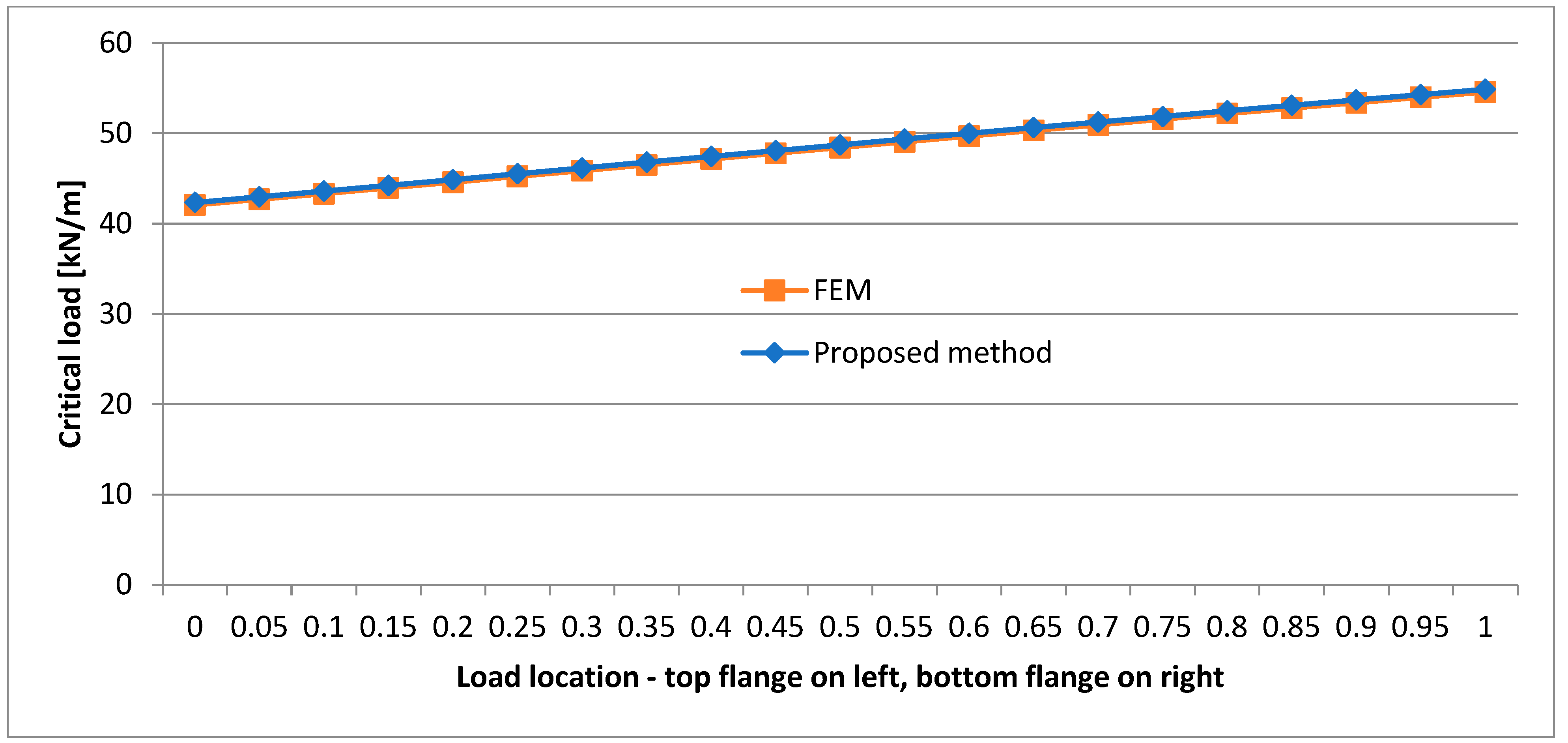
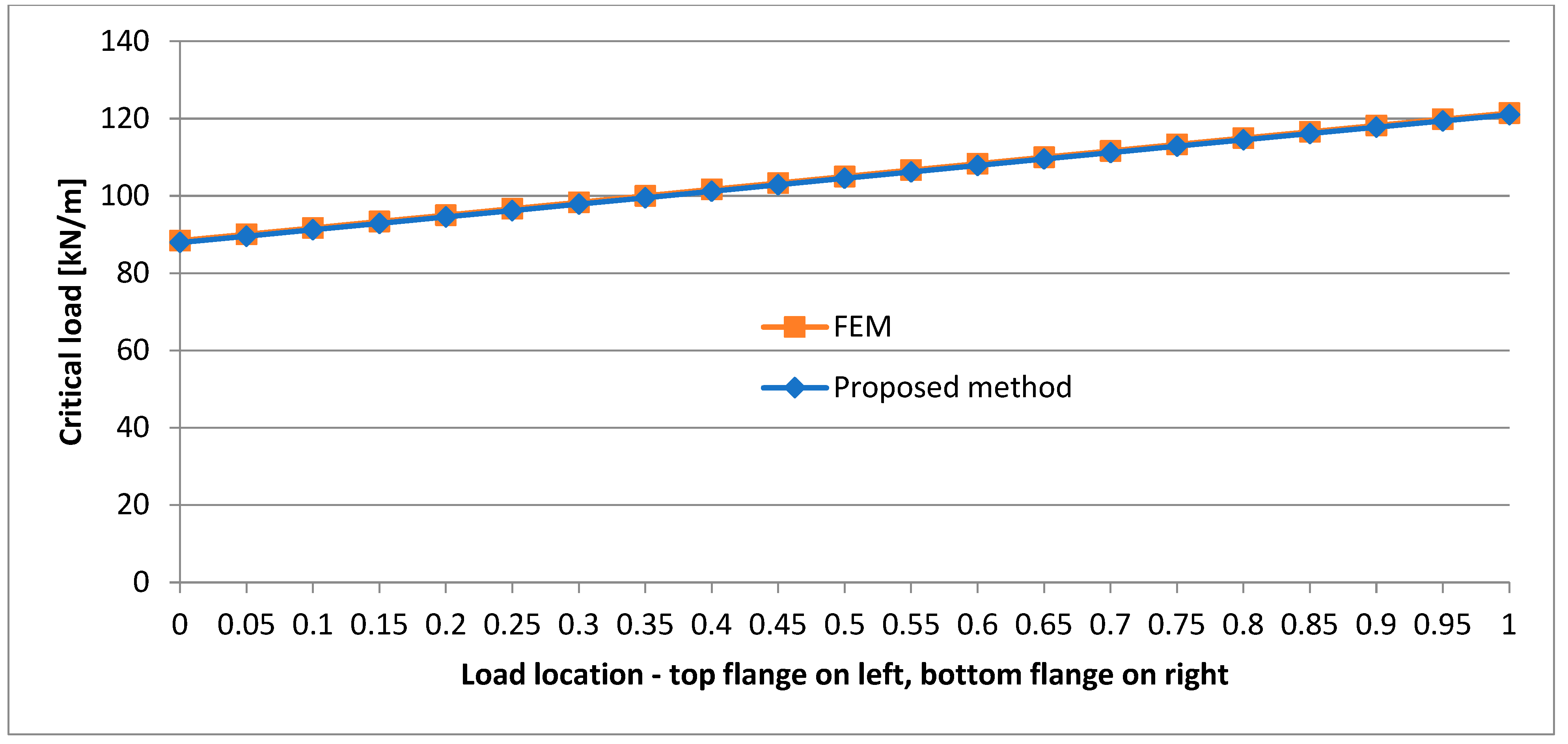
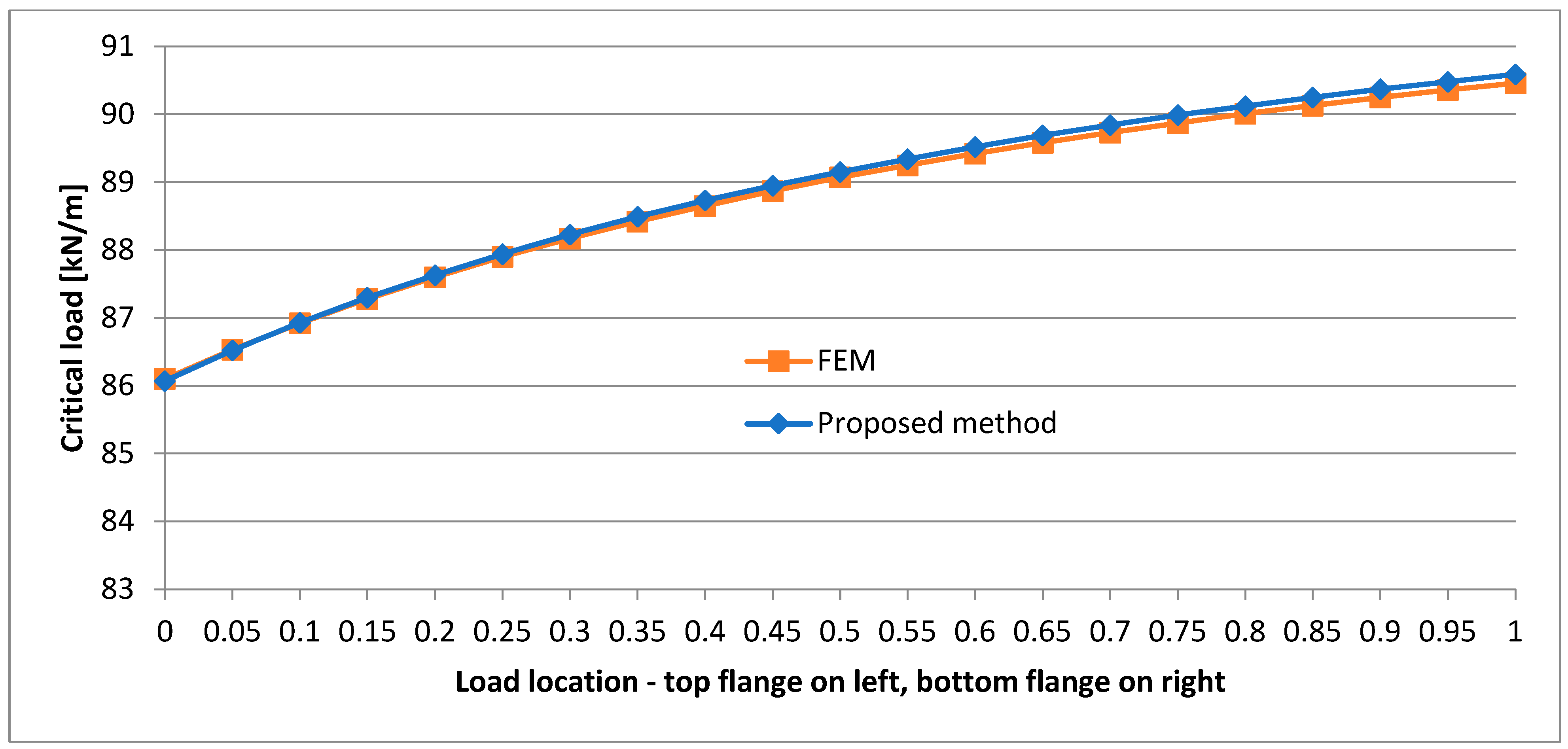
- The location of the load has a significant effect on the critical load value, and the lower the load location, the higher the critical load value.
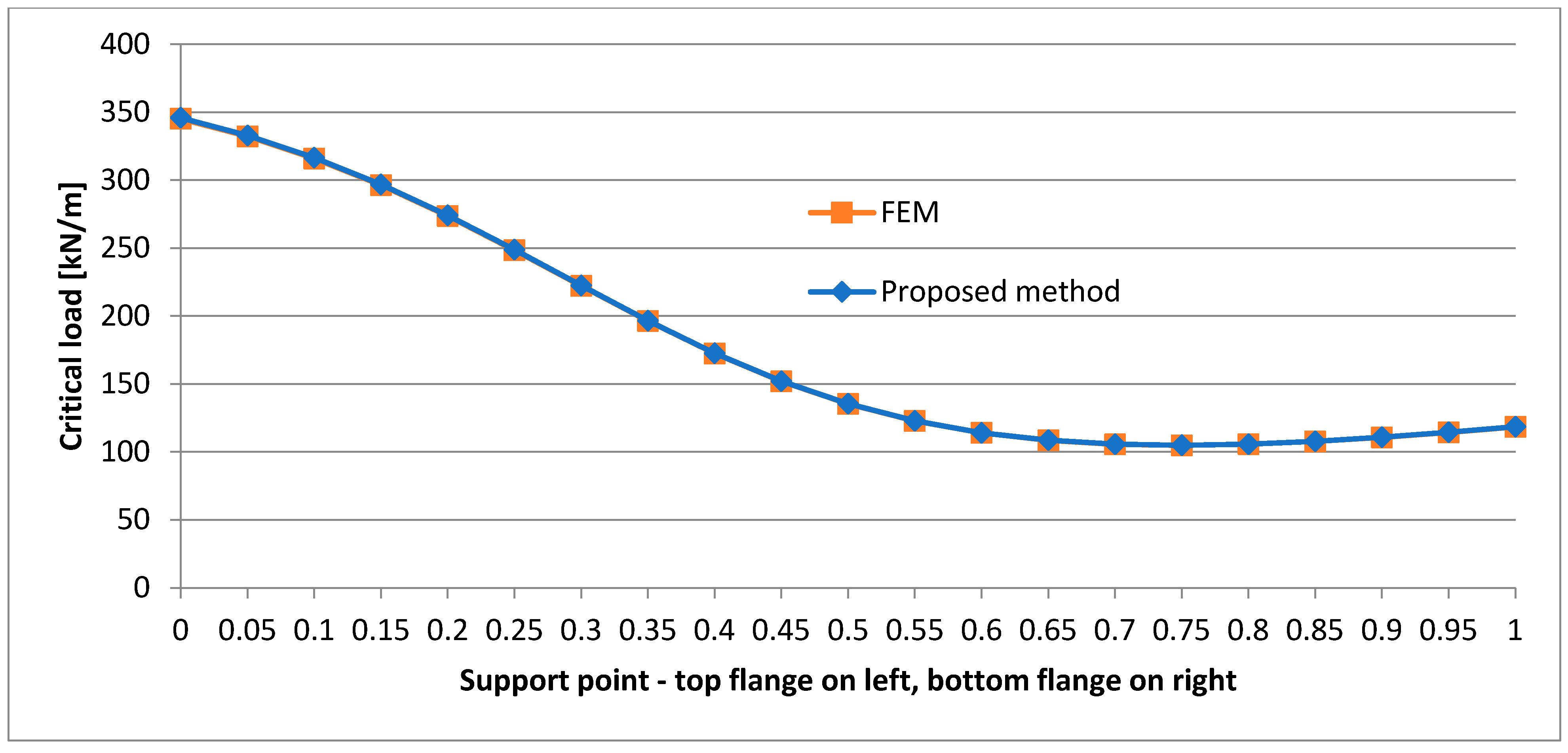
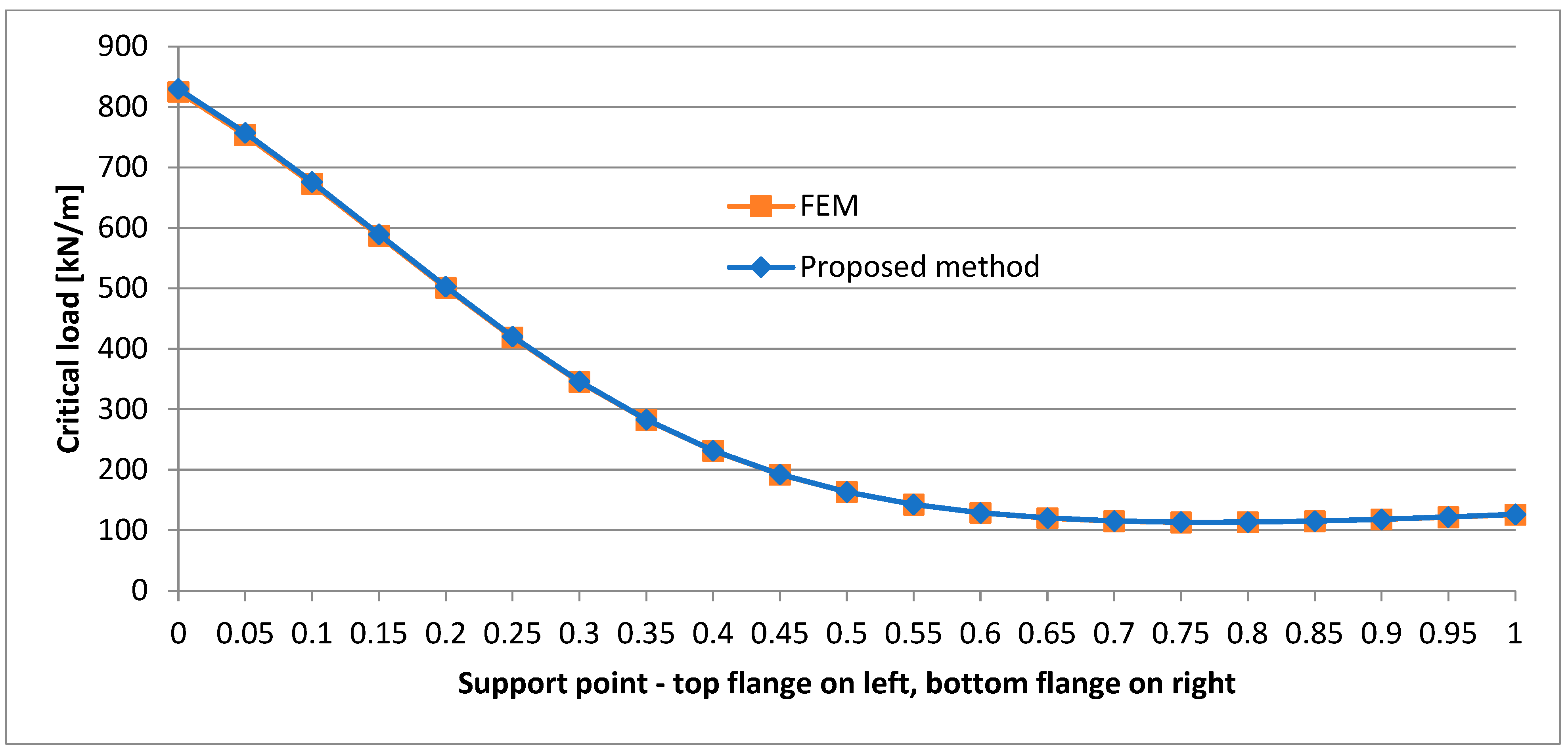
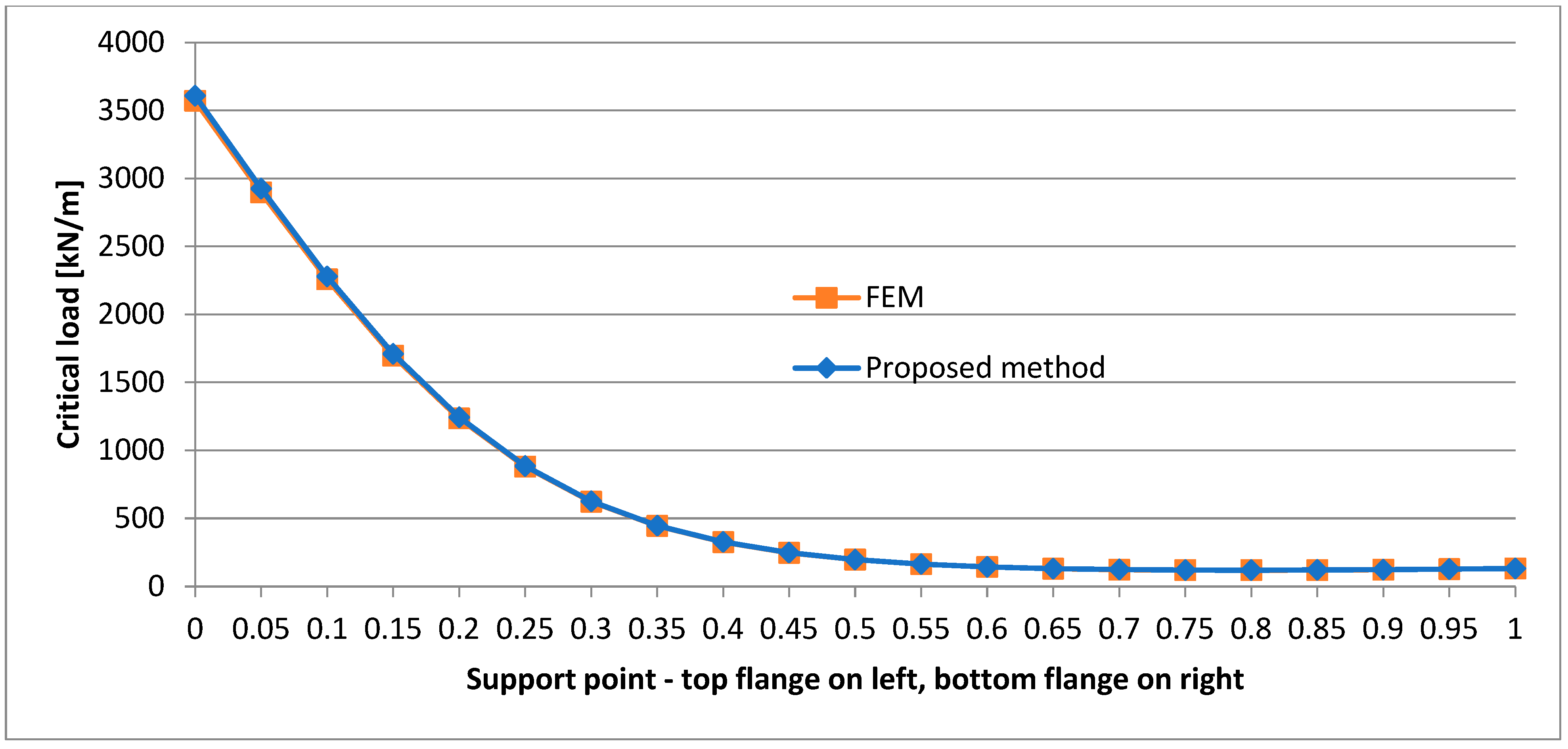
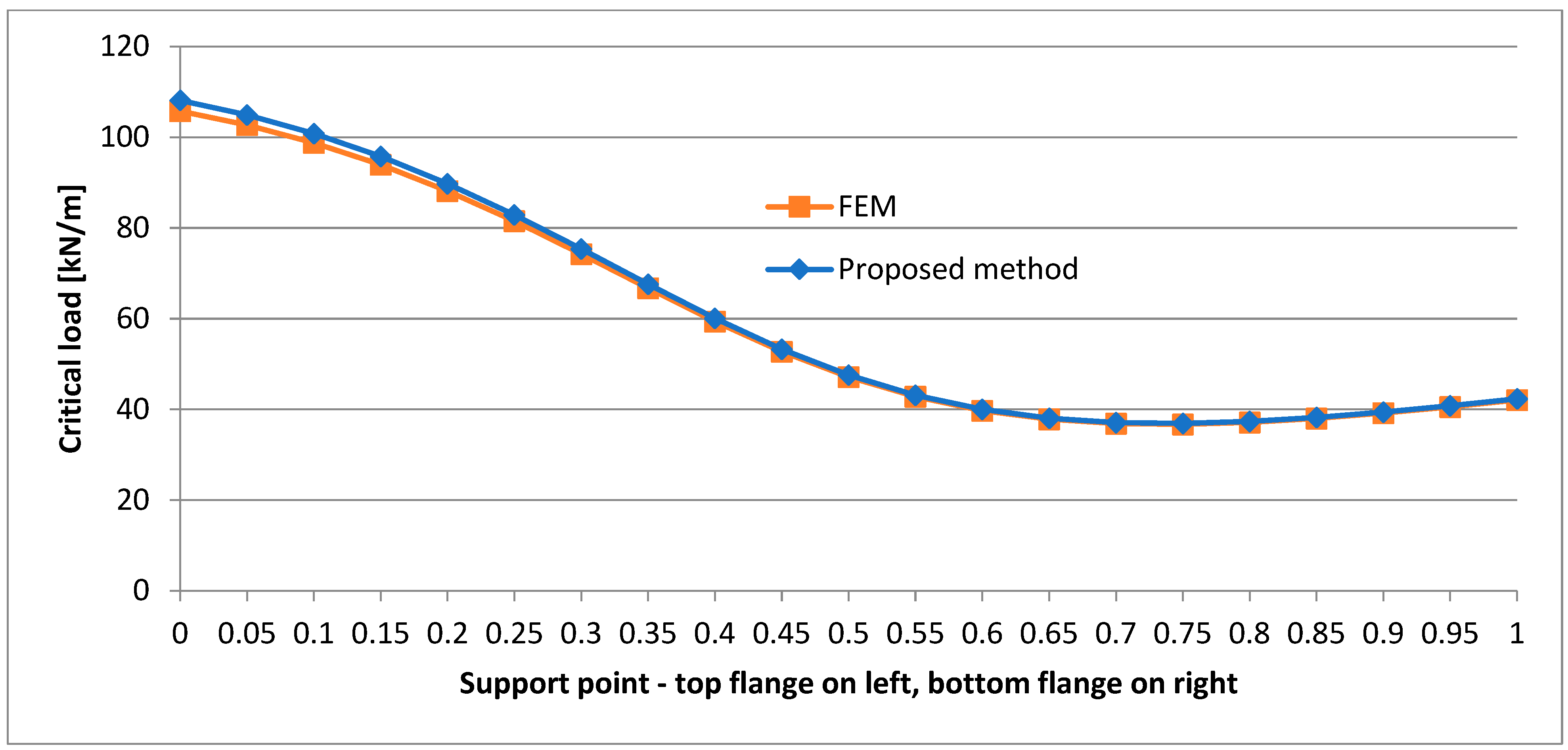
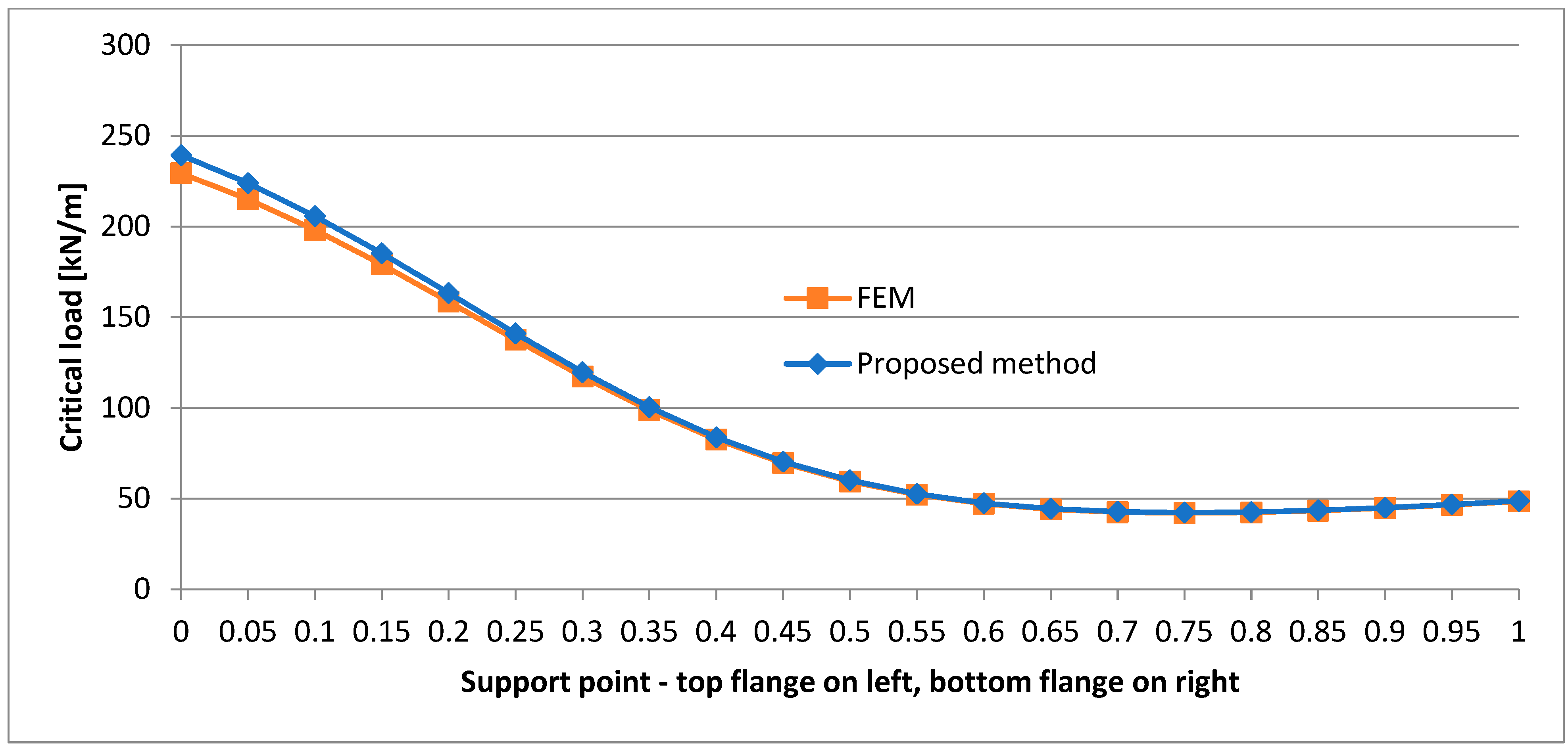
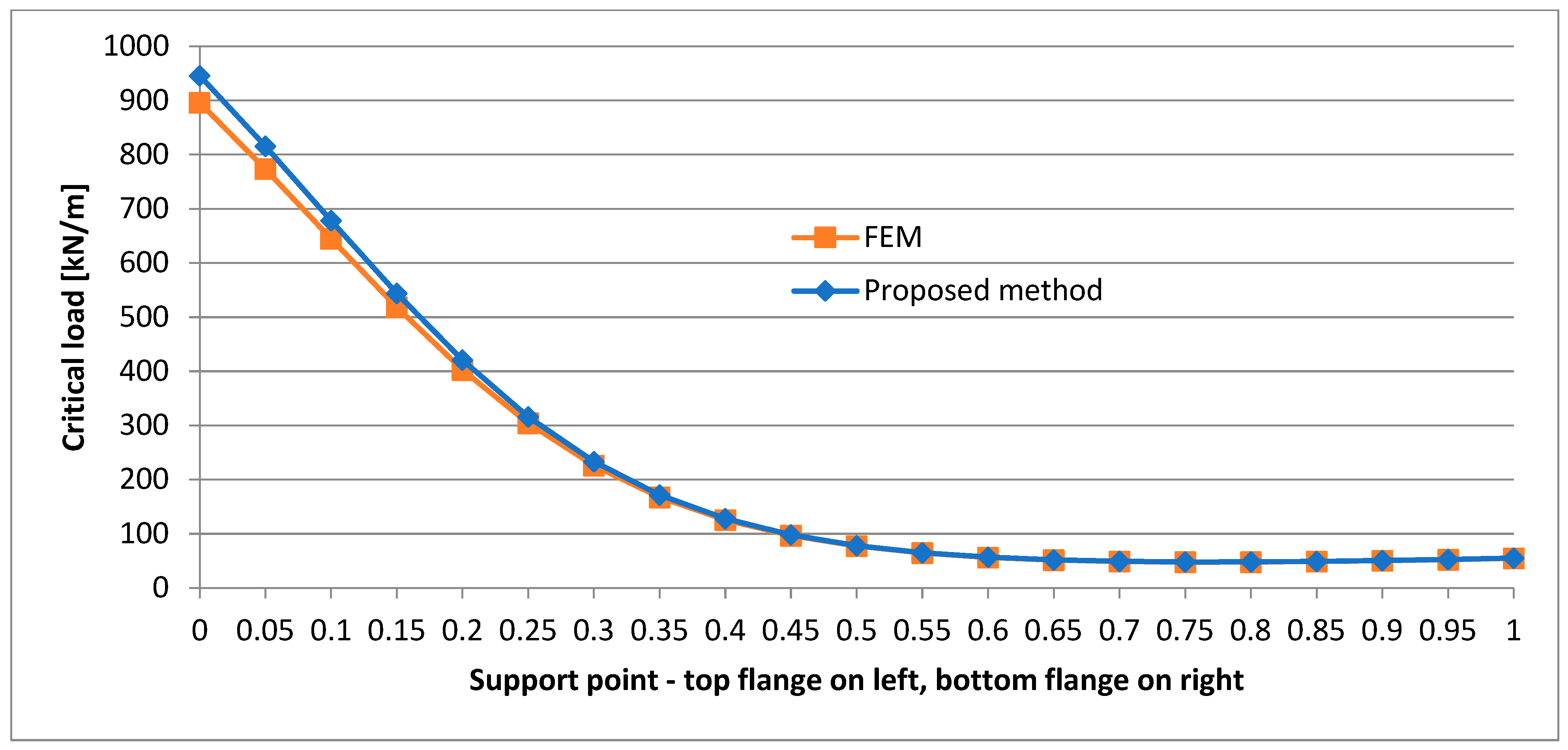
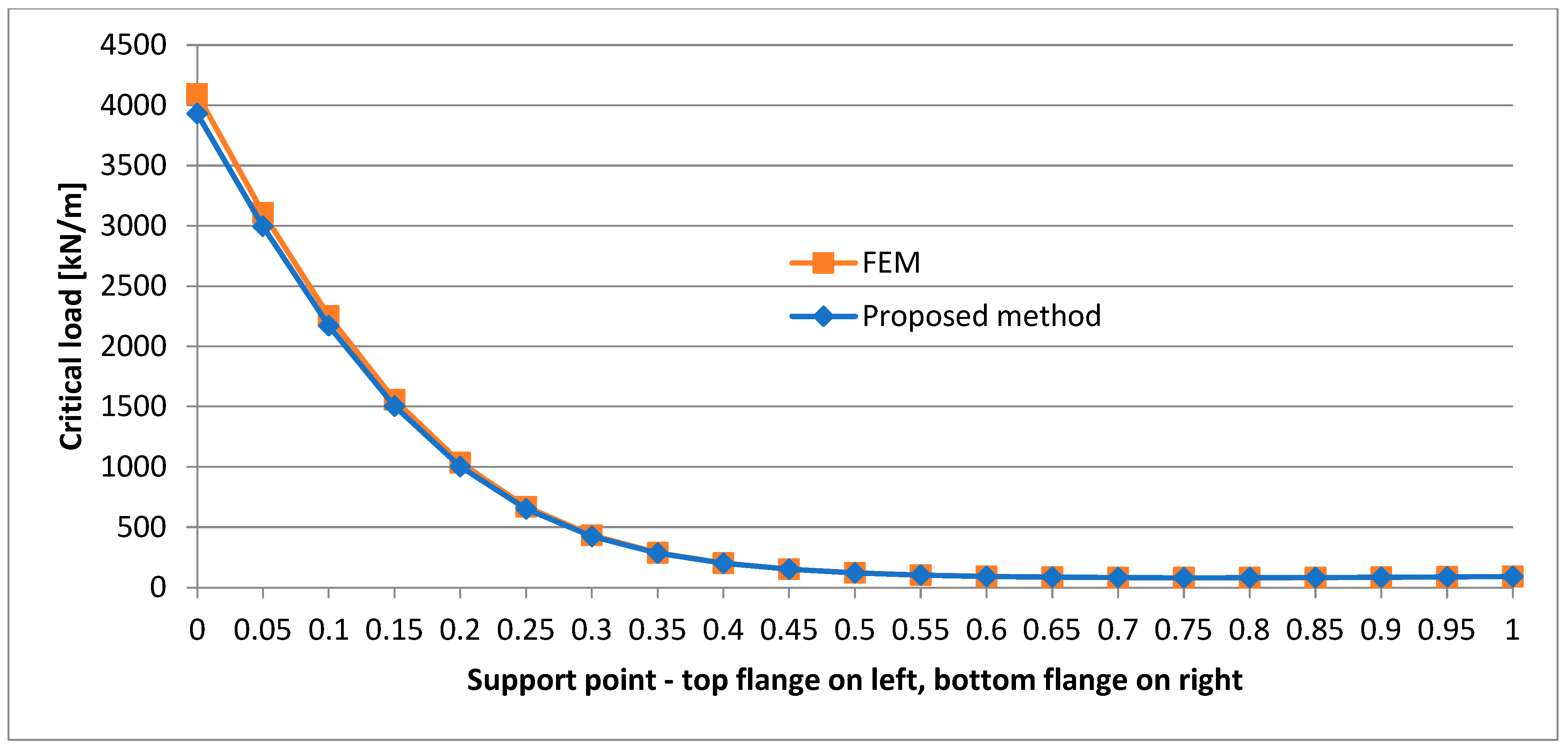
- In the case of the P-P beam, a change in the location of the support point along the height of the cross section leads to significant differences in the critical load. This occurs on each load application level. This phenomenon is strongly nonlinear (as the graphs show), and a significant increase in critical load is observed for support points located above the centre of the web. In such a beam, a considerable axial tension force is generated. The force acts eccentrically, stabilizing the beam and preventing its warping. In the case of a structure capable of transmitting such a considerable horizontal support reaction, this can significantly increase the load bearing capacity of the beam with no need to change its cross section. In some cases, this can be a solution for increasing the critical load capacity of existing buildings through a slight intervention in their structure.
- One can notice that in the case of the I-beam with a smaller top flange, FEM yields a slightly lower critical load value than the method presented in this paper, whereas in the case of the cross section with a smaller bottom flange it is the other way round.
- The support of the P-P beam on the top flange level results in a strongly nonlinear character of the change in critical load when the load shifts along the whole depth of the beam.
- In the case of the P-P beam, the lowest critical load value is obtained when the beam is supported at one fourth of the web’s depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, N.D.; Nguyen, T.K.; Vo, T.P.; Nguyen, T.N.; Lee, S. Vibration and buckling behaviours of thin-walled composite and functionally graded sandwich I-beams. Compos. Part B Eng. 2019, 166, 414–427. [Google Scholar] [CrossRef]
- Andrade, A.; Camotim, D. Lateral-torsional buckling of singly symmetric tapered beams: Theory and applications. J. Eng. Mech. 2005, 131, 586–597. [Google Scholar] [CrossRef]
- Benyamina, A.B.; Meftah, S.A.; Mohri, F.; Daya, E.M. Analytical solutions attempt for lateral torsional buckling of doubly symmetric web-tapered I-beams. Eng. Struct. 2013, 56, 1207–1219. [Google Scholar] [CrossRef]
- Andrade, A.; Camotim, D.; Dinis, P.B. Lateral-torsional buckling of singly symmetric web-tapered thin-walled I-beams: 1D model vs. shell FEA. Comput. Struct. 2007, 85, 1343–1359. [Google Scholar] [CrossRef]
- Asgarian, B.; Soltani, M.; Mohri, F. Lateral-torsional buckling of tapered thin-walled beams with arbitrary cross-sections. Thin-Walled Struct. 2013, 62, 96–108. [Google Scholar] [CrossRef]
- Branford, M.A. Inelastic buckling of tapered monosymmetric I-beams. Eng. Struct. 1989, 11, 119–126. [Google Scholar] [CrossRef]
- Challamel, N.; Andrade, A.; Camotim, D. An analytical study on the lateral-torsional buckling of linearly tapered cantilever strip beams. Int. J. Struct. Stab. Dyn. 2007, 7, 441–456. [Google Scholar] [CrossRef]
- Gupta, P.; Wang, S.T.; Blandford, G.E. Lateral-torsional buckling of nonprismatic I-beams. J. Struct. Eng. 1996, 122, 748–755. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Trahair, N.S. Elastic stability of tapered I-beams. J. Struct. Div. 1972, 98, 713–728. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Trahair, N.S. Elastic behavior of tapered monosymmetric I-beams. J. Struct. Div. 1975, 101, 1661–1678. [Google Scholar] [CrossRef]
- Kuś, J. Stability of Beams with Tapered Cross Sections. Doctoral Dissertation, Opole University of Technology, Opole, Poland, 2012. (In Polish). [Google Scholar]
- Kuś, J. Lateral-torsional buckling steel beams with simultaneously tapered flanges and web. Steel Compos. Struct. 2015, 19, 897–916. [Google Scholar] [CrossRef]
- Kuś, J. Critical moments in the lateral torsional buckling of steel I-beams with linearly variable web depth and flange width. Sci. Pap. Rzesz. Univ. Technol. Constr. Environ. Eng. 2012, 59, 217–224. (In Polish) [Google Scholar]
- Mohri, F.; Brouki, A.; Roth, J.C. Theoretical and numerical stability analyses of unrestrained, mono-symmetric thin-walled beams. J. Constr. Steel Res. 2003, 59, 63–90. [Google Scholar] [CrossRef]
- Osmani, A.; Meftah, S.A. Lateral buckling of tapered thin walled bi-symmetric beams under combined axial and bending loads with shear deformations allowed. Eng. Struct. 2018, 165, 76–87. [Google Scholar] [CrossRef]
- Polyzois, D.; Raftoyiannis, I.G. Lateral-torsional stability of steel web-tapered I-beams. J. Struct. Eng. 1998, 124, 1208–1216. [Google Scholar] [CrossRef]
- Raftoyiannis, I.G.; Adamakos, T. Critical Lateral-Torsional Buckling Moments of Steel Web-Tapered I-beams. Open Constr. Build. Technol. J. 2010, 4, 105–112. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R.; Alepaighamrod, A. Lateral-torsional buckling of functionally graded tapered I-beams considering lateral bracing. Steel Compos. Struct. 2018, 28, 403–414. [Google Scholar] [CrossRef]
- Soltani, M. A novel approach for lateral buckling assessment of double tapered thin-walled laminated composite I-beams. Mech. Adv. Compos. Struct. 2022, 9, 11–23. [Google Scholar] [CrossRef]
- Soltani, M.; Asgarian, B. Exact stiffness matrices for lateral–torsional buckling of doubly symmetric tapered beams with axially varying material properties. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 589–609. [Google Scholar] [CrossRef]
- Soltani, M.; Asgarian, B. Lateral-torsional stability analysis of a simply supported axially functionally graded beam with a tapered I-section. Mech. Compos. Mater. 2020, 56, 39–54. [Google Scholar] [CrossRef]
- Soltani, M.; Asgarian, B.; Mohri, F. Improved finite element model for lateral stability analysis of axially functionally graded nonprismatic I-beams. Int. J. Struct. Stab. Dyn. 2019, 19, 1950108. [Google Scholar] [CrossRef]
- Soltani, M.; Gharebaghi, S.A.; Mohri, F. Lateral stability analysis of steel tapered thin-walled beams under various boundary conditions. J. Numer. Methods Civ. Eng. 2018, 3, 13–25. [Google Scholar] [CrossRef]
- Zhang, L.; Tong, G.S. Lateral buckling of web-tapered I-beams: A new theory. J. Constr. Steel Res. 2008, 64, 1379–1393. [Google Scholar] [CrossRef]
- Giżejowski, M. The lateral torsional buckling of steel beams with limited ability to rotate on their supports. Eng. Constr. 2001, 10, 589–594. (In Polish) [Google Scholar]
- Kim, S.B.; Kim, M.Y. Improved formulation for spatial stability and free vibration of thin-walled tapered beams and space frame. Eng. Struct. 2000, 22, 446–458. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Thang, P.T.; Lee, J. Flexural-torsional stability of thin-walled functionally graded open-section beams. Thin-Walled Struct. 2017, 110, 88–96. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Thang, P.T.; Lee, J. Lateral buckling analysis of thin-walled functionally graded open-section beams. Compos. Struct. 2017, 160, 952–963. [Google Scholar] [CrossRef]
- Pasquino, M.; Marotti de Sciarra, F. Buckling of thin-walled beams with open and generically variable section. Comput. Struct. 1992, 44, 843–849. [Google Scholar] [CrossRef]
- Soltani, M.; Atoufi, F.; Mohri, F.; Dimitri, R. Nonlocal elasticity theory for lateral stability analysis of tapered thin-walled nanobeams with axially varying materials. Thin-Walled Struct. 2021, 159, 107268. [Google Scholar] [CrossRef]
- Soltani, M.; Atoufi, F.; Mohri, F.; Dimitri, R.; Tornabene, F. Nonlocal analysis of the flexural-torsional stability for FG tapered thin-walled beam-columns. Nanomaterials 2021, 11, 1936. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yau, J.D. Stability of beams with tapered I-sections. J. Eng. Mech. 1987, 113, 1337–1357. [Google Scholar] [CrossRef]
- Latalski, J.; Zulli, D. Generalized Beam Theory for Thin-Walled Beams with Curvilinear Open Cross-Sections. Appl. Sci. 2020, 10, 7802. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. A geometrically nonlinear shell theory for thin-walled tubes and beams subjected to large displacements and cross-section deformation. Thin-Walled Struct. 2025, 216, 113583. [Google Scholar] [CrossRef]
- Ruta, P. Application of Chebyshev series to solution of non-prismatic beam vibration problems. J. Sound Vib. 1999, 227, 449–467. [Google Scholar] [CrossRef]
- Ruta, P. Dynamic stability problem of non-prismatic rod. J. Sound Vib. 2002, 250, 445–464. [Google Scholar] [CrossRef]
- Ruta, P.; Szybiński, J. Lateral stability of bending non-prismatic thin-walled beams using orthogonal series. Procedia Eng. 2015, 111, 694–701. [Google Scholar] [CrossRef]
- Szybiński, J.; Ruta, P. An analysis of the effect of a change in the support point location on the vibration of thin-walled beams. Int. J. Struct. Stab. Dyn. 2021, 21, 2150125. [Google Scholar] [CrossRef]
- Szybiński, J.; Ruta, P. Analysis of thin-walled beams with variable monosymmetric cross section by means of Legendre polynomials. Stud. Geotech. Et Mech. 2019, 41, 1–12. [Google Scholar] [CrossRef]
- Szybiński, J.; Ruta, P. Effect of a “slight” curvature of the axis of a thin-walled nonprismatic beam on its free vibration. Int. J. Struct. Stab. Dyn. 2022, 22, 2250041. [Google Scholar] [CrossRef]
- Wilde, P. The torsion of thin-walled rods with variable cross-section. Arch. Mech. 1968, 4, 431–443. [Google Scholar]
- Lewanowicz, S. Construction of a recurrence relation of the lowest order for coefficients of the Gegenbauer series. Appl. Math. 1976, 15, 345–396. [Google Scholar] [CrossRef]
- Paszkowski, S. The Numerical Application of Chebyshev Polynomials and Series; Polish Scientific Publishers: Warsaw, Poland, 1975. (In Polish) [Google Scholar]
- Wolfram. Mathematica 12. Wolfram Research ©Copyright 1988–2019. Available online: https://www.wolfram.com/mathematica/ (accessed on 2 September 2025).






| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 196.97 | 163.33 | 135.41 | 196.74 | 163.17 | 135.30 |
| 0.8 | 178.44 | 148.11 | 122.91 | 177.92 | 147.70 | 122.59 |
| 0.6 | 159.81 | 132.79 | 110.31 | 158.26 | 131.49 | 109.22 |
| 0.4 | 140.98 | 117.31 | 97.59 | 137.34 | 114.19 | 94.91 |
| 0.2 | 121.75 | 101.56 | 84.69 | 114.32 | 95.05 | 79.00 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 1425.94 | 695.36 | 333.53 | 1412.50 | 691.15 | 332.77 |
| 0.8 | 1292.40 | 631.77 | 303.66 | 1277.97 | 626.72 | 302.36 |
| 0.6 | 1167.26 | 570.72 | 274.04 | 1146.45 | 561.85 | 270.66 |
| 0.4 | 1053.37 | 513.24 | 244.89 | 1019.22 | 496.30 | 237.06 |
| 0.2 | 958.45 | 462.12 | 216.92 | 901.96 | 430.24 | 200.24 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 110.33 | 63.88 | 21.14 | 110.37 | 63.79 | 21.14 |
| 0.8 | 111.92 | 66.26 | 22.43 | 104.34 | 62.45 | 23.09 |
| 0.6 | 113.51 | 69.58 | 25.27 | 97.94 | 61.03 | 25.65 |
| 0.4 | 114.92 | 73.92 | 31.10 | 91.07 | 59.51 | 29.07 |
| 0.2 | 115.86 | 79.22 | 43.16 | 83.48 | 57.86 | 33.65 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | |
| 1.0 | 78.13 | 70.71 | 61.49 | 60.05 | 47.56 | 77.24 | 69.93 | 60.86 | 59.45 | 47.15 |
| 0.8 | 72.69 | 65.75 | 57.28 | 55.86 | 44.24 | 71.62 | 64.83 | 56.53 | 55.13 | 43.73 |
| 0.6 | 67.63 | 61.13 | 53.36 | 51.94 | 41.10 | 65.89 | 59.60 | 52.08 | 50.70 | 40.21 |
| 0.4 | 63.30 | 57.14 | 49.97 | 48.51 | 38.32 | 60.08 | 54.28 | 47.55 | 46.18 | 36.59 |
| 0.2 | 60.71 | 54.68 | 47.88 | 46.29 | 36.39 | 54.54 | 49.16 | 43.15 | 41.77 | 33.00 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—load application points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | |
| 1.0 | 427.09 | 316.43 | 200.47 | 185.97 | 97.94 | 412.29 | 304.93 | 193.97 | 180.15 | 96.00 |
| 0.8 | 392.49 | 291.84 | 187.01 | 172.72 | 91.13 | 378.22 | 280.62 | 180.47 | 166.89 | 89.12 |
| 0.6 | 362.33 | 270.92 | 175.96 | 161.60 | 85.11 | 347.20 | 258.71 | 168.39 | 154.87 | 82.59 |
| 0.4 | 339.54 | 256.18 | 169.26 | 154.29 | 80.56 | 321.53 | 241.10 | 159.16 | 145.27 | 76.85 |
| 0.2 | 334.59 | 256.61 | 174.04 | 156.94 | 79.89 | 309.88 | 235.11 | 158.21 | 142.72 | 73.52 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | Bottom Flange | Shear Centre | Centre of Gravity | Centre of the Web | Top Flange | |
| 1.0 | 74.56 | 63.89 | 40.08 | 35.67 | 12.21 | 74.46 | 62.99 | 38.33 | 34.01 | 11.86 |
| 0.8 | 80.05 | 69.69 | 46.62 | 41.35 | 14.10 | 71.31 | 60.95 | 40.12 | 35.86 | 13.39 |
| 0.6 | 85.95 | 76.01 | 54.74 | 48.89 | 17.25 | 68.04 | 58.85 | 41.91 | 37.86 | 15.56 |
| 0.4 | 92.02 | 82.53 | 64.11 | 58.20 | 22.91 | 64.60 | 56.68 | 43.57 | 39.95 | 18.79 |
| 0.2 | 97.71 | 88.62 | 73.58 | 68.62 | 34.28 | 60.96 | 54.41 | 44.96 | 42.02 | 23.77 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | |
| 1.0 | 120.99 | 104.51 | 102.93 | 93.96 | 87.93 | 121.42 | 104.99 | 103.42 | 94.46 | 88.43 |
| 0.8 | 108.57 | 94.15 | 92.67 | 84.89 | 79.56 | 108.83 | 94.48 | 93.01 | 85.25 | 79.93 |
| 0.6 | 95.93 | 83.58 | 82.23 | 75.64 | 71.00 | 95.71 | 83.49 | 82.15 | 75.62 | 71.02 |
| 0.4 | 82.87 | 72.67 | 71.45 | 66.07 | 62.17 | 81.76 | 71.79 | 70.60 | 65.35 | 61.52 |
| 0.2 | 68.76 | 60.95 | 59.92 | 55.85 | 52.74 | 66.22 | 58.76 | 57.77 | 53.90 | 50.94 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | |
| 1.0 | 1117.93 | 574.95 | 530.35 | 321.42 | 228.58 | 1127.56 | 588.78 | 543.95 | 331.62 | 235.65 |
| 0.8 | 1005.83 | 518.46 | 476.05 | 291.91 | 208.34 | 1013.21 | 531.26 | 488.65 | 301.45 | 214.95 |
| 0.6 | 883.68 | 455.74 | 416.22 | 258.49 | 185.49 | 885.09 | 467.21 | 427.62 | 267.37 | 191.58 |
| 0.4 | 736.76 | 382.76 | 347.55 | 219.55 | 159.10 | 730.89 | 392.39 | 357.34 | 227.34 | 164.22 |
| 0.2 | 524.28 | 287.12 | 260.23 | 170.51 | 126.58 | 520.49 | 294.89 | 267.97 | 176.11 | 129.70 |
| Taper Parameter | Proposed Method—Load Application Points [kN/m] | FEM—Load Application Points [kN/m] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | Bottom Flange | Centre of the Web | Centre of Gravity | Shear Centre | Top Flange | |
| 1.0 | 40.59 | 29.41 | 27.77 | 17.99 | 13.24 | 41.09 | 30.03 | 28.43 | 18.59 | 13.63 |
| 0.8 | 40.13 | 28.62 | 26.87 | 17.92 | 13.48 | 38.93 | 28.36 | 26.80 | 18.50 | 14.03 |
| 0.6 | 39.70 | 27.86 | 26.03 | 18.16 | 14.06 | 36.62 | 26.66 | 25.18 | 18.39 | 14.48 |
| 0.4 | 39.23 | 27.21 | 25.42 | 18.82 | 15.12 | 34.08 | 24.94 | 23.58 | 18.28 | 14.98 |
| 0.2 | 38.54 | 26.83 | 25.19 | 20.09 | 16.91 | 31.20 | 23.20 | 22.04 | 18.17 | 15.54 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 118.51 | 135.41 | 345.86 | 118.36 | 135.30 | 345.14 |
| 0.8 | 107.27 | 122.91 | 314.07 | 107.02 | 122.59 | 313.29 |
| 0.6 | 95.72 | 110.31 | 282.61 | 95.06 | 109.22 | 281.32 |
| 0.4 | 83.65 | 97.59 | 252.22 | 82.16 | 94.91 | 249.66 |
| 0.2 | 70.45 | 84.69 | 225.83 | 67.58 | 79.00 | 220.87 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 126.27 | 163.33 | 830.16 | 126.08 | 163.17 | 825.78 |
| 0.8 | 114.30 | 148.11 | 746.18 | 114.04 | 147.70 | 743.79 |
| 0.6 | 101.88 | 132.79 | 663.21 | 101.31 | 131.49 | 665.85 |
| 0.4 | 88.74 | 117.31 | 584.31 | 87.54 | 114.19 | 595.66 |
| 0.2 | 74.04 | 101.56 | 524.09 | 71.86 | 95.05 | 550.95 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 131.74 | 196.97 | 3606.90 | 131.52 | 196.74 | 3570.45 |
| 0.8 | 119.28 | 178.44 | 3145.39 | 119.01 | 177.92 | 3132.98 |
| 0.6 | 106.24 | 159.81 | 2683.88 | 105.75 | 158.26 | 2725.48 |
| 0.4 | 92.30 | 140.98 | 2266.53 | 91.35 | 137.34 | 2362.06 |
| 0.2 | 76.52 | 121.75 | 2002.13 | 74.84 | 114.32 | 2103.04 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 42.34 | 47.56 | 108.16 | 42.07 | 47.15 | 105.77 |
| 0.8 | 38.89 | 44.24 | 100.24 | 38.57 | 43.73 | 97.77 |
| 0.6 | 35.46 | 41.10 | 93.25 | 34.94 | 40.21 | 90.13 |
| 0.4 | 32.07 | 38.32 | 88.02 | 31.13 | 36.59 | 83.43 |
| 0.2 | 28.65 | 36.39 | 87.47 | 27.03 | 33.00 | 80.14 |
| Taper Parameter | Proposed method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 48.72 | 60.05 | 239.35 | 48.43 | 59.45 | 229.30 |
| 0.8 | 44.59 | 55.86 | 219.95 | 44.26 | 55.13 | 210.38 |
| 0.6 | 40.46 | 51.94 | 203.09 | 39.93 | 50.70 | 193.29 |
| 0.4 | 36.28 | 48.51 | 191.16 | 35.38 | 46.18 | 180.11 |
| 0.2 | 31.88 | 46.29 | 193.15 | 30.41 | 41.77 | 180.32 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 54.88 | 78.13 | 945.97 | 54.58 | 77.24 | 895.97 |
| 0.8 | 50.07 | 72.69 | 836.86 | 49.74 | 71.62 | 795.13 |
| 0.6 | 45.19 | 67.63 | 731.08 | 44.71 | 65.89 | 700.63 |
| 0.4 | 40.18 | 63.30 | 644.98 | 39.38 | 60.08 | 618.28 |
| 0.2 | 34.73 | 60.71 | 625.77 | 33.50 | 54.54 | 572.97 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 86.07 | 87.93 | 235.08 | 86.10 | 88.43 | 241.56 |
| 0.8 | 77.96 | 79.56 | 214.26 | 77.91 | 79.93 | 220.81 |
| 0.6 | 69.54 | 71.00 | 192.15 | 69.21 | 71.02 | 199.94 |
| 0.4 | 60.62 | 62.17 | 168.79 | 59.74 | 61.52 | 179.13 |
| 0.2 | 50.47 | 52.74 | 144.75 | 48.84 | 50.94 | 159.73 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 89.15 | 104.51 | 683.10 | 89.07 | 104.99 | 716.89 |
| 0.8 | 80.75 | 94.15 | 612.36 | 80.62 | 94.48 | 647.01 |
| 0.6 | 71.92 | 83.58 | 536.81 | 71.59 | 83.49 | 580.59 |
| 0.4 | 62.38 | 72.67 | 457.70 | 61.69 | 71.79 | 520.34 |
| 0.2 | 51.29 | 60.95 | 379.54 | 50.13 | 58.76 | 479.26 |
| Taper Parameter | Proposed Method Support Point–Critical Load [kN/m] | FEM Support Point–Critical Load [kN/m] | ||||
|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | |
| 1.0 | 90.59 | 120.99 | 3930.28 | 90.46 | 121.42 | 4093.74 |
| 0.8 | 82.08 | 108.57 | 3401.09 | 81.93 | 108.83 | 3572.79 |
| 0.6 | 73.05 | 95.93 | 2840.96 | 72.76 | 95.71 | 3103.10 |
| 0.4 | 63.21 | 82.87 | 2298.52 | 62.65 | 81.76 | 2677.16 |
| 0.2 | 51.67 | 68.76 | 1848.46 | 50.77 | 66.22 | 2329.79 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 76.05 | 90.08 | 230.23 | 25 | 67.61 | 79.10 | 221.45 | ||||||||
| 15 | 70.45 | 84.69 | 225.83 | 50 | 67.58 | 79.00 | 220.87 | ||||||||
| 20 | 70.48 | 84.72 | 225.73 | 75 | 67.57 | 78.98 | 220.76 | ||||||||
| Err10 [%] | Err15 [%] | 7.90 | 0.04 | 6.33 | 0.04 | 1.99 | 0.04 | Err25 [%] | Err50 [%] | 0.06 | 0.01 | 0.15 | 0.03 | 0.31 | 0.05 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 80.36 | 109.11 | 536.67 | 25 | 71.87 | 95.15 | 552.44 | ||||||||
| 15 | 74.04 | 101.56 | 524.09 | 50 | 71.86 | 95.05 | 550.95 | ||||||||
| 20 | 74.08 | 101.61 | 523.37 | 75 | 71.86 | 95.03 | 550.67 | ||||||||
| Err10 [%] | Err15 [%] | 8.48 | 0.05 | 7.38 | 0.05 | 2.54 | 0.14 | Err25 [%] | Err50 [%] | 0.01 | 0.00 | 0.13 | 0.02 | 0.32 | 0.05 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 83.25 | 131.99 | 1986.53 | 25 | 74.84 | 114.41 | 2104.55 | ||||||||
| 15 | 76.52 | 121.75 | 2002.13 | 50 | 74.84 | 114.32 | 2103.04 | ||||||||
| 20 | 76.56 | 121.83 | 1973.75 | 75 | 74.84 | 114.30 | 2102.76 | ||||||||
| Err10 [%] | Err15 [%] | 8.74 | 0.05 | 8.34 | 0.07 | 0.65 | 1.44 | Err25 [%] | Err50 [%] | 0.00 | 0.00 | 0.10 | 0.02 | 0.09 | 0.01 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 30.78 | 38.38 | 88.21 | 25 | 27.05 | 33.04 | 80.35 | ||||||||
| 15 | 28.65 | 36.39 | 87.47 | 50 | 27.03 | 33.00 | 80.14 | ||||||||
| 20 | 28.67 | 36.41 | 87.47 | 75 | 27.03 | 32.99 | 80.10 | ||||||||
| Err10 [%] | Err15 [%] | 7.36 | 0.07 | 5.41 | 0.05 | 0.85 | 0.00 | Err25 [%] | Err50 [%] | 0.07 | 0.00 | 0.15 | 0.03 | 0.31 | 0.05 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 34.55 | 49.26 | 193.94 | 25 | 30.43 | 41.81 | 180.89 | ||||||||
| 15 | 31.88 | 46.29 | 193.15 | 50 | 30.41 | 41.77 | 180.32 | ||||||||
| 20 | 31.90 | 46.32 | 193.05 | 75 | 30.41 | 41.76 | 180.21 | ||||||||
| Err10 [%] | Err15 [%] | 8.31 | 0.06 | 6.35 | 0.06 | 0.46 | 0.05 | Err25 [%] | Err50 [%] | 0.07 | 0.00 | 0.12 | 0.02 | 0.38 | 0.06 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 37.87 | 65.16 | 618.94 | 25 | 33.51 | 54.59 | 574.60 | ||||||||
| 15 | 34.73 | 60.71 | 625.77 | 50 | 33.50 | 54.54 | 572.97 | ||||||||
| 20 | 34.76 | 60.77 | 614.44 | 75 | 33.50 | 54.54 | 572.67 | ||||||||
| Err10 [%] | Err15 [%] | 8.95 | 0.09 | 7.22 | 0.10 | 0.73 | 1.84 | Err25 [%] | Err50 [%] | 0.03 | 0.00 | 0.09 | 0.00 | 0.34 | 0.05 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 54.80 | 56.77 | 149.42 | 25 | 48.85 | 50.99 | 160.10 | ||||||||
| 15 | 50.47 | 52.74 | 144.75 | 50 | 48.84 | 50.94 | 159.73 | ||||||||
| 20 | 50.49 | 52.76 | 144.48 | 75 | 48.84 | 50.93 | 159.66 | ||||||||
| Err10 [%] | Err15 [%] | 8.54 | 0.04 | 7.60 | 0.04 | 3.42 | 0.19 | Err25 [%] | Err50 [%] | 0.02 | 0.00 | 0.12 | 0.02 | 0.28 | 0.04 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 55.87 | 66.25 | 389.86 | 25 | 50.12 | 58.79 | 480.21 | ||||||||
| 15 | 51.29 | 60.95 | 379.54 | 50 | 50.13 | 58.76 | 479.26 | ||||||||
| 20 | 51.31 | 60.97 | 377.30 | 75 | 50.13 | 58.75 | 479.07 | ||||||||
| Err10 [%] | Err15 [%] | 8.89 | 0.04 | 8.66 | 0.03 | 3.33 | 0.59 | Err25 [%] | Err50 [%] | 0.02 | 0.00 | 0.07 | 0.02 | 0.24 | 0.04 |
| Size of the Approximation Base | Proposed Method Support Point–Critical Load [kN/m] | Size of the Approximation Base | FEM Support Point–Critical Load [kN/m] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottom Flange | Centre of the Web | Top Flange | Bottom Flange | Centre of the Web | Top Flange | ||||||||||
| 10 | 56.33 | 75.21 | 1805.57 | 25 | 50,76 | 66,25 | 2326,48 | ||||||||
| 15 | 51.67 | 68.76 | 1848.46 | 50 | 50,77 | 66,22 | 2329,79 | ||||||||
| 20 | 51.69 | 68.79 | 1816.03 | 75 | 50,77 | 66,22 | 2330,42 | ||||||||
| Err10 [%] | Err15 [%] | 8.98 | 0.04 | 9.33 | 0.04 | 0.58 | 1.79 | Err25 [%] | Err50 [%] | 0.02 | 0.00 | 0.05 | 0.00 | 0.17 | 0.03 |
| Cross Section | Bisymmetric | “⏊” | “⏉” | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diagram | P-P | C-C | C-F | P-P | C-C | C-F | P-P | C-C | C-F | |||||||||
| μ [kN] | 0.831 | 0.691 | 0.487 | 0.232 | 0.622 | 0.252 | 0.767 | 0.606 | 0.449 | 0.234 | 0.580 | 0.228 | 0.873 | 0.743 | 0.523 | 0.216 | 0.706 | 0.368 |
| σ [kN] | 0.002 | 0.003 | 0.002 | 0.003 | 0.038 | 0.066 | 0.002 | 0.003 | 0.012 | 0.003 | 0.080 | 0.068 | 0.008 | 0.014 | 0.013 | 0.013 | 0.012 | 0.041 |
| σ [%] | 0.2 | 0.4 | 0.5 | 1.4 | 6.1 | 26.4 | 0.3 | 0.6 | 2.6 | 1.5 | 13.8 | 29.8 | 0.9 | 1.9 | 2.4 | 6.2 | 1.6 | 11.1 |
| Cross Section | Bisymmetric | “⏊” | “⏉” | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load | G–Top Flange | S–Web Centre | D–Bottom Flange | G–Top Flange | S–Web Centre | D–Bottom Flange | G–Top Flange | S–Web Centre | D–Bottom Flange | |||||||||
| μ [kN] | 1.162 | 3.004 | 1.317 | 6.655 | 1.523 | 25.946 | 1.177 | 2.712 | 1.312 | 5.239 | 1.539 | 16.840 | 1.027 | 2.779 | 1.171 | 7.489 | 1.323 | 39.170 |
| σ [kN] | 0.020 | 0.097 | 0.026 | 0.195 | 0.033 | 0.883 | 0.048 | 0.167 | 0.072 | 0.392 | 0.106 | 0.661 | 0.008 | 0.044 | 0.009 | 0.108 | 0.009 | 2.658 |
| σ [%] | 1.7 | 3.2 | 2.0 | 2.9 | 2.2 | 3.4 | 4.1 | 6.2 | 5.5 | 7.5 | 6.9 | 3.9 | 0.8 | 1.6 | 0.7 | 1.4 | 0.7 | 6.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szybiński, J.; Ruta, P. The Effects of Changing the Support Point in a Given Cross Section on Structural Stability. Appl. Sci. 2025, 15, 10774. https://doi.org/10.3390/app151910774
Szybiński J, Ruta P. The Effects of Changing the Support Point in a Given Cross Section on Structural Stability. Applied Sciences. 2025; 15(19):10774. https://doi.org/10.3390/app151910774
Chicago/Turabian StyleSzybiński, Józef, and Piotr Ruta. 2025. "The Effects of Changing the Support Point in a Given Cross Section on Structural Stability" Applied Sciences 15, no. 19: 10774. https://doi.org/10.3390/app151910774
APA StyleSzybiński, J., & Ruta, P. (2025). The Effects of Changing the Support Point in a Given Cross Section on Structural Stability. Applied Sciences, 15(19), 10774. https://doi.org/10.3390/app151910774






