Study of Interface Adhesion Between Polyurethane and Aggregate Based on Surface Free Energy Theory and Molecular Dynamics Simulation

Abstract

In order to eliminate the negative effects caused by traditional pavements, permeable pavements are gradually being used in road construction. In recent years, polyurethane (PU) has been used as a new binder in permeable pavement mixtures. However, compared to traditional pavement mixtures, the adhesion properties between PU and aggregate have not been systematically analyzed. In addition, no clear standards have been established for the performance testing of PU mixtures, posing significant challenges for the selection of materials and the optimization of formulations for PU mixtures. Therefore, this paper proposes new methods for evaluating the performance of PU mixtures from a microscopic point of view, aiming at evaluating the adhesion properties between PU and aggregates. In this study, a PU binder was synthesized. The adhesion properties of this PU binder with aggregate were evaluated by surface free energy measurement and molecular dynamics (MD) simulation. Finally, the effects of different environmental conditions and aggregate types on the PU–aggregate adhesion properties were investigated. The results showed that the adhesion between PU and basalt is consistently better than that with limestone, although the adhesion between PU and aggregate decreased under acidic conditions. It implies that the PU–basalt mixture has better water resistance than the PU–limestone mixture. Furthermore, the results of the surface free energy measurements and MD simulations for the evaluation of adhesion at the PU–aggregate interface showed good correlation with the macroscopic performance experiments, which can be extended to the study of the adhesion properties of other materials.

1. Introduction

As urbanization continues, the urban surface is gradually covered by closed, hardened pavements such as asphalt and cement concrete. The increased coverage of the road network has greatly improved traffic conditions, but the negative impacts have been increasing as the proportion of closed hardened pavements has gradually increased, such as the urban heat island effect (UHI) [1]. Permeable pavement is considered to be one of the effective measures to improve this series of problems. On the one hand, permeable pavement can effectively improve urban drainage capacity, alleviate urban flooding pressure, and regulate the urban hydrological cycle. On the other hand, permeable pavement can realize physical filtration and pollutant removal, maintain the moisture of the pavement structure, reduce the temperature of the pavement, alleviate the heat island effect, and maintain the urban ecological balance [2,3,4].

According to the different pavement materials, the common permeable pavement can be divided into asphalt permeable pavement, cement permeable pavement, resin permeable pavement, and so on [5,6,7,8]. However, the characteristics of traditional asphalt-based permeable pavements and cement-based permeable pavements lie in the low structural strength of their pavements, and their large pore structure will be clogged after a certain number of years, leading to a shorter service life [9,10,11,12]. More importantly, when asphalt is used as a binder, the water stability of asphalt mixtures that are insufficient will make asphalt pavements undergo a series of water damages, such as loosening, spalling, and so on. This is due to the fact that water is more likely to infiltrate the aggregate surface than asphalt, reducing the adhesion properties between asphalt and aggregate, which leads to the constant spalling of asphalt from the aggregate surface. Compared with traditional permeable materials, resin-based materials have the advantages of faster strength formation, excellent water permeability, and better adhesion properties. Therefore, resin-based materials are gradually being used as binders in permeable mixtures, such as epoxy resin (EP), polyurethane (PU), unsaturated polyester (UP), etc. [13,14,15,16]. PU refers to polymers with urethane-containing groups, which are generally made from isocyanates and polyols through polycondensation reactions. In recent years, PU-based materials have been gradually used in the field of road engineering due to their good bond strength, heat resistance, and corrosion resistance [17,18,19]. At present, PU has been widely used in the modification of traditional binders, such as PU-modified asphalt mixtures, which have more excellent high- and low-temperature performance and aging resistance than traditional asphalt mixtures [20,21,22,23,24]. In the latest research, PU can also be used as a new binder, completely replacing the original asphalt, and directly prepared into PU mixtures. Compared with asphalt mixtures, PU mixtures can be mixed at room temperature, which has the advantages of low energy consumption and reduced environmental pollution [25,26,27].

In fact, the strength of the interfacial phase formed between the binder and the aggregate is the key factor affecting the water stability of the mixture. The methods for evaluating the adhesion properties of the binder–aggregate interface mainly include the water boiling method, the water immersion method, the pull-out test, etc. However, such methods are more based on experience for the qualitative evaluation of the adhesion properties and are not capable of evaluating them quantitatively [28]. Therefore, the surface free energy theory began to be used to quantitatively evaluate the adhesion between asphalt and aggregates in the 1990s [29]. The surface free energy theory is an important concept for describing the interaction forces between atoms/molecules on liquid or solid surfaces. From the intermolecular force point of view, molecules in the surface layer of a material are subjected to a higher molecular attractive force, and this molecular attractive force is the surface tension. The higher the surface tension, the higher the intermolecular interaction force. From the energy point of view, the molecules in the surface layer of a material have additional potential energy due to surface tension, and this potential energy is the surface free energy. As an important characteristic of the material itself, it has a significant impact on the interfacial properties and interfacial reactions of the material, such as surface adsorption, wetting, and bonding phenomena, all of which are governed by the surface free energy to a certain extent. Moraes et al. [30] calculated the adhesion work and spalling work between asphalt and aggregate using the contact angle test based on surface free energy theory and compared the results with the bond strength test results, which showed that the results of the adhesion work and spalling work calculations basically verified the results of the asphalt bond strength (ABS) test. Tan et al. [31] found that based asphalt has higher surface free energy compared with modified asphalt through contact angle experiments. In addition to based asphalt and modified asphalt, the surface free energy theory has also been used to evaluate the adhesion properties of reclaimed asphalt. Guo et al. [32] established an adhesion model for warm mix recycled asphalt and aggregate under water and no-water conditions based on the surface free energy theory and evaluated the water stability of warm mix recycled asphalt by calculating the adhesion work under both models. This shows that the surface free energy theory has been widely used to evaluate the adhesion properties between asphalt and aggregates. Although the surface free energy theory has rarely been used to evaluate the adhesion properties of polymer mixtures, many of the above studies on the adhesion properties of asphalt mixtures can be extended to polymer mixtures as well.

Molecular dynamics (MD) is a computational simulation method used to model and study the motion and interactions of atoms or molecules in a given physical environment. By establishing molecular models and microstructures through MD, it is possible to obtain information on various parameters of materials and predict the macroscopic properties of materials from the perspective of micro-mechanisms. In the field of road engineering, MD has been widely used to analyze the rheological properties, aging and reclaimed properties, compatibility, and self-healing properties of road materials [33,34,35,36,37]. In recent years, MD has been gradually used to study the interfacial adhesion properties between road materials, and by studying the interfacial interactions between materials on the nanoscale, the chemical composition of materials can be optimized, and their adhesion properties can be improved. Wu et al. [38] calculated the surface free energy as well as the adhesion work of aggregates with asphalt using MD simulation and compared it with the results of the pull-out test and found that the MD results were in agreement with the pull-out test results. Huang et al. [39] used MD to establish the molecular model of road epoxy resin sealant and studied its adhesion with pavement cracks. The results showed that epoxy resin sealant has better adhesion properties than based asphalt and SBS-modified asphalt. Wu et al. [40] used MD to analyze the adhesion of cold reclaimed emulsified asphalt with aggregate and found that, with the increase in emulsifier, the adhesion of asphalt with aggregates was improved.

Therefore, in this study, a PU binder was prepared, and the adhesive properties between PU and aggregate were investigated using surface free energy theory and molecular dynamics simulation. This multi-scale study connects the macroscopic experimental results of the PU–aggregate interface with the mechanisms of nanoscale interactions, providing a convincing basis for the application of PU mixtures in permeable pavements. In addition, the effects of different environmental conditions and aggregate types on the adhesive properties between PU and aggregates were analyzed. A clear understanding of these influencing factors contributes to the further optimization of PU mixture formulations and serves as a reference for novel permeable pavement materials. The flow chart of this study is shown in Figure 1.

2. Materials and Methods

2.1. Raw Materials

PU prepolymers are usually synthesized through the reaction between isocyanates and polyols. In this paper, diphenyl methane diisocyanate (MDI-50) was chosen for the isocyanate, polytetrahydrofuran diol (PTMEG2000) for the polyol, and demethyl thio-toluene diamine (DMTDA) for the chain extender. The properties of MDI, PTMEG, and DMTDA are shown in

Table 1. Properties of MDI, PTMEG, and DMTDA.

Materials	Molecular Formula	Molecular Weight	Appearance
MDI-50	C15H10N2O2	250.25	White or light-yellow liquid
PTMEG2000	HO[CH2CH2CH2CH2O]nH	2000	White waxy liquid
DMTDA	C9H14N2S2	214	Clear yellow to amber liquid

.

To investigate the effect of aggregate type on adhesion properties, two different aggregates were selected in this paper. The properties of basalt and limestone are shown in

Table 2. Properties of aggregates.

Item	Basalt	Limestone
Apparent density	2.826	2.724
Water absorption (%)	0.40	0.82
Crushed stone value (%)	11.3	15.6
Wear value (%)	15.9	18.7
Polished stone value	46	40

. In addition, two sizes were chosen for both limestone and basalt aggregates: 2.36–4.75 mm and 4.75–9.5 mm. The aggregate gradation is 80% for 2.36–4.75 mm and 20% for 4.75–9.5 mm.

Three reagents with known surface free energy parameters were used to test the contact angle of aggregates and PU. The surface free energy parameters of distilled water, ethylene glycol, and formamide are shown in

Table 3. Surface free energies of three test reagents.

Reagents	Surface Free Energy (mJ/m2)
	${\mathit{\gamma }}_{\mathit{L}}$	${\mathit{\gamma }}_{\mathit{L}}^{\mathit{d}}$	${\mathit{\gamma }}_{\mathit{L}}^{\mathit{p}}$
Distilled water	72.8	21.8	51.0
Ethylene glycol	48.3	29.3	19.0
Formamide	57.9	38.9	19.0

.

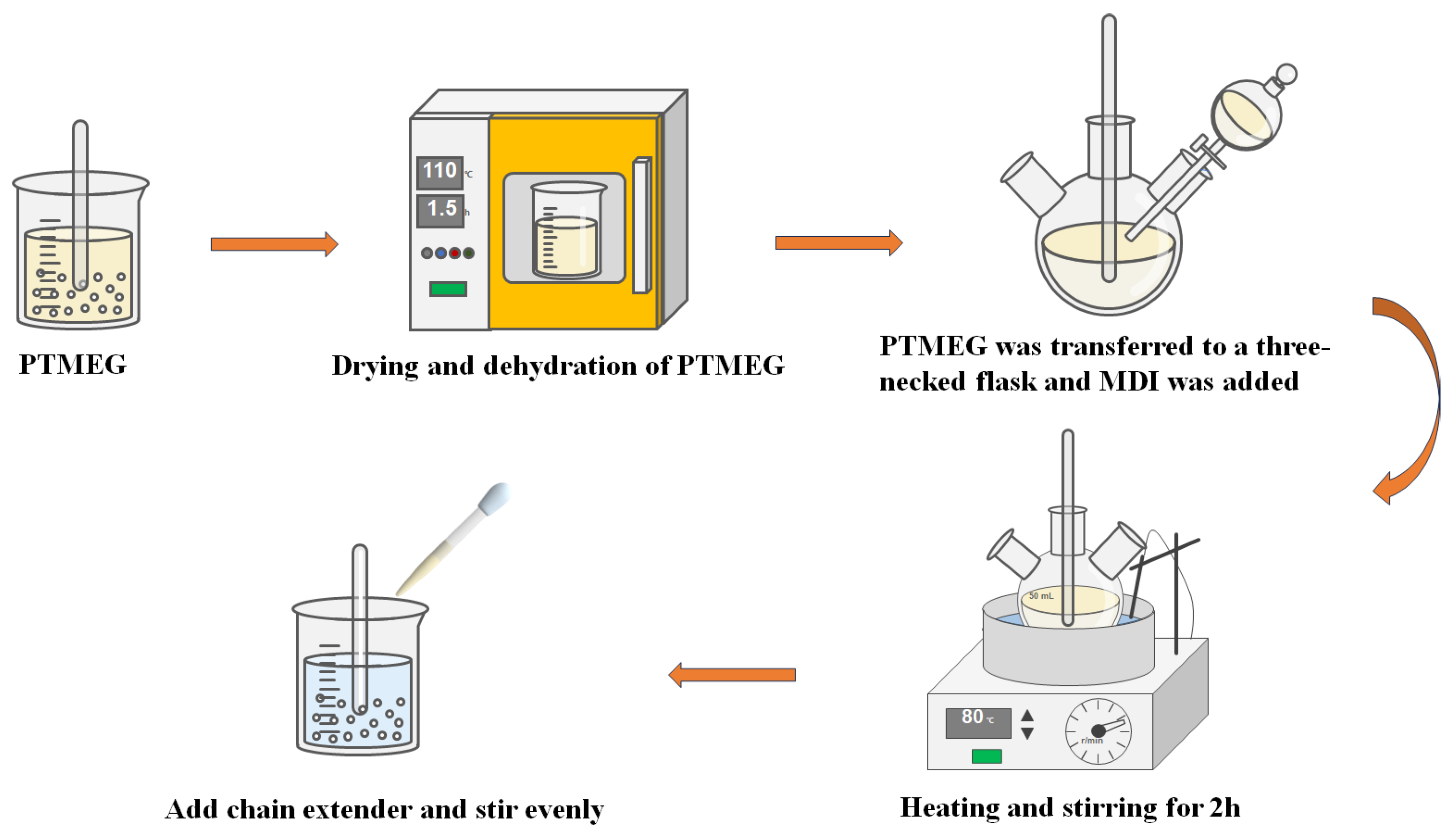
2.2. Synthesis of PU

In this paper, PU is synthesized using a two-step process. The isocyanate is first reacted with a polyol to produce a prepolymer containing isocyanate groups (-NCO) at both ends. Subsequently, a chain extender is added to produce PU. Since the reaction is carried out in two steps and the exotherm is low during the chain extension reaction, the reaction rate is easy to control. The synthesis process of PU is shown in Figure 2. The formula of the synthesized PU was referred to the previous results of this group. The properties of the PU are shown in

Table 4. Properties of PU.

Item	Value
Tensile strength (MPa)	13.6
Elongation at break (%)	672
Shore hardness (HA)	78
Gel time (min)	32.2
Glass transition temperature (°C)	−42.33

.

2.3. Contact Angle Test

Due to the high viscosity of PU, the commonly used method of measuring the surface free energy of liquids is not applicable to PU. Therefore, a solid surface free energy measurement method can be used to determine the surface free energy of PU. The principle of determining the surface free energy parameters of aggregates is the same as that of PU. The molecules inside the solid are more densely arranged and are essentially immobile. Therefore, it is not possible to directly test the surface free energy of solids. Generally, the contact angle method is chosen to measure the contact angle of the smooth plane formed by the liquid after curing and then calculate its surface free energy [41,42].

A clear glass sheet was wiped clean and dried completely, then immersed in PU and held stationary. After 1 min, the glass sheet was raised vertically and left standing upright for 10 min to ensure that the surface liquid did not continue to flow and behaved as a relatively smooth flat surface. In order to investigate the effect of acid rain erosive environments on the adhesion properties of the mixtures, PU was acidified with dilute sulfuric acid solution and recorded as HPU.

2.4. Calculation of Surface Free Energy

Young [43] gave an equation for the relationship between interfacial tension and the contact angle:

$${\gamma }_S={\gamma }_{L}cos\theta +{\gamma }_{SL}$$

(1)

where γ_L is the surface free energy of the liquid. γ_S is the solid surface free energy. γ_SL is the solid–liquid interfacial energy. θ is the solid–liquid contact angle.

Fowkes [44] considered the surface free energy to be the sum of many components, which can be divided into a polar component and a dispersion component:

$${\gamma }_L={\gamma }_L^d+{\gamma }_L^p$$

(2)

$${\gamma }_S={\gamma }_S^d+{\gamma }_S^p$$

(3)

where ${\gamma }_L^d$ is the liquid dispersion component. ${\gamma }_L^p$ is the liquid polar component. ${\gamma }_s^d$ is the solid dispersion component. ${\gamma }_s^p$ is the solid polar component.

The Owen–Wendt equation [45] gave an expression for the surface free energy calculated from the dispersion and polar components:

$${\gamma }_{SL}={\gamma }_S+{\gamma }_L-2\mathrm{}(\sqrt{{{\gamma }_S^d\gamma }_L^d}+\sqrt{{{\gamma }_S^P\gamma }_L^P})$$

(4)

Based on the Young, Fowkes, and Owen–Wendt equations, the relationship between surface free energy and the contact angle can be further derived as follows:

$${\displaystyle \frac{{\gamma }_L\mathrm{}(1+cos\theta )}{2}}{\displaystyle \frac{1}{\sqrt{{\gamma }_L^d}}}=\sqrt{{\gamma }_S^d}+{\displaystyle \frac{\sqrt{{\gamma }_L^p}}{\sqrt{{\gamma }_L^d}}}\sqrt{{\gamma }_S^p}$$

(5)

A linear fit is made to $\sqrt{{{\gamma }_L^d\gamma }_S^p}$ and ${\gamma }_L(1+cos\theta )/2\sqrt{{\gamma }_L^d}$. The goodness of fit determines how reliable the data are. The square of the middle slope of the resulting fitted line is the polar component ${\gamma }_s^p$ and the square of the intercept is the dispersion component ${\gamma }_s^d$.

2.5. Calculation of Adhesion Work and Spalling Work

The adhesion work is defined as the work carried out to separate two phases. The adhesion work reflects the adhesion between the PU and the aggregate; the larger the value, the better the adhesion properties. The principle of calculating the adhesion work is shown in Figure 3.

According to the Young, Fowkes, and Owen–Wendt theory, the adhesion work of PU to aggregate can be characterized in Equations (6) and (7):

$$W_{SL}={\gamma }_S+{\gamma }_L-{\gamma }_{SL}$$

(6)

$$W_{SL}=2 (\sqrt{{{\gamma }_S^d\gamma }_L^d}+\sqrt{{{\gamma }_S^P\gamma }_L^P})$$

(7)

where W_SL is the adhesion work between the solid and the liquid.

After the PU mixture is damaged by water, the PU film will gradually fall off, so that the wrapped aggregate leaks out nakedly, turning into two systems of PU–water and water–aggregate. At this time, the contact area between PU and aggregate decreases, while the contact area between PU and water and water and aggregate increases. The calculation principle of spalling work is shown in Figure 4.

The spalling work of PU with aggregate can be expressed in Equation (8):

$$W_{SPUW}=W_{SW}+W_{PUW}-W_{SPU}$$

(8)

where W_SPUW is the spalling work of PU–aggregate. W_SPU is the adhesion work of PU–aggregate. W_SW is the adhesion work of water–aggregate. W_PUW is the adhesion work of PU–water.

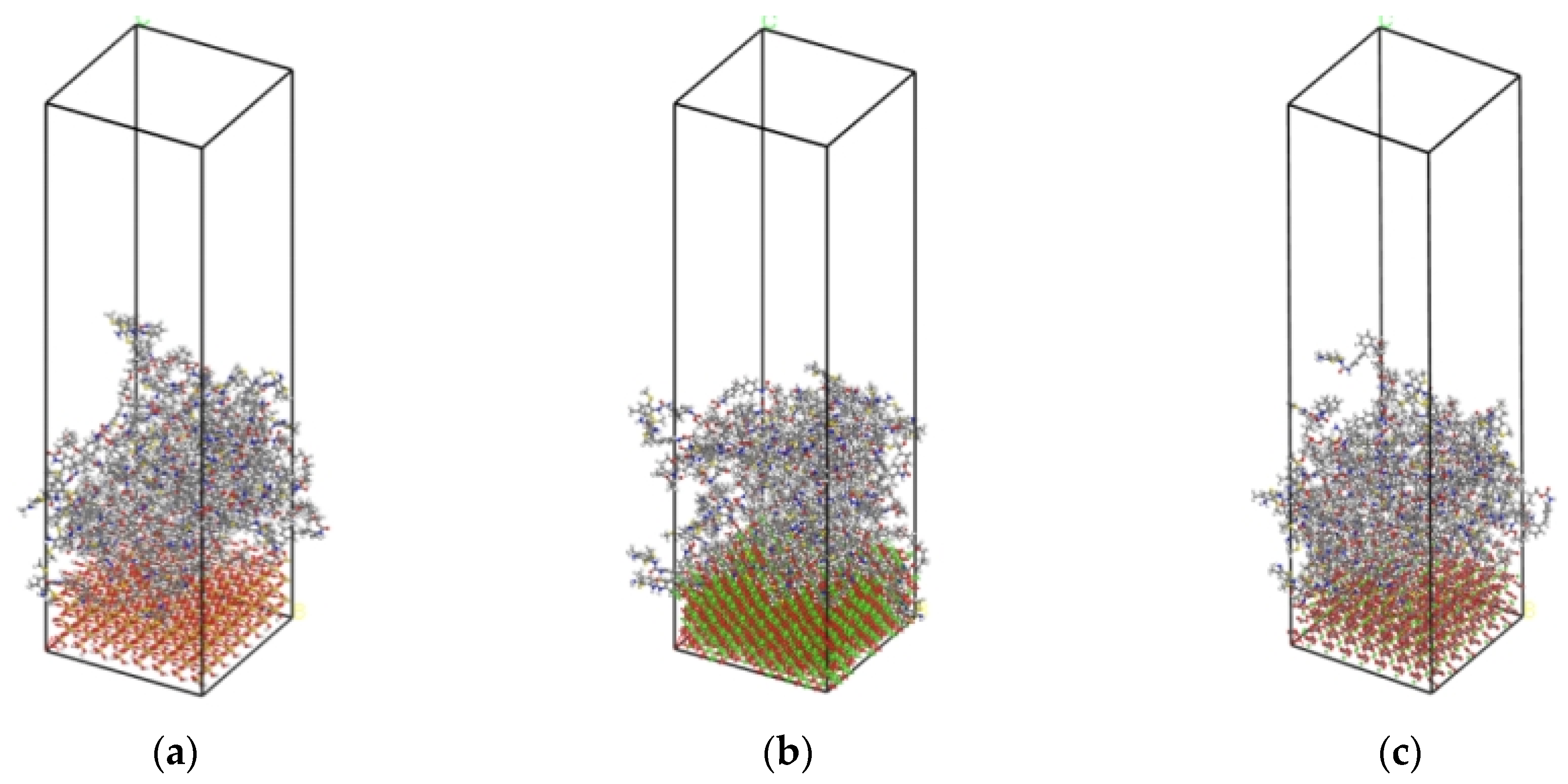
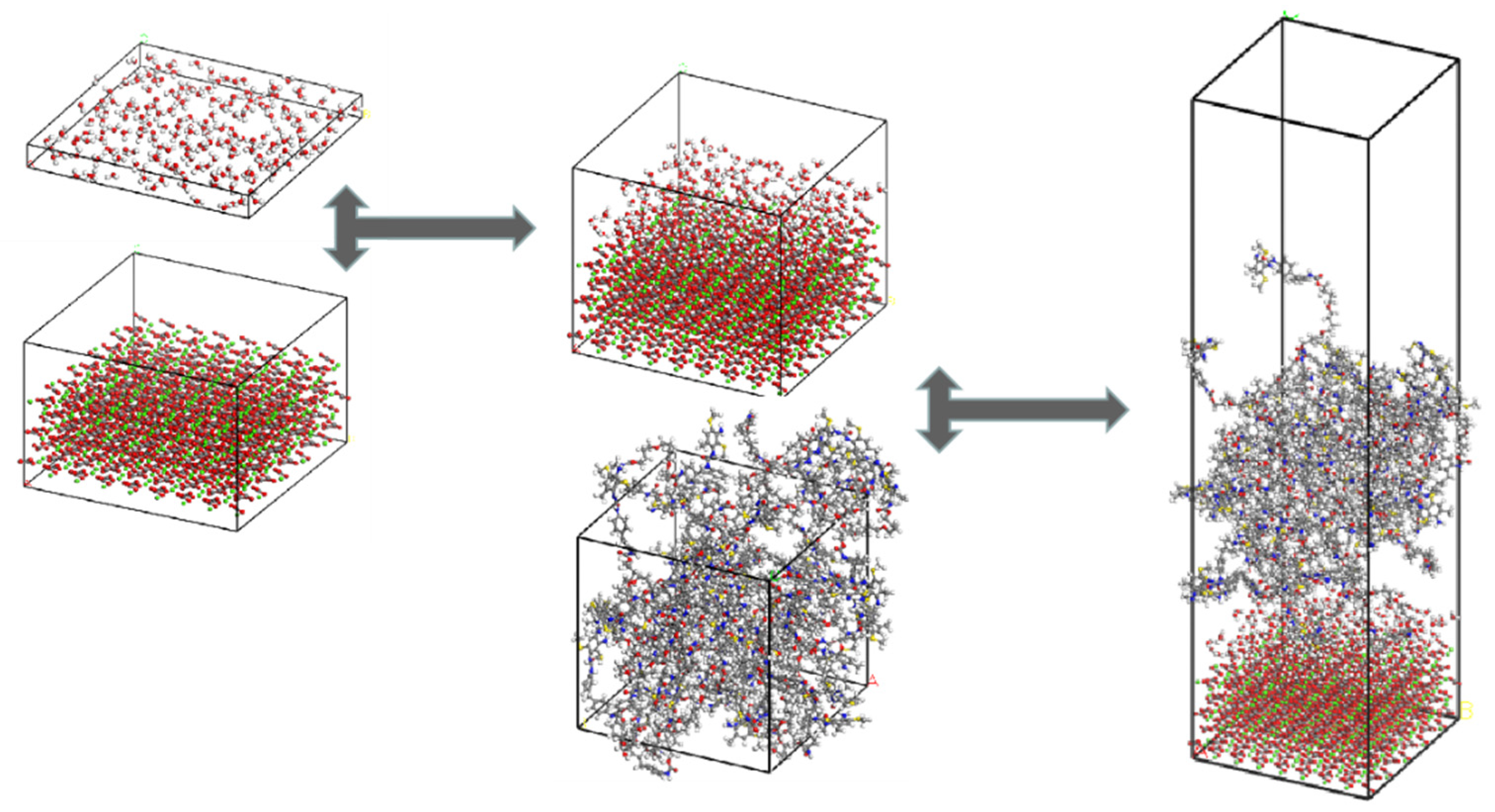
2.6. Construction and Validation of Molecular Models

2.6.1. Molecular Model of PU

The PU molecular model is composed of isocyanates, polyols, and chain extenders. The molecular models of isocyanates, polyols, and chain extenders were manually constructed based on their molecular formulas. The MDI contains two isomeric forms, 2,4′-MDI and 4,4′-MDI. The constructed models underwent geometric optimization to minimize energy. In this study, Ultra-fine was selected for accuracy and Compass II for the force field. The optimized molecular models are shown in Figure 5.

A model was constructed for a PU prepolymer with a degree of polymerization of 3, which consisted of three MDI monomers with two PTMEG2000 monomers. Subsequently, a model of the PU chain generated by the reaction between the chain extender and the prepolymer was constructed. The above molecular models were subjected to geometric optimization and annealing relaxation to make the system stable. The PU molecular box was constructed using the amorphous cell (AC) module. The density was set to 1.18 g/cm³ and the temperature to 298 K. The AC model dimensions were 38 Å × 38 Å × 38 Å. Each PU molecule was constructed with 10 frames, and the frame with the lowest energy was selected for geometric optimization and annealing relaxation. Finally, 100 ps NPT and NVT simulations were conducted to further stabilize the model system. The cell model of PU after optimization is shown in Figure 6.

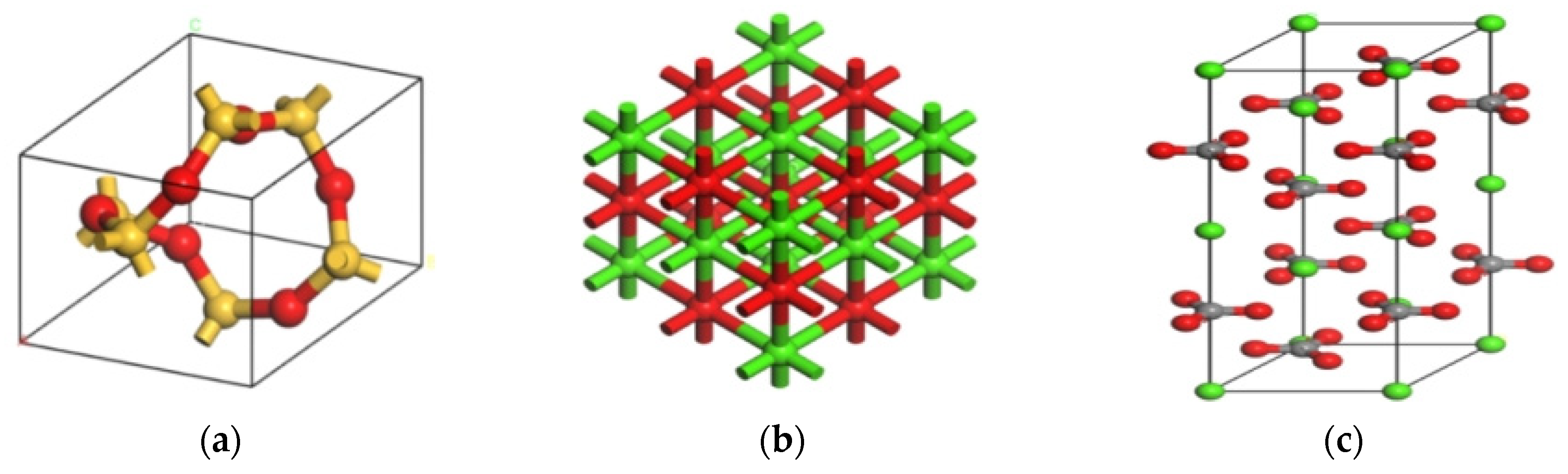
2.6.2. Molecular Model of Aggregate

Most of the aggregates used in roads are granite, basalt, and limestone. Many researchers studied the chemical and mineralogical composition of aggregates using X-ray and found that the main mineral components in aggregates are SiO₂, Al₂O₃, MgO, CaO, Fe₂O₃, etc. [46,47,48]. SiO₂ is the most abundant acid oxide in basalt. CaO is the most alkaline oxide of the common components of basalt. The main mineral component in limestone is CaCO₃. Therefore, SiO₂, CaO, and CaCO₃ were selected as the representative components of aggregates to analyze the interfacial adhesion properties of PU–aggregate. The crystal models of SiO₂, CaO, and CaCO₃ were imported using the Findit v.2017 software, as shown in Figure 7. The crystal parameters are shown in

Table 5. Crystal parameters of SiO₂, CaO, and CaCO₃.

Mineral Types	Lattice Parameters
	a (Å)	b (Å)	c (Å)	A (°)	β (°)	γ (°)
SiO2	4.913	4.913	5.405	90	90	120
CaO	4.810	4.810	4.810	90	90	90
CaCO3	4.990	4.990	17.061	90	90	120

.

Prior to aggregate modeling, the crystal model of the aggregate is usually cell-cut to obtain relatively stable surfaces [49]. Related studies have shown that the (0 0 1) surface usually serves as a stable surface for SiO₂ and CaO, while the (1 0 4) surface serves as a stable surface for CaCO₃. Therefore, the stabilized surfaces of the three mineral molecules were cell-cut. The cell-cut models were subsequently subjected to supercell treatment. The cell models of the three mineral molecules are shown in Figure 8.

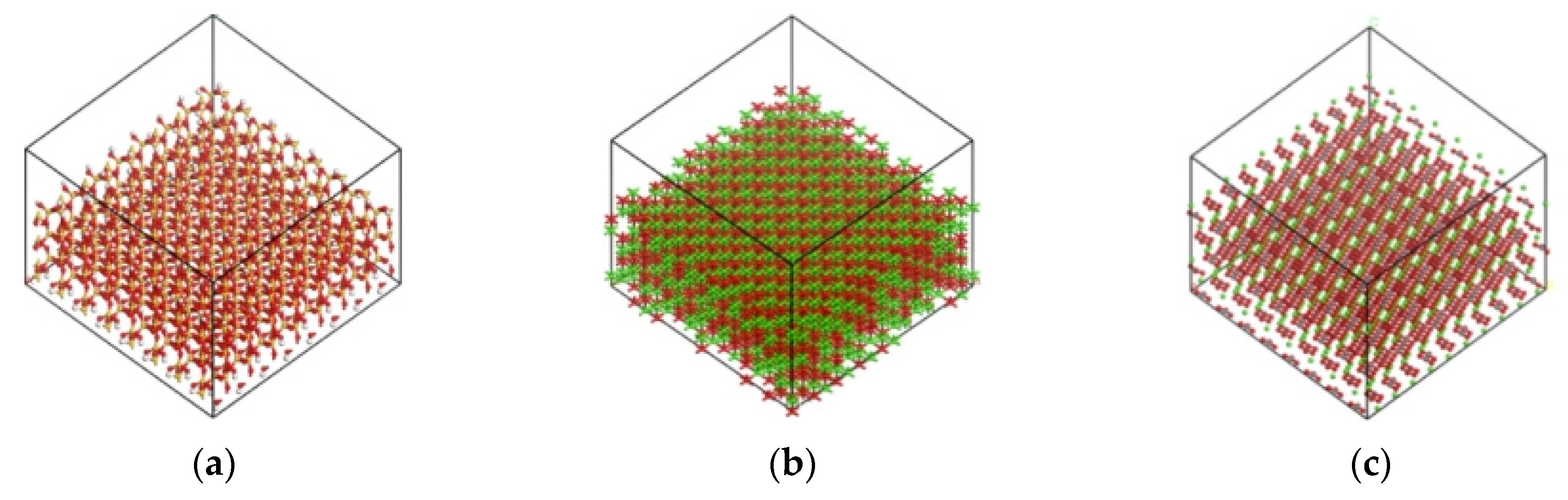
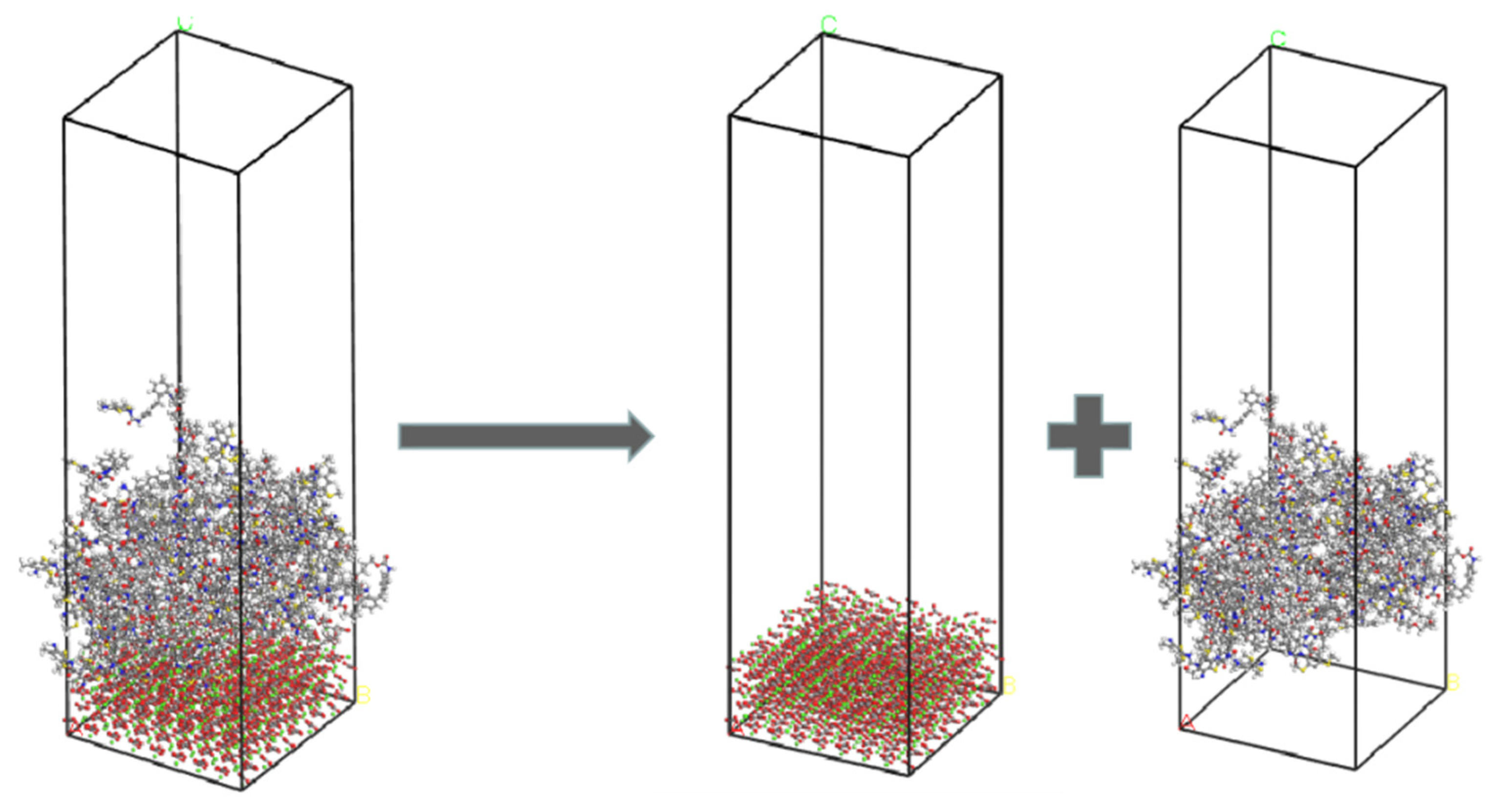
2.6.3. Interface Model of PU–Aggregate

Using the interface construction tool, the PU layer model was combined with the aggregate layer model. The first layer consisted of the mineral supercell layer, followed by the PU layer. To eliminate the influence of three-dimensional periodic boundary conditions, a 50 Å vacuum layer was added at the top of each PU–mineral interface model. The constructed interface models underwent geometric optimization and annealing relaxation, followed by a 200 ps relaxation in the NVT ensemble to obtain a stable interface model. The three interface models are shown in Figure 9.

In order to calculate the spalling work of PU with aggregate, an 8.02 OH/nm² water molecular layer was inserted between the aggregate and the PU. To evaluate the adhesion properties of PU–aggregate under acidic conditions, the H₂O molecular layer was replaced by the H₂SO₄ molecular layer. The interface model of PU–water–aggregate is shown in Figure 10.

2.6.4. Calculation of Interfacial Interaction Energy

The principle of calculation of the interfacial interaction energy is shown in Figure 11. The total potential energy of the system is calculated first, and then the potential energies of the different molecular layers are calculated. The interaction energy can be calculated using Equation (9):

$$E=E_{total}-E_A-E_B$$

(9)

where E is the interaction energy between the surfaces of the two substances. E_A is the potential energy of substance A. E_B is the potential energy of substance B. E_total is the total potential energy of the system.

2.7. Model Validation

In this paper, mean square displacement (MSD) and glass transition temperature (Tg) are used to verify the reasonableness of the molecular model of PU. MSD determines how the particles move over time and is usually used to judge the stability of the system. Tg is usually used to characterize the low-temperature properties of polymer materials. By comparing the molecular model of PU with the measured glass transition temperature of PU, the reasonableness of the model can also be verified.

2.7.1. MSD

A 200 ps simulation in the NPT ensemble was conducted to obtain the reasonable density at different temperatures. Subsequently, a 200 ps simulation in the NVT ensemble was performed on the interface system at this density, yielding the MSD of the PU system. The temperature range for the simulation was set from 200 K to 600 K, with an interval of 50 K. The results of the MSD calculations are shown in Figure 12. The slope of the MSD curve represents the motility of the molecules. The larger the slope, the stronger the motility of the chain segments [49]. At lower temperatures (200 K~400 K), the slope of the MSD curve of PU is smaller, and the slope change is more stable. This indicates that, at low temperatures, the molecular structure of PU is in a more stable state, the intermolecular movement is relatively fixed, and the low-temperature performance is better, which is consistent with the actual performance of PU. When the temperature increases to 450 K, the slope of the MSD curve of PU gradually becomes larger. When the temperature increases to 550 K, the slope of the MSD curve of PU increases sharply, which may be due to the gradual separation of PU molecules at high temperatures. The trend of the MSD of the PU system with the temperature is consistent with the thermal properties of PU, which suggests that the constructed PU model is reliable.

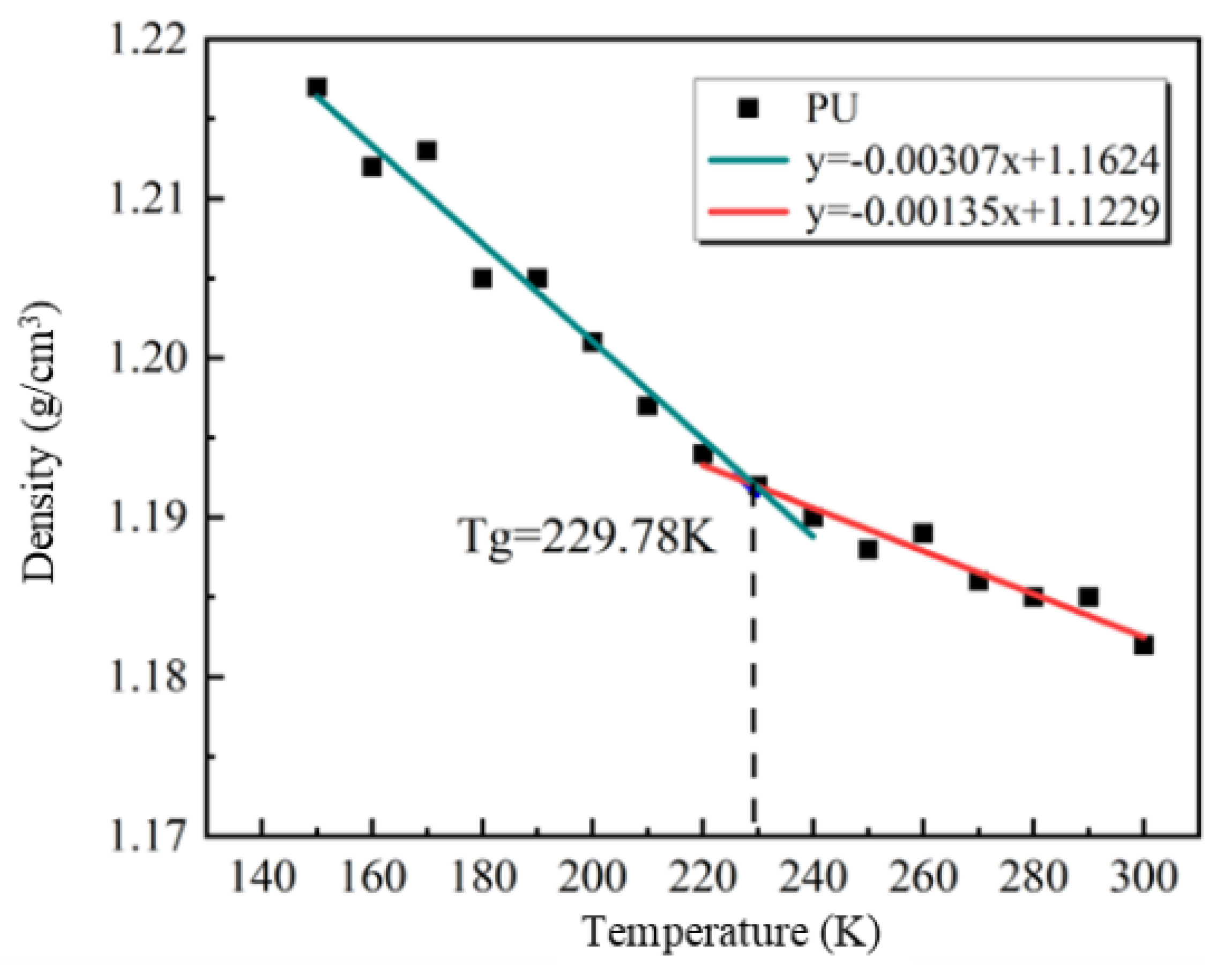
2.7.2. Glass Transition Temperature (Tg)

The free volume theory suggests that the motion of molecular chains is frozen at a certain temperature when the free volume shrinks to the point where it does not provide space to accommodate the motion of the chain segments, and this critical temperature is Tg [50]. Therefore, in this study, a 300 ps NPT ensemble simulation was conducted on the PU molecular model at each temperature (ranging from 140 K to 300 K, with a temperature interval of 10 K) to obtain the density and volume parameters of the PU system under various temperature conditions. The density–temperature curves were plotted, and the glass transition temperature of PU was obtained by fitting the intersection of the curves. As shown in Figure 13, based on the results of the NPT simulation, a segmented linear fit was made to the density and temperature, and the intersection of the two straight lines was taken as the Tg. The Tg obtained from the fitting is 229.78 K (−43.37 °C), which is closer to the measured value of Tg of PU, proving the validity of the molecular model.

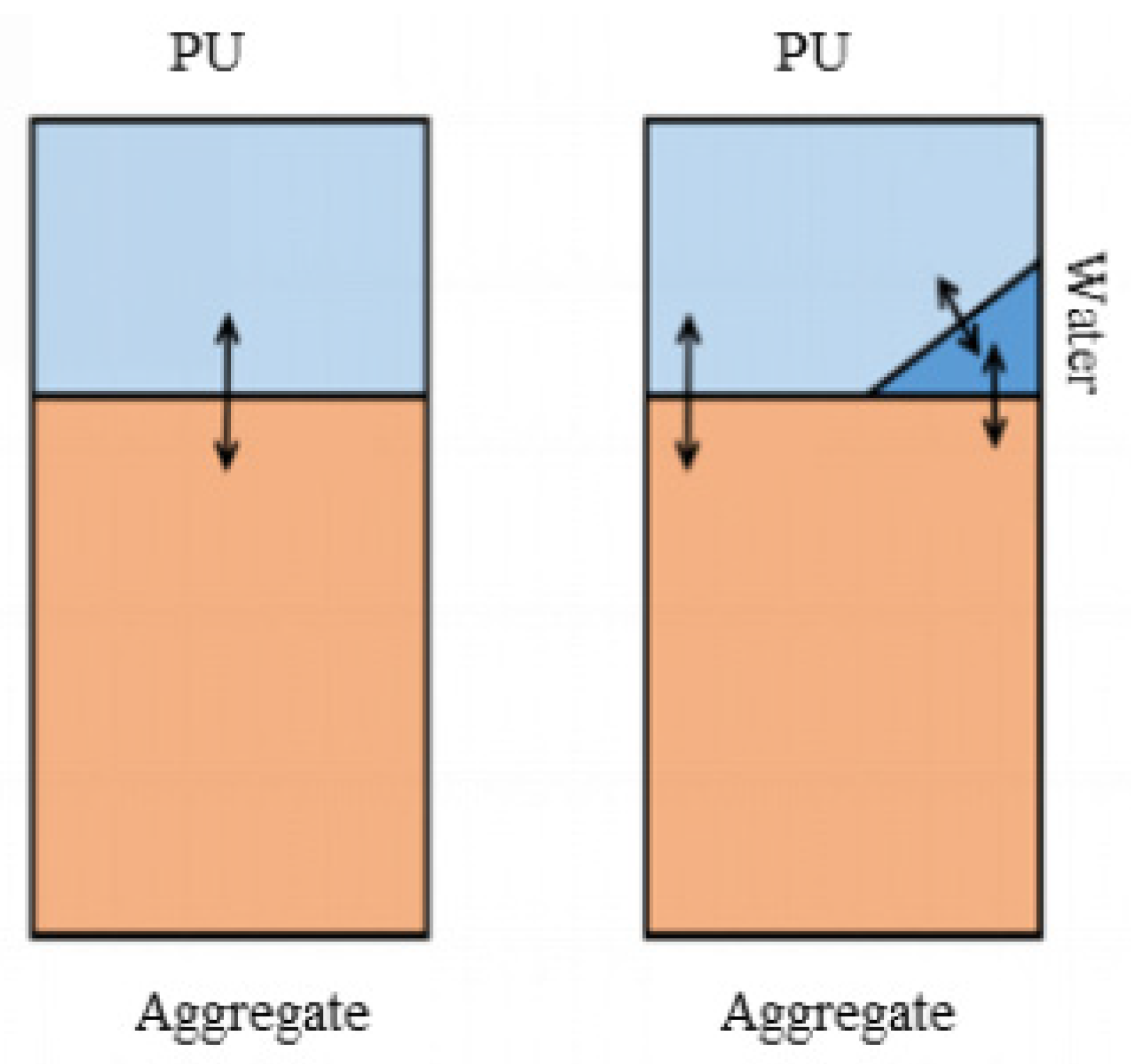
2.8. Water Boiling Method and Water Immersion Method

In this paper, the water boiling method and water immersion method are used to macroscopically evaluate the adhesion properties of PU with aggregates. Refer to T0616-1993 in JTG E20-2011 [51] for the experiments using the water boiling method and water immersion method on PU mixtures. The formulations of PU mixtures refer to the previous results of this group. The adhesion of PU to the aggregate was evaluated by observing the degree of spalling of PU on the surface of the aggregate after water boiling and water immersion. Scanning electron microscopy (SEM) was used to observe the separation process of PU from the aggregate after water immersion. In addition, to quantitatively evaluate the results of the water immersion method, the immersion time of the PU mixtures was extended, and the mass loss after immersion was measured.

3. Results and Discussions

3.1. Contact Angle

3.1.1. Contact Angles of PU

The average contact angles and coefficients of variation between PU and the test reagents before and after acidification are shown in

Table 6. Contact angles of PU.

Materials	Distilled Water		Ethylene Glycol		Formamide		Coefficient of Determination (R2)
	Average/(°)	COV/(%)	Average/(°)	COV/(%)	Average/(°)	COV/(%)
PU	87.6	0.76	61.2	0.78	77.5	0.14	0.9649
HPU	93.1	0.32	79.9	0.41	95.3	0.49	0.9590

. According to the infiltration theory, the hydrophobicity and lipophilicity of the surface of a substance increase with the contact angle [52,53]. The contact angle between acidified PU and distilled water increased, indicating that the hydrophobicity of PU was further enhanced after acidification. Additionally, according to the coefficient of determination, a good linear relationship was observed between $\sqrt{{{\gamma }_L^d\gamma }_S^p}$ and ${\gamma }_L(1+cos\theta )/2\sqrt{{\gamma }_L^d}$ for PU before and after acidification, confirming the validity of the test data.

3.1.2. Contact Angle of Aggregates

The average contact angles and coefficients of variation between aggregates and test reagents are shown in

Table 7. Contact angles of aggregates.

Materials	Distilled Water		Ethylene Glycol		Formamide		Coefficient of Determination (R2)
	Average/(°)	COV/(%)	Average/(°)	COV/(%)	Average/(°)	COV/(%)
Basalt	75.7	0.57	40.1	0.42	59.4	0.63	0.9602
Limestone	72.2	0.21	34.6	0.55	51.9	0.40	0.9882

. It can be seen from the data that the contact angle between aggregates and distilled water is smaller than that between PU and distilled water, indicating that the hydrophilicity of the aggregates is higher than that of PU. In addition, the contact angle of basalt is significantly higher than that of limestone, suggesting that basalt is less hydrophilic than limestone. The coefficient of determination shows a good linear relationship between $\sqrt{{{\gamma }_L^d\gamma }_S^p}$ and ${\gamma }_L(1+cos\theta )/2\sqrt{{\gamma }_L^d}$ for the two aggregates, indicating that the data have sufficient reliability.

3.2. Surface Free Energy

From the linear relationship between $\sqrt{{{\gamma }_L^d\gamma }_S^p}$ and ${\gamma }_L(1+cos\theta )/2\sqrt{{\gamma }_L^d}$, the dispersion and polar components of the surface free energy of the material can be obtained, and then the surface free energy of the material can be calculated according to Equation (3). As shown in

Table 8. Surface free energy of PU and aggregates.

Materials	γ (mJ/m2)	γd (mJ/m2)	γP (mJ/m2)
PU	23.637	14.432	9.205
HPU	16.452	4.244	12.208
Basalt	35.647	26.605	9.042
Limestone	39.673	30.217	9.456

, the surface free energy of HPU is lower than that of PU, which may be due to a certain degree of oxidation in the acidic medium, leading to a reduction in internal strength. Furthermore, the surface free energies of both aggregates are higher than that of PU, with limestone exhibiting a higher surface free energy than basalt. Notably, PU demonstrated polarity similar to that of the aggregates, indicating favorable adhesion properties to the aggregates.

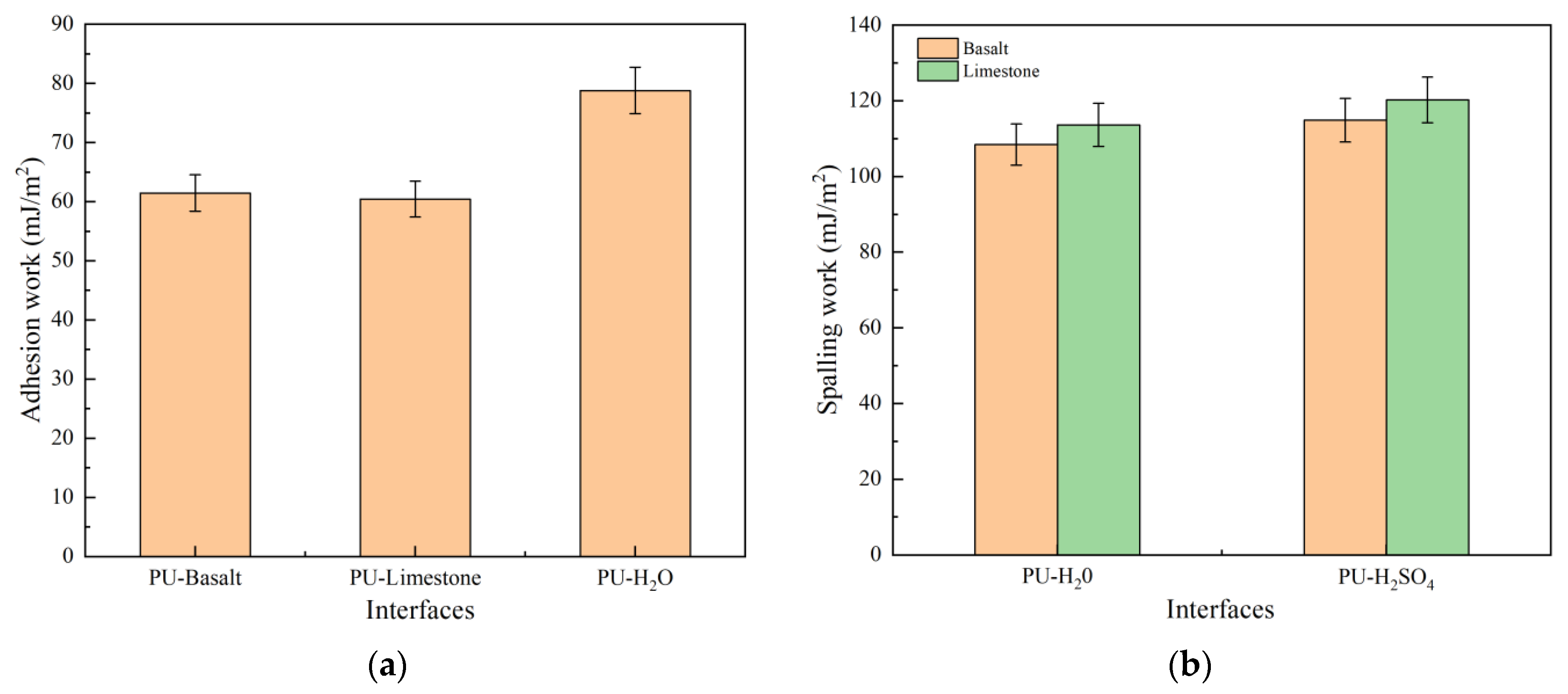
3.3. Adhesion Work and Spalling Work

As shown in Figure 14, the adhesion work and spalling work between PU and aggregates were calculated using Equations (7) and (8). The adhesion work for the PU–basalt interface is higher than that for the PU–limestone interface, indicating better adhesion properties at the PU–basalt interface. The probable reason for this result is that the surface of basalt contains a high proportion of silicate components, which react readily with the isocyanate groups (-NCO) in the PU to form stronger chemical bonds. However, limestone has a more chemically stable surface and is relatively less reactive with PU. When water is added, the spalling work of the PU–basalt interface is less than that of the PU–limestone interface. This indicates that the water stability is better when basalt is used as an aggregate for PU mixtures. Under acidic conditions, the spalling work of PU–basalt and PU–limestone increased by about 5%, implying a reduction in the adhesion properties of PU to aggregates in an acidic environment. A possible reason for this result is that the acid reacts with the metal oxides on the aggregate surface, weakening their ability to chemically bond with the PU.

3.4. Results of Molecular Dynamics Simulation

3.4.1. Interaction Energy

The interaction energy can reflect the stability of the interfacial bonding of two substances. As shown in Figure 15, the interaction energy of the PU–CaO interface is the largest, followed by the SiO₂ interface, and the interaction energy with the CaCO₃ interface is the smallest. This indicates that the PU-CaO system is the most stable, while the PU–CaCO₃ system is the least stable. It is worth noting that the interaction energies between H₂O–SiO₂, H₂O–CaO, H₂SO₄–SiO₂ and H₂SO₄–CaO are smaller than those of PU-SiO₂ and PU-H₂SO₄, but the interaction energies of H₂O–CaCO₃ and H₂SO₄–CaCO₃ are higher than those of PU–CaCO₃, which suggests that the hydrophilicity of limestone is higher than that of basalt. This result can be attributed to the fact that limestone surfaces contain a large number of polar groups (e.g., Ca²⁺ and CO₃²⁻) that attract and bind water molecules, resulting in a higher surface energy that exhibits greater hydrophilicity.

3.4.2. Adhesion Work and Spalling Work

As shown in Figure 16, the adhesion work of the three minerals with PU is ranked as CaO > SiO₂ > CaCO₃, which indicates that the adhesion properties of PU with CaO are better than those of the other minerals. A possible reason for this result is that CaO is an alkaline oxide with a high number of hydroxyl (-OH) and oxygen ions (O²⁻) on its surface, and these reactive groups are able to react chemically with isocyanate groups (-NCO) in PU. The high energy of this chemical bonding enhances the adhesion properties of PU–CaO. In addition, the adhesion work of PU-CaCO₃ is 2.7 mJ/m², which is much lower than that of PU–CaO and PU–SiO₂. The explanation for this result lies in the low surface chemical reactivity of CaCO₃, which makes it difficult to form strong chemical bonds with the polar groups in PU. The ranking of the spalling work of the three minerals with PU is CaO < SiO₂ < CaCO₃. This is due to the fact that calcium oxide reacts violently with water and affects the stability of the PU–CaO interface. The ranking of spalling work also indicates that the mix composed of PU and limestone has poor water stability and is not suitable for areas with high precipitation. Under acidic conditions, the ranking of the spalling work of the three minerals with PU is SiO₂ < CaO < CaCO₃, which indicates that the adhesion properties of PU with basalt are higher than those of limestone under acidic conditions. In addition, under acidic conditions, the spalling work of PU–CaO increased slightly, PU-SiO₂ remained almost unchanged, while PU–CaCO₃ increased from 5.9 mJ/m² to 10.7 mJ/m². This may be due to the fact that SiO₂ is an acidic oxide and is more stable under acidic conditions. However, the chemical properties of CaCO₃ are more active under acidic conditions. It is worth noting that the spalling work of the three minerals with PU increased under acidic conditions, but the spalling work of basalt with PU was still lower than that of limestone, suggesting that basalt has better resistance to acid damage than limestone and is suitable for acid rain-prone areas. In conclusion, PU–basalt is the best material combination for permeable PU mixtures.

3.5. Results of the Water Boiling Method and Water Immersion Method

The optimal material combination obtained by the surface free energy method with molecular dynamics simulations was PU–basalt. In order to verify this conclusion, the adhesion properties of PU with basalt were evaluated using the water boiling method and the water immersion method. As shown in Figure 17, the PU mixture has almost no spalling part, and the integrity of the PU adhesive film is favorable, which indicates that the adhesion properties between PU and basalt are excellent.

The SEM results are shown in Figure 18. Compared to before water immersion, the interface between PU and basalt after water immersion showed cracks, but the width of the cracks was small. Moreover, as shown in Figure 19, the mass loss rate of the PU mixture at 72 h of immersion was less than 1%. The evaluation of the adhesion grade of the PU mixture referred to the section “Adhesion grade of asphalt to aggregates” in JTG E20-2011. The adhesion grade of PU–basalt was determined to be Level 5, which meets the requirements of the standard. This reflects the good adhesion properties between PU and basalt.

4. Conclusions

In this study, a PU binder was synthesized, and the interaction energy, adhesion work, and spalling work between the PU binder and aggregate were calculated based on surface free energy theory and MD to investigate the adhesion properties of the PU–aggregate interface. Additionally, the effects of different environmental conditions and aggregate types on the adhesion properties of the PU–aggregate interface were explored. The main conclusions of this study are as follows:

(1)

The surface free energy of PU showed a polarity similar to that of the aggregate, indicating good adhesion between PU and aggregate. However, the surface free energy of HPU was lower than that of PU, suggesting that adhesion between PU and aggregate decreases under acidic conditions.

(2)

Interaction energies between PU, H₂O, and H₂SO₄ with the three minerals were calculated through MD simulation. In terms of aggregate type, the adhesion of PU with basalt was found to be superior to that with limestone, and limestone exhibited stronger hydrophilicity.

(3)

The adhesion work and spalling work obtained by surface free energy theory and molecular dynamics calculations have the same trend, and the results of the adhesion work and spalling work fully indicate that the adhesion properties of PU with basalt are better than with limestone. While the adhesion properties of PU with limestone and basalt decreased under acidic conditions, the adhesion properties of PU with basalt were better than those of limestone, indicating that the combination of PU–basalt is more suitable for acid rain-prone areas. In addition, the water boiling method and water immersion method verified the rationality of the PU–basalt combination.

(4)

The surface free energy measurement based on the contact angle test and MD simulation provides a multiscale perspective on the adhesion properties between PU and aggregate, enhancing the feasibility of applying permeable PU mixtures. The study of factors affecting PU–aggregate adhesion properties contributes to the further optimization of PU mixture formulations. Moreover, the calculation results of the surface free energy method and MD simulation showed good correlation and were consistent with macroscopic performance tests, which can be extended to the study of the adhesion properties of other materials.