Missed Detection of Entanglement in Two-Mode Squeezed States Based on the Inseparability Criterion

Abstract

The inseparability criterion provides a straightforward and efficient method for identifying and quantifying two-mode Gaussian quantum entanglement, making it a crucial tool in quantum optics experiments. However, it is crucial to recognize that the inseparability criterion serves only as a sufficient condition for entanglement assessment, thereby posing a risk of missed detection during evaluation. This paper investigates the use of the inseparability criterion in assessing two-mode squeezed states, with a particular focus on examining missed entanglement detection due to entanglement asymmetry. The results show that when decoherence symmetrically affects both modes, the inseparability criterion effectively detects entanglement. In contrast, when this symmetry is broken, the criterion may fail to identify entanglement, with the likelihood of missed detection increasing with increasing asymmetry. By comparing these results with the positive partial transpose criterion, which serves as a necessary and sufficient condition, the occurrence of missed detections by the inseparability criterion is confirmed. Our research not only provides valuable insights into the application of the inseparability criterion in quantum information tasks but also deepens the understanding of its operational principles and limitations.

1. Introduction

Quantum entangled states are fundamental resources in quantum information physics, offering unparalleled advantages over classical resources in critical tasks such as information processing [1,2], communication [3,4,5], and computation [6]. Two-mode squeezed states [7], exemplars of continuous-variable entanglement, have attracted significant attention due to their pivotal roles in advancing quantum optics and quantum information technologies. Generated through nonlinear optical processes like optical parametric amplification or oscillation, these states exhibit remarkable squeezing effects in both joint amplitude and phase correlations of the two optical modes in phase space [8], reinforcing their indispensable status in quantum information science. Their significance extends to applications such as quantum illumination [9,10] and continuous-variable quantum key distribution [11,12].

The detection and assessment of quantum entanglement are central topics in quantum information theory, serving as essential prerequisites for the practical deployment of quantum technologies. In quantum communication, accurate entanglement evaluation directly impacts the security and efficiency of information transmission. Similarly, in quantum computation, precise entanglement measurement underpins the achievement of algorithmic acceleration and quantum parallelism. To this end, researchers have developed various entanglement criteria [13], including the Einstein–Podolsky–Rosen (EPR) paradox [14], the positive partial transposition (PPT) criterion [15], relative entanglement entropy [16], and the inseparability criterion [17]. These criteria determine whether a system is in an entangled or separable state by measuring the expectation values of specific observables. Among these, the inseparability criterion, renowned for its simplicity and experimental feasibility, has been extensively employed in quantum optics experiments. Introduced by Duan et al. [17] and Simon [15], the criterion relies on measuring the total variance of EPR-type operator pairs and comparing it with the standard quantum limit to ascertain entanglement. Researchers have leveraged this criterion to explore the dynamical behavior of entangled states in complex environments, such as noisy and lossy channels [18,19,20,21]. Notably, studies like those by D. Buono et al. have validated the robustness of entangled states under strong decoherence using various quantum indicators, including teleportation fidelity, quantum discord, mutual information, and the inseparability criterion [22]. W. P. Bowen et al. investigated the effects of symmetric decoherence on the EPR paradox and inseparability criterion, revealing their qualitative disparities [23]. Furthermore, the inseparability criterion has been extended to assess intricate multi-mode Gaussian quantum entangled states, such as four-mode cluster states [24] and hyperentangled states simultaneously possessing orbital angular momentum and spin angular momentum [25], highlighting its versatility. While previous research primarily focused on symmetric channel decoherence, the increasing importance of asymmetric decoherence phenomena in quantum communication and computation underscores the need for closer examination under asymmetric conditions. Genta Masada has addressed the challenges posed by asymmetric entanglement and channel losses in quantum illumination systems, utilizing the inseparability criterion to analyze the evolution of non-classical correlations [26,27,28,29,30]. Feng et al. [31] and Zhao Hao et al. [32] have also contributed to this field by characterizing the transmission evolution of entangled fields in optical fibers and analyzing the impact of state asymmetry on entanglement properties and robustness [31,32]. Research by Wenhui Zhang et al. further reinforces this trend, emphasizing the significance of exploring quantum entanglement under asymmetric decoherence conditions [33].

The inseparability criterion stands as a sufficient condition for assessing entanglement, proficiently identifying its presence in diverse scenarios. Nevertheless, its non-necessity poses a limitation: in situations characterized by significant asymmetry within the system, particularly those involving asymmetric decoherence or intrinsic quantum state asymmetry, it may fall short of fully and precisely quantifying the extent of entanglement, thereby posing a risk of missed entanglement detections and ultimately leading to an underestimation of the entanglement degree. This limitation transcends specific applications like quantum illumination for target recognition and ranging [34,35], one-sided device-independent quantum key distribution [36], and correlated quadrature asymmetries in entanglement [37,38], posing a tangible threat to the operational integrity of quantum technologies. The complexities inherent in asymmetric quantum systems present a significant challenge to the inseparability criterion, impairing its capacity to fully capture the intricacies of entangled states. As a result, there exists a risk of underestimating the degree of entanglement and missing crucial detections, which could, in turn, jeopardize the practical implementation of quantum technologies. In quantum communication, missed detections may compromise the security of information transmission, while in quantum computation, they may threaten the accuracy of algorithm execution and the reliability of outcomes. Therefore, it is imperative to rigorously evaluate the strengths and limitations of the inseparability criterion in these contexts.

In this paper, we investigate the vulnerability of missed entanglement detections when applying the inseparability criterion to asymmetric two-mode squeezed states. We undertake a comparative analysis with the PPT criterion, known for its superior entanglement detection capabilities, theoretically and experimentally examining how entanglement mode asymmetry modulates the effectiveness of these criteria. Our methodology illuminates the mechanism behind undetected entanglement by the inseparability criterion. By artificially inducing controlled asymmetric optical losses in the distribution of two-mode squeezed states, we simulate experimental asymmetry. Our results reveal a nuanced picture: in symmetric settings, the inseparability criterion aligns with the PPT criterion, fulfilling both sufficiency and necessity for entanglement measurement. Conversely, in asymmetric environments, it reduces to a sufficient condition, incapable of fully and accurately capturing the extent of entanglement. This underscores the crucial importance of judiciously selecting entanglement criteria tailored to specific quantum information processing applications to ensure accurate and reliable entanglement detection. Our contribution aims to propel the advancement of more efficient entanglement verification strategies, indispensable for the robust implementation of real-world quantum systems.

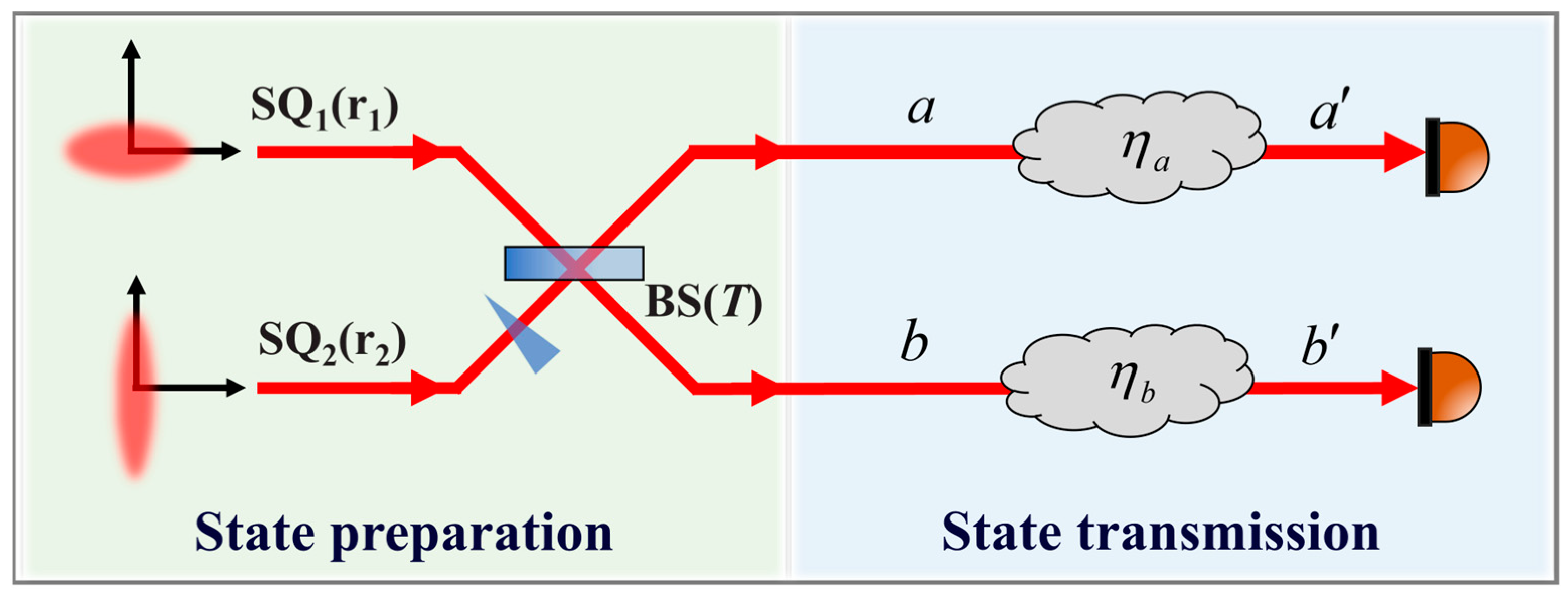
2. Theoretical Analysis

2.1. Asymmetry of Two-Mode Gaussian States

The two-mode squeezed state is a fundamental Gaussian quantum state in quantum optics, typically generated by a type-II nondegenerate optical parametric amplifier (NOPA) or by combining two independent single-mode squeezed fields using a 50/50 beam splitter. Mathematically, this state can be described by the symplectic eigenform of its covariance matrix, denoted as ${\mathit{\sigma }}_{ij}=〈\left(X_i{X}_j+X_j{X}_i\right)〉/2-\langle X_i\rangle -〈X_j〉$, where $X\equiv \left(X_a^{+},X_a^{-},X_b^{+},X_b^{-}\right)$ represents the quadrature components of the field. Here, the subscripts $a$ and $b$ denote the two modes, as illustrated in Figure 1, and the superscripts + and − denote the quadrature amplitude and quadrature phase components, respectively. These quadrature components are related to the annihilation operator $a_i$ and creation operator $a_i^{+}$ of the field as $X_i^{+}=a_i+a_i^{+}$ and $X_i^{-}=i\left(a_i^{+}-a_i\right)$,

$$\mathit{\sigma }=\left[\begin{array}{cc}\mathit{A}& \mathit{C}\\ {\mathit{C}}^{\mathit{T}}& \mathit{B}\end{array}\right]=\left[\begin{array}{cccc}n& 0& c_1& 0\\ 0& n& 0& c_2\\ c_1& 0& m& 0\\ 0& c_2& 0& m\end{array}\right]$$

(1)

where the submatrices $\mathit{A}$ and $\mathit{B}$ correspond to the autocovariance matrices of the two subsystems, while the off-diagonal elements $\mathit{C}$ represent the cross-covariance matrix between the two subsystems [39]. The relevant quantities $n$, $m$, $c_1$, and $c_2$ are determined by four local symplectic invariants: $\det \mathit{\sigma }=\left(nm-c_1^2\right)\left(nm-c_2^2\right)$, $\det \mathit{A}=n^2$, $\det \mathit{B}=m^2$, and $\det \mathit{C}=c_1{c}_2$. Notably, the parameters are not arbitrary but must be subject to specific physical constraints [22]:

$$\mathit{\sigma }+{\displaystyle \frac{i}{2}}\mathit{\omega }\oplus \mathit{\omega }\ge 0$$

(2)

where $\mathit{\omega }\equiv \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$. These constraints can be further elucidated as a function of the symplectic eigenvalues of the matrix elements, providing a deeper understanding of the state’s properties,

$$\det \mathit{A}+\det \mathit{B}+2\det \mathit{C}\le 4\det \mathit{\sigma }+1$$

(3)

A state is termed symmetric when the covariance matrix satisfies $n=m$. For an ideal symmetric state, the parameters in the covariance matrix satisfy both $n=m$ and $c_1=-c_2$.

However, in practical applications, imperfections such as equipment noise and operational inefficiencies often result in asymmetry in two-mode squeezed states [40]. As illustrated in Figure 1, this asymmetry manifests primarily in two aspects: asymmetry in the orthogonal components of inter-mode correlations and asymmetry between the entangled modes. The former refers to the difference between the inter-mode covariance components $c_1$ and $c_2$. This asymmetry typically arises from inconsistencies in the degree of squeezing, squeezing direction, or phase differences between the two squeezed beams (SQ1 and SQ2) used to generate the two-mode squeezed state during the state preparation process [23]. Mode asymmetry, on the other hand, refers to the difference between the local covariance matrices $n$ and $m$ of the two modes. This asymmetry is often a result of the state transmission and detection processes, commonly encountered in quantum information protocols involving asymmetric noise and loss channels, such as quantum illumination and one-sided device-independent quantum key distribution. Asymmetry can significantly impact the results of entanglement criteria, making it crucial to understand and analyze the effects in practical systems.

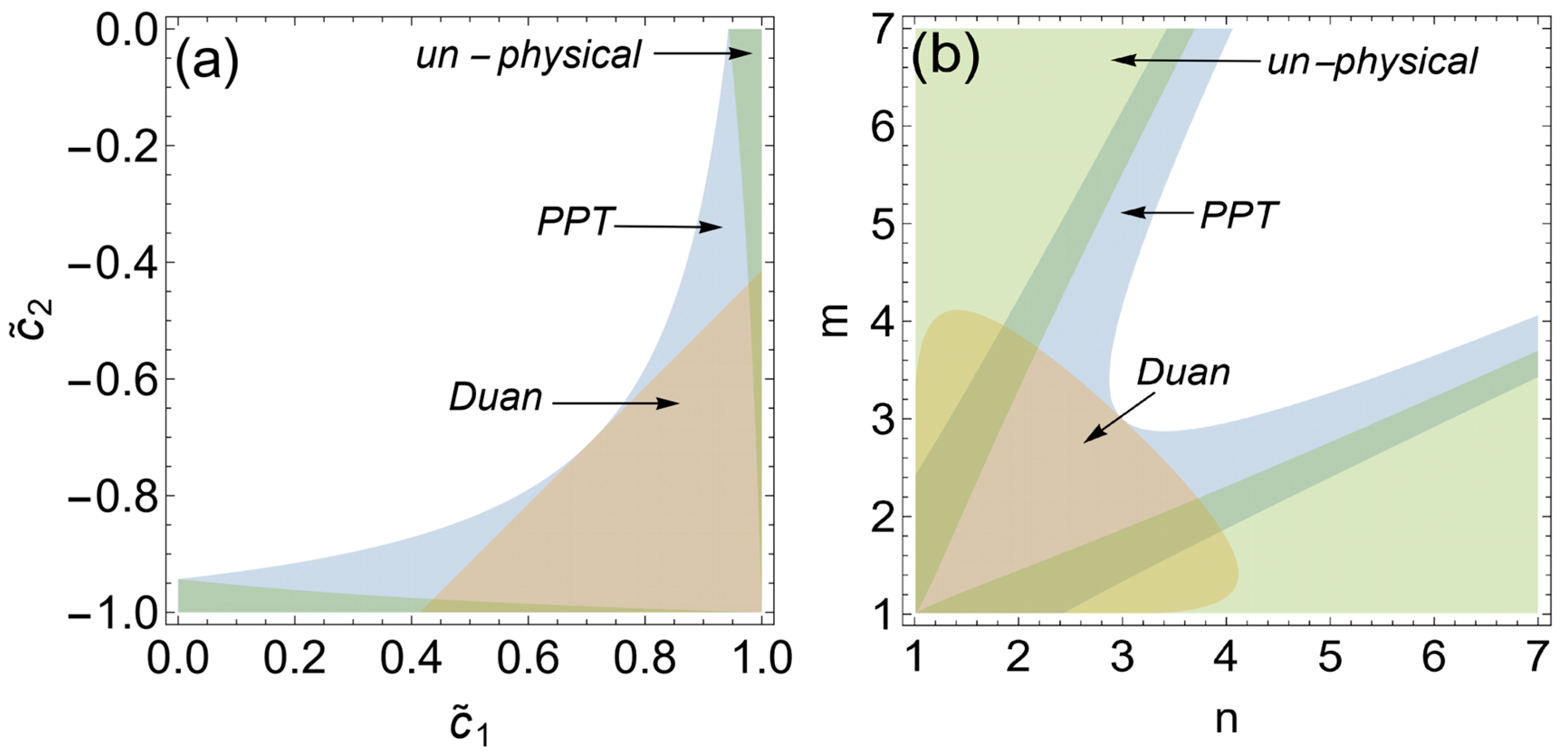
2.2. Missed Detection of Entanglement

The covariance matrix, as a vital representation of quantum state statistical information, provides a comprehensive statistical description of the correlation characteristics of two-mode squeezed states. However, it does not directly reveal the separability or entanglement of a state, nor does it quantify the degree of entanglement, necessitating the use of specific entanglement criteria. Inseparability criteria are widely employed in optical experiments, offering a straightforward and efficient tool for investigating the entanglement properties of continuous-variable quantum systems. The criteria typically equate separability with the positivity of the P-function. For states characterized by Gaussian noise distributions and symmetric correlations in conjugate quadrature components, the criteria can be linked to measurable correlations [6]. Specifically, for two-mode squeezed states, the inequality takes the form of

$$En{t}_{Inse}={\Delta }^2{X}_{a\pm b}^{+}+{\Delta }^2{X}_{a\pm b}^{-}<1$$

(4)

where ${\Delta }^2{X}_{a\pm b}^{+}$ represents the minimum value of the variance of the sum or difference of operators between beams $a$ and $b$, which has been normalized, i.e., ${\Delta }^2{X}_{a\pm b}^{+}=\min 〈{\left(\delta X_a^{+}\pm \delta X_b^{+}\right)}^2〉/4$. The elements of the covariance matrix can be further utilized to calculate these variances:

$$En{t}_{Inse}={\displaystyle \frac{1}{2}}\left[n+m-\left(\right|c_1|-|c_2\left|\right)\right]<1$$

(5)

The value of $En{t}_{Inse}$ directly reflects the strength of entanglement in the quantum state. The closer the value is to zero, the higher the degree of entanglement. It is important to note that the inseparability criterion is merely a sufficient condition for entanglement. Specifically, satisfying this inequality confirms the existence of entanglement. However, this criterion is not necessary—satisfying inequality (4) does not guarantee that the state is separable. The inseparability criterion fails to capture all entangled states, meaning certain entangled states may not satisfy this criterion, posing a risk of missed detections. This could result in misjudgments or errors in practical quantum information tasks, thereby adversely affecting the efficiency and accuracy of these tasks.

We aim to explore the potential risk of missing entangled states when applying the inseparability criterion to asymmetric two-mode squeezed states. To achieve this, we will compare the inseparability criterion with the PPT criterion, which is more reliable in detecting entanglement. The PPT criterion serves as a sufficient and necessary condition for two-mode squeezed states, determining the separability of a state by the positive definiteness of the partial transpose matrix of the two-mode Gaussian state. Specifically, the PPT criterion quantifies the entanglement properties by calculating the minimum symplectic eigenvalue of the covariance matrix [15],

$$En{t}_{PPT}=\sqrt{{\displaystyle \frac{\Gamma -\sqrt{{\Gamma }^2-4\det \mathit{\sigma }}}{2}}}<1$$

(6)

where $\Gamma =\det \mathit{A}+\det \mathit{B}-2\det \mathit{C}$. If the inequality holds, the two-mode Gaussian state is considered entangled; otherwise, it is separable. In Figure 2, we visually compare the inseparability and PPT criteria in defining the entanglement region under two scenarios: asymmetry in the intermodal correlation of orthogonal components and asymmetry in the entanglement modes. Specifically, Figure 2a shows the analysis of missed detections by the inseparability criterion in the case of asymmetry in the intermodal correlation orthogonal components, where we fix $n=m=3$ and analyze the evolution of the criterion by varying the values of ${\tilde{c}}_1$ and ${\tilde{c}}_2$, with ${\tilde{c}}_i=c_i/c_{\max }$, where the state is maximally entangled when ${\tilde{c}}_i=1$; Figure 2b illustrates the analysis of missed detections by the inseparability criterion in the case of asymmetry in the entanglement modes, where we fix ${\tilde{c}}_1=-{\tilde{c}}_2=1/\sqrt{2}$ and vary the values of $n$ and $m$. In each subfigure, the orange region represents the entanglement range defined by the inseparability criterion, while the blue region shows the more comprehensive and rigorous entanglement definition given by the PPT criterion. The green region, a non-physical region, is defined by the constraints of Equation (3), reflecting the range of quantum states that are unattainable in actual physical systems. From the figures, it is evident that compared to the PPT criterion, the inseparability criterion covers a smaller region, entirely contained within the blue region defined by the PPT criterion. This indicates that the inseparability criterion fails to identify some entangled states recognized by the PPT criterion, highlighting the presence of missed entanglement detections. More specifically, in the case of ideal symmetric states (diagonally distributed from top left to bottom right in Figure 2a and anti-diagonally distributed from top right to bottom left in Figure 2b), the boundaries of the two criteria coincide, indicating that their judgments are equivalent: the inseparability criterion is both a sufficient and necessary condition for two-mode squeezed states. However, when this symmetry is broken, whether due to asymmetry in the intermodal correlation orthogonal components or asymmetry inherent in the entanglement modes—a significant divergence between the boundaries of the two criteria emerges, which deepens as asymmetry increases. This phenomenon reveals that under such circumstances, the inseparability criterion serves only as a sufficient condition, rather than a necessary condition, for determining whether a two-mode Gaussian state possesses entanglement properties. Consequently, when dealing with two-mode squeezed states with significant asymmetry, it may be necessary to apply the inseparability criterion more cautiously or consider using a more robust and rigorous criterion (such as the PPT criterion) that is less sensitive to asymmetry to ensure accurate entanglement detection.

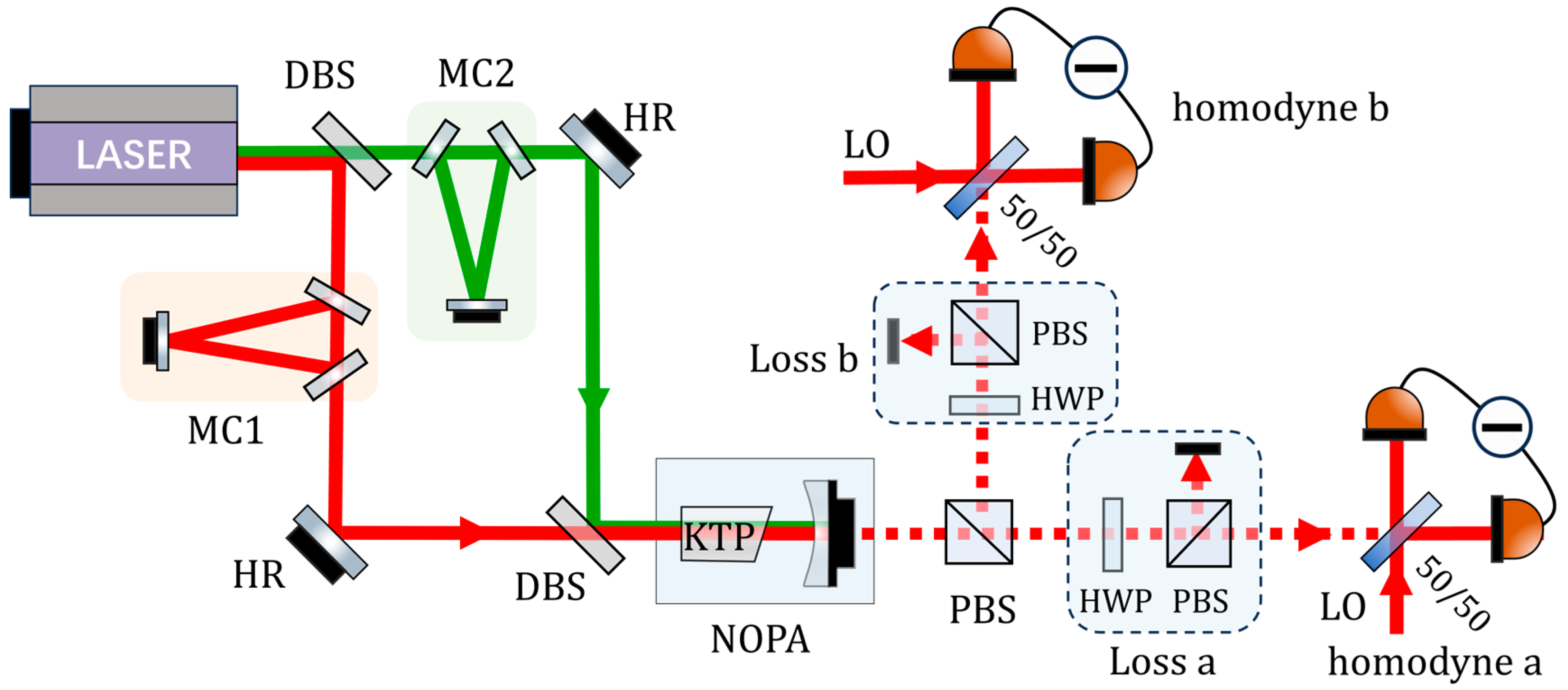
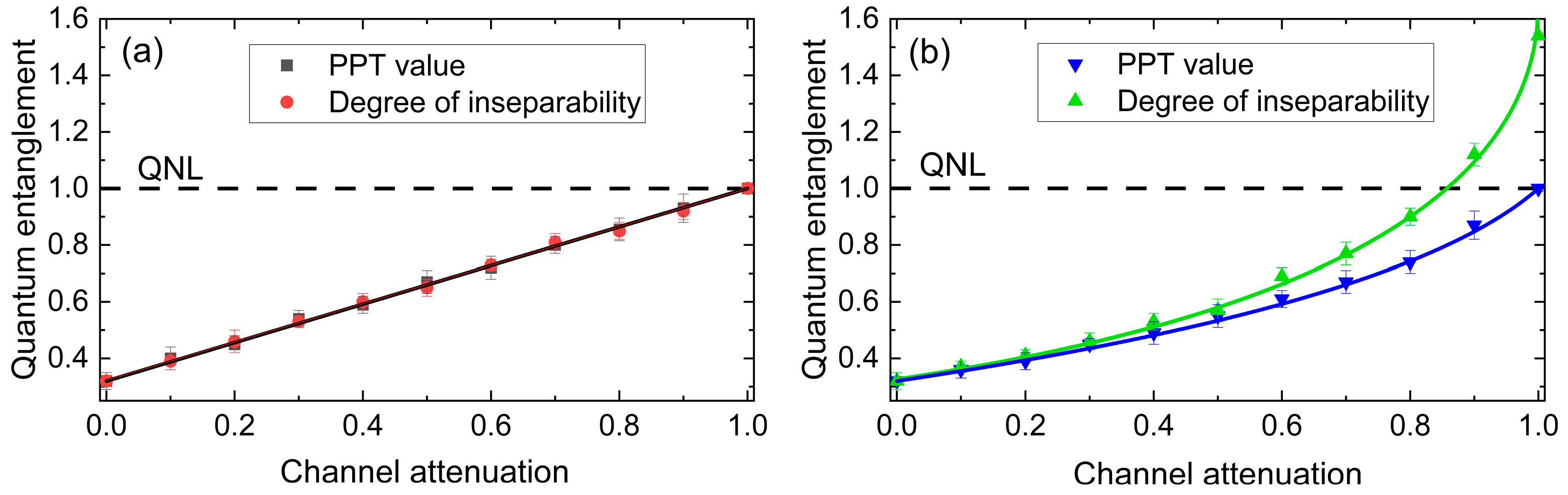
3. Experimental and Results

Our experimental validation was conducted through a NOPA system. Owing to the symmetry of the Hamiltonian, the state generated by NOPA is a fully symmetric state, implying that the elements of the covariance matrix satisfy conditions, specifically $n=m$ and $c_1=-c_2$. Figure 3 illustrates the experimental setup employed to generate the two-mode squeezed state. The NOPA comprises an α-cut type-II phase-matched KTiOPO4 (KTP) crystal (cut at 1°) and a plano-concave mirror. The front surface of the crystal (S1) is highly reflective (HR) at 1080 nm and has a transmission rate of T = 18% at 540 nm, serving as the input coupling mirror. The rear surface (S2) is anti-reflective (AR) coated for both 1080 nm and 540 nm. The plano-concave mirror has a curvature radius of 50 mm and acts as the output coupling mirror, being highly reflective at 540 nm and having a transmission rate of 12.5% for 1080 nm light. The system utilizes 1080 nm infrared light, which is noise-reduced by a three-mirror ring-cavity infrared mode cleaner (MC1), and 540 nm green light, which is noise-reduced by a green light mode cleaner (MC2), as the input and pump beams, respectively. The NOPA cavity is operated below its threshold, and when the relative phase between the pump and input beams is locked to the parametric deamplification state, the output port emits a two-mode squeezed state with orthogonal polarizations (signal field $a$ and idler field $b$). This two-mode squeezed state exhibits anti-correlation in the quadrature amplitudes and positive correlation in the quadrature phases. In the experiment, the two sub-modes $a$ and $b$ of the two-mode squeezed state are separated using a polarizing beam splitter (PBS) and then directed to a balanced homodyne detection system for entanglement measurement. To achieve a lower pump threshold, the NOPA cavity is designed to be triply resonant for the pump, signal, and idler modes. This is experimentally realized by fine-tuning the phase-matching temperature and adjusting the transverse position of the crystal. During measurements, the system is operated at approximately 70% of the threshold power to avoid undesirable non-Gaussian effects. The experiment demonstrates a squeezing of −4.95 dB and an anti-squeezing of 6.53 dB at an analysis frequency of 2 MHz (see Figure 4). The upper trace represents the standard quantum noise limit (QNL), corresponding to approximately −53.8 dBm, which is obtained by blocking the signal light and measuring only the vacuum fluctuations. These measurements were obtained using a balanced homodyne detection system with a total detection efficiency of up to 85%. Complete measurements of the quadrature components allowed for the derivation of the covariance matrix, enabling a comparison between the PPT criterion and the inseparability criterion. The homodyne detection system was calibrated by adjusting the local oscillator (LO) power and balancing the photodetectors to ensure optimal interference and signal-to-noise ratio. Phase stabilization between the signal and LO beams was achieved using a phase-locked loop (PLL). Shot noise levels were calibrated by blocking the signal beam, and electronic noise was confirmed to be at least 10 dB below shot noise. The total uncertainty, including detector efficiency and phase fluctuation effects, was estimated to be within ±0.2 dB.

To introduce asymmetry in the entanglement, we strategically positioned independent beam splitters on the two entangled beams, prior to their arrival at the balanced homodyne detectors. This setup simulates propagation losses inherent quantum channels. These beam splitters were constructed using a half-wave plate and a polarizing beam splitter, enabling us to simulate channel attenuation ranging from 0% to 100% by adjusting the angle of the half-wave plate. The fields $a^{\prime }$ and $b^{\prime }$ preceding the balanced homodyne detectors can be mathematically expressed as $a^{\prime }=\sqrt{{\eta }_a}a+\sqrt{1-{\eta }_a}{a}_v$ and $b^{\prime }=\sqrt{{\eta }_b}b+\sqrt{1-{\eta }_b}{b}_v$, where $\sqrt{{\eta }_a}$ and $\sqrt{{\eta }_b}$ represent the channel transmission, and $a_v$ and $b_v$ are the vacuum fields introduced into the system due to the lossy channels. The two-mode Gaussian state ${\rho }_{a^{\prime }{b}^{\prime }}$, formed by the fields $a^{\prime }$ and $b^{\prime }$, can be effectively characterized by a covariance matrix:

$${\mathit{\sigma }}^{\prime }=\left[\begin{array}{cccc}{\eta }_{a}n+1-{\eta }_A& 0& \sqrt{{\eta }_a{\eta }_b}c& 0\\ 0& {\eta }_{a}n+1-{\eta }_a& 0& -\sqrt{{\eta }_a{\eta }_b}c\\ \sqrt{{\eta }_a{\eta }_b}c& 0& {\eta }_{b}n+1-{\eta }_b& 0\\ 0& -\sqrt{{\eta }_a{\eta }_b}c& 0& {\eta }_{b}n+1-{\eta }_b\end{array}\right]$$

(7)

For each attenuation, the inseparability value and PPT value are obtained by repeating the complete measurement process of the quadrature components. These entanglement criteria can be further formulated as functions of the channel attenuation, with the inseparability value,

$$\begin{array}{cc}\hfill {Ent}_{Inse}^{\prime }& ={\Delta }^2{X}_{a^{\prime }\pm b^{\prime }}^{+}+{\Delta }^2{X}_{a^{\prime }\pm b^{\prime }}^{-}\hfill \\ & ={\displaystyle \frac{1}{2}}\left({\eta }_{a}n+{\eta }_{b}n+\left(1-{\eta }_a\right)+\left(1-{\eta }_b\right)+2\sqrt{{\eta }_a{\eta }_b}c\right)\hfill \end{array}$$

(8)

and PPT value,

$${Ent}_{PPT}^{\prime }=\sqrt{{\displaystyle \frac{{\Gamma }^{\prime }-\sqrt{{{\Gamma }^{\prime }}^2-4\det {\mathit{\sigma }}^{\prime }}}{2}}}$$

(9)

$${\Gamma }^{\prime }={\left({\eta }_{a}n+1-{\eta }_a\right)}^2+{\left({\eta }_{b}n+1-{\eta }_b\right)}^2+2{\eta }_a{\eta }_b{c}^2,$$

$$\det {\mathit{\sigma }}^{\prime }={\left[\left({\eta }_{a}n+1-{\eta }_a\right)\left({\eta }_{b}n+1-{\eta }_b\right)-{\eta }_a{\eta }_b{c}^2\right]}^2,$$

Figure 5 presents the experimental outcomes for entanglement detection utilizing the inseparability criterion. Panels (a) and (b) illustrate the scenarios of symmetric (${\eta }_a={\eta }_b=\eta$) and asymmetric channel attenuation (${\eta }_a=1$ and ${\eta }_b=\eta$), respectively. Value 1 represents QNL, acquired by blocking the entangled light and allowing only the local light to enter the balanced homodyne detection system. The red dots and blue squares correspond to experimental measurements based on the inseparability and PPT criterion, respectively, with their respective theoretical fits depicted by matching colored curves. Data was collected at 10 distinct channel attenuation points, spaced at 0.1 intervals. At zero channel attenuation, the initial entanglement degree was −4.95 dB, accompanied by an anti-squeezing of 6.34 dB, indicative of a state purity of 0.73. In the case of symmetric losses, the results from both criteria coincide, revealing a linear decrease in entanglement with the increasing losses, remaining below 1 within a certain range of channel attenuation $\left[0,1\right)$. Conversely, under asymmetric losses, as the asymmetry intensifies, the inseparability criterion diverges from the PPT criterion. Notably, when the asymmetry exceeds 0.83, the inseparability value surpasses 1, signifying its inability to detect the entangled state. This underscores the intricacies of asymmetric losses in entanglement detection and emphasizes the significance of selecting an appropriate criterion. The close alignment between experimental measurements and theoretical predictions validates both the accuracy of our theoretical analysis and the reliability of the experimental procedure.

In practical experimental setups, the presence of cavity losses and noise effects inherent to optical oscillators necessitates the preparation and manipulation of mixed states rather than pure states. Consequently, these states fail to uphold the minimum uncertainty principle, i.e., ${\Delta }^2{X}_a^{+}·{\Delta }^2{X}_a^{-}={\Delta }^2{X}_b^{+}·{\Delta }^2{X}_b^{-}>1$, yielding a purity metric that falls short of the ideal unity value. To delve into the implications of input state purity on entanglement assessment criteria, we conducted an analysis as illustrated in Figure 6. By systematically varying the purity levels to 1.0, 0.40, 0.138, and 0.04, achieved by maintaining a constant squeezing parameter with $r_1=0.69$ and adjusting the anti-squeezing parameter to 0.69, 1.15, 1.7, and 2.3, respectively, we examined their influence. Figure 6a,b explicitly depict the effects of purity on entanglement criteria under symmetric and asymmetric loss conditions, respectively. Intriguingly, under symmetric losses, the inseparability criterion and the PPT criterion remain invariant to changes in the purity of the two-mode squeezed state, once the initial squeezing factor is established. Conversely, in the presence of asymmetric losses, the PPT criterion remains relatively immune, whereas the inseparability criterion becomes acutely sensitive to state purity. As purity diminishes, the violation of the inseparability criterion intensifies markedly, attributed to the heightened total uncertainty that may hinder the fulfillment of its criteria, ultimately hindering entanglement detection. Furthermore, an overemphasis on squeezing a single quadrature component can potentially lead to erroneous entanglement assessments.

4. Conclusions

This paper delves into the utilization of the inseparability criterion in assessing two-mode squeezed states, with a particular focus on analyzing the phenomenon of entanglement detection failures caused by entanglement asymmetry. To this end, we conducted a comparative analysis with the more stringent necessary and sufficient condition—the PPT criterion, both theoretically and experimentally, investigating the instances where the inseparability criterion fails to detect entanglement. Experimentally, we employed a sub-threshold NOPA to generate two-mode squeezed states and introduced optical losses to induce asymmetry in the entangled modes, thereby validating the limitations of the inseparability criterion. Our results reveal that in the presence of symmetric entanglement, the inseparability criterion aligns with the PPT criterion, constituting a necessary and sufficient condition for two-mode Gaussian states. However, under asymmetric entanglement conditions, significant disparities emerge between the two criteria, with the inseparability criterion only serving as a sufficient condition. Consequently, exclusive reliance on the inseparability criterion may result in missed entanglement detection and erroneous entanglement assessments, with the misjudgment rate escalating alongside the intensification of entanglement asymmetry. Hence, when confronted with highly asymmetric two-mode squeezed states, a more prudent application of the inseparability criterion is warranted. This may involve adjusting the covariance matrix weights, incorporating compensation factors into the inseparability criterion calculation, or adopting stricter criteria to ensure accurate entanglement state determination. Additionally, exploring novel neural network-based methods for continuous-variable entanglement detection [41] offers promising avenues. Recent advancements in discrete-variable entanglement detection, such as machine learning approaches [42] and complex-valued neural networks [43], provide valuable insights and techniques that could potentially be adapted to continuous-variable systems, further advancing the field.

Future research could focus on refining entanglement detection methodologies to address the challenges posed by asymmetric entanglement. This includes developing hybrid criteria that combine traditional mathematical approaches with emerging machine learning-based techniques, which hold significant promise for handling complex quantum systems. Practical applications, such as quantum communication and quantum computing, where secure entanglement distribution and entanglement resource management are critical, stand to benefit greatly from these advancements. For instance, in quantum communication, our findings highlight the importance of robust entanglement detection in ensuring the security and reliability of quantum key distribution protocols, particularly in real-world scenarios involving asymmetric entanglement. In quantum computing, accurate identification of entanglement resources could play a pivotal role in optimizing quantum gate operations and error correction schemes, thereby enhancing computational efficiency. Investigating the role of asymmetric entanglement in quantum networks and sensors also represents an exciting avenue for exploration.

In conclusion, this study offers vital insights into the application and underlying principles of the inseparability criterion in quantum information tasks, while also highlighting its potential limitations. Future quantum information science research should prioritize the impact of asymmetric entanglement, continually refining entanglement detection and measurement methodologies. With ongoing research endeavors and technological advancements, we anticipate harnessing the extraordinary potential of quantum entanglement to propel the rapid evolution of quantum technologies.