Discoloration Characteristics of Mechanochromic Sensors in RGB and HSV Color Spaces and Displacement Prediction
Abstract
1. Introduction
2. Preparation and Methodology
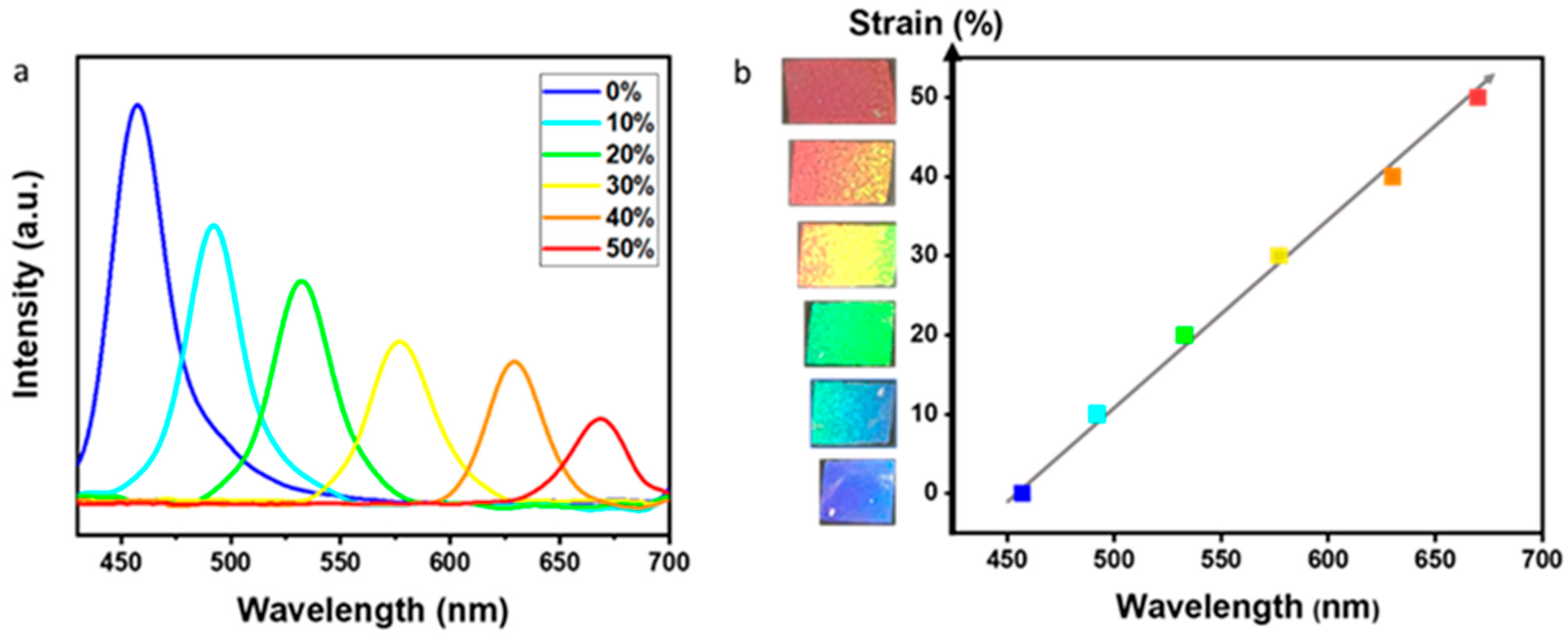
2.1. Fabrication of Mechanochromic Sensor
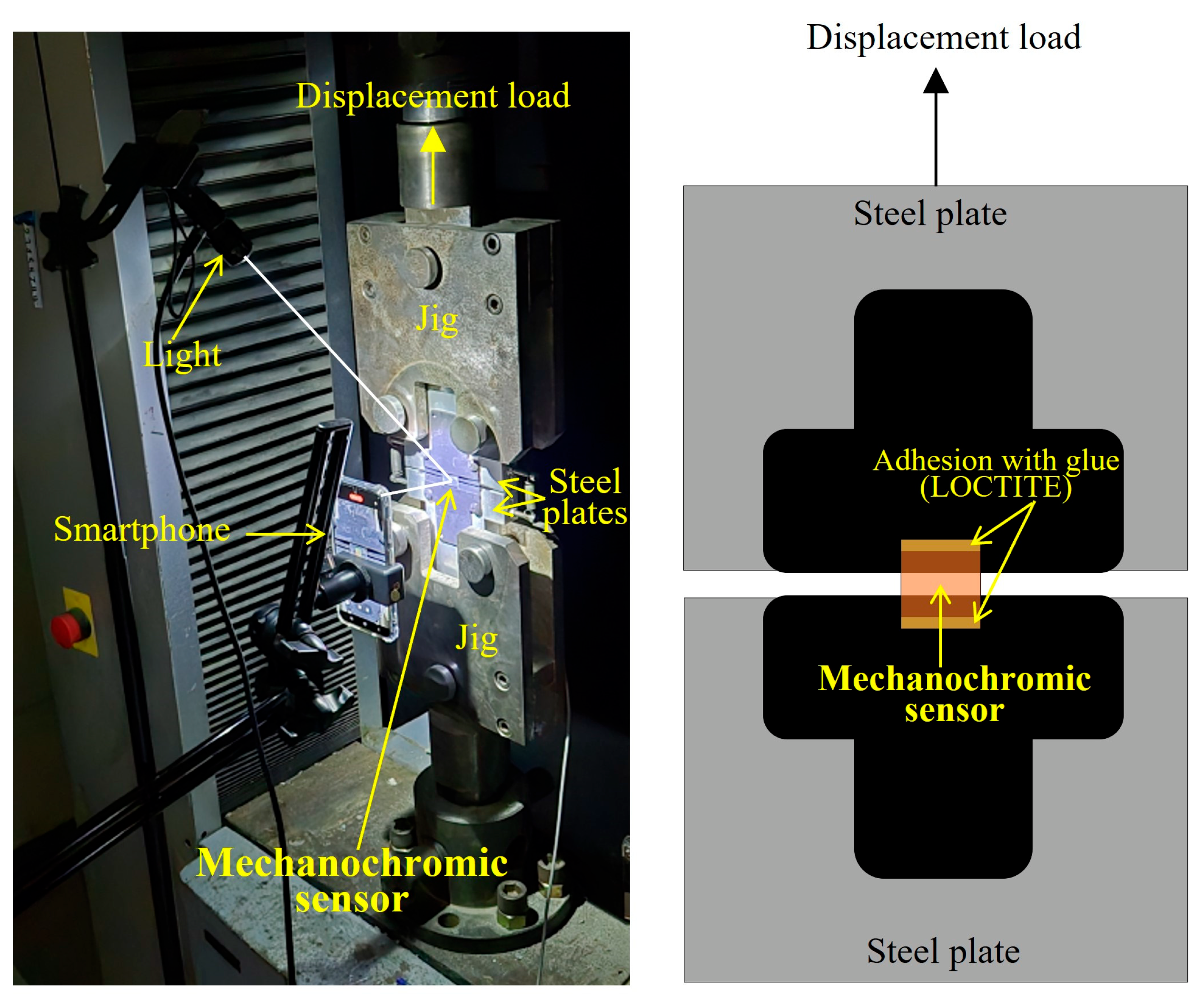
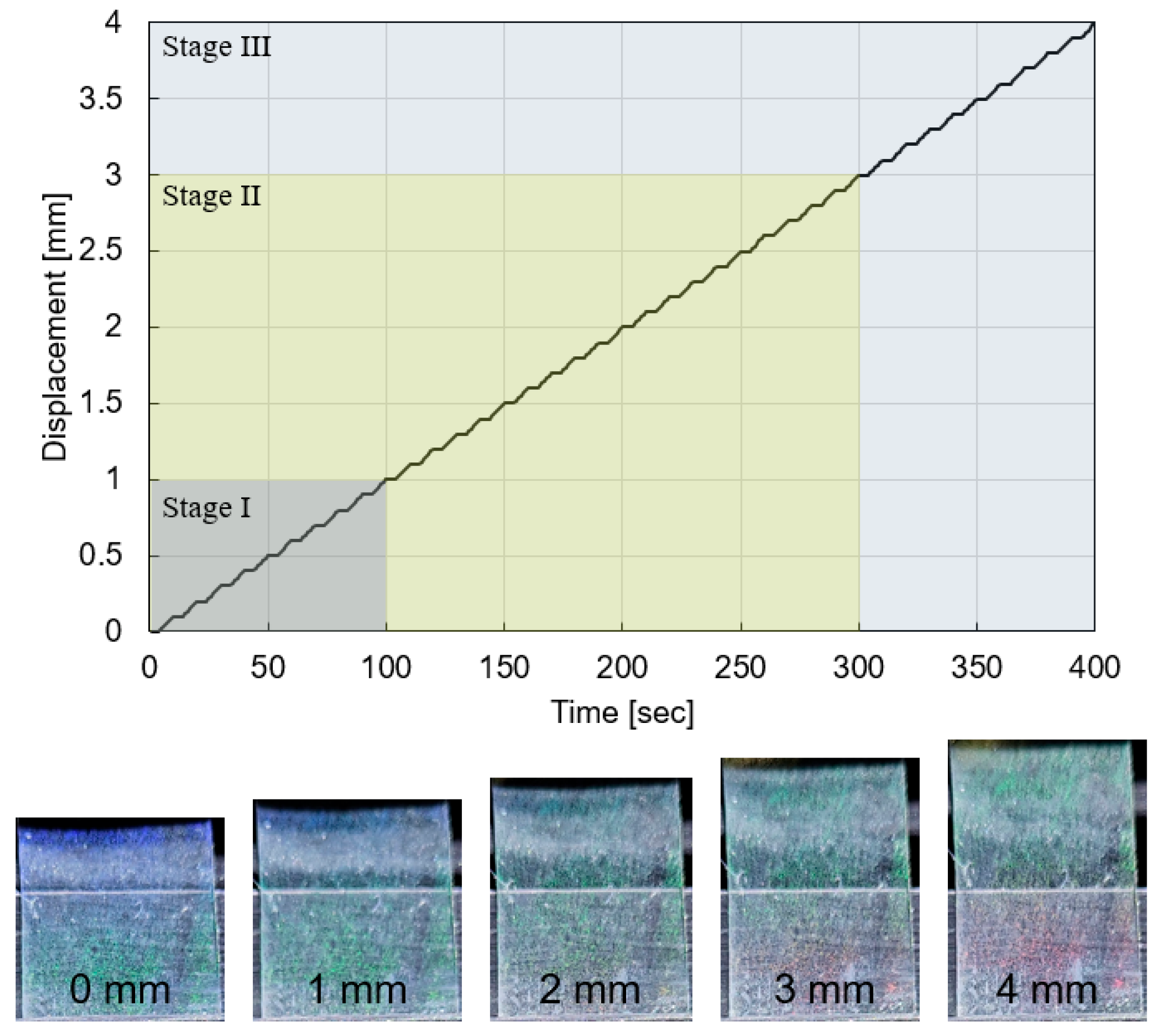
2.2. Measurements of Discoloration and Displacement Under Tensile Load
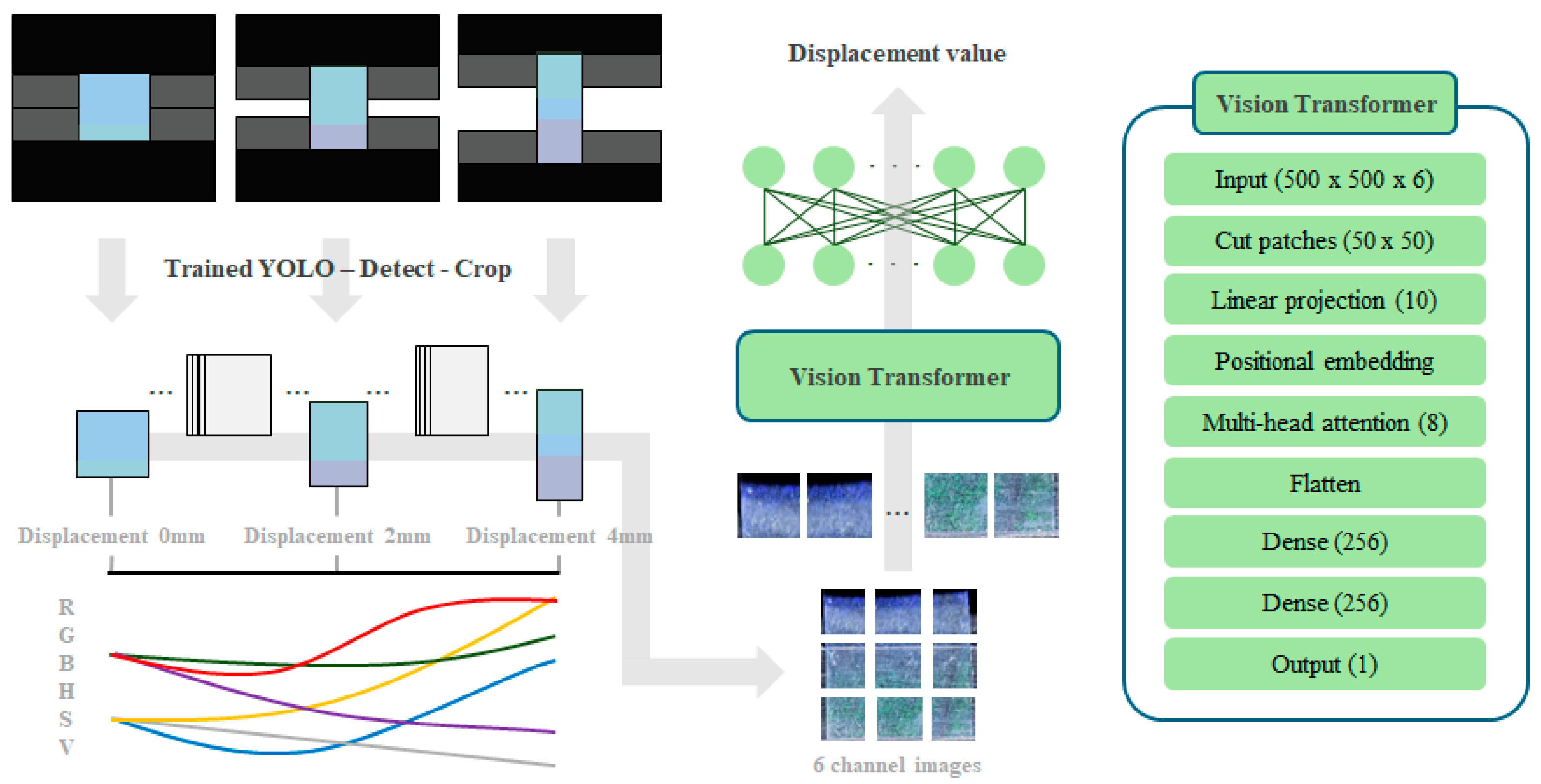
2.3. Methodology of Image Analysis for Quantification of Discoloration
2.3.1. Image Processing
2.3.2. Vision Transformer
3. Results and Discussion
3.1. Relationship Between Deformation and RGB Values
3.2. Relationship Between Deformation and HSV Values
3.3. Sensitivity of the Mechanochromic Sensor and Prediction of Displacement
3.4. Future Works
4. Conclusions
- The RGB color of the mechanochromic sensor showed different discolorations depending on the extent of displacement. B showed significant discoloration at <1 mm displacement, but the discoloration reduced for displacements > 1 mm. At 1.5–2 mm displacement, the discolorations of R and G were dominant, with R showing the largest discoloration behavior at >4 mm displacement.
- HSV also exhibited different behaviors depending on the degree of displacement. In the HSV color space, S exhibited major discoloration at an initial displacement < 1 mm, which was effective up to 3 mm. At displacements between 1–4 mm, the discoloration of H was major.
- For displacements < 1 mm, the discolorations of B and S were the most sensitive and showed the highest fitness for linear relationships, suggesting their suitability for predicting small displacements in concrete. However, owing to the influence of other colors on the small displacement as well as on large displacements, an in-depth study is required to predict the overall displacement.
- The ViT model, built with six RGB and HSV channels, exhibited a high prediction accuracy of R2 = 0.997 for the measured displacement. This presents a novel methodology for predicting displacement through the discoloration of the mechanochromic sensor. However, the different discoloration characteristics depending on the angle of incidence of the mechanochromic sensor should be considered in future studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, S.-J.; You, I.; Kim, S.; Shin, H.-O.; Yoo, D.-Y. Self-Sensing Capacity of Ultra-High-Performance Fiber-Reinforced Concrete Containing Conductive Powders in Tension. Cem. Concr. Compos. 2022, 125, 104331. [Google Scholar] [CrossRef]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced structural health monitoring of concrete structures with the aid of acoustic emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Soman, R.; Wee, J.; Peters, K. Optical fiber sensors for ultrasonic structural health monitoring: A review. Sensors 2021, 21, 7345. [Google Scholar] [CrossRef] [PubMed]
- Fotouhi, M.; Sadeghi, S.; Jalalvand, M.; Ahmadi, M. Analysis of the damage mechanisms in mixed-mode delamination of laminated composites using acoustic emission data clustering. J. Thermoplast. Compos. Mater. 2017, 30, 318–340. [Google Scholar] [CrossRef]
- Hoang Minh, N.H.; Kim, K.; Kang, D.H.; Yoo, Y.-E.; Yoon, J.S. Photonic crystals for dichotomous sensitivity to strain for sensor and indicator applications. ACS Appl. Nano Mater. 2024, 7, 20361–20369. [Google Scholar] [CrossRef]
- Bae, G.; Seo, M.; Lee, S.; Bae, D.; Lee, M. Colorimetric detection of mechanical deformation in metals using thin-film mechanochromic sensor. Adv. Mater. Technol. 2021, 6, 2100479. [Google Scholar] [CrossRef]
- Bae, G.; Seo, M.; Lee, S.; Bae, D.; Lee, M. Angle-insensitive Fabry–Perot mechanochromic sensor for real-time structural health monitoring. Adv. Mater. Technol. 2021, 6, 2100118. [Google Scholar] [CrossRef]
- Tabatabaeian, A.; Liu, S.; Harrison, P.; Schlangen, E.; Fotouhi, M. A review on self-reporting mechanochromic composites: An emerging technology for structural health monitoring. Compos. A 2022, 163, 107236. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, X. A review of mechanochromic polymers and composites: From material design strategy to advanced electronics application. Compos. B Eng. 2021, 227, 109434. [Google Scholar] [CrossRef]
- Tang, C. Fundamental aspects of stretchable mechanochromic materials: Fabrication and characterization. Materials 2024, 17, 3980. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Wang, Q.; Zheng, X. Flexible mechanochromic photonic crystals: Routes to visual sensors and their mechanical properties. J. Mater. Chem. C 2018, 6, 3182–3199. [Google Scholar] [CrossRef]
- Pyeon, S.; Kim, H.; Choe, G.; Lee, M.; Jeon, J.; Kim, G.; Nam, J. Crack evaluation of concrete using mechanochromic Sensor. Materials 2023, 16, 662. [Google Scholar] [CrossRef] [PubMed]
- ACI Committee. 224-Cracking, Causes, Evaluation, and Repair of Cracks in Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2007. [Google Scholar]
- KDS 14 20 30–Serviceability design standard of concrete structure. In Korean Des. Stand. 2021.
- Minh, N.H.; Kim, K.; Kang, D.H.; Yoo, Y.-E.; Yoon, J.S. Fabrication of robust and reusable mold with nanostructures and its application to anti-counterfeiting surfaces based on structural colors. Nanotechnology 2021, 32, 495302. [Google Scholar] [CrossRef]
- Minh, N.H.; Kim, K.; Kang, D.H.; Yoo, Y.-E.; Yoon, J.S. An angle-compensating colorimetric strain sensor with wide working range and its fabrication method. Sci. Rep. 2022, 12, 21926. [Google Scholar] [CrossRef] [PubMed]
- Quan, Y.-J.; Kim, Y.-G.; Kim, M.-S.; Min, S.-H.; Ahn, S.-H. Stretchable Biaxial and Shear Strain Sensors Using Diffractive Structural Colors. ACS Nano 2020, 14, 5392–5399. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2010, arXiv:2010.11929. [Google Scholar]
- Lee, S.H.; Lee, S.; Song, B.C. Vision Transformer for Small-Size Datasets. arXiv 2021, arXiv:2112.13492. [Google Scholar]
- Battisti, A.; Minei, P.; Pucci, A.; Bizzarri, R. Hue-based quantification of mechanochromism towards a cost-effective detection of mechanical strain in polymer systems. Chem. Commun. 2016, 53, 248–251. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Adam, M.L.; Zhao, Y.; Zheng, W.; Gao, L.; Yin, Z.; Zhao, H. Machine Learning-Enhanced Flexible Mechanical Sensing. Nano-Micro Lett. 2023, 15, 55. [Google Scholar] [CrossRef]
- De Castro, L.D.C.; Scabini, L.; Ribas, L.C.; Bruno, O.M.; Oliveir, O.N., Jr. Machine Learning and Image Processing to Monitor Strain and Tensile Forces with Mechanochromic Sensors. Expert Syst. Appl. 2023, 212, 118792. [Google Scholar] [CrossRef]

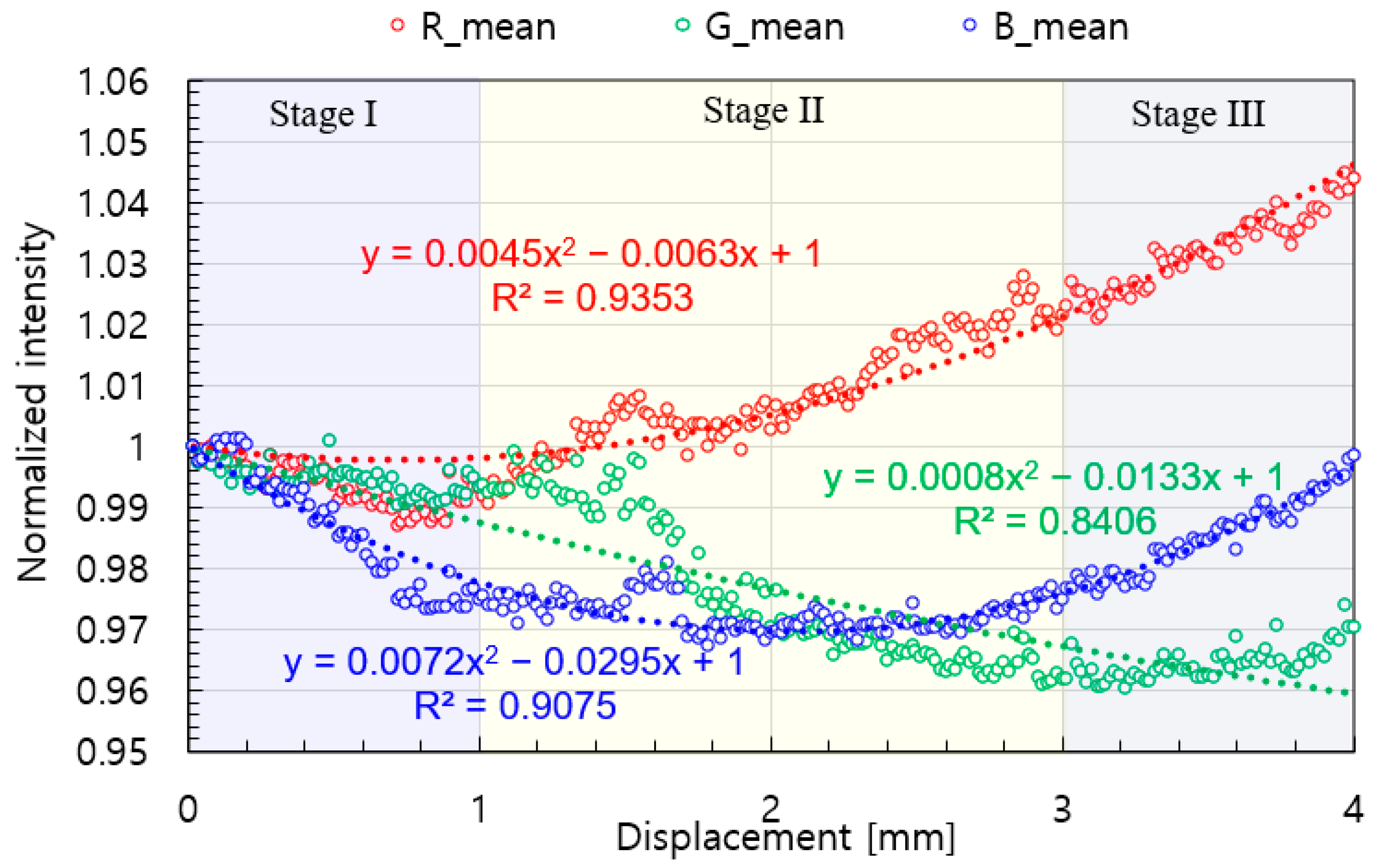



| Normalized Color | I (0–1 mm) | II (1–3 mm) | III (3–4 mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | R2 | a | b | R2 | a | b | R2 | |
| R | −0.012 | 1 | 0.64 | 0.015 | 0.979 | 0.89 | 0.020 | 0.962 | 0.90 |
| G | −0.009 | 1 | 0.38 | −0.020 | 1.016 | 0.88 | 0.007 | 0.942 | 0.47 |
| B | −0.028 | 1 | 0.93 | −0.001 | 0.975 | 0.09 | 0.021 | 0.913 | 0.94 |
| H | −0.027 | 1 | 0.89 | 0.051 | 0.912 | 0.96 | 0.028 | 0.980 | 0.78 |
| S | −0.076 | 1 | 0.87 | −0.048 | 0.950 | 0.69 | −0.004 | 0.828 | 0.00 |
| V | −0.028 | 1 | 0.93 | −0.001 | 0.974 | 0.02 | 0.020 | 0.914 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, W.-J.; Yang, M.; You, I.; Yoon, Y.-S.; Ryu, G.-S.; An, G.-H.; Yoon, J.S. Discoloration Characteristics of Mechanochromic Sensors in RGB and HSV Color Spaces and Displacement Prediction. Appl. Sci. 2025, 15, 1066. https://doi.org/10.3390/app15031066
Choi W-J, Yang M, You I, Yoon Y-S, Ryu G-S, An G-H, Yoon JS. Discoloration Characteristics of Mechanochromic Sensors in RGB and HSV Color Spaces and Displacement Prediction. Applied Sciences. 2025; 15(3):1066. https://doi.org/10.3390/app15031066
Chicago/Turabian StyleChoi, Woo-Joo, Myongkyoon Yang, Ilhwan You, Yong-Sik Yoon, Gum-Sung Ryu, Gi-Hong An, and Jae Sung Yoon. 2025. "Discoloration Characteristics of Mechanochromic Sensors in RGB and HSV Color Spaces and Displacement Prediction" Applied Sciences 15, no. 3: 1066. https://doi.org/10.3390/app15031066
APA StyleChoi, W.-J., Yang, M., You, I., Yoon, Y.-S., Ryu, G.-S., An, G.-H., & Yoon, J. S. (2025). Discoloration Characteristics of Mechanochromic Sensors in RGB and HSV Color Spaces and Displacement Prediction. Applied Sciences, 15(3), 1066. https://doi.org/10.3390/app15031066







