The Multi-Resolution Migration Imaging Method for Grounded Electrical Source Transient Electromagnetic Virtual Wavefield
Abstract
:Featured Application
Abstract
1. Introduction
2. Differential Pulse Spectrum Analysis and 3D Forward Modeling
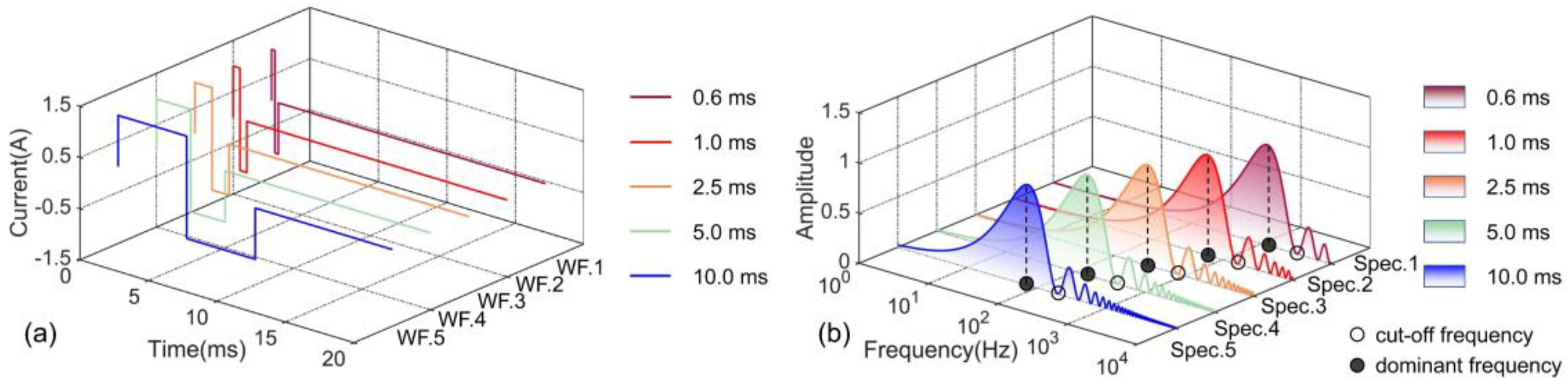
2.1. Differential Pulse Spectrum Analysis
2.2. 3D Forward Modeling of Differential Pulse
2.3. Validation of Magnetic Flux Density for Differential Pulse
3. Preconditioned Precise Integration Time-Sweeping Method
3.1. Preconditioned Precise Integration Algorithm
3.2. Time-Sweeping Wavefield Reverse Transformation Method
4. The Multi-Resolution Pre-Stack Migration Imaging Method
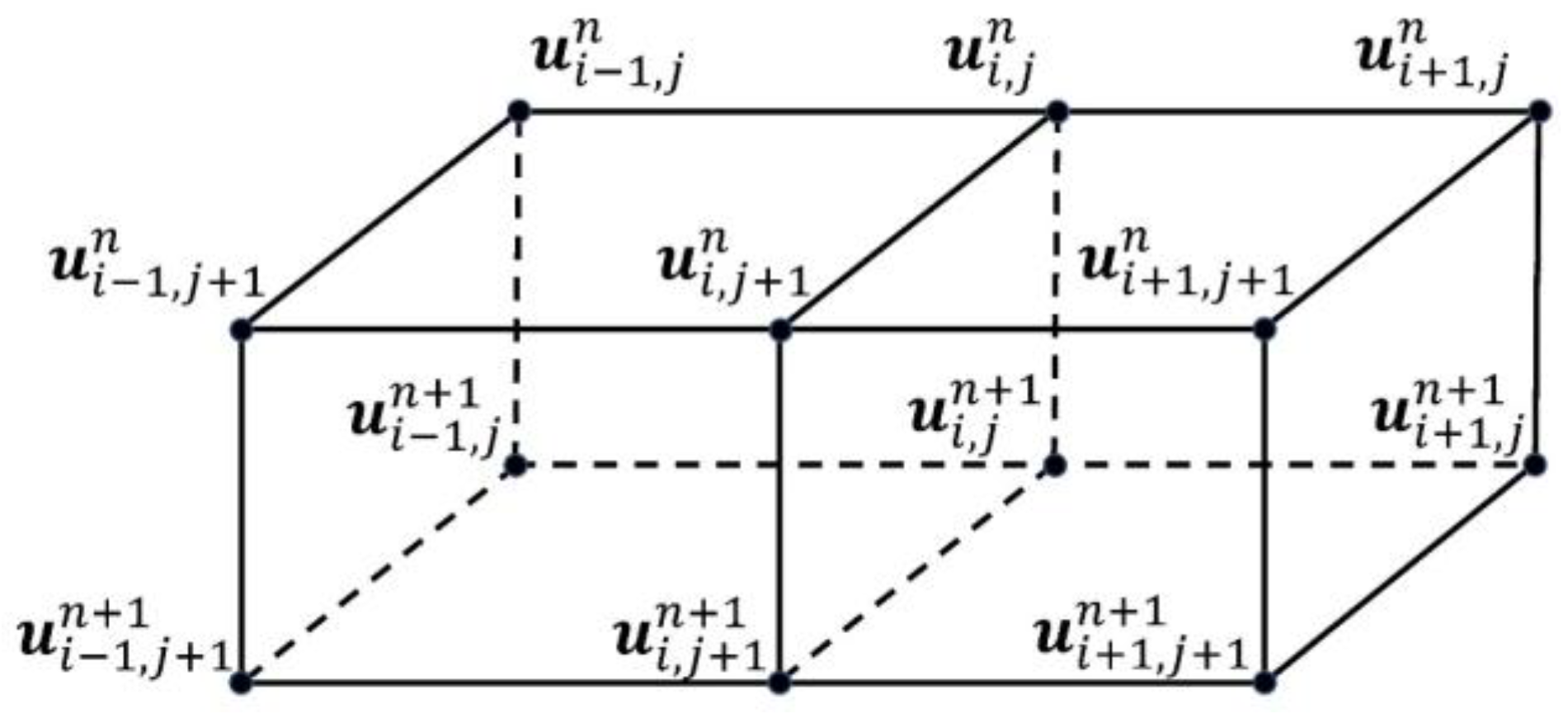
4.1. The Finite-Difference Migration Imaging Method
4.2. The Correlation Stacking Method for Differential Pulse Imaging
5. Numerical Examples
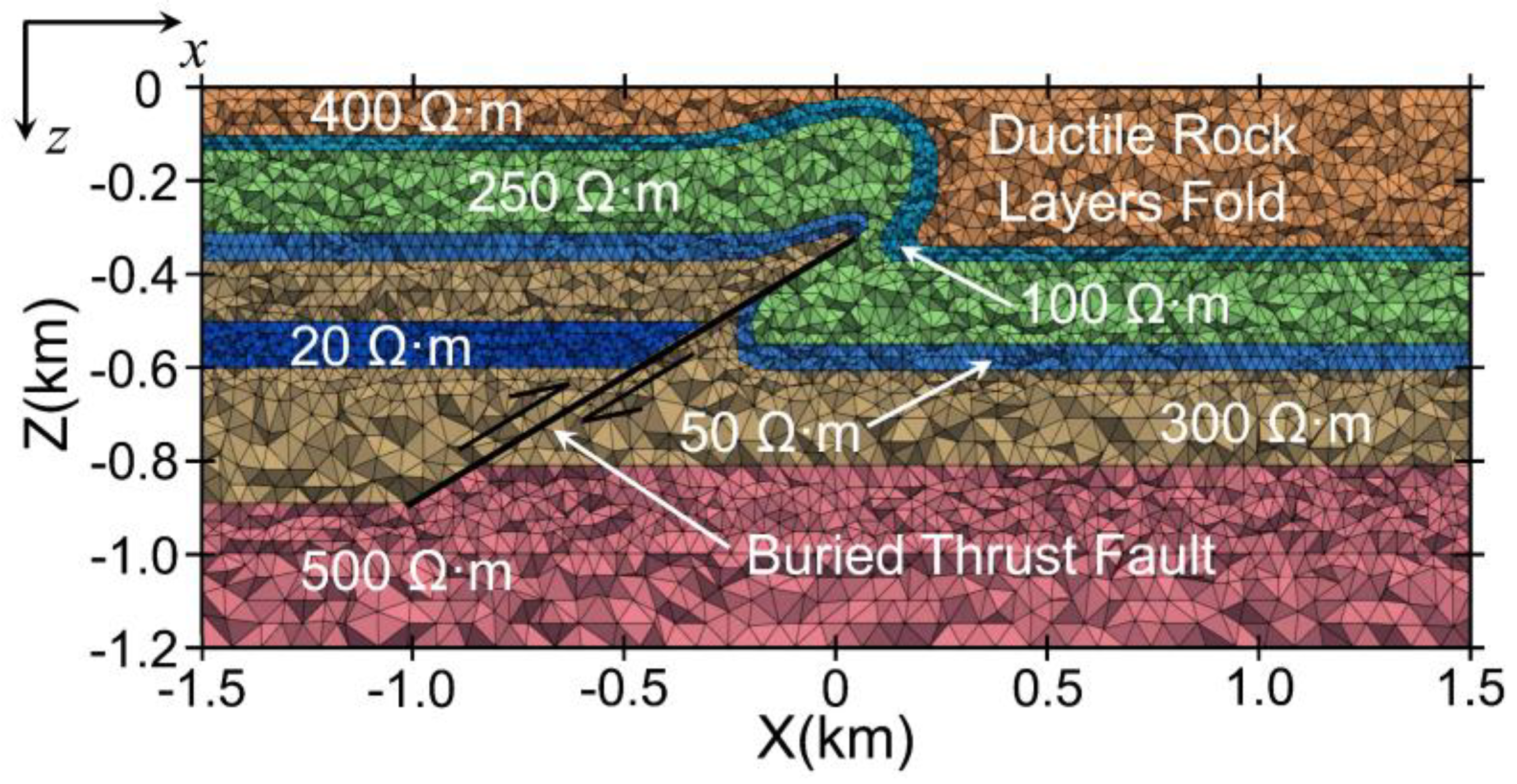
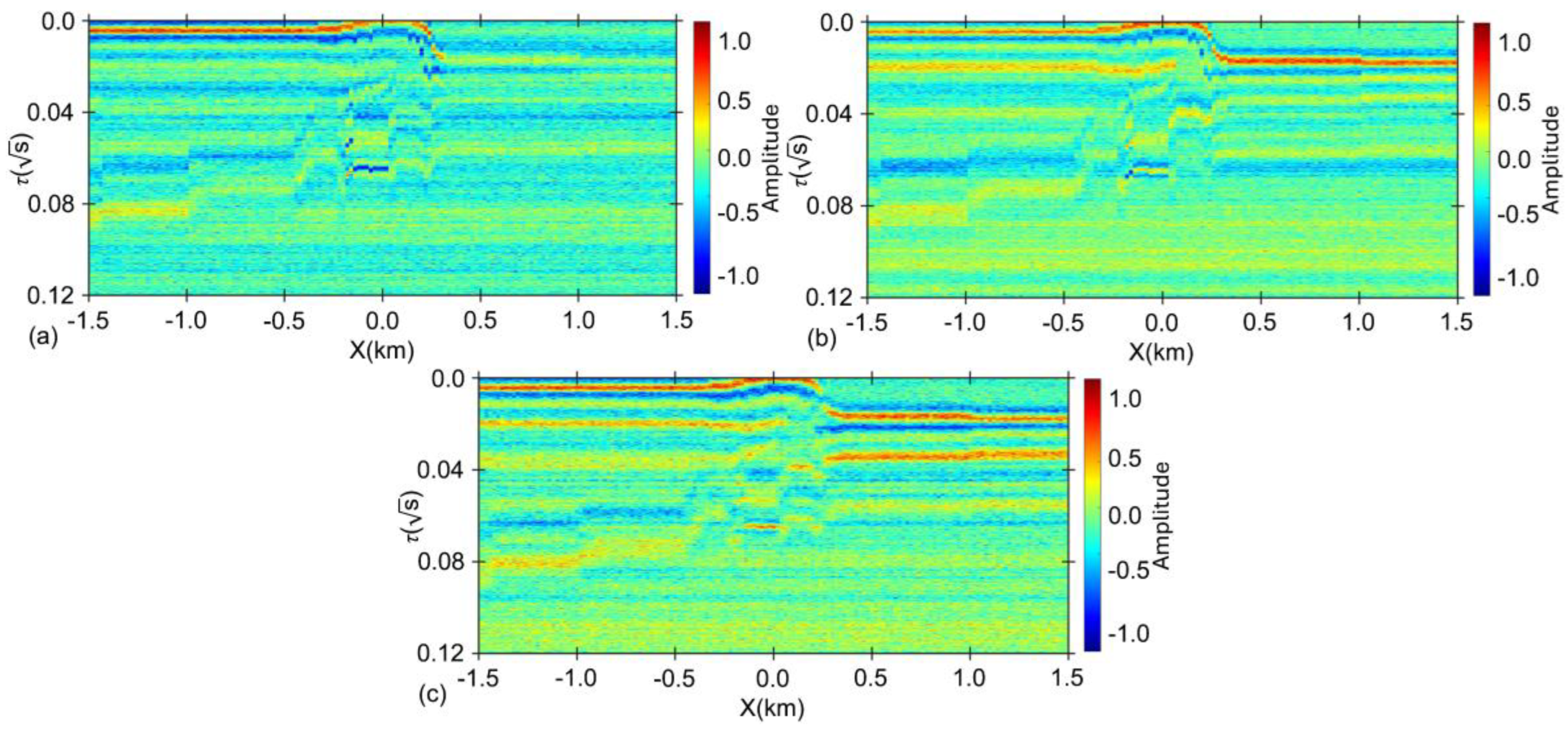
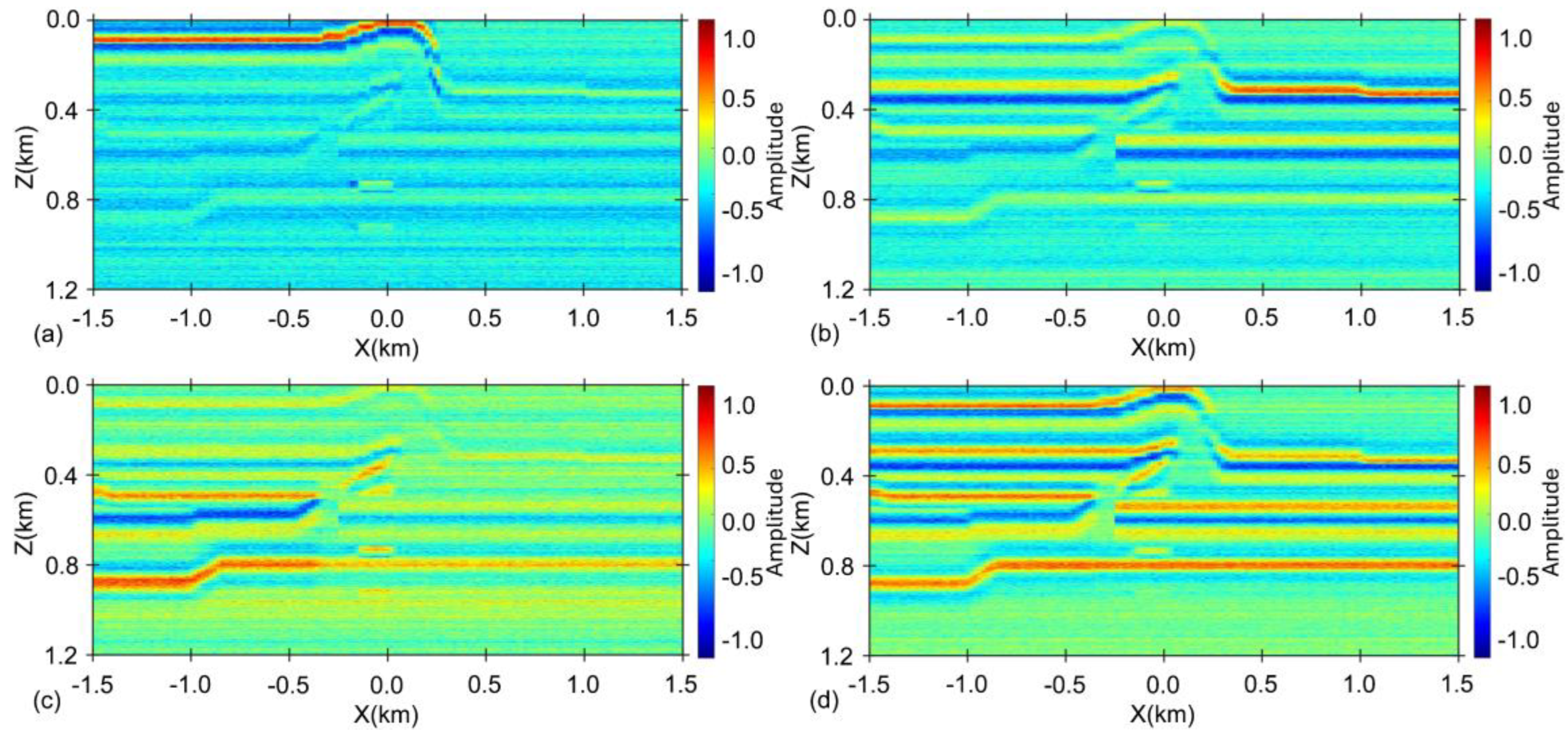
5.1. Buried Thrust Fault Model
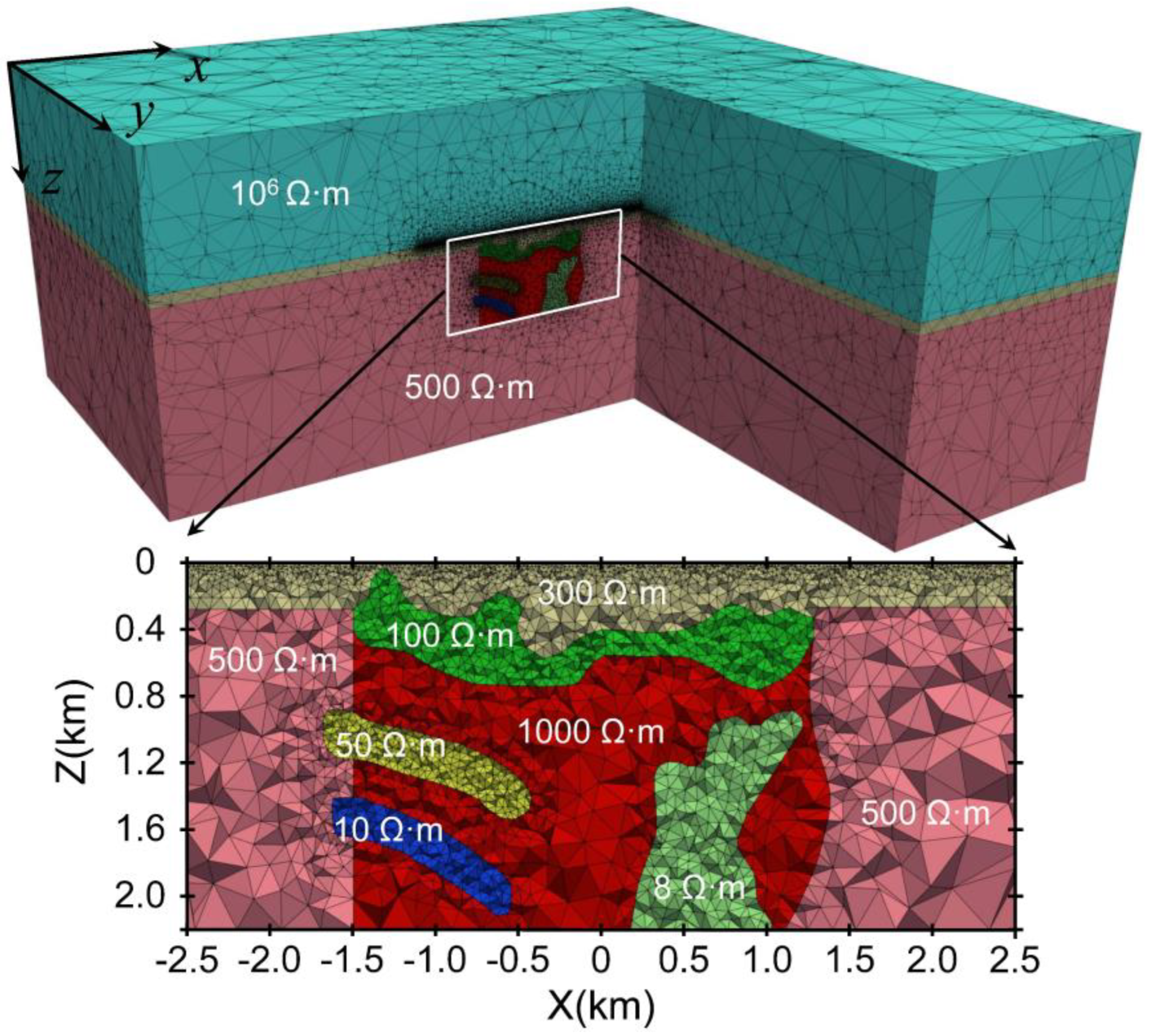
5.2. Complex Geological Model
6. Conclusions
- When square waves are used as the excitation waveform, the dominance of low-frequency harmonics hinders the achievement of high-resolution detection. In contrast, differential pulses effectively enhance high-frequency harmonics, thereby mitigating the impact of low-frequency harmonics on detection performance.
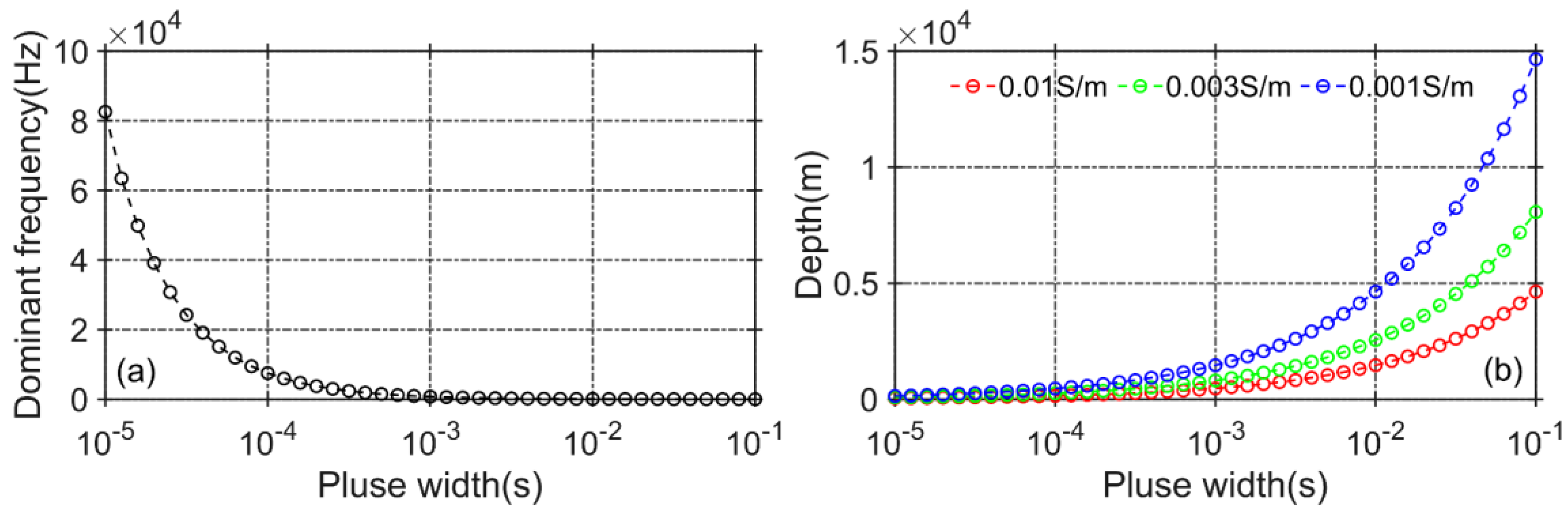
- Based on the buried thrust fault model, square waves and differential pulses with different pulse widths were used as excitation sources. From the relative anomaly maps of bz, it is observed that the anomaly response increased by 53.7%, indicating that differential pulses provide higher detection resolution.
- The TEM diffusion field exhibits a stronger volumetric effect. Converting it into a virtual wavefield can effectively mitigate the impact of the volumetric effect. However, the virtual wavefield cannot accurately represent the subsurface features, and it is necessary to apply migration imaging methods to obtain the geometric shapes of the stratigraphic interfaces.
- Square waves with different pulse widths can effectively reflect the geometric characteristics of the shallow subsurface layers. As the pulse width of the square wave increases, although the resolution of the deep subsurface layers improves to some extent, the enhancement remains limited.
- Imaging results from the buried thrust fault model and the complex geological model demonstrate that differential pulses enable multi-resolution detection across different depth ranges, which can subsequently be used to obtain high-resolution imaging through correlation stacking.
- This paper investigates the use of differential pulses with varying pulse widths to excite transient electromagnetic fields, and employs migration imaging methods to image the interfaces of geological anomalies. Future research will focus on developing resistivity imaging methods using differential pulses with different pulse widths.
- This study primarily addresses the fundamental theoretical research on transient electromagnetic multi-resolution detection. The corresponding equipment is currently in the final stage of debugging. We plan to conduct the first experimental validation once the equipment is completed, with the experimental validation expected to begin in August 2025. At that time, a systematic evaluation of the proposed method will be conducted.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xue, G.Q.; Wu, X.; Chen, K.; Lei, K.X.; Zhao, Y.; Lv, P.F.; Shi, J.J. An analysis of the shadow effect for the short-offset transient electromagnetic method. J. Appl. Geophys. 2022, 206, 104833. [Google Scholar] [CrossRef]
- Fournier, D.; Kang, S.; McMillan, M.; Oldenburg, D. Inversion of airborne geophysics over the DO-27/DO-18 kimberlites-Part 2: Electromagnetics. Interpretation 2017, 5, T313–T325. [Google Scholar] [CrossRef]
- Di, Q.Y.; Xue, G.Q.; Yin, C.C.; Li, X. New methods of controlled-source electromagnetic detection in China. Sci. China Earth Sci. 2020, 50, 1219–1227. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Liu, L.B.; Liu, S.C.; Yue, J.H. Surface-to-Underground Transient Electromagnetic Detection of Water-Bearing Goaves. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5303–5318. [Google Scholar] [CrossRef]
- Gottschalk, L.; Knight, R.; Asch, T.; Abraham, J.; Cannia, J. Using an airborne electromagnetic method to map saltwater intrusion in the Northern Salinas Valley, CA. Geophysics 2019, 85, B119–B131. [Google Scholar] [CrossRef]
- Li, S.C.; Sun, H.F.; Lu, X.S.; Li, X. Three-dimensional modeling of transient electromagnetic responses of water-bearing structures in front of a tunnel face. J. Environ. Eng. Geophys. 2014, 19, 13–32. [Google Scholar] [CrossRef]
- Xue, G.Q.; Li, X.; Yu, S.B.; Chen, W.Y.; Ji, Y.J. The application of ground-airborne TEM systems for underground cavity detection in China. J. Environ. Eng. Geophys. 2018, 23, 103–113. [Google Scholar] [CrossRef]
- Li, X.; Hu, W.M.; Xue, G.Q. 3D modeling of multi-radiation source semi-airborne transient electromagnetic response. Chin. J. Geophys. 2021, 64, 716–723. [Google Scholar]
- Lu, K.L.; Li, X.; Fan, Y.N.; Zhou, J.M.; Qi, Z.P.; Li, W.H.; Li, H. The application of multi-grounded source transient electromagnetic method in the detections of coal seam goafs in Gansu Province, China. J. Geophys. Eng. 2021, 18, 515–528. [Google Scholar] [CrossRef]
- Qi, Y.F.; Yin, C.C.; Liu, Y.H.; Cai, J. 3D time-domain airborne EM full-wave forward modeling based on instantaneous current pulse. Chin. J. Geophys. 2017, 60, 369–382. [Google Scholar]
- Cao, H.K.; Qi, Z.P.; Li, X.; Qi, Y.F.; Cheng, W.S. Transient electromagnetic apparent resistivity calculation considering turn-off time and shallow resolution analysis of different waveforms. Prog. Geophys. 2022, 37, 1704–1716. [Google Scholar]
- Qi, Z.P.; Li, X.; Lu, X.S.; Zhang, Y.Y.; Yao, W.H. Inverse transformation algorithm of transient electromagnetic field and its high-resolution continuous imaging interpretation method. J. Geophys. Eng. 2015, 12, 242–252. [Google Scholar] [CrossRef]
- Li, W.H.; Liu, B.; Li, S.C.; Li, H.; Lu, K.L.; Li, X. Study on multi-resolution imaging method of urban underground space based on high performance transient electromagnetic source. Chin. J. Geophys. 2020, 63, 4553–4564. [Google Scholar]
- Zeng, S.H.; Hu, X.Y.; Li, J.H.; Farquharson, C.G.; Wood, P.C.; Lu, X.S.; Peng, R.H. Effects of full transmitting-current waveforms on transient electromagnetics: Insights from modeling the Albany graphite deposit. Geophysics 2019, 84, E255–E268. [Google Scholar] [CrossRef]
- Li, J.H.; Wang, Y. Effects of base frequency, duty cycle, and waveform repetition on transient electromagnetic responses: Insights from models of a deep-buried conductor. Geophysics 2024, 89, E165–E176. [Google Scholar] [CrossRef]
- Liu, G.M. Effect of transmitter current waveform on airborne TEM response. Explor. Geophys. 1998, 29, 34–41. [Google Scholar] [CrossRef]
- Chen, S.D.; Lin, J.; Zhang, S. Effect of transmitter current waveform on TEM response. Chin. J. Geophys. 2012, 55, 709–716. [Google Scholar]
- Yin, C.C.; Ren, X.Y.; Liu, Y.H.; Cai, J. Exploration capability of airborne TEM systems for typical targets in the subsurface. Chin. J. Geophys. 2015, 58, 3370–3379. [Google Scholar]
- Zhao, Y.; Xu, F.; Li, X.; Lu, K.L. Exploration capability of transmitter current waveform on shallow water TEM response. Chin. J. Geophys. 2019, 62, 1526–1540. [Google Scholar]
- Xue, G.Q.; Gelius, L.J.; Li, X.; Qi, Z.P.; Chen, W.Y. 3D pseudo-seismic imaging of transient electromagnetic data—A feasibility study. Geophys. Prospect. 2013, 61, 561–571. [Google Scholar] [CrossRef]
- Li, X.; Xue, G.Q.; Zhi, Q.Q.; Li, H.; Zhong, H.S. TEM pseudo-wave field extractions using a modified algorithm. J. Environ. Eng. Geophys. 2018, 23, 33–45. [Google Scholar] [CrossRef]
- Fan, Y.N.; Lu, K.L.; Li, X.; Qi, Z.P.; Ma, J.; Fan, K.R. Mapping coal water-filled zones using multi-radiation source transient electromagnetic pseudo-seismic Born approximation imaging and apparent resistivity imaging in Gansu, China. J. Appl. Geophys. 2022, 203, 104717. [Google Scholar] [CrossRef]
- Lu, K.L.; Fan, Y.N.; Li, X.; Zhou, J.M.; Fan, K.R. Transient electromagnetic pseudo wavefield imaging based on the sweep-time preconditioned precise integration algorithm. J. Appl. Geophys. 2023, 209, 104937. [Google Scholar] [CrossRef]
- Fan, K.R.; Guo, J.L.; Wang, G.; Xu, L.; Lu, K.L.; Sun, S.Q.; He, P.; Li, Z.Q.; Wang, N. A Self-adaptive Algorithm of Inverse Wavefield Transform for the Vertically Magnetic Components of the Loop-source Transient Electromagnetic Data. IEEE Geosci. Remote Sens. Lett. 2025, 22, 7501005. [Google Scholar] [CrossRef]
- Lu, K.L.; Li, X.; Qi, Z.P.; Fan, Y.N.; Zhou, J.M.; Li, W.H.; Li, H.; Zhang, M.J.; Wang, Y.Z. A precise integration transform algorithm for transformation from the transient electromagnetic diffusion field into the pseudo wave field. Chin. J. Geophys. 2021, 64, 3379–3390. [Google Scholar]
- Xue, J.J.; Cheng, J.L.; Gelius, L.J.; Wu, X.; Zhao, Y. Full waveform inversion of transient electromagnetic data in the time domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2006408. [Google Scholar] [CrossRef]
- Li, X.; Xue, G.Q.; Song, J.P.; Guo, W.B.; Wu, J.J. An optimize method for transient electromagnetic field-wave field conversion. Chin. J. Geophys. 2005, 48, 1185–1190. [Google Scholar] [CrossRef]
- Qi, Z.P.; Li, X.; Wu, Q.; Sun, H.F.; Yang, Z.L. A new algorithm for full-time-domain wave-field transformation based on transient electromagnetic method. Chin. J. Geophys. 2013, 56, 3581–3595. [Google Scholar]
- Xue, J.J.; Cheng, J.L.; Xue, G.Q.; Li, H.; Zhong, H.S.; Lei, K.X.; Li, X. Extracting Pseudo Wave Fields from Transient Electromagnetic Fields Using a Weighting Coefficients Approach. J. Environ. Eng. Geophys. 2019, 24, 351–359. [Google Scholar] [CrossRef]
- Li, X.; Yang, H.; Qi, Z.P.; Sun, N.Q. Virtual wave field characteristic extractions based on multi-window time-sweep wave field transformation. J. Appl. Geophys. 2022, 204, 104701. [Google Scholar] [CrossRef]
- Li, X.; Qi, Z.P.; Xue, G.Q.; Fan, T.; Zhu, H.W. Three dimensional curved surface continuation image based on TEM pseudo wave-field. Chin. J. Geophys. 2010, 53, 3005–3011. [Google Scholar]
- Xue, G.Q.; Li, X.; Qi, Z.P.; Fan, T.; Zhou, N.N. Study of sharpen the wave-form of TEM pseudo-seismic. Chin. J. Geophys. 2011, 54, 1384–1390. [Google Scholar]
- Lu, K.L.; Fan, Y.N.; Li, X.; Zhou, J.M. Finite difference transient electromagnetic migration imaging for grounded sources. Chin. J. Geophys. 2023, 66, 854–869. [Google Scholar]
- Lu, K.L.; Zhou, J.M.; Li, X.; Fan, Y.N.; Qi, Z.P.; Cao, H.K. 3D large-scale transient electromagnetic modeling using a Shift-and-Invert Krylov subspace method. J. Appl. Geophys. 2022, 198, 104573. [Google Scholar] [CrossRef]
- Yin, C.C.; Qi, Y.F.; Liu, Y.H.; Cai, J. 3D time-domain airborne EM forward modeling with topography. J. Appl. Geophys. 2016, 134, 11–22. [Google Scholar] [CrossRef]
- Börner, R.U.; Renst, O.G.; Güttel, S. Three-dimensional transient electromagnetic modelling using rational Krylov methods. Geophys. J. Int. 2015, 202, 2025–2043. [Google Scholar] [CrossRef]
- Zhou, J.M.; Lu, K.L.; Li, X.; Liu, W.T.; Qi, Z.P.; Qi, Y.F. 3-D large-scale TEM modeling using restarting polynomial Krylov method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Lu, K.L.; Fan, Y.N.; Zhou, J.M.; Li, X.; Li, H.; Fan, J.R. 3D anisotropic TEM modeling with loop source using model reduction method. J. Geophys. Eng. 2022, 19, 403–417. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Li, W.H.; Xue, J.J.; Li, X. Development of multi resolution transient electromagnetic virtual wave-field migration imaging method. J. Appl. Geophys. 2024, 222, 105314. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Li, X.; Yue, J.; Fan, Y.; Yang, Q.; Teng, X. The Multi-Resolution Migration Imaging Method for Grounded Electrical Source Transient Electromagnetic Virtual Wavefield. Appl. Sci. 2025, 15, 1107. https://doi.org/10.3390/app15031107
Lu K, Li X, Yue J, Fan Y, Yang Q, Teng X. The Multi-Resolution Migration Imaging Method for Grounded Electrical Source Transient Electromagnetic Virtual Wavefield. Applied Sciences. 2025; 15(3):1107. https://doi.org/10.3390/app15031107
Chicago/Turabian StyleLu, Kailiang, Xiu Li, Jianhua Yue, Ya’nan Fan, Qinrun Yang, and Xiaozhen Teng. 2025. "The Multi-Resolution Migration Imaging Method for Grounded Electrical Source Transient Electromagnetic Virtual Wavefield" Applied Sciences 15, no. 3: 1107. https://doi.org/10.3390/app15031107
APA StyleLu, K., Li, X., Yue, J., Fan, Y., Yang, Q., & Teng, X. (2025). The Multi-Resolution Migration Imaging Method for Grounded Electrical Source Transient Electromagnetic Virtual Wavefield. Applied Sciences, 15(3), 1107. https://doi.org/10.3390/app15031107




