Analysis of Shell Egg Pasteurization Using Computational Fluid Dynamics
Abstract
:Featured Application
Abstract
1. Introduction
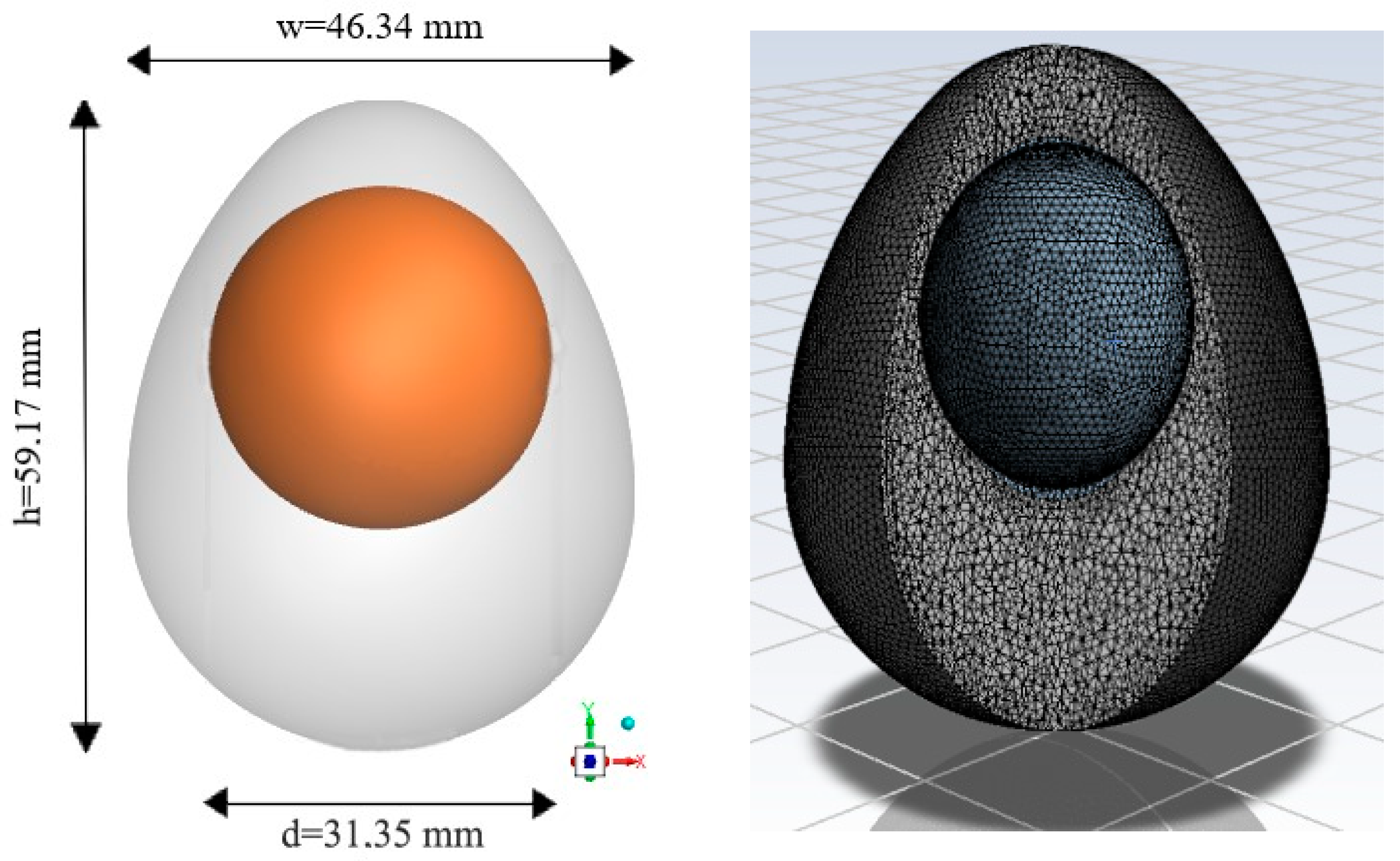
2. Materials and Methods
2.1. Convective Heat Transfer Coefficient
2.2. Validation Experiments
2.3. Thermal Process Calculations
2.4. Quality Degradation
3. Results and Discussion
3.1. Convective Heat Transfer Coefficient
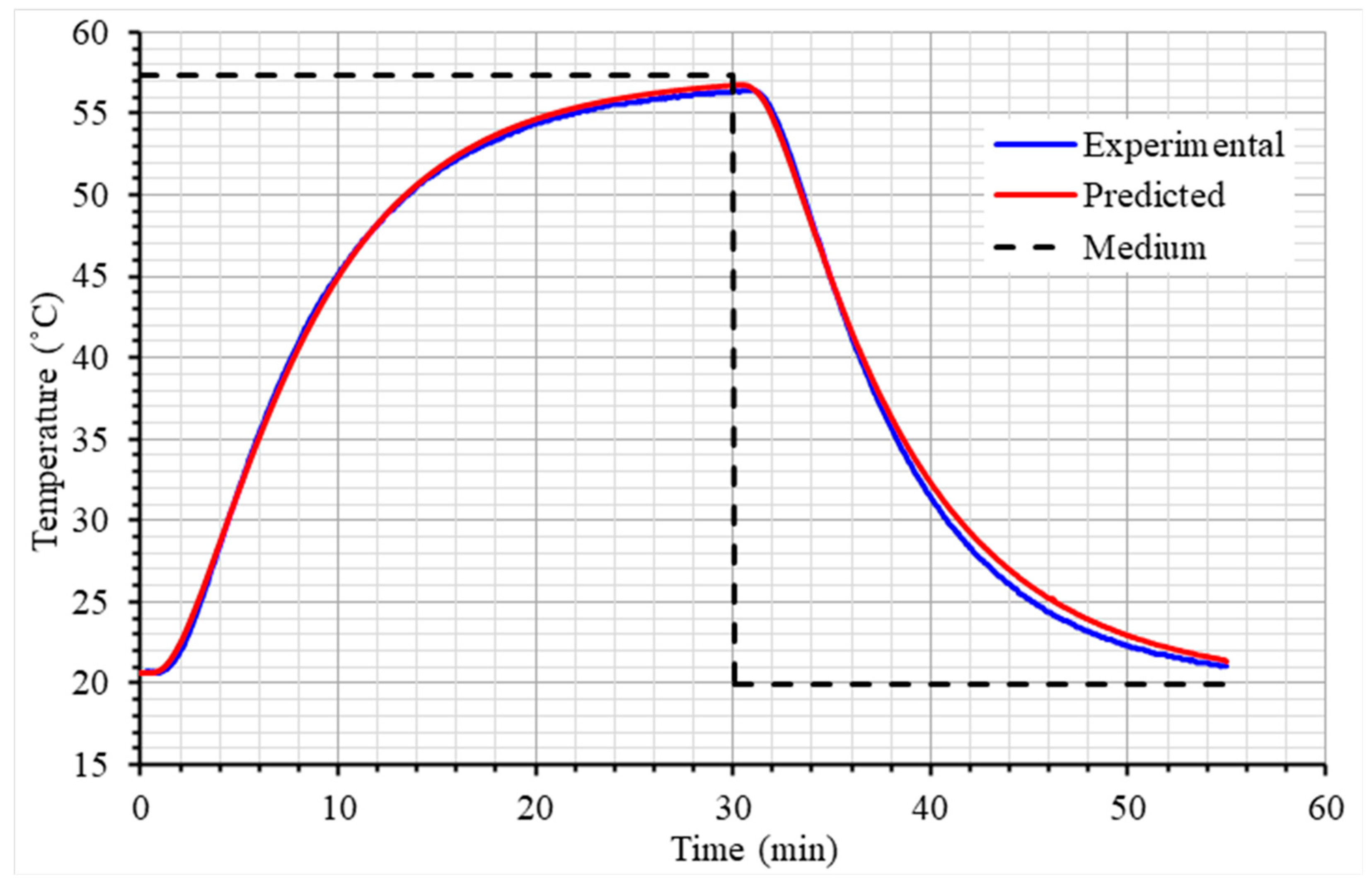
3.2. Validation Experiments
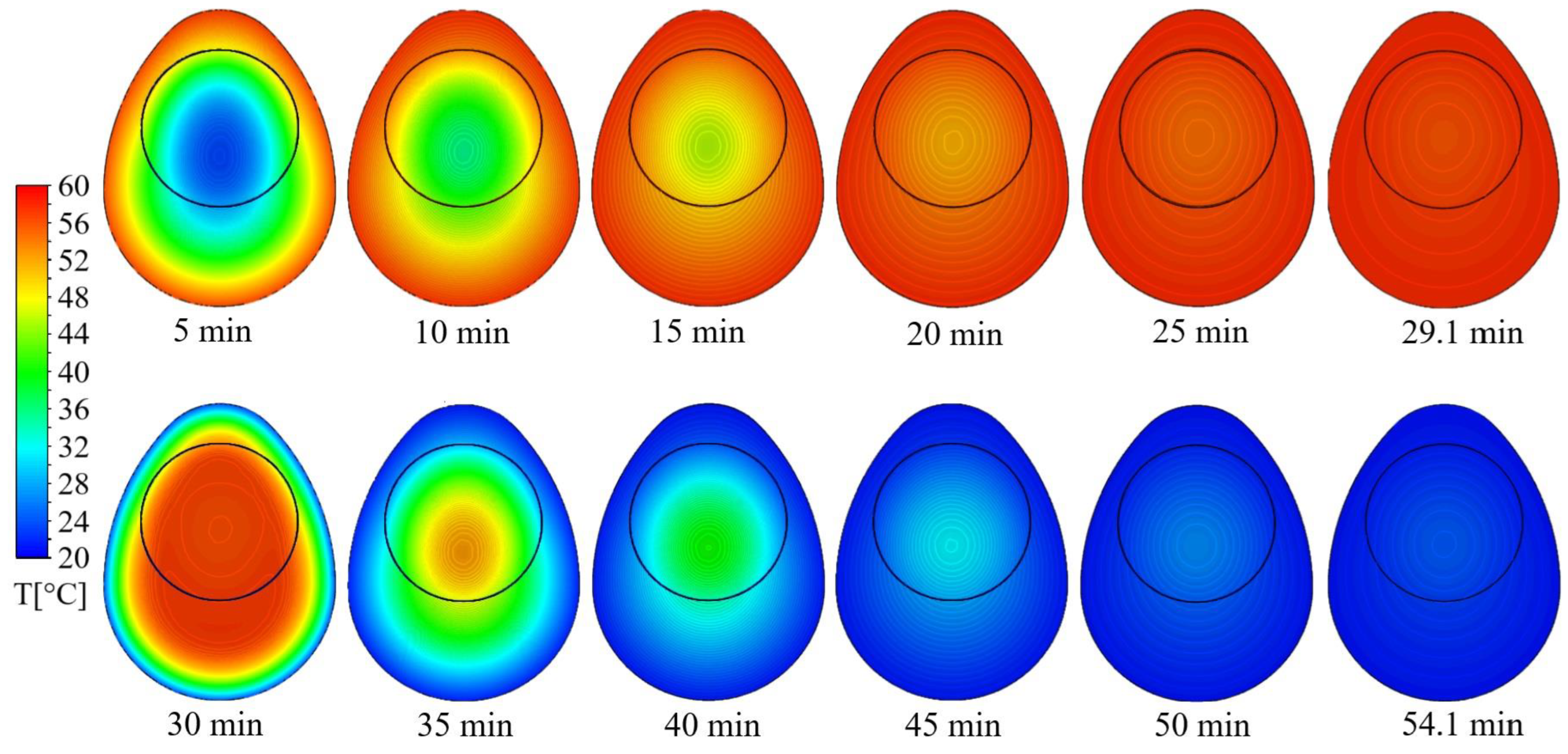
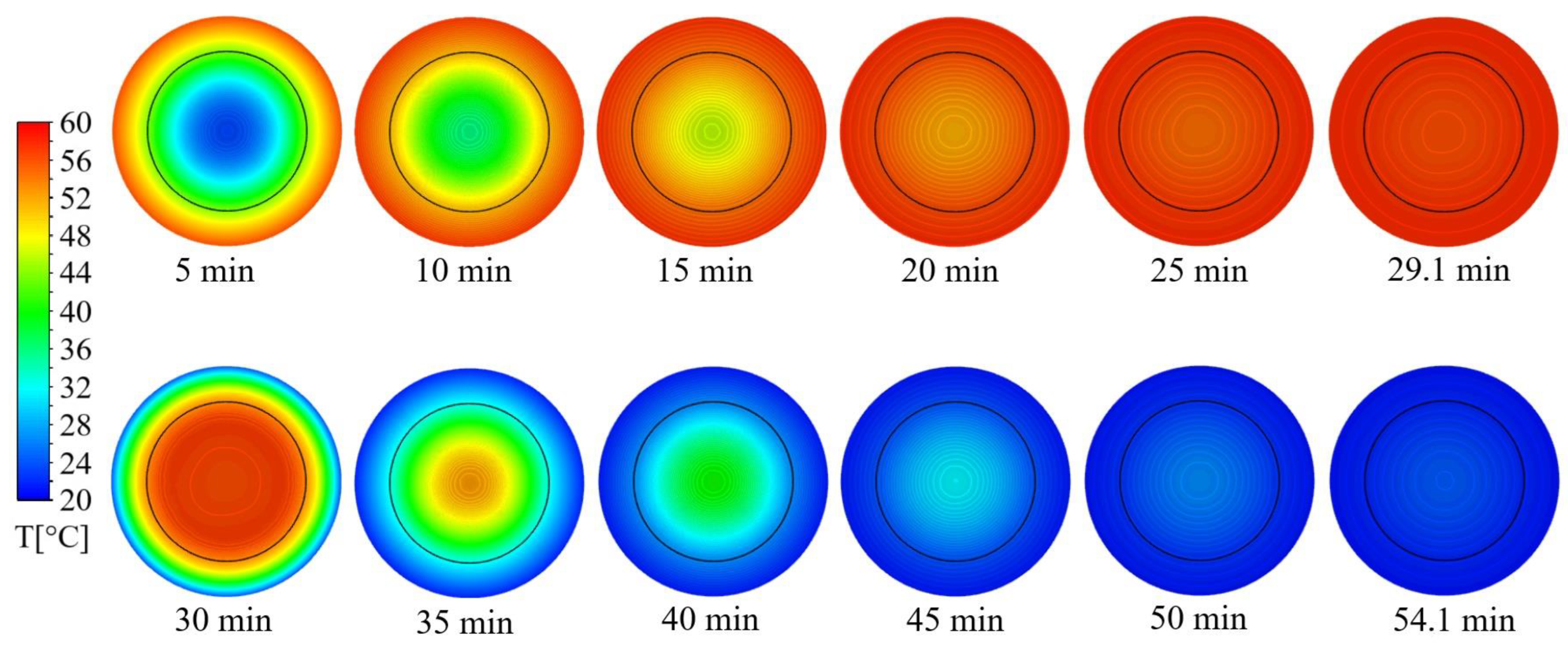
3.3. Thermal Process Calculations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | heat transfer area, m2 |
| B | required heating time, min |
| C | concentration of a heat labile substance, number of microorganisms/mL, spores per container, g/mL, or any other appropriate unit |
| Cp | specific heat of the product, J/(kg·K) |
| DT | (noted also as D) decimal reduction time or death rate constant—time at a constant temperature required to reduce by 90% the initial spore load (or, in general, time required for 90% reduction of a heat labile substance), min |
| m | mass, kg |
| (or simply F) time at a constant temperature, T, required to destroy a given percentage of microorganisms whose thermal resistance is characterized by z, | |
| or the equivalent processing time of a hypothetical thermal process at a constant temperature that produces the same effect (in terms of spore destruction) as the actual thermal process, min | |
| h | convective heat transfer coefficient between the heating or cooling medium and the product, W/(m2K) |
| T | product temperature, °C |
| t | time, s or min |
| x, y, z | orthogonal coordinates |
| z | temperature difference required to achieve a decimal change of the DT value, °C |
| Subscripts | |
| cooling | referring to the cooling cycle |
| heating | referring to the heating cycle |
| IT | initial condition |
| p | process |
| process | process value |
| required | required value |
| total | cumulative value |
| ∞ | heating or cooling medium |
References
- Rehault-Godbert, S.; Guyot, N.; Nys, Y. The golden egg: Nutritional value, bioactivities, and emerging benefits for human health. Nutrients 2019, 11, 684. [Google Scholar] [CrossRef] [PubMed]
- FDA. 21 CFR Parts 16 and 118. Prevention of Salmonella enteritidis in Shell Eggs During Production, Storage, and Transportation. Fed. Regist. 2009, 74, 33030–33101. [Google Scholar]
- Li, L.; McWhorter, A.; Chousalkar, K. Ensuring egg safety: Salmonella survival, control, and virulence in the supply chain. Compr. Rev. Food Sci. Food Saf. 2025, 24, e70075. [Google Scholar] [CrossRef] [PubMed]
- Gantois, I.; Ducatelle, R.; Pasmans, F.; Haesebrouck, F.; Gast, R.; Humphrey, T.J.; Immerseel, F.V. Mechanisms of egg contamination by Salmonella enteritidis. FEMS Microbiol. Rev. 2009, 33, 718–738. [Google Scholar] [CrossRef] [PubMed]
- Keener, K. Shell Egg Pasteurization. In Egg Innovations and Strategies for Improvements; Hester, P.Y., Ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2017; pp. 165–175. [Google Scholar] [CrossRef]
- Ebel, E.; Schlosser, W. Estimating the annual fraction of eggs contaminated with Salmonella enteritidis in the United States. Int. J. Food Microbiol. 2000, 61, 51–62. [Google Scholar] [CrossRef] [PubMed]
- EFSA, European Food Safety Authority and the European Centre for Disease Prevention and Control. The European Union One Health 2018 Zoonoses Report. EFSA J. 2019, 17, 5926. [Google Scholar] [CrossRef]
- EFSA, European Food Safety Authority and the European Centre for Disease Prevention and Control. Multi-country outbreak of Salmonella enteritidis sequence type (ST)11 infections linked to eggs and egg products. EFSA Support. Publ. 2022, 19, 7180E. [Google Scholar] [CrossRef]
- FSN. Food Safety News: Salmonella Outbreak in Sweden Linked to Eggs. Available online: https://www.foodsafetynews.com/2023/01/salmonella-outbreak-in-sweden-linked-to-eggs/ (accessed on 24 January 2023).
- Abbasnezhad, B.; Hamdami, N.; Shahedi, M.; Vatankhah, H. Thermophysical and rheological properties of liquid egg white and yolk during thermal pasteurization of intact eggs. Food Meas. Charact. 2014, 8, 259–269. [Google Scholar] [CrossRef]
- Abbasnezhad, B.; Hamdami, N.; Monteau, J.Y.; Vatankhah, H. Numerical modeling of heat transfer and pasteurizing value during thermal processing of intact egg. Food Sci. Nutr. 2015, 4, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Bermudez-Aguirre, D.; Niemira, B.A. A review on egg pasteurization and disinfection: Traditional and novel processing technologies. Compr. Rev. Food Sci. Food Saf. 2022, 22, 756–784. [Google Scholar] [CrossRef] [PubMed]
- Hou, H.; Singh, R.K.; Muriana, P.M.; Stadelman, W.J. Pasteurization of intact shell eggs. Food Microbiol. 1996, 13, 93–101. [Google Scholar] [CrossRef]
- Schuman, J.D.; Sheldon, B.W.; Vandepopuliere, J.M.; Ball, H.R., Jr. Immersion heat treatments for inactivation of salmonella enteritidis with intact eggs. J. Appl. Microbiol. 1997, 83, 438–444. [Google Scholar] [CrossRef] [PubMed]
- Denys, S.; Pieters, J.G.; Dewettinck, K. Computational fluid dynamics analysis of combined conductive and convective heat transfer in model eggs. J. Food Eng. 2004, 63, 281–290. [Google Scholar] [CrossRef]
- Denys, S.; Pieters, J.G.; Dewettinck, K. Computational fluid dynamics analysis for process impact assessment during thermal pasteurization of intact eggs. J. Food Prot. 2005, 68, 366–374. [Google Scholar] [CrossRef] [PubMed]
- Park, H.W.; Yoon, W.B. Computational fluid dynamics (CFD) modelling and application for sterilization of foods: A Review. Processes 2018, 6, 62. [Google Scholar] [CrossRef]
- Szpicer, A.; Bińkowska, W.; Stelmasiak, A.; Zalewska, M.; Wojtasik-Kalinowska, I.; Piwowarski, K.; Piepiórka-Stepuk, J.; Półtorak, A. Computational fluid dynamics simulation of thermal processes in food technology and their applications in the food industry. Appl. Sci. 2025, 15, 424. [Google Scholar] [CrossRef]
- Dixon, R. Mathographics; Dover Publications Inc.: Mineola, NY, USA, 1991; pp. 3–11. [Google Scholar]
- Sun, D.W. Computational Fluid Dynamics in Food Processing; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2007; p. 760. [Google Scholar]
- European Commission. Commission Regulation (EC) No. 589/2008 of 23 June 2008 laying down detailed rules for implementing Council Regulation (EC) No. 1234/2007 as regards marketing standards for eggs. Off. J. Eur. Union (EN) 2008, 50, 6–23. [Google Scholar]
- Romanoff, A.; Romanoff, A. The Avian Egg; John Wiley and Sons, Inc.: New York, NY, USA, 1949. [Google Scholar]
- Badin, E.E.; Mercatante, M.M.; Mascheroni, R.H.; Quevedo-Leon, R.; Ibarz, A.; Ribotta, P.D.; Lespinard, A.R. Effect of pasteurization on color, ascorbic acid and lycopene of crushed tomato: A computational study with experimental validation. J. Food Eng. 2023, 337, 111218. [Google Scholar] [CrossRef]
- Heldman, D.R.; Singh, R.P. Food Process Engineering, 2nd ed.; The AVI Publishing Company, Inc.: Baton Rouge, LA, USA, 1981; p. 481. [Google Scholar]
- ASM Handbook Committee. ASM Handbook Volume 2, Properties and Selection: Nonferrous Alloys and Special-Purpose Materials, 10th ed.; ASM International/The Materials Information Company: Russell Township, OH, USA, 1990. [Google Scholar]
- Ball, C.O.; Olson, F.C.W. Sterilization in Food Technology. Theory, Practice and Calculations; McGraw-Hill Book Co.: New York, NY, USA, 1957. [Google Scholar]
- Stoforos, N.G. Thermal Processing. In Handbook of Food Processing: Food Preservation; Varzakas, T., Tzia, C., Eds.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2015; pp. 27–56. [Google Scholar]
- Jin, T.; Zhang, H.; Boyd, G.; Tang, J. Thermal resistance of Salmonella enteritidis and Escherichia coli K12 in liquid egg determined by thermal-death-time disks. J. Food Eng. 2008, 84, 608–614. [Google Scholar] [CrossRef]
- Lund, D.B. Design of thermal processes for maximizing nutrient retention. Food Technol. 1977, 31, 71–78. [Google Scholar]



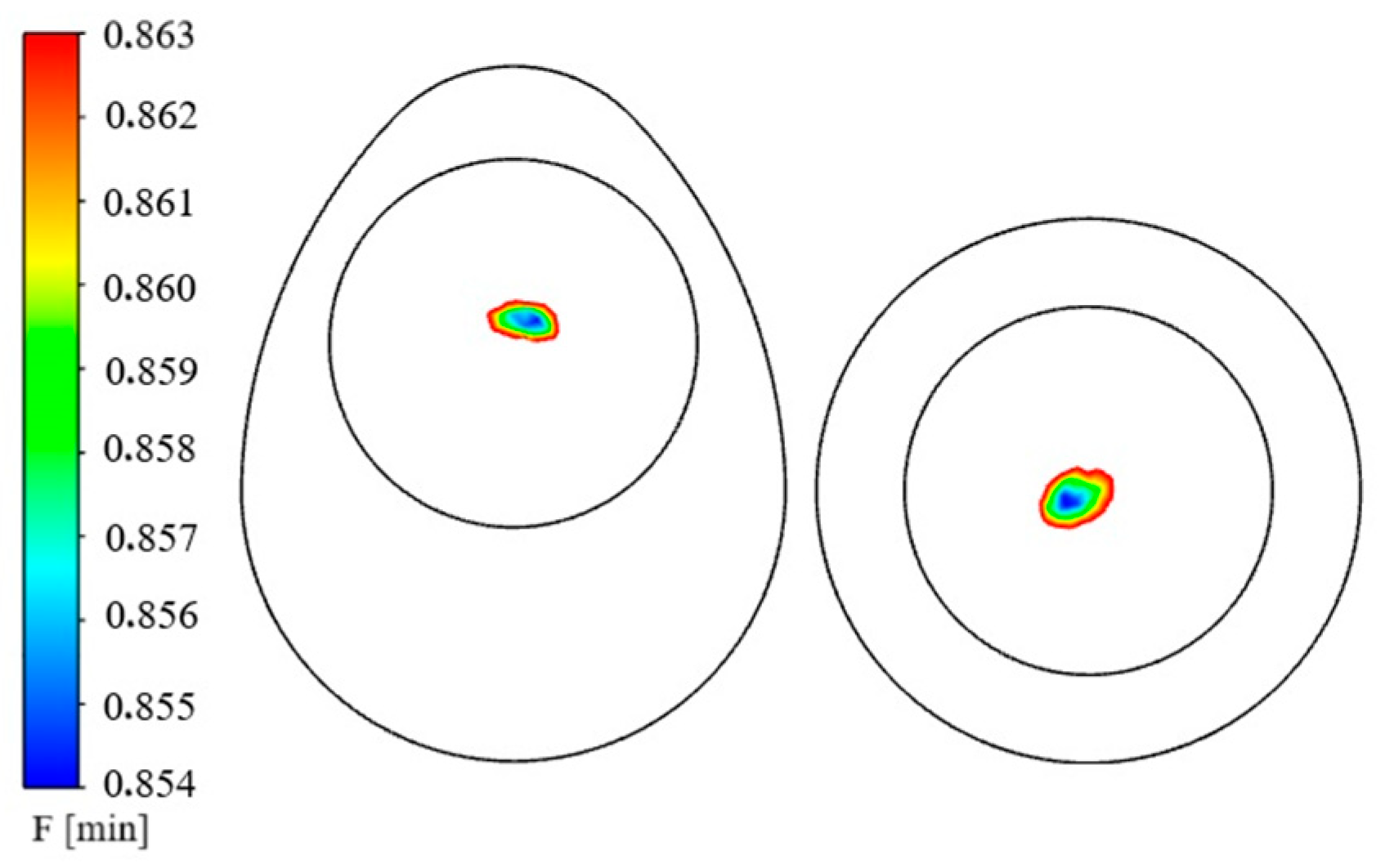
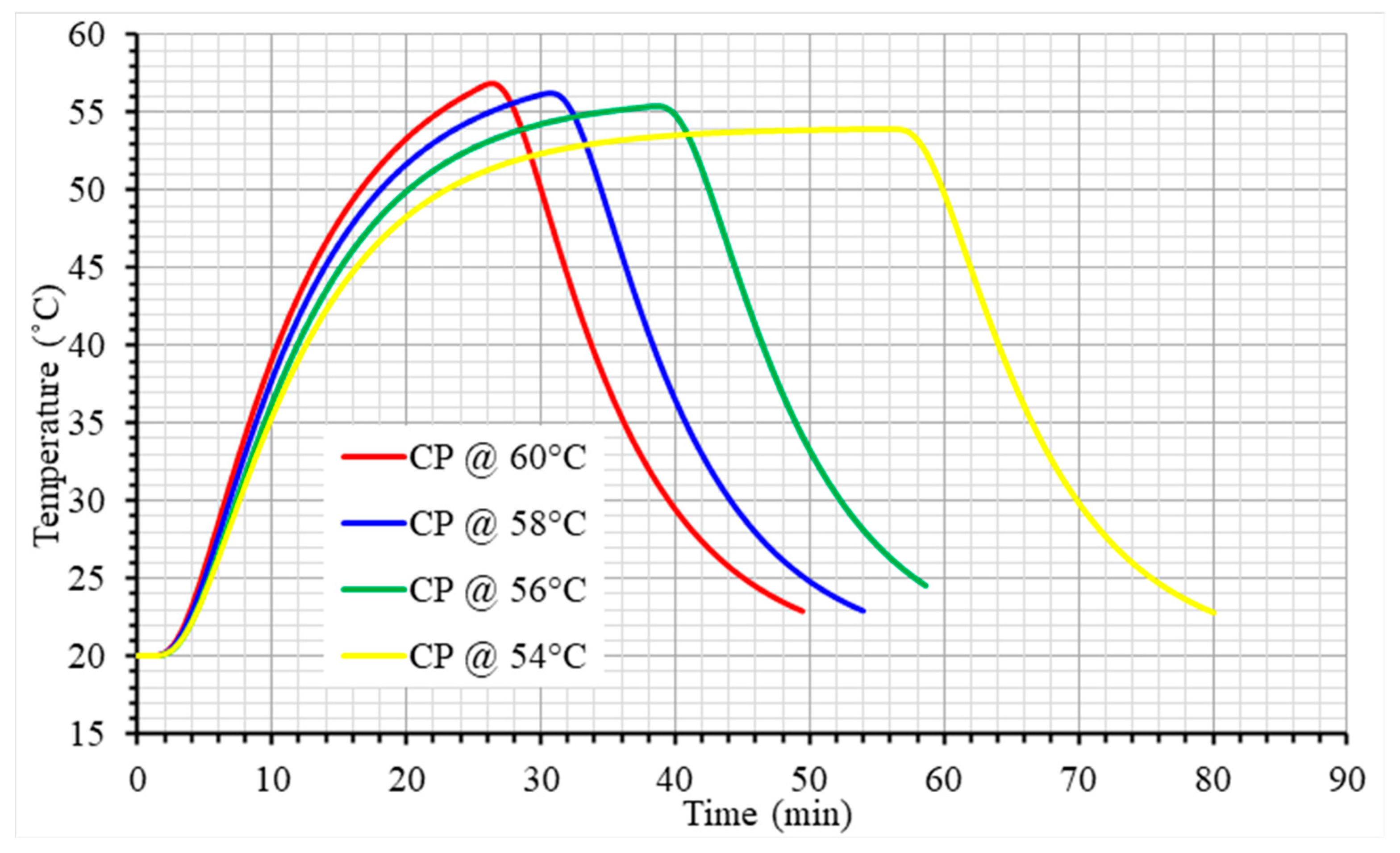
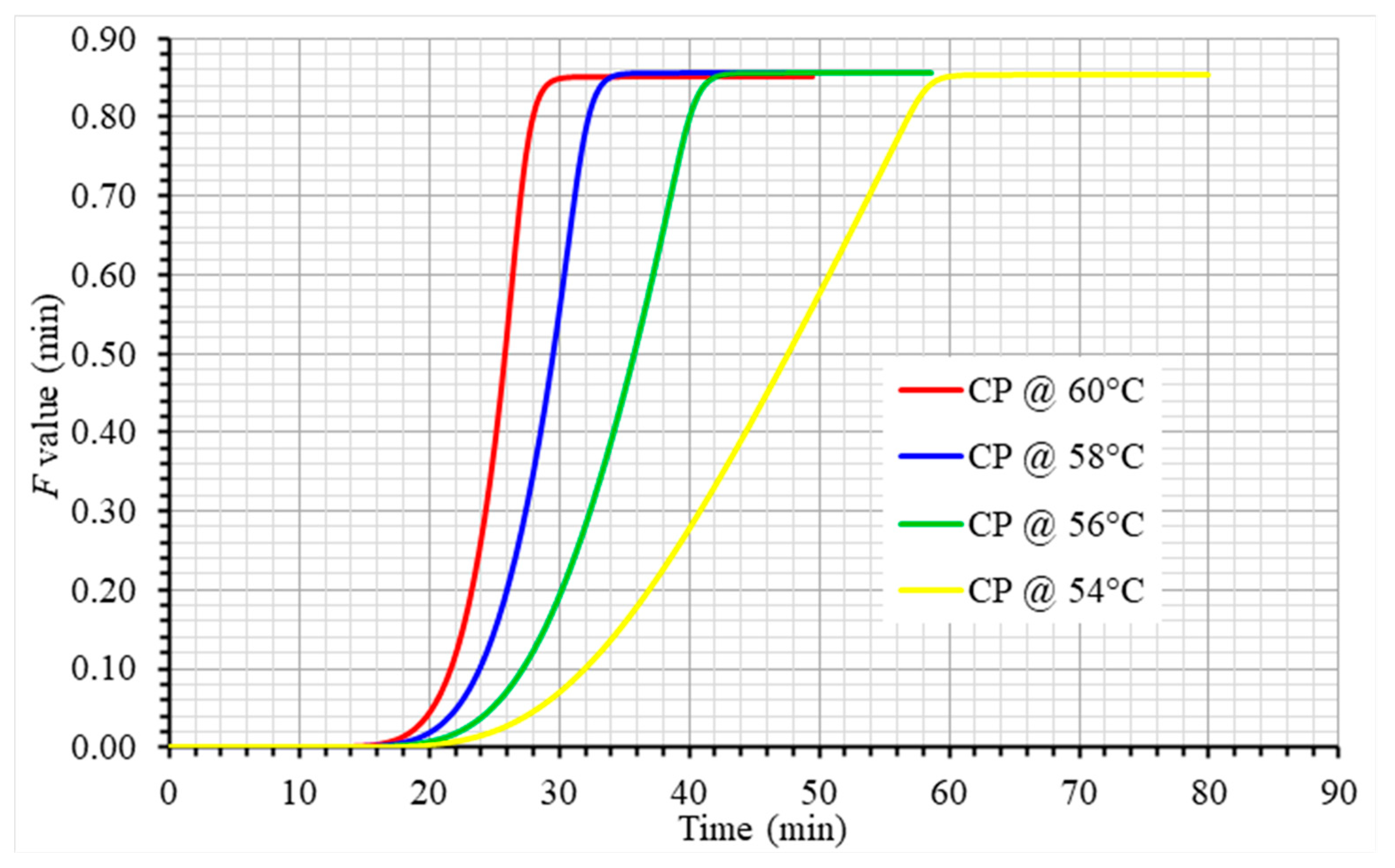
| Property (Units) | Egg Component | Value/ Equation 1 | Reference |
|---|---|---|---|
| Density (ρ) (kg/m3) | Egg white | 1048 | [22] |
| Yolk | 1035 | [22] | |
| Shell | 2300 | [16] | |
| Specific heat (Cp) (J/kg·K) | Egg white | 3560 | [22] |
| Yolk | 3560 | [22] | |
| Shell | 888 | [15] | |
| Thermal conductivity (k) (W/m·K) | Egg white | 0.43 + 0.00055 × Τ | [22] |
| Yolk | 0.337 | [22] | |
| Shell | 2.25 | [15] | |
| Viscosity (μ) (Pa·s) | Egg white | 3.12 − 0.0089 × Τ | [22] |
| Yolk | 1.60 − 0.0048 × Τ | [22] | |
| Shell | - | - |
| Egg Size | Heating Medium T (°C) | Heating Time B (min) | Ftotal (min) | Fheating (min) | Fcooling (min) | % Contribution of Cooling Lethality |
|---|---|---|---|---|---|---|
| Medium | 54 | 53.1 | 0.85 | 0.75 | 0.10 | 11.8 |
| 56 | 35.5 | 0.85 | 0.62 | 0.23 | 27.1 | |
| 58 | 27.8 | 0.86 | 0.49 | 0.37 | 43.5 | |
| 60 | 23.4 | 0.86 | 0.41 | 0.45 | 52.9 | |
| Large | 54 | 55.1 | 0.85 | 0.74 | 0.11 | 13.0 |
| 56 | 37.2 | 0.86 | 0.6 | 0.26 | 29.9 | |
| 58 | 29.1 | 0.86 | 0.46 | 0.40 | 46.2 | |
| 60 | 24.5 | 0.86 | 0.32 | 0.53 | 62.3 | |
| Extra Large | 54 | 56.8 | 0.85 | 0.71 | 0.14 | 16.5 |
| 56 | 38.8 | 0.86 | 0.54 | 0.32 | 37.6 | |
| 58 | 30.5 | 0.86 | 0.37 | 0.49 | 57.6 | |
| 60 | 25.8 | 0.87 | 0.25 | 0.62 | 72.9 |
| Heating Medium T (°C) | Heating Time B (min) | D121.11°C (min) | z (°C) | D121.11°C (min) | z (°C) | D121.11°C (min) | z (°C) | D121.11°C (min) | z (°C) |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 20 | 1000 | 20 | 100 | 50 | 1000 | 50 | ||
| 54 | 55.1 | 99.95 | 100.00 | 94.22 | 99.41 | ||||
| 56 | 37.2 | 99.96 | 100.00 | 95.77 | 99.57 | ||||
| 58 | 29.1 | 99.97 | 100.00 | 96.34 | 99.63 | ||||
| 60 | 24.5 | 99.97 | 100.00 | 96.67 | 99.66 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sampanis, P.-A.; Chatzidakis, S.M.; Stoforos, G.N.; Stoforos, N.G. Analysis of Shell Egg Pasteurization Using Computational Fluid Dynamics. Appl. Sci. 2025, 15, 1263. https://doi.org/10.3390/app15031263
Sampanis P-A, Chatzidakis SM, Stoforos GN, Stoforos NG. Analysis of Shell Egg Pasteurization Using Computational Fluid Dynamics. Applied Sciences. 2025; 15(3):1263. https://doi.org/10.3390/app15031263
Chicago/Turabian StyleSampanis, Pavlos-Antonios, Stylianos M. Chatzidakis, George N. Stoforos, and Nikolaos G. Stoforos. 2025. "Analysis of Shell Egg Pasteurization Using Computational Fluid Dynamics" Applied Sciences 15, no. 3: 1263. https://doi.org/10.3390/app15031263
APA StyleSampanis, P.-A., Chatzidakis, S. M., Stoforos, G. N., & Stoforos, N. G. (2025). Analysis of Shell Egg Pasteurization Using Computational Fluid Dynamics. Applied Sciences, 15(3), 1263. https://doi.org/10.3390/app15031263







