Adaptive Impedance Control of a Human–Robotic System Based on Motion Intention Estimation and Output Constraints
Abstract
1. Introduction
- (1)
- Compared with the existing impedance control methods in [12,15], which use a predefined trajectory for the exoskeleton, this paper proposes a novel neural network-based motion intention estimation method for human–robot interaction, where the exoskeleton is able to actively interact with the patient.
- (2)
- (3)
- In this paper, an RBFNN is used to compensate for the uncertainties in the exoskeleton dynamics, further improving the accuracy of the system. Additionally, strict stability analysis is carried out to ensure the effectiveness of the rehabilitation training.
2. Preliminaries
2.1. System Dynamics
2.2. Human Limb Model
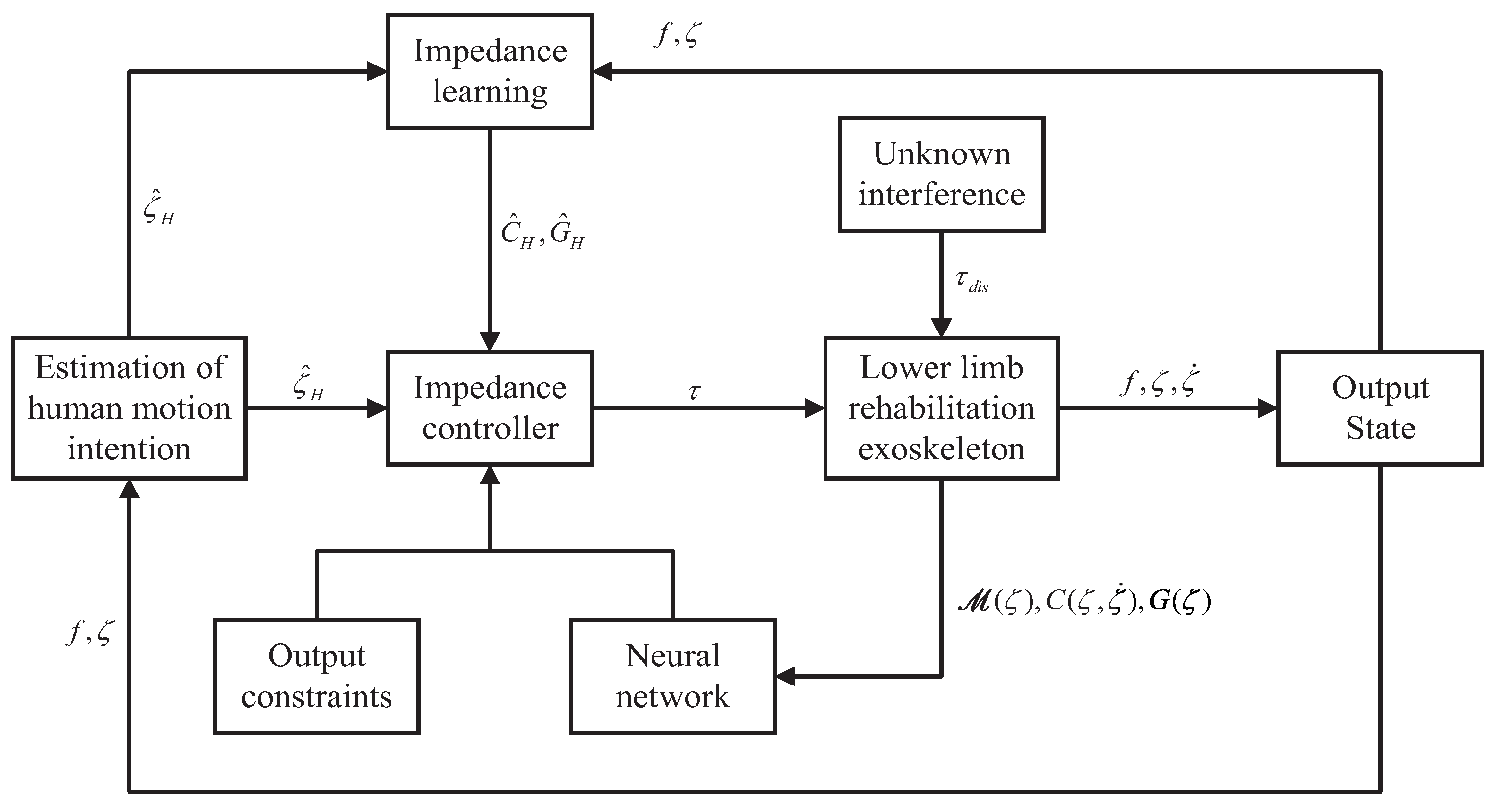
3. Controller Design
3.1. NN-Based Motion Intention Estimation
3.2. Human Impedance Learning
3.3. Output Constraints Tracking Control
3.3.1. Model-Based (MB) Impedance Control
3.3.2. Adaptive NN Impedance Control
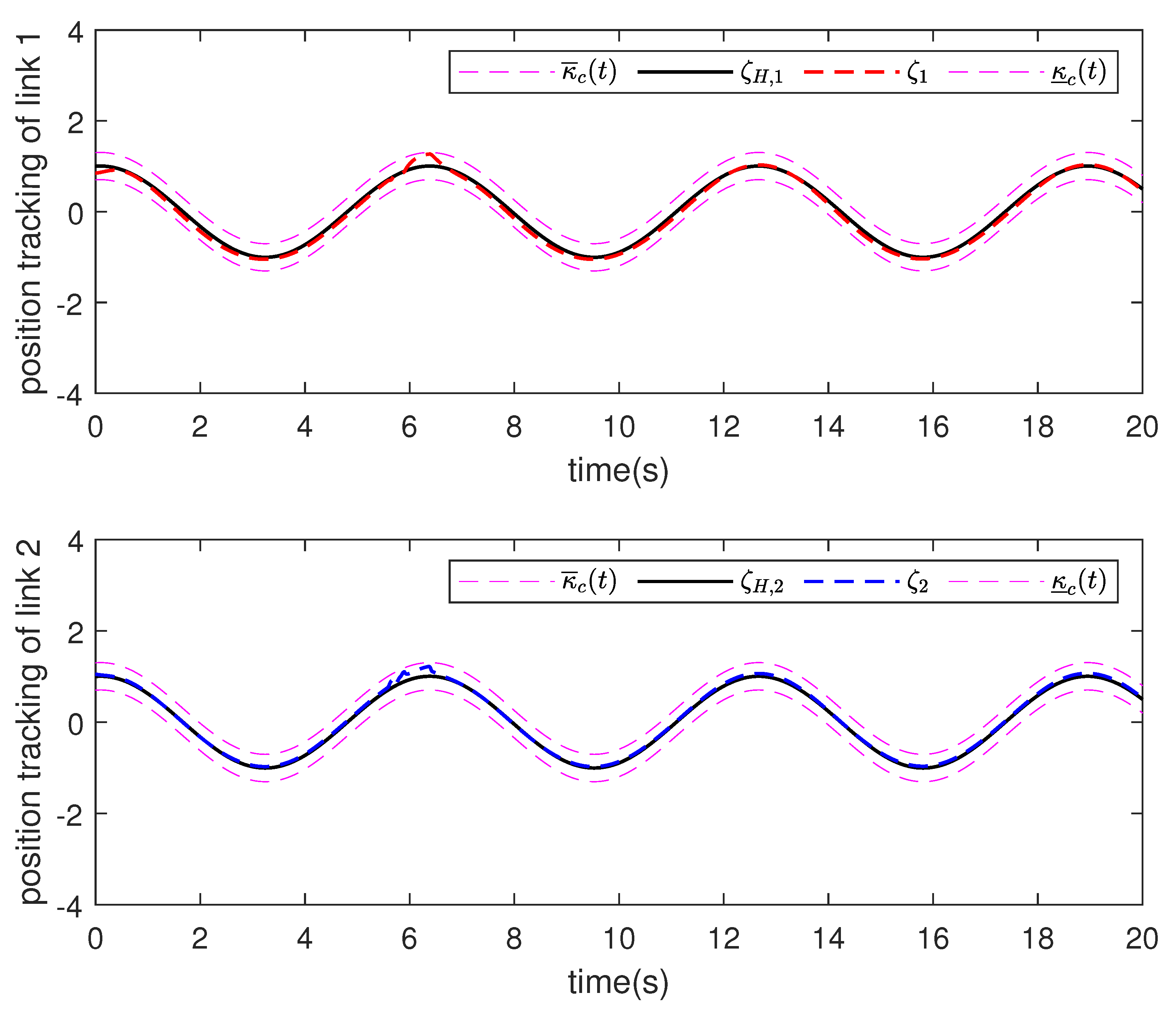
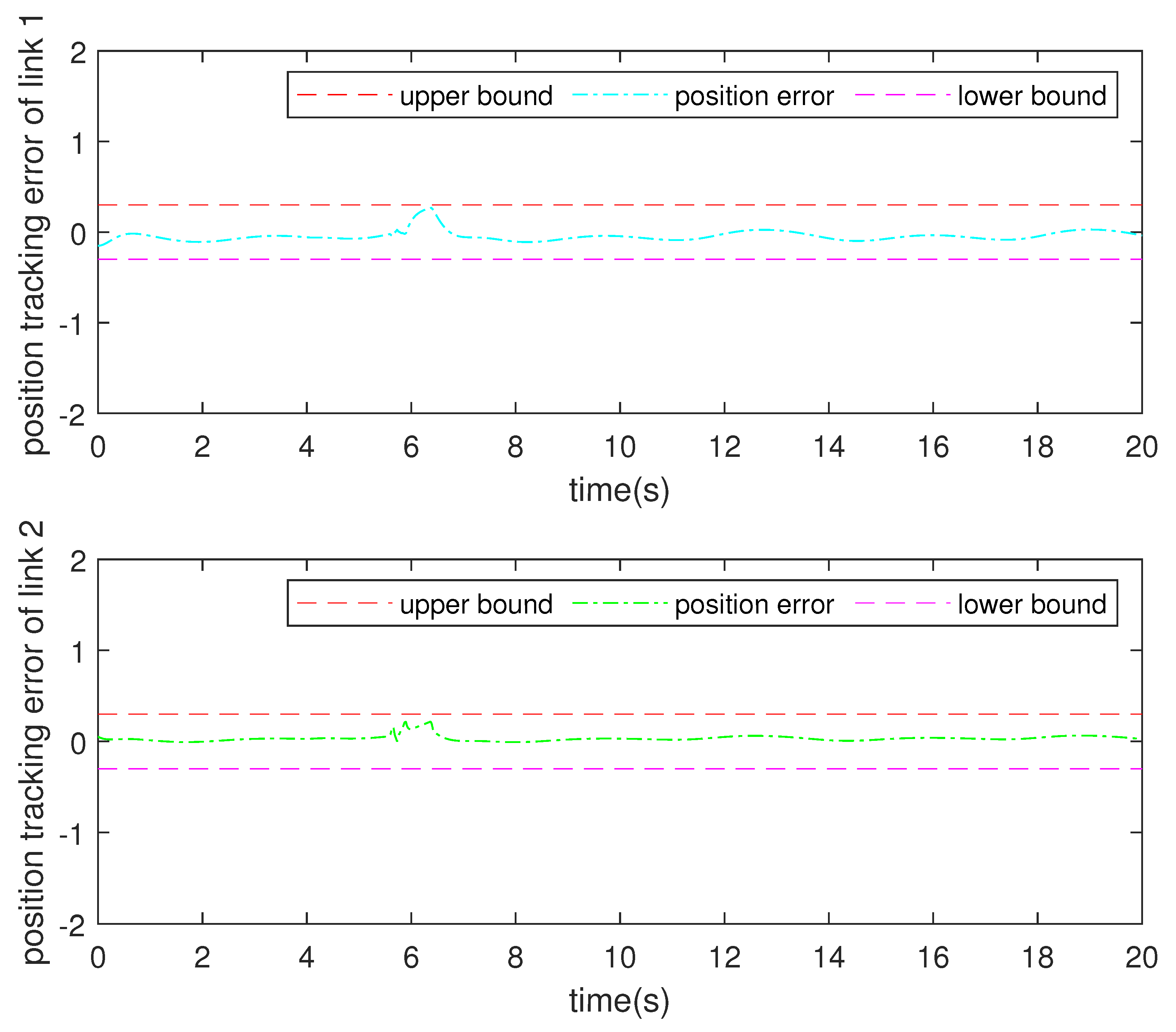
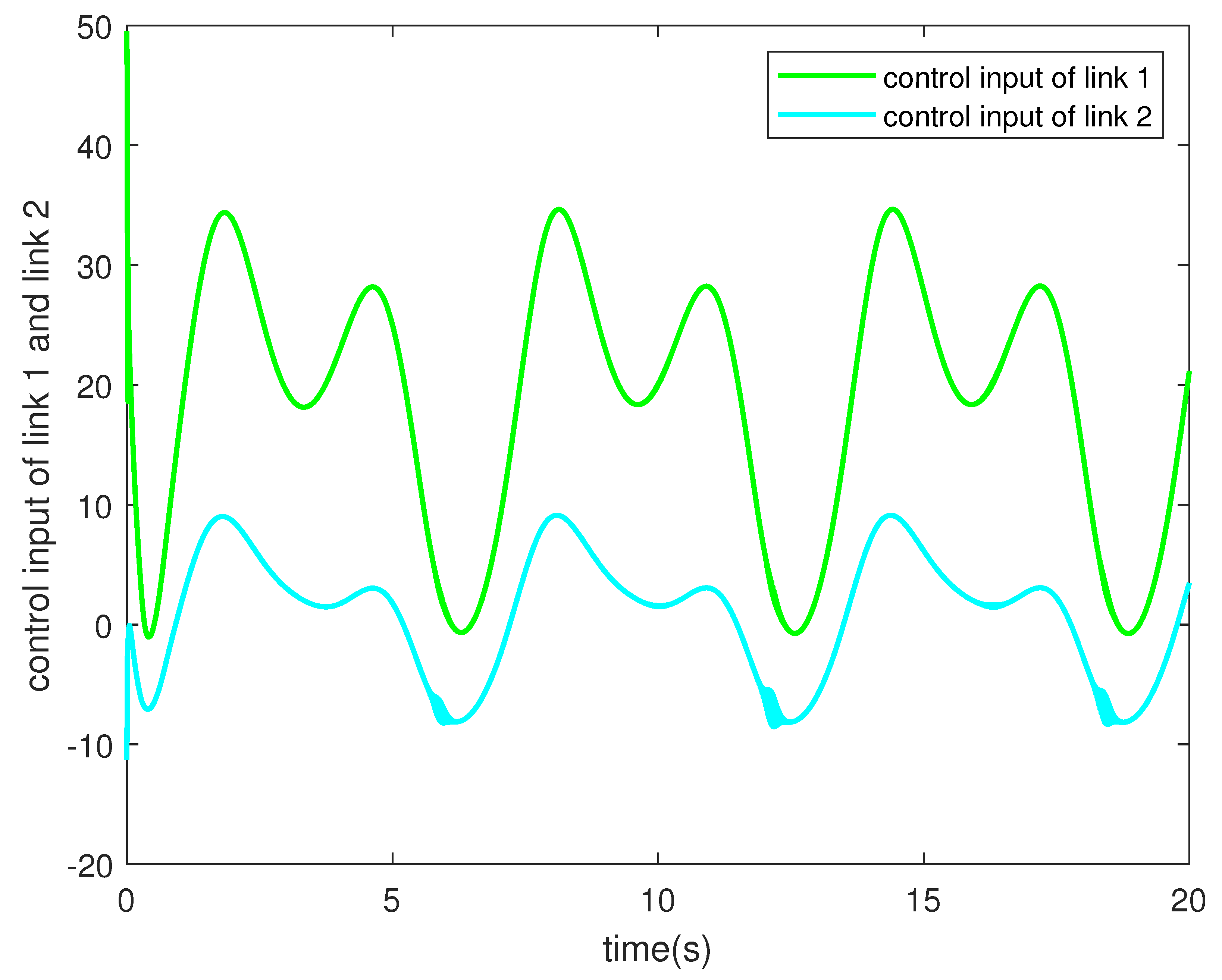
4. Numerical Simulation
4.1. Controller Simulation
4.2. Comprehensive Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huo, Y.X.; Li, X.; Zhang, X.; Li, X.; Sun, D. Adaptive Intention-Driven Variable Impedance Control for Wearable Robots with Compliant Actuators. IEEE Trans. Control Syst. Technol. 2023, 31, 1308–1323. [Google Scholar] [CrossRef]
- Zhang, P.F.; Gao, X.S.; Miao, M.D.; Zhao, P. Design and Control of a Lower Limb Rehabilitation Robot Based on Human Motion Intention Recognition with Multi-Source Sensor Information. Machines 2023, 10, 1125. [Google Scholar] [CrossRef]
- Du, G.M.; Ding, Z.; Guo, H.; Song, M.C.; Jiang, F. Estimation of Lower Limb Joint Angles Using sEMG Signals and RGB-D Camera. Bioengineering 2024, 11, 1026. [Google Scholar] [CrossRef] [PubMed]
- Plaza, A.; Hernandez, M.; Puyuelo, G.; Garces, E.; Garcia, E. Lower-Limb Medical and Rehabilitation Exoskeletons: A Review of the Current Designs. IEEE Rev. Biomed. Eng. 2023, 16, 278–291. [Google Scholar] [CrossRef]
- Jenhani, S.; Gritli, H.; Narayan, J. Robust Position Control of a Knee-Joint Rehabilitation Exoskeleton Using a Linear Matrix Inequalities-Based Design Approach. Appl. Sci. 2025, 15, 404. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, H.F.; Sue, S.; Song, S. Spatiotemporal Compliance Control for a Wearable Lower Limb Rehabilitation Robot. IEEE Trans. Biomed. Eng. 2023, 70, 1858–1868. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Lan, C.R.; Liang, P.; Zhong, M.Y.; Shi, X.L.; Lv, Y.L. Research on Interactive Force Acquisition and Active–Passive Mode Determination of Rehabilitation Robot. Measurement 2023, 220, 113340. [Google Scholar] [CrossRef]
- Matinfar, M.; Hashtrudi-Zaad, K. Optimization-Based Robot Compliance Control: Geometric and Linear Quadratic Approaches. Int. J. Robot. Res. 2005, 24, 645–656. [Google Scholar] [CrossRef]
- Lu, W.-S.; Meng, Q.-H. Impedance Control with Adaptation for Robotic Manipulations. IEEE Trans. Robot. Autom. 1991, 7, 408–415. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Yan, F.; Chen, J.W.; Ju, F.; Chen, B. A New Adaptive Time-Delay Control Scheme for Cable-Driven Manipulators. IEEE Trans. Ind. Inform. 2019, 15, 3469–3481. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control: An Approach to Manipulation. Part I: Theory; Part II: Implementation; Part III: Applications. J. Dyn. Syst. Meas. Control 1985, 107, 8–16. [Google Scholar] [CrossRef]
- Sun, Y.H.; Hu, J.P.; Huang, R. Negative-Stiffness Structure Vibration-Isolation Design and Impedance Control for a Lower Limb Exoskeleton Robot. Actuators 2023, 12, 147. [Google Scholar] [CrossRef]
- Liu, L.; Illian, M.; Leonhardt, S.; Misgeld, B.J.E. Iterative Learning Control for Cascaded Impedance-Controlled Compliant Exoskeleton with Adaptive Reaction to Spasticity. IEEE Trans. Instrum. Meas. 2023, 72, 4008211. [Google Scholar] [CrossRef]
- Zhang, Q.; Si, J.; Tu, X.K.; Li, M.H.; Lewek, M.D.; Huang, H. Toward Task-Independent Optimal Adaptive Control of a Hip Exoskeleton for Locomotion Assistance in Neurorehabilitation. IEEE Trans. Syst. Man Cybern.-Syst. 2024, 54, 7592–7604. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, D.Q.; Jin, C.W.; Liu, X.; Li, Y.A. Neural Learning Impedance Control of Lower Limb Rehabilitation Exoskeleton with Flexible Joints in the Presence of Input Constraints. Int. J. Robust Nonlinear Control 2022, 33, 4191–4209. [Google Scholar] [CrossRef]
- Lee, H.Y.W.; Lee, J.N.; Keppler, M.; Oh, S. Robust Elastic Structure Preserving Control for High Impedance Rendering of Series Elastic Actuator. IEEE Robot. Autom. Lett. 2024, 9, 3601–3608. [Google Scholar] [CrossRef]
- Li, L.S.; Wang, F.; Tang, H.; Liang, Y.B. Variable-Parameter Impedance Control of Manipulator Based on RBFNN and Gradient Descent. Sensors 2024, 25, 49. [Google Scholar] [CrossRef]
- Sun, Y.H.; Peng, Z.A.; Hu, J.P.; Ghosh, B.K. Event-Triggered Critic Learning Impedance Control of Lower Limb Exoskeleton Robots in Interactive Environments. Neurocomputing 2024, 564, 126963. [Google Scholar] [CrossRef]
- Li, J.W.; Lu, L.; Zhao, L.D.; Wang, C.; Li, J.H. An Integrated Approach for Robotic Sit-to-Stand Assistance: Control Framework Design and Human Intention Recognition. Control Eng. Pract. 2021, 107, 104680. [Google Scholar] [CrossRef]
- Tang, C.Y.; Xu, Z.Y.; Occhipinti, E.; Yi, W.T.; Xu, M.Z.; Kumar, S.; Virk, G.S.; Gao, S.; Occhipinti, L.G. From Brain to Movement: Wearables-Based Motion Intention Prediction Across the Human Nervous System. Nano Energy 2023, 115, 108712. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, C.J.; Zhao, Z.X.; Hu, T.L.; Zhang, J.H. Robot Teaching System Based on Hand-Robot Contact State Detection and Motion Intention Recognition. Robot. Comput.-Integr. Manuf. 2023, 81, 102492. [Google Scholar] [CrossRef]
- Kueper, N.; Kim, S.K.; Kirchner, E.A. Avoidance of Specific Calibration Sessions in Motor Intention Recognition for Exoskeleton-Supported Rehabilitation Through Transfer Learning on EEG Data. Sci. Rep. 2024, 14, 16690. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.J.; Gu, X.P.; Yu, H.L. A Comparison of Four Neural Networks Algorithms on Locomotion Intention Recognition of Lower Limb Exoskeleton Based on Multi-Source Information. J. Bionic Eng. 2024, 21, 224–235. [Google Scholar] [CrossRef]
- Sharifi, M.; Azimi, V.; Mushahwar, V.K.; Tavakoil, M. mpedance Learning-Based Adaptive Control for Human–Robot Interaction. IEEE Trans. Control Syst. Technol. 2022, 30, 1345–1358. [Google Scholar] [CrossRef]
- Kim, B.; Park, J.; Park, S.; Kang, S. Impedance Learning for Robotic Contact Tasks Using Natural Actor-Critic Algorithm. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 2010, 40, 433–443. [Google Scholar]
- Tsuji, T.; Ito, K.; Morasso, P.G. Neural Network Learning of Robot Arm Impedance in Operational Space. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 1996, 26, 290–298. [Google Scholar] [CrossRef][Green Version]
- Chang, P.H.; Park, K.; Kang, S.H.; Krebs, H.I.; Hogan, N. Stochastic Estimation of Human Arm Impedance Using Robots with Nonlinear Frictions: An Experimental Validation. IEEE-ASME Trans. Mechatron. 2013, 18, 775–786. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Zhang, J.X.; Xiong, G.L.; Gao, Y.F.; Feng, Y. Research on Adaptive Fuzzy Impedance Control of Human-Massage Robot Interaction Based on Kelvin-Voigt Modeling. IEEE Access 2024, 12, 89562–89572. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.A.; Liu, X.; Huang, D.Q. Adaptive Neural Network Control for a Hydraulic Knee Exoskeleton with Valve Deadband and Output Constraint Based on Nonlinear Disturbance Observer. Neurocomputing 2022, 473, 14–23. [Google Scholar] [CrossRef]
- Xu, M.M.; Wu, Y.Q. Event-Based Fuzzy Stabilization Controller for Uncertain Nonholonomic Systems with Output Constraints: Application to Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Yang, S.Y.; Pei, J.F.; Liu, Y.Y.; Chen, Y.H. Robust Tracking Control Design with a Novel Leakage-Type Adaptive Mechanism for an Uncertain Lower Limb Exoskeleton Robot. J. Vib. Control 2023, 29, 2681–2695. [Google Scholar] [CrossRef]
- Sun, J.J.; Wang, J.; Yang, P.; Guo, S.J. Fractional-Order Prescribed Performance Sliding-Mode Control with Time-Delay Estimation for Wearable Exoskeletons. IEEE Trans. Ind. Inform. 2023, 19, 8274–8284. [Google Scholar] [CrossRef]
- Tee, K.P.; Ren, B.B.; Ge, S.S. Control of Nonlinear Systems with Time-Varying Output Constraints. Automatica 2011, 47, 2511–2516. [Google Scholar] [CrossRef]
- Li, Z.J.; Yuan, W.; Chen, Y.; Ke, F.; Chu, X.L.; Chen, C.L.P. Neural-Dynamic Optimization-Based Model Predictive Control for Tracking and Formation of Nonholonomic Multirobot Systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6113–6122. [Google Scholar] [CrossRef] [PubMed]
- Le, Q.D.; Yang, E.F. Adaptive Fault-Tolerant Tracking Control for Multi-Joint Robot Manipulators via Neural Network-Based Synchronization. Sensors 2024, 24, 6837. [Google Scholar] [CrossRef] [PubMed]
- Yin, M.; Shang, D.Y.; Cao, W.J.; Ma, Y.; Li, J.K.; Tian, D.K.; Wu, X.Y. Rotation Angle Control Strategy for the Hip Joint of an Exoskeleton Robot Assisted by Paraplegic Patients Considering Time-Varying Inertia. IEEE Trans. Autom. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Yang, G.C.; Yao, J.Y. Multilayer Neurocontrol of High-Order Uncertain Nonlinear Systems with Active Disturbance Rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Wang, H.T.; Liu, Q.S.; Xu, C.T. Predefined-Time Distributed Optimization and Anti-Disturbance Control for Nonlinear Multi-Agent System with Neural Network Estimator: A Hierarchical Framework. Neural Netw. 2024, 175, 106270. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, J.W.; Park, J.H.; Zhang, J.; Shen, H. Improved Disturbance Observer-Based Fixed-Time Adaptive Neural Network Consensus Tracking for Nonlinear Multi-Agent System. Neural Netw. 2023, 162, 490–501. [Google Scholar] [CrossRef] [PubMed]
- Espinosa-Espejel, K.I.; Rosales-Luengas, Y.; Salazar, S.; López-Gutiérrez, R.; Lozano, R. Active Disturbance Rejection Control via Neural Networks for a Lower-Limb Exoskeleton. Sensors 2024, 24, 6546. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dong, X.C.; Huang, D.Q. Enhanced Neural Network Control of Lower Limb Rehabilitation Exoskeleton by Add-On Repetitive Learning. Neurocomputing 2019, 323, 256–264. [Google Scholar] [CrossRef]
- Khatib, O.; Warren, J.; Sapio, V.D.; Sentis, L. Human-Like Motion from Physiologically-Based Potential Energies. Adv. Robot Kinemat. 2004, 149–163. Available online: https://link.springer.com/chapter/10.1007/978-1-4020-2249-4_16 (accessed on 2 December 2024).
- Lalitharatne, T.; Teramoto, K.; Hayashi, Y.; Kiguchi, K. Evaluation of Perception-Assist with an Upper-Limb Powerassist Exoskeleton Using EMG and EEG Signals. In Proceedings of the 11th IEEE International Conference on Networking, Sensing and Control, Sensing and Control, ICNSC 2014, Marseille, France, 25–27 October 2014; pp. 524–529. [Google Scholar]
- Ge, S.S.; Lee, T.H.; Harris, C.J. Adaptive Neural Network Control of Robotic Manipulators; World Scientific: Singapore, 1998. [Google Scholar]




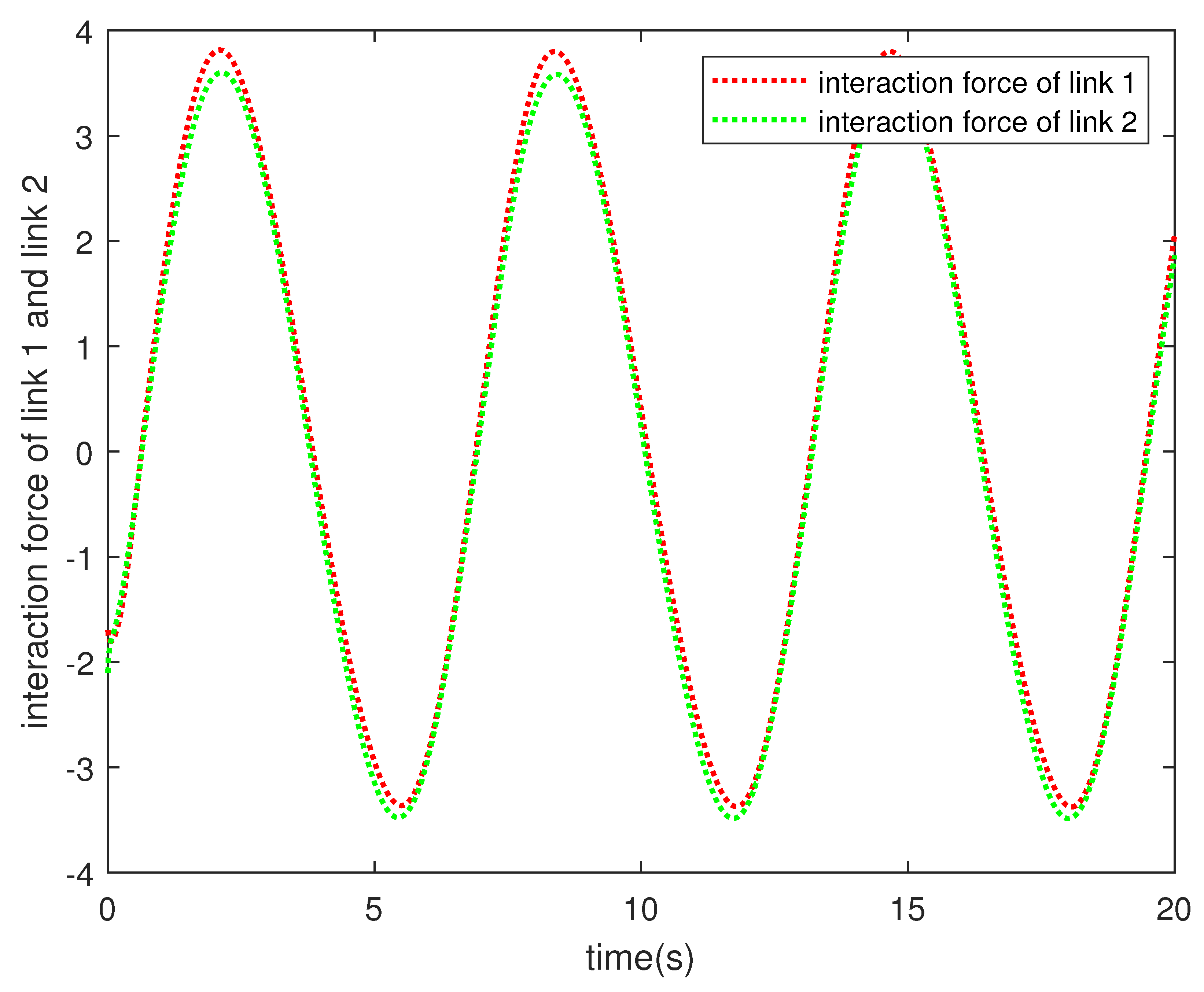
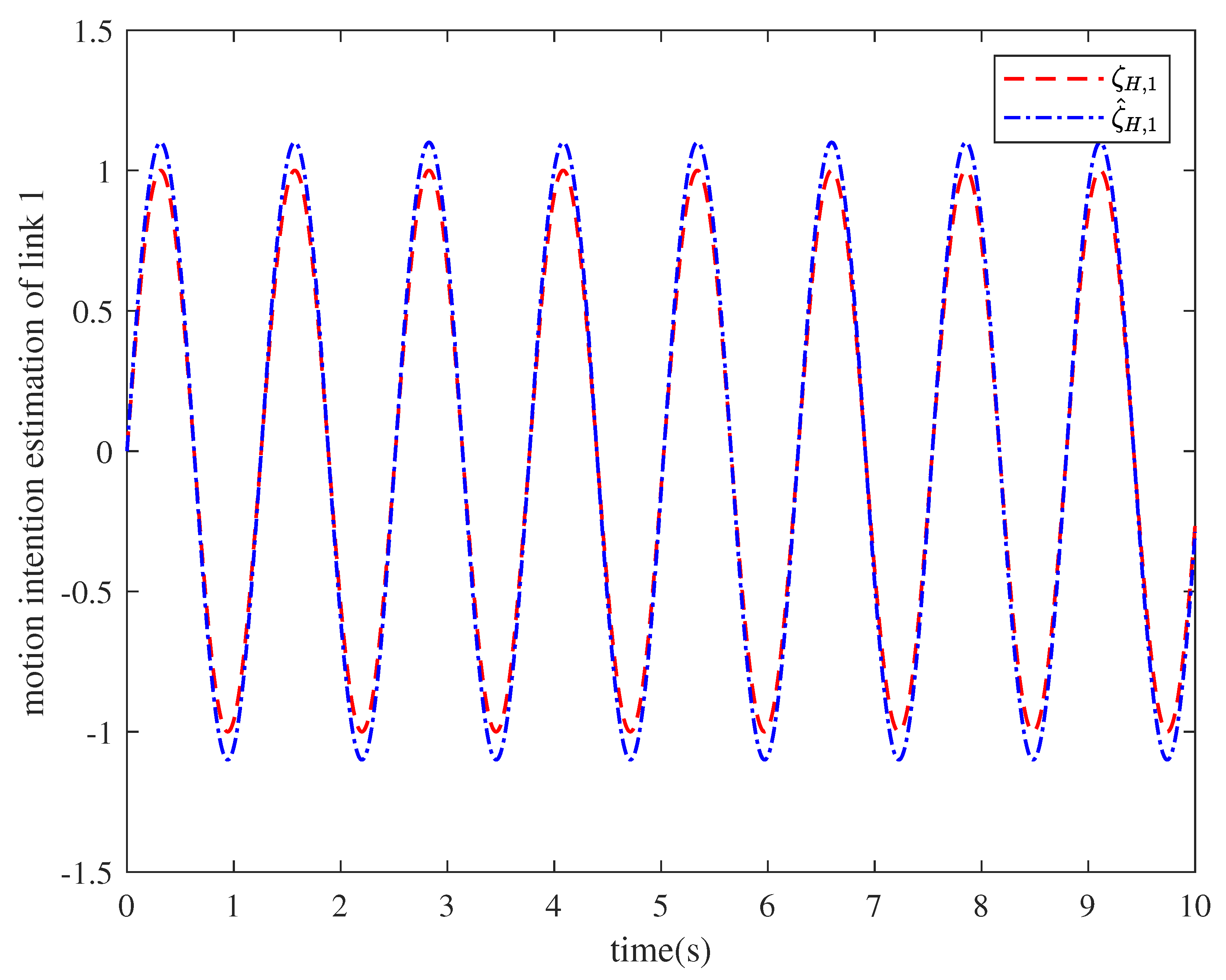
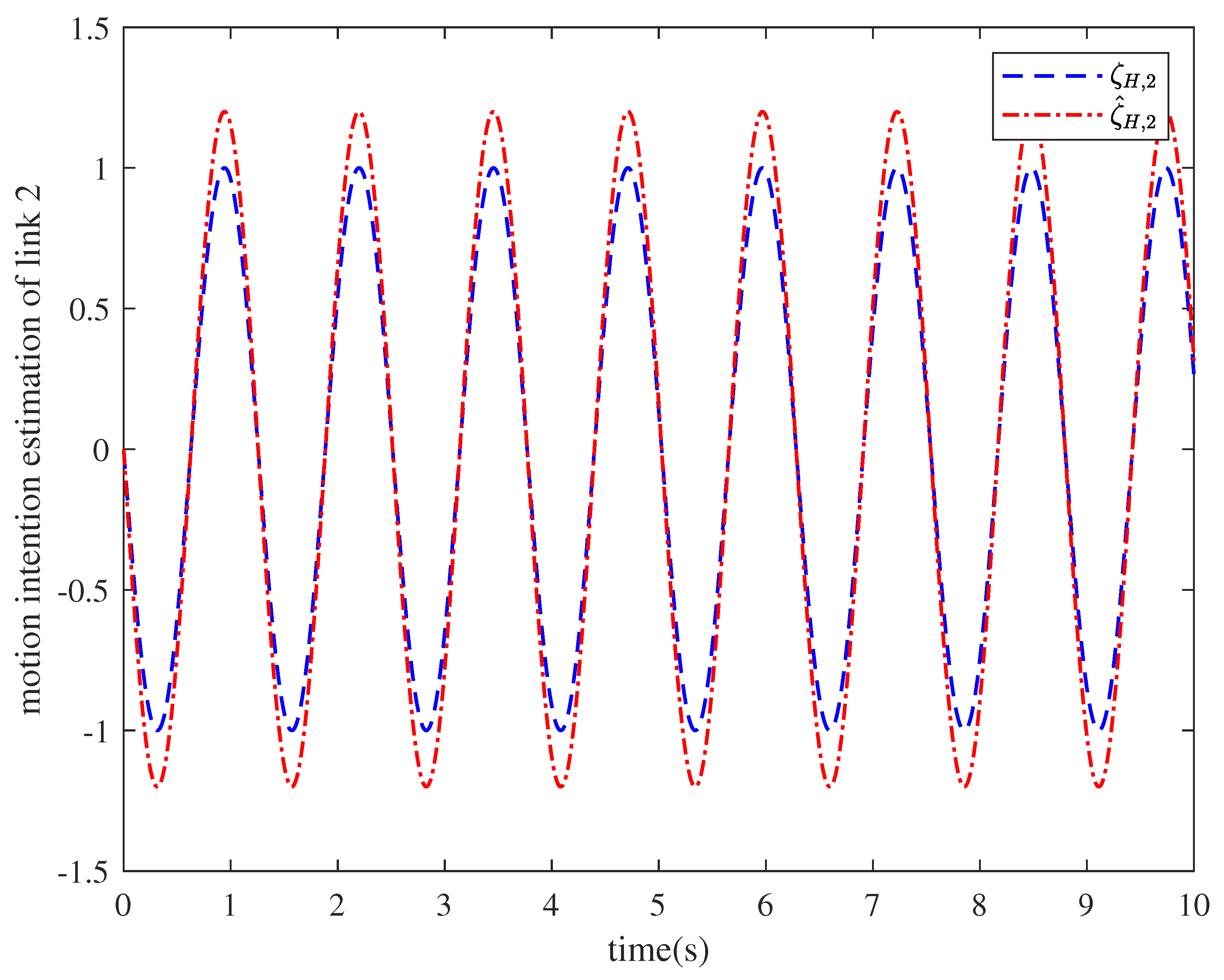
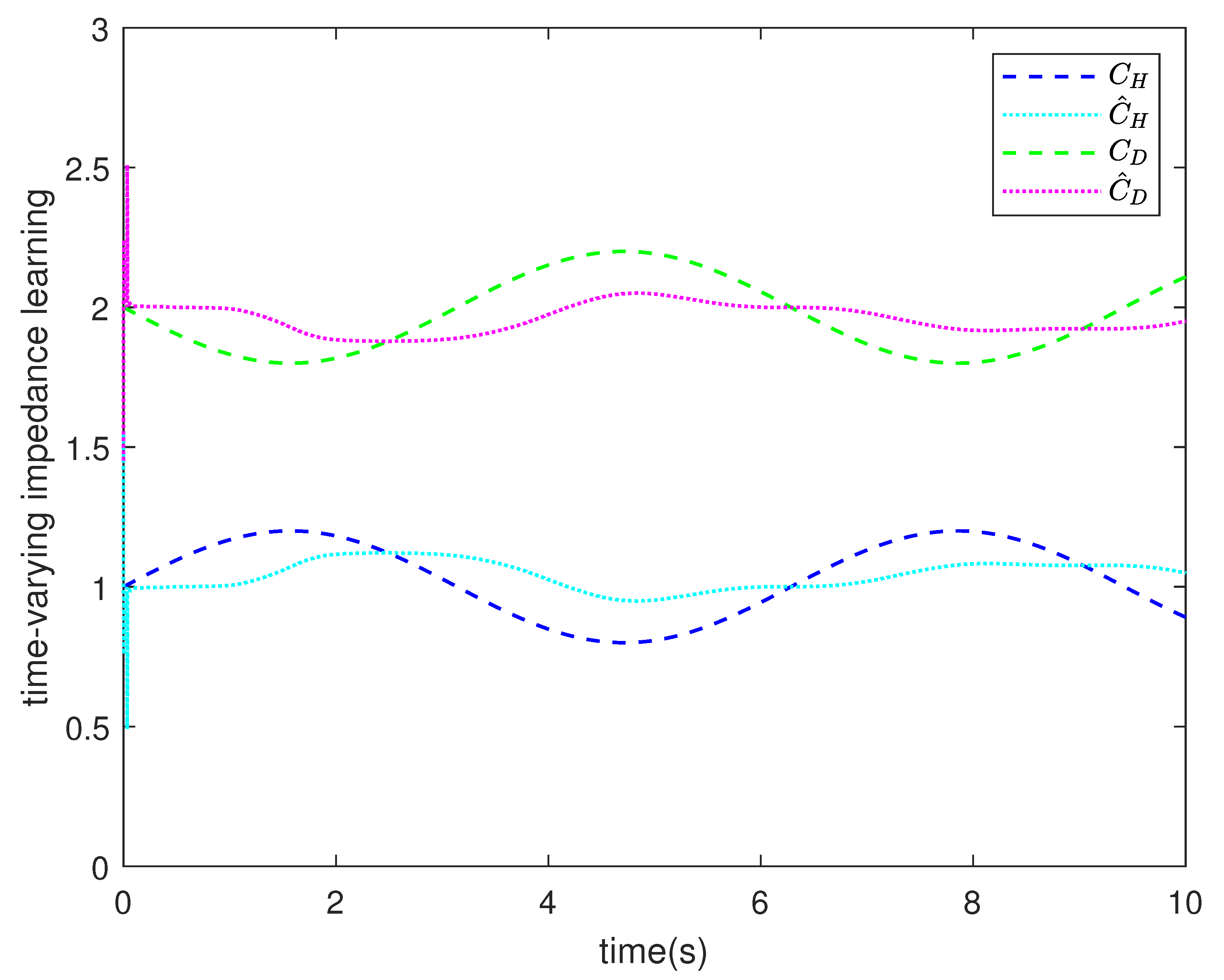
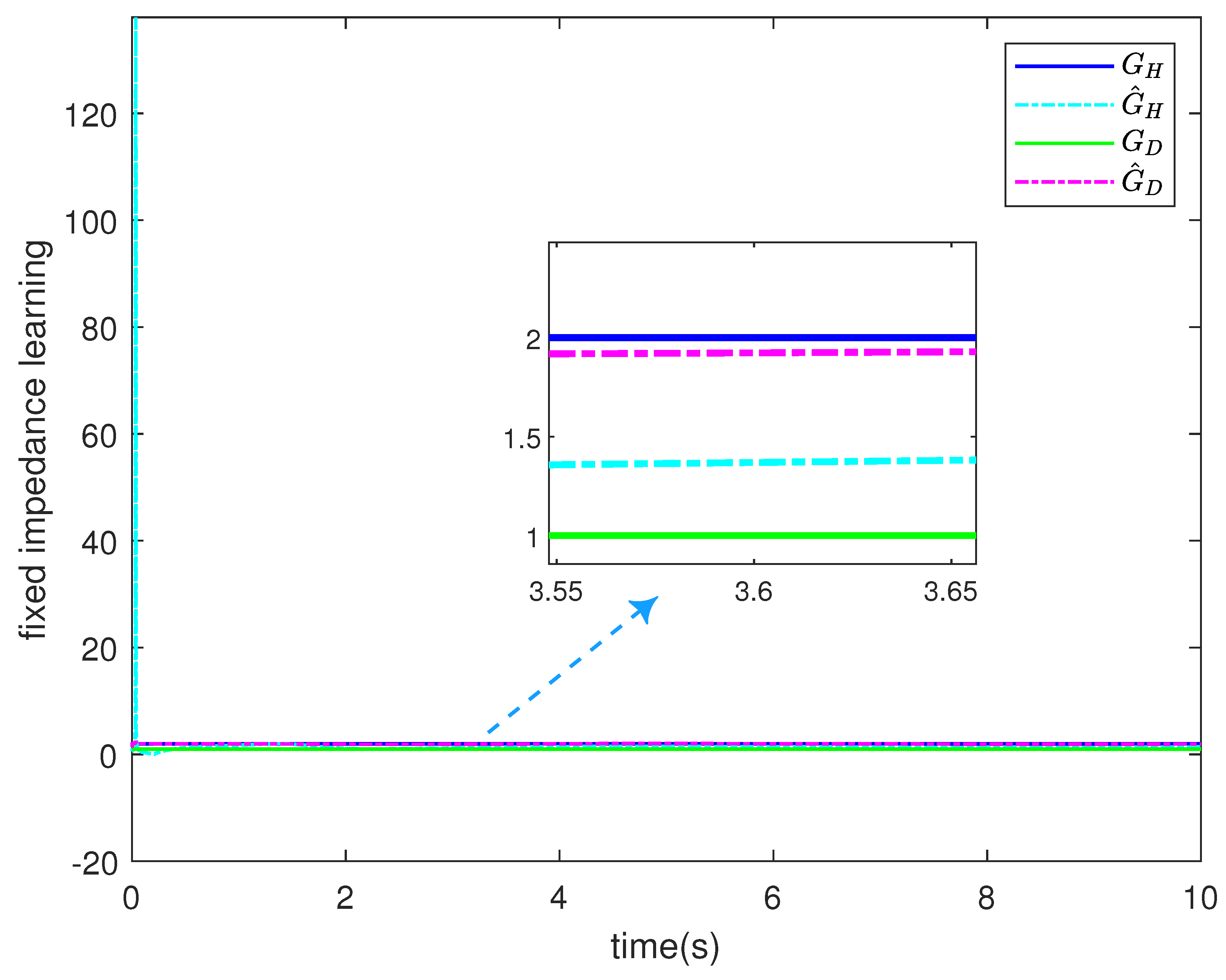
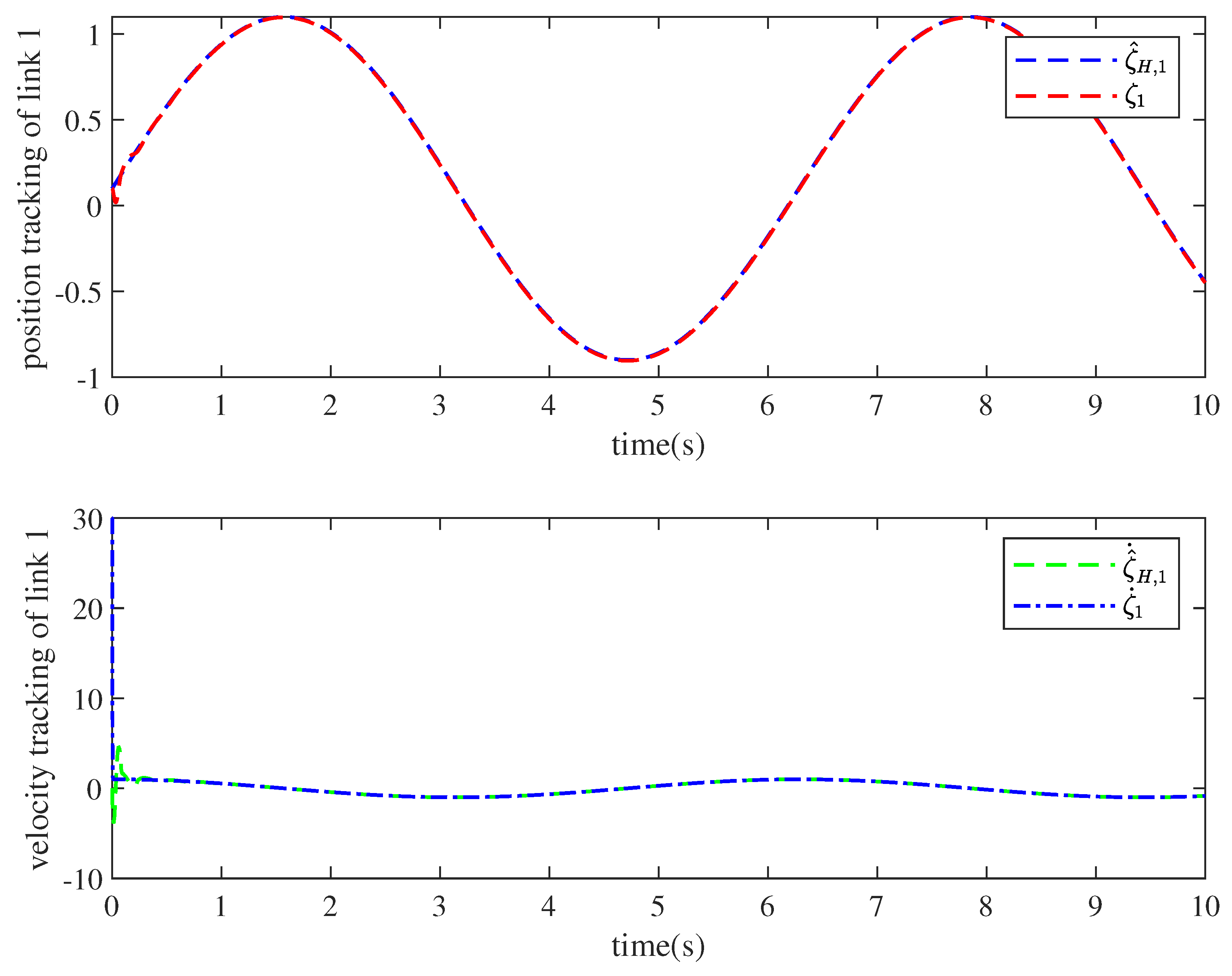
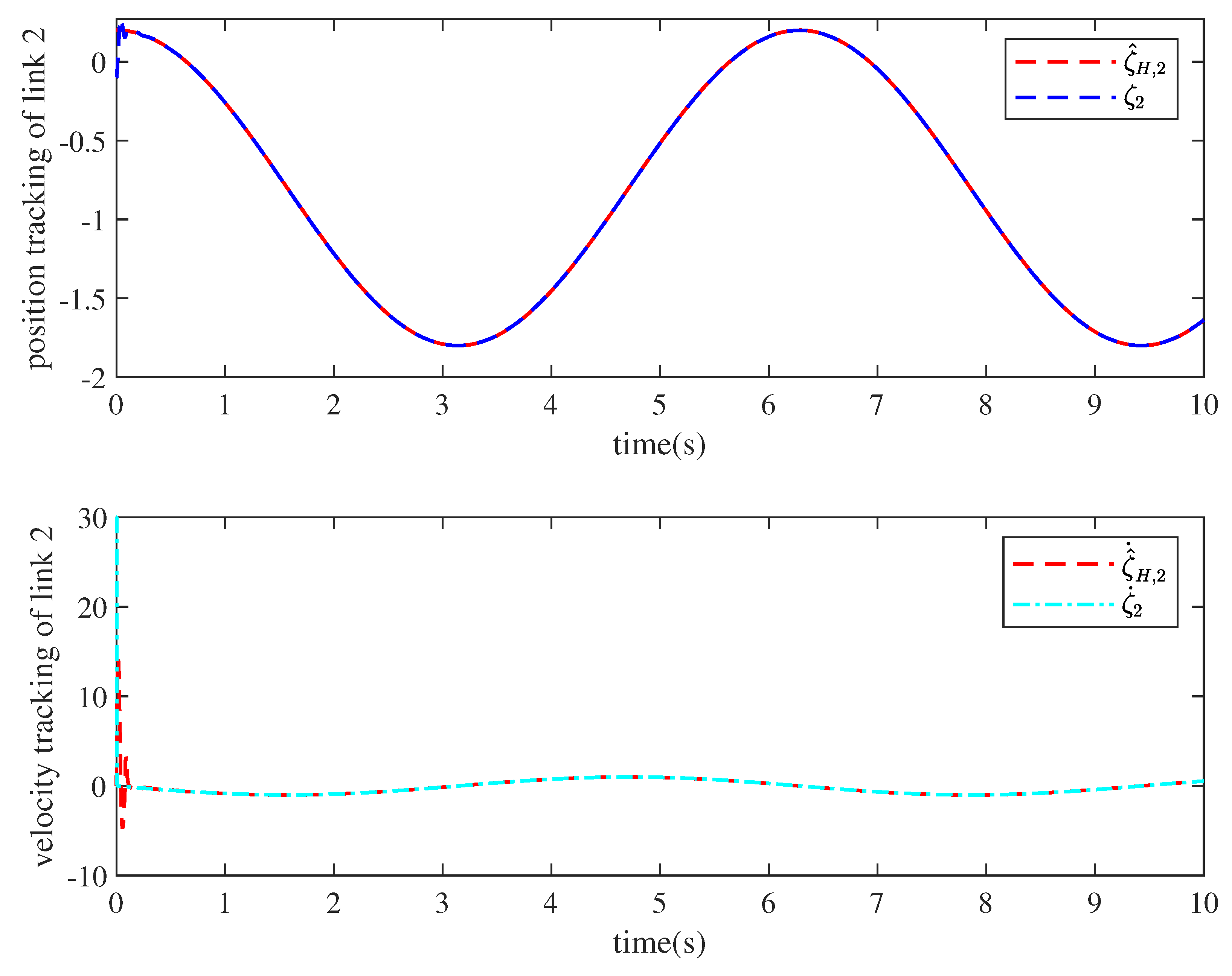
| Parameter | Description | Value |
|---|---|---|
| Mass of link 1 | ||
| Mass of link 2 | ||
| Length of link 1 | ||
| Length of link 2 | ||
| Inertia of link 1 | ||
| Inertia of link 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Chen, H.; Liu, X.; Yang, Y.; Huang, D. Adaptive Impedance Control of a Human–Robotic System Based on Motion Intention Estimation and Output Constraints. Appl. Sci. 2025, 15, 1271. https://doi.org/10.3390/app15031271
Ma J, Chen H, Liu X, Yang Y, Huang D. Adaptive Impedance Control of a Human–Robotic System Based on Motion Intention Estimation and Output Constraints. Applied Sciences. 2025; 15(3):1271. https://doi.org/10.3390/app15031271
Chicago/Turabian StyleMa, Junjie, Hongjun Chen, Xinglan Liu, Yong Yang, and Deqing Huang. 2025. "Adaptive Impedance Control of a Human–Robotic System Based on Motion Intention Estimation and Output Constraints" Applied Sciences 15, no. 3: 1271. https://doi.org/10.3390/app15031271
APA StyleMa, J., Chen, H., Liu, X., Yang, Y., & Huang, D. (2025). Adaptive Impedance Control of a Human–Robotic System Based on Motion Intention Estimation and Output Constraints. Applied Sciences, 15(3), 1271. https://doi.org/10.3390/app15031271





