Quasi-Experimental Design for Medical Studies with the Method of the Fuzzy Pseudo-Control Group
Abstract
:Featured Application
Abstract
1. Definition and Necessity of Pseudo-Control Groups
- If we observed a favorable change in X that is due to the cumulative effect of factors unaccounted for in the study rather than to intervention R (that only weakly contributed to the situation, did not contribute, or even contributed unfavorably), then our conclusion that the effect of R over X for objects from P was favorable would be incorrect.
- If we observed an unfavorable change in X that is due to the cumulative effect of factors unaccounted for in the study and not due to intervention R (that only weakly worsened the situation, did not contribute, or even contributed favorably), then our conclusion that the effect of R over X for objects from P was unfavorable would be incorrect.
- If we observed a negligible change in X that combined the favorable effect of R over X and the cumulative unfavorable effect of the factors unaccounted for in the study, then our conclusion that there was no effect of R over X for objects from P would be incorrect.
- If we observed a negligible change in X that combined the unfavorable effect of R over X and the cumulative favorable effect of the factors unaccounted for in the study, then our conclusion that there was no effect of R over X for objects from P would be incorrect.
- Eb is the sample that contains the values of parameter X for the experimental group at the beginning of the experiment.
- Kb is the sample that contains the values of parameter X for the control group at the beginning of the experiment.
- Ee is the sample that contains the values of parameter X for the experimental group at the end of the experiment, after the group has been subjected to the base intervention V and the investigated intervention R.
- Ke is the sample that contains the values of parameter X for the experimental group at the end of the experiment, after the group has been subjected to the base intervention V.
- We test the samples Ee and Ke for equality:
- If the values X in Ee are statistically significantly more favorable than in Ke, then intervention R over parameter X is proven to be statistically favorable.
- If the values X in Ee are statistically significantly less favorable than in Ke, then intervention R over parameter X is proven to be statistically unfavorable.
- If Ee and Ke have statistically indistinguishable values of X, then the effect of intervention R over parameter X is considered statistically unproven.
- We test, for nullity, the change in X in the paired samples Eb and Ee and the change in X in the paired samples Kb and Ke:
- If the temporal change (TC) in the experimental group is statistically significantly favorable, whereas the TC in the control group is statistically significantly unfavorable, then the effect of intervention R over parameter X is proven to be statistically favorable.
- If the TC in the experimental group is not statistically significant, whereas the TC in the control group is statistically significantly unfavorable, then the effect of intervention R over parameter X is proven to be statistically favorable.
- If the TC in the experimental group is statistically significantly unfavorable, whereas the TC in the control group is statistically significantly favorable, then the effect of intervention R over parameter X is proven to be statistically unfavorable.
- If the TC in the experimental group is not statistically significant, whereas the TC in the control group is statistically significantly favorable, then the effect of intervention R over parameter X is proven to be statistically unfavorable.
- If the TC in both groups are either simultaneously statistically significantly favorable, simultaneously statistically insignificant, or simultaneously statistically significantly unfavorable, then the effect of intervention R over parameter X is considered statistically unproven.
- Eb is the sample that contains the values of parameter X for the experimental group at the beginning of the experiment.
- PCb is the sample that contains the values of parameter X for the pseudo-control group at the beginning of the experiment.
- Ee is the sample that contains the values of parameter X for the experimental group at the end of the experiment after the group has been subjected to the base intervention V and the investigated intervention R.
- PCe is the sample that contains the values of parameter X for the pseudo-control group at the end of the experiment after the group has been subjected to the base intervention V.
- The task depends on whether parameter X is discrete or continuous.
- We should conduct the task using several statistical tests whose results should match.
- The results from the tests should have high sensitivity and specificity, as judging the effect of intervention R over parameter X is based on the differences in the equality tests before and after the intervention.
2. State of the Art in Bootstrap Statistical Testing with Fuzzy Samples
- BM1: Fuzzy Bootstrap with quasi-equal-information generation using an ECDF. In each pseudo-reality, any synthetic sample is generated from the ECDF (constructed using (3) from the original sample) so that the degree of membership sum is almost identical to the same sum for the original sample. It is unlikely that the synthetic and original samples will have the same cardinality.
- BM2: Fuzzy Bootstrap with quasi-equal-information generation using a FECDF. In each pseudo-reality, any synthetic sample is generated from the FECDF (constructed using (4) from the original sample) so that the degree of membership sum is almost identical to the same sum at the original sample. It is unlikely that the synthetic and original samples will have the same cardinality.
- BM3: Fuzzy Bootstrap with equal-size generation using an ECDF. In each pseudo-reality, any synthetic sample is generated from the ECDF (constructed using (3) from the original sample) with cardinality equal to the cardinality of the original sample. It is unlikely that the synthetic and original samples will have the same degree of membership sums.
- BM4: Fuzzy Bootstrap with equal-size generation using a FECDF. In each pseudo-reality, any synthetic sample is generated from the FECDF (constructed using (4) from the original sample) with cardinality equal to the cardinality of the original sample. It is unlikely that the synthetic and original samples will have the same degree of membership sums.
3. The Method of the Fuzzy Pseudo-Control Group
- An expert-based definition of the optimal values of parameter X.
- A favorability assessment of the differences between the populations.
- The identification of the statistical significance of differences between populations.
- The categorization of differences between populations.
- The classification of the MFPCG result.
3.1. An Expert-Based Definition of the Optimal Values of Parameter X
3.2. A Favorability Assessment of the Difference Between Populations
Stage 2 Algorithm: A Favorability Assessment of the Difference Between the Fuzzy Central Tendencies of Two Populations
3.3. The Identification of the Statistical Significance of Differences Between Populations
- Test 1: Fuzzy Bootstrap Kuiper test for equality of population distributions (FBT1).
- Test 2. Fuzzy two-tail Bootstrap test for equality of population means (FBT2).
- Test 3. Fuzzy one-tail Bootstrap test for equality of population means (FBT3).
- Test 4. Fuzzy two-tail Bootstrap test for equality of population medians (FBT4).
- Test 5. Fuzzy one-tail Bootstrap test for equality of population medians (FBT5).
- Test 6. Fuzzy two-tail Bootstrap test for equality of population variances (FBT6).
- Test 7. Fuzzy one-tail Bootstrap test for equality of population variances (FBT7).
- Test 8. Fuzzy two-tail Bootstrap test for equality of population interquartile ranges (FBT8).
- Test 9. Fuzzy one-tail Bootstrap test for equality of population interquartile ranges (FBT9).
Stage 3 Algorithm: Defining the Statistical Significance of Differences Between Two Populations
3.4. The Categorization of Differences Between Populations
- If one of the measures of the location of X in the target population P is statistically significantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is neither statistically significantly nor borderline statistically significantly less favorable than that of the pseudo-control population Q, then categorize in C+1.
- If one of the measures of location of X in the target population P is statistically significantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is borderline statistically significantly less favorable than that of the pseudo-control population Q, and the First Condition holds, then categorize in C+1.
- If one of the measures of location of X in the target population P is borderline statistically significantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either borderline statistically significantly more favorable, or statistically indistinguishable, or neutral to that in the pseudo-control population Q, and the First Condition holds, then categorize in C+1.
- If one of the measures of location of X in the target population P is statistically insignificantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either statistically insignificantly more favorable or neutral compared to that in the pseudo-control population Q, and the Second Condition holds, then categorize in C+1.
- If one of the measures of location of X in the target population P is statistically significantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is neither statistically significantly nor borderline statistically significantly more favorable than that in the pseudo-control population Q, then categorize in C−1.
- If one of the measures of location of X in the target population P is statistically significantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is borderline statistically significantly more favorable than that in the pseudo-control population Q, and the First Condition holds, then categorize in C−1.
- If one of the measures of location of X in the target population P is borderline statistically significantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either borderline statistically significantly less favorable, or statistically indistinguishable, or neutral compared to that in the pseudo-control population Q, and the First Condition holds, then categorize in C−1.
- If one of the measures of location of X in the target population P is statistically insignificantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either statistically insignificantly less favorable or neutral compared to that in the pseudo-control population Q, and the Second Condition holds, then categorize in C−1.
- If one of the measures of location of X in the target population P is statistically significantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is borderline statistically significantly less favorable than that in the pseudo-control population Q, then categorize in C+1/2.
- If one of the measures of location of X in the target population P is borderline statistically significantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either borderline statistically significantly more favorable, or statistically indistinguishable, or neutral with that in the pseudo-control population Q, then categorize in C+1/2.
- If one of the measures of location of X in the target population P is statistically insignificantly more favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either statistically insignificantly more favorable or neutral with that in the pseudo-control population Q, and the Third Condition holds, then categorize in C+1/2.
- If one of the measures of location of X in the target population P is statistically significantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is borderline statistically significantly more favorable than that in the pseudo-control population Q, then categorize in C−1/2.
- If one of the measures of location of X in the target population P is borderline statistically significantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either borderline statistically significantly less favorable, or statistically indistinguishable, or neutral with that in the pseudo-control population Q, then categorize in C−1/2.
- If one of the measures of location of X in the target population P is statistically insignificantly less favorable than that in the pseudo-control population Q, whereas the other measure of location in the target population P is either statistically insignificantly less favorable or neutral with that in the pseudo-control population Q, and the Third Condition holds, then categorize in C−1/2.
- If none of Rules 1 to 14 apply, then categorize in C0.
3.5. The Classification of the MFPCG Result
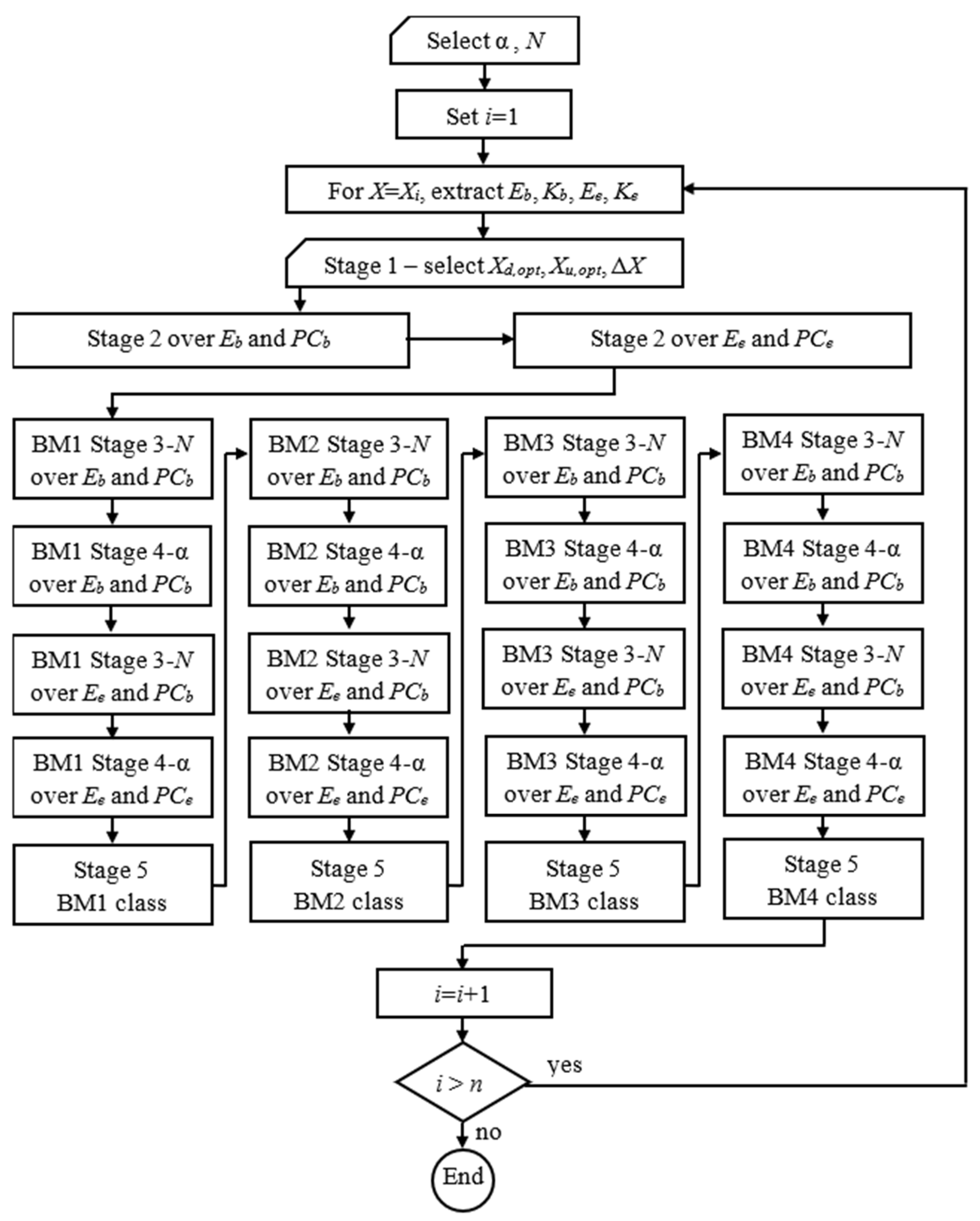
3.6. MFPCG Algorithm and Flowchat of the Method
MFPCG Algorithm
- Select the significance level, α, and the number of pseudo-realities, N, of the Bootstrap statistical tests.
- Set i = 1.
- Choose X = Xi.
- Extract from the database the fuzzy samples Eb, PCb, Ee, and PCe for this X.
- Perform stage 1 of MFPCG and expertly determine for X the optimal value margins Xd,opt, Xu,opt, and the insignificant change threshold ΔX.
- Perform stage 2 of MFPCG for Eb and PCb.
- Perform stage 2 of MFPCG for Ee and PCe.
- Repeat for Bootstrap Modification BMk (k = 1, 2, 3, 4):
- 8.1.
- Perform stage 3 of MFPCG for Eb and PCb using Bootstrap Modification BMk with N pseudo-realities for each Bootstrap test using significance level α.
- 8.2.
- Perform stage 4 of MFPCG for Eb and PCb using Bootstrap Modification BMk.
- 8.3.
- Perform stage 3 of MFPCG for Ee and PCe using Bootstrap Modification BMk with N pseudo-realities for each Bootstrap test using significance level α.
- 8.4.
- Perform stage 4 of MFPCG for Ee and PCe using Bootstrap Modification BMk.
- 8.5.
- Perform stage 5 of MFPCG for Bootstrap Modification BMk and find the BMk class.
- Set i = i + 1.
- If i < n, then go to step 3. Otherwise, end the algorithm.
4. Annuloplasty Favorability Case Study
- (1)
- Traditionally, the classification of patients is based on subjective expertise. There is no specific measure of how typical a patient is to a given group.
- (2)
- The groups are not homogenous. Therefore, comparing them is complicated.
4.1. Database
- Those with a comparatively preserved medical state (A1 and B1)
- Those with a comparatively deteriorated medical state (A2 and B2).
- 20 identifiers;
- 18 anamnesis and clinical preoperative parameters; and
- 13 three-dimensional (triple) echocardiographic parameters.
4.2. Division into Groups with Fuzzy Degrees of Membership
4.3. Assessing the Effect of Annuloplasty for Patients with Severe IMR Using Fuzzy Pseudo-Control Groups
- (Task 1)
- Assess the effect of annuloplasty over RF for patients with a relatively preserved medical state.
- (Task 2)
- Assess the effect of annuloplasty over MR for patients with a relatively preserved medical state.
- (Task 3)
- Assess the effect of annuloplasty over RF for patients with a relatively deteriorated medical state.
- (Task 4)
- Assess the effect of annuloplasty over MR for patients with a relatively deteriorated medical state.
- Eb is a fuzzy sample that contains the values of X and their degrees of membership to the experimental group Ai before the combined intervention.
- PCb is a fuzzy sample that contains the values of X and their degrees of membership to the pseudo-control group Bi before the isolated intervention.
- Ee is a fuzzy sample that contains the values of X and their degrees of membership to the experimental group Ai late after the combined intervention.
- PCe is a fuzzy sample that contains the values of X and their degrees of membership to the pseudo-control group Bi late after the isolated intervention.
4.3.1. Effect of Annuloplasty over RF for Patients with Relatively Preserved Medical State (Task 1)
4.3.2. Effect of Annuloplasty over MR for Patients with Relatively Preserved Medical State (Task 2)
4.3.3. Effect of Annuloplasty over RF for Patients with Relatively Deteriorated Medical State (Task 3)
4.3.4. Effect of Annuloplasty over MR for Patients with Relatively Deteriorated Medical State (Task 4)
4.4. Summary
5. Validation of the Case Study Conclusions
5.1. External Validation
- In this study, we used data for all available patients, whereas the cited sources analyzed the data after rejecting outliers (which comprised about 20% of the data).
- Here, we discuss the typicality of patients to a respective subgroup for the first time, whereas in earlier works, the classification is considered absolute (crisp).
- The statistical support for a favorable effect of annuloplasty is efficiently completed using only two integral parameters. In contrast, the earlier works used a double-digit count of parameters to reach the same conclusions.
5.2. Fuzzy DID Method (FDID)
FDID Algorithm
- Select the significance level, α, and the number of pseudo-realities, N, to construct the Bootstrap CIs.
- Set i = 1.
- Choose X = Xi.
- Extract from the database the fuzzy samples Eb, PCb, Ee, and PCe for this X.
- Estimate the fuzzy mean values of the four samples ME,b, MPC,b, ME,e, and MPC,e using (8).
- Estimate the fuzzy DID estimator as the ATE:
- 7.
- Find the index of the empirical α/2-quantile from the Bootstrap distribution of ATE, as Nd = round(N × α/2).
- 8.
- Find the index of the empirical (1–α/2)-quantile from the Bootstrap distribution of ATE, as Nu = round(N − N × α/2).
- 9.
- Repeat for Bootstrap Modification BMk (k = 1, 2, 3, 4):
- 9.1.
- Repeat for pseudo-reality r (r = 1, 2, …, N):
- 9.1.1.
- From sample Eb, generate sEb,r, using Bootstrap Modification BMk.
- 9.1.2.
- From sample PCb, generate sPCb,r, using Bootstrap Modification BMk.
- 9.1.3.
- From sample Ee, generate sEe,r, using Bootstrap Modification BMk.
- 9.1.4.
- From sample PCe, generate sPCe,r, using Bootstrap Modification BMk.
- 9.1.5.
- Estimate the fuzzy mean values of the four synthetic samples sME,b,r, sMPC,b,r, sME,e,r, and sMPC,e,r using (8).
- 9.1.6.
- Estimate the fuzzy DID estimator as sATEr in the r-th pseudo-reality:sATEr = (sME,e,r − sMPC,e,r) − (sME,b,r − sMPC,b,r)
- 9.2.
- Sort the synthetic sATEr in ascending order and obtain sATEsort,r (r = 1, 2, …, N).
- 9.3.
- Estimate the Reverse Percentile 100 × (1 – α)%-CI for ATE using Bootstrap Modification BMk:Pr{2 × ATE – sATEsort,Nu < ATE < 2 × ATE – sATEsort,Nd} = 1 – α
- 10.
- Set i = i+1.
- 11.
- If i < n, then go to step 3. Otherwise, end the algorithm.
5.3. Case Study Solved with FDID
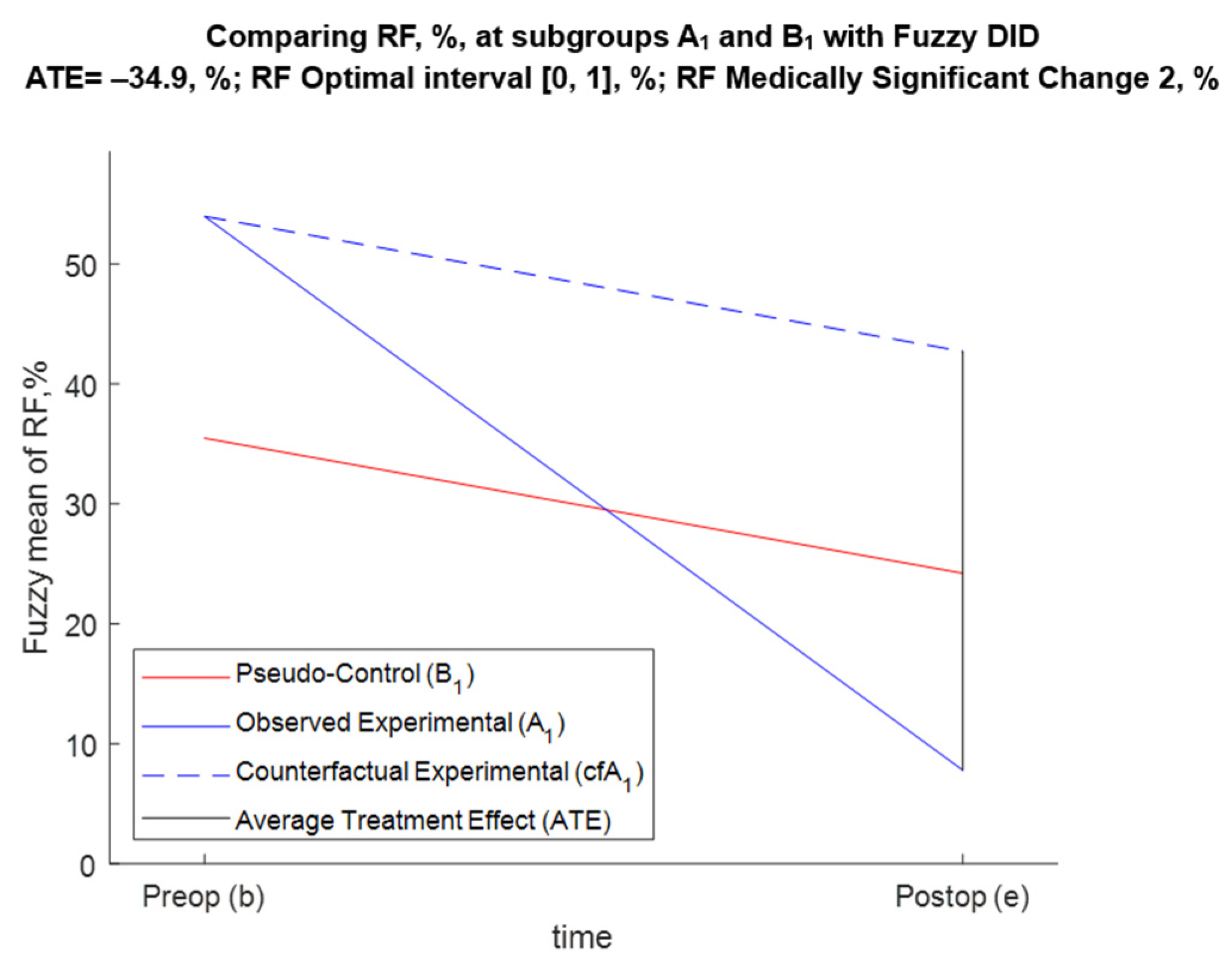
5.3.1. FDID Solution of Task 1 (Effect of Annuloplasty over RF for A1 and B1 Patients)
- For BM1, Pr{−43.7 < ATE < −26.1} = 0.95;
- For BM2, Pr{−44.6 < ATE < −27.1} = 0.95;
- For BM3, Pr{−44.1 < ATE < −26} = 0.95;
- For BM4, Pr{−44.4 < ATE < −26.9} = 0.95.
5.3.2. FDID Solution of Task 2 (Effect of Annuloplasty over MR for A1 and B1 Patients)
- For BM1, Pr{−3.97 < ATE < −2.67} = 0.95;
- For BM2, Pr{−3.91 < ATE < −2.54} = 0.95;
- For BM3, Pr{−4 < ATE < −2.64} = 0.95 = 0.95;
- For BM4, Pr{−3.9 < ATE < −2.54} = 0.95 = 0.95.
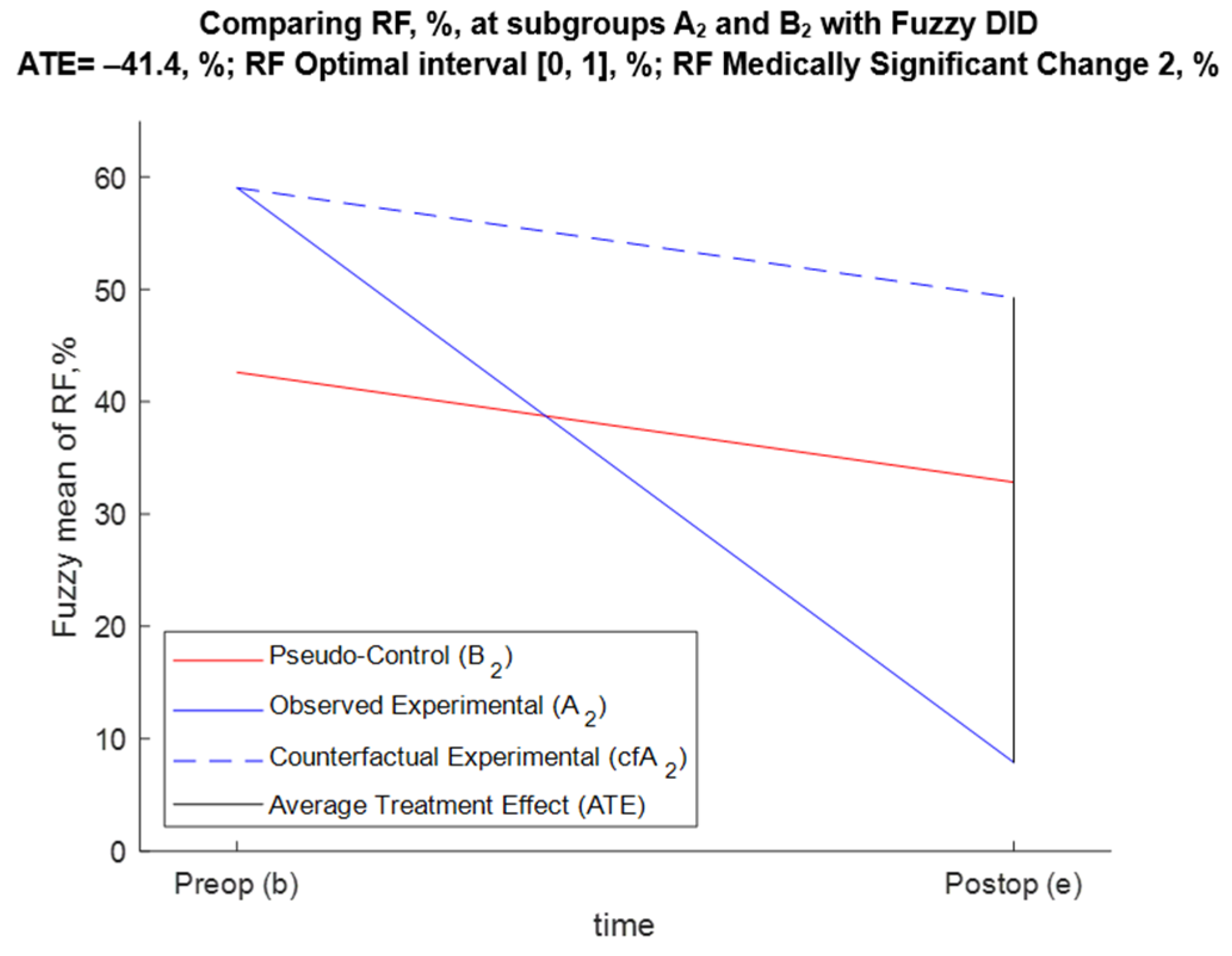
5.3.3. FDID Solution of Task 3 (Effect of Annuloplasty over RF for A2 and B2 Patients)
- For BM1, Pr{−52.5 < ATE < −29.5} = 0.95;
- For BM2, Pr{−54.5 < ATE < −29.7} = 0.95;
- For BM3, Pr{−52.7 < ATE < −30.5} = 0.95;
- For BM4, Pr{−54 < ATE < −29.9} = 0.95.
5.3.4. FDID Solution of Task 4 (Effect of Annuloplasty over MR for A2 and B2 Patients)
- For BM1, Pr{−4.62 < ATE < −3.17} = 0.95;
- For BM2, Pr{−4.56 < ATE < −3.1} = 0.95;
- For BM3, Pr{−4.63 < ATE < −3.15} = 0.95;
- For BM4, Pr{−4.62 < ATE < −3.09} = 0.95.
5.4. Internal Validation with FDID
- The results from FDID are conditional upon the assumptions of the method. We do not have a way of proving the parallel trend assumption, as shown in Figure 2, Figure 3, Figure 4 and Figure 5. We also cannot prove that, in this particular case, the classical normal linear regression model (CNLRM) assumptions [9,60] about nullity, homoskedasticity, normality, correlation, multicollinearity, and linearity hold.
- Both methods use data for all available patients without rejecting outliers.
- Both methods use a cluster of tests instead of individual p-values.
- Both methods consider the typicality of patients to a respective subgroup.
- MFPCG produces qualitative results that annuloplasty is favorable for patients with an average or average-to-severe IMR. At the same time, the FDID produced quantitative results as to how much the annuloplasty improved the outcome for those patients compared with patients with isolated CABG.
5.5. Internal Validation with Fuzzy RDD (FRDD)
6. Discussion and Conclusions
6.1. Basic Idea and Adaptability of MFPCG
6.2. Limitations of MFPCG
6.3. Synergies of MFPCG, FRDD, and FDID
- FDID always produces a quantitative assessment of the influence, and FRDD sometimes produces a quantitative assessment of the influence, whereas MFPCG sometimes produces a qualitative assessment of that influence.
- FRDD and FDID apply only to monotonic preferences over X, whereas MFPCG deals with hill preferences that are very applicable in medical studies, especially in the current age of overmedication in Western societies.
- FDID uses many assumptions that are hard to verify (the same is true to a smaller extent about FRDD), unlike MFPCG.
- FRDD and FDID only deal with mean values, whereas the more complex MFPCG operates on distributions, means, medians, standard deviations, and interquartile ranges.
- FRDD and FDID are incapable of assessing the practical significance of observed changes regardless of their statistical significance, whereas this aspect is incorporated in MFPCG.
- FRDD and FDID are easy to implement, whereas MFPCG is computationally challenging.
- There is considerable knowledge of how to implement and modify FRDD and FDID to deal with different problems since these are well known, whereas MFPCG is a new approach.
- (1)
- We should always start by applying FRDD. It generally works when there are large experimental and pseudo-control groups. The quantitative result, if any, statistically proves that the pseudo-control sample is, in fact, the control one, since there is no statistically significant difference between the pre-intervention samples. If the values of X in the fuzzy samples are in the region of monotonic preferences, the results of FRDD would be useful.
- (2)
- We then try MFPCG. If the method works, it will provide a very reliable qualitative assessment of the positive or negative influence of the intervention R.
- (3)
- We can finish with FDID. The reliability of the quantitative result depends on the validity of the assumptions of the method. If the values of X in the fuzzy samples are in the region of monotonic preferences, the results of FDID would be useful.
6.4. Applications of MFPCG
6.5. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hinkelmann, K.; Kempthorne, O. Design and Analysis of Experiments, Volume I: Introduction to Experimental Design, 2nd ed.; Wiley Series of Probability and Statistics: Washington, DC, USA, 2008. [Google Scholar]
- Bailey, R.A. Design of Comparative Experiments; Cambridge University Press: Cambridge, UK, 2008; ISBN 978-0-521-68357-9. [Google Scholar]
- Everitt, B.S. The Cambridge Dictionary of Statistics; Cambridge University Press: Cambridge, UK, 2002; ISBN 0-521-81099-X. [Google Scholar]
- Chalmers, T.C.; Smith, H.; Blackburn, B.; Silverman, B.; Schroeder, B.; Reitman, D.; Ambroz, A. A method for assessing the quality of a randomized control trial. Control. Clin. Trials 1981, 2, 31–49. [Google Scholar] [CrossRef]
- Eddy, D.M. Evidence-based medicine: A unified approach. Health Aff. 2005, 24, 9–17. [Google Scholar] [CrossRef]
- Robson, L.S.; Shannon, H.S.; Goldenhar, L.M.; Hale, A.R. Quasi-experimental and experimental designs: More powerful evaluation designs. In Guide to Evaluating the Effectiveness of Strategies for Preventing Work Injuries; Department of Health and Human Services, National Institute for Occupational Safety and Health: Cincinnati, OH, USA, 2001; pp. 29–42. [Google Scholar]
- Kampenes, V.B.; Dybå, T.; Hannay, J.E.; Sjøberg, D.I.K. A systematic review of quasi-experiments in software engineering. Inf. Softw. Technol. 2009, 51, 71–82. [Google Scholar] [CrossRef]
- Roth, J.; Sant’Anna, P.H.C.; Bilinski, A.; Poe, J. What’s trending in difference-in-differences? A synthesis of the recent econometrics literature. J. Econom. 2023, 235, 2218–2244. [Google Scholar] [CrossRef]
- Poole, M.A.; O’Farrell, P.N. The assumptions of the linear regression model. Trans. Inst. Br. Geogr. 1971, 52, 145–158. [Google Scholar] [CrossRef]
- Ryan, A.M.; Burgess, J.F., Jr.; Dimick, J.B. Why we should not be indifferent to specification choices for difference-in-differences. Health Res. Educ. Trust. 2015, 50, 1211–1235. [Google Scholar] [CrossRef]
- Abadie, A. Semiparametric difference-in-differences estimators. Rev. Econ. Stud. 2005, 72, 1–19. [Google Scholar] [CrossRef]
- Imbens, G.; Lemieux, T.H. Regression Discontinuity Designs: A Guide to Practice. National Bureau of Economic Research Technical Working Paper 337. 2007. Available online: http://www.nber.org/papers/t0337 (accessed on 10 January 2025).
- Nikolova, N.; Rodríguez, R.M.; Symes, M.; Toneva, D.; Kolev, K.; Tenekedjiev, K. Outlier detection algorithms over fuzzy data with weighted least squares. Int. J. Fuzzy Syst. 2021, 23, 1234–1256. [Google Scholar] [CrossRef]
- Farkas, Á.Z.; Farkas, V.J.; Gubucz, I.; Szabó, L.; Bálint, K.; Tenekedjiev, K.; Nagy, A.I.; Sótonyi, P.; Hidi, L.; Nagy, Z.; et al. Neutrophil extracellular traps in thrombi retrieved during interventional treatment of ischemic arterial diseases. Thromb. Res. 2019, 175, 46–52. [Google Scholar] [CrossRef]
- Mihaylova, N. Bootstrap-Based Simulation Platform for Analysis of Medical Information. Ph.D. Thesis, Nikola Vaptsarov Naval Academy, Varna, Bulgaria, 2015. [Google Scholar]
- Panayotova, D. Application of echocardiographic methods for fuzzy stratification determining the volume of surgery in patients with ischemic mitral regurgitation. In Medical Academic Repository; Medical University: Varna, Bulgaria, 2023; Available online: https://repository.mu-varna.bg/handle/nls/3461 (accessed on 23 December 2024).
- Faugeras, O.P. Maximal coupling of empirical copulas for discrete vectors. J. Multivar. Anal. 2015, 137, 179–186. [Google Scholar] [CrossRef]
- Tenekedjiev, K.; Dimitrakiev, D.; Nikolova, N. Building frequentist distributions of continuous random variables. Mach. Mech. 2002, 47, 164–168. [Google Scholar]
- Gao, S.; Zhong, Y.; Gu, C. Random weighting estimation of confidence intervals for quantiles. Aust. N. Z. J. Stat. 2013, 55, 43–53. [Google Scholar] [CrossRef]
- Poe, G.; Giraud, K.; Loomis, J. Computational methods for measuring the difference of empirical distributions. Am. J. Agric. Econ. 2005, 87, 353–365. [Google Scholar] [CrossRef]
- Wasserman, L. The Bootstrap and the Jackknife. In All of Nonparametric Statistics; Springer Texts in Statistics; Springer: New York, NY, USA, 2006; pp. 27–41. [Google Scholar] [CrossRef]
- Henderson, R. The Bootstrap: A technique for data-driven statistics. Using computer-intensive analyses to explore experimental data. Clin. Chim. Acta 2005, 359, 1–26. [Google Scholar] [CrossRef]
- González-Rodríguez, G.; Montenegro, M.; Colubi, A.; Gil, M.-A. Bootstrap techniques and fuzzy random variables: Synergy in hypothesis testing with fuzzy data. Fuzzy Sets Syst. 2006, 157, 2608–2613. [Google Scholar] [CrossRef]
- Politis, D. Computer-intensive methods in statistical analysis. Signal Process. Mag. 1998, 15, 39–55. [Google Scholar] [CrossRef]
- Chernobai, A.; Rachev, S.T.; Fabozzi, F.J. Composite goodness-of-fit tests for left-truncated loss samples. In Handbook of Financial Econometrics and Statistics; Lee, C.F., Lee, J., Eds.; Springer: New York, NY, USA, 2015; pp. 575–596. [Google Scholar] [CrossRef]
- Groebner, D.F.; Shannon, P.W.; Fry, P.C. Business Statistics—A Decision-Making Approach, 10th ed.; Pearson: London, UK, 2018; pp. 387–434. [Google Scholar]
- Böhm, W.; Hornik, K. A Kolmogorov-Smirnov test for r samples. Res. Rep. Ser. Dep. Stat. Math. 2010, 105, 103–125. [Google Scholar] [CrossRef]
- Lemeshko, B.; Gobrunova, A.A. Application and power of the nonparametric Kuiper, Watson, and Zhang tests of goodness-of-fit. Meas. Tech. 2013, 56, 465–475. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes—The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007; Volume 732, p. 737. [Google Scholar]
- Nikolova, N.; Ivanova, S.; Chin, C.; Tenekedjiev, K. Calculation of the Kolmogorov-Smirnov and Kuiper statistics over fuzzy samples. Proc. Jangjeon Math. Soc. 2017, 20, 269–311. [Google Scholar]
- Nikolova, N.; Chai, S.; Ivanova, S.; Kolev, K.; Tenekedjiev, K. Bootstrap Kuiper testing of the identity of 1D continuous distributions using fuzzy samples. Int. J. Comput. Intell. Syst. 2015, 8, 63–75. [Google Scholar] [CrossRef]
- Nikolova, N.; Mihaylova, N.; Tenekedjiev, K. Bootstrap tests for mean value differences over fuzzy samples. IFAC-PapersOnLine 2015, 48, 7–14. [Google Scholar] [CrossRef]
- Tenekedjiev, K.; Nikolova, N.; Rodriguez, R.M.; Hirota, K. Bootstrap testing of central tendency nullity over paired fuzzy samples. Int. J. Fuzzy Syst. 2021, 23, 1934–1954. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic. In Granular, Fuzzy, and Soft Computing; Lin, T.Y., Liau, C.J., Kacprzyk, J., Eds.; Encyclopedia of Complexity and Systems Science Series; Springer: New York, NY, USA, 2009; pp. 19–49. [Google Scholar] [CrossRef]
- Bickel, P.J.; Ren, J.-J. The Bootstrap in hypothesis testing. Lect. Notes-Monogr. Ser. 2001, 36, 91–112. Available online: http://www.jstor.org/stable/4356107 (accessed on 5 January 2025).
- Wehrens, R.; Putter, H.; Buydens, L.M.C. The Bootstrap: A tutorial. Chemom. Intell. Lab. Syst. 2000, 54, 35–52. [Google Scholar] [CrossRef]
- Cahoy, D.O. A Bootstrap test for equality of variances. Comput. Stat. Data Anal. 2010, 54, 2306–2316. [Google Scholar] [CrossRef]
- Greco, L.; Luta, G.; Wilcox, R. On testing the equality between interquartile ranges. Comput. Stat. 2024, 39, 2873–2898. [Google Scholar] [CrossRef]
- Hidi, L.; Komorowicz, E.; Kovács, G.I.; Szeberin, Z.; Garbaisz, D.; Nikolova, N.; Tenekedjiev, K.; Szabó, L.; Kolev, K.; Sótonyi, P. Cryopreservation moderates the thrombogenicity of arterial allografts during storage. PLoS ONE 2021, 16, e0255114. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Nikolova, N.; Hirota, K.; Kobashikawa, C.; Tenekedjiev, K. Elicitation of non-monotonic preferences of a fuzzy rational decision maker. Inf. Technol. Control. 2006, 4, 36–50. [Google Scholar]
- Coats, A.J.S.; Anker, S.D.; Baumbach, A.; Alfieri, O.; von Bardeleben, R.S.; Bauersachs, J.; Bax, J.J.; Boveda, S.; Čelutkienė, J.; Cleland, J.G.; et al. The management of secondary mitral regurgitation in patients with heart failure: A joint position statement from the Heart Failure Association (HFA), European Association of Cardiovascular Imaging (EACVI), European Heart Rhythm Association (EHRA), and European Association of Percutaneous Cardiovascular Interventions (EAPCI) of the ESC. Eur. Heart J. 2021, 42, 1254–1269. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Mazin, I.; Arad, M.; Freimark, D.; Goldenberg, I.; Kuperstein, R. The prognostic role of mitral valve regurgitation severity and left ventricle function in acute heart failure. J. Clin. Med. 2022, 11, 4267. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Vajapey, R.; Kwon, D. Guide to functional mitral regurgitation: A contemporary review. Cardiovasc. Diagn. Ther. 2021, 11, 781–792. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Chan, K.M.; Punjabi, P.P.; Flather, M.; Wage, R.; Symmonds, K.; Roussin, I.; Rahman-Haley, S.; Pennell, D.J.; Kilner, P.J.; Dreyfus, G.D.; et al. Coronary artery bypass surgery with or without mitral valve annuloplasty in moderate functional ischemic mitral regurgitation: Final results of the Randomized Ischemic Mitral Evaluation (RIME) trial. Circulation 2012, 126, 2502–2510. [Google Scholar] [CrossRef] [PubMed]
- Cully, M. Mitral valve repair with CABG surgery. Nat. Rev. Cardiol. 2013, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Acker, M.A.; Parides, M.K.; Perrault, L.P.; Moskowitz, A.J.; Gelijns, A.C.; Voisine, P.; Smith, P.K.; Hung, J.W.; Blackstone, E.H.; Puskas, J.D.; et al. Mitral-valve repair versus replacement for severe ischemic mitral regurgitation. N. Engl. J. Med. 2014, 370, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.; Moskowitz, A.J.; Gelijns, A.C.; Ailawadi, G.; Parides, M.K.; Perrault, L.P.; Hung, J.W.; Voisine, P.; Dagenais, F.; Gillinov, A.M.; et al. Two-year outcomes of surgical treatment of severe ischemic mitral regurgitation. N. Engl. J. Med. 2016, 374, 344–353. [Google Scholar] [CrossRef]
- Andalib, A.; Chetrit, M.; Eberg, M.; Filion, K.B.; Thériault-Lauzier, P.; Lange, R.; Buithieu, J.; Martucci, G.; Eisenberg, M.; Bolling, S.F.; et al. A systematic review and meta-analysis of outcomes following mitral valve surgery in patients with significant functional mitral regurgitation and left ventricular dysfunction. J. Heart Valve Dis. 2016, 25, 696–707. [Google Scholar]
- Dayan, V.; Soca, G.; Cura, L.; Mestres, C.A. Similar survival after mitral valve replacement or repair for ischemic mitral regurgitation: A meta-analysis. Ann. Thorac. Surg. 2014, 97, 758–765. [Google Scholar] [CrossRef]
- Lio, A.; Miceli, A.; Varone, E.; Canarutto, D.; Di Stefano, G.; Della Pina, F.; Gilmanov, D.; Murzi, M.; Solinas, M.; Glauber, M. Mitral valve repair versus replacement in patients with ischaemic mitral regurgitation and depressed ejection fraction: Risk factors for early and mid-term mortality dagger. Interdiscip. Cardiovasc. Thorac. Surg. 2014, 19, 64–69. [Google Scholar] [CrossRef]
- LaPar, D.J.; Ailawadi, G.; Isbell, J.M.; Crosby, I.K.; Kern, J.A.; Rich, J.B.; Speir, A.M.; Kron, I.L. Mitral valve repair rates correlate with surgeon and institutional experience. J. Thorac. Cardiovasc. Surg. 2014, 148, 995–1003; Discussion 3–4. [Google Scholar] [CrossRef]
- Maltais, S.; Schaff, H.V.; Daly, R.C.; Suri, R.M.; Dearani, J.A.; Sundt, T.M., 3rd; Enriquez-Sarano, M.; Topilsky, Y.; Park, S.J. Mitral regurgitation surgery in patients with ischemic cardiomyopathy and ischemic mitral regurgitation: Factors that influence survival. J. Thorac. Cardiovasc. Surg. 2011, 142, 995–1001. [Google Scholar] [CrossRef] [PubMed]
- Panayotov, P.; Panayotova, D.; Nikolova, N.; Donchev, N.; Ivanova, S.; Mircheva, L.; Petrov, V.; Tenekedjiev, K. Algorithms for formal stratification of patients with ischemic mitral regurgitation. Scr. Sci. Medica 2018, 50, 33–38. [Google Scholar] [CrossRef]
- Nikolova, N.; Panayotov, P.; Panayotova, D.; Ivanova, S.; Tenekedjiev, K. Using fuzzy sets in surgical treatment selection and homogenizing stratification of patients with significant chronic ischemic mitral regurgitation. Int. J. Comput. Intell. Syst. 2019, 12, 1075–1090. [Google Scholar] [CrossRef]
- Oxorn, D.C.; Otto, C.M. Atlas of Intraoperative Transesophageal Echocardiography; W.B. Saunders Company: Philadelphia, PA, USA, 2006. [Google Scholar]
- Armstrong, W.F.; Ryan, T.H. Feigenbaum’s Echocardiography, 7th ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2010. [Google Scholar]
- Charles, E.J.; Kronn, I.L. Data, not dogma, for ischemic mitral regurgitation. J. Thorac. Cardiovasc. Surg. 2017, 154, 137–138. [Google Scholar] [CrossRef] [PubMed]
- Doig, F.; Lu, Z.-Q.; Smith, S.; Naidoo, R. Long term survival after surgery for ischaemic mitral regurgitation: A single centre Australian experience. Heart Lung Circ. 2021, 30, 612–619. [Google Scholar] [CrossRef] [PubMed]
- El-Hag-Aly, M.A.; El Swaf, Y.F.; Elkassas, M.H.; Hagag, M.G.; Allam, H.K. Moderate ischemic mitral incompetence: Does it worth more ischemic time? Gen. Thorac. Cardiovasc. Surg. 2020, 68, 492–498. [Google Scholar] [CrossRef]
- Gujarati, D. Basic Econometrics, 4th ed.; Tata McGraw Hill: New York, NY, USA, 2004; pp. 148–149+378+947–948. [Google Scholar]
- Raska, A.; Kálmán, K.; Egri, B.; Csikós, P.; Beinrohr, L.; Szabó, L.; Tenekedjiev, K.; Nikolova, N.; Longstaff, C.; Roberts, I.; et al. Synergism of red blood cells and tranexamic acid in the inhibition of fibrinolysis. J. Thromb. Haemost. 2024, 22, 794–804. [Google Scholar] [CrossRef]
- Tóth, E.; Beinrohr, L.; Gubucz, I.; Szabó, L.; Tenekedjiev, K.; Nikolova, N.; Nagy, A.I.; Hidi, L.; Sótonyi, P.; Szikora, I.; et al. Fibrin to von Willebrand factor ratio in arterial thrombi is associated with plasma levels of inflammatory biomarkers and local abundance of extracellular DNA. Thromb. Res. 2022, 209, 8–15. [Google Scholar] [CrossRef]
- Lytsy, P. P in the right place: Revisiting the evidential value of p-values. J. Evid. Based Med. 2018, 11, 288–291. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]


| CM | CMED | Generalized Condition | Ct | Rule |
|---|---|---|---|---|
| M+1 | MED+1 | C+1 | 1 | |
| M+1 | MED+1/2 | C+1 | 1 | |
| M+1 | MED+0 | C+1 | 1 | |
| M+1 | MED00 | C+1 | 1 | |
| M+1 | MED–0 | C+1 | 1 | |
| M+1 | MED–1/2 | Cond1 = T | C+1 | 2 |
| M+1 | MED–1/2 | Cond1 = F | C+1/2 | 9 |
| M+1 | MED–1 | C0 | 15 | |
| M+1/2 | MED+1 | C+1 | 1 | |
| M+1/2 | MED+1/2 | Cond1 = T | C+1 | 3 |
| M+1/2 | MED+1/2 | Cond1 = F | C+1/2 | 10 |
| M+1/2 | MED+0 | Cond1 = T | C+1 | 3 |
| M+1/2 | MED+0 | Cond1 = F | C+1/2 | 10 |
| M+1/2 | MED00 | Cond1 = T | C+1 | 3 |
| M+1/2 | MED00 | Cond1 = F | C+1/2 | 10 |
| M+1/2 | MED–0 | Cond1 = T | C+1 | 3 |
| M+1/2 | MED–0 | Cond1 = F | C+1/2 | 10 |
| M+1/2 | MED–1/2 | C0 | 15 | |
| M+1/2 | MED–1 | Cond1 = T | C–1 | 6 |
| M+1/2 | MED–1 | Cond1 = F | C–1/2 | 12 |
| M+0 | MED+1 | C+1 | 1 | |
| M+0 | MED+1/2 | Cond1 = T | C+1 | 3 |
| M+0 | MED+1/2 | Cond1 = F | C+1/2 | 10 |
| M+0 | MED+0 | Cond2 = T | C+1 | 4 |
| M+0 | MED+0 | Cond2 = F and Cond3 = T | C+1/2 | 11 |
| M+0 | MED+0 | Cond2 = F and Cond3 = F | C0 | 15 |
| M+0 | MED00 | Cond2 = T | C+1 | 4 |
| M+0 | MED00 | Cond2 = F and Cond3 = T | C+1/2 | 11 |
| M+0 | MED00 | Cond2 = F and Cond3 = F | C0 | 15 |
| M+0 | MED–0 | C0 | 15 | |
| M+0 | MED–1/2 | Cond1 = T | C–1 | 7 |
| M+0 | MED–1/2 | Cond1 = F | C–1/2 | 13 |
| M+0 | MED–1 | C–1 | 5 | |
| M00 | MED+1 | C+1 | 1 | |
| M00 | MED+1/2 | Cond1 = T | C+1 | 3 |
| M00 | MED+1/2 | Cond1 = F | C+1/2 | 10 |
| M00 | MED+0 | Cond2 = T | C+1 | 4 |
| M00 | MED+0 | Cond2 = F and Cond3 = T | C+1/2 | 11 |
| M00 | MED+0 | Cond2 = F and Cond3 = F | C0 | 15 |
| M00 | MED00 | C0 | 15 | |
| M00 | MED–0 | Cond2 = T | C–1 | 8 |
| M00 | MED–0 | Cond2 = F and Cond3 = T | C–1/2 | 14 |
| M00 | MED–0 | Cond2 = F and Cond3 = F | C0 | 15 |
| M00 | MED–1/2 | Cond1 = T | C–1 | 7 |
| M00 | MED–1/2 | Cond1 = F | C–1/2 | 13 |
| M00 | MED–1 | C–1 | 5 | |
| M–0 | MED+1 | C+1 | 1 | |
| M–0 | MED+1/2 | Cond1 = T | C+1 | 3 |
| M–0 | MED+1/2 | Cond1 = F | C+1/2 | 10 |
| M–0 | MED+0 | C0 | 15 | |
| M–0 | MED00 | Cond2 = T | C–1 | 8 |
| M–0 | MED00 | Cond2 = F and Cond3 = T | C–1/2 | 14 |
| M–0 | MED00 | Cond2 = F and Cond3 = F | C0 | 15 |
| M–0 | MED–0 | Cond2 = T | C–1 | 8 |
| M–0 | MED–0 | Cond2 = F and Cond3 = T | C–1/2 | 14 |
| M–0 | MED–0 | Cond2 = F and Cond3 = F | C0 | 15 |
| M–0 | MED–1/2 | Cond1 = T | C–1 | 7 |
| M–0 | MED–1/2 | Cond1 = F | C–1/2 | 13 |
| M–0 | MED–1 | C–1 | 5 | |
| M–1/2 | MED+1 | Cond1 = T | C+1 | 2 |
| M–1/2 | MED+1 | Cond1 = F | C+1/2 | 9 |
| M–1/2 | MED+1/2 | C0 | 15 | |
| M–1/2 | MED+0 | Cond1 = T | C–1 | 7 |
| M–1/2 | MED+0 | Cond1 = F | C–1/2 | 13 |
| M–1/2 | MED00 | Cond1 = T | C–1 | 7 |
| M–1/2 | MED00 | Cond1 = F | C–1/2 | 13 |
| M–1/2 | MED–0 | Cond1 = T | C–1 | 7 |
| M–1/2 | MED–0 | Cond1 = F | C–1/2 | 13 |
| M–1/2 | MED–1/2 | Cond1 = T | C–1 | 7 |
| M–1/2 | MED–1/2 | Cond1 = F | C–1/2 | 13 |
| M–1/2 | MED–1 | C–1 | 5 | |
| M–1 | MED+1 | C0 | 15 | |
| M–1 | MED+1/2 | Cond1 = T | C–1 | 6 |
| M–1 | MED+1/2 | Cond1 = F | C–1/2 | 12 |
| M–1 | MED+0 | C–1 | 5 | |
| M–1 | MED00 | C–1 | 5 | |
| M–1 | MED–0 | C–1 | 5 | |
| M–1 | MED–1/2 | C–1 | 5 | |
| M–1 | MED–1 | C–1 | 5 |
| Sample | Eb | PCb | R Favorability | Ee | PCe | R Favorability |
|---|---|---|---|---|---|---|
| No. of observations | 34 | 43 | N/A | 32 | 41 | N/A |
| Fuzzy mean, % | 54 | 35.5 | unfavorable | 7.79 | 24.2 | favorable |
| Fuzzy median, % | 55.1 | 35.2 | unfavorable | 0 | 20.7 | favorable |
| Fuzzy STD, % | 10.8 | 11.8 | N/A | 12.1 | 20.1 | N/A |
| Fuzzy IQR, % | 19.9 | 12.3 | N/A | 12.8 | 26.6 | N/A |
| Modification | Time | FBT1 | FBT2 | FBT3 | FBT4 | FBT5 | FBT6 | FBT7 | FBT8 | FBT9 |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.4995 | 0.2480 | 0.1690 | 0.0975 |
| BM1 | Late_Postop | 0.0010 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0335 | 0.0270 | 0.1870 | 0.1800 |
| BM2 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.5360 | 0.2565 | 0.1785 | 0.1170 |
| BM2 | Late_Postop | 0.0010 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.0285 | 0.0160 | 0.1745 | 0.1495 |
| BM3 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.5310 | 0.2670 | 0.2075 | 0.1155 |
| BM3 | Late_Postop | 0.0010 | 0.0000 | 0.0000 | 0.0010 | 0.0000 | 0.0340 | 0.0320 | 0.1735 | 0.1670 |
| BM4 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.5410 | 0.2420 | 0.1720 | 0.1135 |
| BM4 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.0320 | 0.0195 | 0.1500 | 0.1300 |
| Modification | Time | CM | CMED | Cond1 | Cond2 | Cond3 | Ct | Rule | Result of MFPCG | Class |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM1 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM2 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM2 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM3 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM3 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM4 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM4 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 |
| Sample | Eb | PCb | R Favorability | Ee | PCe | R Favorability |
|---|---|---|---|---|---|---|
| No. of observations | 34 | 43 | N/A | 32 | 41 | N/A |
| Fuzzy mean | 5.28 | 3.48 | unfavorable | 0.878 | 2.4 | favorable |
| Fuzzy median | 5 | 3 | unfavorable | 0 | 2 | favorable |
| Fuzzy STD | 0.865 | 0.507 | N/A | 1.2 | 1.46 | N/A |
| Fuzzy IQR | 1 | 1 | N/A | 2 | 2 | N/A |
| Modification | Time | FBT1 | FBT2 | FBT3 | FBT4 | FBT5 | FBT6 | FBT7 | FBT8 | FBT9 |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.9985 |
| BM1 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0115 | 0.0010 | 0.3015 | 0.1735 | 1.0000 | 0.5240 |
| BM2 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 1.0000 | 0.9875 |
| BM2 | Late_Postop | 0.0010 | 0.0000 | 0.0000 | 0.0080 | 0.0010 | 0.3480 | 0.1570 | 1.0000 | 0.5735 |
| BM3 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.9980 |
| BM3 | Late_Postop | 0.0010 | 0.0000 | 0.0000 | 0.0080 | 0.0020 | 0.3000 | 0.1715 | 1.0000 | 0.4940 |
| BM4 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.9945 |
| BM4 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0080 | 0.0005 | 0.3165 | 0.1450 | 1.0000 | 0.5945 |
| Modification | Time | CM | CMED | Cond1 | Cond2 | Cond3 | Ct | Rule | Result of MFPCG | Class |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | M−1 | MED−1 | F | F | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM1 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM2 | Preop | M−1 | MED−1 | F | F | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM2 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM3 | Preop | M−1 | MED−1 | F | F | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM3 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM4 | Preop | M−1 | MED−1 | F | F | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM4 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 |
| Sample | Eb | PCb | R Favorability | Ee | PCe | R Favorability |
|---|---|---|---|---|---|---|
| No. of observations | 53 | 39 | N/A | 44 | 32 | N/A |
| Fuzzy mean, % | 59 | 42.6 | unfavorable | 7.89 | 32.8 | favorable |
| Fuzzy median, % | 61 | 44.7 | unfavorable | 0 | 27.1 | favorable |
| Fuzzy STD, % | 11.9 | 13.2 | N/A | 11.1 | 25.6 | N/A |
| Fuzzy IQR, % | 18 | 21 | N/A | 13.4 | 39.1 | N/A |
| Modification | Time | FBT1 | FBT2 | FBT3 | FBT4 | FBT5 | FBT6 | FBT7 | FBT8 | FBT9 |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.4730 | 0.2180 | 0.5005 | 0.3030 |
| BM1 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0020 | 0.0020 | 0.0000 | 0.0000 | 0.0460 | 0.0460 |
| BM2 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0010 | 0.0010 | 0.4715 | 0.3350 | 0.6020 | 0.4405 |
| BM2 | Late_Postop | 0.0005 | 0.0000 | 0.0000 | 0.0025 | 0.0025 | 0.0000 | 0.0000 | 0.0475 | 0.0475 |
| BM3 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0035 | 0.0030 | 0.4670 | 0.1880 | 0.5025 | 0.2865 |
| BM3 | Late_Postop | 0.0005 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0570 | 0.0570 |
| BM4 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0020 | 0.0020 | 0.4475 | 0.3070 | 0.5635 | 0.4270 |
| BM4 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0015 | 0.0015 | 0.0000 | 0.0000 | 0.0475 | 0.0475 |
| Modification | Time | CM | CMED | Cond1 | Cond2 | Cond3 | Ct | Rule | Result of MFPCG | Class |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM1 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM2 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM2 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM3 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM3 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 | ||
| BM4 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM4 | Late_Postop | M+1 | MED+1 | F | F | F | C+1 | 1 |
| Sample | Eb | PCb | R Favorability | Ee | PCe | R Favorability |
|---|---|---|---|---|---|---|
| No. of observations | 53 | 38 | N/A | 44 | 32 | N/A |
| Fuzzy mean | 5.7 | 3.92 | unfavorable | 0.827 | 2.92 | favorable |
| Fuzzy median | 6 | 4 | unfavorable | 0 | 2.64 | favorable |
| Fuzzy STD | 0.802 | 0.813 | N/A | 1.13 | 1.53 | N/A |
| Fuzzy IQR | 1 | 0.101 | N/A | 2 | 2 | N/A |
| Modification | Time | FBT1 | FBT2 | FBT3 | FBT4 | FBT5 | FBT6 | FBT7 | FBT8 | FBT9 |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.9650 | 0.4540 | 0.5010 | 0.4145 |
| BM1 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.1550 | 0.0915 | 1.0000 | 0.5060 |
| BM2 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.9675 | 0.6010 | 0.5290 | 0.3650 |
| BM2 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1925 | 0.0775 | 1.0000 | 0.5125 |
| BM3 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.9690 | 0.4135 | 0.5175 | 0.4340 |
| BM3 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.1795 | 0.1165 | 1.0000 | 0.4925 |
| BM4 | Preop | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.9690 | 0.6085 | 0.5365 | 0.3895 |
| BM4 | Late_Postop | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 | 0.1885 | 0.0860 | 1.0000 | 0.5335 |
| Modification | Time | CM | CMED | Cond1 | Cond2 | Cond3 | Ct | Rule | Result of MFPCG | Class |
|---|---|---|---|---|---|---|---|---|---|---|
| BM1 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM1 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM2 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM2 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM3 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM3 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 | ||
| BM4 | Preop | M−1 | MED−1 | T | T | F | C−1 | 5 | (Cb, Ce) = (C−1, C+1) | YES+ |
| BM4 | Late_Postop | M+1 | MED+1 | T | T | F | C+1 | 1 |
| A1 (E) | B1 (PC) | Difference (D) | |
|---|---|---|---|
| Preop (b) | ME,b = +54, % | MPC,b = +35.5, % | Db = +18.5, % |
| Postop (e) | ME,e = +7.79, % | MPC,e = +24.2, % | De = −16.4, % |
| Temporal change (TC) | TCE = −46.2, % | TCPC = −11.3, % | ATE = −34.9, % |
| A1 (E) | B1 (PC) | Difference (D) | |
|---|---|---|---|
| Preop (b) | ME,b = +5.28, % | MPC,b = +3.48, % | Db = +1.8, % |
| Postop (e) | ME,e = +0.878, % | MPC,e = +2.4, % | De = −1.52, % |
| Temporal change (TC) | TCE = −4.4, % | TCPC = −1.08, % | ATE = −3.31, % |
| A2 (E) | B2 (PC) | Difference (D) | |
|---|---|---|---|
| Preop (b) | ME,b = +59, % | MPC,b = +42.6, % | Db = +16.4, % |
| Postop (e) | ME,e = +7.89, % | MPC,e = +32.8, % | De = −24.9, % |
| Temporal change (TC) | TCE = −51.1, % | TCPC = −9.78, % | ATE = −41.4, % |
| A2 (E) | B2 (PC) | Difference (D) | |
|---|---|---|---|
| Preop (b) | ME,b = +5.7, % | MPC,b = +3.92, % | Db = +1.78, % |
| Postop (e) | ME,e = +0.827, % | MPC,e = +2.92, % | De = −2.09, % |
| Temporal change (TC) | TCE = −4.87, % | TCPC = −1, % | ATE = −3.87, % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tenekedjiev, K.; Panayotova, D.; Daboos, M.; Ivanova, S.; Symes, M.; Panayotov, P.; Nikolova, N. Quasi-Experimental Design for Medical Studies with the Method of the Fuzzy Pseudo-Control Group. Appl. Sci. 2025, 15, 1370. https://doi.org/10.3390/app15031370
Tenekedjiev K, Panayotova D, Daboos M, Ivanova S, Symes M, Panayotov P, Nikolova N. Quasi-Experimental Design for Medical Studies with the Method of the Fuzzy Pseudo-Control Group. Applied Sciences. 2025; 15(3):1370. https://doi.org/10.3390/app15031370
Chicago/Turabian StyleTenekedjiev, Kiril, Daniela Panayotova, Mohamed Daboos, Snejana Ivanova, Mark Symes, Plamen Panayotov, and Natalia Nikolova. 2025. "Quasi-Experimental Design for Medical Studies with the Method of the Fuzzy Pseudo-Control Group" Applied Sciences 15, no. 3: 1370. https://doi.org/10.3390/app15031370
APA StyleTenekedjiev, K., Panayotova, D., Daboos, M., Ivanova, S., Symes, M., Panayotov, P., & Nikolova, N. (2025). Quasi-Experimental Design for Medical Studies with the Method of the Fuzzy Pseudo-Control Group. Applied Sciences, 15(3), 1370. https://doi.org/10.3390/app15031370








