Cost-Effective FEM Simulation Through Solid Bodies of the Thermal Behavior of Lattice Structures Printed via PBF-LB
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Procedure for the Characterization of Inconel 718’s Thermal Properties
2.2. Methodology
2.2.1. LB-PBF Lattice Structure Printing
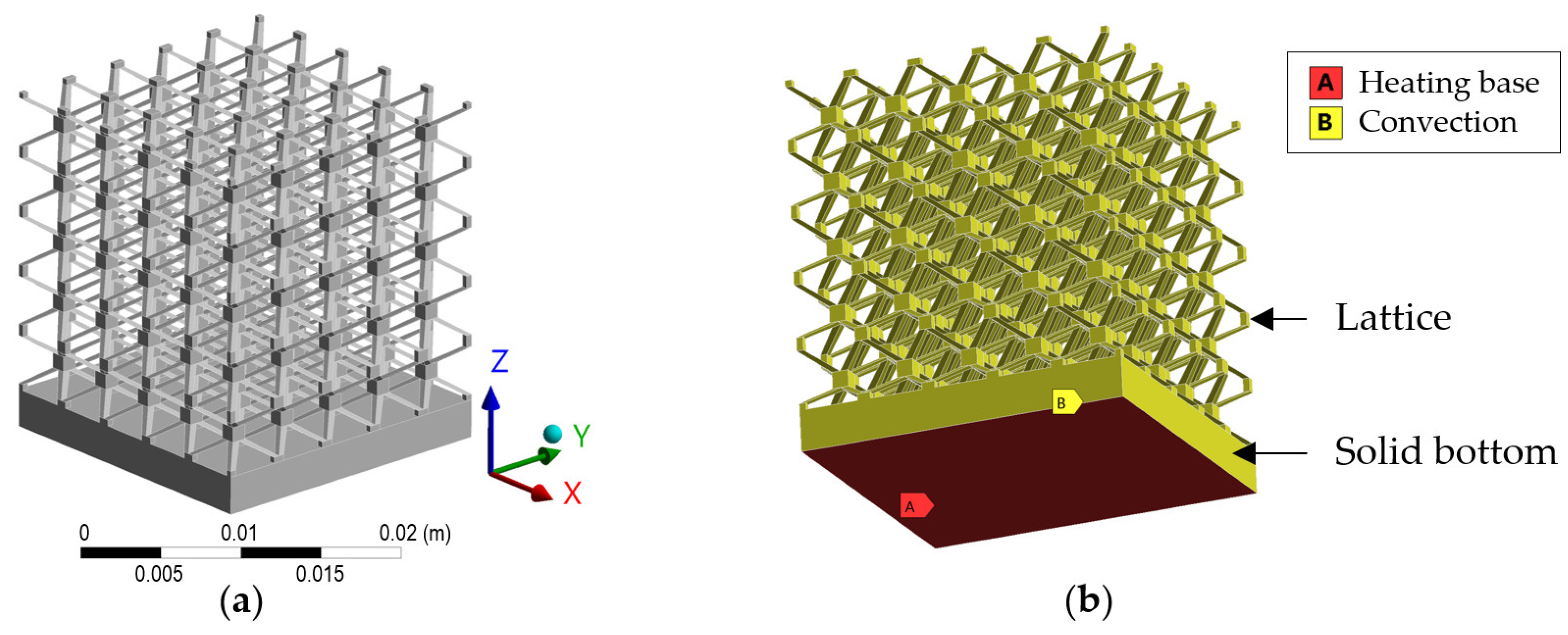
2.2.2. Simulation of the Lattice Structure
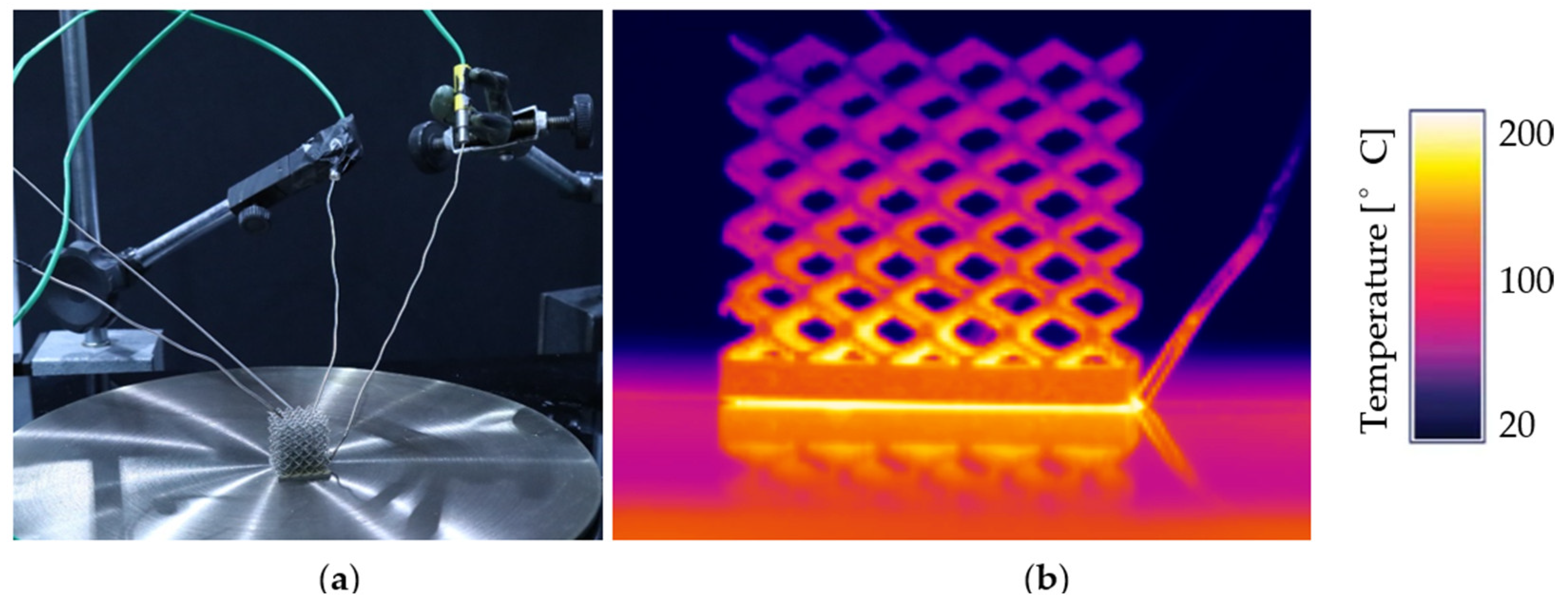
2.2.3. Experimental Testing
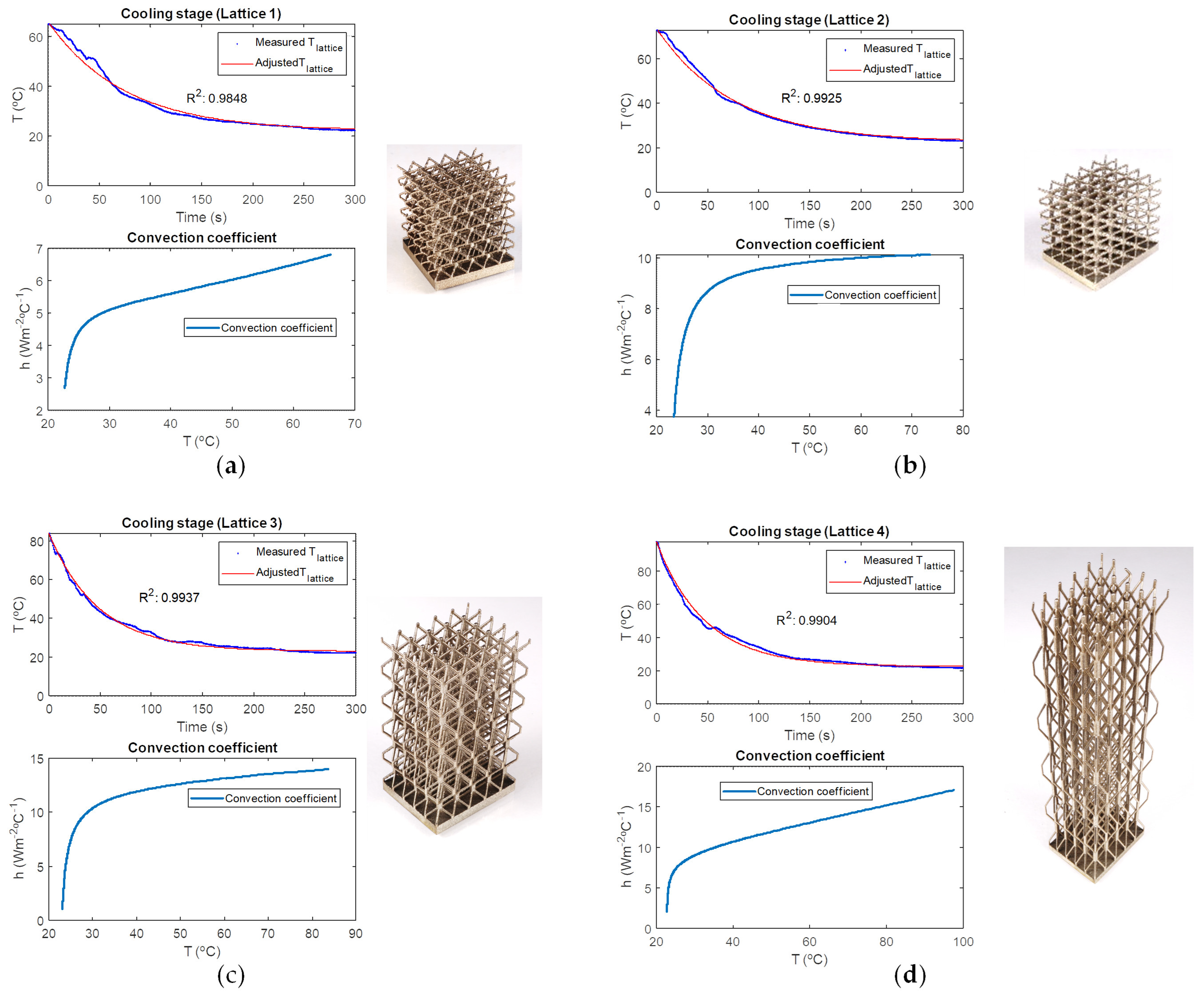
Convection Coefficient Determination
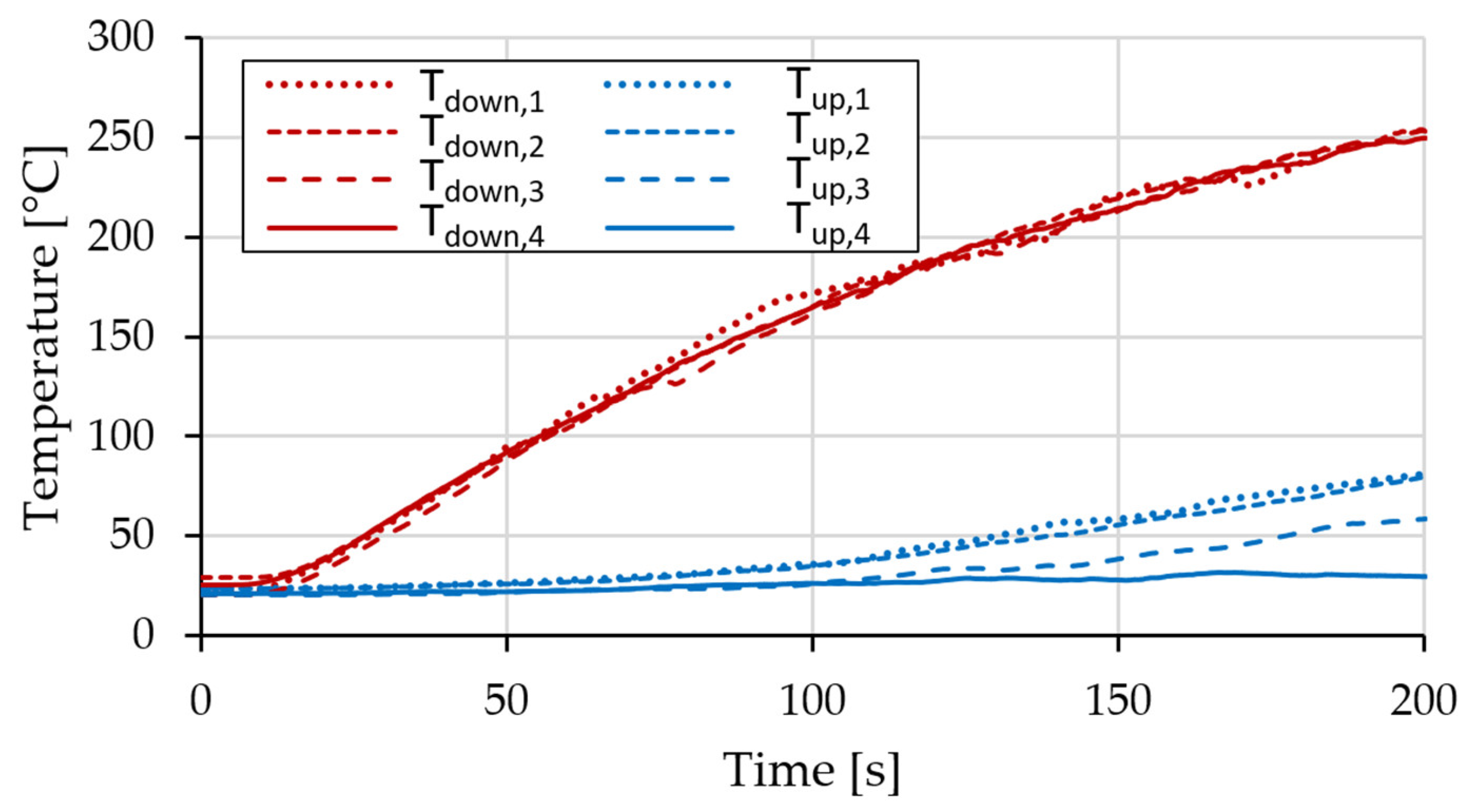
Heat Transfer Capability of the Lattice Structure
3. Results
3.1. Thermal Properties of the Additively Manufactured Inconel 718
3.2. Lattice Structure Design and Part Printing
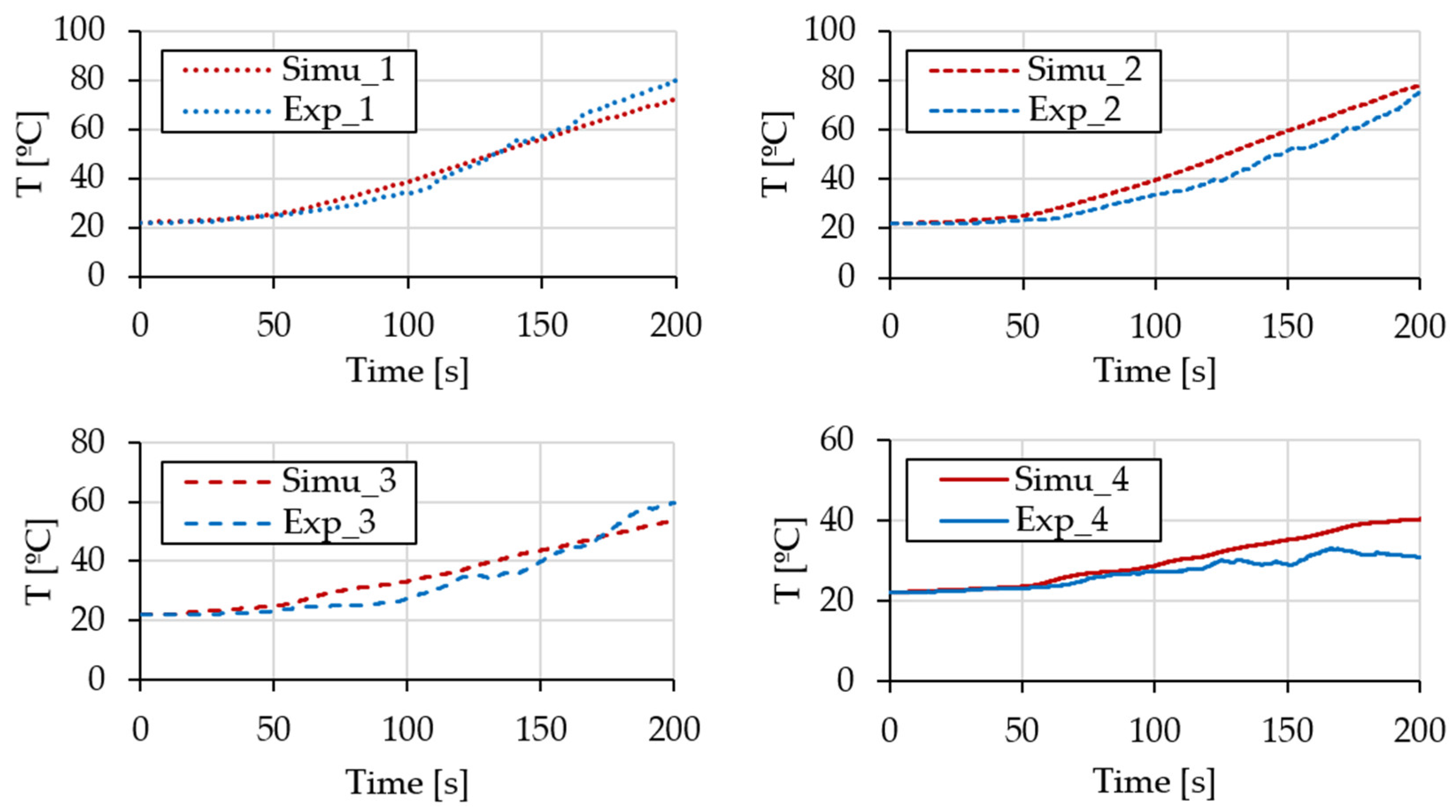
3.3. Experimental Study of the Lattice Structure
3.3.1. Convection Coefficient Determination
3.3.2. Heat Transfer Capabilities of the Lattice Structure
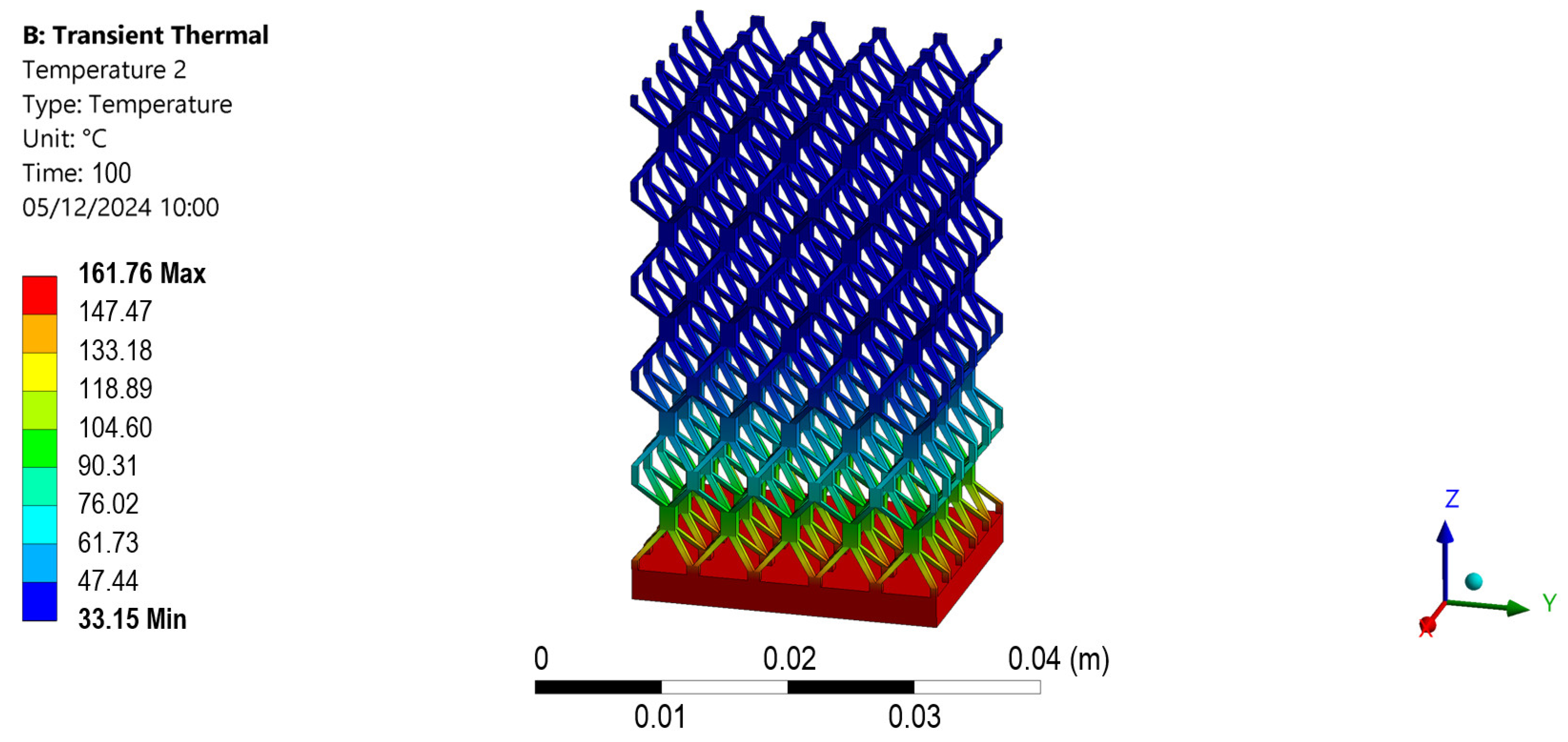
3.4. Thermal Simulation of the Lattice Structures
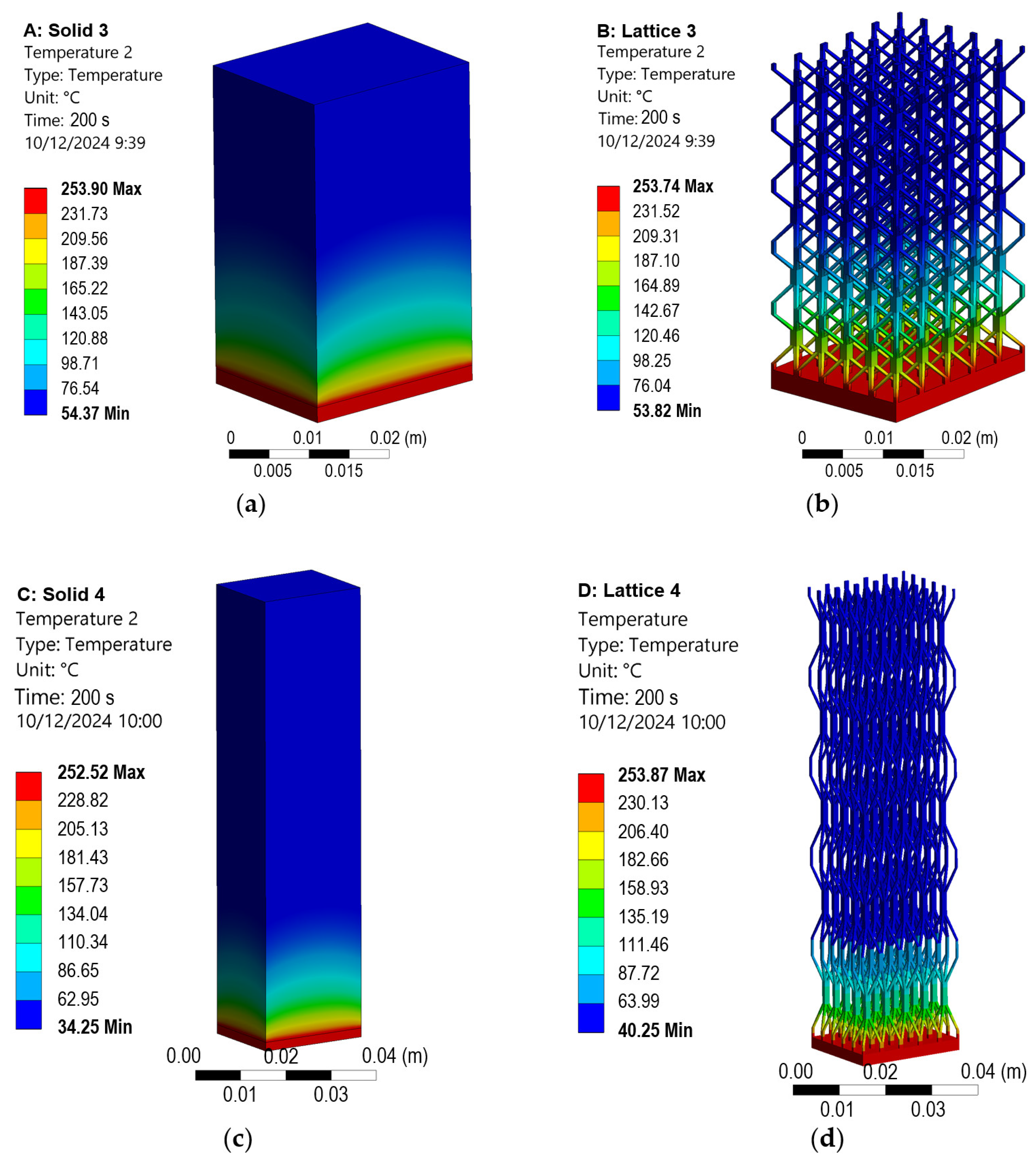
3.5. Approximation of the Lattice Structures Through Solid Bodies
4. Discussion
5. Conclusions
- (1)
- It is feasible to simulate the thermal behavior of lattice structures by means of solid blocks composed of fictitious materials whose properties have been adapted accordingly. An error rate below 2% is obtained between the simulated lattice and the solid block composed of the fictitious material.
- The density of the fictitious material is proportional to the fill percentage of the lattice structure.
- The specific heat of the fictitious material remains constant.
- The effective thermal conductivity of the fictitious material needs to be adjusted based on the fill percentage and the shape of the lattice structure.
- (2)
- Thanks to the developed methodology, the computational cost required for the simulation of lattice structures can be reduced by up to 90%.
- (3)
- The convection coefficient is approximated as a linear function with regard to the temperature. The more stretched the lattice, the lower the resistance that it poses to the airflow and, therefore, the higher the convection coefficient. In order to consider the equivalent convection in the solid body, it has to be escalated according to the area ratio.
- (4)
- Once the convection coefficient has been adjusted experimentally, the thermal simulation of the lattice structures presents the same behavior as in the experimental tests.
- (5)
- Lastly, the obtained results open the door to the design of anisotropic components based on lattice structures and their topological optimization once the effective conductivity of a lattice structure is characterized.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Temp. [°C] | Diff. (mm2·s−1) | Dens. (g·cm−3) | Cp (J·kg−1·K−1) | K (W·m−1·K−1) |
|---|---|---|---|---|
| 50 | 3.077 | 8.200 | 462.345 | 11.666 |
| 100 | 3.208 | 8.180 | 464.060 | 12.178 |
| 200 | 3.504 | 8.140 | 489.665 | 13.965 |
| 300 | 3.803 | 8.110 | 506.020 | 15.605 |
| 400 | 4.056 | 8.070 | 512.165 | 16.762 |
| 500 | 4.293 | 8.030 | 547.670 | 18.880 |
| 600 | 4.540 | 7.990 | 634.025 | 22.999 |
| 700 | 4.862 | 7.960 | 627.000 | 24.266 |
| 800 | 4.700 | 7.920 | 722.965 | 26.912 |
| 900 | 4.743 | 7.880 | 602.065 | 22.502 |
| 1000 | 5.026 | 7.860 | 424.235 | 18.732 |
References
- Gloria, A.; Montanari, R.; Richetta, M.; Varone, A. Alloys for Aeronautic Applications: State of the Art and Perspectives. Metals 2019, 9, 662. [Google Scholar] [CrossRef]
- Yang, W.; He, W.; Hu, Z.; Duan, W.; Ni, X.; Deng, X.; Wang, A.; Luo, Y.; Xie, F.; Chen, Z.; et al. Fabrication of Inconel 718 composites reinforced with TiCN via laser powder bed fusion: Integration of triply periodic minimal surface lattice structures. J. Mater. Res. Technol. 2024, 32, 2443–2458. [Google Scholar] [CrossRef]
- Beyer, C.; Figueroa, D. Design and Analysis of Lattice Structures for Additive Manufacturing. J. Manuf. Sci. Eng. 2016, 138, 121014. [Google Scholar] [CrossRef]
- Chowdhury, S.; Yadaiah, N.; Prakash, C.; Ramakrishna, S.; Dixit, S.; Gupta, L.R.; Buddhi, D. Laser powder bed fusion: A state-of-the-art review of the technology, materials, properties & defects, and numerical modelling. J. Mater. Res. Technol. 2022, 20, 2109–2172. [Google Scholar] [CrossRef]
- Popovich, V.A.; Borisov, E.V.; Popovich, A.A.; Sufiiarov, V.S.; Masaylo, D.V.; Alzina, L. Functionally graded Inconel 718 processed by additive manufacturing: Crystallographic texture, anisotropy of microstructure and mechanical properties. Mater. Des. 2017, 114, 441–449. [Google Scholar] [CrossRef]
- Flores, I.; Kretzschmar, N.; Azman, A.H.; Chekurov, S.; Pedersen, D.B.; Chaudhuri, A. Implications of lattice structures on economics and productivity of metal powder bed fusion. Addit. Manuf. 2020, 31, 100947. [Google Scholar] [CrossRef]
- Mahshid, R.; Hansen, H.N.; Højbjerre, K.L. Strength analysis and modeling of cellular lattice structures manufactured using selective laser melting for tooling applications. Mater. Des. 2016, 104, 276–283. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Williams, H.; Yang, E.; Alghamdi, A.; Lozanovski, B.; Zhang, X.; Shidid, D.; Farahbod-Sternahl, L.; Witt, G.; et al. Inconel 625 lattice structures manufactured by selective laser melting (SLM): Mechanical properties, deformation and failure modes. Mater. Des. 2018, 157, 179–199. [Google Scholar] [CrossRef]
- Sajjad, U.; Rehman, T.U.; Ali, M.; Park, C.W.; Yan, W.M. Manufacturing and potential applications of lattice structures in thermal systems: A comprehensive review of recent advances. Int. J. Heat Mass Transf. 2022, 198, 123352. [Google Scholar] [CrossRef]
- Piacquadio, S.; Schirp-Schoenen, M.; Mameli, M.; Filippeschi, S.; Schröder, K.U. Experimental analysis of the thermal energy storage potential of a phase change material embedded in additively manufactured lattice structures. Appl. Therm. Eng. 2022, 216, 119091. [Google Scholar] [CrossRef]
- Gao, T.; Zhang, W.H.; Zhu, J.H.; Xu, Y.J.; Bassir, D.H. Topology optimization of heat conduction problem involving design-dependent heat load effect. Finite Elem. Anal. Des. 2008, 44, 805–813. [Google Scholar] [CrossRef]
- Iga, A.; Nishiwaki, S.; Izui, K.; Yoshimura, M. Topology optimization for thermal conductors considering design-dependent effects, including heat conduction and convection. Int. J. Heat Mass Transf. 2009, 52, 2721–2732. [Google Scholar] [CrossRef]
- Yamada, T.; Izui, K.; Nishiwaki, S. A Level Set-Based Topology Optimization Method for Maximizing Thermal Diffusivity in Problems Including Design-Dependent Effects. J. Mech. Des. 2011, 133, 031011. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, S.; Liu, T.; Li, P.; Duan, F. Effective heat conduction evaluation of lattice structures from selective laser melting printing. Int. J. Heat Mass Transf. 2024, 218, 124790. [Google Scholar] [CrossRef]
- Foteinopoulos, P.; Papacharalampopoulos, A.; Stavropoulos, P. Additive manufacturing simulations: An approach based on space partitioning and dynamic 3D mesh adaptation. Addit. Manuf. Lett. 2024, 11, 100256. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.; González-Barrio, H.; Sanz-Calle, M.; Gómez-Escudero, G.; Munoa, J.; de Lacalle, L.L. Machining stability improvement in LPBF printed components through stiffening by crystallographic texture control. CIRP Ann. 2023, 72, 141–144. [Google Scholar] [CrossRef]
- Certificate of Analysis, Osprey® 718. Available online: https://www.metalpowder.sandvik/globalassets/webshop/osprey-718/certificate-of-analysis-osprey-718-53-15.pdf (accessed on 23 January 2025).
- Terpilowski, J.; Józwiak, S.; Woroniak, G.; Szczepaniak, R. Thermal Diffusivity Characteristics of the IN718 Alloy Tested with the Modified Pulse Method. Materials 2022, 15, 7881. [Google Scholar] [CrossRef] [PubMed]




| Equipment | Measured Property | Sample Dimensions (mm) |
|---|---|---|
| Linseis L75 Platinum Dilatometer | Density () | Ø 5 × 15 |
| MicroFlash® 457 Laser Flash | Thermal diffusivity () | Ø 10 × 3 |
| 449 F3 Jupiter DSC STA | Specific heat () | Ø 5 × 1 |
| Parameter | Value |
|---|---|
| Hatch distance [µm] | 80 |
| Layer thickness [µm] | 60 |
| Laser power [W] | 200 |
| Inert gas [-] | Argon |
| Scan speed (mm·s−1) | 1250 |
| Case | Dimensions X × Y × Z [mm3] | Fill % | Lattice Volume [mm3] | Baseplate Volume [mm3] | Solid Block Volume [mm3] |
|---|---|---|---|---|---|
| 1 | 20 × 20 × 20 | 5.16 | 613.19 | 800 | 8800 |
| 2 | 20 × 25 × 20 | 5.16 | 766.49 | 1000 | 11,000 |
| 3 | 20 × 25 × 40 | 5.16 | 1282.15 | 1000 | 21,000 |
| 4 | 20 × 25 × 100 | 5.16 | 2829.64 | 1000 | 50,000 |
| Case | mlattice (kg) | Alattice (m2) |
|---|---|---|
| 1 | 0.0125 | 0.0049 |
| 2 | 0.0161 | 0.0059 |
| 3 | 0.0195 | 0.0084 |
| 4 | 0.0306 | 0.0174 |
| Case | h(T) (W·m−2·K−1) |
|---|---|
| 1 | 0.05·T + 3.5 |
| 2 | 0.05·T + 6.5 |
| 3 | 0.10·T + 6.0 |
| 4 | 0.133·T + 5.0 |
| Case | R | Lattice Experimental T [°C] | Lattice Simulation T [°C] | Solid Block Simulation T [°C] | Solid Block Error [%] | k% | Solid Block Simulation T [°C] If k = Fill % |
|---|---|---|---|---|---|---|---|
| 1 | 2.27 | 80.79 | 77.08 | 77.58 | 0.65 | 0.98% | 131.80 |
| 2 | 2.36 | 77.14 | 78.07 | 77.10 | −1.24 | 1.85% | 128.01 |
| 3 | 1.96 | 58.64 | 53.88 | 54.95 | 1.99 | 2.85% | 69.57 |
| 4 | 1.79 | 29.82 | 40.38 | 40.06 | 0.54 | 4.00% | 46.38 |
| Case | Lattice | Solid | ||||
|---|---|---|---|---|---|---|
| Number of Elements | Elapsed Time | MAPDL Result File Size | Number of Elements | Elapsed Time | MAPDL Result File Size | |
| 1 | 41,993 | 2 h 3 min | 89.698 GB | 2066 | 15 min 11 s | 4.47 GB |
| 2 | 42,530 | 2 h 6 min | 92.439 GB | 2054 | 18 min 5 s | 3.80 GB |
| 3 | 35,848 | 1 h 41 min | 88.872 GB | 3016 | 21 min 34 s | 5.27 GB |
| 4 | 43,631 | 2 h 12 min | 112.02 GB | 2736 | 23 min 15 s | 7.16 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arrizubieta, J.I.; Gómez, G.; Lamikiz, A.; Legorburu, J.; Agirre, X.; Galdos, L.; Sainz, S. Cost-Effective FEM Simulation Through Solid Bodies of the Thermal Behavior of Lattice Structures Printed via PBF-LB. Appl. Sci. 2025, 15, 1372. https://doi.org/10.3390/app15031372
Arrizubieta JI, Gómez G, Lamikiz A, Legorburu J, Agirre X, Galdos L, Sainz S. Cost-Effective FEM Simulation Through Solid Bodies of the Thermal Behavior of Lattice Structures Printed via PBF-LB. Applied Sciences. 2025; 15(3):1372. https://doi.org/10.3390/app15031372
Chicago/Turabian StyleArrizubieta, Jon Iñaki, Gaizka Gómez, Aitzol Lamikiz, June Legorburu, Xabier Agirre, Lander Galdos, and Shandra Sainz. 2025. "Cost-Effective FEM Simulation Through Solid Bodies of the Thermal Behavior of Lattice Structures Printed via PBF-LB" Applied Sciences 15, no. 3: 1372. https://doi.org/10.3390/app15031372
APA StyleArrizubieta, J. I., Gómez, G., Lamikiz, A., Legorburu, J., Agirre, X., Galdos, L., & Sainz, S. (2025). Cost-Effective FEM Simulation Through Solid Bodies of the Thermal Behavior of Lattice Structures Printed via PBF-LB. Applied Sciences, 15(3), 1372. https://doi.org/10.3390/app15031372










