Using Multiple-Hop Assessments and Reactive Strength Indices to Differentiate Sprinting Performance in Sportsmen

Abstract

Multiple-hop tests are commonly used in both performance and rehabilitation settings to assess neuromuscular function. This study aimed to explore the relationship between hop performance and sprint ability. Specifically, it focused on three goals: (1) examining the connection between 3-Hop and 5-Hop distances and sprint performance and comparing the strength of relationship between hop kinetics and sprint times; (2) investigating two methods of calculating the 3-Hop and 5-Hop Reactive Strength Indexes (RSI_hors) and their relationship to sprinting; and (3) assessing whether hop ratios or kinetic variables could distinguish sprinters of varying abilities. Forty-four male sportsmen participated, completing 3-Hop and 5-Hop tests and sprint times (5–45 m) over 54 inground force platforms. Ground reaction forces (GRFs) were collected during hop trials and horizontal and vertical hop propulsive and braking kinetics were determined. Results showed strong negative correlations between hop distances and sprint times (r = −0.700 to −0.796), while kinetic variables showed weaker relationships with sprint performance (r = −0.554 to 0.017). RSI_hor, derived from hop distance, correlated more strongly with sprint performance than RSI_hor from flight time. Hop ratios (5-Hop/3-Hop) did not differentiate fast from slow sprinters, and maximal vertical force and horizontal propulsive impulse were the best predictors of 10 m and 40 m sprint times. These findings suggest that hop distance and RSI_hor are valuable tools for assessing sprint performance and reactive strength.

1. Introduction

Multiple hops and jumps, specifically triple (3-Hop) and quintuple hops (5-Hop), have been found to be valid and reliable tools for evaluating athletes’ physical capabilities [1,2,3,4,5]. Moreover, these types of hop and stop tests are considered suitable for late-stage rehabilitation assessment and for improving athletic performance, such as sprinting, as their execution requires high neuromuscular demands, and in turn necessitates a significant tolerance for stretch load through cyclical expressions of unilateral propulsive and braking forces [6]. Four research groups [7,8,9,10] have examined the relationship between 3-Hop distance and short (10–20 m) sprint performances (times and velocities), with some variability observed between these studies (r = 0.33 to −0.89). A very large negative correlation (r = −0.86) between 3-Hop distance and 20 m sprint time was reported in recreationally engaged male sports athletes [8], and strong correlations (r = 0.68) with 10-yard sprint time, again in a cohort of mixed sub-elite level male athletes [10]. Habibi et al. observed similarly high correlations (r = 0.89) for sub-elite male sprinters with 10 m block starts [7]; however, a previous identical study found weak correlations (r = 0.24 to 0.33) in an elite group of male sprinters [9]. Due to this variation, Maulder et al. (2006) [9] suggested that horizontal jump measures might be more effective for predicting sprint performance in athletes participating in sports requiring a variety of sprint running expressions but may not be valid for competitive level sprinters. They also considered that multiple jump measures, such as force and power, might better represent the dynamics of sprint running compared to jump distance alone. Nevertheless, given the relationship between jump distance and sprint performance, it can be hypothesized that the strength qualities required for achieving greater hop distances may also confer benefits to sprinting ability.

In addition to those investigating the relationship between 3-Hop tests and sprint performance, a 5-step jump test was reported to have very large negative correlations (r = −0.81) to 40 m sprint time [11] in a cohort of male sub-elite sports athletes. In the sprint training literature [6,12] the 5-Hop test has been used extensively to determine readiness for competition and, therefore, is also worthy of further investigation to determine the relationship between 3-Hop and sprint performance, and additionally whether the 5-Hop test is a stronger predictor of sprint performance. Moreover, as Maulder et al. (2006) [9] suggested, it would be useful for a deterministic purpose, i.e., to quantify this relationship, to use kinetic measures (force or power) rather than just distance hopped.

Reactive strength, the ability to efficiently couple eccentric–concentric contractions [the stretch–shorten cycle (SSC)] is a metric that has garnered considerable attention. It is thought to be a fundamental determinant of many athletic qualities [13] and has shown to be highly correlated with vertical leg-spring stiffness [14]. This strength quality is typically represented as a strength index (RSI), measured by the ratio between jump height and contact time in a drop jump [15] or by the ratio between jump height and time to take off (RSI_mod) in the countermovement jump [16], or the ratio of flight time to ground contact time [17], and it is sometimes referred to as the reactive strength ratio [18,19]. Given the principle of specificity, it may make sense to calculate the RSI parallel to the principal line of movement when explicitly calculating a horizontal reactive strength index (RSI_hor) for sprinting performance. Davey et al. (2021) [20] examined whether such a measure (the ratio between flight and contact time) was reliable using a 3-Hop test. The between-session coefficients of variation were less than 5.5%, and the intraclass correlation coefficients greater than 0.70 across hops. Sarabon et al. (2023) [21], however, quantified the reliability of the 3-Hop flight time, hop distance, and contact time, and reported only moderate reliability (ICC = 0.67–0.74). Assuming that this reliability is acceptable, it is important to determine whether RSI_hor as a metric has a high association with performance, thereby establishing its value as a tool for athletic monitoring and exercise prescription. A recent study [21] has investigated the utility of RSI_hor from a 3-Hop test, finding variable correlations with 505 test performance (r = −0.76 to 0.23) and 10 m sprint performance (r = −0.50 to 0.43) in male volleyball players. RSI_hor measures calculated from flight and ground contact times of unilateral multiple hopping tasks have also been shown to have a negligible to moderate relationship with sprint performances, ranging from 10 to 100 m (r = 0.00 to −0.38) [22]. This was the first study to investigate RSI_hor further than the 3-Hop test, and it noted that RSI continued to increase until the fifth hop, suggesting that a 5-Hop test should be enough multiple hops in series to understand an athlete’s capability. However, further research is required to better understand the relationship between RSI_hor and athletic performance, particularly in athletes accustomed to horizontal-focused movements over longer sprint distances.

Interestingly, both 3-Hop and 5-Hop assessments have been used for assessing elite sprinter’s training readiness for competition, and to provide key insights into “an athlete’s ability to express repeated peaks of strength in exercise with faster and faster movements” [6,12]. According to Vittori [12], sprinters with good strength expression should hop seventy percent further for a 5-Hop than a 3-Hop. Whether this is the case has not been documented, and it may be that other measures, such as the RSI_hor, provide better insight as to that which differentiates sprint performance.

The 3-Hop is a movement that is implemented a great deal by practitioners interested in the neuromuscular function of athletes during rehabilitation and sports performance. The 5-Hop is less well researched, possibly due to the higher neuromuscular demands associated with the latter hops. The authors have noted increases of ~56% in maximal vertical force, ~236% in vertical braking impulse, and ~1147% in horizontal braking impulse across steps. Given the higher neuromuscular demands, the 5-Hop may be a better differentiator of sprint ability as compared to the 3-Hop test. Based on this and the preceding information, the aims of this study were threefold: (1) to examine the relationship between 3-Hop and 5-Hop distance with sprint performance and determine whether hop kinetic variables provide stronger relationships to sprinting ability than the kinematic/hop distances; (2) to explore the relationship between two methods of determining 3-Hop and 5-Hop RSI_hor and sprint performance; and (3) to investigate whether the 5-Hop/3-Hop ratio or RSI_hor or other kinetic measures could differentiate between sprinters of different ability. It was hypothesized that (1) the correlations between 3-Hop and 5-Hop distances/sprint performances would be strong and that kinetic variables would provide stronger correlations to sprinting ability; (2) both methods (flight and distance) for determining RSI_hor would be similarly correlated with sprint performance; and (3) the faster sprinters would have a greater percentage difference between their 3-Hop and 5-Hop ratios. The findings will provide practitioners with valuable insights into the potential utility of multiple-hop tests for assessing, rehabbing and enhancing athletic performance.

2. Methodology

2.1. Participants

Forty-four male sportsmen (age 20.1 ± 1.4 years; body mass 71.2 ± 8.6 kg; stature 171.9 ± 5.1 cm) from across various university sports (kendo, baseball, rowing, track athletics, field athletics, windsurfing, cycling, soccer, and basketball) volunteered to participate. All participants were required to be healthy and injury-free at the time of testing. Potential participants were excluded if they had any significant historic injuries (e.g., previous ruptures or tears to major tendons or ligaments [Achilles, ACL]), regardless of the post-injury training time. The study procedures followed the Declaration of Helsinki, and ethical approval was granted by the Auckland University of Technology Review Board (reference: 17/133) and the National Institute of Fitness and Sports in Kanoya Review Board (reference: 8-123). Informed consent was obtained before inclusion in the study. Body mass was measured to the nearest 0.1 kg, and stature was measured according to the methodology set out by the International Society for the Advancement of Kinanthropometry [23] on a digital scale and stadiometer (Tanita DC-217A, Tokyo, Japan).

2.2. Procedures

Each participant attended a familiarization session a minimum of three days prior to the first testing session, which included a standardized warm-up protocol that was repeated before the testing session. The warm-up included dynamic limb flexibility exercises (upper and lower), general movement to raise body temperature, explosive bounding movements to mimic test demands, and gradually intense sprinting over 30 m. The testing process started five minutes after the warm-up was completed.

The 3-Hop test protocol involved three hops on the same leg (Figure 1), while the 5-Hop test involved five hops on the same leg. Because of the very high stretch-load demands placed on the body by this test, three trials for 3-Hop and two trials for 5-Hop were completed in a randomized order for dominant and non-dominant limbs, minimizing the risk of injury, reducing acute overuse, and reducing fatigue effects. There was a two-minute rest period between the efforts before hopping on the other leg. Each hop began with the subject balancing on their hopping leg before propelling themselves forward for the number of contacts specified in the test. For all tests, the subjects landed on two feet after the final hop; contact with the ground with their hands after landing was permitted if the hopping foot did not move further forward during landing. This was performed to encourage each subject to achieve maximal horizontal displacement. Upper-limb motion was permitted during the hops, which replicated the motor patterns associated with athletic movements. Each subject was instructed to “reach the furthest horizontal distance in the shortest possible time”.

The hop trials were conducted on an indoor synthetic track surface (Hasegawa Sports Facilities, Tokyo, Japan) that covered 54 inground force platforms in series (TF-90100, Tec Gihan, Kyoto, Japan), and were linked to a single computer that collected GRFs at a sampling rate of 1000 Hz. Force plate data were captured for each trial, exported, tagged, and stored for later analysis. The GRF signals collected during the hop trials were filtered using a 4th-order Butterworth low-pass digital filter with a 50 Hz cutoff frequency, and horizontal and vertical hop propulsive and braking kinetics were determined, with associated impulses calculated via the integration of force for each of the required periods. All variables were computed using a custom algorithm (MATLAB R2021a, Mathworks Inc., Natick, MA, USA).

2.3. Data Processing and Outcome Measures

Touch-down and take-off detection were identified in the filtered data by a 20 N vertical GRF threshold. Horizontal center of mass (COM) velocity (V_H as a function of time) was calculated from the initial movement to the end of the trial using the methods outlined by Colyer, Nagahara, and Salo [24]. Per this method, the impulse–momentum relationship was used to determine instantaneous V_H throughout the entire sprint from the IMP_AP and estimated aerodynamic drag [25]. Sprint times (5 to 45 m) were derived from the integral of the V_H data. Hop ratios were determined by dividing the mean 5-Hop distance by the mean 3-Hop distance. RSI was determined using the methods outlined by Sarabon et al. [21] for each step and also as an average (Total RSI_hor) for each hop trial using two methods; firstly, RSI_hor-DIST was calculated by dividing the hop distance by the previous ground contact time, and secondly, RSI_hor-FT was calculated by dividing the hop flight time (FT) by the previous ground contact time. Total RSI_hor was determined by dividing total hop distance or total flight time by the sum of all ground contacts.

2.4. Statistical Analysis

Statistical analyses were performed with Jeffrey’s Amazing Statistics Program (JASP) software (version 0.18.3; Amsterdam, The Netherlands). Using descriptive statistics (means and standard deviations), centrality and spread were calculated and presented in the tables. Assumptions of univariate normality, outliers, and sphericity were assessed. Outlier analysis was conducted using boxplots, and values larger than three standard deviations (SD) were manually omitted from any further analysis. The Shapiro–Wilk test [26] was used to evaluate normality, and Q-Q plots were used to visually assess kurtosis and skewness. Of interest was whether the kinematic and kinetic variables could distinguish between sprinters of different ability. A paired sample t-test was conducted to assess whether there were significant differences between the dominant and non-dominant limbs, no statistically significant differences between the two limbs were detected, prompting the pooling of the data for subsequent analysis. The sportsmen were divided into two groups (fast and slow), consisting of the top fifteen and bottom fifteen performers for 10 m and 40 m sprint times, which were used as proxies for accelerative and top speed capability. Independent t-tests were conducted to identify any significant differences (p < 0.05) in kinetics, hop ratios, and RSI_hor between these groups. A Levene’s test was used to test the assumption that variances are equal across both groups. To explore the relationship between hop distance, RSI_hor, and sprint performance, a series of Pearson’s correlations were conducted, with the significance set at p < 0.05 and interpreted as weak (0.1–0.3), moderate (0.4–0.6), or strong (0.7–0.9) [27].

3. Results

The inter-relationship between speed measures and total hop distances is presented in

Table 1. Inter-relationships between speed measures and 3-Hop and 5-Hop distance.

		10 m	20 m	40 m
3-Hop distance	Pearson’s r	−0.705	−0.760	−0.795
	p-value	<0.001	<0.001	<0.001
5-Hop distance	Pearson’s r	−0.700	−0.759	−0.796
	p-value	<0.001	<0.001	<0.001

. A near-perfect correlation was observed between the 3-Hop and 5-Hop distances. As the distance increased from 10 m to 40 m, the strength of the correlations between the sprint times and both the 3-Hop and 5-Hop distances also increased, with very high negative and statistically significant (p < 0.05) correlations ranging from r = −0.700 to −0.796. The differences in the 3-Hop and 5-Hop correlations were negligible, ranging from 0.006 to 0.011.

The means and standard deviations for the kinetic variables for 3-Hop and 5-Hop are provided in

Table 2. Descriptive statistics and Pearson (r) correlations and p-values between kinetic variables (3-Hop, 5-Hop) and sprint times (10 and 40 m).

	3-Hop					5-Hop
		10 m		40 m			10 m		40 m
Kinetic Variable	Mean ± SD	r	p	r	p	Mean ± SD	r	p	r	p
Maximal Vertical Force 1	32.5 ± 4.63	−0.366	0.016	−0.451	0.002	32.1 ± 4.22	−0.279	0.070	−0.350	0.021
Maximal Vertical Force 2	42.0 ± 7.60	−0.416	0.005	−0.501	<0.001	39.7 ± 7.15	−0.484	0.001	−0.553	<0.001
Maximal Vertical Force 3						45.1 ± 8.76	−0.336	0.026	−0.467	0.001
Maximal Vertical Force 4						50.7 ± 10.5	−0.452	0.002	−0.554	<0.001
Net Vertical Impulse 1	5.67 ± 0.439	−0.296	0.051	−0.310	0.040	5.48 ± 0.442	−0.286	0.060	−0.307	0.043
Net Vertical Impulse 2	5.87 ± 0.338	−0.337	0.029	−0.335	0.030	5.48 ± 0.415	−0.319	0.037	−0.358	0.018
Net Vertical Impulse 3						5.60 ± 0.397	−0.270	0.080	−0.338	0.027
Net Vertical Impulse 4						5.88 ± 0.343	−0.311	0.048	−0.360	0.021
Vertical Braking Impulse 1	1.33 ± 0.626	−0.043	0.785	−0.054	0.736	1.04 ± 0.579	0.066	0.672	0.026	0.019
Vertical Braking Impulse 2	2.58 ± 0.461	−0.110	0.477	−0.155	0.314	2.02 ± 0.372	−0.148	0.337	−0.190	0.218
Vertical Braking Impulse 3						2.80 ± 0.373	−0.023	0.884	−0.136	0.389
Vertical Braking Impulse 4						3.55 ± 0.580	−0.267	0.080	−0.339	0.024
Vertical Propulsive Impulse 1	4.36 ± 0.431	−0.250	0.101	−0.237	0.122	4.46 ± 0.396	−0.404	0.007	−0.368	0.015
Vertical Propulsive Impulse 2	3.32 ± 0.481	−0.209	0.173	−0.179	0.246	3.51 ± 0.293	−0.242	0.128	−0.283	0.073
Vertical Propulsive Impulse 3						2.85 ± 0.243	−0.330	0.029	−0.262	0.085
Vertical Propulsive Impulse 4						2.42 ± 0.509	0.037	0.810	0.059	0.703
Net Horizontal Impulse 1	0.700 ± 0.157	−0.306	0.046	−0.354	0.020	0.780 ± 0.154	−0.436	0.003	−0.449	0.002
Net Horizontal Impulse 2	0.305 ± 0.148	−0.148	0.337	−0.162	0.292	0.461 ± 0.091	−0.171	0.280	−0.200	0.205
Net Horizontal Impulse 3						0.196 ± 0.094	−0.234	0.135	−0.185	0.242
Net Horizontal Impulse 4						−0.050 ± 0.186	0.141	0.366	0.147	0.346
Horizontal Braking Impulse 1	−0.048 ± 0.023	−0.164	0.306	−0.224	0.160	−0.033 ± 0.017	−0.179	0.263	−0.178	0.266
Horizontal Braking Impulse 2	−0.191 ± 0.048	−0.095	0.541	−0.142	0.356	−0.113 ± 0.035	−0.026	0.869	0.017	0.912
Horizontal Braking Impulse 3						−0.257 ± 0.044	0.118	0.470	0.165	0.308
Horizontal Braking Impulse 4						−0.400 ± 0.094	0.211	0.180	0.259	0.098
Horizontal Propulsive Impulse 1	0.756 ± 0.135	−0.332	0.028	−0.354	0.018	0.820 ± 0.138	−0.477	0.001	−0.477	0.001
Horizontal Propulsive Impulse 2	0.500 ± 0.109	−0.177	0.250	−0.191	0.214	0.583 ± 0.074	−0.281	0.068	−0.337	0.027
Horizontal Propulsive Impulse 3						0.445 ± 0.069	−0.368	0.014	−0.324	0.032
Horizontal Propulsive Impulse 4						0.350 ± 0.105	0.033	0.834	0.032	0.836

SD = standard deviation; force variables = N.kg; impulse variables = Ns.kg.

. In terms of the relationship between 3-Hop and 5-Hop kinetic measures and sprint times (10 and 40 m) the following was observed: the relationships between the kinetic measures and 10 and 40 m sprint times were weak to moderate (r < −0.554). Among the kinetic measures, relative maximal vertical force exhibited the strongest correlation, particularly across the 3-Hop and 5-Hop sequences (r = −0.554 to −0.350). Relative net vertical impulse was found to have a weak relationship across steps with sprint times (r = −0.360 to −0.270), as too was the relative vertical braking impulse across (r = −0.339 to 0.066). Moderate to negligible correlations were found between relative vertical propulsive impulse with sprint times (r = −0.404 to 0.059), with the strongest relationships observed in the initial steps, particularly for shorter sprint distances. Moderate to weak correlations were observed between net relative horizontal impulse and sprint times (r = −0.449 to 0.147), with stronger relationships observed in the first step across all sprint distances. A weak relationship was seen between relative horizontal braking impulse and sprint times (r = −0.224 to 0.259). Moderate to negligible correlations were seen between relative horizontal propulsive impulse and sprint times (r = −0.477 to 0.033), with stronger associations in the initial steps and weaker correlations in the final step.

The means and standard deviations for all RSI variables are presented in

Table 3. Descriptive statistics of 3-Hop and 5-Hop RSI variables (m·s⁻¹) and Pearson (r) correlations and p-values with sprint performance.

	Mean ± SD	Range	5 m		10 m		20 m		40 m
3-Hop			r	p	r	p	r	p	r	p
Step 1–2 RSIhor-DIST	7.26 ± 1.39	4.94 to 10.51	−0.468	0.001	−0.535	<0.001	−0.595	<0.001	−0.641	<0.001
Step 1–2 RSIhor-FT	1.18 ± 0.25	0.68 to 1.82	−0.350	0.020	−0.438	0.003	−0.496	<0.001	−0.549	<0.001
Step 2–3 RSIhor-DIST	10.71 ± 2.18	7.12 to 15.72	−0.477	0.001	−0.555	<0.001	−0.626	<0.001	−0.680	<0.001
Step 2–3 RSIhor-FT	1.71 ± 0.34	1.09 to 2.46	−0.434	0.003	−0.518	<0.001	−0.590	<0.001	−0.647	<0.001
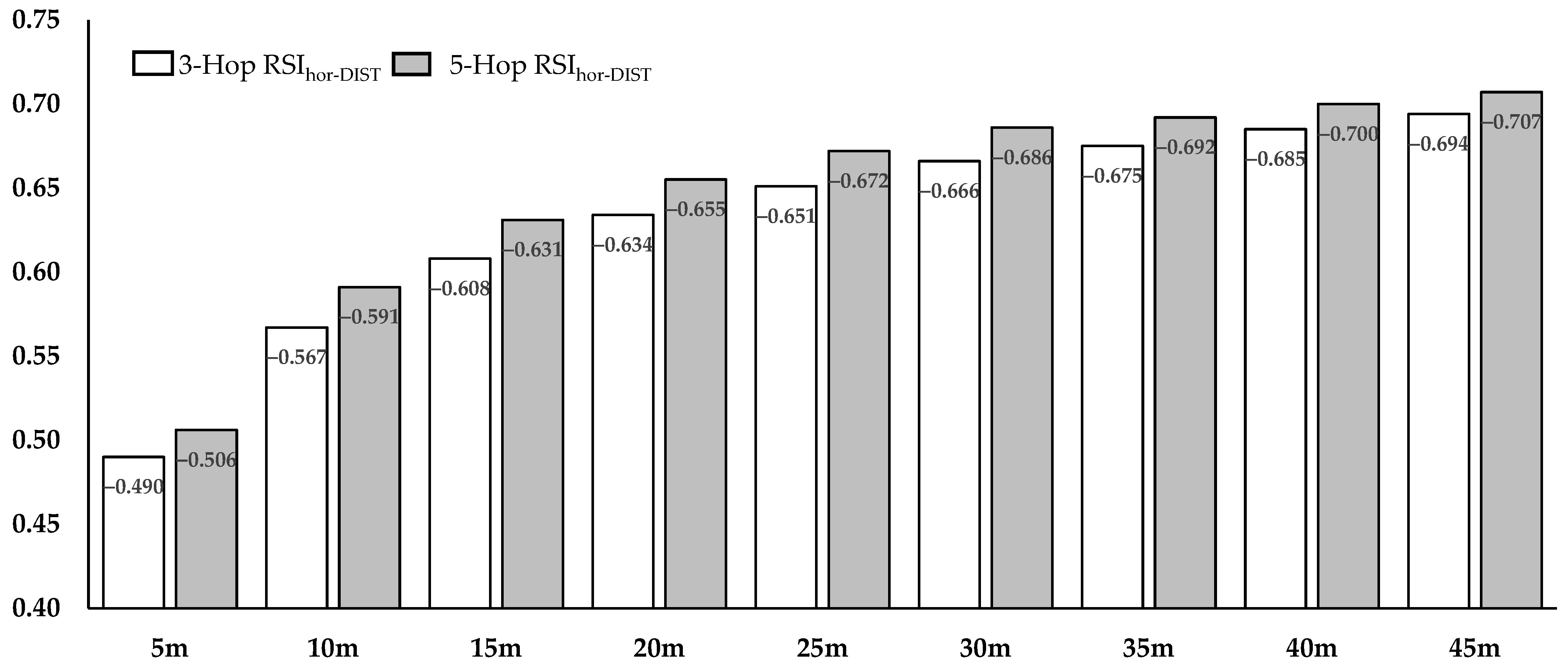
Total RSIhor-DIST	11.99 ± 2.21	8.48 to 16.78	−0.490	<0.001	−0.567	<0.001	−0.634	<0.001	−0.685	<0.001
Total RSIhor-FT	1.44 ± 0.28	0.88 to 2.12	−0.391	0.009	−0.482	<0.001	−0.544	<0.001	−0.562	<0.001
5-Hop
Step 1–2 RSIhor-DIST	7.30 ± 1.23	4.74 to 10.19	−0.467	0.001	−0.547	<0.001	−0.609	<0.001	−0.653	<0.001
Step 1–2 RSIhor-FT	1.17 ± 0.23	0.72 to 1.82	−0.270	0.076	−0.357	0.017	−0.408	0.006	−0.455	0.002
Step 2–3 RSIhor-DIST	9.12 ± 1.69	5.90 to 12.93	−0.453	0.002	−0.548	<0.001	−0.619	<0.001	−0.671	<0.001
Step 2–3 RSIhor-FT	1.36 ± 0.27	0.80 to 2.07	−0.319	0.035	−0.413	0.005	−0.480	<0.001	−0.539	<0.001
Step 3–4 RSIhor-DIST	9.93 ± 2.03	6.28 to 14.0	−0.461	0.002	−0.532	<0.001	−0.597	<0.001	−0.643	<0.001
Step 3–4 RSIhor-FT	1.46 ± 0.31	0.83 to 2.30	−0.315	0.037	−0.403	0.007	−0.475	0.001	−0.542	<0.001
Step 4–5 RSIhor-DIST	12.18 ± 2.82	7.74 to 18.4	−0.507	<0.001	−0.583	<0.001	−0.639	<0.001	−0.674	<0.001
Step 4–5 RSIhor-FT	1.89 ± 0.43	1.04 to 2.78	−0.467	0.001	−0.553	<0.001	−0.615	<0.001	−0.661	<0.001
Total RSIhor-DIST	11.17 ± 2.02	7.33 to 15.6	−0.506	<0.001	−0.591	<0.001	−0.655	<0.001	−0.700	<0.001
Total RSIhor-FT	1.45 ± 0.28	0.84 to 2.15	−0.391	<0.001	−0.482	<0.001	−0.544	<0.001	−0.597	<0.001

SD = standard deviation; RSI = reactive strength index; _hor-DIST = horizontal distance/ground contact time; _hor-FT = horizontal flight time/ground contact time.

. RSI_hor-DIST (r = −0.453 to −0.707) was found to have stronger relationships with sprint performance than RSI_hor-FT (r = −0.270 to −0.668) across all steps and particularly over the initial 5–10 m shorter distances and between fast and slow groups (Table 3). The strength of association of Total RSI_hor increased with sprinting distance (0.490 to 0.707; p < 0.001) for both 3-Hop and 5-Hop (Figure 2).

The means and standard deviations for the 10 and 40 m fast and slow groups and their differences are shown in

Table 4. Descriptive statistics for 3-Hop variables and t-test for independent samples with p-values and effect sizes for slow and fast sprint groups (10 and 40 m).

	10 m				40 m
	Slow	Fast			Slow	Fast
Kinetic Variable	Mean ± SD	Mean ± SD	p	d	Mean ± SD	Mean ± SD	p	d
Maximal Vertical Force 1	30.2 ± 3.80	33.5 ± 3.47	0.024	0.892	30.1 ± 3.83	34.3 ± 3.61	0.006	1.120
Maximal Vertical Force 2	37.9 ± 6.05	44.8 ± 7.04	0.008	1.046	38.2 ± 5.98	46.2 ± 6.86	0.002	1.240
Net Vertical Impulse 1	5.57 ± 0.447	5.76 ± 0.447	0.245	0.433	5.51 ± 0.424	5.72 ± 0.442	0.188	0.493
Net Vertical Impulse 2	5.78 ± 0.416	5.98 ± 0.337	0.166	0.529	5.74 ± 0.379	5.96 ± 0.334	0.102	0.629
Vertical Braking Impulse 1	1.22 ± 0.642	1.31 ± 0.480	0.651	0.170	1.21 ± 0.665	1.26 ± 0.475	0.803	0.096
Vertical Braking Impulse 2	2.44 ± 0.441	2.52 ± 0.446	0.663	0.161	2.49 ± 0.510	2.53 ± 0.461	0.803	0.092
Vertical Propulsive Impulse 1	4.32 ± 0.480	4.44 ± 0.405	0.460	0.274	4.35 ± 0.523	4.45 ± 0.405	0.550	0.221
Vertical Propulsive Impulse 2	3.29 ± 0.303	3.51 ± 0.524	0.185	0.496	3.21 ± 0.402	3.44 ± 0.585	0.222	0.456
Net Horizontal Impulse 1	0.655 ± 0.144	0.751 ± 0.143	0.080	0.664	0.669 ± 0.159	0.777 ± 0.134	0.055	0.731
Net Horizontal Impulse 2	0.299 ± 0.102	0.367 ± 0.166	0.182	0.500	0.289 ± 0.121	0.356 ± 0.173	0.223	0.455
Horizontal Braking Impulse 1	0.054 ± 0.027	−0.047 ± 0.017	0.420	0.304	−0.052 ± 0.029	−0.043 ± 0.019	0.343	0.359
Horizontal Braking Impulse 2	−0.193 ± 0.038	−0.180 ± 0.052	0.416	0.301	−0.193 ± 0.037	−0.177 ± 0.053	0.362	0.339
Horizontal Propulsive Impulse 1	0.725 ± 0.119	0.808 ± 0.123	0.070	0.689	0.735 ± 0.129	0.830 ± 0.107	0.037	0.800
Horizontal Propulsive Impulse 2	0.492 ± 0.078	0.551 ± 0.123	0.130	0.570	0.482 ± 0.093	0.545 ± 0.120	0.119	0.587

SD = standard deviation; force variables = N.kg; impulse variables = Ns.kg; d = Cohen’s d for effect size.

and

Table 5. Descriptive statistics for 5-Hop kinetic variables and t-test for independent samples with p-values and effect sizes for slow and fast sprint groups (10 and 40 m).

	10 m				40 m
	Slow	Fast			Slow	Fast
Kinetic Variable	Mean ± SD	Mean ± SD	p	d	Mean ± SD	Mean ± SD	p	d
Maximal Vertical Force 1	30.4 ± 2.94	33.0 ± 3.59	0.044	0.784	30.5 ± 2.87	33.5 ± 3.74	0.021	0.909
Maximal Vertical Force 2	35.9 ± 6.13	43.4 ± 6.24	0.002	1.214	35.9 ± 6.10	45.1 ± 6.00	<0.001	1.514
Maximal Vertical Force 3	40.7 ± 7.02	47.0 ± 7.52	0.025	0.864	40.9 ± 6.89	50.0 ± 7.88	0.002	1.236
Maximal Vertical Force 4	44.0 ± 6.95	55.4 ± 10.2	0.001	1.306	44.5 ± 6.76	58.0 ± 9.45	<0.001	1.644
Net Vertical Impulse 1	5.39 ± 0.444	5.56 ± 0.477	0.303	0.383	5.31 ± 0.406	5.55 ± 0.457	0.131	0.568
Net Vertical Impulse 2	5.42 ± 0.494	5.59 ± 0.368	0.298	0.387	5.35 ± 0.468	5.62 ± 0.374	0.091	0.640
Net Vertical Impulse 3	5.55 ± 0.448	5.71 ± 0.373	0.299	0.383	5.49 ± 0.450	5.73 ± 0.380	0.121	0.585
Net Vertical Impulse 4	5.79 ± 0.390	5.97 ± 0.352	0.192	0.497	5.75 ± 0.368	5.94 ± 0.333	0.158	0.550
Vertical Braking Impulse 1	1.14 ± 0.604	0.945 ± 0.542	0.367	−0.303	1.04 ± 0.663	0.985 ± 0.504	0.794	−0.098
Vertical Braking Impulse 2	2.02 ± 0.474	2.00 ± 0.273	0.914	−0.040	1.97 ± 0.484	2.07 ± 0.308	0.539	0.227
Vertical Braking Impulse 3	2.81 ± 0.339	2.77 ± 0.392	0.786	−0.102	2.76 ± 0.370	2.82 ± 0.372	0.649	0.171
Vertical Braking Impulse 4	3.27 ± 0.604	3.47 ± 0.405	0.278	0.404	3.32 ± 0.655	3.56 ± 0.553	0.303	0.383
Vertical Propulsive Impulse 1	4.28 ± 0.424	4.64 ± 0.360	0.021	0.909	4.30 ± 0.439	4.49 ± 0.342	0.055	0.747
Vertical Propulsive Impulse 2	3.43 ± 0.271	3.60 ± 0.325	0.134	0.564	3.40 ± 0.238	3.57 ± 0.321	0.120	0.585
Vertical Propulsive Impulse 3	2.80 ± 0.279	2.97 ± 0.242	0.088	0.645	2.78 ± 0.265	2.92 ± 0.229	0.117	0.590
Vertical Propulsive Impulse 4	2.57 ± 0.517	2.56 ± 0.390	0.991	−0.004	2.47 ± 0.580	2.50 ± 0.474	0.916	0.039
Net Horizontal Impulse 1	0.701 ± 0.132	0.843 ± 0.127	0.006	1.096	0.721 ± 0.155	0.863 ± 0.121	0.009	1.020
Net Horizontal Impulse 2	0.431 ± 0.082	0.483 ± 0.095	0.129	0.594	0.446 ± 0.010	0.473 ± 0.098	0.476	0.274
Net Horizontal Impulse 3	0.168 ± 0.085	0.219 ± 0.098	0.143	0.561	0.186 ± 0.101	0.217 ± 0.076	0.357	0.348
Net Horizontal Impulse 4	0.039 ± 0.130	−0.005 ± 0.162	0.422	−0.303	0.010 ± 0.182	−0.019 ± 0.175	0.661	−0.165
Horizontal Braking Impulse 1	−0.036 ± 0.013	−0.031 ± 0.015	0.296	0.404	−0.034 ± 0.014	−0.029 ± 0.015	0.385	0.334
Horizontal Braking Impulse 2	−0.123 ± 0.033	−0.109 ± 0.035	0.295	0.390	−0.116 ± 0.037	−0.113 ± 0.037	0.846	0.072
Horizontal Braking Impulse 3	−0.256 ± 0.052	−0.269 ± 0.029	0.424	−0.307	−0.253 ± 0.052	−0.261 ± 0.031	0.643	−0.180
Horizontal Braking Impulse 4	−0.351 ± 0.082	−0.386 ± 0.076	0.249	−0.438	−0.349 ± 0.085	−0.393 ± 0.085	0.174	−0.529
Horizontal Propulsive Impulse 1	0.746 ± 0.114	0.879 ± 0.116	0.004	1.159	0.764 ± 0.1355	0.897 ± 0.105	0.006	1.094
Horizontal Propulsive Impulse 2	0.555 ± 0.065	0.611 ± 0.074	0.036	0.818	0.563 ± 0.075	0.606 ± 0.074	0.130	0.580
Horizontal Propulsive Impulse 3	0.422 ± 0.057	0.480 ± 0.076	0.025	0.864	0.428 ± 0.061	0.470 ± 0.072	0.097	0.627
Horizontal Propulsive Impulse 4	0.370 ± 0.103	0.377 ± 0.103	0.847	0.071	0.359 ± 0.112	0.368 ± 0.110	0.832	0.078

SD = standard deviation; force variables = N.kg; impulse variables = Ns.kg; d = Cohen’s d for effect size.

. In terms of the 10 m times, faster sprinters were found to produce significantly greater maximal vertical force across all hops (8.55 to 25.6% Δ) for both the 3-Hop and 5-Hop testing (ES = 0.784–1.306), significantly greater vertical propulsive impulse (8.41% Δ) on the first hop of 5-Hop testing, significantly greater net horizontal impulse on the first hop (20.3% Δ) of the 5-Hop test, and significantly greater horizontal propulsive impulse across the first three hops (10.1 to 17.8% Δ) in the 5-Hop test (ES = 0.818–1.159). With regards to the 40 m times, faster sprinters were found to produce significantly greater maximal vertical force across all hops (9.84 to 30.3% Δ) for both the 3-Hop and 5-Hop testing (ES = 0.909–1.644), significantly greater net horizontal impulse on the first hop (19.7% Δ) in the 5-Hop test, and significantly greater horizontal propulsive impulse in the first hop (12.9 to 17.4% Δ) in the 3-Hop and 5-Hop tests.

Hop ratios did not distinguish (p < 0.05) between fast and slow groups for sprinting (

Table 6. The sprint times and hop ratios for groups, separated by 10 and 40 m times.

	Sprint Time (s)	Hop Ratio	p	3-Hop RSIhor-DIST	p	5-Hop RSIhor-DIST	p
10 m Sprint
Group 1 (fast)	1.60	1.73 ± 0.034	-	13.1 ± 2.10	-	11.8 ± 1.08	-
Group 2 (slow)	1.78	1.71 ± 0.044	0.222	10.5 ± 1.52	<0.001	10.1 ± 1.01	<0.001
40 m Sprint
Group 1 (fast)	5.10	1.72 ± 0.036	-	13.8 ± 2.20	-	12.8 ± 1.92	-
Group 2 (slow)	5.71	1.71 ± 0.046	0.434	10.7 ± 1.55	<0.001	9.9 ± 1.59	<0.001

). The fast group 5-Hop distance was approximately 72.5% greater than the 3-Hop distance for both the 10 m and 40 m, whereas the slower group differences were 71% across both sprint distances. However, the 3-Hop and 5-Hop RSI_hor measures were found to be significantly different between the fast and slow sprinters. The differences between the 3-Hop and 5-Hop RSI_hor values of the fastest and slowest groups was ~14.5 to 22.5% (p < 0.001) for both the 10 and 40 m distances.

4. Discussion

The 3-Hop and to a lesser extent the 5-Hop are movements that provide physiotherapists, as well as strength and conditioning coaches and technical coaches, with valuable insights into neuromuscular function. Improving understanding around the utility of these jumps and their associated measures provided an overarching focus for this research. Specifically the aims of this study were threefold: (1) to examine the relationship between 3-Hop and 5-Hop distance and sprint performance, and to determine whether hop kinetic variables provide stronger relationships to sprinting ability than kinematic/hop distances; (2) to explore the relationship between two methods of determining 3-Hop and 5-Hop RSI_hor and sprint performance; (3) to investigate whether the 5-Hop/3-Hop ratio or RSI_hor and other kinetic measures could differentiate between sprinters of different ability. The main findings were as follows: (1) 3-Hop and 5-Hop distances were strongly correlated with 10, 20, and 40 m sprint times (r = 0.70 to 0.80), while the relationship between the kinetic measures and sprint times was weak to moderate (r < −0.55); (2) the strength of the association between RSI_hor and sprint performance increased with sprint distance (r = 0.49 to 0.71; p < 0.001), and RSI_hor calculated from jump distance was a stronger predictor of sprint performance than calculation from flight time; (3) hop ratios did not differentiate between fast and slow sprinters, whereas RSI_hor was able to; (4) there were significant differences in some kinetic measures of 3-Hop and 5-Hop tests that differentiated fast and slow sprinters; and (5) given the small differences between the 3-Hop and 5-Hop results, there would seem little value in including both hops in the assessment of sprint-related performance.

The 3-Hop and 5-Hop distances were strongly correlated with 10, 20, and 40 m sprint times (r = 0.70 to 0.80), with the strength of association increasing with sprint distance. The results of this study were consistent with the previously reported relationships between multiple hop distances and sprint performance, both for recreational (r = 0.68 to 0.86) athletes [8,10] and sub-elite (r = 0.84 to 0.89) sprinters [7].

Maulder et al. (2006) [9] proposed that predictions of sprint performance using horizontal jump measures might be more effective for athletes involved in sports requiring a wide range of sprinting expressions, but less applicable for competitive-level sprinters. They also suggested that more sensitive measures, such as force and power, might provide a better reflection of what occurs during sprint running compared to jumping distance alone. Our findings in this cohort of sportsmen suggests that while kinetic variables can explain some of the variance associated with sprinting, they were not strong predictors of sprint performance in this cohort. The general relationships between the hop GRFs and sprint performance were weak to moderate (r < −0.55). The maximal vertical forces seen in both 3-Hop and 5-Hop tests were shown to have the strongest relationship with sprint performance, and the strength of this relationship increased with sprinting distance over 5 m to 45 m. This finding was consistent with previously reported characteristics of performance in elite sprinters [28].

Of interest was the relationship between the two methods of calculating 3-Hop and 5-Hop RSI_hor and their relationship to sprint performance. The strength of the association between RSI_hor and sprint performance increased with sprint distance (r = 0.49 to 0.71; p < 0.001), with RSI_hor calculated from jump distance showing a stronger correlation with sprint performance than when calculated from flight time (see Figure 2). Sarabon et al. (2023) [21] investigated the utility of RSI_hor-DIST during 3-Hop assessments, finding small to moderate negative correlations with 505 change-of-direction test performance (r = −0.15 to −0.45) and 10 m sprint performance (r = −0.03 to −0.16) in male volleyball players. They reported RSI_hor-DIST values ranging from 5.24 to 7.57 m·s⁻¹, whereas in this study, 3-Hop assessments yielded values between 7.26 and 10.71 m·s⁻¹, with stronger correlations with sprint performance (r = −0.49 to −0.69). This stronger relationship may be attributed to the higher reactive strength capacity of the subjects in this study. The mean hop distance in our sample was 6.43 m (±0.67), compared to 5.91 m (±0.51) in the Sarabon et al. [21] study, with our participants also demonstrating shorter ground contact times, which also amplifies the resulting RSI.

Another focus of the research was to determine whether the 5-Hop/3-Hop ratio or RSI_hor could differentiate between sprinters of differing ability. According to Vittori, sprinters with a capacity to express strength whilst sprinting should be able to hop approximately 70% further in a 5-Hop compared to a 3-Hop. However, our findings indicated that the hop ratio could not (p < 0.05) differentiate between fast and slow sprinters, as both group 5-Hop to 3-Hop differences were 71 to 72.5% (p > 0.05). While it might seem intuitive that athletes capable of achieving higher stretch-loads in a 5-Hop would also demonstrate faster sprinting speeds, our study, conducted with a heterogeneous sample, did not provide any evidence to support this hypothesis. Rather, it seems that RSI_hor is a better variable to differentiate sprinting ability, and, therefore, most likely a better variable to measure and monitor. It also appears that RSI_hor values from the 3-Hop assessments were just as strongly correlated with sprint distance as those from the 5-Hop test, suggesting that the additional injury risk associated with the 5-Hop may not be justified in a training-assessment context. Nevertheless, in a training environment, the 5-Hop might still be valuable for eliciting the higher stretch–load stimuli for those athletes ready for such incremental loading.

5. Conclusions and Practical Applications

Multiple hops offer an easy, valid, and reliable method for assessing neuromuscular function and are commonly used by physiotherapists, strength and conditioning coaches, and technical coaches. The utility and interpretation of these tests is usually based on the distance jumped. The focus of this article was to determine if other kinematic and kinetic measures could enhance the diagnostic value of 3-Hop and 5-Hop assessments, within a sports performance/sprint context. With this in mind, the findings were as follows.

Both 3-Hop and 5-Hop distances were strongly correlated with 10, 20, and 40 m sprint times, which have applications for assessment and training. For example, changes in the distance jumped should correspond to quicker sprint times (especially for longer distance sprints), which could be monitored between official timing light or radar assessments. In terms of training, using multiple hops as a training option to improve sprint times is certainly supported by the results of this study.

RSI_hor calculated from jump distance was a stronger predictor of sprint performance than calculation from flight time, and it is recommended as the variable of choice for measuring horizontal reactivity. This can be performed with force plates, or by using more readily available smartphone AI-based digitizing applications, such as Vuemotion (Sydney, Australia); however, using flight time in the calculation can offer a more practical approach for field assessments for those without expensive analysis tools, as simple smartphone video technology has been shown to be both valid and reliable for this purpose [1,2].

Most of the movement strategy kinetic variables did not correlate strongly to the outcome variables (jump distance/sprint times) in this cohort. Of the kinetic measures investigated, maximal vertical force and horizontal propulsive impulse were found to be correlated best with the 10 and 40 m times, and, as such, are potentially the best variables to measure, monitor, and train athletes if force plate technology is available.

It would seem that the hop ratio between the 3-Hop and 5-Hop cannot differentiate sprint ability in sportsmen; however, RSI_hor can, and, therefore, this measure could be used to measure and monitor athletes, or for talent identification purposes.

Given the high collinearity between the 3-Hop and 5-Hop tests, it would seem prudent to measure and monitor only one of the hops. The stretch loads associated with the 5-Hop exceed that of the 3-Hop, and, therefore, decisions on the hop used in an assessment battery may be made around the unilateral strength–power qualities and athleticism of the athletes who are involved.

One limitation of this study was the homogeneity of the sample. While it encompassed a diverse range of participants from various sports requiring both skill and a variety of strength qualities, the sample was limited to university-aged male participants. Future researchers should aim to include a more diverse range of ages and should include female athletes to enhance the generalizability of the findings. Secondly, a more in-depth analysis of the kinetic data, particularly focusing on the power and work involved in completing both the 3-Hop and 5-Hop tasks, could provide deeper insights into the storage and utilization of the elastic energy capacity of athletes across hops.