Computational Fluid Dynamics of Compartment Fires: A Review of Methods and Applications
Abstract
:1. Introduction
2. Validation in CFD Simulation
3. CFD Simulation in Compartment Fires
3.1. Computational Mesh
3.2. Boundary Conditions
- Thermal Boundary Conditions: Thermal boundary conditions directly influence heat losses to walls, floors, and ceilings, which in turn affect fire spread, flame temperature, and product gases. For example, a well-insulated boundary can trap heat, causing higher temperatures and more intense fire growth, while highly conductive boundaries may slow fire development by reducing available thermal energy. Accurate representation of these boundary conditions is therefore essential for capturing realistic compartment fire behavior.
- Material and Surface Properties: Material properties directly influence the boundary conditions in CFD simulations by affecting heat flux, temperature profiles, and the fire spread rate. For accurate fire modeling, these properties must be carefully selected and validated based on experimental data to replicate real-world conditions.
- Flow Boundary Conditions: Flow boundary conditions at inlets and outlets such as doors, windows, and vents are essential to define how air enters the compartment and how product gases exit. These boundaries control the oxygen supply, smoke evacuation, and pressure gradients within the compartment, all of which impact the fire dynamics and its growth.
- Burning Rate and Pyrolysis Boundary Conditions: Burning rate and pyrolysis boundary conditions describe how combustible materials are set up to burn, including parameters for pyrolysis and feedback mechanisms (e.g., temperature, and heat flux) affecting fuel release rates. This is critical for accurately modeling the growth phase of compartment fires.
- Initial Condition: Initial condition describes how the initial setup, like ambient temperatures and initial pressures, affects boundary conditions over time, influencing fire spread predictions.
3.3. Physical Models
3.3.1. Turbulence Modeling
- RANS sees the flow properties (e.g., velocity, pressure, etc.) as the composition of mean and fluctuating components and solves the Navier–Stokes equations in a time-averaged manner. As a result, turbulence is modeled using transport equations.
- LES resolves large turbulent eddies (which carry most of the turbulent energy) in the flow while modeling the smaller scales (turbulent eddies at the scales are smaller than the grid size, i.e., sub-grid scale). The method that is used to model sub-grid scale eddies will be presented in following section called sub-grid scale modeling.
- The DNS method resolves all scales of turbulence without any modeling, solving the Navier–Stokes equations directly and completely. It requires extremely fine computational grids and small time-steps to capture the whole range of turbulent scales.
- DES is based on benefiting from LES modeling while keeping the advantages of RANS mode where LES is computationally expensive. The main idea of DES is to use RANS adjacent to the surfaces (such as walls) to neglect the need for fine mesh resolution (as in LES) and switch to LES in other regions where larger scale eddies are present and resolving them is computationally feasible.
- VLES is a flexible approach in turbulence modeling and has been designed to cover a wide range of turbulence modeling modes. It adapts its operation based on the grid resolution and required turbulence details: VLES works in RANS mode and most of the turbulent motions are not resolved when the grid size is very coarse. Finer grids can move it to a transitional approach between RANS and LES and more of the turbulence spectrum is resolved. VLES becomes pure LES when the grids are finer than the previous mode. And finally, if the computational grids are fine enough to resolve all turbulent scales, VLES works as DNS. This was first introduced by Speziale [47] and improved by Han et al. [48,49].
Sub-Grid Scale (SGS) Modeling
3.3.2. Pyrolysis
- Gases: Volatile compounds like hydrogen, methane, carbon monoxide, and other light hydrocarbons.
- Liquids: Condensable products such as tar, oil, or other heavy hydrocarbons.
- Solid Residue: Char or ash.
- Solid Fuels
- Liquid Fuels
3.3.3. Combustion and Kinetics
- Infinite rate chemistry: it is assumed that fuel and oxygen can interact with each other instantly and the only limiting criteria is mixing [12], eliminating the influence of chemical kinetics.
- Finite-rate chemistry: consider the actual chemical reaction rates and their dependency on temperature, pressure, and concentration of reactants.
3.3.4. Heat Transfer: Radiation Transport
- Emission—radiation emitted by the media itself;
- Absorption—radiation absorbed by media and reducing the intensity of radiation passing through it;
- Scattering—radiation deflected by particles in the media, changing its direction without being absorbed.
- P1 [103,104]: This is the simplest method which simplifies the RTE by assuming that radiation is isotropic and diffusive in nature, making it computationally efficient and easy to implement. It approximates RTE based on the spherical harmonics method. It assumes isotropic radiation and works well for optically thick media (such as smoke and flames in fires). P1 is less accurate in optically thin media (to overpredict radiative fluxes from localized heat sources or sinks in optically thin media [104]) but is suitable for optically thick cases, such as fires with heavy smoke. Optically thin media and walls exposed to uncertain boundary conditions may result in the inaccuracy of the P1 method [94]. P1 considers scattering without any additional computational cost [104].
- Discrete Ordinates Method (DOM) [105]: This is is a finite volume method which solves the RTE by dividing the angular space into several discrete directions and solving for each direction. DOM can model anisotropic radiation and complex geometries, although it requires higher computational resources compared to P1, especially when fine angular resolution is needed. Furthermore, in optically thin regions, errors arise because DOM does not inherently treat scattering accurately and can produce ray effects where artificial patterns of radiation appear.
- Discrete Transfer Ray-Tracing Method (DTRM) [99]: This method traces rays from heat sources to surfaces, calculating radiation directly along these paths. DTRM assumes negligible scattering and is less accurate in optically thick media or for environments with strong scattering effects such as soot. In flows where fire is dominant (such as compartment fire), soot is the determining factor rather than product gases in thermal radiation [7]. Therefore, DTRM is not a good choice in a CFD simulation of a compartment fire.
- S2S Model (opaque Solid): This is a technique to simulate radiative heat transfer between surfaces in systems where the media between the surfaces is non-participating (i.e., it does not absorb, emit, or scatter radiation). This model simplifies radiative heat transfer by only considering radiation exchange between solid surfaces. The S2S model cannot account for the effects of soot, smoke, or combustion gases on radiation, which limits its application. But, in case of compartment fire, it can be used for the radiation model of solid surfaces such as walls, ceilings, floors, furnishing, and objects inside the compartment.
- Line-by-Line (LBL): This method considers the actual spectral lines of radiatively active gases, resolving absorption coefficients at very high spectral resolution. LBL is used when high accuracy is required. It is the most accurate model for radiative transfer because it considers every spectral line. Due to the intensive computational requirements of resolving individual absorption lines across the entire spectrum, it is not widely implemented in CFD tools like FDS or OpenFOAM.
- Spectral Band Models: These models divide the spectrum of gas radiation into discrete spectral bands:
- Narrow Band Models (NBM): These models divide the spectrum into small narrow bands and treat radiative properties as varying within each band. They offer a more manageable approximation compared to LBL but still retain some spectral detail.
- Statistical Narrow Band (SNB): This incorporates statistical methods to represent spectral lines within each narrow band. It is the most accurate model to replicate the LBL method, especially in high temperature gases.
- Wide Band Model (WBM): This is a simplified version of SNB. It categorizes the radiation spectrum into wider bands rather than treating individual spectral lines. Each band represents a broader wavelength range, where the absorption and emission properties are relatively similar. In other words, the model assumes that within each band, the gas properties, such as absorption coefficients, are constant or vary in a predictable manner. It can result in significantly less computational cost compared to NBM. WBM offers good accuracy, especially for gases like CO2 and H2O which have strong and wide absorption bands. This model is available on FDS (Box Model) [12] and OpenFOAM (WideBandAbsorptionEmission) [112].
- Global Models: These models, including the Gray Gas and Weighted-Sum-of-Gray-Gases (WSGG) models, simplify the radiative transfer by treating the gas as absorbing/emitting uniformly across all wavelengths (or a few representative gray gases with different absorption coefficients). They are commonly available in CFD tools such as FDS, OpenFOAM, and FireFOAM.
- Gray Gas Model: To reduce the required computation time for solving RTE, gases are often assumed to be gray. It helps the RTE to be solved more efficiently by treating the gas as having uniform radiative properties and eliminates the need for detailed spectral calculations (i.e., no spectral variation is considered), which involves resolving the radiative transfer across a wide range of wavelengths. By treating the gas as gray, the simulation ignores the fine structure of how different wavelengths are absorbed and emitted by gases like CO2 and H2O, which are computationally expensive to resolve [94]. This can decrease the accuracy of the simulation in the case of oxyfuel combustion (i.e., more concentrated CO2 and H2O in the product gases) and optically thin flames [62] (i.e., soot yield is lower than CO2 and H2O yield).
- WSGG Model [111]: This model improves the gray gas approximation by dividing the radiation spectrum into a sum of gray gases with different absorption coefficients, each weighted by temperature and concentration. When dealing with mixtures of gases such as CO2, H2O, and soot, the absorption spectra can overlap. The WSGG model may not handle these interactions effectively, leading to reduced accuracy when modeling multi-gas combustion environments. For similar conditions, the computational cost of WSGG was shown to be around 3.5 times that of the Gray Gas Model [38].
3.3.5. Extinction
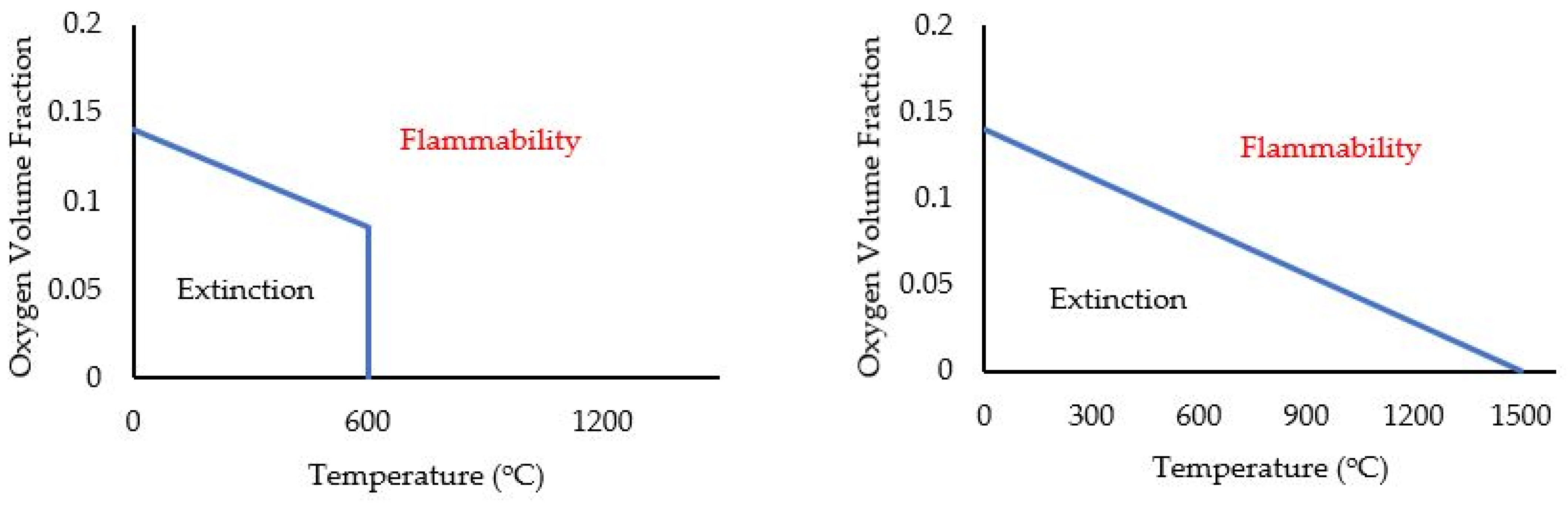
- A critical flame temperature (CFT) (a constant value in the range of 1450–1780 K) which does not consider the effects of turbulence [121];
- A critical Damkohler number to model flame extinction, which is defined as Equation (6).
4. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amokrane, A.; Sapa, B. Large Scale Multi-Compartment and Multi-Source Fire Modelling Using the Peatross & Beyler Correlation. Fire Saf. J. 2023, 138, 103810. [Google Scholar] [CrossRef]
- Shen, R.; Jiao, Z.; Parker, T.; Sun, Y.; Wang, Q. Recent Application of Computational Fluid Dynamics (CFD) in Process Safety and Loss Prevention: A Review. J. Loss Prev. Process Ind. 2020, 67, 104252. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; De Cachinho Cordeiro, I.M.; Chen, T.B.Y.; Chen, Q.; Liu, H.; Yeoh, G.H. Multiphase CFD Modelling for Enclosure Fires—A Review on Past Studies and Future Perspectives. Exp. Comput. Multiph. Flow. 2022, 4, 1–25. [Google Scholar] [CrossRef]
- Lngason, H.; Persson, B. Prediction of Optical Density Using CFD. Fire Saf. Sci. 2000, 6, 817–828. [Google Scholar] [CrossRef]
- Wen, J.X. Fire Modelling: The Success, the Challenges, and the Dilemma from a Modeller’s Perspective. Fire Saf. J. 2024, 144, 104087. [Google Scholar] [CrossRef]
- Cox, G. Fire Research in the 21st Century. Fire Saf. J. 1999, 32, 203–219. [Google Scholar] [CrossRef]
- Beji, T.; Hidalgo, J.P.; Fateh, T.; Floyd, J.; Prétrel, H.; Hamins, A. Compartment Fires: Challenges for Fire Modeling as a Tool for a Safe Design (IAFSS Workshop, April 2021). Fire Saf. J. 2024, 144, 104109. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics; Wiley: Hoboken, NJ, USA, 2011; ISBN 9780470319031. [Google Scholar]
- Novozhilov, V. Computational Fluid Dynamics Modeling of Compartment Fires. Prog. Energy Combust. Sci. 2001, 27, 611–666. [Google Scholar] [CrossRef]
- Lucherini, A.; Jovanović, B.; Torero, J.L.; Van Coile, R.; Merci, B. Thermal Characterisation of the Cooling Phase of Post-Flashover Compartment Fires. Int. J. Therm. Sci. 2024, 199, 108933. [Google Scholar] [CrossRef]
- Lucherini, A.; Torero, J.L. Defining the Fire Decay and the Cooling Phase of Post-Flashover Compartment Fires. Fire Saf. J. 2023, 141, 103965. [Google Scholar] [CrossRef]
- McGrattan, K.; McDermott, R.; Weinschenk, C.; Forney, G. Fire Dynamics Simulator, Technical Reference Guide, 6th ed.; Special Publication (NIST SP), National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar] [CrossRef]
- Institut de Radioprotection et de Sûreté Nucléaire. Available online: https://www.irsn.fr/actualites/isis-version-200-disponible (accessed on 16 September 2024).
- FM Global. Available online: https://www.fm.com/about-us/our-engineering-approach/engineering-methods/open-source-fire-modeling (accessed on 16 September 2024).
- ASTM E1355; Standard Guide for Evaluating Predictive Capability of Deterministic Fire Models. American Society for Testing and Materials: West Conshohoken, PA, USA, 2005.
- Rein, G.; Torero, J.L.; Jahn, W.; Stern-Gottfried, J.; Ryder, N.L.; Desanghere, S.; Lázaro, M.; Mowrer, F.; Coles, A.; Joyeux, D.; et al. Round-Robin Study of a Priori Modelling Predictions of the Dalmarnock Fire Test One. Fire Saf. J. 2009, 44, 590–602. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.; Lee, S.; Shin, W.G. Validation of the Fire Dynamics Simulator (FDS) Model for Fire Scenarios with Two Liquid Pool Fires in Multiple Compartments. Fire Saf. J. 2023, 141, 103892. [Google Scholar] [CrossRef]
- Skarsbø, L.R. An Experimental Study of Pool Fires and Validation of Different CFD Fire Models. Master’s Thesis, University of Bergen, Bergen, Norway, 2011. [Google Scholar]
- McGrattan, K.; Floyd, J. Current and Future Parameters Used by FDS. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=933774 (accessed on 2 September 2024).
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa Publishers: Albuquerque, NM, USA, 1998. [Google Scholar]
- Roache, P.J. Verification of Codes and Calculations. AIAA J. 1998, 36, 696–702. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and Validation in Computational Fluid Dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]
- Terminology for Model Credibility. Simulation 1979, 32, 103–104. [CrossRef]
- Merci, B.; Li, J.; Maragkos, G. On the Importance of the Heat Release Rate in Numerical Simulations of Fires in Mechanically Ventilated Air-tight Enclosures. Proc. Combust. Inst. 2023, 39, 3647–3672. [Google Scholar] [CrossRef]
- Suard, S.; Lapuerta, C.; Kaiss, A.; Porterie, B. Sensitivity Analysis of a Fire Field Model in the Case of a Large-Scale Compartment Fire Scenario. Numer. Heat Transf. Part A Appl. 2013, 63, 879–905. [Google Scholar] [CrossRef]
- Yeoh, G.; Yuen, K.K. Computational Fluid Dynamics in Fire Engineering: Theory, Modelling and Practice; Butterworth-Heinemann: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Hasib, R.; Kumar, R.; Shashi; Kumar, S. Simulation of an Experimental Compartment Fire by CFD. Build. Environ. 2007, 42, 3149–3160. [Google Scholar] [CrossRef]
- Khan, A.A.; Khan, M.A.; Domada, R.V.V.; Huang, X.; Usmani, A.; Bakhtiyari, S.; Ashtiani, M.J.; Garivani, S.; Aghakouchak, A.A. Fire Modelling Framework for Investigating Tall Building Fire: A Case Study of the Plasco Building. Case Stud. Therm. Eng. 2023, 45, 103018. [Google Scholar] [CrossRef]
- Husted, B.P.; Li, Y.Z.; Huang, C.; Andersson, J.; Svensson, R.; Ingason, H.; Runefors, M.; Wahlqvist, J. Verification, Validation and Evaluation of FireFOAM as a Tool for Performance Based Design; TVBB No. 3176, Brandforsk Rapport Vol. 2017, No. 2; Lund University, Department of Fire Safety Engineering: Lund, Sweden, 2018. [Google Scholar]
- Wang, J.; Wu, Z.; Xiao, X.; He, Y. Selection of computational domain in numerical simulation of building fires. Fire Saf. Sci. 2006, 15, 232–240. [Google Scholar]
- He, Y.; Jamieson, C.; Jeary, A.; Wang, J. Effect of Computation Domain on Simulation of Small Compartment Fires. Fire Saf. Sci. 2008, 9, 1365–1376. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, M.; Wang, J.; He, Y. Effects of Computational Domain on Numerical Simulation of Building Fires. J. Fire Prot. Eng. 2010, 20, 225–251. [Google Scholar] [CrossRef]
- Lu, Y.; Li, P.; Liu, J.-H.; Chen, Q.-P.; Wang, J. Selection and Its Criteria of Computational Domain on Numerical Simulation of Building Fires. In Proceedings of the 2nd Annual International Conference on Electronics, Electrical Engineering and Information Science (EEEIS 2016), Xi’an, China, 2–4 December 2016; Atlantis Press: Paris, France, 2017. [Google Scholar]
- Quintiere, J.G. An Introduction to Fire Dynamics. Fire Saf. J. 1986, 10, 161–162. [Google Scholar] [CrossRef]
- McGrattan, K.B.; Baum, H.R.; Rehm, R.G. Large Eddy Simulations of Smoke Movement. Fire Saf. J. 1998, 30, 161–178. [Google Scholar] [CrossRef]
- Hietaniemi, J.; Hostikka, S.; Vaari, J.; Building, V. Transport FDS Simulation of Fire Spread—Comparison of Model Results with Experimental Data; VTT Building and Transport: Espoo, Finland, 2004. [Google Scholar]
- Cai, N.; Chow, W.K. Numerical Studies on Heat Release Rate in Room Fire on Liquid Fuel under Different Ventilation Factors. Int. J. Chem. Eng. 2012, 2012, 910869. [Google Scholar] [CrossRef]
- Maragkos, G.; Merci, B. Influence of Radiation Modelling in Under-Resolved FDS Free-Burn Simulations. Int. J. Heat Fluid Flow 2024, 107, 109437. [Google Scholar] [CrossRef]
- Sahu, D.; Jain, S.; Gupta, A.; Kumar, S. Numerical Studies on Methanol Pool Fire Inside the Enclosure. In Advances in Mechanical Engineering: Select Proceedings of CAMSE 2020; Springer: Singapore, 2021; pp. 257–269. [Google Scholar]
- OpenCFD Ltd. OpenFOAM Docs. Available online: https://doc.openfoam.com/2306/tools/processing/boundary-conditions/ (accessed on 15 October 2024).
- CALIFS-ISIS V6: Physical Modeling. Available online: https://gforge.irsn.fr/#/project/isis/docs/Tutorial (accessed on 15 November 2024).
- National Fire Protection Association. NFPA 921: Guide for Fire and Explosion Investigations, 2004 ed.; National Fire Protection Association: Quincy, MA, USA, 2004. [Google Scholar]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 1493925652. [Google Scholar]
- Reynolds, O. IV.On the Dynamical Theory of Incompressible Viscous Fluids and the Determination of the Criterion. Philos. Trans. R. Soc. Lond. A 1895, 186, 123–164. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Spalart, P.; Jou, W.-H.; Strelets, M.; Allmaras, S. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Louisiana Tech University, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Charles, G. Speziale A Combined Large-Eddy Simulation and Time-Dependent RANS Capability for High-Speed Compressible Flows. J. Sci. Comput. 1998, 13, 253–274. [Google Scholar]
- Han, X.; Krajnović, S. An Efficient Very Large Eddy Simulation Model for Simulation of Turbulent Flow. Int. J. Numer. Methods Fluids 2013, 71, 1341–1360. [Google Scholar] [CrossRef]
- Han, X.; Krajnović, S. Very-Large-Eddy Simulation Based on k-ω Model. AIAA J. 2015, 53, 1103–1108. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid. Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Hwang, C.-H.; Lock, A.; Bundy, M.; Johnsson, E.; Ko, G.H. Studies on Fire Characteristics in Over- and Underventilated Full-Scale Compartments. J. Fire Sci. 2010, 28, 459–486. [Google Scholar] [CrossRef]
- Chow, W.K.; Yin, R. A New Model on Simulating Smoke Transport with Computational Fluid Dynamics. Build. Environ. 2004, 39, 611–620. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Heidarinejad, G.; Pasdarshahri, H. Verification of Temperature and Toxic Species in Methane Compartment Fire Using Flamelet Generated Manifold with Radiation Effect. Int. J. Therm. Sci. 2022, 176, 107499. [Google Scholar] [CrossRef]
- Jowsey, A. Fire Imposed Heat Fluxes for Structural Analysis. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2006. Available online: https://era.ed.ac.uk/handle/1842/1480 (accessed on 1 January 2025).
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A Dynamic Subgrid-scale Eddy Viscosity Model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Moin, P.; Squires, K.; Cabot, W.; Lee, S. A Dynamic Subgrid-scale Model for Compressible Turbulence and Scalar Transport. Phys. Fluids A Fluid Dyn. 1991, 3, 2746–2757. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow. Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Vreman, A.W. An Eddy-Viscosity Subgrid-Scale Model for Turbulent Shear Flow: Algebraic Theory and Applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Deardorff, J.W. Stratocumulus-Capped Mixed Layers Derived from a Three-Dimensional Model. Bound. Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Deardorff, J.W. A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Numbers. J. Fluid. Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- OpenFOAM User Guide. Available online: https://www.openfoam.com/documentation/guides/latest/doc/guide-turbulence-les-k-eqn.html (accessed on 15 October 2024).
- McGrattan, K.; McDermott, R.; Weinschenk, C.; Forney, G. Fire Dynamics Simulator Users Guide, 6th ed.; Special Publication (NIST SP), National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; ISBN 3540264035. [Google Scholar]
- Kim, W.-W.; Menon, S. A New Dynamic One-Equation Subgrid-Scale Model for Large Eddy Simulations. In Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1995. [Google Scholar]
- Kim, T. Modeling of Wood Crib Fires Using a Detailed Pyrolysis Model. Therm. Sci. Eng. Prog. 2024, 47, 102339. [Google Scholar] [CrossRef]
- Yuan, S.; Zhang, J. Large Eddy Simulation of Compartment Fire with Solid Combustibles. Fire Saf. J. 2009, 44, 349–362. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, G.; Fukumoto, K.; Zhao, M.; Zhang, X.; Wang, C.; Li, C. Experimental and Numerical Simulation of Multi-Component Combustion of Typical No-Charring Material. Energy 2023, 262, 125555. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, C.; Lu, S. Modeling the Pyrolysis of Wet Wood Using FireFOAM. Energy Convers. Manag. 2015, 98, 500–506. [Google Scholar] [CrossRef]
- Markus, E.; Snegirev, A.; Kuznetsov, E.; Tanklevskiy, L. Application of the Thermal Pyrolysis Model to Predict Flame Spread over Continuous and Discrete Fire Load. Fire Saf. J. 2019, 108, 102825. [Google Scholar] [CrossRef]
- Hostikka, S.; Mcgrattan, K.; Hamins, A. Numerical Modeling of Pool Fires Using Les and Finite Volume Method for Radiation. Fire Saf. Sci. 2003, 7, 383–394. [Google Scholar] [CrossRef]
- Hong, M.C.; Merci, B.; Beji, T. On the Use of Natural and Forced Convection Correlations in Predictive CFD Simulations of Liquid Pool Fires. Fire Saf. J. 2023, 137, 103765. [Google Scholar] [CrossRef]
- Hong, M.-C.; Merci, B.; Beji, T. Numerical Simulations of Oscillatory Combustion and Extinction of a Liquid Pool Fire in a Reduced-Scale and Mechanically-Ventilated Enclosure. Fire Saf. J. 2023, 141, 104005. [Google Scholar] [CrossRef]
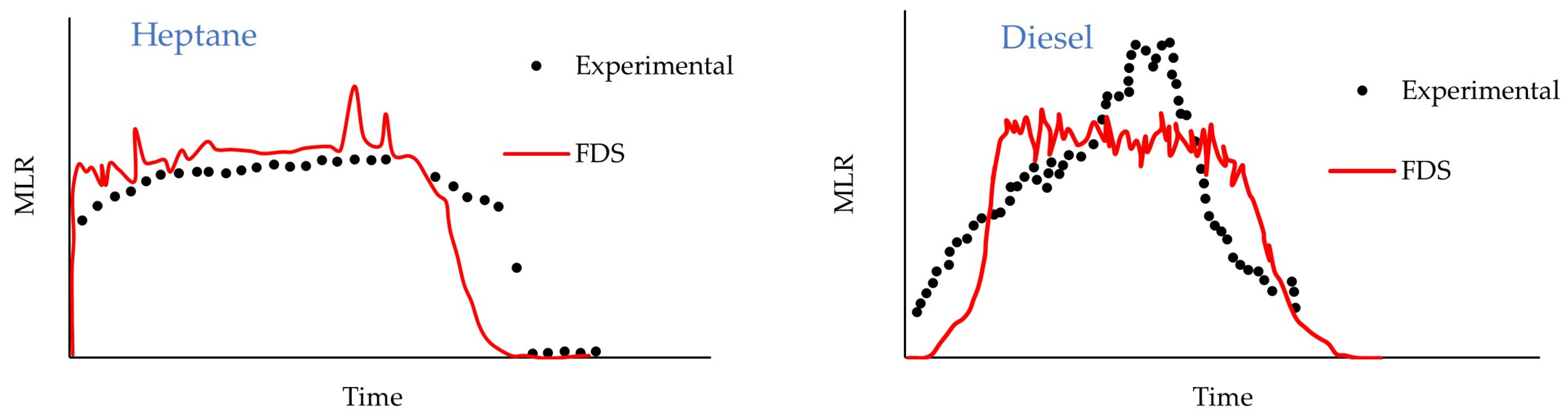
- Stewart, J.R.; Phylaktou, H.N.; Andrews, G.E.; Burns, A.D. Evaluation of CFD Simulations of Transient Pool Fire Burning Rates. J. Loss Prev. Process Ind. 2021, 71, 104495. [Google Scholar] [CrossRef]
- Kassem, H.I.; Saqr, K.M.; Aly, H.S.; Sies, M.M.; Wahid, M.A. Implementation of the Eddy Dissipation Model of Turbulent Non-Premixed Combustion in OpenFOAM. Int. Commun. Heat Mass Transf. 2011, 38, 363–367. [Google Scholar] [CrossRef]
- Huang, Y.-L.; Shiu, H.-R.; Chang, S.-H.; Wu, W.-F.; Chen, S.-L. Comparison of Combustion Models in Cleanroom Fire. J. Mech. 2008, 24, 267–275. [Google Scholar] [CrossRef]
- Spalding, D.B. Development of the Eddy-Break-up Model of Turbulent Combustion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1977; Volume 16, pp. 1657–1663. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H. On Mathematical Modeling of Turbulent Combustion with Special Emphasis on Soot Formation and Combustion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1977; Volume 16, pp. 719–729. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Chen, T.B.Y.; Chan, Q.N.; Wang, C.; Li, D.D. Comparison of Detailed Soot Formation Models for Sooty and Non-Sooty Flames in an under-Ventilated ISO Room. Int. J. Heat Mass Transf. 2017, 115, 717–729. [Google Scholar] [CrossRef]
- Van Oijen, J.A.; De Goey, L.P.H. Modelling of Premixed Laminar Flames using Flamelet-Generated Manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef]
- van Oijen, J.A.; Donini, A.; Bastiaans, R.J.M.; ten Thije Boonkkamp, J.H.M.; de Goey, L.P.H. State-of-the-Art in Premixed Combustion Modeling Using Flamelet Generated Manifolds. Prog. Energy Combust. Sci. 2016, 57, 30–74. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H.; Olsen, J.G.; Bhaduri, D. Effects of Turbulent Structure and Local Concentrations on Soot Formation and Combustion in C2H2 Diffusion Flames. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1979; Volume 17, pp. 1383–1393. [Google Scholar] [CrossRef]
- Pope, S.B. PDF Methods for Turbulent Reactive Flows. Prog. Energy Combust. Sci. 1985, 11, 119–192. [Google Scholar] [CrossRef]
- Petit, A.-T.; Dulong, P.-L. Recherches sur quelques points importants de la Théorie de la Chaleur. Ann. Chim. Phys. 1819, 10, 395–413. (In French) [Google Scholar]
- Goldin, G.M.; Menon, S. A Comparison of Scalar PDF Turbulent Combustion Models. Combust. Flame 1998, 113, 442–453. [Google Scholar] [CrossRef]
- Xue, H.; Ho, J.C.; Cheng, Y.M. Comparison of Different Combustion Models in Enclosure Fire Simulation. Fire Saf. J. 2001, 36, 37–54. [Google Scholar] [CrossRef]
- Maragkos, G.; Beji, T.; Merci, B. Advances in Modelling in CFD Simulations of Turbulent Gaseous Pool Fires. Combust. Flame 2017, 181, 22–38. [Google Scholar] [CrossRef]
- Heidarinejad, G.; PasdarShahri, H.; Safarzadeh, M. The Importance of the Compatible Combustion and Sub-Grid Scale Models on the Simulation of Large-Scale Pool Fire. Amirkabir J. Mech. Eng. 2019, 52, 2425–2442. [Google Scholar]
- Safarzadeh, M.; Heidarinejad, G.; Pasdarshahri, H. Simulation of Pool and Compartment Fire Using Flamelet Generated Manifold With/Without Radiation Coupling. Arab. J. Sci. Eng. 2021, 46, 7239–7248. [Google Scholar] [CrossRef]
- Razeghi, S.M.J.; Safarzadeh, M.; Pasdarshahri, H. Comparison of Combustion Models Based on Fast Chemistry Assumption in Large Eddy Simulation of Pool Fire. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 208. [Google Scholar] [CrossRef]
- At Thabari, J.; Maragkos, G.; Snegirev, A.; Merci, B. Numerical Study of the Impact of the EDC Formulation and Finite-Rate Chemistry Mechanisms in CFD Simulations of Fire Plumes. Fire Saf. J. 2023, 141, 103950. [Google Scholar] [CrossRef]
- Peters, N.; Rogg, B. Reduced Kinetic Mechanisms for Applications in Combustion Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 15, ISBN 3540475435. [Google Scholar]
- Yuen, A.C.Y.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.P.; Barber, T.J. Importance of Detailed Chemical Kinetics on Combustion and Soot Modelling of Ventilated and Under-Ventilated Fires in Compartment. Int. J. Heat Mass Transf. 2016, 96, 171–188. [Google Scholar] [CrossRef]
- Sikic, I.; Dembele, S.; Wen, J. Non-Grey Radiative Heat Transfer Modelling in LES-CFD Simulated Methanol Pool Fires. J. Quant. Spectrosc. Radiat. Transf. 2019, 234, 78–89. [Google Scholar] [CrossRef]
- Porter, R.; Liu, F.; Pourkashanian, M.; Williams, A.; Smith, D. Evaluation of Solution Methods for Radiative Heat Transfer in Gaseous Oxy-Fuel Combustion Environments. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2084–2094. [Google Scholar] [CrossRef]
- Beshir, M.; Wang, Y.; Centeno, F.; Hadden, R.; Welch, S.; Rush, D. Semi-Empirical Model for Estimating the Heat Release Rate Required for Flashover in Compartments with Thermally-Thin Boundaries and Ultra-Fast Fires. Fire Saf. J. 2021, 120, 103124. [Google Scholar] [CrossRef]
- Centeno, F.R.; Beshir, M.; Rush, D. Influence of Wind on the Onset of Flashover within Small-Scale Compartments with Thermally-Thin and Thermally-Thick Boundaries. Fire Saf. J. 2020, 117, 103211. [Google Scholar] [CrossRef]
- Wen, J.X.; Huang, L.Y.; Roberts, J. The Effect of Microscopic and Global Radiative Heat Exchange on the Field Predictions of Compartment Fires. Fire Saf. J. 2001, 36, 205–223. [Google Scholar] [CrossRef]
- Liu, Y.; Rogg, B. Prediction of Radiative Heat Transfer in Laminar Flames. Combust. Sci. Technol. 1996, 118, 127–145. [Google Scholar] [CrossRef]
- Lockwood, F.C.; Shah, N.G. A New Radiation Solution Method for Incorporation in General Combustion Prediction Procedures. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1981; Volume 18, pp. 1405–1414. [Google Scholar] [CrossRef]
- Zhang, J.; Dembele, S.; Wen, J. Effect of Radiation Models on Cfd Simulations of Upward Flame Spread. Fire Saf. Sci. 2005, 8, 421–432. [Google Scholar] [CrossRef]
- Krishnamoorthy, G. A Computationally Efficient P1 Radiation Model for Modern Combustion Systems Utilizing Pre-Conditioned Conjugate Gradient Methods. Appl. Therm. Eng. 2017, 119, 197–206. [Google Scholar] [CrossRef]
- OpenFOAM User Guide. Available online: https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1radiation_1_1noRadiation.html#details (accessed on 17 October 2024).
- Cheng, P. Two-Dimensional Radiating Gas Flow by a Moment Method. AIAA J. 1964, 2, 1662–1664. [Google Scholar] [CrossRef]
- Sazhin, S.S.; Sazhina, E.M.; Faltsi-Saravelou, O.; Wild, P. The P-1 Model for Thermal Radiation Transfer: Advantages and Limitations. Fuel 1996, 75, 289–294. [Google Scholar] [CrossRef]
- Fiveland, W.A. Discrete-Ordinates Solutions of the Radiative Transport Equation for Rectangular Enclosures. J. Heat Transf. 1984, 106, 699–706. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Trouvé, A. Large Eddy Simulation of the Unstable Flame Structure and Gas-to-Liquid Thermal Feedback in a Medium-Scale Methanol Pool Fire. Combust. Flame 2021, 225, 237–254. [Google Scholar] [CrossRef]
- Trivic, D.N. Modeling of 3-D Non-Gray Gases Radiation by Coupling the Finite Volume Method with Weighted Sum of Gray Gases Model. Int. J. Heat Mass Transf. 2004, 47, 1367–1382. [Google Scholar] [CrossRef]
- Chu, H.; Liu, F.; Zhou, H. Calculations of Gas Thermal Radiation Transfer in One-Dimensional Planar Enclosure Using LBL and SNB Models. Int. J. Heat Mass Transf. 2011, 54, 4736–4745. [Google Scholar] [CrossRef]
- Goody, R.M. A Statistical Model for Water-vapour Absorption. Q. J. R. Meteorol. Soc. 1952, 78, 165–169. [Google Scholar] [CrossRef]
- Smith, T.F.; Shen, Z.F.; Friedman, J.N. Evaluation of Coefficients for the Weighted Sum of Gray Gases Model. J. Heat Mass Transf. 1982, 104, 602–608. [Google Scholar] [CrossRef]
- Eckert, E.R.G. Radiative Transfer, H.C. Hottel and A. F. Sarofim, McGraw-Hill Book Company, New York, 1967. 52 Pages. AIChE J. 1969, 15, 794–796. [Google Scholar] [CrossRef]
- OpenFOAM User Guide. Available online: https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1radiation_1_1wideBandAbsorptionEmission.html (accessed on 17 October 2024).
- White, J.P.; Vilfayeau, S.; Marshall, A.W.; Trouvé, A.; McDermott, R.J. Modeling Flame Extinction and Reignition in Large Eddy Simulations with Fast Chemistry. Fire Saf. J. 2017, 90, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Vilfayeau, S.; Ren, N.; Wang, Y.; Trouvé, A. Numerical Simulation of Under-Ventilated Liquid-Fueled Compartment Fires with Flame Extinction and Thermally-Driven Fuel Evaporation. Proc. Combust. Inst. 2015, 35, 2563–2571. [Google Scholar] [CrossRef]
- Loo, A.S.-X.; Coppalle, A.; Aîné, P. Flame Extinction in a Ventilation-Controlled Compartment. Procedia Eng. 2013, 62, 301–308. [Google Scholar] [CrossRef]
- Beyler, C. A Brief History of the Prediction of Flame Extinction Based upon Flame Temperature. Fire Mater. 2005, 29, 425–427. [Google Scholar] [CrossRef]
- Quintiere, J.G.; Rangwala, A.S. A Theory for Flame Extinction Based on Flame Temperature. Fire Mater. 2004, 28, 387–402. [Google Scholar] [CrossRef]
- Beyler, C. Flammability Limits of Premixed and Diffusion Flames. In SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 529–553. [Google Scholar]
- Utiskul, Y.; Quintiere, J.G.; Rangwala, A.S.; Ringwelski, B.A.; Wakatsuki, K.; Naruse, T. Compartment Fire Phenomena under Limited Ventilation. Fire Saf. J. 2005, 40, 367–390. [Google Scholar] [CrossRef]
- Maragkos, G.; Snegirev, A.; At Thabari, J.; Merci, B. Flame Ignition and Extinction Modelling Using Infinitely Fast Chemistry in Large Eddy Simulations of Fire-Related Reacting Flows. Fire Saf. J. 2023, 141, 103952. [Google Scholar] [CrossRef]
- Ren, N.; Zeng, D.; Meredith, K.V.; Wang, Y.; Dorofeev, S.B. Modeling of Flame Extinction/Re-Ignition in Oxygen-Reduced Environments. Proc. Combust. Inst. 2019, 37, 3951–3958. [Google Scholar] [CrossRef]
- Hewson, J.C.; Kerstein, A.R. Local Extinction and Reignition in Nonpremixed Turbulent CO/H 2 /N 2 Jet Flames. Combust. Sci. Technol. 2002, 174, 35–66. [Google Scholar] [CrossRef]
- Fancello, A. Dynamic and Turbulent Premixed Combustion Using Flamelet Generated Manifold in OpenFOAM. Doctoral Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2014. Available online: https://pure.tue.nl/ws/portalfiles/portal/3869475/781467.pdf (accessed on 17 February 2025).
- Han, C.; Wang, H. A Comparison of Different Approaches to Integrate Flamelet Tables with Presumed-Shape PDF in Flamelet Models for Turbulent Flames. Combust. Theory Model. 2017, 21, 603–629. [Google Scholar] [CrossRef]
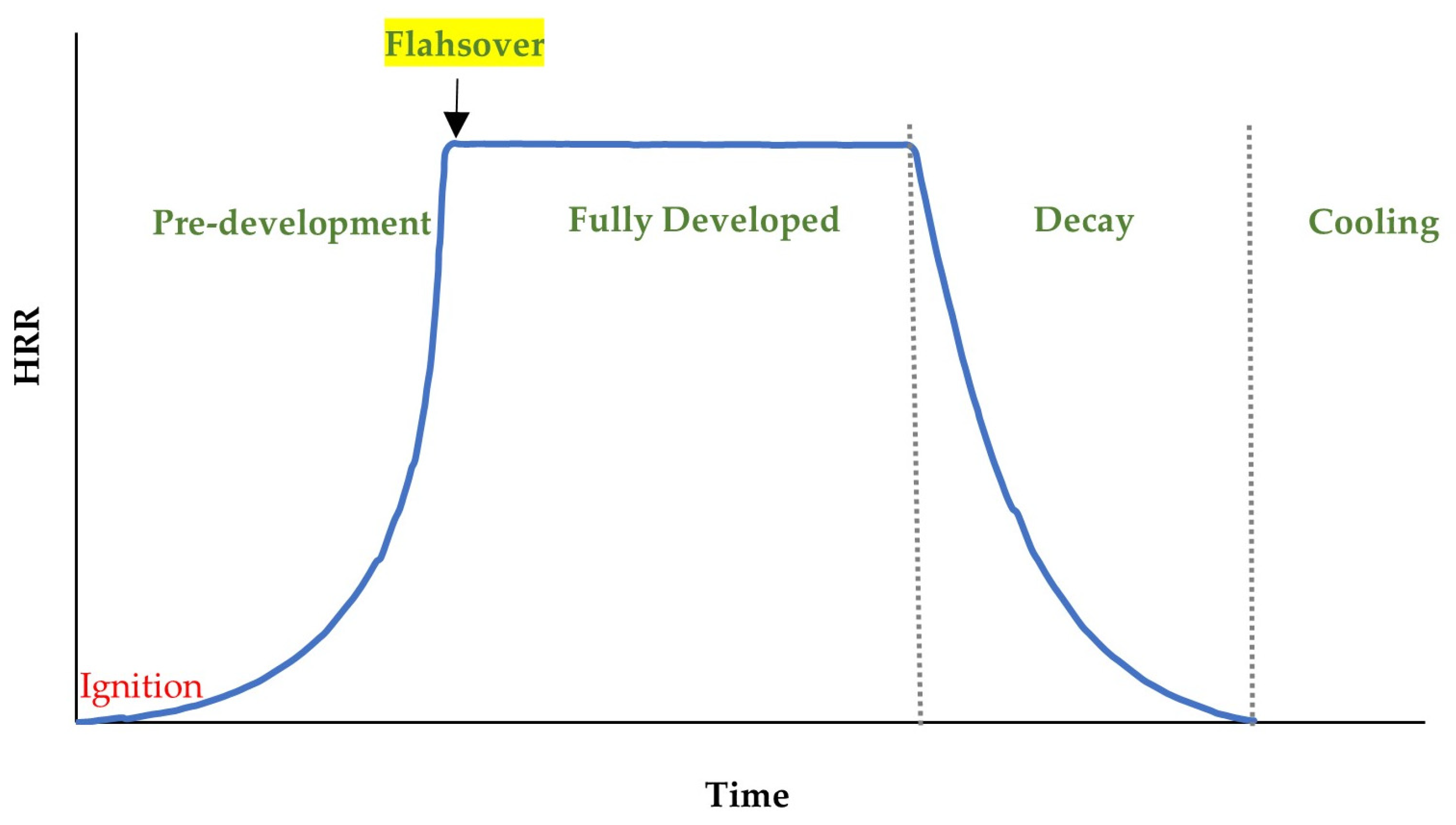

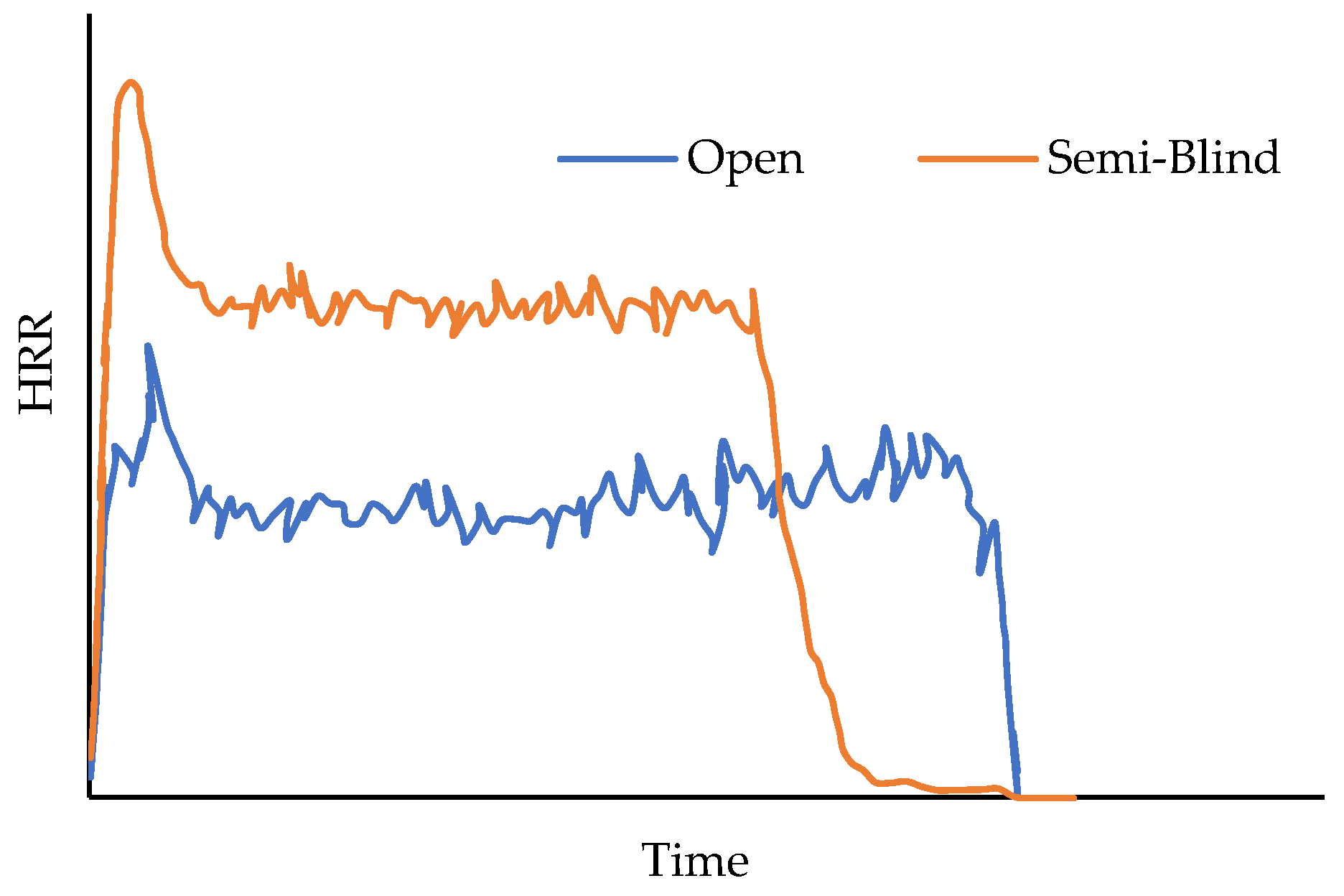
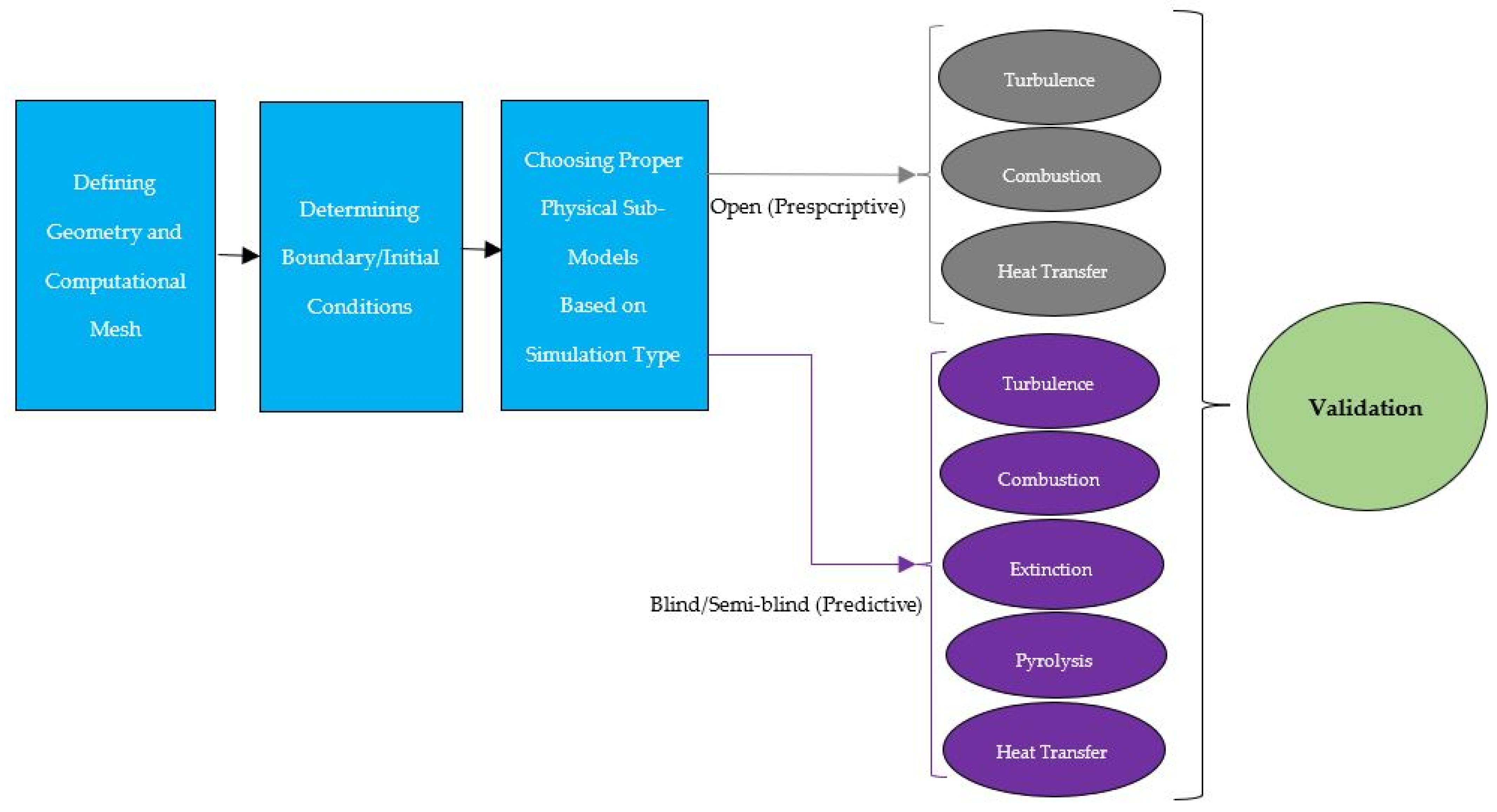
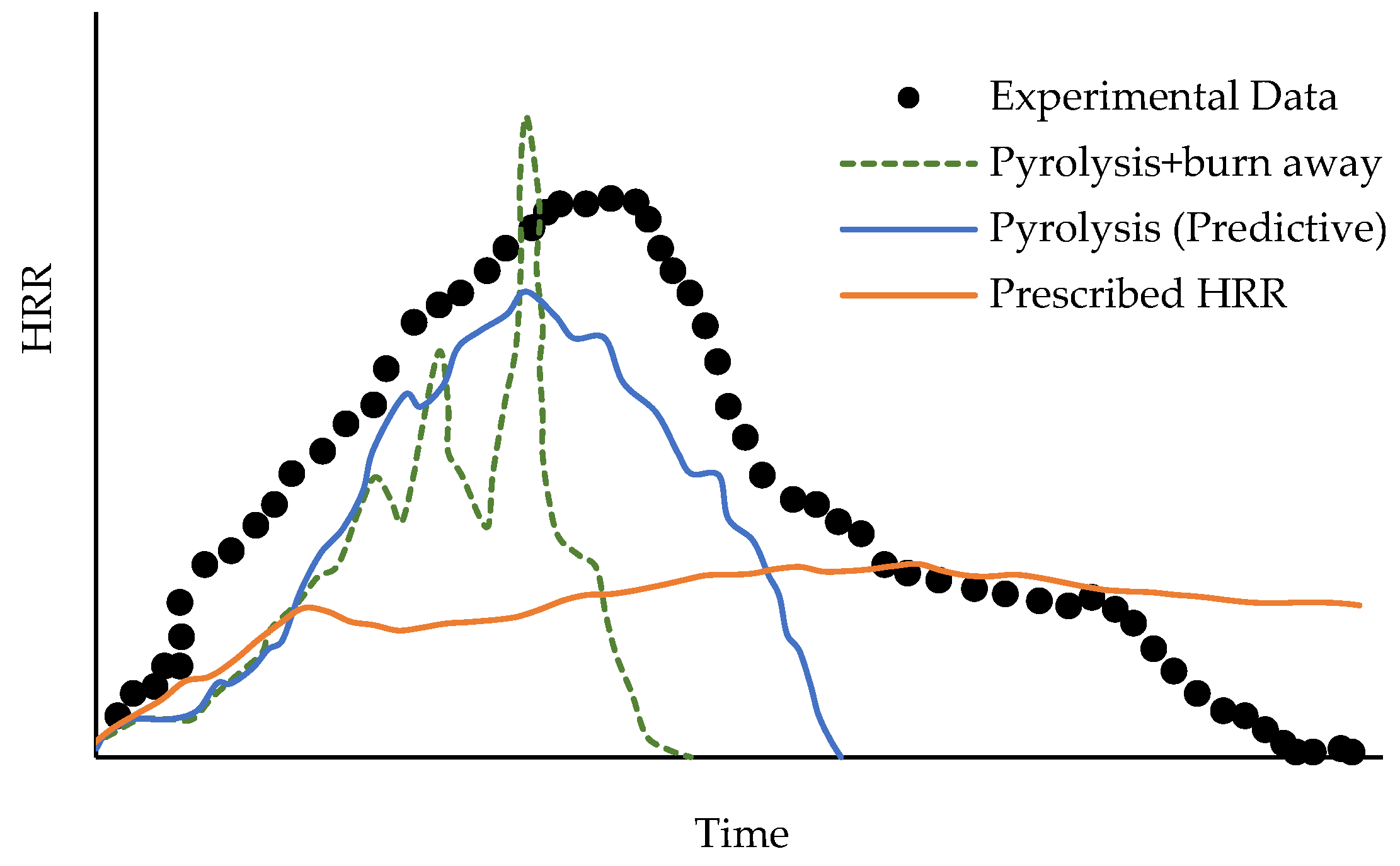
| Method | Turbulence Approach | Turbulence Modeling | Grid Resolution Requirement | Pros | Cons |
|---|---|---|---|---|---|
| RANS | Models all turbulent scales | Uses transport equations for turbulence | Relatively coarse grids | Low computational cost | Unable to capture unsteady/transient flow such as in compartment fires |
| LES | Resolves the large eddies, models sub-grid scales | Sub-grid scale models | Finer than RANS, coarser than DNS | Captures transient and large-scale turbulent structures accurately | Requires a fine grid near walls (such as for compartment fires): increases computational cost |
| DNS | Resolves all turbulent scales | No model needed | Extremely fine grids | Most reliable method | Very high computational cost and resources |
| DES | RANS near walls and LES away from walls | A combination of RANS models and LES sub-grid models | Coarser near the walls and finer in other regions | Balanced computational cost and accuracy between RANS and LES | Accuracy depends on grid resolution and transition between RANS and LES (determining switching criteria between RANS and LES) |
| VLES | Based on grid resolution, wide spectrum from RANS to DNS | Adapts with grid resolution, either modeled in coarse grids or resolved in fine grids | From course to very fine, depends on the application | Adaptive approach, flexible for different case | May require local refinement strategies (e.g., adaptive mesh refinement). |
| SGS Model | CFD Tool | Weakness |
|---|---|---|
| Constant Smagorinsky |
|
|
| Deardorff |
|
|
| Dynamic Smagorinsky |
|
|
| WALE |
|
|
| Vreman |
|
|
| K equation |
|
|
| Dynamic K equation |
|
|
| Model | CFD Tool | Pros | Cons |
|---|---|---|---|
| P1 |
| Computationally efficient Works well in optically thick media | Less accurate for non-homogeneous media Assumes isotropic radiation |
| DOM |
| Handles complex geometries More accurate than P1 in some cases | Computationally expensive Can introduce ray effects (false directional patterns) |
| DTRM |
| Handles complex geometries Accurate for optically thin media Works well with complex geometries | Computationally expensive Does not inherently include scattering effects |
| S2S |
| Efficient for surface-to-surface radiation | Does not account for gas-phase radiation and soot absorption or scattering |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parsa, V.; Santiago, A.; Laím, L. Computational Fluid Dynamics of Compartment Fires: A Review of Methods and Applications. Appl. Sci. 2025, 15, 2342. https://doi.org/10.3390/app15052342
Parsa V, Santiago A, Laím L. Computational Fluid Dynamics of Compartment Fires: A Review of Methods and Applications. Applied Sciences. 2025; 15(5):2342. https://doi.org/10.3390/app15052342
Chicago/Turabian StyleParsa, Vahid, Aldina Santiago, and Luís Laím. 2025. "Computational Fluid Dynamics of Compartment Fires: A Review of Methods and Applications" Applied Sciences 15, no. 5: 2342. https://doi.org/10.3390/app15052342
APA StyleParsa, V., Santiago, A., & Laím, L. (2025). Computational Fluid Dynamics of Compartment Fires: A Review of Methods and Applications. Applied Sciences, 15(5), 2342. https://doi.org/10.3390/app15052342








