Lattice Design of an Intermediate-Energy Electron Storage Ring Dedicated to Materials Research
Abstract
1. Introduction
2. Linear Optics Design
3. Nonlinear Optics Optimization
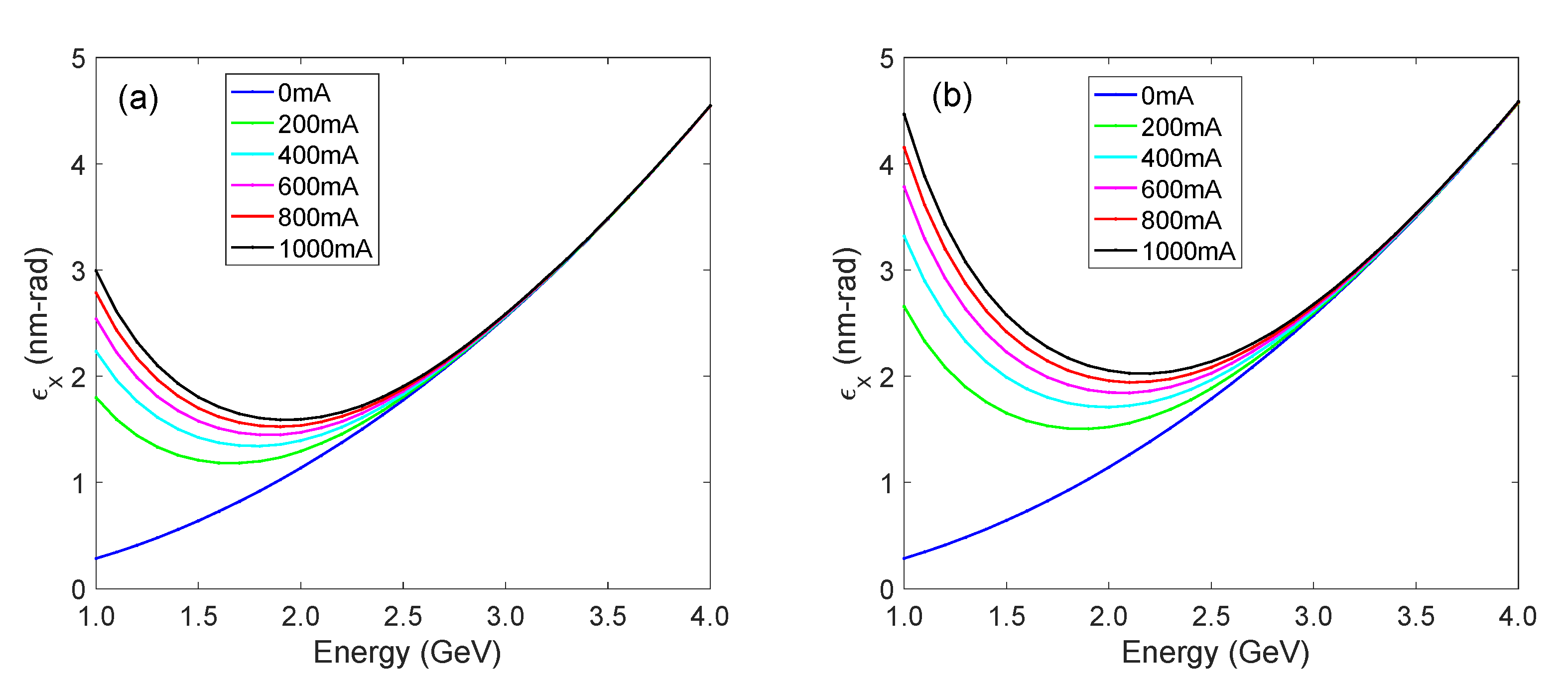
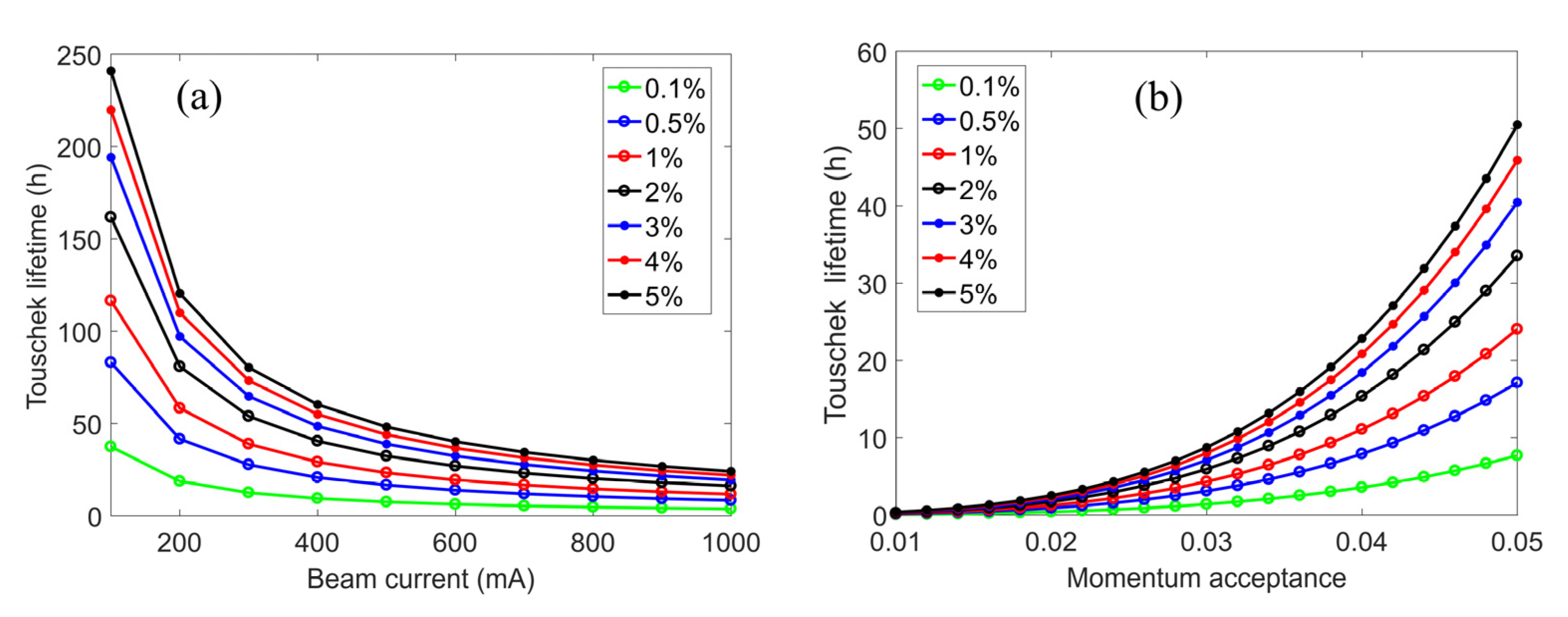
4. Intra-Beam Scattering (IBS) and Touschek Scattering
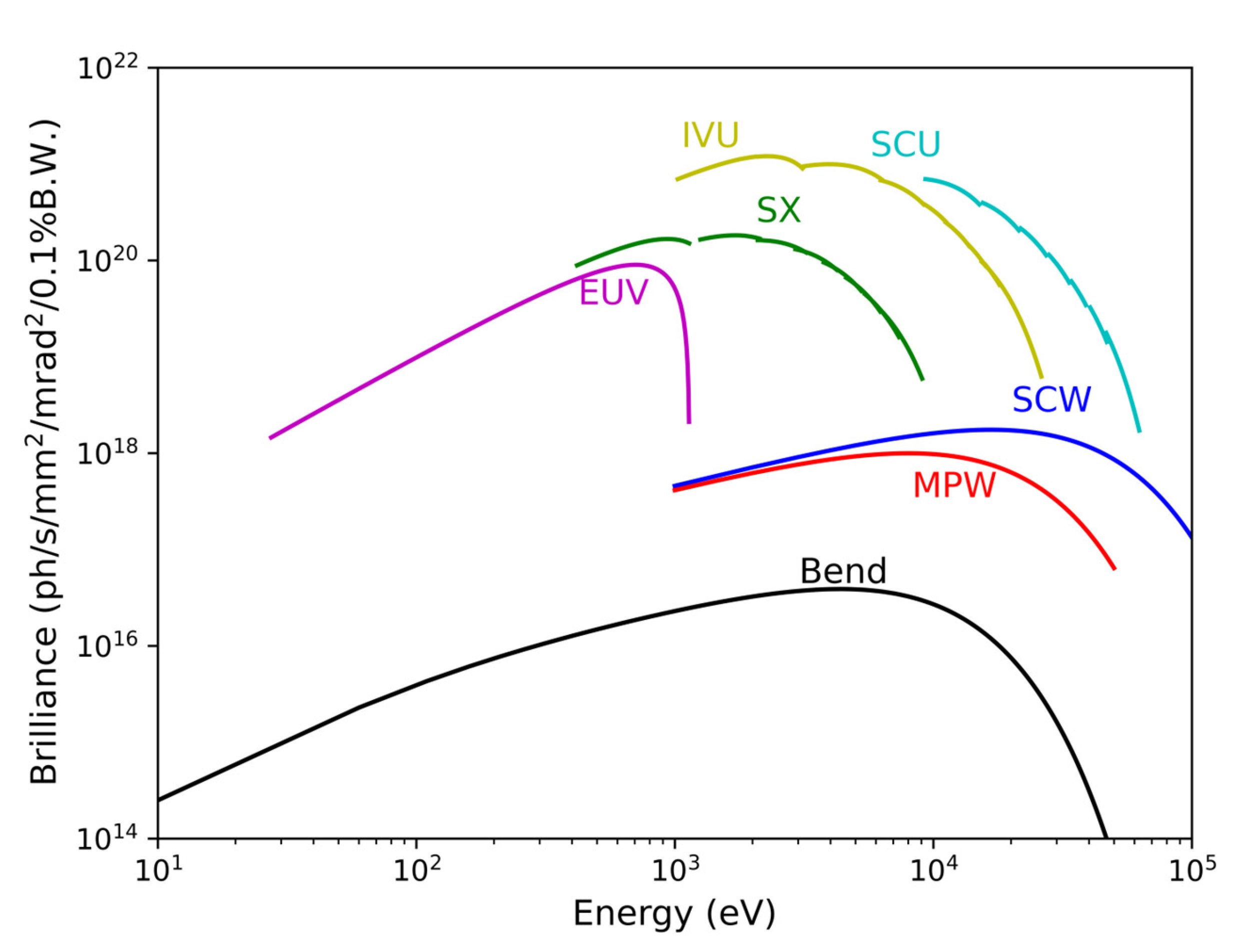
5. Photon Performance
6. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Z.T. Storage ring light sources. Rev. Accel. Sci. Technol. 2010, 03, 57. [Google Scholar] [CrossRef]
- Einfeld, D.; Plesko, M.; Schaper, J. First multi-bend achromat lattice consideration. Synchrotron Radiat. 2014, 21, 856–861. [Google Scholar] [CrossRef] [PubMed]
- Tavares, P.F.; Leemann, S.C.; Sjöström, M.; Andersson, Å. The MAX IV storage ring project. Synchrotron Radiat. 2014, 21, 862–877. [Google Scholar] [CrossRef] [PubMed]
- Tavares, P.F.; Dmour, E.A.; Andersson, Å.; Cullinan, F.; Jensen, B.N.; Olsson, D.K.; Sjöström, M.; Tarawneh, H.; Thorin, S.; Vorozhtsov, A. Commissioning and first-year operational results of the MAX IV 3 GeV ring. Synchrotron Radiat. 2018, 25, 1291–1316. [Google Scholar] [CrossRef]
- Liu, L.; Milas, N.; Mukai, A.H.; Resende, X.R.; de Sá, F.H. The Sirius project. Synchrotron Radiat. 2014, 21, 904–911. [Google Scholar] [CrossRef]
- Raimondi, P.; Benabderrahmane, C.; Berkvens, P.; Biasci, J.C.; Borowiec, P.; Bouteille, J.-F.; Brochard, T.; Brookes, N.B.; Carmignani, N.; Carver, L.R.; et al. The Extremely Brilliant Source storage ring of the European Synchrotron Radiation Facility. Commun. Phys. 2023, 6, 82. [Google Scholar] [CrossRef]
- Raimondi, P.; Carmignani, N.; Carver, L.R.; Chavanne, J.; Farvacque, L.; Le Bec, G.; Martin, D.; Liuzzo, S.M.; Perron, T.; White, S. Commissioning of the hybrid multibend achromat lattice at the European Synchrotron Radiation Facility. Phys. Rev. Accel. Beams 2021, 24, 110701. [Google Scholar] [CrossRef]
- Borland, M.; Berenc, T.; Sun, Y.; Sajaev, V. Lower emittance lattice for the Advanced Photon Source Upgrade using reverse bending magnets. In Proceedings of the NAPAC2016, Chicago, IL, USA, 9–14 October 2016; pp. 877–880. [Google Scholar]
- Jiao, Y.; Xu, G.; Cui, X.H.; Duan, Z.; Guo, Y.Y.; He, P.; Ji, D.H.; Li, J.Y.; Li, X.Y.; Meng, C.; et al. The HEPS project. Synchrotron Radiat. 2018, 25, 1611–1618. [Google Scholar] [CrossRef]
- Agapov, I.; Antipov, S.; Bartolini, R.; Brinkmann, R.; Chae, Y.C.; Einfeld, D.; Hellert, T.; Hüening, M.; Jebramcik, M.; Keil, J.; et al. Petra IV storage ring design. In Proceedings of the IPAC2022, Bangkok, Thailand, 12–17 June 2022; pp. 1431–1434. [Google Scholar]
- Tanaka, H. Current status of the SPring-8 upgrade project. Synchrotron Radiat. News 2014, 27, 23–26. [Google Scholar] [CrossRef]
- Jang, G.S.; Shin, S.; Yoon, M.; Ko, J.; Yoon, Y.D.; Lee, J.; Oh, B.-H. Low emittance lattice design for Korea-4GSR. Nucl. Instrum. Methods Phys. Res. A 2022, 1034, 166779. [Google Scholar] [CrossRef]
- Alekou, A.; Bartolini, R.; Bartolini, R.; Carmignani, N.; Walker, R.; Pulampong, T.; Liuzzo, S.M. Study of a double triple bend achromat (DTBA) lattice for a 3 GeV light source. In Proceedings of the IPAC2016, Busan, Republic of Korea, 8–13 May 2016; pp. 2940–2942. [Google Scholar]
- Zhao, Y.; Jiao, Y.; Li, Z.; Liu, W.; Wang, S. Improving the MWI threshold of the modified hybrid-7BA lattice design for SAPS. Nucl. Instrum. Methods Phys. Res. A 2023, 1056, 168565. [Google Scholar] [CrossRef]
- Kim, J.; Huang, X.; Raimondi, P.; Safranek, J.A.; Song, M.; Tian, K. A hybrid multi-bend achromat lattice design for SSRL-X. In Proceedings of the IPAC2022, Bangkok, Thailand, 12–17 June 2022; pp. 207–209. [Google Scholar]
- Loulergue, A.; Blanco-Garcia, O.R.; Blanco-García, O.; Gamelin, A.; Nadji, A.; Tordeux, M.A.; Brunelle, P.; Foosang, W.; Nadolski, L. TDR baseline lattice for SOLEIL II upgrade project. In Proceedings of the IPAC2023, Venice, Italy, 7–12 May 2023; pp. 689–691. [Google Scholar]
- Streun, A.; Aiba, M.; Böge, M.; Calzolaio, C.; Ehrlichman, M.; Negrazus, M.; Riemann, B.; Vrankovic, V. Swiss Light Source upgrade lattice design. Phys. Rev. Accel. Beams 2023, 26, 091601. [Google Scholar] [CrossRef]
- Karantzoulis, E.; Barletta, W. Aspects of the Elettra 2.0 design. Nucl. Instrum. Methods Phys. Res. A 2019, 927, 70. [Google Scholar] [CrossRef]
- Bai, Z.; Feng, G.; He, T.; Li, W.; Li, W.; Liu, G.; Wang, L.; Yang, P.; Zhang, S. Progress on the storage ring physics design of Hefei advanced light facility (HALF). In Proceedings of the IPAC2023, Venice, Italy, 7–12 May 2023; pp. 703–706. [Google Scholar]
- Hellert, T.; Steier, C.; Venturini, M. Lattice correction and commissioning simulation of the Advanced Light Source upgrade storage ring. Phys. Rev. Accel. Beams 2022, 25, 110701. [Google Scholar] [CrossRef]
- Farvacque, L.; Carmignani, N.; Chavanne, J.; Franchi, A.; Le Bec, G.; Liuzzo, S.; Nash, B.; Perron, T.; Raimondi, P. A low-emittance lattice for the ESRF. In Proceedings of the IPAC2013, Shanghai, China, 12–17 May 2013; pp. 79–81. [Google Scholar]
- Verdier, A. Resonance free lattices for A.G. machines. In Proceedings of the PAC1999, New York, NY, USA, 29 March–2 April 1999; pp. 398–400. [Google Scholar]
- Cai, Y.; Bane, K.; Hettel, R.; Nosochkov, Y.; Wang, M.-H.; Borland, M. Ultimate storage ring based on fourth-order geometric achromats. Phys. Rev. Accel. Beams 2012, 15, 054002. [Google Scholar] [CrossRef]
- Nishimori, N. A new compact 3GeV light source in Japan. In Proceedings of the IPAC2022, Bangkok, Thailand, 12–17 June 2022; pp. 2402–2406. [Google Scholar]
- Klysubun, P.; Sudmuang, P.; Pulampong, T.; Chanwattana, T.; Jummunt, S.; Sunwong, P.; Prawanta, S.; Kwankasem, A.; Juntong, N.; Phimsen, T. SPS-II: A 4th generation synchrotron light source in southeast Asia. In Proceedings of the IPAC2022, Bangkok, Thailand, 12–17 June 2022; pp. 764–768. [Google Scholar]
- Bartolini, R.; Abraham, C.; Apollonio, M.; Bailey, C.P.; Cox, M.P.; Day, A.; Fielder, R.T.; Hammond, N.P.; Heron, M.T.; Holdsworth, R.; et al. Double-double bend achromat cell upgrade at the Diamond Light Source: From design to commissioning. Phys. Rev. Accel. Beams 2018, 21, 050701. [Google Scholar] [CrossRef]
- Project Web Site. Available online: http://ados.web.psi.ch/opa/ (accessed on 20 December 2024).
- Borland, M. Elegant: A flexible SDDS-compliant code for accelerator simulation. In Proceedings of the 6th International Computational Accelerator Physics Conference, Darmstadt, Germany, 11–14 September 2000. Advanced Photon Source Report 2000, No. LS-287. [Google Scholar]
- Robin, D.; Steier, C. Global dynamics of the advanced light source revealed through experimental frequency map analysis. Phys. Rev. Lett. 2000, 85, 558. [Google Scholar] [CrossRef]
- Jiao, Y.; Duan, Z. Statistical analysis of the limitation of half integer resonances on the available momentum acceptance of the High Energy Photon Source. Nucl. Instrum. Methods Phys. Res. A 2017, 841, 97–103. [Google Scholar] [CrossRef][Green Version]
- Nagaokaa, R.; Baneb, K.L.F. Collective effects in a diffraction-limited storage ring. Synchrotron Radiat. 2014, 21, 937–960. [Google Scholar] [CrossRef]
- Piwinski, A. Intra-beam-scattering. In Proceedings of the 9th International Conference on High Energy Accelerators, Stanford, CA, USA, 2–7 May 1974; SLAC: Stanford, CA, USA, 1974; pp. 405–409. [Google Scholar]
- Bjorken, J.D.; Mtingwa, S.K. Intrabeam scattering. Part. Accel. 1983, 13, 115–143. [Google Scholar]
- Dowd, R.; Boland, M.; LeBlanc, G.; Tan, Y.-R.E. Achievement of ultralow emittance coupling in the Australian Synchrotron storage ring. Phys. Rev. Accel. Beams 2011, 14, 012804. [Google Scholar] [CrossRef]
- Tanaka, T.; Kitamura, H. SPECTRA: A synchrotron radiation calculation code. Synchrotron Radiat. 2001, 8, 1221–1228. [Google Scholar] [CrossRef] [PubMed]



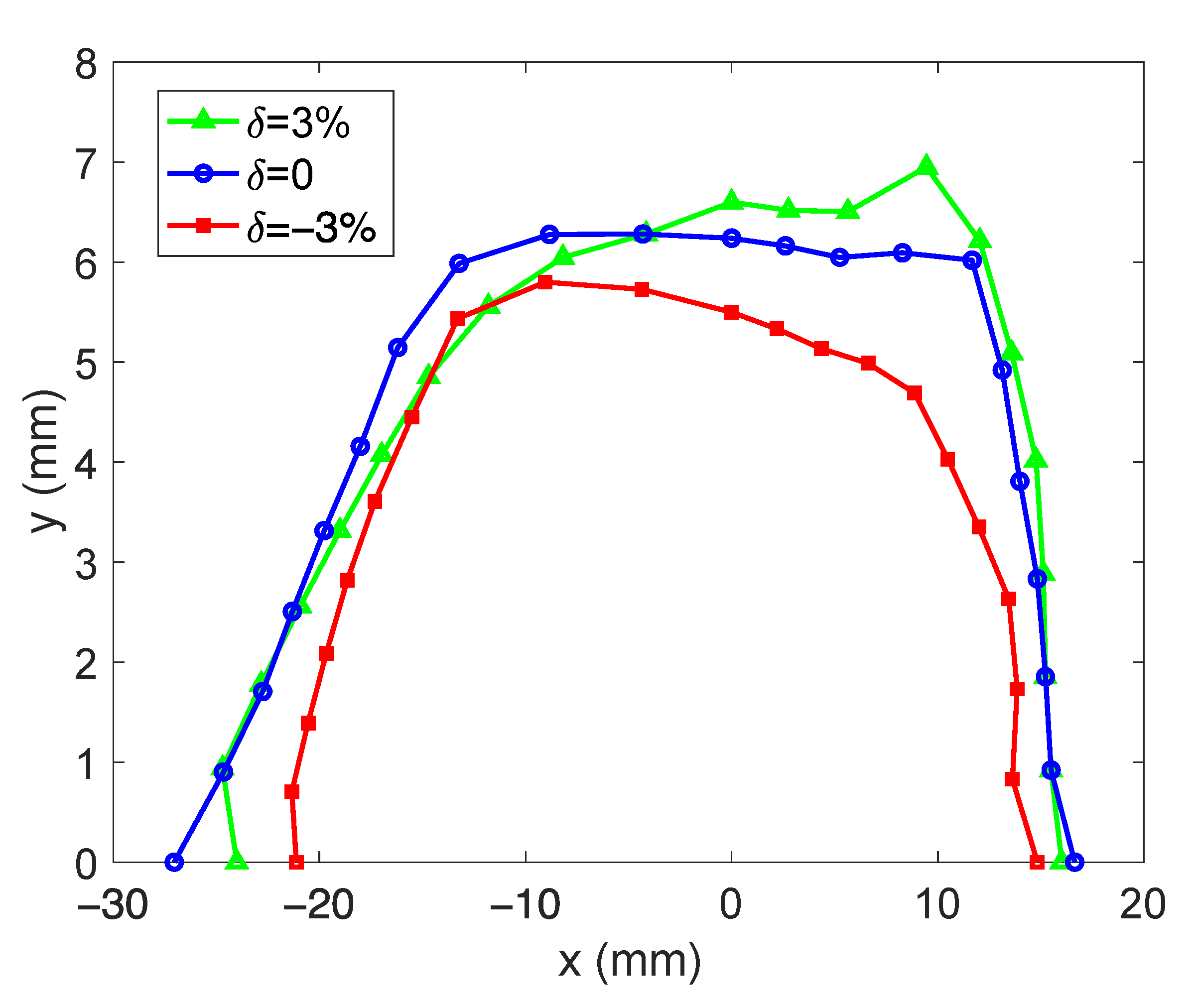
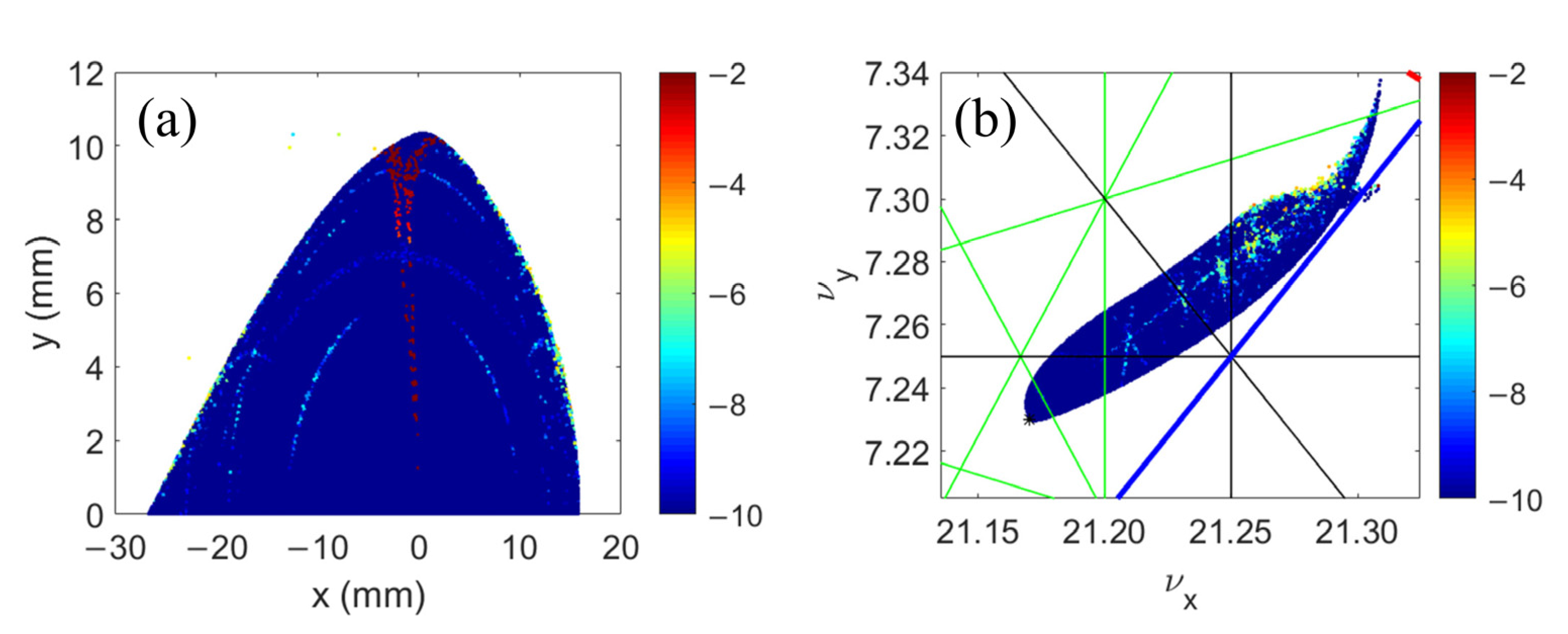

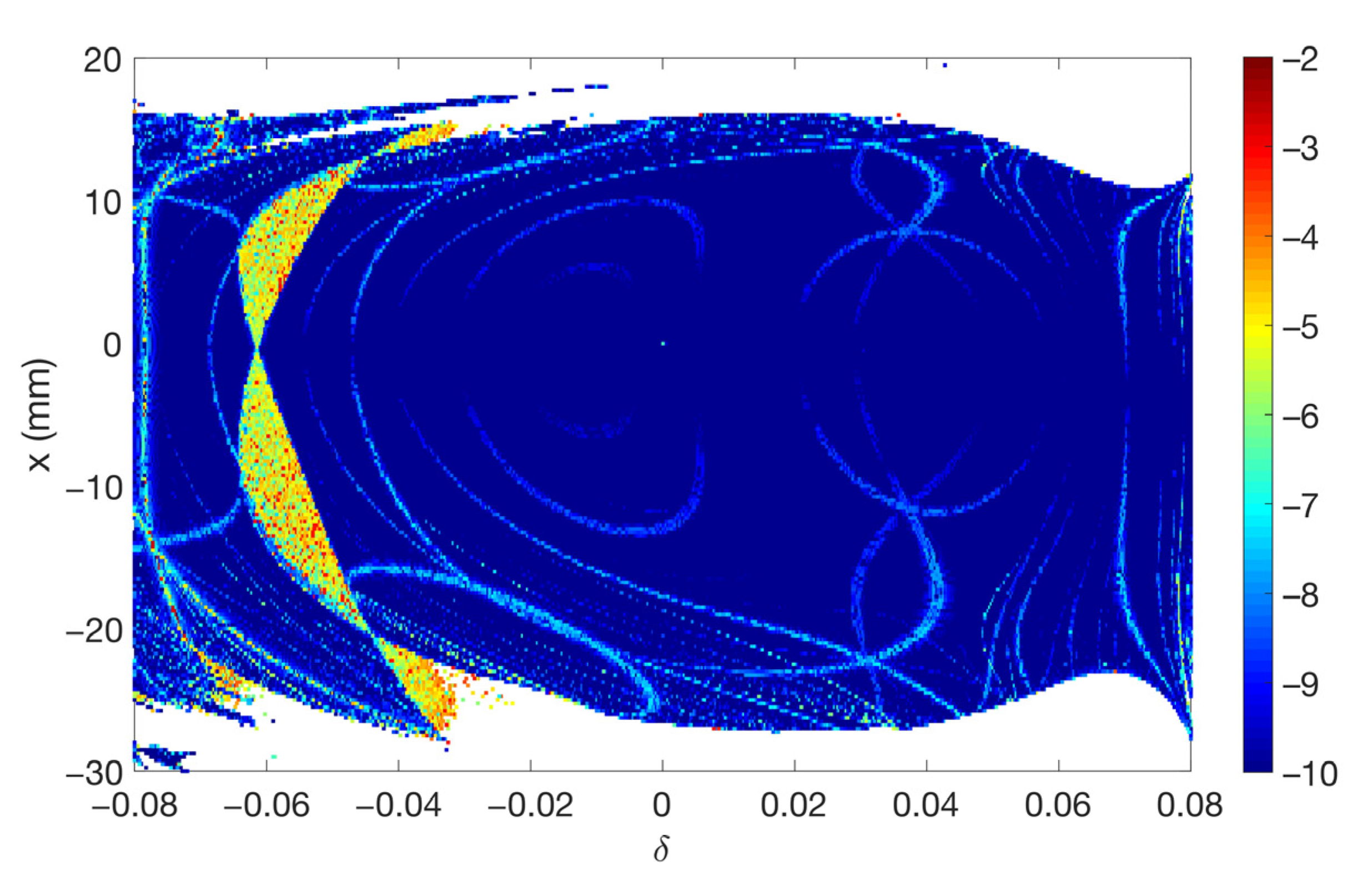
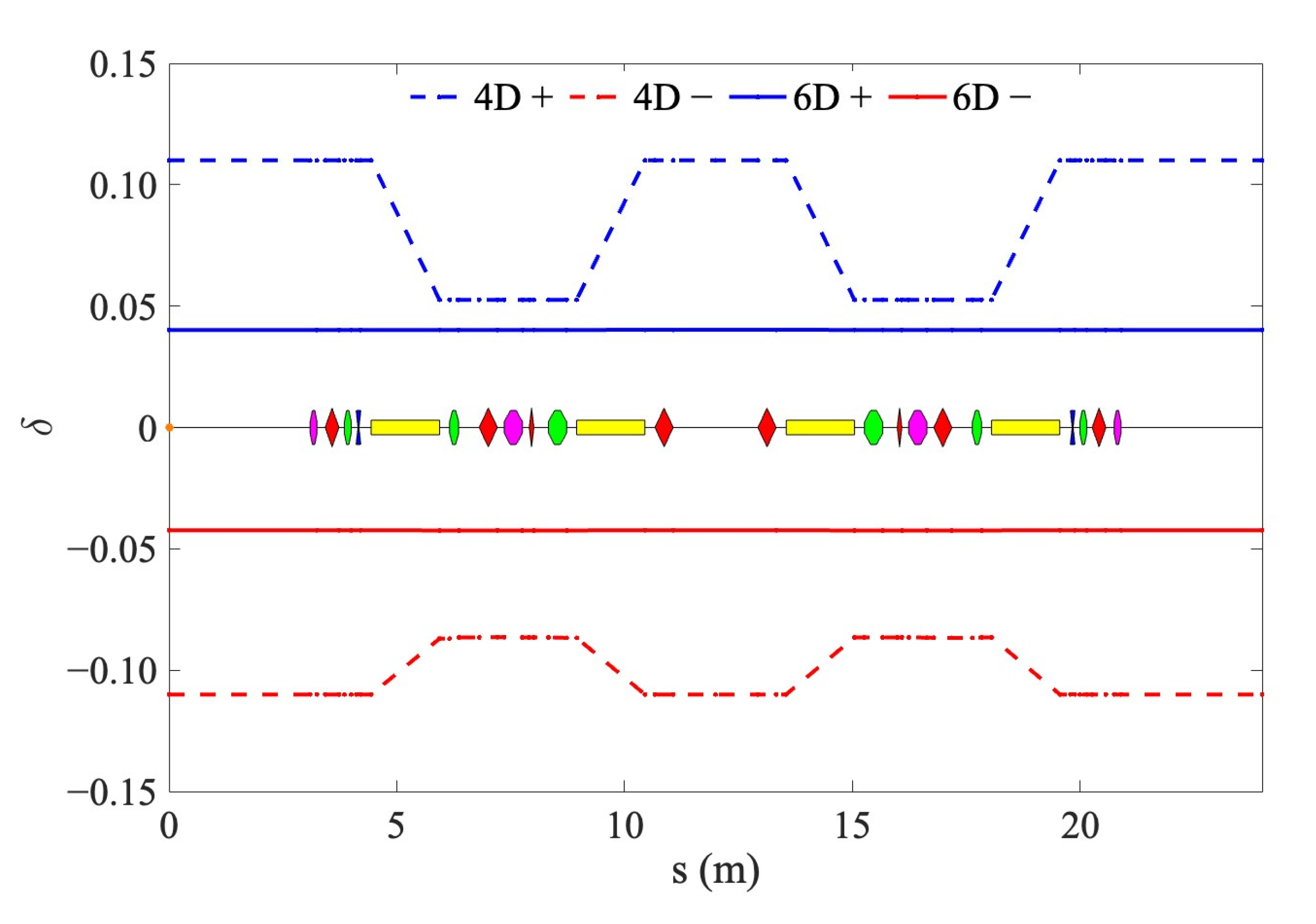
| Parameter | Value |
|---|---|
| Beam energy | 3 GeV |
| Circumference | 288 m |
| Lattice type | 12 × DBA |
| Tunes | 21.17, 7.23 |
| Horizontal emittance | 2.57 nm rad |
| Energy spread | 8.64 × 10−4 |
| Natural chromaticity | −51.60, −30.45 |
| Corrected chromaticity | 1.0, 1.0 |
| Momentum compaction factor | 8.23 × 10−4 |
| Energy loss per turn | 0.625 MeV |
| Damping partition numbers | 1.46, 1, 1.54 |
| Damping time | 6.33 ms, 9.22 ms, 5.97 ms |
| Long straight section | 12 × 6.20 m |
| Short straight section | 12 × 1.86 m |
| Twiss at LSS (betax, betay, etax) | 18.0 m, 3.20 m, 0 m |
| Twiss at SSS (betax, betay, etax) | 3.41 m, 2.85 m, 0.065 m |
| RF frequency | 499.654 MHz |
| Harmonic number | 480 |
| RF voltage | 4.0 MV |
| RF bucket height | 4.06% |
| RMS bunch length | 3.58 mm |
| Magnet | Name | Length | Strength | Bore Diameters |
|---|---|---|---|---|
| Combined dipoles | B | 1.50 m | 0.87 T, −5.27 T/m | - |
| Quadrupoles | Q1 | 0.30 m | 22.37 T/m | 50 mm |
| Q2 | 0.10 m | −7.37 T/m | 50 mm | |
| Q3 | 0.40 m | 24.33 T/m | 50 mm | |
| Q4 | 0.10 m | 7.37 T/m | 50 mm | |
| Q5 | 0.40 m | 22.12 T/m | 50 mm | |
| Sextupoles | S1 | 0.15 m | 687.58 T/m2 | 56 mm |
| S2 | 0.15 m | −824.57 T/m2 | 56 mm | |
| SD1 | 0.20 m | −368.87 T/m2 | 56 mm | |
| SF | 0.40 m | 430.02 T/m2 | 56 mm | |
| SD2 | 0.40 m | −483.10 T/m2 | 56 mm |
| ID Type | Period (mm) | Number Periods | Max B(T) |
|---|---|---|---|
| IVU | 22 | 190 | 1.15 |
| MPW | 100 | 13 | 1.6 |
| Apple-II (EUV) | 75 | 53 | 1.08 |
| Apple-II (SX *) | 56 | 71 | 0.44 |
| SC wiggler | 48 | 22 | 4.2 |
| SC undulator | 10 | 116 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Chen, J.; Wu, H.; Zhang, Q.; Wang, K. Lattice Design of an Intermediate-Energy Electron Storage Ring Dedicated to Materials Research. Appl. Sci. 2025, 15, 2541. https://doi.org/10.3390/app15052541
Li C, Chen J, Wu H, Zhang Q, Wang K. Lattice Design of an Intermediate-Energy Electron Storage Ring Dedicated to Materials Research. Applied Sciences. 2025; 15(5):2541. https://doi.org/10.3390/app15052541
Chicago/Turabian StyleLi, Changliang, Jianhui Chen, Hailong Wu, Qinglei Zhang, and Kun Wang. 2025. "Lattice Design of an Intermediate-Energy Electron Storage Ring Dedicated to Materials Research" Applied Sciences 15, no. 5: 2541. https://doi.org/10.3390/app15052541
APA StyleLi, C., Chen, J., Wu, H., Zhang, Q., & Wang, K. (2025). Lattice Design of an Intermediate-Energy Electron Storage Ring Dedicated to Materials Research. Applied Sciences, 15(5), 2541. https://doi.org/10.3390/app15052541







