Evaluating the Resilience of Mountainous Sparse Road Networks in High-Risk Geological Disaster Areas: A Case Study in Tibet, China
Abstract
:Featured Application
Abstract
1. Introduction
- Proposing a two-layer topological modeling approach suitable for road networks in regions prone to frequent geological and meteorological disasters.
- Developing a dynamic resilience evaluation method for sparse road networks under high-frequency cumulative disaster events.
2. Related Research
2.1. Network Topology Construction
2.2. Transportation Network Resilience Assessment
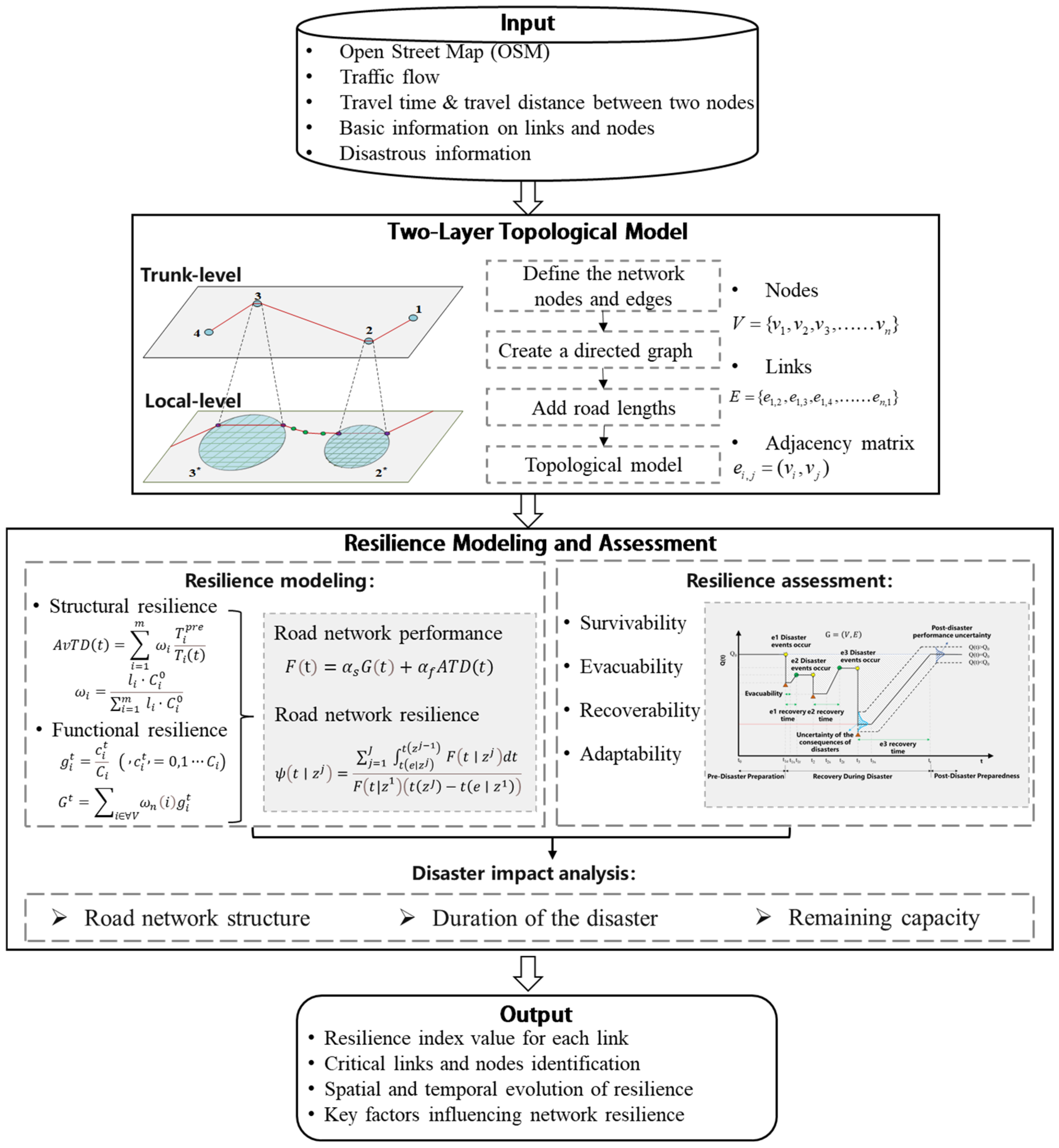
3. Methodology
3.1. Two-Layer Topological Model for Sparse Road Networks
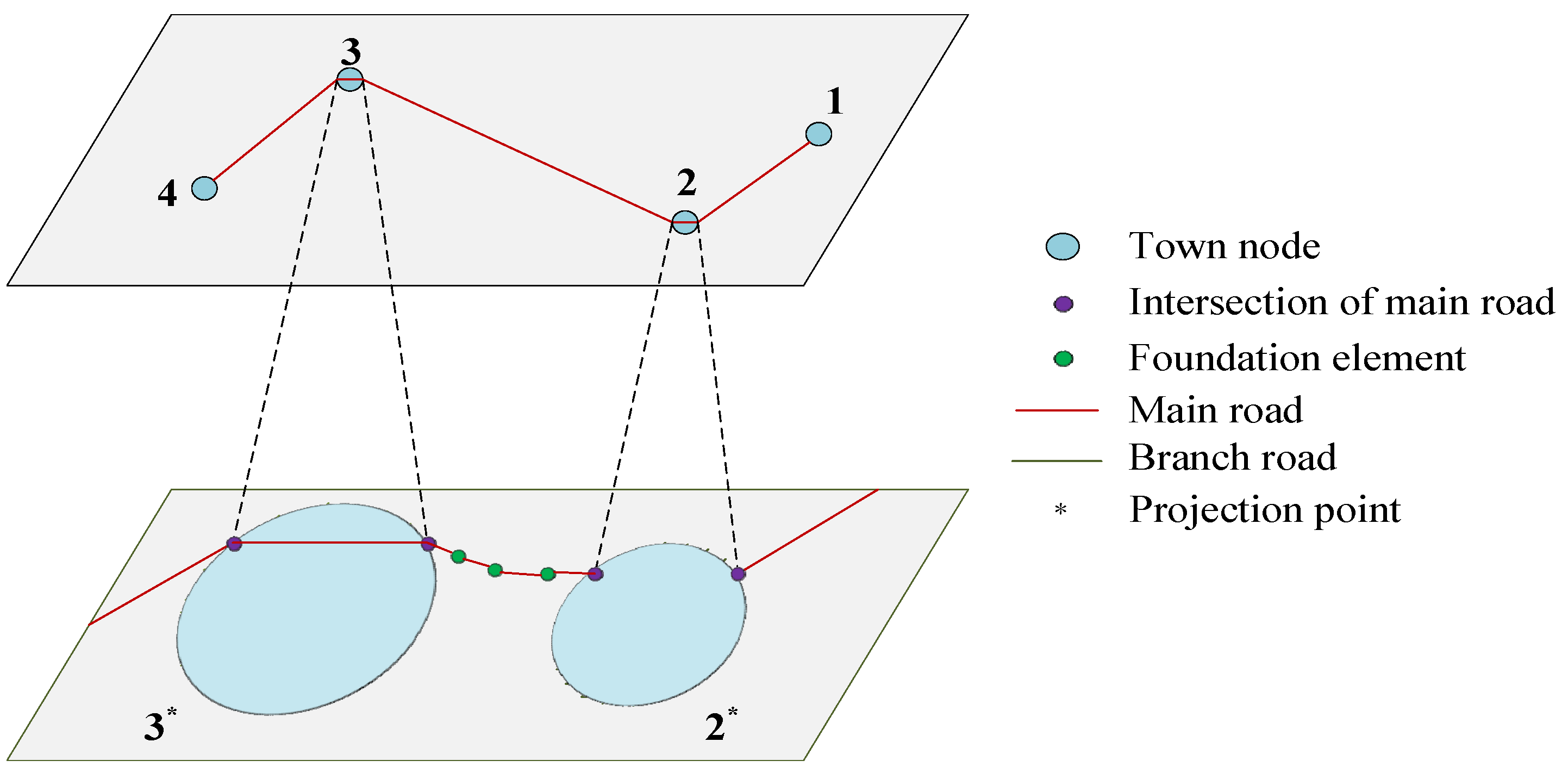
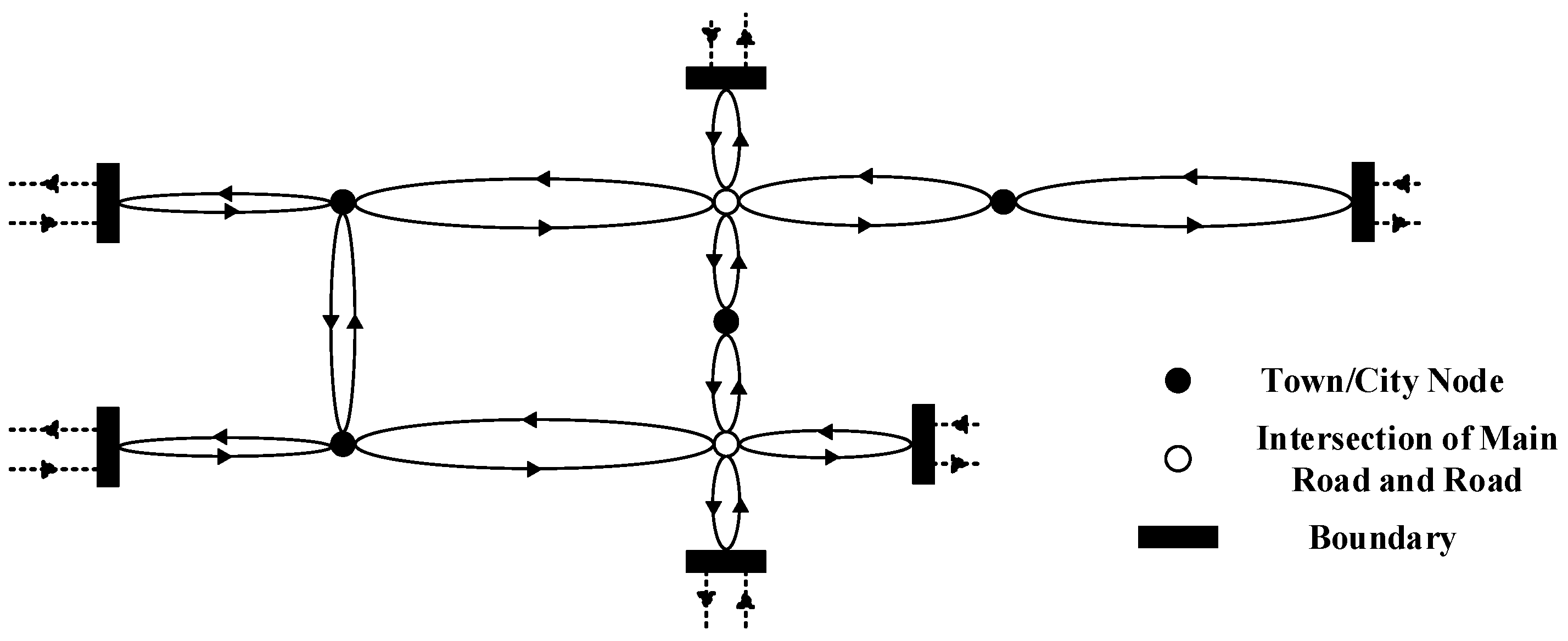
3.1.1. Trunk-Level Road Network Topology
- Delete urban roads within the target area, retaining highways, national roads, and provincial roads;
- Remove internal road nodes and merge multiple connected roads without branches into a single structure;
- Eliminate auxiliary roads that are short and do not affect the overall connectivity of the main road network;
- Merge internal road nodes of cities (municipalities), counties (districts), and towns within the target area into a single node.
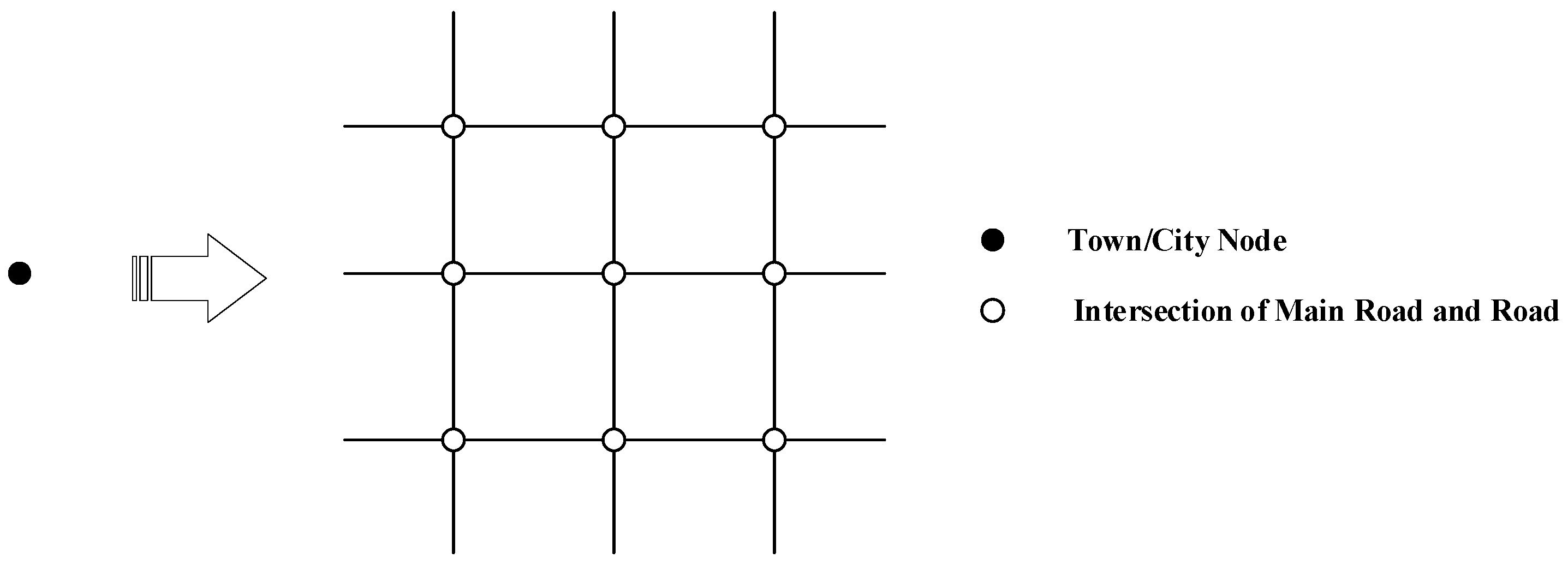
3.1.2. Local-Level Road Network Topology
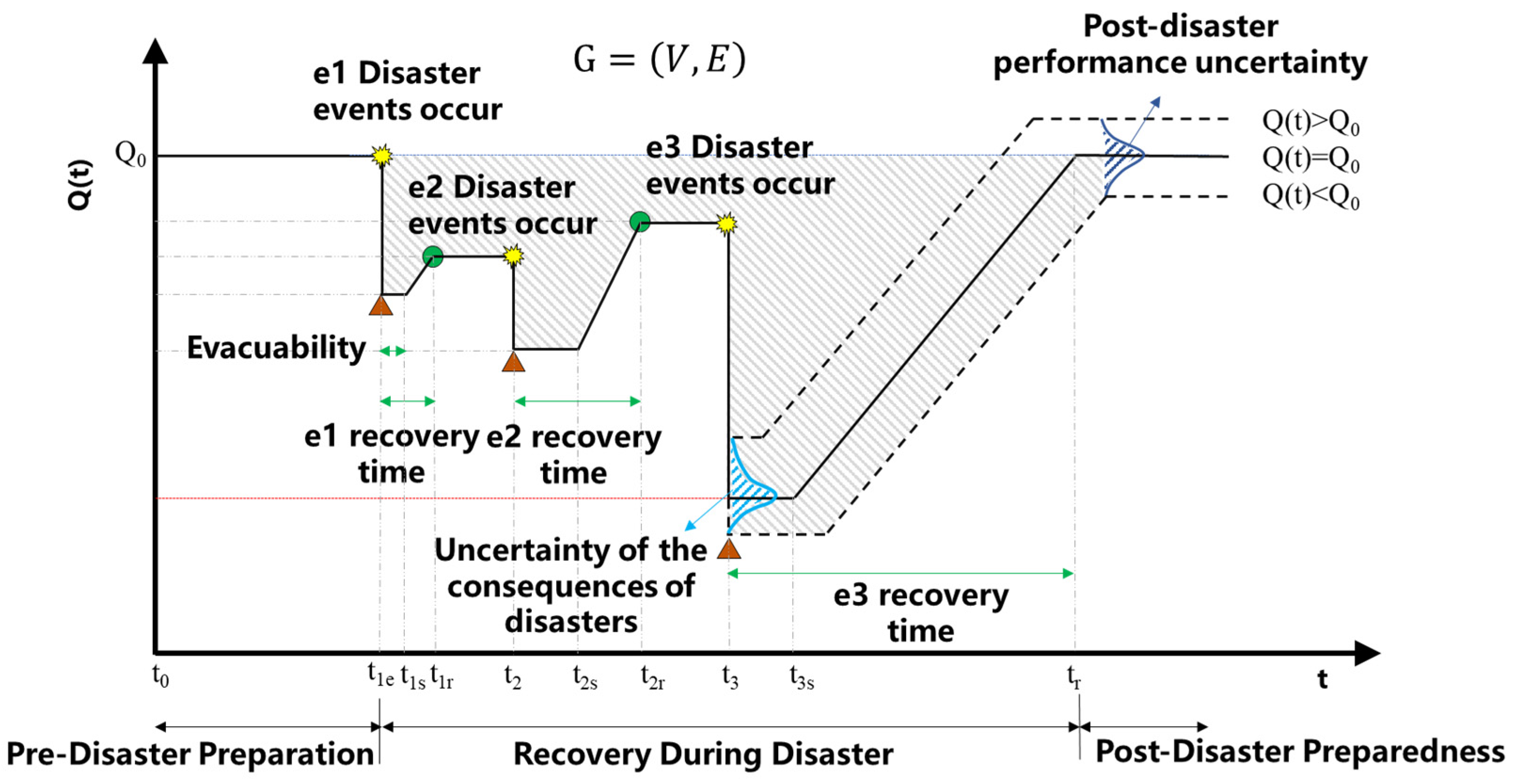
3.2. Connotation of Resilience of Sparse Road Networks
3.3. Quantifying the Resilience of Sparse Road Networks
3.3.1. Average Travel Delay
3.3.2. Network Accessibility
3.4. Quantifying the Performance of Sparse Road Networks
3.5. Resilience Assessment of Sparse Road Networks
3.5.1. Survivability
3.5.2. Evacuability
3.5.3. Recoverability
3.5.4. Adaptability
3.6. Repair Time Estimation Model
4. Case Study
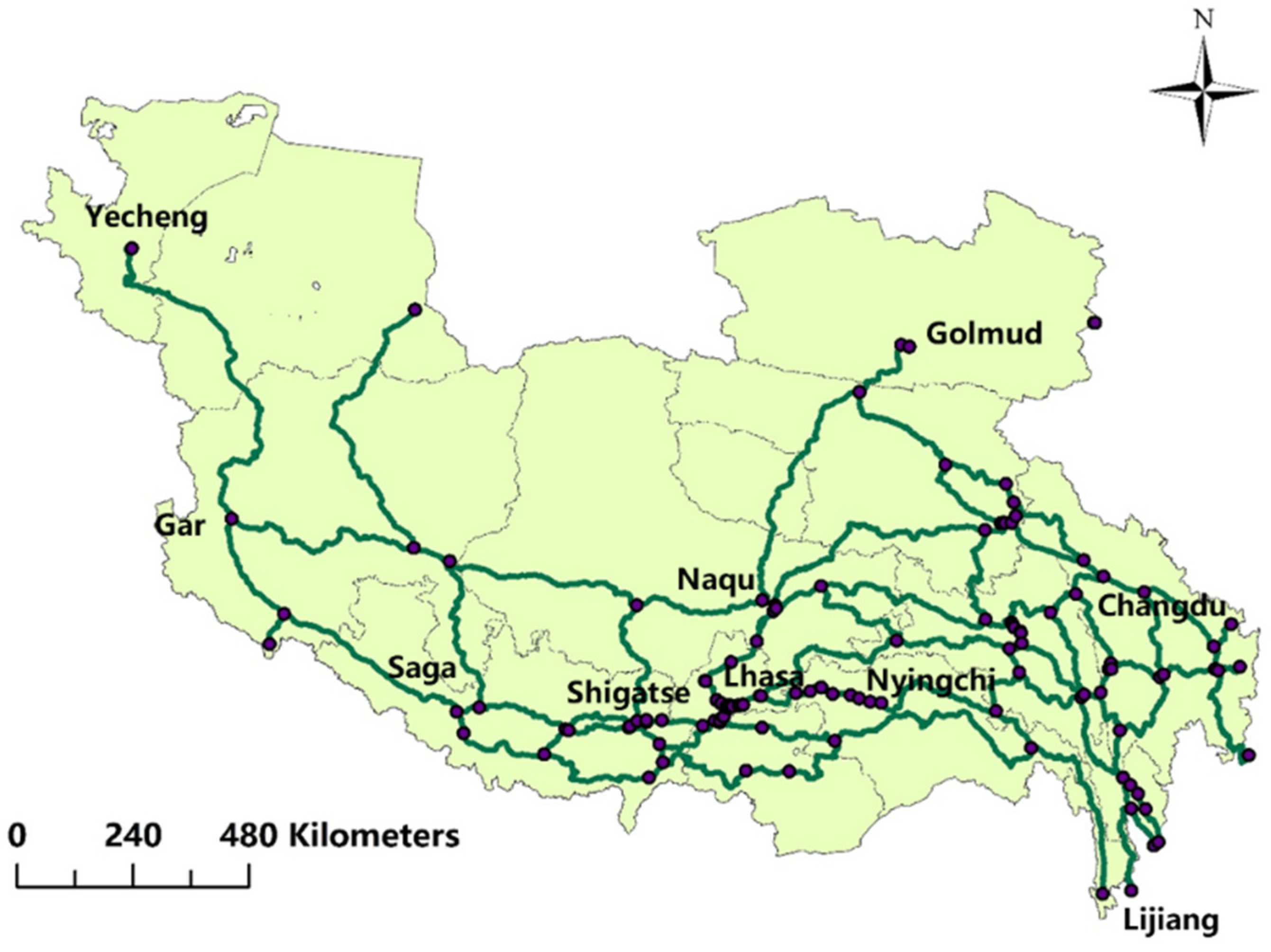
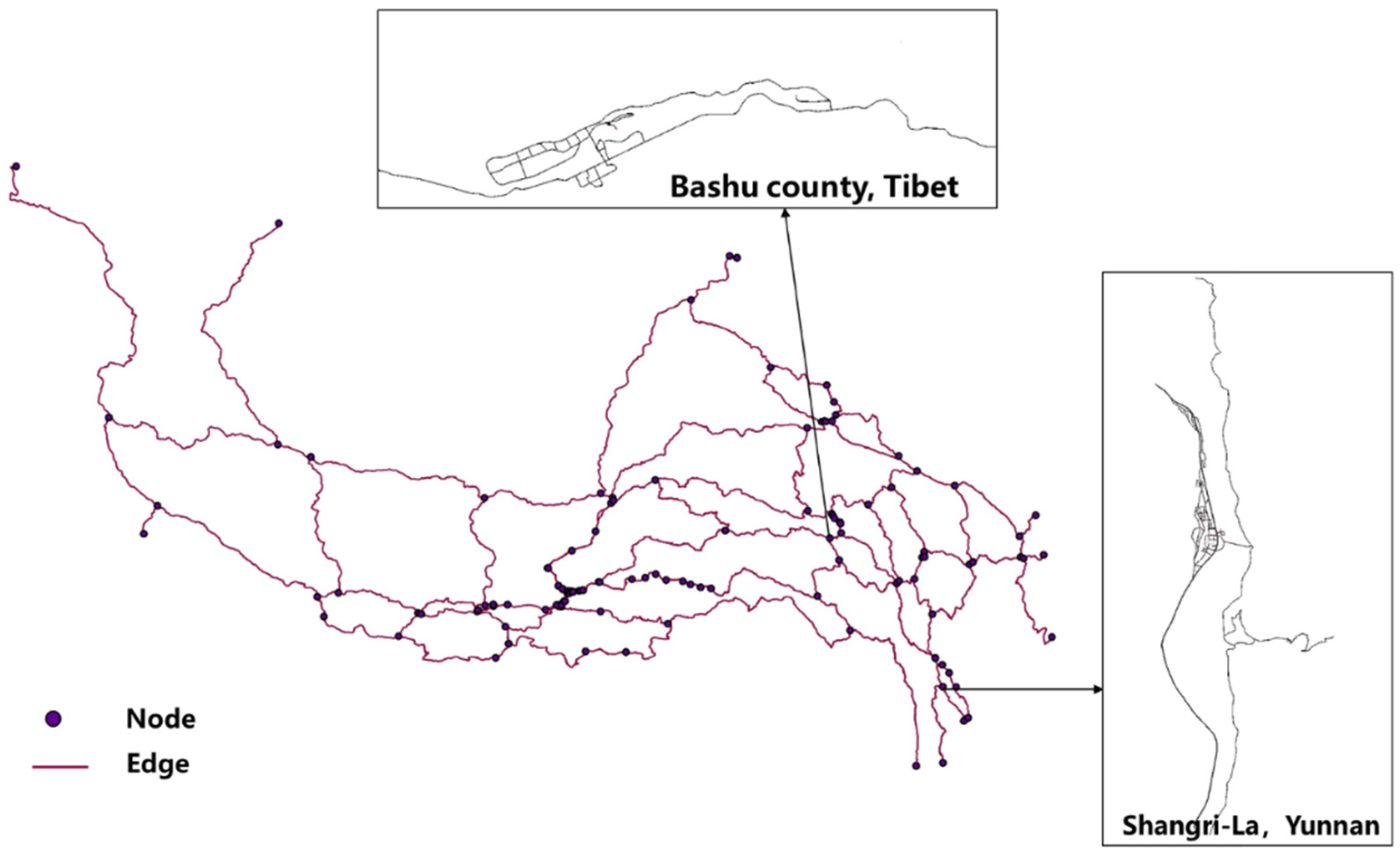
4.1. Study Area
4.2. Data Preparation
4.2.1. Road Network Topology Data
4.2.2. Traffic Flow Data
4.2.3. Travel Time Data
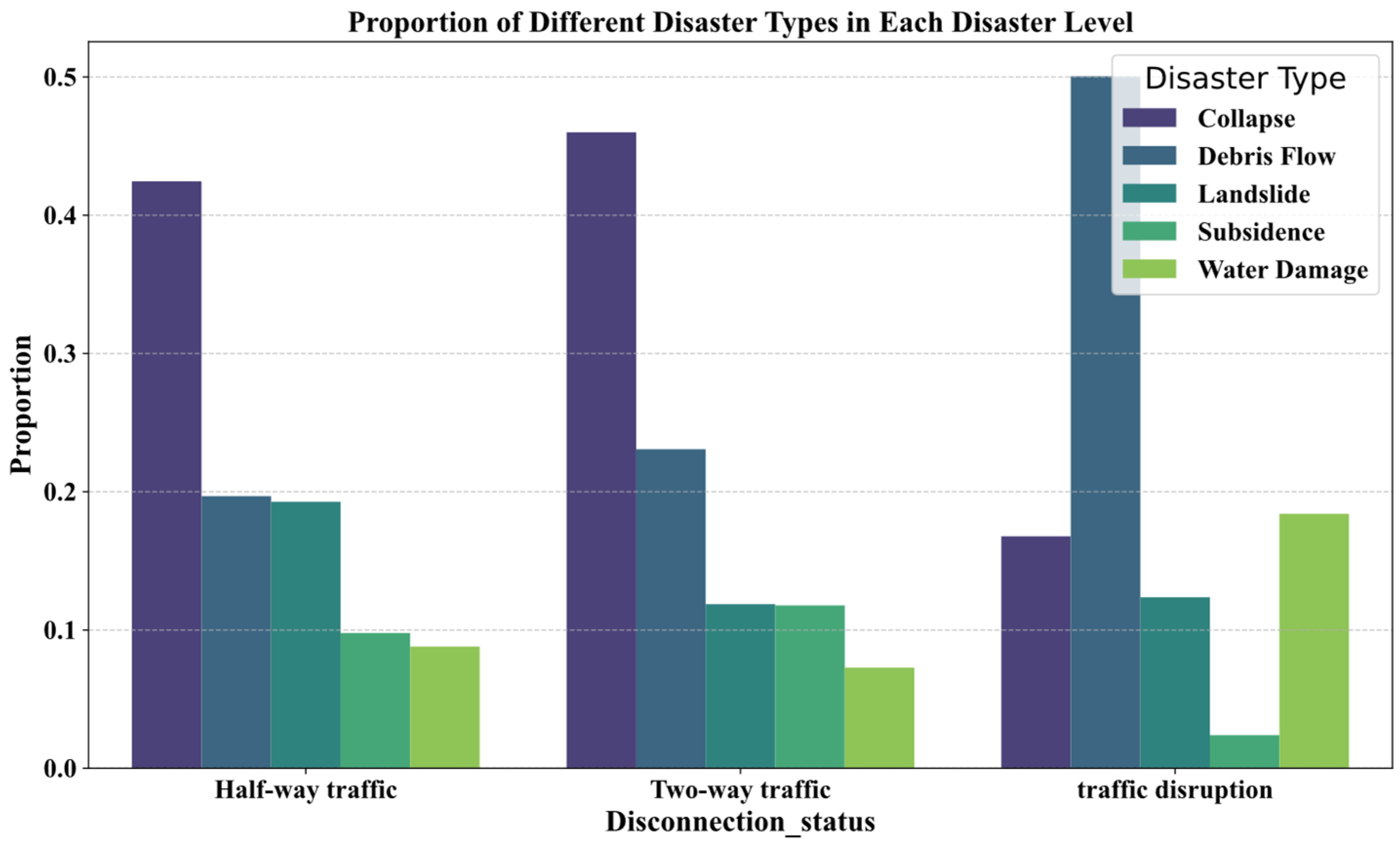
4.2.4. Disaster Event Data
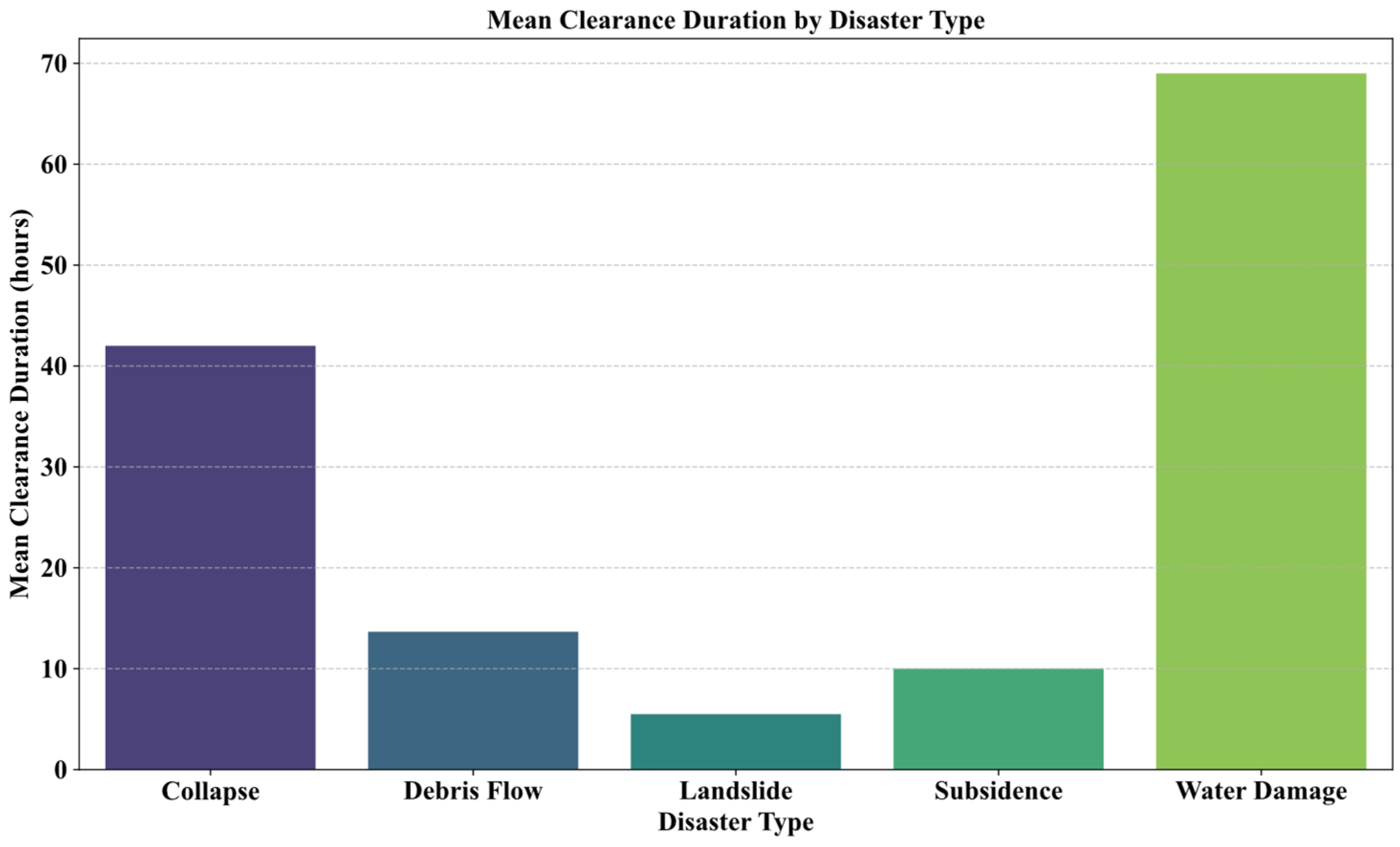
4.2.5. Repair Time Data
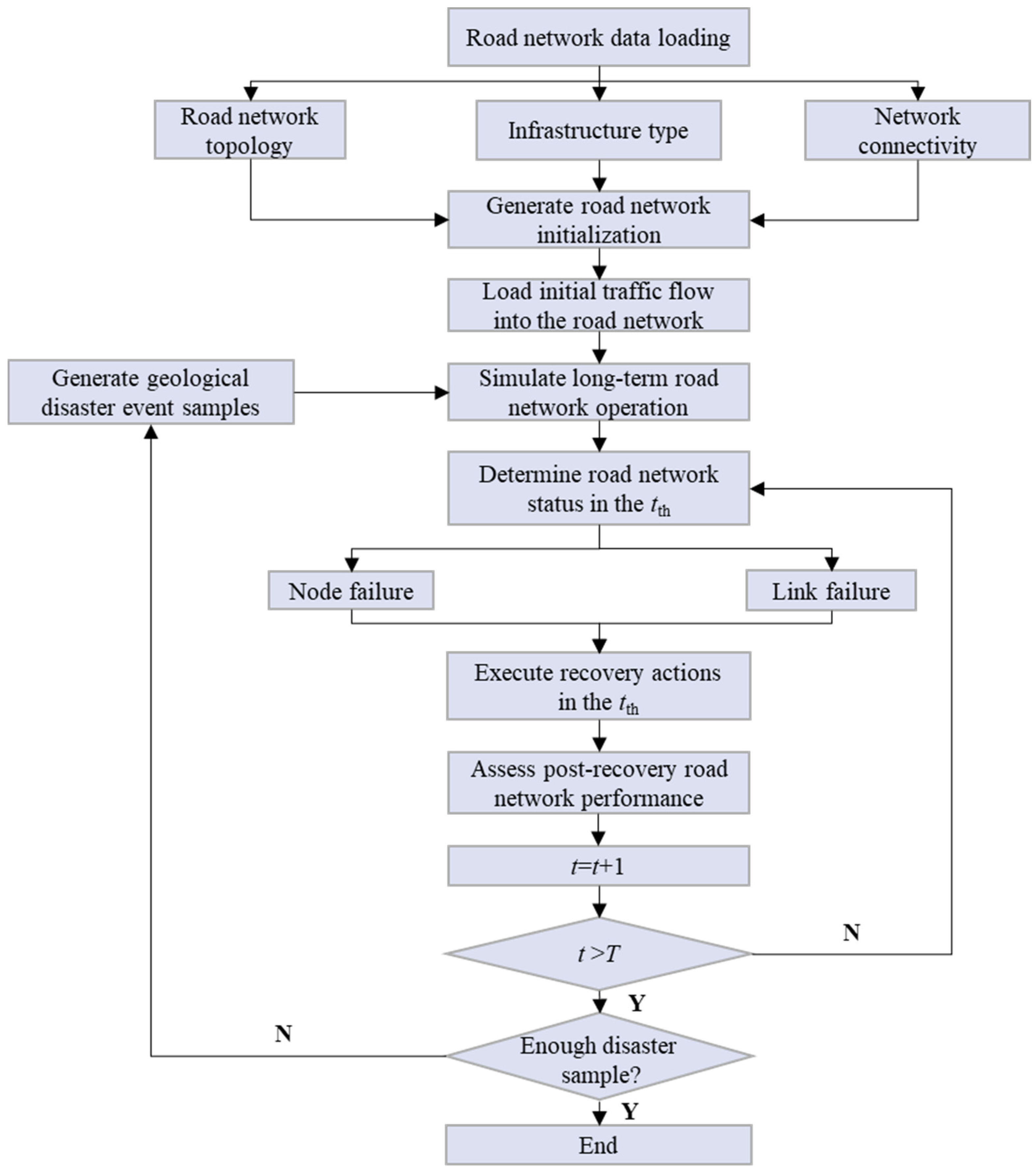
4.3. Simulation Process
4.4. Model Results
4.4.1. Sparse Road Network Topology Models
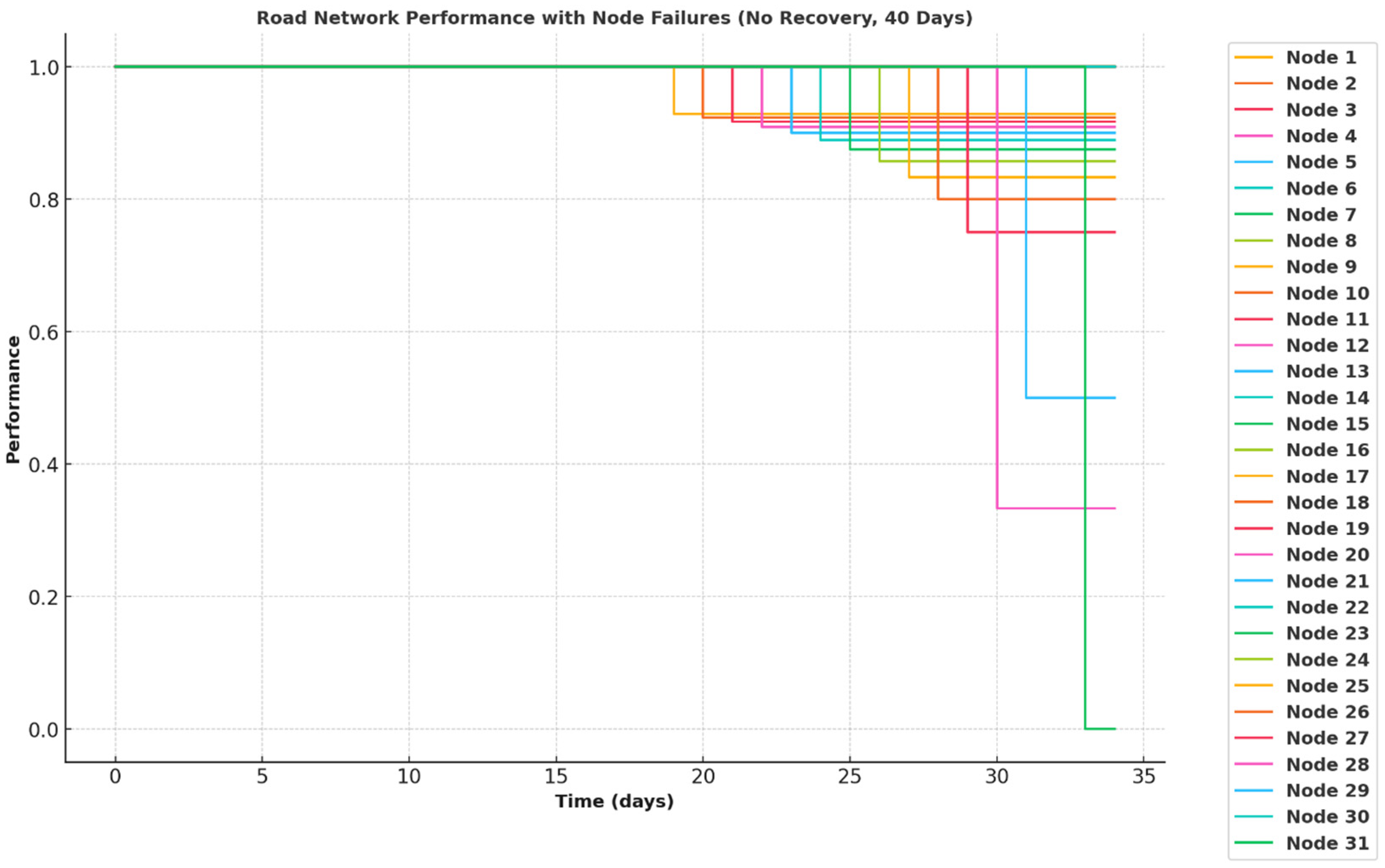
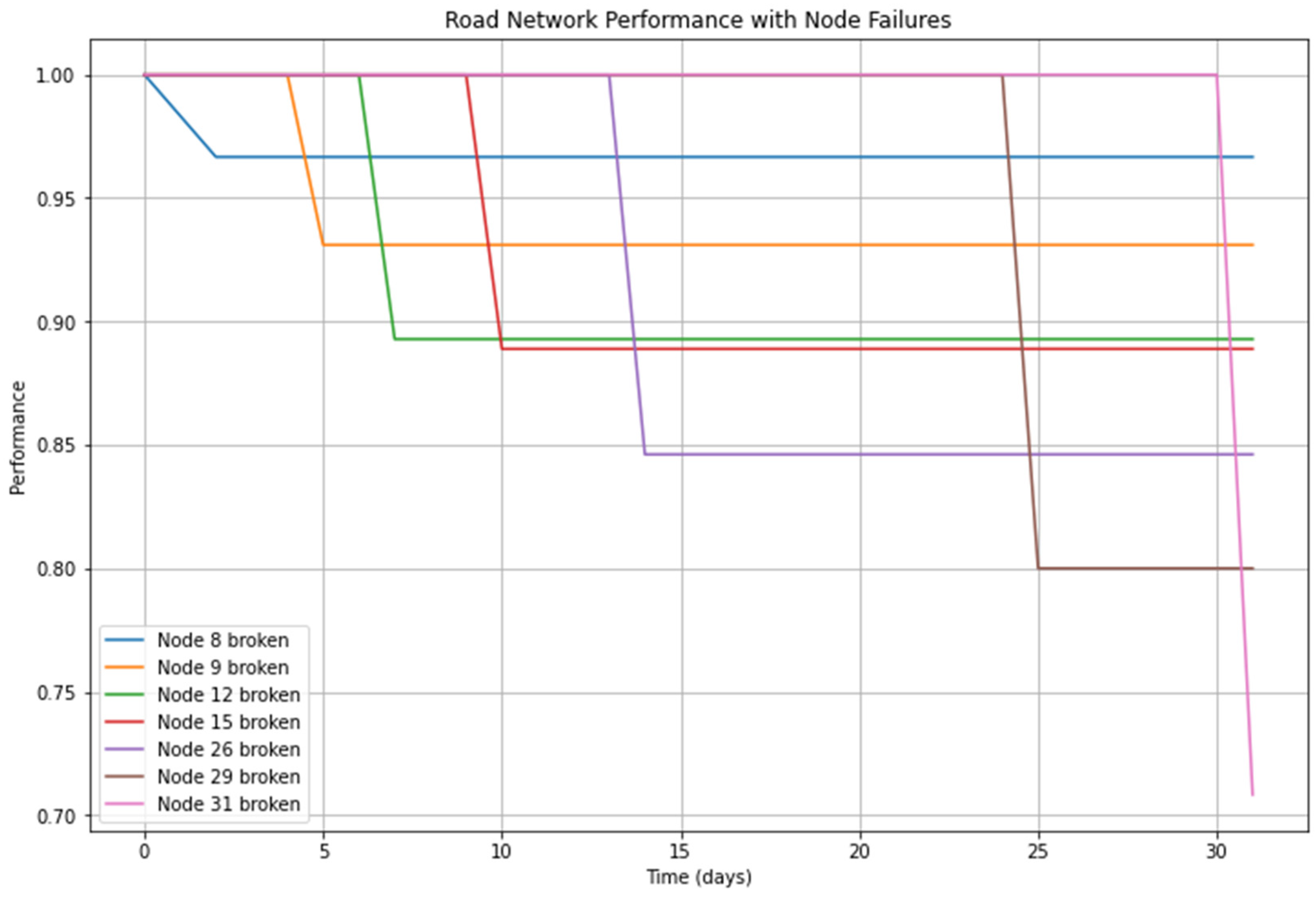
4.4.2. Analyzing Sparse Road Network Resilience
- (1)
- Sparse Road Network Structure
- (2)
- Duration of the Disaster Event
- (3)
- Remaining Capacity
5. Conclusions and Recommendations
5.1. Conclusions
5.2. Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J. Transport policymaking that accounts for COVID-19 and future public health threats: A PASS approach. Transp. Policy 2020, 99, 405–418. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-W.; Peng, Z.-R.; Wang, D.; Meng, Y.; Wu, T.; Sun, W.; Lu, Q.-C. Evaluation and prediction of transportation resilience under extreme weather events: A diffusion graph convolutional approach. Transp. Res. Part C Emerg. Technol. 2020, 115, 102619. [Google Scholar] [CrossRef]
- Yu, G.; Lin, D.; Xie, J.; Wang, Y.K. A Novel Approach for Modeling and Evaluating Road Operational Resilience Based on Pressure-State-Response Theory and Dynamic Bayesian Networks. Appl. Sci. 2023, 13, 7481. [Google Scholar] [CrossRef]
- McMichael, A.J.; Lindgren, E. Climate change: Present and future risks to health, and necessary responses. J. Intern. Med. 2011, 270, 401–413. [Google Scholar] [CrossRef] [PubMed]
- Shabani, K.; Nassiri, H. Reliability of Tehran transportation network during earthquakes. Sci. Iran. 2016, 23, 1618–1626. [Google Scholar] [CrossRef]
- Younes, S.; Oloufa, A. Applying Topological Information for Routing Commercial Vehicles Around Traffic Congestion. Appl. Sci. 2024, 14, 10134. [Google Scholar] [CrossRef]
- Esfeh, M.A.; Kattan, L.; Lam, W.H.; Salari, M.; Esfe, R.A. Road network vulnerability analysis considering the probability and consequence of disruptive events: A spatiotemporal incident impact approach. Transp. Res. Part C Emerg. Technol. 2022, 136, 103549. [Google Scholar] [CrossRef]
- Cats, O. Topological evolution of a metropolitan rail transport network: The case of Stockholm. J. Transp. Geogr. 2017, 62, 172–183. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Z.; Wu, H.; Sun, P.; Zhou, F. Evaluation of Urban Transportation Resilience under Extreme Weather Events. Appl. Sci. 2024, 14, 4947. [Google Scholar] [CrossRef]
- Liu, C.; Su, X.; Wu, Z.; Zhang, Y.; Zhou, C.; Wu, X.; Huang, Y. Exploration of the Mountainous Urban Rail Transit Resilience Under Extreme Rainfalls: A Case Study in Chongqing, China. Appl. Sci. 2025, 15, 735. [Google Scholar] [CrossRef]
- Gao, W.; Hu, X.; Wang, N. Resilience analysis in road traffic systems to rainfall events: Road environment perspective. Transp. Res. Part D Transp. Environ. 2024, 126, 104000. [Google Scholar] [CrossRef]
- Silva-Lopez, R.; Baker, J.W. Use of corridors to select bridges to retrofit in road networks in seismic regions. Sustain. Resil. Infrastruct. 2022, 7, 901–917. [Google Scholar] [CrossRef]
- Mebarki, A.; Jerez, S.; Prodhomme, G.; Reimeringer, M. Natural hazards, vulnerability and structural resilience: Tsunamis and industrial tanks. Geomat. Nat. Hazards Risk 2016, 7, 5–17. [Google Scholar] [CrossRef]
- Watson, G.; Ahn, J.E. A systematic review: To increase transportation infrastructure resilience to flooding events. Appl. Sci. 2022, 12, 12331. [Google Scholar] [CrossRef]
- Singh, P.; Sinha, V.S.P.; Vijhani, A.; Pahuja, N. Vulnerability assessment of urban road network from urban flood. Int. J. Disaster Risk Reduct. 2018, 28, 237–250. [Google Scholar] [CrossRef]
- Tong, J.; Zhang, W.; Li, C.; Yuan, D.; Lou, H.; Wang, Q.; Wang, H.; Zhai, J. Review of Resilience Evaluation Methods in Operational Highway Tunnel: Analysis of Index Systems and Evaluation Frameworks. J. Adv. Transp. 2024, 2024, 9273719. [Google Scholar] [CrossRef]
- Xu, C.; Hu, H.; Wang, H. A theoretical study on the resilience evaluation method of operational road tunnel systems. Appl. Sci. 2023, 13, 13279. [Google Scholar] [CrossRef]
- Allen, E.; Costello, S.B.; Henning, T.F.; Chamorro, A.; Echaveguren, T. Integration of resilience and risk to natural hazards into transportation asset management of road networks: A systematic review. Struct. Infrastruct. Eng. 2023, 1–19. [Google Scholar] [CrossRef]
- Serdar, M.Z.; Koç, M.; Al-Ghamdi, S.G. Urban transportation networks resilience: Indicators, disturbances, and assessment methods. Sustain. Cities Soc. 2022, 76, 103452. [Google Scholar] [CrossRef]
- Li, C.; Fang, Q.; Ding, L.; Cho, Y.K.; Chen, K. Time-dependent resilience analysis of a road network in an extreme environment. Transp. Res. Part D Transp. Environ. 2020, 85, 102395. [Google Scholar] [CrossRef]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Wang, S.; Yu, D.; Kwan, M.-P.; Zhou, H.; Li, Y.; Miao, H. The Evolution and Growth Patterns of the Road Network in a Medium-Sized Developing City: A Historical Investigation of Changchun, China, from 1912 to 2017. Sustainability 2019, 11, 5307. [Google Scholar] [CrossRef]
- Tian, J.; Guo, Q. A progressive approach to the generalization of an urban street network. In Geoinformatics 2007: Cartographic Theory and Models; SPIE: Nanjing, China, 2007; pp. 134–143. [Google Scholar] [CrossRef]
- Ji, T.; Yao, Y.; Dou, Y.; Deng, S.; Yu, S.; Zhu, Y.; Liao, H. The Impact of Climate Change on Urban Transportation Resilience to Compound Extreme Events. Sustainability 2022, 14, 3880. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Nettis, A.; Uva, G. A MTInSAR-based early warning system to appraise deformations in simply supported concrete girder bridges. Struct. Control Health Monit. 2024, 2024, 8978782. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Doglioni, A.; Morga, M.; Nettis, A.; Simeone, V.; Uva, G. Probabilistic-based assessment of subsidence phenomena on the existing built heritage by combining MTInSAR data and UAV photogrammetry. Struct. Infrastruct. Eng. 2024, 1–16. [Google Scholar] [CrossRef]
- Vugrin, E.D.; Warren, D.E.; Ehlen, M.A.; Camphouse, R.C. A framework for assessing the resilience of infrastructure and economic systems. In Sustainable and Resilient Critical Infrastructure Systems: Simulation, Modeling, and Intelligent Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 77–116. [Google Scholar] [CrossRef]
- Pregenzer, A.L. Systems Resilience: A New Analytical Framework for Nuclear Nonproliferation; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2011. [Google Scholar]
- Zhang, M.; Yang, X.; Zhang, J.; Li, G. Post-earthquake resilience optimization of a rural “road-bridge” transportation network system. Reliab. Eng. Syst. Saf. 2022, 225, 108570. [Google Scholar] [CrossRef]
- Calvert, S.C.; Snelder, M. A methodology for road traffic resilience analysis and review of related concepts. Transp. A Transp. Sci. 2018, 14, 130–154. [Google Scholar] [CrossRef]
- Zhu, C.; Wu, J.; Liu, M.; Luan, J.; Li, T.; Hu, K. Cyber-physical resilience modelling and assessment of urban roadway system interrupted by rainfall. Reliab. Eng. Syst. Saf. 2020, 204, 107095. [Google Scholar] [CrossRef]
- Allenby, B.; Fink, J. Toward inherently secure and resilient societies. Science 2005, 309, 1034–1036. [Google Scholar] [CrossRef]
- Azolin, L.G.; da Silva, A.N.R.; Pinto, N. Incorporating public transport in a methodology for assessing resilience in urban mobility. Transp. Res. Part D Transp. Environ. 2020, 85, 102386. [Google Scholar] [CrossRef]
- Janić, M. Reprint of “Modelling the resilience, friability and costs of an air transport network affected by a large-scale disruptive event”. Transp. Res. Part A Policy Pract. 2015, 81, 77–92. [Google Scholar] [CrossRef]
- Barker, K.; Ramirez-Marquez, J.E.; Rocco, C.M. Resilience-based network component importance measures. Reliab. Eng. Syst. Saf. 2013, 117, 89–97. [Google Scholar] [CrossRef]
- Ouyang, M.; Dueñas-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Saf. 2012, 36, 23–31. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Ma, F.; Ao, Y.; Wang, X.; He, H.; Liu, Q.; Yang, D.; Gou, H. Assessing and enhancing urban road network resilience under rainstorm waterlogging disasters. Transp. Res. Part D Transp. Environ. 2023, 123, 103928. [Google Scholar] [CrossRef]
- Zobel, C.W.; Khansa, L. Characterizing multi-event disaster resilience. Comput. Oper. Res. 2014, 42, 83–94. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Hoff, P.D.; Raftery, A.E.; Handcock, M.S. Latent space approaches to social network analysis. J. Am. Stat. Assoc. 2002, 97, 1090–1098. [Google Scholar] [CrossRef]
- Geisberger, R.; Sanders, P.; Schultes, D.; Vetter, C. Exact routing in large road networks using contraction hierarchies. Transp. Sci. 2012, 46, 388–404. [Google Scholar] [CrossRef]
- Faturechi, R.; Miller-Hooks, E. Travel time resilience of roadway networks under disaster. Transp. Res. Part B Methodol. 2014, 70, 47–64. [Google Scholar] [CrossRef]
- Aghababaei, M.T.S.; Costello, S.B.; Ranjitkar, P. Measures to evaluate post-disaster trip resilience on road networks. J. Transp. Geogr. 2021, 95, 103154. [Google Scholar] [CrossRef]
- Luathep, P.; Sumalee, A.; Ho, H.; Kurauchi, F. Large-scale road network vulnerability analysis: A sensitivity analysis based approach. Transportation 2011, 38, 799–817. [Google Scholar] [CrossRef]
- Henry, E.; Furno, A.; Faouzi, N.-E.E. Approach to quantify the impact of disruptions on traffic conditions using dynamic weighted resilience metrics of transport networks. Transp. Res. Rec. 2021, 2675, 61–78. [Google Scholar] [CrossRef]
- Xu, Z.; Ramirez-Marquez, J.E.; Liu, Y.; Xiahou, T. A new resilience-based component importance measure for multi-state networks. Reliab. Eng. Syst. Saf. 2020, 193, 106591. [Google Scholar] [CrossRef]
- Li, S. Dynamic traffic flow-based post-earthquake road network restoration and relief logistics. Acta Tech. 2017, 62, 149–160. [Google Scholar]
- Duque, P.A.M.; Dolinskaya, I.S.; Sörensen, K. Network repair crew scheduling and routing for emergency relief distribution problem. Eur. J. Oper. Res. 2016, 248, 272–285. [Google Scholar] [CrossRef]
- GB/T 40112-2021; Specifications for Risk Assessment of Geological Hazard. Standards Press of China: Beijing, China, 2021.
- JTG B01-2014; Technical Standard of Highway Engineering. China Communications Press: Beijing, China, 2015.







| Definitions | References |
|---|---|
| Resilience is the ability of a system to maintain its function and structure in the face of internal and external changes, and to gracefully degrade when necessary. | Allenby and Fink et al. [32] |
| Resilience encompasses the system’s ability to resist, adapt to, and absorb the consequences of interruptions, maintain normal function levels, and recover from shocks. | Azolin et al. [33] |
| Network resilience is the ability to maintain planned functions under the influence of disruptive events and the speed at which the network returns to its expected state. | Janic et al. [34] |
| Resilience is categorized into four stages: anticipation, absorption, adaptation, and recovery, based on the system’s performance characteristics at different phases of disturbance. | Barker et al. [35] |
| Dynamic resilience comprises four key attributes: robustness, redundancy, resourcefulness, and recovery speed. | Ouyang et al. [36] |
| Resilience is the dynamic service capacity of a road network under frequent disaster impacts. | Li et al. [20] |
| Site Name | Anduo | Bange | Nagqu | Xijiao | Naiji | Sigong | |
|---|---|---|---|---|---|---|---|
| Date | 1 January 2021 | 1 March 2021 | 1 December 2021 | 1 July 2022 | 5 January 2023 | 1 June 2023 | |
| Vehicles (units) | Light Trucks | 69 | 175 | 40 | 359 | 65 | 48 |
| Medium Trucks | 15 | 1140 | 15 | 166 | 13 | 26 | |
| Heavy Trucks | 9 | 36 | 5 | 129 | 16 | 14 | |
| Extra-Heavy Trucks | 866 | 317 | 749 | 944 | 1146 | 1513 | |
| Containers | 0 | 0 | 0 | 0 | 0 | 0 | |
| Small Passenger Vehicles | 464 | 560 | 254 | 1239 | 1337 | 695 | |
| Large Passenger Vehicles | 11 | 8 | 8 | 33 | 18 | 23 | |
| Subtotal | 1434 | 2236 | 1071 | 2870 | 2595 | 2319 | |
| Motorcycles (units) | 28 | 18 | 17 | 73 | 13 | 22 | |
| Tractors (units) | 2 | 0 | 1 | 0 | 0 | 0 | |
| Total (units) | 1464 | 2254 | 1089 | 2943 | 2608 | 2341 | |
| Disaster Type 1 | Road Segment | Bridge | Tunnel |
|---|---|---|---|
| small-scale | 1 | 1.5 | 2 |
| medium-scale | 2 | 3 | 4 |
| large-scale | 5 | 7.5 | 10 |
| extra-large-scale | 15 | 22.5 | 30 |
| O-D | Travel Demand | O-D | Travel Demand | O-D | Travel Demand | O-D | Travel Demand |
|---|---|---|---|---|---|---|---|
| (4,1) | 6000 | (5,1) | 6000 | (6,1) | 4500 | (7,1) | 5000 |
| (4,2) | 6500 | (5,2) | 5500 | (6,2) | 5500 | (7,2) | 6000 |
| (4,3) | 7000 | (5,3) | 6000 | (6,3) | 6500 | (7,3) | 8000 |
| Disaster Type | Survivability | Evacuability | Recoverability | Adaptability |
|---|---|---|---|---|
| Duration of disaster | ||||
| Collapse (42 h) | 0.65 | 0.89 | 0.0036 | 0.35 |
| Debris flow (14 h) | 0.20 | 0.78 | 0.047 | 0.80 |
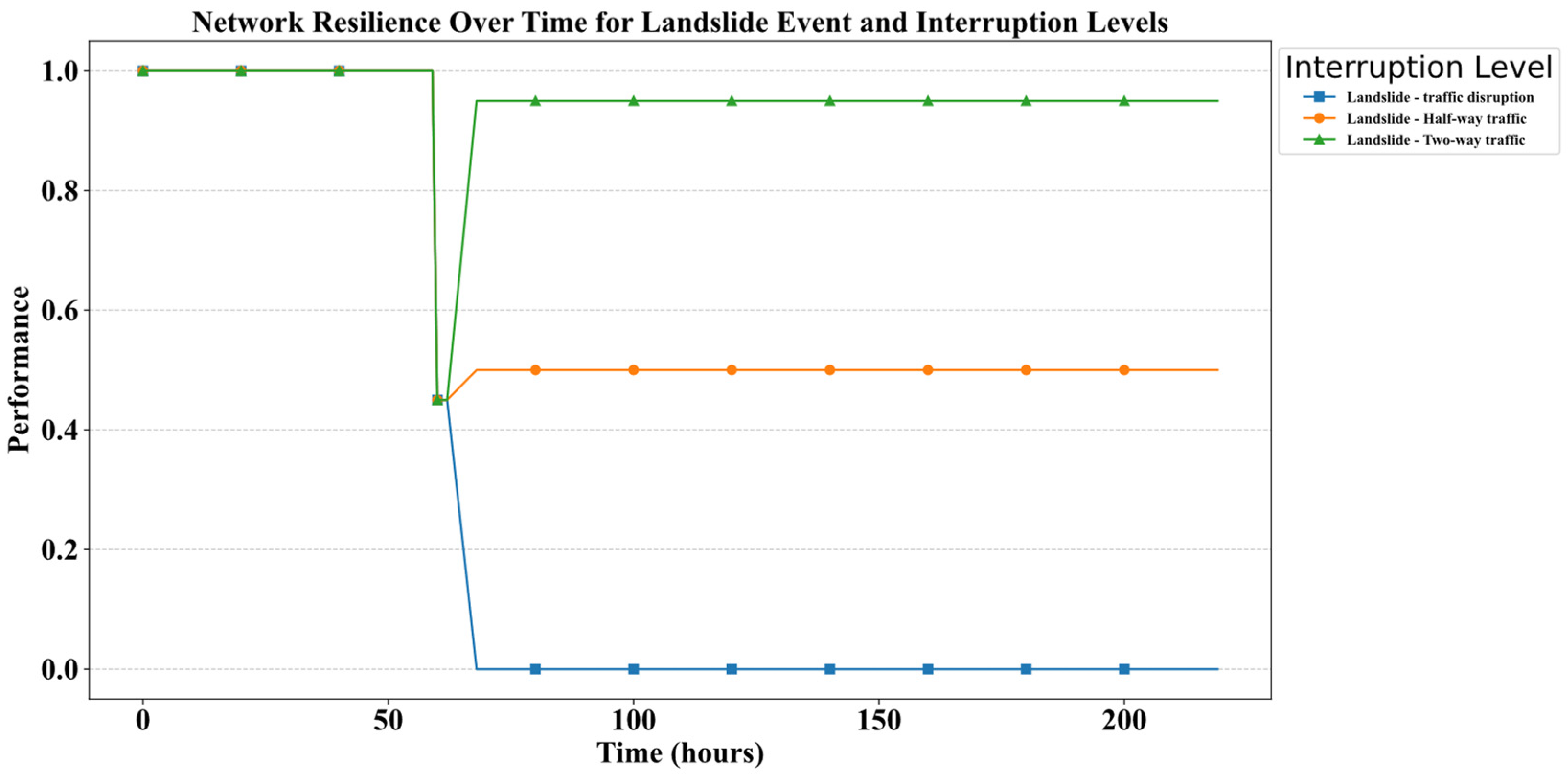
| Landslide (6 h) | 0.45 | 0.73 | 0.075 | 0.55 |
| Subsidence (10 h) | 0.35 | 0.62 | 0.04 | 0.65 |
| Water damage (69 h) | 0.50 | 0.55 | 0.0069 | 0.50 |
| Acceptable service level | ||||
| Traffic disruption | 0.0000 | 0.6864 | 0 | 0 |
| Half-way traffic | 0.4500 | 0.7273 | 0.0008 | 0.9500 |
| Two-way traffic | 0.4500 | 0.7273 | 0.075 | 0.5500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Yang, Z.; Wang, M.; Xu, G.; Bai, S. Evaluating the Resilience of Mountainous Sparse Road Networks in High-Risk Geological Disaster Areas: A Case Study in Tibet, China. Appl. Sci. 2025, 15, 2688. https://doi.org/10.3390/app15052688
Xie S, Yang Z, Wang M, Xu G, Bai S. Evaluating the Resilience of Mountainous Sparse Road Networks in High-Risk Geological Disaster Areas: A Case Study in Tibet, China. Applied Sciences. 2025; 15(5):2688. https://doi.org/10.3390/app15052688
Chicago/Turabian StyleXie, Shikun, Zhen Yang, Mingxuan Wang, Guilong Xu, and Shuming Bai. 2025. "Evaluating the Resilience of Mountainous Sparse Road Networks in High-Risk Geological Disaster Areas: A Case Study in Tibet, China" Applied Sciences 15, no. 5: 2688. https://doi.org/10.3390/app15052688
APA StyleXie, S., Yang, Z., Wang, M., Xu, G., & Bai, S. (2025). Evaluating the Resilience of Mountainous Sparse Road Networks in High-Risk Geological Disaster Areas: A Case Study in Tibet, China. Applied Sciences, 15(5), 2688. https://doi.org/10.3390/app15052688





