Analysis of Structural Performance and Design Optimization of Prefabricated Cantilever Systems Under Traffic Loads
Abstract
:1. Introduction
2. Development and Validation of the Scaled-Down PCS Model
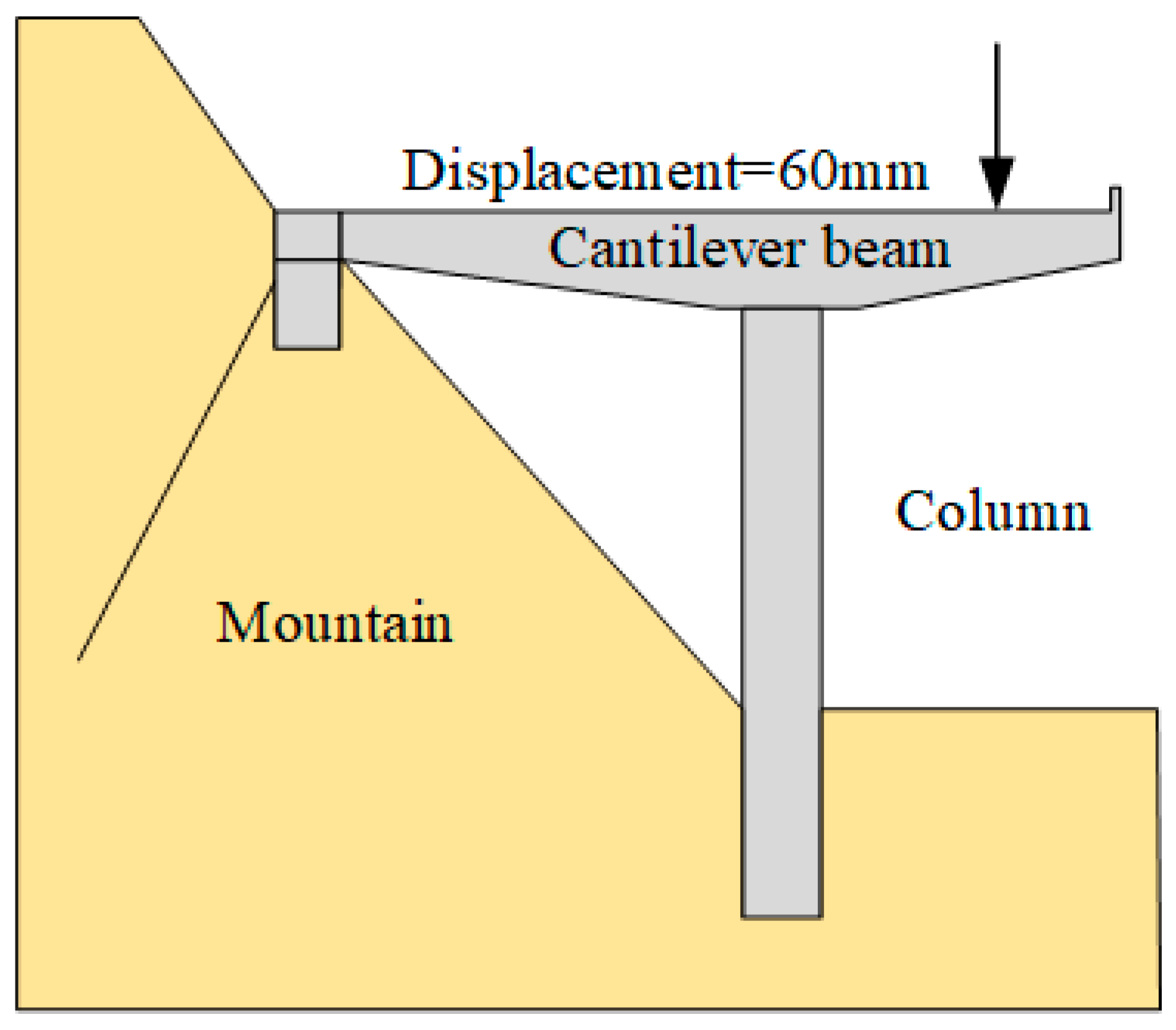
2.1. Design and Testing of the Scaled-Down PCS
2.2. Scaled-Down PCS Model Construction
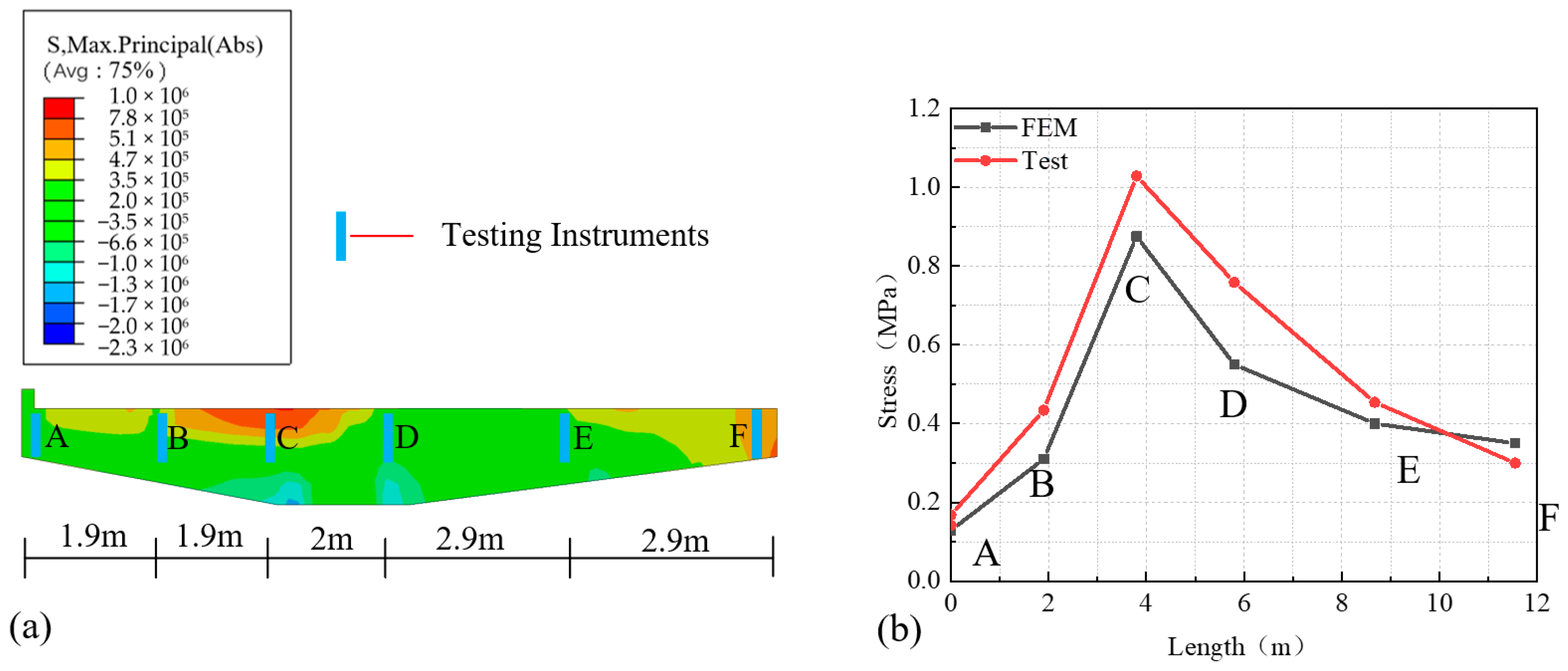
2.3. Scaled-Down PCS Model Validation
3. Full-Scale PCS Model Development and Validation
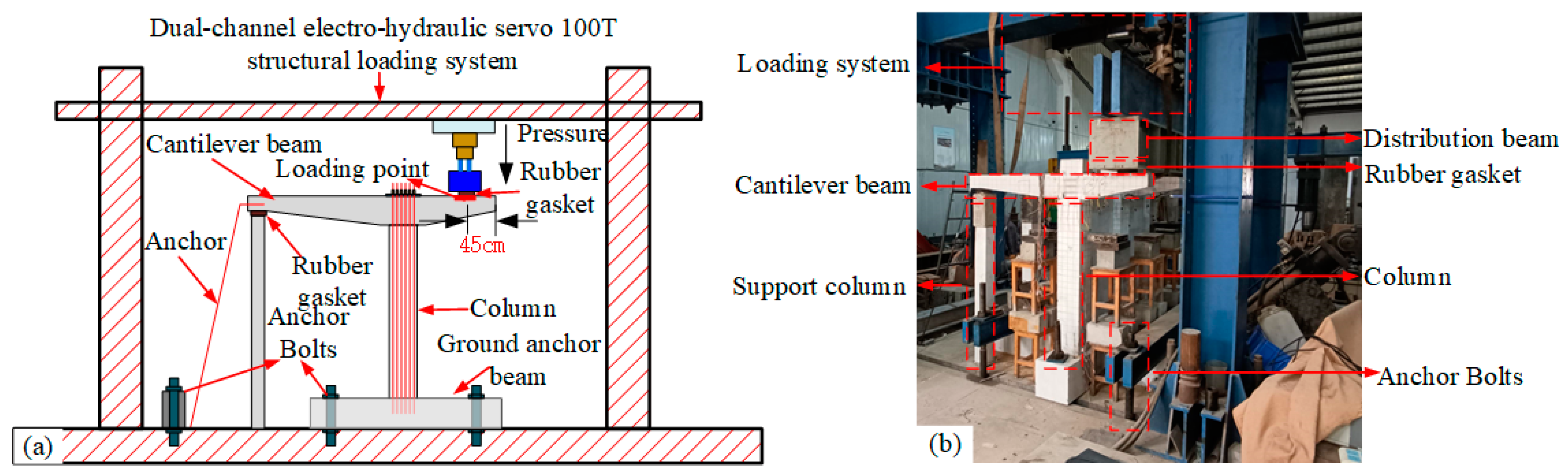
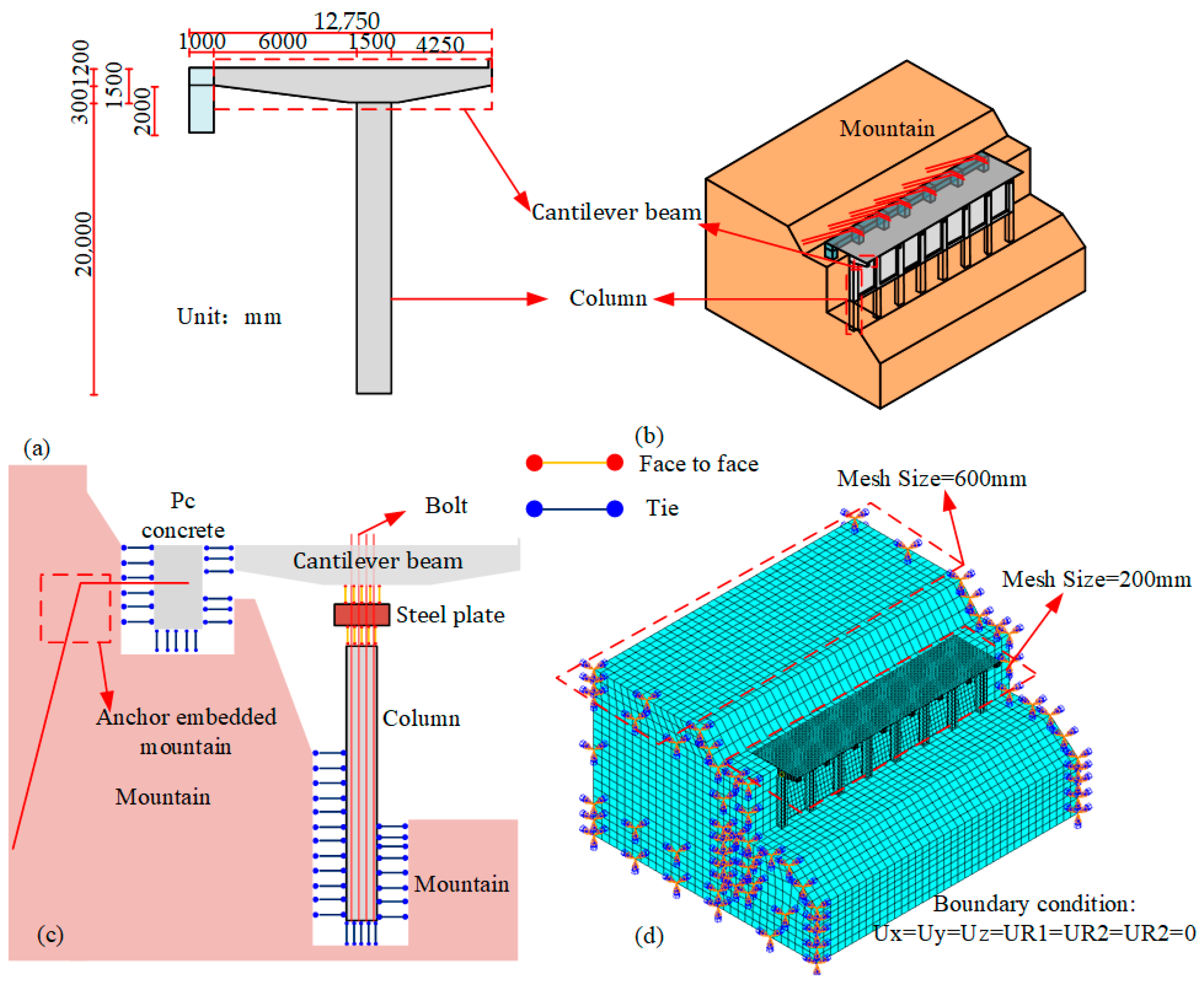
3.1. Full-Scale PCS Testing
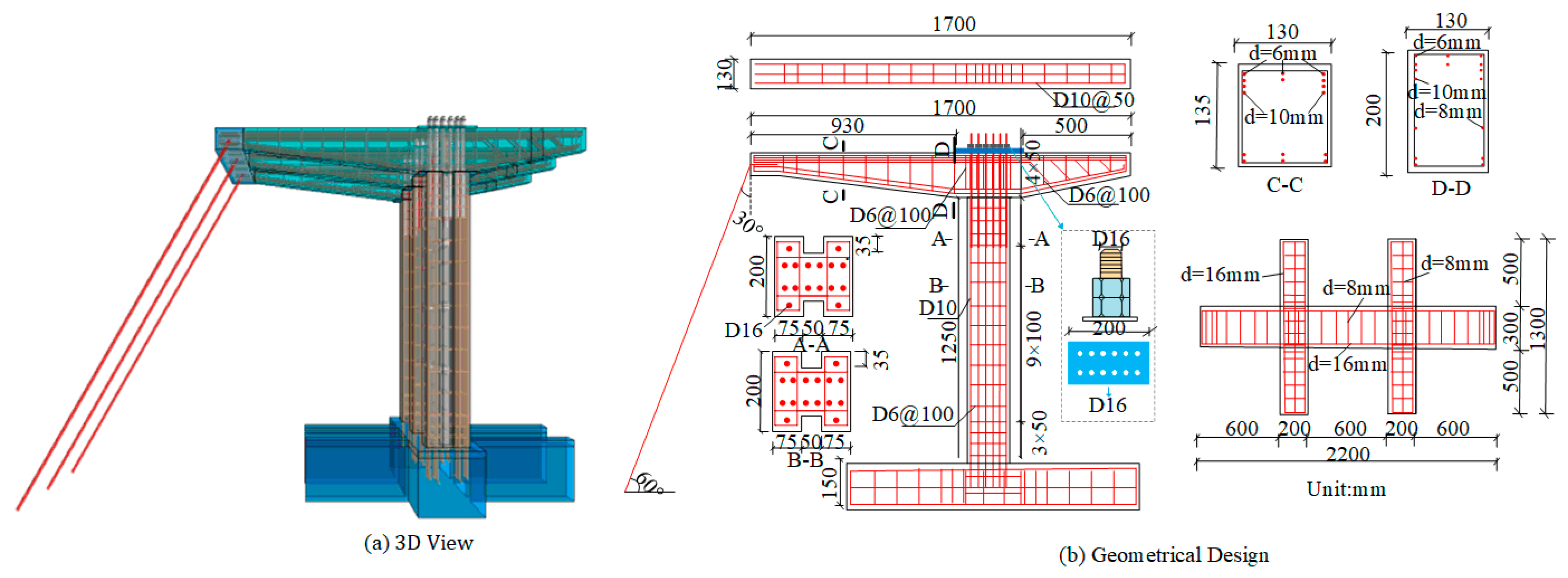
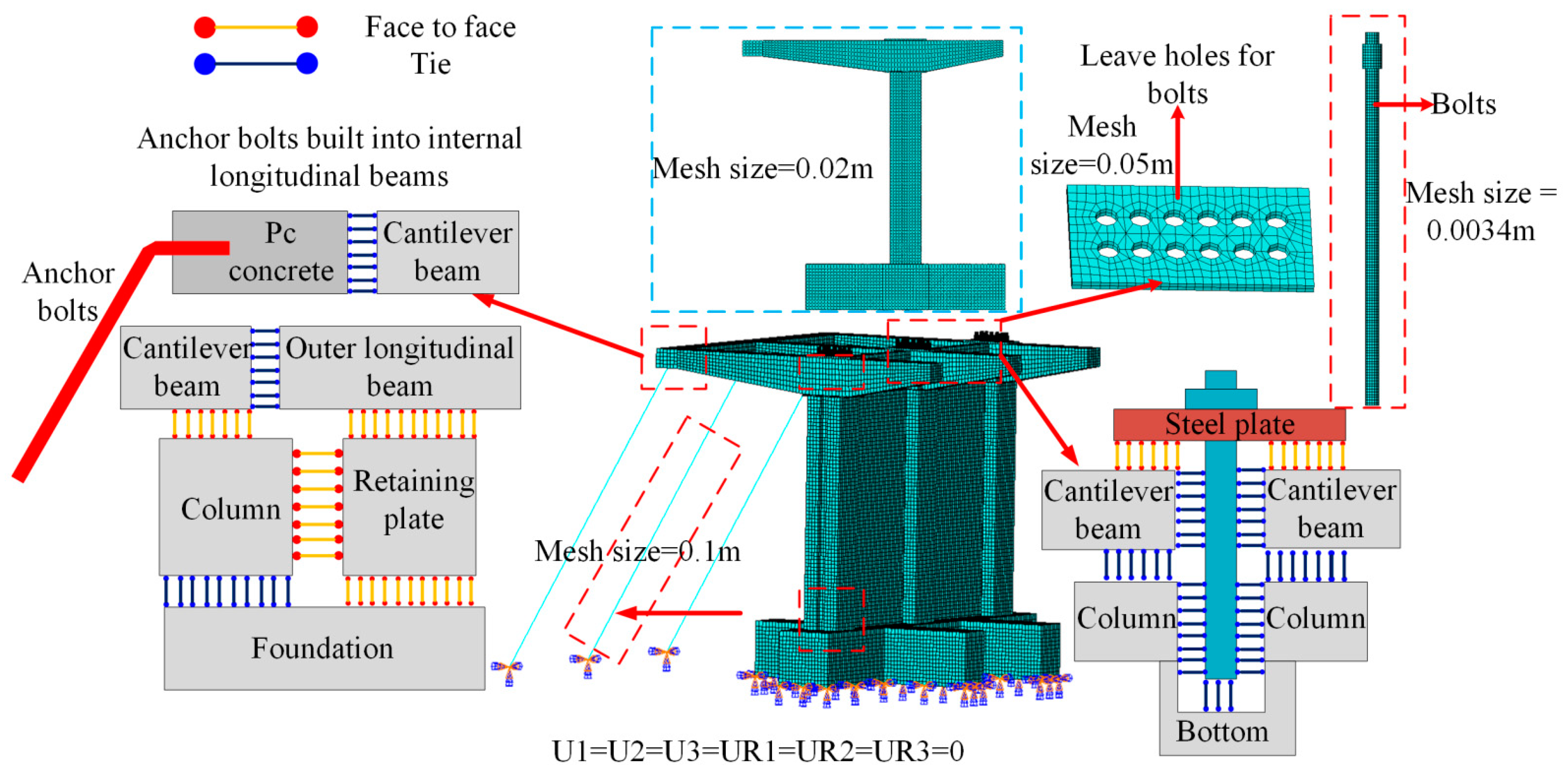
3.2. Full-Scale PCS Development
3.3. Full-Scale PCS Model Validation
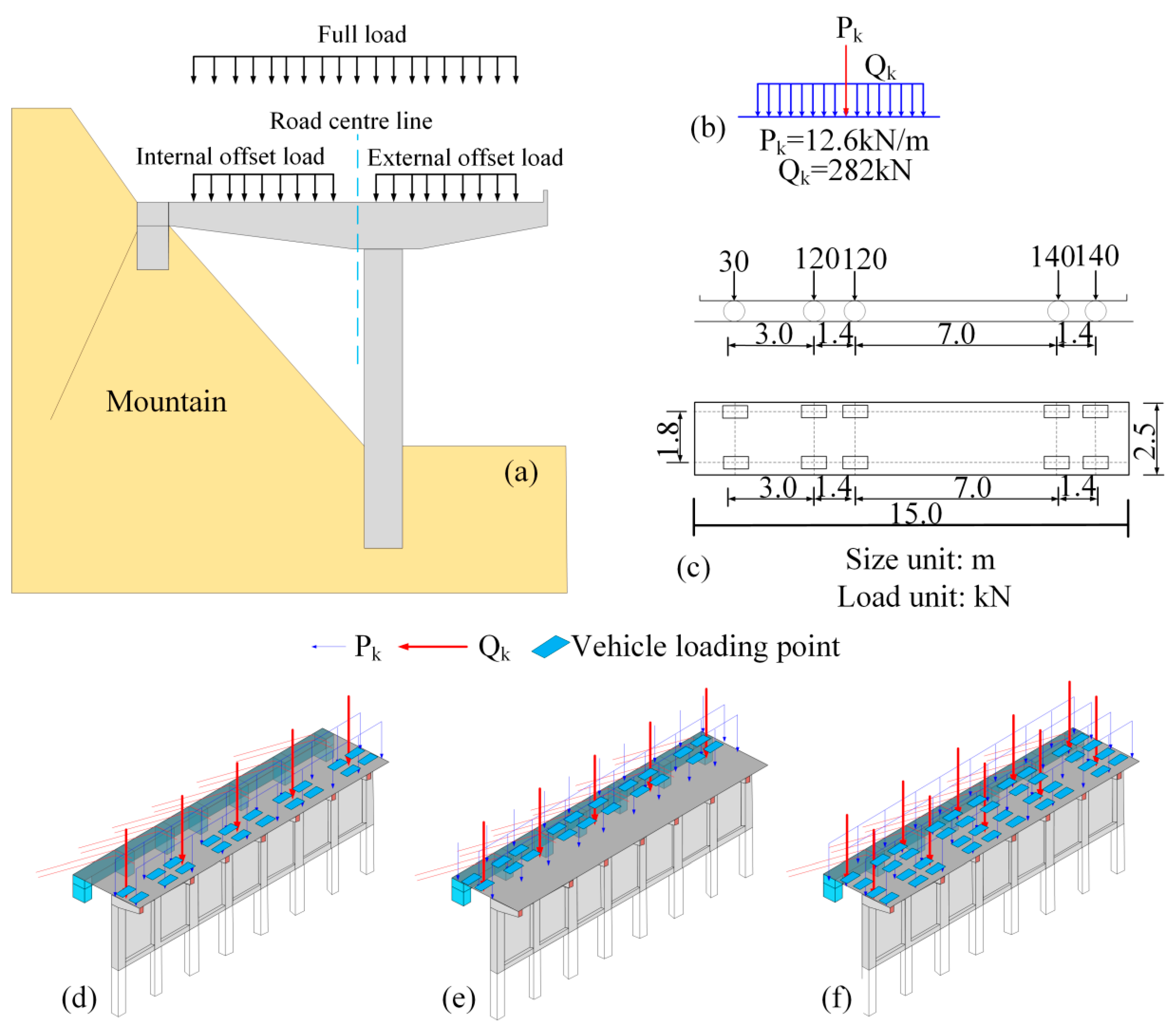
4. Full-Scale PCS Response Analysis and Optimization Under Traffic Load
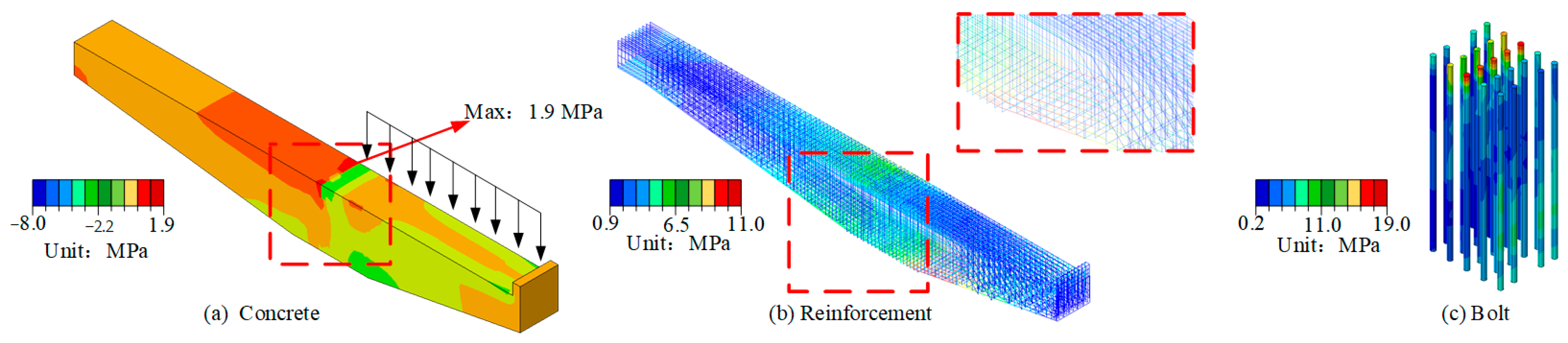
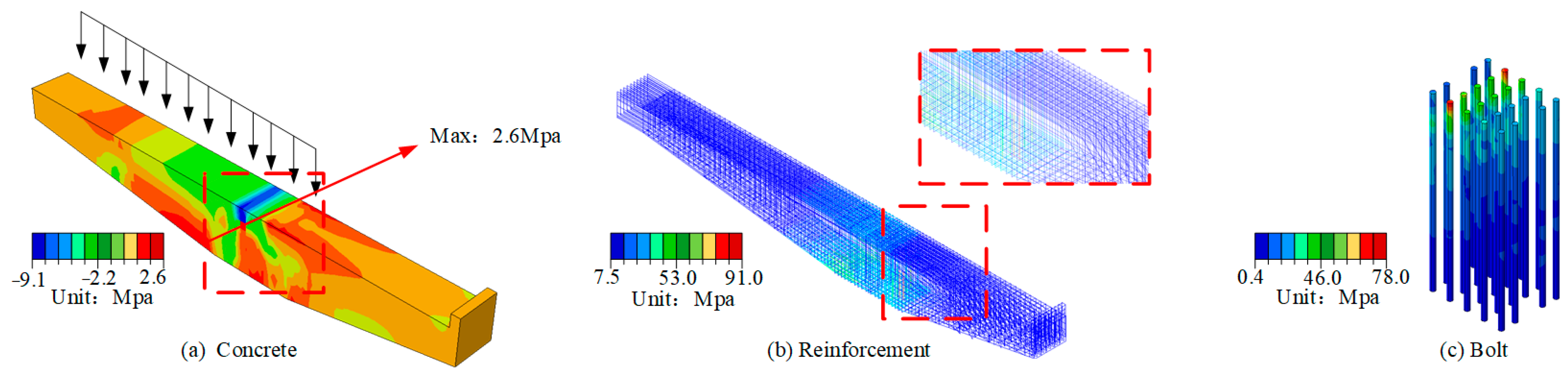
4.1. Structural Response Analysis
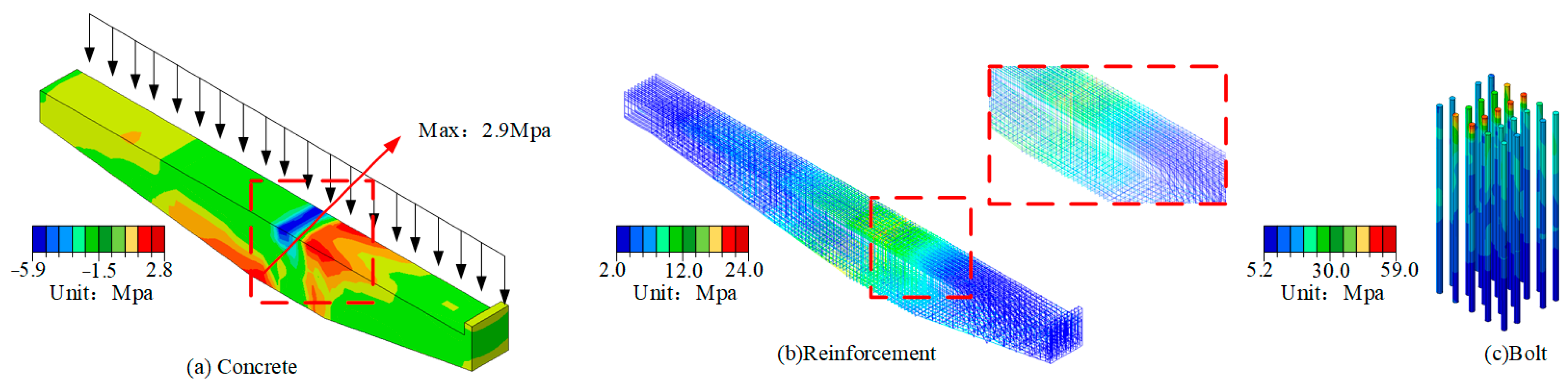
4.2. Structural Optimization Based on the Numerical Design
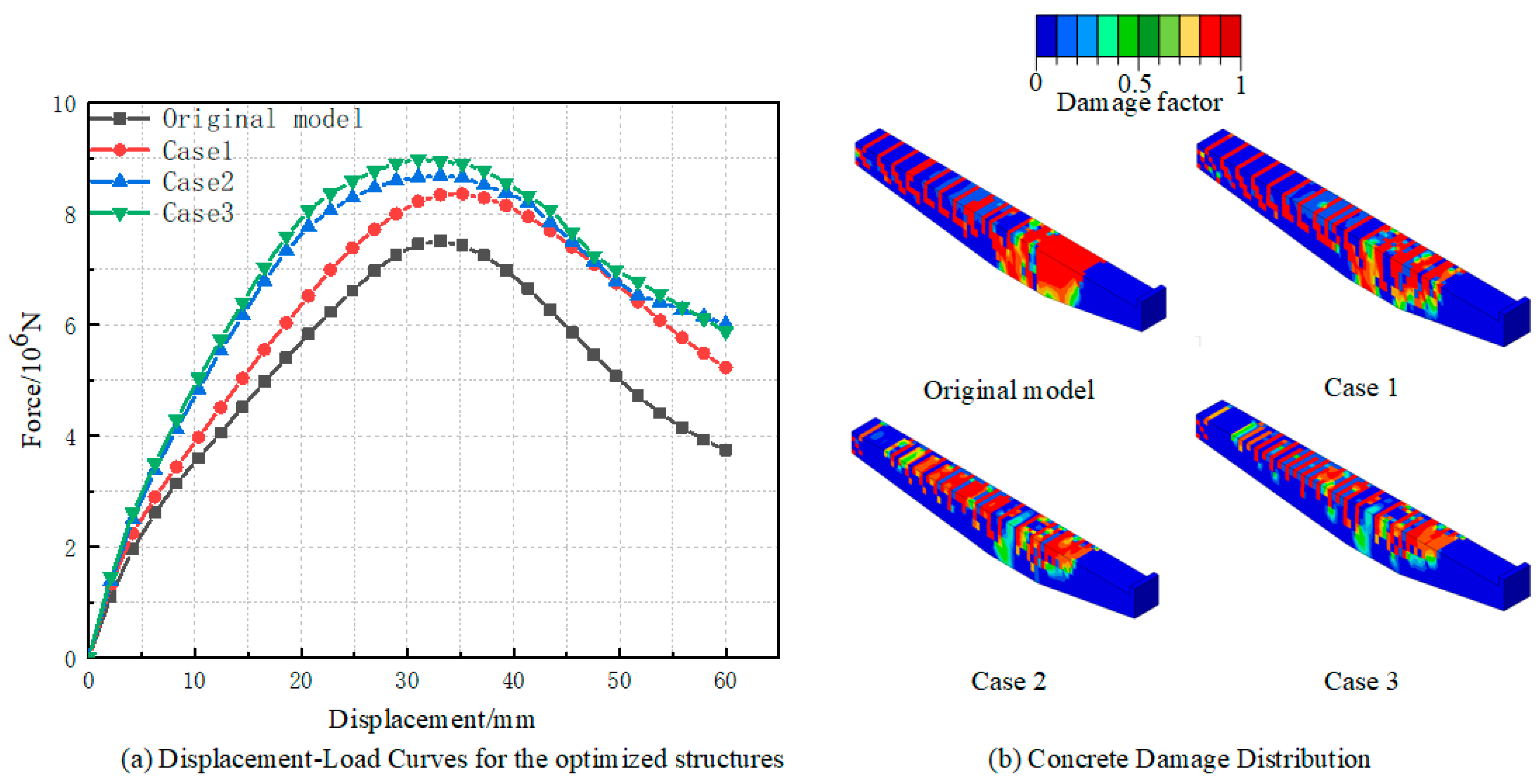
4.3. Load-Bearing Capacity of Optimized Structures
5. Conclusions
- (1)
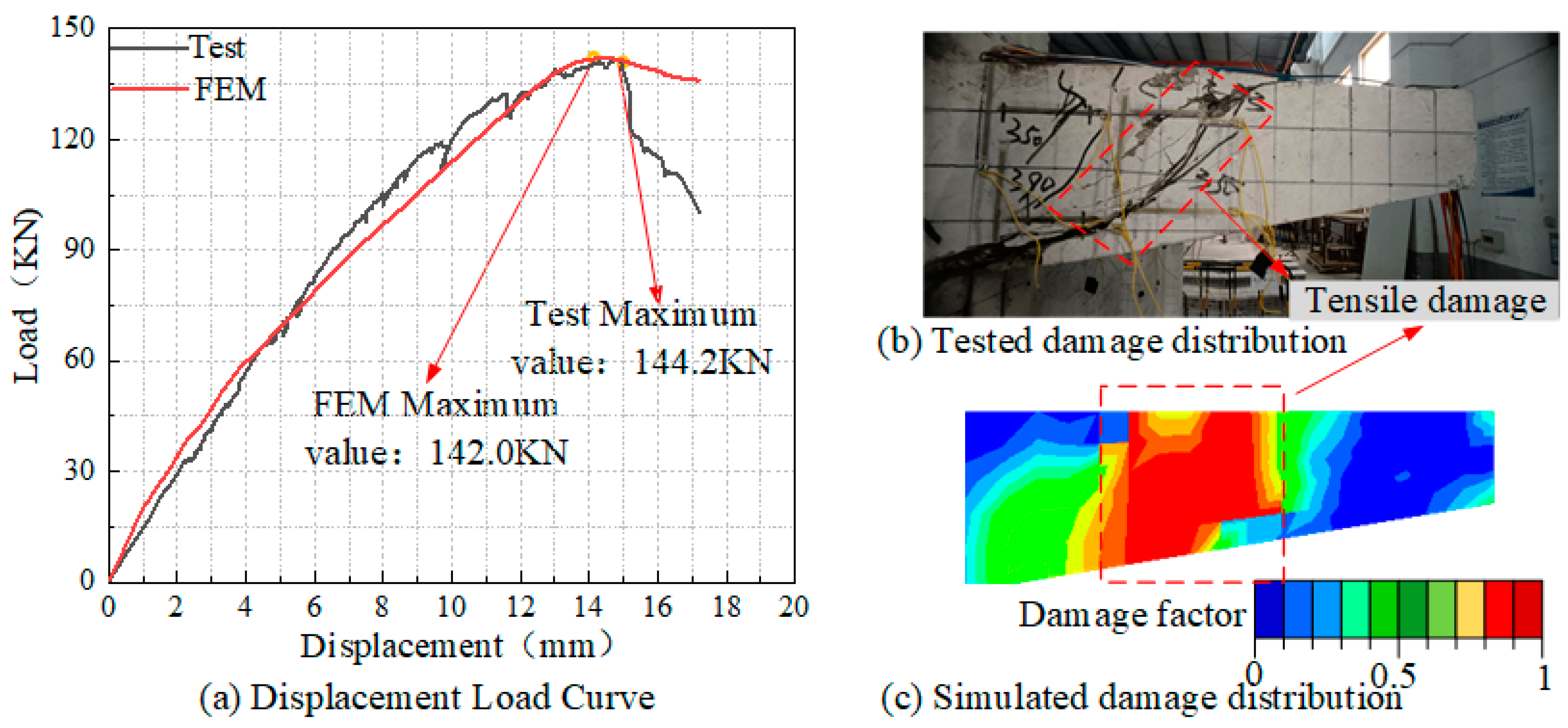
- The prefabricated cantilever structure model presented in this study effectively replicates the real-world stress and failure characteristics of the structure. In the scaled model, the load-bearing capacity curves derived from both simulations and laboratory experiments demonstrate a high degree of consistency. For the full-scale model, comparisons between simulated and actual stresses on the cantilever beams during paving further corroborate the model’s accuracy, verifying its robustness and reliability.
- (2)
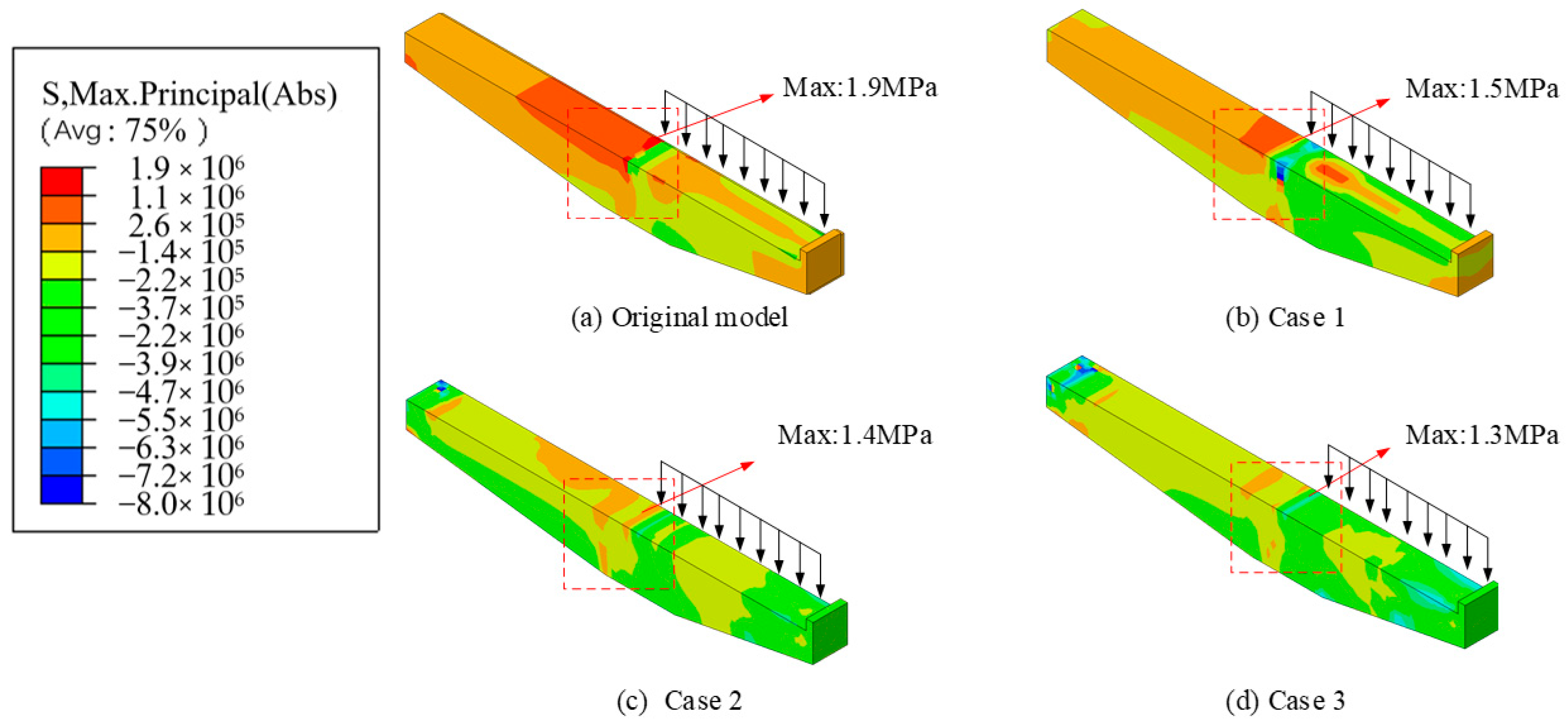
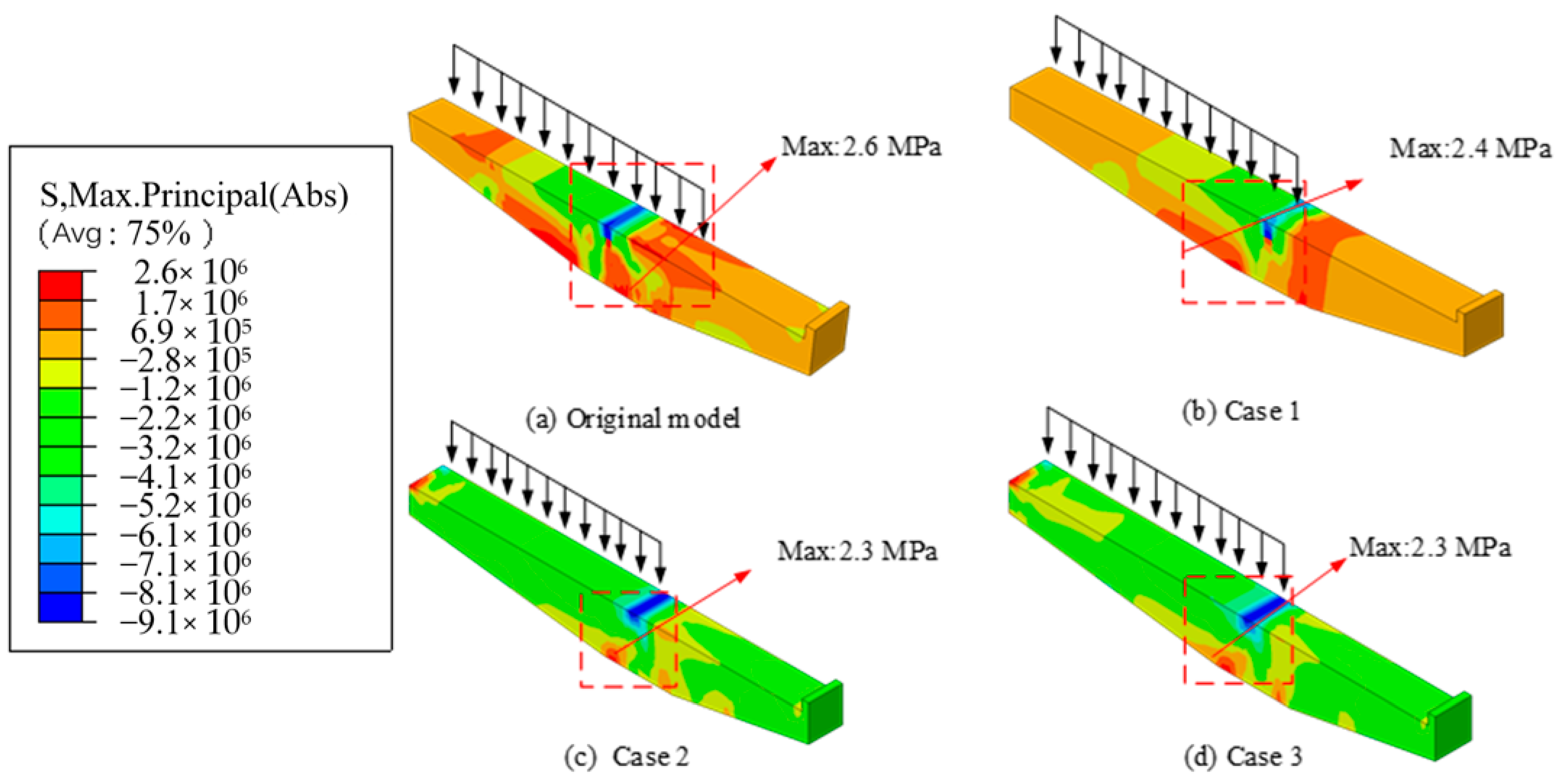
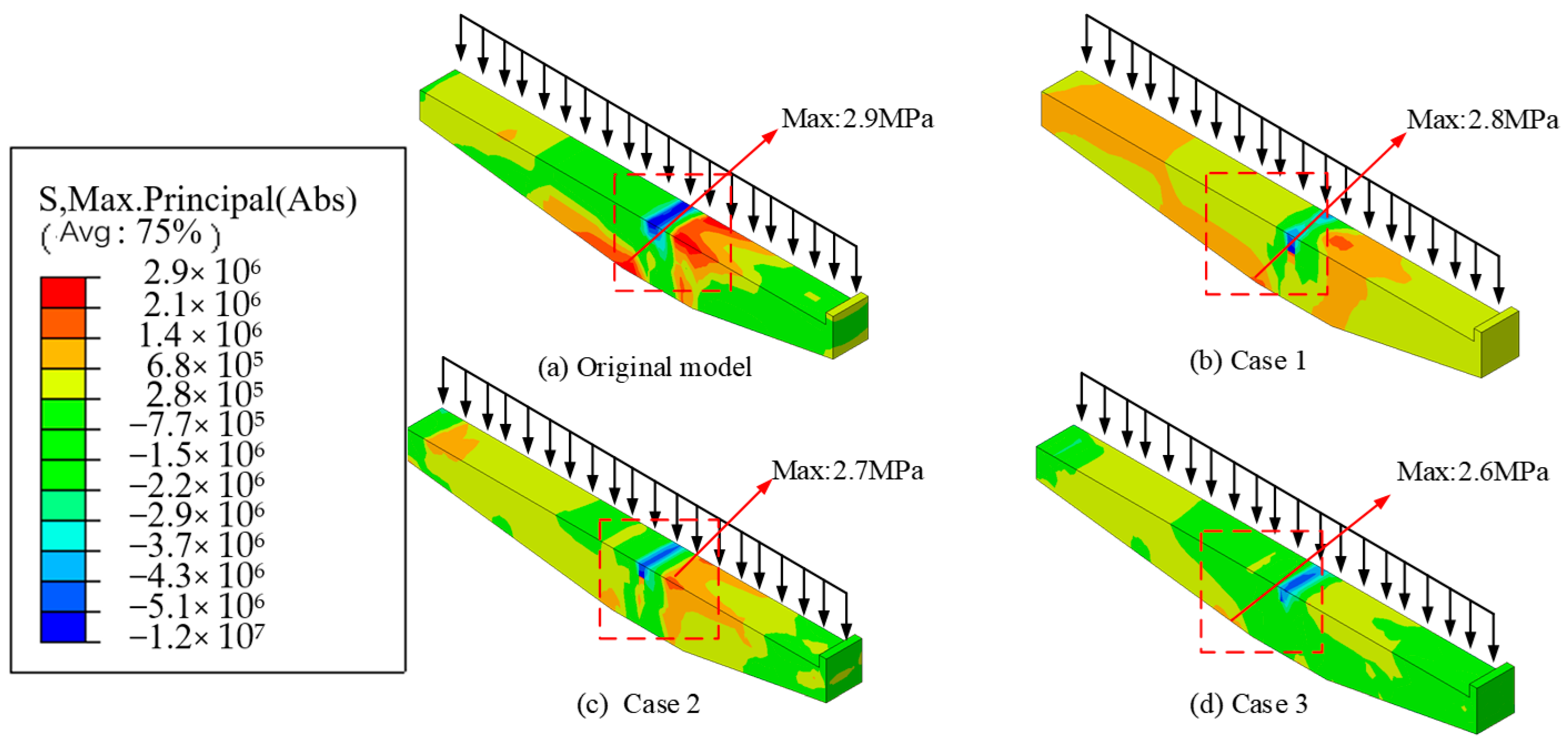
- Under varying vehicular loads, the connection between the cantilever beam and the column is identified as a critical weak point, characterized by significant stress concentration. While the reinforcements in this region endure high stress, the tensile strength of the concrete is relatively low. However, once cracking occurs in the concrete, the tensile stress will be borne by the steel bars, and failure could result from either the yielding of the steel bars or the failure of the concrete compression surface, potentially leading to the collapse of the entire structure.
- (3)
- The incorporation of prestressed rebars in the tension zone of the cantilever beams optimizes the internal stress distribution, alleviating stress concentration, and leading to a more uniform overall stress distribution, thus improving the structural performance. Positioning prestressed rebars at both the inner and outer top surfaces of the cantilever beams significantly enhances stress distribution under both external and internal eccentric loads. Additionally, adding prestressed rebars at the bottom of the inner cantilever beam further refines stress distribution under full loading conditions.
- (4)
- Incorporating prestressed rebars into the cantilever beams improves the structure’s overall stiffness, load-bearing capacity, and ductility, while delaying the initiation of structural damage. Simulations of the optimized structure under ultimate load conditions show that the inclusion of prestressed rebars, especially at the top inner and outer cantilever beam surfaces, notably enhances the initial slope and peak load of the displacement-load curve, along with a reduced descending slope. The damage distribution analysis indicates that adding prestressed rebars, particularly at the top inner and outer sides, significantly mitigates damage at critical beam–column connections, improving stress distribution and preventing rapid damage propagation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lou, C.H.; Dong, F.H. Study of overturning stability safety factors of continuous girder bridges during cantilever construction. Eng. J. Wuhan Univ. 2017, 50, 2. (In Chinese) [Google Scholar]
- Jeon, B.S.; Yoon, H.H.; Bollinger, K.; Jeong, Y.K. Design and Construction of the 85 m Cantilever Roof: Busan Cinema Centre, Korea. Struct. Eng. Int. 2012, 22, 62–65. [Google Scholar] [CrossRef]
- Bakholdin, B.V.; Dranitsyn, A.V. Procedure for monitoring the bearing capacity of cast-in-place piles from results of their. Soil Mech. Found. Eng. 2007, 44, 18–23. [Google Scholar] [CrossRef]
- Kazakov, Y.N.; Bulankin, N.F. Experience with Installation of Cast-In-Place Piles of Increased Bearing Capacity. Soil Mech. Found. Eng. 2015, 52, 15–17. [Google Scholar] [CrossRef]
- Chen, Z.; Li, H.; Chen, A.; Yu, Y.; Wang, H. Research on pretensioned modular frame test and simulations. Eng. Struct. 2017, 151, 774–787. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Yan, M.; Meng, W.; Lu, X.; Chen, K.; Bao, Y. Cyclic behavior of joints assembled using prefabricated beams and columns with Engineered Cementitious Composite (ECC). Eng. Struct. 2021, 247, 113115. [Google Scholar] [CrossRef]
- Wang, J.X.; Shen, Y.J.; Gao, S.; Wang, W.D. Anti-collapse performance of concrete-filled steel tubular composite frame with assembled tensile steel brace under middle column removal. Eng. Struct. 2022, 266, 114635. [Google Scholar] [CrossRef]
- Pan, J.; Lu, W.; Tang, X. Nonlinear stability analysis of cable-stayed bridges in cantilever construction state. J. Wuhan Univ. Technol. Transp. Sci. Eng. 2008, 32, 225–228. (In Chinese) [Google Scholar]
- Singh, A.P.; Chatterjee, K. Ground Settlement and Deflection Response of Cantilever Sheet Pile Wall Subjected to Surcharge Loading. Indian Geotech. J. 2020, 50, 540–549. [Google Scholar] [CrossRef]
- Qin, X.; Wang, Y.; Cui, S.; Liu, S.; Liu, S.; Wangari, V.W. Post-assessment of the eco-environmental impact of highway construction- A case study of Changbai Mountain Ring Road. Environ. Impact Assess. Rev. 2023, 98, 106963. [Google Scholar] [CrossRef]
- Yan, G.; Liu, B.; Li, Y.; Wang, M.; Yan, T. Antecedents of Electricity-Saving Behavior in Mountain Road Tunnel-Construction Sites: A Multi-Level Modeling Analysis. Sustainability 2024, 16, 2593. [Google Scholar] [CrossRef]
- Choudhari, S.; Tindwani, A. Logistics optimisation in road construction project. Constr. Innov. 2017, 17, 158–179. [Google Scholar] [CrossRef]
- Donaldson, L. Concrete revolutionises road construction. Mater. Today 2010, 13, 10. [Google Scholar] [CrossRef]
- Qi, H.; Li, Y.; Chen, X.; Duan, J.; Sun, J. Nonlinear analysis of a tall building with large cantilevered steel truss under expected rare earthquake through ABAQUS. World Earthq. Eng. 2015, 31, 210–215. [Google Scholar]
- Chen, P.; Cao, P.; Shi, F.T.; Chen, L.; Pei, X.; Tan, Z.F. Bolted connections in prefabricated cantilevered cap beam-column structures: A comprehensive experimental and numerical study. Eng. Struct. 2024, 310, 118124. [Google Scholar] [CrossRef]
- Veganzones, J.J.; Pacoste, C.; Karoumi, R. Width and Edge Beam Effects on the Ultimate Behaviour of RC Bridge Overhangs. Nord. Concr. Res. 2019, 61, 131–152. [Google Scholar] [CrossRef]
- Bu, L.T.; Wang, W.Y.; He, F.L. Shear behavior of RC overhanging beams strengthened with PVA-ECC. J. Hunan Univ. Nat. Sci. 2014, 41, 52–56. (In Chinese) [Google Scholar]
- Munoz, J.J.V.; Pacoste, C.; Pettersson, L.; Karoumi, R. Influence of Edge Beam on Behavior of Bridge Overhangs. ACI Struct. J. 2018, 115, 957–970. [Google Scholar] [CrossRef]
- Donduren, M.S. Determination of displacement and failure loads formed in reinforced concrete construction with overhang and without overhang by ANN modeling. Sci. Eng. Compos. Mater. 2012, 19, 169–176. [Google Scholar] [CrossRef]
- Kim, S.H.; Heo, W.H.; You, D.W.; Choi, J.-G. Vehicle Loads for Assessing the Required Load Capacity Considering the Traffic Environment. Appl. Sci. 2017, 7, 365. [Google Scholar] [CrossRef]
- Lu, Y.; Li, D.; Wang, K.; Jia, S. Study on Solar Radiation and the Extreme Thermal Effect on Concrete Box Girder Bridges. Appl. Sci. 2021, 11, 6332. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, X.; Casas, J.R.; Zhang, M. Probabilistic Modeling of Congested Traffic Scenarios on Long-Span Bridges. Appl. Sci. 2024, 14, 9525. [Google Scholar] [CrossRef]
- Desrosiers, J.; Laporte, G.; Sauve, M.; Soumis, F.; Taillefer, S. Vehicle routing with full loads. Comput. Oper. Res. 1988, 15, 219–226. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Yang, X.S. Random vehicle flow load effect considering axle load. J. Zhejiang Univ. Eng. Sci. 2019, 53, 78–88. (In Chinese) [Google Scholar]
- Wang, B.L.; Lu, P.M. Treatment of vehicle load and axle load model. J. Zhengzhou Univ. Eng. Sci. 2008, 29, 127–131. (In Chinese) [Google Scholar]
- Deng, L.; Wang, W.; Cai, C.S. Effect of pavement maintenance cycle on the fatigue reliability of simply-supported steel I-girder bridges under dynamic vehicle loading. Eng. Struct. 2017, 133, 124–132. [Google Scholar] [CrossRef]
- Ding, L.; Hao, H.; Xia, Y.; Deeks, A.J. Evaluation of Bridge Load Carrying Capacity Using Updated Finite Element Model and Nonlinear Analysis. Adv. Struct. Eng. 2012, 15, 1739–1750. [Google Scholar] [CrossRef]
- Chi, M.R.; Zhang, W.H.; Zeng, J. Influence of partial load on riding quality of vehicle. J. Traffic Transp. Eng. 2010, 10, 38–41. [Google Scholar]
- Gong, J.; Li, W.; Zhao, J.; Feng, M. Research on Probabilistic Model of Highway Bridge Vehicle Loads Non-controlling Area. J. Highw. Transp. Res. Dev. 2010, 27, 40–45, 57. [Google Scholar]
- Lv, G.; Lv, H.; Chen, Z.; Chu, W.; Mao, J. Research on inertia transfer in load simulation of tracked vehicle under complex working conditions. Front. Mater. 2023, 10, 1188411. [Google Scholar] [CrossRef]
- Sun, H.; Guan, X.; Bao, Y.; Xu, Y.; Li, H. Normalising flow-based vehicle load modeling for bridges. Struct. Infrastruct. Eng. 2023. [Google Scholar] [CrossRef]
- Pinkney, B.; Dagenais, M.A.; Wight, G. Dynamic load testing of a modular truss bridge using military vehicles. Eng. Struct. 2022, 254, 113822. [Google Scholar] [CrossRef]
- Chen, Z.; Bao, Y.; Chen, J.; Li, H. Modelling the spatial distribution of heavy vehicle loads on long-span bridges based on undirected graphical model. Struct. Infrastruct. Eng. 2019, 15, 1485–1499. [Google Scholar] [CrossRef]
- Sun, J.S.; Yang, C.F.; Dou, Y.M.; Li, B. Study on the vehicle load of bridge design on heavy traffic highway based on traffic investigation. J. Hebei Univ. Technol. 2009, 38, 91–95. (In Chinese) [Google Scholar]
- Zhang, Y.; Wong, R.C.K. Static and dynamic responses of buried steel pipe under truck load: An experimental study. Eng. Struct. 2024, 312, 118253. [Google Scholar] [CrossRef]
- Ndong, A.K.; Sherif, M.M.; Kassner, B.; Ozbulut, O.E.; Harris, D.K. Refined analysis of steel girder bridges for computation of live load distribution factors considering effects of freight and emergency vehicles. Eng. Struct. 2023, 293, 116630. [Google Scholar] [CrossRef]
- Zou, S.; Cao, R.; Deng, L.; Wang, W. Effect of stress reversals on fatigue life evaluation of OSD considering the transverse distribution of vehicle loads. Eng. Struct. 2022, 265, 114400. [Google Scholar] [CrossRef]
- Yuan, Y.; Han, W.; Li, G.; Xie, Q.; Guo, Q. Time-dependent reliability assessment of existing concrete bridges including non-stationary vehicle load and resistance processes. Eng. Struct. 2019, 197, 109426. [Google Scholar] [CrossRef]
- Sun, Z.; Siringoringo, D.M.; Fujino, Y. Load-carrying capacity evaluation of girder bridge using moving vehicle. Eng. Struct. 2021, 229, 111645. [Google Scholar] [CrossRef]
- Luccioni, B.; Oller, S.; Danesi, R. Coupled plastic-damaged model. Comput. Methods Appl. Mech. Eng. 1996, 129, 81–89. [Google Scholar] [CrossRef]
- Sarikaya, A.; Erkmen, R.E. A plastic-damage model for concrete under compression. Int. J. Mech. Sci. 2019, 150, 584–593. [Google Scholar] [CrossRef]
- GB50011-2010; Concrete Structure Design Code. China Academy of Building Research: Beijing, China, 2010.
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Zarate Garnica, G.I.; Lantsoght, E.O.L.; Yang, Y. Monitoring structural responses during load testing of reinforced concrete bridges: A review. Struct. Infrastruct. Eng. 2022, 18, 1558–1580. [Google Scholar] [CrossRef]
- De Domenico, D.; Messina, D.; Recupero, A. Quality control and safety assessment of prestressed concrete bridge decks through combined field tests and numerical simulation. Structures 2022, 39, 1135–1157. [Google Scholar] [CrossRef]
- Sun, X.Y.; Xu, C.; Wang, H.L.; Chu, J.F. Overloading simulation fatigue experiment of bridge member with and without CFRP reinforcement. J. Zhejiang Univ. Eng. Sci. 2012, 46, 1585–1591. [Google Scholar]
- Shi, Y.; Li, S.; Cong, Y.A. Influence of Dead-load Based Overload on Reliability of Flexural Members of In-service Bridges. J. Highw. Transp. Res. Dev. 2009, 26, 77–81. [Google Scholar]
- Janga, B.; Mohammadi, J. Impact of fatigue damage from overloads on bridge life-cycle cost analysis. Bridge Struct. 2019, 15, 181–186. [Google Scholar] [CrossRef]
- Deng, L.; Yan, W.; Nie, L. A simple corrosion fatigue design method for bridges considering the coupled corrosion-overloading effect. Eng. Struct. 2019, 178, 309–317. [Google Scholar] [CrossRef]
- Ahmed, M.; El Hadi, K.M.; Hasan, M.A.; Mallick, J.; Ahmed, A. Evaluating the co-relationship between concrete flexural tensile strength and compressive strength. Int. J. Struct. Eng. 2014, 5, 115–131. [Google Scholar] [CrossRef]
- Liao, W.C.; Chen, P.S.; Hung, C.W.; Wagh, S.K. An Innovative Test Method for Tensile Strength of Concrete by Applying the Strut-and-Tie Methodology. Materials 2020, 13, 2776. [Google Scholar] [CrossRef]
- Sadovskaya, E.A.; Leonovich, S.N.; Zhdanok, S.A.; Polonina, E.N. Tensile Strength of Nanofibrous Concrete. J. Eng. Phys. Thermophys. 2020, 93, 1015–1019. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Chen, Y.T. Seismic performance of reinforced concrete beam-column joints with diagonal bars wrapped by steel tubes: Experimental, numerical and analytical study. Structures 2024, 59, 105734. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Chen, Y.T.; Tizani, W. Experimental and numerical study on reinforced concrete beam-column joints with diagonal bars: Effects of bonding condition and diameter. Structures 2022, 37, 905–918. [Google Scholar] [CrossRef]
- Shen, X.; Li, B.; Chen, Y.T.; Tizani, W.; Jiang, Y. Relocating plastic hinges in reinforced concrete beam-column joints by mechanically anchored diagonal bars. Eng. Struct. 2022, 251, 113468. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Jiang, H.; Zhuge, P. Experimental Study on the Flexural and Shear Performance of Concrete Beams Strengthened with Prestressed CFRP Tendons. Appl. Sci. 2024, 14, 1237. [Google Scholar] [CrossRef]
- Zhao, L.; Dou, T.; Cheng, B.; Xia, S.; Yang, J.; Zhang, Q.; Li, M.; Li, X. Theoretical Study and Application of the Reinforcement of Prestressed Concrete Cylinder Pipes with External Prestressed Steel Strands. Appl. Sci. 2019, 9, 5532. [Google Scholar] [CrossRef]
- Kim, S.H.; Joung, J.Y.; Choi, K.T.; Jung, C.Y. Experimental load-carrying capacity evaluation of thermal prestressed H beam with steel brackets. J. Constr. Steel Res. 2013, 88, 309–320. [Google Scholar] [CrossRef]
- Osofero, A.I.; Wadee, M.A.; Gardner, L. Numerical Studies on the Buckling Resistance of Prestressed Stayed Columns. Adv. Struct. Eng. 2013, 16, 487–498. [Google Scholar] [CrossRef]

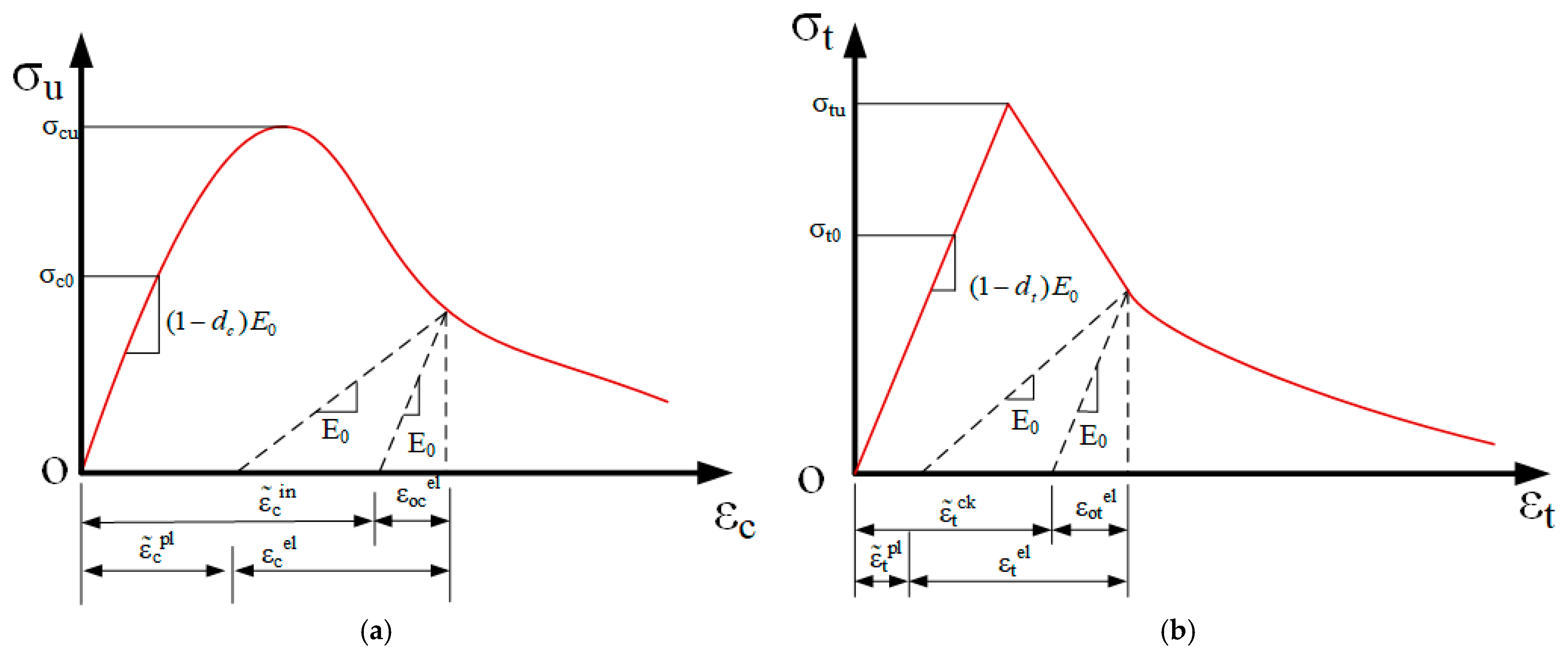
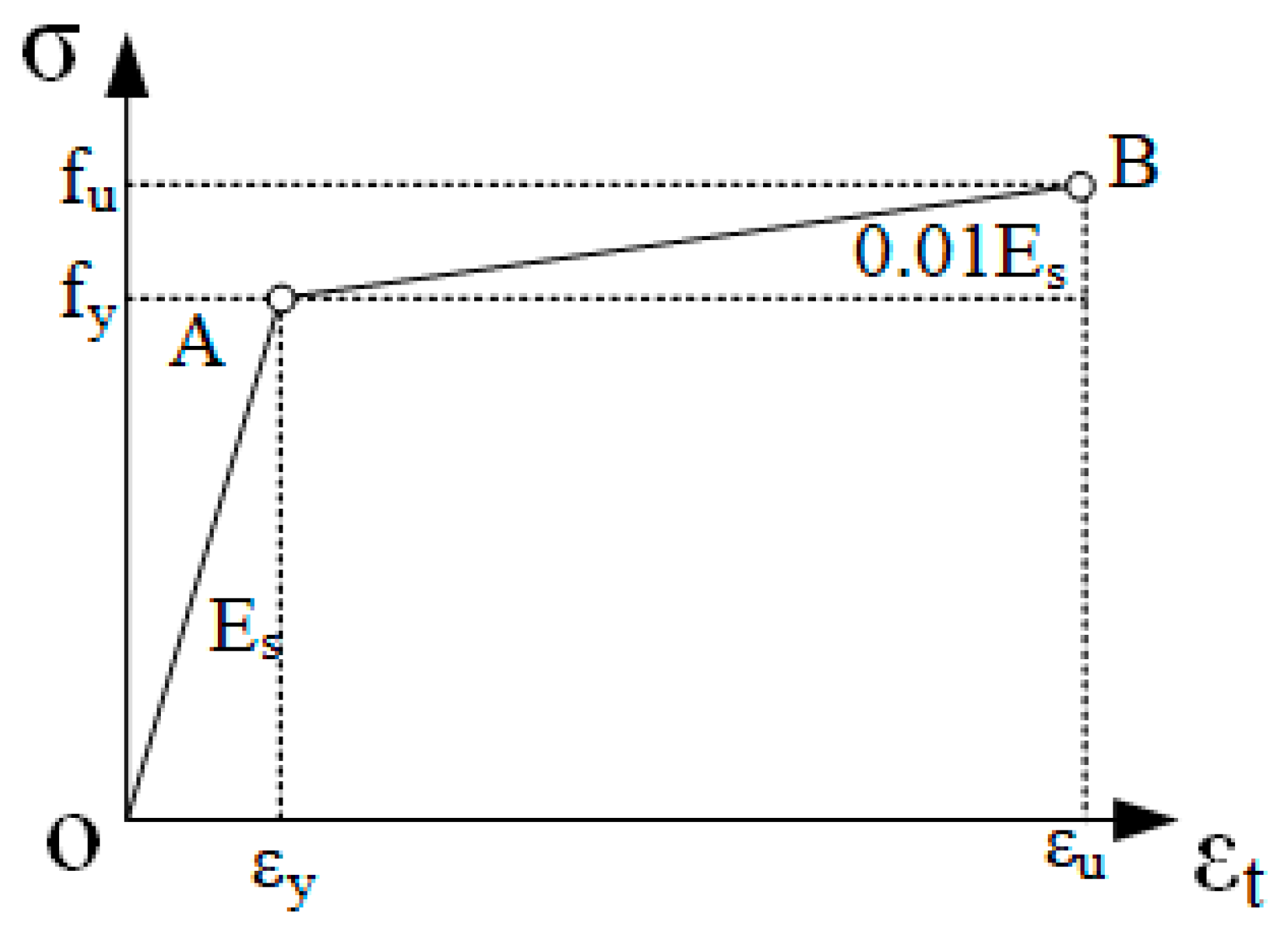


| C50 Concrete | |||||
|---|---|---|---|---|---|
| Compressive Behavior | Tensile Behavior | ||||
| Stress (MPa) | Cracking Strain | Damaged Factor | Stress (MPa) | Inelastic Strain | Damaged Factor |
| 38.19948 | 0 | 0 | 2.34521 | 0 | 0 |
| 43.10004 | 0.00009 | 0.03588 | 2.69435 | 0.00001 | 0.0381 |
| 46.86577 | 0.00018 | 0.05958 | 2.99498 | 0.00001 | 0.05135 |
| 49.21496 | 0.0003 | 0.09141 | 3.21325 | 0.00002 | 0.07359 |
| 50 | 0.00047 | 0.13119 | 3.3 | 0.00003 | 0.10934 |
| 46.18227 | 0.00097 | 0.23777 | 3.08616 | 0.00005 | 0.17877 |
| 42.67332 | 0.00126 | 0.29604 | 2.73549 | 0.00007 | 0.25975 |
| 38.95815 | 0.00156 | 0.35185 | 2.39215 | 0.00009 | 0.33492 |
| 24.30413 | 0.00294 | 0.56056 | 2.09564 | 0.00011 | 0.40014 |
| 22.32143 | 0.00319 | 0.58953 | 1.84995 | 0.00014 | 0.45551 |
| 20.58501 | 0.00344 | 0.61531 | 0.98002 | 0.00025 | 0.67277 |
| 19.06016 | 0.00367 | 0.63835 | 0.91809 | 0.00027 | 0.69023 |
| 12.92085 | 0.005 | 0.73606 | 0.86384 | 0.00028 | 0.70585 |
| 12.2334 | 0.00521 | 0.74764 | 0.81598 | 0.00029 | 0.71989 |
| 11.60991 | 0.00542 | 0.75829 | 0.77345 | 0.00031 | 0.73259 |
| 11.0424 | 0.00563 | 0.76811 | 0.73544 | 0.00032 | 0.74411 |
| 10.5241 | 0.00584 | 0.77718 | 0.70128 | 0.00034 | 0.75463 |
| 10.04921 | 0.00604 | 0.78559 | 0.48623 | 0.00047 | 0.82462 |
| 9.61277 | 0.00625 | 0.7934 | 0.47243 | 0.00048 | 0.82936 |
| 9.21053 | 0.00645 | 0.80068 | 0.4595 | 0.0005 | 0.83382 |
| 8.17443 | 0.00706 | 0.81979 | 0.30496 | 0.00076 | 0.88947 |
| 7.87662 | 0.00726 | 0.82539 | 0.167 | 0.00153 | 0.94216 |
| 3.63523 | 0.01333 | 0.91146 | 0.15656 | 0.00166 | 0.9462 |
| 2.12355 | 0.02106 | 0.94601 | 0.14757 | 0.00179 | 0.94966 |
| 1.92258 | 0.02298 | 0.95082 | 0.13974 | 0.00192 | 0.95268 |
| Expansion Angle | Eccentricity | fb0/fc0 | K | υ |
|---|---|---|---|---|
| 35° | 0.1 | 1.16 | 0.6667 | 0.0005 |
| Material | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| C50 | 2400 | 35 | 0.2 |
| C30 | 2400 | 30 | 0.2 |
| Q345 | 7850 | 210 | 0.3 |
| HRB400 | 7850 | 200 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Yang, S.; Xie, H.; Tan, Z. Analysis of Structural Performance and Design Optimization of Prefabricated Cantilever Systems Under Traffic Loads. Appl. Sci. 2025, 15, 2781. https://doi.org/10.3390/app15052781
Chen L, Yang S, Xie H, Tan Z. Analysis of Structural Performance and Design Optimization of Prefabricated Cantilever Systems Under Traffic Loads. Applied Sciences. 2025; 15(5):2781. https://doi.org/10.3390/app15052781
Chicago/Turabian StyleChen, Liang, Shengwei Yang, Haihui Xie, and Zhifei Tan. 2025. "Analysis of Structural Performance and Design Optimization of Prefabricated Cantilever Systems Under Traffic Loads" Applied Sciences 15, no. 5: 2781. https://doi.org/10.3390/app15052781
APA StyleChen, L., Yang, S., Xie, H., & Tan, Z. (2025). Analysis of Structural Performance and Design Optimization of Prefabricated Cantilever Systems Under Traffic Loads. Applied Sciences, 15(5), 2781. https://doi.org/10.3390/app15052781






