Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study
Abstract
1. Introduction
- How does twisting angle (or lay length) affect for multi-segment cables under typical operating frequencies?
- What is the relative difference in AC losses between very short (tightly twisted) and large (nearly parallel) lay lengths?
- Can an analytical or semi-empirical model describe the trend as a function of lay length?
2. Cable Model and Effective Length in 3D Twisted Conductors
2.1. Overview of the Baseline Cable
2.2. Introducing Twisting: Lay Length Definition
2.2.1. Helical Transformation
2.2.2. Range of Lay Lengths Studied
- LayLength sets the total helical pitch (0.1–5 m), while NumberOfDivisions controls how many increments ( and VGEN) will be used to create the continuous twist;
- The variables OffSetAng and OffSetZ are computed, ensuring a uniform and persise helical extrusion in cylindrical coordinates;
- A DO loop (from lines *DO,i,3,88,1) selects each 2D area in turn (ASEL), then extrudes (VEXT) and replicates (VGEN) the geometry with the appropriate angular and z-axis offset (Figure 4b,c);
- Once the single-fifth twist is complete, it is repeated five times (VGEN,5,ALL) to form the full 360° cross-section (Figure 4d).
2.3. The Effective Length in 3D Models
2.3.1. Numerical Calculation of the Effective Length
2.3.2. Practical Computation of the Effective Length
- Model the cable, including twists, in the FE environment using tetrahedral elements that cover the entire conductor volume;
- Compute the total cable volume V and the total cross-sectional area A for each model;
- From “volume equals to length times cross section area”, infer the effective twisted length .
2.4. Definition of DC Resistances
2.5. Definition of Total Power Loss and AC Resistance
- () is the total power loss due to resistive heating;
- I() is the total current flowing through the conductor;
- () is the conductor’s AC resistance;
- J() is the current density at each point of the volume;
- () is the electrical conductivity of the conductor material;
- represents the infinitesimal volume element.
2.6. Frequency Range and Material Properties
- DC Condition () to confirm that twisting does not change the purely ohmic resistance. is obtained from simulations at this frequency which will then be compared to the numerically calculated DC resistance ;
- AC Condition () as the fundamental cable frequency, representing the predominant frequency in most of the power systems globally. Skin and proximity effects are expected to increase the ohmic power loss in these simulations. These simulations will yield which will then be compared to .
3. Finite-Element Setup
3.1. Geometry and 2D-to-3D Extrusion
3.2. Element Type and Meshing
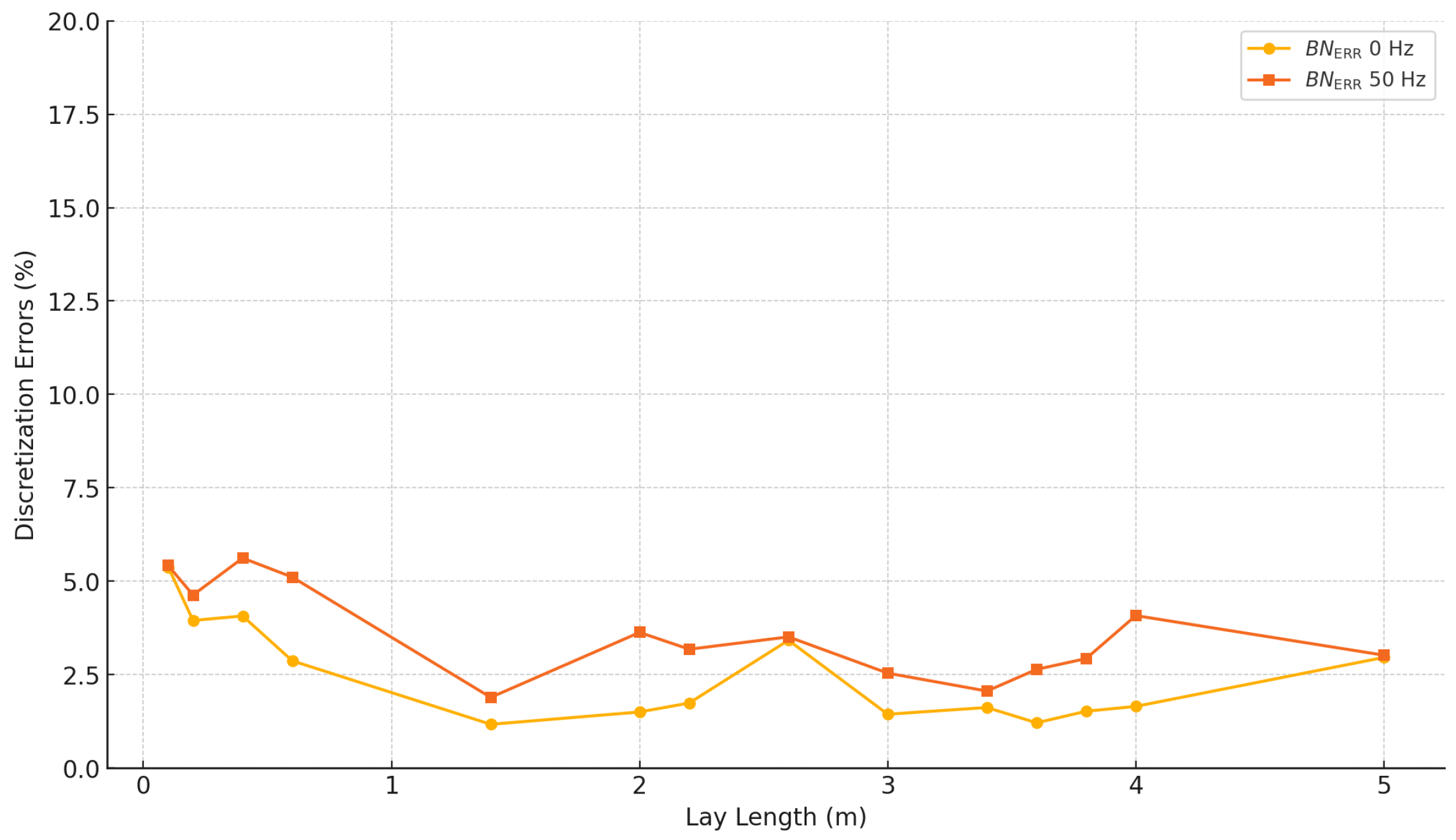
3.3. FE Error Estimates
3.4. Boundary Conditions
4. Two-Dimensional Benchmark Cases
- A solid circular conductor with the same cross-sectional area as the five-segment design;
- The five-segment model, corresponding to a 3D cable with an infinite lay length.
4.1. Solid Circular Conductor
4.2. Five-Segment Conductor (Infinite Lay Length)
5. Results and Discussion
5.1. DC Condition (0 Hz)
5.2. AC Condition (50 Hz)
5.3. Exponential-Saturation Model for
5.4. Total Cable Resistance vs. Per-Unit-Length Resistance
6. Conclusions
- Influence of Lay Length on AC Losses: Over the tested range of lay lengths (0.1 m–5.0 m at 50 Hz), the AC-to-DC resistance ratio varied from about 1.32 (for very tight twists) to nearly 1.72 (for gentle twists). This demonstrates that twisting can markedly change the current distribution and resultant AC losses;
- 3D FE Accuracy vs. 2D Simplifications: Two-dimensional models assume parallel sub-conductors and thus overestimate eddy-current losses, effectively treating lay length as infinite. By contrast, the proposed 3D model reveals how shorter lay lengths help redistribute current more uniformly;
- Exponential-Saturation Relationship: An exponential-saturation model was found to predict with high accuracy () across all studied twists, offering a convenient analytical tool for cable designers;
- Total Cable Resistance vs. Per-Meter Perspective: Although the per-unit-length AC resistance is reduced at shorter lay lengths, the overall helical path is longer, which can increase the total cable resistance. Understanding both effects is key to balancing mechanical robustness with minimal AC losses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okamura, S. Electrical Cables Handbook, 3rd ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Lavers, J.L. Advanced Electromagnetic Analysis of Power Cables: Theory and Practice; IET Press: Stevenage, UK, 2020. [Google Scholar]
- Paice, D.A. Skin effect in multi-layer conductors—The proximity effect. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 1137–1145. [Google Scholar]
- Gross, E.E. Proximity effect in systems of conductors. AIEE Trans. Power Appar. Syst. 1959, 78, 1352–1360. [Google Scholar]
- Rosskopf, A.; Bär, E.; Joffe, C. Influence of Inner Skin- and Proximity Effects on Conduction in Litz Wires. IEEE Trans. Power Electron. 2014, 29, 5454–5461. [Google Scholar] [CrossRef]
- Acero, J.; Lope, I.; Burdío, J.M.; Carretero, C. Loss Analysis of Multistranded Twisted Wires by Using 3D-FEA Simulation. In Proceedings of the Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014. [Google Scholar]
- Reddy, P.B.; Jahns, T.M.; Bohn, T.P. Transposition Effects on Bundle Proximity Losses in High-Speed PM Machines. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 1919–1926. [Google Scholar]
- Sullivan, C.R.; Zhang, R.Y. Analytical Model for Effects of Twisting on Litz-Wire Losses. In Proceedings of the 2014 Conference on Magnetics and Power Electronics, Santander, Spain, 22–25 June 2014. [Google Scholar]
- Plumed, E.; Acero, J.; Lope, I.; Carretero, C. 3D Finite Element Simulation of Litz Wires with Multilevel Bundle Structure. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Piwonski, A.; Dular, J.; Rezende, R.S.; Schuhmann, R. 2-D Eddy Current Boundary Value Problems for Power Cables with Helicoidal Symmetry. IEEE Trans. Magn. 2023, 59, 6300204. [Google Scholar] [CrossRef]
- Morgan, R.B.; Fink, D.G. Method for computing skin and proximity effects in cable conductors. IEEE Trans. Power Appar. Syst. 1975, 94, 344–354. [Google Scholar]
- International Electrotechnical Commission. IEC 60287: Electric Cables—Calculation of the Current Rating; International Electrotechnical Commission: Geneva, Switzerland, 2020. [Google Scholar]
- Brauer, J.R. Magnetic Actuators and Sensors; IEEE Press: New York, NY, USA, 2006. [Google Scholar]
- Saldanha, N. High-frequency modeling of power cables. IEEE Trans. Power Deliv. 2013, 28, 247–256. [Google Scholar]
- Khan, S.; Grattan, K.T.V.; Attwood, J.R. Finite Element Modelling of Skin and Proximity Effects in High Voltage Power Cables. In Proceedings of the COMPUMAG, Evian, France, 2–5 July 2001; pp. 2–5. [Google Scholar]
- Silva, F.J. Power Cables and Their Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- McAllister, R. Handbook of Electrical Engineering Calculations; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- ANSYS Inc. ANSYS Electromagnetics Documentation; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
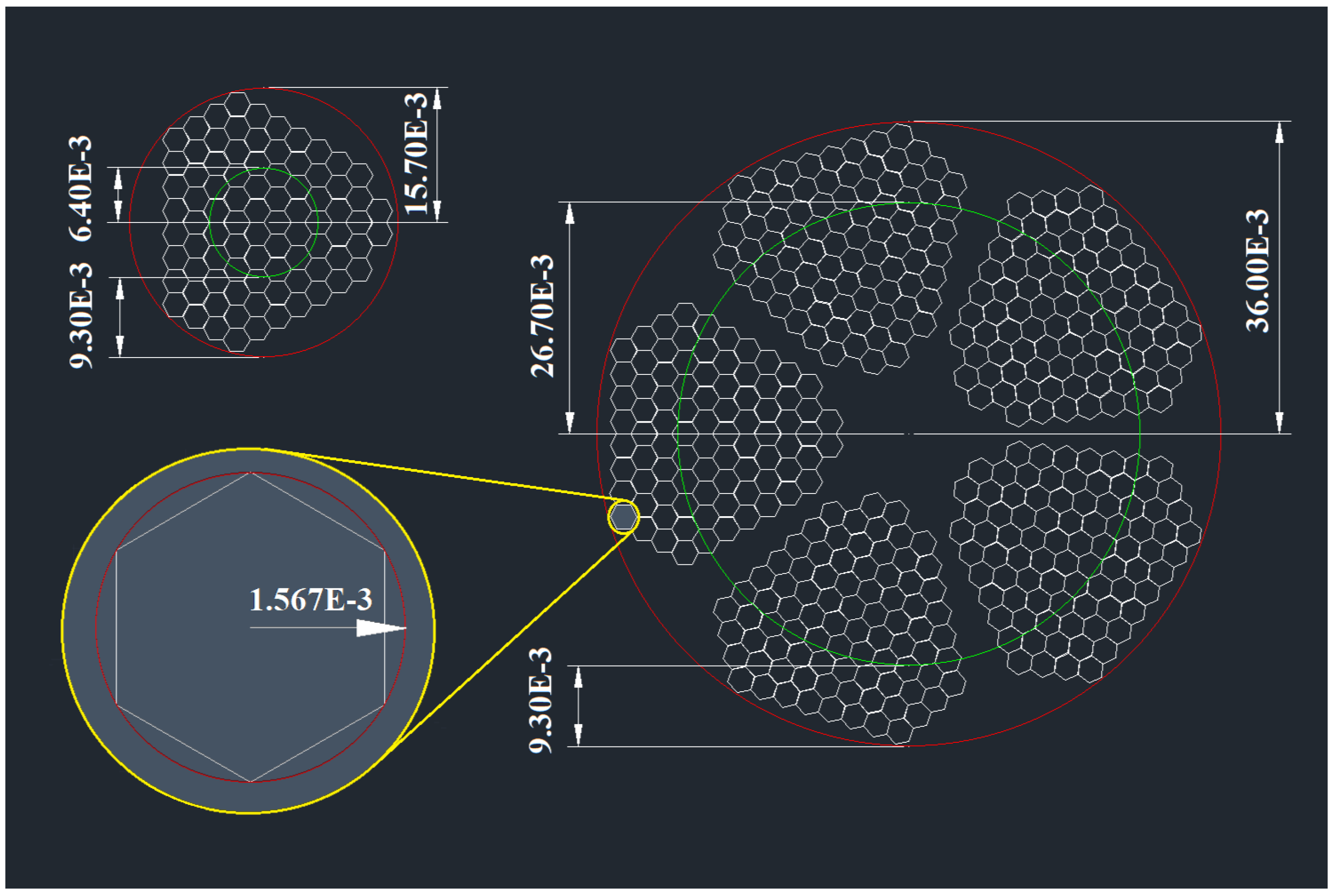
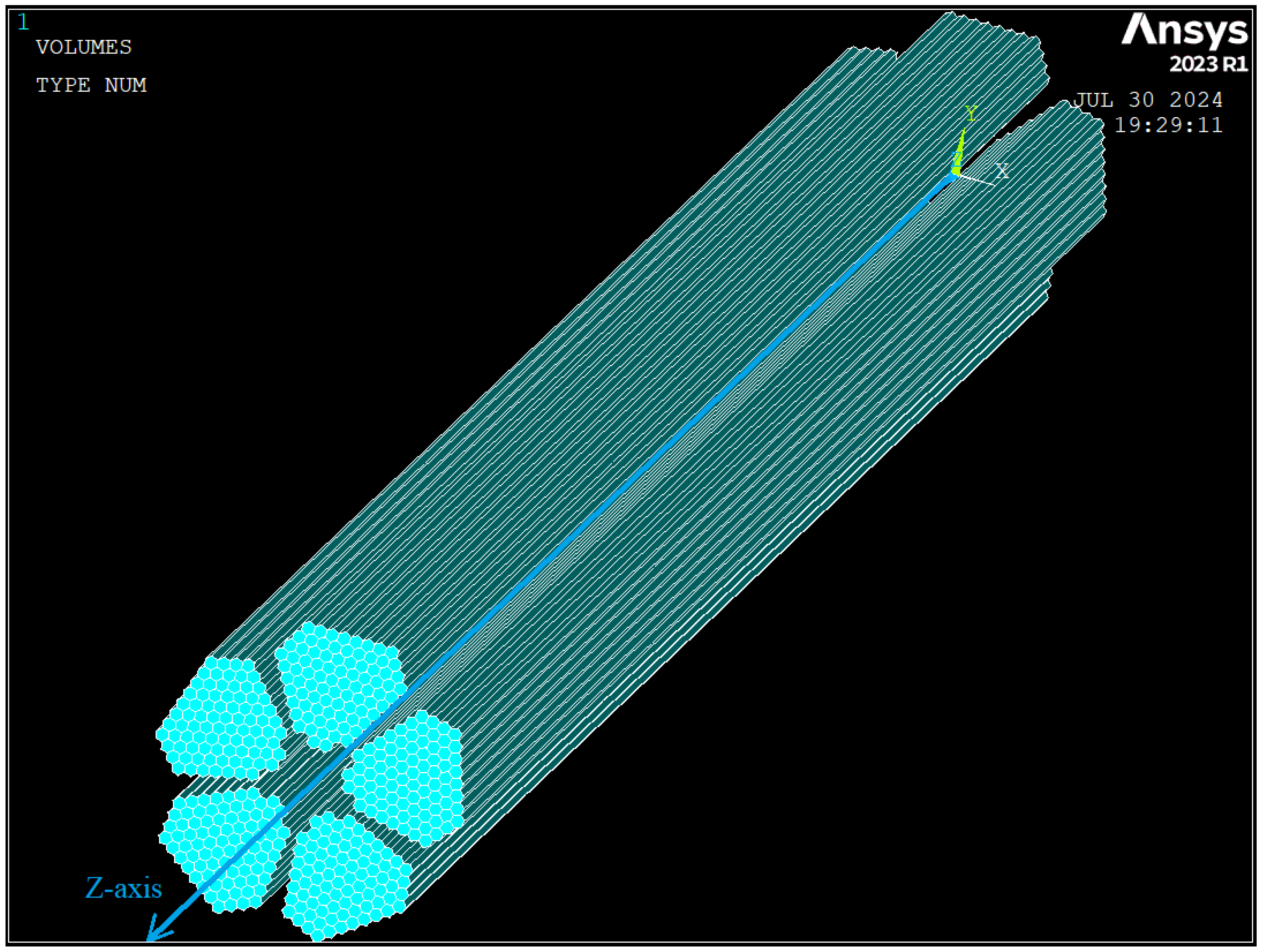
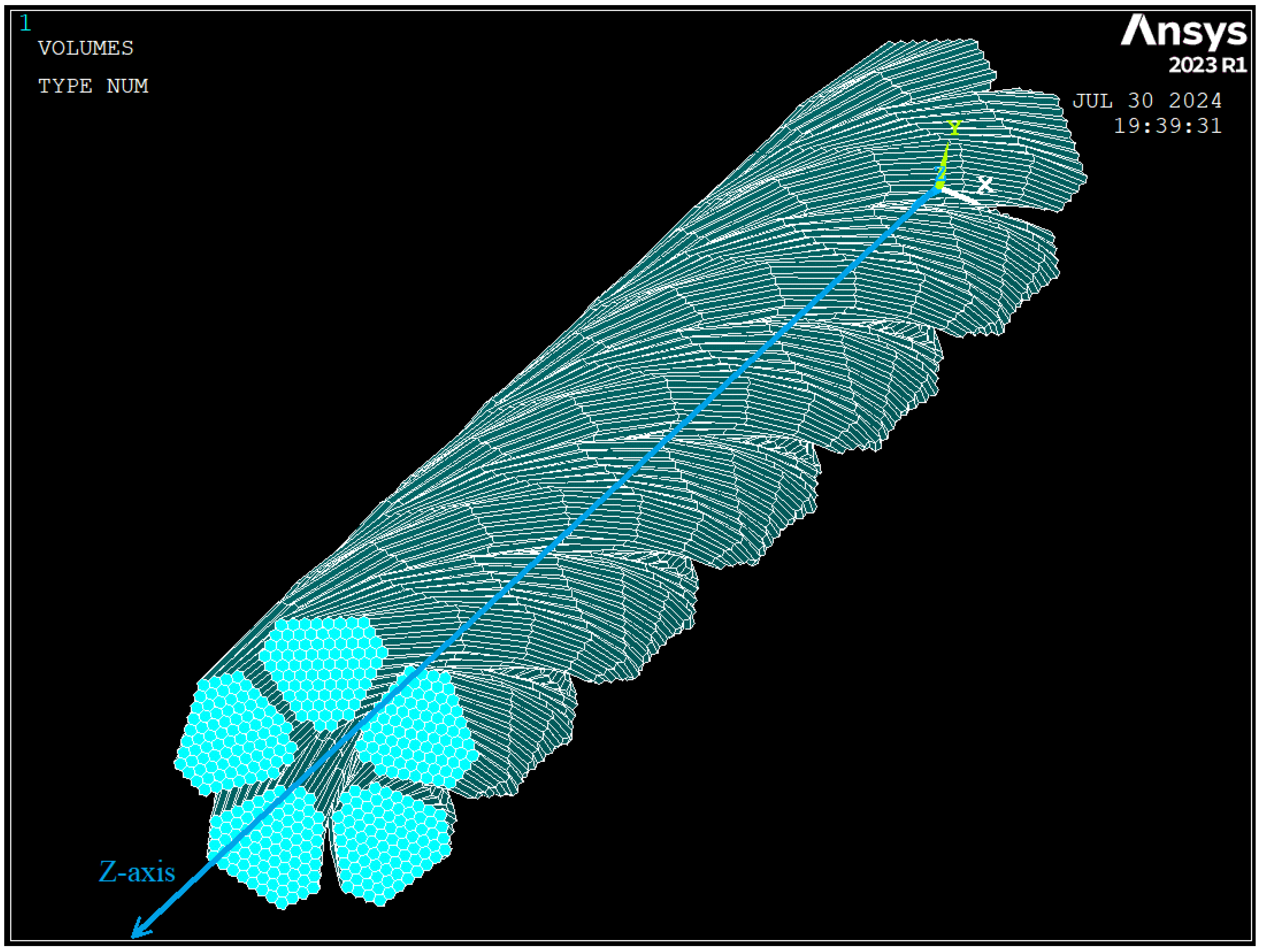
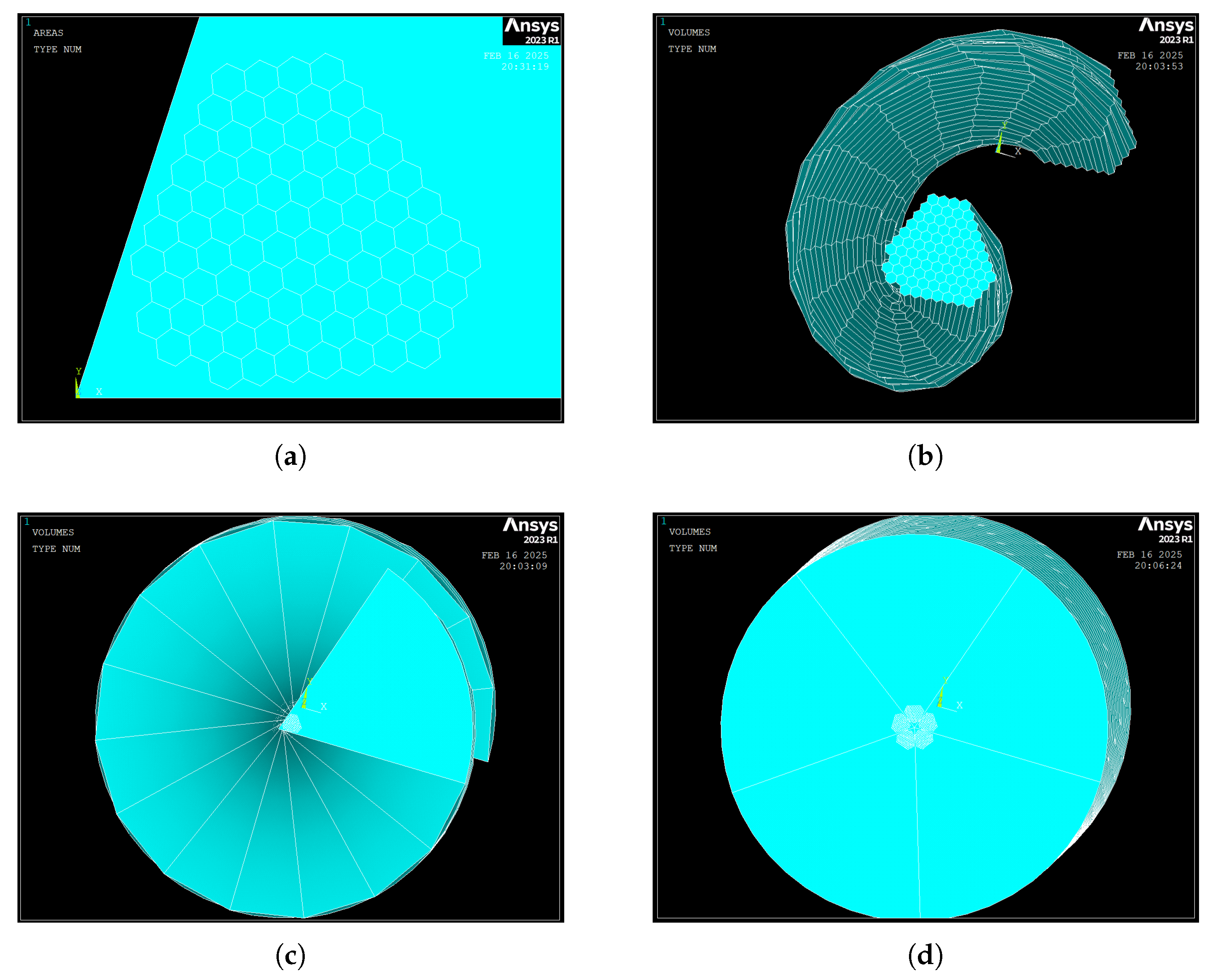





| Material | |||
|---|---|---|---|
| Copper | 1 | ||
| Air | 1 |
| Lay Length (m) | Total Elements | Total Nodes | 0 Hz (%) | 50 Hz (%) |
|---|---|---|---|---|
| 1,016,991 | 1,362,014 | 5.38 | 5.42 | |
| 506,993 | 679,553 | 3.95 | 4.63 | |
| 736,796 | 985,645 | 4.07 | 5.62 | |
| 2,972,972 | 3,963,554 | 2.87 | 5.11 | |
| 3,409,389 | 4,513,492 | 1.17 | 1.89 | |
| 4,742,205 | 6,285,546 | 1.50 | 3.63 | |
| 5,101,876 | 6,760,819 | 1.74 | 3.18 | |
| 5,978,288 | 7,921,663 | 3.42 | 3.51 | |
| 6,754,232 | 8,945,680 | 1.44 | 2.54 | |
| 7,954,225 | 10,535,941 | 1.62 | 2.06 | |
| 8,312,148 | 11,009,740 | 1.21 | 2.64 | |
| 8,713,383 | 11,539,800 | 1.52 | 2.93 | |
| 9,158,742 | 12,127,533 | 1.65 | 4.08 | |
| 11,454,819 | 15,163,705 | 2.96 | 3.02 |
| 2D Model | () | () | |
|---|---|---|---|
| Solid Round Conductor | 6.36 | 11.72 | 1.843 |
| Five-Segment | 6.36 | 11.07 | 1.741 |
(m) | (mW) | () | (m) | () | () | |
|---|---|---|---|---|---|---|
| 0.1 | 0.1709 | 1.709 | 0.2688 | 6.36 | 6.36 | 1.00 |
| 0.2 | 0.1892 | 1.892 | 0.2975 | 6.36 | 6.36 | 1.00 |
| 0.4 | 0.2922 | 2.922 | 0.4594 | 6.36 | 6.36 | 1.00 |
| 0.6 | 0.4127 | 4.127 | 0.6490 | 6.36 | 6.36 | 1.00 |
| 1.4 | 0.9230 | 9.230 | 1.4513 | 6.36 | 6.36 | 1.00 |
| 2.0 | 1.3117 | 13.117 | 2.0625 | 6.36 | 6.36 | 1.00 |
| 2.2 | 1.4416 | 14.416 | 2.2668 | 6.36 | 6.36 | 1.00 |
| 2.6 | 1.7017 | 17.017 | 2.6758 | 6.36 | 6.36 | 1.00 |
| 3.0 | 1.9621 | 19.621 | 3.0852 | 6.36 | 6.36 | 1.00 |
| 3.4 | 2.2226 | 22.226 | 3.4948 | 6.36 | 6.36 | 1.00 |
| 3.6 | 2.3529 | 23.529 | 3.6997 | 6.36 | 6.36 | 1.00 |
| 3.8 | 2.4832 | 24.832 | 3.9046 | 6.36 | 6.36 | 1.00 |
| 4.0 | 2.6135 | 26.135 | 4.1096 | 6.36 | 6.36 | 1.00 |
| 5.0 | 3.2654 | 32.654 | 5.1346 | 6.36 | 6.36 | 1.00 |
(m) | (mW) | () | (m) | () | () | |
|---|---|---|---|---|---|---|
| 0.1 | 0.2263 | 2.263 | 0.2688 | 8.42 | 6.36 | 1.324 |
| 0.2 | 0.2898 | 2.898 | 0.2975 | 9.74 | 6.36 | 1.532 |
| 0.4 | 0.4846 | 4.846 | 0.4594 | 10.55 | 6.36 | 1.659 |
| 0.6 | 0.6974 | 6.974 | 0.6490 | 10.75 | 6.36 | 1.690 |
| 1.4 | 1.5798 | 15.798 | 1.4513 | 10.89 | 6.36 | 1.712 |
| 2.0 | 2.2495 | 22.495 | 2.0625 | 10.91 | 6.36 | 1.715 |
| 2.2 | 2.4732 | 24.732 | 2.2668 | 10.91 | 6.36 | 1.716 |
| 2.6 | 2.9206 | 29.206 | 2.6758 | 10.91 | 6.36 | 1.716 |
| 3.0 | 3.3685 | 33.685 | 3.0852 | 10.92 | 6.36 | 1.717 |
| 3.4 | 3.8165 | 38.165 | 3.4948 | 10.92 | 6.36 | 1.717 |
| 3.6 | 4.0405 | 40.405 | 3.6997 | 10.92 | 6.36 | 1.717 |
| 3.8 | 4.2646 | 42.646 | 3.9046 | 10.92 | 6.36 | 1.717 |
| 4.0 | 4.4887 | 44.887 | 4.1096 | 10.92 | 6.36 | 1.717 |
| 5.0 | 5.6095 | 56.095 | 5.1346 | 10.92 | 6.36 | 1.718 |
(m) | (m) | () | (/m) | (/m) |
|---|---|---|---|---|
| 0.1 | 0.2688 | 2.263 | 8.42 | 22.63 |
| 0.2 | 0.2975 | 2.898 | 9.74 | 14.49 |
| 0.4 | 0.4594 | 4.846 | 10.55 | 12.12 |
| 0.6 | 0.6490 | 6.974 | 10.75 | 11.62 |
| 1.4 | 1.4513 | 15.798 | 10.89 | 11.28 |
| 2.0 | 2.0625 | 22.495 | 10.91 | 11.25 |
| 2.2 | 2.2668 | 24.732 | 10.91 | 11.24 |
| 2.6 | 2.6758 | 29.206 | 10.91 | 11.24 |
| 3.0 | 3.0852 | 33.685 | 10.92 | 11.23 |
| 3.4 | 3.4948 | 38.165 | 10.92 | 11.22 |
| 3.6 | 3.6997 | 40.405 | 10.92 | 11.22 |
| 3.8 | 3.9046 | 42.646 | 10.92 | 11.22 |
| 4.0 | 4.1096 | 44.887 | 10.92 | 11.22 |
| 5.0 | 5.1346 | 56.095 | 10.92 | 11.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, S.; Khan, S.H.; Grattan, K.T.V. Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study. Appl. Sci. 2025, 15, 2814. https://doi.org/10.3390/app15052814
Ahmadi S, Khan SH, Grattan KTV. Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study. Applied Sciences. 2025; 15(5):2814. https://doi.org/10.3390/app15052814
Chicago/Turabian StyleAhmadi, Soheil, S. H. Khan, and K. T. V. Grattan. 2025. "Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study" Applied Sciences 15, no. 5: 2814. https://doi.org/10.3390/app15052814
APA StyleAhmadi, S., Khan, S. H., & Grattan, K. T. V. (2025). Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study. Applied Sciences, 15(5), 2814. https://doi.org/10.3390/app15052814





