Privacy Illusion: Subliminal Channels in Schnorr-like Blind-Signature Schemes

Featured Application

The mitigation techniques presented in this work should be implemented in client-side applications interfacing devices that implement protocols based on blind-signature schemes for critical purposes (such as self-sovereign identity, anonymous credentials, etc.).

Abstract

Blind signatures are one of the key techniques of Privacy-Enhancing Technologies (PETs). They appear as a component of many schemes, including, in particular, the Privacy Pass technology. Blind-signature schemes provide provable privacy: the signer cannot derive any information about a message signed at user’s request. Unfortunately, in practice, this might be just an illusion. We consider a novel but realistic threat model where the user does not participate in the protocol directly but instead uses a provided black-box device. We then show that the black-box device may be implemented in such a way that, despite a provably secure unblinding procedure, a malicious signer can link the signing protocol transcript with a resulting unblinded signature. Additionally, we show how to transmit any short covert message between the black-box device and the signer. We prove the stealthiness of these attacks in anamorphic cryptography model, where the attack cannot be detected even if all private keys are given to an auditor. At the same time, an auditor will not detect any irregular behavior even if the secret keys of the signer and the device are revealed for audit purposes (anamorphic cryptography model). We analyze the following schemes: (1) Schnorr blind signatures, (2) Tessaro–Zhu blind signatures, and their extensions. We provide a watchdog countermeasure and conclude that similar solutions are necessary in practical implementations to defer most of the threats.

1. Introduction

In recent years, blind signatures, first introduced by Chaum in [1], became a popular tool for implementing various privacy-enhancing applications. For example, they are a core component of some anonymous credentials protocols [2]. Another application (widely used in practice) is a protocol for issuing one-time anonymous authentication tokens—Privacy Pass [3]. The tokens of Privacy Pass are blindly signed random values. A token can be redeemed at any time, and it proves that the person redeeming it is known to the token issuer (and, consequently, is not a bot). Similar techniques for anonymous authentication were used by Google One VPN (Virtual Private Network) [4] and are currently used by Apple Private Relay [5]. Moreover, these techniques have even been proposed as an anonymous authentication method for phone users connecting to 4G/5G networks [6].

Further applications of blind signatures may emerge together with the introduction of the European Digital Identity Wallet (EDIW) according to eIDAS 2.0 regulation [7]. (In fact, the consensus of the cryptographic community is that anonymous credentials protocols should be used to implement the EDIW [8], while, as we mentioned earlier, blind signatures are often their main technical component). The eIDAS 2.0 regulation aims to provide space for certificates of attributes and identification/authentication schemes that reveal only the information that is strictly required for a given purpose. For example, an EDIW should be able to prove that its holder is of legal age, e.g., to let them purchase alcoholic beverages. At the same time, neither the seller nor the issuer of the EDIW should be able to learn the buyer’s identity according to the data-minimization security paradigm. Attribute certificates issued with blind-signature protocols may solve this problem of privacy-preservingprotecting age verification. A similar situation may involve certain sensitive healthcare services, where the health insurance company should be able to check the eligibility of a medical transaction but not necessarily the patient’s identity.

In many countries, there are strict rules regarding privacy protection. The GDPR (General Data Protection Regulation) [9] of the European Union states that all information systems must implement privacy protection by design and by default. Moreover, implementing these principles must be demonstrable (accountability principle). Thus, deploying a well-researched technical solution like a blind-signature scheme may be a pragmatic option where demonstrating compliance with the GDPR rules is cheap, easy, and non-disputable.

Sometimes, the situation enforces rapid progress in privacy protection on a global scale, as it was the case with contact-tracing systems during the COVID-19 pandemic. At this time, the need arose to create a method of contact tracing to help identify potentially infected people and alert them before they infect more people. Phone apps notifying users of exposure have been created to address that problem. Of course, such a system had to be developed in a privacy-preserving manner, as information about who interacts with whom can be critical for personal and public security. This privacy-by-design approach was the key feature of the exposure notification privacy-preserving analytics system [10], developed jointly by Apple and Google. As long as users’ smartphones follow the protocol, the users do not have to worry that the generated data will be misused, say, by criminals. This was the key acceptance condition for this technology in countries like Germany, where residents care a lot about their privacy.

1.1. Cryptographic Schemes Versus Black-Box Implementations

Most cryptographic schemes require some secret keys for protocol participants. These keys must be protected, as the sheer possibility of unauthorized use undermines the whole security concept. This philosophy leads to the strategy of encapsulating cryptographic operations and data in a secure environment and restricting access to this environment so that only the requests specified in the cryptographic scheme are processed. In particular, no direct read access to the memory of this secure environment should be granted. This is a sound strategy, as a seemingly innocent read operation might be an element of an unknown attack. Consequently, it is a good practice to use such black-box devices (implemented either in hardware or software) to run cryptographic procedures.

The concept of a cryptographic black box is a double-edged sword. As long as an implementation follows the specification to the letter, the cryptographic security arguments apply. However, how do we know what is executed by a black-box device? It may only look like an honest and flawless implementation of the scheme. In reality, intentional and non-intentional deviations from the ideal implementation might invalidate the security and privacy arguments. A prominent example of this situation was the flaw in Estonian electronic personal identity cards, where a faulty RSA key-generation procedure resulted in citizens’ public keys being compromised [11]. In an ideal situation, an auditor could conclude that the implementation is correct and secure by analyzing the device’s behavior (output correctness on test data, execution time, power consumption, etc.). Unfortunately, this is almost never the case for cryptographic products. First, a lot of effort is put into ensuring that side-channel analysis does not provide any information about the operations performed. This protects the system from attacks but simultaneously limits the auditor’s capabilities.

Given this, the problem is that a protocol implementation may deviate from the specification and cryptography may provide an indistinguishability proof for it. In that case, unless a fundamental cryptographic assumption is broken, no distinguisher has a non-negligible advantage in distinguishing a genuine implementation from a modified one based solely on the device’s input and output. Of course, this does not preclude detection during a destructive physical inspection in a specialized lab.

An attacker might have various goals when manipulating a protocol implementation. The first goal might be to transmit data to a designated receiver covertly. Classic subliminal channels [12] fall into this category. Another purpose of modification might be to leak secret keys stored on the device (and possibly generated there) to the attacker (and to nobody else). Then, these modifications fall into the category of kleptography [13]. Recently, anamorphic channels received a lot of interest: their additional feature in comparison to subliminal channels is undetectability even if the protocol participants are forced to surrender all secret keys present in the protocol according to the original specification to a distinguisher [14].

Subliminal information channels can be used for evil (like kleptography) and good purposes. For example, a malicious implementation of the popular FIDO2 standard may be used to break the unlinkability properties against a designated party [15]. On the other hand, one can hide information (a watermark) in standard signatures created by legitimate devices so that signatures forged by a third party after breaking the public key can be recognized and nulled [16].

In the case of blind signatures, the malicious goal might be to break anonymity guarantees: a malicious device may enable the signer to link the unblinded signature to the device and thereby to its owner. An attack may also involve transmitting covert data in either direction (e.g., the device’s private keys or description of some tasks to be carried out by the device).

We are mainly concerned with devices, like the future European Digital Identity Wallet (EDIW), which must be developed according to the privacy-by-design approach while implementing digital signature schemes and strong authentication protocols with user attributes. This inevitably leads to an architecture where the cryptographic functionalities are executed in a black box.

Research Problem

The problem we consider in this paper is the following:

Problem 1.

Are blind-signature schemes immune against malicious implementation setups that invalidate the privacy properties of blind signatures and are undetectable from the point of view of an auditor in the anamorphic cryptography model, where an auditor can request the secret keys?

If yes, are such latent attacks simple enough to be applicable in practice? Is it possible to prevent them in a pragmatic way?

1.2. Our Contribution

We introduce a formal model for creating covert/subliminal channels in blind-signature schemes with a black-box device. We present multiple methods of creating such subliminal channels in blind Schnorr signatures [17,18] and recent extensions of Schnorr signatures [19,20,21]. We then show how to use these subliminal channels to break the blindness/unlinkability property of the aforementioned schemes and how to securely transmit covert messages in the presence of a powerful auditor. These attacks remain undetectable even if the auditor requests private keys that exist according to the system specification (anamorphic cryptography model [14]).

We also show methods of mitigating subliminal channels for the schemes mentioned. Typically, the defense is based on an external watchdog, which serves as a proxy between the client’s black-box device and the signing server. In the context of this work, the watchdog can be considered an open-source client application trusted by the user.

1.3. Impact of the Findings

The goal of this paper is to provide strong arguments for caution in putting to use cryptographic products promising privacy protection. We show that we cannot rely solely on the cryptographic strength of blind-signature schemes—including the most prominent ones—and we have to control the actual implementation effectively. Otherwise, a product promising privacy-by-design might turn out to be a Trojan horse and serve rather as a Big Brother system. We show what can and will go wrong.

Understanding the attack potential is the first step of preventing them. As blind signatures may become an essential primitive in the context of the GDPR and eIDAS2.0 regulations and the concept of Self-Sovereign Identity (SSI), the issues discussed here may profoundly impact security and privacy protection in the wild. Note that online information systems will often have to deal with sensitive personal information, so we expect widespread use of blind signatures shortly, e.g., for attribute-based authentication and authentication tokens.

In the paper, we show simple and fairly straightforward methods of muting (closing) the subliminal channels and thus mitigating the aforementioned attacks. We believe that these countermeasures should be implemented in all client applications that interface black-box devices as long as we are not absolutely sure about the black-box implementation.

1.4. Structure of the Article

In Section 2, we present related work. In Section 3, we describe the mathematical notation used in the paper and introduce cryptographic models for the blind-signature schemes with a black-box device on the user’s side. We also discuss types of attacks in our model alongside our assumptions and their rationale. In Section 4, we briefly recall the Schnorr blind-signature scheme and present attacks. We start with a secret key agreement, and then expand it to linking attacks (revealing which device has created an unblinded signature). Finally, we show how to create covert channels between the user’s device and the signing server, undetectable for the user and for the auditor. The attack details differ depending on whether the attack results are available after presenting an unblinded signature or immediately after blind-signature creation. Then, we show that a watchdog between the user device and the signing service would effectively block the attacks. In Section 5, we perform a similar analysis for the Tessaro–Zhu blind-signature scheme and its extensions proposed recently. We show that the modifications made to these constructions to strengthen their model turn into weaknesses in the more realistic setting, as they allow for anamorphic channels. Again, we show that there is an effective defense based on a watchdog. Section 6 is reserved for conclusions and laying out future work.

2. Related Work

Blind-signature schemes have been around for a long time. Due to that, they are quite well researched and have a well-scrutinized security model [22,23] that captures the properties of one-more-unforgeability and malicious signer blindness. Many works are enhancing blind signatures with additional features, like, e.g., non-interactivity [24], post-quantum security [25], partial blindness [26], etc.

Anamorphic channels in generic signature schemes have been studied in [27]. The Dictator model used in [27] and in our work has been introduced in [14].

The watchdog countermeasure implemented in this work is somewhat similar to the concept of trusted “amalgamation” functions defined in [28] (where the suspected subverted protocol $\mathrm{\Pi }$ is decomposed into multiple parts and then amalgamated by some trusted function in a way that closes the subliminal channel) and used, e.g., in [29] to achieve subversion resilience.

3. Methods

In this section we describe the notation, define cryptographic models, and present the threat model and assumptions used in subsequent analysis.

3.1. Notation

In the paper, we use multiplicative group notation, although a target implementation may be based on elliptic curves, where additive group notation is typically used. For simplicity of presentation, we assume that the computations are performed $\mathrm{mod}p$ for a prime number p unless stated otherwise. Let $g\in {\mathbb{Z}}_p$ be an element of prime order q. We use a subgroup $\langle g\rangle$ of ${\mathbb{Z}}_p$ generated by g. However, most considerations apply almost directly to elliptic curve groups. If any non-trivial modification is required, we indicate the necessary changes.

We define a cryptographically secure hash function ${\mathrm{H}}_1:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_q^{\ast }$ that maps any bit string to a number in ${\mathbb{Z}}_q^{\ast }$. In addition, when we use without any index, we refer to any standard cryptographically secure hash function such as, e.g., SHA-3.

By $(a,b,c,\dots )$, we denote applying the function to a single input $a\parallel b\parallel c\parallel \dots$, where ∥ denotes concatenation. Sampling uniformly at random, an element x from set S is denoted by $xS$. We also define the $\mathsf{bitlen}\left(x\right)$ function to return $\lceil \log x\rceil$ (the bit length of x). We let $a_{\{i,\dots ,j\}}$ denote the substring of a starting at position i and terminating at position j. By $x=\mathsf{PRNG}\left(\mathit{seed}\right)$, we mean taking a value x from a pseudorandom number generator $\mathsf{PRNG}$ seeded with the value $\mathit{seed}$. The exact format of the value x will follow from the context of invocation of $\mathsf{PRNG}$. (For simplicity, we overload the notation; sometimes we need $\mathsf{PRNG}$ to return, e.g., a 32-byte number, and other times to return an element from ${\mathbb{Z}}_q^{\ast }$.)

For interactive algorithms $\mathcal{A}$ and $\mathcal{B}$, by $(a,b)\leftarrow \langle \mathcal{A}\left(x\right),\mathcal{B}\left(y\right)\rangle$ we denote joint execution, where x is the private input of $\mathcal{A}$, y is the private input of $\mathcal{B}$, a is the private output of $\mathcal{A}$, and b is the private output of $\mathcal{B}$.

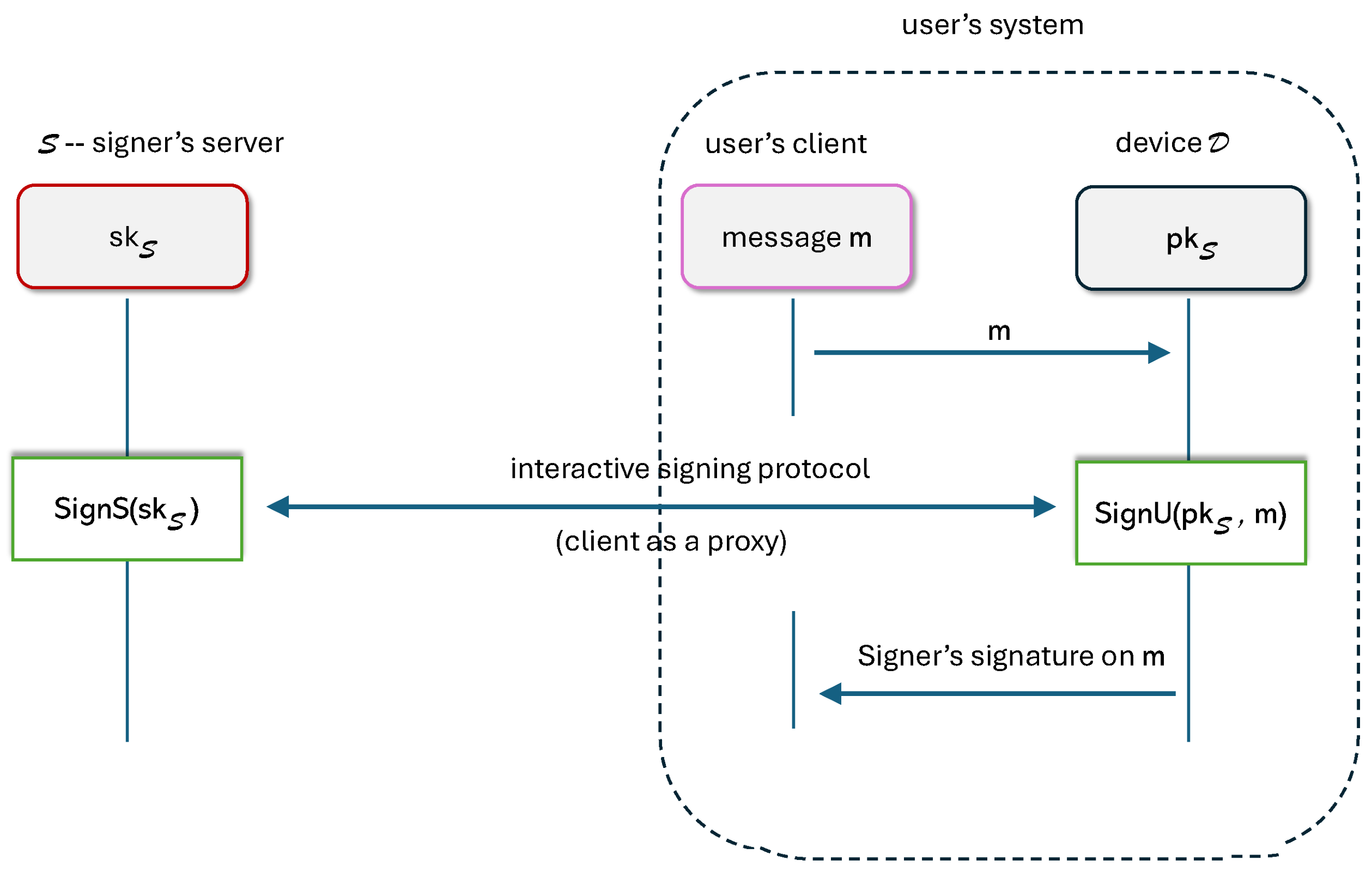
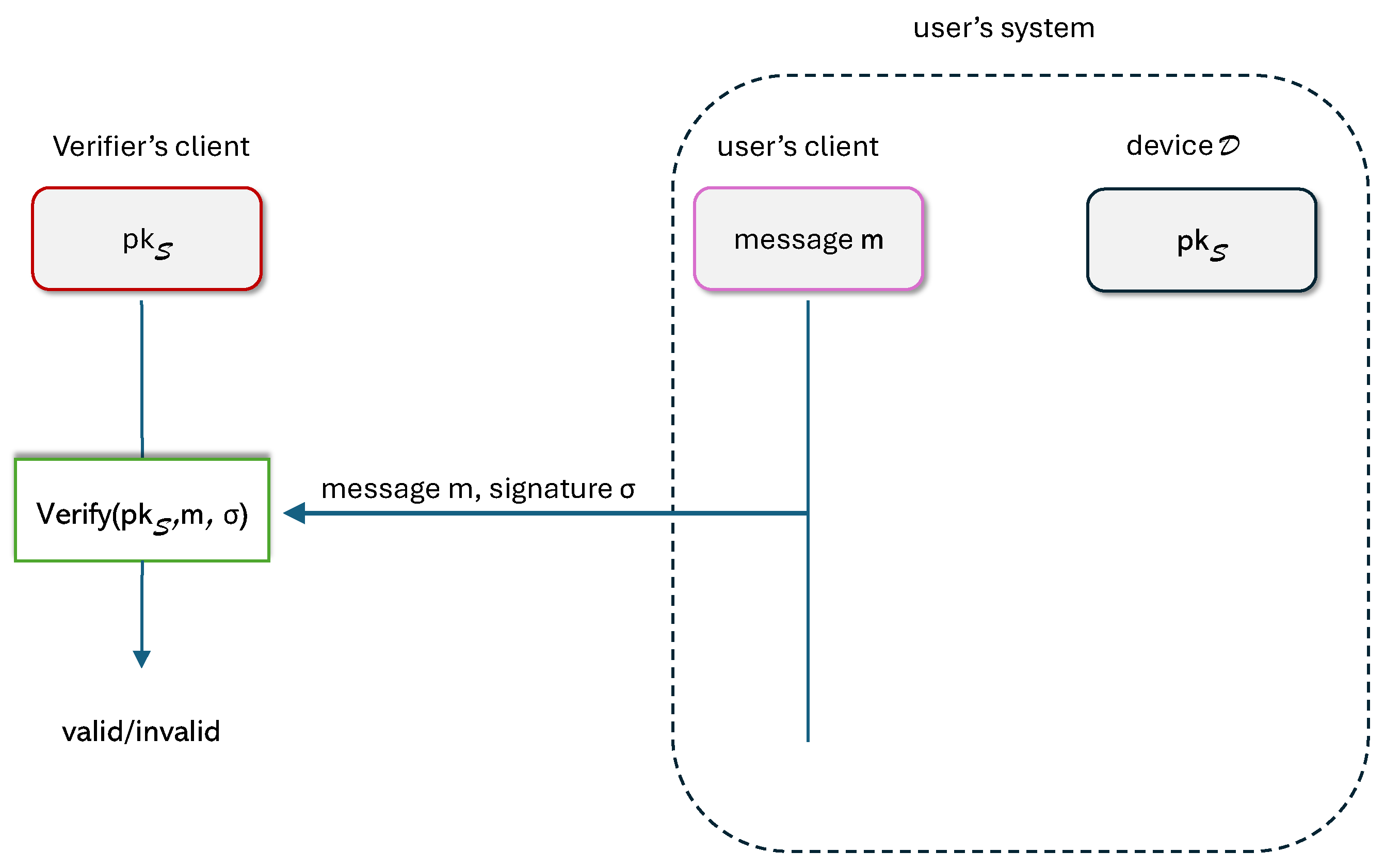
3.2. Blind Signatures

A blind-signature scheme enables a User $\mathcal{U}$ to obtain digital signatures of a Signer $\mathcal{S}$ for arbitrarily chosen messages. The key feature of a blind-signature scheme is that $\mathcal{S}$ not only does not see the signatures created in interaction with the User but also cannot determine which message has been signed for whom if all these signatures are presented to $\mathcal{S}$.

In more detail, there are the following roles in the protocol:

• Signer $\mathcal{S}$ is a party that holds private signing keys and signs (blindly) messages on request of Users,
• User $\mathcal{U}$ is a party that requests signatures of $\mathcal{S}$ over chosen messages; all cryptographic operations of the scheme are executed by a black-box device $\mathcal{D}$ of $\mathcal{U}$ (we assume that $\mathcal{D}$ may have a pair of keys ${\mathsf{sk}}_{\mathcal{D}}\in {\mathbb{Z}}_q^{\ast },{\mathsf{pk}}_{\mathcal{D}}=g^{{\mathsf{sk}}_{\mathcal{D}}}$ used, e.g., for authentication);
• A verifier $\mathcal{V}$ checks the signatures allegedly created by $\mathcal{S}$.

A practical use case of a blind-signature scheme according to our model can be seen on Figure 1 (User login), Figure 2 (blind-signature creation) and Figure 3 (signature verification). Sometimes, the Signer and the Verifier are the same party, as the Signer can apply the verification procedure to signatures that appear on the market. Note that, in practice, $\mathcal{U}$ stands also for some electronic devices, but, in contrast to $\mathcal{D}$, it can be controlled (at least to some extent) by its owner— a physical person.

A blind-signature scheme consists of three procedures:

Definition 1.

(Blind-Signature Scheme). A blind-signature scheme Π is a tuple of algorithms $\mathrm{\Pi }=(\mathsf{Gen},\langle \mathsf{SignS},\mathsf{SignU}\rangle ,\mathsf{Verify})$, where:

1.

The  key-generation procedure  $\mathsf{Gen}\left({\mathsf{1}}^{\mathsf{n}}\right)$ takes as input the security parameter n and outputs a pair of signing keys $(\mathsf{sk},\mathsf{pk})$ for the Signer $\mathcal{S}$.

2.

The  signing procedure is an interactive protocol, where $\mathcal{S}$ runs $\mathsf{SignS}\left(\mathsf{sk}\right)$, and $\mathcal{D}$ runs $\mathsf{SignU}(\mathsf{pk},\mathsf{m})$ on behalf of a User:

$$(\perp ,\sigma )\leftarrow \langle \mathsf{BSignS}\left(\mathsf{sk}\right),\mathsf{SignU}(\mathsf{pk},\mathsf{m})\rangle$$

For message $\mathsf{m}\in \mathcal{M}$ ($\mathcal{M}$ is the set of possible messages to be signed), the joint execution outputs a signature σ on the side of the User $\mathcal{U}$. A transcript $\mathcal{T}$ of the interaction (all messages exchanged between $\mathcal{S}$ and $\mathcal{D}$ during joint execution) is visible to all parties (including, in particular, the User).

3.

The verification procedure $\mathsf{Verify}(\mathsf{pk},\mathsf{m},\sigma )$ takes as input a public key $\mathsf{pk}$, a message $\mathsf{m}$, and a signature σ. It returns a bit $b\in \{0,1\}$, where 1 stands for ‘the signature is valid’.

For  correctness, we require that for any keypair $(\mathsf{sk},\mathsf{pk})$ generated by $\mathsf{Gen}$ and a message $\mathsf{m}\in \mathcal{M}$:

$$\mathbf{if}(\perp ,\sigma )\leftarrow \langle \mathsf{SignS}\left(\mathsf{sk}\right),\mathsf{SignU}(\mathsf{pk},\mathsf{m}))\rangle ,\mathbf{then}\mathsf{Verify}(\mathsf{pk},\mathsf{m},\sigma )=1.$$

Properties of Blind Signatures

There are two fundamental security and privacy properties of blind signatures:

• One-more unforgeablity: This property captures the unforgeability of signatures: no signature can be created without running the interactive procedure with $\mathcal{S}$. Namely, in the security game, the Adversary can interact with $\mathcal{S}$ and receive valid signatures ${\sigma }_i$ for $i\in \{1,\dots ,n\}$ on messages ${\mathsf{m}}_i$ of their choice. The Adversary wins if they can present a valid signature ${\sigma }_{\ast }\notin \{{\sigma }_1,\dots ,{\sigma }_n\}$.
  The scheme satisfies one-more unforgeability property if the probability of winning the game by the Adversary is negligible.
• Blindness: This property captures the fact that $\mathcal{S}$ cannot link the signatures with the sessions executed with the User. It is expressed by the following game: first, the Adversary chooses messages ${\mathsf{m}}_0$, ${\mathsf{m}}_1$, generates signing keys $(\mathsf{sk},\mathsf{pk})$, and sends ${\mathsf{m}}_0$ and ${\mathsf{m}}_1$ to the User. Next, the User chooses a bit b at random. Then, two instances of blind signing procedures are started (and possibly run concurrently) with the Adversary being the Signer. In the first instance, the User obtains a valid signature of ${\mathsf{m}}_b$ signed with $\mathsf{sk}$; in the second, it obtains a valid signature for ${\mathsf{m}}_{1-b}$ signed with $\mathsf{sk}$. The resulting valid unblinded signatures ${\sigma }_0,{\sigma }_1$ are presented to the Adversary. The Adversary presents a bit $b^{\prime }$ and wins the game if $b=b^{\prime }$.
  The scheme satisfies the blindness property if the probability of winning the game by the Adversary is ${\displaystyle \frac{1}{2}}+ϵ$, where $ϵ$ is a negligibly small value.

In a standard use case, the User is authenticated before starting the signature creation procedure by the Signer $\mathcal{S}$, since typically, signing blindly is a service offered only to entitled Users. Hence, by presenting a valid signature $\sigma$ of $\mathcal{S}$, the User implicitly proves that $\sigma$ has been obtained by an eligible party.

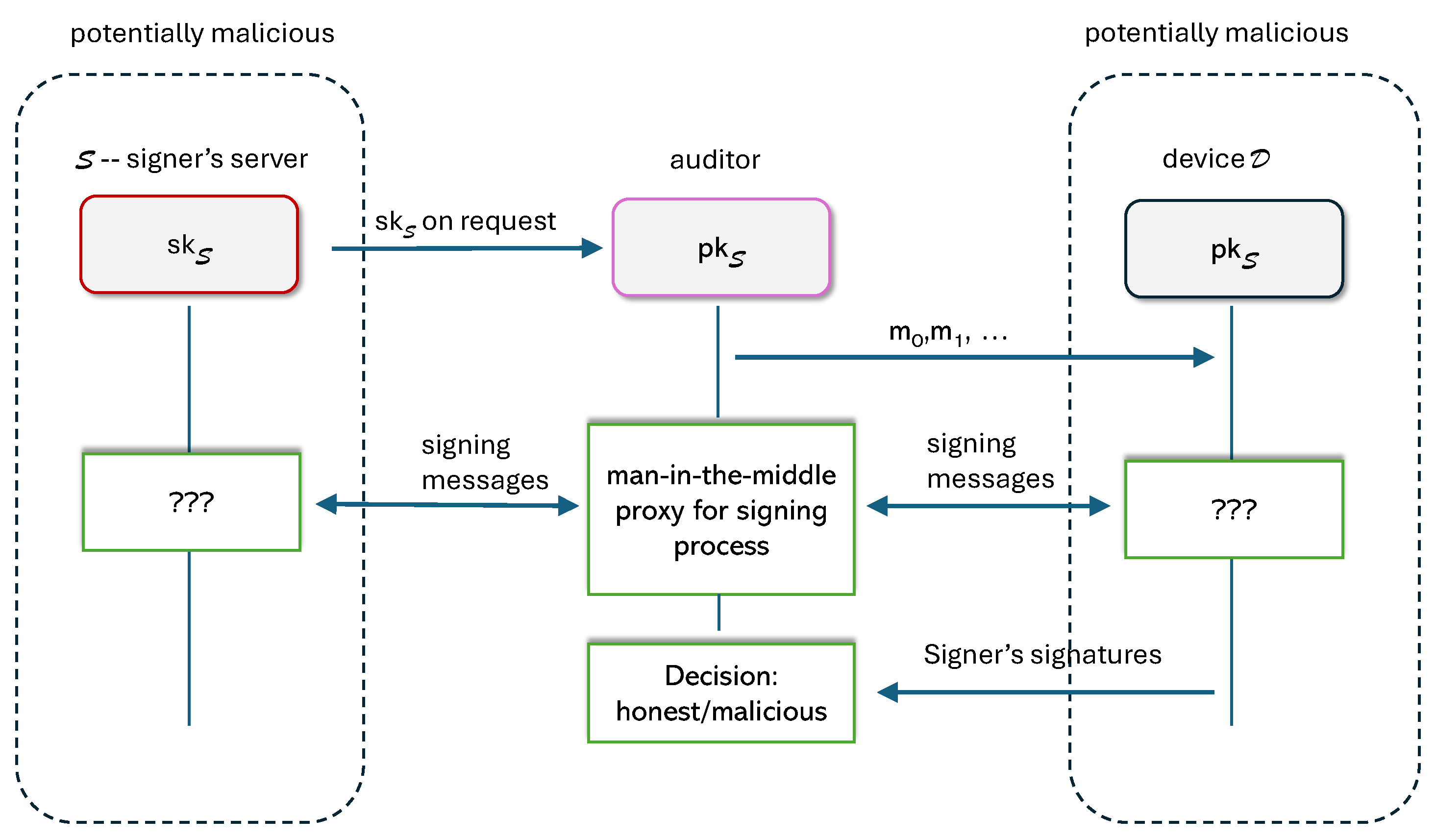
3.3. Audit and Threat Model

We consider blind-signature schemes for which cryptographic proofs for blindness and one-more-unforgeability features already exist. For these proofs, the Adversary is either a malicious Signer (eager to learn what he signs) or a malicious User (aiming to derive more signatures of $\mathcal{S}$ than requested).

The scenario that we consider is different but motivated by privacy protection in the wild: we consider the case where the Signer $\mathcal{S}$ and a device $\mathcal{D}$ attempt to cheat the User holding $\mathcal{D}$. In almost all cases, the User can neither inspect the Signer nor check $\mathcal{D}$. All the User can do is eavesdrop on the messages exchanged between $\mathcal{S}$ and $\mathcal{D}$ and, possibly, inspect some security declarations and/or certificates for $\mathcal{D}$ and $\mathcal{S}$ issued by third parties. Persuaded by the certificates and provable but theoretical properties of a blind-signature scheme, the User may have a false sense of security and privacy. Namely, the certificates and declarations might be meaningless since the User may be given a malicious device different from those that undergo the certification process, and $\mathcal{S}$ may run the services not as declared. As long as there are no observable protocol deviations, the User might be in a lost position.

There are a few attack vectors carried out by the colluding Signer $\mathcal{S}$ and device $\mathcal{D}$:

• Unblinding known signatures: This attack enables $\mathcal{S}$ to decide whether a given signature $\sigma$ has been created during a given session with $\mathcal{D}$ (effectively showing which device has derived $\sigma$); the attack may require the message signed by $\sigma$. If effective, this attack dismantles privacy protection for signatures that emerge on the market.
• Immediate unblinding: This attack enables $\mathcal{S}$ to derive the same unblinded signature as that obtained by $\mathcal{D}$ while running the blind-signature creation procedure;
• Covert transmission to Signer: In this attack, $\mathcal{D}$ sends a covert message to $\mathcal{S}$ during blind-signature creation. In particular, the covert message can contain the message to be signed blindly for immediate unblinding.
• Covert transmission to device: In this attack, $\mathcal{D}$ sends a covert message to $\mathcal{S}$ during blind-signature creation. In particular, the covert message can contain secret instructions for the device.

In all the above cases, the Signer, which has been deployed as an important component of the privacy protection ecosystem, turns out to be a “Big Brother” spying on its Users.

To prevent the mentioned attacks, one must either redesign the schemes so that the Users obtain more control over the situation or run an appropriate audit and certification framework together with a strict evaluation of the cryptographic schemes. Somehow, the second approach is the strategy more frequently implemented in practice.

3.3.1. Auditor Model

In this paper, we consider the model of a Dictator (in our work called an Auditor) borrowed from [14] and subsequently also applied to digital signatures [27].

Definition 2

(Auditor). An Auditor $\mathcal{J}$ can observe any interaction between $\mathcal{S}$ and $\mathcal{D}$ (see Figure 4). Following the anamorphic cryptography concept, $\mathcal{J}$ may require $\mathcal{S}$ and/or $\mathcal{D}$ to hand over all private keys they should hold for protocol execution. In particular, this concerns the signing key of $\mathcal{S}$ and data used to authenticate $\mathcal{D}$ against $\mathcal{S}$. Based on that, $\mathcal{J}$ can analyze all past interactions between $\mathcal{S}$ and $\mathcal{D}$ (presumably recorded for this purpose).

Note that Definition 2 makes a silent assumption that after surrendering the keys to $\mathcal{J}$, the public key $\mathsf{pk}$ of the Signer $\mathcal{S}$ must be revoked. Indeed, one cannot claim anymore that a signature verified with $\mathsf{pk}$ originates from $\mathcal{S}$.

Note that according to the definition, $\mathcal{J}$ will obtain any private key created outside the scope of scheme specification (so-called dual keys according to the terminology in [14]). The queried parties can claim that such keys do not exist.

In anamorphic cryptography, the name “Dictator” is used for the entity that requests the private keys from protocol participants. In our case, the Dictator is on the “good” side, helping to thwart the attacks against Users’ privacy. Hence, we use a neutral Auditor term to avoid confusion. In real-world applications, it is easy to imagine that in cases of a suspected attack of the described kind, a competent authority may request access to valid keys from the legal entity that provides the blind signing service and access to the keys used by the devices. These prerogatives can be well motivated by obligations to supervise critical trust services.

Last but not least, due to advances in cryptanalytic algorithms and hardware, the Signer’s public key can be broken at some point. So, the model considered applies immediately.

3.3.2. Indistinguishability

The main objective of malicious parties $\mathcal{S}$ and $\mathcal{D}$ is to run the blind-signature scheme so that the goals of an attack are fulfilled, while on the other hand, $\mathcal{J}$ has no chance to detect deviations from the original protocol. “Impossibility” can be captured formally by the following left-or-right game.

Definition 3

(Indistinguishability Game). The game consists of the following phases:

• $\mathcal{S}$ and $\mathcal{D}$ choose jointly a bit $b\in \{0,1\}$ uniformly at random,
• If $b=0$, they install the original blind-signature scheme Π. If $b=1$, they install a modified scheme ${\mathrm{\Pi }}^{\prime }$ implementing the attack.
• $\mathcal{J}$ inspects $\mathcal{S}$ and $\mathcal{D}$ as described in Definition 2.
• $\mathcal{J}$ outputs a bit $b^{\prime }$.

If $b^{\prime }=b$, then $\mathcal{J}$ wins the game.

Definition 4.

We say that the schemes ${\mathrm{\Pi }}^{\prime },\mathrm{\Pi }$ are indistinguishable for an auditor $\mathcal{J}$ if $\mathcal{J}$ wins the game from Definition 3 with probability ${\displaystyle \frac{1}{2}}+ϵ$, where ϵ is a negligible value.

3.4. Watchdog Defense

We shall find that for many important blind-signature schemes $\mathrm{\Pi }$, one can find a modified malicious scheme ${\mathrm{\Pi }}^{\prime }$ implementing one of the above-mentioned attacks so that $\mathrm{\Pi }$ and ${\mathrm{\Pi }}^{\prime }$ are indistinguishable. In this situation, due to the fundamental role of blind signatures in many trust services, it is necessary to find a remedy to the situation.

In our opinion, the easiest way is to create a watchdog $\mathcal{W}$ running in the User’s system and serving as a man-in-the-middle between $\mathcal{S}$ and $\mathcal{D}$. For pragmatic reasons, $\mathcal{W}$ should be in some sense transparent to $\mathcal{S}$ and $\mathcal{D}$: if they run their protocol honestly, they will not notice any change in the protocol behavior. However, if they run a modified malicious protocol, $\mathcal{W}$ should prevent them from achieving attack goals.

Typically, a watchdog randomizes any nondeterministic element transmitted between the protocol participants. In that way, almost all potential channels to transmit covert data between malicious participants are blocked (we say “almost”, as, for example, there is still a possibility of leaking data by interrupting the execution, introducing transmission failures, etc., or by abusing the probabilistic nature of signatures via rejection sampling).

For both Schnorr blind signatures and Tessaro–Zhu blind signatures, we show that a watchdog that randomizes values on the wire is provably effective. In particular, we show that such a watchdog makes it impossible for the Signer and device to link the unblinded signature with a signing session using subliminal channels in the signing procedure and, by extension, mitigates these subliminal channels. Unfortunately, linking can still be carried out using other subliminal channels, e.g., in the message $\mathsf{m}$ (e.g., if $\mathsf{m}$ is a random element selected by the device) or in the unblinded signature $\sigma$ itself by means of rejection sampling, as mentioned earlier.

4. Blind Schnorr Signatures—Results and Discussion

The blind Schnorr signature scheme [17,18] is one of the most straightforward realizations of blind signatures but it suffers from some security shortcomings regarding the one-more unforgeability property [30,31] when concurrent signing sessions are allowed. Still, with some caution, it can be safely utilized in most practical use cases. The Signer holds a private key ${\mathsf{sk}}_{\mathcal{S}}\in {\mathbb{Z}}_q^{\ast }$ and the corresponding public key ${\mathsf{pk}}_{\mathcal{S}}=g^{{\mathsf{sk}}_{\mathcal{S}}}$. The signing procedure is presented on Figure 5 (one could alternatively consider a variant of the scheme where the signature is $\sigma =(R^{\prime },s^{\prime })$). The verification procedure of a signature $\sigma$ on a message $\mathsf{m}$ with regard to a public key $\mathsf{pk}$ is exactly the same as for the regular Schnorr signatures and proceeds as in Figure 5.

4.1. Establishing a Shared Secret by $\mathcal{S}$ and $\mathcal{D}$

The first step of most of our attacks is to establish a shared secret (anamorphic key) $\mathsf{ak}$ between the Signer $\mathcal{S}$ and the device $\mathcal{D}$. The difficulty lies in the fact that no out-of-bound channel can be used; the key agreement must be undetectable and well hidden in the regular interaction.

The simplest way to establish a shared key is a static–static Diffie–Hellman (DH) protocol, where public keys ${\mathsf{pk}}_{\mathcal{S}}$ and ${\mathsf{pk}}_{\mathcal{D}}=g^{{\mathsf{sk}}_{\mathcal{D}}}$ are used to derive a shared secret $\mathsf{ak}={\mathsf{pk}}_{\mathcal{D}}^{{\mathsf{sk}}_{\mathcal{S}}}={\mathsf{pk}}_{\mathcal{S}}^{{\mathsf{sk}}_{\mathcal{D}}}$. However, the problem is that the Auditor $\mathcal{J}$ may ask for secret keys that are kept by $\mathcal{S}$ and $\mathcal{D}$ according to the system specification (the request to surrender the private keys may concern any keys, not only ${\mathsf{sk}}_{\mathcal{S}}$). In that case, $\mathcal{J}$ would calculate the shared secret $\mathsf{ak}$ derived as above. In that case, any information transferred between $\mathcal{S}$ and $\mathcal{D}$ and hidden with the key $\mathsf{ak}$ would be readable for the Auditor $\mathcal{J}$.

For the same reason, the static–ephemeral Diffie–Hellman protocol for deriving the shared secret is not applicable in the attack. Indeed, the Auditor needs to request just one secret key to derive the shared secret. So, the only choice seems to be an ephemeral–ephemeral Diffie–Hellman key exchange.

On the side of the Signer, one can attempt to use R as a share for Diffie–Hellman key exchange. The Auditor cannot ask for r, as $\mathcal{S}$ can claim that it has been erased after the protocol execution for security reasons (or just to conserve space). However, it does not help if $\mathcal{S}$ finalizes the protocol execution with $s=r+c·{\mathsf{sk}}_{\mathcal{S}}\mathrm{mod}q$: after gaining ${\mathsf{sk}}_{\mathcal{S}}$, the Auditor would be able to derive r from this equality.

We have to conclude that to hide manipulations in the protocol, the secret key $\mathsf{ak}$ has to be established from the Diffie–Hellman shares, where $\mathcal{S}$ and $\mathcal{D}$ either forget the discrete logarithms effectively or claim not to know them at any time after the protocol is completed.

Our plan is to create shares of ephemeral–ephemeral Diffie–Hellman key exchange using exclusively the messages exchanged during the creation of blind signatures. The hidden key agreement will require a few steps, as presented below.

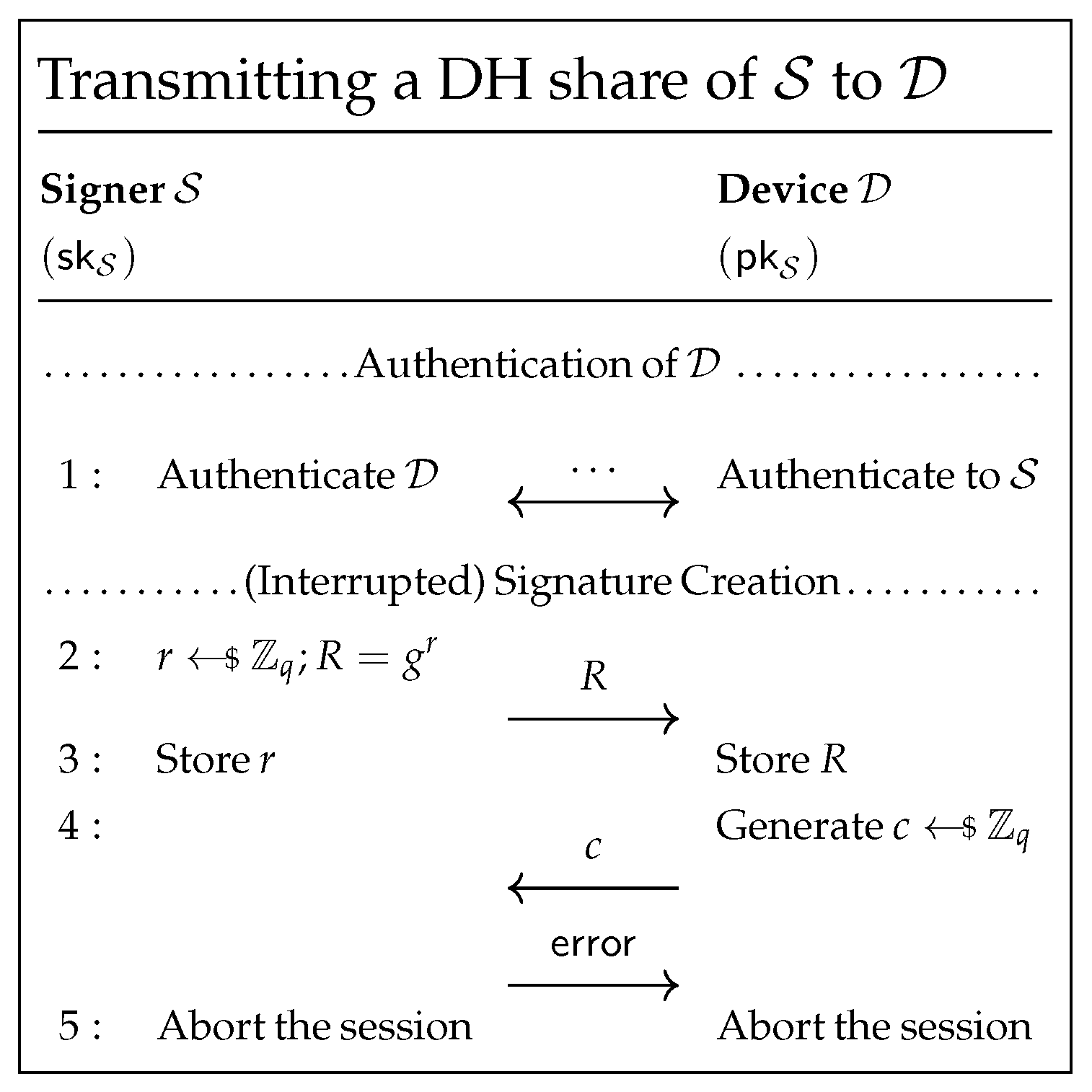
4.1.1. Transmitting a Diffie–Hellman Ephemeral Share from $\mathcal{S}$ to $\mathcal{D}$

The trick is to use the element $R=g^r$ as the share of $\mathcal{S}$. This may seem to contradict what we have said above (r can be derived by $\mathcal{J}$ when ${\mathsf{sk}}_{\mathcal{S}}$ is surrendered). However, the strategy of $\mathcal{S}$ is to interrupt the protocol execution and report an error for some reasonable reason (e.g., “server overloaded”). In this case, the corresponding value s is not transmitted to $\mathcal{D}$ and the only element dependent on r and visible to $\mathcal{J}$ is $R=g^r$. So, we are in the situation of the DH key-exchange protocol. The details are given in Figure 6.

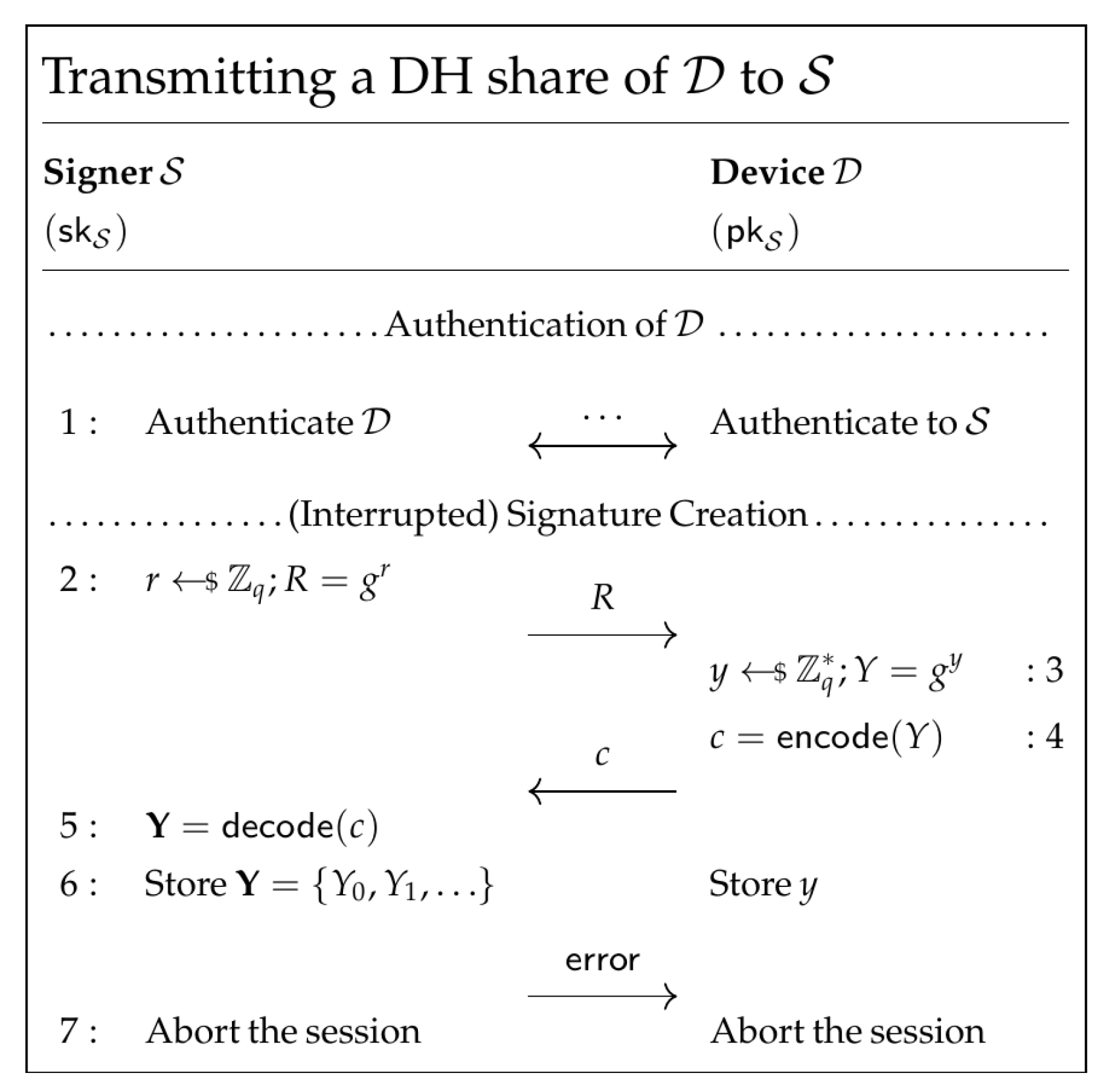
4.1.2. Transmitting a DH Ephemeral Share from $\mathcal{D}$ to $\mathcal{S}$

Transmitting a DH share from $\mathcal{D}$ to $\mathcal{S}$ is more complicated. The share should be hidden inside c, as it is the only element sent by $\mathcal{D}$. Fortunately, c is in some sense random, as $c=c^{\prime }+\beta \mathrm{mod}q$, where $\beta$ can be freely chosen. However, c is not a group element but belongs to ${\mathbb{Z}}_q$. So, we need to somehow encode a random group element as an element of ${\mathbb{Z}}_q$. It is impossible to do it perfectly, but achieving this goal with some redundancy will suffice.

In the first step, $\mathcal{D}$ chooses $y\in {\mathbb{Z}}_q^{\ast }$ at random and calculates $Y=g^y$. At this moment, Y must be mapped into ${\mathbb{Z}}_q$ and $c=\mathsf{encode}\left(Y\right)$ for the chosen function $\mathsf{encode}$. As already mentioned, this might be difficult. In the following, we show an example where the inversion mapping $\mathsf{decode}\left(Y\right)$ provides more than one candidate for Y.

Recall that for the sake of simplicity, we consider a subgroup of ${\mathbb{Z}}_p$ of prime order q, where $p=2q+1$ (it is the case for a strong DDH-secure Schnorr group). In this case, we may choose a mapping $\mathsf{encode}\left(Y\right)=Y\mathrm{mod}q$. Note that since $q={\displaystyle \frac{p-1}{2}}$, we have that either $Y=c$ or $Y=c+q\mathrm{mod}p$. In this case, $\mathsf{decode}\left(Y\right)=\{Y,Y+q\mathrm{mod}p\}$.

With more effort, one can define analogous mappings for elliptic curve groups. Attention should be paid to the resulting probability distribution of c: it should be indistinguishable from the uniform distribution in ${\mathbb{Z}}_q$. This can be technically involved (compare [32]).

The details of the described procedure are shown in Figure 7. Note that the attack can be detected if $\mathcal{D}$ is immediately asked for a Schnorr signature resulting from this interaction. Namely, $\mathcal{D}$ would have to find $c^{\prime }$ such that $c^{\prime }={\mathsf{H}}_1(g^{\alpha }·R·{\mathsf{pk}}_{\mathcal{S}}^{c-c^{\prime }\mathrm{mod}q},\mathsf{m})$. Solving this equation for $c^{\prime }$ is infeasible, even if one can freely choose $\alpha$. So again, a good choice is to create a “server error” instead of sending the response s.

Note that as long as the mapping $\mathsf{encode}$ on random group elements yields the elements of ${\mathbb{Z}}_q$ with probability distribution not distinguishable from the uniform distribution, the above execution is indistinguishable by the Auditor $\mathcal{J}$ from an execution of the original protocol.

4.1.3. Generating $\mathsf{ak}$

On the side of $\mathcal{D}$, there are shares $R,Y=g^y$ and $\mathcal{D}$ knows y, so it can derive the shared key $K=\mathsf{KDF}\left(R^y\right)$ (where $\mathsf{KDF}$ is some secure key-derivation function). On the side of $\mathcal{S}$, the situation is more complicated, as $\mathsf{decode}\left(c\right)$ may provide more than one candidate for the share of $\mathcal{D}$. In particular, for the example mapping defined above, $\mathcal{S}$ can compute two candidates for $\mathsf{ak}$:

$${\mathsf{ak}}_0=\mathsf{KDF}\left(c^r\mathrm{mod}p\right),{\mathsf{ak}}_1=\mathsf{KDF}\left({(c+q)}^r\mathrm{mod}p\right).$$

As there are no further messages from $\mathcal{D}$ to $\mathcal{S}$ during a single protocol invocation, there is no way to inform $\mathcal{S}$ which out of ${\mathsf{ak}}_0$ and ${\mathsf{ak}}_1$ is the correct shared value.

If matching between $\mathsf{ak}$ and one of ${\mathsf{ak}}_0$ and ${\mathsf{ak}}_1$ is necessary, one can use the next protocol invocation. Then, $\mathcal{D}$ can choose the challenge $c_1={\mathsf{H}}_1(g^{{\alpha }_1}·R_1·{\mathsf{pk}}_{\mathcal{S}}^{{\beta }_1},{\mathsf{m}}_1)$ to carry this message. For example, $\mathcal{D}$ can choose $c_1<q/2$ (by randomizing blinding factors $\alpha ,\beta$ until the hash function outputs value in the desired range) if $Y=c$ in the previous protocol invocation, and $c_1\ge q/2$ otherwise.

4.2. Linking with the Shared Key $\mathsf{ak}$

We assume that $\mathcal{D}$ and $\mathcal{S}$ already share a secret $\mathsf{ak}$. The goal of the attack described below is to enable linking a Schnorr signature $\sigma$ derived by $\mathcal{D}$ with an interaction between $\mathcal{S}$ and $\mathcal{D}$. As $\mathcal{D}$ is not anonymous during this interaction, such linking reveals the User who received $\sigma$. Thus, the attack aims to break the blindness property. As a side effect of the proposed construction, the device $\mathcal{D}$ can also create a hidden ciphertext that is readable only by $\mathcal{S}$.

The key point for linking is creating a hidden relation between $\alpha$ and $\beta$ by $\mathcal{D}$. Namely, first assume that $\alpha$ is created at random, as in the original scheme, while $\beta$ depends on $\alpha$, the session, and a hidden message $m^{\prime }$. For example, let ${\mathsf{m}}^{\prime }<q/2^{20}$ be a covert message. Then, $\beta$ is calculated as

$$\beta =\alpha +\mathsf{PRNG}(0,\mathsf{ak},R)+{\mathsf{m}}^{\prime }\mathrm{mod}q$$

where $\mathsf{PRNG}$ is a pseudorandom number generator that yields elements of ${\mathbb{Z}}_q$, and R is the element sent by $\mathcal{S}$ as the first message in the current session. So, we use a one-time pad in ${\mathbb{Z}}_q$, where the key is session-specific and depends on the shared secret $\mathsf{ak}$. Note that the link between $\alpha ,\beta$ and $\mathcal{D}$ is witnessed by the fact that

$$\beta -\alpha -\mathsf{PRNG}(0,\mathsf{ak},R)\mathrm{mod}q<q/2^{20}$$

In the case of using a wrong key $\mathsf{ak}$, the calculated number is a random element of ${\mathbb{Z}}_q$, so the probability of a false positive is about $2^{-20}$. Of course, the choice of ${\mathsf{m}}^{\prime }<q/2^{20}$ is somewhat arbitrary but seems to be good enough in practice.

In order to extend the bandwidth of a covert channel, $\mathcal{D}$ may generate $\alpha$ not at random but derive it with $\mathsf{ak},R$ and the second covert message ${\mathsf{m}}^{\prime \prime }<q$. Namely,

$$\alpha =\mathsf{PRNG}(1,\mathsf{ak},R)+{\mathsf{m}}^{\prime \prime }\mathrm{mod}q$$

(note that we use the same arguments $\mathsf{ak}$ and R as before, but slightly change the input to obtain a different pseudorandom element).

The details of the procedure executed by $\mathcal{D}$ during signature creation are shown in Figure 8. The only difference is that $\alpha$ and $\beta$ are generated in a modified way. Note that the change is undetectable by the auditor $\mathcal{J}$ as long as the output of $\mathsf{PRNG}$ is not distinguishable from random sampling in ${\mathbb{Z}}_q$. However, $\mathsf{ak}$ is not available to $\mathcal{J}$, so we may use a cryptographically strong generator $\mathsf{PRNG}$ with this property.

Now, let us discuss how a signature can be linked with a transcript of a signing procedure. So assume that $\mathcal{S}$ holds a transcript $(R,c,s)$ of an interaction with $\mathcal{D}$ and a signature $(s^{\prime },c^{\prime })$ found in the cyberspace. The goal is to check whether $(s^{\prime },c^{\prime })$ corresponds to this interaction (consequently, whether $(s^{\prime },c^{\prime })$ has been used by the owner of $\mathcal{D}$). In the positive case, the covert messages ${\mathsf{m}}^{\prime }$ and ${\mathsf{m}}^{\prime \prime }$ should be retrieved as well. The test details are given in Figure 8. First, $\alpha ,\beta$ are recalculated by computing

1.

${\alpha }^{\prime }=s^{\prime }-s\mathrm{mod}q$,

2.

${\beta }^{\prime }=c-c^{\prime }\mathrm{mod}q$,

Then, one can test whether the link is correct by deriving

$${\mathsf{m}}^{\prime }={\beta }^{\prime }-{\alpha }^{\prime }-\mathsf{PRNG}(0,\mathsf{ak},R)\mathrm{mod}q$$

and checking that

$${\mathsf{m}}^{\prime }<q/2^{20}$$

If this is the case, then ${\mathsf{m}}^{\prime }$ and ${\mathsf{m}}^{\prime \prime }={\beta }^{\prime }-{\alpha }^{\prime }-\mathsf{PRNG}(1,\mathsf{ak},R)\mathrm{mod}q$ are accepted as covert messages from $\mathcal{D}$.

Comments

First, if $\mathcal{S}$ has two candidates ${\mathsf{ak}}_0$ and ${\mathsf{ak}}_1$ for the shared key, then the test is performed both for ${\mathsf{ak}}_0$ and ${\mathsf{ak}}_1$. The only effect is that it increases the probability of a false-positive result from $2^{-20}$ to about $2^{-19}$.

Another important issue is that $\mathcal{S}$ does not need to hold the message $\mathsf{m}$ for which $(c^{\prime },s^{\prime })$ is a valid signature. This makes linking easier since sometimes the signatures are available, but the data signed are still undisclosed due to data protection issues.

Unblinding During Signature Creation

The presented attack can be slightly adjusted, so that during blind-signature creation, $\mathcal{S}$ learns the message $\mathsf{m}$. The only prerequisite is that the domain of potential messages $\mathcal{M}$ is small enough to run a test for all messages $\mathsf{m}\in \mathcal{M}$. Moreover, $\mathcal{J}$ cannot inject hidden messages ${\mathsf{m}}^{\prime }$, ${\mathsf{m}}^{\prime \prime }$ anymore.

For this attack, the parameters $\alpha$, $\beta$ are calculated by $\mathcal{D}$ in a slightly simplified way (as before, $\mathsf{PRNG}$ is assumed to return numbers from ${\mathbb{Z}}_q$ and be indistinguishable from a true random number generator):

1.

$\alpha =\mathsf{PRNG}(0,\mathsf{ak},R)$,

2.

$\beta =\mathsf{PRNG}(1,\mathsf{ak},R)$.

The remaining steps of the blind-signature creation are unchanged. In particular, note that for the Auditor $\mathcal{J}$, the numbers $\alpha ,\beta$ are not distinguishable from a pair of elements of ${\mathbb{Z}}_q$ selected at random. Hence, $\mathcal{J}$ cannot detect any deviation from the original protocol.

Apart from the steps specified by the original protocol, $\mathcal{S}$ can run the procedure shown in Figure 9. Its main idea is to recalculate $\alpha ,\beta$, then derive $R^{\prime }$ and $c^{\prime }$, and check the hash value for each message from $\mathcal{M}$ until a match is found.

Since $\mathcal{S}$ can compute $s^{\prime }$ as $s^{\prime }=s+\alpha \mathrm{mod}q$, the signature $(s^{\prime },c^{\prime })$ can be immediately attributed to $\mathcal{D}$.

Comment

Note that if blind signatures are used for tasks like e-voting, then all possible plaintexts (the message space $\mathcal{M}$) are known. Indeed, they must not be modified in any way; otherwise, the decrypted ballot would serve as a witness about the vote cast. Moreover, the number of voting options in $\mathcal{M}$ is small. So, $\mathcal{S}$ can immediately verify the signature $(c^{\prime },s^{\prime })$ for each voting option and learn the vote cast with $\mathcal{D}$. This would be a disaster from the point of view of an election process.

4.3. Linking Without the Shared Key $\mathsf{ak}$

Now we assume that $\mathcal{S}$ does not know any public keys representing $\mathcal{D}$ and there is no secret $\mathsf{ak}$ computed as described before and shared by $\mathcal{S}$ with $\mathcal{D}$. Nevertheless, we shall see that malicious $\mathcal{D}$ and $\mathcal{S}$ can break the blindness property in an undetectable way. A single asymmetric key will be used.

The first stage of the attack is the same as in Section 4.1.1: as a result, $\mathcal{S}$ holds $r_0$ associated with $\mathcal{D}$, while $\mathcal{D}$ holds $R_0=g^{r_0}$.

Equipped with the key $R_0$, the device $\mathcal{D}$ can create $\alpha ,\beta$ so that they are in a relation recognizable by a party holding r and completely random from the point of view of an Auditor $\mathcal{J}$. An instantiation of such relation is creating an ElGamal ciphertext of R (from the current interaction) and then mapping both parts of the ciphertext to ${\mathbb{Z}}_q$, as has been carried out in Section 4.1.2. The rest of the signing protocol is unchanged (see Figure 10).

ElGamal ciphertexts $(R_0^k·R,g^k)$ are not distinguishable from random pairs of group elements, so, for a proper mapping $\mathsf{encode}$, we can conclude that an Auditor $\mathcal{J}$ will see no difference between the execution from Figure 10 and the original one.

Now, let us focus on the linking mechanism. When a signature $(c^{\prime },s^{\prime })$ has to be compared with a transcript $(R,c,s)$, the first step is to derive candidate values $\alpha =s^{\prime }-s\mathrm{mod}q$ and $\beta =c-c^{\prime }\mathrm{mod}q$. Then, we can apply the $\mathsf{decode}$ function to $\alpha$ and $\beta$. Every combination of the results can be treated as an ElGamal ciphertext created with the public key $R_0$. It can be decrypted with $r_0$ and tested whether the result is R. For details, see Figure 11.

Comment

The above construction can be modified slightly to enable $\mathcal{D}$ to insert a covert message for $\mathcal{S}$. Namely, instead of encrypting R, one can encrypt a bit string M representing an element of the group, where

$$M=\mathsf{H}{\left(R\right)}_{\{\ell -t+1,\dots ,\ell \}}\parallel {\mathsf{m}}^{\prime }$$

(ℓ is the bit length of the output of the $\mathsf{H}$ function.)

Now, the test procedure will not check equality with R but with the last t bits of $\mathsf{H}\left(R\right)$. If t is big enough (say, $t=40$), then the false-positive probability is practically negligible, while there are plenty of bit positions left for the message ${\mathsf{m}}^{\prime }$.

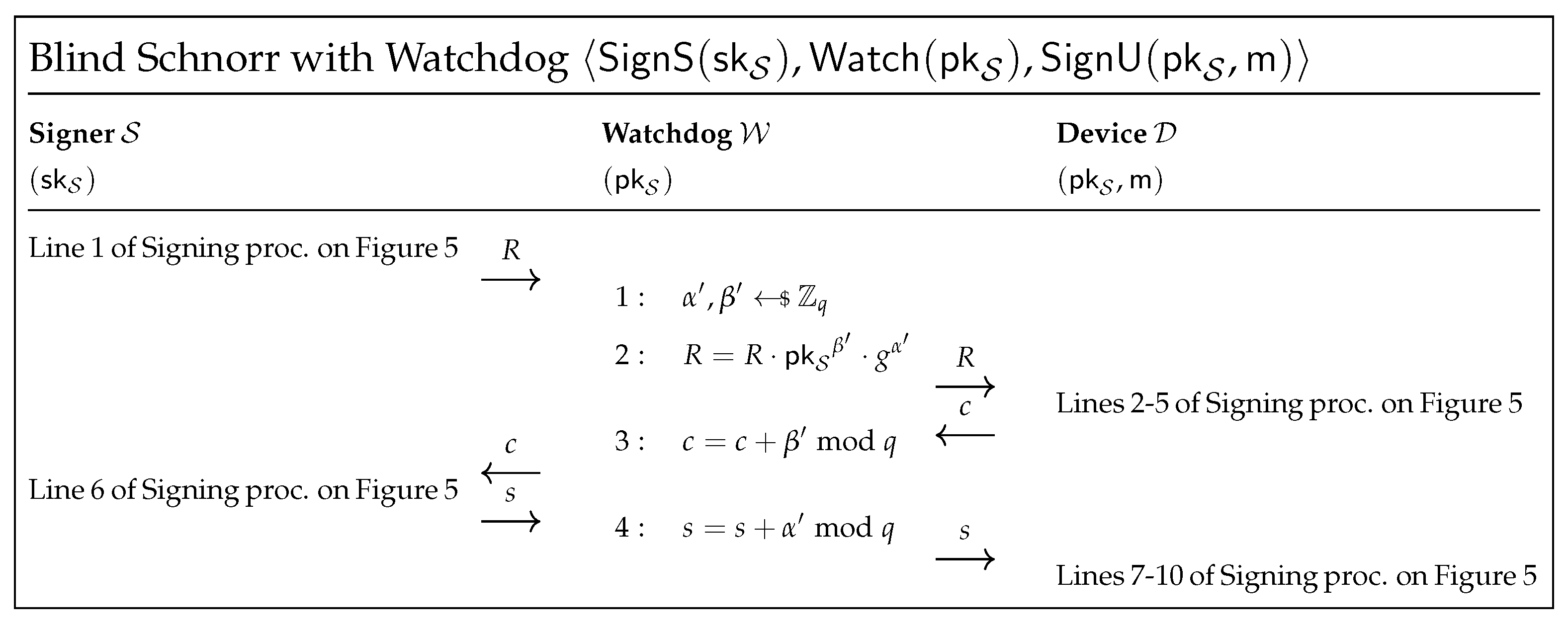
4.4. Countermeasures

The simplest solution to the problem of a black-box device $\mathcal{D}$ and $\mathcal{S}$ corrupting the blind-signature scheme is to use a watchdog. The watchdog serves as a proxy between $\mathcal{D}$ and $\mathcal{S}$ that modifies exchanged messages in an oblivious manner. In a real-life scenario, the watchdog could be a trusted software client for a hardware signing device. In case an Auditor wants to implement it, they can force the signing protocol users to run all communication through their proxy.

The watchdog influences the communication between Alice and Bob using randomly chosen ${\alpha }^{\prime }$ and ${\beta }^{\prime }$ (see Figure 12):

• instead of passing R, the watchdog delivers $R=R·{{\mathsf{pk}}_{\mathcal{S}}}^{{\beta }^{\prime }}·g^{{\alpha }^{\prime }}$;
• instead of passing c, the watchdog delivers $c=c+{\beta }^{\prime }\mathrm{mod}q$;
• instead of passing s, the watchdog delivers $s=s+{\alpha }^{\prime }\mathrm{mod}q$.

Since the order q is a prime number, the elements $R,c$ are randomized so that the result is uniformly distributed in the respective group. The third message s computed by $\mathcal{S}$ is deterministic and must be adjusted by setting $s=s+{\alpha }^{\prime }\mathrm{mod}q$ to obtain a valid signature. For honest parties, the protocol is indistinguishable from the one without a watchdog.

The effectiveness of the watchdog protection follows from the following property:

Theorem 1.

Consider invocations ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$ of blind Schnorr signature creation executed by $\mathcal{S}$ with devices ${\mathcal{D}}_1$, ${\mathcal{D}}_2$ (where ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ might be the same). Let the messages seen by $\mathcal{S}$ during the execution of ${\mathrm{\Pi }}_1$ be $R_1,c_1,s_1$. Let $R_2,c_2,s_2$ be the messages seen by ${\mathcal{D}}_2$ during execution of ${\mathrm{\Pi }}_2$. Then, there is a valid execution of the signing procedure with a watchdog, where the messages exchanged are $R_1,c_1,s_1$ from the point of view of $\mathcal{S}$, and $R_2,c_2,s_2$ from the point of view of ${\mathcal{D}}_2$.

In other words, given a signature $(c^{\prime },s^{\prime })$ and the full history of interactions with the clients, the Signer $\mathcal{S}$ cannot exclude any session for being the one where $(c^{\prime },s^{\prime })$ was created. This means that it is impossible to link an unblinded signature with the signing session using subliminal channels in the signing procedure. As we will see later, it does not mean that all attacks are stopped, as it is still possible to carry out a linking attack using a subliminal channel in the unblinded signature $\sigma$.

Proof. 

We have to find ${\alpha }^{\prime },{\beta }^{\prime }$ that “couple” both executions. First, let ${\beta }^{\prime }=c_1-c_2\mathrm{mod}q$. Then, we have to show that there is ${\alpha }^{\prime }$ such that

$$R_2=R_1·{\mathsf{pk}}_S^{{\beta }^{\prime }}·g^{{\alpha }^{\prime }}$$

That is, we ask for ${\alpha }^{\prime }$ such that

$$g^{{\alpha }^{\prime }}=R_2/R_1·{\mathsf{pk}}_S^{{\beta }^{\prime }}.$$

The value on the right-hand side is already fixed, and g is a group generator, so there is such ${\alpha }^{\prime }$.

Finally, we observe that in this case, we automatically have $s_2=s_1+{\alpha }^{\prime }\mathrm{mod}q$. Indeed, due to correctness, we have

$$g^{s_2}=R_2·{\mathsf{pk}}_{\mathcal{S}}^{c_2},g^{s_1}=R_1·{\mathsf{pk}}_{\mathcal{S}}^{c_1}$$

By substitutions and reductions, we obtain the following equivalent equalities:

$$\begin{array}{ccc}\hfill s_2& \stackrel{?}{=}& s_1+{\alpha }^{\prime }\mathrm{mod}q\hfill \\ \hfill g^{s_2}& \stackrel{?}{=}& g^{s_1+{\alpha }^{\prime }}\hfill \\ \hfill R_2·{\mathsf{pk}}_{\mathcal{S}}^{c_2}& \stackrel{?}{=}& R_1·{\mathsf{pk}}_{\mathcal{S}}^{c_1}·g^{{\alpha }^{\prime }}\hfill \\ \hfill R_1·{\mathsf{pk}}_S^{{\beta }^{\prime }}·g^{{\alpha }^{\prime }}·{\mathsf{pk}}_{\mathcal{S}}^{c_2}& \stackrel{?}{=}& R_1·{\mathsf{pk}}_{\mathcal{S}}^{c_1}·g^{{\alpha }^{\prime }}\hfill \\ \hfill {\mathsf{pk}}_S^{{\beta }^{\prime }}·{\mathsf{pk}}_{\mathcal{S}}^{c_2}& \stackrel{?}{=}& {\mathsf{pk}}_{\mathcal{S}}^{c_1}\hfill \end{array}$$

The last equation holds, as ${\beta }^{\prime }+c_2=c_1\mathrm{mod}q$. □

Corollary 1.

If $\mathcal{S}$ links a signature $(c^{\prime },s^{\prime })$ and a transcript $(R,c,s)$ with a device $\mathcal{D}$, it must occur independently of $(R,c,s)$.

In Section 4.5, we show that $\mathcal{D}$ has only some limited possibilities to inject its own identifier to a signature $(c^{\prime },s^{\prime })$. Indeed, the only non-deterministic step is freely choosing $\alpha$ and $\beta$. The problem is that $\alpha$ and $\beta$ are only used to transform R to $R^{\prime }$. The element $R^{\prime }$ will be reconstructed during signature verification and potentially can be the source of information on $\mathcal{D}$. However, the mapping $R\to R^{\prime }=R$ is a kind of one-way function as $R^{\prime }=g^{\alpha }·R·{\mathsf{pk}}_{\mathcal{S}}^{\beta }$. So, any intelligent way of choosing $\alpha$ and $\beta$ is doomed to fail.

Comments

Let us note that the watchdog also protects against executions where $\mathcal{D}$ or $\mathcal{S}$ send error messages. If $\mathcal{D}$ interrupts, then there is no advantage for malicious $\mathcal{S}$ and $\mathcal{D}$, as $\mathcal{D}$ gets an element stochastically independent of the element sent by $\mathcal{S}$. So, the same effect can be achieved by simulating the message received.

If the protocol is interrupted by $\mathcal{S}$ after receiving the modified c, then the communication transcripts on the side of $\mathcal{S}$ and $\mathcal{D}$ are stochastically independent. So again, the same effect can be achieved by simulating the responses. On the other hand, without communication, no data can be transmitted between $\mathcal{D}$ and $\mathcal{S}$.

4.5. The Remaining Threat—Rejection Sampling Attack

Let us note that a malicious device $\mathcal{D}$ has an opportunity to partially disclose its identity in a blind signature due to the rejection sampling technique, and no watchdog can prevent it. For this purpose, $\mathcal{D}$ must use a hidden key $K_A$ of an adversary. The details are presented in Figure 13.

The idea of the attack is to adjust $R^{\prime }$ so that $\mathsf{H}(R^{\prime },K_A)$ has prefix bits identical with $I_{\mathcal{D}}$. Since $\mathsf{H}$ is a pseudorandom function, the only way to find such $R^{\prime }$ is by random sampling the values of $R^{\prime }$. So, in the case of failure detected at Step 5, we simply backtrack to Step 3. Note that the parameter k must be small (e.g., $k=4$) to skip backtracking in a reasonable time. So, only a few bits of information on the identity of $\mathcal{D}$ can be leaked.

The reconstruction of $I_{\mathcal{D}}$ from a signature $(c^{\prime },s^{\prime })$ is immediate, as $R^{\prime }$ is recalculated during the signature verification process as $g^{s^{\prime }}·{\mathsf{pk}}_{\mathcal{S}}^{-c^{\prime }}$. Then, the adversary knowing $K_A$ can compute $\mathsf{H}(R^{\prime },K_A)$ and truncate it to $I_{\mathcal{D}}$. On the other hand, an Auditor $\mathcal{J}$ cannot derive any information on $\mathsf{H}(R^{\prime },K_A)$ without $K_A$, if $\mathsf{H}$ is a correlated-input secure hash function [33].

Note that no watchdog can prevent this attack without introducing additional message exchange and modifying the blind-signature creation protocol. The reason is that $R^{\prime }$ is determined on the side of $\mathcal{D}$ immediately after choosing $\alpha ,\beta$ and remains unchanged until signature verification, where it is used as an argument of $\mathsf{H}$.

Despite the short length of $I_{\mathcal{D}}$ (and lack of uniqueness in most scenarios), the presented attack must be considered as a serious risk in some situations. For example, if blind signatures are used for e-voting in a small committee, there is a serious risk of vote deanonymization by the Adversary holding $K_A$.

5. Tessaro–Zhu Blind Signatures—Results and Discussion

The Tessaro–Zhu protocol [19] is a blind-signature scheme based on blind Schnorr signatures. The motivation to extend blind Schnorr signatures was that their security is based on the assumption of hardness of the ROS problem [30]: in the case of solving ROS, the one-more unforgeability property will be automatically broken. This has only been a theoretical issue until, in 2020, an efficient way of solving the ROS problem was presented [31]. This renders blind Schnorr signatures (if created concurrently) formally insecure.

The Tessaro–Zhu blind-signature scheme has been designed so that the ROS problem does not affect its security. It breaks the linearity of the Schnorr system by introducing additional random values exchanged between the parties. Below, we show that while solving one problem, the new construction opens doors for wide subliminal channels. First, we analyze the $\mathsf{BS}\mathsf{1}$ variant from [19], which seems to be most commonly referred to.

The signing and verification procedures for the $\mathsf{BS}\mathsf{1}$ variant of Tessaro–Zhu blind signatures are presented on Figure 14.

Note that each signature component $c^{\prime },s^{\prime },y^{\prime }$ is randomized by $\mathcal{D}$ using fresh random values (by, respectively, $r_2$, $r_1$, and $\gamma$).

5.1. Establishing a Shared Key $\mathsf{ak}$

Obviously, $\mathcal{S}$ and $\mathcal{D}$ can use the methods presented for the blind Schnorr signatures to send their shares for hidden Diffie–Hellman key exchange. However, surprisingly, for Tessaro–Zhu signatures, there are additional opportunities for malicious parties to increase the attack potential.

5.1.1. Transmitting the Share of $\mathcal{S}$

The key observation is that transmitting the share of $\mathcal{S}$ to $\mathcal{D}$ does not require interruption with an error message anymore. Namely, instead of using A as a share, $\mathcal{S}$ can transmit its share in y. Instead of choosing y at random, the following steps are executed:

1.

$z_{\mathcal{S}}{\mathbb{Z}}_q^{\ast }$,

2.

$Z_{\mathcal{S}}=g^{z_{\mathcal{S}}}$,

3.

$y=\mathsf{encode}\left(Z_{\mathcal{S}}\right)+\mathsf{H}\left(A\right)\mathrm{mod}q$

where $\mathsf{encode}$ is the mapping from Section 4.1.2. The element $\mathsf{H}\left(A\right)$ is used as a pseudorandom shift.

Note that $\mathcal{D}$ will have more than one candidate for the share of $\mathcal{S}$ after applying $\mathsf{decode}(y-\mathsf{H}(A\left)\mathrm{mod}q\right)$. This will lead to multiple candidate keys $\mathsf{ak}$, but this does not prevent the linking attacks, as before.

5.1.2. Transmitting the Share of $\mathcal{D}$

One can avoid an error message by encoding the share of $\mathcal{D}$ in $\gamma$: Instead of choosing $\gamma$ at random, $\mathcal{D}$ executes the following steps:

1.

$z_{\mathcal{D}}{\mathbb{Z}}_q$,

2.

$Z_{\mathcal{D}}=g^{z_{\mathcal{D}}}$,

3.

$\gamma =\mathsf{encode}\left(Z_{\mathcal{D}}\right)+\mathsf{H}(Y,A)\mathrm{mod}q$

The only difference is that $\gamma$ is not visible immediately to $\mathcal{S}$. However, $\mathcal{D}$ can make the signature $(c^{\prime },s^{\prime },y^{\prime })$ somehow available to $\mathcal{S}$. Then, $\gamma$ can be derived as $y^{\prime }/y\mathrm{mod}q$.

Later, we shall see that the keys $\mathsf{ak}$ can be confirmed during linking attacks. So, $\mathcal{S}$ can crawl through all available signatures, compute candidate parameters $\gamma$, derive corresponding candidates for $\mathsf{ak}$, and detect the matches.

5.1.3. Generating $\mathsf{ak}$

As before, the shared key can be calculated as $K=\mathsf{KDF}\left(Z_{\mathcal{D}}^{z_{\mathcal{S}}}\right)=\mathsf{KDF}\left(Z_{\mathcal{S}}^{z_{\mathcal{D}}}\right)$. Multiple candidates are possible as well.

5.2. Linking with a Shared Secret

The attack from Section 4.2 can now be extended as instead of $\alpha ,\beta \in {\mathbb{Z}}_q$, the device $\mathcal{D}$ now uses three elements $r_1,r_2,\gamma$ in the same way as $\alpha$ and $\beta$ before. This increases the space available for covert messages by more than 50%.

5.3. Linking with No Shared Key

As transmitting the dedicated public key from $\mathcal{S}$ to $\mathcal{D}$ can be achieved in a single valid execution of the blind-signature creation procedure, one can focus more attention on extending the attack from Section 4.3. The difference is that for Schnorr blind signatures, we had elements $\alpha ,\beta \in {\mathbb{Z}}_q$ that carried a single ElGamal ciphertext. Now, the elements $r_1,r_2,\gamma$ can play a similar role.

To perform the attack, we need two hidden public keys ${\mathsf{pk}}_1,{\mathsf{pk}}_2$ of $\mathcal{S}$ dedicated to $\mathcal{D}$. Simply, ${\mathsf{pk}}_1$ is set during the first interaction with $\mathcal{D}$, while ${\mathsf{pk}}_2$ is determined during the second interaction with $\mathcal{D}$.

When ${\mathsf{pk}}_1,{\mathsf{pk}}_2$ are set, one can create linkable signatures that additionally contain covert messages ${\mathsf{m}}_1<q/2^{20},{\mathsf{m}}_2<q/2^{20}$. Instead of calculating $r_1,r_2,\gamma$ at random, the following steps are executed:

1.

$\psi {\mathbb{Z}}_q$,

2.

$\gamma =\mathsf{encode}\left(g^{\psi }\right)$,

3.

$r_1=\mathsf{encode}({\mathsf{pk}}_1^{\psi }·{\mathsf{m}}_1)$

4.

$r_2=\mathsf{encode}({\mathsf{pk}}_2^{\psi }·{\mathsf{m}}_2)$

The conditions ${\mathsf{m}}_1<q/2^{20},{\mathsf{m}}_2<q/2^{20}$ are somewhat arbitrary, but their purpose is:

1.

Eliminate wrong guesses for the identity of $\mathcal{D}$ (for wrong keys of $\mathcal{D}$, after decryption we would obtain random elements of ${\mathbb{Z}}_q$, hence not in the required range with a high probability;

2.

Eliminate wrong elements delivered by $\mathsf{decode}$.

5.4. Attacks on Related Schemes

The blind-signature scheme BS1 from [19] has been followed by related schemes:

1.

Scheme BS3 from the same paper [19];

2.

Schemes BS and BSr3 from [34] (see also CRYPTO’23 version [21]);

3.

Schemes BS1, BS2, BS3 from [35] (see also CRYPTO’24 version [20]).

These schemes differ from the point of view of security proof and underlying assumptions needed for the proof. The price to be paid for stronger security and privacy statements is their complexity: the schemes become more complicated, and many new elements and messages appear during protocol execution.

Unfortunately, these stronger protocols are even more vulnerable to our attacks and due to protocol complexities, there is even more room for covert messages. In the following, we do not provide specifications of the mentioned schemes (as they are too long) but instead indicate what parameters can be used for the attack so that an interested reader can easily reproduce the attacks. We slightly change the notation—for all papers, we assume that the group order is q and not p as in [34,35].

5.4.1. Establishing a Public Key of $\mathcal{S}$ Dedicated for $\mathcal{D}$

As before, the scenario is that during the first interaction between $\mathcal{S}$ and $\mathcal{D}$, the Signer presents a public key $\mathsf{pk}$ to $\mathcal{D}$ in a way that $\mathcal{S}$ can claim to be unaware of the related secret key. This key is used for static–ephemeral Diffie–Hellman key exchange during the following interactions. The public key—an element of the main group can be encoded by an element or elements of ${\mathbb{Z}}_q$ that are transmitted in clear from $\mathcal{S}$ to $\mathcal{D}$ during the first interaction between $\mathcal{S}$ and $\mathcal{D}$. These elements are:

• Scheme BS3 from [19]:$t\in {\mathbb{Z}}_q$, $y\in {\mathbb{Z}}_q^{\ast }$ selected by $\mathcal{S}$ in ${\mathsf{BS}}_3.{\mathsf{S}}_1$ and revealed to $\mathcal{D}$ as the output of ${\mathsf{BS}}_3.{\mathsf{S}}_2$ (compare page 22 of [19]);
• Scheme BS from [34]:$b,y\in {\mathbb{Z}}_q$ selected by $\mathcal{S}$ during the first step of $\mathsf{BS}.\mathsf{ISign}$ and revealed to $\mathcal{D}$ in the last message of this procedure (compare page 13 of [34]);
• Scheme BSr3 from [34]:$b,y\in {\mathbb{Z}}_q$ selected by $\mathcal{S}$ during the first step of $\mathsf{BSr}{\mathsf{3}}_3.\mathsf{ISign}$ and revealed to $\mathcal{D}$ in the third message (compare page 14 of [34]);
• Scheme BS1 from [35]:$z_1,e\in {\mathbb{Z}}_q$ selected by $\mathcal{S}$ during ${\mathsf{BS}}_1.{\mathsf{S}}_1$. They are transferred to $\mathcal{D}$ in the final step of ${\mathsf{BS}}_1.{\mathsf{S}}_2$ (compare page 10 of [35]);
• Scheme BS2 from [35]:$z_1,e\in {\mathbb{Z}}_q$ selected by $\mathcal{S}$ during ${\mathsf{BS}}_2.{\mathsf{S}}_1$. They are transferred to $\mathcal{D}$ in the final step of ${\mathsf{BS}}_2.{\mathsf{S}}_3$ (compare page 19 of [35]);
• Scheme BS3 from [35]:$z_1,e\in {\mathbb{Z}}_q$, ${\mathsf{crnd}}_{\overline{S}},{\mathsf{crnd}}_{\overline{R}}\in {\mathbb{Z}}_q^2$ (so, together, 6 elements of ${\mathbb{Z}}_q$!); they are selected by $\mathcal{S}$ during the execution of ${\mathsf{BS}}_3.{\mathsf{S}}_1$ and revealed in the message sent by $\mathcal{S}$ in the last step of ${\mathsf{BS}}_3.{\mathsf{S}}_2$ (compare page 34 of [35]).

5.4.2. Linkable Signature Creation Details

Similarly as before, we use random elements of ${\mathbb{Z}}_q$ from the original scheme to carry the covert data. The elements are specific to the schemes, as well as their recovery when a signature is compared with an interaction transcript: The random elements used are:

• Scheme BS3 from [19]:$r_1,r_2,{\gamma }_1\in {\mathbb{Z}}_p,{\gamma }_2\in {\mathbb{Z}}_p^{\ast }$ selected by $\mathcal{D}$ during execution of ${\mathsf{BS}}_3.{\mathsf{U}}_1$ (compare page 22 of [19]). They can be recalculated by $\mathcal{S}$ as follows:

  –

  ${\gamma }_1=y^{\prime }/y\mathrm{mod}q$ (compare ${\mathsf{BS}}_3.{\mathsf{U}}_2$);

  –

  ${\gamma }_2=c/c^{\prime }\mathrm{mod}q$ (compare ${\mathsf{BS}}_3.{\mathsf{U}}_1$));

  –

  $r_1=s^{\prime }-({\gamma }_1/{\gamma }_2)·s\mathrm{mod}q$ (compare ${\mathsf{BS}}_3.{\mathsf{U}}_2$);

  –

  $r_2=t^{\prime }-{\gamma }_1·t\mathrm{mod}q$ (compare ${\mathsf{BS}}_3.{\mathsf{U}}_2$).

  Note that $c^{\prime },s^{\prime },y^{\prime },t^{\prime }$ are the components of the signature compared with an interaction with messages containing $s,y,t$ (message sent by $\mathcal{S}$ as the output of ${\mathsf{BS}}_3.{\mathsf{S}}_2$) and c (message sent by $\mathcal{D}$ as the output of ${\mathsf{BS}}_3.\mathsf{ISign}$).
• Scheme BS from [34]:$\alpha ,\beta ,r\in {\mathbb{Z}}_q$ (in some cases, $\in {\mathbb{Z}}_q^{\ast }$) selected by $\mathcal{D}$ (compare $\mathsf{BS}\left[f_1\right].{\mathsf{USign}}_1$ and $\mathsf{BS}\left[f_2\right].{\mathsf{USign}}_1$ on page 13 of [34]). They can be recovered by $\mathcal{S}$ as follows (compare $\mathsf{BS}\left[f_1\right].{\mathsf{USign}}_1$, $\mathsf{BS}\left[f_1\right].{\mathsf{USign}}_2$ and $\mathsf{BS}\left[f_2\right].{\mathsf{USign}}_1$, $\mathsf{BS}\left[f_2\right].{\mathsf{USign}}_2$ on page 13 of [34]):

  –

  $\alpha =\overline{y}/y\mathrm{mod}q$,

  –

  $\beta =c/\overline{c}\mathrm{mod}q$ (the version with $f_2$) or $\beta =c-\overline{c}{\alpha }^{-5}\mathrm{mod}q$ (the version with $f_1$),

  –

  $r=\overline{z}-\alpha {\beta }^{-1}z-\alpha b\mathrm{mod}q$ (the version with $f_2$) or $r=\overline{z}-{\alpha }^{5}z-\alpha b\mathrm{mod}q$ (the version with $f_2$),

• Scheme BSr3 from [34]: the elements $\beta ,s\in {\mathbb{Z}}_q$. Note that random s is sent in clear during blind-signature creation so it can be used to calculate the shared ephemeral secret used to derive $\beta$. In turn, $\beta$ can be derived by $\mathcal{S}$ as $c/\overline{c}\mathrm{mod}q$, where $\overline{c}$ is recalculated according to the regular verification procedure (compare page 14 of [34]);
• Scheme BS1 from [35]: the elements ${\alpha }_0,{\alpha }_1,{\gamma }_0,{\gamma }_1\in {\mathbb{Z}}_q$ selected freely by $\mathcal{D}$ during ${\mathsf{BS}}_1.{\mathsf{U}}_2$. They can be recalculated by $\mathcal{S}$ during the linking test as: ${\gamma }_0=d^{\prime }-d\mathrm{mod}q$, ${\gamma }_1=e^{\prime }-e\mathrm{mod}q$, ${\alpha }_0=z_0^{\prime }-z_0\mathrm{mod}q$, ${\alpha }_1=z_1^{\prime }-z_1\mathrm{mod}q$ (recall that $d^{\prime },e^{\prime },z_0^{\prime },z_1^{\prime }$ are components of the blind signature, while $d,e,z_0,z_1$ are transmitted by $\mathcal{S}$ in the last step of ${\mathsf{BS}}_1.{\mathsf{S}}_2$ (compare page 10 of [35]);
• Scheme BS2 from [35]: the elements ${\alpha }_0,{\alpha }_1,{\gamma }_0,{\gamma }_1\in {\mathbb{Z}}_q$ selected by $\mathcal{D}$ during ${\mathsf{BS}}_2.{\mathsf{U}}_1$ (compare page 19 of [35]). They can be recalculated by $\mathcal{S}$ during the linking test as: ${\gamma }_0=d^{\prime }-d\mathrm{mod}q$, ${\gamma }_1=e^{\prime }-e\mathrm{mod}q$, ${\alpha }_0=z_0^{\prime }-z_0\mathrm{mod}q$, ${\alpha }_1=z_1^{\prime }-z_1\mathrm{mod}q$. Recall that $d^{\prime },e^{\prime },z_0^{\prime },z_1^{\prime }$ are components of the blind signature, while $d,e,z_0,z_1$ are transmitted by $\mathcal{S}$ in the last step of ${\mathsf{BS}}_2.{\mathsf{S}}_3$.
• Scheme BS3 from [35]: the elements ${\alpha }_1,{\gamma }_0,{\gamma }_1\in {\mathbb{Z}}_q$ and ${\delta }_S,{\delta }_R\in {\mathbb{Z}}_q^2$ selected by $\mathcal{D}$ during the execution of ${\mathsf{BS}}_3.{\mathsf{U}}_2$ (compare page 34 of [35]). They can be recalculated by $\mathcal{S}$ during the linking test as:

  –

  ${\alpha }_1=z_1^{\prime }-z_1\mathrm{mod}q$.

  –

  ${\gamma }_0=d^{\prime }-d\mathrm{mod}q$;

  –

  ${\gamma }_1=e^{\prime }-e\mathrm{mod}q$;

  –

  ${\delta }_S={\mathsf{crnd}}_{\overline{S}}^{\prime }-{\mathsf{crnd}}_{\overline{S}}\mathrm{mod}{\mathbb{Z}}_q$ (these are component-wise calculations on vectors of length 2);

  –

  ${\delta }_R={\mathsf{crnd}}_{\overline{R}}^{\prime }-{\mathsf{crnd}}_{\overline{R}}-{\gamma }_0·{\mathsf{crnd}}_{\overline{S}}^{\prime }\mathrm{mod}{\mathbb{Z}}_q$ (again, these are vector operations)

  (compare ${\mathsf{BS}}_3.{\mathsf{U}}_3$ on page 34 of [35]). Note that these calculations can be performed by $\mathcal{S}$ as $d^{\prime },e^{\prime },z_1^{\prime },{\mathsf{crnd}}_{\overline{S}}^{\prime },{\mathsf{crnd}}_{\overline{R}}^{\prime }$ are the components of the final signature (see the output of ${\mathsf{BS}}_3.{\mathsf{U}}_3$), while $d,e,z_1,{\mathsf{crnd}}_{\overline{S}},{\mathsf{crnd}}_{\overline{R}}$ are contained in the message sent by $\mathcal{S}$ in the last step of ${\mathsf{BS}}_3.{\mathsf{S}}_2$.

We see that except for BSr3, there are at least three elements of ${\mathbb{Z}}_q$ available for the attack. So, apart from linking, one can transmit at least two hidden messages. In the case of BS3 from CRYPTO’24, the scheme most attractive from the point of view of formal security analysis provided in [35], there is room for six messages.

5.5. Countermeasures

Similarly as for the blind Schnorr signature scheme, a properly implemented watchdog can mask the values sent on the wire so that no subliminal channel in the signing procedure can be used for the linking attack. The watchdog is presented on Figure 15.

Let us check that the output on the side of $\mathcal{D}$ is a valid Tessaro–Zhu signature. The key point is to check that

$$A^{\prime }=g^{s^{\prime }}·{\mathsf{pk}}_{\mathcal{S}}^{-c^{\prime }·y^{\prime }}$$

as the right-hand side expression replaces $A^{\prime }$ under the hash during the verification procedure. Recall that

$$\begin{array}{ccc}\hfill A^{\ast }& =& g^{r_1^{\ast }}·A^{{\gamma }^{\ast }}·Y^{{\gamma }^{\ast }·r_2^{\ast }}\hfill \\ \hfill A^{\prime }& =& g^{r_1}·{\left(A^{\ast }\right)}^{\gamma }·{\left(Y^{\ast }\right)}^{\gamma ·r_2}\hfill \\ & =& g^{r_1}·{(g^{r_1^{\ast }}·A^{{\gamma }^{\ast }}·Y^{{\gamma }^{\ast }·r_2^{\ast }})}^{\gamma }·Y^{{\gamma }^{\ast }·\gamma ·r_2}\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·\gamma \ast }·Y^{{\gamma }^{\ast }·\gamma ·(r_2^{\ast }+r_2)}\hfill \end{array}$$

On the other hand,

$$\begin{array}{ccc}\hfill g^{s^{\prime }}·{\mathsf{pk}}_{\mathcal{S}}^{-c’·y^{\prime }}& =& g^{s^{\ast }·\gamma +r_1}·{\mathsf{pk}}_{\mathcal{S}}^{-c’·y^{\ast }·\gamma }\hfill \\ & =& g^{(s·{\gamma }^{\ast }+r_1^{\ast })·\gamma +r_1}·{\mathsf{pk}}_{\mathcal{S}}^{-c’·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{((a+c·y·{\mathsf{sk}}_{\mathcal{S}})·{\gamma }^{\ast }+r_1^{\ast })·\gamma +r_1}·{\mathsf{pk}}_{\mathcal{S}}^{-c’·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·{\gamma }^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·{\gamma }^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c·y·{\gamma }^{\ast }·\gamma }·{\mathsf{pk}}_{\mathcal{S}}^{-c’·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·{\gamma }^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c·y·{\gamma }^{\ast }·\gamma }·{\mathsf{pk}}_{\mathcal{S}}^{-(c-r_2^{\ast }-r_2)·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·{\gamma }^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{(r_2^{\ast }+r_2)·y·{\gamma }^{\ast }·\gamma }\hfill \\ & =& g^{r_1+r_1^{\ast }·\gamma }·A^{\gamma ·{\gamma }^{\ast }}·Y^{(r_2^{\ast }+r_2)·{\gamma }^{\ast }·\gamma }=A^{\prime }\hfill \end{array}$$

For the constructed watchdog, we can show a result similar to Theorem 1.

Theorem 2.

Consider invocations ${\mathrm{\Pi }}_1$, ${\mathrm{\Pi }}_2$ of blind Tessaro–Zhu signature creation executed by $\mathcal{S}$ with devices ${\mathcal{D}}_1$, ${\mathcal{D}}_2$ (where ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ might be the same). Let the messages seen by $\mathcal{S}$ during the execution of ${\mathrm{\Pi }}_1$ be $A_1,Y_1,c_1,s_1,y_1$. Let $A_2,Y_2,c_2,s_2,y_2$ be the messages seen by ${\mathcal{D}}_2$ during the execution of ${\mathrm{\Pi }}_2$. Then, there is a valid execution of the signing procedure with the watchdog, where the messages exchanged are $A_1,Y_1,c_1,s_1,y_1$ from the point of view of $\mathcal{S}$, and $A_2,Y_2,c_2,s_2,y_2$ from the point of view of ${\mathcal{D}}_2$.

Proof. 

We have to show that there are the blinding factors $r_1^{\ast },r_2^{\ast },{\gamma }^{\ast }$ that can be used to “couple” both executions. Since, according to the protocol specification $c^{\ast }=c+r_2^{\ast }\mathrm{mod}q$, we immediately obtain the value for $r_2^{\ast }=c_1-c_2\mathrm{mod}q$. Similarly, since $y^{\ast }=y·{\gamma }^{\ast }\mathrm{mod}q$, we set ${\gamma }^{\ast }=y_2/y_1\mathrm{mod}q$. The value $r_1^{\ast }$ should satisfy the equality

$$A_2=g^{r_1^{\ast }}·A_1^{{\gamma }^{\ast }}·{\left(Y_2\right)}^{r_2^{\ast }}$$

In the above equality, all values are fixed apart from $r_1^{\ast }$. As g is the group generator, there is a unique $r_1^{\ast }<q$ such that $g^{r_1^{\ast }}=A_2·A_1^{-{\gamma }^{\ast }}·{\left(Y_2\right)}^{-r_2^{\ast }}$.

So it remains to check that $s_2=s_1·{\gamma }^{\ast }+r_1^{\ast }$. As the group has prime order, it suffices to show that $g^{s_2}=g^{s_1·{\gamma }^{\ast }+r_1^{\ast }}$. Before we start, let us recall that

$$s_1=a_1+c_1·y_1·{\mathsf{sk}}_{\mathcal{S}}\mathrm{mod}q,s_2=a_2+c_2·y_2·{\mathsf{sk}}_{\mathcal{S}}\mathrm{mod}q.$$

Hence, also

$$g^{s_1}=A_1·{\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1},g^{s_2}=A_2·{\mathsf{pk}}_{\mathcal{S}}^{c_2·y_2}.$$

By substitutions and reductions, we obtain the following equivalent equalities:

$$\begin{array}{ccc}\hfill g^{s_2}& \stackrel{?}{=}& g^{s_1·{\gamma }^{\ast }+r_1^{\ast }}\hfill \\ \hfill A_2·{\mathsf{pk}}_{\mathcal{S}}^{c_2·y_2}& \stackrel{?}{=}& {(A_1·{\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1})}^{{\gamma }^{\ast }}·g^{r_1^{\ast }}\hfill \\ \hfill g^{r_1^{\ast }}·A_1^{{\gamma }^{\ast }}·{\left(Y_2\right)}^{r_2^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c_2·y_2}& \stackrel{?}{=}& A_1^{{\gamma }^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}·g^{r_1^{\ast }}\hfill \\ \hfill {\left(Y_2\right)}^{r_2^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{c_2·y_2}& \stackrel{?}{=}& {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}\hfill \\ \hfill {\mathsf{pk}}_{\mathcal{S}}^{y_2·r_2^{\ast }}·{\mathsf{pk}}_{\mathcal{S}}^{(c_1-r_2^{\ast })·y_2}& \stackrel{?}{=}& {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}\hfill \\ \hfill {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_2}& \stackrel{?}{=}& {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}\hfill \\ \hfill {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}& \stackrel{?}{=}& {\mathsf{pk}}_{\mathcal{S}}^{c_1·y_1·{\gamma }^{\ast }}\hfill \end{array}$$

As the last equality is true, so is the first, and both points of view can originate from the same computation. □

6. Conclusions

Let us start the conclusions by addressing Problem 1. We have shown that blind-signature schemes are vulnerable to malicious implementation setups that invalidate privacy properties of blind signatures while being undetectable from the point of view of the Auditor. Subliminal channels exist in each one of the discussed protocols, and in case of a malicious, black-box implementation, allow for breaking the blindness property and for sending covert messages. We argue that these attacks are easily applicable in practice.

Given that, we believe that blind-signature schemes should be implemented on the client side with great care. Answering the second part of Problem 1, we have presented a solution for preventing the aforementioned attacks in a pragmatic way. This problem can be solved by a properly implemented, transparent watchdog, provided the user can trust the watchdog not to collude with the client’s device. This can be achieved by implementing the watchdog as a publicly auditable, open-source software. We have presented formal proofs of watchdog’s effectiveness. The only remaining problem not solved by the watchdog is rejection sampling, which may still leak a few bits per signature. This is because the watchdog only stops the subliminal channels that are contained within the singing procedure, i.e., in values $(R,c,s)$ exchanged between $\mathcal{D}$ and $\mathcal{S}$, as per Theorems 1 and 2. Then, a subliminal channel can still exist in the unblinded signature $(c^{\prime },s^{\prime })$ or even in the signed message $\mathsf{m}$ itself. While we do not have any solution that would not require modifying the schemes, we argue that, according to current knowledge (e.g., [27]), rejection sampling is in fact the only way to abuse the channel in the signature $(c^{\prime },s^{\prime })$ due to both of its random elements being a result of a one-way function of sorts. The anamorphic channel in $\mathsf{m}$ can only exist in use cases where the signed message is a random value chosen by the device (e.g., a random token as in Privacy Pass [3]). It can only be stopped by carefully designing the implementation to not allow any randomness in messages. Having all of this in mind, watchdogs seem to be the optimal solution, especially given their transparency—there is no need to modify existing blind-signature implementations.

For future work, similar analysis should be provided for other blind-signature schemes, e.g., blind RSA signatures, privately verifiable tokens based on verifiable oblivious pseudorandom functions (used in Privacy Pass) and post-quantum schemes. What is more, any work that improves rejection sampling will also improve the practicality of using it to break blind-signature schemes. Currently, one would require a large number of signatures to make it work (e.g., 50–100 signatures to establish a 256-bit Diffie–Hellman anamorphic key $\mathsf{ak}$). Reducing this number to, say, 10 signatures could make the attack much more practical.