Study on the Stability of High and Steep Slopes of Open-Air Dump with Various Slope Ratios Under Rainfall Conditions

Abstract

As a crucial component in mining engineering, the instability of waste dumps can lead to severe engineering accidents and significant economic losses. This study focuses on the stability of steep slopes in open-pit waste dumps, particularly under short-duration heavy rainfall conditions, and analyzes the stability performance of slopes with different slope ratios. Using a manganese mine waste dump in Guangxi Province as a case study, a 2D numerical model was developed using GeoStudio software (2022.1). The model incorporated local soil parameters and rainfall data to calculate the safety factors of single-step slopes with heights ranging from 5 to 30 m under the maximum local rainfall, which lasted for 10 h. The slope ratios considered were 1:1.5, 1:1.75, 1:2.0, and 1:2.25. The study found that as the slope ratio and rainfall duration increased, the stability of the slope significantly decreased. For slope ratios of 1:1.5, 1:1.75, and 1:2.0, the safety factors dropped below 1.1 as the step height increased. However, for slopes with a ratio of 1:2.25 and step heights ≤ 30 m, the safety factors remained above 1.1, meeting the stability requirements. This research provides a theoretical basis for addressing the stability issues of waste dumps in rainfall-prone regions and for the implementation of stabilization measures in single-step waste dump slopes.

1. Introduction

A waste dump is a massive artificial loose accumulation structure. Once destabilized, it may trigger mining disasters and major engineering accidents, which not only disrupt normal mining operations but also result in substantial economic losses and threaten downstream facilities and personnel safety [1,2,3]. In practical engineering, rainfall is one of the primary factors affecting slope stability. Globally, thousands of landslides are triggered by rainfall each year [4,5,6]. Rainfall infiltration saturates the soil, increases its weight, and reduces its shear strength, thereby inducing slope instability [7]. Prolonged or intense rainfall events significantly heighten the risk of slope failure, particularly in loose, poorly drained soils. For instance, the Three Gorges Reservoir area has experienced multiple rainfall-induced landslides [8]. Therefore, studying the stability of steep high slopes under rainfall conditions, especially under varying slope ratios, is crucial for preventing and mitigating geological disasters.

In recent years, progress has been made in understanding slope stability, particularly the effects of rainfall infiltration. Sun [9] demonstrated that the stability of heterogeneous slopes under different water-level drawdown conditions is significantly influenced by the heterogeneity coefficient of soil properties. Zhang and Wu [10,11] investigated the impact of rainfall infiltration on slope stability, finding that rainfall rapidly increases surface saturation and causes water accumulation at the interface between weak interlayers and bedrock, leading to shear failure. Su [12] conducted simulation experiments on slopes with varying basal inclinations and concluded that displacement and strain increments positively correlate with basal inclination. Liang [13] proposed a novel three-dimensional stability calculation method, integrating the shear resistance and sliding force of micro-column units to establish a spatial shape equation for composite slopes. Numerous researchers have employed numerical simulation software, such as FLAC 3D and GeoStudio, to explore slope stability under various conditions [14,15,16]. Guo Xiaogang [17] addressed the stability control requirements for reverse stacking in weak foundation dumps, establishing a relationship between stacking height rate and weak soil layer strength parameters, and proposed a stability analysis method for dump slopes under different stacking height rates. Wang [18] developed a slope stability prediction model based on a genetic algorithm-optimized BP neural network, considering six key slope characteristics: unit weight (γ), cohesion (c), internal friction angle (φ), slope angle (α), slope height (H), and pore water pressure (ru). Li [19] conducted model experiments to study the response of weathered rock slopes to rainfall infiltration under different conditions, concluding that excavation angle and moisture distribution are critical factors influencing slope stability. The finite element method (FEM) is widely used due to its advantages in handling complex geometries and heterogeneous materials [20]. In recent years, the strength reduction method based on FEM has become an important tool for slope stability assessment. Su [12] proposed a new three-dimensional slope stability analysis method based on finite element stress calculations. This method aligns with the rigid limit equilibrium assumption regarding the sliding direction, making it convenient for calculating three-dimensional sliding directions. Mebrahtu [21] assessed the stability of slopes with complex geometries composed of hyaloclastite basalt, porphyritic basalt, ignimbrite, and debris layers (poorly sorted clayey sand to silty sand) using both the limit equilibrium method and the shear strength reduction method based on finite element analysis.

Many studies rely on limited sample data, which may restrict the generalization ability and predictive accuracy of models. The stability of steep slopes is a common issue in open-pit mining and large-scale civil engineering projects, particularly in regions with frequent rainfall, where the risk of slope failure is significantly heightened. Compared to FLAC3D or PLAXIS, which require complex three-dimensional modeling and extensive computational time, the two-dimensional modeling approach in GeoStudio ensures computational accuracy while significantly reducing computational costs, making it well-suited for parametric studies involving multiple slope ratios and heights. GeoStudio’s SEEP/W module accurately simulates unsaturated seepage and the dynamic variation of pore water pressure, while the SLOPE/W module seamlessly integrates seepage results for limit equilibrium analysis. Furthermore, the reliability of GeoStudio’s limit equilibrium method was validated in numerous slope stability studies.

In this study, a two-dimensional numerical model was established using GeoStudio, incorporating existing data and regional soil parameters to evaluate the safety factors of single-step slopes under a 10 h short-duration intense rainfall. The study considered different slope ratios (1:1.5, 1:1.75, 1:2.0, and 1:2.25), which are commonly adopted in open-pit dump slope designs. In southern China, where frequent rainfall poses a significant challenge, slope ratios ranging from 1:1.5 to 1:2.25 are widely employed to balance safety and economic feasibility. This study contributes to the existing body of research on slope stability under varying slope ratios, providing scientific guidance for optimizing slope design parameters and laying a foundation for more complex future studies on slope stability.

2. Study Area Overview

The study area is located in the northern part of Guangxi, where a large-scale open-pit mine is being operated. The site is characterized by steep topography and unstable slopes, which present significant challenges for slope stability. The main geological features of the area include Quaternary artificial fill layers (Q₄^ml), loess-like fill soils, and residual soil layers from the Quaternary period (Q₄^el+dl), composed of silty clay, along with underlying bedrock layers such as the Silurian Wuzhishan Formation (D₃w) and Carboniferous Yanshan Formation (C₁y¹). These geological characteristics significantly influence the stability of the mine’s waste dumps and surrounding infrastructure.

The waste dump is situated on the northeastern side of the mining area and is constructed on a mountain slope. It is an open-pit dump with a total waste rock disposal volume of approximately 1.821 million cubic meters. The elevation of the dump ranges from 367.0 m to 430.9 m, with a stacking height of about 63.9 m. The dump uses a multi-step construction method, with the top elevations of the first, second, third, and fourth steps at approximately 400.0 m, 409.0 m, 417.0 m, and 422.0 m, respectively. The single-step slope ratio is about 1:1.25, and the safety platform width ranges from 3.0 to 5.0 m. The overall slope angle of the dump is 12.1°.

According to meteorological data, the local highest daily rainfall recorded was 183.2 mm (on 26 September 2008). The largest continuous rainfall event was 261.1 mm (24–27 September 2008), lasting for 4 days. The longest continuous rainfall event lasted for 26 days, with a total rainfall of 405.10 mm (27 July–21 August 1971). The maximum annual rainfall over the years was 1796.90 mm, while the minimum was 1073.10 mm, with an average annual rainfall of 1302.40 mm. Rainfall is most concentrated between April and September, with the heaviest rain occurring from June to August, accounting for 54.63% of the total annual rainfall, marking this period as the peak rainy season. Given the steep topography, unstable soil conditions, and heavy rainfall, the region faces a high risk of slope instability, making it an ideal site for studying the factors affecting slope stability in open-pit dumps under various rainfall conditions. The local instability of the spoil dump is shown in Figure 1.

3. Data and Methods

3.1. Soil Parameters

The basic physical and mechanical properties of the fill material, derived from the waste dump’s site investigation report, in situ testing data, and triaxial test results, are summarized in

Table 1. Basic physical and mechanical parameters of surface fill in the dump.

Geotechnical Parameters	Numerical Value
Heavy γ (kN/m3)	16.7
Cohesive force C (kPa)	8
Internal friction angle Φ (°)	9
relative density	2.7
Plastic limit (ω p/%)	27.3
Liquid limit (ω I/%)	56.1
Plasticity index (Ip)	28.8
Original soil dry density (ρ d/g/cm3)	1.67
Undisturbed soil moisture content (ω/%)	54.2

. The soil is gray-brown in color. Based on the Technical Specifications for Geotechnical Engineering of Tailings Dams and fundamental soil physical parameters, the sample is classified as silty clay with a plastic consistency.

3.2. Numerical Simulation Software and Steps

This study employs GeoStudio software to analyze the stability of dump site slopes, which are characterized by their complex geometric configurations, mixed distribution of multi-layered soil and rock materials, and significant seepage effects. Slope stability issues become particularly pronounced under the influence of external factors such as rainfall and groundwater fluctuations, as well as internal factors like stacking loads and geostress redistribution. GeoStudio integrates multiple modules and combines the Limit Equilibrium Method (LEM) with the Finite Element Method (FEM), making it highly suitable for addressing such complex slope stability problems.

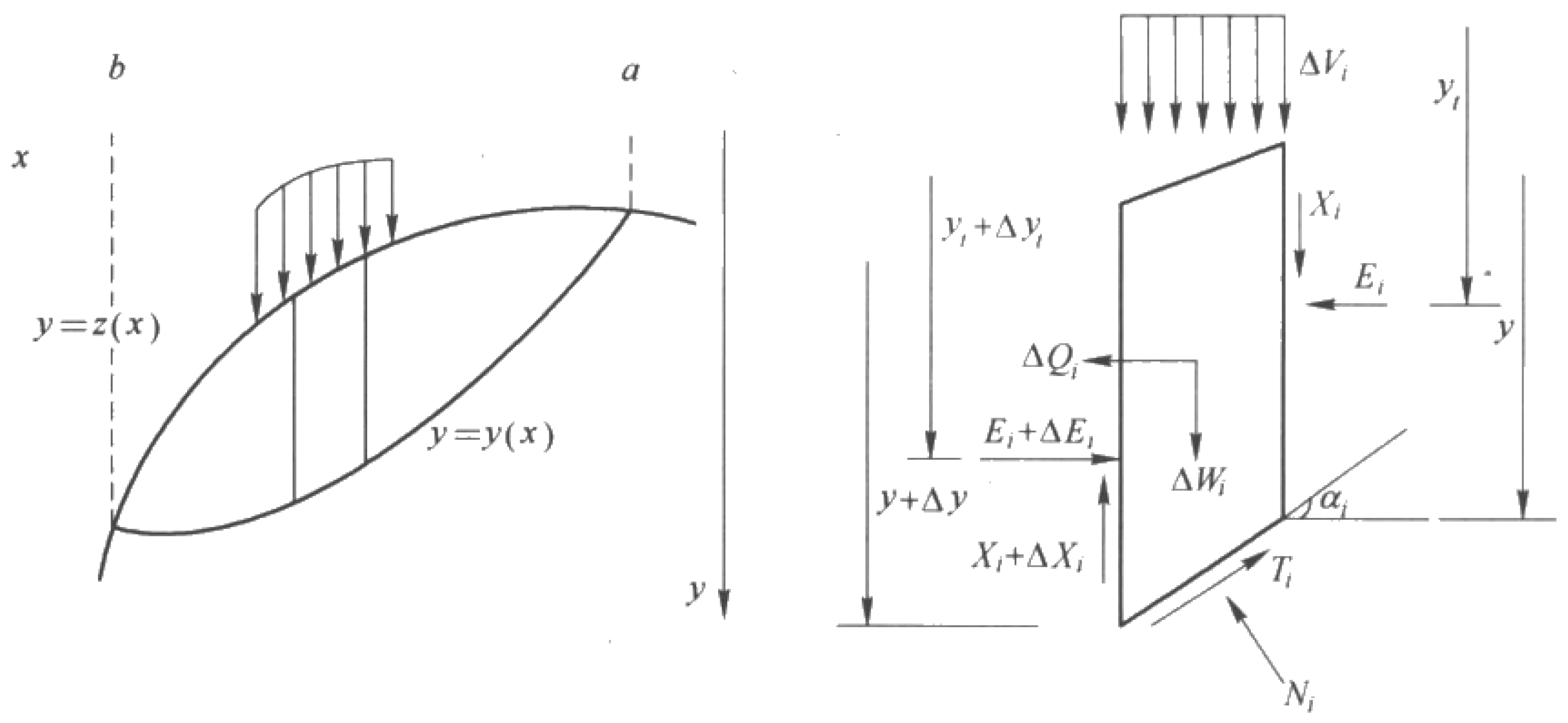
3.2.1. The Basic Principle of Limit Equilibrium Method

The traditional Limit Equilibrium Method (LEM) is often a simplified approach based on the assumption that the safety factor (K) of the slope can be determined. When the shear strength parameters of the slope are reduced by a factor of FFF (the slope safety factor), a critical slip surface, representing the most dangerous potential sliding surface, is assumed to exist within the slope under limiting equilibrium conditions.

LEM typically assumes that failure occurs along a predefined sliding surface within the rock or soil mass. Based on the static equilibrium conditions of the sliding mass and the Mohr–Coulomb failure criterion, the method evaluates the likelihood of sliding along this surface, quantified by the safety factor or the probability of failure. Multiple potential sliding surfaces are systematically analyzed in the same manner to calculate the corresponding safety factors or failure probabilities. The sliding surface with the smallest safety factor or highest failure probability is identified as the most likely failure surface.

Commonly used LEM approaches include the Swedish slice method, Bishop’s method, Spencer’s method, and the Morgenstern–Price (M–P) method. In this stability analysis, the M–P method was employed for calculations. The calculation diagram is shown in Figure 2.

Morgenstern and Price proposed a general approach, assuming that:

X_i/E_i = tanβ = f₀ (x) + λf₁ (x)

(1)

Here, λ is to be determined, and f₁(x) is an artificially assumed function (f₁(x) = kx + m, where k and m are constants).

(1)

The deadweight of the soil strip ΔW_i, its magnitude, position and direction of action point are known.

(2)

The normal stress at the bottom of the strip is N_i, and the tangential stress is T_i. Assume that N_i and T_i act at the midpoint of the sliding surface, and their magnitudes are unknown.

(3)

The normal forces on both sides of the soil strip are E_i and E_i + ΔE_i, and the vertical shear forces are X_i and X_i + ΔX_i.

(4)

ΔQ_i is the horizontal inertial force (i.e., horizontal seismic force), and the distance between its action point and the soil strip is h_ei.

(5)

The vertical load qΔx on the slope surface.

(6)

The angle between the normal line (i.e., the radius of the arc) of the sliding surface of soil strip i and the vertical line is α_i; the cohesion of the soil on the sliding surface is c, and the internal friction angle is φ.

Horizontal force balance:

T_i cosα_i − N_i sinα_i = ΔQ_i − ΔE_i

(2)

Vertical force balance:

T_i sinα_i + N_i cosα_i = ΔW_i + ΔV_i − ΔX_i

(3)

Satisfy the limit equilibrium condition:

T_i = c_e Δxsecα_i + N_i tanφ_e

(4)

Eliminating T_i and N_i, we can obtain:

tan (φ_e − α_i) = c_e xsec² α_i + (ΔW_i + ΔV_i)(tanφ_e − tanα_i) − ΔQ_i (1 + tanφ_e tanα_i)

(5)

When Δx → 0:

−(dE_i)/dx (1 + tanφ_e tanα_i) + (dX_i)/dx (tanφ_e − tanα_i) = c_e sec² α_i+
((dW_i)/dx + (dV_i)/dx)(tanφ_e − tanα_i) − (dQ_i)/dx(1 + tanφ_e tanα_i)

(6)

Using the moment equilibrium condition of the soil strip, take the moment at the bottom midpoint of the soil strip:

(X_i + ΔX_i) Δx/2 + X_i Δx/2 + (E_i + ΔE_i)[y + Δy − (y_t + Δy_t)-Δy/2] − E_i (y-y_t + Δy/2) − ΔQ_i h_ei = 0

(7)

Simplified:

X_i Δx − E_i Δy_t + ΔE_i (y − y_t) − ΔQ_i h_ei = 0

(8)

When Δx → 0:

X_i = −y (dE_i)/dx + d(y_t E_i)/dx + dQ/dx h_ei

(9)

3.2.2. Numerical Simulation Steps

To study the stability of single-step slopes in dump sites, the soil is assumed to be a homogenous material under ideal conditions. Based on this assumption, simplified numerical models for single-step slopes of varying heights and slope ratios were established using the finite element software GeoStudio. The models adopt an elastoplastic constitutive model and the Mohr–Coulomb strength criterion, with the grid discretization employing a combination of quadrilateral and triangular elements.

To more accurately simulate rainfall infiltration, the SEEP/W module in GeoStudio was utilized to simulate and analyze the seepage lines representing groundwater level changes. By leveraging numerical simulation techniques, the variation of pore water pressure within the slope was determined through the analysis of infiltration lines. The analysis employed the seepage equation implemented in the SEEP/W module [22].

∂Q/∂t = ∂/∂x (k_x ∂h/∂x) + ∂/∂_y (k_y ∂h/∂y) + q

(10)

In the above equation, h represents the total head, k_x_ and k_y denote the permeability coefficients in the x and y directions, respectively, q is the boundary recharge rate, q also represents the unit storage capacity, and t is time.

Van-Genuchten (VG) proposed a mathematical model for fitting the soil–water characteristic curve. The model can be expressed as [23]:

θ = S_e = 1/[1 + (aψ)ⁿ]^m

(11)

The parameter relationships among a, n, and m significantly influence the predictive accuracy of the van Genuchten (VG) model. The inclusion of the maximum matrix suction point depends on the discreteness and range of a, m, and n. The VG model aims to optimize the parameter relationships to improve curve-fitting accuracy and enhance predictive precision. Compared to fine-grained soils, the VG model generally achieves better predictive accuracy for coarse-grained soils.

In this simulation experiment, the soil’s volumetric water content function and permeability coefficient function were established based on the VG model, derived from the basic physical parameters of the soil. Using rainfall data provided by the meteorological bureau, the unit rainfall intensity for this 10 h short-duration heavy rainfall was set at 0.05 m³/h/m². The height of the single-step slope varied between 5 and 30 m, with slope ratios selected as 1:1.5, 1:1.75, 1:2.0, and 1:2.25.

Using the limit equilibrium theory and the Morgenstern–Price (M–P) method, the stability performance of each slope ratio under heights ranging from 5 to 30 m was calculated for the 10 h continuous rainfall event, with stability analyzed hourly. The modeling process utilized GeoStudio software. First, the SEEP/W module was employed to create a two-dimensional single-step slope model, applying seepage and boundary conditions, along with volumetric water content and permeability coefficient functions, to perform seepage calculations. Subsequently, the SLOPE/W module was used to incorporate geotechnical parameters for limit equilibrium analysis. Models were developed for slopes with heights of 5–30 m and slope ratios of 1:1.5, 1:1.75, 1:2.0, and 1:2.25. An example model of a slope with a height of 5 m and a slope ratio of 1:1.5 is shown in Figure 3.

4. Stability Analysis of Single-Step Slope with Different Slope Ratios Under Rainfall Conditions

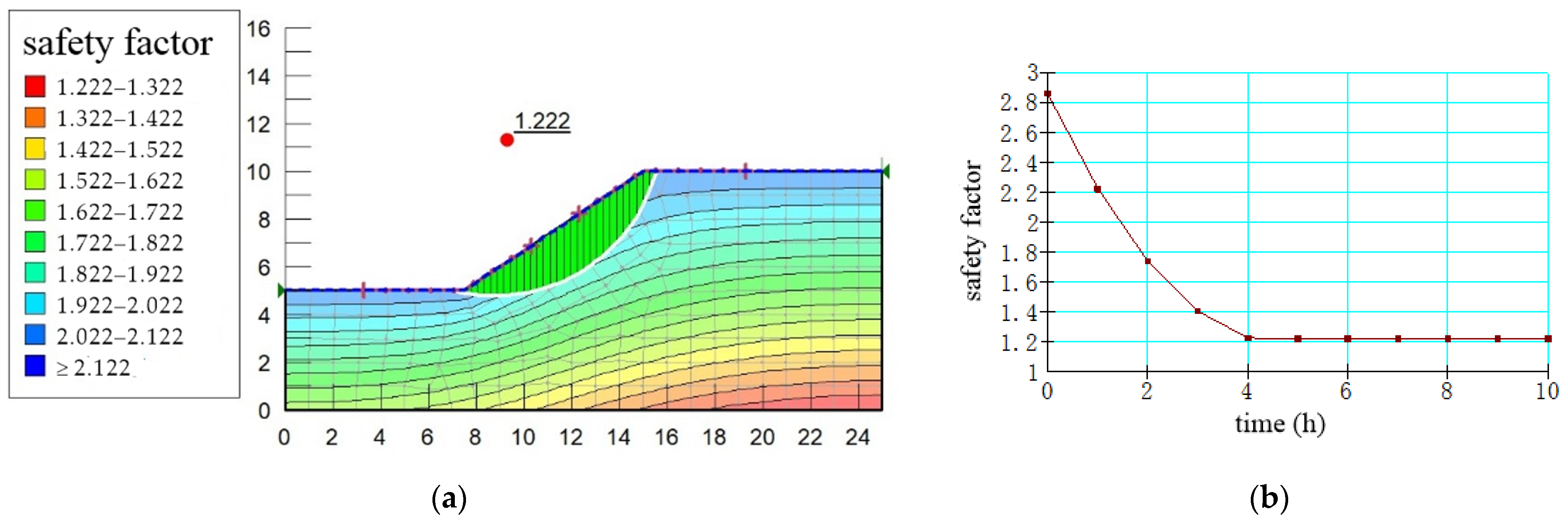
4.1. Changes in Slope Stability Under Continuous Rainfall

Figure 4 illustrates the final state of a single-step slope composed of tailings clay with a slope ratio of 1:1.5 and a height of 5 m under 10 h of continuous heavy rainfall, as well as the slope stability performance at various time intervals during the rainfall event. In the initial stages of rainfall, the stability factor exhibits significant variation, but the rate of change begins to decrease as time progresses. After 4 h of continuous rainfall, the slope stability factor starts to stabilize.

Based on the simulation results, the single-step slope with a height of 5 m and a slope ratio of 1:1.5 does not experience failure under these conditions. However, during continuous rainfall, its stability decreases sharply. This can be attributed to the infiltration of rainwater into the soil, which gradually increases the soil’s water content and reduces matric suction. Matric suction plays a critical role in maintaining the stability of unsaturated soils. As matric suction decreases, the effective stress within the soil diminishes, leading to a reduction in soil strength and, consequently, a decrease in slope stability.

4.2. Changes in Slope Stability at Different Step Heights with the Same Slope Ratio Under Continuous Rainfall

To investigate the stability variations of single-step slopes with different heights under the same slope ratio during continuous rainfall, Figure 5 presents the stability calculation contour maps for single-step slopes with a height of 10 m and slope ratios of 1:1.5 and 1:1.75. Figure 6 shows the variation curves of the safety factors over 10 h of continuous rainfall for slope ratios of 1:1.5 and 1:1.75 at different time intervals.

Based on the simulation results, the single-step slope with a height of 10 m and a slope ratio of 1:1.5 begins to fail after 7 h of rainfall, with slope damage occurring. After 8 h of rainfall, the safety factor approaches its minimum value, reaching only 0.9. However, under the same conditions, when the slope ratio is reduced to 1:1.75, the safety factor reaches its lowest point of 1.11 after 8 h of rainfall, showing a significant improvement compared to the 1:1.5 slope ratio, and the slope remains stable. This indicates that steeper slopes lead to lower slope stability.

The choice of slope ratio affects the geometric shape of the slope, and the geometry is directly related to the distribution and potential sliding surfaces. For steeper slopes, the self-weight strain per unit area increases, leading to higher shear strain in the soil or rock, which reduces the strength of the slope material. A steeper slope also tends to shorten the natural drainage paths, increasing the likelihood of water retention within the soil or rock, leading to higher pore water pressure, which further reduces shear strength. On the other hand, gentler slope ratios typically enhance slope stability. A gentler slope distributes stresses more evenly, reducing shear forces along the potential sliding surface, and thereby lowering the risk of landslides. Additionally, a gentler slope often improves the natural drainage capacity for rainwater or groundwater, decreasing the accumulation of pore water pressure and helping maintain the strength of the soil.

4.3. Stability Changes of Different Slope Ratios Under Short-Term Heavy Rainfall

To investigate the stability of slopes with different slope ratios under rainfall conditions for slope heights ranging from 5 to 30 m, Figure 7 presents the safety factor variation curves over time for slopes with slope ratios from 1:1.5 to 1:2.25 and heights ranging from 5 to 30 m, under identical rainfall conditions.

As shown in Figure 7, after 10 h of heavy rainfall, the safety factors for slopes with heights of 15 m, 20 m, and 25 m and a slope ratio of 1:2.0 are 1.187, 1.194, and 1.088, respectively. Therefore, when the step height is ≥25 m, a slope ratio of 1:2.0 no longer meets the stability requirements. However, for slopes with heights of 25 m and 30 m, a slope ratio of 1:2.25 yields safety factors of 1.301 and 1.300, both of which satisfy the stability criteria. Initially, as rainfall infiltrates the slope, the overall stability of the slope declines sharply. For slopes with a height of ≤15 m, the safety factor decreases rapidly at first, then stabilizes. For slopes taller than 15 m, the safety factor curve declines slowly for the first 4–5 h. However, as the rainfall infiltration continues, the safety factor curve begins to drop sharply, eventually stabilizing.

5. Discussion

(1)

The simulation results indicate that rainfall infiltration significantly affects slope stability. During the 10 h rainfall simulation, the following trends were observed: In the early stages of rainfall, the safety factor decreases sharply as water begins to infiltrate the slope. This is due to the rapid increase in pore water pressure, which results in a corresponding reduction in effective stress. After 4–5 h of rainfall, the soil reaches saturation, and the rate of decrease in the safety factor slows down. At this point, the permeability and drainage rate of the soil tend to reach equilibrium. After 10 h of rainfall, the safety factors of some slopes approach critical values, especially for steeper slopes, indicating that the slope is on the verge of instability due to increased pore water pressure caused by water accumulation in the soil.

(2)

The impact of slope ratio on stability is significant. Under rainfall conditions, steeper slopes exhibit poorer stability. The rate of decrease in the safety factor for steep slopes (e.g., 1:1.5) is much faster than for gentler slopes (e.g., 1:2.25). This is attributed to the fact that steeper slopes concentrate the forces acting on the soil, thereby increasing shear stress and reducing shear strength, making the slope more prone to failure. For slopes with ratios of 1:1.5 and 1:1.75, failure occurs after 7–8 h of rainfall, especially for slopes exceeding 10 m in height, where the safety factor decreases significantly, reaching a minimum of 0.9. In contrast, slopes with gentler ratios (1:2.0 and 1:2.25) exhibit better stability. For example, a slope with a ratio of 1:2.25 maintains a safety factor above 1.1 even after 10 h of rainfall.

(3)

The results of this study have important implications for slope design and maintenance in areas prone to rainfall and erosion. In regions with frequent rainfall, slope designs should adopt gentler slope ratios (e.g., 1:2.0 or 1:2.25) to minimize the risk of instability. Steep slopes, especially those with greater heights, should be avoided, as they are more susceptible to collapse during prolonged rainfall. For existing slopes, measures such as improving drainage, reducing water infiltration, or using stabilization techniques (e.g., slope reduction and counterpressure at the slope foot) can help maintain stability during heavy rainfall events.

(4)

Although the results provide a solid basis for decision-making, this study also has some limitations. The study relied entirely on numerical simulation for stability analysis, and the model was not calibrated and verified by physical experimental models or field monitoring data. Although the simulation results are consistent with theoretical expectations, they are not directly compared with the actual slope behavior, which may affect the applicability of the model in real complex geological conditions. In the future, the numerical model should be verified by physical experiments and field monitoring data to improve the empirical reliability of the results; the simulation assumes homogeneous soil conditions, while in reality, the cohesion, permeability and compaction of the soil may vary. Future research should also consider the impact of soil heterogeneity on slope stability. In addition, this study focuses on short-term heavy rainfall events, while long-term low-intensity rainfall may have different effects on slope stability. Future research should explore the impact of such events on long-term slope stability. Although the numerical simulation results provide valuable theoretical insights, further field studies and verification using real data are needed to confirm the research results and improve modeling techniques.

6. Conclusions

This study used GeoStudio software to establish a 2D model of the slope, and based on this model, a 10 h short-duration heavy rainfall simulation was conducted for single-step slopes with heights ranging from 5 to 30 m. The M–P method was applied to analyze the stability of slopes with slope ratios of 1:1.5, 1:1.75, 1:2, and 1:2.25, leading to the following conclusions:

(1)

As rainfall infiltrates the slope soil, the soil moisture content gradually increases. When the soil pores approach saturation, the capillary tension and suction in the soil decrease, leading to a reduction in matric suction and weakening the soil strength. During rainfall, if the infiltration rate exceeds the drainage rate, water accumulates within the soil, increasing pore water pressure. As pore water pressure rises, the effective stress in the soil decreases, causing the slope to lose its original shear strength.

(2)

Steeper slopes are more prone to accumulating large amounts of surface runoff under heavy rainfall or prolonged precipitation, which increases the soil moisture content and pore water pressure, thereby weakening the soil’s shear strength and increasing the risk of instability. In contrast, gentler slope ratios allow for a more uniform distribution of stresses, reducing localized stress concentrations and enhancing the overall stability of the slope. Additionally, gentler slopes aid in drainage, reducing pore water pressure buildup and mitigating the negative impacts of rainfall infiltration on slope stability.

(3)

According to the stability analysis results of single-step slopes under sustained rainfall, when the slope height is less than or equal to 5 m, a slope ratio of 1:1.5 is appropriate. For step heights between 5 and 15 m, a slope ratio of 1:1.75 meets the stability requirements. For step heights ranging from 15 to 25 m, a slope ratio of 1:2.0 can be selected. A slope ratio of 1:2.25 is suitable for single-step slopes with heights up to 30 m.

(4)

In slope design and remediation, the slope ratio should be chosen based on the specific conditions. For high and steep slopes, measures such as slope reduction, drainage systems, and counterpressure at the slope foot should be implemented to improve stability. In areas with dense cracks, it is recommended to enhance the drainage design to prevent excessive water accumulation within the soil, which may lead to instability.

(5)

To address local instability within the internal slopes of the dump site, several stabilization measures can be implemented. One approach is to construct a placement platform at the toe of the dump slope to exert a certain amount of counteracting horizontal pressure, which is particularly suitable for areas with sufficient space at the slope toe and where additional support for the toe embankment is required. Another method involves slope trimming to reduce the overall slope gradient and increase platform areas, thereby decreasing the slope height. If the earthwork volume required for slope trimming is excessive, a combined approach incorporating counterweight berms at the slope toe can be considered. In addition to these two remediation methods, further measures should be taken to ensure the long-term stability of the dump site. These include the installation of retaining structures, drainage interception and discharge systems, monitoring facilities, and land reclamation initiatives. These measures help ensure that the dump site meets the requirements of relevant standards and regulations, thereby enhancing overall stability and safety.