The Seismic Dynamic Response Characteristics of the Steep Bedding Rock Slope Are Investigated Using the Hilbert–Huang Transform and Marginal Spectrum Theory
Abstract
1. Introduction
2. Numerical Simulation Scheme
2.1. Establishing the Numerical Model
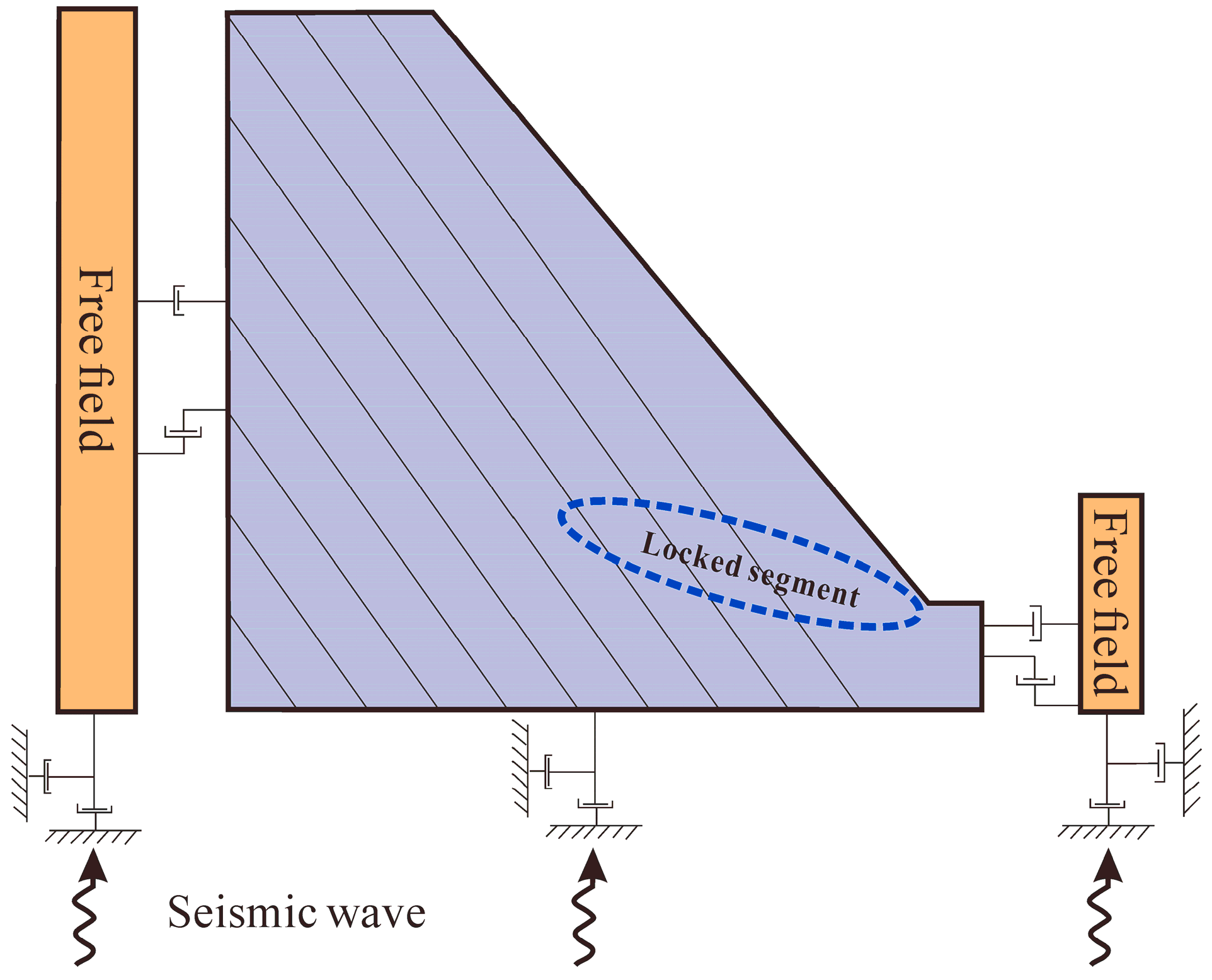
2.2. Boundary Conditions and Loading Conditions
3. Results and Discussion
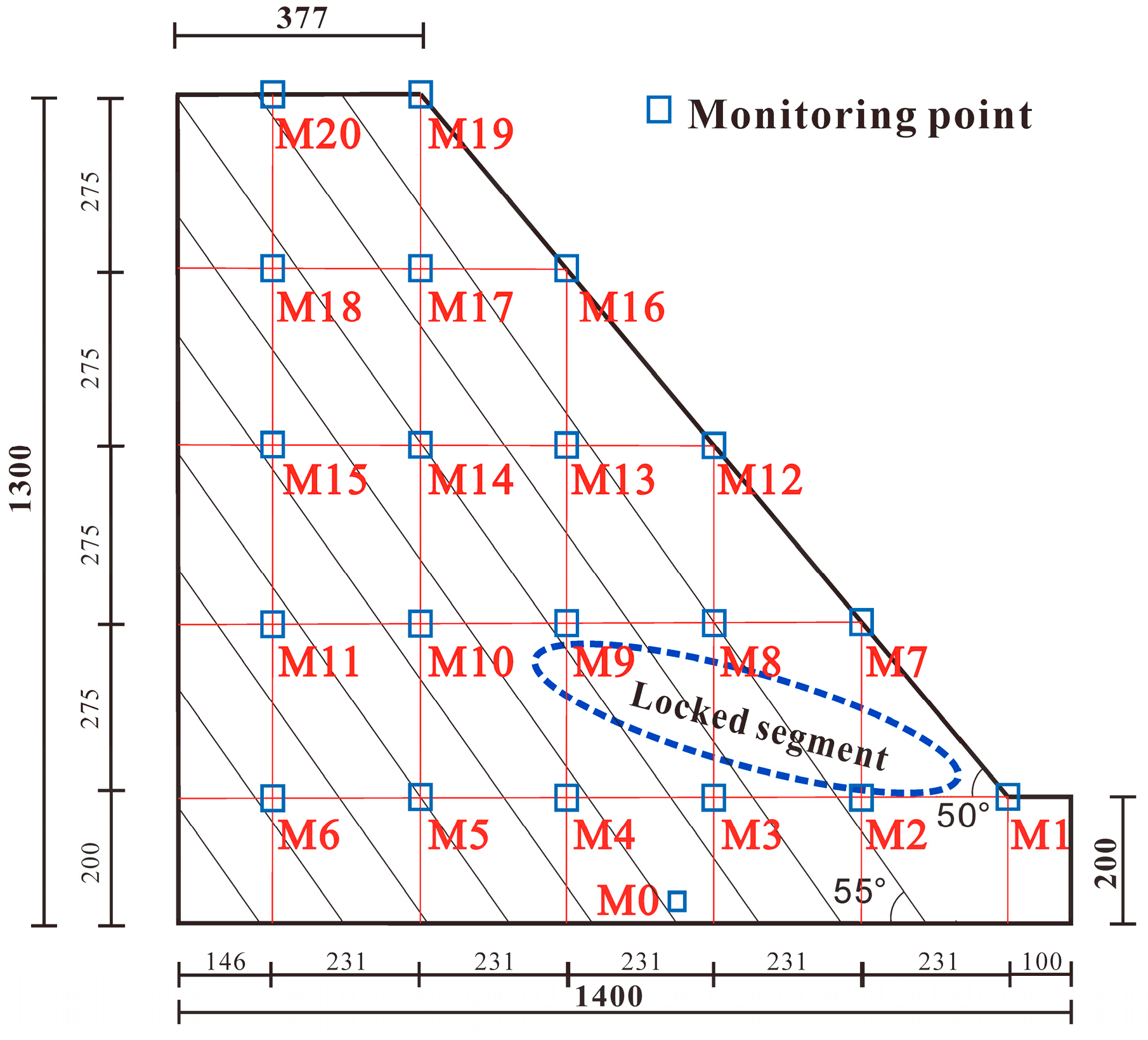
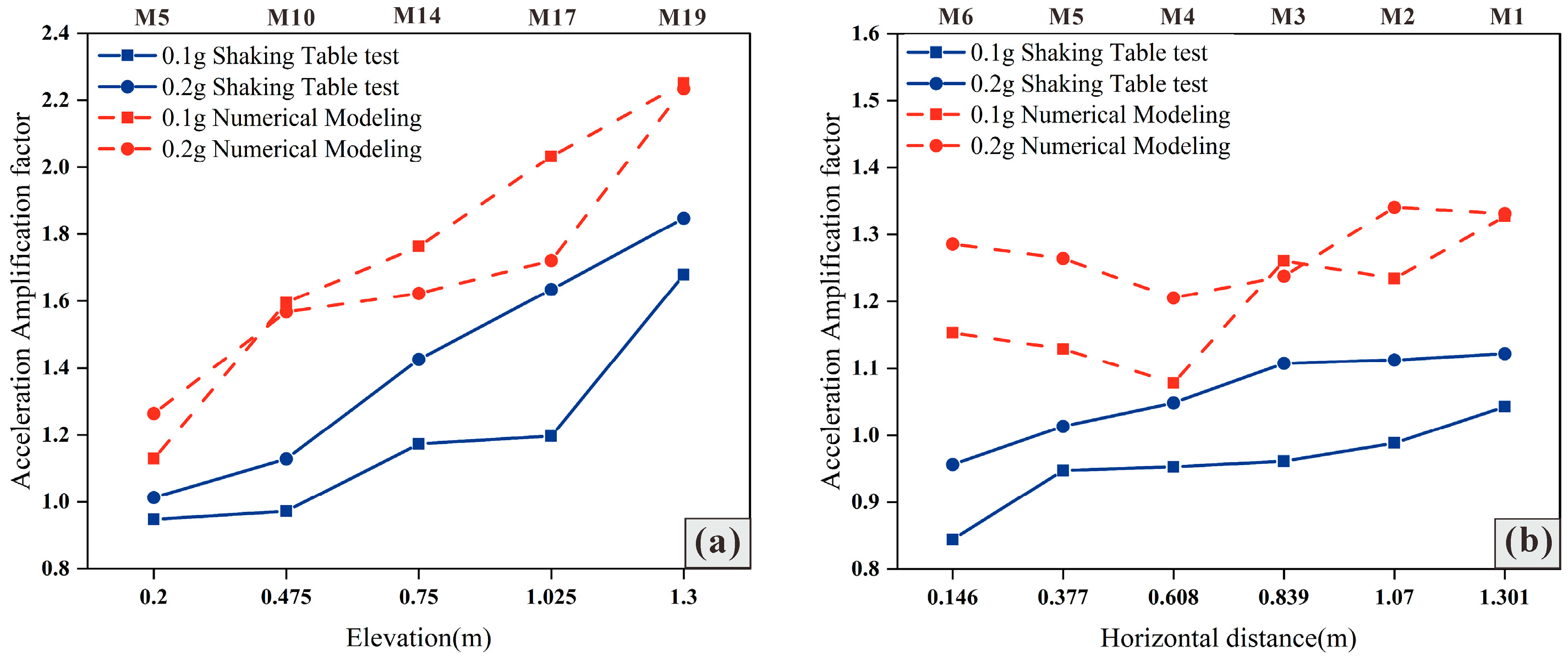
3.1. The Law of Acceleration Response Characteristics
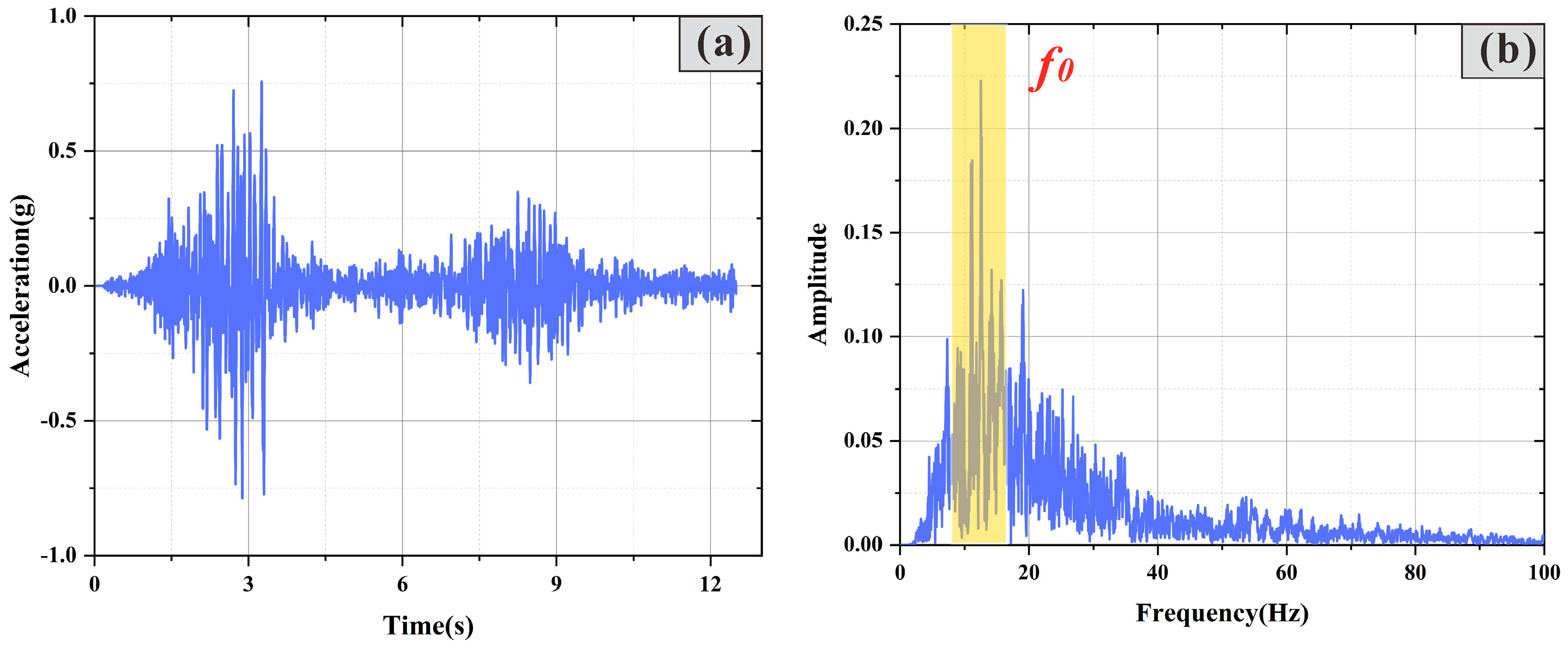
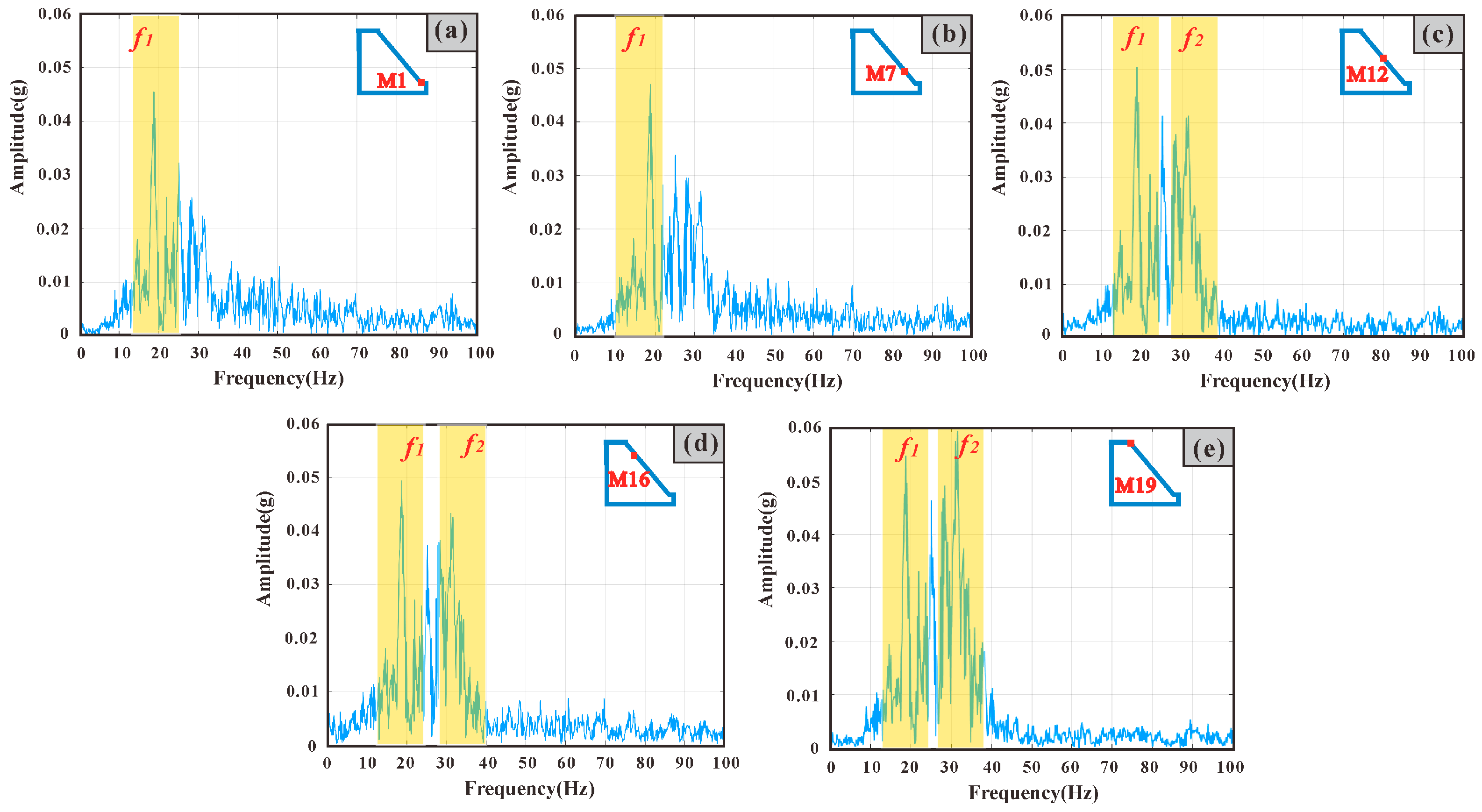
3.2. Fourier Spectrum Analysis of Acceleration
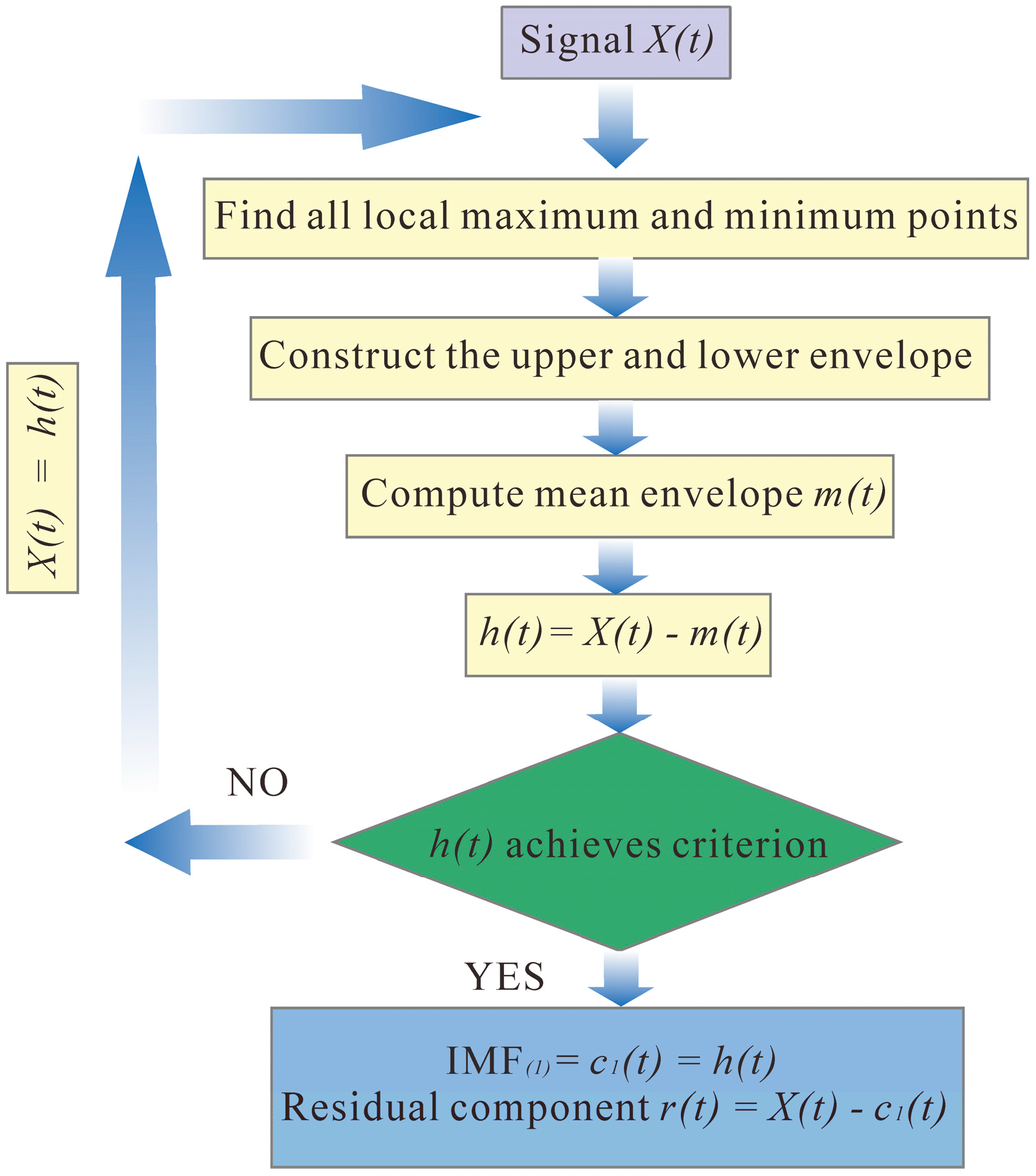
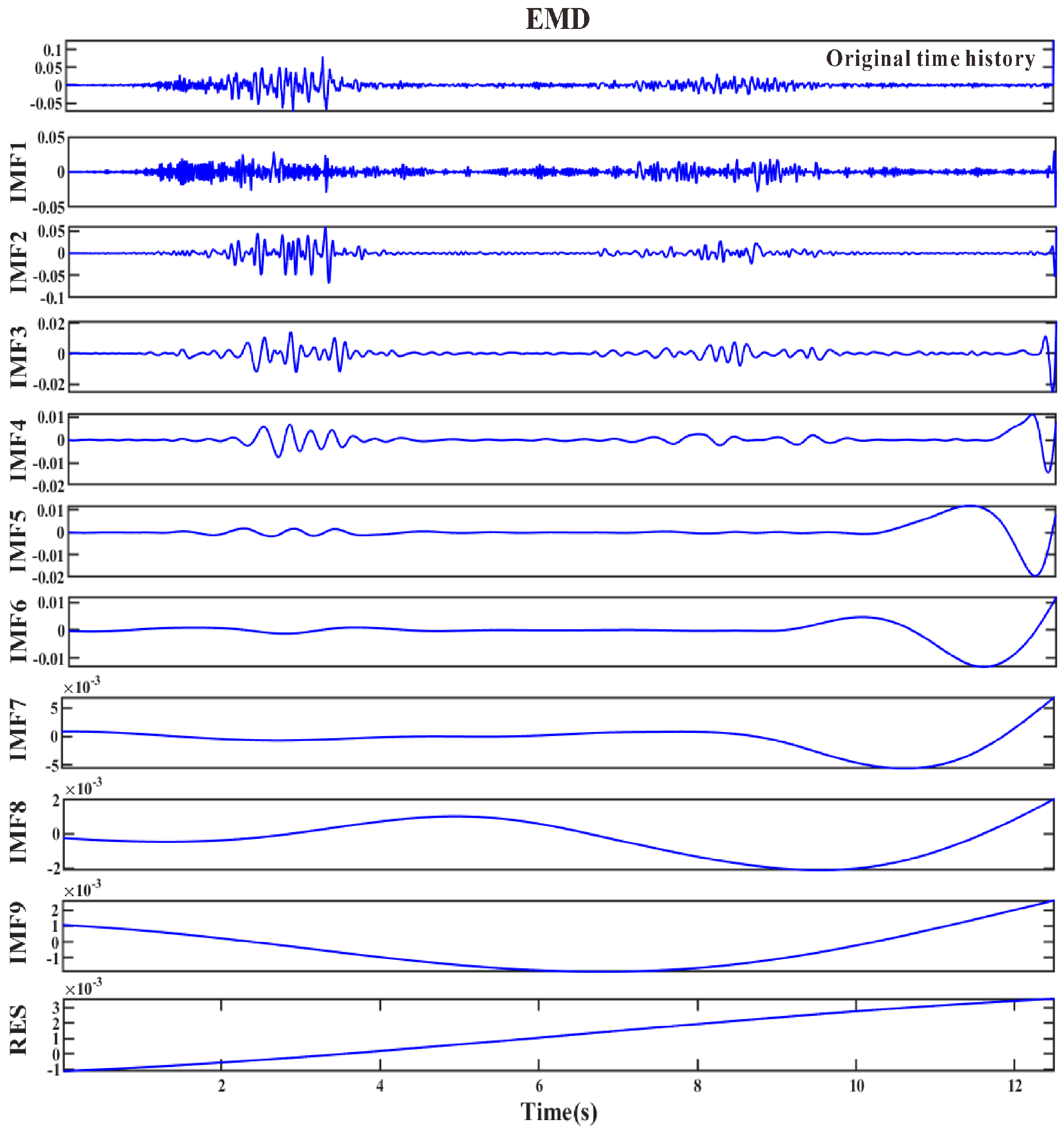
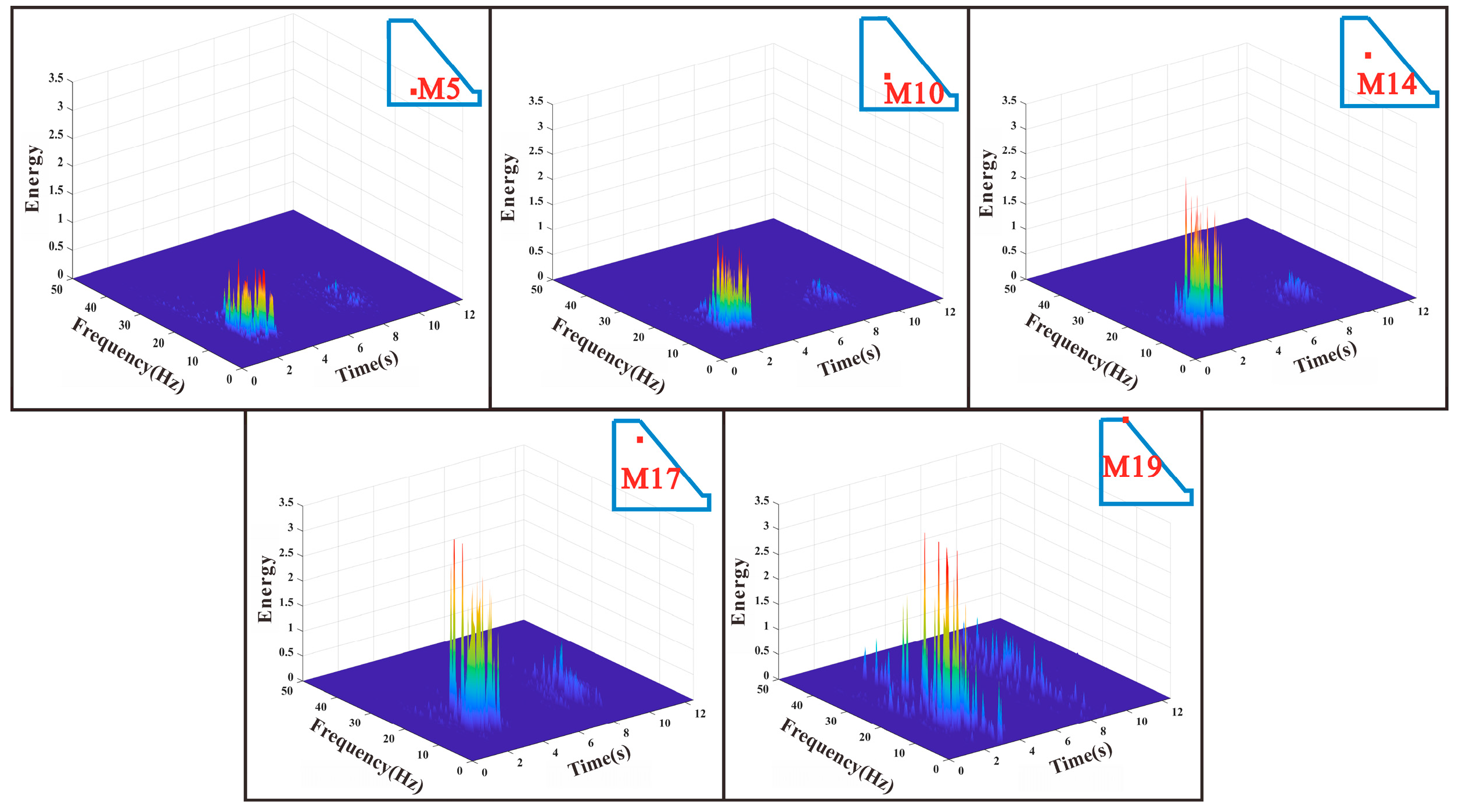
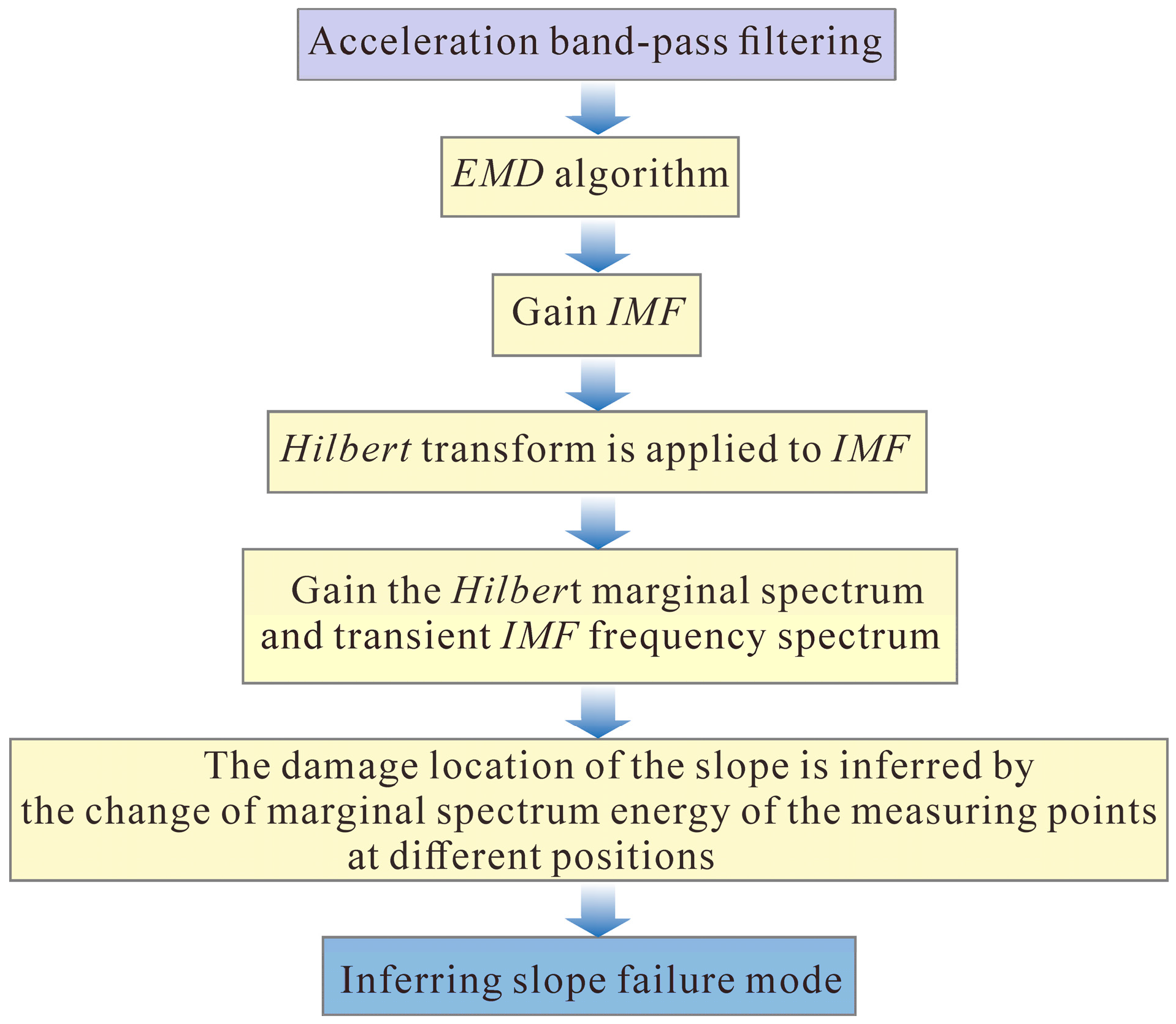
3.3. Analysis of Hilbert Spectrum
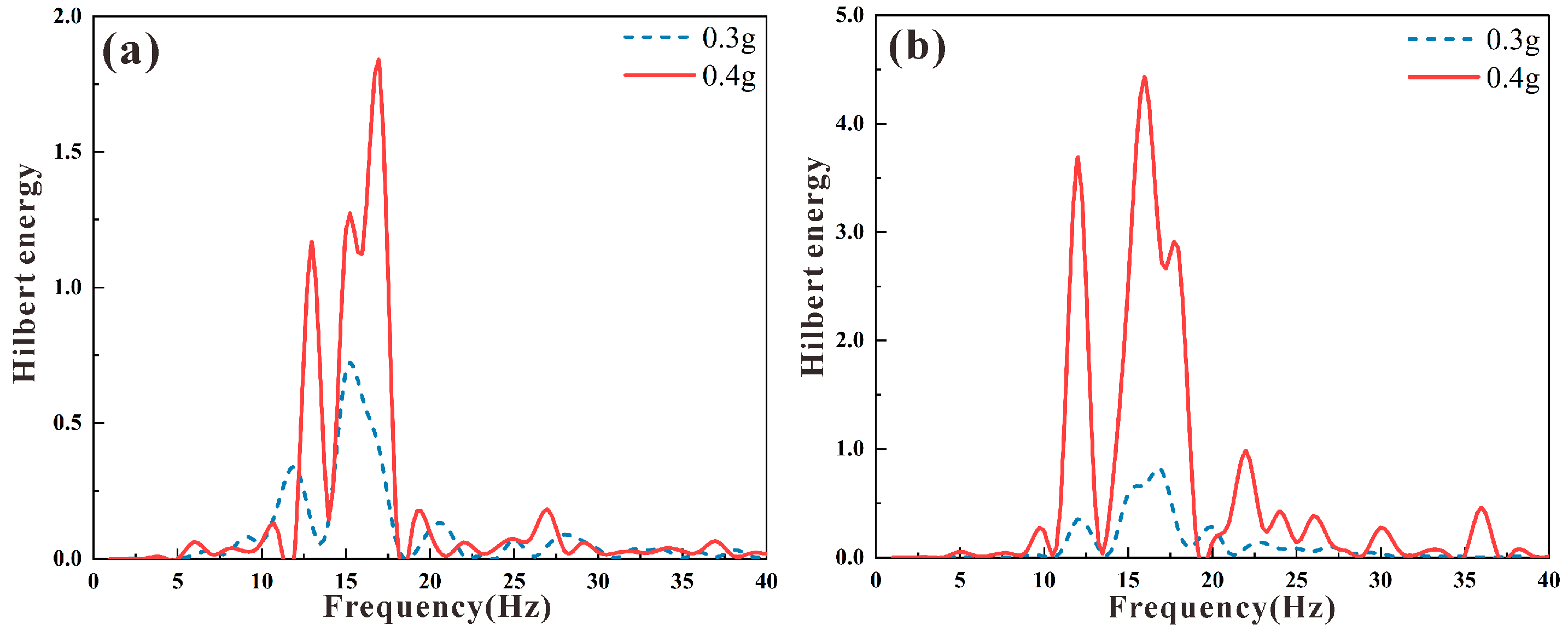
3.4. Analysis of the Marginal Spectrum
4. Conclusions
- (1)
- The acceleration amplification factor AAF of the slope under seismic action shows an obvious ’elevation effect’ and ’surface effect’. Simultaneously, the slope surface monitoring point’s acceleration Fourier spectrum gradually changes from a single peak to a double peak as its elevation rises. The amplitude of the high-frequency peak is more noticeable with the elevation amplification effect than the low-frequency peak, indicating that the slope acceleration Fourier spectrum’s amplification effect is somewhat selective.
- (2)
- Both the elevation and weak layers amplify the transmission of Hilbert energy, and the comparison of the Hilbert spectrums of an SBRS with weak layers and a homogeneous slope reveals a greater amplification of the high-frequency component of Hilbert energy. Because of this, the weak layer at the top of the slope is often damaged first when an earthquake happens. The final instability of the SBRS results from the progressive extension of the tensile fractures in the slope downhill and the progressive cutting and joining of the locked section at the toe of the slope.
- (3)
- The peak value of the marginal spectrum’s Hilbert energy corresponding to the main earthquake frequency will be considerably boosted as the seismic wave amplitude grows, according to a comparison of the SBRS’s marginal spectrum under different seismic wave amplitudes. This implies that when the Hilbert energy of the marginal spectrum being regulated by seismic waves progressively takes over, the slope is harmed and distorted. Additionally, there is a precursor even though there is no penetration damage because the Hilbert energy in the high-frequency band of the marginal spectrum at the locked segment’s upper monitoring point will suddenly rise before penetration damage occurs in the locked segment close to the base of the slope. This suggests that the top portion of the internal portion of the locked section has begun to sustain damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAF | Acceleration Amplification Factor |
| EMD | Empirical Modal Decomposition |
| HHT | Hilbert–Huang Transform |
| MSP | Marginal Spectrum |
| SBRS | Steep Bedding Rock Slope |
References
- Wang, X.; Chen, L.; Chen, Q.-F. Evaluation of 3D Crustal Seismic Velocity Models in Southwest China: Model Performance, Limitation, and Prospects. Sci. China Earth Sci. 2024, 67, 604–619. [Google Scholar] [CrossRef]
- Yao, H.; Liu, Y.; Zhang, Z. CSES Community Velocity Models in Southwest China. In China Seismic Experimental Site: Theoretical Framework and Ongoing Practice; Li, Y.-G., Zhang, Y., Wu, Z., Eds.; Springer Nature: Singapore, 2022; pp. 53–90. ISBN 9789811686078. [Google Scholar]
- Wang, Y.; Ling, Y.; Chan, T.O.; Awange, J. High-Resolution Earthquake-Induced Landslide Hazard Assessment in Southwest China through Frequency Ratio Analysis and LightGBM. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103947. [Google Scholar] [CrossRef]
- Dai, L.; Fan, X.; Wang, X.; Fang, C.; Zou, C.; Tang, X.; Wei, Z.; Xia, M.; Wang, D.; Xu, Q. Coseismic Landslides Triggered by the 2022 Luding Ms6.8 Earthquake, China. Landslides 2023, 20, 1277–1292. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, D.; Zheng, W.; Yang, J.; Chen, G.; Duan, L.; Liang, S.; Peng, H. Interaction of Earthquake-Triggered Landslides and Local Relief: Evidence from the 2008 Wenchuan Earthquake. Landslides 2023, 20, 757–770. [Google Scholar] [CrossRef]
- Li, L. Seismic Stability of Steep Consequent Rockslides with Different Lithology Assemblies: A Comparative Study. Bull. Eng. Geol. Environ. 2024, 83, 353. [Google Scholar] [CrossRef]
- Xia, C.; Shi, Z.; Liu, M.; Li, B.; Yu, S.; Xue, J. Dynamic Analysis of Field-Scale Rockslides Based on Three-Dimensional Discontinuous Smoothed Particle Hydrodynamics: A Case Study of Tangjiashan Rockslide. Eng. Geol. 2024, 336, 107558. [Google Scholar] [CrossRef]
- Yang, J.; Shi, Z.; Peng, M.; Zheng, H.; Soares-Frazão, S.; Zhou, J.; Shen, D.; Zhang, L. Quantitative Risk Assessment of Two Successive Landslide Dams in 2018 in the Jinsha River, China. Eng. Geol. 2022, 304, 106676. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Liu, W.; Hu, M.; Dong, J. The Comprehensive Risk Assessment of the Tangjiashan Landslide Dam Incident, China. Environ. Sci. Pollut. Res. 2023, 30, 73913–73927. [Google Scholar] [CrossRef]
- Chen, X.Q.; Cui, P.; Li, Y.; Zhao, W.Y. Emergency Response to the Tangjiashan Landslide-Dammed Lake Resulting from the 2008 Wenchuan Earthquake, China. Landslides 2011, 8, 91–98. [Google Scholar] [CrossRef]
- Pei, X.; Cui, S.; Liang, Y.; Wang, H. The Multiple Earthquakes Induced Progressive Failure of the Xinmo Landslide, China: Based on Shaking Table Tests. Environ. Earth Sci. 2023, 82, 465. [Google Scholar] [CrossRef]
- Chen, J.; Che, A.; Wang, L.; Zhou, H. Investigating the Failure Mechanism of Loess-Mudstone Landslides with a High Water Content Interface Subjected to Earthquakes through the Shaking Table Test. Soil Dyn. Earthq. Eng. 2024, 177, 108406. [Google Scholar] [CrossRef]
- Feng, Z.-Y.; Lu, Y.-R.; Shen, Z.-R. A Numerical Simulation of Seismic Signals of Coseismic Landslides. Eng. Geol. 2021, 289, 106191. [Google Scholar] [CrossRef]
- Li, L.; Xue, L.; Jiang, T.; Huang, K.; Li, Z. A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics. Sustainability 2024, 16, 9623. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Shi, X.; Yang, L.; Liu, R.; Lu, N. Exploring Mechanism of Hidden, Steep Obliquely Inclined Bedding Landslides Using a 3DEC Model: A Case Study of the Shanyang Landslide in Shaanxi Province, China. China Geol. 2024, 7, 303–314. [Google Scholar] [CrossRef]
- Xin, C.; Yang, F.; Feng, W.; Wang, Z.; Li, W. Seismic Responses and Shattering Cumulative Effects of Bedding Parallel Stepped Rock Slope: Model Test and Numerical Simulation. J. Rock Mech. Geotech. Eng. 2024, 6, 1614. [Google Scholar] [CrossRef]
- Tan, X.; Ren, Y.; Li, T.; Zhou, S.; Zhang, J.; Zhou, S. In-Situ Direct Shear Test and Numerical Simulation of Slate Structural Planes with Thick Muddy Interlayer along Bedding Slope. Int. J. Rock Mech. Min. Sci. 2021, 143, 104791. [Google Scholar] [CrossRef]
- Wang, C.; Guo, M.; Chen, X.; Gu, K.; Gong, Y.; Qi, Y.; Yuan, D.; Zhu, C.; Chen, B. Damage Evolution of the Bedding Rock Landslide and Debris Landslide under Earthquakes in the Three-Rivers Basin. Eng. Geol. 2024, 339, 107631. [Google Scholar] [CrossRef]
- Zang, M.; Yang, G.; Dong, J.; Qi, S.; He, J.; Liang, N. Experimental Study on Seismic Response and Progressive Failure Characteristics of Bedding Rock Slopes. J. Rock Mech. Geotech. Eng. 2022, 14, 1394–1405. [Google Scholar] [CrossRef]
- Dong, J.; Wang, C.; Huang, Z.; Yang, J.; Xue, L. Shaking Table Model Test to Determine Dynamic Response Characteristics and Failure Modes of Steep Bedding Rock Slope. Rock Mech. Rock. Eng. 2022, 55, 3645–3658. [Google Scholar] [CrossRef]
- Garcia, S.R.; Romo, M.P.; Alcántara, L. Analysis of Non-Linear and Non-Stationary Seismic Recordings of Mexico City. Soil Dyn. Earthq. Eng. 2019, 127, 105859. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, J.; Wu, J.; Yan, K. Dynamic Response and Dynamic Failure Mode of a Weak Intercalated Rock Slope Using a Shaking Table. Rock Mech. Rock Eng. 2016, 49, 3243–3256. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, L.-M.; Zhang, J.-J.; Ouyang, F. Energy-Based Analysis of Mechanisms of Earthquake-Induced Landslide Using Hilbert–Huang Transform and Marginal Spectrum. Rock Mech. Rock Eng. 2017, 50, 2425–2441. [Google Scholar] [CrossRef]
- Song, D.; Chen, Z.; Chao, H.; Ke, Y.; Nie, W. Numerical Study on Seismic Response of a Rock Slope with Discontinuities Based on the Time-Frequency Joint Analysis Method. Soil Dyn. Earthq. Eng. 2020, 133, 106112. [Google Scholar] [CrossRef]
- Song, D.; Liu, X.; Huang, J.; Zhang, J. Energy-Based Analysis of Seismic Failure Mechanism of a Rock Slope with Discontinuities Using Hilbert-Huang Transform and Marginal Spectrum in the Time-Frequency Domain. Landslides 2021, 18, 105–123. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Wang, P.; Che, A. Failure Mechanism Investigation on Loess–Mudstone Landslides Based on the Hilbert–Huang Transform Method Using a Large-Scale Shaking Table Test. Eng. Geol. 2022, 302, 106630. [Google Scholar] [CrossRef]
- Lei, H.; Wu, H.; Qian, J. Seismic Failure Mechanism and Interaction of the Cross Tunnel-Slope System Using Hilbert-Huang Transform. Tunn. Undergr. Space Technol. 2023, 131, 104820. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite Element Method Accuracy for Wave Propagation Problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Qi, S.; He, J.; Zhan, Z. A Single Surface Slope Effects on Seismic Response Based on Shaking Table Test and Numerical Simulation. Eng. Geol. 2022, 306, 106762. [Google Scholar] [CrossRef]
- Xue, L.; Li, L.; Xu, C.; Cui, Y.; Ding, H.; Huang, K.; Li, Z. A Multi-Objective Optimization Evaluation Model for Seismic Performance of Slopes Reinforced by Pile-Anchor System. Sci. Rep. 2024, 14, 5044. [Google Scholar] [CrossRef] [PubMed]
- Antwi Buah, P.; Zhang, Y.; He, J.; Yu, P.; Xiang, C.; Fu, H.; He, Y.; Liu, J. Evaluating the Dynamic Response and Failure Process of a Rock Slope under Pulse-like Ground Motions. Geomat. Nat. Hazards Risk 2023, 14, 2167613. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Tai, D.; Qi, S.; Zheng, B.; Luo, G.; He, J.; Guo, S.; Zou, Y.; Wang, Z. Effect of Excitation Frequency and Joint Density on the Dynamic Amplification Effect of Slope Surface on Jointed Rock Slopes. Eng. Geol. 2024, 330, 107385. [Google Scholar] [CrossRef]
- Nussbaumer, H.J. The Fast Fourier Transform. In Fast Fourier Transform and Convolution Algorithms; Nussbaumer, H.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 80–111. ISBN 978-3-642-81897-4. [Google Scholar]
- Liu, H.; Xu, Q.; Li, Y.; Fan, X. Response of High-Strength Rock Slope to Seismic Waves in a Shaking Table Test. Bull. Seismol. Soc. Am. 2013, 103, 3012–3025. [Google Scholar] [CrossRef]
- Song, D.; Che, A.; Chen, Z.; Ge, X. Seismic Stability of a Rock Slope with Discontinuities under Rapid Water Drawdown and Earthquakes in Large-Scale Shaking Table Tests. Eng. Geol. 2018, 245, 153–168. [Google Scholar] [CrossRef]
- Huang, N.E.; Long, S.R.; Shen, Z. The Mechanism for Frequency Downshift in Nonlinear Wave Evolution. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1996; Volume 32, pp. 59–117, 117A, 117B, 117C. [Google Scholar]

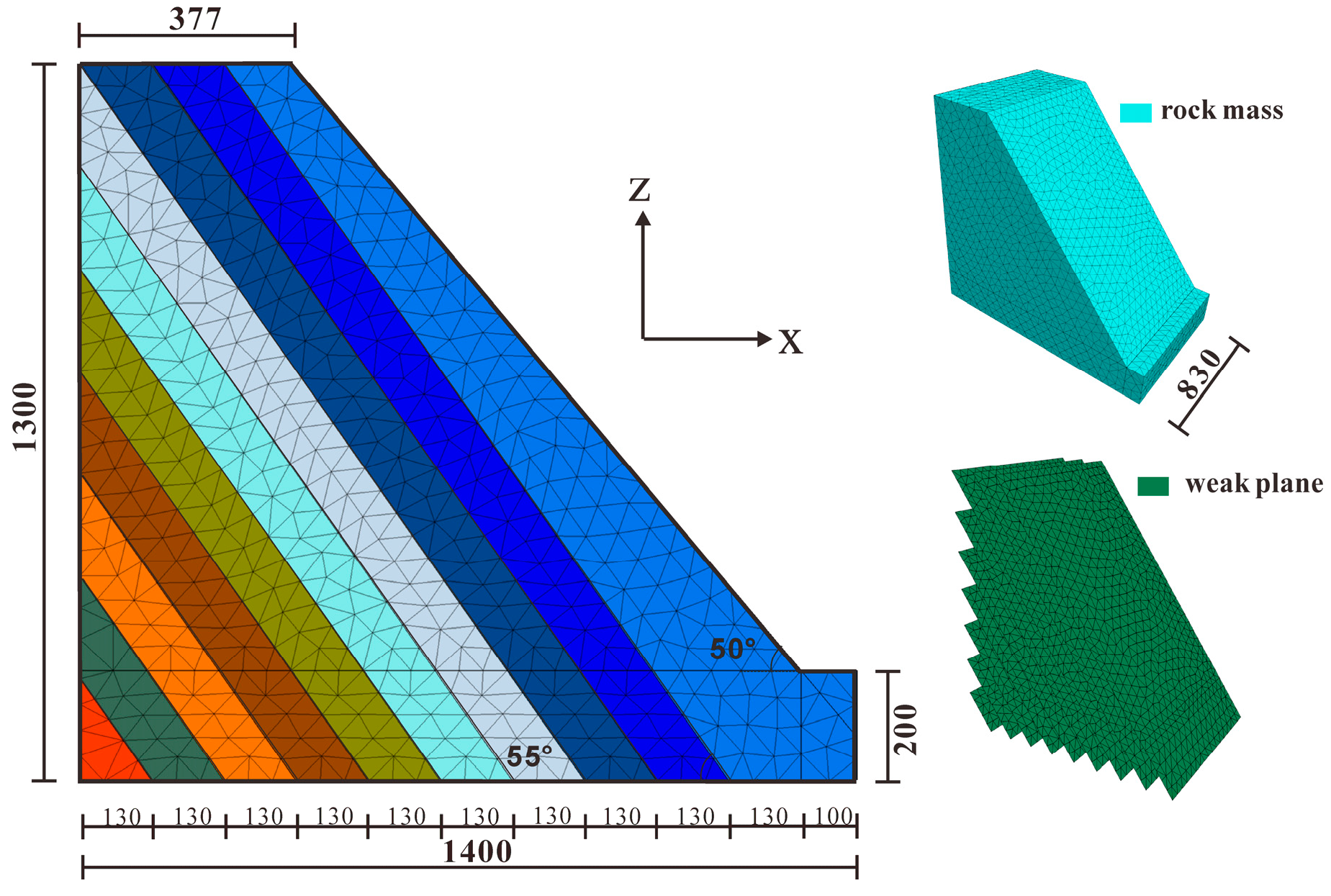

| (a) | |||||
| Item | Density (g/cm3) | Young Modulus (MPa) | Poisson Ratio | Friction Angle (°) | Cohesion (kPa) |
| Rock mass | 2.50 | 124.46 | 0.12 | 34.8 | 294.0 |
| (b) | |||||
| Item | Stiffness—Normal (Pa) | Stiffness—Shear (Pa) | Friction Angle (°) | Cohesion (kPa) | |
| Weak layer | 2.00 × 1010 | 2.00 × 1010 | 30 | 200.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, L.; Huang, K.; Xue, L.; Jiang, T.; Dong, J.; Wang, C.; Ding, H. The Seismic Dynamic Response Characteristics of the Steep Bedding Rock Slope Are Investigated Using the Hilbert–Huang Transform and Marginal Spectrum Theory. Appl. Sci. 2025, 15, 3078. https://doi.org/10.3390/app15063078
Li Z, Li L, Huang K, Xue L, Jiang T, Dong J, Wang C, Ding H. The Seismic Dynamic Response Characteristics of the Steep Bedding Rock Slope Are Investigated Using the Hilbert–Huang Transform and Marginal Spectrum Theory. Applied Sciences. 2025; 15(6):3078. https://doi.org/10.3390/app15063078
Chicago/Turabian StyleLi, Zhuan, Longfei Li, Kun Huang, Lei Xue, Tong Jiang, Jinyu Dong, Chuang Wang, and Hao Ding. 2025. "The Seismic Dynamic Response Characteristics of the Steep Bedding Rock Slope Are Investigated Using the Hilbert–Huang Transform and Marginal Spectrum Theory" Applied Sciences 15, no. 6: 3078. https://doi.org/10.3390/app15063078
APA StyleLi, Z., Li, L., Huang, K., Xue, L., Jiang, T., Dong, J., Wang, C., & Ding, H. (2025). The Seismic Dynamic Response Characteristics of the Steep Bedding Rock Slope Are Investigated Using the Hilbert–Huang Transform and Marginal Spectrum Theory. Applied Sciences, 15(6), 3078. https://doi.org/10.3390/app15063078





