Role Contribution and Interpersonal Coordination in Partner-Assisted Flight According to Pair Experience
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Characterization
2.2. Data Analysis Procedures
2.3. Statistical Analysis
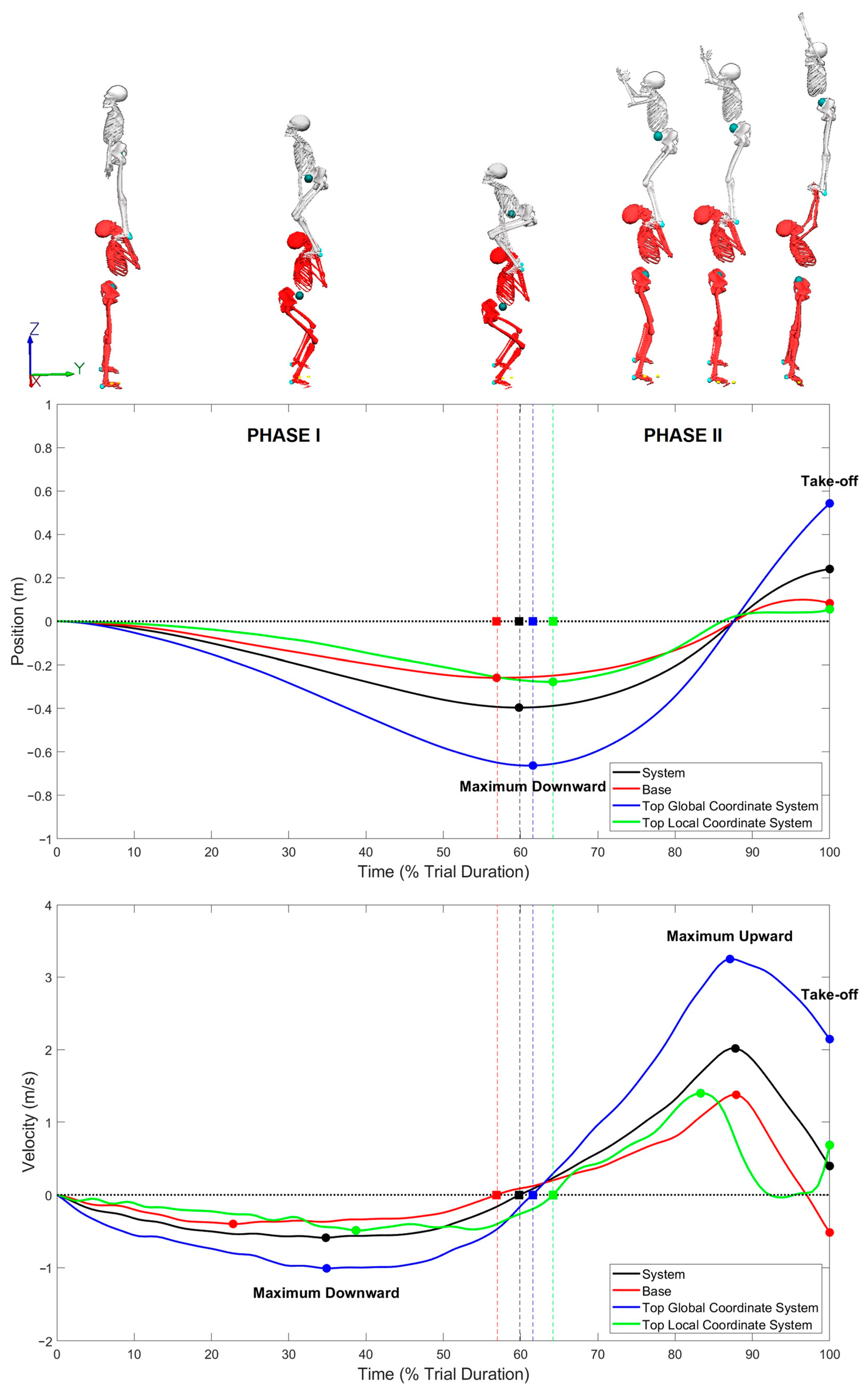
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pozzo, T.; Studeny, C. Théorie et Pratique des Sports Acrobatiques; Vigot: Paris, France, 1987; p. 196. [Google Scholar]
- León-Prados, J.A.; Jemni, M. Reliability and agreement in technical and artistic scores during real-time judging in two European acrobatic gymnastic events. Int. J. Perform. Anal. Sport 2022, 22, 132–148. [Google Scholar] [CrossRef]
- Fédération Internationale de Gymnastique. Acrobatic Gymnastics Code of Points 2022–2024. Available online: https://www.gymnastics.sport/publicdir/rules/files/en_2022-2024%20ACRO%20CoP.pdf (accessed on 13 September 2023).
- Leite, I.; Fonseca, P.; Ávila-Carvalho, L.; Vilas-Boas, J.P.; Goethel, M.; Mochizuki, L.; Conceição, F. Biomechanical Research Methods Used in Acrobatic Gymnastics: A Systematic Review. Biomechanics 2023, 3, 52–68. [Google Scholar] [CrossRef]
- Leite, I.; Fonseca, P.; Ávila-Carvalho, L.; Vilas-Boas, J.P.; Goethel, M.; Mochizuki, L.; Conceição, F. The state of the art in Acrobatic Gymnastics: A bibliometric analysis. Sci. Gymnast. J. 2023, 15, 47–64. [Google Scholar] [CrossRef]
- Kimura, A.; Yokozawa, T.; Ozaki, H. Clarifying the Biomechanical Concept of Coordination Through Comparison with Coordination in Motor Control. Front. Sports Act. Living 2021, 3, 753062. [Google Scholar] [CrossRef] [PubMed]
- Passos, P.; Davids, K.; Chow, J.Y. Interpersonal Coordination and Performance in Social Systems, 1st ed.; Routledge: New York, NY, USA, 2016. [Google Scholar]
- Lund, O.; Ravn, S.; Christensen, M.K. Jumping together: Apprenticeship learning among elite trampoline athletes. Phys. Educ. Sport Pedagog. 2014, 19, 383–397. [Google Scholar] [CrossRef]
- Feigean, M.; R’Kiouak, M.; Bootsma, R.J.; Bourbousson, J. Effects of Intensive Crew Training on Individual and Collective Characteristics of Oar Movement in Rowing as a Coxless Pair. Front. Psychol. 2017, 8, 1139. [Google Scholar] [CrossRef]
- de Brouwer, A.J.; de Poel, H.J.; Hofmijster, M.J. Don’t rock the boat: How antiphase crew coordination affects rowing. PLoS ONE 2013, 8, e54996. [Google Scholar] [CrossRef]
- Cuijpers, L.S.; Zaal, F.T.; de Poel, H.J. Rowing Crew Coordination Dynamics at Increasing Stroke Rates. PLoS ONE 2015, 10, e0133527. [Google Scholar] [CrossRef]
- Cuijpers, L.S.; Passos, P.J.M.; Murgia, A.; Hoogerheide, A.; Lemmink, K.; de Poel, H.J. Rocking the boat: Does perfect rowing crew synchronization reduce detrimental boat movements? Scand. J. Med. Sci. Sports 2017, 27, 1697–1704. [Google Scholar] [CrossRef]
- Harrison, S.J.; Richardson, M.J. Horsing Around: Spontaneous Four-Legged Coordination. J. Mot. Behav. 2009, 41, 519–524. [Google Scholar] [CrossRef]
- Eckardt, F.; Witte, K. Horse-Rider Interaction: A New Method Based on Inertial Measurement Units. J. Equine Vet. Sci. 2017, 55, 1–8. [Google Scholar] [CrossRef]
- Wolframm, I.A.; Bosga, J.; Meulenbroek, R.G. Coordination dynamics in horse-rider dyads. Hum. Mov. Sci. 2013, 32, 157–170. [Google Scholar] [CrossRef] [PubMed]
- Fumery, G.; Turpin, N.A.; Claverie, L.; Fourcassié, V.; Moretto, P. A biomechanical study of load carriage by two paired subjects in response to increased load mass. Sci. Rep. 2021, 11, 4346. [Google Scholar] [CrossRef] [PubMed]
- Leite, I.; Goethel, M.; Conceição, F.; Ávila-Carvalho, L. How Does the Jumping Performance Differs between Acrobatic and Rhythmic Gymnasts? Biomechanics 2023, 3, 457–468. [Google Scholar] [CrossRef]
- Lake, J.P.; Mundy, P.D.; Comfort, P. Power and Impulse Applied During Push Press Exercise. J. Strength. Cond. Res. 2014, 28, 2552–2559. [Google Scholar] [CrossRef]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the Key Phases of the Countermovement Jump Force-Time Curve. Strength. Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
- Mizuguchi, S.; Sands, W.A.; Wassinger, C.A.; Lamont, H.S.; Stone, M.H. A new approach to determining net impulse and identification of its characteristics in countermovement jumping: Reliability and validity. Sports Biomech. 2015, 14, 258–272. [Google Scholar] [CrossRef]
- Gathercole, R.; Sporer, B.; Stellingwerff, T. Countermovement Jump Performance with Increased Training Loads in Elite Female Rugby Athletes. Int. J. Sports Med. 2015, 36, 722–728. [Google Scholar] [CrossRef]
- Laffaye, G.; Wagner, P.P.; Tombleson, T.I. Countermovement jump height: Gender and sport-specific differences in the force-time variables. J. Strength. Cond. Res. 2014, 28, 1096–1105. [Google Scholar] [CrossRef]
- Linthorne, N.P. Analysis of standing vertical jumps using a force platform. Am. J. Phys. 2001, 69, 1198–1204. [Google Scholar] [CrossRef]
- Renals, L.; Lake, J.; Keogh, J.; Austin, K. Strongman Log Push Press: The Effect Log Diameter has on Force-Time Characteristics. J. Strength. Cond. Res. 2018, 32, 2693–2700. [Google Scholar] [CrossRef] [PubMed]
- Bradley, E.; Harrington, K.; Tiffin, C. A comparison of a tucked back somersault between novice and experienced acrobatic gymnasts: An inertial measurement approach. In Proceedings of the ISBS Proceedings Archive: ISBS Conference 2020, Liverpool, UK, 20–24 July 2020. [Google Scholar]
- Hiley, M.J.; Yeadon, M.R. The margin for error when releasing the high bar for dismounts. J. Biomech. 2003, 36, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Huchez, A.; Haering, D.; Holvoet, P.; Barbier, F.; Begon, M. Differences between expert and novice gymnasts performance of a counter movement forward in flight on uneven bars. Sci. Gymnast. J. 2016, 8, 31–41. [Google Scholar]
- Takei, Y. The roche vault performed by elite gymnasts: Somersaulting technique, deterministic model, and judges’ scores. J. Appl. Biomech. 2007, 23, 1–11. [Google Scholar] [CrossRef]
- Chang, M.; O’Dwyer, N.; Adams, R.; Cobley, S.; Lee, K.Y.; Halaki, M. Whole-body kinematics and coordination in a complex dance sequence: Differences across skill levels. Hum. Mov. Sci. 2020, 69, 102564. [Google Scholar] [CrossRef]
- Hiley, M.J.; Schmid, N.; Yeadon, M.R. How do technique and coordination change during learning of a whole-body task: Application to the upstart in gymnastics. J. Sports Sci. 2019, 37, 2374–2380. [Google Scholar] [CrossRef] [PubMed]
- Münz, A.; Eckardt, F.; Witte, K. Horse–rider interaction in dressage riding. Hum. Mov. Sci. 2014, 33, 227–237. [Google Scholar] [CrossRef]
- Leite, I.; Ávila-Carvalho, L.; Goethel, M.; Mochizuki, L.; Conceição, F. How do base and top acrobatic gymnasts organize their movement patterns to perform partner-assisted flight? In Proceedings of the 9th Gymnastics National Congress/7th International Congress: Gymnastics in the Global Society, Vila Real, Portugal, 11–13 October 2024; pp. 49–50. [Google Scholar]
- Robertson, D.G.E.; Caldwell, G.E.; Hamill, J.; Kamen, G.; Whittlesey, S. Research Methods in Biomechanics, 2nd ed.; Human Kinetics: Champaign, IL, USA, 2014. [Google Scholar]
- Parise, C.V.; Spence, C.; Ernst, M.O. When Correlation Implies Causation in Multisensory Integration. Curr. Biol. 2012, 22, 46–49. [Google Scholar] [CrossRef]
- Moura, F.A.; van Emmerik, R.E.A.; Santana, J.E.; Martins, L.E.B.; Barros, R.M.L.d.; Cunha, S.A. Coordination analysis of players’ distribution in football using cross-correlation and vector coding techniques. J. Sports Sci. 2016, 34, 2224–2232. [Google Scholar] [CrossRef]
- Ervilha, U.F.; Mochizuki, L.; Figueira, A., Jr.; Hamill, J. Are muscle activation patterns altered during shod and barefoot running with a forefoot footfall pattern? J. Sports Sci. 2017, 35, 1697–1703. [Google Scholar] [CrossRef]
- Nelson-Wong, E.; Howarth, S.; Winter, D.A.; Callaghan, J.P. Application of autocorrelation and cross-correlation analyses in human movement and rehabilitation research. J. Orthop. Sports Phys. Ther. 2009, 39, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. Journal of experimental psychology. J. Exp. Psychol. General 2012, 141, 2–18. [Google Scholar] [CrossRef]
- Cohen, B.H. Explaining Psychological Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: New York, NY, USA, 1988; p. 567. [Google Scholar]
- Prassas, S.; Kwon, Y.H.; Sands, W.A. Biomechanical research in artistic gymnastics: A review. Sports Biomech. 2006, 5, 261–291. [Google Scholar] [CrossRef]
- Taboada-Iglesias, Y.; Gutierrez-Sanchez, A.; Vernetta Santana, M. Anthropometric profile of elite acrobatic gymnasts and prediction of role performance. J. Sports Med. Phys. Fit. 2016, 56, 433–442. [Google Scholar]
- King, M.A.; Yeadon, M.R. Coping with perturbations to a layout somersault in tumbling. J. Biomech. 2003, 36, 921–927. [Google Scholar] [CrossRef]
- Yeadon, M.R. Airborne Movements: Somersaults and Twists. In Handbook of Human Motion; Müller, B., Wolf, S.I., Brueggemann, G.-P., Deng, Z., McIntosh, A., Miller, F., Selbie, W.S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–19. [Google Scholar]
- Burgess, R.C.; Noffal, G.J. Kinematic analysis of the back salto take-off in a tumbling series: Advanced vs. beginner techniques. In Proceedings of the Biomechanics Symposia, San Francisco, CA, USA, 8–11 August 2001; pp. 8–11. [Google Scholar]
- Marinsek, M.; Cuk, I. Landing errors in the men’s floor exercise are caused by flight characteristics. Biol. Sport 2010, 27, 123–128. [Google Scholar] [CrossRef]
- Gómez-Landero, L.A.; Leal Del Ojo, P.; Walker, C.; Floría, P. Static balance performance differs depending on the test, age and specific role played in acrobatic gymnastics. Gait Posture 2021, 90, 48–54. [Google Scholar] [CrossRef]
- Leite, I.; Goethel, M.; Fonseca, P.; Vilas-Boas, J.P.; Ávila-Carvalho, L.; Mochizuki, L.; Conceição, F. A Hierarchy of Variables That Influence the Force–Velocity Profile of Acrobatic Gymnasts: A Tool Based on Artificial Intelligence. Appl. Sci. 2024, 14, 3191. [Google Scholar] [CrossRef]
- Hochmuth, G. Biomecánica de los Movimientos Deportivos; Instituto Nacional de Educación Física: Madrid, Spain, 1973.
- Floría, P.; Harrison, A.J. The influence of range of motion versus application of force on vertical jump performance in prepubescent girls and adult females. Eur. J. Sport. Sci. 2014, 14, S197–S204. [Google Scholar] [CrossRef]
- Loram, I.D.; Lakie, M.; Gawthrop, P.J. Visual control of stable and unstable loads: What is the feedback delay and extent of linear time-invariant control? J. Physiol. 2009, 587, 1343–1365. [Google Scholar] [CrossRef]
- Urbán, T.; Gutiérrez, Ó.; Moreno, F.J. Effects of Unstable Conditions on Kinematics and Performance Variables in Young Handball Players. J. Hum. Kinet. 2015, 46, 39–48. [Google Scholar] [CrossRef]
- Ostrowski, S.J.; Carlson, L.A.; Lawrence, M.A. Effect of an Unstable Load on Primary and Stabilizing Muscles During the Bench Press. J. Strength. Cond. Res. 2017, 31, 430–434. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Lavender, S.A.; Sommerich, C. The Effects of Load Stability and Visual Access During Asymmetric Lifting Tasks on Back and Upper Extremity Biomechanical Responses. Hum. Factors 2019, 61, 712–721. [Google Scholar] [CrossRef] [PubMed]
- Leal Del Ojo, P.; Floría, P.; Walker, C.; Gómez-Landero, L.A. Is acrobatic pyramid performance determined by the individual balance of the gymnasts? Sports Biomech. 2023, 22, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Hiley, M.J.; Wangler, R.; Predescu, G. Optimization of the felge on parallel bars. Sports Biomech. 2009, 8, 39–51. [Google Scholar] [CrossRef]
- McCluskey, L.; Lynskey, S.; Leung, C.K.; Woodhouse, D.; Briffa, K.; Hopper, D. Throwing velocity and jump height in female water polo players: Performance predictors. J. Sci. Med. Sport 2010, 13, 236–240. [Google Scholar] [CrossRef]
- Freeston, J.; Ferdinands, R.; Rooney, K. Throwing velocity and accuracy in elite and sub-elite cricket players: A descriptive study. Eur. J. Sport Sci. 2007, 7, 231–237. [Google Scholar] [CrossRef]
- Buszard, T. On Learning to Anticipate in Youth Sport. Sports Med. 2022, 52, 2303–2314. [Google Scholar] [CrossRef]
- Clayton, H.M.; MacKechnie-Guire, R.; Hobbs, S.J. Riders’ Effects on Horses—Biomechanical Principles with Examples from the Literature. Animals 2023, 13, 3854. [Google Scholar] [CrossRef]
- Jingguang, Q.; Yiling, M.; Xiao, T.; Zhaoxia, L.; Chen, W. A Finite Element Model for Estimation of Contact Dynamics. J. Hum. Kinet. 2020, 73, 59–72. [Google Scholar] [CrossRef]
- Matsushima, M. Relation between downward and upward phases on the trampoline bed during jumping. Sci. Gymnast. J. 2023, 15, 367–374. [Google Scholar] [CrossRef]
| LE (N = 7) | ME (N = 5) | |||
|---|---|---|---|---|
| Variables | Base | Top | Base | Top |
| Age (years) | 18.00 (7.00) | 14.00 (5.00) | 16.00 (0.00) | 12.00 (1.00) |
| Mass (kg) | 70.10 (15.60) | 36.40 (9.20) | 61.10 (5.40) | 32.80 (0.10) |
| Height (m) | 1.68 (0.07) | 1.49 (0.10) | 1.64 (0.09) | 1.45 (0.05) |
| Experience as a pair (years) | 0.25 (0.17) | 2.00 (1.75) | ||
| Variables | Unit | BASE | TOP GCS | TOP LCS | SYSTEM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LE | ME | p (ES) | LE | ME | p (ES) | LE | ME | p (ES) | LE | ME | p (ES) | ||
| Trial Duration | s | 1.72 (1.47) | 1.58 (0.14) | <0.001 (0.80) | 1.72 (0.47) | 1.58 (0.14) | <0.001 (0.80) | 1.72 (0.47) | 1.58 (0.14) | <0.001 (0.80) | 1.72 (0.47) | 1.58 (0.14) | <0.001 (0.80) |
| Phase I | s | 1.11 (0.42) | 0.95 (0.24) | <0.001 (0.61) | 1.13 (0.41) | 0.99 (0.20) | <0.001 (0.72) | 1.18 (0.37) | 1.03 (0.11) | <0.001 (0.82) | 1.12 (0.41) | 0.98 (0.22) | <0.001 (0.67) |
| %time | 63.09 (7.89) | 59.44 (11.66) | 0.02 (0.43) | 65.18 (7.49) | 61.99 (6.19) | <0.001 (0.68) | 66.68 (6.24) | 64.49 (4.17) | <0.001 (0.77) | 64.14 (8.49) | 60.79 (7.82) | <0.001 (0.62) | |
| Phase II | s | 0.61 (0.06) | 0.56 (0.11) | <0.001 (0.60) | 0.58 (0.06) | 0.58 (0.07) | 0.37 (0.16) | 0.56 (0.10) | 0.56 (0.09) | 0.45 (0.14) | 0.58 (0.05) | 0.56 (0.09) | 0.04 (0.37) |
| %time | 36.91 (7.89) | 40.56 (11.66) | 0.02 (0.43) | 34.82 (7.49) | 38.01 (6.19) | <0.001 (0.68) | 33.32 (6.24) | 35.51 (4.17) | <0.001 (0.77) | 35.86 (8.49) | 39.21 (7.82) | <0.001 (0.62) | |
| MD Pos | m | −0.24 (0.03) | −0.25 (0.03) | 0.89 (0.03) | −0.61 (0.08) | −0.63 (0.06) | 0.02 (0.43) | −0.27 (0.06) | −0.29 (0.03) | 0.13 (0.27) | −0.37 (0.03) | −0.39 (0.03) | 0.07 (0.33) |
| stature | −0.14 (0.02) | −0.15 (0.02) | 0.30 (0.19) | −0.42 (0.03) | −0.46 (0.03) | <0.001 (0.67) | −0.19 (0.04) | −0.20 (0.02) | 0.02 (0.41) | −0.12 (0.01) | −0.13 (0.01) | 0.005 (0.53) | |
| TO Pos | m | 0.09 (0.04) | 0.09 (0.02) | 0.06 (0.35) | 0.67 (0.05) | 0.63 (0.07) | <0.001 (0.75) | 0.08 (0.04) | 0.09 (0.04) | 0.05 (0.36) | 0.30 (0.05) | 0.27 (0.05) | <0.001 (0.77) |
| stature | 0.06 (0.02) | 0.05 (0.02) | 0.17 (0.25) | 0.45 (0.06) | 0.45 (0.05) | 0.11 (0.29) | 0.06 (0.03) | 0.07 (0.03) | 0.02 (0.43) | 0.10 (0.01) | 0.09 (0.02) | 0.009 (0.50) | |
| MD Vel | m/s | −0.44 (0.15) | −0.48 (0.18) | 0.06 (0.35) | −1.12 (0.38) | −1.21 (0.29) | <0.001 (0.64) | −0.56 (0.28) | −0.62 (0.15) | 0.005 (0.53) | −0.66 (0.23) | −0.72 (0.22) | 0.007 (0.51) |
| stature/s | −0.44 (0.15) | −0.48 (0.18) | 0.01 (0.45) | −0.75 (0.21) | −0.88 (0.23) | <0.001 (0.75) | −0.36 (0.19) | −0.44 (0.09) | <0.001 (0.63) | −0.21 (0.07) | −0.23 (0.08) | <0.001 (0.64) | |
| MU Vel | m/s | 1.39 (0.18) | 1.45 (0.15) | 0.02 (0.41) | 3.59 (0.32) | 3.47 (0.31) | 0.02 (0.43) | 1.60 (0.27) | 1.37 (0.23) | <0.001 (0.90) | 2.13 (0.23) | 2.18 (0.24) | 0.68 (0.08) |
| stature/s | 1.39 (0.18) | 1.45 (0.15) | <0.001 (0.61) | 2.47 (0.24) | 2.48 (0.18) | 0.68 (0.07) | 1.08 (0.13) | 0.98 (0.14) | <0.001 (0.73) | 0.69 (0.05) | 0.72 (0.10) | <0.001 (0.31) | |
| TO Vel | m/s | −0.55 (0.16) | −0.55 (0.14) | 0.84 (0.04) | 2.45 (0.39) | 2.54 (0.51) | 0.48 (0.13) | 2.03 (0.54) | 2.04 (0.95) | 0.45 (0.14) | 0.51 (0.17) | 0.53 (0.22) | 0.97 (0.01) |
| stature/s | −0.33 (0.10) | −0.34 (0.11) | 0.34 (0.17) | 1.68 (0.29) | 1.81 (0.31) | 0.07 (0.33) | 1.39 (0.43) | 1.42 (0.57) | 0.81 (0.04) | 0.16 (0.05) | 0.18 (0.08) | 0.59 (0.01) | |
| Variables | TOP GCS-BASE | TOP LCS-BASE | ||||
|---|---|---|---|---|---|---|
| LE | ME | p (ES) | LE | ME | p (ES) | |
| Position rmax | 0.98 (0.01) | 0.98 (0.01) | 0.45 (0.14) | 0.97 (0.02) | 0.98 (0.01) | 0.02 (0.43) |
| Position r0 | 0.98 (0.02) | 0.98 (0.01) | 0.81 (0.04) | 0.95 (0.04) | 0.96 (0.02) | <0.001 (0.64) |
| Position lag (%movement) | 0.90 (1.00) | 0.65 (1.00) | 0.03 (0.39) | 2.80 (2.60) | 1.40 (4.00) | <0.001 (0.62) |
| Velocity rmax | 0.95 (0.03) | 0.96 (0.02) | 0.20 (0.24) | 0.84 (0.10) | 0.85 (0.05) | 0.28 (0.20) |
| Velocity r0 | 0.82 (0.10) | 0.82 (0.06) | 0.36 (0.17) | 0.78 (0.16) | 0.82 (0.07) | 0.01 (0.48) |
| Velocity lag (% movement) | 5.10 (2.20) | 5.75 (1.00) | 0.01 (0.47) | −1.20 (4.50) | −1.75 (3.80) | 0.06 (0.34) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leite, I.; Gómez-Landero, L.A.; Fonseca, P.; Ávila-Carvalho, L.; Vilas-Boas, J.P.; Goethel, M.; Mochizuki, L.; Conceição, F. Role Contribution and Interpersonal Coordination in Partner-Assisted Flight According to Pair Experience. Appl. Sci. 2025, 15, 3085. https://doi.org/10.3390/app15063085
Leite I, Gómez-Landero LA, Fonseca P, Ávila-Carvalho L, Vilas-Boas JP, Goethel M, Mochizuki L, Conceição F. Role Contribution and Interpersonal Coordination in Partner-Assisted Flight According to Pair Experience. Applied Sciences. 2025; 15(6):3085. https://doi.org/10.3390/app15063085
Chicago/Turabian StyleLeite, Isaura, Luis Arturo Gómez-Landero, Pedro Fonseca, Lurdes Ávila-Carvalho, João Paulo Vilas-Boas, Márcio Goethel, Luis Mochizuki, and Filipe Conceição. 2025. "Role Contribution and Interpersonal Coordination in Partner-Assisted Flight According to Pair Experience" Applied Sciences 15, no. 6: 3085. https://doi.org/10.3390/app15063085
APA StyleLeite, I., Gómez-Landero, L. A., Fonseca, P., Ávila-Carvalho, L., Vilas-Boas, J. P., Goethel, M., Mochizuki, L., & Conceição, F. (2025). Role Contribution and Interpersonal Coordination in Partner-Assisted Flight According to Pair Experience. Applied Sciences, 15(6), 3085. https://doi.org/10.3390/app15063085








