A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions
Abstract
:1. Introduction
2. Recent Review Articles
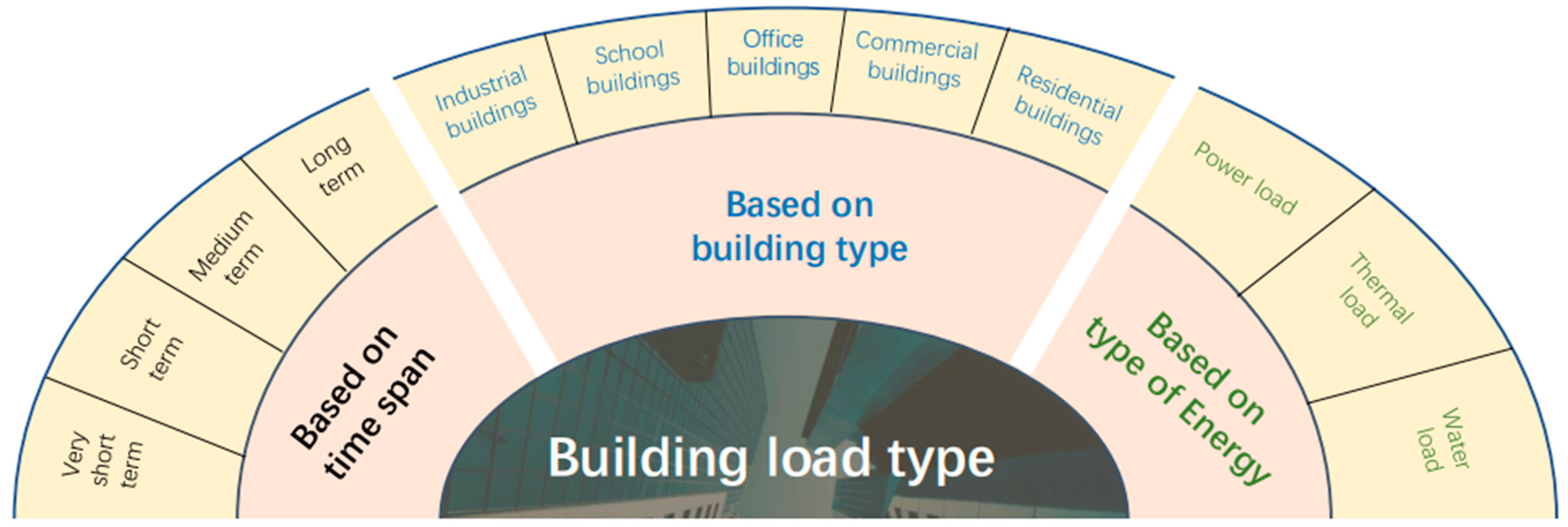
3. Building Load Type
3.1. Classify Based on Time Span
3.1.1. Very Short Term Load Forecasting
3.1.2. Short Term Load Forecasting
3.1.3. Medium Term Load Forecasting
3.1.4. Long Term Load Forecasting
3.2. Classify Based on Building Type
3.2.1. Industrial Buildings
3.2.2. Educational Buildings
3.2.3. Office Buildings
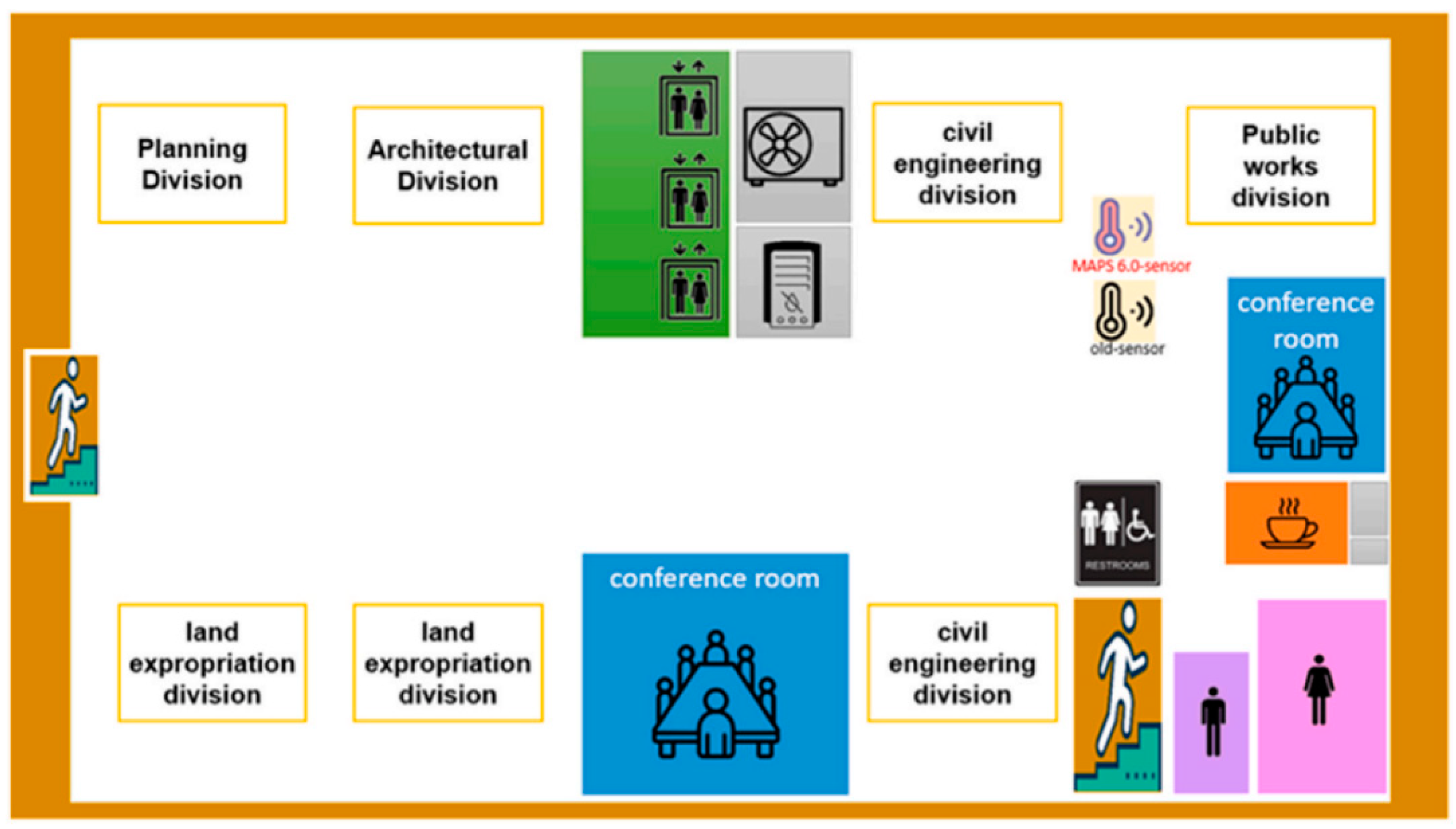
3.2.4. Commercial Buildings
3.2.5. Residential Buildings
3.3. Classify Based on Energy Type
3.3.1. Power Load
3.3.2. Thermal Load
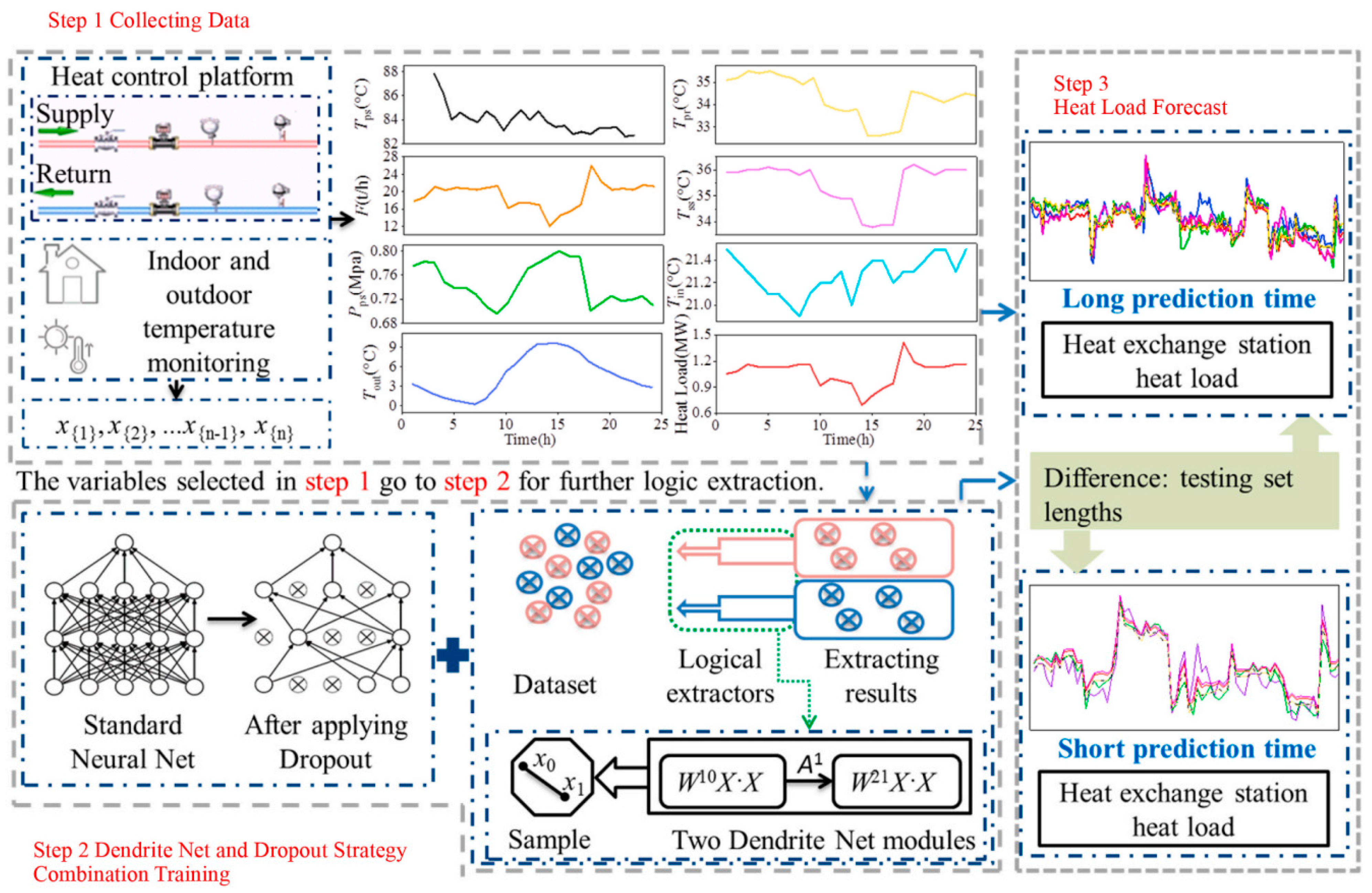
3.3.3. Water Load
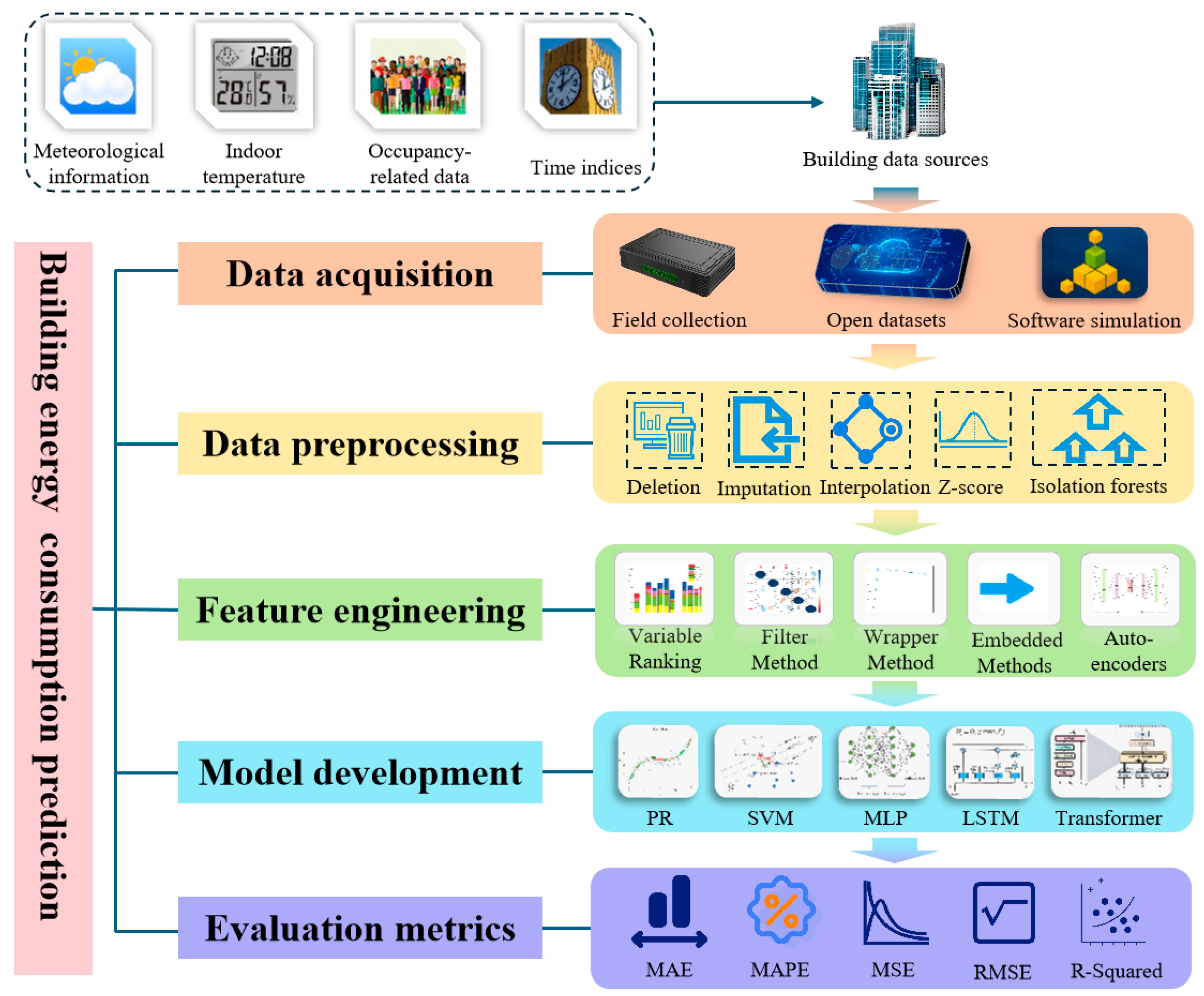
4. Data-Driven Framework for Building Energy Consumption Prediction
4.1. Data Acquisition
4.2. Data Preprocessing
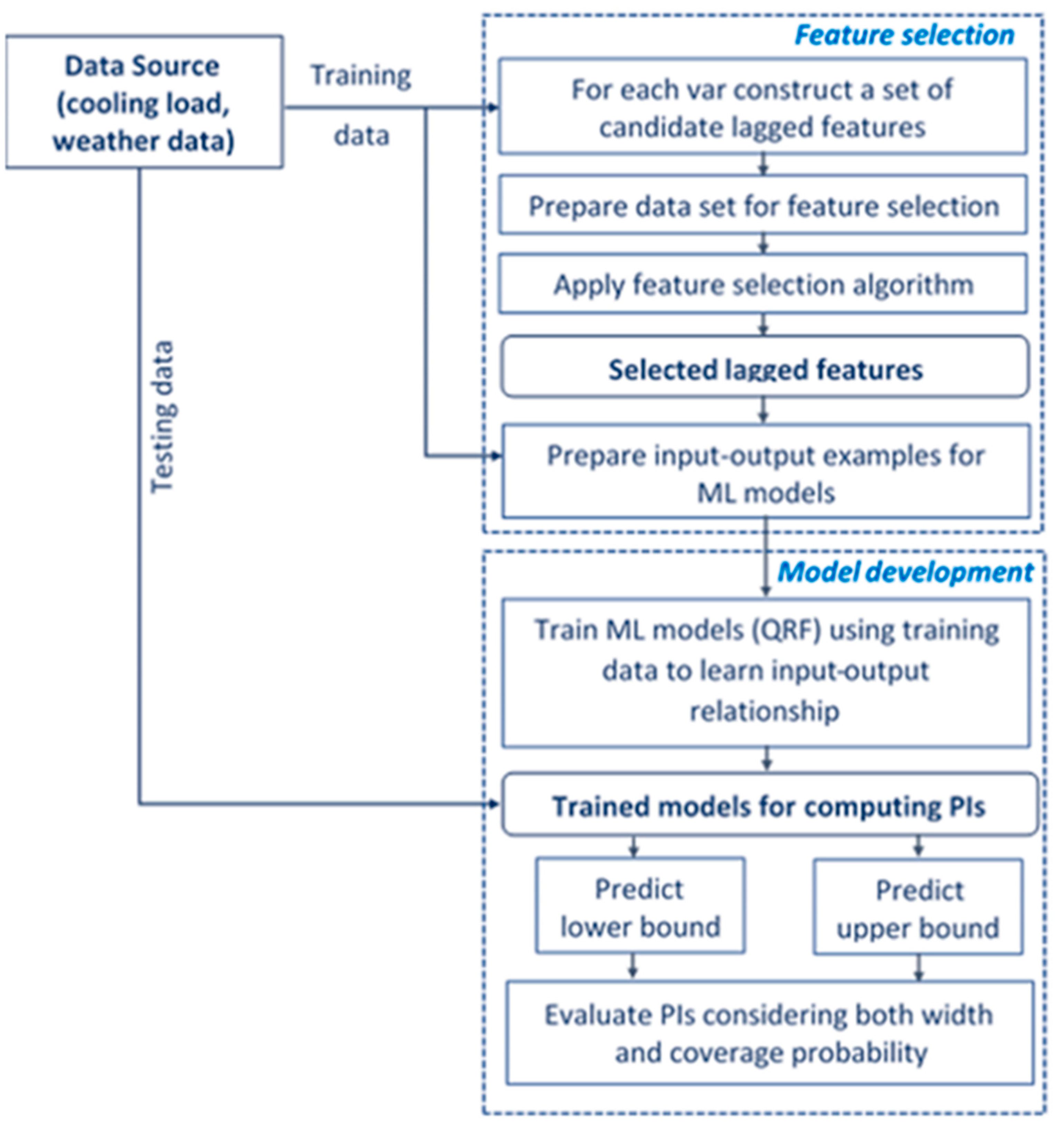
4.3. Feature Engineering
- (1)
- Variable ranking is employed, which involves identifying the most relevant features to the target variable through techniques such as correlation analysis. Notable examples of this approach include the use of the Pearson correlation coefficient and the Spearman rank correlation coefficient.
- (2)
- There are filtering and wrapper methods, which assess the predictive performance of individual features or subsets of features to determine the optimal feature set. Principal component analysis (PCA) and random forest (RF) are among the commonly used techniques within this category.
- (3)
- Embedded methods represent another significant approach, wherein feature selection is seamlessly integrated into the learning algorithm itself. Lasso regression is a prime example, as it inherently performs feature selection as part of its regression process.
- (4)
- Autoencoders (AEs) utilize deep learning techniques to learn nonlinear representations of the input data, thereby effectively extracting useful features. This method leverages the power of neural networks to uncover complex patterns within the data.
4.4. Model for Prediction
4.4.1. Polynomial Regression
4.4.2. SVR
4.4.3. MLP
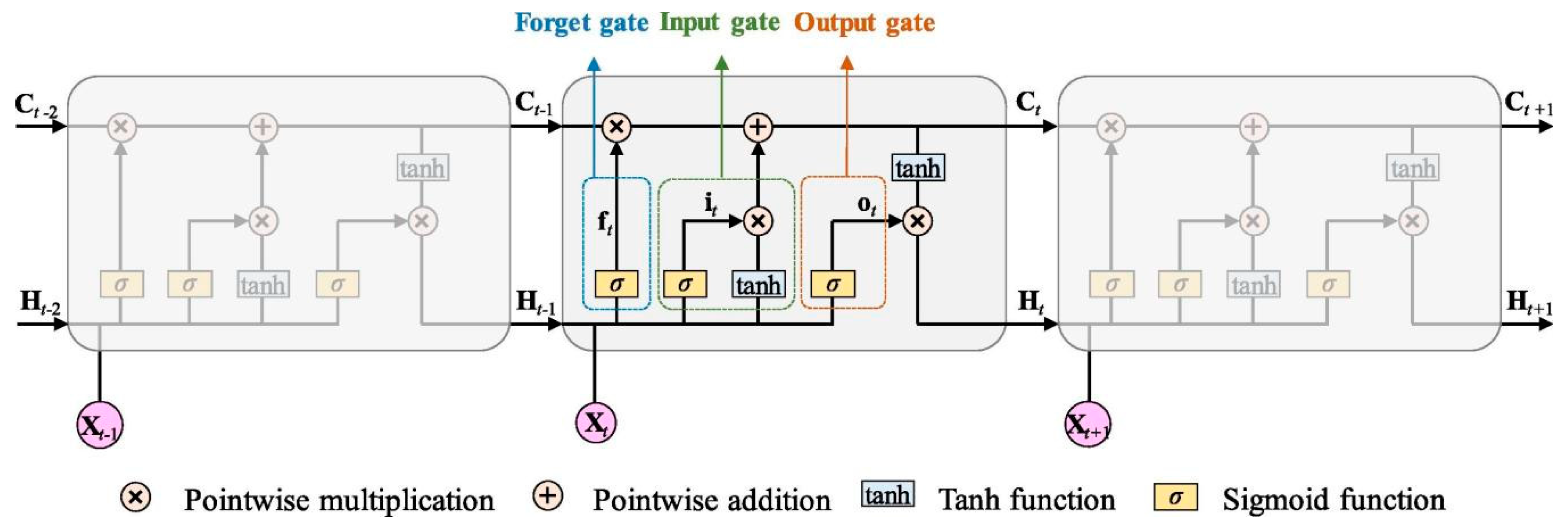
4.4.4. LSTM
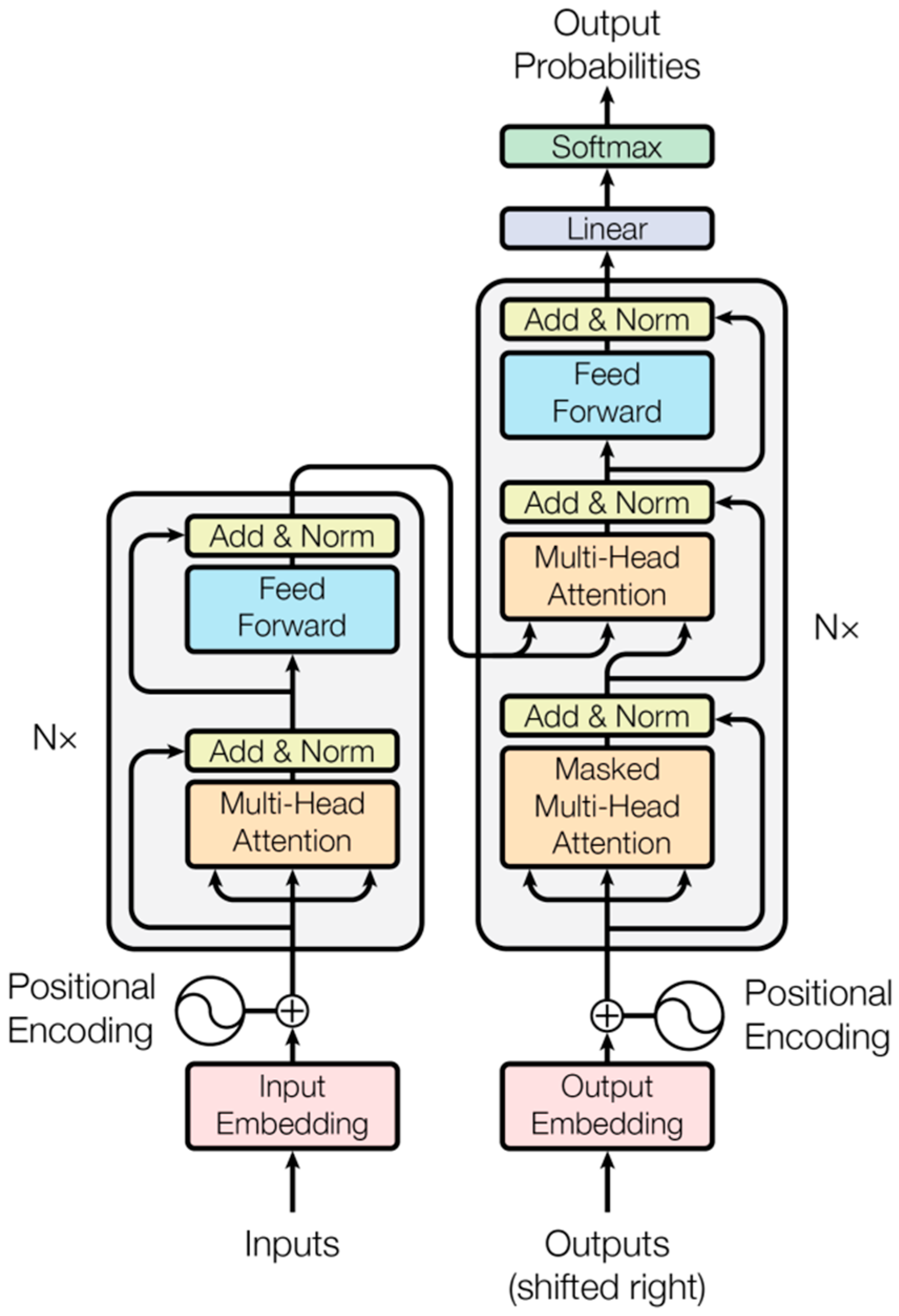
4.4.5. Transformer
4.4.6. K-Nearest Neighbors
4.4.7. CNN
4.4.8. Tree-Based Models
4.4.9. Ensemble Models
4.5. Evaluation Metrics
5. Discussion
5.1. Opportunities for Further Works
- (1)
- Multi-agent collaboration for energy load forecasting and optimization. Confronted with the complex energy systems composed of diverse building types within cities or industrial parks, the intricate interplay among various energy loads poses unprecedented challenges for accurately forecasting overall energy loads. The multi-agent collaboration approach, with its distinct advantages of distributed processing, adaptability, and efficient coordination, offers an innovative solution to this dilemma. By simulating the behavioral patterns of different buildings as independent agents, this method can capture and process the dynamic interactions among buildings and with the external environment, thereby achieving high-precision forecasting and intelligent optimization of the regional comprehensive energy loads, providing robust support for energy management decision-making.
- (2)
- Optimization and efficiency enhancement of deep learning model frameworks in building energy consumption prediction. Deep learning models, with their formidable data-fitting capabilities, have demonstrated immense potential in building energy consumption predictions. However, their high demands for training data volume and quality, as well as the substantial computational resources required, constitute bottlenecks in practical applications. Consequently, future research should concentrate on refining deep learning model frameworks, aiming to strike an optimal balance between computational efficiency and prediction accuracy with minimal computational resources. This encompasses strategies such as designing lightweight network structures, exploring efficient training algorithms, and optimizing data preprocessing procedures, with the goal of maintaining or even enhancing prediction accuracy and timeliness while reducing resource consumption.
- (3)
- Exploration of generative pre-trained models in building energy consumption prediction. As large language models proliferate across industries, their robust semantic understanding and generation capabilities have sparked new insights into the realm of time-series analysis [180]. Particularly in building energy consumption prediction [181], the introduction and targeted fine-tuning of generative pre-trained models can harness their extensive context awareness and vast prior knowledge to uncover hidden complex patterns and trends within load data. This approach excels at capturing the nonlinear characteristics of load variations more precisely, enhancing the robustness and generalization capabilities of prediction models, thereby charting a promising new avenue for future research in building energy consumption prediction.
- (4)
- Multi-source data fusion for building energy consumption forecasting. With the advancement of Internet of Things (IoT) and smart sensor technologies, building energy consumption data can originate from multiple sources, including building management systems, smart meters, and weather stations [182]. These data sources vary in terms of temporal resolution, spatial granularity, and quality levels [183]. Future research should focus on effectively merging these diverse data sources to improve the accuracy and reliability of forecasts. This may involve the development of data cleaning, matching, transformation, and fusion algorithms.
- (5)
- Edge computing has important applications in building energy consumption prediction. Edge computing is capable of performing data processing at devices close to data sources or at the network edge, reducing data transmission latency and increasing data processing efficiency. In the context of building energy consumption prediction, by deploying edge-computing nodes on intelligent devices within buildings, the locally-collected energy-consumption data can be analyzed in real-time. This not only enables a rapid response to real-time changes in building energy consumption and the timely adjustment of prediction-model parameters but also eases the burden on the cloud-computing center and safeguards data privacy. For example, edge computing can perform preliminary processing on the high-frequency energy-consumption data generated in real-time by smart meters. After extracting key features, the data are then transmitted to the cloud for in-depth analysis, thus enhancing the timeliness and accuracy of the overall prediction.
- (6)
- Blockchain technology plays a facilitating role in the management of building energy consumption data. Blockchain, with its characteristics of decentralization, immutability, and traceability, provides new ideas for the management of building energy consumption data. In the field of building energy-consumption prediction, data from different sources may have trust-related issues, and blockchain can ensure data authenticity and integrity. For instance, through blockchain technology, the energy-consumption data collected from building management systems, smart meters, and other devices is recorded. The entry of each data item requires verification by multiple nodes, ensuring that the data cannot be maliciously tampered with. This helps to improve the credibility of data when integrating multi-source data, laying a foundation for constructing a more reliable energy-consumption prediction model. Meanwhile, the smart-contract function of blockchain can also be used to automate the sharing and trading of energy-consumption data, promoting data circulation and rational utilization.
- (7)
- There is potential to be tapped for crowdsourced data in building energy consumption prediction. Crowdsourced data, sourced from a large number of users, has advantages such as a large volume of data and wide coverage. In building energy-consumption prediction, information about building usage habits and users’ perception of environmental comfort can be collected through crowdsourcing platforms. These data can supplement the deficiencies of data collected by traditional sensors and reveal the influencing factors of building energy consumption from the perspective of user behavior. For example, users can upload information such as their indoor temperature-adjustment preferences and the frequency of electrical-appliance use in the building through a mobile application. Combining these crowdsourced data with the actual energy-consumption data of the building can lead to a more comprehensive understanding of the complex patterns of building energy consumption, thereby optimizing the energy-consumption prediction model and improving the accuracy and comprehensiveness of the prediction.
- (8)
- Interpretability and transparency in building energy consumption forecasting. The pervasive use of deep learning models for building energy consumption forecasting introduces challenges related to interpretability and transparency due to their complexity and “black box” nature [184]. Future research can explore methods to enhance the interpretability of deep learning models, making their predictions more transparent and trustworthy. For instance, investigations could focus on employing interpretable machine learning techniques such as LIME and SHAP to elucidate deep learning model predictions, thereby aiding building managers in understanding the decision-making processes of these models. Moreover, research could aim to design deep learning models that inherently possess explanatory capabilities, automatically generating interpretive information during the forecasting process.
- (9)
- Real-time and dynamic building energy consumption forecasting. As energy systems evolve to become increasingly complex and dynamic, building energy consumption forecasts must not only achieve high precision but also exhibit real-time capabilities and dynamic adjustment abilities [185]. Future research could explore strategies for delivering real-time energy consumption forecasts and dynamically adjusting model parameters to account for variations in building usage patterns and environmental conditions [186]. For example, researchers could investigate the application of online and incremental learning techniques to enable models to update and adjust dynamically based on real-time data. Additionally, research could integrate reinforcement learning techniques to allow models to continually optimize their forecasting strategies during real-time prediction.
- (10)
- Collaborative optimization of building energy consumption forecasting and smart grids. The synergistic optimization of building energy consumption forecasting and smart grid operations is vital for achieving efficient energy utilization [187]. Future research could examine methods to integrate building energy consumption forecasting with the scheduling and optimization processes of smart grids, realizing collaborative synergies between buildings and the grid [188]. For example, researchers could explore how to leverage building energy consumption forecasts to optimize grid load scheduling, mitigating peak loads and fluctuations within the grid. Furthermore, investigations could focus on combining demand response technologies, enabling buildings to adapt dynamically to grid load conditions for mutually beneficial outcomes.
- (11)
- Incorporating renewable energy fluctuations and uncertainties in building energy consumption forecasting [189]. As the utilization of renewable energy sources within buildings becomes more prevalent, building energy consumption forecasting must account for the inherent variability and uncertainties associated with renewable energy supplies [190]. Future research could explore methodologies for integrating building energy consumption forecasts with renewable energy predictions, facilitating the collaborative optimization of energy consumption and renewable energy utilization [191]. For example, investigations could focus on optimizing the use of renewable energy based on building energy consumption forecasts to reduce reliance on traditional energy sources. Additionally, research could examine the integration of energy storage technologies, enabling buildings to utilize storage devices to supplement energy during periods of insufficient renewable energy supply.
5.2. Challenges
- (1)
- In practical applications, data-related issues pose numerous challenges to building energy consumption prediction. In terms of data quality and integrity, data often suffers from noise, missing values, and inconsistent formats. For example, sensor failures can lead to data loss, and differences in device data formats impede integration. There is an urgent need for efficient data cleaning and preprocessing techniques. Data privacy and security are also crucial. As the data encompasses more information, preventing data leakage and safeguarding user privacy while achieving effective energy consumption prediction during data sharing and transmission is a difficult problem. For instance, when cloud platforms process data, strict control over encryption and access rights is required. Moreover, multi-source data integration is extremely challenging. Data from different sources vary greatly in time resolution, spatial granularity, and quality. For example, meteorological data and smart meter data have different time scales. How to match and integrate them to improve prediction accuracy remains to be further studied.
- (2)
- Model-related challenges restrict the practical application of building energy consumption prediction models. Regarding model complexity and interpretability, although deep-learning models are accurate in prediction, their structures are complex, and they are in a “black-box” state. Building managers and energy professionals find it difficult to understand their decision-making processes. For example, the Transformer model has poor interpretability when used for commercial building cooling load prediction. Therefore, developing interpretable deep-learning models or combining interpretable technologies is an important direction. The adaptability and generalization ability of models are insufficient. Different buildings vary in structure, usage patterns, and environments, and existing models struggle to quickly adapt to different scenarios. For example, a model for northern residential buildings cannot be directly applied to southern commercial buildings. The real-time performance and dynamic adjustment of models also urgently need improvement. The dynamic nature of the energy system requires models to be updated rapidly based on real-time data to respond to changes in building usage patterns and the environment. For example, when there is a sudden increase in personnel activities leading to a rise in energy consumption, the model needs to adjust the prediction results in real-time.
- (3)
- Multiple factors in the actual application environment pose challenges to building energy consumption prediction. The building operation environment is constantly changing. Equipment aging, renovation, and changes in user behavior affect energy consumption characteristics, and existing models have difficulty capturing these in real-time. For example, the prediction accuracy of the model is easily affected when energy-saving lighting equipment is replaced or air-conditioning usage habits change. Policy, regulatory, and market factors cannot be ignored. Changes in energy policies and regulations and fluctuations in energy market prices can change building energy consumption patterns, but these are often not fully considered in models. For example, when an energy-saving subsidy policy is introduced, it needs to be incorporated into the model to conform to reality. In addition, the coordinated optimization of multiple systems is difficult. Building energy consumption prediction needs to be coordinated with smart grids and regional energy systems, but the coordination mechanisms among systems are complex and involve multiple stakeholders. For example, how to adjust power consumption strategies reasonably based on building energy consumption predictions during peak grid loads to achieve a win-win situation is a key challenge.
5.3. Comparative Analysis and Application Considerations of Prediction Models
5.4. Multi-Step Prediction Strategies and Performance Analysis in Different Building Energy Consumption Prediction Models
- (1)
- Direct strategy
- (2)
- Recursive/rolling strategy
- (3)
- Sequential strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, Y.; Zuo, W.; Wang, G. A comprehensive review of energy-related data for U.S. commercial buildings. Energy Build. 2019, 186, 126–137. [Google Scholar] [CrossRef]
- Cheng, Y.L.; Lim, M.H.; Hui, K.H. Impact of internet of things paradigm towards energy consumption prediction: A systematic literature review. Sustain. Cities Soc. 2022, 78, 103624. [Google Scholar] [CrossRef]
- Kumar Mohapatra, S.; Mishra, S.; Tripathy, H.K.; Alkhayyat, A. A sustainable data-driven energy consumption assessment model for building infrastructures in resource constraint environment. Sustain. Energy Technol. Assess. 2022, 53, 102697. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Srinivasan, R.S. A novel ensemble learning approach to support building energy use prediction. Energy Build. 2018, 159, 109–122. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Data-driven estimation of building energy consumption with multi-source heterogeneous data. Appl. Energy 2020, 268, 114965. [Google Scholar] [CrossRef]
- Yoshino, H.; Hong, T.; Nord, N. IEA EBC annex 53: Total energy use in buildings—Analysis and evaluation methods. Energy Build. 2017, 152, 124–136. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Li, H.; Lou, Y.; Li, J. A behavior-orientated prediction method for short-term energy consumption of air-conditioning systems in buildings blocks. Energy 2023, 263, 125940. [Google Scholar] [CrossRef]
- Qiao, Q.; Yunusa-Kaltungo, A.; Edwards, R.E. Towards developing a systematic knowledge trend for building energy consumption prediction. J. Build. Eng. 2021, 35, 101967. [Google Scholar] [CrossRef]
- Sha, H.; Xu, P.; Yan, C.; Ji, Y.; Zhou, K.; Chen, F. Development of a key-variable-based parallel HVAC energy predictive model. Build. Simul. 2022, 15, 1193–1208. [Google Scholar] [CrossRef]
- Zhan, S.; Wichern, G.; Laughman, C.; Chong, A.; Chakrabarty, A. Calibrating building simulation models using multi-source datasets and meta-learned Bayesian optimization. Energy Build. 2022, 270, 112278. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, L.; Han, X.; Zhao, T. Reconstituted data-driven air conditioning energy consumption prediction system employing occupant-orientated probability model as input and swarm intelligence optimization algorithms. Energy 2024, 288, 129799. [Google Scholar] [CrossRef]
- Bucarelli, N.; El-Gohary, N. Sensor deployment configurations for building energy consumption prediction. Energy Build. 2024, 308, 113888. [Google Scholar] [CrossRef]
- Song, C.; Yang, H.; Meng, X.-B.; Yang, P.; Cai, J.; Bao, H.; Xu, K. A novel deep-learning framework for short-term prediction of cooling load in public buildings. J. Clean. Prod. 2024, 434, 139796. [Google Scholar] [CrossRef]
- El-Maraghy, M.; Metawie, M.; Safaan, M.; Saad Eldin, A.; Hamdy, A.; El Sharkawy, M.; Abdelaty, A.; Azab, S.; Marzouk, M. Predicting energy consumption of mosque buildings during the operation stage using deep learning approach. Energy Build. 2024, 303, 113829. [Google Scholar] [CrossRef]
- Lei, L.; Shao, S.; Liang, L. An evolutionary deep learning model based on EWKM, random forest algorithm, SSA and BiLSTM for building energy consumption prediction. Energy 2024, 288, 129795. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H.; Guo, Y.; Wang, J. A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review. Energy Build. 2018, 165, 301–320. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Tian, W.; Heo, Y.; de Wilde, P.; Li, Z.; Yan, D.; Park, C.S.; Feng, X.; Augenbroe, G. A review of uncertainty analysis in building energy assessment. Renew. Sustain. Energy Rev. 2018, 93, 285–301. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Fu, Q.; Han, Z.; Chen, J.; Lu, Y.; Wu, H.; Wang, Y. Applications of reinforcement learning for building energy efficiency control: A review. J. Build. Eng. 2022, 50, 104165. [Google Scholar] [CrossRef]
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, M.; Chen, Z.; Chen, Z.; Ji, Y. Physical energy and data-driven models in building energy prediction: A review. Energy Rep. 2022, 8, 2656–2671. [Google Scholar] [CrossRef]
- Ardabili, S.; Abdolalizadeh, L.; Mako, C.; Torok, B.; Mosavi, A. Systematic Review of Deep Learning and Machine Learning for Building Energy. Front. Energy Res. 2022, 10, 786027. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, C.; Xiao, F.; Li, A.; Miller, C. A review and reflection on open datasets of city-level building energy use and their applications. Energy Build. 2023, 285, 112911. [Google Scholar] [CrossRef]
- Gao, H.; Wang, X.; Wu, K.; Zheng, Y.; Wang, Q.; Shi, W.; He, M. A Review of Building Carbon Emission Accounting and Prediction Models. Buildings 2023, 13, 1617. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Liu, Y.; Wu, H. A Review of Data-Driven Building Energy Prediction. Buildings 2023, 13, 532. [Google Scholar] [CrossRef]
- Afzal, S.; Ziapour, B.M.; Shokri, A.; Shakibi, H.; Sobhani, B. Building energy consumption prediction using multilayer perceptron neural network-assisted models; comparison of different optimization algorithms. Energy 2023, 282, 128446. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Owolabi, H.; Akanbi, L.; Ganiyu, S. Data-Driven Tools for Building Energy Consumption Prediction: A Review. Energies 2023, 16, 2574. [Google Scholar] [CrossRef]
- Chen, Z.; Xiao, F.; Guo, F.; Yan, J. Interpretable machine learning for building energy management: A state-of-the-art review. Adv. Appl. Energy 2023, 9, 100123. [Google Scholar] [CrossRef]
- Balali, Y.; Chong, A.; Busch, A.; O’Keefe, S. Energy modelling and control of building heating and cooling systems with data-driven and hybrid models—A review. Renew. Sustain. Energy Rev. 2023, 183, 113496. [Google Scholar] [CrossRef]
- Eren, Y.; Küçükdemiral, İ. A comprehensive review on deep learning approaches for short-term load forecasting. Renew. Sustain. Energy Rev. 2024, 189, 114031. [Google Scholar] [CrossRef]
- Afzal, S.; Shokri, A.; Ziapour, B.M.; Shakibi, H.; Sobhani, B. Building energy consumption prediction and optimization using different neural network-assisted models; comparison of different networks and optimization algorithms. Eng. Appl. Artif. Intell. 2024, 127, 107356. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, S.; Ding, Y.; Kim, M.K.; Yang, B.; Tian, Z.; Liu, J. Exploring the comprehensive integration of artificial intelligence in optimizing HVAC system operations: A review and future outlook. Results Eng. 2025, 25, 103765. [Google Scholar] [CrossRef]
- Beltrán-Velamazán, C.; Monzón-Chavarrías, M.; López-Mesa, B. Predicting Energy and Emissions in Residential Building Stocks: National UBEM with Energy Performance Certificates and Artificial Intelligence. Appl. Sci. 2025, 15, 514. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Zhang, M.; Han, Y.; Zalhaf, A.S.; Wang, C.; Yang, P.; Wang, C.; Zhou, S.; Xiong, T. Accurate ultra-short-term load forecasting based on load characteristic decomposition and convolutional neural network with bidirectional long short-term memory model. Sustain. Energy Grids Netw. 2023, 35, 101129. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Besanger, Y.; Tran, Q.T. Self-updating machine learning system for building load forecasting—Method, implementation and case-study on COVID-19 impact. Sustain. Energy Grids Netw. 2022, 32, 100873. [Google Scholar] [CrossRef]
- Gilbert, C.; Browell, J.; Stephen, B. Probabilistic load forecasting for the low voltage network: Forecast fusion and daily peaks. Sustain. Energy Grids Netw. 2023, 34, 100998. [Google Scholar] [CrossRef]
- Liu, F.; Liang, C. Short-term power load forecasting based on AC-BiLSTM model. Energy Rep. 2024, 11, 1570–1579. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Dedinec, A.; Filiposka, S.; Dedinec, A.; Kocarev, L. Deep belief network based electricity load forecasting: An analysis of Macedonian case. Energy 2016, 115, 1688–1700. [Google Scholar] [CrossRef]
- Oliveira Panão, M.J.N.; Brito, M.C. Modelling aggregate hourly electricity consumption based on bottom-up building stock. Energy Build. 2018, 170, 170–182. [Google Scholar] [CrossRef]
- Etxegarai, G.; Zapirain, I.; Camblong, H.; Ugartemendia, J.; Hernandez, J.; Curea, O. Photovoltaic Energy Production Forecasting in a Short Term Horizon: Comparison between Analytical and Machine Learning Models. Appl. Sci. 2022, 12, 12171. [Google Scholar] [CrossRef]
- Ruano, A.E.; Pesteh, S.; Silva, S.; Duarte, H.; Mestre, G.; Ferreira, P.M.; Khosravani, H.R.; Horta, R. The IMBPC HVAC system: A complete MBPC solution for existing HVAC systems. Energy Build. 2016, 120, 145–158. [Google Scholar] [CrossRef]
- Salehi, S.; Kavgic, M.; Bonakdari, H.; Begnoche, L. Comparative study of univariate and multivariate strategy for short-term forecasting of heat demand density: Exploring single and hybrid deep learning models. Energy AI 2024, 16, 100343. [Google Scholar] [CrossRef]
- Lu, Y.; Tian, Z.; Zhang, Q.; Zhou, R.; Chu, C. Data augmentation strategy for short-term heating load prediction model of residential building. Energy 2021, 235, 121328. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Zhang, C.; Fan, C. Attention-based interpretable neural network for building cooling load prediction. Appl. Energy 2021, 299, 117238. [Google Scholar] [CrossRef]
- Lu, C.; Li, S.; Reddy Penaka, S.; Olofsson, T. Automated machine learning-based framework of heating and cooling load prediction for quick residential building design. Energy 2023, 274, 127334. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Z.; Deng, Q.; Tang, P.; Yang, C.; Li, X.; Gui, W. A knowledge embedded graph neural network-based cooling load prediction method using dynamic data association. Energy Build. 2023, 278, 112635. [Google Scholar] [CrossRef]
- Atef, S.; Nakata, K.; Eltawil, A.B. A deep bi-directional long-short term memory neural network-based methodology to enhance short-term electricity load forecasting for residential applications. Comput. Ind. Eng. 2022, 170, 108364. [Google Scholar] [CrossRef]
- Dab, K.; Henao, N.; Nagarsheth, S.; Dubé, Y.; Sansregret, S.; Agbossou, K. Consensus-based time-series clustering approach to short-term load forecasting for residential electricity demand. Energy Build. 2023, 299, 113550. [Google Scholar] [CrossRef]
- Khan, Z.A.; Ullah, A.; Ul Haq, I.; Hamdy, M.; Maria Mauro, G.; Muhammad, K.; Hijji, M.; Baik, S.W. Efficient Short-Term Electricity Load Forecasting for Effective Energy Management. Sustain. Energy Technol. Assess. 2022, 53, 102337. [Google Scholar] [CrossRef]
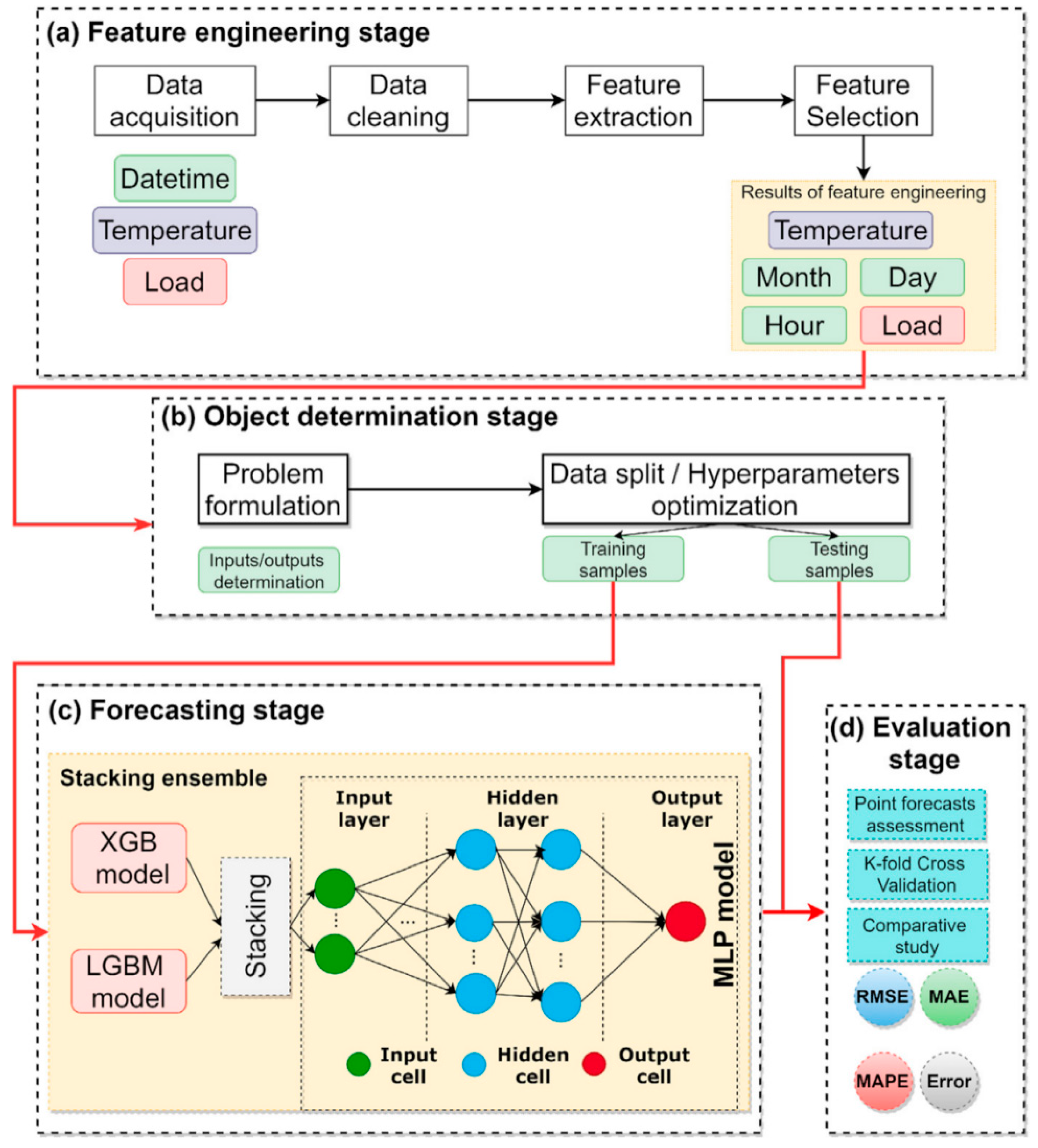
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T. Research on short-term and ultra-short-term cooling load prediction models for office buildings. Energy Build. 2017, 154, 254–267. [Google Scholar] [CrossRef]
- Waheed, W.; Xu, Q. Data-driven short term load forecasting with deep neural networks: Unlocking insights for sustainable energy management. Electr. Power Syst. Res. 2024, 232, 110376. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nizami, A.; Khazen, M.; Nik-Bakht, M. Medium-Term Regional Electricity Load Forecasting through Machine Learning and Deep Learning. Designs 2021, 5, 27. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, J.; Liu, J.; Chen, Y.; Ouyang, H. Regional midterm electricity demand forecasting based on economic, weather, holiday, and events factors. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 225–234. [Google Scholar] [CrossRef]
- Lee, J.; Cho, Y. National-scale electricity peak load forecasting: Traditional, machine learning, or hybrid model? Energy 2022, 239, 122366. [Google Scholar] [CrossRef]
- Butt, F.M.; Hussain, L.; Mahmood, A.; Lone, K.J. Artificial Intelligence based accurately load forecasting system to forecast short and medium-term load demands. Math. Biosci. Eng. 2021, 18, 400–425. [Google Scholar] [CrossRef] [PubMed]
- Eya, C.U.; Salau, A.O.; Braide, S.L.; Chigozirim, O.D. Improved Medium Term Approach for Load Forecasting of Nigerian Electricity Network Using Artificial Neuro-Fuzzy Inference System: A Case Study of University of Nigeria, Nsukka. Procedia Comput. Sci. 2023, 218, 2585–2593. [Google Scholar] [CrossRef]
- Bashiri Behmiri, N.; Fezzi, C.; Ravazzolo, F. Incorporating air temperature into mid-term electricity load forecasting models using time-series regressions and neural networks. Energy 2023, 278, 127831. [Google Scholar] [CrossRef]
- Wu, X.; Dou, C.; Yue, D. Electricity load forecast considering search engine indices. Electr. Power Syst. Res. 2021, 199, 107398. [Google Scholar] [CrossRef]
- Gao, T.; Niu, D.; Ji, Z.; Sun, L. Mid-term electricity demand forecasting using improved variational mode decomposition and extreme learning machine optimized by sparrow search algorithm. Energy 2022, 261, 125328. [Google Scholar] [CrossRef]
- Mystakidis, A.; Koukaras, P.; Tsalikidis, N.; Ioannidis, D.; Tjortjis, C. Energy Forecasting: A Comprehensive Review of Techniques and Technologies. Energies 2024, 17, 1662. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Gao, Y.; Wu, J.; Zhao, S.; Ding, Z. An effective dimensionality reduction approach for short-term load forecasting. Electr. Power Syst. Res. 2022, 210, 108150. [Google Scholar] [CrossRef]
- Subbiah, S.S.; Chinnappan, J. Deep learning based short term load forecasting with hybrid feature selection. Electr. Power Syst. Res. 2022, 210, 108065. [Google Scholar] [CrossRef]
- Moral-Carcedo, J.; Pérez-García, J. Integrating long-term economic scenarios into peak load forecasting: An application to Spain. Energy 2017, 140, 682–695. [Google Scholar] [CrossRef]
- Cai, Z.; Dai, S.; Ding, Q.; Zhang, J.; Xu, D.; Li, Y. Gray wolf optimization-based wind power load mid-long term forecasting algorithm. Comput. Electr. Eng. 2023, 109, 108769. [Google Scholar] [CrossRef]
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- An, W.; Gao, B.; Liu, J.; Ni, J.; Liu, J. Predicting hourly heating load in residential buildings using a hybrid SSA–CNN–SVM approach. Case Stud. Therm. Eng. 2024, 59, 104516. [Google Scholar] [CrossRef]
- Medeiros, M.; Vasconcelos, G.; Veiga, A.; Zilberman, E. Forecasting Inflation in a Data-Rich Environment: The Benefits of Machine Learning Methods. J. Bus. Econ. Stat. 2019, 39, 1–45. [Google Scholar] [CrossRef]
- Chen, Y.; Xiao, C.; Yang, S.; Yang, Y.; Wang, W. Research on long term power load grey combination forecasting based on fuzzy support vector machine. Comput. Electr. Eng. 2024, 116, 109205. [Google Scholar] [CrossRef]
- Tong, C.; Zhang, L.; Li, H.; Ding, Y. Temporal inception convolutional network based on multi-head attention for ultra-short-term load forecasting. IET Gener. Transm. Distrib. 2022, 16, 1680–1696. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Bakker, S.J.; Sartori, I. Modelling electric and heat load profiles of non-residential buildings for use in long-term aggregate load forecasts. Util. Policy 2019, 58, 63–88. [Google Scholar] [CrossRef]
- Lei, L.; Wu, B.; Fang, X.; Chen, L.; Wu, H.; Liu, W. A dynamic anomaly detection method of building energy consumption based on data mining technology. Energy 2023, 263, 125575. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, D. Integrated performance optimization of industrial buildings in relation to thermal comfort and energy consumption: A case study in hot summer and cold winter climate. Case Stud. Therm. Eng. 2023, 46, 102991. [Google Scholar] [CrossRef]
- Kapp, S.; Choi, J.-K.; Hong, T. Predicting industrial building energy consumption with statistical and machine-learning models informed by physical system parameters. Renew. Sustain. Energy Rev. 2023, 172, 113045. [Google Scholar] [CrossRef]
- Banti, N. Existing industrial buildings—A review on multidisciplinary research trends and retrofit solutions. J. Build. Eng. 2024, 84, 108615. [Google Scholar] [CrossRef]
- Chou, J.-S.; Nguyen, H.-M. Simulating long-term energy consumption prediction in campus buildings through enhanced data augmentation and metaheuristic-optimized artificial intelligence. Energy Build. 2024, 312, 114191. [Google Scholar] [CrossRef]
- Javid, A.S.; Aramoun, F.; Bararzadeh, M.; Avami, A. Multi objective planning for sustainable retrofit of educational buildings. J. Build. Eng. 2019, 24, 100759. [Google Scholar] [CrossRef]
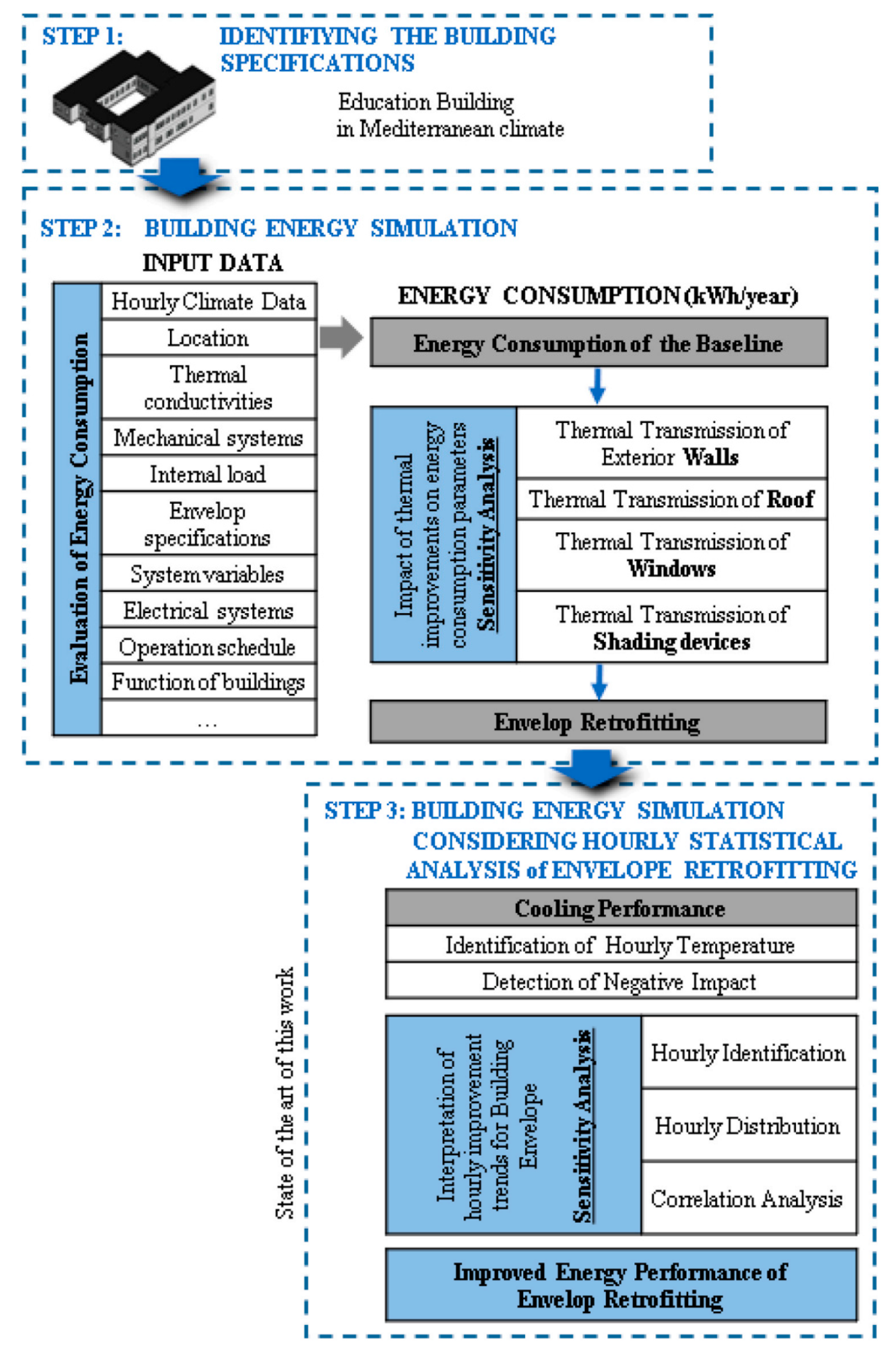
- Zafaranchi, M.; Sozer, H. Enhancing energy efficiency through hourly assessments of passive interventions in educational-office buildings: A case study in a Mediterranean climate. Energy Rep. 2024, 11, 423–441. [Google Scholar] [CrossRef]
- Alam, M.; Devjani, M.R. Analyzing energy consumption patterns of an educational building through data mining. J. Build. Eng. 2021, 44, 103385. [Google Scholar] [CrossRef]
- Cao, W.; Yu, J.; Chao, M.; Wang, J.; Yang, S.; Zhou, M.; Wang, M. Short-term energy consumption prediction method for educational buildings based on model integration. Energy 2023, 283, 128580. [Google Scholar] [CrossRef]
- Himeur, Y.; Elnour, M.; Fadli, F.; Meskin, N.; Petri, I.; Rezgui, Y.; Bensaali, F.; Amira, A. AI-big data analytics for building automation and management systems: A survey, actual challenges and future perspectives. Artif. Intell. Rev. 2023, 56, 4929–5021. [Google Scholar] [CrossRef]
- Zhao, J.; Yuan, X.; Duan, Y.; Li, H.; Liu, D. An artificial intelligence (AI)-driven method for forecasting cooling and heating loads in office buildings by integrating building thermal load characteristics. J. Build. Eng. 2023, 79, 107855. [Google Scholar] [CrossRef]
- Chen, T.-J.G.; Liu, Y.-T.; Lee, C.-Y.; Chang, Y.-C.W.; Cheng, C.-P.; Lee, M.-H.; Chan, Y.-C.; Huang, J.-C.; Chao, K.-Y.C. Effects of weather forecasting on indoor comfort and energy savings in office buildings. Build. Environ. 2022, 221, 109280. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, P.; Chu, Y.; Li, W.; Wu, Y.; Ni, L.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Skomski, E.; Lee, J.-Y.; Kim, W.; Chandan, V.; Katipamula, S.; Hutchinson, B. Sequence-to-sequence neural networks for short-term electrical load forecasting in commercial office buildings. Energy Build. 2020, 226, 110350. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T.; Yang, K. Model input selection for building heating load prediction: A case study for an office building in Tianjin. Energy Build. 2018, 159, 254–270. [Google Scholar] [CrossRef]
- Xuan, Z.; Xuehui, Z.; Liequan, L.; Zubing, F.; Junwei, Y.; Dongmei, P. Forecasting performance comparison of two hybrid machine learning models for cooling load of a large-scale commercial building. J. Build. Eng. 2019, 21, 64–73. [Google Scholar] [CrossRef]
- Chiu, M.-C.; Hsu, H.-W.; Chen, K.-S.; Wen, C.-Y. A hybrid CNN-GRU based probabilistic model for load forecasting from individual household to commercial building. Energy Rep. 2023, 9, 94–105. [Google Scholar] [CrossRef]
- Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust short-term electrical load forecasting framework for commercial buildings using deep recurrent neural networks. Appl. Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
- Rana, M.; Sethuvenkatraman, S.; Goldsworthy, M. A data-driven approach based on quantile regression forest to forecast cooling load for commercial buildings. Sustain. Cities Soc. 2022, 76, 103511. [Google Scholar] [CrossRef]
- Asadinejad, A.; Rahimpour, A.; Tomsovic, K.; Qi, H.; Chen, C.-f. Evaluation of residential customer elasticity for incentive based demand response programs. Electr. Power Syst. Res. 2018, 158, 26–36. [Google Scholar] [CrossRef]
- Goude, Y.; Nedellec, R.; Kong, N. Local Short and Middle Term Electricity Load Forecasting With Semi-Parametric Additive Models. IEEE Trans. Smart Grid 2014, 5, 440–446. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Hawash, H.; Sallam, K.; Askar, S.S.; Abouhawwash, M. STLF-Net: Two-stream deep network for short-term load forecasting in residential buildings. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 4296–4311. [Google Scholar] [CrossRef]
- Haben, S.; Giasemidis, G.; Ziel, F.; Arora, S. Short term load forecasting and the effect of temperature at the low voltage level. Int. J. Forecast. 2019, 35, 1469–1484. [Google Scholar] [CrossRef]
- Shaqour, A.; Ono, T.; Hagishima, A.; Farzaneh, H. Electrical demand aggregation effects on the performance of deep learning-based short-term load forecasting of a residential building. Energy AI 2022, 8, 100141. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S. Load demand forecasting of residential buildings using a deep learning model. Electr. Power Syst. Res. 2020, 179, 106073. [Google Scholar] [CrossRef]
- Irankhah, A.; Yaghmaee, M.H.; Ershadi-Nasab, S. Optimized short-term load forecasting in residential buildings based on deep learning methods for different time horizons. J. Build. Eng. 2024, 84, 108505. [Google Scholar] [CrossRef]
- Somu, N.; M R, G.R.; Ramamritham, K. A hybrid model for building energy consumption forecasting using long short term memory networks. Appl. Energy 2020, 261, 114131. [Google Scholar] [CrossRef]
- He, Y.; Wu, P.; Li, Y.; Wang, Y.; Tao, F.; Wang, Y. A generic energy prediction model of machine tools using deep learning algorithms. Appl. Energy 2020, 275, 115402. [Google Scholar] [CrossRef]
- Mohsenimanesh, A.; Entchev, E. Charging Strategies for Electric Vehicles Using a Machine Learning Load Forecasting Approach for Residential Buildings in Canada. Appl. Sci. 2024, 14, 11389. [Google Scholar] [CrossRef]
- Bellahsen, A.; Dagdougui, H. Aggregated short-term load forecasting for heterogeneous buildings using machine learning with peak estimation. Energy Build. 2021, 237, 110742. [Google Scholar] [CrossRef]
- Chen, H.; Wang, S.; Wang, S.; Li, Y. Day-ahead aggregated load forecasting based on two-terminal sparse coding and deep neural network fusion. Electr. Power Syst. Res. 2019, 177, 105987. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Z.; Chen, Y.; Kong, D.; Wang, Y.-G. A new hybrid model to predict the electrical load in five states of Australia. Energy 2019, 166, 598–609. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector field-based support vector regression for building energy consumption prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.-G.; Tian, Y.-C.; Burrage, K.; Cao, T. Support vector regression with asymmetric loss for optimal electric load forecasting. Energy 2021, 223, 119969. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q.; Yan, J.; Zhang, S.; Xu, J. A novel asynchronous deep reinforcement learning model with adaptive early forecasting method and reward incentive mechanism for short-term load forecasting. Energy 2021, 236, 121492. [Google Scholar] [CrossRef]
- Jeong, D.; Park, C.; Ko, Y.M. Short-term electric load forecasting for buildings using logistic mixture vector autoregressive model with curve registration. Appl. Energy 2021, 282, 116249. [Google Scholar] [CrossRef]
- Wang, Z.; Qiu, Y.; Zhou, S.; Tian, Y.; Zhu, X.; Liu, J.; Lu, S. Enhancing Air Conditioning System Efficiency Through Load Prediction and Deep Reinforcement Learning: A Case Study of Ground Source Heat Pumps. Energies 2025, 18, 199. [Google Scholar] [CrossRef]
- Fouladfar, M.H.; Soppelsa, A.; Nagpal, H.; Fedrizzi, R.; Franchini, G. Adaptive thermal load prediction in residential buildings using artificial neural networks. J. Build. Eng. 2023, 77, 107464. [Google Scholar] [CrossRef]
- Lv, R.; Yuan, Z.; Lei, B.; Zheng, J.; Luo, X. Building thermal load prediction using deep learning method considering time-shifting correlation in feature variables. J. Build. Eng. 2022, 61, 105316. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, G.; Kwon, G.-Y.; Kim, D.-I.; Shin, Y.-J. Deep Learning Based on Multi-Decomposition for Short-Term Load Forecasting. Energies 2018, 11, 3433. [Google Scholar] [CrossRef]
- Santoyo Alum, A.; Fay, T.-A.; Cigarini, F.; Göhlich, D. Assessment of Thermal Comfort in an Electric Bus Based on Machine Learning Classification. Appl. Sci. 2023, 13, 11190. [Google Scholar] [CrossRef]
- Yuan, J.; Zhou, Z.; Tang, H.; Wang, C.; Lu, S.; Han, Z.; Zhang, J.; Sheng, Y. Identification heat user behavior for improving the accuracy of heating load prediction model based on wireless on-off control system. Energy 2020, 199, 117454. [Google Scholar] [CrossRef]
- Geysen, D.; De Somer, O.; Johansson, C.; Brage, J.; Vanhoudt, D. Operational thermal load forecasting in district heating networks using machine learning and expert advice. Energy Build. 2018, 162, 144–153. [Google Scholar] [CrossRef]
- Suryanarayana, G.; Lago, J.; Geysen, D.; Aleksiejuk, P.; Johansson, C. Thermal load forecasting in district heating networks using deep learning and advanced feature selection methods. Energy 2018, 157, 141–149. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Xu, X.; Liu, F.; Guo, Y.; Yang, Z.; Hu, T. High spatial granularity residential heating load forecast based on Dendrite net model. Energy 2023, 269, 126787. [Google Scholar] [CrossRef]
- de Santiago, J.; Rodriguez-Villalón, O.; Sicre, B. The generation of domestic hot water load profiles in Swiss residential buildings through statistical predictions. Energy Build. 2017, 141, 341–348. [Google Scholar] [CrossRef]
- Sanzana, M.R.; Abdulrazic, M.O.M.; Wong, J.Y.; Maul, T.; Yip, C.-C. Charging water load prediction for a thermal-energy-storage air-conditioner of a commercial building with a multilayer perceptron. J. Build. Eng. 2023, 75, 107016. [Google Scholar] [CrossRef]
- Edwards, S.; Beausoleil-Morrison, I.; Laperrière, A. Representative hot water draw profiles at high temporal resolution for simulating the performance of solar thermal systems. Sol. Energy 2015, 111, 43–52. [Google Scholar] [CrossRef]
- Jeong, Y. A Study on the BIM Evaluation, Analytics, and Prediction (EAP) Framework and Platform in Linked Building Ontologies and Reasoners with Clouds. Adv. Civ. Eng. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Lovell, L.J.; Davies, R.J.; Hunt, D.V.L. Building Information Modelling Facility Management (BIM-FM). Appl. Sci. 2024, 14, 3977. [Google Scholar] [CrossRef]
- Oktora, D.; Ting, Y.-H. Sukoyo Multi-Objective Optimization of Injection Parameters and Energy Consumption Based on ANN-Differential Evolution. Appl. Sci. 2025, 15, 826. [Google Scholar] [CrossRef]
- Grubinger, T.; Chasparis, G.C.; Natschläger, T. Generalized online transfer learning for climate control in residential buildings. Energy Build. 2017, 139, 63–71. [Google Scholar] [CrossRef]
- Ribeiro, M.; Grolinger, K.; ElYamany, H.F.; Higashino, W.A.; Capretz, M.A.M. Transfer learning with seasonal and trend adjustment for cross-building energy forecasting. Energy Build. 2018, 165, 352–363. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Xiao, F.; Ma, J.; Lee, D.; Wang, J.; Tseng, Y.C. Statistical investigations of transfer learning-based methodology for short-term building energy predictions. Appl. Energy 2020, 262, 114499. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Li, X.; Li, G.; Liu, Z.; Xie, Y.; Li, K.; Liu, B. Transfer learning-based strategies for fault diagnosis in building energy systems. Energy Build. 2021, 250, 111256. [Google Scholar] [CrossRef]
- Mathumitha, R.; Rathika, P.; Manimala, K. Intelligent deep learning techniques for energy consumption forecasting in smart buildings: A review. Artif. Intell. Rev. 2024, 57, 35. [Google Scholar] [CrossRef]
- Roda-Sanchez, L.; Cirillo, F.; Solmaz, G.; Jacobs, T.; Garrido-Hidalgo, C.; Olivares, T.; Kovacs, E. Building a Smart Campus Digital Twin: System, Analytics, and Lessons Learned From a Real-World Project. IEEE Internet Things J. 2024, 11, 4614–4627. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Santos, V.; Dias, M.S.; Mahmoud, A.N. A hybrid model of self-organizing map and deep learning with genetic algorithm for managing energy consumption in public buildings. J. Clean. Prod. 2024, 434, 140040. [Google Scholar] [CrossRef]
- Yu, X.; Ergan, S.; Dedemen, G. A data-driven approach to extract operational signatures of HVAC systems and analyze impact on electricity consumption. Appl. Energy 2019, 253, 113497. [Google Scholar] [CrossRef]
- Roodkoly, S.H.; Fard, Z.Q.; Tahsildoost, M.; Zomorodian, Z.; Karami, M. Development of a simulation-based ANN framework for predicting energy consumption metrics: A case study of an office building. Energy Effic. 2024, 17, 5. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398. [Google Scholar] [CrossRef]
- Mishra, A.; Lone, H.R.; Mishra, A. DECODE: Data-driven energy consumption prediction leveraging historical data and environmental factors in buildings. Energy Build. 2024, 307, 113950. [Google Scholar] [CrossRef]
- Cao, S.; Zhou, S.; Liu, J.; Liu, X.; Zhou, Y. Wood classification study based on thermal physical parameters with intelligent method of artificial neural networks. BioResources 2022, 17, 1187–1204. [Google Scholar] [CrossRef]
- Cui, M.; Ning, B.; Wu, X.; Kim, M.K.; Yang, B.; Tian, Z.; Liu, J. The development of radiant floor cooling system (RFCS): System type, control strategy, and application. Results Eng. 2024, 23, 102544. [Google Scholar] [CrossRef]
- Sun, Y.; Haghighat, F.; Fung, B.C.M. A review of the-state-of-the-art in data-driven approaches for building energy prediction. Energy Build. 2020, 221, 110022. [Google Scholar] [CrossRef]
- Alberini, A.; Prettico, G.; Shen, C.; Torriti, J. Hot weather and residential hourly electricity demand in Italy. Energy 2019, 177, 44–56. [Google Scholar] [CrossRef]
- Thieblemont, H.; Haghighat, F.; Moreau, A.; Lacroix, G. Control of electrically heated floor for building load management: A simplified self-learning predictive control approach. Energy Build. 2018, 172, 442–458. [Google Scholar] [CrossRef]
- Chammas, M.; Makhoul, A.; Demerjian, J. An efficient data model for energy prediction using wireless sensors. Comput. Electr. Eng. 2019, 76, 249–257. [Google Scholar] [CrossRef]
- Shetty, S.S.; Hoang, D.C.; Gupta, M.; Panda, S.K. Learning desk fan usage preferences for personalised thermal comfort in shared offices using tree-based methods. Build. Environ. 2019, 149, 546–560. [Google Scholar] [CrossRef]
- Wei, Y.; Xia, L.; Pan, S.; Wu, J.; Zhang, X.; Han, M.; Zhang, W.; Xie, J.; Li, Q. Prediction of occupancy level and energy consumption in office building using blind system identification and neural networks. Appl. Energy 2019, 240, 276–294. [Google Scholar] [CrossRef]
- Sala-Cardoso, E.; Delgado-Prieto, M.; Kampouropoulos, K.; Romeral, L. Activity-aware HVAC power demand forecasting. Energy Build. 2018, 170, 15–24. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Wang, S. Development of prediction models for next-day building energy consumption and peak power demand using data mining techniques. Appl. Energy 2014, 127, 1–10. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Pour Rahimian, F.; Rastogi, P.; Glesk, I. Tuning machine learning models for prediction of building energy loads. Sustain. Cities Soc. 2019, 47, 101484. [Google Scholar] [CrossRef]
- He, Y.; Qin, Y.; Wang, S.; Wang, X.; Wang, C. Electricity consumption probability density forecasting method based on LASSO-Quantile Regression Neural Network. Appl. Energy 2019, 233–234, 565–575. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, X.; Zhou, G.; Fan, C.; Ding, P.; Chen, Q. An online physical-based multiple linear regression model for building’s hourly cooling load prediction. Energy Build. 2022, 254, 111574. [Google Scholar] [CrossRef]
- Ravichandran, C.; Gopalakrishnan, P. Estimating cooling loads of Indian residences using building geometry data and multiple linear regression. Energy Built Environ. 2024, 5, 741–771. [Google Scholar] [CrossRef]
- Liu, H.; Yu, J.; Dai, J.; Zhao, A.; Wang, M.; Zhou, M. Hybrid prediction model for cold load in large public buildings based on mean residual feedback and improved SVR. Energy Build. 2023, 294, 113229. [Google Scholar] [CrossRef]
- Khajavi, H.; Rastgoo, A. Improving the prediction of heating energy consumed at residential buildings using a combination of support vector regression and meta-heuristic algorithms. Energy 2023, 272, 127069. [Google Scholar] [CrossRef]
- Cai, W.; Wen, X.; Li, C.; Shao, J.; Xu, J. Predicting the energy consumption in buildings using the optimized support vector regression model. Energy 2023, 273, 127188. [Google Scholar] [CrossRef]
- Xu, Y.; Li, F.; Asgari, A. Prediction and optimization of heating and cooling loads in a residential building based on multi-layer perceptron neural network and different optimization algorithms. Energy 2022, 240, 122692. [Google Scholar] [CrossRef]
- Lima-Junior, F.R.; Carpinetti, L.C.R. Predicting supply chain performance based on SCOR® metrics and multilayer perceptron neural networks. Int. J. Prod. Econ. 2019, 212, 19–38. [Google Scholar] [CrossRef]
- Koschwitz, D.; Frisch, J.; van Treeck, C. Data-driven heating and cooling load predictions for non-residential buildings based on support vector machine regression and NARX Recurrent Neural Network: A comparative study on district scale. Energy 2018, 165, 134–142. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Faiq, M.; Geok Tan, K.; Pao Liew, C.; Hossain, F.; Tso, C.-P.; Li Lim, L.; Khang Wong, A.Y.; Mohd Shah, Z. Prediction of energy consumption in campus buildings using long short-term memory. Alex. Eng. J. 2023, 67, 65–76. [Google Scholar] [CrossRef]
- Zhang, C.; Li, J.; Zhao, Y.; Li, T.; Chen, Q.; Zhang, X. A hybrid deep learning-based method for short-term building energy load prediction combined with an interpretation process. Energy Build. 2020, 225, 110301. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust framework based on hybrid deep learning approach for short term load forecasting of building electricity demand. Energy 2023, 268, 126660. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Walser, T.; Sauer, A. Typical load profile-supported convolutional neural network for short-term load forecasting in the industrial sector. Energy AI 2021, 5, 100104. [Google Scholar] [CrossRef]
- Somu, N.; Raman M R, G.; Ramamritham, K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Li, L.; Su, X.; Bi, X.; Lu, Y.; Sun, X. A novel Transformer-based network forecasting method for building cooling loads. Energy Build. 2023, 296, 113409. [Google Scholar] [CrossRef]
- Ni, Z.; Zhang, C.; Karlsson, M.; Gong, S. A study of deep learning-based multi-horizon building energy forecasting. Energy Build. 2024, 303, 113810. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Ding, Z.; Zheng, T.; Hu, J.; Zhang, K. A Transformer-Based Method of Multienergy Load Forecasting in Integrated Energy System. IEEE Trans. Smart Grid 2022, 13, 2703–2714. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y. Interpretable deep learning model for building energy consumption prediction based on attention mechanism. Energy Build. 2021, 252, 111379. [Google Scholar] [CrossRef]
- Lu, S.; Cui, M.; Gao, B.; Liu, J.; Ni, J.; Liu, J.; Zhou, S. A Comparative Analysis of Machine Learning Algorithms in Predicting the Performance of a Combined Radiant Floor and Fan Coil Cooling System. Buildings 2024, 14, 1659. [Google Scholar] [CrossRef]
- An, W.; Zhu, X.; Yang, K.; Kim, M.K.; Liu, J. Hourly Heat Load Prediction for Residential Buildings Based on Multiple Combination Models: A Comparative Study. Buildings 2023, 13, 2340. [Google Scholar] [CrossRef]
- Kim, M.K.; Cremers, B.; Liu, J.; Zhang, J.; Wang, J. Prediction and correlation analysis of ventilation performance in a residential building using artificial neural network models based on data-driven analysis. Sustain. Cities Soc. 2022, 83, 103981. [Google Scholar] [CrossRef]
- Ren, L.; An, F.; Su, M.; Liu, J. Exposure Assessment of Traffic-Related Air Pollution Based on CFD and BP Neural Network and Artificial Intelligence Prediction of Optimal Route in an Urban Area. Buildings 2022, 12, 1227. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Cheng, M.; Luo, Y.; Li, Z. Generative Pretrained Hierarchical Transformer for Time Series Forecasting. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, Barcelona, Spain, 25–29 August 2024; pp. 2003–2013. [Google Scholar]
- Zhang, C.; Lu, J.; Zhao, Y. Generative pre-trained transformers (GPT)-based automated data mining for building energy management: Advantages, limitations and the future. Energy Built Environ. 2024, 5, 143–169. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Lin, L.; Wu, S.; Kang, Y.; Sepasgozar, S. Exploring the Benefits and Limitations of Digital Twin Technology in Building Energy. Appl. Sci. 2023, 13, 8814. [Google Scholar] [CrossRef]
- Gao, B.; Zhu, X.; Ren, J.; Ran, J.; Kim, M.K.; Liu, J. Multi-objective optimization of energy-saving measures and operation parameters for a newly retrofitted building in future climate conditions: A case study of an office building in Chengdu. Energy Rep. 2023, 9, 2269–2285. [Google Scholar] [CrossRef]
- Park, J.; Kang, D. Artificial Intelligence and Smart Technologies in Safety Management: A Comprehensive Analysis Across Multiple Industries. Appl. Sci. 2024, 14, 11934. [Google Scholar] [CrossRef]
- Su, M.; Liu, J.; Zhou, S.; Miao, J.; Kim, M.K. Dynamic prediction of the pre-dehumidification of a radiant floor cooling and displacement ventilation system based on computational fluid dynamics and a back-propagation neural network: A case study of an office room. Indoor Built Environ. 2022, 31, 2386–2410. [Google Scholar] [CrossRef]
- Mariano-Hernández, D.; Hernández-Callejo, L.; Solís, M.; Zorita-Lamadrid, A.; Duque-Perez, O.; Gonzalez-Morales, L.; Santos-García, F. A Data-Driven Forecasting Strategy to Predict Continuous Hourly Energy Demand in Smart Buildings. Appl. Sci. 2021, 11, 7886. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, M.K.; Fu, N.; Liu, J.; Wang, J.; Srebric, J. Investigating the impact of data normalization methods on predicting electricity consumption in a building using different artificial neural network models. Sustain. Cities Soc. 2025, 118, 105570. [Google Scholar] [CrossRef]
- Bondok, A.; Abdelsalam, O.; Badr, M.; Mahmoud, M.; Alsabaan, M.; Alsaqhan, M.; Ibrahem, M.I. Accurate Power Consumption Predictor and One-Class Electricity Theft Detector for Smart Grid “Change-and-Transmit” Advanced Metering Infrastructure. Appl. Sci. 2024, 14, 9308. [Google Scholar] [CrossRef]
- Cui, M.; Song, Y.; Mao, Y.; Yang, K.; Liu, J.; Tian, Z. Potential application of radiant floor cooling systems for residential buildings in different climate zones. Build. Simul. 2024, 17, 543–560. [Google Scholar] [CrossRef]
- Liu, J.; Su, M.; Kim, M.K.; Song, S. Developing simplified numerical calculation and BP neural network modeling for the cooling capacity in a radiant floor cooling system. J. Asian Archit. Build. Eng. 2024, 23, 754–772. [Google Scholar] [CrossRef]
- Cordeiro-Costas, M.; Villanueva, D.; Eguía-Oller, P. Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques. Appl. Sci. 2021, 11, 7991. [Google Scholar] [CrossRef]





| Ref. | Year | Building Type | Load Type | Prediction Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ind | Edu | Off | Com | Res | PL | TL | WL | Clust | Reg | MLP | DL | ||
| Amasyali et al. [8] | 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Ahmad et al. [18] | 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| Wei et al. [19] | 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Tian et al. [20] | 2018 | ✓ | ✓ | ✓ | |||||||||
| Fan et al. [21] | 2019 | ✓ | ✓ | ||||||||||
| Bourdeau et al. [22] | 2019 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Ahmad et al. [23] | 2020 | ✓ | ✓ | ✓ | ✓ | ||||||||
| Fu et al. [24] | 2022 | ✓ | ✓ | ✓ | ✓ | ||||||||
| Lu et al. [25] | 2022 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Chen et al. [26] | 2022 | ✓ | ✓ | ✓ | ✓ | ||||||||
| Ardabili et al. [27] | 2022 | ✓ | ✓ | ✓ | |||||||||
| Jin et al. [28] | 2023 | ✓ | ✓ | ✓ | ✓ | ||||||||
| Gao et al. [29] | 2023 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Liu et al. [30] | 2023 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Afzal et al. [31] | 2023 | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| Olu-Ajayi et al. [32] | 2023 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| Chen et al. [33] | 2023 | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| Balali et al. [34] | 2023 | ✓ | ✓ | ||||||||||
| Eren et al. [35] | 2024 | ✓ | ✓ | ✓ | |||||||||
| Afzal et al. [36] | 2024 | ✓ | ✓ | ✓ | ✓ | ||||||||
| Lu et al. [37] | 2025 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Num. | Feature Types | Contents |
|---|---|---|
| 1 | Meteorological information | Outdoor temperature, humidity, wind speed, solar radiation, rain- fall, air pressure, and other factors. |
| 2 | Indoor environmental information | Set temperature, indoor temperature, humidity, carbon dioxide concentration. |
| 3 | Occupancy-related data | The number of occupants and types of activities. |
| 4 | Time indices | Date, day of the week, time of day, and holidays. |
| 5 | Building characteristic data | Compactness, surface area, wall area, roof area, height, orientation, glass area, thermal transmittance coefficient, and other factors. |
| 6 | Socio-economic information | Income levels, electricity prices, GDP, population. |
| 7 | Historical data | Historical meteorological data, historical energy consumption data. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Lu, S.; Zhou, S.; Tian, Z.; Kim, M.K.; Liu, J.; Liu, X. A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions. Appl. Sci. 2025, 15, 3086. https://doi.org/10.3390/app15063086
Chen G, Lu S, Zhou S, Tian Z, Kim MK, Liu J, Liu X. A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions. Applied Sciences. 2025; 15(6):3086. https://doi.org/10.3390/app15063086
Chicago/Turabian StyleChen, Guanzhong, Shengze Lu, Shiyu Zhou, Zhe Tian, Moon Keun Kim, Jiying Liu, and Xinfeng Liu. 2025. "A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions" Applied Sciences 15, no. 6: 3086. https://doi.org/10.3390/app15063086
APA StyleChen, G., Lu, S., Zhou, S., Tian, Z., Kim, M. K., Liu, J., & Liu, X. (2025). A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions. Applied Sciences, 15(6), 3086. https://doi.org/10.3390/app15063086










