Numerical Simulation Study on Cavitation Characteristics of Circular Arc Spiral Gear Pump at High Speed
Abstract
1. Introduction
2. Materials and Methods
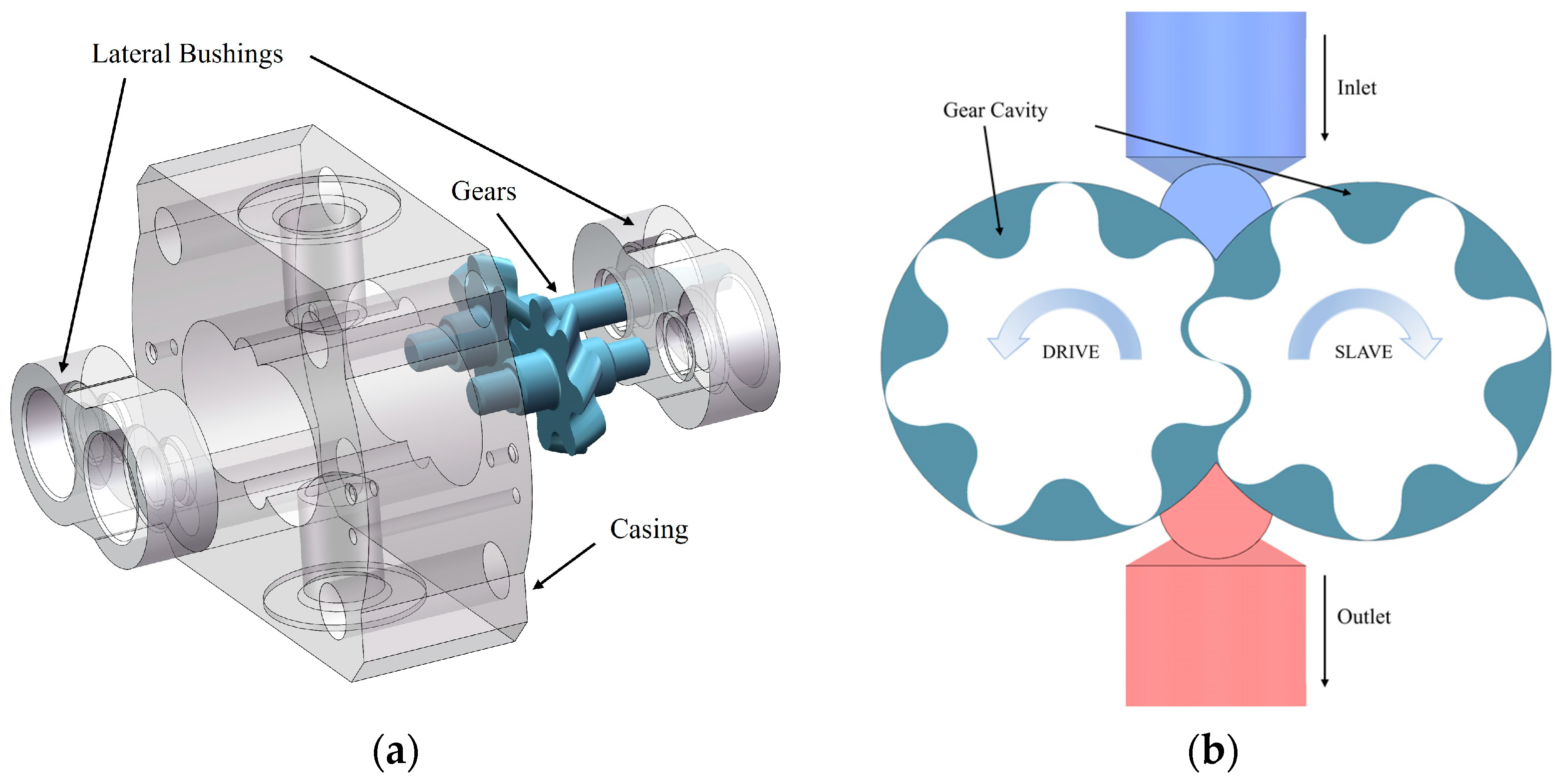
2.1. Design of Gear Pump Structural Parameters
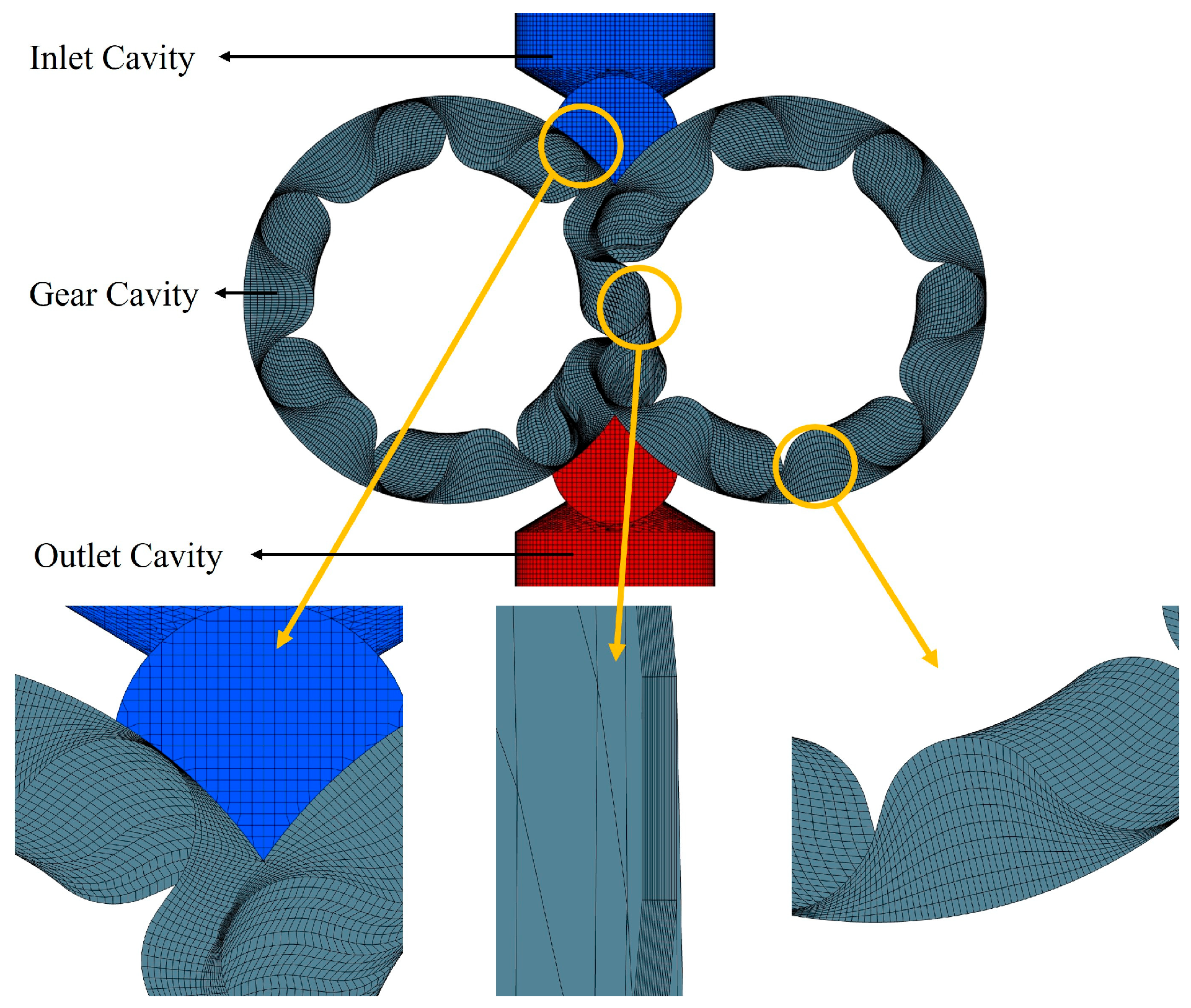
2.2. Mesh Division and Boundary Conditions
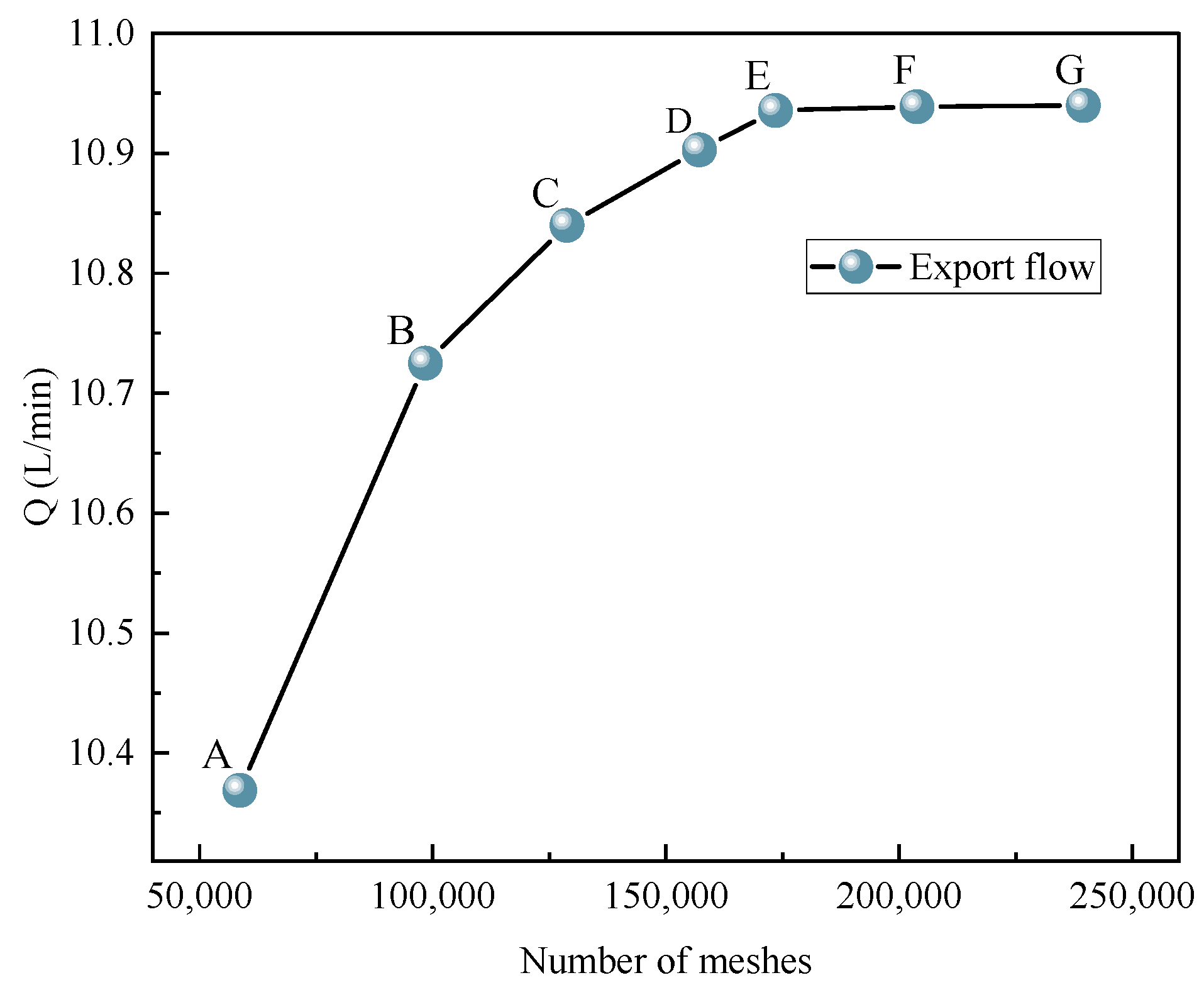
2.3. Mesh Independence Verification
2.4. Turbulence Model and Cavitation Model
2.5. Gear Pump Outlet Flow and Volumetric Efficiency
3. Results and Discussion
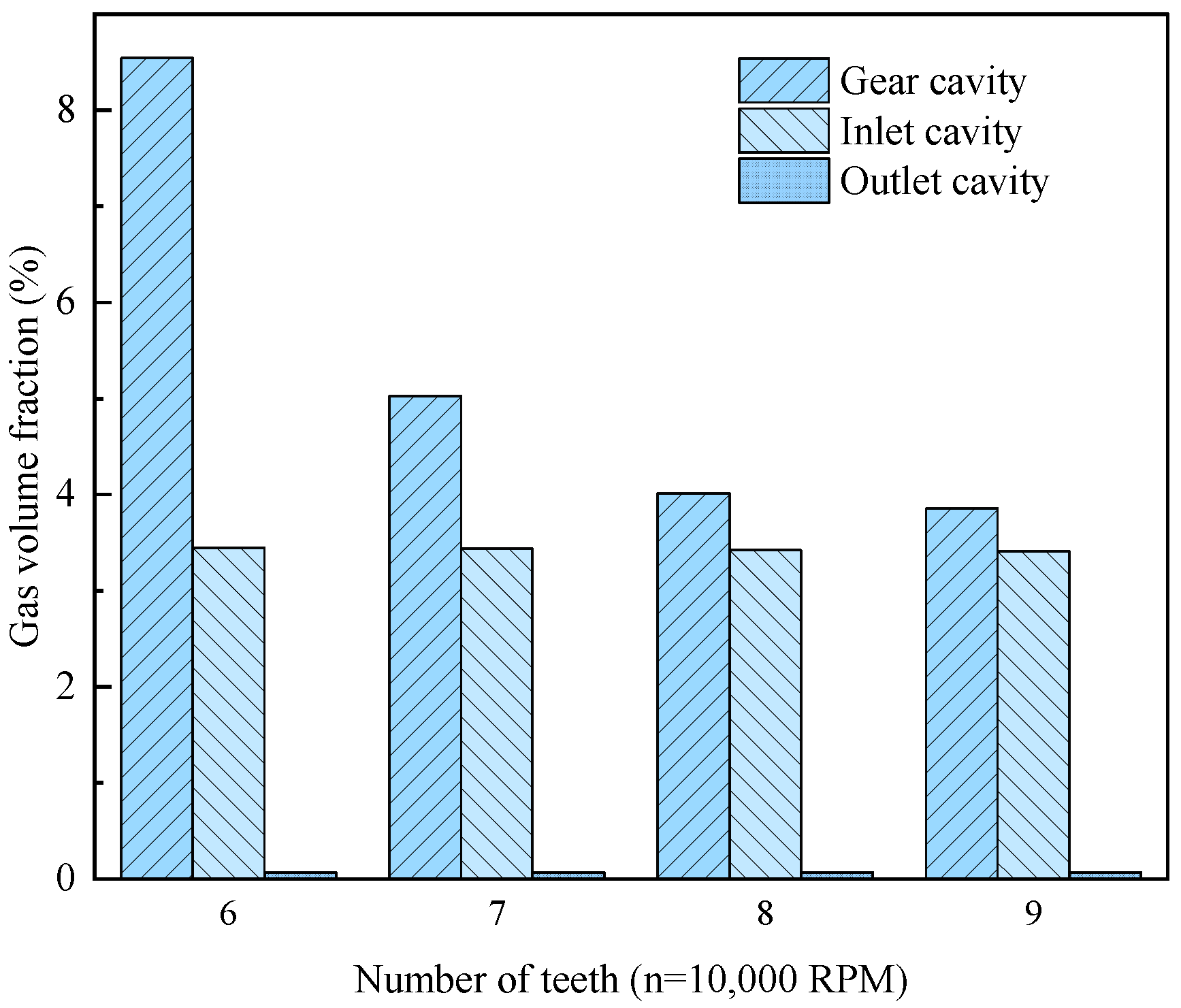
3.1. The Influence of the Number of Teeth on the Volume Fraction of Gas in Key Parts
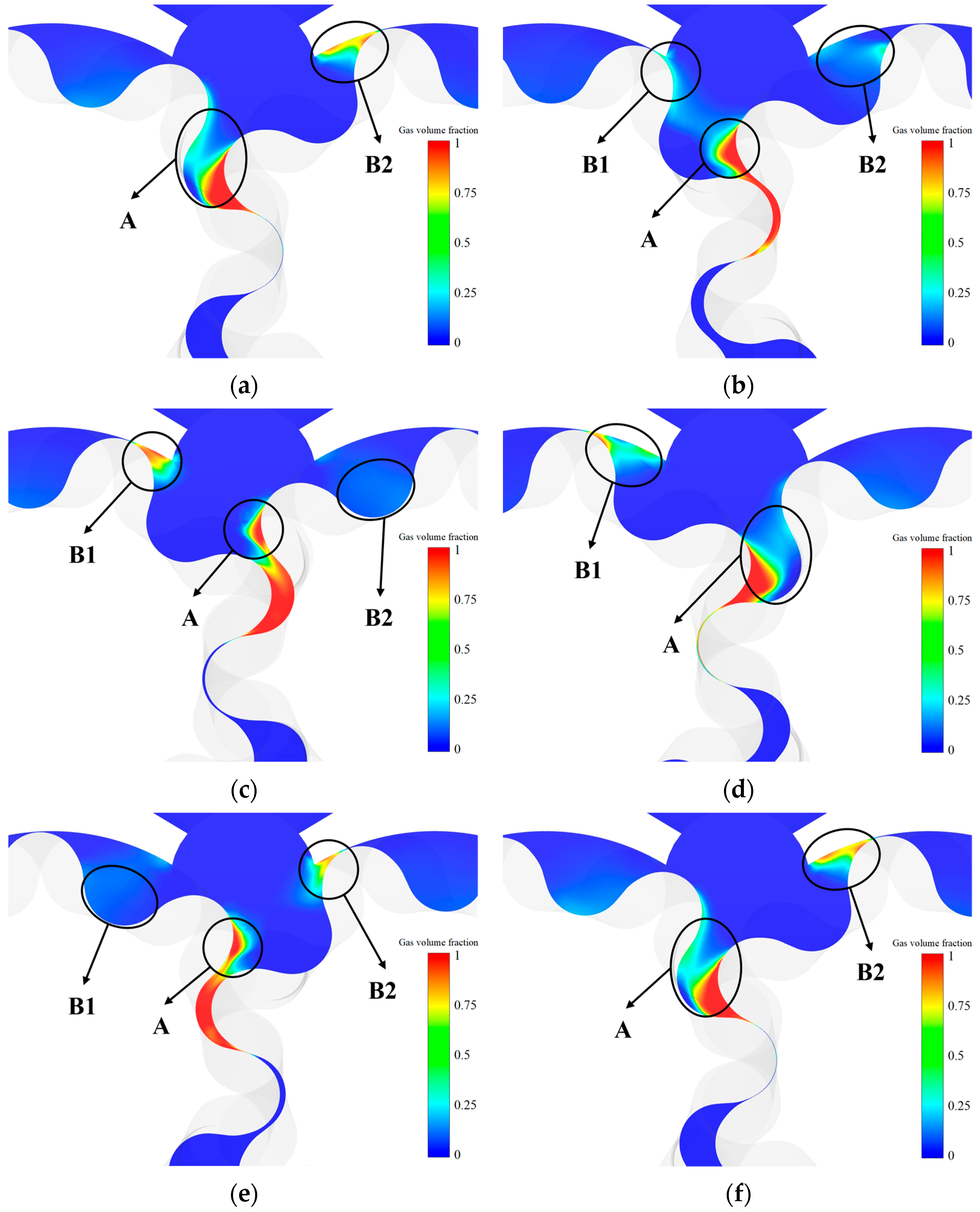
3.2. Cavitation Evolution Process of Gear Cavity
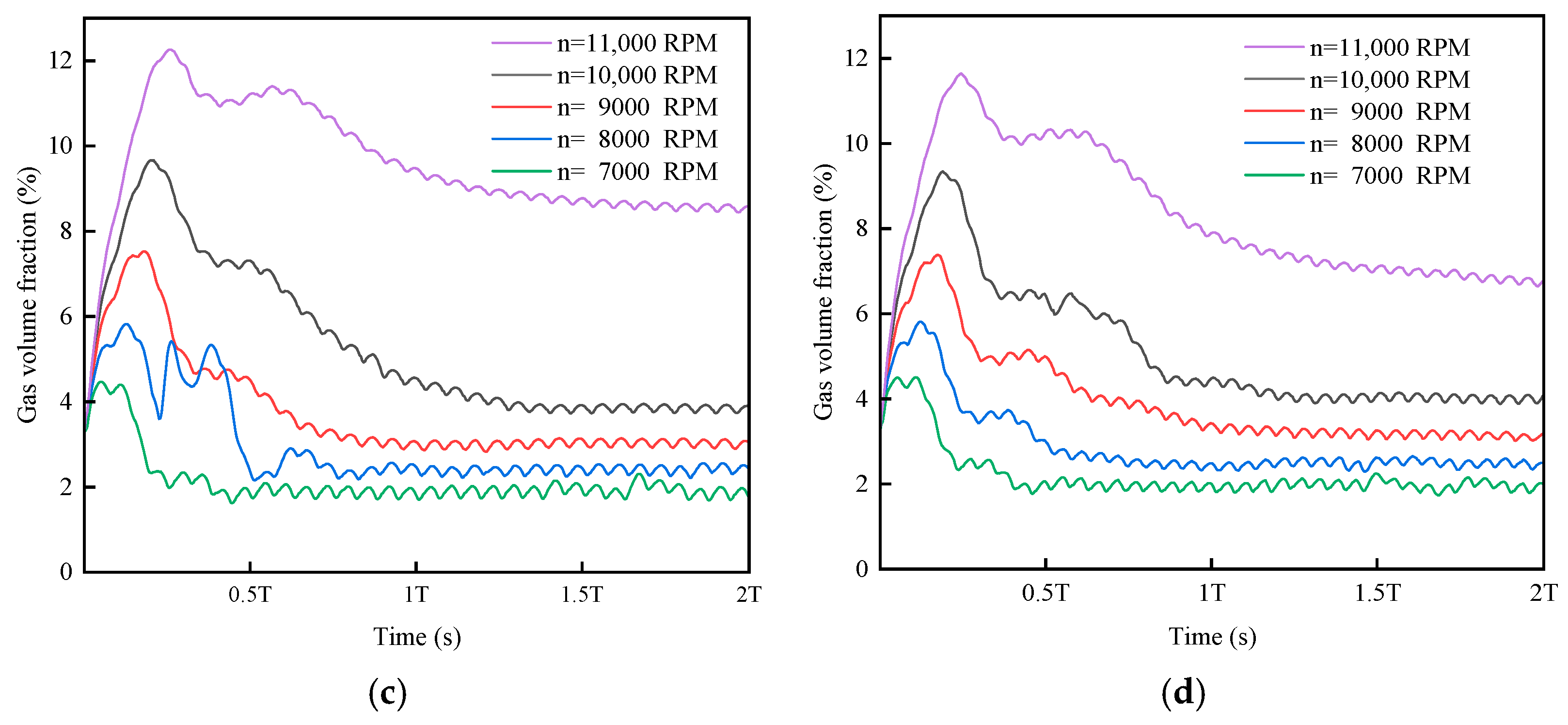
3.3. Influence of Speed on the Volume Fraction of Gas in the Gear Cavity
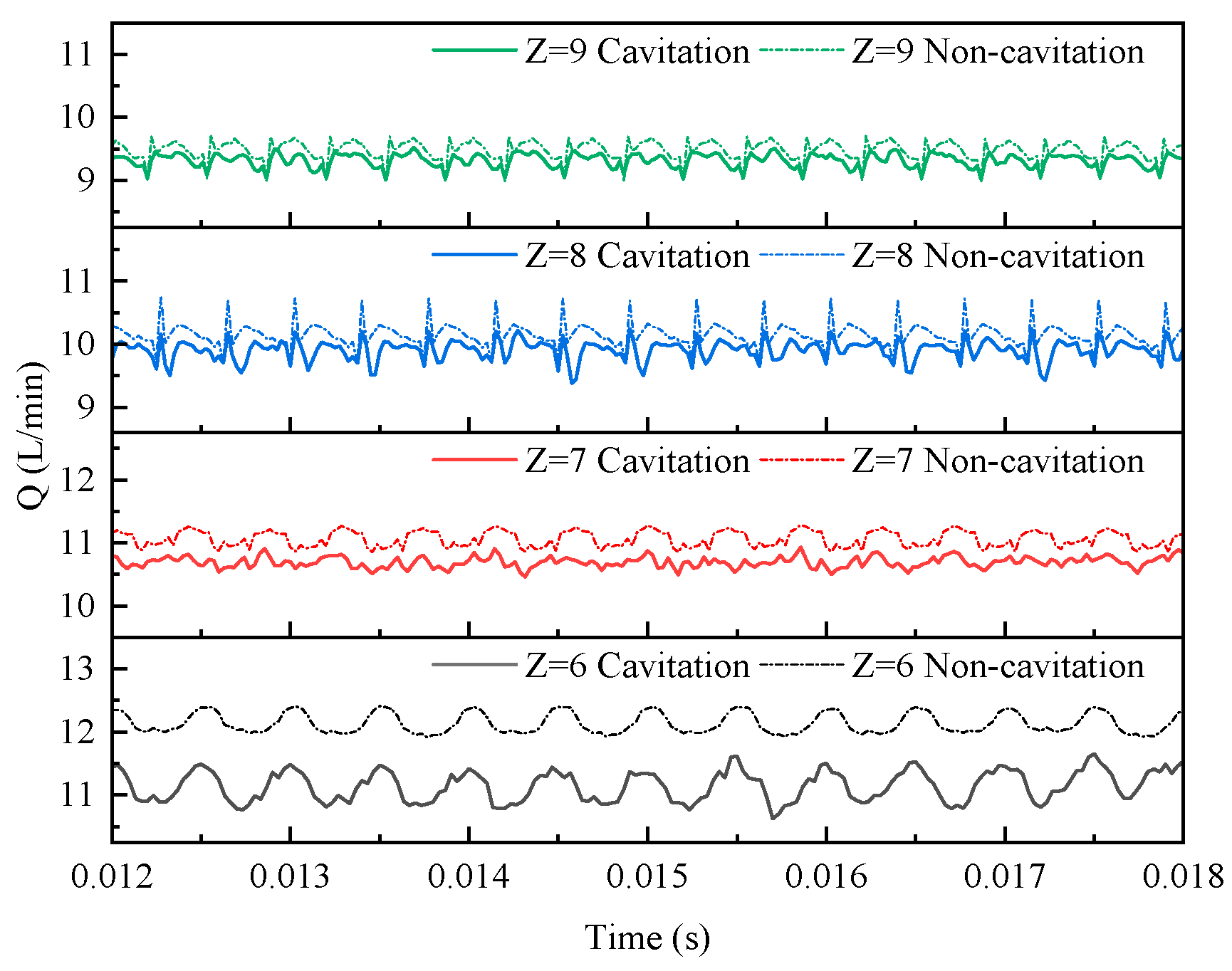
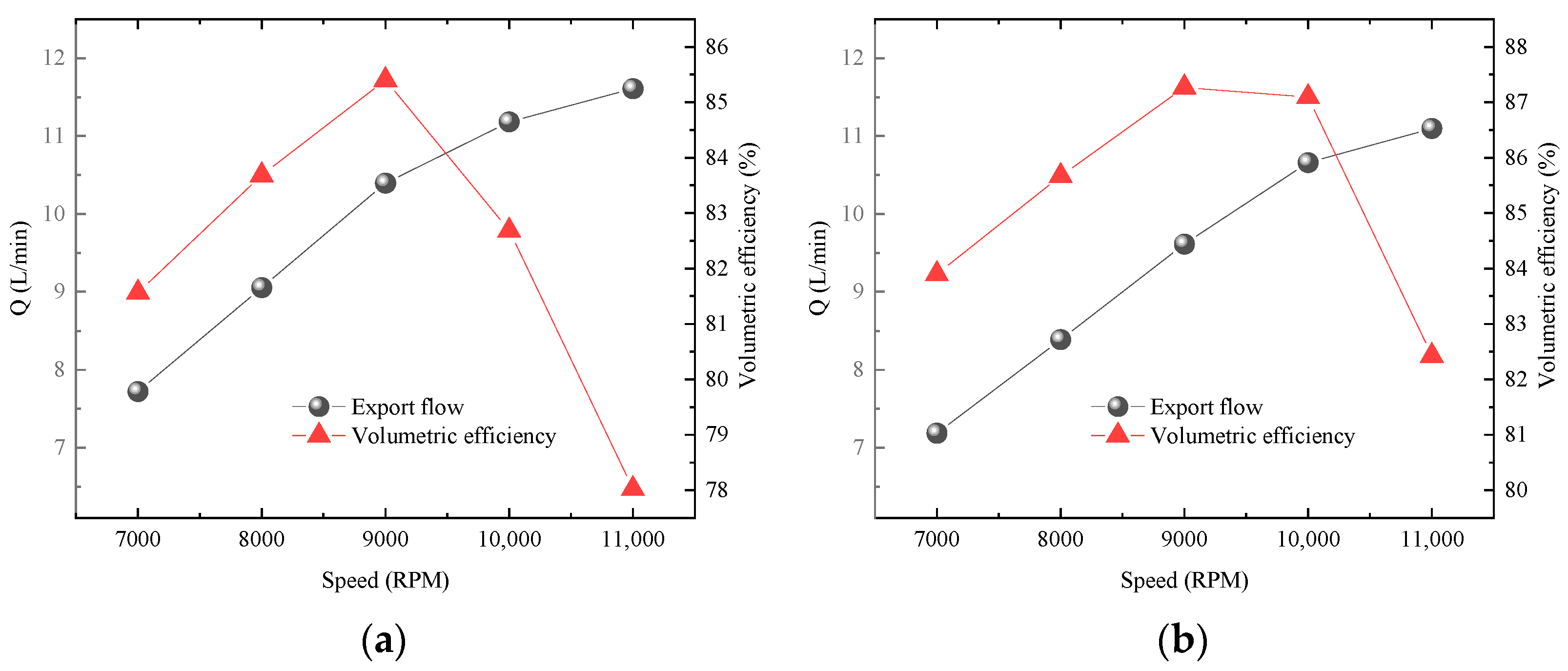
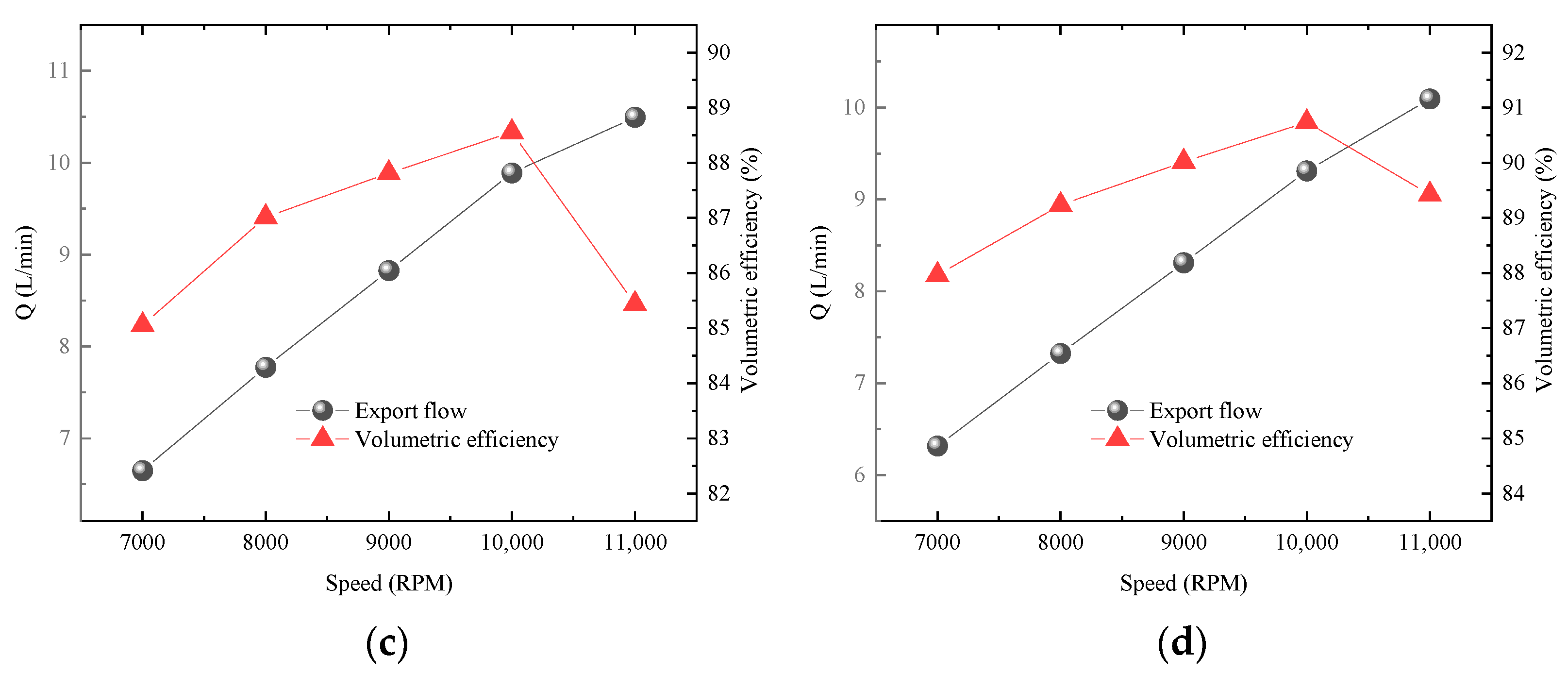
3.4. Influence of Cavitation on Flow Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| A | Center distance | [m] |
| B | Gear width | [m] |
| R | Gear pitch circle radius | [m] |
| Radius of toothed apex | [m] | |
| β | Helix angle | [°] |
| De | Diameter of tooth tip | [m] |
| Z | Tooth number | |
| n | Rotation speed | [r/min] |
| Turbulent kinetic energy | [kg/(ms3)] | |
| Turbulent viscosity | ||
| Empirical constant | ||
| Turbulent kinetic energy | [m2/s2] | |
| Flow energy dissipation rate | [m2/s2] | |
| Mass fraction of vapor | ||
| Mass fraction of air | ||
| Fluid velocity, fluid surface velocity | [m/s] | |
| Vapor diffusion coefficient | [m2/s] | |
| Turbulent Schmidt number | ||
| Vapor generation rate, gas phase condensation rate | ||
| r | Bubble radius | [m] |
| Surface tension coefficient | ||
| P | Pressure | [MPa] |
| Saturated vapor pressure | [Pa] | |
| Density of gas-bearing fluid, density of steam, density of air, density of fluid in oil | [kg/m3] | |
| Gas volume fraction | [m3] | |
| Cavitating region volume | [m3] | |
| Volume of gear pump cavity | [m3] | |
| Volumetric efficiency | [%] | |
| Actual average discharge rate of pump | [L/min] | |
| Theoretical average pump outlet flow | [L/min] | |
| Theoretical flow rate of gear pump per revolution of pump | [m3] | |
| T | Time period for one complete rotation of gear pump | [s] |
References
- Ertürk, N.; Vernet, A.; Castilla, R.; Gamez-Montero, P.J.; Ferre, J.A. Experimental analysis of the flow dynamics in the suction chamber of an external gear pump. Int. J. Mech. Sci. 2011, 53, 135–144. [Google Scholar] [CrossRef]
- Gregory, W.P. External gear pumps for accurate and reliable metering duties. World Pumps 2006, 2006, 34–36. [Google Scholar] [CrossRef]
- Dearn, R. The fine art of gear pump selection and operation. World Pumps 2001, 2001, 38–40. [Google Scholar] [CrossRef]
- Antoniak, P.; Stryczek, J. Visualization study of the flow processes and phenomena in the external gear pump. Arch. Civ. Mech. Eng. 2018, 18, 1103–1115. [Google Scholar] [CrossRef]
- Stryczek, J.; Antoniak, P.; Jakhno, O.; Kostyuk, D.; Kryuchkov, A.; Belov, G.; Rodionov, L. Visualisation research of the flow processes in the outlet chamber–outlet bridge–inlet chamber zone of the gear pumps. Arch. Civ. Mech. Eng. 2015, 15, 95–108. [Google Scholar] [CrossRef]
- Chen, Y.; Xiong, D.F.; Li, Y.T.; Gao, Y.C.; Li, C.C.; Wang, B.Q.; Wang, J. Lubrication Characteristics of Gear End Face Friction Pairs of Aviation High-speed Gear Pumps. China Mech. Eng. 2024, 35, 1178–1187. [Google Scholar]
- Koukouvinis, P.; Naseri, H.; Gavaises, M. Performance of turbulence and cavitation models in prediction of incipient and developed cavitation. Int. J. Engine Res. 2017, 18, 333–350. [Google Scholar] [CrossRef]
- Lin, J.N.; Tseng, Y.T.; Chang, Y.Z.; Chou, Y.A.; Tsai, G.L.; Lan, T.S. Cavitation of Flow Field in Gear Pump. Sensor. Mater. 2022, 34, 2293. [Google Scholar] [CrossRef]
- Del Campo, D.; Castilla, R.; Raush, G.A.; Gamez Montero, P.J.; Codina, E. Numerical analysis of external gear pumps including cavitation. J. Fluids Eng. 2012, 134, 081105. [Google Scholar] [CrossRef]
- Del Campo, D.; Castilla, R.; Raush, G.A.; Gamez-Montero, P.J.; Codina, E. Pressure effects on the performance of external gear pumps under cavitation. J. Mech. Eng. Sci. 2014, 228, 2925–2937. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Numerical modeling of the power losses in geared transmissions: Windage, churning and cavitation simulations with a new integrated approach that drastically reduces the computational effort. Tribol. Int. 2016, 103, 58–68. [Google Scholar] [CrossRef]
- Ransegnola, T.; Zappaterra, F.; Vacca, A. A strongly coupled simulation model for external gear machines considering fluid-structure induced cavitation and mixed lubrication. Appl. Math. Model. 2022, 104, 721–749. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Wang, L.Q.; Zhu, Z.C. Numerical study on flow characteristics of rotor pumps including cavitation. J. Mech. Eng. Sci. 2015, 229, 2626–2638. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.F.; Wang, F.J.; Liu, W.C. Cavitation behavior study in the pump mode of a reversible pump-turbine. Renewable Energy 2018, 125, 655–667. [Google Scholar] [CrossRef]
- Yan, S.; Jiang, Y.; Hu, M.Y. Study on the cavitation suppression mechanism of axial piston pump. Int. J. Aerospace Eng. 2022, 1, 9913739. [Google Scholar] [CrossRef]
- Lian, J.; Wang, W.J.; Wang, X.Q.; Wang, X.C.; Zou, Y.Q.; Wu, G. Numerical simulation and experimental study on cavitation of micro high-speed fuel pump. Fluid Mach. 2024, 52, 58–66. [Google Scholar]
- Zhao, Z.J.; Fu, J.F.; Wei, S.J.; Wei, P.F.; Tong, L.; Jiang, Y. Analysis of the Influence Laws of Inlet Condition on the Volumetric Efficiency of the High-Speed Fuel Gear Pump. ICMAE 2022, 13, 184–189. [Google Scholar]
- Novakovic, B.; Radovanovic, L.; Zuber, N.; Radosav, D.; Dordevic, L.; Kavalic, M. Analysis of the influence of hydraulic fluid quality on external gear pump performance. Eksploat. Niezawodn. 2022, 24, 260–268. [Google Scholar] [CrossRef]
- Han, G.Z.; Huang, K.; Xiong, Y.S.; Kong, L.B.; Cang, D.J. Fluid analysis of the cavitation of the microsegment gear pump operating at high-pressure condition. J. Process Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Ouyang, T.C.; Mo, X.Y.; Lu, Y.C.; Wang, J.X. CFD-vibration coupled model for predicting cavitation in gear transmissions. Int. J. Mech. Sci. 2022, 225, 107377. [Google Scholar] [CrossRef]
- Chao, Q.; Xu, Z.; Tao, J.F.; Liu, C.L.; Zhai, J. Cavitation in a high-speed aviation axial piston pump over a wide range of fluid temperatures. J. Power Energy 2022, 236, 727–737. [Google Scholar] [CrossRef]
- Yang, G.L.; Li, H.; Guo, J.X.; Zhang, Z.C.; He, H. Limiting Speed Characteristics of External Gear Pump Under the Influence of Suction Pressure. Chin. Hydraul. Pneum. 2021, 2, 91–94. [Google Scholar]
- Zhou, Y.; Hao, S.; Hao, M. Design and performance analysis of a circular-arc gear pump operating at high pressure and high speed. J. Mech. Eng. Sci. 2016, 230, 189–205. [Google Scholar] [CrossRef]
- Li, G.Q.; Zhang, L.F.; Han, W.F.; Deng, X.Z.; Feng, Y. Pulsation Characteristics Analysis and Tooth Profile Design of Double-circular-arc Helical Gear Pumps. China Mech. Eng. 2018, 29, 186–192. [Google Scholar]
- Castilla, R.; Gamez-Montero, P.J.; Campo, D.; Raush, G.; Garcia-Vilchez, M.; Codina, E. Three-Dimensional Numerical Simulation of an External Gear Pump With Decompression Slot and Meshing Contact Point. J. Fluids Eng. 2015, 137, 041105. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Fang, X.; Yu, X.; Wu, X.; Du, T. Cloud cavitating flow over a submerged axisymmetric projectile and comparison between two-dimensional RANS and three-dimensional large-eddy simulation methods. J. Fluids Eng. 2016, 138, 061102. [Google Scholar] [CrossRef]
- Franc, J.-P.; Michel, J.-M. Fundamentals of Cavitation; Moreau, R., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2005; Volume 76, ISBN 1-4020-2232-8. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Yash, G.S.; Andrea, V.; Sadegh, D. Air Release and Cavitation Modeling with a Lumped Parameter Approach Based on the Rayleigh–Plesset Equation: The Case of an External Gear Pump. Energies 2018, 11, 3472. [Google Scholar] [CrossRef]
- Wu, B.; Ke, S.Y.; Wang, B.; Ye, Z.F. Study on Cavitation Performance of Three Gear Pump for Aircraft Engines. Mach. Build. Autom. 2022, 51, 61–64. [Google Scholar]
- Yang, J.L.; Lee, K.H.; Lee, C.H. Research on Cavitation Characteristics and Influencing Factors of Herringbone Gear Pump. CMES-Comp. Model. Eng. 2024, 139, 2917–2946. [Google Scholar] [CrossRef]
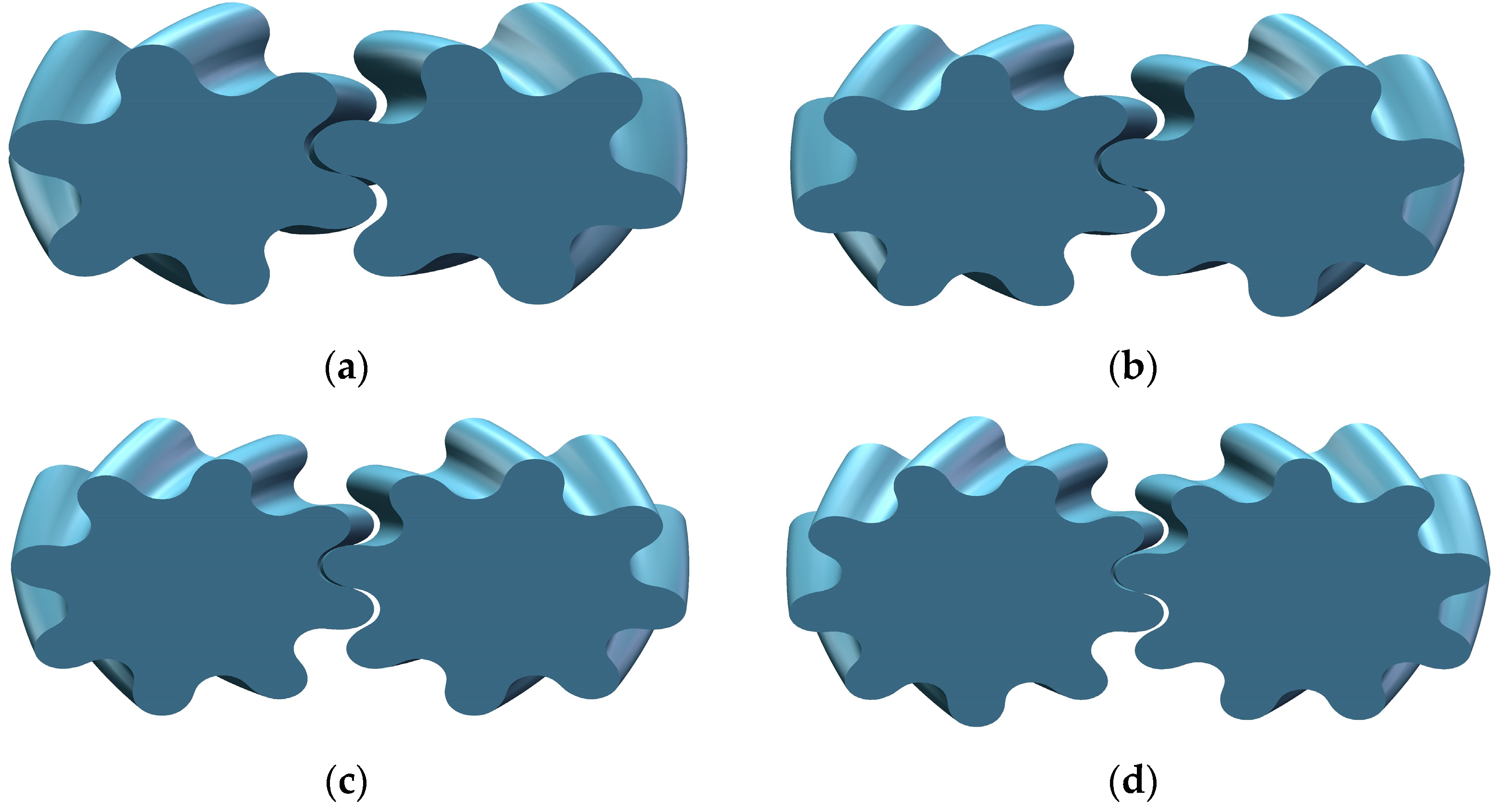

| Tooth Number | 6 | 7 | 8 | 9 |
|---|---|---|---|---|
| Center distance (mm) | 20.48 | 21.02 | 21.46 | 21.828 |
| Gear width (mm) | 4 | 4 | 4 | 4 |
| Helix angle (°) | 30 | 25.714 | 22.5 | 20 |
| Gas Volume Fraction | 7000 RPM | 8000 RPM | 9000 RPM | 10,000 RPM | 11,000 RPM |
|---|---|---|---|---|---|
| 6 | 1.888% | 2.484% | 3.311% | 8.541% | |
| 7 | 1.886% | 2.443% | 3.117% | 5.036% | |
| 8 | 1.884% | 2.425% | 3.033% | 3.853% | 8.394% |
| 9 | 1.935% | 2.485% | 3.123% | 4.014% | 6.665% |
| Average value | 1.898% | 2.459% | 3.146% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, H.; Li, G.; Li, T. Numerical Simulation Study on Cavitation Characteristics of Circular Arc Spiral Gear Pump at High Speed. Appl. Sci. 2025, 15, 3141. https://doi.org/10.3390/app15063141
Wang S, Wang H, Li G, Li T. Numerical Simulation Study on Cavitation Characteristics of Circular Arc Spiral Gear Pump at High Speed. Applied Sciences. 2025; 15(6):3141. https://doi.org/10.3390/app15063141
Chicago/Turabian StyleWang, Shuai, Hao Wang, Geqiang Li, and Tianxing Li. 2025. "Numerical Simulation Study on Cavitation Characteristics of Circular Arc Spiral Gear Pump at High Speed" Applied Sciences 15, no. 6: 3141. https://doi.org/10.3390/app15063141
APA StyleWang, S., Wang, H., Li, G., & Li, T. (2025). Numerical Simulation Study on Cavitation Characteristics of Circular Arc Spiral Gear Pump at High Speed. Applied Sciences, 15(6), 3141. https://doi.org/10.3390/app15063141






