Impact Load Compensation Inverter Based on Nonlinear Adaptive Multiple Input Multiple Output Control Strategy
Abstract
:1. Introduction
2. Mathematical Models
2.1. Mathematical Model of Compensation System Output Power
2.2. Mathematical Model of Generation Output Power
2.3. Dynamic Characteristics Analysis of Open Loop System
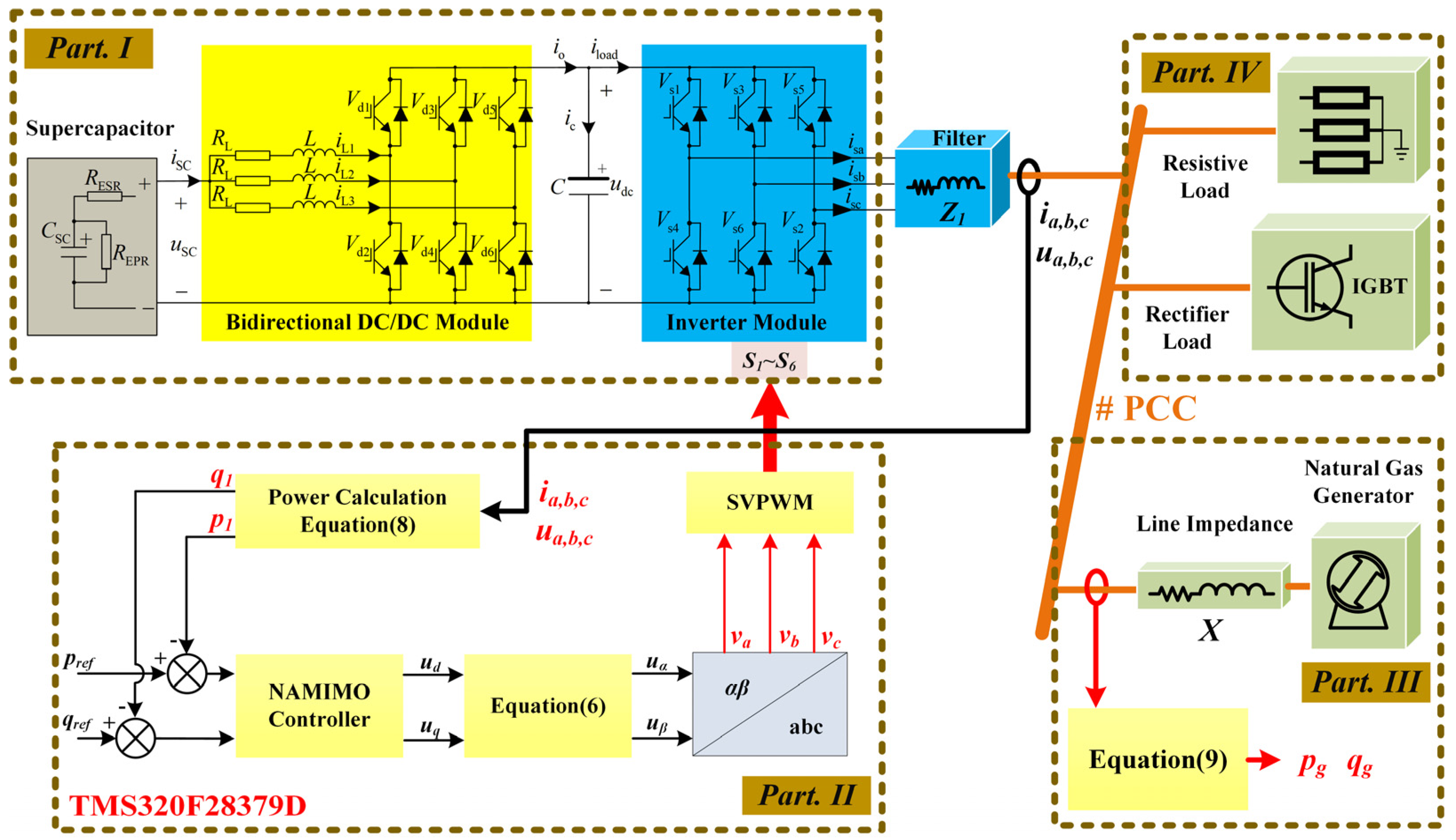
3. Control Strategies
3.1. Description of the Closed-Loop System
3.2. NAMIMO Controller Design and Stability Analysis
4. Simulation and Experimental Results Analysis
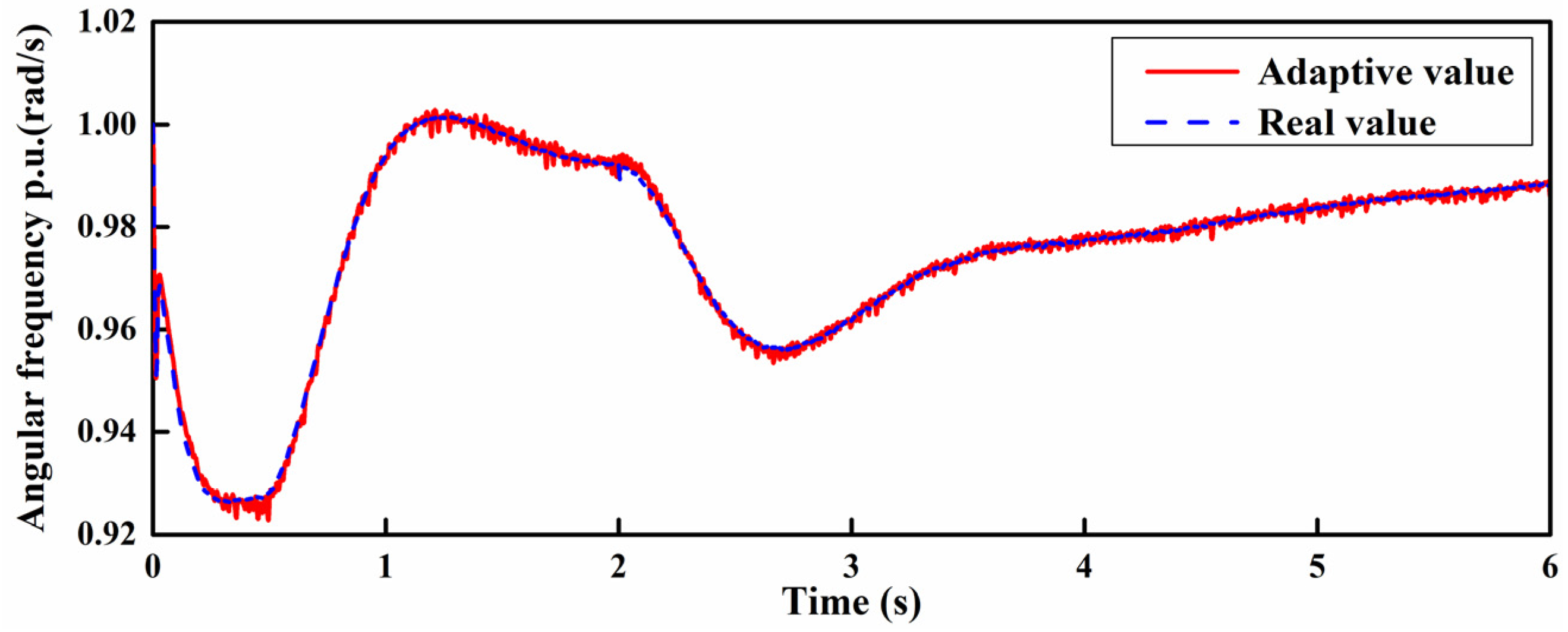
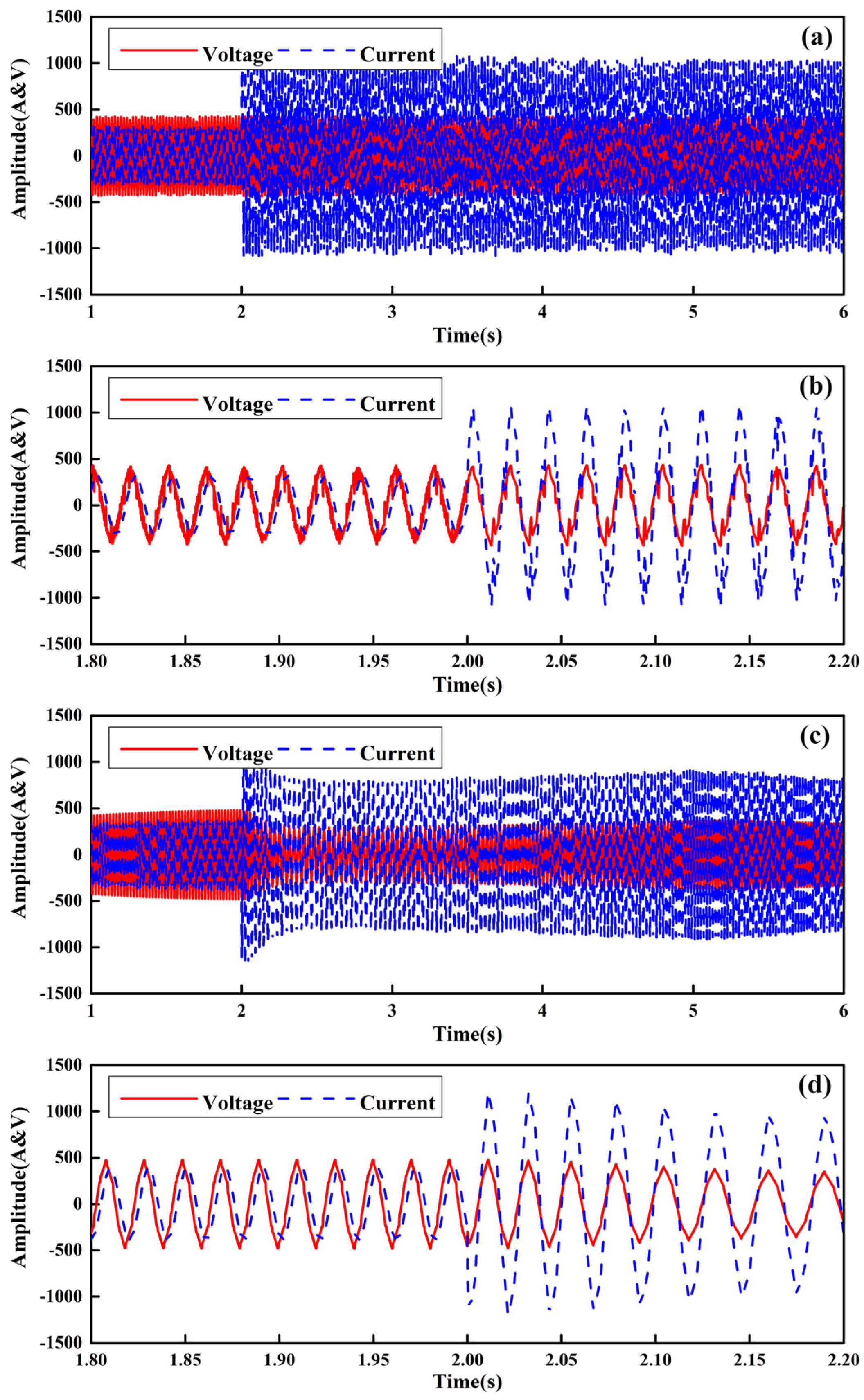
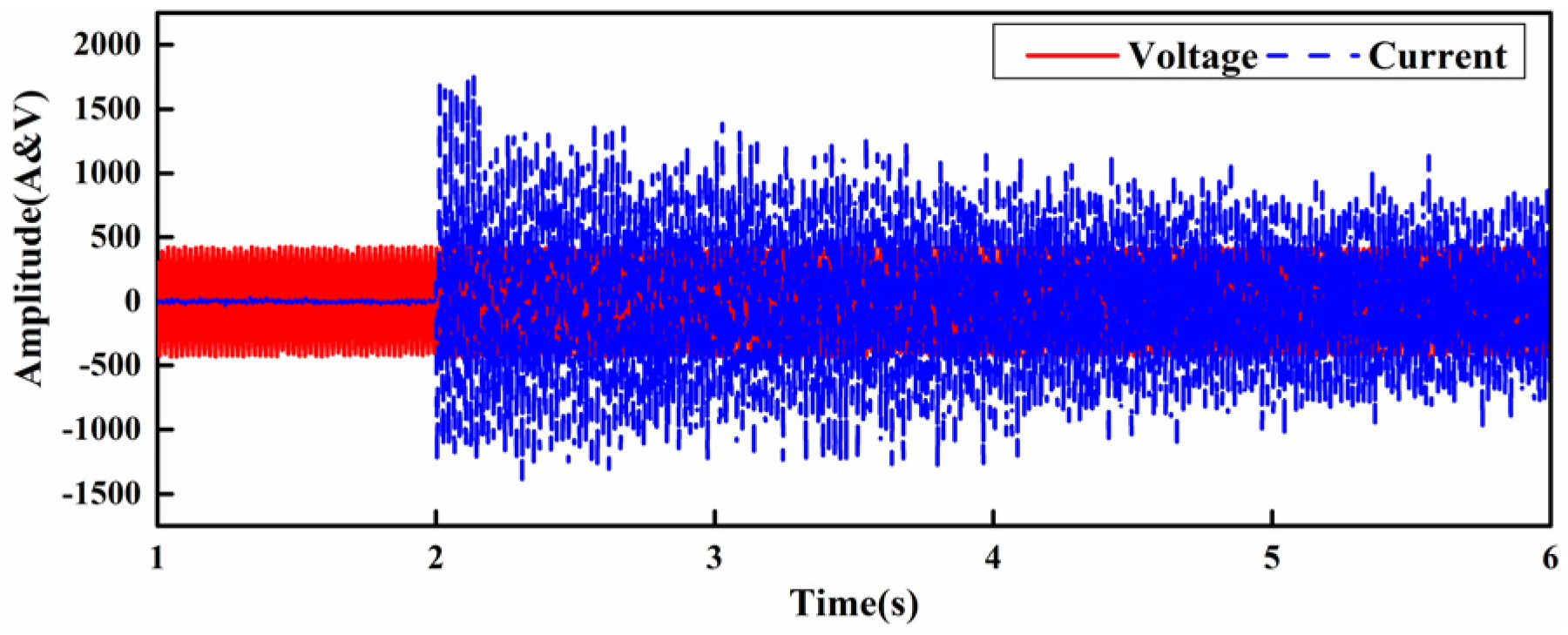
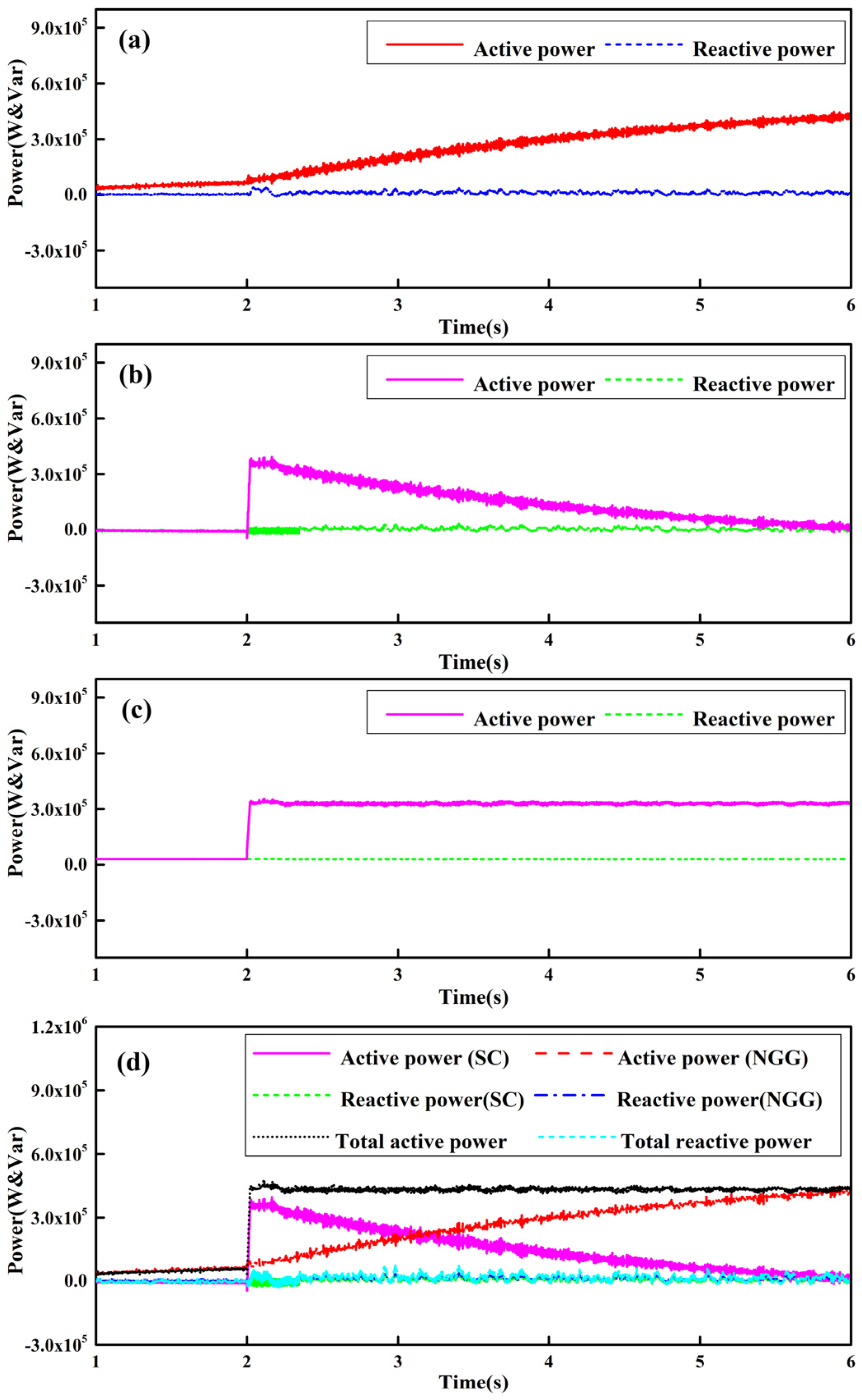
4.1. Simulation Analysis of the Compensation System Response
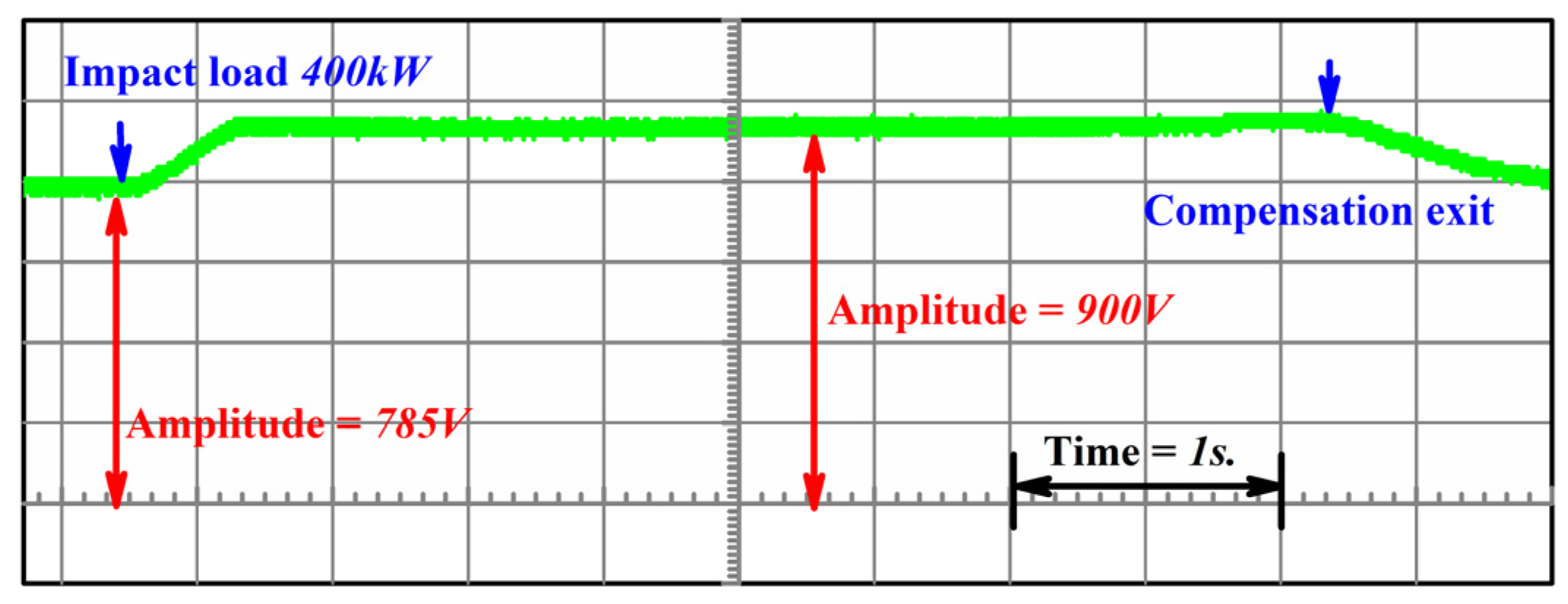
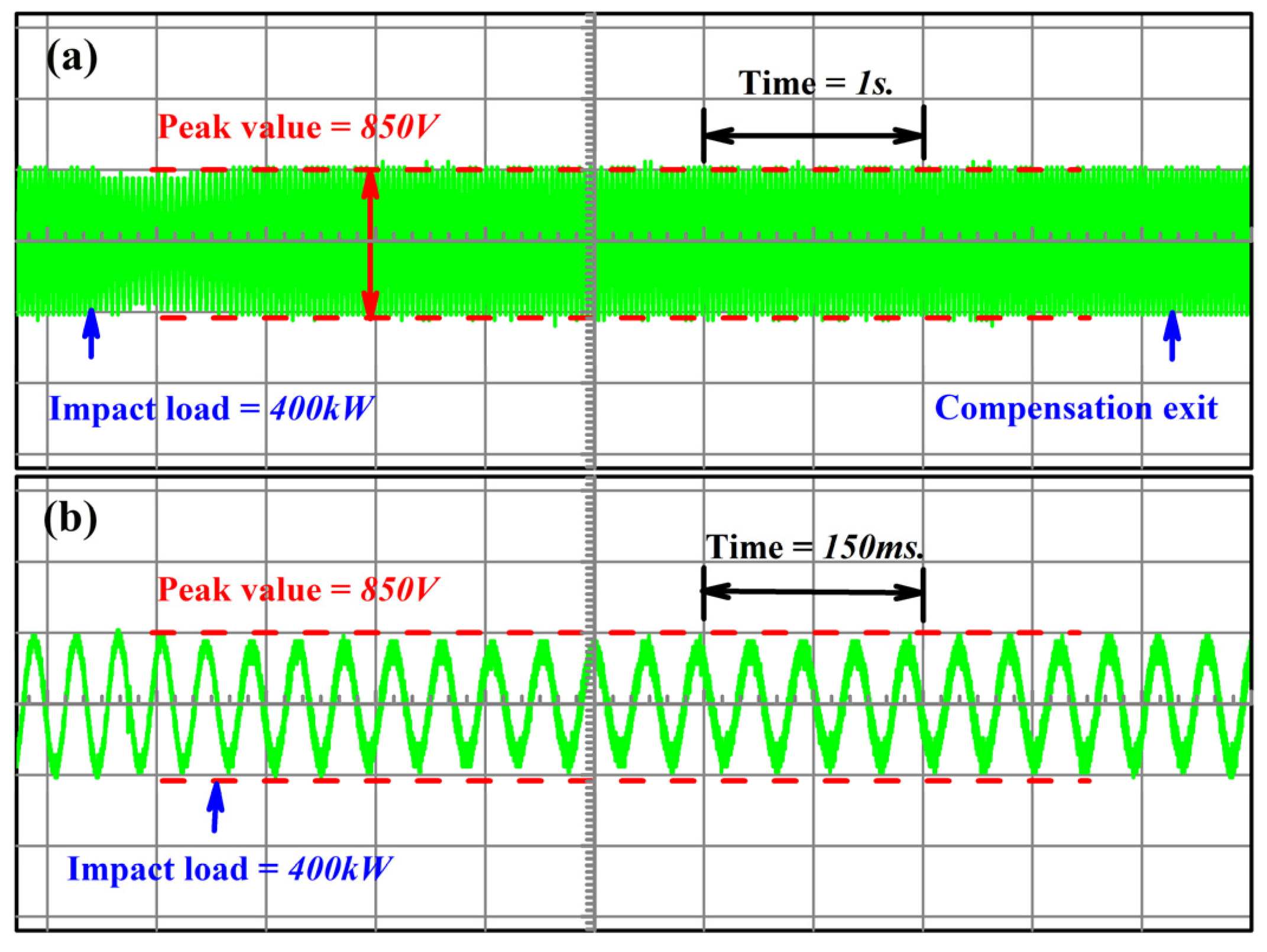
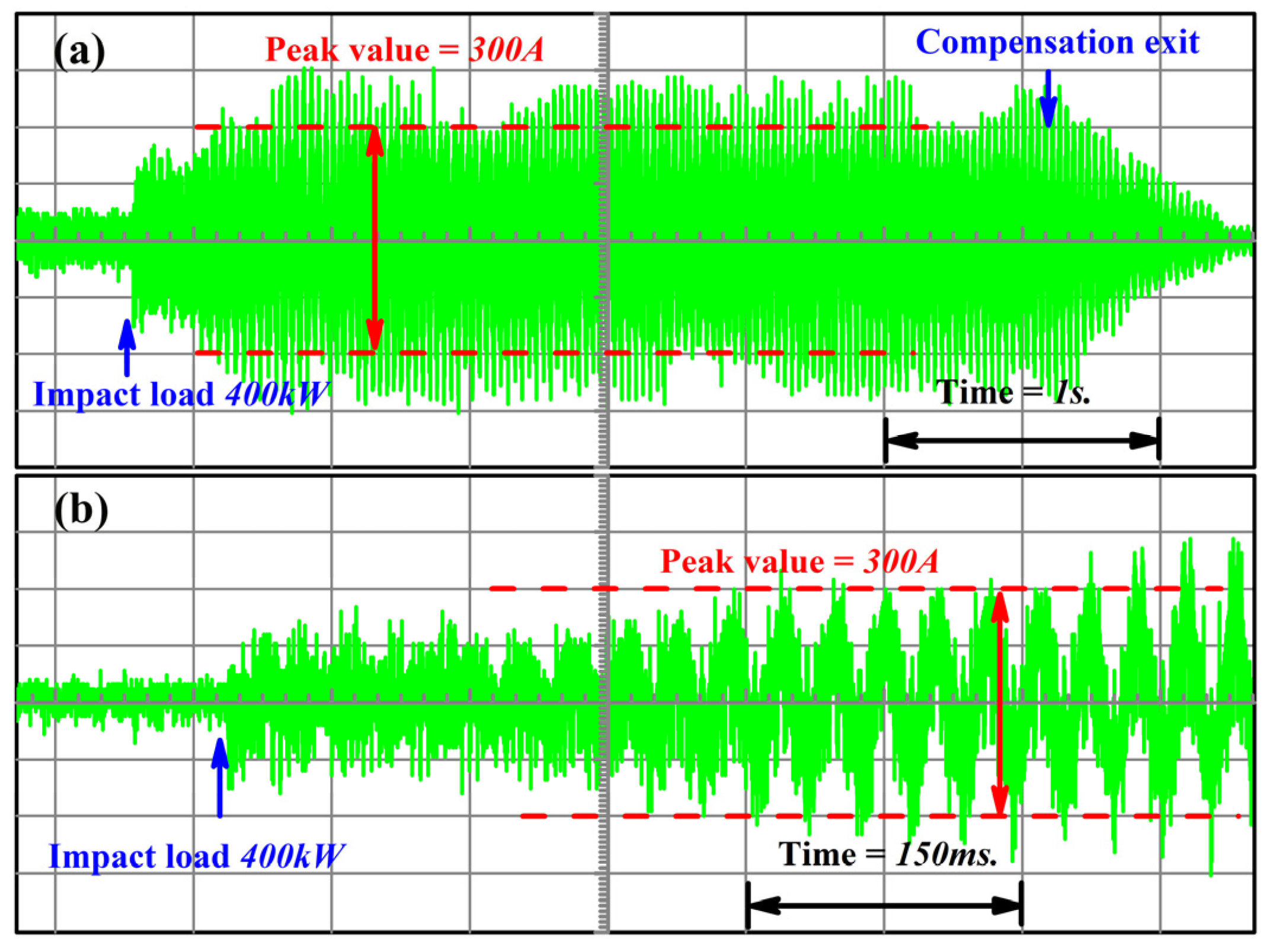
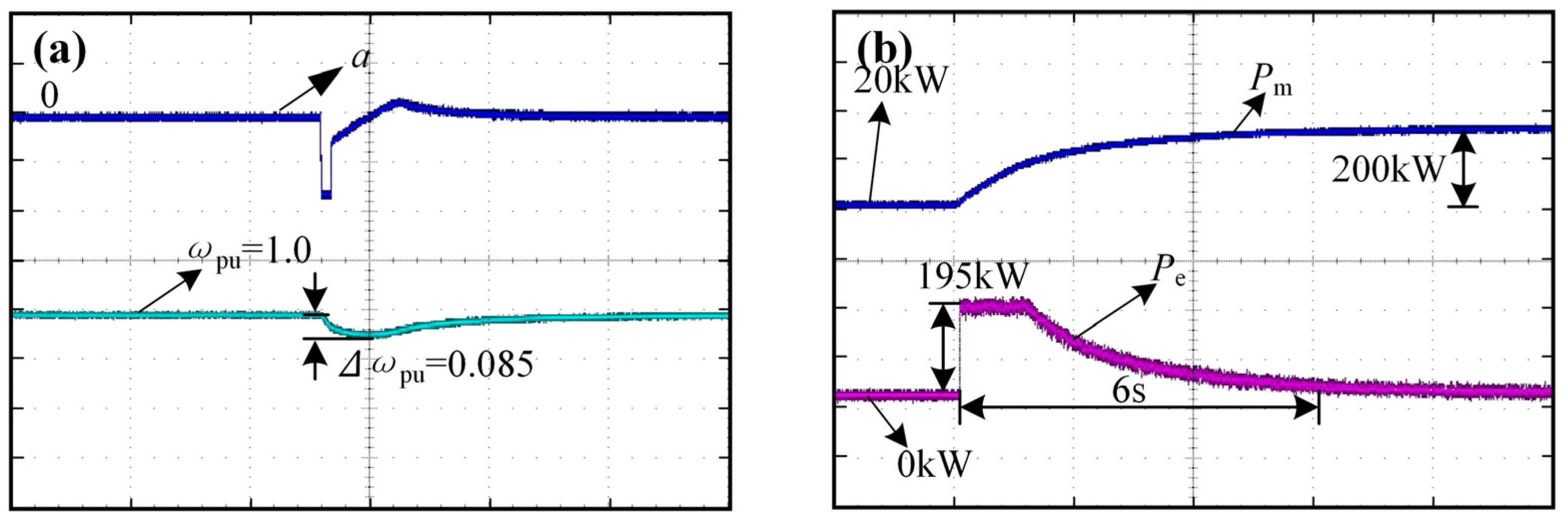
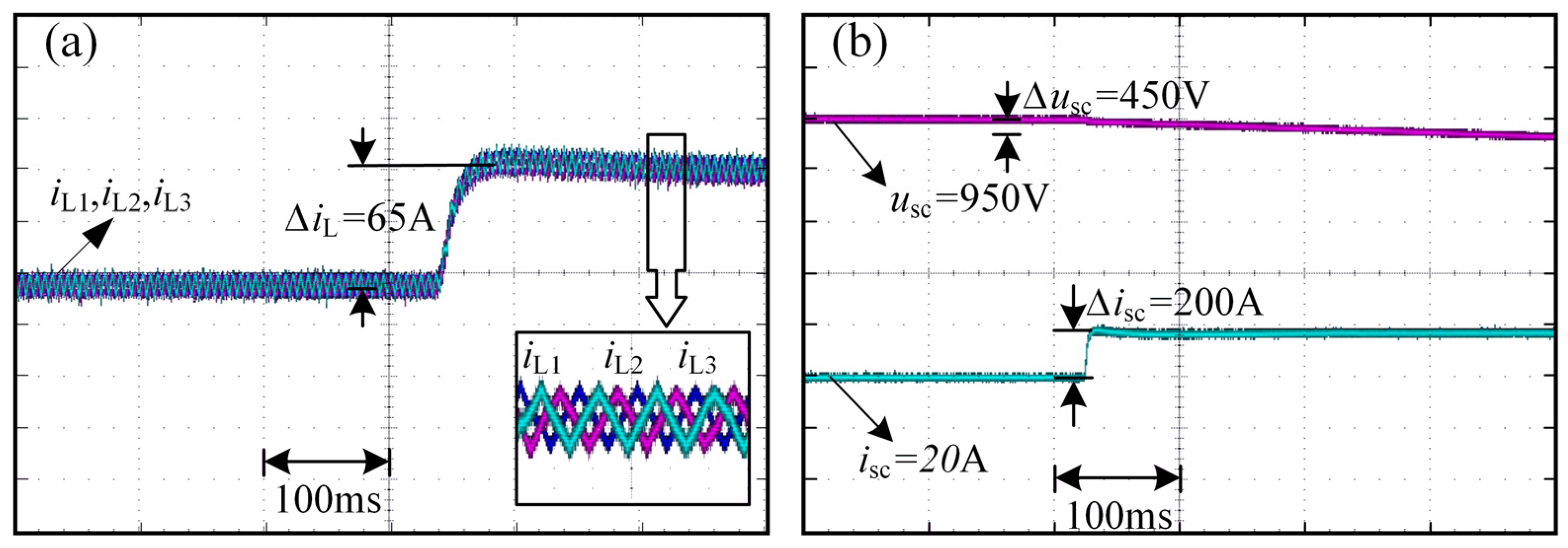
4.2. Experiment Analysis of the Compensation System Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Odetayo, B.; Kazemi, M.; MacCormack, J. A Chance Constrained Programming Approach to the Integrated Planning of Electric Power Generation, Natural Gas Network and Storage. IEEE Trans. Smart Grid. 2018, 33, 6883–6893. [Google Scholar] [CrossRef]
- Xiao, J.; Bai, L.; Li, F. Sizing of Energy Storage and Diesel Generators in an Isolated Microgrid Using Discrete Fourier Transform (DFT). IEEE Trans. Sustain. Energy 2014, 5, 907–916. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Wind in Weak Grids: Low-Frequency Oscillations, Subsynchronous Oscillations, and Torsional Interactions. IEEE Trans. Power Syst. 2020, 35, 109–117. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Guo, H.; Wang, L.K. Computer Modeling of the Eddy Current Losses of Metal Fasteners in Rotor Slots of a Large Nuclear Steam Turbine Generator Based on Finite-Element Method and Deep Gaussian Process Regression. IEEE Trans. Ind. Electron. 2020, 67, 5349–5359. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.B.; Dakyo, B. Transient Power Control for Diesel-Generator Assistance in Electric Boat Applications Using Supercapacitors and Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 416–428. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Wang, Y.J. Sizing Optimization and Energy Management Strategy for Hybrid Energy Storage System Using Multiobjective Optimization and Random Forests. IEEE Trans. Power Electron. 2021, 36, 11421–11430. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Chen, Z.Q.; Huang, D.Y. Model Prediction and Rule Based Energy Management Strategy for a Plug-in Hybrid Electric Vehicle with Hybrid Energy Storage System. IEEE Trans. Power Electron. 2021, 36, 5926–5940. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Lee, B.K. High-Efficiency Adaptive-Current Charging Strategy for Electric Vehicles Considering Variation of Internal Resistance of Lithium-Ion Battery. IEEE Trans. Power Electron. 2019, 34, 3041–3052. [Google Scholar] [CrossRef]
- Kotra, S.; Mishra, M.K. Design and Stability Analysis of DC Microgrid with Hybrid Energy Storage System. IEEE Trans. Sustain. Energy. 2019, 10, 1603–1610. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G. Experimental Study on a Semi-Active Battery-Supercapacitor Hybrid Energy Storage System for Electric Vehicle Application. IEEE Trans. Power Electron. 2020, 35, 1014–1021. [Google Scholar] [CrossRef]
- Hou, J.; Song, Z.; Hofmann, H.F. Control Strategy for Battery/Flywheel Hybrid Energy Storage in Electric Shipboard Microgrids. IEEE Trans. Ind. Inform. 2021, 17, 1089–1099. [Google Scholar] [CrossRef]
- Charalambous, A.; Hadjidemetriou, L.; Kyriakides, E. A Coordinated Voltage–Frequency Support Scheme for Storage Systems Connected to Distribution Grids. IEEE Trans. Power Electron. 2021, 36, 8464–8475. [Google Scholar] [CrossRef]
- Oskouee, S.S.; Kamali, S.; Amraee, T. Primary Frequency Support in Unit Commitment Using a Multi-Area Frequency Model with Flywheel Energy Storage. IEEE Trans. Power Syst. 2021, 36, 5105–5119. [Google Scholar] [CrossRef]
- Nguyen, T.; Yoo, H.; Kim, H. Applying Model Predictive Control to SMES System in Microgrids for Eddy Current Losses Reduction. IEEE Trans. Appl. Supercond. 2016, 25, 5400405. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Ren, L.; Xu, C.; Tang, Y.; Li, J.; Chen, L.; Jia, B. Research on the Application of Superconducting Magnetic Energy Storage in Microgrids for Smoothing Power Fluctuation Caused by Operation Mode Switching. IEEE Trans. Appl. Supercond. 2018, 28, 5701306. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, C.; Lu, R.; Chan, C.C. Improved Study of Temperature Dependence Equivalent Circuit Model for Supercapacitors. IEEE Trans. Plasma Sci. 2013, 41, 1267–1271. [Google Scholar]
- Zhu, D.; Zhou, S.; Zou, X. Improved Design of PLL Controller for LCL-Type Grid-Connected Converter in Weak Grid. IEEE Trans. Power Electron. 2020, 35, 4715–4727. [Google Scholar] [CrossRef]
- Guo, X.; Guerrero, J.M.; Wu, B. Space Vector Modulation for DC-Link Current Ripple Reduction in Back-to-Back Current-Source Converters for Microgrid Applications. IEEE Trans. Ind. Electron. 2015, 62, 6008–6013. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.; Krim, F. Predictive Direct Power Control of Three-Phase Pulsewidth Modulation (PWM) Rectifier Using Space-Vector Modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of Phase-Locked Loop Low-Frequency Stability in Three-Phase Grid-Connected Power Converters Considering Impedance Interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Silwal, S.; Taghizadeh, S.; Karimi-Ghartemani, M.; Hossain, M.J. An Enhanced Control System for Single-Phase Inverters Interfaced with Weak and Distorted Grids. IEEE Trans. Power Electron. 2019, 34, 12538–12551. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2018, 32, 1775–1787. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Hou, X.; Han, H. Quantitative Parameters Design of VSG Oriented to Transient Synchronization Stability. IEEE Trans. Power Syst. 2019, 38, 4978–4981. [Google Scholar] [CrossRef]
- Koiwa, K.; Inoo, K.; Zanma, T.; Liu, K.-Z. Virtual Voltage Control of VSG for Overcurrent Suppression Under Symmetrical and Asymmetrical Voltage Dips. IEEE Trans. Ind. Electron. 2022, 69, 11177–11186. [Google Scholar] [CrossRef]
- Li, G.; Song, W.; Liu, X. A Quasi-Harmonic Voltage Feedforward Control for Improving Power Quality in VSG-Based Islanded Microgrid. IEEE J. Emerg. Sel. Topics Power Electron. 2024, 12, 2994–3004. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Blaabjerg, F. Vector Current Control Derived from Direct Power Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 9224–9235. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, J.; Liu, J.; Gao, J. Direct Power Control of PWM Rectifier with Feedforward Compensation of DC-Bus Voltage Ripple Under Unbalanced Grid Conditions. IEEE Trans. Ind. Appl. 2019, 55, 2890–2901. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, J.; Liu, J. Direct Power Control of PWM Rectifiers with Online Inductance Identification Under Unbalanced and Distorted Network Conditions. IEEE Trans. Power Electron. 2019, 34, 12524–12537. [Google Scholar] [CrossRef]
- Sato, A.; Noguchi, T. Voltage-Source PWM Rectifier–Inverter Based on Direct Power Control and Its Operation Characteristics. IEEE Trans. Power Electron. 2011, 26, 1559–1567. [Google Scholar] [CrossRef]
- Kelly, R.; Santibanez, V.; Loria, A. Control of Robot Manipulators in Joint Space; Springer: Berlin/Heidelberg, Germany, 2005; pp. 392–394. [Google Scholar]


| Generator Parameter | Unit | Value |
|---|---|---|
| Rated power | kW | 300 |
| Rated voltage | V | 600 |
| Rated frequency | Hz | 50 |
| Rated power factor | 0.8 | |
| Rated speed | rpm | 1500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhao, K.; Duan, J.; Sun, L. Impact Load Compensation Inverter Based on Nonlinear Adaptive Multiple Input Multiple Output Control Strategy. Appl. Sci. 2025, 15, 3167. https://doi.org/10.3390/app15063167
Wang S, Zhao K, Duan J, Sun L. Impact Load Compensation Inverter Based on Nonlinear Adaptive Multiple Input Multiple Output Control Strategy. Applied Sciences. 2025; 15(6):3167. https://doi.org/10.3390/app15063167
Chicago/Turabian StyleWang, Shuai, Ke Zhao, Jiandong Duan, and Li Sun. 2025. "Impact Load Compensation Inverter Based on Nonlinear Adaptive Multiple Input Multiple Output Control Strategy" Applied Sciences 15, no. 6: 3167. https://doi.org/10.3390/app15063167
APA StyleWang, S., Zhao, K., Duan, J., & Sun, L. (2025). Impact Load Compensation Inverter Based on Nonlinear Adaptive Multiple Input Multiple Output Control Strategy. Applied Sciences, 15(6), 3167. https://doi.org/10.3390/app15063167






