Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review
Abstract
1. Introduction
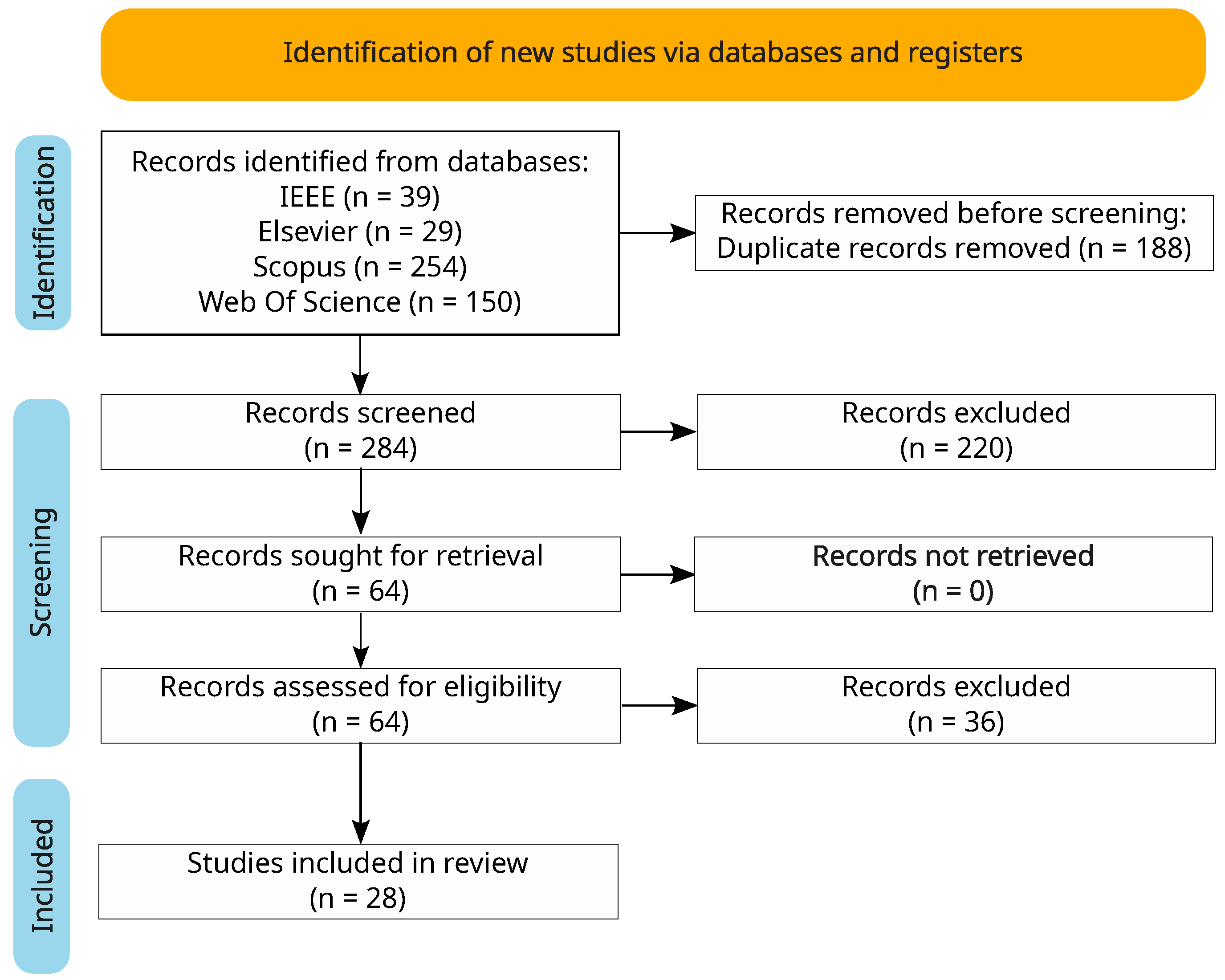
2. Methodology
2.1. Search Strategy
- First, the following set of keywords was used: (“earthquake magnitude” OR “earthquake early warning”) AND (prediction OR forecasting OR estimation OR forecast) AND (“machine learning” OR “deep learning” OR “artificial intelligence”).
- Subsequently, an additional search was performed with the following keywords: (“earthquake magnitude” OR “earthquake early warning”) AND (prediction OR forecasting OR estimation OR classification) AND (“machine learning” OR “deep learning” OR “artificial intelligence”).
- Finally, duplicate articles from both searches were identified and removed, resulting in a unified set of relevant articles.
2.2. Screening and Eligibility Results
- Articles focusing on machine learning methods for early earthquake magnitude estimation.
- Articles published in English.
- Articles published between 2014 and 7 March 2025.
- Conference papers.
- Systematic review articles.
- Articles in which machine learning was not applied to early earthquake magnitude estimation.
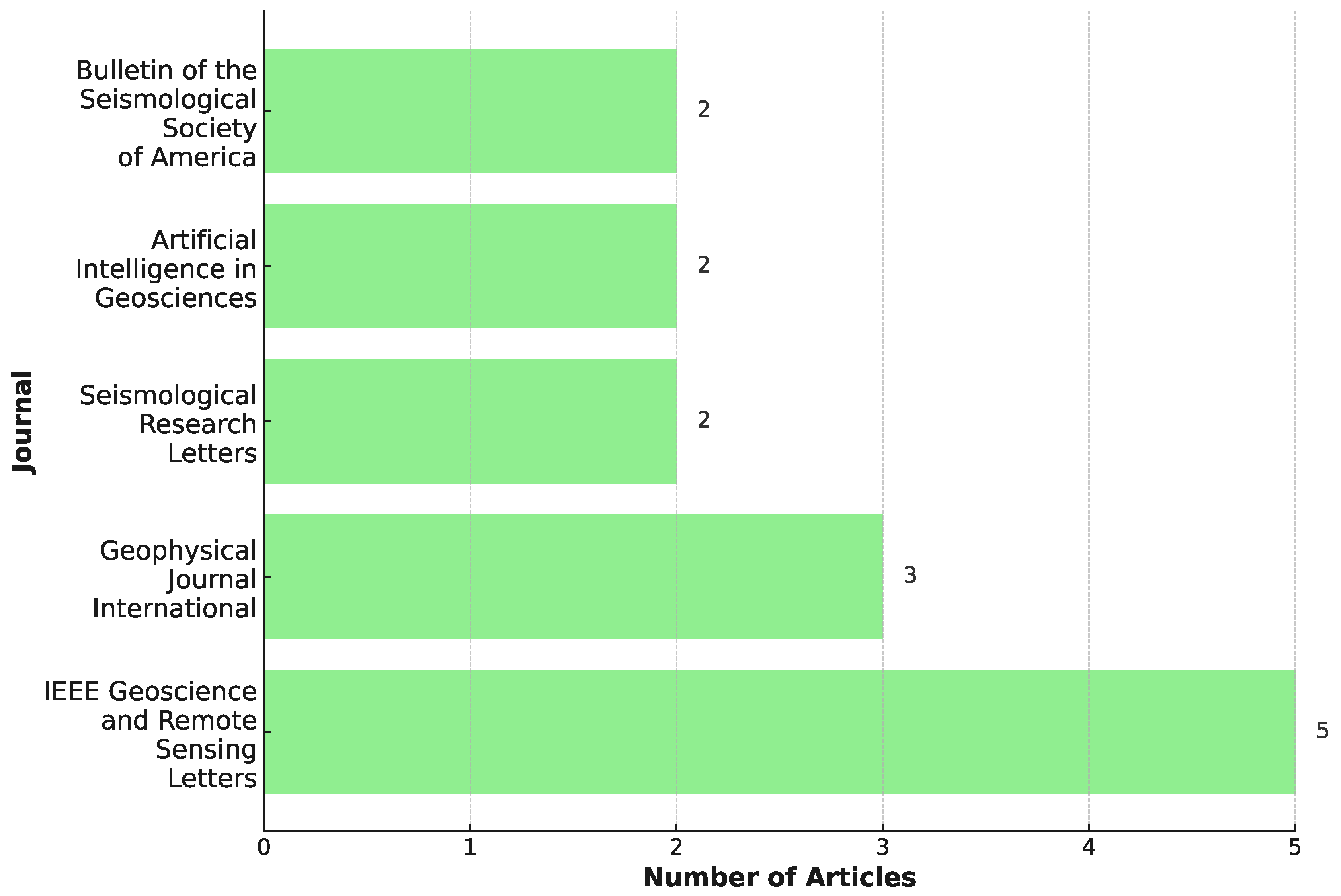
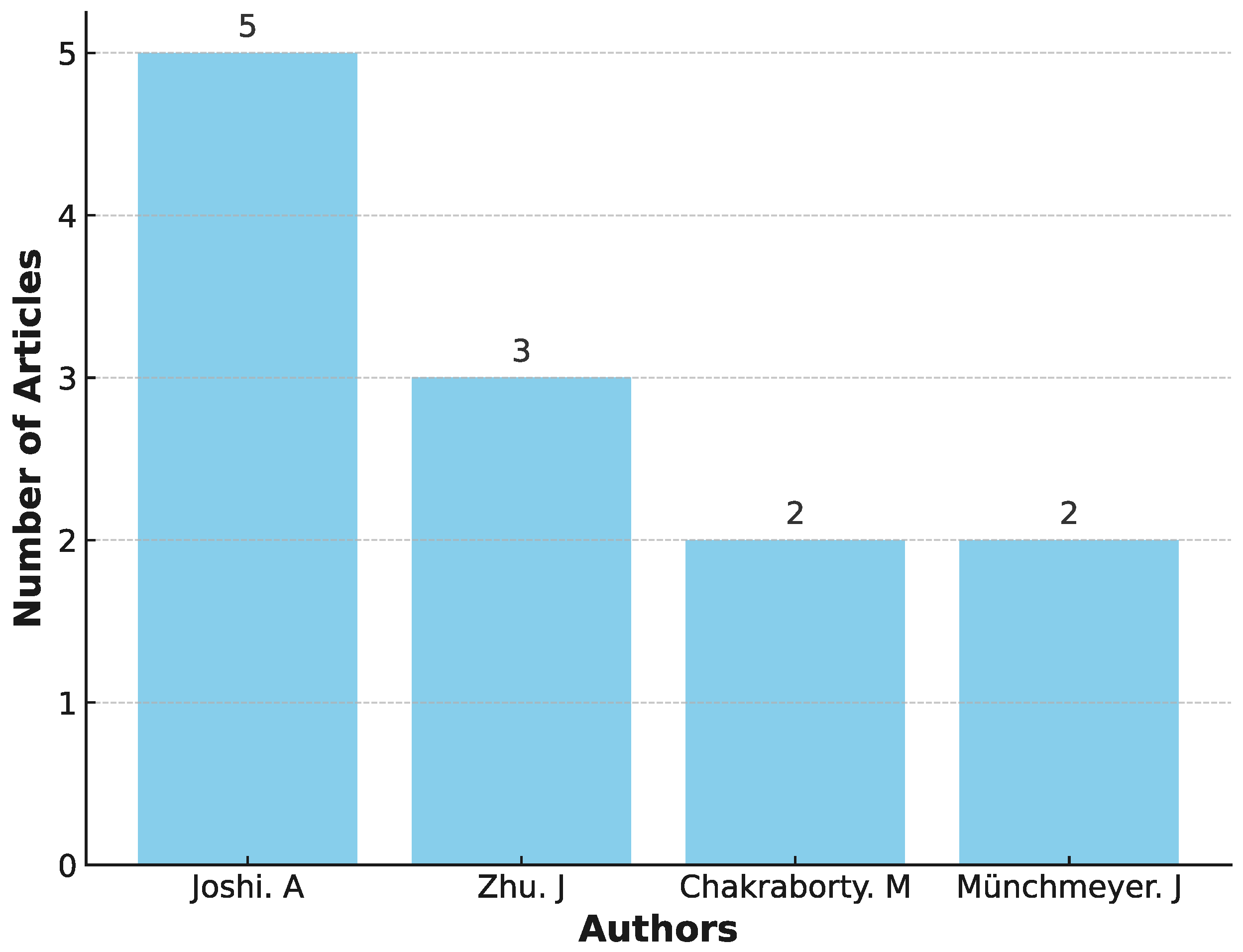
3. Results
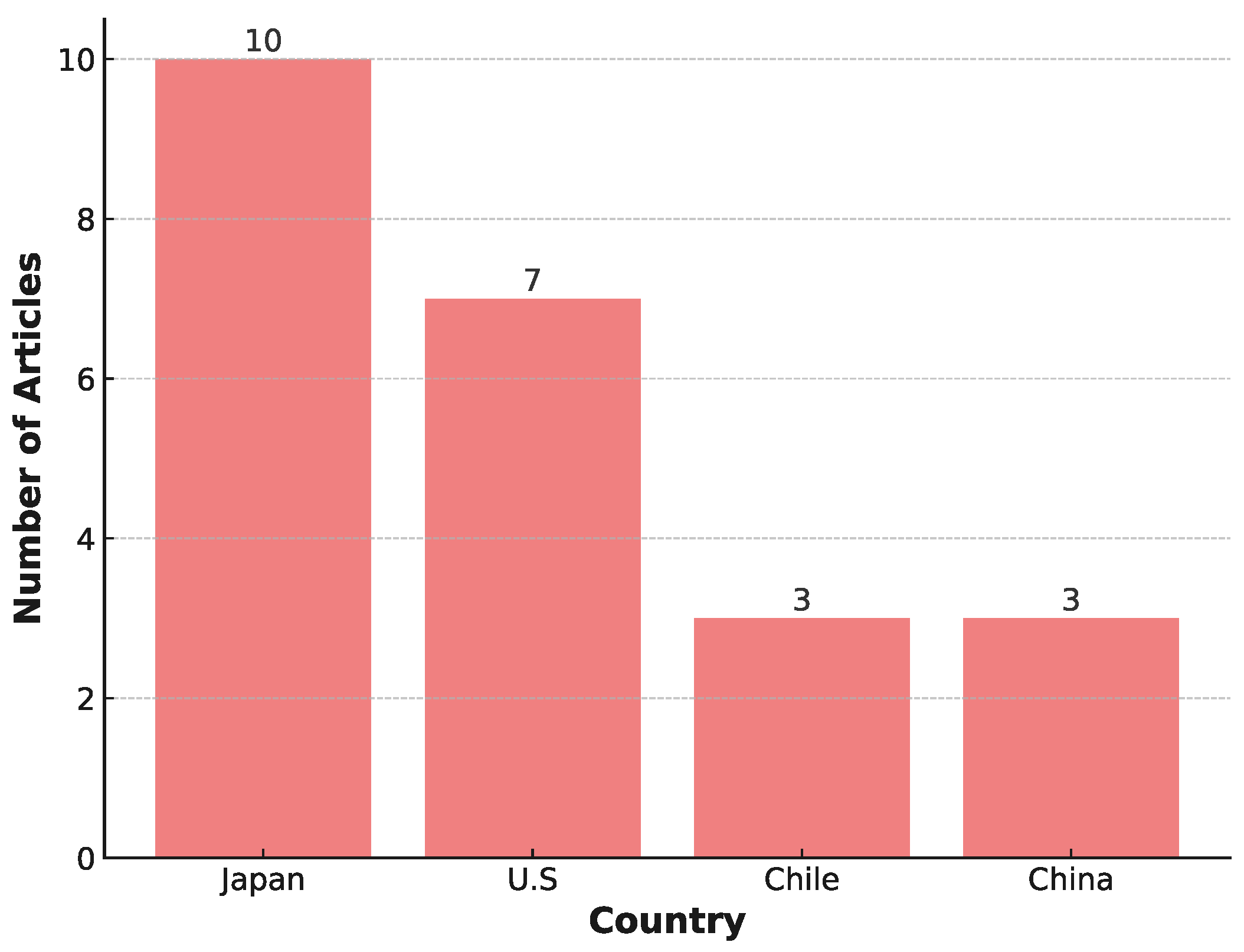
| Author, Year, Country, Ref. | Dataset Size Country | Target Features | AI Model | Performance Index Name | Performance Value (Unit) |
|---|---|---|---|---|---|
| Zhu et al., 2022, China, [40] | K-NET 1837 earthquakes 57,789 waveforms Japan | Magnitude | SVM-M | 0.297 | |
| Song et al., 2022, China, [32] | K-NET 1205 earthquakes 69,033 waveforms Japan | Magnitude | MEANet: CNN-RNN-AM | 0 < error < 0.5 0.5 < error < 1.0 1.0 < error | 0.9422 0.0525 0.42 |
| Wang et al., 2023, China, [41] | KiK-net 30,756 waveforms Japan | Magnitude | CNN | PME Mean | 0.40 0.8421 −0.06 |
| Quinteros-Cartaya et al., 2024, Germany, [42] | Synthetic 36,800 waveforms Chile | Magnitude | CNN | Synthetic data: RMS Real data: RMS | Synthetic data: 0.06 Real data: 0.09 |
| Münchmeyer et al., 2020, Germany, [43] | IPOC 101,601 earthquakes Chile | Magnitude | Boosting Regression Tree | RMSE | 0.117 |
| Kuang et al., 2021, China, [44] | CSES 21,700 synthetic earthquakes China | Magnitude | Fully Convolutional Network (FCN) | 3 < M < 5.9: Mean, 2.3 < M < 3.5: Mean, | 3 < M < 5.9: −0.017, 0.21 2.3 < M < 3.5: −0.011, 0.14 |
| Mousavi et al., 2020, USA, [7] | STEAD 300 k waveforms Global | Local magnitude Duration magnitude | CNN-LSTM | Mean | −0.1 0.24 |
| Joshi et al., 2024, India, [45] | K-NET 20 k waveforms Japan | Magnitude | LSTM-Bi-LSTM- XGBoost RF-LightGBM- SVR | MAE RMSE | 0.24 0.29 0.17 |
| Joshi et al., 2024, India, [31] | K-NET 2960 waveforms Japan | Magnitude | XGBoost | APE | 0.004 ± 0.57 |
| Jin et al., 2024, South Korea, [33] | STEAD 1.2 M waveforms KPED 335 k waveforms Global | Earthquake/Noise Magnitude | Conformer: Convolutional- augmented Transformer | STEAD Dataset: Classification: Accuracy Precision Recall F1 Score Magnitude: MAE KPED Dataset: Classification: Accuracy Precision Recall F1 Score Magnitude: MAE | STEAD Dataset: Classification: 0.9999 0.9999 0.9999 0.9999 Magnitude: 0.1278 KPED Dataset: Classification: 1 1 1 1 Magnitude: 0.1925 |
| Münchmeyer et al., 2021, Germany, [46] | Chile: 1.6 M waveforms Italy: 494,183 waveforms Japan: 372,661 waveforms | Location Magnitude | TEAM-LM (Transformer) | Chile: RMSE (magnitude), Mean error (location) Italy: RMSE (magnitude), Mean error (location) Japan: RMSE (magnitude), Mean error (location) | Chile: 0.08 19 km a 0.5 s 2 km a 25 s Italy: 0.20 2 km a 7 km Japan: 0.22 14 km a 22 km |
| Chakraborty et al., 2022, Germany, [47] | STEAD 1.2 M waveforms Global | Earthquake/Noise Magnitude | CNN-Bi-LSTM | Accuracy | 0.9386 |
| Ristea et al., 2022, Romania, [48] | STEAD 1.2 M waveforms Global | Epicentral distance Depth Magnitude | Complex CNN | Epicentral distance: MAE Depth: MAE Magnitude: MAE | Epicentral distance: 4.51 km Depth: 6.15 km Magnitude: 0.26 |
| Joshi et al., 2022, India, [49] | K-NET 2951 waveforms Japan | Magnitude | EEWPEnsembleStack: AdaBoost-XGBoost LightGBM-DT Lasso regression | MAE | 0.419 0.63 |
| Cofre et al., 2022, Chile, [50] | CSN 7580 earthquakes Chile | Magnitude | LSTM | M > 4: MAPE M < 4: MAPE | M > 4: 0.401 M < 4: 0.804 |
| Wang et al., 2024, China, [51] | STEAD 200 k waveforms Global | Local magnitude Duration magnitude | Graph Neural Network CNN-RCGL | : RMSE Mean : RMSE Mean (RMSE): 0–1, 1–2, 2–3, 3–4, ≥4 (RMSE): 0–1, 1–2, 2–3, ≥3 ( add-SNR dB): −2, −1, 0, 1, 2, 3, 5, 15 ( add-SNR dB): −2, −1, 0, 1, 2, 3, 5, 15 | : 0.9303 0.1844 0.0054 0.1843 : 0.8621 0.2575 0.0422 0.2540 : 0.1512, 0.1788, 0.2619, 0.3640, 0.6324 : 0.3020, 0.2289, 0.2586, 0.3083 : 0.872, 0.872, 0.873, 0.875, 0.876, 0.880, 0.885, 0.892 : 0.792, 0.796, 0.797, 0.802, 0.808, 0.815, 0.837, 0.850 |
| Zhu et al., 2024, China, [52] | K-NET 129,513 waveforms 2794 earthquakes Japan | Magnitude | MCFrame: (CNN-RNN-AM) SVM, RF, DNN | M < 5.5 a 3 s: Accuracy M ≥ 5.5 a 3 s: Accuracy M < 5.5 a 1 s: Accuracy M ≥ 6 a 1 s: Accuracy M ≥ 6 a 3 s: Accuracy M ≥ 6 a 5 s: Accuracy 5 < M < 6 a 5 s: Accuracy | M < 5.5 a 3 s 0.98 M ≥ 5.5 a 3 s 0.89 M < 5.5 a 1 s 0.99 M ≥ 6 a 1 s 0.90 M ≥ 6 a 3 s 0.95 M ≥ 6 a 5 s 0.97 5 < M < 6 a 5 s 0.78 |
| Yoon et al., 2023, South Korea, [53] | STEAD 260 k waveforms KiK-net 130 k waveforms Global/Japan | Magnitude Epicentral distance | CRNN | STEAD Dataset (epicentral distance, magnitude): MAE KiK-net (epicentral distance, magnitude): MAE Inference time: (GPU, CPU) | STEAD Dataset (epicentral distance, magnitude): 2.2736, 0.1337 KiK-net (epicentral distance, magnitude): 5.0040, 0.1448 Inference time (ms): 796.4, 5.68 |
| Shakeel et al., 2022, Japan, [54] | STEAD 93,144 waveforms Global | Magnitude | 3D Convolutional Recurrent Neural Network (3D-CNN-RNN) | 0 < M < 1 Precision Recall F1 Score 1 < M < 2 Precision Recall F1 Score 2 < M < 3 Precision Recall F1 Score 3 < M < 4 Precision Recall F1 Score 4 < M < 8 Precision Recall F1 Score Earthquake/Noise: Precision Recall F1 Score | 0 < M < 1 0.97 0.50 0.66 1 < M < 2 0.98 0.69 0.81 2 < M < 3 0.83 0.51 0.63 3 < M < 4 0.93 0.90 0.91 4 < M < 8 0.84 0.81 0.82 Earthquake/Noise: 0.99 0.87 0.92 |
| Ren et al., 2023, China, [55] | STEAD/CENC 1097 earthquakes 4166 waveforms China/Global/Italy | Magnitude | CNN | General accuracy Medium and large earthquake: Precision Recall F1 Score Small earthquake: Precision Recall F1 Score | 0.9765 Medium and large earthquake: 0.9827 0.9693 0.9769 Small earthquake: 0.9796 0.9834 0.9770 |
| Dybing et al., 2024, USA, [56] | USGS (MLAAPDE) 2.4 M waveforms Global | Magnitude | AIMag: CNN-RNN | Mean Precision ( to ) | ±0.5 |
| Meng et al., 2023, China, [57] | CENC 324,266 waveforms China | Magnitude | EEWMagNet: CNN | Accuracy Precision Recall F1 Score | 0.9023 0.8935 0.9108 0.9021 |
| Hou et al., 2024, China, [58] | 8144 earthquakes Japan | Magnitude | Transformer LSTM-CNN | First 3 s: RMSE MAE First 14 s: RMSE MAE | First 3 s: 0.38 0.29 0.38 First 14 s: 0.20 0.15 0.20 |
| Chanda et al., 2021, India, [59] | SPECFEM3D 400 earthquakes Synthetic data | Magnitude Location | SVM | Magnitude: RMSE MSE MAE Hypocentral dist: RMSE MSE MAE Azimuth: RMSE MSE MAE Elevation: RMSE MSE MAE | Magnitude: 0.0412 1.0 0.00169 0.009419 Hypocentral dist: 485.53 1.0 235,700 268.64 Azimuth: 68.85 0.58 4741.5 58.94 Elevation: 0.0056422 1.0 0.00003 0.0015 |
| Chakraborty et al., 2022, Germany, [4] | STEAD 32,356 waveforms INSTANCE 135,347 waveforms Global/Italy | P-wave arrival time Earthquake/Noise Magnitude | CNN Bi-LSTM | STEAD Dataset Classification: Accuracy Precision Recall F1 Score Magnitude: Mean error RMSE MAE P-wave arrival time: Mean error RMSE MAE INSTANCE Classification: Accuracy Precision Recall F1 Score Magnitude: Mean error RMSE MAE P-wave arrival time: Mean error RMSE MAE | STEAD Dataset Classification: 0.9858 0.9964 0.9831 0.9897 Magnitude: −0.06 0.60 0.61 0.46 P-wave arrival time: −0.05 0.10 0.12 0.05 INSTANCE Classification: 0.9759 0.9866 0.9753 0.9810 Magnitude: −0.02 0.69 0.69 0.54 P-wave arrival time: 0.01 0.52 0.52 0.29 |
| Zhu et al., 2022, China, [60] | CSMNC 7236 waveforms 461 earthquakes China | Magnitude | SVM | Estimation error: , and Estimation error: and Average error | Estimation error: , and ±0.3 units 1 s Estimation error: and ±0.3 units 13 s 0.31 0.41 |
| Joshi et al., 2025, India, [61] | 18,994 waveforms Japan | Magnitude | MagPred XGBoost-LightGBM CatBoost-RF | First 3 s: MAE RMSE First 4 s: MAE RMSE First 5 s: MAE RMSE | First 3 s: 0.42 0.56 First 4 s: 0.40 0.54 First 5 s: 0.39 0.53 |
| Joshi et al., 2025, India, [34] | 26,279 waveforms Japan | Magnitude PGA | DFTQuake AM-NN-LightGBM XGBoost-RF | Magnitude: MAE RMSE Training time (s) Parameters PGA: MAE RMSE Training time (s) Parameters | Magnitude: 0.66 0.85 3.81 0.12 62.22 ∼2.4 M PGA: 0.25 0.32 95.19 99.78 62.22 ∼2.4 M |
3.1. Early Earthquake Magnitude Estimation as a Classification Task
3.2. Early Earthquake Magnitude Estimation as a Regression Task
3.3. Key Insights into Machine Learning and Deep Learning Models for Magnitude Estimation
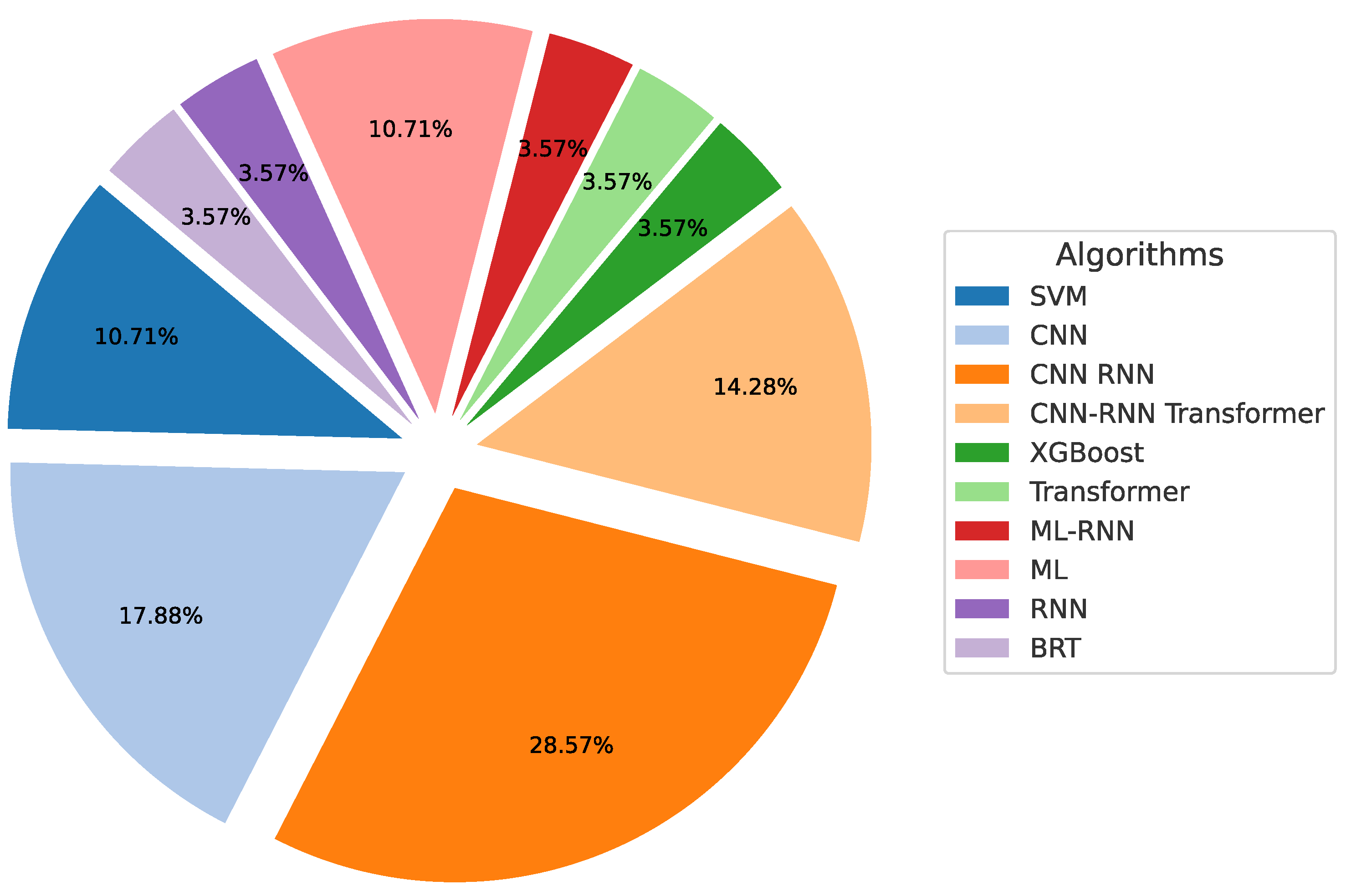
- Dominance of DL models: Architectures such as Bi-LSTM [7], Transformers [46], CNN-based networks [32], and hybrid approaches like MEANet [32] and MCFrame [52] have demonstrated high capability in capturing temporal and spatial features of seismic signals. These models improve early magnitude prediction by leveraging complex feature extraction mechanisms.
- Optimization strategies: Some studies employ ensemble learning models, such as EEWPEnsembleStack [49], which combine multiple predictors to reduce variance and enhance generalization across diverse seismic datasets.
- Computational considerations: While DL models offer superior accuracy, their computational demands can pose challenges for real-time applications, particularly in resource-constrained environments. In contrast, simpler models like SVM-M [40] perform well on small datasets but may struggle to maintain accuracy and scalability for complex, large-scale earthquake events.
- Balance between speed and accuracy: In early warning systems, rapid and accurate predictions are crucial. Models like MagNet [44] and real-time CNN-based approaches have been designed to operate efficiently, making them suitable for emergency response scenarios.
- Challenges and future directions: Despite advances in magnitude estimation, accurate prediction of large earthquakes ( 6) remains challenging due to limited training data in this range. Additionally, generalizing models to different geological regions is still an open issue that requires further investigation.
3.4. Comparison Between Machine Learning Techniques and Traditional Methods
3.4.1. Quantitative Comparison
3.4.2. Considerations
- Interpretability and trustworthiness: Traditional methods like and are based on well-established physical principles, making them transparent and easy to validate. In contrast, ML/DL models function as “black boxes”, where the decision-making process is not easily interpretable. However, recent advancements in explainable AI (XAI) [69] have introduced techniques to enhance interpretability, such as Grad-CAM [70], SHapley Additive Explanations (SHAP) [71], and local interpretable model-agnostic explanations (LIME) [72]. Although these techniques have been applied in various fields, such as healthcare [73], finance [74], and image recognition [75], their potential in seismology remains largely unexplored. Further research is needed to assess their effectiveness in improving the transparency of ML/DL models for seismic applications, ensuring that these methods can be reliably integrated into real-time earthquake early warning systems.
- Generalization and adaptability across different seismic regions: Traditional empirical models have well-defined calibration parameters that can be adapted with minimal regional data, whereas ML/DL models require large datasets to prevent overfitting. The variability in tectonic conditions across different regions can significantly impact the performance of ML/DL approaches [4,68]. To improve model adaptability, researchers have explored techniques such as fine-tuning [76] and domain adaptation [77].
- Robustness in data-limited or noisy conditions: In regions with low-density seismic networks, traditional methods can still function with minimal data, whereas ML/DL models require large-scale datasets for training and may fail when encountering unseen or noisy data. To address these limitations, researchers have explored techniques such as data augmentation [78] and self-supervised learning [79].
- Regulatory and approval constraints in EEW systems:The deployment of new ML/DL models in operational seismic warning systems requires extensive validation, certification, and regulatory approval. Traditional methods have been used and optimized for decades, whereas ML-based approaches must undergo a rigorous evaluation before being integrated into national or regional networks [34,56].
- Practical benefits and real-world impact: Although ML-based models have demonstrated superior accuracy in magnitude estimation, their actual contribution to improving EEW performance and reducing earthquake-related losses remains an open research topic. Some studies suggest that ML models can reduce false alarms and missed detections, thereby improving public trust in EEW systems [4,7]. However, large-scale evaluations and real-world implementation studies are still needed to quantify their effectiveness in reducing casualties and economic damage. Future research should focus on systematic field tests that assess the real-time performance of ML-driven EEW systems in operational environments [61].
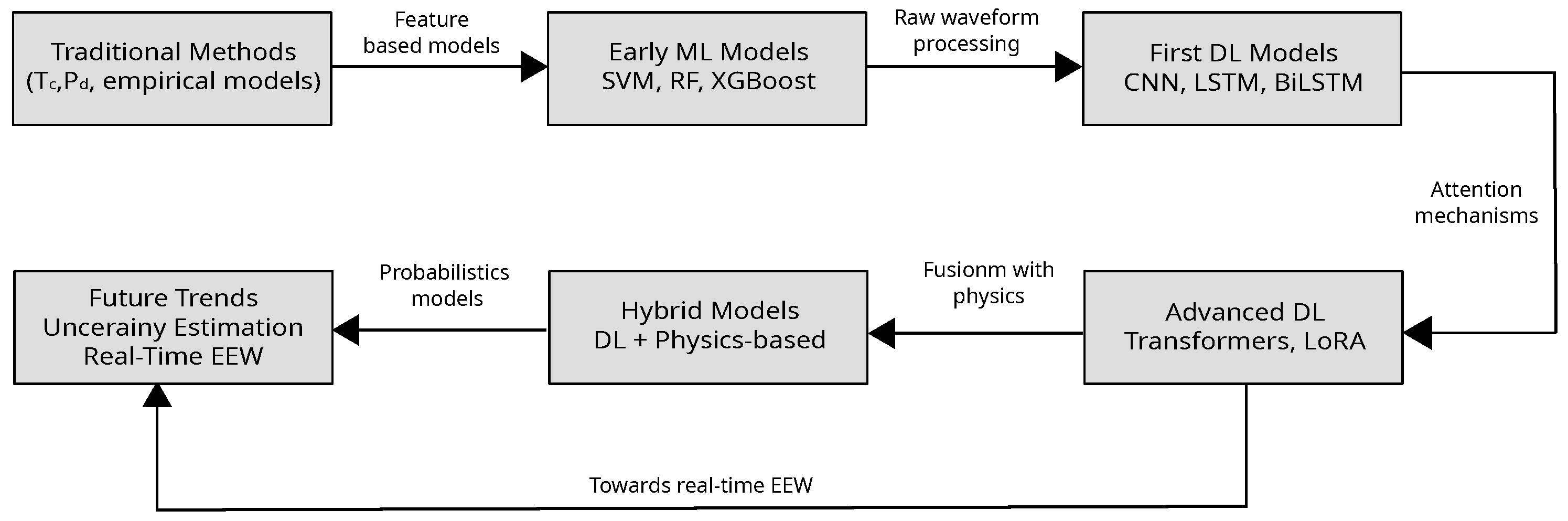
4. Trends and Future Work
Real-World Usage Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| AM | attention mechanism |
| APE | average prediction error |
| Bi-GRU | bidirectional gated recurrent unit |
| Bi-LSTM | bidirectional long short-term memory |
| BRT | boosted regression tree |
| CENC | China Earthquake Networks Center |
| CNN | convolutional neural network |
| CReLU | complex-valued convolutional layer |
| CRNN | convolutional recurrent neural network |
| CSES | China Seismic Experimental Site |
| CSN | community seismic network |
| CTGAN | conditional tabular generative adversarial network |
| DL | deep learning |
| DNN | deep neural network |
| DT | decision tree |
| EEW | earthquake early warning |
| FCN | fully convolutional network |
| GAP | global average pooling |
| GNN | graph neural network |
| GRU | gated recurrent unit |
| HR-GNSS | high-frequency global navigation satellite system |
| INSTANCE | The Italian Seismic Dataset for Machine Learning |
| IPOC | Integrated Plate Boundary Observatory Chile |
| K-NET | Kyoshin Network |
| KiK-net | Kiban Kyoshin Network |
| LIME | local interpretable model-agnostic explanations |
| LoRA | low-rank adaptation |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| MCFrame | machine learning magnitude classification framework |
| ML | machine learning |
| MLP | multilayer perceptron |
| MSE | mean squared error |
| MTL | multitask learning |
| moment magnitude | |
| PGA | peak ground acceleration |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| RCGLs | residual connection graph layers |
| RF | random forest |
| RMS | root mean square |
| RMSE | root mean square error |
| RNN | recurrent neural network |
| SNR | signal-to-noise ratio |
| SGWO | sanitized gray wolf optimizer |
| SHAP | SHapley Additive Explanations |
| STA/LTA | short-time-average/long-time-average |
| STEAD | Stanford Earthquake Dataset |
| STFT | short-time Fourier transform |
| SVM | support vector machine |
| SVR | support vector regression |
| USGS | United States Geological Survey |
| ViT | Vision Transformer |
| XGBoost | extreme gradient boosting |
| body-wave magnitude | |
| duration magnitude | |
| local magnitude | |
| surface-wave magnitude | |
| Japan Meteorological Agency Magnitude | |
| peak displacement | |
| determination coefficient | |
| standard deviation | |
| effective average period | |
| predominant period |
Appendix A
| Journal | Year |
|---|---|
| Geodesy and Geodynamics | 2025 |
| Engineering Applications of Artificial Intelligence | 2025 |
| Neural Computing and Applications | 2024 |
| Journal of Earth System Science | 2024 |
| Journal of South American | 2024 |
| Earth, Planets and Space | 2024 |
| Gondwana Research | 2023 |
| Solid Earth | 2023 |
| Journal of Asian Earth Sciences: X | 2022 |
| Geophysics | 2022 |
| Applied Sciences (Switzerland) | 2022 |
| Journal of Geophysical Research: Solid Earth | 2022 |
| Geophysical Research Letters | 2020 |
| Pure and Applied Geophysics | 2020 |
Appendix B
| Author | Year |
|---|---|
| Jin Y | 2024 |
| Wang Z | 2024 |
| Quinteros-Cartaya C | 2024 |
| Hou B | 2024 |
| Dybing S N | 2024 |
| Wang Y | 2023 |
| Yoon D | 2023 |
| Ren T | 2023 |
| Meng F | 2023 |
| Ristea N | 2022 |
| Cofre A | 2022 |
| Song J | 2022 |
| Shakeel M | 2022 |
| Kuang W | 2021 |
| Mousavi S | 2020 |
| Chanda S | 2020 |
Appendix C
| Country | Year |
|---|---|
| U.S.–Japan | 2023 |
| China–U.S.–Italy | 2023 |
| Chile–Italy–Japan | 2021 |
| Synthetics | 2020 |
| U.S.–Italy | 2020 |
References
- Asim, K.M.; Martínez-Álvarez, F.; Basit, A.; Iqbal, T. Earthquake magnitude prediction in Hindukush region using machine learning techniques. Nat. Hazards 2017, 85, 471–486. [Google Scholar]
- Geller, R.J.; Jackson, D.D.; Kagan, Y.Y.; Mulargia, F. Earthquakes Cannot Be Predicted. Science 1997, 275, 1616. [Google Scholar]
- Zhang, D.; Fu, J.; Li, Z.; Wang, L.; Li, J.; Wang, J. A Synchronous Magnitude Estimation with P-Wave Phases’ Detection Used in Earthquake Early Warning System. Sensors 2022, 22, 4534. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, M.; Fenner, D.; Li, W.; Faber, J.; Zhou, K.; Rümpker, G.; Stoecker, H.; Srivastava, N. CREIME—A Convolutional Recurrent Model for Earthquake Identification and Magnitude Estimation. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024595. [Google Scholar]
- Richter, C.F. An instrumental earthquake magnitude scale. Bull. Seismol. Soc. Am. 1935, 25, 1–32. [Google Scholar]
- Chung, D.H.; Bernreuter, D.L. Regional relationships among earthquake magnitude scales. Rev. Geophys. 1981, 19, 649–663. [Google Scholar]
- Mousavi, S.M.; Beroza, G.C. A Machine-Learning Approach for Earthquake Magnitude Estimation. Geophys. Res. Lett. 2020, 47, e2019GL085976. [Google Scholar]
- Nakamura, Y. On the Urgent Earthquake Detection and Alarm System (UrEDAS). In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo/Kyoto, Japan, 2–9 August 1988; Volume VII. pp. 673–678. [Google Scholar]
- Kanamori, H. Real-time seismology and earthquake damage mitigation. Annu. Rev. Earth Planet. Sci. 2005, 33, 195–214. [Google Scholar]
- Kanamori, H.; Allen, R.M. Earthquake Early Warning Systems. Science 2003, 300, 786–789. [Google Scholar]
- Böse, M.; Hauksson, E.; Solanki, K.; Kanamori, H.; Heaton, T.H. Real-time testing of the on-site warning algorithm in southern California and its performance during the July 29 2008 Mw5.4 Chino Hills earthquake. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Sarker, I.H. A machine learning based robust prediction model for real-life mobile phone data. Internet Things 2019, 5, 180–193. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.M.; Beroza, G.C. Machine Learning in Earthquake Seismology. Annu. Rev. Earth Planet. 2023, 51, 105–129. [Google Scholar] [CrossRef]
- Wilkins, A.H.; Strange, A.; Duan, Y.; Luo, X. Identifying microseismic events in a mining scenario using a convolutional neural network. Comput. Geosci. 2020, 137, 104418. [Google Scholar] [CrossRef]
- Kuyuk, H.S.; Susumu, O. Real-Time Classification of Earthquake using Deep Learning. Procedia Comput. Sci. 2018, 140, 298–305. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Zhu, W.; Sheng, Y.; Beroza, G.C. CRED: A Deep Residual Network of Convolutional and Recurrent Units for Earthquake Signal Detection. Sci. Rep. 2019, 9, 10267. [Google Scholar] [CrossRef]
- Wang, T.; Bian, Y.; Zhang, Y.; Hou, X. Classification of earthquakes, explosions and mining-induced earthquakes based on XGBoost algorithm. Comput. Geosci. 2023, 170, 105242. [Google Scholar] [CrossRef]
- Zainab, T.; Karstens, J.; Landsiedel, O. LightEQ: On-Device Earthquake Detection with Embedded Machine Learning. In Proceedings of the ACM International Conference Proceeding Series, San Antonio, TX, USA, 9–12 May 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 130–143. [Google Scholar]
- Agathos, L.; Avgoustis, A.; Avgoustis, N.; Vlachos, I.; Karydis, I.; Avlonitis, M. Identifying Earthquakes in Low-Cost Sensor Signals Contaminated with Vehicular Noise. Appl. Sci. 2023, 13, 10884. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, P.; Liu, J.; Wang, M.; Wan, J. LCANet: Lightweight Context-Aware Attention Networks for Earthquake Detection and Phase-Picking on IoT Edge Devices. IEEE Syst. J. 2022, 16, 4024–4035. [Google Scholar] [CrossRef]
- Lim, J.; Jung, S.; JeGal, C.; Jung, G.; Yoo, J.H.; Gahm, J.K.; Song, G. LEQNet: Light Earthquake Deep Neural Network for Earthquake Detection and Phase Picking. Front. Earth Sci. 2022, 10, 848237. [Google Scholar] [CrossRef]
- Zhu, W.; Beroza, G.C. PhaseNet: A deep-neural-network-based seismic arrival-time picking method. Geophys. J. Int. 2019, 216, 261–273. [Google Scholar] [CrossRef]
- Choi, S.; Lee, B.; Kim, J.; Jung, H. Deep-Learning-Based Seismic-Signal P-Wave First-Arrival Picking Detection Using Spectrogram Images. Electronics 2024, 13, 229. [Google Scholar] [CrossRef]
- Sugondo, R.A.; Machbub, C. P-Wave detection using deep learning in time and frequency domain for imbalanced dataset. Heliyon 2021, 7, e08605. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Hao, M.; Cui, Z. A High-Resolution Aftershock Catalog for the 2014 Ms 6.5 Ludian (China) Earthquake Using Deep Learning Methods. Appl. Sci. 2024, 14, 1997. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Wu, R.T.; Liang, C.W.; Kuo, C.H.; Lin, C.M. Peak ground acceleration estimation using P-wave parameters and horizontal-to-vertical spectral ratios. Terr. Atmos. Ocean. Sci. 2020, 31, 1–8. [Google Scholar] [CrossRef]
- Mandal, P.; Mandal, P. Peak ground acceleration prediction using supervised machine learning algorithm for the seismically hazardous Kachchh rift zone, Gujarat, India. Nat. Hazards 2024, 120, 1821–1840. [Google Scholar] [CrossRef]
- Somala, S.N.; Chanda, S.; Alhamaydeh, M.; Mangalathu, S. Explainable XGBoost-SHAP Machine-Learning Model for Prediction of Ground Motion Duration in New Zealand. Nat. Hazards Rev. 2024, 25. [Google Scholar] [CrossRef]
- Khosravikia, F.; Clayton, P. Machine learning in ground motion prediction. Comput. Geosci. 2021, 148, 104700. [Google Scholar] [CrossRef]
- Joshi, A.; Vishnu, C.; Mohan, C.K.; Raman, B. Application of XGBoost model for early prediction of earthquake magnitude from waveform data. J. Earth Syst. Sci. 2024, 133, 5. [Google Scholar] [CrossRef]
- Song, J.; Zhu, J.; Li, S. MEANet: Magnitude Estimation Via Physics-based Features Time Series, an Attention Mechanism, and Neural Networks. Geophysics 2022, 88, V33–V43. [Google Scholar] [CrossRef]
- Jin, Y.; Kim, G.; Ko, H. Classification and Magnitude Estimation of Global and Local Seismic Events Using Conformer and Low-Rank Adaptation Fine-Tuning. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar]
- Joshi, A.; Vedium, N.R.; Raman, B. DFTQuake: Tripartite Fourier attention and dendrite network for real-time early prediction of earthquake magnitude and peak ground acceleration. Eng. Appl. Artif. Intell. 2025, 144, 110077. [Google Scholar]
- Li, H.; Liu, C.; Wang, P.; Xiong, W.; Xu, X. Efficient GPU-accelerated seismic wave propagation simulations for nuclear structural safety assessment. Comput. Methods Appl. Mech. Eng. 2024, 415, 116305. [Google Scholar]
- Xu, J.; Wang, Y.; Zhang, T.; Liu, R. A spatio-temporal model for real-time casualty estimation in earthquake-affected urban areas. Nat. Hazards 2025, 110, 203–221. [Google Scholar]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Int. J. Surg. 2021, 88, 105906. [Google Scholar]
- Mousavi, S.M.; Sheng, Y.; Zhu, W.; Beroza, G.C. Stanford Earthquake Dataset (STEAD): A Global Data Set of Seismic Signals for AI. IEEE Access 2019, 7, 179464–179476. [Google Scholar]
- Michelini, A.; Cianetti, S.; Gaviano, S.; Giunchi, C.; Jozinović, D.; Lauciani, V. INSTANCE-the Italian seismic dataset for machine learning. Earth Syst. Sci. Data 2021, 13, 5509–5544. [Google Scholar]
- Zhu, J.; Li, S.; Song, J. Magnitude Estimation for Earthquake Early Warning with Multiple Parameter Inputs and a Support Vector Machine. Seismol. Res. Lett. 2022, 93, 126–136. [Google Scholar]
- Wang, Y.; Li, X.; Wang, Z.; Liu, J. Deep learning for magnitude prediction in earthquake early warning. Data Driven Model. 2023, 123, 164–173. [Google Scholar] [CrossRef]
- Quinteros-Cartaya, C.; Köhler, J.; Li, W.; Faber, J.; Srivastava, N. Exploring a CNN model for earthquake magnitude estimation using HR-GNSS data. J. S. Am. Earth Sci. 2024, 136, 104815. [Google Scholar] [CrossRef]
- Münchmeyer, J.; Bindi, D.; Sippl, C.; Leser, U.; Tilmann, F. Low uncertainty multifeature magnitude estimation with 3-D corrections and boosting regression tree: Application to North Chile. Geophys. J. Int. 2020, 220, 142–159. [Google Scholar] [CrossRef]
- Kuang, W.; Yuan, C.; Zhang, J. Network-based earthquake magnitude determination via deep learning. Seismol. Res. Lett. 2021, 92, 2245–2254. [Google Scholar] [CrossRef]
- Joshi, A.; Raman, B.; Mohan, C.K. An integrated approach for prediction of magnitude using deep learning techniques. Neural Comput. Appl. 2024, 36, 16991–17006. [Google Scholar] [CrossRef]
- Münchmeyer, J.; Bindi, D.; Leser, U.; Tilmann, F. Earthquake magnitude and location estimation from real time seismic waveforms with a transformer network. Geophys. J. Int. 2021, 226, 1086–1104. [Google Scholar] [CrossRef]
- Chakraborty, M.; Li, W.; Faber, J.; Rümpker, G.; Stoecker, H.; Srivastava, N. A study on the effect of input data length on a deep-learning-based magnitude classifier. Solid Earth 2022, 13, 1721–1729. [Google Scholar]
- Ristea, N.C.; Radoi, A. Complex Neural Networks for Estimating Epicentral Distance, Depth, and Magnitude of Seismic Waves. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Joshi, A.; Vishnu, C.; Mohan, C.K. Early detection of earthquake magnitude based on stacked ensemble model. J. Asian Earth Sci. X 2022, 8, 100122. [Google Scholar] [CrossRef]
- Cofre, A.; Marin, M.; Pino, O.V.; Galleguillos, N.; Riquelme, S.; Barrientos, S.; Yoma, N.B. End-to-End LSTM-Based Earthquake Magnitude Estimation with a Single Station. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Zhang, H. EQGraphNet: Advancing single-station earthquake magnitude estimation via deep graph networks with residual connections. Artif. Intell. Geosci. 2024, 5, 100089. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, Y.; Liu, H.; Jiao, C.; Li, S.; Fan, T.; Wei, Y.; Song, J. Rapid Earthquake Magnitude Classification Using Single Station Data Based on the Machine Learning. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Yoon, D.; Li, Y.; Ku, B.; Ko, H. Estimation of Magnitude and Epicentral Distance From Seismic Waves Using Deeper CRNN. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3000305. [Google Scholar]
- Shakeel, M.; Nishida, K.; Itoyama, K.; Nakadai, K. 3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification. Appl. Sci. 2022, 12, 2195. [Google Scholar] [CrossRef]
- Ren, T.; Liu, X.; Chen, H.; Dimirovski, G.M.; Meng, F.; Wang, P.; Zhong, Z.; Ma, Y. Seismic severity estimation using convolutional neural network for earthquake early warning. Geophys. J. Int. 2023, 234, 1355–1362. [Google Scholar]
- Dybing, S.N.; Yeck, W.L.; Cole, H.M.; Melgar, D. Rapid Estimation of Single-Station Earthquake Magnitudes with Machine Learning on a Global Scale. Bull. Seismol. Soc. Am. 2024, 114, 1523–1538. [Google Scholar]
- Meng, F.; Ren, T.; Liu, Z.; Zhong, Z. Toward earthquake early warning: A convolutional neural network for rapid earthquake magnitude estimation. Artif. Intell. Geosci. 2023, 4, 39–46. [Google Scholar] [CrossRef]
- Hou, B.; Zhou, Y.; Li, S.; Wei, Y.; Song, J. Real-time earthquake magnitude estimation via a deep learning network based on waveform and text mixed modal. Earth Planets Space 2024, 76, 1. [Google Scholar]
- Chanda, S.; Somala, S.N. Single-Component/Single-Station–Based Machine Learning for Estimating Magnitude and Location of an Earthquake: A Support Vector Machine Approach. Pure Appl. Geophys. 2021, 178, 1959–1976. [Google Scholar]
- Zhu, J.; Li, S.; Ma, Q.; He, B.; Song, J. Support Vector Machine-Based Rapid Magnitude Estimation Using Transfer Learning for the Sichuan-Yunnan Region, China. Bull. Seismol. Soc. Am. 2022, 112, 894–904. [Google Scholar]
- Joshi, A.; Raman, B.; Mohan, C.K. Real-time earthquake magnitude prediction using designed machine learning ensemble trained on real and CTGAN generated synthetic data. Geod. Geodyn. 2025, 17, 18–29. [Google Scholar] [CrossRef]
- Mousavi, S.; Ellsworth, W.; Zhu, W.; Chuang, L.; Beroza, G. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar]
- Zhou, Y.; Yue, H.; Zhou, S.; Kong, Q. Hybrid event detection and phase-picking algorithm using convolutional and recurrent neural networks. Seismol. Res. Lett. 2019, 90, 1079–1087. [Google Scholar]
- Zhu, L.; Peng, Z.; McClellan, J.; Li, C.; Yao, D.; Li, Z.; Fang, L. Deep learning for seismic phase detection and picking in the aftershock zone of 2008 Mw7.9 Wenchuan Earthquake. Phys. Earth Planet. Inter. 2019, 293, 106261. [Google Scholar]
- Allen, R.V. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar]
- Lomax, A.; Michelini, A.; Jozinović, D. An Investigation of Rapid Earthquake Characterization Using Single-Station Waveforms and a Convolutional Neural Network. Seismol. Res. Lett. 2019, 90, 517–529. [Google Scholar]
- Mousavi, S.M.; Beroza, G.C. Bayesian-Deep-Learning Estimation of Earthquake Location from Single-Station Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8211–8224. [Google Scholar]
- Zollo, A.; Amoroso, O.; Lancieri, M.; Wu, Y.-M.; Kanamori, H. A threshold-based earthquake early warning using dense accelerometer networks. Geophys. J. Int. 2010, 183, 963–974. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4766–4775. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar]
- Holzinger, A.; Langs, G.; Denk, H.; Zatloukal, K.; Müller, H. Causability and explainability of artificial intelligence in medicine. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1312. [Google Scholar]
- Samek, W.; Montavon, G.; Vedaldi, A.; Hansen, L.K.; Müller, K.R. Explainable AI: Interpreting, Explaining and Visualizing Deep Learning. Lect. Notes Comput. Sci. 2019, 11700, 1–8. [Google Scholar]
- Zhang, Q.; Zhu, S.C. Visual Interpretability for Deep Learning: A Survey. Front. Inf. Technol. Electron. Eng. 2018, 19, 27–39. [Google Scholar]
- Howard, J.; Ruder, S. Universal language model fine-tuning for text classification. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (ACL), Melbourne, Australia, 15–20 July 2018; Volume 1, pp. 328–339. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning (ICML), Online, 13–18 July 2020; pp. 1575–1585. [Google Scholar]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Seismic Signal Denoising and Decomposition Using Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9476–9488. [Google Scholar] [CrossRef]
- Cui, X.Z.; Hong, H.P. Use of discrete orthonormal s-transform to simulate earthquake ground motions. Bull. Seismol. Soc. Am. 2020, 110, 565–575. [Google Scholar]
- Zhao, Q.; Rong, M.; Wang, J.; Li, X. An end-to-end multi-task network for early prediction of the instrumental intensity and magnitude in the north–south seismic belt of China. J. Asian Earth Sci. 2024, 276, 106369. [Google Scholar]
- Löberich, E.; Long, M.D. Follow the Trace: Becoming a Seismo-Detective with a Campus-Based Raspberry Shake Seismometer. Seismol. Res. Lett. 2024, 95, 2538–2553. [Google Scholar]
- Zheng, Z.; Wang, J.; Shi, L.; Zhao, S.; Hou, J.; Sun, L.; Dong, L. Generating phone-quality records to train machine learning models for smartphone-based earthquake early warning. J. Seismol. 2022, 26, 439–454. [Google Scholar]
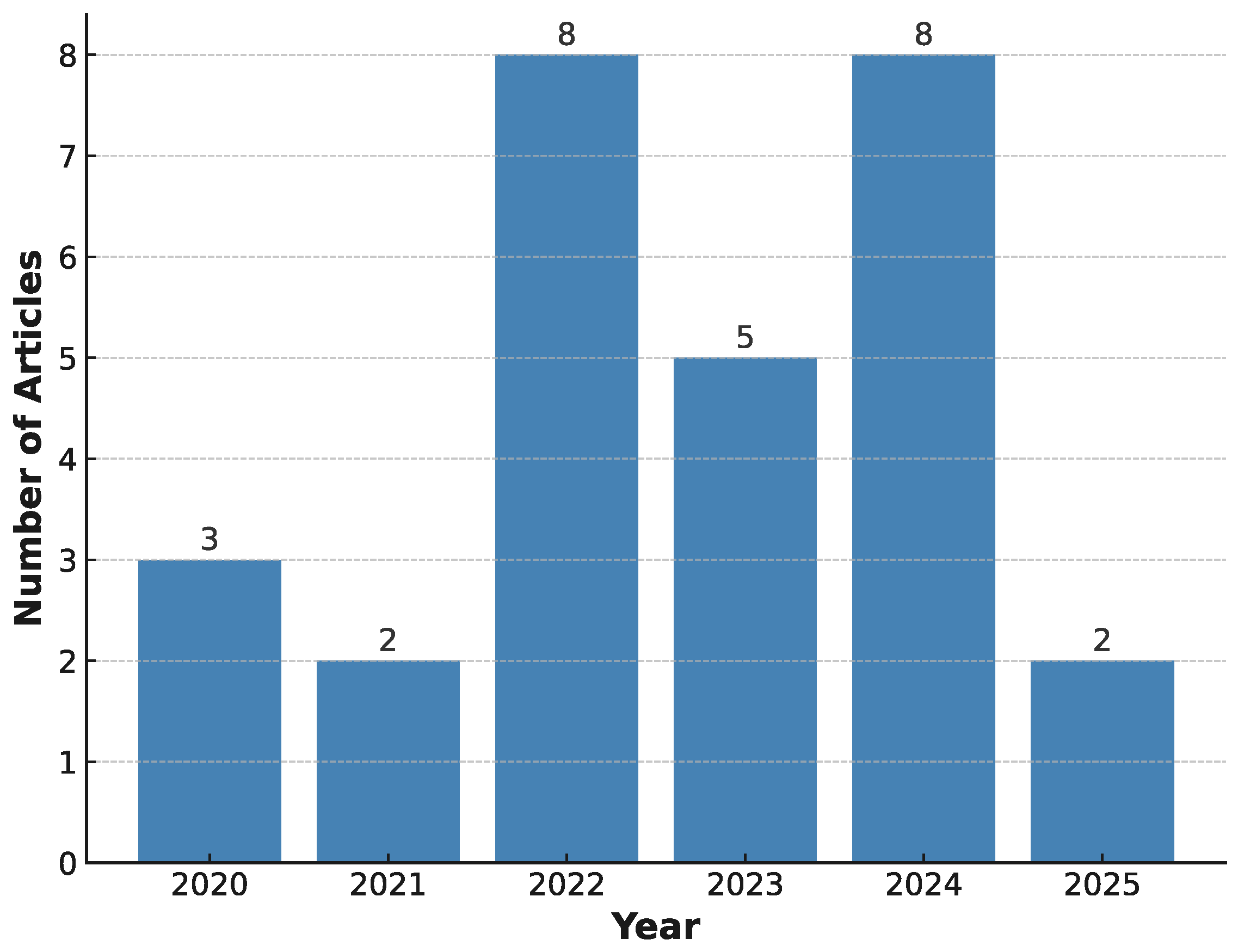


| ML/DL Model | Advantages | Disadvantages | Application in Magnitude Estimation | Real-Time Feasibility |
|---|---|---|---|---|
| Bi-LSTM [7] | Captures long-term dependencies in seismic signals, robust to temporal distortions, effective for time-series prediction. | Higher computational cost than simple RNNs, requires large training datasets, prone to vanishing gradients in long sequences. | Used for direct magnitude regression based on waveform sequences, enhances feature extraction in hybrid architectures. | Efficient if optimized with pruning/quantization. |
| TEAM-LM [46] | Captures global dependencies, highly parallelizable, effective in handling large datasets. | High memory consumption, complex architecture, requires extensive pre-training. | Optimized for fast magnitude estimation, potential in regional/global earthquake monitoring. | Requires substantial GPU resources. LoRA fine-tuning improves feasibility. |
| MEANet [32] | Fast feature extraction, robust to noise, minimal manual preprocessing. | Limited to spatial features, lacks the ability to capture temporal dependencies. | Designed for rapid magnitude estimation from the initial P-wave signals, with potential applications in EEW. | Demonstrates high-speed processing, but has potential for EEW applications. |
| SVM-M [40] | Works well with small datasets, interpretable, effective for binary magnitude classification. | Scalability issues with large datasets, less effective in highly non-linear relationships. | Applied in magnitude classification rather than direct regression. | Provides a rapid initial estimate and can guide early response decisions. |
| MagNet [44] | Reduces noise through deep convolutions, and generates probabilistic magnitude estimates. | Requires large labeled datasets, sensitive to data distribution changes. | Used in probabilistic magnitude estimation and uncertainty quantification. | Deployable in real-time but requires fine-tuning for regional variations. |
| MCFrame [52] | Combines CNN feature extraction with RNN for temporal dependencies. | High computational cost, difficult to fine-tune hyperparameters. | Used in event-based magnitude classification and real-time seismic monitoring. | Requires optimizations for real-time use, but has potential for EEW applications. |
| EEWPEnsembleStack [49] | Combines multiple models to reduce bias and variance; improves accuracy. | Computationally expensive; requires careful feature engineering/hyperparameter tuning. | Reduces uncertainty in magnitude estimation, used in multi-source seismic data fusion. | Requires substantial processing power, limiting real-time deployment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro-Rodríguez, A.; Castro-Artola, O.A.; García-Guerrero, E.E.; Aguirre-Castro, O.A.; Tamayo-Pérez, U.J.; López-Mercado, C.A.; Inzunza-Gonzalez, E. Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review. Appl. Sci. 2025, 15, 3492. https://doi.org/10.3390/app15073492
Navarro-Rodríguez A, Castro-Artola OA, García-Guerrero EE, Aguirre-Castro OA, Tamayo-Pérez UJ, López-Mercado CA, Inzunza-Gonzalez E. Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review. Applied Sciences. 2025; 15(7):3492. https://doi.org/10.3390/app15073492
Chicago/Turabian StyleNavarro-Rodríguez, Andrés, Oscar Alberto Castro-Artola, Enrique Efrén García-Guerrero, Oscar Adrian Aguirre-Castro, Ulises Jesús Tamayo-Pérez, César Alberto López-Mercado, and Everardo Inzunza-Gonzalez. 2025. "Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review" Applied Sciences 15, no. 7: 3492. https://doi.org/10.3390/app15073492
APA StyleNavarro-Rodríguez, A., Castro-Artola, O. A., García-Guerrero, E. E., Aguirre-Castro, O. A., Tamayo-Pérez, U. J., López-Mercado, C. A., & Inzunza-Gonzalez, E. (2025). Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review. Applied Sciences, 15(7), 3492. https://doi.org/10.3390/app15073492









