Next Article in Journal
Sewer Cleaning Robot: A Visually Assisted Cleaning Robot for Sewers
Next Article in Special Issue
Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review
Previous Article in Journal
Camera-Based Continuous Heart and Respiration Rate Monitoring in the ICU
Previous Article in Special Issue
Application of Machine Learning Models to Multi-Parameter Maximum Magnitude Prediction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 7
10.3390/app15073424
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Microseismic Phase Picking and Polarity Determination Model Based on the Earthquake Transformer

by
Ling Peng
1,2,
Lei Li
1,2,3,* and
Xiaobao Zeng
1,2
1
Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Ministry of Education, Changsha 410083, China
2
School of Geosciences and Info–Physics, Central South University, Changsha 410083, China
3
Department of Geophysics, Stanford University, Stanford, CA 94305, USA
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(7), 3424; https://doi.org/10.3390/app15073424
Submission received: 4 March 2025 / Revised: 17 March 2025 / Accepted: 18 March 2025 / Published: 21 March 2025
(This article belongs to the Special Issue Machine Learning Applications in Seismology: 2nd Edition)
Browse Figures
Versions Notes

Abstract

Phase arrival times and polarities provide essential kinematic constraints for and dynamic insights into seismic sources, respectively. This information serves as fundamental data in seismological study. For microseismic events with smaller magnitudes, reliable phase picking and polarity determination are even more challenging but play a crucial role in source location and focal mechanism inversion. This study innovatively proposes a deep learning model suitable for simultaneous phase picking and polarity determination with continuous microseismic waveforms. Building upon the Earthquake Transformer (EQT) model, we implemented structural improvements through four distinct decoders specifically designed for three tasks of P-wave picking, S-wave picking, and P-wave first-motion polarity determination and named the model EQT-Plus (EQTP). Notably, the polarity determination task was decomposed into two independent decoders to enhance the learning of polarity characteristics. Through training on a northern California dataset and testing on microseismic events (Md < 3) in the Geysers region, the results demonstrate that the EQTP model achieves superior performance in both phase picking and polarity determination compared to the PhaseNet+ model. It not only provides accurate phase picking but also shows higher consistency with manual picking results in polarity determination. We further validated the good generalization ability of the model with the DiTing dataset from China. This study not only advances the adaptation of the Transformer model in seismology but also reliably delivers fundamental information essential for refined microseismic inversion, offering an alternative and advanced tool for the seismological community.

1. Introduction

Microseismic monitoring technology is a critical geophysical tool for both geo-energy exploitation, subsurface fault/fracture characterization, and seismic hazard assessment [1]. Microseismic activity exhibits significant correlations with various geodynamic processes, particularly in unconventional hydrocarbon and geothermal reservoir development, where hydraulic stimulation involves rock fracturing and abundant microseismic activities [2]. By utilizing continuous waveform data acquired from dense monitoring networks, combined with advanced source parameter inversion techniques, we can accurately characterize the tempo-spatial distribution of subsurface mechanical parameters and interpret the evolution of fracture networks. These critical geophysical insights provide essential guidance for optimizing geo-energy development strategies and assessing engineering safety. Phase picking provides essential kinematic constraints through precise identification of P/S-wave arrivals, while first-motion polarity determination offers dynamic insights into rupture process and stress states [3]. The two components are fundamental inputs for subsequent source parameter inversion, including the seismic source location, source mechanism analysis, and seismic hazard assessment. More precise phase picking and polarity determination allow more reliable source parameter inversion, facilitating the rigorous characterization of source physics and the underlying mechanisms governing fracture dynamics [4,5].
During the past decades, significant progress has been made by introducing methods for phase picking such as the Short-Term Average to Long-Term Average ratio (STA/LTA) and Akaike Information Criterion (AIC) methods based on waveform statistical information [6,7], as well as methods for P-wave polarity determination using the amplitude envelope ratio, Bayesian algorithms, and the cross-correlation method [8,9]. For example, the PhasePApy software package integrates an AIC criterion for initial picking and determines polarity based on seismic amplitude and noise levels, calculating the polarity uncertainties using the root mean square errors of feature functions [10]. PhasePApy demonstrates notable computational efficiency, ensuring accuracy while significantly reducing the processing time.
However, traditional methods for phase picking and polarity determination encounter significant limitations as seismic datasets continue to grow in scale and complexity [11]. Firstly, the exponential increase in data volume, especially small-magnitude and low signal-to-noise ratio (SNR) microearthquakes, imposes substantial computational burdens, severely impairing the operational efficiency of statistical-based initial picking methods and making it increasingly challenging to meet real-time processing requirements. Secondly, the intensification of complex seismic wavefield characteristics in large datasets exposes the inherent adaptability weaknesses of conventional approaches, particularly when dealing with seismic data under intricate geological conditions. Furthermore, local variations in subsurface geological properties, such as hydraulic stimulation, mining, and other similar industrial activities, significantly affect seismic wave propagation patterns, and these subtle, yet critical, changes yield additional challenges for reliable phase picking and polarity determination.
In recent years, artificial intelligence (AI) technologies have emerged as transformative tools in seismology, leveraging their powerful learning capabilities to address complex challenges [12,13,14,15]. Among these, neural networks demonstrate remarkable proficiency in automatically extracting intricate features from massive and complex seismic datasets [16]. Specifically, convolutional neural networks (CNNs), as one of the most prevalent deep learning architectures, have gained widespread adoption in phase picking and polarity determination [17,18,19,20,21,22,23]. End-to-end neural networks handle entire tasks as a single unit, mapping directly from raw inputs to final outputs without explicitly separating and designing intermediate modules, significantly reducing the system complexity and design challenges. The U-Net network, a typical end-to-end model, has achieved tremendous success in image segmentation, offering efficient and robust solutions for phase picking in seismic data [24]. Furthermore, the PhaseNet model has established itself as a benchmark in seismic data processing, while its enhanced version, PhaseNet+ (PN+), extends its capabilities by incorporating polarity determination, enabling comprehensive multi-task processing of seismic data [25]. Complementing these developments, the encoder–decoder structure offers flexible handling of variable-length input and output sequences. The encoder dynamically extracts feature representations from inputs of varying lengths, while the decoder generates appropriately sized output sequences tailored to specific task requirements [26]. The Transformer model, a pioneering deep learning architecture for sequence data processing, has demonstrated exceptional capabilities in natural language processing tasks [27]. Its adaptation to seismic waveform analysis has led to the development of the Earthquake Transformer (EQT) model, which integrates global and local attention mechanisms to efficiently manage multi-task seismic data processing while achieving robust accuracy in practical applications [28]. To address challenges in low signal-to-noise scenarios, the Siamese Earthquake Transformer (S-EqT) leverages the strengths of Siamese Networks and Transformer architectures, significantly enhancing the model’s ability to discern low SNR seismic signals [29]. Further innovations include DiTingMotion, a deep learning model designed for polarity classification, which incorporates holistic edge detection techniques to achieve superior performance and unique design advancements [30]. Additionally, the FocMech-Flow workflow employs deep learning to automate P-wave polarity identification and source mechanism inversion, as demonstrated in the study of the 2021 Yangbi earthquake sequence, where it achieved an impressive accuracy rate of 98.49% in P-wave polarity determination [31]. Meanwhile, EQPolarity, a specialized deep learning method, has been developed for P-wave polarity determination and has shown remarkable efficacy in seismic source mechanism inversion, highlighting its potential for broader applications [32]. Beyond supervised approaches, unsupervised learning—a distinct subclass of machine learning—has emerged as a powerful tool for phase picking and polarity determination [33,34,35]. By leveraging clustering, dimensionality reduction, and other advanced techniques, unsupervised methods can uncover latent patterns in massive seismic waveform datasets without relying on extensive labeled data. This approach enables the automatic detection of P-wave characteristics, precise picking of arrival times, and the effective determination of P-wave polarities, thereby elevating seismic monitoring and analysis to unprecedented levels of accuracy and efficiency.
In the realm of microseismic monitoring and analysis, a persistent challenge has been the concurrent treatment of phase picking and polarity determination. Most existing approaches handle the two tasks separately, which not only escalates the complexity of the analytical process but also potentially undermines the accuracy and reliability of the final results due to insufficient information exchange between these two critical tasks. To address this issue, an attention mechanism-based multi-task neural network has been introduced to independently processes waveform data to predict both phase picking and polarities probabilities while simultaneously inferring source mechanisms across various scales [36]. This sophisticated model has exhibited robust performance and exceptional adaptability in multi-regional tests, proving its efficacy in real-time earthquake monitoring systems.
Building on these advancements and leveraging the cutting-edge EQT architecture, our study introduces an enhanced variant: the EQT-Plus (EQTP) model. This novel development aims to seamlessly integrate and unify the outputs of phase picking and P-wave polarity determination. Considering the continuous, massive, and complex data characteristic of practical microseismic monitoring scenarios, the EQTP model is specifically designed to perform continuous, stable, and precise analysis of continuous waveforms. This enhancement not only streamlines the process but also substantially improves both the efficiency and accuracy of subsequent earthquake analysis and source parameter inversion.

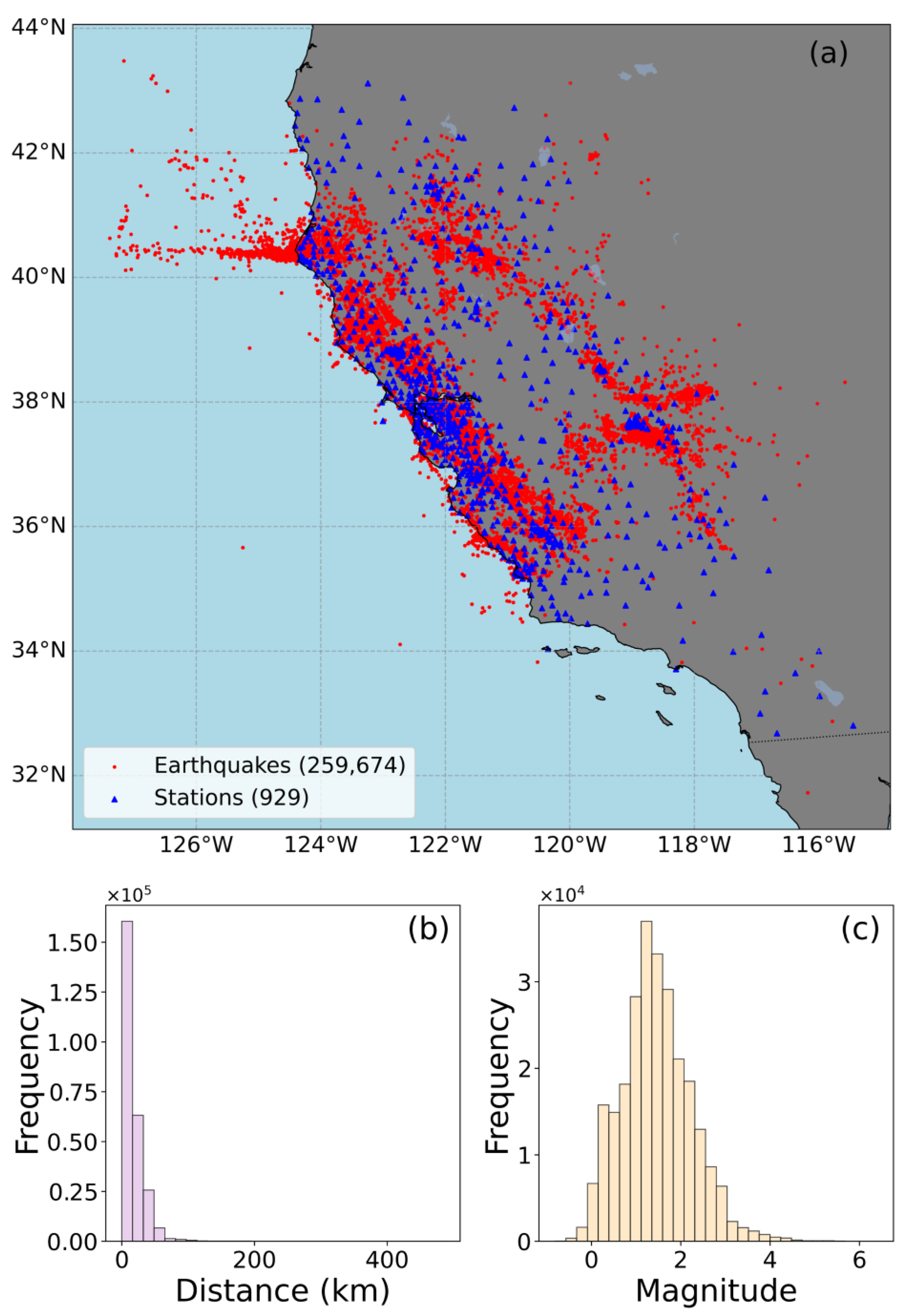
2. Data

The Northern California Earthquake Data Center (NCEDC) serves as a permanent archive and real-time data distribution hub for a unique and comprehensive collection of seismic and geophysical datasets covering northern and central California [37]. Since 1984, NCEDC has recorded over 900,000 seismic events, providing event catalogs, parametric information, moment tensors, first-motion mechanisms, and time series data [38].
In this study, 259,674 three-component seismic waveforms recorded by 929 stations in northern and central California between 2019 and 2023 were utilized (Figure 1). The waveform and polarity data were retrieved from the California Earthquake Event Dataset (CEED) [38]. These waveforms have magnitude distributions ranging from −0.81 to 6.4 and epicentral distance distributions from 0 to 480 km, with the majority being less than 50 km. Figure 2 shows the phase picking and polarity labels along with waveforms for an example event from the dataset. Each waveform trace consists of 12,000 sampling points at a 100 Hz sampling rate. The dataset was split into training (181,771), validation (25,967), and testing (51,926) sets following a 7:1:2 ratio.
The Geysers dataset is a microseismic dataset from the Geysers geothermal field in northern California, USA. The Geysers geothermal field has been developed and operated for over 50 years and is the world’s largest steam-dominated geothermal field in terms of power generation. Geothermal extraction activities in this area induce tens of thousands of microseismic events each year. The majority of these events have a duration magnitude (Md) of less than magnitude 1 [37,39,40]. In this study, we downloaded 10-day continuous microseismic waveform data (with a sampling rate of 500 Hz) from the BG network (a total of 37 three-component geophones) from 0:00 on 1 December 2023 to 24:00 on 10 December 2023, through the NCEDC. The continuous seismic waveforms were cropped into 120 s waveform data according to the double-difference earthquake catalog provided on the official NCEDC website (the start time of the waveform has a random shift between 10 and 80 s relative to the origin time for each event). A total of 434 earthquake events were statistically identified, with the magnitude ranging from Md −0.38 to Md 2.75.
In addition, we used the DiTing dataset to validate the generalization ability of the proposed model. The DiTing dataset is a large-scale and high-quality seismological training dataset covering natural earthquake events in mainland China and its neighboring regions from 2013 to 2020 [41]. This dataset includes three-component seismic waveforms for events with magnitudes (e.g., ML, Ms) from 0 to 8, with a sampling rate of 50 Hz and 9000 sampling points per waveform. The DiTing dataset provides key information such as the P-wave arrival time, S-wave arrival time, and P-wave first-motion polarity.

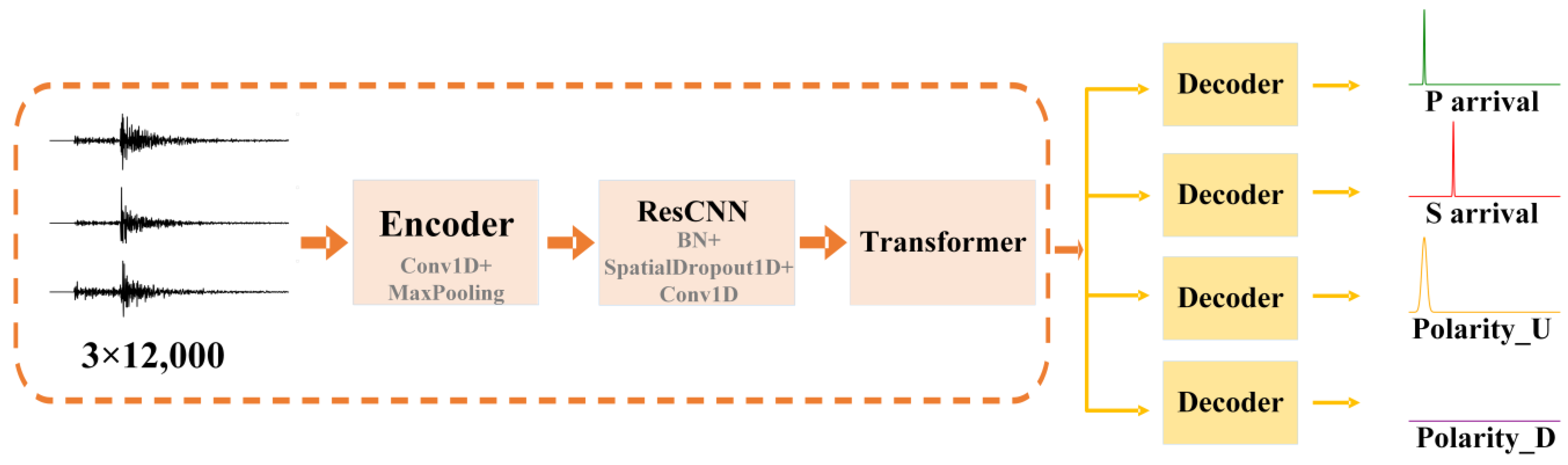
3. Model

3.1. Model Building

Based on the EQT model, this study proposes the EQTP model, which simultaneously performs microseismic phase picking and P-wave first-motion polarity determination. The SeisBench (v0.7) toolbox, an open-source Python (v3.9) toolbox for machine learning in seismology, was used to improve and train the EQTP model for evaluation [42].
The EQTP model removes the event detection task from the original EQT model while adding the P-wave first-motion polarity determination task. The model structure primarily consists of CNN, ResCNN, and two Transformer layers, and it ultimately completes three tasks—P-wave picking, S-wave picking, and P-wave first-motion polarity determination—through four different decoders, as shown in Figure 3. The first-motion polarity determination is divided into two decoders to better learn the characteristics of different polarities. The Transformer serves as the core structure, utilizing a global attention mechanism to focus on global waveform features and a local attention mechanism in the phase task decoder to focus on seismic phases.
When processing long sequential data, BiLSTM layers often struggle with gradient vanishing, limiting their ability to accurately capture long-term dependencies and identify trends. Additionally, the inherently sequential processing nature makes training time-consuming [43,44]. In contrast, the Transformer model, with its self-attention mechanism, excels at capturing long-range dependencies without relying on sequential processing. This allows it to handle complex time-series data more effectively while leveraging parallel computing to significantly reduce the training time and enhance the overall efficiency. These advantages make the Transformer highly adaptable and well-suited for various sequential data processing tasks [45,46,47]. By removing the BiLSTM layers from EQT, the computational complexity is reduced, mitigating gradient vanishing or explosion issues and making the training process more stable and efficient. The training time of the model was reduced from 50 h to 40 h after removing the BiLSTM layers.

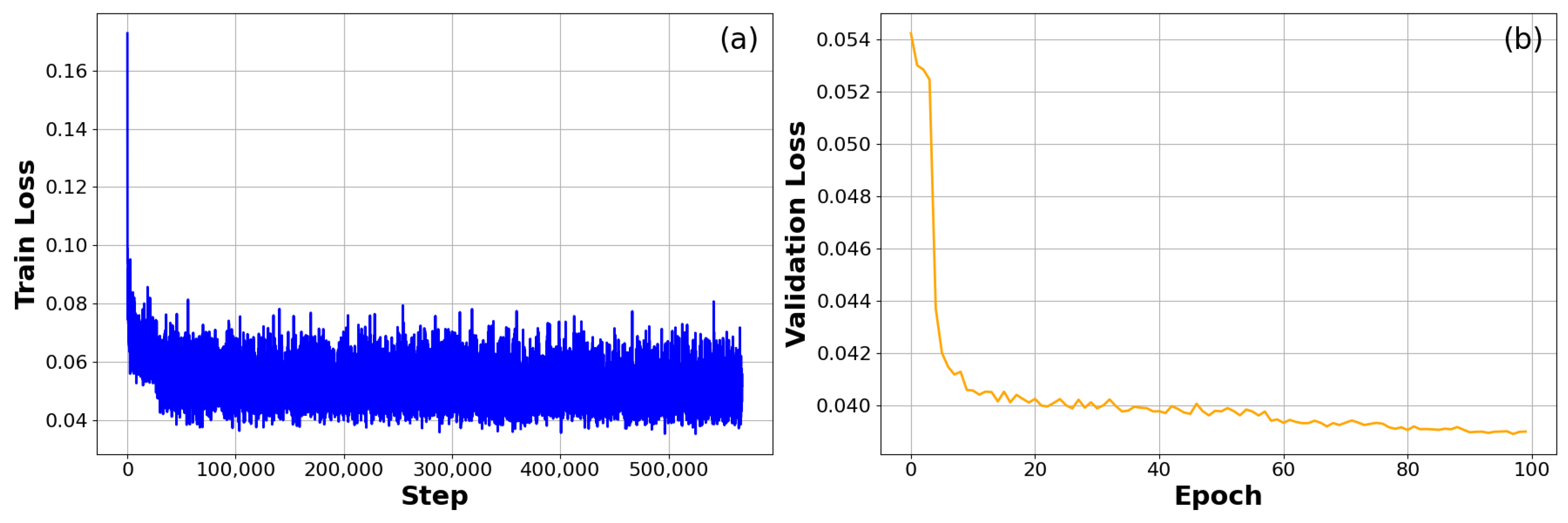
3.2. Model Training

To ensure the optimal performance of the model, several crucial parameters were meticulously tuned in the training process. The iteration count was set at 100. Through multiple rounds of experimental validation, this configuration allowed the model to converge adequately on the training set. It effectively alleviated both overfitting and underfitting issues, thus attaining excellent generalization capabilities. The batch size was set to 32. This value struck an ideal balance between memory utilization and training stability. It not only ensured the efficacy of each gradient update but also avoided memory overflow problems that could arise from an excessively large batch size. The initial learning rate was set at 0.001, and a learning rate scheduler based on the performance metrics of the validation set was employed. As the training progressed, the learning rate gradually decreased. This enabled the model to converge more precisely in the later stages of training. For the training, an NVIDIA RTX 3060 GPU was utilized. The training loss and validation loss during the training are presented in Figure 4.

4. Results

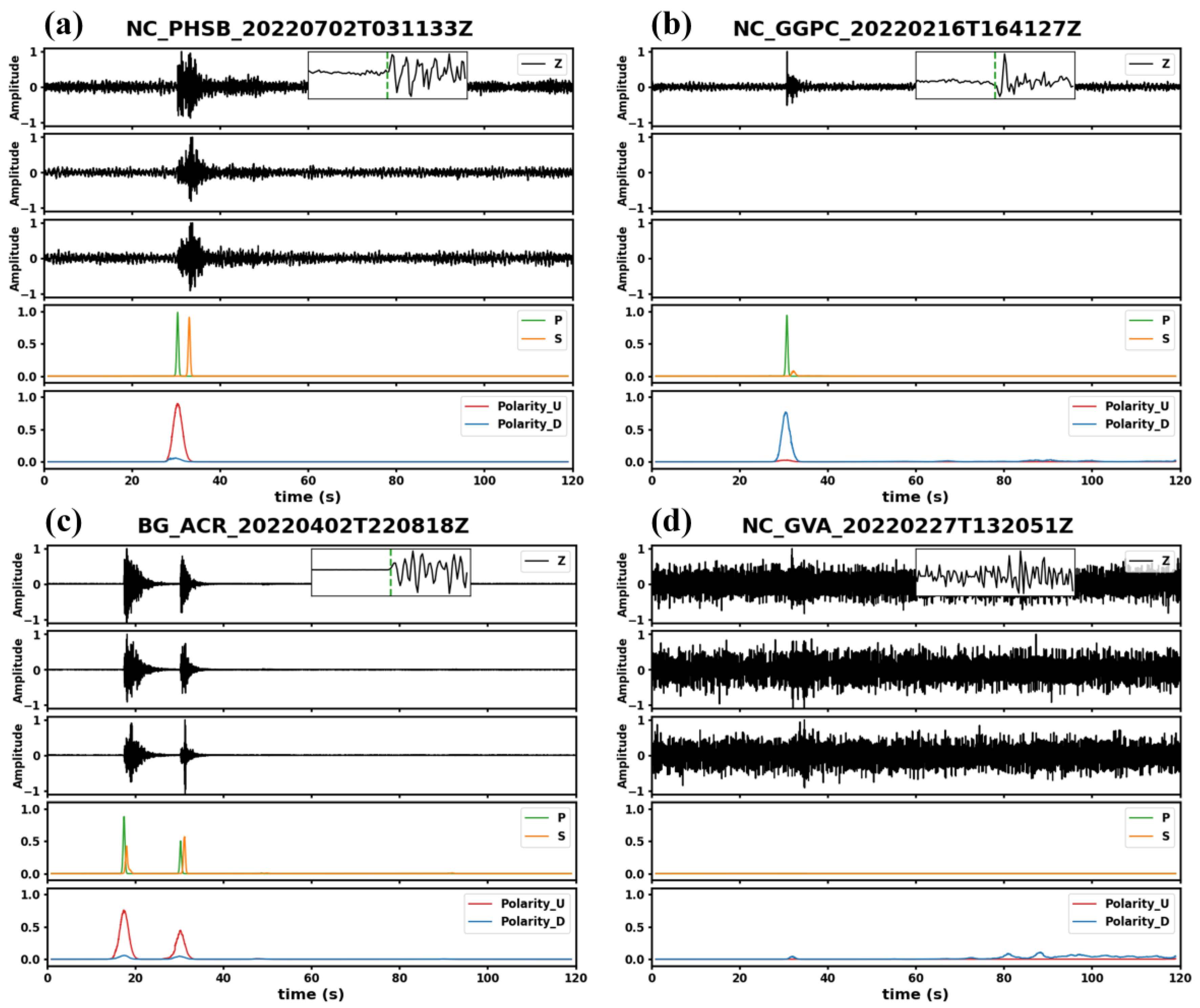
4.1. Test Set Analysis

In the EQT model, the thresholds for event detection and phase picking were set at 0.5 and 0.3, respectively. The OBSTransformer model test further confirmed the effectiveness of these thresholds in the EQT model [48]. Adjusting the thresholds may enhance the model performance to a certain extent for specific datasets, but the improvement would not be significant and generalizable. A lower threshold may increase the number of candidate samples, thereby improving the recall, but can produce a higher false positive rate [49]. Conversely, a higher threshold effectively reduces false positives but may lead to an increase in false negatives. Based on prior research findings, this study aligned with the commonly used choices of the thresholds for phase picking and polarity determination as 0.3. Meanwhile, a pick was judged as a correct pick only if the error was less than 100 sampling points (i.e., 1 s). For polarity determination, an additional threshold of picking error was set at 10 sampling points (i.e., 0.1 s) to filter out the potential polarity uncertainty and bias. Prior to the performance evaluation of the model, the waveform polarity data that did not meet the picking accuracy requirements were excluded. The model performance was quantitatively assessed using a confusion matrix (see Table 1). The classification criterion for the N-pre category is defined as follows: if neither the positive (U-pre) nor the negative (D-pre) polarity probability reaches the predefined polarity determination threshold, the polarity is classified as N (indicating no clear polarity or a noise event).
Figure 5 shows four sample results of the testing dataset. The EQTP model can simultaneously pick the phase arrivals and determine the polarity correctly for both single-event and multi-event waveforms. Through inspection and analysis, most of the waveforms that could not be accurately picked and whose polarities could not be correctly determined mainly originated from extremely low SNRs (Figure 5d). In addition, there were also some waveforms with annotation errors.
F P R = F P F P + T N
F N R = F N F N + T P
In this study, to achieve a quantitative evaluation of the model performance, the false positive rate (FPR) and false negative rate (FNR) were calculated based on the confusion matrix [50], and key evaluation metrics such as the precision, recall, and F1-score were also analyzed. Among them, the precision is closely related to the FPR, and the recall is closely associated with the FNR. As an important metric that comprehensively considers precision and recall, the F1-score can effectively balance the model’s performance in different dimensions. The results show that EQTP performs quite well in seismic phase picking. The evaluation metrics for both P-waves and S-waves are close to 1, with the mean value close to 0 s, and both the standard deviation and the mean absolute error are less than 0.2 s (see Table 2). Although affected by data errors, with the FPR being 12.74% and the FNR being 9.65%, the key indicators of first-arrival polarity determination still exhibit a high level (around 0.9). The polarity determination failure rate (N-pre/Total) is only 0.5%.

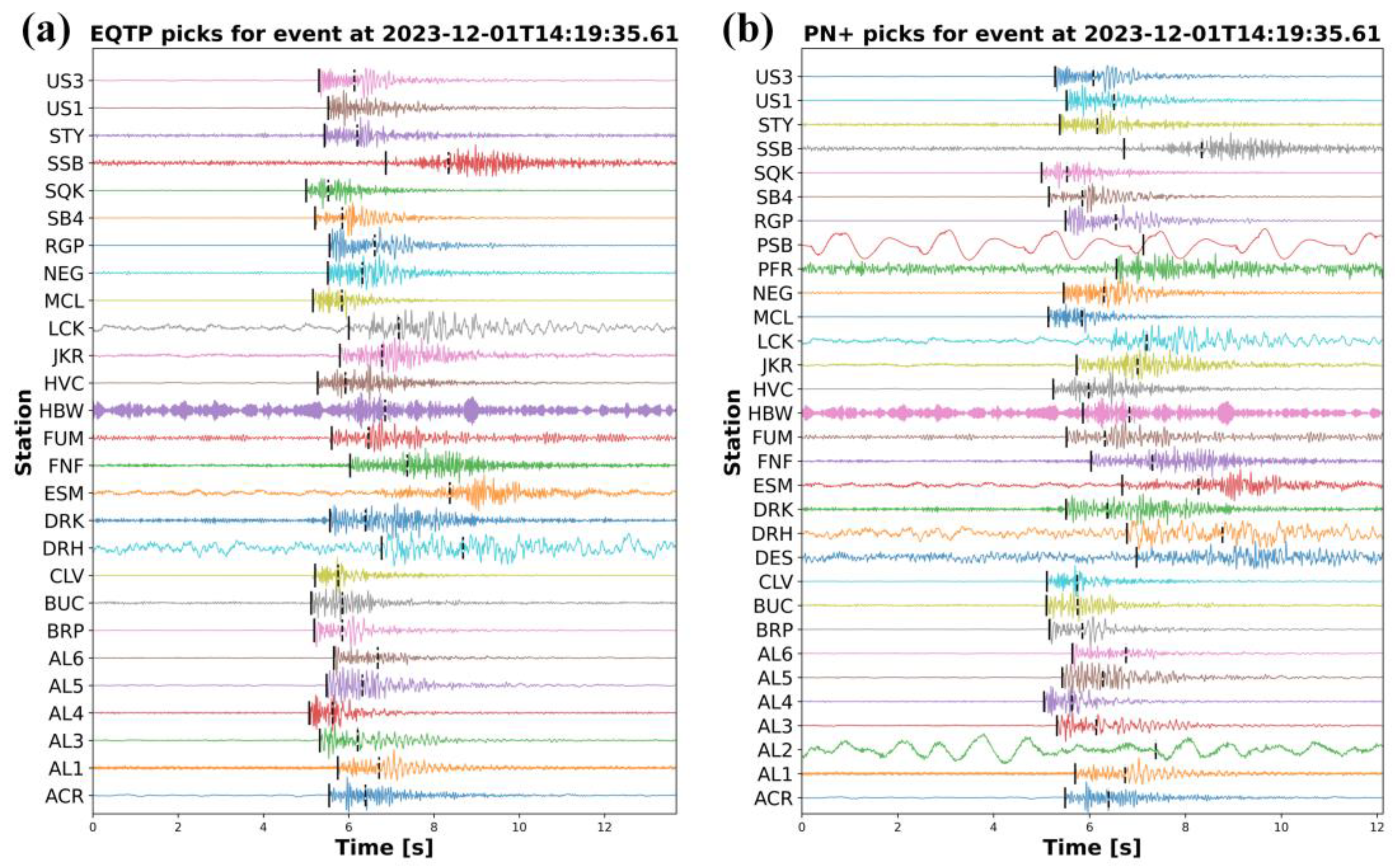
4.2. The Geysers Dataset Analysis

4.2.1. Phase Picking Analysis

The EQTP model was applied to the Geysers dataset for seismic phase picking and first-arrival polarity determination, and the results were verified and analyzed in comparison with those of the PN+ model. Through an experimental test, we set the thresholds for P-wave and S-wave picking of the two methods as 0.5 and 0.3, respectively, and the threshold for polarity picking was set at 0.6 for further analysis. Increasing the threshold for P-wave phase picking is beneficial to the accuracy of polarity determination, and the threshold for polarity determination also exhibits high stability. The microseismic phases were associated and located using GaMMA [51] and then compared with the double-difference location earthquake catalog (Figure 6). The EQTP detected 426 events, with eight missed. Statistical analysis showed that a total of 13,096 valid P-waves and 13,534 valid S-waves were picked, among which the first-arrival polarity was determined 8415 times (accounting for approximately 64%). The PN+ detected 465 events, with 31 events over-detected. Statistical analysis showed that a total of 18,405 valid P-waves and 15,054 valid S-waves were picked, among which the first-arrival polarity was determined 10,047 times (accounting for approximately 54%). Compared with the PN+ model, the EQTP model proposed in this study has more accurate detection, avoiding a large number of incorrect picks (as shown in Figure 7, obvious noise channels such as at the AL2, PSB, and PFR stations were not picked by EQTP). It is worth noting that GaMMA only produced relatively rough absolute locations, which can be further enhanced by, e.g., hypoDD [52] relocation algorithms, which is beyond the scope of the current study.

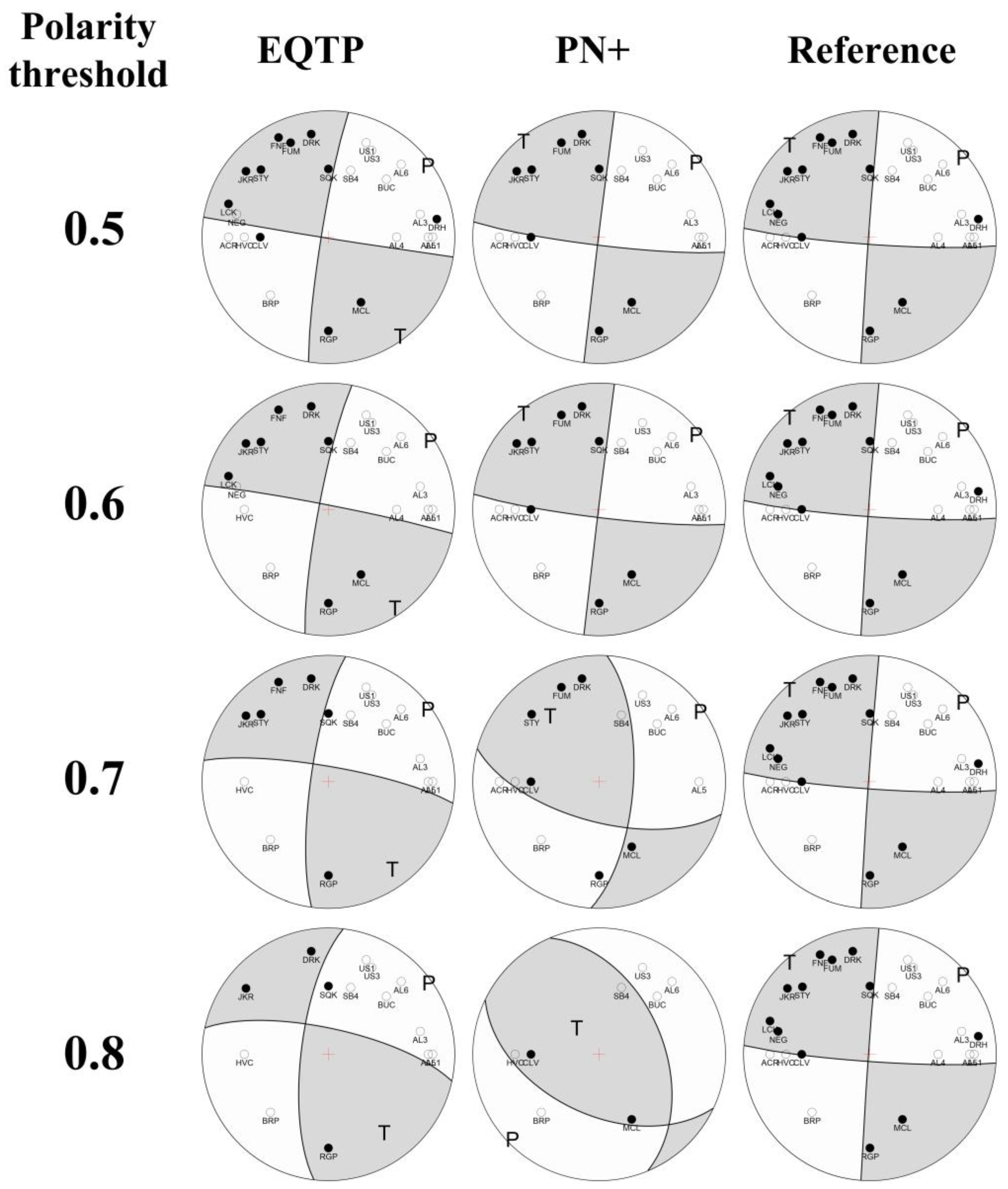
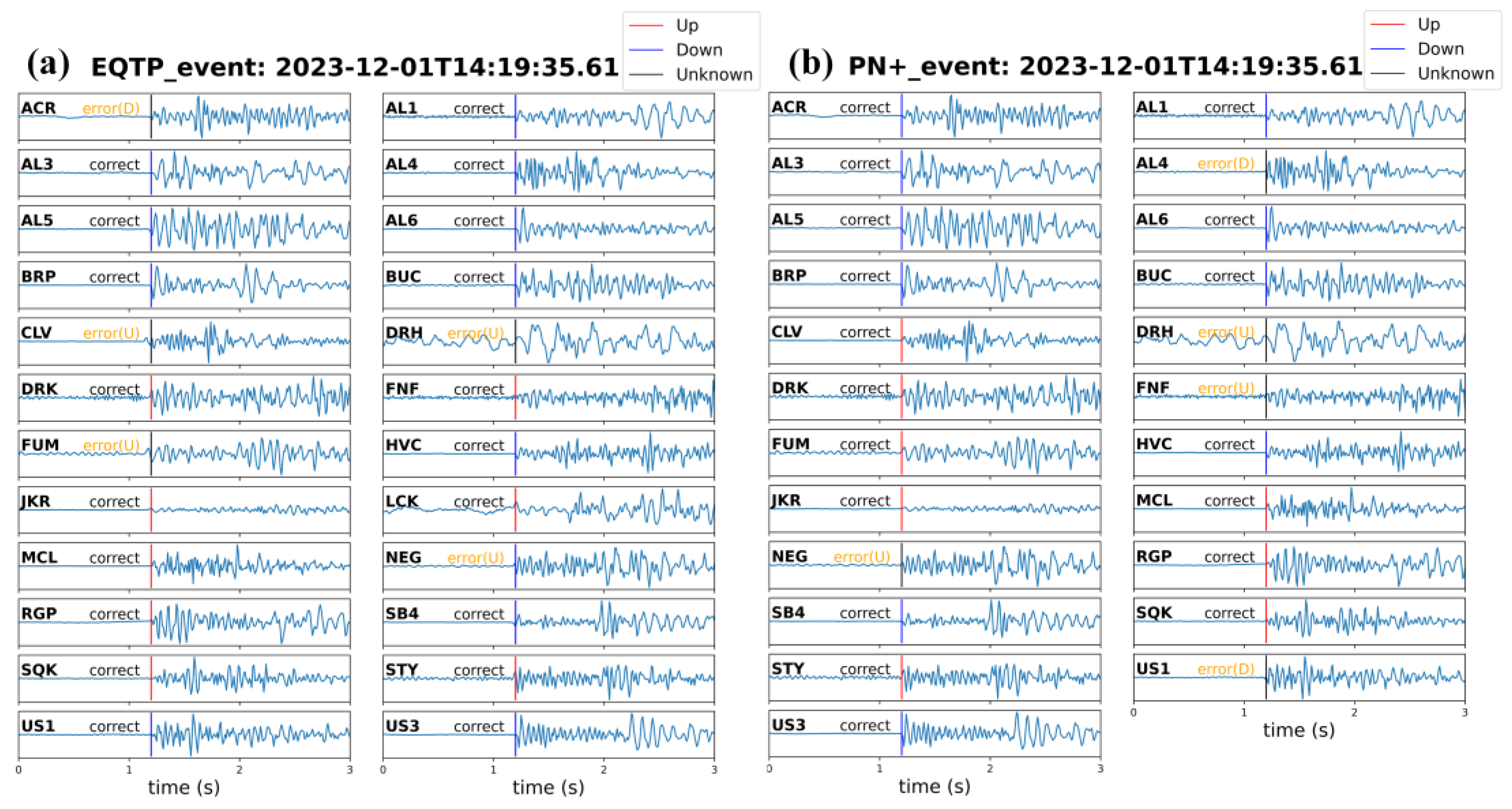
4.2.2. First-Arrival Polarity Determination Analysis

To deeply explore the performance of the EQTP model in first-arrival polarity determination, we selected two representative microseismic events for analysis. They are the event at 14:19:35.61 on 1 December 2023 (magnitude Md 0.82, hereinafter referred to as Event 1) and the event at 08:09:10.97 on 2 December 2023 (magnitude Md 1.27, hereinafter referred to as Event 2). The open-source software package HybridMT v1.6.2 [53] for focal mechanism inversion based on the first-arrival polarity and amplitude of P-waves was used for the two microseismic events. Meanwhile, to accurately verify the impact of the selection of first-arrival polarities with different thresholds on the focal mechanism inversion results, we specifically set four different thresholds of 0.5, 0.6, 0.7, and 0.8 for both the EQTP model and the PN+ model.
For Event 1, when the polarity threshold was set to 0.5 and 0.6, the focal mechanism inversion associated with EQTP showed a higher similarity to the manually-picked results (Figure 8). When the polarity threshold was 0.5, the EQTP model can reserve more stations (AL4, DRH, FNF, LCK, NEG, US1). Additional polarity constraints from the LCK and NEG stations make the focal mechanism associated with EQTP more reliable. As the threshold gradually increased, the number of corresponding stations for both models decreased, and obvious differences began to appear in the inversion results (when the number of stations is small, the constraint on the focal mechanism will be reduced). When the polarity threshold reaches 0.8, although EQTP removed some stations, the impact on the focal mechanism results was still small. However, after PN+ removed some stations, it led to a huge deviation in the focal mechanism. The inversion results of the EQTP model show stronger stability compared with those of the PN+ model. The results corresponding to polarity threshold 0.6 in Figure 9 show that under the same constraints, the EQTP model excluded stations such as ACR, HVC, DRH, and FUM. Most of these stations have interference in the first arrivals, or the waveform has a relatively low SNR.
For Event 2 (as shown in Figure 10), when the polarity threshold gradually increased, the uncertain polarities of some stations in the picking results of EQTP were removed. For stations SSB and AL4, the polarity determination results were consistent with the manual picking results. As the threshold increased, they were excluded; yet, this had a minor impact on the focal mechanism solution. However, the reversed polarity of station FFA was still reversed, which was also consistent with the manually-picked result. There may have been some temporary disturbances at this station. For most stations, the polarity picking results of the two models are relatively close, but EQTP better removes the stations with obvious polarity reversal, which is beneficial to the extended analysis of the full moment tensor inversion. The EQTP model obtained more first-arrival polarity results than the PN+ model. After careful and repeated manual tests, we observed that the EQT inversion demonstrated strong robustness under different polarity determination thresholds. The PN+ model will fail to obtain reliable focal mechanisms when polarities from certain key stations are excluded as the polarity threshold increases [54]. Figure 11 shows the first-arrival polarity results of Event 2 (polarity threshold = 0.6). Both EQTP and PN+ have excluded some stations (HBW, RTB) with low-probability picks. However, PN+ failed to determine the polarity correctly for multiple stations (AL1, AL3, AL5). EQTP also had incorrect polarity determinations for the stations PSB and SRB, mainly due to the noise contamination in the vertical components.

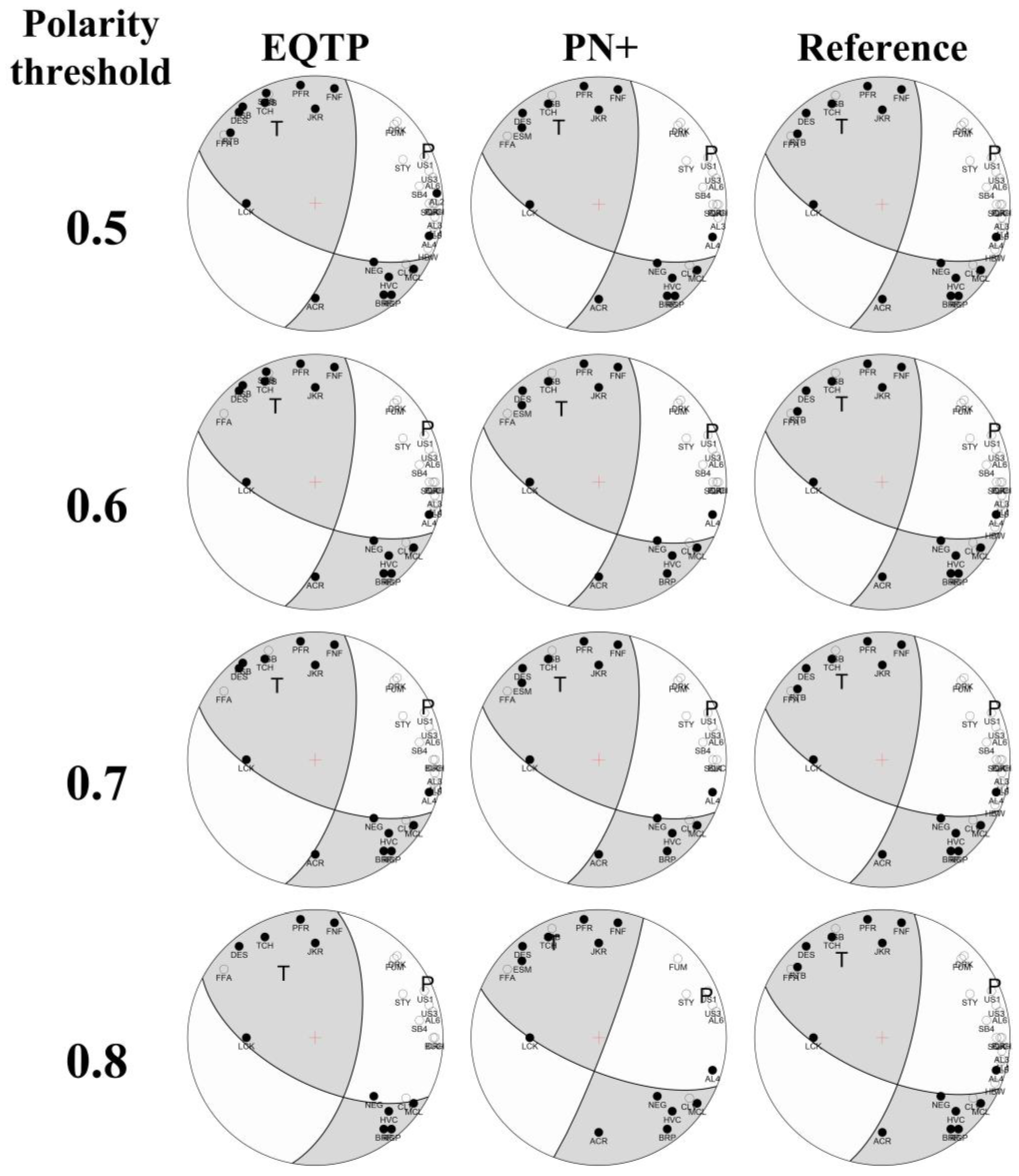
4.3. Generalization Ability Analysis

To further evaluate the generalization capability of the EQTP model across different magnitudes and geological regions, we randomly selected around 67,000 three-component seismic waveforms from the DiTing dataset for analysis. Among them, around 6000 waveforms correspond to earthquakes with magnitudes equal to or greater than 3, while around 61,000 waveforms correspond to earthquakes with magnitudes below 3. From the confusion matrix analysis in Table 3, the EQTP model (values outside the brackets) exhibits a higher accuracy in polarity determination compared to the PN+ model (values in the brackets). Specifically, the FNR of the EQTP model (2.8%) is lower than that of the PN+ model (3.8%), while its FPR (9.6%) is slightly higher than PN+ (7.9%). The determination failure rate of EQTP (0.4%) is significantly lower than that of PN+ (3.1%). From the evaluation metrics in Table 4, the EQTP model demonstrates relatively better overall performance, and most statistical metrics of the EQTP model are superior to those of the PN+ model. The results suggest that the EQTP model exhibits a better generalization ability across difference regions and datasets.

5. Discussion and Conclusions

This study focuses on the challenges of microseismic phase picking and first-motion polarity determination and innovatively proposes the EQTP model. The model adopts a cutting-edge network architecture, enabling it to efficiently process massive amounts of continuous waveform data. Compared with the PN+ model, the EQTP model shows a superior performance for both phase picking and polarity determination and exhibits a better generalization ability across different datasets. Compared with traditional methods, the EQTP model significantly shortens the data processing cycle and can quickly complete the preliminary analysis of massive microseismic events within seconds, producing reliable phase picks and P-wave first-motion polarities. For multi-event waveforms, the traditional binary classification model has difficulty in simultaneously predicting the first-motion polarities corresponding to multiple first arrivals. The EQTP model can not only identify multi-event seismic phases simultaneously but also automatically predict the polarities associated with these phases. The accurate phase picking and polarity determination results from EQTP ensure reliable source parameter inversion, providing a reliable data basis for subsurface reservoir monitoring and seismic hazard assessment.
Data quality is crucial to the performance of the EQTP model. Issues such as noise, missing data, and outliers can significantly impact the accuracy of phase picking and first-motion polarity determination. To address these challenges, future work can focus on developing advanced data preprocessing techniques, such as deep learning-based denoising autoencoders. Additionally, multi-model ensemble picking can be used to enhance dataset quality by integrating results from deep learning models and traditional algorithms. By applying label constraints, abnormal labels can be identified and corrected or removed [48]. This approach improves the quality of training datasets for the EQTP model, enabling it to learn more precise and effective features. Additionally, developing uncertainty quantification methods specifically for polarity classification would help the model better identify low-confidence samples, further improving the precision of polarity determination.
In field applications, the EQTP model may encounter challenges, particularly in adapting to highly complex and variable geological conditions. In regions with significant geological heterogeneity, the model may struggle to achieve optimal performance. Future work could explore methods such as transfer learning to enhance adaptability. For example, a stacked machine learning (Stacked ML) approach could be employed [55]. In this framework, base models such as EQTP, PhaseNet+, and EQT are trained independently to generate preliminary predictions. A meta-learner, such as logistic regression, then assigns weights to these predictions, effectively integrating the strengths of different models. By leveraging this ensemble strategy, the model can achieve more accurate and robust predictions across diverse geological environments.

Author Contributions

Formal analysis, L.P., L.L. and X.Z.; Funding acquisition, L.L.; Investigation, L.P. and L.L.; Methodology, L.P., L.L. and X.Z.; Software, L.P. and X.Z.; Supervision, L.L.; Writing—original draft, L.P. and L.L.; Writing—review and editing, L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China, grant number 42374076; Central South University Innovation−Driven Research Programme, grant number 2023CXQD063; and the Fundamental Research Funds for the Central Universities of Central South University.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The CEED dataset, the Geysers dataset, and the DiTing dataset can be downloaded through references [38], [37] and [41], respectively.

Acknowledgments

We acknowledge the discussion with affiliates of the Stanford Center for Induced and Triggered Seismicity (SCITS). We thank S. Mostafa Mousavi for the helpful discussion on the EQT model structure and Zhengguang Zhao for the preparation of the manuscript. We appreciate the feedback from two anonymous reviewers, which significantly improved the quality of the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Eaton, D.W. Passive Seismic Monitoring of Induced Seismicity: Fundamental Principles and Application to Energy Technologies; Cambridge University Press: Cambridge, UK, 2018; ISBN 978-1-107-14525-2. [Google Scholar]
  2. Li, L.; Tan, J.; Wood, D.A.; Zhao, Z.; Becker, D.; Lyu, Q.; Shu, B.; Chen, H. A Review of the Current Status of Induced Seismicity Monitoring for Hydraulic Fracturing in Unconventional Tight Oil and Gas Reservoirs. Fuel 2019, 242, 195–210. [Google Scholar] [CrossRef]
  3. Li, L.; Tan, J.; Tan, Y.; Pan, X.; Zhao, Z. Chapter Eight—Microseismic Analysis to Aid Gas Reservoir Characterization. In Sustainable Geoscience for Natural Gas Subsurface Systems; Wood, D.A., Cai, J., Eds.; The Fundamentals and Sustainable Advances in Natural Gas Science and Eng; Gulf Professional Publishing: Houston, TX, USA, 2022; Volume 2, pp. 219–242. ISBN 978-0-323-85465-8. [Google Scholar]
  4. Xu, J.; Zhang, W.; Chen, X.; Guo, Q. An Effective Polarity Correction Method for Microseismic Migration-Based Location. Geophysics 2020, 85, KS115–KS125. [Google Scholar] [CrossRef]
  5. Barthwal, H.; van der Baan, M. Microseismicity Observed in an Underground Mine: Source Mechanisms and Possible Causes. Geomech. Energy Environ. 2020, 22, 100167. [Google Scholar] [CrossRef]
  6. Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
  7. Allen, R.V. Automatic Earthquake Recognition and Timing from Single Traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar] [CrossRef]
  8. Pugh, D.J.; White, R.S.; Christie, P.A.F. Automatic Bayesian Polarity Determination. Geophys. J. Int. 2016, 206, 275–291. [Google Scholar] [CrossRef]
  9. Kim, J.; Woo, J.-U.; Rhie, J.; Kang, T.-S. Automatic Determination of First-Motion Polarity and Its Application to Focal Mechanism Analysis of Microseismic Events. Geosci. J. 2017, 21, 695–702. [Google Scholar] [CrossRef]
  10. Chen, C.; Holland, A.A. PhasePApy: A Robust Pure Python Package for Automatic Identification of Seismic Phases. Seismol. Res. Lett. 2016, 87, 1384–1396. [Google Scholar] [CrossRef]
  11. Tomassi, A.; de Franco, R.; Trippetta, F. High-Resolution Synthetic Seismic Modelling: Elucidating Facies Heterogeneity in Carbonate Ramp Systems. Pet. Geosci. 2025, 31, petgeo2024-47. [Google Scholar] [CrossRef]
  12. Anikiev, D.; Birnie, C.; bin Waheed, U.; Alkhalifah, T.; Gu, C.; Verschuur, D.J.; Eisner, L. Machine Learning in Microseismic Monitoring. Earth Sci. Rev. 2023, 239, 104371. [Google Scholar] [CrossRef]
  13. Lin, L.; Zhong, Z.; Li, C.; Gorman, A.; Wei, H.; Kuang, Y.; Wen, S.; Cai, Z.; Hao, F. Machine Learning for Subsurface Geological Feature Identification from Seismic Data: Methods, Datasets, Challenges, and Opportunities. Earth Sci. Rev. 2024, 257, 104887. [Google Scholar] [CrossRef]
  14. Yu, S.; Ma, J. Deep Learning for Geophysics: Current and Future Trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
  15. Li, L.; Zeng, X.; Pan, X.; Peng, L.; Tan, Y.; Liu, J. Microseismic Velocity Inversion Based on Deep Learning and Data Augmentation. Appl. Sci. 2024, 14, 2194. [Google Scholar] [CrossRef]
  16. LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
  17. Chen, Y.; Zhang, G.; Bai, M.; Zu, S.; Guan, Z.; Zhang, M. Automatic Waveform Classification and Arrival Picking Based on Convolutional Neural Network. Earth Space Sci. 2019, 6, 1244–1261. [Google Scholar] [CrossRef]
  18. Dokht, R.M.H.; Kao, H.; Visser, R.; Smith, B. Seismic Event and Phase Detection Using Time–Frequency Representation and Convolutional Neural Networks. Seismol. Res. Lett. 2019, 90, 481–490. [Google Scholar] [CrossRef]
  19. Hara, S.; Fukahata, Y.; Iio, Y. P-Wave First-Motion Polarity Determination of Waveform Data in Western Japan Using Deep Learning. Earth Planets Space 2019, 71, 127. [Google Scholar] [CrossRef]
  20. Ross, Z.E.; Meier, M.-A.; Hauksson, E. P Wave Arrival Picking and First-Motion Polarity Determination with Deep Learning. J. Geophys. Res. Solid Earth 2018, 123, 5120–5129. [Google Scholar] [CrossRef]
  21. Tian, X.; Zhang, W.; Zhang, X.; Zhang, J.; Zhang, Q.; Wang, X.; Guo, Q. Comparison of Single-trace and Multiple-trace Polarity Determination for Surface Microseismic Data Using Deep Learning. Seismol. Res. Lett. 2020, 91, 1794–1803. [Google Scholar] [CrossRef]
  22. Uchide, T. Focal Mechanisms of Small Earthquakes beneath the Japanese Islands Based on First-Motion Polarities Picked Using Deep Learning. Geophys. J. Int. 2020, 223, 1658–1671. [Google Scholar] [CrossRef]
  23. Guo, T.Y.; Vanorio, T.; Ding, J. A Deep-Learning P-Wave Arrival Picker for Laboratory Acoustic Emissions: Model Training and Its Performance. Rock Mech. Rock Eng. 2024. [Google Scholar] [CrossRef]
  24. Shen, T.; Jiang, X.; Wang, S.; Peng, G. Improved U-Net3+ Network for First Arrival Picking of Noisy Earthquake Recordings. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5912511. [Google Scholar] [CrossRef]
  25. Zhu, W.; Beroza, G.C. PhaseNet: A Deep-Neural-Network-Based Seismic Arrival Time Picking Method. Geophys. J. Int. 2019, 216, 261–273. [Google Scholar] [CrossRef]
  26. Chakraborty, M.; Cartaya, C.Q.; Li, W.; Faber, J.; Rümpker, G.; Stoecker, H.; Srivastava, N. PolarCAP—A Deep Learning Approach for First Motion Polarity Classification of Earthquake Waveforms. Artif. Intell. Geosci. 2022, 3, 46–52. [Google Scholar] [CrossRef]
  27. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Newry, UK, 2017; Volume 30. [Google Scholar]
  28. Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake Transformer—An Attentive Deep-Learning Model for Simultaneous Earthquake Detection and Phase Picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
  29. Xiao, Z.; Wang, J.; Liu, C.; Li, J.; Zhao, L.; Yao, Z. Siamese Earthquake Transformer: A Pair-Input Deep-Learning Model for Earthquake Detection and Phase Picking on a Seismic Array. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021444. [Google Scholar] [CrossRef]
  30. Zhao, M.; Xiao, Z.; Zhang, M.; Yang, Y.; Tang, L.; Chen, S. DiTingMotion: A Deep-Learning First-Motion-Polarity Classifier and Its Application to Focal Mechanism Inversion. Front. Earth Sci. 2023, 11, 1103914. [Google Scholar] [CrossRef]
  31. Li, S.; Fang, L.; Xiao, Z.; Zhou, Y.; Liao, S.; Fan, L. FocMech-Flow: Automatic Determination of P-Wave First-Motion Polarity and Focal Mechanism Inversion and Application to the 2021 Yangbi Earthquake Sequence. Appl. Sci. 2023, 13, 2233. [Google Scholar] [CrossRef]
  32. Chen, Y.; Saad, O.M.; Savvaidis, A.; Zhang, F.; Chen, Y.; Huang, D.; Li, H.; Aziz Zanjani, F. Deep Learning for P-Wave First-Motion Polarity Determination and Its Application in Focal Mechanism Inversion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5917411. [Google Scholar] [CrossRef]
  33. Chen, Y. Automatic Microseismic Event Picking via Unsupervised Machine Learning. Geophys. J. Int. 2020, 222, 1750–1764. [Google Scholar] [CrossRef]
  34. Li, H.; He, J.; Tuo, X.; Wen, X.; Yang, Z. Self-Supervised Convolutional Clustering for Picking the First Break of Microseismic Recording. IEEE Geosci. Remote Sens. Lett. 2024, 21, 7501105. [Google Scholar] [CrossRef]
  35. Mousavi, S.M.; Zhu, W.; Ellsworth, W.; Beroza, G. Unsupervised Clustering of Seismic Signals Using Deep Convolutional Autoencoders. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1693–1697. [Google Scholar] [CrossRef]
  36. Zhang, J.; Li, Z.; Zhang, J. Simultaneous Seismic Phase Picking and Polarity Determination with an Attention-based Neural Network. Seismol. Res. Lett. 2023, 94, 813–828. [Google Scholar] [CrossRef]
  37. NCEDC. Northern California Earthquake Data Center. UC Berkeley Seismological Laboratory. Dataset 2014. [Google Scholar] [CrossRef]
  38. Zhu, W.; Wang, H.; Rong, B.; Yu, E.; Zuzlewski, S.; Tepp, G.; Taira, T.; Marty, J.; Husker, A.; Allen, R.M. California Earthquake Dataset for Machine Learning and Cloud Computing. arXiv 2025, arXiv:2502.11500. [Google Scholar]
  39. Martínez-Garzón, P.; Kwiatek, G.; Sone, H.; Bohnhoff, M.; Dresen, G.; Hartline, C. Spatiotemporal Changes, Faulting Regimes, and Source Parameters of Induced Seismicity: A Case Study from The Geysers Geothermal Field. J. Geophys. Res. Solid Earth 2014, 119, 8378–8396. [Google Scholar] [CrossRef]
  40. Yu, C.; Vavryčuk, V.; Adamová, P.; Bohnhoff, M. Moment Tensors of Induced Microearthquakes in The Geysers Geothermal Reservoir From Broadband Seismic Recordings: Implications for Faulting Regime, Stress Tensor, and Fluid Pressure. J. Geophys. Res. Solid Earth 2018, 123, 8748–8766. [Google Scholar] [CrossRef]
  41. Zhao, M.; Xiao, Z.; Chen, S.; Fang, L. DiTing: A Large-Scale Chinese Seismic Benchmark Dataset for Artificial Intelligence in Seismology. Earthq. Sci. 2023, 36, 84–94. [Google Scholar] [CrossRef]
  42. Woollam, J.; Münchmeyer, J.; Tilmann, F.; Rietbrock, A.; Lange, D.; Bornstein, T.; Diehl, T.; Giunchi, C.; Haslinger, F.; Jozinović, D.; et al. SeisBench—A Toolbox for Machine Learning in Seismology. Seismol. Res. Lett. 2022, 93, 1695–1709. [Google Scholar] [CrossRef]
  43. Yin, X.; Liu, Z.; Liu, D.; Ren, X. A Novel CNN-Based Bi-LSTM Parallel Model with Attention Mechanism for Human Activity Recognition with Noisy Data. Sci. Rep. 2022, 12, 7878. [Google Scholar] [CrossRef]
  44. Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the 2019 IEEE International Conference on Big Data (big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
  45. Sun, J.; Zhang, X.; Wang, J. Lightweight Bidirectional Long Short-Term Memory Based on Automated Model Pruning with Application to Bearing Remaining Useful Life Prediction. Eng. Appl. Artif. Intell. 2023, 118, 105662. [Google Scholar] [CrossRef]
  46. Bashir, T.; Wang, H.; Tahir, M.; Zhang, Y. Wind and Solar Power Forecasting Based on Hybrid CNN-ABiLSTM, CNN-Transformer-MLP Models. Renew. Energy 2025, 239, 122055. [Google Scholar] [CrossRef]
  47. Choi, Y.; Nguyen, H.-T.; Han, T.H.; Choi, Y.; Ahn, J. Sequence Deep Learning for Seismic Ground Response Modeling: 1D-CNN, LSTM, and Transformer Approach. Appl. Sci. 2024, 14, 6658. [Google Scholar] [CrossRef]
  48. Niksejel, A.; Zhang, M. OBSTransformer: A Deep-Learning Seismic Phase Picker for OBS Data Using Automated Labelling and Transfer Learning. Geophys. J. Int. 2024, 237, 485–505. [Google Scholar] [CrossRef]
  49. Shi, P.; Meier, M.-A.; Villiger, L.; Tuinstra, K.; Selvadurai, P.A.; Lanza, F.; Yuan, S.; Obermann, A.; Mesimeri, M.; Münchmeyer, J.; et al. From Labquakes to Megathrusts: Scaling Deep Learning Based Pickers over 15 Orders of Magnitude. J. Geophys. Res. Mach. Learn. Comput. 2024, 1, e2024JH000220. [Google Scholar] [CrossRef]
  50. Youden, W.J. Index for Rating Diagnostic Tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
  51. Zhu, W.; McBrearty, I.W.; Mousavi, S.M.; Ellsworth, W.L.; Beroza, G.C. Earthquake Phase Association Using a Bayesian Gaussian Mixture Model. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023249. [Google Scholar] [CrossRef]
  52. Waldhauser, F. A Double-Difference Earthquake Location Algorithm: Method and Application to the Northern Hayward Fault, California. Bull. Seismol. Soc. Am. 2000, 90, 1353–1368. [Google Scholar] [CrossRef]
  53. Kwiatek, G.; Martínez-Garzón, P.; Bohnhoff, M. HybridMT: A MATLAB/Shell Environment Package for Seismic Moment Tensor Inversion and Refinement. Seismol. Res. Lett. 2016, 87, 964–976. [Google Scholar] [CrossRef]
  54. Celli, N.L.; Nooshiri, N.; Bean, C.J.; Grigoli, F.; Obermann, A.; Wiemer, S. Manual MT Inversions in Microseismic Areas: Good Practices and Building a Reference Database for the Hengill Region, Iceland. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-11721. [Google Scholar]
  55. Kazemi, F.; Asgarkhani, N.; Jankowski, R. Optimization-Based Stacked Machine-Learning Method for Seismic Probability and Risk Assessment of Reinforced Concrete Shear Walls. Expert Syst. Appl. 2024, 255, 124897. [Google Scholar] [CrossRef]
Applsci 15 03424 g001
Figure 1. Earthquake and station distribution in northern and central California. (a) The red dots represent the locations of 259,674 earthquakes, while the blue triangles indicate the positions of 929 seismic monitoring stations. The earthquake distribution is widespread, with some regions showing high concentrations, and the stations are primarily deployed in seismically active areas. (b) The distribution of horizontal epicentral distances, with most events occurring within 50 km. (c) The magnitude (duration magnitude Md) distribution of earthquakes, mainly ranging from 0 to 3, with a high proportion of events with magnitudes below 2.
Figure 1. Earthquake and station distribution in northern and central California. (a) The red dots represent the locations of 259,674 earthquakes, while the blue triangles indicate the positions of 929 seismic monitoring stations. The earthquake distribution is widespread, with some regions showing high concentrations, and the stations are primarily deployed in seismically active areas. (b) The distribution of horizontal epicentral distances, with most events occurring within 50 km. (c) The magnitude (duration magnitude Md) distribution of earthquakes, mainly ranging from 0 to 3, with a high proportion of events with magnitudes below 2.
Applsci 15 03424 g001
Applsci 15 03424 g002
Figure 2. NCEDC waveform data. (a) Z-channel waveform. (b) N-channel waveform. (c) Magnified view of the P-wave arrival in the Z-channel. The blue and red lines indicate the P-wave and S-wave arrival times, respectively. The red arrows represent positive polarity of P-wave, while the blue arrows indicate negative polarity.
Figure 2. NCEDC waveform data. (a) Z-channel waveform. (b) N-channel waveform. (c) Magnified view of the P-wave arrival in the Z-channel. The blue and red lines indicate the P-wave and S-wave arrival times, respectively. The red arrows represent positive polarity of P-wave, while the blue arrows indicate negative polarity.
Applsci 15 03424 g002
Applsci 15 03424 g003
Figure 3. EQTP model architecture. The orange dashed box represents the waveform feature extraction layer, where a three-component waveform is input and processed through the Encoder, ResCNN, and Transformer layers to obtain waveform features. These features are then passed through four different decoders to generate probability curves for P arrival, S arrival, Polarity_U (positive polarity), and Polarity_D (negative polarity).
Figure 3. EQTP model architecture. The orange dashed box represents the waveform feature extraction layer, where a three-component waveform is input and processed through the Encoder, ResCNN, and Transformer layers to obtain waveform features. These features are then passed through four different decoders to generate probability curves for P arrival, S arrival, Polarity_U (positive polarity), and Polarity_D (negative polarity).
Applsci 15 03424 g003
Applsci 15 03424 g004
Figure 4. Loss curves. (a) Training loss; (b) validation loss.
Figure 4. Loss curves. (a) Training loss; (b) validation loss.
Applsci 15 03424 g004
Applsci 15 03424 g005
Figure 5. Sample results of the testing set data. (a) Positive polarity event with noise interference; (b) negative polarity event with only a single Z component; (c) multi-event waveforms with two positive polarities; (d) noise event.
Figure 5. Sample results of the testing set data. (a) Positive polarity event with noise interference; (b) negative polarity event with only a single Z component; (c) multi-event waveforms with two positive polarities; (d) noise event.
Applsci 15 03424 g005
Applsci 15 03424 g006
Figure 6. Location results of 434 earthquake events from 1 December 2023 to 10 December 2023. (a) The horizontal profile showing the locations of 37 monitoring stations (black triangles), the reference double-difference locations (red dots), the events located by GaMMA with the EQTP model-based picks (blue dots), and those with the PN+ model-based picks (green dots). (b) The event locations along the depth profile.
Figure 6. Location results of 434 earthquake events from 1 December 2023 to 10 December 2023. (a) The horizontal profile showing the locations of 37 monitoring stations (black triangles), the reference double-difference locations (red dots), the events located by GaMMA with the EQTP model-based picks (blue dots), and those with the PN+ model-based picks (green dots). (b) The event locations along the depth profile.
Applsci 15 03424 g006
Applsci 15 03424 g007
Figure 7. The earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82). (a) The picking results of the EQTP model; (b) the picking results of the PN+ model. The black solid line represents the arrival time of the P-wave, and the black dashed line represents the arrival time of the S-wave.
Figure 7. The earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82). (a) The picking results of the EQTP model; (b) the picking results of the PN+ model. The black solid line represents the arrival time of the P-wave, and the black dashed line represents the arrival time of the S-wave.
Applsci 15 03424 g007
Applsci 15 03424 g008
Figure 8. Inversion results of the earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82). The first column shows the inversion results of the focal mechanism of the first-motion polarity by the EQTP model, the second column corresponds to those by the PN+ model, the third column shows the same inversion results of the focal mechanism of the manually picked first-motion polarity. Each row represents different first-motion polarity thresholds; from top to bottom, these are 0.5, 0.6, 0.7, and 0.8, respectively.
Figure 8. Inversion results of the earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82). The first column shows the inversion results of the focal mechanism of the first-motion polarity by the EQTP model, the second column corresponds to those by the PN+ model, the third column shows the same inversion results of the focal mechanism of the manually picked first-motion polarity. Each row represents different first-motion polarity thresholds; from top to bottom, these are 0.5, 0.6, 0.7, and 0.8, respectively.
Applsci 15 03424 g008
Applsci 15 03424 g009
Figure 9. The earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82) (polarity threshold = 0.6). (a) The phase picking and polarity determination results of EQTP; (b) the phase picking and polarity determination results of PN+. Those consistent with the manually picked results are marked as “correct”, and those inconsistent are marked as “error”. The green short lines represent positive polarities, the blue short lines represent negative polarities, and the black short lines represent unknown polarities. The marked positions are the first arrival positions of P-waves.
Figure 9. The earthquake event at 14:19:35.61 on 1 December 2023 (Md 0.82) (polarity threshold = 0.6). (a) The phase picking and polarity determination results of EQTP; (b) the phase picking and polarity determination results of PN+. Those consistent with the manually picked results are marked as “correct”, and those inconsistent are marked as “error”. The green short lines represent positive polarities, the blue short lines represent negative polarities, and the black short lines represent unknown polarities. The marked positions are the first arrival positions of P-waves.
Applsci 15 03424 g009
Applsci 15 03424 g010
Figure 10. Inversion results of the earthquake event at 08:09:10.97 on 2 December 2023 (Md 1.27). The first column shows the inversion results of the focal mechanism of the first-motion polarity by the EQTP model, the second column corresponds to those by the PN+ model, T, and the third column shows the same inversion results of the focal mechanism of the manually picked first-motion polarity. Each row represents different first-motion polarity thresholds; from top to bottom, these are 0.5, 0.6, 0.7, and 0.8, respectively.
Figure 10. Inversion results of the earthquake event at 08:09:10.97 on 2 December 2023 (Md 1.27). The first column shows the inversion results of the focal mechanism of the first-motion polarity by the EQTP model, the second column corresponds to those by the PN+ model, T, and the third column shows the same inversion results of the focal mechanism of the manually picked first-motion polarity. Each row represents different first-motion polarity thresholds; from top to bottom, these are 0.5, 0.6, 0.7, and 0.8, respectively.
Applsci 15 03424 g010
Applsci 15 03424 g011
Figure 11. The earthquake event at 08:09:10.97 on 2 December 2023 (Md 1.27) (polarity threshold = 0.6). (a) The first-motion polarity results of EQTP; (b) the first-motion polarity results of PN+. Those consistent with the manually picked results are marked as “correct”, and those inconsistent are marked as “error”. The green short lines represent positive polarities, the blue short lines represent negative polarities, and the black short lines represent unknown polarities. The marked positions are the first arrival positions of P-waves.
Figure 11. The earthquake event at 08:09:10.97 on 2 December 2023 (Md 1.27) (polarity threshold = 0.6). (a) The first-motion polarity results of EQTP; (b) the first-motion polarity results of PN+. Those consistent with the manually picked results are marked as “correct”, and those inconsistent are marked as “error”. The green short lines represent positive polarities, the blue short lines represent negative polarities, and the black short lines represent unknown polarities. The marked positions are the first arrival positions of P-waves.
Applsci 15 03424 g011
Table 1. Confusion matrix for the determination of the first-motion polarity in the testing set.
Table 1. Confusion matrix for the determination of the first-motion polarity in the testing set.
UD
U-pre18,8652196
D-pre185616,748
N-pre9779
Total20,81819,023
Table 2. Table of evaluation indicator results for the testing set.
Table 2. Table of evaluation indicator results for the testing set.
PrecisionRecallF1Mean(s)Std(s)MAE(s)Precision
(Polarity)		Recall
(Polarity)		F1
(Polarity)
P1.001.001.000.000.050.020.900.890.90
S1.000.991.000.010.150.09
Table 3. Confusion matrix for the determination of the first-motion polarity in the DiTing dataset.
Table 3. Confusion matrix for the determination of the first-motion polarity in the DiTing dataset.
UD
U-pre30,485 (29,398)2113 (1672)
D-pre863 (1150)19,960 (19,588)
N-pre100 (783)137 (876)
Total31,448 (31,331)22,210 (22,136)
Table 4. Table of evaluation indicator results for the DiTing dataset.
Table 4. Table of evaluation indicator results for the DiTing dataset.
PrecisionRecallF1Mean(s)Std(s)MAE(s)Precision
(Polarity)		Recall
(Polarity)		F1
(Polarity)
P1.00 (1.00)0.99 (0.88)1.00 (0.94)0.01 (−0.01)0.05 (0.05)0.03 (0.03)0.94 (0.95)0.94 (0.92)0.94 (0.93)
S1.00 (1.00)0.97 (0.80)0.98 (0.89)0.04 (0.04)0.20 (0.17)0.12 (0.10)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Peng, L.; Li, L.; Zeng, X. A Microseismic Phase Picking and Polarity Determination Model Based on the Earthquake Transformer. Appl. Sci. 2025, 15, 3424. https://doi.org/10.3390/app15073424

AMA Style

Peng L, Li L, Zeng X. A Microseismic Phase Picking and Polarity Determination Model Based on the Earthquake Transformer. Applied Sciences. 2025; 15(7):3424. https://doi.org/10.3390/app15073424

Chicago/Turabian Style

Peng, Ling, Lei Li, and Xiaobao Zeng. 2025. "A Microseismic Phase Picking and Polarity Determination Model Based on the Earthquake Transformer" Applied Sciences 15, no. 7: 3424. https://doi.org/10.3390/app15073424

APA Style

Peng, L., Li, L., & Zeng, X. (2025). A Microseismic Phase Picking and Polarity Determination Model Based on the Earthquake Transformer. Applied Sciences, 15(7), 3424. https://doi.org/10.3390/app15073424

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop