Numerical Simulation of the Elastic–Plastic Ejection from Grooved Aluminum Surfaces Under Double Supported Shocks Using the SPH Method
Abstract
1. Introduction
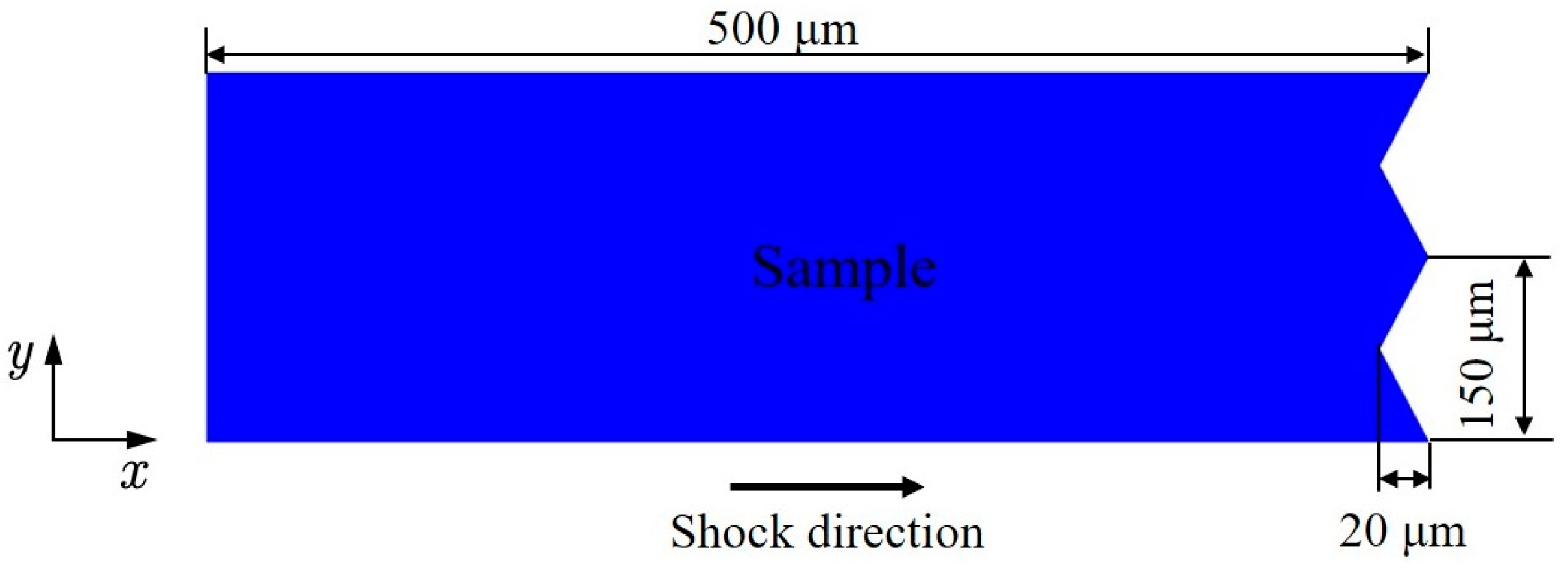
2. Materials and Methods
3. Results
3.1. Numerical Validations
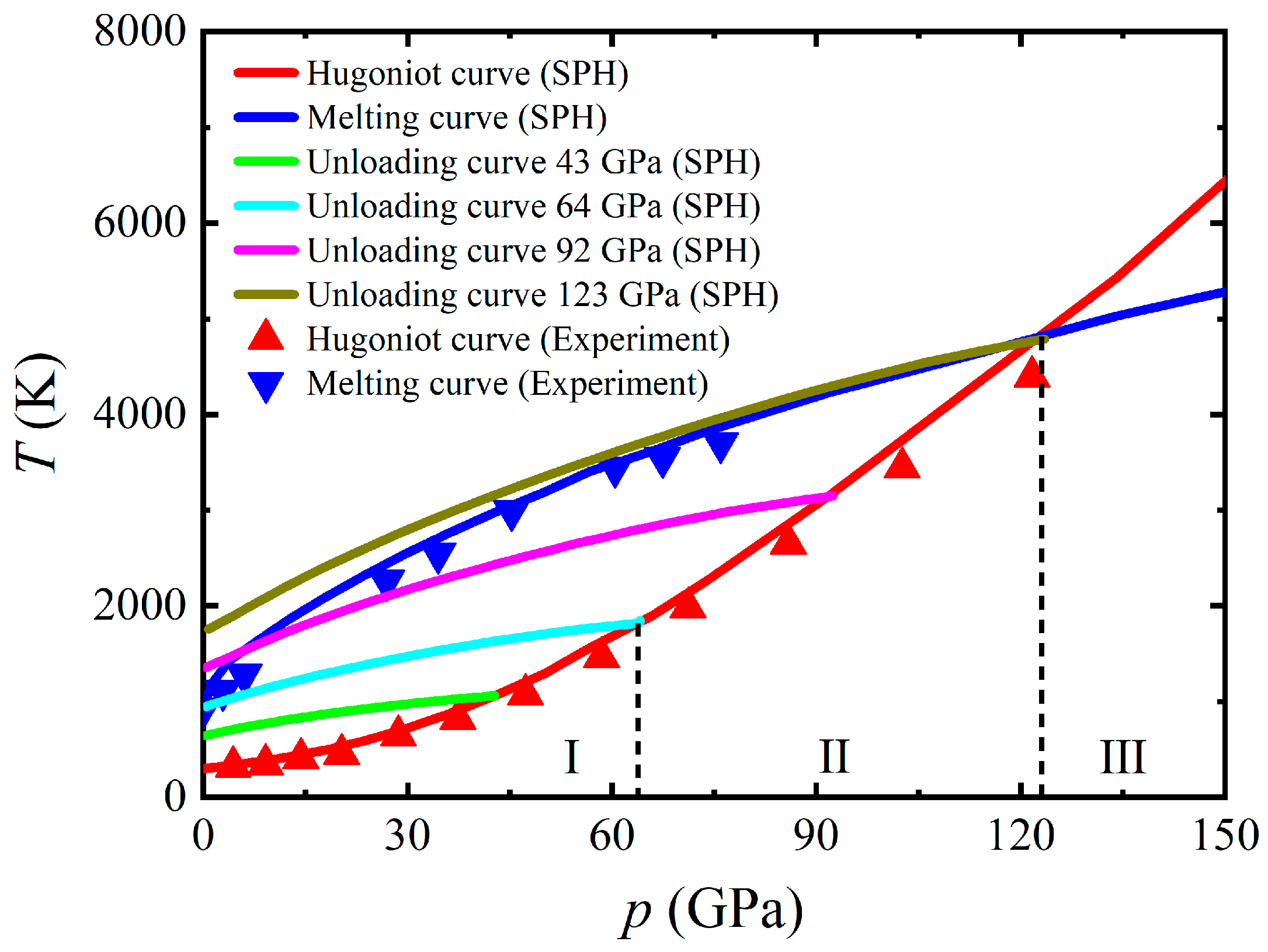
3.1.1. Pressure–Temperature Curve
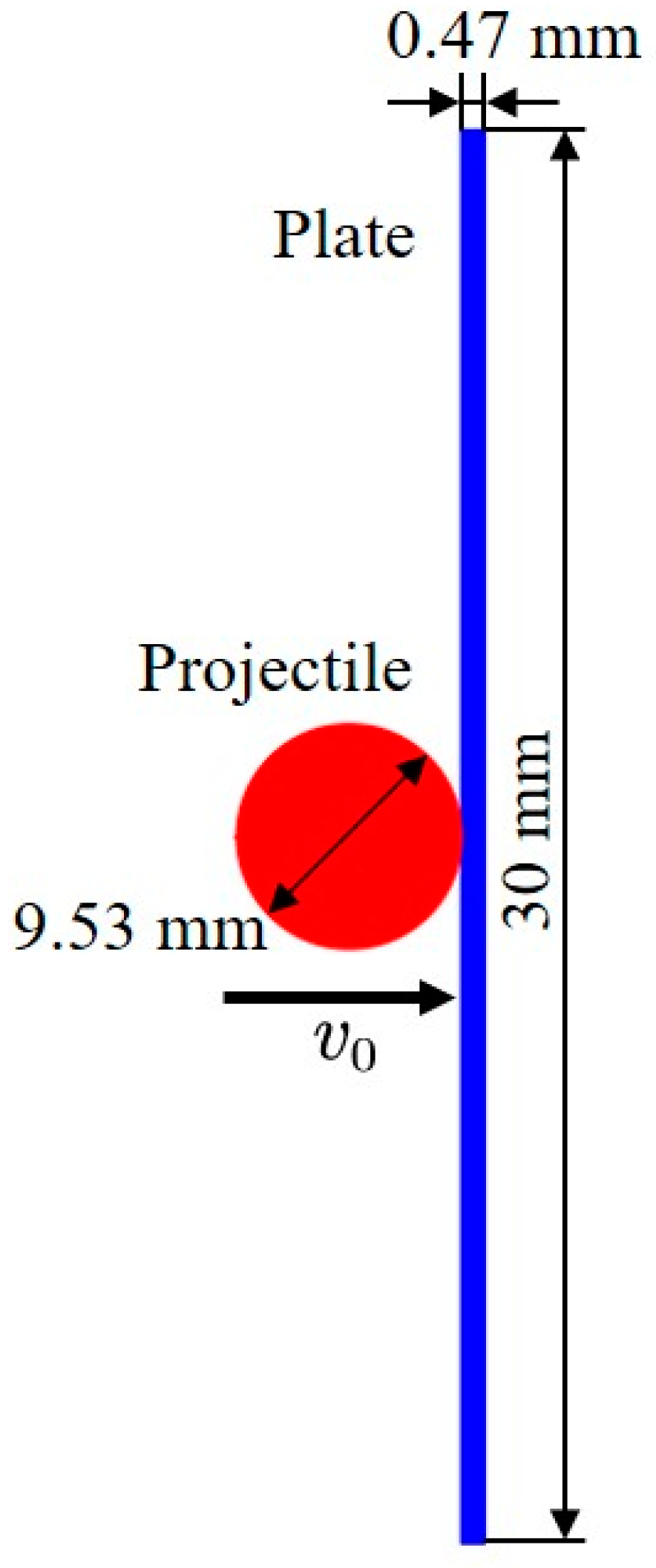
3.1.2. D High-Velocity Impact
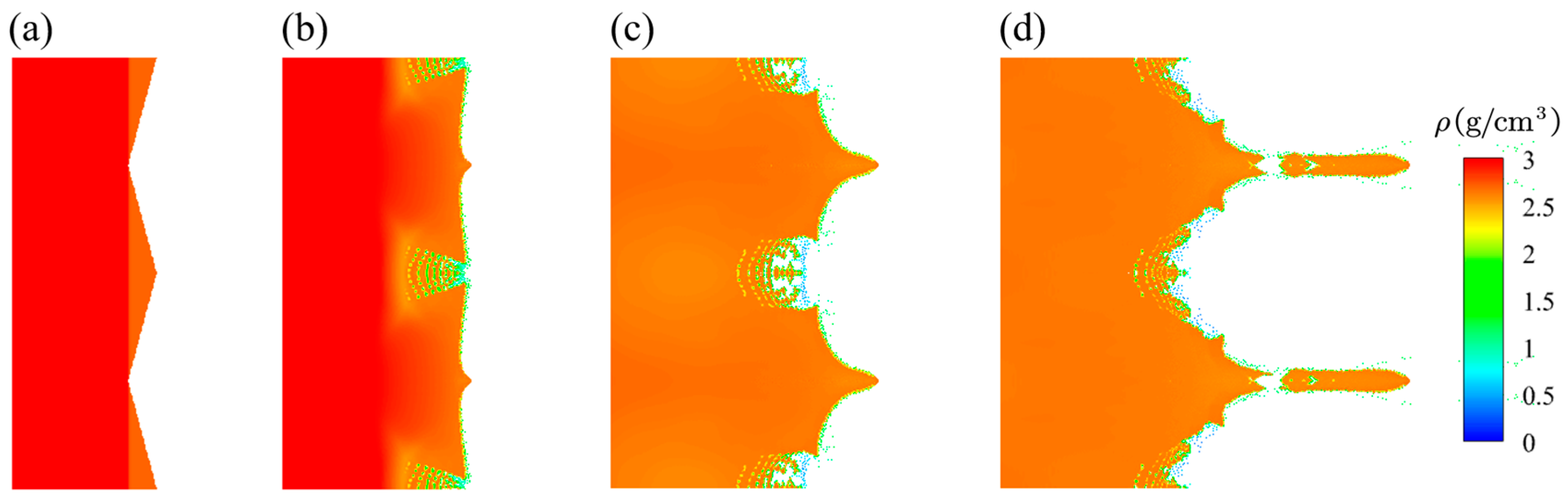
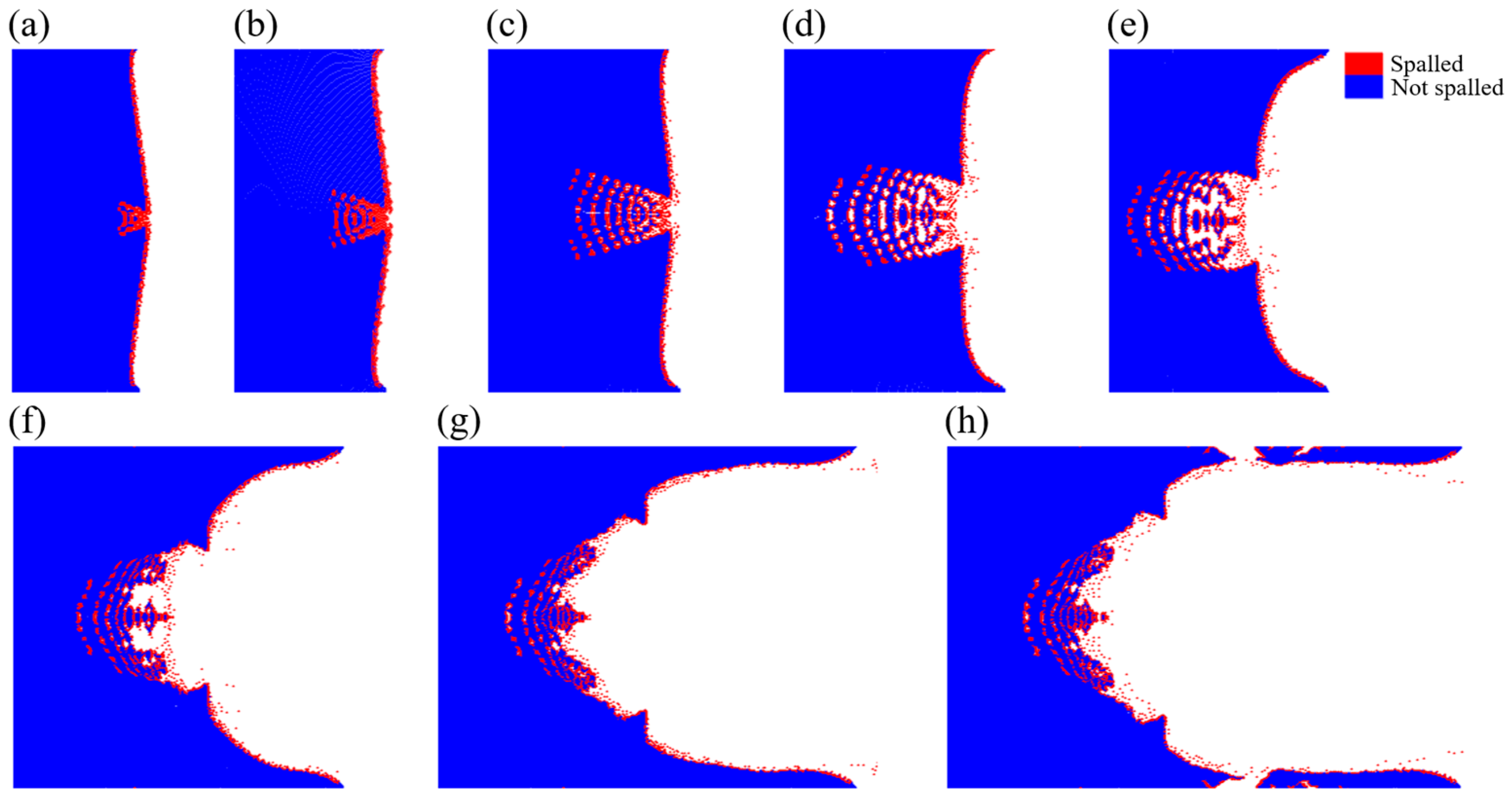
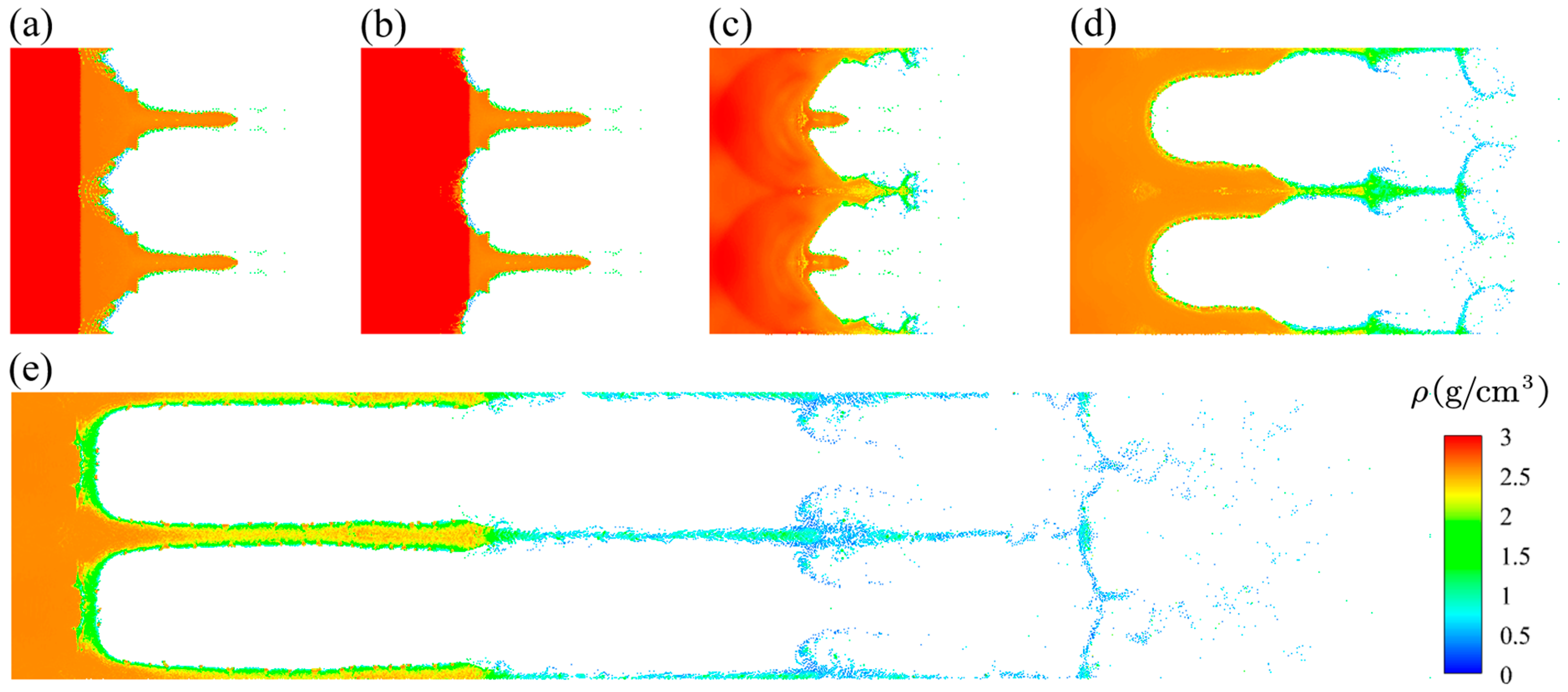
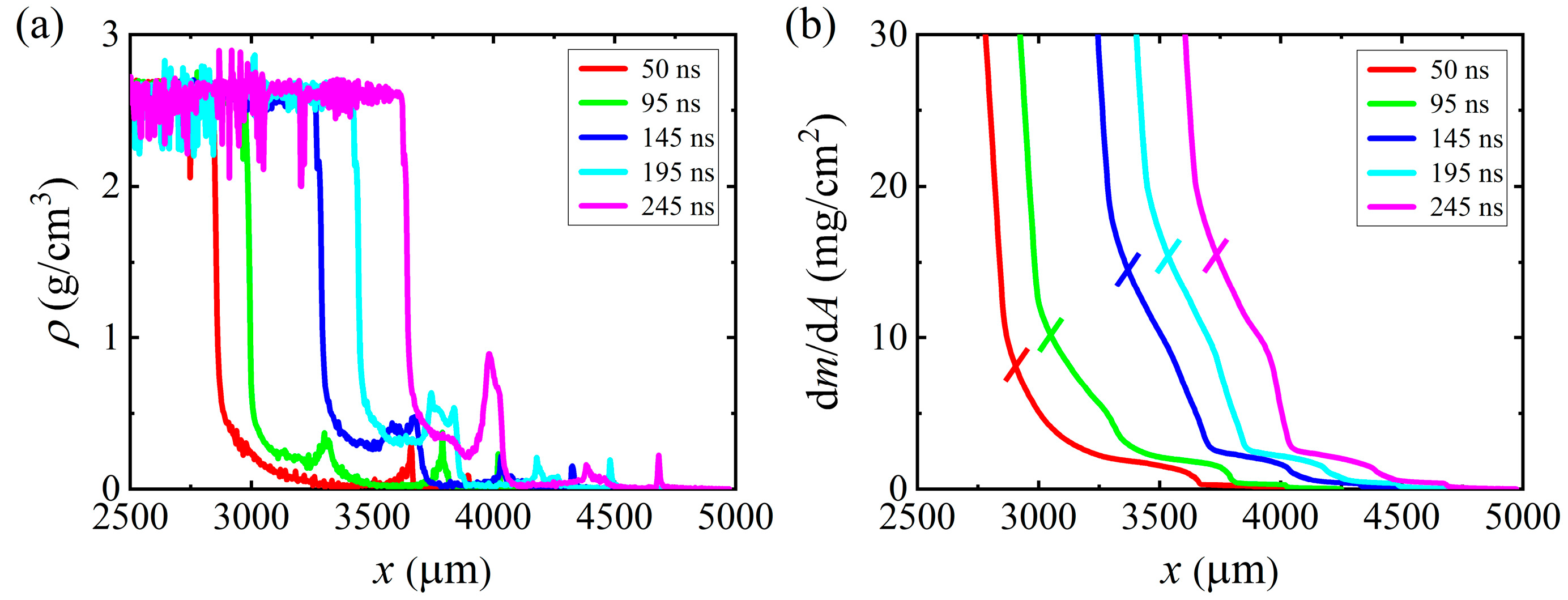
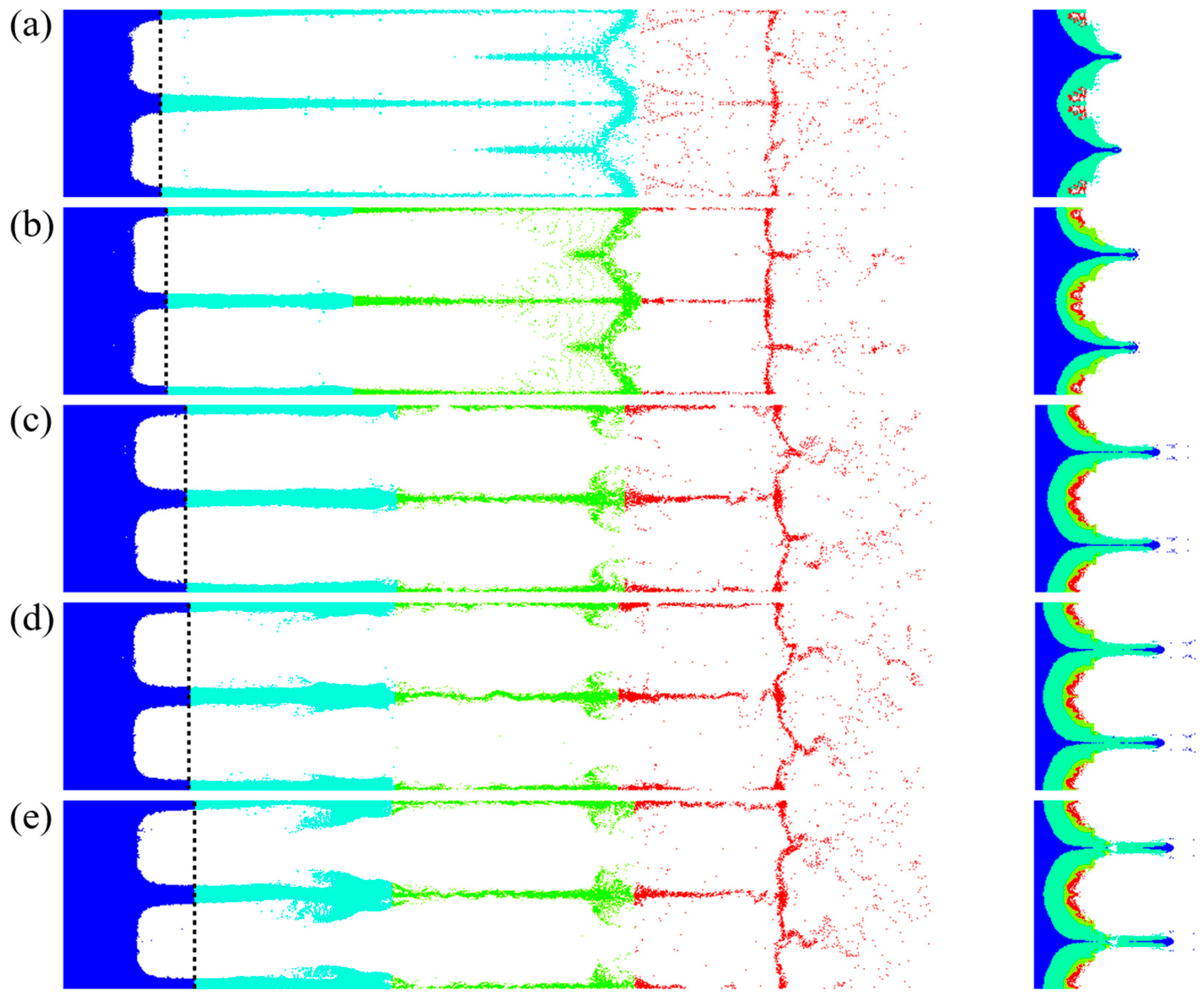
3.2. Elastic–Plastic Ejection Under Double Supported Shocks
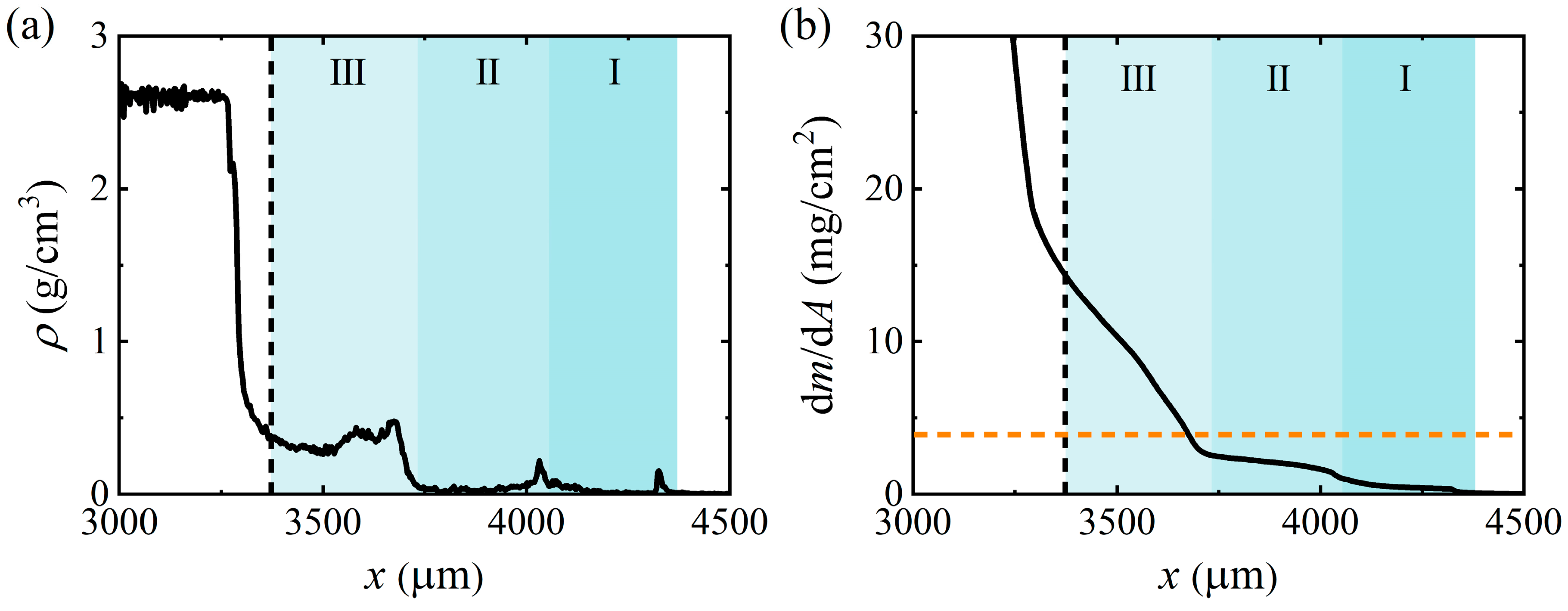
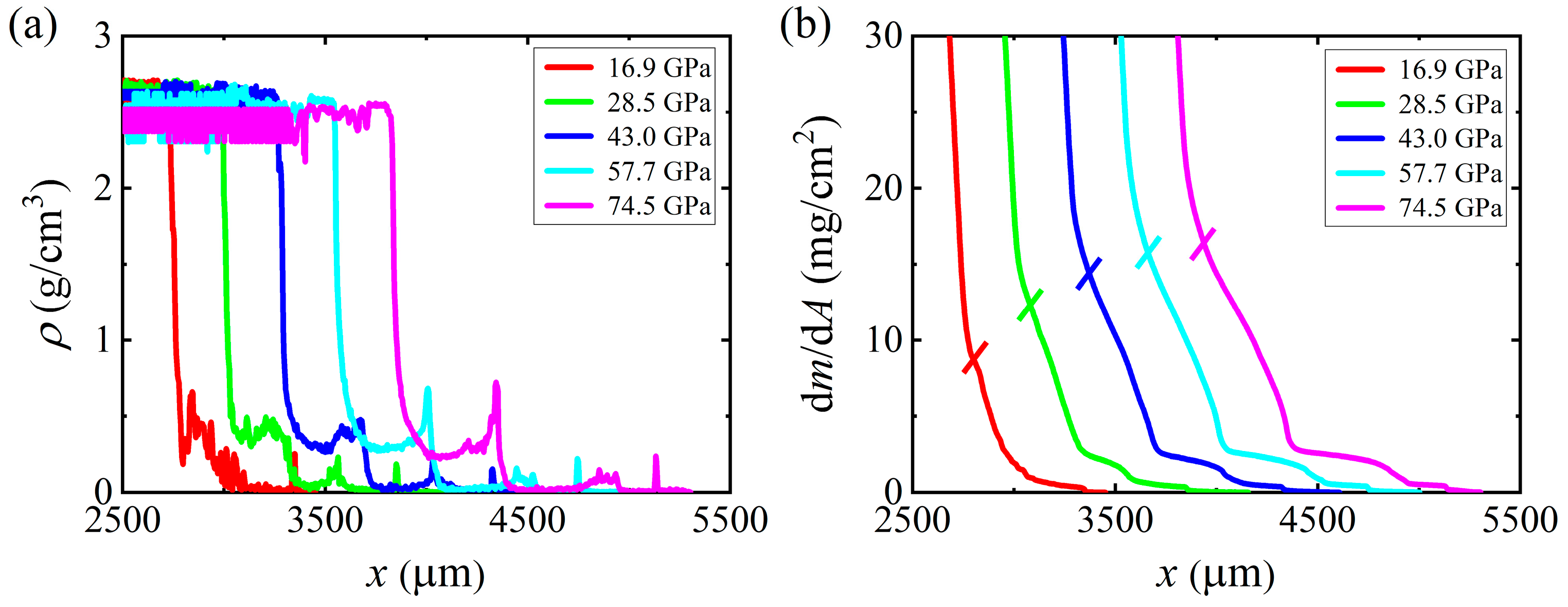
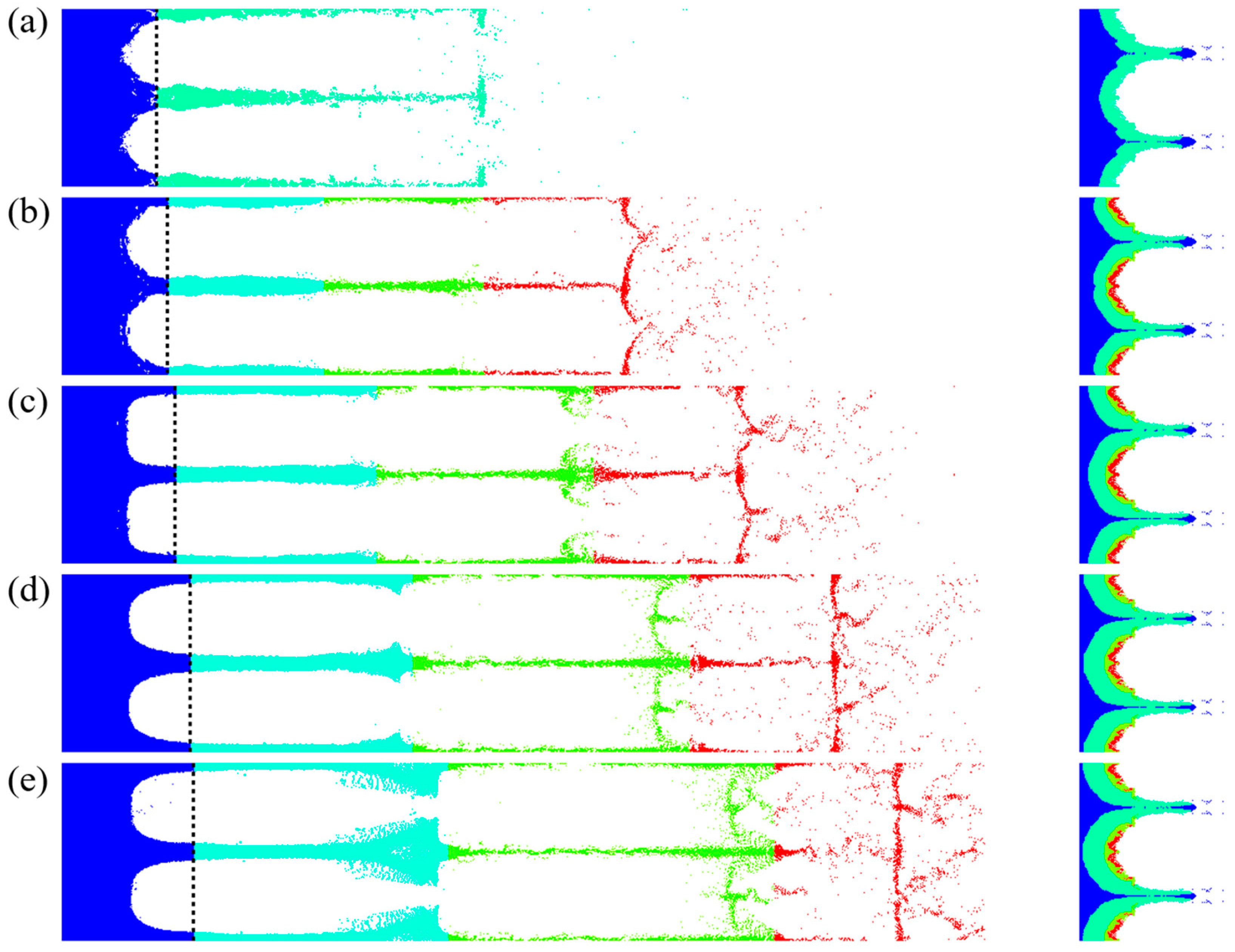
3.3. Effect of the Second Shock Pressure on the Second Ejection
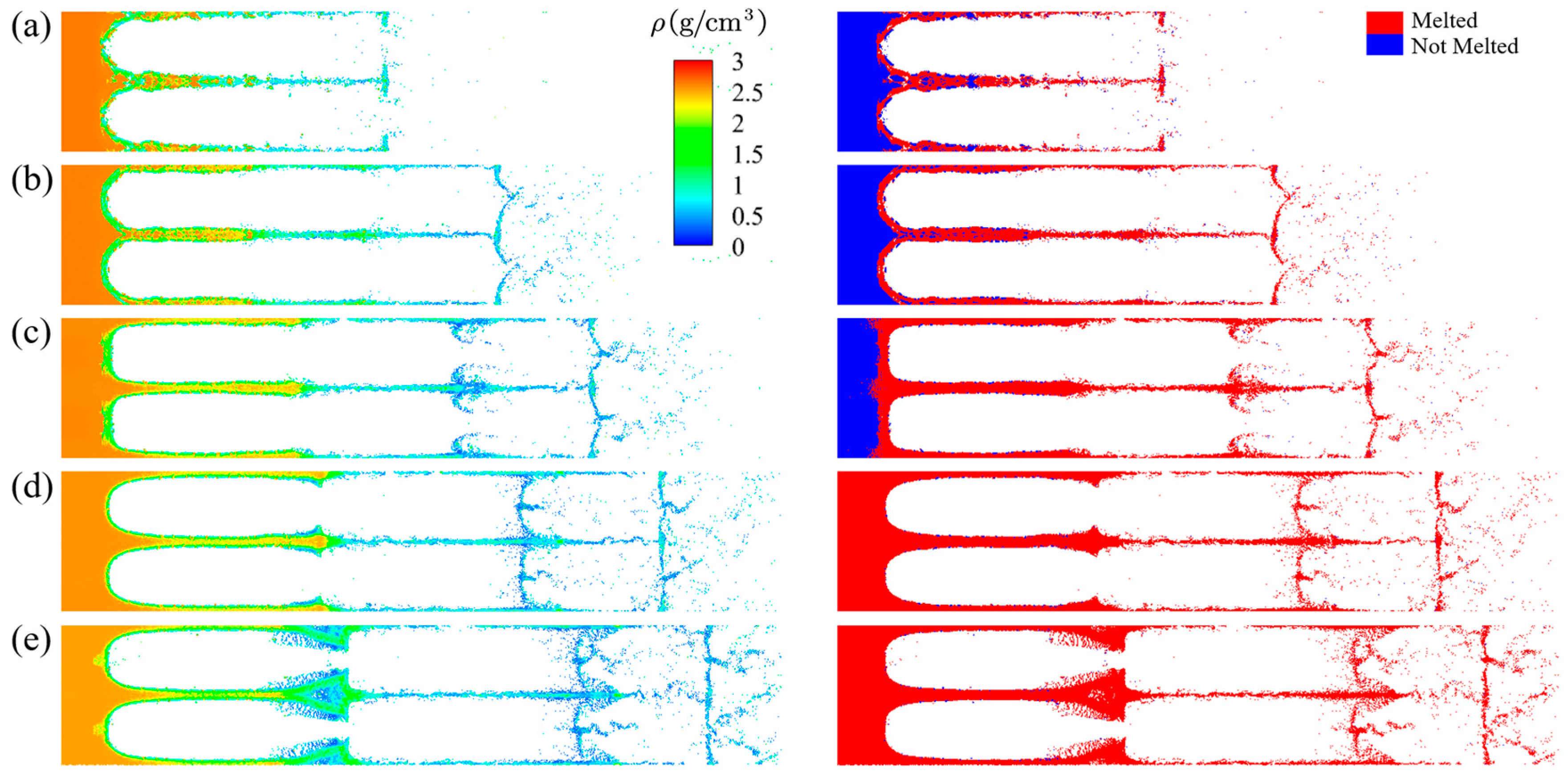
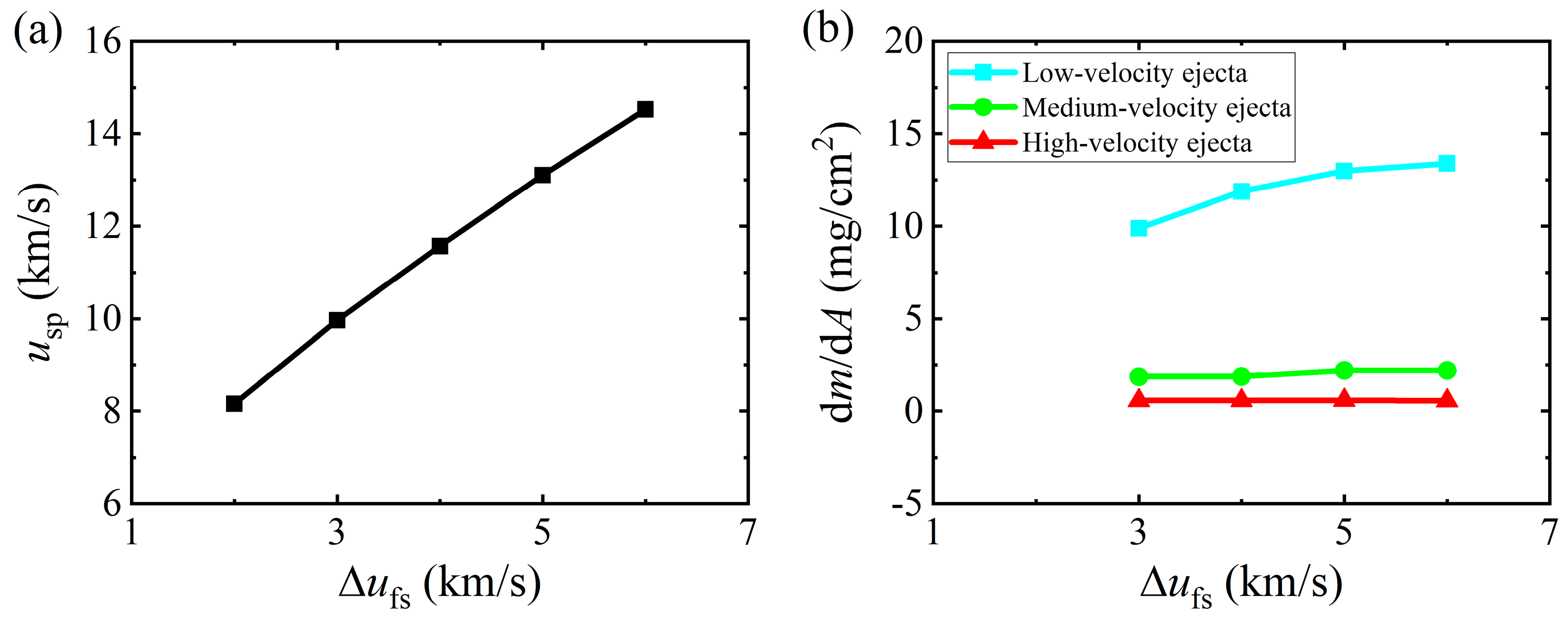
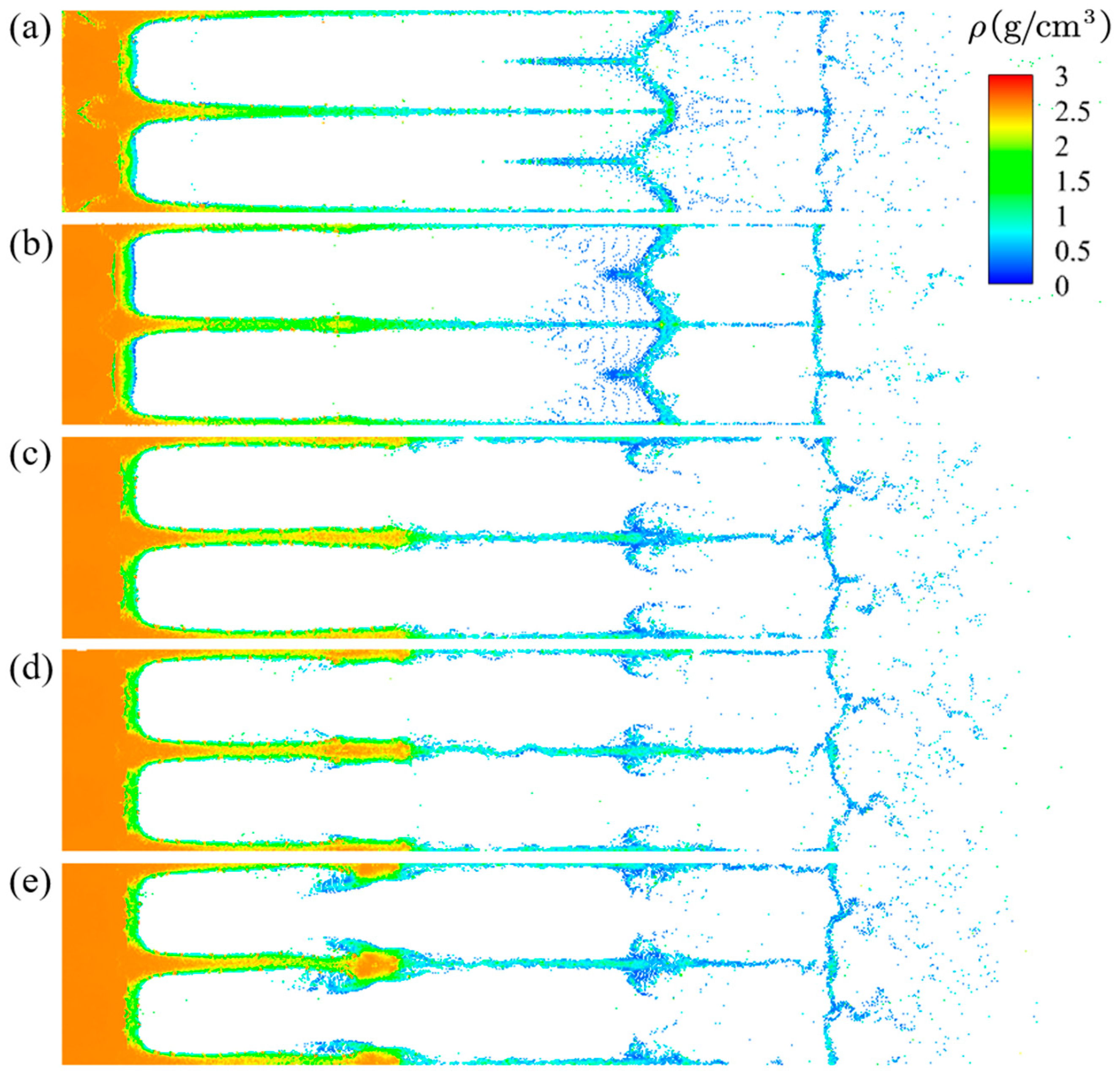
3.4. Effect of the Time Interval on the Second Ejection
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buttler, W.T.; Williams, R.J.R.; Najjar, F.M. Foreword to the Special Issue on Ejecta. J. Dyn. Behav Mater. 2017, 3, 151–155. [Google Scholar]
- Wang, P.; He, A.M.; Shao, J.L.; Sun, H.Q.; Chen, D.W.; Liu, W.B.; Liu, J. Numerical and theoretical investigations of shock-induced material ejection and ejecta-gas mixing. Sci. China Phys. Mech. Astron. 2018, 48, 094608. (In Chinese) [Google Scholar]
- Zellner, M.B.; Byers, M.; Dimonte, G.; Hammerberg, J.E.; Germann, T.C.; Rigg, P.A.; Buttler, W.T. Influence of shockwave profile on ejecta. AIP Conf. Proc. 2009, 1195, 1047–1050. [Google Scholar]
- Monfared, S.K.; Oŕo, D.M.; Grover, M.; Hammerberg, J.E.; LaLone, B.M.; Pack, C.L.; Schauer, M.M.; Stevens, G.D.; Stone, J.B.; Turley, W.D.; et al. Experimental observations on the links between surface perturbation parameters and shock-induced mass ejection. J. Appl. Phys. 2014, 116, 063504. [Google Scholar]
- de Rességuier, T.; Prudhomme, G.; Roland, C.; Brambrink, E.; Loison, D.; Jodar, B.; Lescoute, E.; Sollier, A. Picosecond x-ray radiography of microjets expanding from laser shock-loaded grooves. J. Appl. Phys. 2018, 124, 065106. [Google Scholar]
- Xu, M.Y.; Song, W.D.; Wang, C.; Wang, P.; Shao, J.L.; Tang, E.L. Theoretical and experimental study on the hypervelocity impact induced microjet from the grooved metal surface. Int. J. Impact Eng. 2021, 156, 103944. [Google Scholar]
- Bober, D.B.; Mackay, K.K.; Akin, M.C.; Najjar, F.M. Understanding the evolution of liquid and solid microjets from grooved Sn and Cu samples using radiography. J. Appl. Phys. 2021, 130, 045901. [Google Scholar]
- Shao, J.L.; Wang, P.; He, A.M.; Duan, S.Q.; Qin, C.S. Atomistic simulations of shock-induced microjet from a grooved aluminium surface. J. Appl. Phys. 2013, 113, 153501. [Google Scholar]
- Liu, W.B.; Ma, D.J.; He, A.M.; Wang, P. Ejecta from periodic grooved Sn surface under unsupported shocks. Chin. Phys. B 2018, 27, 016202. [Google Scholar]
- Wang, F.; Liu, J.; He, A.M.; Wang, P.; Wang, J.G. Ejecta production from metal Sn into inert gases. J. Appl. Phys. 2020, 127, 195901. [Google Scholar]
- Durand, O.; Soulard, L.; Colombet, L.; Prat, R. Influence of the phase transitions of shock-loaded tin on microjetting and ejecta production using molecular dynamics simulations. J. Appl. Phys. 2020, 127, 175901. [Google Scholar] [CrossRef]
- Mackay, K.K.; Najjar, F.M.; Ali, S.J.; Eggert, J.H.; Rinderknecht, H.G.; Stan, C.V.; Saunders, A.M. Hydrodynamic computations of high-power laser drives generating metal ejecta jets from surface grooves. J. Appl. Phys. 2020, 128, 215904. [Google Scholar] [CrossRef]
- Buttler, W.T.; Oŕo, D.M.; Preston, D.L.; MIkaelian, K.O.; Cherne, F.J.; Hixson, R.S.; Mariam, F.G.; Morris, C.; Stone, J.B.; Terrones, G.; et al. Unstable Richtmyer-Meshkov growth of solid and liquid metals in vacuum. J. Fluid Mech. 2012, 703, 60–84. [Google Scholar] [CrossRef]
- Dimonte, G.; Terrones, G.; Cherne, F.J.; Ramaprabhu, P. Ejecta source model based on the nonlinear Richtmyer-Meshkov instability. J. Appl. Phys. 2013, 113, 024905. [Google Scholar] [CrossRef]
- Karkhanis, V.; Ramaprabhu, P.; Cherne, F.J.; Hammerberg, J.E.; Andrews, M.J. A numerical study of bubble and spike velocities in shock-driven liquid metals. J. Appl. Phys. 2018, 123, 025902. [Google Scholar] [CrossRef]
- Cherne, F.J.; Hammerberg, J.E.; Andrews, M.J.; Karkhanis, V.; Ramaprabhu, P. On shock driven jetting of liquid from non-sinusoidal surfaces into a vacuum. J. Appl. Phys. 2015, 118, 185901. [Google Scholar] [CrossRef]
- He, A.M.; Liu, J.; Liu, C.; Wang, P. Numerical and theoretical investigation of jet formation in elastic-plastic solids. J. Appl. Phys. 2018, 124, 185902. [Google Scholar] [CrossRef]
- Buttler, W.T.; Oŕo, D.M.; Olson, R.T.; Cherne, F.J.; Hammerberg, J.E.; Hixson, R.S.; Monfared, S.K.; Pack, C.L.; Rigg, P.A.; Stone, J.B.; et al. Second shock ejecta measurements with an explosively driven two-shockwave drive. J. Appl. Phys. 2014, 116, 103519. [Google Scholar] [CrossRef]
- Liu, W.B.; Xi, T.; He, A.M.; Zhou, T.T.; Xin, J.T.; Liu, N.S.; Wang, P. Numerical and experimental study of the second ejection from a grooved tin surface under laser-driven shock loading. Int. J. Impact Eng. 2022, 161, 104135. [Google Scholar] [CrossRef]
- Karkhanis, V.; Ramaprabhu, P.; Buttler, W.T.; Hammerberg, J.E.; Cherne, F.J.; Andrews, M.J. Ejecta production from second shock: Numerical simulations and experiments. J. Dyn. Behav Mater. 2017, 3, 265–279. [Google Scholar] [CrossRef]
- Lucy, L.B. Numerical approach to testing of fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar]
- Lind, S.J.; Rogers, B.D.; Stansby, P.K. Review of smoothed particle hydrodynamics: Towards converged Lagrangian flow modelling. Proc. R. Soc. A. 2020, 476, 20190801. [Google Scholar]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Zhang, A.M. The plus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar]
- Ye, T.; Pan, D.Y.; Huang, C.; Liu, M.B. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids. 2019, 21, 011301. [Google Scholar] [CrossRef]
- Antona, R.; Vacondio, R.; Avesani, D.; Righetti, M.; Renzi, M. Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction. Water 2021, 13, 2432. [Google Scholar] [CrossRef]
- Xu, X.Y.; Cheng, J.; Peng, S.; Yu, P. Numerical simulations of Phan-Thien-Tanner viscoelastic fluid flows based on the SPH method. Eng. Anal. Bound. Elem. 2024, 158, 473–485. [Google Scholar]
- Sugiura, K.; Inutsuka, S. An extension of Godunov SPH II: Application to elastic dynamics. J. Comput. Phys. 2017, 333, 78–103. [Google Scholar]
- Wang, L.; Xu, F.; Yang, Y. An improved total Lagrangian SPH method for modeling solid deformation and damage. Eng. Anal. Bound. Elem. 2021, 133, 286–302. [Google Scholar]
- Rahimi, M.N.; Moutsanidis, G. A smoothed particle hydrodynamics approach for phase field modeling of brittle fracture. Comput. Methods Appl. Mech. Eng. 2022, 398, 115191. [Google Scholar]
- Antuono, M.; Pilloton, C.; Colagrossi, A.; Durante, D. Clone particles: A simplified technique to enforce solid boundary conditions in SPH. Comput. Methods Appl. Mech. Eng. 2023, 409, 115973. [Google Scholar]
- Liu, W.B.; Duan, Z.P.; Liu, Y.; Huang, F.L. 3D hybrid particle contact method for ignition response of high explosives and high velocity impact. Appl. Math. Model. 2025, 140, 115911. [Google Scholar]
- Zhang, A.M.; Sun, P.N.; Ming, F.R.; Colagrossi, A. Smoothed particle hydrodynamics and its applications in fluid-structure interactions. J. Hydrodyn. 2017, 29, 187–216. [Google Scholar]
- Gao, T.R.; Qiu, H.H.; Fu, L. A block-based adaptive particle refinement SPH method for fluid-structure interaction problems. Comput. Methods Appl. Mech. Eng. 2022, 399, 115356. [Google Scholar]
- Khayyer, A.; Gotoh, H.; Shimizu, Y.; Gotoh, T. An improved Riemann SPH-Hamiltonian SPH coupled solver for hydroelastic fluid-structure interactions. Eng. Anal. Bound. Elem. 2024, 158, 332–355. [Google Scholar]
- Feng, R.F.; Fourtakas, G.; Rogers, B.D.; Lombardi, D. A general smoothed particle hydrodynamics (SPH) formulation for coupled liquid flow and solid deformation in porous media. Comput. Methods Appl. Mech. Eng. 2024, 419, 116581. [Google Scholar]
- Bao, T.T.; Hu, J.; Wang, S.J.; Huang, C.; Yu, H.; Shakibaeinia, A. An entirely SPH-based FSI solver and numerical investigations on hydrodynamic characteristics of the flexible structure with an ultra-thin characteristic. Comput. Methods Appl. Mech. Eng. 2024, 431, 117255. [Google Scholar]
- Fan, H.F.; Bergel, G.L.; Li, S.F. A hybrid peridynamics–SPH simulation of soil fragmentation by blast loads of buried explosive. Int. J. Impact Eng. 2016, 87, 14–27. [Google Scholar]
- Zhang, Z.L.; Liu, M.B. Smoothed particle hydrodynamics with kernel gradient correction for modeling high velocity impact in two- and three-dimensional spaces. Eng. Anal. Bound. Elem. 2017, 83, 141–157. [Google Scholar]
- Peng, Y.X.; Zhang, A.M.; Ming, F.R. Numerical simulation of structural damage subjected to the near-field underwater explosion based on SPH and RKPM. Ocean. Eng. 2021, 222, 108576. [Google Scholar]
- Chen, J.Y.; Feng, D.L.; Liu, J.H.; Yu, S.Y.; Lu, Y. Numerical modeling of the damage mechanism of concrete soil multilayered medium subjected to underground explosion using the GPU-accelerated SPH. Eng. Anal. Bound. Elem. 2023, 151, 265–274. [Google Scholar]
- Ceri, S.; Khodaei, Z.S. Numerical investigation of hypervelocity impact simulation with FEM/SPH formulation for space structures. Int. J. Impact Eng. 2024, 187, 104926. [Google Scholar]
- Liu, W.B.; He, A.M.; Wang, P. Effect of shock breakout pressure on material ejection from tin surface under unsupported shocks. AIP Adv. 2018, 8, 095023. [Google Scholar]
- Xin, J.T.; He, A.M.; Liu, W.B.; Chu, G.B.; Yu, M.H.; Fan, W.; Wu, W.C.; Xi, T.; Shui, M.; Zhao, Y.Q.; et al. X-ray radiography of microjetting from grooved surfaces in tin sample subjected to laser driven shock. J. Micromech. Microeng. 2019, 29, 095011. [Google Scholar]
- Liu, W.B.; He, A.M.; Wang, K.; Xin, J.T.; Shao, J.L.; Liu, N.S.; Wang, P. An improved model of damage depth of shock-melted metal in microspall under triangular wave loading. Chin. Phys. B 2021, 30, 096202. [Google Scholar]
- Libersky, L.D.; Petschek, A.G.; Carney, T.C.; Hipp, J.R.; Allahdadi, F.A. High strain lagrangian hydrodynamics: A three-dimensional SPH code for dynamic material response. J. Comput. Phys. 1993, 109, 67–75. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar]
- Shao, J.R.; Li, H.Q.; Liu, G.R.; Liu, M.B. An improved SPH method for modeling liquid sloshing dynamics. Comput. Struct. 2012, 100–101, 18–26. [Google Scholar]
- Gray, J.P.; Monaghan, J.J.; Swift, R.P. SPH elastic dynamics. Comput. Methods Appl. Mech. Eng. 2001, 190, 6641–6662. [Google Scholar]
- Benz, W. Smooth Particle Hydrodynamics: A Review; Springer: Dordrecht, The Netherlands, 1990; pp. 269–288. [Google Scholar]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at highstrain rate. J. Appl. Phys. 1980, 51, 1498. [Google Scholar]
- Xiang, M.Z.; Jiang, S.Q.; Chen, J. Theoretical investigations on melting/crystallization kinetics in overheated/overcooled aluminum at high pressures. J. Appl. Phys. 2019, 126, 125113. [Google Scholar] [CrossRef]
- Tang, W.H. Shock Wave Physics; Science Press: Beijing, China, 2011; pp. 162–247. (In Chinese) [Google Scholar]
- Kanel, G.I. Unusual behaviour of usual materials in shock waves. J. Phys. Conf. Ser. 2014, 500, 012001. [Google Scholar] [CrossRef]
- Ran, X.W.; Tang, W.H.; Tan, H.; Dai, C.D. Calculation of shock temperature by considering electronic contribution. Chin. J. High. Pressure Phys. 2006, 20, 153–156. (In Chinese) [Google Scholar]
- Mehta, S. Theoretical melt curves of Al, Cu, Ta and Pb. AIP Conf. Proc. 2006, 845, 258–261. [Google Scholar]
- Kanel, G.I.; Baumung, K.; Rush, D.; Singer, J.; Razorenov, S.V.; Utkin, A.V. Melting of shock-compressed metals in release. AIP Conf. Proc. 1998, 429, 155–158. [Google Scholar]
- Piekutowski, A.J. Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates. Int. J. Impact Eng. 1993, 14, 573–586. [Google Scholar] [CrossRef]
- Wu, B.; He, A.M.; Wang, X.X.; Sun, H.Q.; Wang, P. Numerical investigation of ejecta mass of twice-shocked liquid Sn. J. Appl. Phys. 2023, 133, 165903. [Google Scholar] [CrossRef]
- Jiang, D.D.; Shao, J.L.; Wu, B.; Wang, P.; He, A.M. Sudden change of spall strength induced by shock defects based on atomistic simulation of single crystal aluminum. Scr. Mater. 2022, 210, 114474. [Google Scholar] [CrossRef]
- Wang, J.N.; Wu, F.C.; Wang, P.; He, A.M.; Wu, H.A. Double-shock-induced spall and recompression processes in copper. J. Appl. Phys. 2020, 127, 135903. [Google Scholar] [CrossRef]
- Zhang, Q.; He, A.M.; Zhao, F.Q.; Zhou, T.T.; Wang, P. Understanding the spall behaviors of single crystalline aluminum under double decaying shock loadings: Atomistic simulations and theoretical models. Eur. J. Mech. A/Solids 2024, 105, 105237. [Google Scholar] [CrossRef]
- Sui, H.N.; Wang, X.X.; Wu, B.; Bao, Q.; Zhang, F.H.; Sun, H.Q.; He, A.M.; Wang, P. Cooperative competition between melt-phase and void during micro-spallation and recompression. Int. J. Mech. Sci. 2024, 275, 109276. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Xiao, H. Numerical Simulation of the Elastic–Plastic Ejection from Grooved Aluminum Surfaces Under Double Supported Shocks Using the SPH Method. Appl. Sci. 2025, 15, 3498. https://doi.org/10.3390/app15073498
Liu W, Xiao H. Numerical Simulation of the Elastic–Plastic Ejection from Grooved Aluminum Surfaces Under Double Supported Shocks Using the SPH Method. Applied Sciences. 2025; 15(7):3498. https://doi.org/10.3390/app15073498
Chicago/Turabian StyleLiu, Wenbin, and Han Xiao. 2025. "Numerical Simulation of the Elastic–Plastic Ejection from Grooved Aluminum Surfaces Under Double Supported Shocks Using the SPH Method" Applied Sciences 15, no. 7: 3498. https://doi.org/10.3390/app15073498
APA StyleLiu, W., & Xiao, H. (2025). Numerical Simulation of the Elastic–Plastic Ejection from Grooved Aluminum Surfaces Under Double Supported Shocks Using the SPH Method. Applied Sciences, 15(7), 3498. https://doi.org/10.3390/app15073498





