Dynamic Energy Consumption Modeling for HVAC Systems in Electric Vehicles
Abstract
1. Introduction
2. Materials and Methods
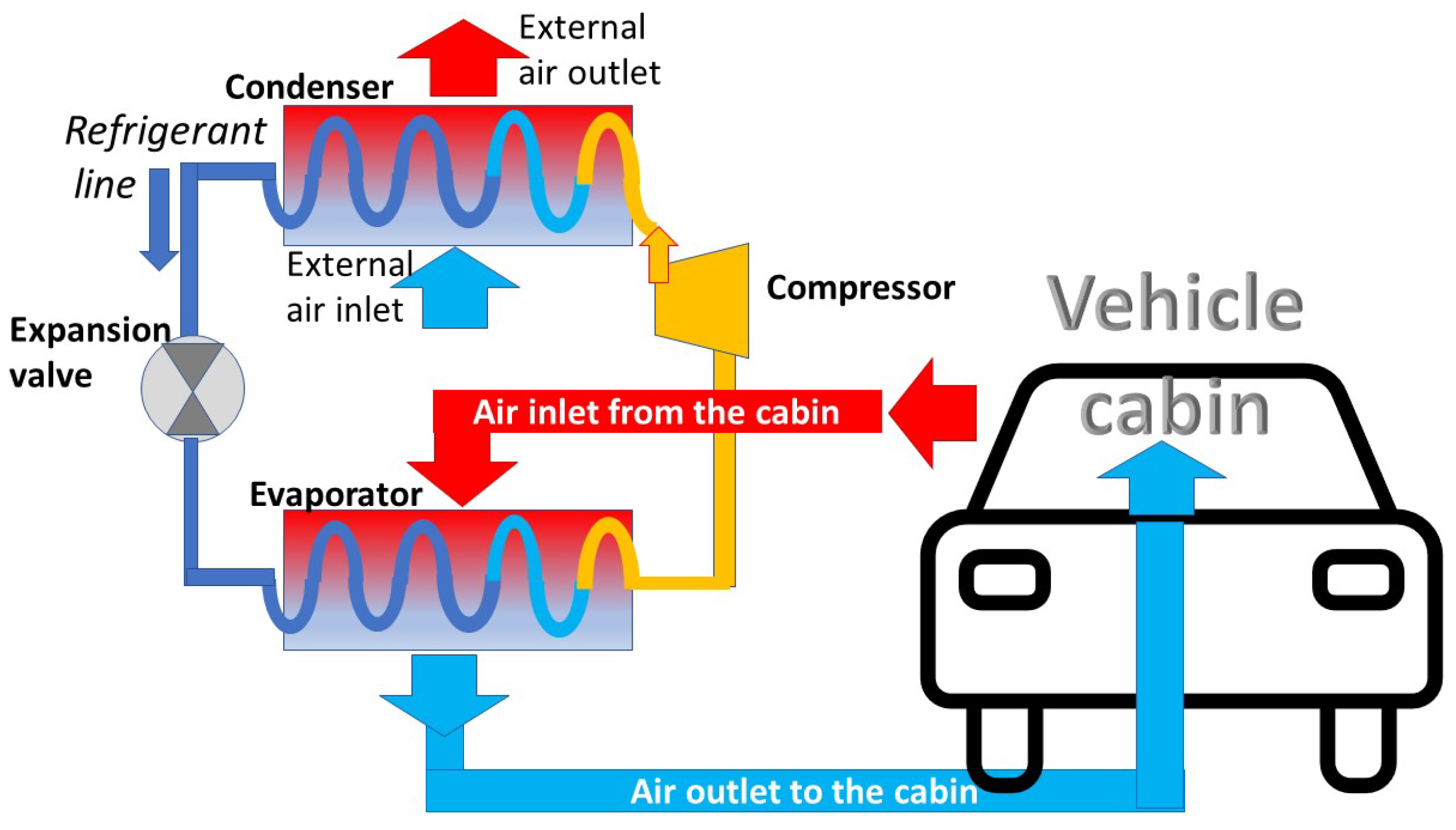
2.1. The HVAC Model
2.1.1. Evaporator
2.1.2. Compressor
2.1.3. Condenser
2.1.4. Expansion Valve
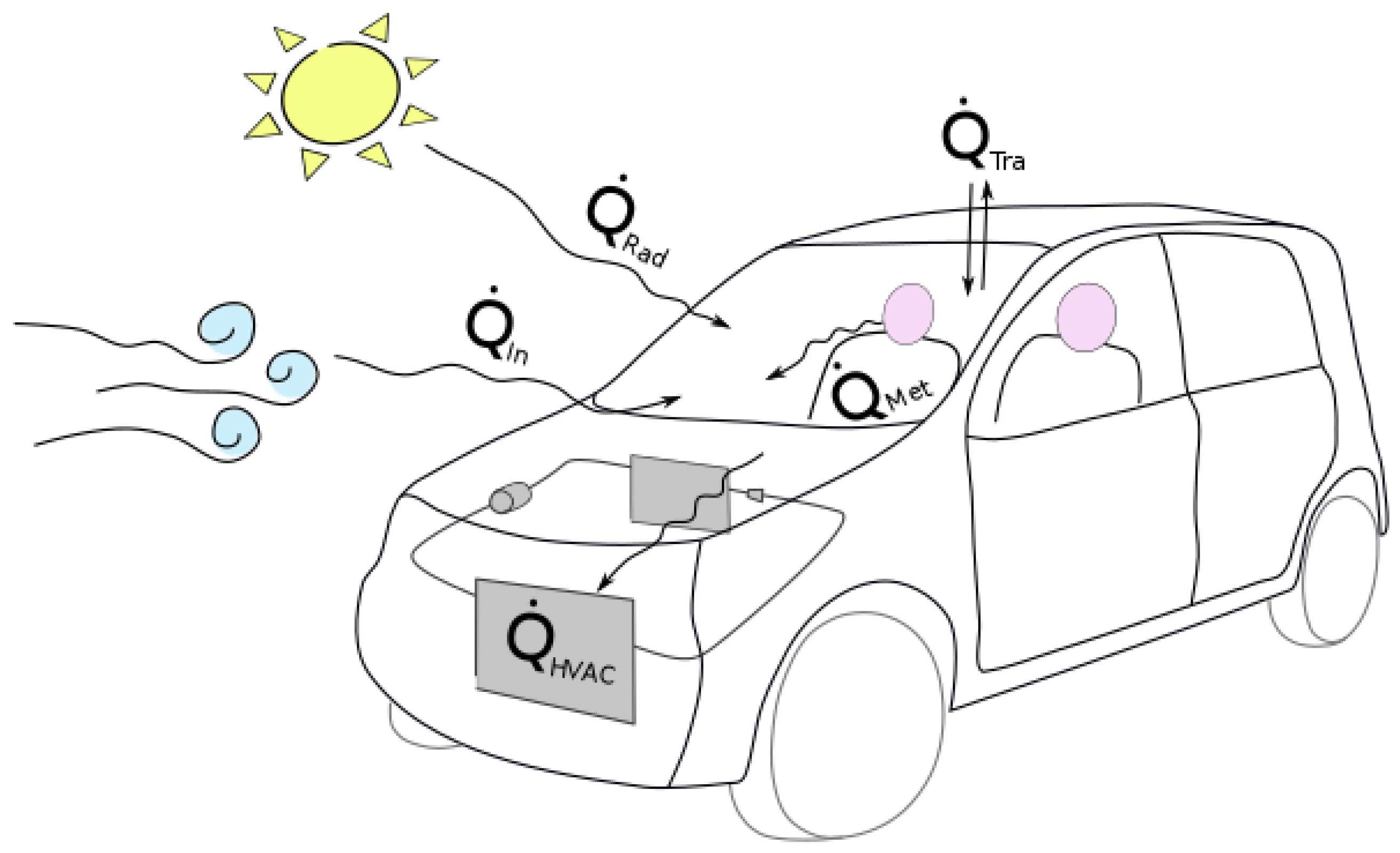
2.2. The Cabin Model
2.2.1. Solar Radiation
- Direct solar radiation, depending on the incident angle of the normal solar radiance with respect to the normal of the surface.
- Diffuse sky radiation .
- Albedo , depending on reflections from the ground and surrounding surfaces.
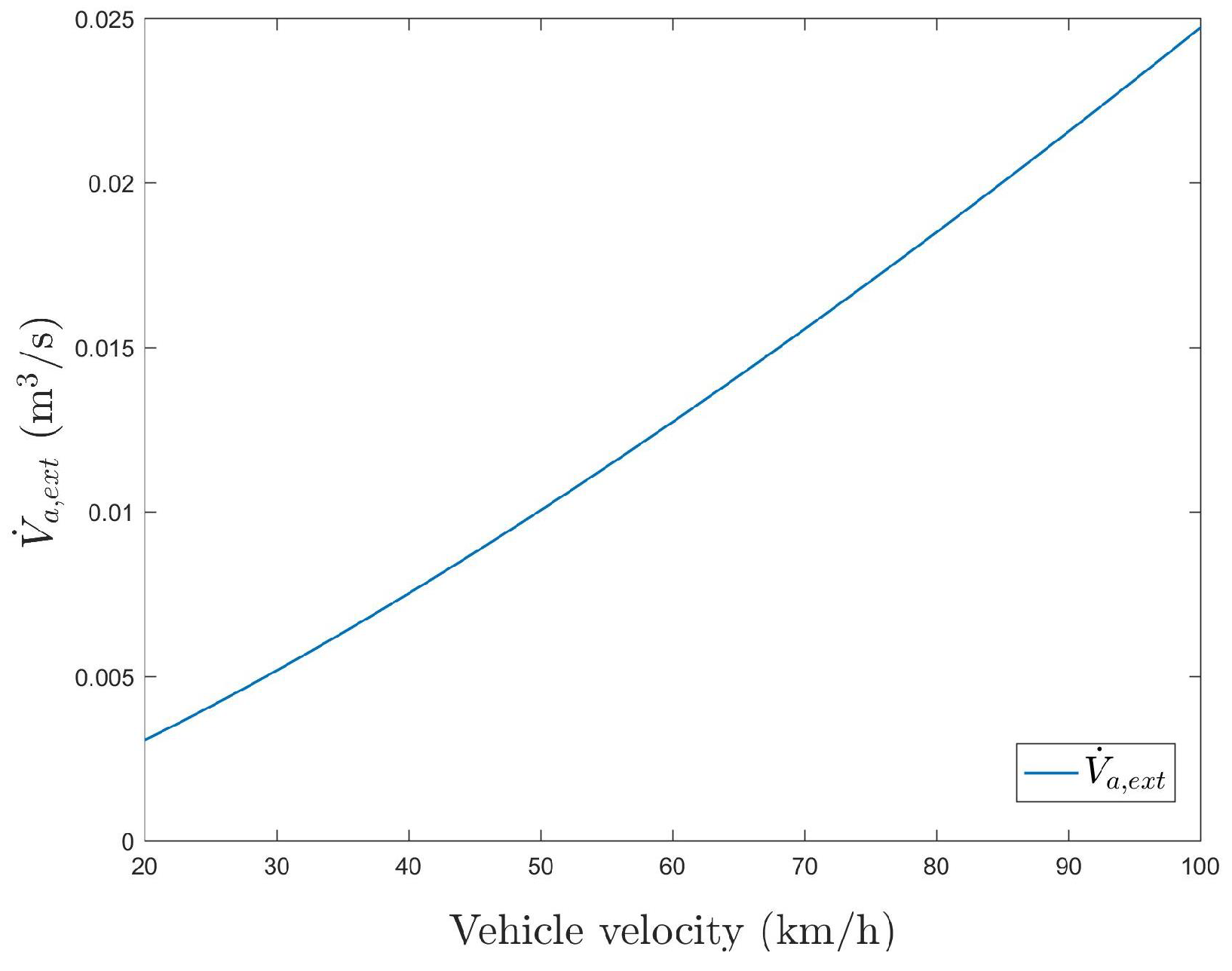
2.2.2. Ventilation and Infiltration
2.2.3. Heat Transmission Through the Vehicle Envelope
2.2.4. Metabolic Load
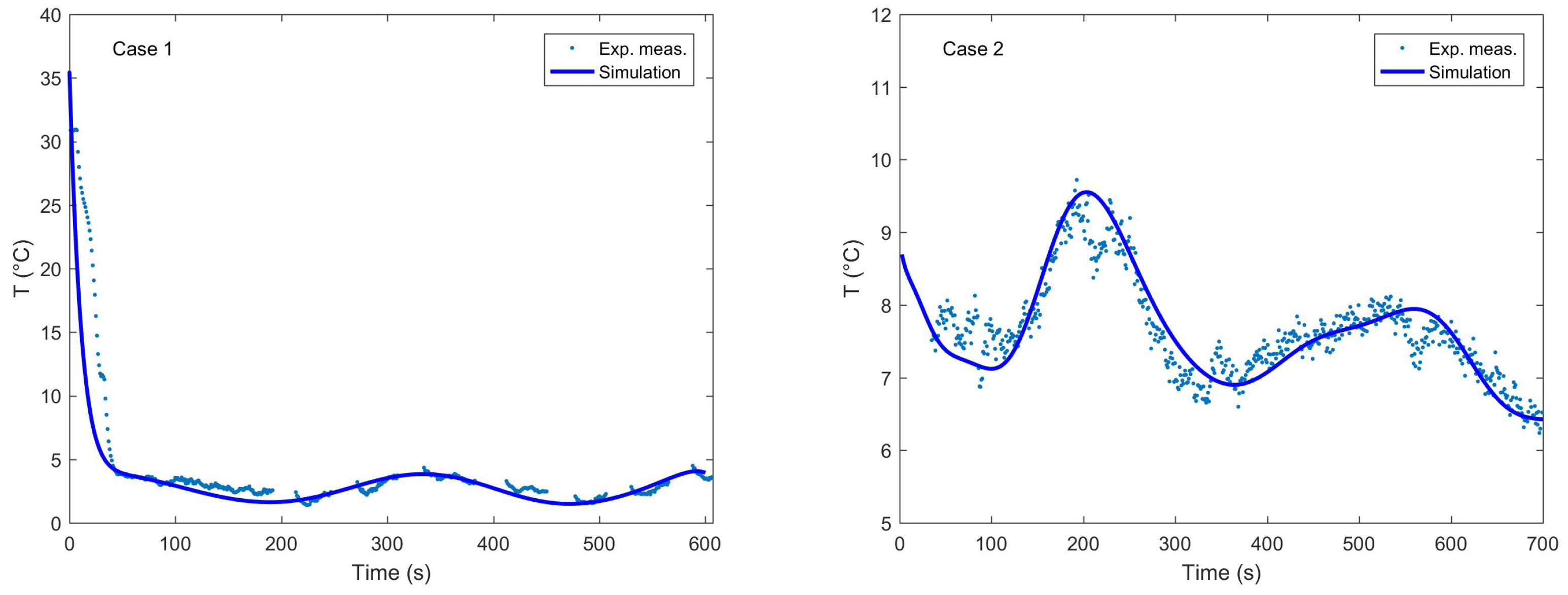
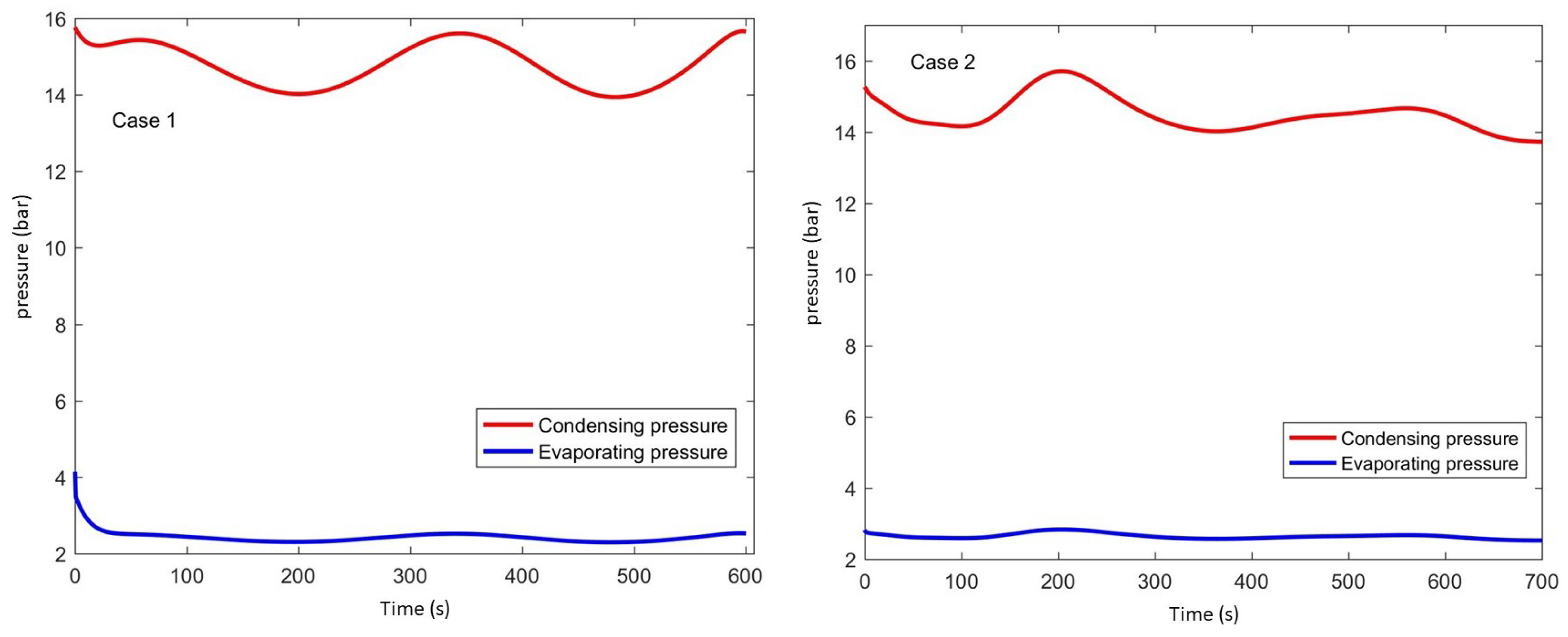
3. Validation of the Model
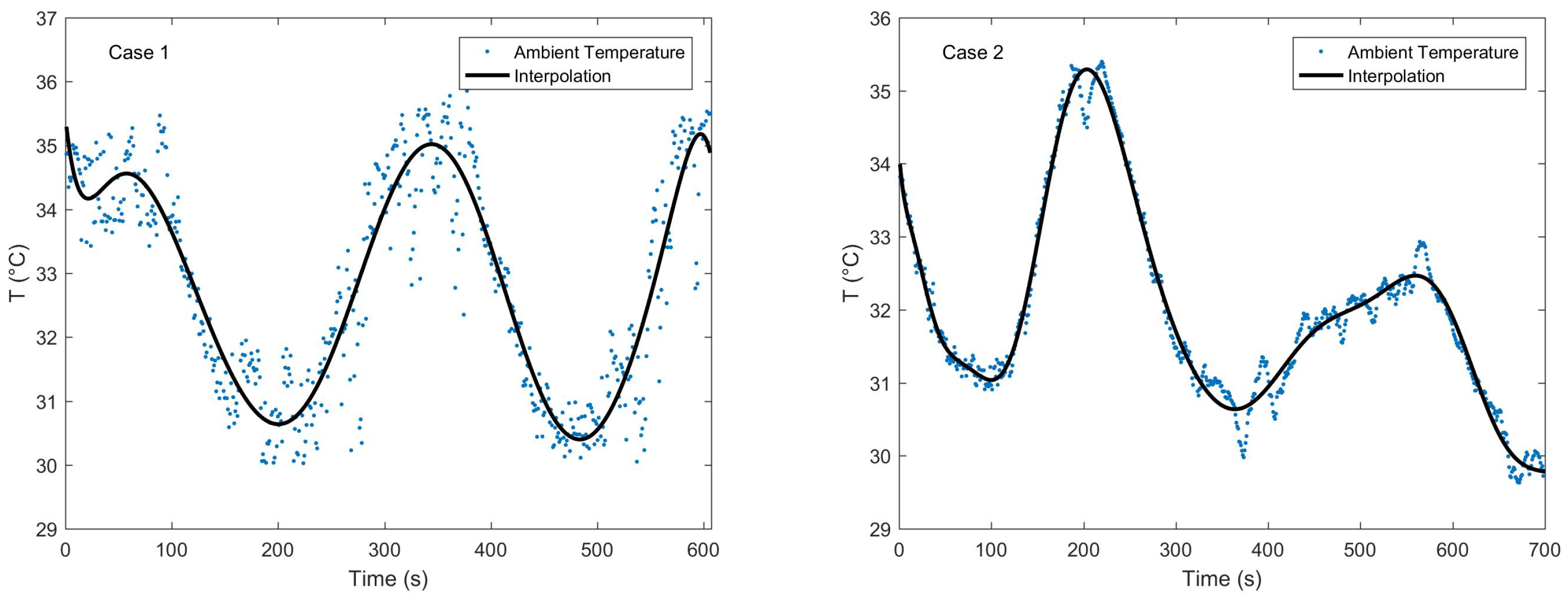
Test Conditions
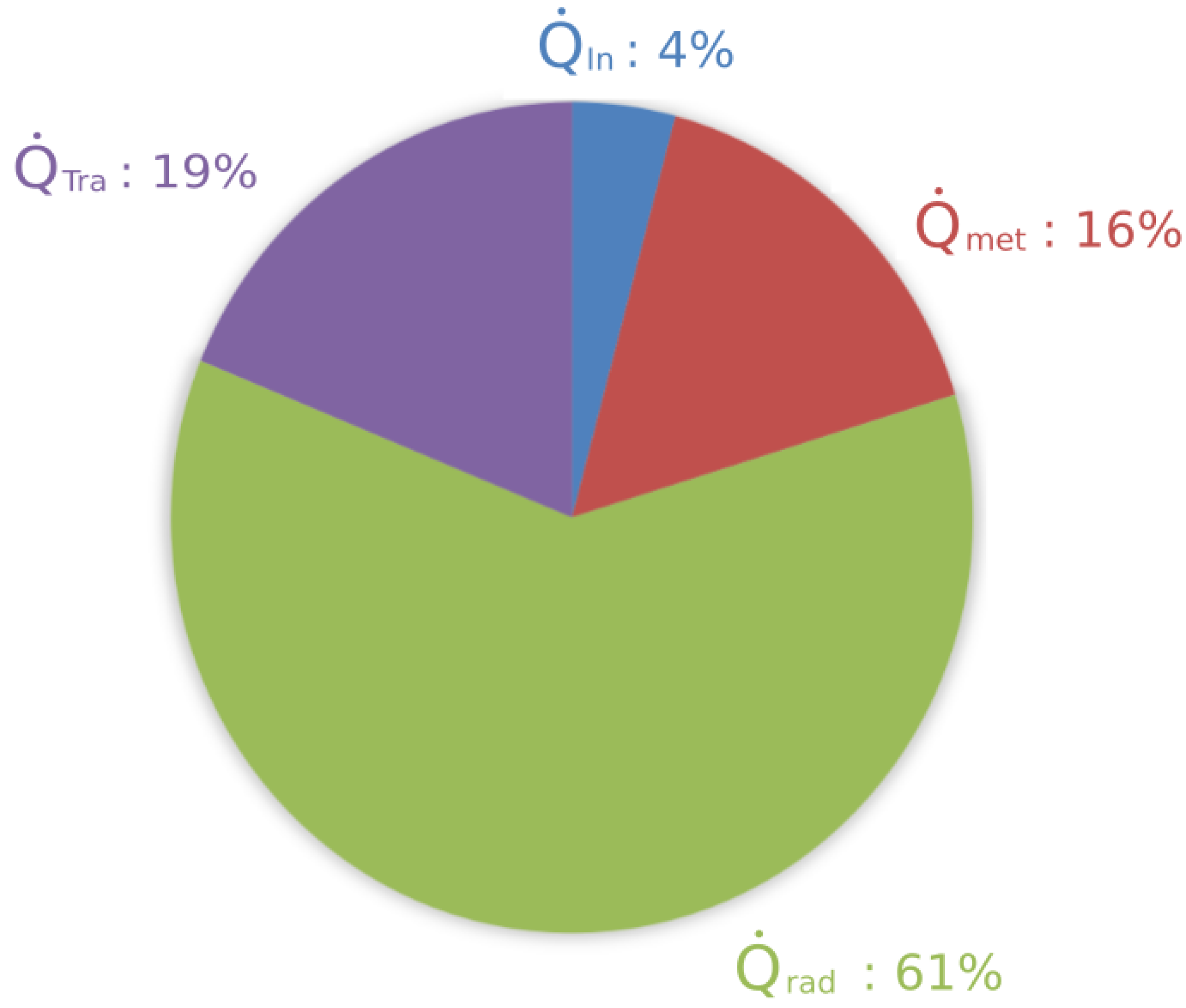
4. Results and Discussion
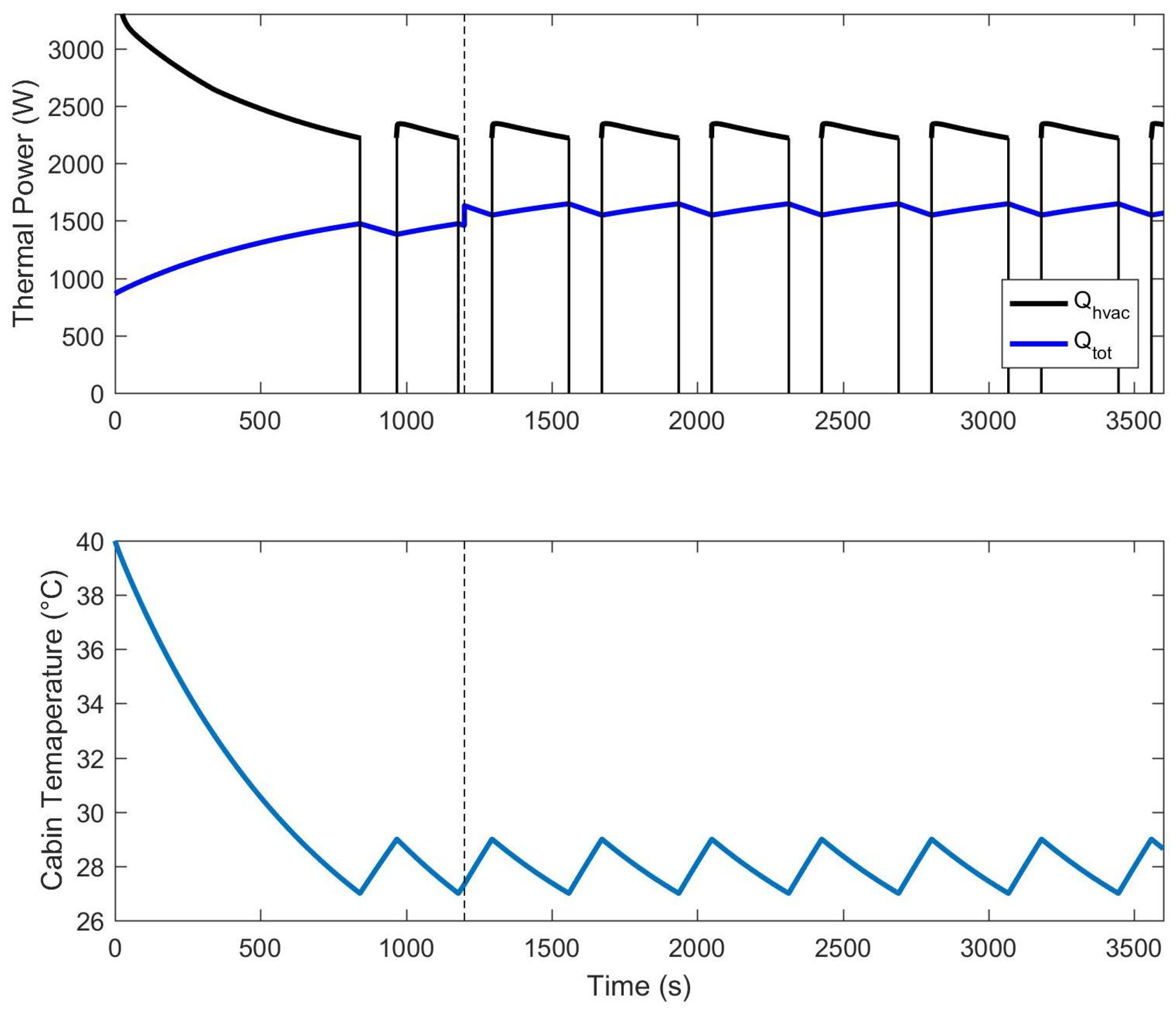
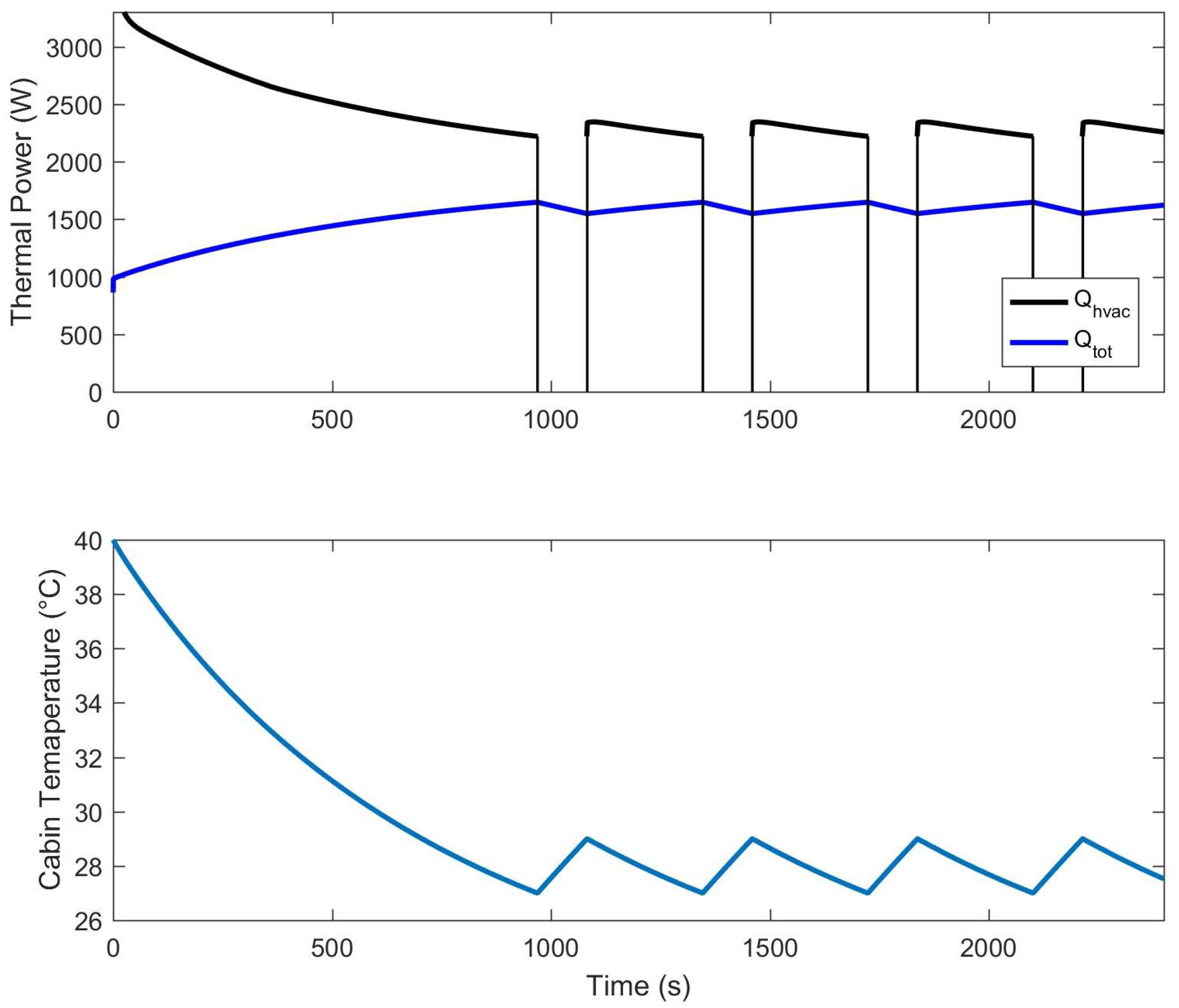
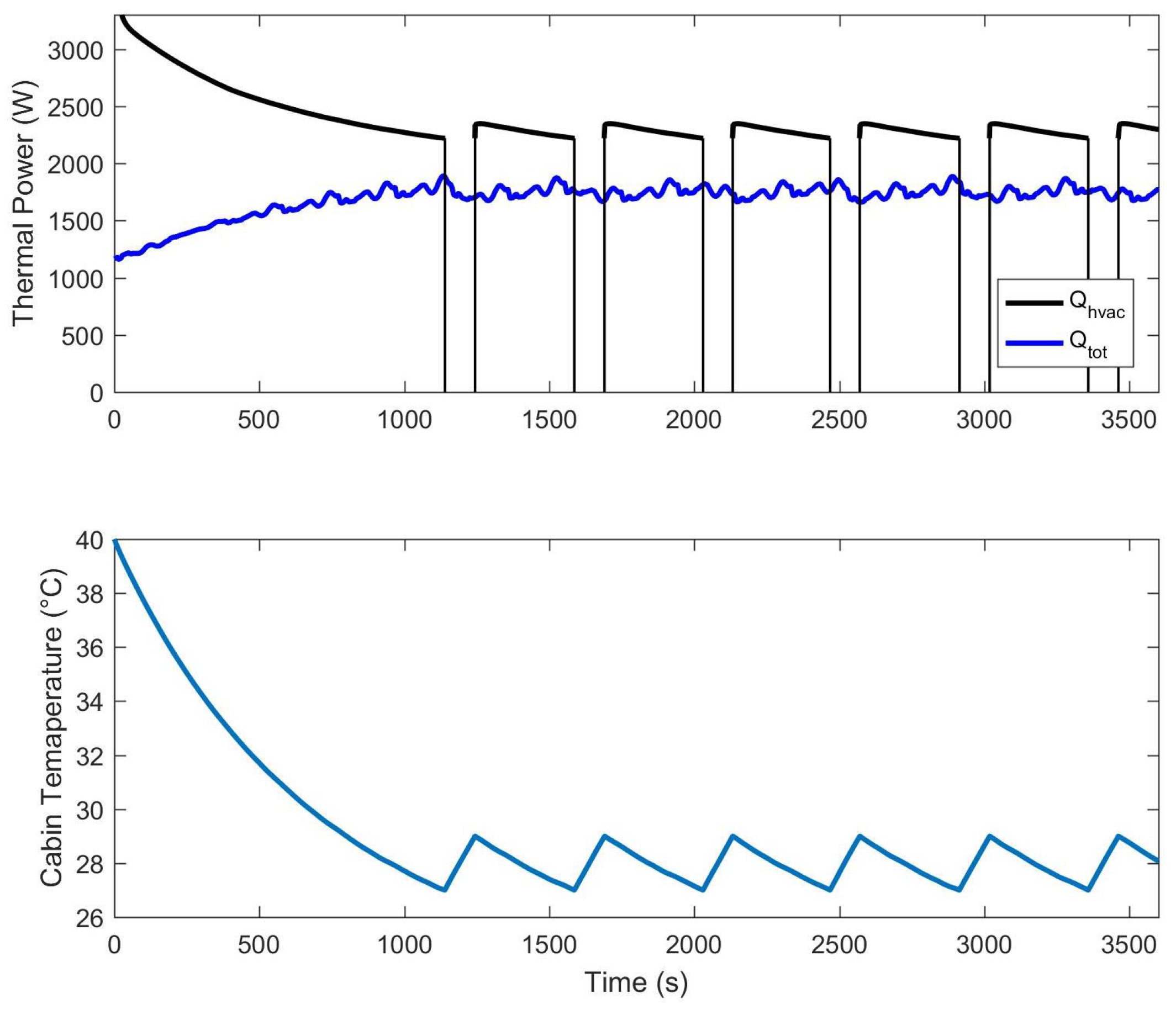
4.1. Constant Speed Driving Condition and the Influence of Precooling Phase
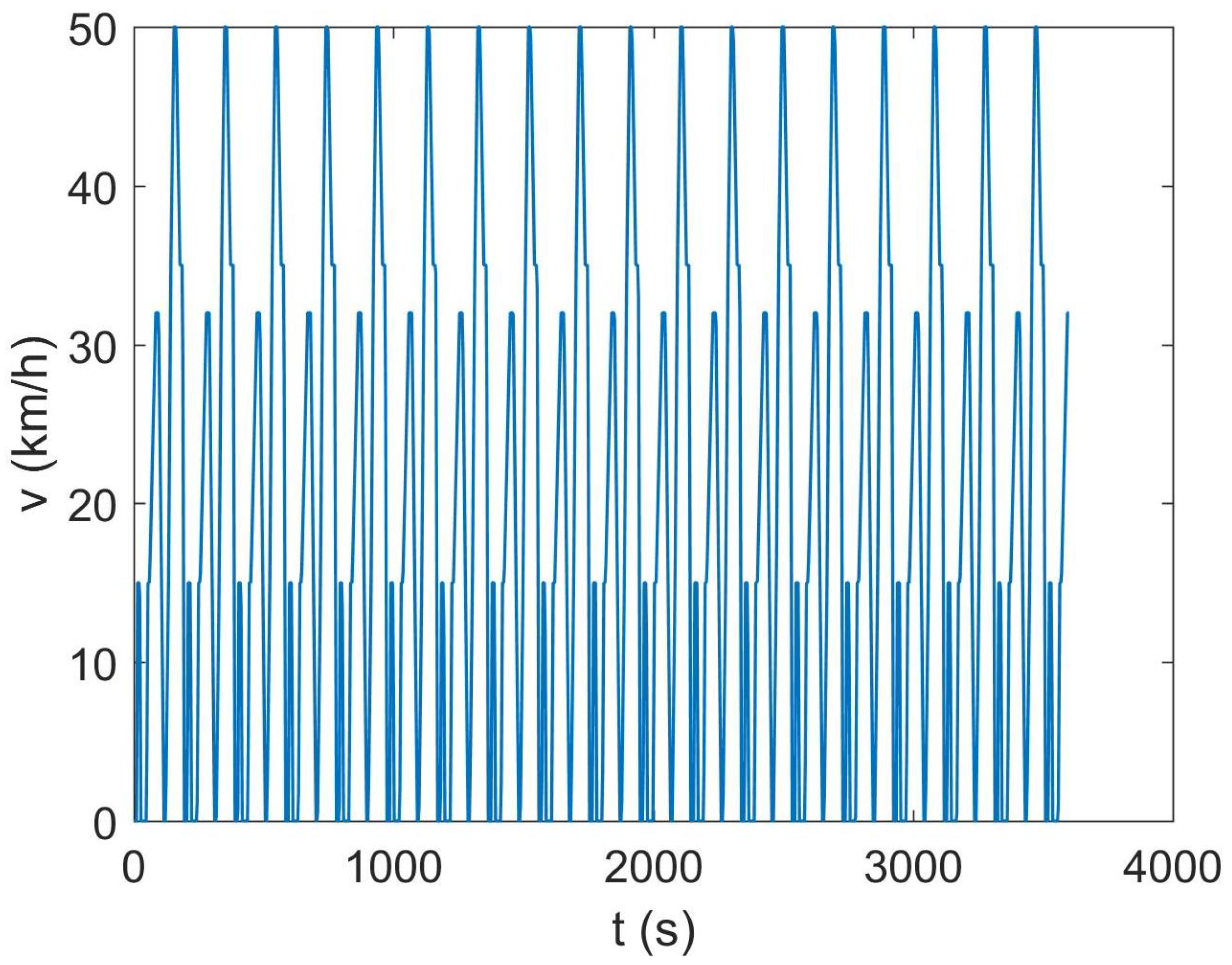
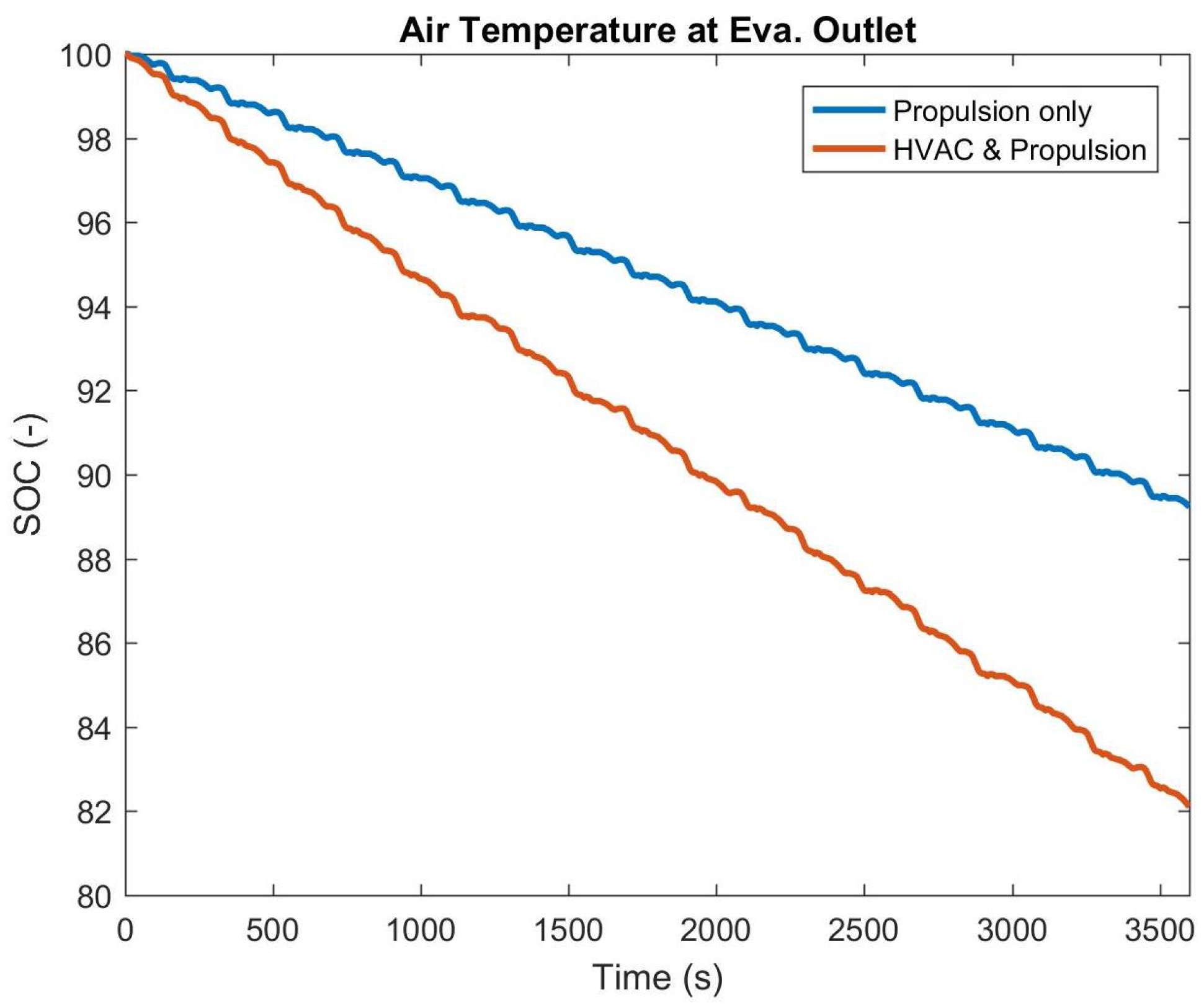
4.2. ECE 15 Driving Cycle
5. Conclusions
- Model and validation: Accurate correlations for refrigerant and air-side heat transfer coefficients are integrated into the model to represent a realistic HVAC system designed for electric vehicles. These correlations are sourced from the literature and are based on the geometry of the heat exchangers used in the experiments. The model’s results were validated through comparisons with experimental measurements performed in a climatic chamber, demonstrating excellent agreement.
- Unsteady analysis of energy consumption: Two different HVAC working conditions were considered for the unsteady analysis of energy consumption. The first condition involves one person in the car, driving at a constant speed for 40 min on a hot summer day. The analysis compares the energy consumed by the HVAC during the drive period in two scenarios: one in which the driver enters a hot car and starts driving immediately and another where the driver enters a car that has undergone a precooling phase. The comparison shows that the energy consumption during the driving period without a precooling phase is 16% greater than with a precooling phase. However, the total energy consumed with precooling is 25% higher than without precooling, but this does not affect the energy delivered by the batteries during the drive. The second condition simulates the behavior of the HVAC system during a regulated driving cycle (ECE 15 driving cycle) that simulates urban mobility. In this case, the HVAC system increases the total energy consumption of the electric vehicle by 40%.
- Importance and future work: The contribution of the HVAC system is significant in the overall energy consumption of an electric vehicle. Therefore, a computational model that allows us to evaluate the electrical consumption of the HVAC system is crucial to improving the efficiency of electric mobility. The methodology framework proposed in this article can be extended to other HVAC systems and applied in different scenarios, allowing more robust optimization techniques for such systems. This approach shows potential practical implications, such as in a tool for describing the dynamic behavior of systems in the vehicle to compare different solutions. In an example, one can compare the energy consumption with different heat exchangers in the evaporator or condenser before building a prototype. Moreover, the dynamic simulation shown in this paper can be a basis for the optimization of a control system for the HVAC system. Hence, the methodologies presented in this paper are very useful for electric vehicle manufacturers or HVAC system developers.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Catano, J.; Zhang, T.; Wen, J.T.; Jensen, M.K.; Peles, Y. Vapor compression refrigeration cycle for electronic cooling—Part I: Dynamic modeling and experimental validation. Int. J. Heat Mass Transf. 2013, 66, 911–921. [Google Scholar] [CrossRef]
- Nunes, T.; Vargas, J.; Ordonez, J.; Shah, D.; Martinho, L. Modeling, simulation and optimization of a vapor compression refrigeration system dynamic and steady state response. Appl. Energy 2015, 158, 540–555. [Google Scholar] [CrossRef]
- Heimel, M.; Berger, E.; Posch, S.; Stupnik, A.; Hopfgartner, J.; Almbauer, R. Transient cycle simulation of domestic appliances and experimental validation. Int. J. Refrig. 2016, 69, 28–41. [Google Scholar]
- Yin, X.; Wang, X.; Li, S.; Cai, W. Energy-efficiency-oriented cascade control for vapor compression refrigeration cycle systems. Energy 2016, 116, 1006–1019. [Google Scholar] [CrossRef]
- Wang, W.; Ren, J.; Yin, X.; Qiao, Y.; Cao, F. Energy-efficient operation of the thermal management system in electric vehicles via integrated model predictive control. J. Power Sources 2024, 603, 234415–234427. [Google Scholar]
- Liang, K.; Wang, M.; Gao, C.; Dong, B.; Feng, C.; Zhou, X.; Liu, J. Advances and challenges of integrated thermal management technologies for pure electric vehicles. Sustain. Energy Technol. Assessments 2021, 46, 101319. [Google Scholar] [CrossRef]
- Ibrahim, A.; Jiang, F. The electric vehicle energy management: An overview of the energy system and related modeling and simulation. Renew. Sustain. Energy Rev. 2021, 144, 111049. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, Q.; Wang, Z. A systematic review on modelling the thermal environment of vehicle cabins. Appl. Therm. Eng. 2024, 257, 124142. [Google Scholar] [CrossRef]
- He, L.; Jing, H.; Zhang, Y.; Li, P.; Gu, Z. Review of thermal management system for battery electric vehicle. J. Energy Storage 2023, 59, 106443. [Google Scholar] [CrossRef]
- Karimshoushtari, M.; Kordestani, M.; Shojaei, S.; Dönmez, B.; Rashid, M.; Weslati, F.; Bouyoucef, K. On the applicability of advanced model-based strategies to control of electrified vehicle thermal systems. Energy 2023, 283, 128791. [Google Scholar] [CrossRef]
- Narimani, M.; Emami, S.; Banazadeh, A.; Modarresi, A. A unified thermal management framework for electric vehicles: Design and test bench implementation. Appl. Therm. Eng. 2024, 248, 123057. [Google Scholar] [CrossRef]
- Lahn, F.; Chen, J.; Li, W. Effect of urban microclimates on dynamic thermal characteristics of a vehicle cabin. Case Stud. Therm. Eng. 2023, 49, 103162. [Google Scholar] [CrossRef]
- Barlow, T.; Latham, S.; McCrae, I.; Boulter, P. A Reference Book of Driving Cycles For Use in The Measurement of Road Vehicle Emissions; TRL Published Project Report; Crowthorne House: Berkshire, UK, 2009. [Google Scholar]
- Fayazbakhsh, M.A.; Bahrami, M. Comprehensive Modeling of Vehicle Air Conditioning Loads Using Heat Balance Method; SAE Technical Paper 2013-01-1507; SAE: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Özışık, M. Heat Transfer: A Basic Approach; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Wagner, W.; PrussVaghela, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, Y.; Sun, Y.; Chen, J. Development of a mini-channel evaporator model using {R1234yf} as working fluid. Int. J. Refrig. 2012, 35, 2166–2178. [Google Scholar] [CrossRef]
- Mendoza-Miranda, J.; Ramírez-Minguela, J.; Muñoz-Carpio, V.; Navarro-Esbrí, J. Development and validation of a micro-fin tubes evaporator model using {R134a} and {R1234yf} as working fluids. Int. J. Refrig. 2015, 50, 32–43. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Steinke, M.E. Predicting heat transfer during flow boiling in minichannels and microchannels. Trans. Am. Soc. Heat. Refrig. Air Cond. Eng. 2003, 109, 667–676. [Google Scholar]
- Kandlikar, S.G. A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes. J. Heat Transf. 1990, 112, 219–228. [Google Scholar] [CrossRef]
- Petukhov, B.; Popov, V. Theoretical calculation of heat exchange and frictional resistance in turbulent flow in tubes of an incompressible fluid with variable physical properties (Heat exchange and frictional resistance in turbulent flow of liquids with variable physical properties through tubes). High Temp. 1963, 1, 69–83. [Google Scholar]
- Gnielinski, V. New equations for heat and mass-transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Kakaç, S.; Shah, R.; Aung, W. Handbook of Single-Phase Convective Heat Transfer, (Chapter 3) Laminar Convective Heat Transfer in Ducts; A Wiley Interscience Publication, Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Chang, Y.J.; Wang, C.C. A generalized heat transfer correlation for Iouver fin geometry. Int. J. Heat Mass Transf. 1997, 40, 533–544. [Google Scholar] [CrossRef]
- Cavallini, A.; Del Col, D.; Doretti, L.; Matkovic, M.; Rossetto, L.; Zilio, C.; Censi, G. Condensation in Horizontal Smooth Tubes: A New Heat Transfer Model for Heat Exchanger Design. Heat Transf. Eng. 2006, 27, 31–38. [Google Scholar] [CrossRef]
- ASHRAE Handbook. Fundamentals; American Society of Heating, Refrigerating and Air-conditioning Engineers: Peachtree Corners, GA, USA, 1997. [Google Scholar]
- Bolz, R. CRC Handbook of Tables for Applied Engineering Science; CRC Handbook Series; Taylor & Francis: Boca Raton, FL, USA, 1973. [Google Scholar]
- Fletcher, B.; Saunders, C. Air change rates in stationary and moving motor vehicles. J. Hazard. Mater. 1994, 38, 243–256. [Google Scholar] [CrossRef]
- ISO 8996:2004; Ergonomics of the Thermal Environment—Determination of Metabolic Rate. International Organization for Standardization: Geneva, Switzerland, 2004.
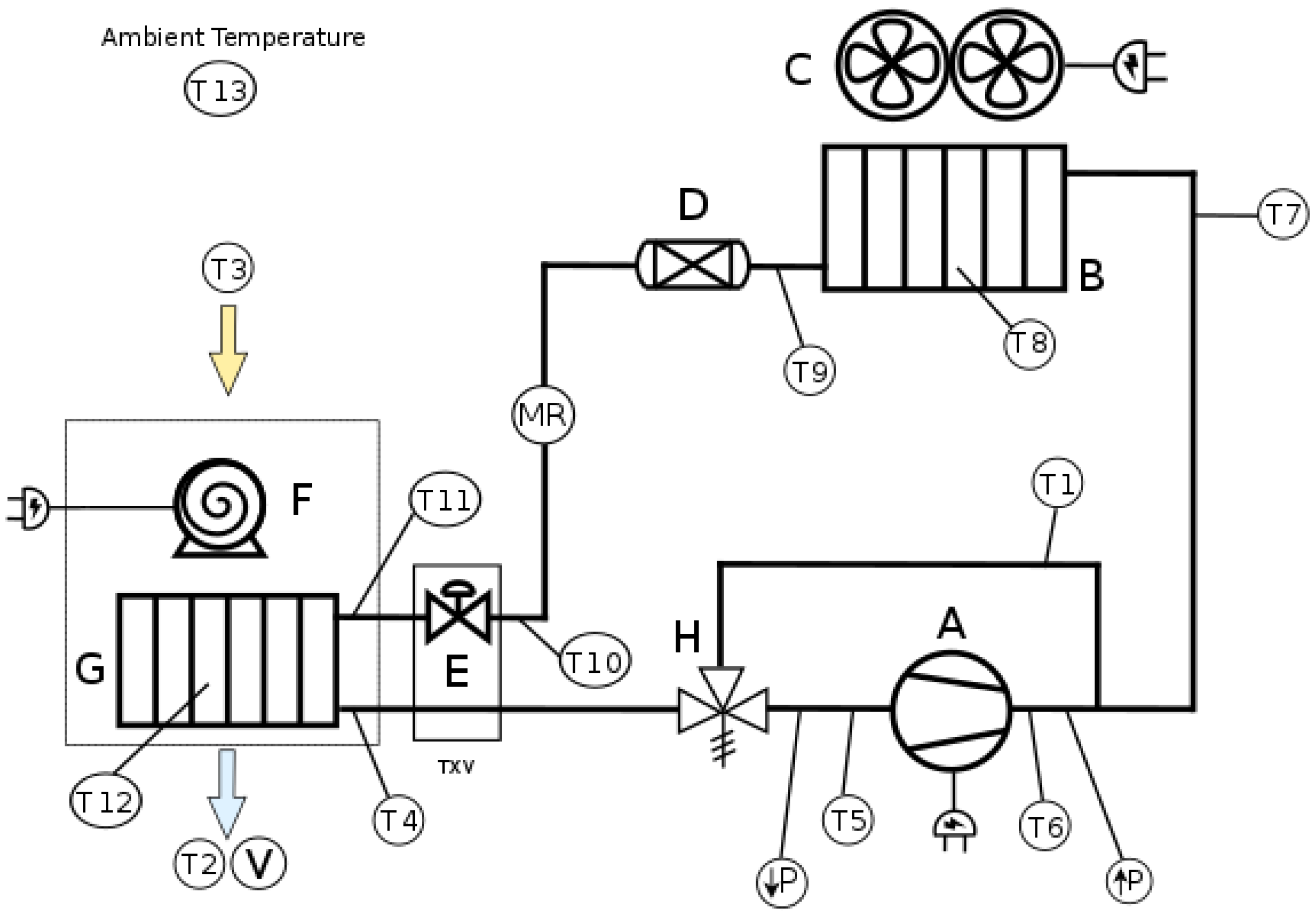
| Description | Uncertainty |
|---|---|
| T-type thermocouples | ±0.5 °C |
| Low-pressure gauge | ±0.2 bar |
| High-pressure gauge | ±0.5 bar |
| Refrigerant mass flow rate | ±0.5% of reading |
| Volumetric air flow rate | ±3% of reading |
| Description | Case | Simulation | Measurements |
|---|---|---|---|
| High pressure | 1 | 14.8 | 15.5 ± 0.5 |
| Low pressure | 1 | 2.1 | 2.0 ± 0.2 |
| High pressure | 2 | 14.4 | 15.0 ± 0.5 |
| Low pressure | 2 | 2.3 | 2.0 ± 0.2 |
| Imposed Condition | Values | |
|---|---|---|
| Outdoor temperature | 35 °C | |
| Initial inner temperature | 40 °C | |
| Relative humidity | 35% | |
| Solar thermal load | 1100 W | |
| Passenger number | 1 |
| With Precooling | |
|---|---|
| Simulation time | 3600 s |
| Average vehicle velocity (t < ) | 0 km/h |
| Average vehicle velocity (t > ) | 20 km/h |
| Without Precooling | |
| Simulation time | 2400 s |
| Average vehicle velocity | 20 km/h |
| Imposed Condition | Values | |
|---|---|---|
| Simulation time | 3600 s | |
| Outdoor temperature | 35 °C | |
| Initial inner temperature | 40 °C | |
| Relative humidity | 35% | |
| Solar thermal load | 1100 W | |
| Passenger number | 2 | |
| Set-point temperature | 28 °C | |
| Total distance covered | 19.8 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pulvirenti, B.; Puccetti, G.; Semprini, G. Dynamic Energy Consumption Modeling for HVAC Systems in Electric Vehicles. Appl. Sci. 2025, 15, 3514. https://doi.org/10.3390/app15073514
Pulvirenti B, Puccetti G, Semprini G. Dynamic Energy Consumption Modeling for HVAC Systems in Electric Vehicles. Applied Sciences. 2025; 15(7):3514. https://doi.org/10.3390/app15073514
Chicago/Turabian StylePulvirenti, Beatrice, Giacomo Puccetti, and Giovanni Semprini. 2025. "Dynamic Energy Consumption Modeling for HVAC Systems in Electric Vehicles" Applied Sciences 15, no. 7: 3514. https://doi.org/10.3390/app15073514
APA StylePulvirenti, B., Puccetti, G., & Semprini, G. (2025). Dynamic Energy Consumption Modeling for HVAC Systems in Electric Vehicles. Applied Sciences, 15(7), 3514. https://doi.org/10.3390/app15073514












