Effective Ductile Fracture Characterization of 17-4PH and Ti6Al4V by Shear–Tension Tests: Experiments and Damage Models Calibration †
Abstract
1. Introduction
2. Theoretical Background
3. Materials and Methods
- Driemeier’s specimens (RB, RNB, Pos10, and Pos30);
- Mohr’s specimens (RB, RNB, Mohr00, and Mohr15);
- Driemeier and Mohr’s specimens (RB, RNB, Pos10, Pos30, Mohr00, and Mohr15);
- All tests (RB, RNB, PS, Tors, Pos10, Pos30, Mohr00, and Mohr15).
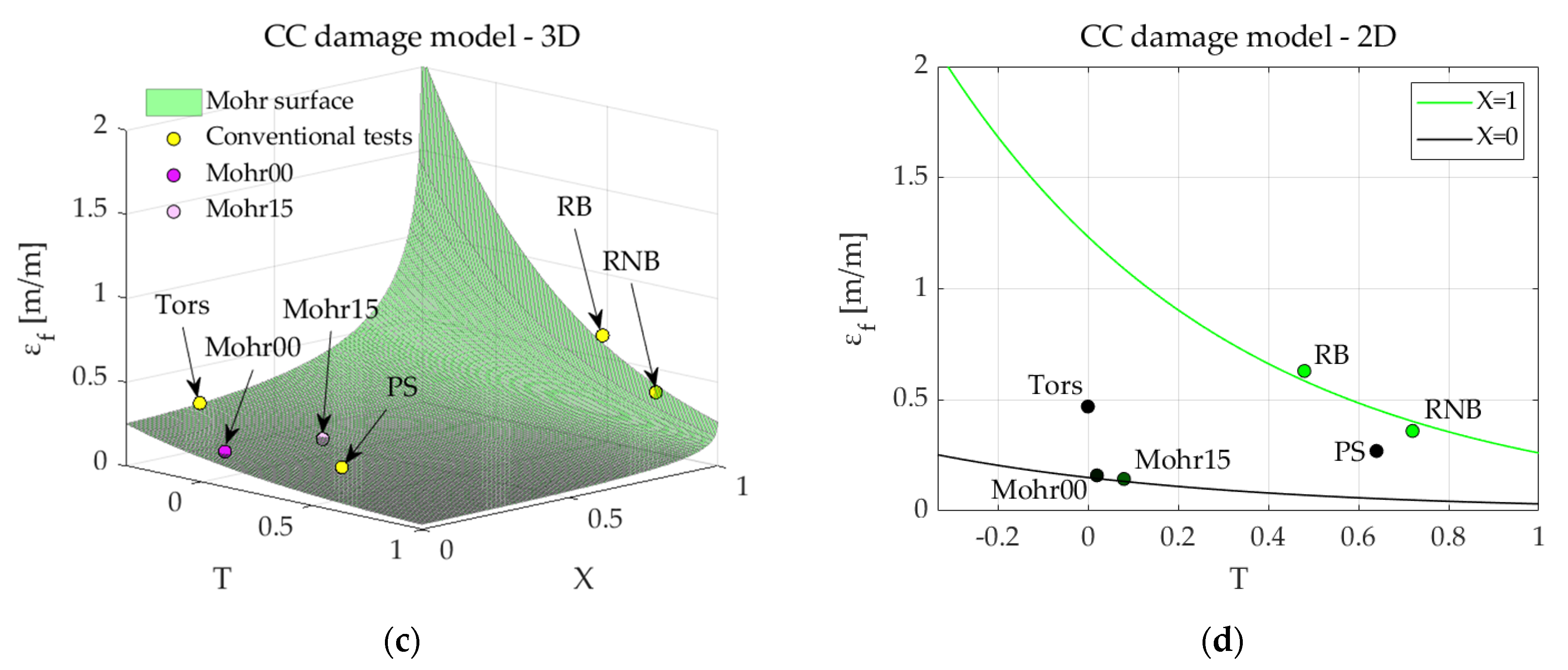
4. Results and Discussion
5. Conclusions
- ▪
- The Driemeier and Mohr’s test specimens are capable of generating several mixed tensile–shear stress states in a low triaxiality regime using only a uniaxial testing machine;
- ▪
- It is possible to vary the tensile-to-shear ratio of the stress state just by changing the machined geometry and dimensions (Driemeier), or just by clamping the samples at a different angle (Mohr) through a purposely designed gripping system;
- ▪
- The ductility of a 17-4PH and of a Ti6Al4V alloys could be estimated with the same accuracy level achievable using a more typical complex multiaxial testing and calibration procedure;
- ▪
- The prediction effectiveness of the Modified Mohr–Coulomb, Coppola–Cortese, and Hosford–Coulomb damage models was investigated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vural, H.; Erdogan, C.; Fenercioğlu, T.O.; Yalcinkaya, T. Ductile failure prediction during the flow forming process. Procedia Struct. Integr. 2022, 35, 25–33. [Google Scholar] [CrossRef]
- Mohamed, M.; Amer, M.; Shazly, M.; Masters, I. Assessment of different ductile damage models of AA5754 for cold forming. Int. J. Adv. Manuf. Technol. 2021, 114, 1219–1231. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Rosenbusch, D.; Wester, H.; Althaus, P. Comparison of three different ductile damage models for deep drawing simulation of high-strength steels. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1238, 012021. [Google Scholar] [CrossRef]
- McClintock, F.A. A criterion for ductile fracture by growth of holes. ASME J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Hancock, J.W.; Mackenzie, A.C. On the mechanism of ductile failure in high-strength steel subjected to multi-axial stresses. J. Mech. Phys. Solids 1976, 24, 147–160. [Google Scholar] [CrossRef]
- Thomason, P. A three-dimensional model for ductile fracture by the growth and coalescence of microvoids. Acta Metall. 1985, 33, 1087–1095. [Google Scholar] [CrossRef]
- Rousselier, G. Ductile fracture models and their potential in local approach of fracture. Nucl. Eng. Des. 1987, 105, 97–111. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I Yield criteria and flow rules for porous ductile media. ASME J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Kachanov, L.M. Time of the rupture process under creep conditions. Izv. Akad. Nauk SSSR Otd. Tekh. Nauk 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. Creep Problems in Structural Members; North-Holland Series in Applied Mathematics and Mechanics; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1969; Volume 7, 803p. [Google Scholar]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. ASME J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Chaboche, J.-L. Damage induced anisotropy: On the difficulties associated with the active/passive unilateral condition. Int. J. Damage Mech. 1992, 1, 148–171. [Google Scholar] [CrossRef]
- Chandrakanth, S.; Pandey, P.C. An isotropic damage model for ductile material. Eng. Fract. Mech. 1995, 50, 457–465. [Google Scholar] [CrossRef]
- Chaboche, J.; Boudifa, M.; Saanouni, K. A CDM approach of ductile damage with plastic compressibility. Int. J. Fract. 2006, 137, 51–75. [Google Scholar] [CrossRef]
- Zhang, K.; Badreddine, H.; Hfaiedh, N.; Saanouni, K.; Liu, J. Enhanced CDM model accounting of stress triaxiality and Lode angle for ductile damage prediction in metal forming. Int. J. Damage Mech. 2021, 30, 260–282. [Google Scholar] [CrossRef]
- Bonora, N. A nonlinear CDM model for ductile failure. Eng. Fract. Mech. 1997, 58, 11–28. [Google Scholar] [CrossRef]
- Bonora, N.; Testa, G. Plasticity damage self-consistent model incorporating stress triaxiality and shear controlled fracture mechanisms—Model formulation. Eng. Fract. Mech. 2022, 271, 108634. [Google Scholar] [CrossRef]
- Bonora, N.; Testa, G. Plasticity damage self-consistent model incorporating stress triaxiality and shear controlled fracture mechanisms—Model verification and validation. Eng. Fract. Mech. 2022, 271, 108635. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture; McGraw-Hill: New York, NY, USA, 1952; p. 177. [Google Scholar] [CrossRef]
- Gurson, A.L. Plastic Flow and Fracture Behavior of Ductile Materials Incorporating Void Nucleation, Growth and Interaction. Ph.D. Thesis, Brown University, Providence, RI, USA, 1975. [Google Scholar]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.-W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Barsoum, I. Ductile Failure and Rupture Mechanisms in Combined Tension and Shear. Licentiate Thesis No 96 Stockholm. Ph.D. Thesis, KTH Solid Mechanics, Stockholm, Sweden, 2006. [Google Scholar]
- Coppola, T.; Cortese, L.; Folgarait, P. The effect of stress invariants on ductile fracture limit in steels. Eng. Fract. Mech. 2009, 76, 1288–1302. [Google Scholar] [CrossRef]
- Mohr, D.; Mercadet, J.S. Micromechanically-motivated phenomenological Hosford-Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Lode, W. Versuche über den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel. Z. Phys. 1926, 36, 913–939. [Google Scholar] [CrossRef]
- Driemeier, L.; Brünig, M.; Micheli, G.; Alves, M. Experiments on stress-triaxiality dependence of material behavior of aluminium alloys. Mech. Mater. 2010, 42, 207–217. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Optimized butterfly specimen for the fracture testing of sheet materials under combined normal and shear loading. Eng. Fract. Mech. 2011, 78, 2919–2934. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Ductile fracture experiments with locally proportional loading histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, K.; Cerik, B.C.; Choung, J. Ductile fracture prediction of EH36 grade steel based on Hosford–Coulomb model. Ships Offshore Struct. 2019, 14 (Suppl. 1), 219–230. [Google Scholar] [CrossRef]
- Park, S.-J.; Kim, K. Localized Necking Model for Punching Fracture Simulation in Unstiffened and Stiffened Panels. Appl. Sci. 2021, 11, 3774. [Google Scholar] [CrossRef]
- Cerik, B.C.; Park, B.; Park, S.-J.; Choung, J. Modeling; testing and calibration of ductile crack formation in grade DH36 ship plates. Mar. Struct. 2019, 66, 27–43. [Google Scholar] [CrossRef]
- Yu, R.; Li, X.; Yue, Z.; Li, A.; Zhao, Z.; Wang, X.; Zhou, H.; Lu, T.J. Stress state sensitivity for plastic flow and ductile fracture of L907A low-alloy marine steel: From tension to shear. Mater. Sci. Eng. A 2022, 835, 142689. [Google Scholar] [CrossRef]
- Wilson-Heid, A.E.; Furton, E.T.; Beese, A.M. Contrasting the Role of Pores on the Stress State Dependent Fracture Behavior of Additively Manufactured Low and High Ductility Metals. Materials 2021, 14, 3657. [Google Scholar] [CrossRef]
- Ma, H.; Qu, R.; Song, K.; Liu, F. Notch strength of ductile materials with different work-hardening behaviors. J. Mater. Res. Technol. 2024, 33, 8974–8982. [Google Scholar] [CrossRef]
- Olsen, J.S.; Zhang, Z.L.; Lu, H.; Van der Eijk, C. Fracture of notched round-bar NiTi-specimens. Eng. Fract. Mech. 2012, 84, 1–14. [Google Scholar] [CrossRef]
- Nalli, F.; Imbimbo, B.; Cortese, L. Design of non-conventional biaxial tensile-shear tests for the structural characterization and ductile damage assessment of ductile engineering materials. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012068. [Google Scholar] [CrossRef]
- Cortis, G.; Nalli, F.; Piacenti, M. A direct methodology for the calibration of ductile damage models from a simple multiaxial test. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1214, 012016. [Google Scholar] [CrossRef]
- Moreno-Garibaldi, P.; Alvarez-Vera, M.; Beltrán-Fernández, J.A.; Carrera-Espinoza, R.; Hdz-García, H.M.; Díaz-Guillen, J.C.; Muñoz-Arroyo, R.; Ortega, J.A.; Molenda, P. Characterization of Microstructural and Mechanical Properties of 17-4 PH Stainless Steel by Cold Rolled and Machining vs. DMLS Additive Manufacturing. J. Manuf. Mater. Process. 2024, 8, 48. [Google Scholar] [CrossRef]
- Shunmugavel, M.; Polishetty, A.; Littlefair, G. Microstructure and Mechanical Properties of Wrought and Additive Manufactured Ti-6Al-4V Cylindrical. Procedia Technol. 2015, 20, 231–236. [Google Scholar] [CrossRef]
- Cortis, G.; Broggiato, G.B.; Cortese, L. Ductility assessment of a 17-4PH steel through simple multiaxial tests. In Proceedings of the 2023 IOP Conference Series: Materials Science and Engineering, Padova, Italy, 7–10 September 2022. [Google Scholar] [CrossRef]
- Nalli, F.; Cortese, L.; Concli, F. Ductile damage assessment of Ti6Al4V, 17-4PH and AlSi10Mg for additive manufacturing. Eng. Fract. Mech. 2021, 241, 107395. [Google Scholar] [CrossRef]
- Cortese, L.; Nalli, F.; Broggiato, G.B.; Coppola, T. An effective experimental-numerical procedure for damage assessment of Ti6Al4V. In Residual Stress, Thermomechanics & Infrared Imaging, Hybrid Techniques and Inverse Problems, Volume 9, Proceedings of the 2015 Annual Conference on Experimental and Applied Mechanics, Costa Mesa, CA, USA, 8–11 June 2015; Bossuyt, S., Schajer, G., Carpinteri, A., Eds.; Conference Proceedings of the Society for Experimental Mechanics Series (CPSEMS); Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
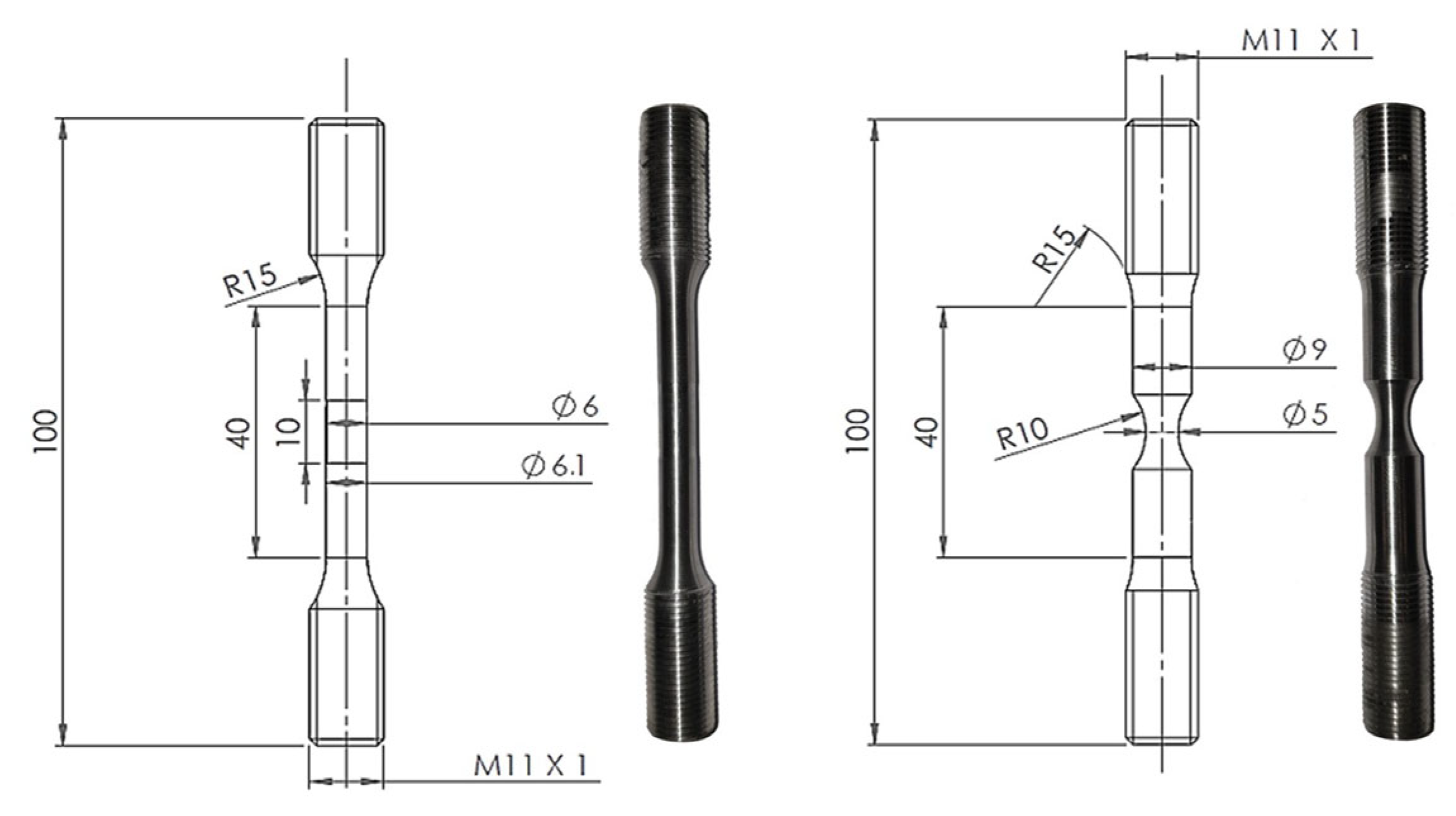


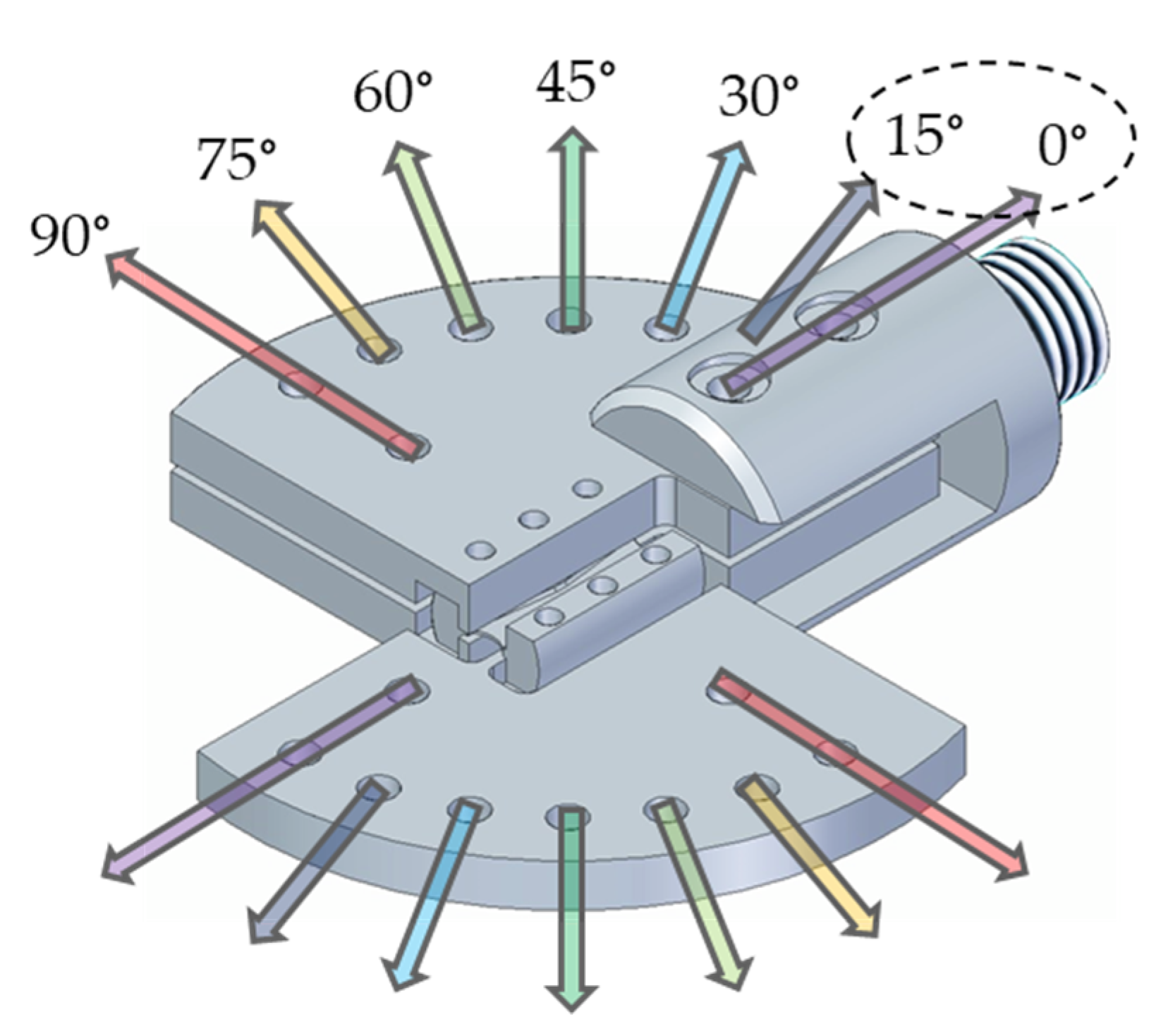
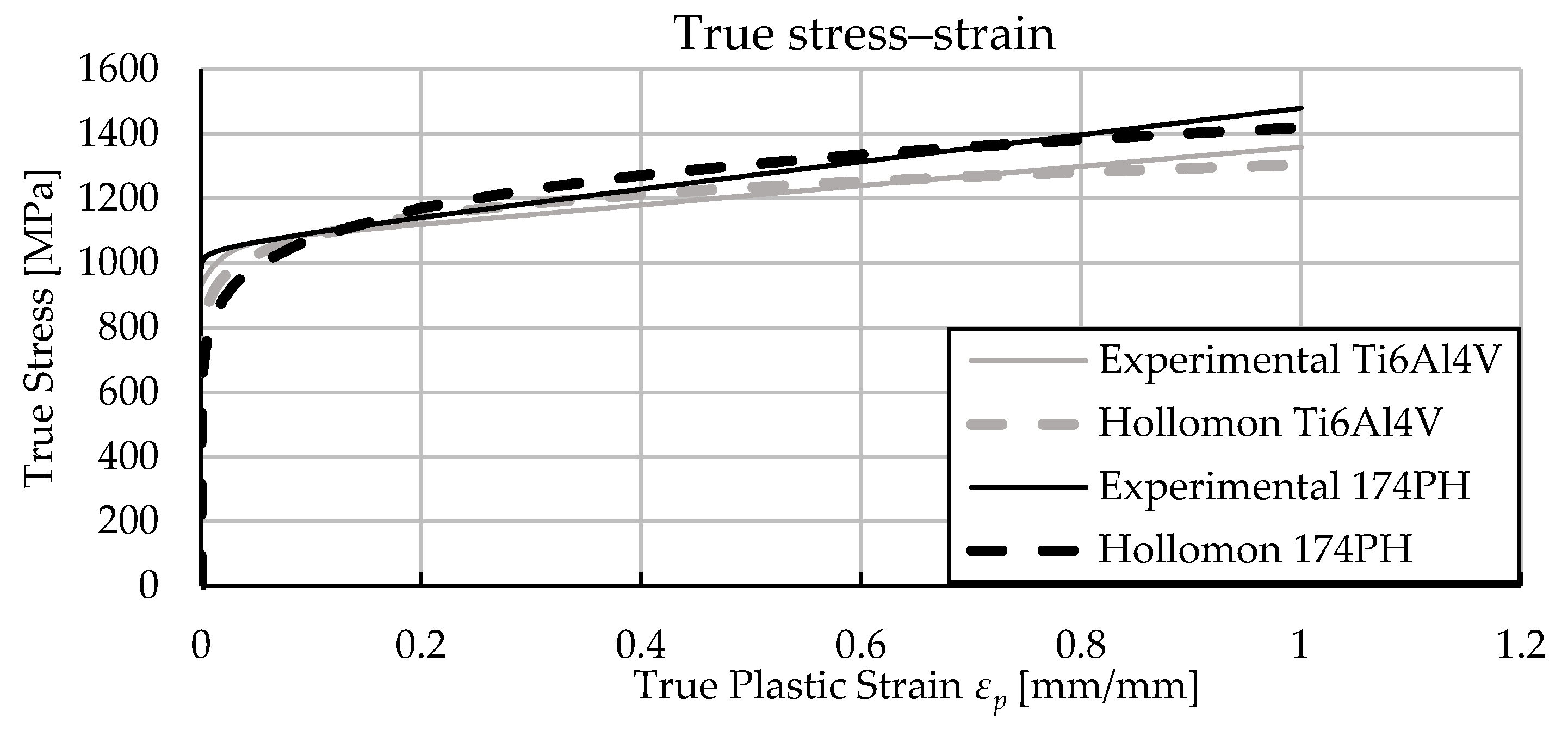

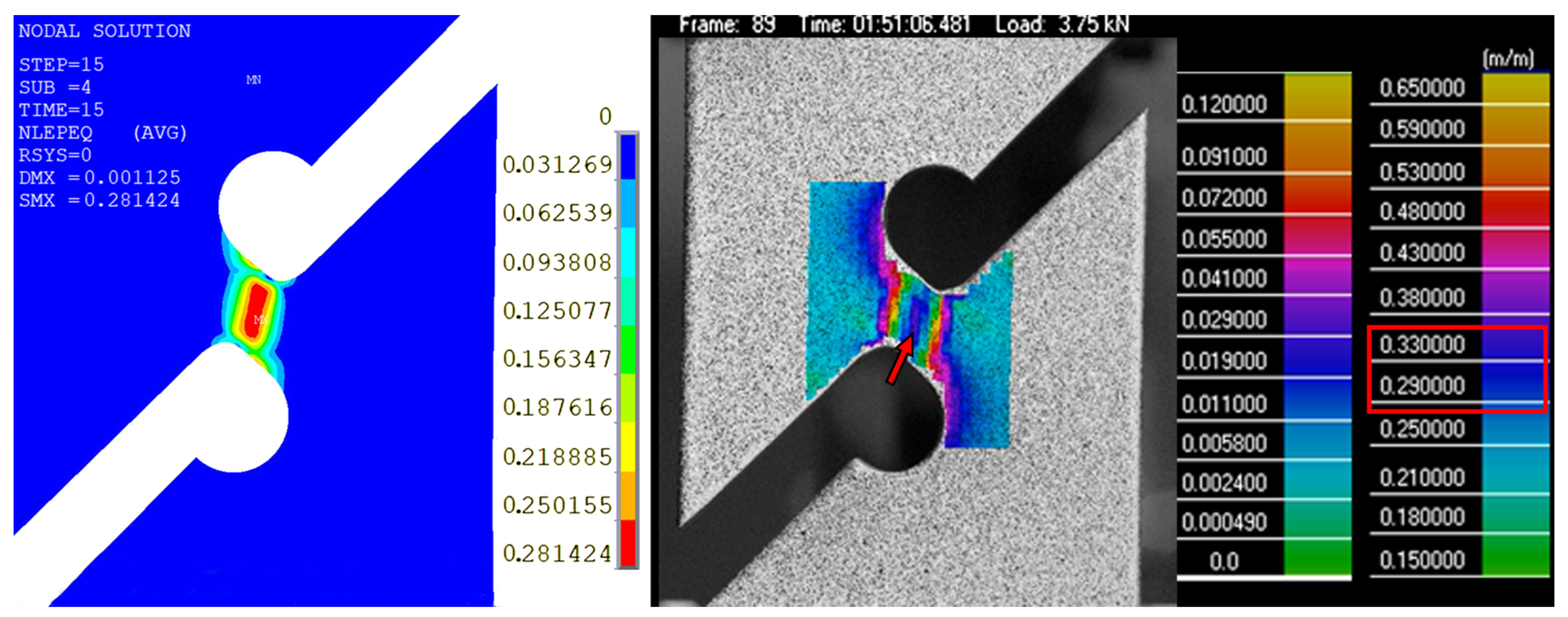
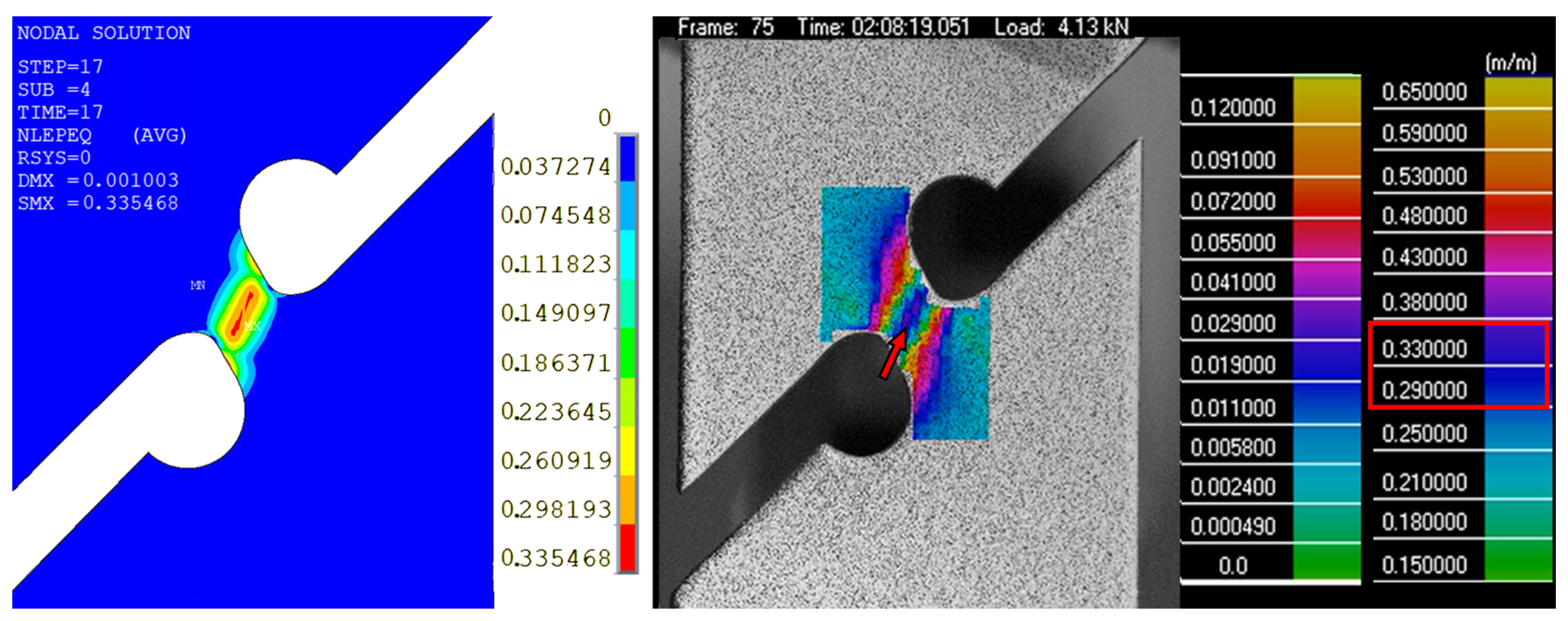


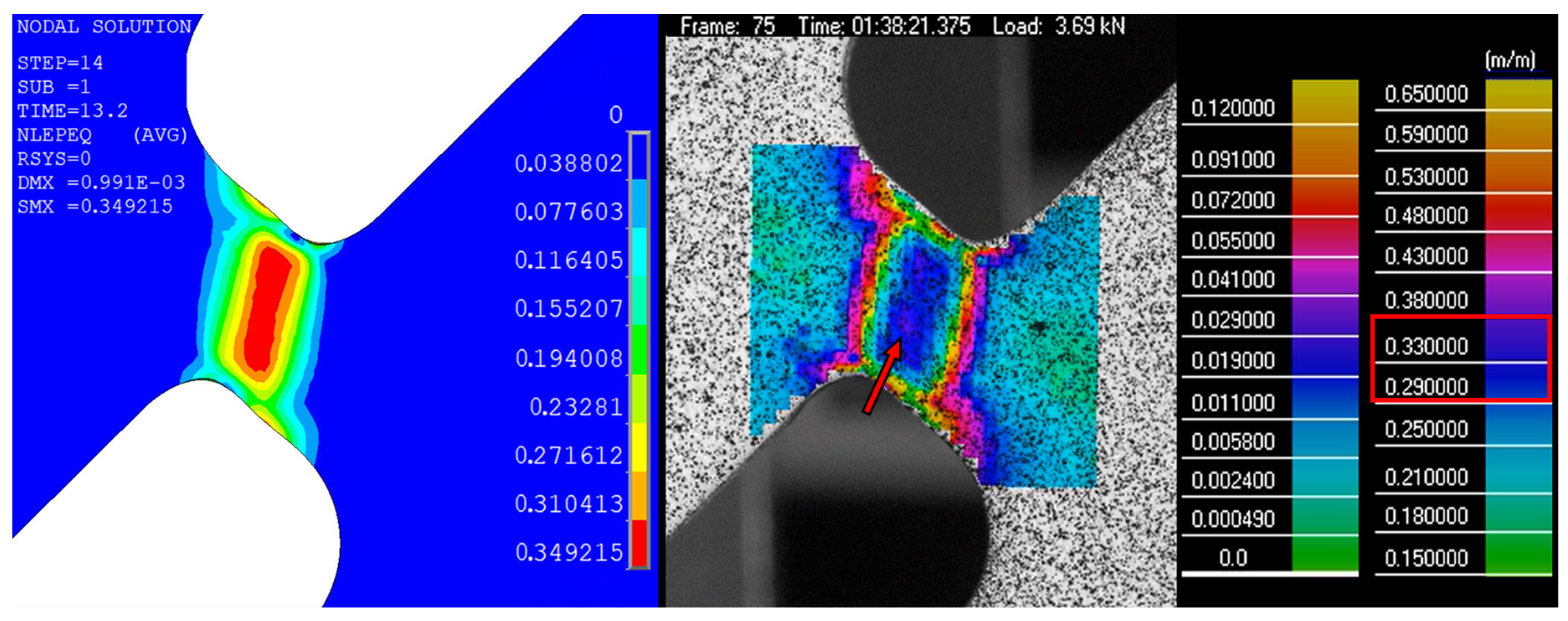
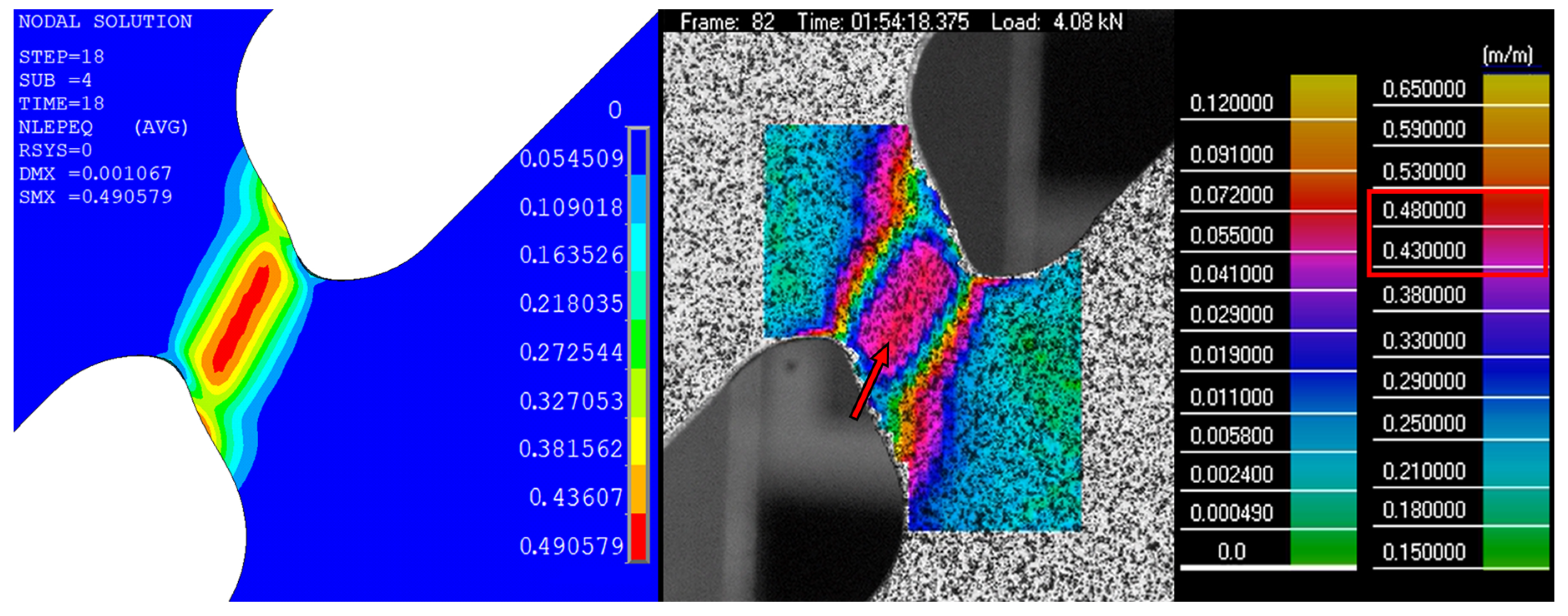


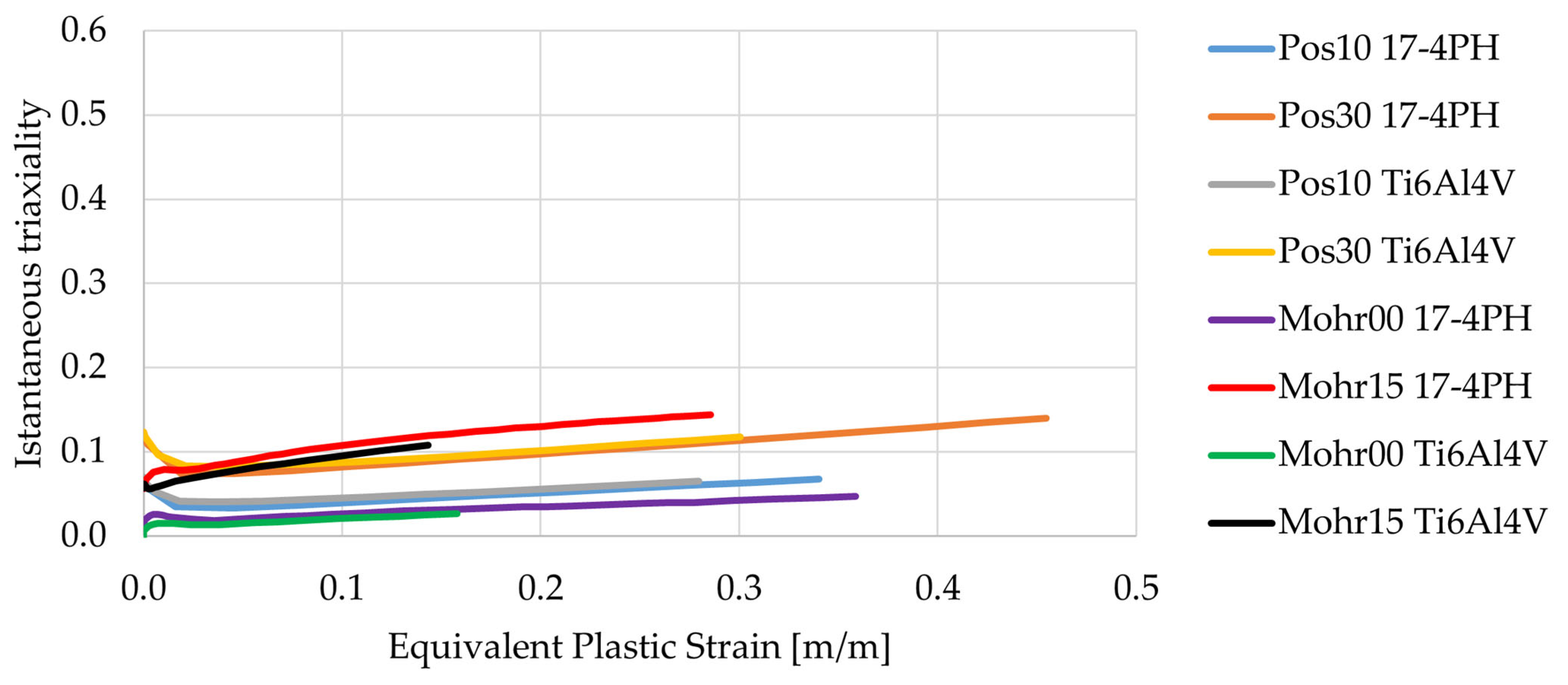
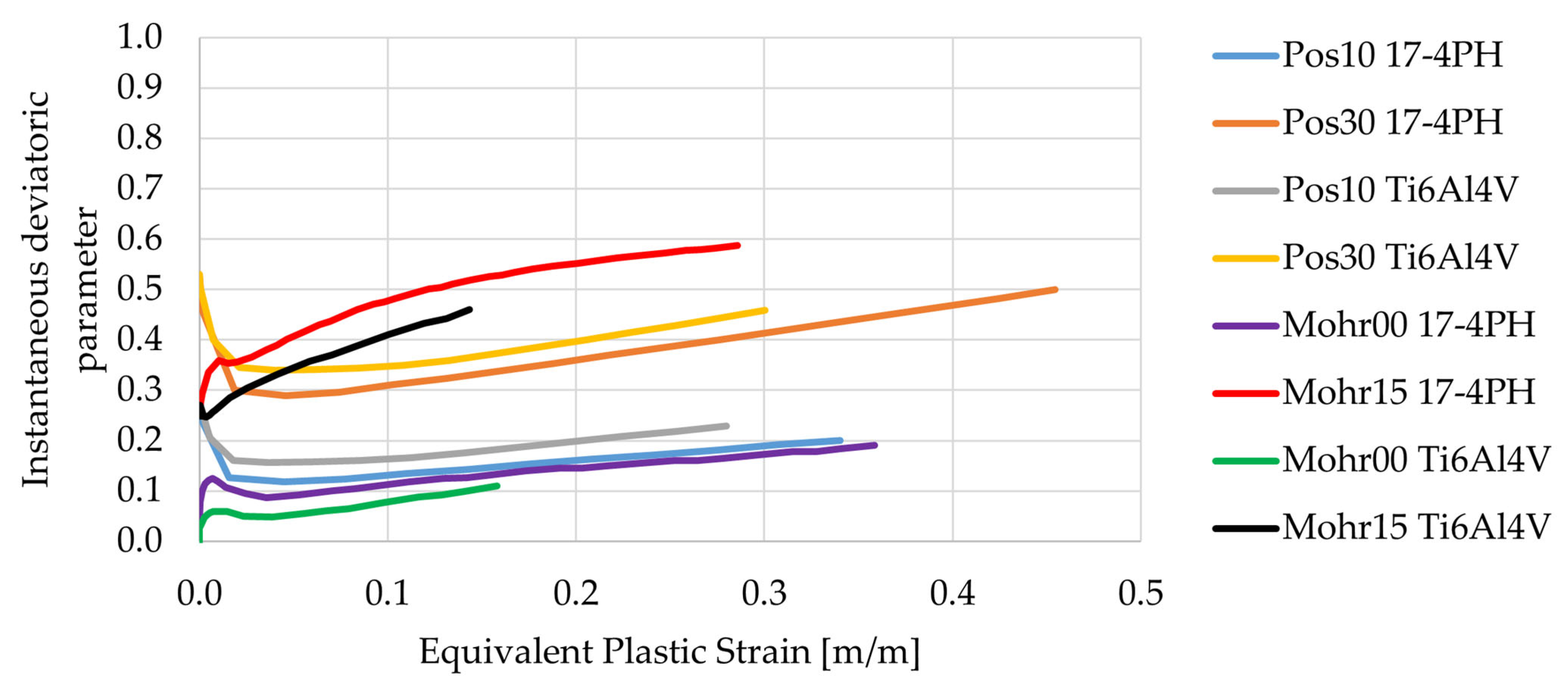
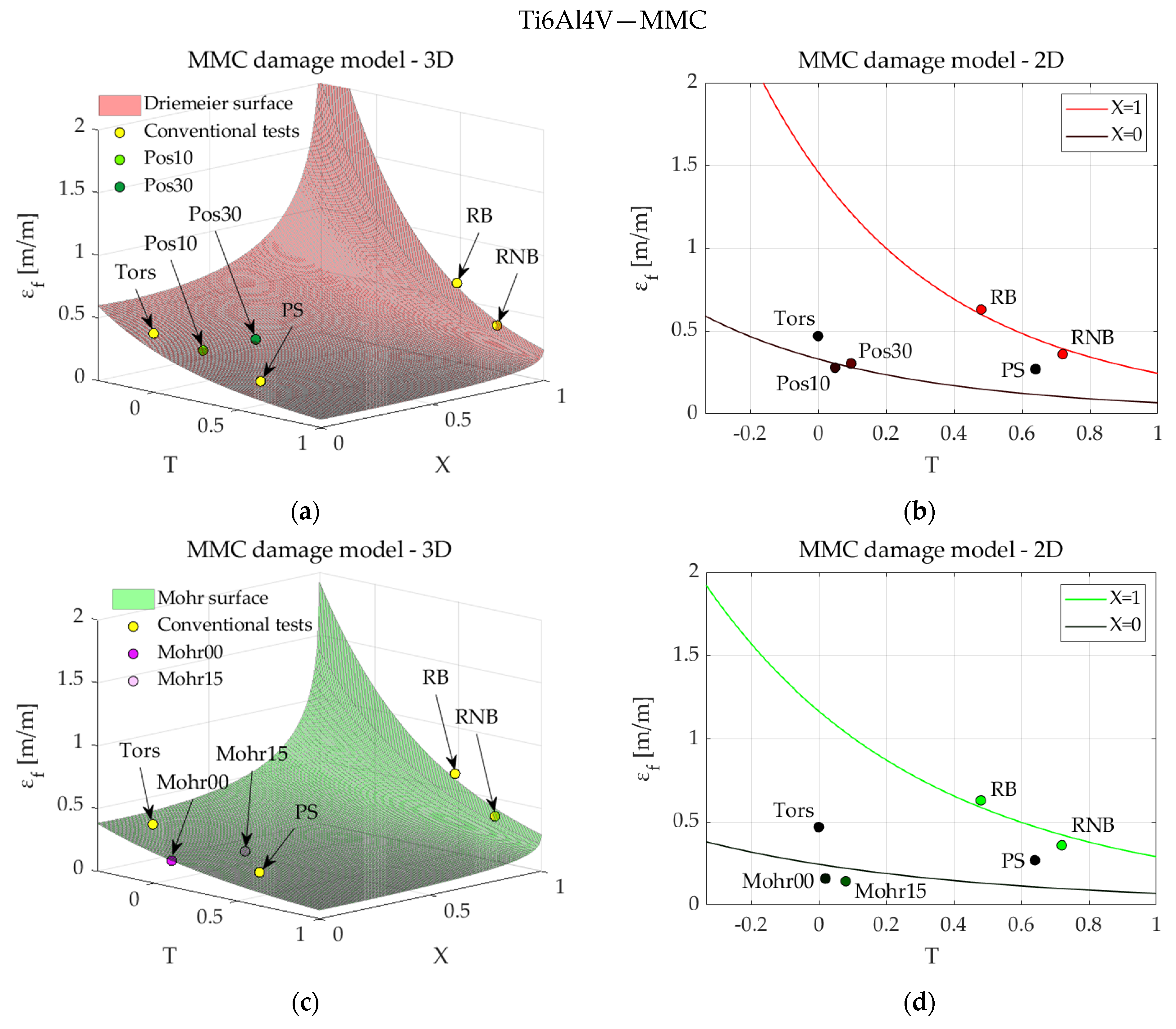
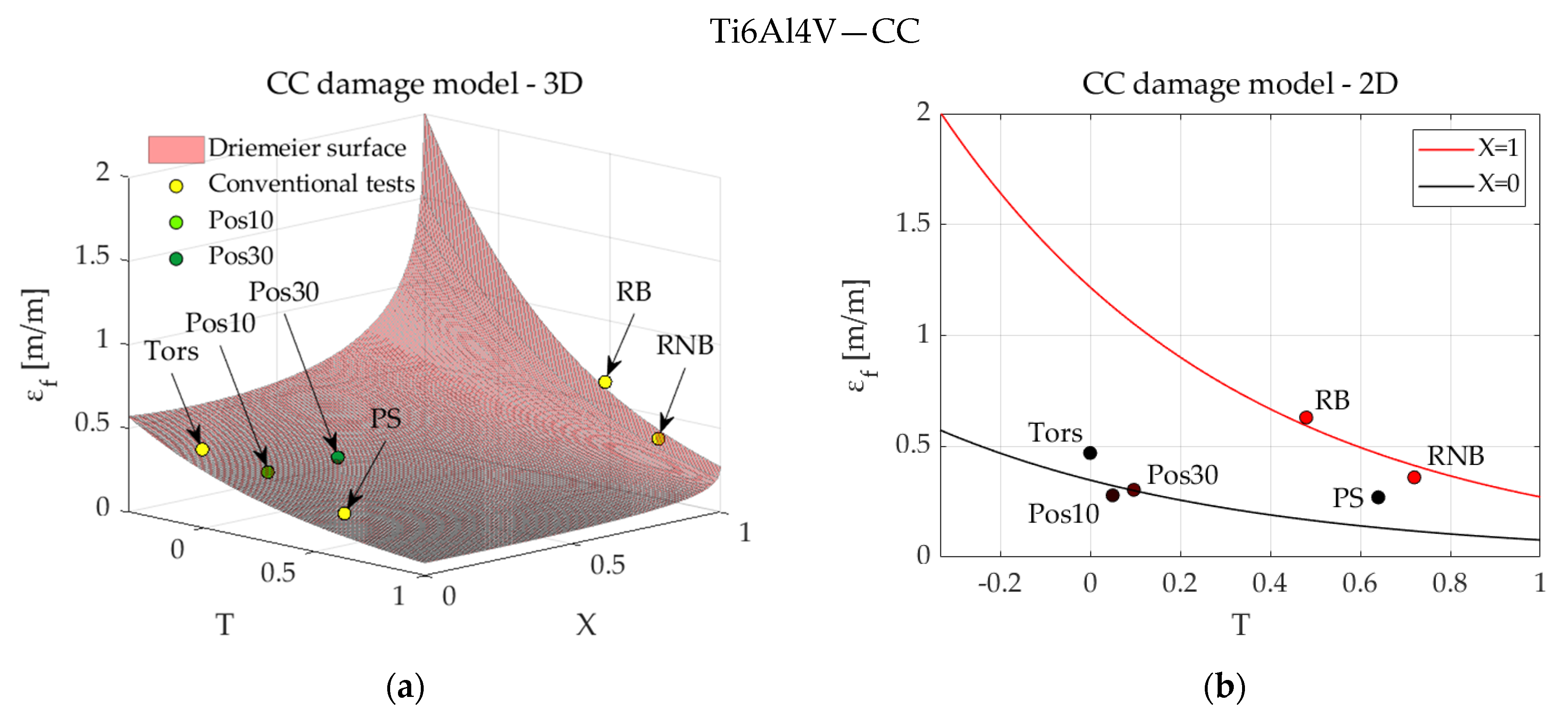



| Ti6Al4V | 17-4PH | |||||
|---|---|---|---|---|---|---|
| Test | [m/m] | [m/m] | ||||
| Pos10 | 0.05 | 0.18 | 0.28 | 0.05 | 0.16 | 0.35 |
| Pos30 | 0.10 | 0.39 | 0.30 | 0.10 | 0.38 | 0.46 |
| Mohr00 | 0.02 | 0.07 | 0.16 | 0.03 | 0.14 | 0.35 |
| Mohr15 | 0.08 | 0.36 | 0.15 | 0.11 | 0.49 | 0.28 |
| RB | 0.48 | 0.99 | 0.63 | 0.61 | 0.99 | 1.17 |
| RNB | 0.72 | 0.99 | 0.36 | 0.76 | 0.99 | 0.81 |
| PS | 0.64 | 0.00 | 0.27 | 0.70 | 0.00 | 0.36 |
| Tors | 0.00 | 0.00 | 0.47 | 0.00 | 0.00 | 0.47 |
| Ti6Al4V | 17-4PH | |||||||
|---|---|---|---|---|---|---|---|---|
| Pos10 | Pos30 | Mohr00 | Mohr15 | Pos10 | Pos30 | Mohr00 | Mohr15 | |
| Std. dev. T (±) | 0.01 | 0.02 | 0.01 | 0.02 | 0.01 | 0.02 | 0.01 | 0.03 |
| Std. dev. X (±) | 0.05 | 0.07 | 0.04 | 0.10 | 0.05 | 0.08 | 0.06 | 0.11 |
| Ti6Al4V | 17-4PH | |||||||
|---|---|---|---|---|---|---|---|---|
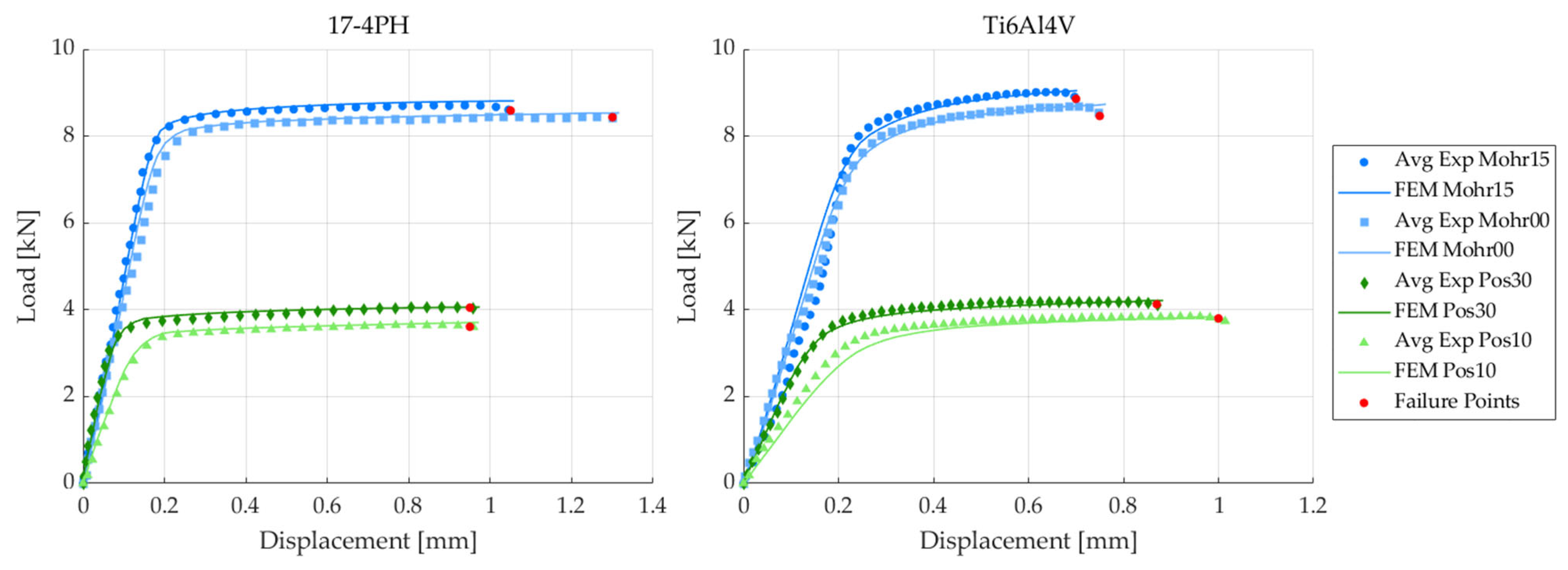
| Test | [mm] | [kN] | [kN] | [m/m] | [mm] | [kN] | [kN] | [m/m] |
| Pos10 | 1.00 | 3.75 | 3.85 | 0.32 | 0.95 | 3.69 | 3.70 | 0.33 |
| Pos30 | 0.87 | 4.13 | 4.23 | 0.33 | 0.95 | 4.08 | 4.05 | 0.46 |
| Mohr00 | 0.74 | 8.66 | 8.72 | 0.16 | 1.30 | 8.43 | 8.54 | 0.34 |
| Mohr15 | 0.68 | 9.06 | 9.05 | 0.15 | 1.05 | 8.59 | 8.81 | 0.30 |
| Ti6Al4V | MMC | CC | HC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | SDErr | SDErr | SDErr | |||||||||
| Driemeier | 0.079 | 692.4 | 0.03 | 0.82 | 1.50 | 0.853 | 1.000 | 0.04 | 1.00 | 0.80 | 0.550 | 0.05 |
| Mohr | 0.060 | 675.0 | 0.08 | 0.81 | 1.55 | 1.080 | 1.000 | 0.03 | 1.00 | 0.68 | 0.020 | 0.07 |
| Conventional | 0.090 | 710.0 | 0.09 | 0.80 | 1.55 | 0.997 | 0.925 | 0.07 | 1.10 | 0.80 | 0.070 | 0.04 |
| Driemeier and Mohr | 0.060 | 673.9 | 0.07 | 0.81 | 1.55 | 1.470 | 0850 | 0.07 | 1.00 | 0.74 | 0.036 | 0.15 |
| All specimens | 0.075 | 689.0 | 0.11 | 0.90 | 1.32 | 0.840 | 1.000 | 0.11 | 1.00 | 0.78 | 0.047 | 0.11 |
| 17-4PH | MMC | CC | HC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | SDErr | SDErr | SDErr | |||||||||
| Driemeier | 0.013 | 742.0 | 0.14 | 0.51 | 1.02 | 1.970 | 0.750 | 0.09 | 1.02 | 1.36 | 0.017 | 0.12 |
| Mohr | 0.013 | 725.0 | 0.15 | 0.50 | 1.05 | 1.450 | 0.990 | 0.11 | 1.05 | 1.10 | 0.000 | 0.05 |
| Conventional | 0.020 | 751.0 | 0.13 | 0.53 | 0.85 | 1.130 | 0.986 | 0.11 | 1.03 | 1.42 | 0.020 | 0.11 |
| Driemeier and Mohr | 0.010 | 721.1 | 0.12 | 0.50 | 1.03 | 1.240 | 1.000 | 0.10 | 1.00 | 1.38 | 0.015 | 0.20 |
| All specimens | 0.020 | 732.2 | 0.11 | 0.60 | 0.74 | 1.110 | 1.000 | 0.11 | 1.06 | 1.20 | 0.010 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortis, G.; Cortese, L. Effective Ductile Fracture Characterization of 17-4PH and Ti6Al4V by Shear–Tension Tests: Experiments and Damage Models Calibration. Appl. Sci. 2025, 15, 3645. https://doi.org/10.3390/app15073645
Cortis G, Cortese L. Effective Ductile Fracture Characterization of 17-4PH and Ti6Al4V by Shear–Tension Tests: Experiments and Damage Models Calibration. Applied Sciences. 2025; 15(7):3645. https://doi.org/10.3390/app15073645
Chicago/Turabian StyleCortis, Gabriele, and Luca Cortese. 2025. "Effective Ductile Fracture Characterization of 17-4PH and Ti6Al4V by Shear–Tension Tests: Experiments and Damage Models Calibration" Applied Sciences 15, no. 7: 3645. https://doi.org/10.3390/app15073645
APA StyleCortis, G., & Cortese, L. (2025). Effective Ductile Fracture Characterization of 17-4PH and Ti6Al4V by Shear–Tension Tests: Experiments and Damage Models Calibration. Applied Sciences, 15(7), 3645. https://doi.org/10.3390/app15073645






