Optimizing Police Patrol Strategies in Real-World Scenarios: A Modified PPS-MOEA/D Approach for Constrained Multi-Objective Optimization
Abstract
1. Introduction
2. Related Work
2.1. Single-Objective Optimization Approaches
2.2. Multi-Objective Optimization Approaches
3. Model Formulation
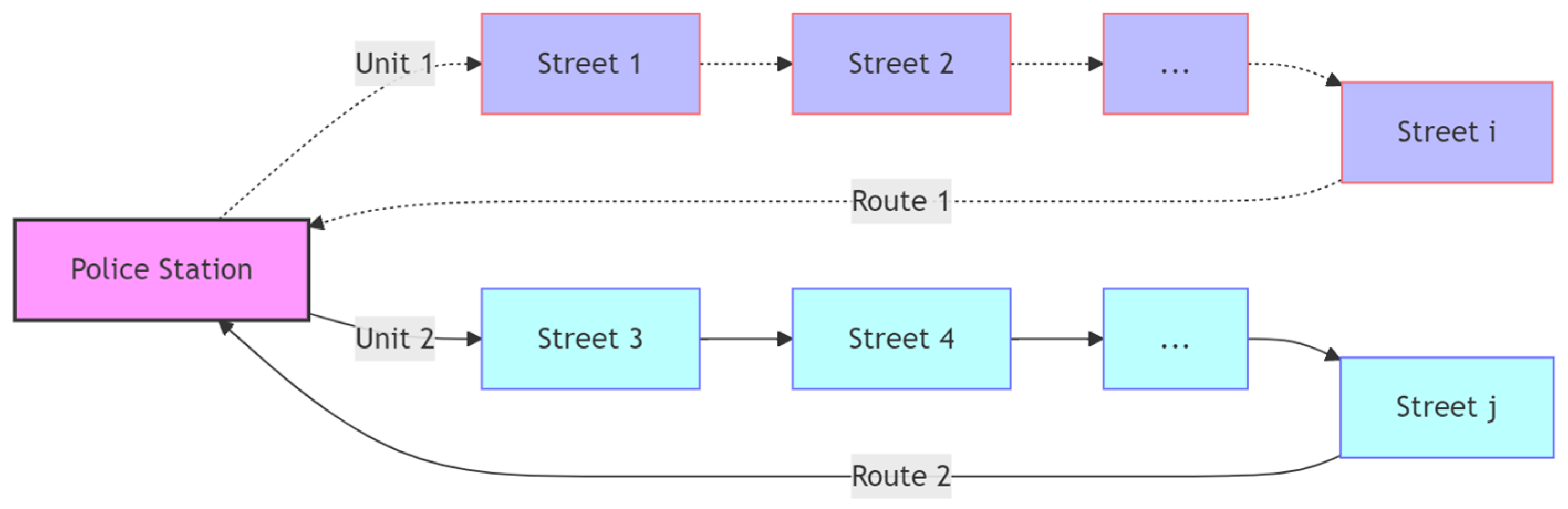
3.1. Problem Definition
3.2. Objective Function
3.3. Constraints
4. Algorithm Implementation
4.1. Initialization
4.2. Differential Evolution
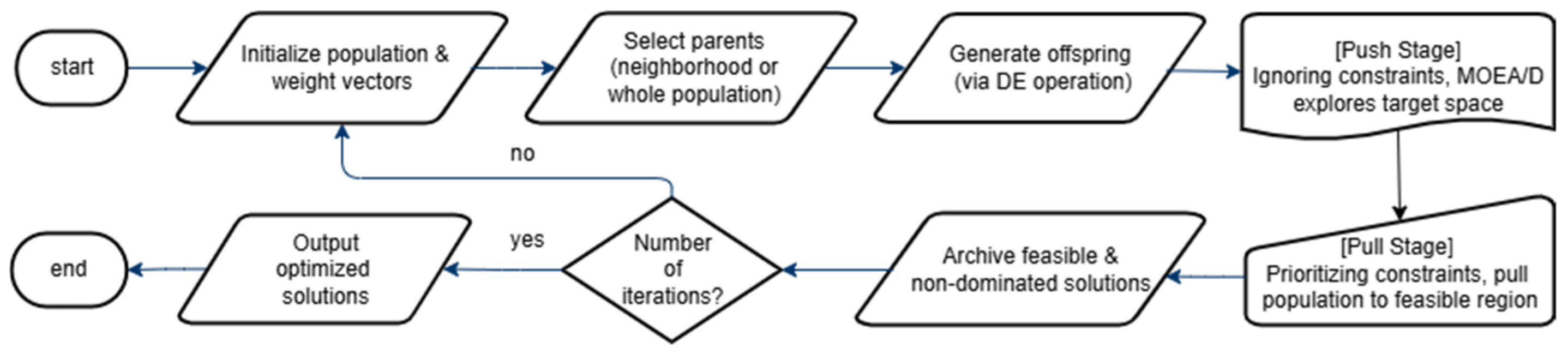
4.3. Push and Pull Phases
4.4. Preservation of Feasible Non-Dominated Solutions
5. Simulation Settings
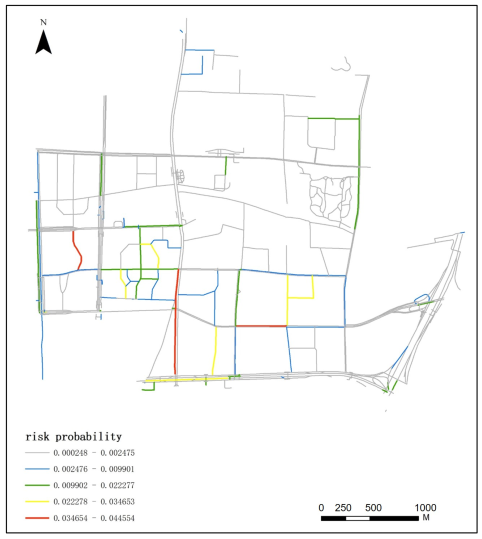
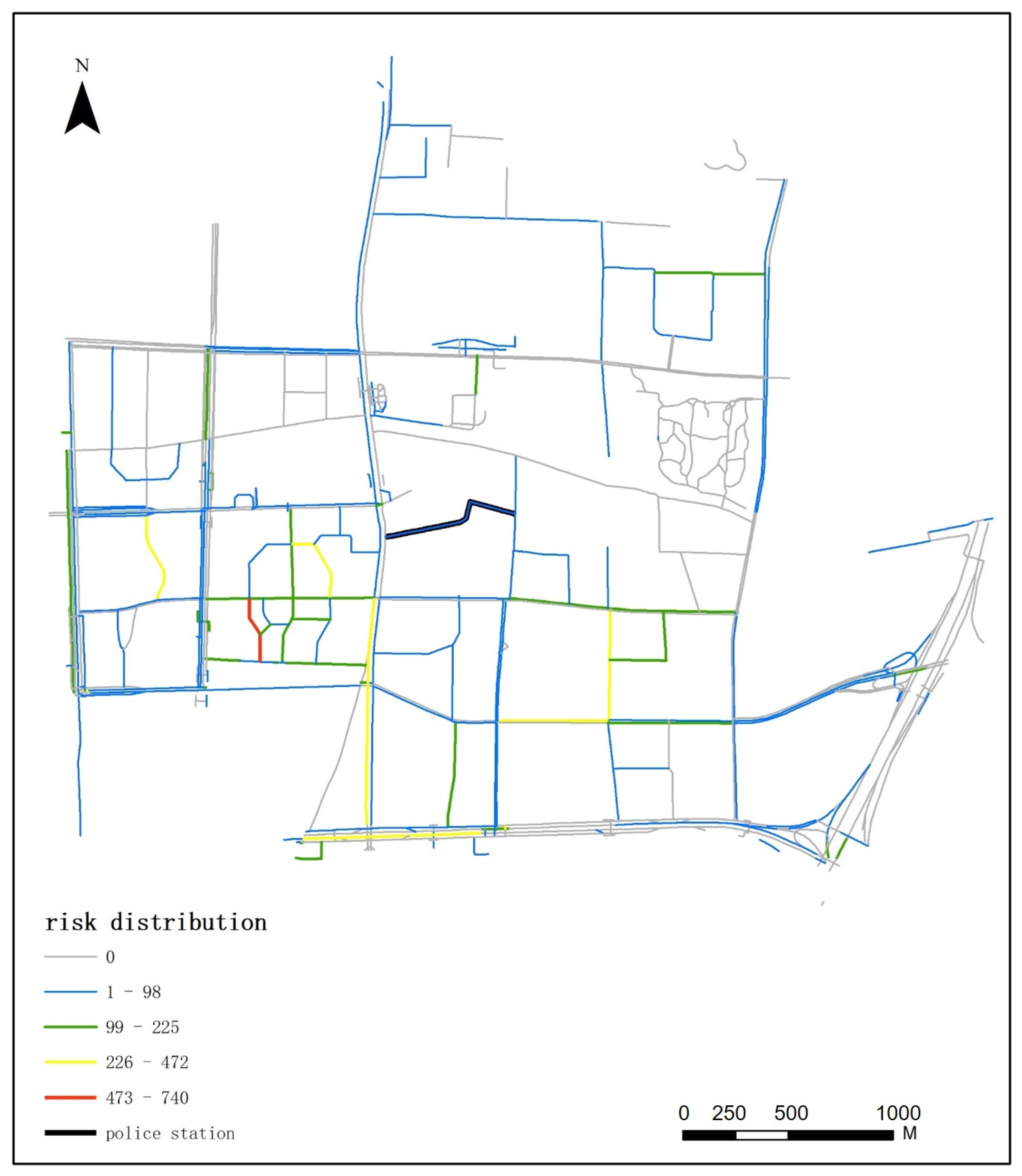
5.1. 110 Incident Risk Distribution
5.2. Street Length and Distance Matrix
5.3. Baseline Algorithms and Parameter Settings
5.4. Performance Metrics
5.5. Hardware and Platform
6. Simulation Results
6.1. Comparative Analysis
6.2. Optimization Objectives Comparison
7. Discussion
7.1. Trends and Insights
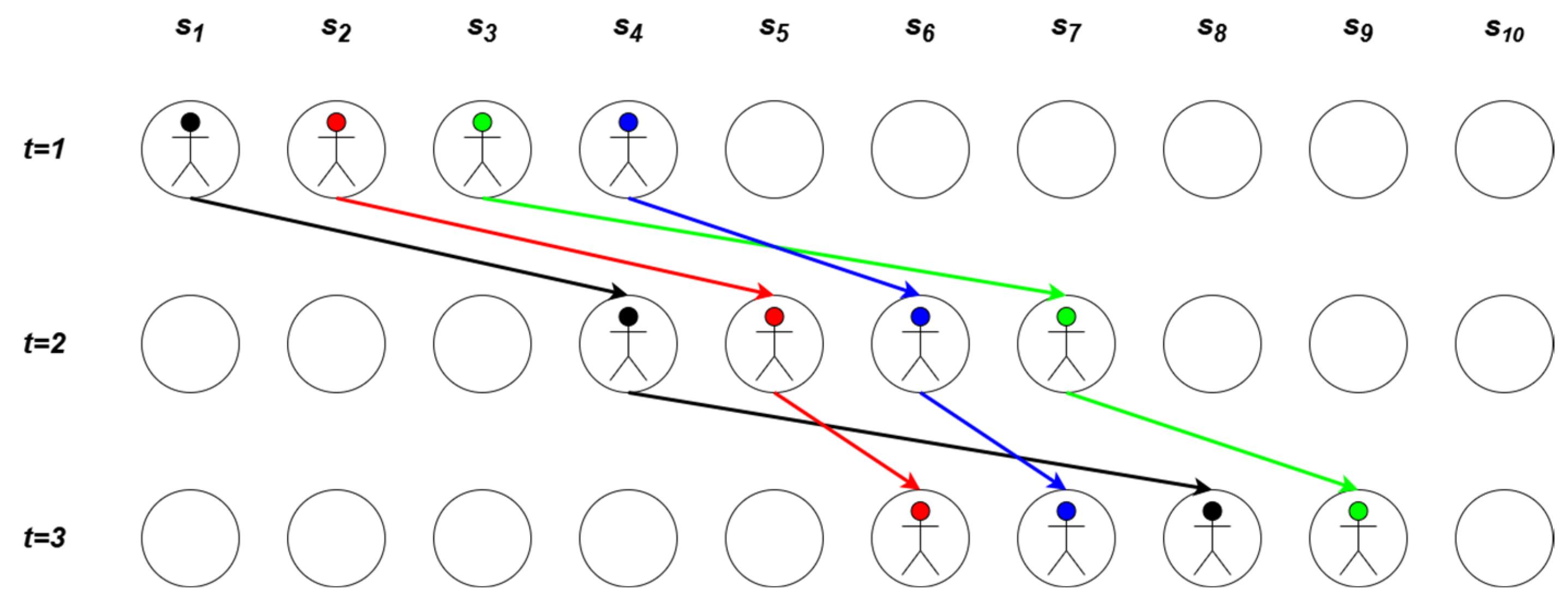
7.2. Visualization of Optimal Solutions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Temporal Variations of Incident Risk
Appendix A.1. Spatial–Temporal Distribution of 110 Incident Risk at 16:00

Appendix A.2. Spatial–Temporal Distribution of 110 Incident Risk at 17:00
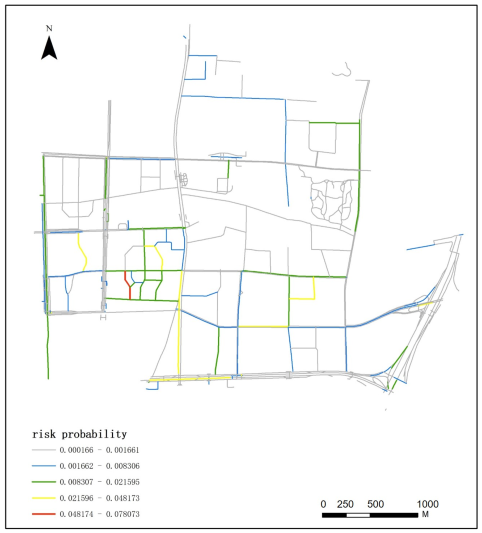
Appendix A.3. Spatial–Temporal Distribution of 110 Incident Risk at 18:00
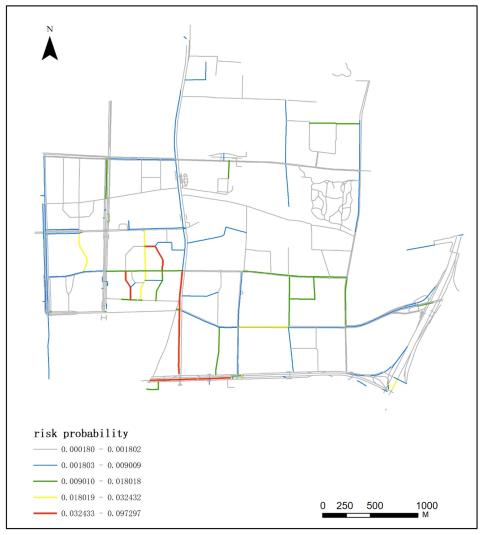
Appendix A.4. Spatial–Temporal Distribution of 110 Incident Risk at 19:00

Appendix A.5. Spatial–Temporal Distribution of 110 Incident Risk at 20:00

Appendix A.6. Spatial–Temporal Distribution of 110 Incident Risk at 21:00
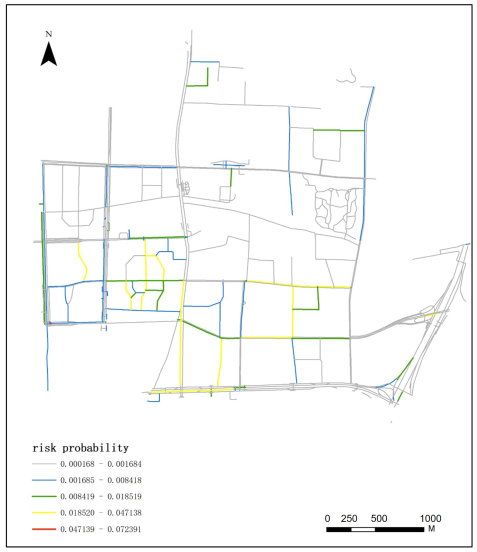
Appendix A.7. Spatial–Temporal Distribution of 110 Incident Risk at 22:00
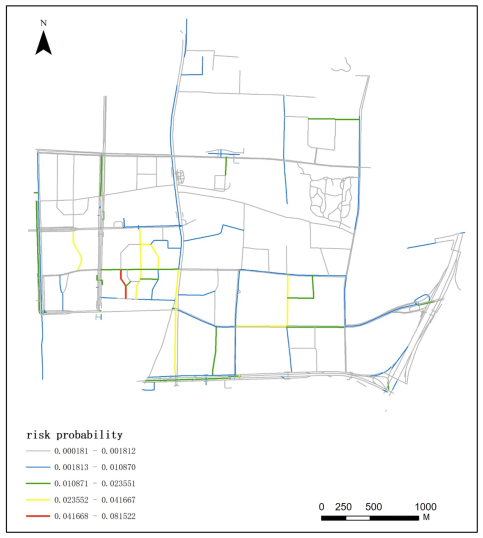
Appendix A.8. Spatial–Temporal Distribution of 110 Incident Risk at 23:00
Appendix B. Simulation Results
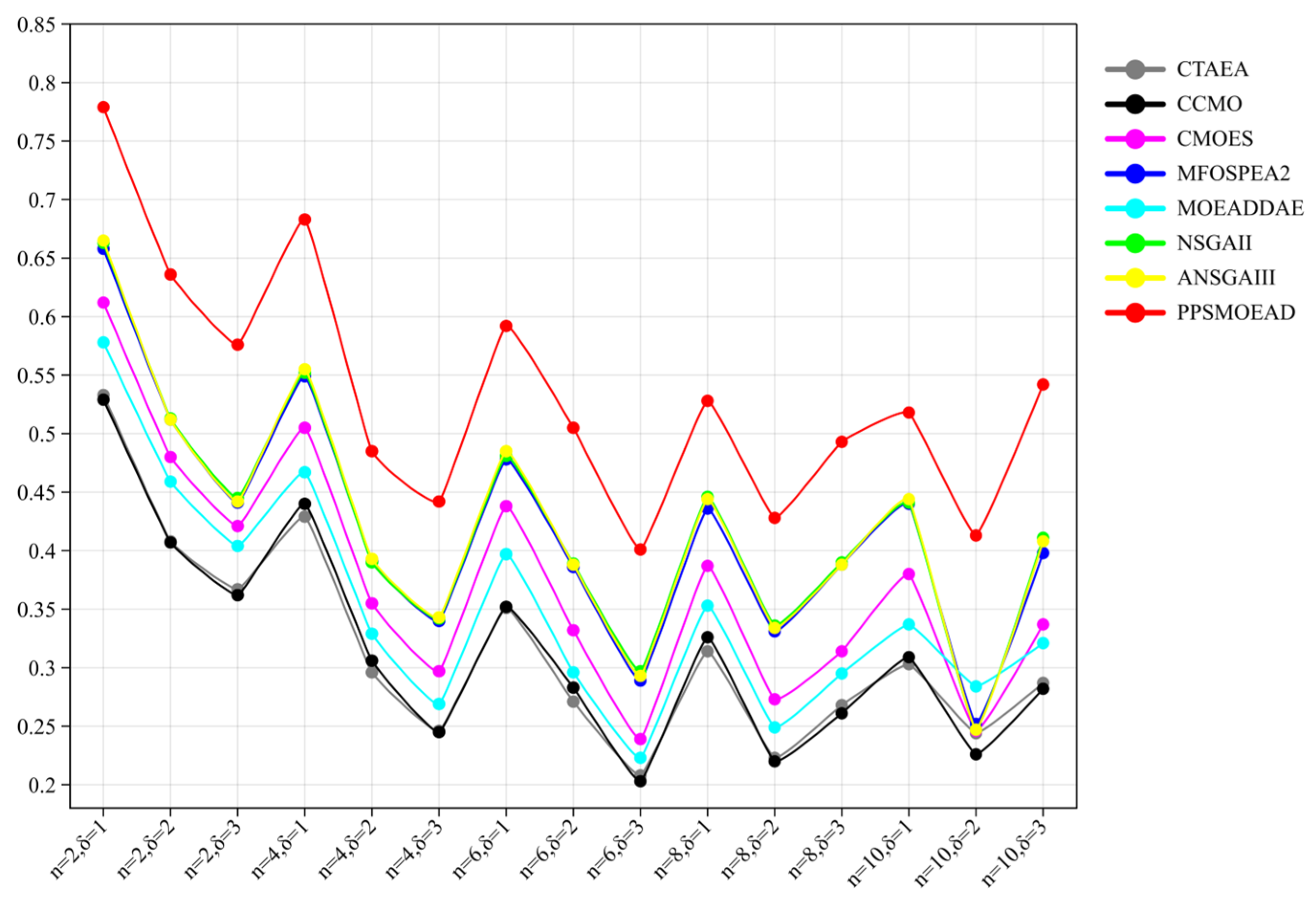
Appendix B.1. Simulation Results of HVs
| Scenario | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 5.3348 × 10−1 (3.13 × 10−3) | 5.2857 × 10−1 (2.16 × 10−2) | 6.1166 × 10−1 (1.49 × 10−2) | 6.5773 × 10−1 (9.12 × 10−3) | 5.7799 × 10−1 (1.47 × 10−2) | 6.6272 × 10−1 (9.72 × 10−3) | 6.6462 × 10−1 (7.26 × 10−3) | 7.7935 × 10−1 (4.67 × 10−2) |
| n = 2, δ = 2 | 4.0827 × 10−1 (3.85 × 10−3) | 4.0660 × 10−1 (1.42 × 10−2) | 4.8040 × 10−1 (9.87 × 10−3) | 5.1152 × 10−1 (6.44 × 10−3) | 4.5867 × 10−1 (7.81 × 10−3) | 5.1307 × 10−1 (7.58 × 10−3) | 5.1213 × 10−1 (4.29 × 10−3) | 6.3647 × 10−1 (3.31 × 10−2) |
| n = 2, δ = 3 | 3.6728 × 10−1 (2.95 × 10−3) | 3.6240 × 10−1 (1.02 × 10−2) | 4.2126 × 10−1 (7.35 × 10−3) | 4.4073 × 10−1 (4.63 × 10−3) | 4.0363 × 10−1 (7.16 × 10−3) | 4.4485 × 10−1 (5.54 × 10−3) | 4.4239 × 10−1 (4.93 × 10−3) | 5.7622 × 10−1 (4.13 × 10−2) |
| n = 4, δ = 1 | 4.2870 × 10−1 (4.60 × 10−3) | 4.3964 × 10−1 (1.85 × 10−2) | 5.0468 × 10−1 (1.33 × 10−2) | 5.4931 × 10−1 (9.64 × 10−3) | 4.6681 × 10−1 (1.22 × 10−2) | 5.5185 × 10−1 (1.01 × 10−2) | 5.5515 × 10−1 (8.91 × 10−3) | 6.8301 × 10−1 (3.62 × 10−2) |
| n = 4, δ = 2 | 2.9579 × 10−1 (2.69 × 10−3) | 3.0601 × 10−1 (1.51 × 10−2) | 3.5539 × 10−1 (7.37 × 10−3) | 3.9056 × 10−1 (6.55 × 10−3) | 3.2916 × 10−1 (6.29 × 10−3) | 3.9047 × 10−1 (7.10 × 10−3) | 3.9262 × 10−1 (5.05 × 10−3) | 4.8496 × 10−1 (3.51 × 10−2) |
| n = 4, δ = 3 | 2.4611 × 10−1 (2.48 × 10−3) | 2.4537 × 10−1 (1.05 × 10−2) | 2.9719 × 10−1 (9.64 × 10−3) | 3.3987 × 10−1 (1.19 × 10−2) | 2.6864 × 10−1 (6.42 × 10−3) | 3.4220 × 10−1 (1.13 × 10−2) | 3.4274 × 10−1 (5.81 × 10−3) | 4.4168 × 10−1 (3.06 × 10−2) |
| n = 6, δ = 1 | 3.5132 × 10−1 (4.68 × 10−3) | 3.5204 × 10−1 (3.08 × 10−2) | 4.3786 × 10−1 (8.90 × 10−3) | 4.7803 × 10−1 (1.18 × 10−2) | 3.9703 × 10−1 (8.56 × 10−3) | 4.8144 × 10−1 (1.41 × 10−2) | 4.8459 × 10−1 (9.71 × 10−3) | 5.9185 × 10−1 (4.63 × 10−2) |
| n = 6, δ = 2 | 2.7068 × 10−1 (3.67 × 10−3) | 2.8270 × 10−1 (1.79 × 10−2) | 3.3246 × 10−1 (9.77 × 10−3) | 3.8599 × 10−1 (7.26 × 10−3) | 2.9647 × 10−1 (7.74 × 10−3) | 3.8864 × 10−1 (8.24 × 10−3) | 3.8777 × 10−1 (6.32 × 10−3) | 5.0533 × 10−1 (3.73 × 10−2) |
| n = 6, δ = 3 | 2.0817 × 10−1 (3.11 × 10−3) | 2.0326 × 10−1 (1.53 × 10−2) | 2.3883 × 10−1 (1.44 × 10−2) | 2.8852 × 10−1 (4.55 × 10−3) | 2.2332 × 10−1 (1.10 × 10−2) | 2.9690 × 10−1 (5.77 × 10−3) | 2.9288 × 10−1 (5.24 × 10−3) | 4.0057 × 10−1 (3.59 × 10−2) |
| n = 8, δ = 1 | 3.1359 × 10−1 (4.02 × 10−3) | 3.2640 × 10−1 (1.97 × 10−2) | 3.8671 × 10−1 (8.16 × 10−3) | 4.3602 × 10−1 (6.67 × 10−3) | 3.5260 × 10−1 (7.02 × 10−3) | 4.4603 × 10−1 (1.23 × 10−2) | 4.4436 × 10−1 (9.44 × 10−3) | 5.2777 × 10−1 (3.48 × 10−2) |
| n = 8, δ = 2 | 2.2254 × 10−1 (2.39 × 10−3) | 2.2038 × 10−1 (1.80 × 10−2) | 2.7292 × 10−1 (7.58 × 10−3) | 3.3128 × 10−1 (6.34 × 10−3) | 2.4899 × 10−1 (6.33 × 10−3) | 3.3554 × 10−1 (7.15 × 10−3) | 3.3391 × 10−1 (6.39 × 10−3) | 4.2829 × 10−1 (2.87 × 10−2) |
| n = 8, δ = 3 | 2.6826 × 10−1 (2.67 × 10−3) | 2.6109 × 10−1 (1.45 × 10−2) | 3.1354 × 10−1 (1.29 × 10−2) | 3.8758 × 10−1 (6.59 × 10−3) | 2.9511 × 10−1 (6.62 × 10−3) | 3.8964 × 10−1 (8.84 × 10−3) | 3.8803 × 10−1 (8.53 × 10−3) | 4.9269 × 10−1 (4.27 × 10−2) |
| n = 10, δ = 1 | 3.0287 × 10−1 (2.85 × 10−3) | 3.0894 × 10−1 (1.87 × 10−2) | 3.7972 × 10−1 (1.31 × 10−2) | 4.4016 × 10−1 (9.30 × 10−3) | 3.3668 × 10−1 (7.51 × 10−3) | 4.4097 × 10−1 (1.02 × 10−2) | 4.4418 × 10−1 (1.13 × 10−2) | 5.1766 × 10−1 (4.09 × 10−2) |
| n = 10, δ = 2 | 2.4442 × 10−1 (3.04 × 10−3) | 2.2647 × 10−1 (1.83 × 10−2) | 2.4613 × 10−1 (3.15 × 10−2) | 2.5201 × 10−1 (5.41 × 10−3) | 2.8382 × 10−1 (4.97 × 10−3) | 2.4699 × 10−1 (5.88 × 10−3) | 2.4722 × 10−1 (4.64 × 10−3) | 4.1269 × 10−1 (3.02 × 10−2) |
| n = 10, δ = 3 | 2.8740 × 10−1 (2.46 × 10−3) | 2.8164 × 10−1 (2.16 × 10−2) | 3.3663 × 10−1 (1.16 × 10−2) | 3.9801 × 10−1 (5.60 × 10−3) | 3.2058 × 10−1 (9.19 × 10−3) | 4.1145 × 10−1 (8.09 × 10−3) | 4.0758 × 10−1 (6.19 × 10−3) | 5.4163 × 10−1 (5.13 × 10−2) |
| +/−/= | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 |
Appendix B.2. Simulation Results of Spacings
| Scenario | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 6.5818 × 10−3 (9.16 × 10−4) | 9.1561 × 10−3 (1.11 × 10−3) | 7.4419 × 10−3 (1.91 × 10−3) | 8.3420 × 10−3 (1.30 × 10−3) | 1.3628 × 10−2 (4.43 × 10−3) | 8.0466 × 10−3 (1.31 × 10−3) | 7.8801 × 10−3 (1.10 × 10−3) | 5.9009 × 10−3 (1.96 × 10−3) |
| n = 2, δ = 2 | 7.2718 × 10−3 (9.97 × 10−4) | 8.4616 × 10−3 (7.43 × 10−4) | 8.0992 × 10−3 (4.21 × 10−3) | 8.7339 × 10−3 (1.39 × 10−3) | 1.5838 × 10−2 (4.92 × 10−3) | 9.2630 × 10−3 (1.24 × 10−3) | 8.6895 × 10−3 (1.19 × 10−3) | 6.5355 × 10−3 (1.85 × 10−3) |
| n = 2, δ = 3 | 7.9941 × 10−3 (1.29 × 10−3) | 5.7245 × 10−3 (6.22 × 10−4) | 7.9817 × 10−3 (1.58 × 10−3) | 8.6194 × 10−3 (1.17 × 10−3) | 1.6438 × 10−2 (9.65 × 10−3) | 8.6248 × 10−3 (1.40 × 10−3) | 9.0894 × 10−3 (1.24 × 10−3) | 7.3637 × 10−3 (1.82 × 10−3) |
| n = 4, δ = 1 | 7.3373 × 10−3 (9.41 × 10−4) | 9.4965 × 10−3 (1.18 × 10−3) | 8.8465 × 10−3 (1.01 × 10−3) | 1.0318 × 10−2 (1.18 × 10−3) | 1.5295 × 10−2 (7.18 × 10−3) | 1.0004 × 10−2 (1.81 × 10−3) | 9.1592 × 10−3 (1.29 × 10−3) | 7.1025 × 10−3 (1.86 × 10−3) |
| n = 4, δ = 2 | 8.2588 × 10−3 (1.13 × 10−3) | 8.3543 × 10−3 (1.36 × 10−3) | 9.9683 × 10−3 (2.04 × 10−3) | 1.0789 × 10−2 (1.28 × 10−3) | 1.4847 × 10−2 (4.47 × 10−3) | 1.0888 × 10−2 (1.41 × 10−3) | 1.0950 × 10−2 (1.68 × 10−3) | 9.2828 × 10−3 (3.54 × 10−3) |
| n = 4, δ = 3 | 8.0457 × 10−3 (1.45 × 10−3) | 1.0590 × 10−2 (1.41 × 10−3) | 9.2606 × 10−3 (1.82 × 10−3) | 1.0944 × 10−2 (1.88 × 10−3) | 1.4683 × 10−2 (4.24 × 10−3) | 1.0411 × 10−2 (1.56 × 10−3) | 1.0757 × 10−2 (1.48 × 10−3) | 8.6537 × 10−3 (6.87 × 10−3) |
| n = 6, δ = 1 | 1.0195 × 10−2 (1.08 × 10−3) | 7.3334 × 10−3 (7.89 × 10−4) | 1.0349 × 10−2 (5.07 × 10−3) | 1.3157 × 10−2 (2.19 × 10−3) | 1.9295 × 10−2 (6.11 × 10−3) | 1.2003 × 10−2 (2.07 × 10−3) | 1.2825 × 10−2 (2.09 × 10−3) | 7.9827 × 10−3 (3.27 × 10−3) |
| n = 6, δ = 2 | 8.7095 × 10−3 (1.09 × 10−3) | 1.0669 × 10−2 (1.41 × 10−3) | 9.5790 × 10−3 (3.45 × 10−4) | 1.1537 × 10−2 (1.69 × 10−3) | 1.5809 × 10−2 (4.70 × 10−3) | 1.1008 × 10−2 (1.74 × 10−3) | 1.1550 × 10−2 (1.60 × 10−3) | 6.7823 × 10−3 (3.01 × 10−3) |
| n = 6, δ = 3 | 1.0716 × 10−2 (2.37 × 10−3) | 6.6066 × 10−3 (3.39 × 10−3) | 8.4693 × 10−3 (3.01 × 10−3) | 1.0556 × 10−2 (1.45 × 10−3) | 1.4818 × 10−2 (6.36 × 10−3) | 1.0304 × 10−2 (1.55 × 10−3) | 1.0034 × 10−2 (1.54 × 10−3) | 4.7195 × 10−3 (2.83 × 10−3) |
| n = 8, δ = 1 | 1.0063 × 10−2 (1.33 × 10−3) | 9.6572 × 10−3 (9.84 × 10−4) | 1.0377 × 10−2 (5.84 × 10−4) | 1.2151 × 10−2 (1.56 × 10−3) | 1.6886 × 10−2 (5.38 × 10−3) | 1.2111 × 10−2 (1.87 × 10−3) | 1.2705 × 10−2 (1.60 × 10−3) | 8.4812 × 10−3 (3.45 × 10−3) |
| n = 8, δ = 2 | 9.5034 × 10−3 (1.90 × 10−3) | 1.2068 × 10−3 (3.14 × 10−3) | 8.5870 × 10−3 (1.81 × 10−3) | 1.1927 × 10−2 (1.54 × 10−3) | 1.5408 × 10−2 (4.34 × 10−3) | 1.1699 × 10−2 (1.47 × 10−3) | 1.2034 × 10−2 (2.43 × 10−3) | 6.9181 × 10−3 (6.03 × 10−3) |
| n = 8, δ = 3 | 8.7741 × 10−3 (1.35 × 10−3) | 6.8553 × 10−4 (2.78 × 10−3) | 8.1039 × 10−3 (1.54 × 10−3) | 1.1620 × 10−2 (1.93 × 10−3) | 1.4346 × 10−2 (4.99 × 10−3) | 1.1752 × 10−2 (1.90 × 10−3) | 1.1614 × 10−2 (1.57 × 10−3) | 6.0393 × 10−3 (5.08 × 10−3) |
| n = 10, δ = 1 | 9.2486 × 10−3 (1.16 × 10−3) | 1.1389 × 10−2 (1.54 × 10−3) | 1.0777 × 10−2 (1.45 × 10−3) | 1.2465 × 10−2 (1.99 × 10−3) | 1.5472 × 10−2 (3.69 × 10−3) | 1.2154 × 10−2 (2.01 × 10−3) | 1.2186 × 10−2 (2.17 × 10−3) | 9.9395 × 10−3 (5.08 × 10−3) |
| n = 10, δ = 2 | 1.0917 × 10−2 (1.82 × 10−3) | 6.1531 × 10−3 (3.26 × 10−3) | 8.5457 × 10−3 (2.36 × 10−3) | 1.1245 × 10−2 (1.35 × 10−3) | 1.5906 × 10−2 (4.62 × 10−3) | 9.9491 × 10−3 (9.71 × 10−4) | 1.0682 × 10−2 (1.23 × 10−3) | 3.5137 × 10−3 (1.74 × 10−3) |
| n = 10, δ = 3 | 8.4370 × 10−3 (1.15 × 10−3) | 2.9216 × 10−4 (1.04 × 10−3) | 7.4574 × 10−3 (1.89 × 10−3) | 1.0371 × 10−2 (1.41 × 10−3) | 1.3705 × 10−2 (3.80 × 10−3) | 1.0791 × 10−2 (1.74 × 10−3) | 1.1029 × 10−2 (1.57 × 10−3) | 5.0337 × 10−3 (5.02 × 10−3) |
| +/−/= | 3/12/0 | 4/11/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 |
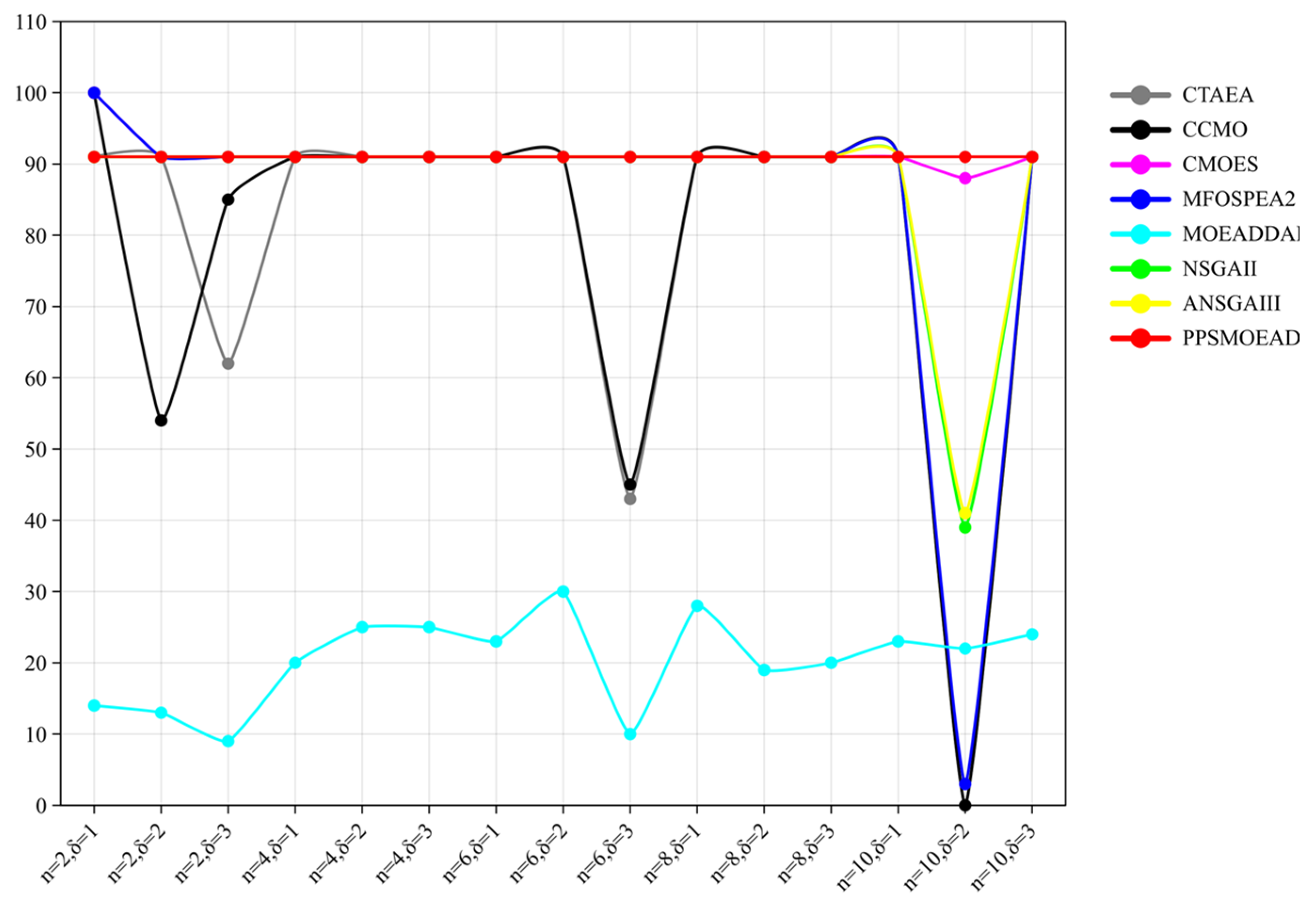
Appendix B.3. Simulation Results of Feasible Solutions
| Scenario | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 9.1000 × 101 (0.00 × 100) | 1.0000 × 102 (0.00 × 100) | 1.0000 × 102 (0.00 × 100) | 1.0000 × 102 (0.00 × 100) | 1.4000 × 101 (2.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 2, δ = 2 | 9.1000 × 101 (0.00 × 100) | 5.4667 × 101 (2.47 × 101) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 1.3667 × 101 (2.08 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 2, δ = 3 | 6.2667 × 101 (6.11 × 100) | 8.5333 × 101 (6.03 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.3333 × 100 (3.06 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 4, δ = 1 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.0667 × 101 (4.51 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 4, δ = 2 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.5000 × 101 (2.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 4, δ = 3 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.5000 × 101 (4.36 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 6, δ = 1 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.3000 × 101 (2.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 6, δ = 2 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 3.0333 × 101 (5.03 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 6, δ = 3 | 4.3333 × 101 (7.57 × 100) | 4.5000 × 101 (4.50 × 101) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 1.0333 × 101 (5.77 × 10−1) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 8, δ = 1 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.8333 × 101 (1.15 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 8, δ = 2 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 1.9000 × 101 (5.57 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 8, δ = 3 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.0333 × 101 (9.45 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 10, δ = 1 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.3333 × 101 (9.02 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| n = 10, δ = 2 | 0.0000 × 100 (0.00 × 100) | 0.0000 × 100 (0.00 × 100) | 8.8000 × 101 (0.00 × 100) | 3.3333 × 100 (3.21 × 100) | 2.2667 × 101 (1.02 × 101) | 3.9000 × 101 (9.54 × 100) | 4.1667 × 101 (1.29 × 101) | 9.1000 × 101 (0.00 × 100) |
| n = 10, δ = 3 | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 2.4000 × 101 (7.81 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) | 9.1000 × 101 (0.00 × 100) |
| +/−/= | 0/3/12 | 1/4/10 | 1/0/14 | 1/1/13 | 0/15/0 | 0/1/14 | 0/1/14 |
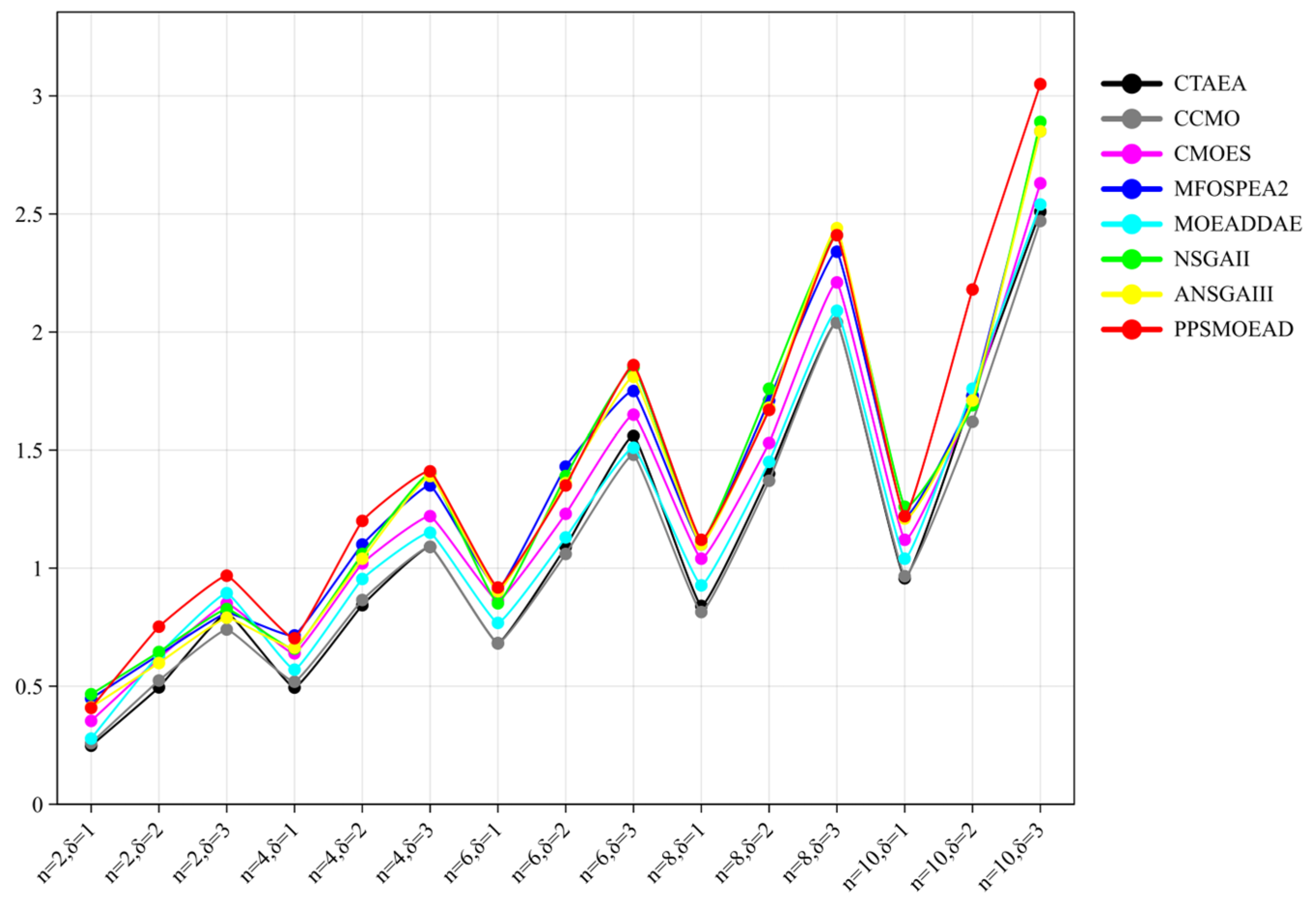
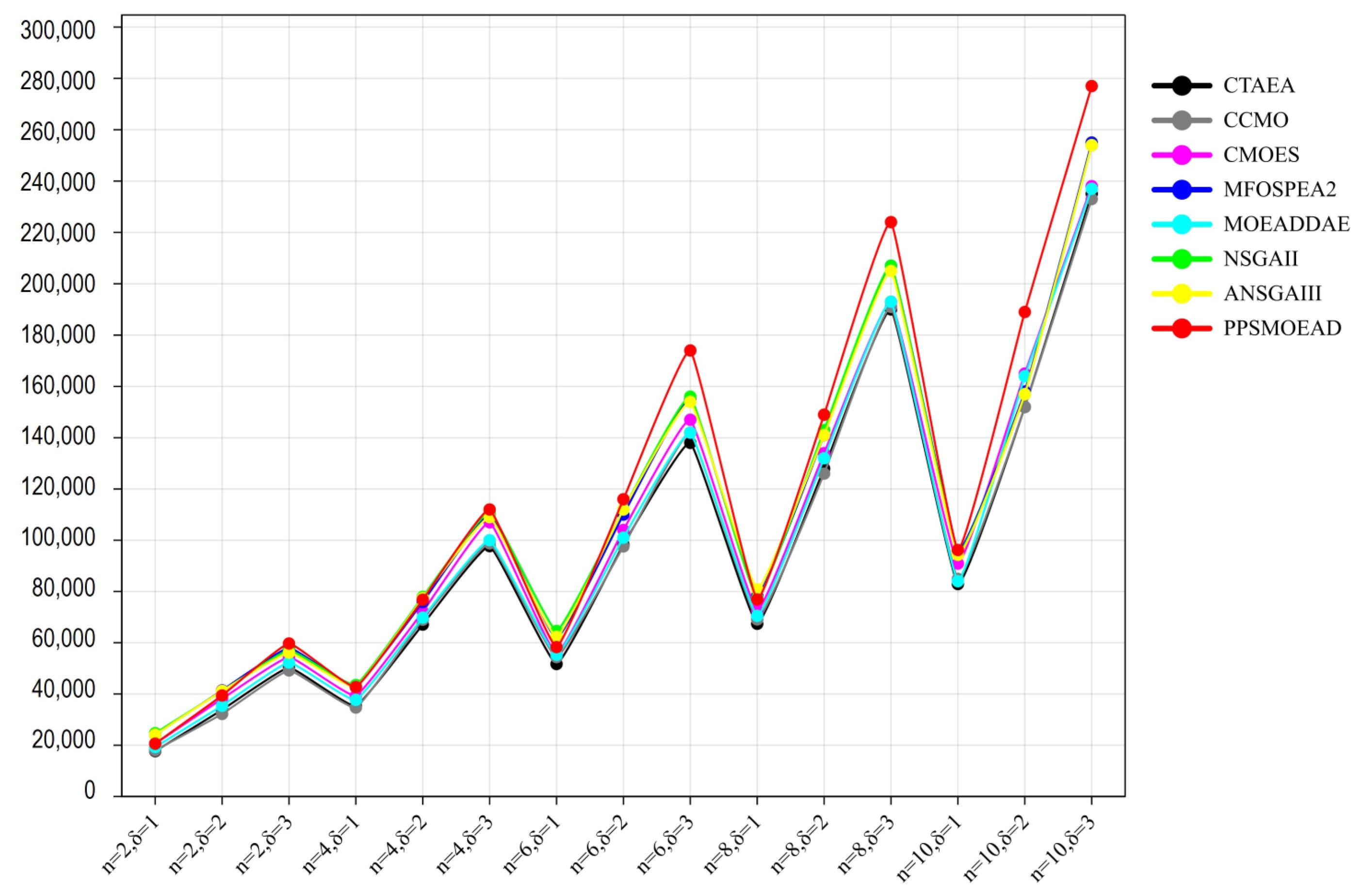
Appendix B.4. Simulation Results of Objective 1
| Scenario | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 2.4817 × 10−1 (1.26 × 10−3) | 2.5932 × 10−1 (2.80 × 10−2) | 3.5309 × 10−1 (2.11 × 10−2) | 4.4772 × 10−1 (1.38 × 10−2) | 2.7817 × 10−1 (1.36 × 10−2) | 4.6625 × 10−1 (2.95 × 10−3) | 4.1123 × 10−1 (2.23 × 10−2) | 4.0792 × 10−1 (1.35 × 10−2) |
| n = 2, δ = 2 | 4.9522 × 10−1 (7.51 × 10−3) | 5.2383 × 10−1 (4.65 × 10−2) | 6.1791 × 10−1 (1.97 × 10−2) | 6.3325 × 10−1 (3.61 × 10−2) | 6.3355 × 10−1 (4.63 × 10−2) | 6.4490 × 10−1 (5.99 × 10−2) | 5.9804 × 10−1 (2.00 × 10−2) | 7.5154 × 10−1 (3.08 × 10−2) |
| n = 2, δ = 3 | 8.1012 × 10−1 (1.09 × 10−2) | 7.3987 × 10−1 (2.89 × 10−2) | 8.5003 × 10−1 (5.24 × 10−2) | 8.0960 × 10−1 (3.45 × 10−2) | 8.9352 × 10−1 (6.85 × 10−2) | 8.2722 × 10−1 (6.11 × 10−2) | 7.8969 × 10−1 (2.66 × 10−2) | 9.6774 × 10−1 (4.99 × 10−2) |
| n = 4, δ = 1 | 4.9363 × 10−1 (1.02 × 10−2) | 5.1893 × 10−1 (2.88 × 10−2) | 6.3893 × 10−1 (2.31 × 10−2) | 7.1475 × 10−1 (2.26 × 10−2) | 5.6962 × 10−1 (1.14 × 10−2) | 6.5933 × 10−1 (1.50 × 10−2) | 6.6272 × 10−1 (3.23 × 10−2) | 7.0257 × 10−1 (4.98 × 10−2) |
| n = 4, δ = 2 | 8.4295 × 10−1 (9.26 × 10−3) | 8.6454 × 10−1 (6.74 × 10−3) | 1.0166 × 100 (4.99 × 10−2) | 1.1016 × 100 (1.94 × 10−2) | 9.5372 × 10−1 (3.20 × 10−2) | 1.0595 × 100 (3.27 × 10−2) | 1.0399 × 100 (7.74 × 10−2) | 1.1984 × 100 (2.46 × 10−2) |
| n = 4, δ = 3 | 1.0945 × 100 (7.57 × 10−3) | 1.0927 × 100 (3.74 × 10−2) | 1.2188 × 100 (4.19 × 10−2) | 1.3479 × 100 (4.20 × 10−2) | 1.1461 × 100 (9.38 × 10−3) | 1.4049 × 100 (2.75 × 10−2) | 1.3939 × 100 (2.17 × 10−2) | 1.4071 × 100 (1.01 × 10−1) |
| n = 6, δ = 1 | 6.8233 × 10−1 (1.33 × 10−2) | 6.8118 × 10−1 (6.17 × 10−2) | 8.6174 × 10−1 (7.72 × 10−2) | 9.0913 × 10−1 (1.68 × 10−2) | 7.6764 × 10−1 (3.87 × 10−2) | 8.5093 × 10−1 (3.84 × 10−2) | 9.0246 × 10−1 (1.68 × 10−2) | 9.1786 × 10−1 (3.19 × 10−2) |
| n = 6, δ = 2 | 1.0891 × 100 (2.92 × 10−3) | 1.0615 × 100 (8.06 × 10−2) | 1.2306 × 100 (1.84 × 10−2) | 1.4326 × 100 (4.79 × 10−2) | 1.1270 × 100 (4.09 × 10−4) | 1.3935 × 100 (3.21 × 10−2) | 1.3630 × 100 (3.05 × 10−2) | 1.3539 × 100 (5.37 × 10−2) |
| n = 6, δ = 3 | 1.5612 × 100 (2.76 × 10−2) | 1.4803 × 100 (4.44 × 10−2) | 1.6517 × 100 (4.96 × 10−2) | 1.7485 × 100 (2.44 × 10−2) | 1.5143 × 100 (7.32 × 10−3) | 1.8495 × 100 (3.39 × 10−2) | 1.8136 × 100 (8.47 × 10−3) | 1.8570 × 100 (7.76 × 10−2) |
| n = 8, δ = 1 | 8.3965 × 10−1 (3.23 × 10−3) | 8.1370 × 10−1 (4.94 × 10−2) | 1.0404 × 100 (4.57 × 10−2) | 1.0991 × 100 (2.11 × 10−2) | 9.2728 × 10−1 (2.23 × 10−2) | 1.1058 × 100 (6.77 × 10−2) | 1.1006 × 100 (5.41 × 10−2) | 1.1188 × 100 (7.55 × 10−2) |
| n = 8, δ = 2 | 1.3957 × 100 (3.41 × 10−3) | 1.3735 × 100 (1.61 × 10−2) | 1.5348 × 100 (4.47 × 10−2) | 1.7119 × 100 (3.28 × 10−2) | 1.4531 × 100 (1.36 × 10−2) | 1.7565 × 100 (8.31 × 10−3) | 1.6848 × 100 (1.73 × 10−2) | 1.6690 × 100 (6.62 × 10−2) |
| n = 8, δ = 3 | 2.0392 × 100 (1.56 × 10−2) | 2.0418 × 100 (5.52 × 10−2) | 2.2068 × 100 (3.41 × 10−2) | 2.3407 × 100 (5.11 × 10−2) | 2.0882 × 100 (2.17 × 10−2) | 2.4116 × 100 (4.70 × 10−2) | 2.4392 × 100 (3.89 × 10−2) | 2.4071 × 100 (6.05 × 10−2) |
| n = 10, δ = 1 | 9.5739 × 10−1 (3.22 × 10−3) | 9.6618 × 10−1 (1.64 × 10−2) | 1.1217 × 100 (2.03 × 10−2) | 1.2225 × 100 (6.11 × 10−2) | 1.0409 × 100 (2.69 × 10−3) | 1.2584 × 100 (1.48 × 10−2) | 1.2097 × 100 (3.61 × 10−2) | 1.2242 × 100 (2.65 × 10−2) |
| n = 10, δ = 2 | 1.7291 × 100 (9.14 × 10−3) | 1.6209 × 100 (1.57 × 10−2) | 1.7113 × 100 (1.48 × 10−1) | 1.7272 × 100 (1.57 × 10−2) | 1.7584 × 100 (2.94 × 10−2) | 1.6935 × 100 (8.17 × 10−3) | 1.7085 × 100 (2.41 × 10−2) | 2.1771 × 100 (1.24 × 10−1) |
| n = 10, δ = 3 | 2.5061 × 100 (5.22 × 10−3) | 2.4677 × 100 (2.68 × 10−2) | 2.6333 × 100 (3.19 × 10−2) | 2.8504 × 100 (6.03 × 10−2) | 2.5354 × 100 (2.12 × 10−2) | 2.8915 × 100 (4.65 × 10−2) | 2.8543 × 100 (5.37 × 10−2) | 3.0549 × 100 (1.62 × 10−1) |
| +/−/= | 0/15/0 | 0/15/0 | 0/15/0 | 4/11/0 | 0/15/0 | 5/10/0 | 4/11/0 |
Appendix B.5. Simulation Results of Objective 2
| Instance | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 1.7727 × 104 (1.43 × 102) | 1.8022 × 104 (1.29 × 102) | 2.0588 × 104 (1.14 × 103) | 2.4076 × 104 (7.37 × 102) | 1.9263 × 104 (3.74 × 102) | 2.4688 × 104 (8.85 × 102) | 2.4127 × 104 (6.38 × 102) | 2.0638 × 104 (4.69 × 102) |
| n = 2, δ = 2 | 3.3822 × 104 (4.64 × 102) | 3.2241 × 104 (2.04 × 102) | 3.8145 × 104 (1.20 × 103) | 4.1432 × 104 (4.83 × 102) | 3.5377 × 104 (4.04 × 102) | 4.1059 × 104 (4.47 × 102) | 4.1152 × 104 (1.35 × 103) | 3.9393 × 104 (5.58 × 102) |
| n = 2, δ = 3 | 5.0284 × 104 (2.44 × 102) | 4.9192 × 104 (1.22 × 103) | 5.4440 × 104 (1.76 × 103) | 5.7983 × 104 (3.70 × 102) | 5.2263 × 104 (9.42 × 102) | 5.7121 × 104 (7.92 × 102) | 5.6060 × 104 (1.06 × 103) | 5.9698 × 104 (1.09 × 103) |
| n = 4, δ = 1 | 3.5272 × 104 (3.62 × 102) | 3.4690 × 104 (1.26 × 103) | 3.9287 × 104 (1.12 × 103) | 4.3048 × 104 (7.46 × 102) | 3.7738 × 104 (4.72 × 102) | 4.3508 × 104 (1.02 × 103) | 4.2714 × 104 (7.26 × 102) | 4.2682 × 104 (3.58 × 103) |
| n = 4, δ = 2 | 6.7110 × 104 (7.83 × 101) | 6.8976 × 104 (7.57 × 102) | 7.2056 × 104 (1.79 × 103) | 7.5904 × 104 (1.43 × 103) | 6.9781 × 104 (6.86 × 102) | 7.7915 × 104 (1.19 × 103) | 7.7411 × 104 (2.13 × 103) | 7.6844 × 104 (2.12 × 103) |
| n = 4, δ = 3 | 9.7741 × 104 (3.84 × 102) | 9.8781 × 104 (1.80 × 103) | 1.0692 × 105 (4.98 × 103) | 1.1029 × 105 (1.80 × 103) | 1.0005 × 105 (1.51 × 103) | 1.1123 × 105 (5.02 × 102) | 1.0932 × 105 (1.06 × 103) | 1.1187 × 105 (2.09 × 103) |
| n = 6, δ = 1 | 5.1724 × 104 (3.05 × 102) | 5.4440 × 104 (7.61 × 102) | 5.5556 × 104 (1.19 × 103) | 6.1670 × 104 (1.08 × 103) | 5.5295 × 104 (8.51 × 102) | 6.4550 × 104 (1.64 × 103) | 6.2320 × 104 (1.33 × 103) | 5.8331 × 104 (1.87 × 103) |
| n = 6, δ = 2 | 9.8313 × 104 (2.09 × 102) | 9.7560 × 104 (4.14 × 103) | 1.0449 × 105 (2.08 × 103) | 1.1013 × 105 (1.05 × 103) | 1.0053 × 105 (1.06 × 103) | 1.1247 × 105 (7.75 × 102) | 1.1230 × 105 (1.85 × 103) | 1.1595 × 105 (6.06 × 103) |
| n = 6, δ = 3 | 1.3832 × 105 (2.01 × 102) | 1.4163 × 105 (3.69 × 103) | 1.4660 × 105 (2.91 × 103) | 1.5496 × 105 (1.09 × 103) | 1.4202 × 105 (1.94 × 103) | 1.5588 × 105 (9.57 × 102) | 1.5359 × 105 (7.29 × 102) | 1.7371 × 105 (8.88 × 103) |
| n = 8, δ = 1 | 6.7441 × 104 (2.78 × 102) | 6.9070 × 104 (3.49 × 103) | 7.2571 × 104 (1.81 × 103) | 7.8538 × 104 (2.45 × 103) | 7.0495 × 104 (1.22 × 102) | 7.7522 × 104 (1.47 × 103) | 8.0767 × 104 (5.68 × 102) | 7.6902 × 104 (2.69 × 103) |
| n = 8, δ = 2 | 1.2778 × 105 (6.84 × 101) | 1.2569 × 105 (3.65 × 103) | 1.3437 × 105 (1.58 × 103) | 1.4098 × 105 (2.48 × 103) | 1.3207 × 105 (1.42 × 103) | 1.4308 × 105 (2.19 × 103) | 1.4060 × 105 (1.84 × 103) | 1.4925 × 105 (2.05 × 103) |
| n = 8, δ = 3 | 1.9028 × 105 (4.46 × 102) | 1.9089 × 105 (6.08 × 103) | 1.9299 × 105 (1.70 × 103) | 2.0709 × 105 (1.85 × 103) | 1.9274 × 105 (1.08 × 103) | 2.0701 × 105 (1.05 × 103) | 2.0459 × 105 (9.39 × 102) | 2.2425 × 105 (1.25 × 104) |
| n = 10, δ = 1 | 8.2917 × 104 (4.49 × 102) | 8.4949 × 104 (1.30 × 103) | 9.0857 × 104 (1.62 × 103) | 9.5876 × 104 (1.57 × 103) | 8.4002 × 104 (1.23 × 103) | 9.4965 × 104 (1.55 × 103) | 9.4282 × 104 (1.15 × 103) | 9.6150 × 104 (2.49 × 102) |
| n = 10, δ = 2 | 1.5193 × 105 (1.11 × 103) | 1.5152 × 105 (2.67 × 103) | 1.6486 × 105 (8.78 × 103) | 1.5767 × 105 (8.00 × 101) | 1.6403 × 105 (2.06 × 103) | 1.5699 × 105 (1.42 × 103) | 1.5711 × 105 (1.12 × 103) | 1.8937 × 105 (2.94 × 103) |
| n = 10, δ = 3 | 2.3515 × 105 (2.63 × 102) | 2.3337 × 105 (3.53 × 103) | 2.3846 × 105 (3.58 × 103) | 2.5497 × 105 (2.41 × 103) | 2.3726 × 105 (1.26 × 103) | 2.5447 × 105 (4.72 × 103) | 2.5390 × 105 (2.64 × 103) | 2.7748 × 105 (6.40 × 103) |
| +/−/= | 0/15/0 | 0/15/0 | 0/15/0 | 5/10/0 | 0/15/0 | 6/9/0 | 6/9/0 |
Appendix B.6. Simulation Results of Objective 3
| Instance | CTAEA | CCMO | CMOES | MFOSPEA2 | MOEADDAE | NSGAII | ANSGAIII | PPSMOEAD |
| n = 2, δ = 1 | 1.2919 × 105 (1.35 × 103) | 1.2839 × 105 (1.83 × 102) | 1.1826 × 105 (1.88 × 103) | 1.1443 × 105 (1.14 × 103) | 1.2171 × 105 (3.65 × 103) | 1.1372 × 105 (1.40 × 103) | 1.1252 × 105 (1.50 × 103) | 7.5361 × 104 (3.16 × 103) |
| n = 2, δ = 2 | 2.7239 × 105 (7.65 × 102) | 2.7738 × 105 (2.18 × 103) | 2.5961 × 105 (4.43 × 103) | 2.5567 × 105 (2.20 × 103) | 2.6387 × 105 (2.10 × 103) | 2.5443 × 105 (3.27 × 103) | 2.5230 × 105 (3.25 × 103) | 1.7882 × 105 (1.47 × 104) |
| n = 2, δ = 3 | 4.2055 × 105 (1.64 × 103) | 4.1639 × 105 (4.62 × 103) | 4.0550 × 105 (5.57 × 102) | 3.9671 × 105 (3.09 × 103) | 4.0551 × 105 (6.65 × 103) | 3.9399 × 105 (1.17 × 103) | 3.9379 × 105 (2.43 × 103) | 2.9215 × 105 (8.22 × 103) |
| n = 4, δ = 1 | 2.4098 × 105 (5.24 × 102) | 2.3753 × 105 (1.33 × 104) | 2.2364 × 105 (4.93 × 103) | 2.1782 × 105 (5.31 × 103) | 2.2975 × 105 (3.66 × 103) | 2.1643 × 105 (1.40 × 103) | 2.1552 × 105 (3.82 × 103) | 1.3194 × 105 (8.98 × 103) |
| n = 4, δ = 2 | 5.0742 × 105 (1.23 × 103) | 4.9994 × 105 (1.37 × 104) | 4.7946 × 105 (7.65 × 103) | 4.7885 × 105 (5.40 × 103) | 4.9697 × 105 (5.34 × 103) | 4.7530 × 105 (1.03 × 103) | 4.7989 × 105 (4.16 × 103) | 3.6180 × 105 (1.68 × 104) |
| n = 4, δ = 3 | 7.8411 × 105 (1.61 × 103) | 7.9697 × 105 (2.53 × 104) | 7.6126 × 105 (7.16 × 103) | 7.4288 × 105 (5.39 × 103) | 7.6981 × 105 (3.79 × 103) | 7.3724 × 105 (6.99 × 103) | 7.3935 × 105 (4.67 × 103) | 5.3602 × 105 (2.56 × 104) |
| n = 6, δ = 1 | 3.3590 × 105 (7.14 × 102) | 3.3709 × 105 (9.05 × 103) | 3.0870 × 105 (3.12 × 103) | 3.0525 × 105 (2.10 × 103) | 3.2724 × 105 (7.76 × 103) | 3.0529 × 105 (1.08 × 104) | 3.0693 × 105 (4.01 × 103) | 1.9522 × 105 (1.65 × 104) |
| n = 6, δ = 2 | 7.1079 × 105 (1.50 × 103) | 7.0456 × 105 (3.20 × 104) | 6.8745 × 105 (4.84 × 103) | 6.5767 × 105 (1.95 × 103) | 7.0125 × 105 (5.11 × 103) | 6.5358 × 105 (4.52 × 103) | 6.6843 × 105 (6.47 × 103) | 4.6995 × 105 (4.43 × 104) |
| n = 6, δ = 3 | 1.0855 × 106 (6.48 × 103) | 1.1004 × 106 (1.21 × 104) | 1.0632 × 106 (1.14 × 104) | 1.0322 × 106 (2.93 × 103) | 1.0780 × 106 (1.19 × 104) | 1.0336 × 106 (8.82 × 103) | 1.0345 × 106 (2.37 × 103) | 7.7564 × 105 (2.23 × 104) |
| n = 8, δ = 1 | 4.2071 × 105 (2.30 × 103) | 4.1537 × 105 (8.78 × 103) | 3.9588 × 105 (5.10 × 103) | 3.8614 × 105 (3.55 × 103) | 4.0899 × 105 (1.67 × 103) | 3.8687 × 105 (5.55 × 103) | 3.8388 × 105 (9.64 × 103) | 3.0375 × 105 (2.53 × 103) |
| n = 8, δ = 2 | 8.8451 × 105 (3.10 × 103) | 8.9239 × 105 (2.28 × 104) | 8.5474 × 105 (4.11 × 103) | 8.2790 × 105 (3.08 × 103) | 8.7196 × 105 (7.20 × 103) | 8.3360 × 105 (1.17 × 104) | 8.2955 × 105 (1.22 × 104) | 6.1058 × 105 (1.69 × 104) |
| n = 8, δ = 3 | 1.3454 × 106 (4.19 × 103) | 1.3274 × 106 (2.14 × 104) | 1.3194 × 106 (9.78 × 103) | 1.2680 × 106 (3.76 × 103) | 1.3199 × 106 (2.50 × 103) | 1.2740 × 106 (1.30 × 104) | 1.2739 × 106 (5.92 × 103) | 9.7669 × 105 (1.01 × 104) |
| n = 10, δ = 1 | 5.0129 × 105 (1.04 × 103) | 5.0015 × 105 (1.49 × 104) | 4.8192 × 105 (4.26 × 103) | 4.5969 × 105 (3.77 × 103) | 4.8550 × 105 (4.63 × 103) | 4.5871 × 105 (5.93 × 103) | 4.6011 × 105 (2.80 × 103) | 3.3833 × 105 (2.41 × 104) |
| n = 10, δ = 2 | 1.0403 × 106 (6.76 × 103) | 1.0609 × 106 (2.78 × 104) | 1.0555 × 106 (1.73 × 104) | 1.0412 × 106 (5.75 × 102) | 1.0225 × 106 (1.28 × 104) | 1.0481 × 106 (8.41 × 103) | 1.0505 × 106 (6.88 × 103) | 7.3307 × 105 (1.06 × 104) |
| n = 10, δ = 3 | 1.5821 × 106 (3.20 × 103) | 1.5879 × 106 (1.90 × 104) | 1.5642 × 106 (9.22 × 103) | 1.5147 × 106 (9.67 × 103) | 1.5629 × 106 (1.14 × 104) | 1.5031 × 106 (6.47 × 102) | 1.5062 × 106 (7.84 × 103) | 1.1677 × 106 (1.75 × 104) |
| +/−/= | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 | 0/15/0 |
References
- Samanta, S.; Sen, G.; Ghosh, S.K. A Literature Review on Police Patrolling Problems. Ann. Oper. Res. 2022, 316, 1063–1106. [Google Scholar] [CrossRef]
- Dai, M.; Xia, Y.; Han, R. Temporal Variations in Calls for Police Service During COVID-19: Evidence from China. Crime Delinq. 2022, 68, 1183–1206. [Google Scholar] [CrossRef]
- Weisburd, D.; Majmundar, M.K. Proactive Policing: Effects on Crime and Communities; National Academies Press: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Bullock, K. Community, Intelligence-Led Policing and Crime Control. Polic. Soc. 2013, 23, 125–144. [Google Scholar] [CrossRef]
- Jenkins, M.J. Police Support for Community Problem-Solving and Broken Windows Policing. Am. J. Crim. Justice 2016, 41, 220–235. [Google Scholar] [CrossRef]
- Sindall, K.; Sturgis, P. Austerity Policing: Is Visibility More Important than Absolute Numbers in Determining Public Confidence in the Police? Eur. J. Criminol. 2013, 10, 137–153. [Google Scholar] [CrossRef]
- Yesberg, J.; Brunton-Smith, I.; Bradford, B. Police Visibility, Trust in Police Fairness, and Collective Efficacy: A Multilevel Structural Equation Model. Eur. J. Criminol. 2023, 20, 712–737. [Google Scholar] [CrossRef]
- Alamdari, S.; Fata, E.; Smith, S.L. Persistent Monitoring in Discrete Environments: Minimizing the Maximum Weighted Latency between Observations. Int. J. Robot. Res. 2014, 33, 138–154. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Franchi, A.; Bullo, F. On Cooperative Patrolling: Optimal Trajectories, Complexity Analysis, and Approximation Algorithms. IEEE Trans. Robot. 2012, 28, 592–606. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Gutierrez-Moizant, R.; Melendez-Useros, M.; Lopez Boada, M.J. Static Output Feedback Control for Vehicle Platoons with Robustness to Mass Uncertainty. Electronics 2025, 14, 139. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Melendez-Useros, M.; Jimenez-Salas, M.; Boada, M.J.L. Fault-Tolerant Robust Output-Feedback Control of a Vehicle Platoon Considering Measurement Noise and Road Disturbances. IET Intell. Transp. Syst. 2025, 19, e70007. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and Pull Search for Solving Constrained Multi-Objective Optimization Problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Weisburd, S. Police Presence, Rapid Response Rates, and Crime Prevention. Rev. Econ. Stat. 2021, 103, 280–293. [Google Scholar] [CrossRef]
- Andresen, M.A.; Lau, K.C.Y. An Evaluation of Police Foot Patrol in Lower Lonsdale, British Columbia. Police Pract. Res. 2014, 15, 476–489. [Google Scholar] [CrossRef]
- Andresen, M.A.; Shen, J.-L. The Spatial Effect of Police Foot Patrol on Crime Patterns: A Local Analysis. Int. J. Offender Ther. Comp. Criminol. 2019, 63, 1446–1464. [Google Scholar] [CrossRef]
- Ratcliffe, J.; Sorg, E. Foot Patrol: Rethinking the Cornerstone of Policing; Springer: New York, NY, USA, 2017. [Google Scholar]
- Basilico, N.; Gatti, N.; Amigoni, F. Patrolling Security Games: Definition and Algorithms for Solving Large Instances with Single Patroller and Single Intruder. Artif. Intell. 2012, 184–185, 78–123. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, T.; Wise, S. Developing an Online Cooperative Police Patrol Routing Strategy. Comput. Environ. Urban Syst. 2017, 62, 19–29. [Google Scholar] [CrossRef]
- Leigh, J.; Dunnett, S.; Jackson, L. Predictive Police Patrolling to Target Hotspots and Cover Response Demand. Ann. Oper. Res. 2019, 283, 395–410. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Wu, D.; Chi, C. A Game Theory Approach for Assessment of Risk and Deployment of Police Patrols in Response to Criminal Activity in San Francisco. Risk Anal. 2020, 40, 534–549. [Google Scholar] [CrossRef]
- Chase, J.; Phong, T.; Long, K.; Le, T.; Lau, H.C. GRAND-VISION: An Intelligent System for Optimized Deployment Scheduling of Law Enforcement Agents. ICAPS 2021, 31, 459–467. [Google Scholar] [CrossRef]
- Chainey, S.P.; Matias, J.A.S.; Nunes Junior, F.C.F.; Coelho Da Silva, T.L.; De Macêdo, J.A.F.; Magalhães, R.P.; De Queiroz Neto, J.F.; Silva, W.C.P. Improving the Creation of Hot Spot Policing Patrol Routes: Comparing Cognitive Heuristic Performance to an Automated Spatial Computation Approach. ISPRS Int. J. Geo-Inf. 2021, 10, 560. [Google Scholar] [CrossRef]
- Guevara, C.; Santos, M. Smart Patrolling Based on Spatial-Temporal Information Using Machine Learning. Mathematics 2022, 10, 4368. [Google Scholar] [CrossRef]
- Wang, W.; Dong, Z.; An, B.; Jiang, Y. Toward Efficient City-Scale Patrol Planning Using Decomposition and Grafting. IEEE Trans. Intell. Transport. Syst. 2021, 22, 747–757. [Google Scholar] [CrossRef]
- Wang, W.; Tao, H.; Jiang, Y. Efficient Online City-Scale Patrolling by Exploiting Offline Model-Based Coordination Policy. IEEE Trans. Intell. Transport. Syst. 2022, 23, 13805–13818. [Google Scholar] [CrossRef]
- Che, Q.; Wang, W.; Liu, G.; Zhang, W.; Jiang, J.; Jiang, Y. An Offline–Online Integration Approach for Security Traffic Patrolling with Frequency Constraints. IEEE Trans. Comput. Soc. Syst. 2024, 11, 2383–2396. [Google Scholar] [CrossRef]
- Joe, W.; Lau, H.C.; Pan, J. Reinforcement Learning Approach to Solve Dynamic Bi-Objective Police Patrol Dispatching and Rescheduling Problem. ICAPS 2022, 32, 453–461. [Google Scholar] [CrossRef]
- Joe, W.; Lau, H.C. Learning to Send Reinforcements: Coordinating Multi-Agent Dynamic Police Patrol Dispatching and Rescheduling via Reinforcement Learning. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, International Joint Conferences on Artificial Intelligence Organization, Macau, China, 19–25 August 2023; pp. 153–161. [Google Scholar]
- Jiang, Y.; Li, H.; Feng, B.; Wu, Z.; Zhao, S.; Wang, Z. Street Patrol Routing Optimization in Smart City Management Based on Genetic Algorithm: A Case in Zhengzhou, China. ISPRS Int. J. Geo-Inf. 2022, 11, 171. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A Comprehensive Survey on NSGA-II for Multi-Objective Optimization and Applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Computat. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Computat. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. TIK Rep. 2001, 103, 1–22. [Google Scholar]
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective Evolutionary Algorithms: A Survey of the State of the Art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-Based Selection in Multiobjective Search. In Proceedings of the Parallel Problem Solving from Nature—PPSN VIII, Birmingham, UK, 18–22 September 2004; Yao, X., Burke, E.K., Lozano, J.A., Smith, J., Merelo-Guervós, J.J., Bullinaria, J.A., Rowe, J.E., Tiňo, P., Kabán, A., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Bader, J.; Zitzler, E. HypE: An Algorithm for Fast Hypervolume-Based Many-Objective Optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Ban, X.; Yu, K.; Qu, B.; Qiao, K.; Yue, C.; Chen, K.; Tan, K.C. A Survey on Evolutionary Constrained Multiobjective Optimization. IEEE Trans. Evol. Computat. 2023, 27, 201–221. [Google Scholar] [CrossRef]
- Asafuddoula, M.; Ray, T.; Sarker, R. A Decomposition-Based Evolutionary Algorithm for Many Objective Optimization. IEEE Trans. Evol. Computat. 2015, 19, 445–460. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y. Shift-Based Penalty for Evolutionary Constrained Multiobjective Optimization and Its Application. IEEE Trans. Cybern. 2023, 53, 18–30. [Google Scholar] [CrossRef]
- Liu, Z.-Z.; Wang, B.-C.; Tang, K. Handling Constrained Multiobjective Optimization Problems via Bidirectional Coevolution. IEEE Trans. Cybern. 2022, 52, 10163–10176. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J. Comparative Study of Distributed Consensus Gossip Algorithms for Network Size Estimation in Multi-Agent Systems. Future Internet 2021, 13, 134. [Google Scholar] [CrossRef]
- Lohitha, N.S.; Pounambal, M. Integrated Publish/Subscribe and Push-Pull Method for Cloud Based IoT Framework for Real Time Data Processing. Meas. Sens. 2023, 27, 100699. [Google Scholar] [CrossRef]
- Sui, J.; Chen, P.; Gu, H. Deep Spatio-Temporal Graph Attention Network for Street-Level 110 Call Incident Prediction. Appl. Sci. 2024, 14, 9334. [Google Scholar] [CrossRef]
- Chainey, S.P.; Monteiro, J. The Dispersion of Crime Concentration during a Period of Crime Increase. Secur. J. 2019, 32, 324–341. [Google Scholar] [CrossRef]
- Curman, A.S.N.; Andresen, M.A.; Brantingham, P.J. Crime and Place: A Longitudinal Examination of Street Segment Patterns in Vancouver, BC. J. Quant. Criminol. 2015, 31, 127–147. [Google Scholar] [CrossRef]
- Weisburd, D.; Telep, C.W.; Lawton, B.A. Could Innovations in Policing Have Contributed to the New York City Crime Drop Even in a Period of Declining Police Strength?: The Case of Stop, Question and Frisk as a Hot Spots Policing Strategy. Justice Q. 2014, 31, 129–153. [Google Scholar] [CrossRef]
- Dau, P.M.; Vandeviver, C.; Dewinter, M.; Witlox, F.; Vander Beken, T. Policing Directions: A Systematic Review on the Effectiveness of Police Presence. Eur. J. Crim. Policy Res. 2023, 29, 191–225. [Google Scholar] [CrossRef]
- Doyle, M.; Frogner, L.; Andershed, H.; Andershed, A.-K. Feelings of Safety in the Presence of the Police, Security Guards, and Police Volunteers. Eur. J. Crim. Policy Res. 2016, 22, 19–40. [Google Scholar] [CrossRef]
- Pilgrim, B. Munkres’ Assignment Algorithm, Modified for Rectangular Matrices. Available online: https://ww2.mathworks.cn/matlabcentral/fileexchange/20652-hungarian-algorithm-for-linear-assignment-problems-v2-3?s_tid=FX_rc1_behav (accessed on 11 February 2025).
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Jiao, R.; Xue, B.; Zhang, M. A Multiform Optimization Framework for Constrained Multiobjective Optimization. IEEE Trans. Cybern. 2023, 53, 5165–5177. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 303–315. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A Coevolutionary Framework for Constrained Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2021, 25, 102–116. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Jin, Y. Even Search in a Promising Region for Constrained Multi-Objective Optimization. IEEE/CAA J. Autom. Sin. 2024, 11, 474–486. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Q.; Lin, Q. A Constrained Multiobjective Evolutionary Algorithm with Detect-and-Escape Strategy. IEEE Trans. Evol. Comput. 2020, 24, 938–947. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Schott, J.R. Fault Tolerant Design Using Single and Multi-Criteria Genetic Algorithms. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. Volume 37. pp. 1–13. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]







| t = 1\t = 2 | ||||
|---|---|---|---|---|
| 3000 | 4000 | 3000 | 6000 | |
| 4000 | 3000 | 4000 | 5000 | |
| 5000 | 4000 | 3000 | 4000 | |
| Inf | 3000 | 2000 | 4000 |
| t = 1\t = 2 | ||||
|---|---|---|---|---|
| 0 | 1000 | 0 | 3000 | |
| 1000 | 0 | 1000 | 2000 | |
| 2000 | 1000 | 1000 | 1000 | |
| Inf | 1000 | 0 | 2000 |
| t = 1\t = 2 | ||||
|---|---|---|---|---|
| 0 | 1000 | 0 | 2000 | |
| 1000 | 0 | 1000 | 1000 | |
| 2000 | 1000 | 1000 | 0 | |
| Inf | 1000 | 0 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, J.; Chen, P.; Jiang, H. Optimizing Police Patrol Strategies in Real-World Scenarios: A Modified PPS-MOEA/D Approach for Constrained Multi-Objective Optimization. Appl. Sci. 2025, 15, 3651. https://doi.org/10.3390/app15073651
Sui J, Chen P, Jiang H. Optimizing Police Patrol Strategies in Real-World Scenarios: A Modified PPS-MOEA/D Approach for Constrained Multi-Objective Optimization. Applied Sciences. 2025; 15(7):3651. https://doi.org/10.3390/app15073651
Chicago/Turabian StyleSui, Jinguang, Peng Chen, and Huan Jiang. 2025. "Optimizing Police Patrol Strategies in Real-World Scenarios: A Modified PPS-MOEA/D Approach for Constrained Multi-Objective Optimization" Applied Sciences 15, no. 7: 3651. https://doi.org/10.3390/app15073651
APA StyleSui, J., Chen, P., & Jiang, H. (2025). Optimizing Police Patrol Strategies in Real-World Scenarios: A Modified PPS-MOEA/D Approach for Constrained Multi-Objective Optimization. Applied Sciences, 15(7), 3651. https://doi.org/10.3390/app15073651





