Abstract
In multi-UAV collaborative power grid inspection, the system efficiency of existing methods is limited by the performance of both task assignment and path planning, which is critical in large-scale task scenarios, resulting in a huge computational cost and a high possibility to local optimality. To address these challenges, a bilevel optimization framework based on GA-NSGA-II and task segmentation is proposed to balance the total inspection distance and the distance standard deviation of UAVs, where the outer optimization employs the NSGA-II to assign task units to each UAV evenly, while the inner optimization deploys an adaptive genetic algorithm with an elite retention strategy to optimize the inspection direction and order in each task domain to obtain a Pareto-optimal solution set under constraints. To avoid the dimensionality disaster, the massive inspection points are combined into task units based on the UAV’s endurance. In scenarios with 284 tower task points, the proposed algorithm has reduced the standard deviation of UAV flight distances by 41.91% to 84.63% and the longest flight distance by 29.41% to 43.98% compared to the GA-GA bilevel optimization. Against task-adaptive clustering optimization, it decreased the standard deviation by 18.25% to 94.93% and the longest flight distance by 15.97% to 37.33%. Applying it to 406 tower task points also confirmed the GA-NSGA-II bilevel optimization’s effectiveness in minimizing the total inspection distance and balancing UAV workloads.
1. Introduction
As the scale of power grids continues to expand, the maintenance of transmission systems is becoming increasingly difficult, especially in harsh environments and complex terrain conditions, where traditional inspection methods are inefficient and cannot achieve full coverage, affecting the quality of power grid inspections. Owing to its characteristics of rapid response, high flexibility, high safety, and strong imaging capabilities, the unmanned aerial vehicle (UAV) can effectively cover areas that are hard to reach by manual inspections, can significantly improve the efficiency and accuracy of power grid inspections, and has promising potential in application. Currently, the UAV inspection approach has become the mainstream method, but its overall efficiency is still limited by the quality of task assignment and path planning. Therefore, the study on UAV-based power grid inspection, especially for its task assignment and path planning, has great significance to improve the power grid inspection efficiency, energy security, and economic development [1,2,3,4,5,6].
Compared to manual inspections, UAV-based inspections offer advantages such as lower costs and reduced security risks [7]. However, single UAV inspections often face limitations, such as a restricted range and higher failure risks. Multi-UAV cooperative inspection technology mitigates these risks by expanding the inspection coverage, enhancing efficiency through redundancy, and offering flexibility in adjusting inspection strategies [8,9,10,11], which makes it more valuable in practical applications. Despite these benefits, the implementation of multi-UAV collaborative inspections still encounters several challenges: Balanced task assignment: To optimize inspection efficiency, tasks must be allocated evenly among UAVs to prevent overloading any single unit [12,13]. Optimal path planning: it is crucial to plan the most efficient inspection route for each UAV to minimize energy consumption and enhance inspection efficiency, all while ensuring task completion [14,15]. Expansion of inspection scope: extending the inspection strategy to cover large-scale power grids is necessary to improve system adaptability and coverage [16,17].
Task assignment in multi-UAV power grid inspections is a typical multiple traveling salesman problem (MTSP) with constrains [18]. In the literature, various methods have been proposed, including exact algorithms like linear programming, heuristic approaches such as simulated annealing, neural network-based methods like self-organizing neural networks, and a hybrid combination of these approaches. Heuristic algorithms, including genetic algorithms, particle swarm optimization, ant colony optimization, and clustering methods, are particularly effective for large-scale task assignment and path planning, as they can quickly approximate optimal solutions through heuristic rules [19,20]. Li et al. improved bidirectional ant colony and honey badger algorithms for task assignment and path planning in challenging environments, but their algorithms are computationally intensive and unsuitable for large-scale scenarios [21]. Ma et al. developed a coordination optimization algorithm using k-means clustering and genetic algorithms to reduce flight distances, but it struggles with balanced task assignment due to its reliance on geographical clustering [22]. Huo et al. proposed a simulated annealing algorithm for small-scale scenarios, but its efficiency declines in large-scale applications [23]. Optimization methods such as dynamic programming, depth-first and breadth-first search, and mixed integer linear programming have also been explored [24]. Wu et al. introduced a dynamic ant colony division model to track heterogeneous UAVs’ positions in real time, showing strong self-organization and adaptability to dynamic environments [25]. Zhang et al. proposed a discrete particle swarm optimization algorithm for dynamic task assignment in changing environments [26]. Li et al. combined mixed integer linear programming with reinforcement learning and adaptive large neighborhood search for UAV transmission line inspections, demonstrating superior optimization and stability, though the approach still faces challenges in computational complexity and real-time performance [27]. Finally, Rubens et al. used model predictive control in a mixed integer linear programming approach to handle task assignment and trajectory planning in obstacle-rich environments with connectivity constraints [28]. Heuristic algorithms have significant advantages over exact algorithms. First, heuristic algorithms can quickly solve problems in polynomial time, making them suitable for large-scale task planning. This avoids the issue of excessive solution time caused by the exponential growth of computational complexity in exact algorithms. For example, Wang and Liu et al. developed a FIFO-based genetic algorithm to optimize the scheduling of heterogeneous UAVs for package delivery. They did this because the mixed-integer programming model is difficult to solve within a reasonable time for large-scale instances, thereby verifying the reasonable solution time of heuristic algorithms compared to exact algorithms [29]. Second, heuristic algorithms have good adaptability and robustness. In power grid inspection, complex terrain and dynamically changing environments pose challenges for path planning. Heuristic algorithms can effectively deal with environmental changes and avoid local optima by introducing randomness, dynamic adjustment mechanisms, or combining with other algorithms. Xu et al. proposed a model based on dynamic ant colony labor division to address the dynamic task assignment problem in UAV swarms. Through simulation experiments, they demonstrated the high self-organization, flexibility, and real-time responsiveness of heuristic algorithms in dynamic environments for task assignment [30]. Moreover, heuristic algorithms perform well in multi-objective optimization. Multi-UAV inspection tasks often involve multiple optimization objectives, such as minimizing the total flight distance, energy consumption, and mission completion time. Heuristic algorithms can flexibly balance these objectives to find compromise solutions. Hu et al. developed a fuzzy multi-objective optimization method based on pigeon-inspired optimization (PIO) to solve the task assignment problem for UAVs targeting multiple objectives. The study established a multi-objective integer programming model with three objective functions and employed the PIO algorithm to address task assignment. This work validated the superiority of heuristic algorithms in multi-objective optimization [31]. Finally, heuristic algorithms are simple to implement and consume low resources, making them suitable for UAV systems with limited resources. For example, Ermağan et al. proposed a learning-based heuristic algorithm to solve the charging station docking problem in UAV path planning. The algorithm demonstrates high efficiency in resource-constrained scenarios and can generate high-quality path planning solutions in a short time [32]. So, heuristic algorithms are capable of quickly generating high-quality solutions for multi-UAV power grid inspection task assignment and adapting to complex and dynamic environments while demonstrating good robustness and scalability. Compared to exact algorithms, they are an effective approach for solving task assignment problems within the framework of the MTSP.
Given the complexity of large-scale power grid inspection tasks and the limitations of computational resources, this study adopts an offline path planning method. Although this method cannot respond to environmental changes in real time, it completes path planning before task execution, efficiently utilizing computational resources to ensure global optimality in large-scale scenarios. Moreover, this method is not limited to a specific type of UAV. Since path planning is based on UAV battery capacity for task segmentation, it can accommodate various types and performance levels of UAVs, demonstrating strong versatility. Additionally, the method is applicable to multiple types of tasks, including fault detection and routine inspection. This is because its underlying assumptions cover the power lines between transmission towers and the towers themselves, and the planning process has already accounted for the time required for UAVs to locate fault points and take photos at the towers. Therefore, this method can be widely applied to various task scenarios. While many existing methods can effectively address multi-UAV task assignment in small-scale scenarios, significant challenges remain in large-scale scenarios. For example, how to achieve rational task assignment among multi-UAVs while ensuring the shortest total travel distance is still an urgent problem to be solved. To address this challenge, this paper proposes an innovative bilevel optimization algorithm based on GA-NSGA-II for multi-UAV task assignment and path planning for large-scale power grid inspections. The main innovations are as follows:
- Power line segmentation: the extensive power grid lines are divided into several unit tasks based on external constraints and UAV battery capacity for subsequent optimization.
- Multi-UAV task assignment based on the NSGA-II algorithm: the chromosome encoding strategy of the NSGA-II algorithm is innovatively applied to allocate the segmented unit tasks to each UAV.
- Path optimization with the adaptive genetic algorithm based on the elitist preservation strategy: for the inspection unit tasks allocated to each UAV, an adaptive genetic algorithm based on the elitist preservation strategy is innovatively used to optimize the inspection sequence and direction of the unit tasks.
- The GA-NSGA-II bilevel optimization algorithm: An innovative bilevel optimization framework combining the adaptive genetic algorithm with the elitist preservation strategy and NSGA-II is proposed. This framework aims to minimize the total inspection distance of UAVs while ensuring balanced task distribution among them.
The specific procedure of the entire algorithm is as follows: First, according to the proposed constraints and UAV battery capacity, the power grid lines are segmented into several unit tasks. Next, these unit tasks are allocated to different UAVs using the chromosome encoding strategy of the NSGA-II algorithm. Subsequently, in the inner optimization layer, the adaptive genetic algorithm based on the elitist preservation strategy is employed to optimize the sequence and direction of the unit tasks assigned to each UAV, thereby minimizing the UAV’s flight distance. Finally, in the outer layer, the genetic selection mechanism of the NSGA-II algorithm is used to screen for the optimal results that meet the conditions.
2. Problem Description
2.1. Scenario Description
The problem of multi-UAV cooperative inspections and task assignment can be described as follows: For the inspection task composed of multiple transmission towers in multiple transmission lines in three-dimensional space, multi-UAVs can maximize the cooperative operation efficiency of UAVs through reasonable task segmentation, balanced distribution, and path planning. In the execution of the task, the UAV needs to take off from the designated charging station (hive) and return to the hive after the completion of the task. There are a certain number of redundant hives for the UAV to charge. Because the transmission towers in different lines belong to different entrusting parties, there are various types of inspection tasks in the scenario. The inspection task defines a number of checkpoints and auxiliary points for each tower. The UAV needs to hover at the checkpoint to take photos and complete operations such as turning at the auxiliary point. Figure 1 shows a scenario example with three transmission lines, two power change hives, and a total of 51 towers to be inspected.
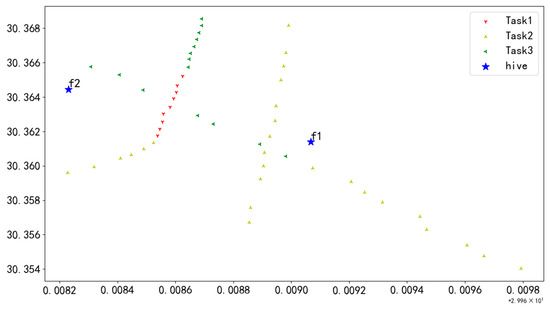
Figure 1.
Top view of the transmission line scene.
2.2. Symbol Definition and Description
To construct a multi-UAV inspection scheduling algorithm based on bilevel optimization, system modeling and optimization and constraint definition involve a large number of variables and parameters, as shown in Table 1 and Table 2.

Table 1.
Element symbols and definitions.

Table 2.
Variables, parameter symbols, and their definitions.
2.3. Constraint Establishment
This paper takes the total flight distance of UAVs and the standard deviation of flight distances among UAVs as optimization objectives. It aims to ensure that the total flight distance of UAVs is minimized while balancing the flight distances of each UAV, thereby guaranteeing the feasibility of multi-UAV task assignment and path planning. The objective functions are defined as follows:
The total flight distance D represents the combined flight distance of all UAVs, which is calculated as follows:
The standard deviation of multi-UAV flight distance, denoted as µ, is defined as a measure of the variation in flight distances among individual UAVs. A smaller value of µ indicates that the flight distances of the UAVs are closer to each other, suggesting a more balanced task assignment and higher efficiency in path planning. Conversely, a larger value of µ may imply uneven task distribution, with some UAVs having to fly longer distances. The mathematical expression for µ is as follows:
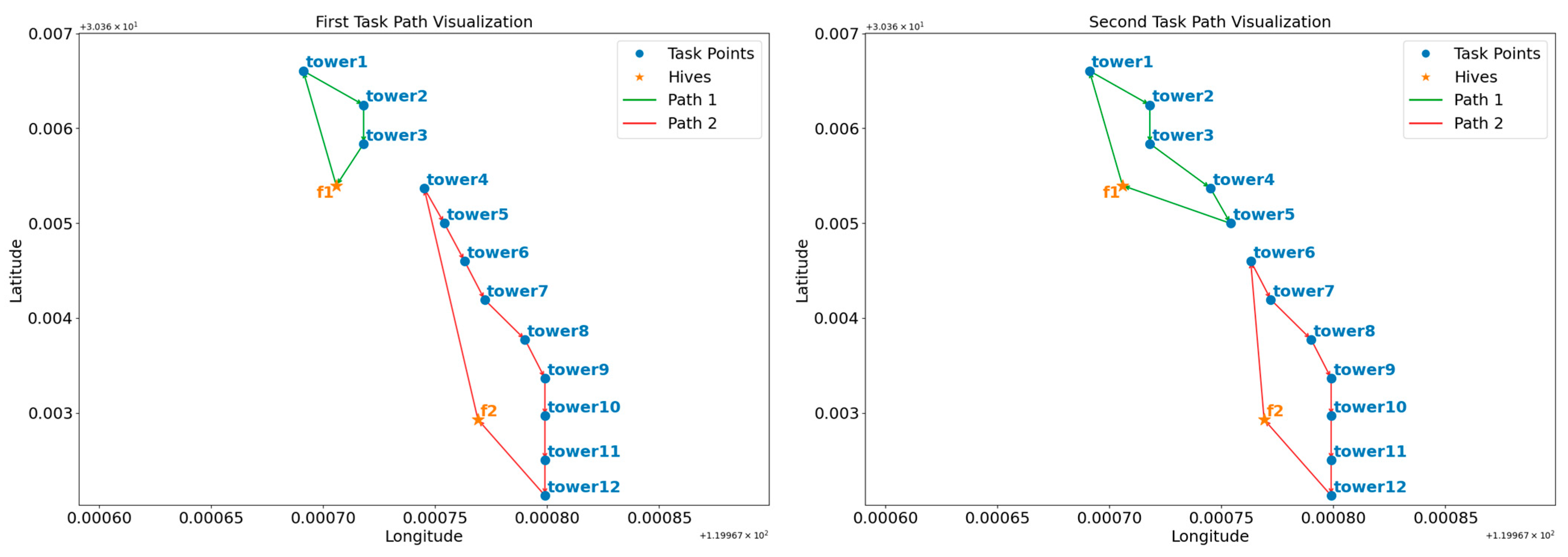
Figure 2 clearly illustrates the impact of task balance constraints on the flight path planning of UAVs. The left diagram represents the flight routes of the two UAVs without considering task balance constraints. In contrast, the right diagram shows the flight routes after the introduction of task balance constraints. By comparison, it is evident that the difference in flight distances between the two UAVs has been significantly reduced following the optimization with task balance constraints. This change not only enhances the overall flight efficiency but also effectively minimizes the waiting time incurred when one UAV completes its tasks ahead of the other, thereby improving the collaborative efficiency of the UAVs. Furthermore, this optimization approach helps to equalize the workload of the two UAVs, preventing the waste of resources and further enhancing the overall efficiency of task execution.
Figure 2.
Comparison of task distribution before and after balancing.
The constraints are as follows:
Among them, Constraint (3) is the matching constraint between UAVs and hives, ensuring that the number of UAVs is equal to the number of hives; Constraints (4–8) are constraints on power grid line segmentation, and Constraint (4) ensures that all transmission towers are assigned to the task to ensure the comprehensiveness of the inspection; Constraint (5) ensures that each transmission tower is only assigned to a single UAV unit task to avoid repetitive inspection tasks, while Constraints (6–7) are used to restrict the cumulative power consumption of a single takeoff and landing of the UAV so that it does not exceed its endurance margin; Constraint (8) ensures that the generation of new unit tasks is stopped when the task is segmented to the end of each transmission line and ensures the continuity of task assignment; Constraints (9–11) are the outer task assignment constraint, and Constraint (9) ensures that each UAV is assigned at least one small task; Constraint (10) ensures that any unit task is performed by one UAV, ensuring that the task is performed exclusively. Constraint (11) emphasizes the balance of task assignment; that is, the task quantity of each UAV matches its performance; Constraint (12) refers to the cross-line task execution constraint, which is used to prohibit UAVs from performing tasks across lines to avoid confusion in task execution; Constraint (13) stipulates that each UAV must be positioned in distinct hives at both the initial and final stages of the task. This ensures that every UAV is located in separate hives at the start and end of the mission, thereby efficiently avoiding various conflicts and ensuring the smooth operation of the multi-UAV system as well as the efficient completion of the task; Constraints (14–16) are constraints on the value range of variables to ensure that all decision variables are within a reasonable range, ensuring the solvability and practicability of the model.
3. Solution Algorithm
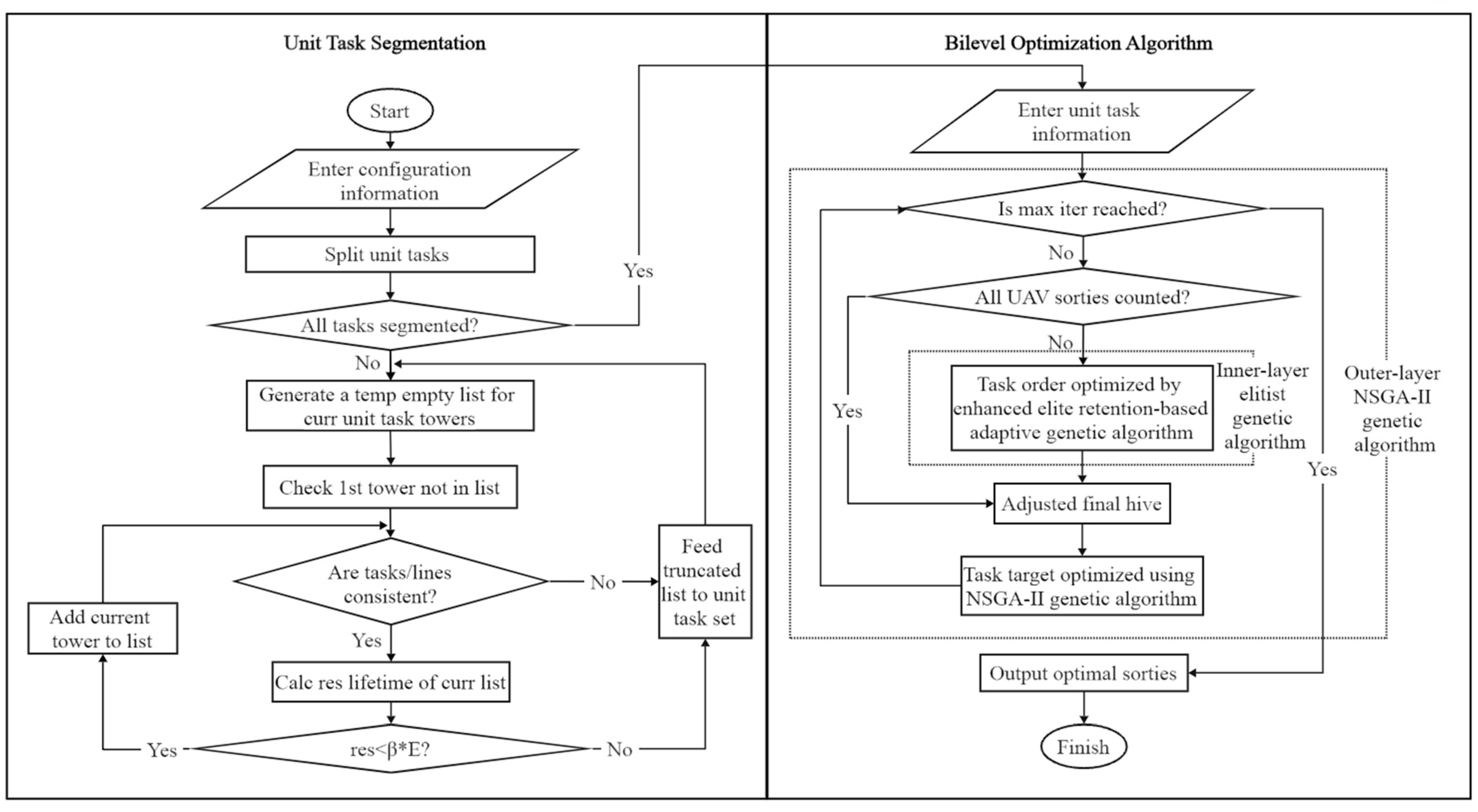
In response to the multi-UAV power grid inspection scheduling problem, this paper innovatively proposes a bilevel optimization-based GA-NSGA-II algorithm framework, as shown in Figure 3. Through the segmentation of power grid lines, the large-scale inspection task is decomposed into smaller and easy to manage unit tasks, and each unit task is regarded as the minimum dispatching unit. The algorithm employs a bilevel optimization strategy: the inner-layer optimization uses an adaptive genetic algorithm to optimize the task execution sequence within a single UAV’s domain, while the outer-layer optimization utilizes the NSGA-II algorithm for task assignment and optimization.
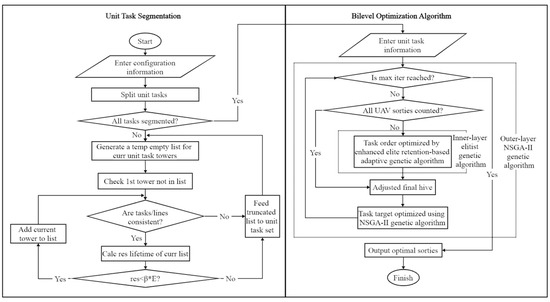
Figure 3.
Framework of the bilevel optimization algorithm.
3.1. Unit Task Segmentation
In power grid inspections, the complexity and diversity of inspection tasks make it almost impossible for drones to complete all inspections within a single flight range. Therefore, how to effectively divide inspection tasks to ensure that UAVs can complete effective inspections within their safe flight range has become an urgent problem to be solved. To address this issue, this paper proposes a method for dividing inspection tasks based on the endurance capability of a single UAV.
Firstly, the UAV configuration information and geographical data are input as parameters. Then, a temporary list is created to store the power grid towers in the current unit task. For the first power grid tower that has not yet been added to the list, the algorithm first verifies whether it matches the line number of the current unit task. If it does not match, the task is divided to form a unit task, which is constrained by Constraint (12) to prohibit drones from crossing different transmission lines to avoid confusion during task execution. If it matches, the algorithm proceeds to the next step to calculate the remaining endurance of the drone after removing all the power grid towers from the current list. If Constraints (6) and (7) are not satisfied, the upper limit for task division is set at 80% of the UAV’s single-flight endurance capability to divide the task and obtain a new unit task. If the constraints are satisfied, the algorithm continues to check the next tower until all towers have been inspected. Finally, all generated unit tasks are input into the bilevel optimization section. The entire process is shown in the left half of Figure 2.
Throughout the division process, Constraints (4) and (5) must be satisfied. Constraint (4) ensures that all transmission towers are allocated to the tasks, while Constraint (5) ensures that each tower is assigned to only one task to avoid duplication.
3.2. Nested Bilevel Optimization Algorithm
To minimize the total flight distance of multi-UAVs while balancing the task distribution among them, this paper proposes a bilevel optimization framework based on the NSGA-II algorithm and an adaptive elitist retention strategy in genetic algorithms.
3.2.1. Task Assignment Based on the NSGA-II Algorithm
In the outer-layer optimization, the NSGA-II algorithm is adopted to encode and assign the unit tasks. The steps are as follows:
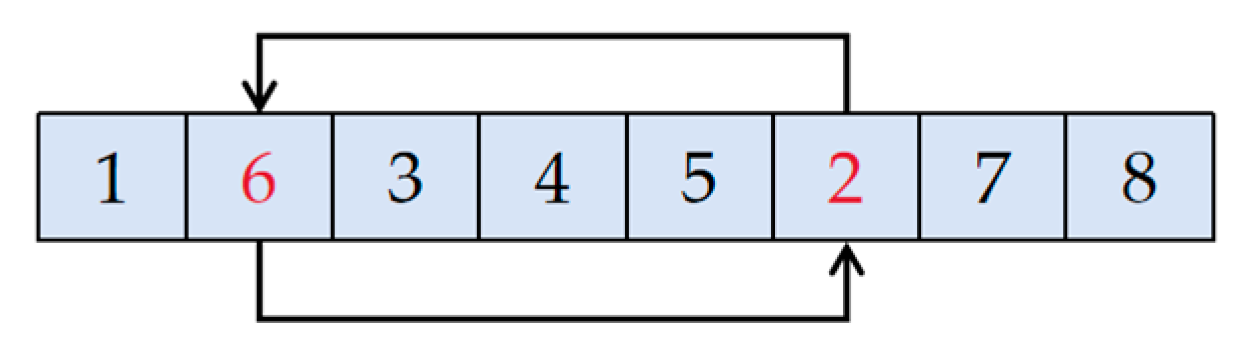
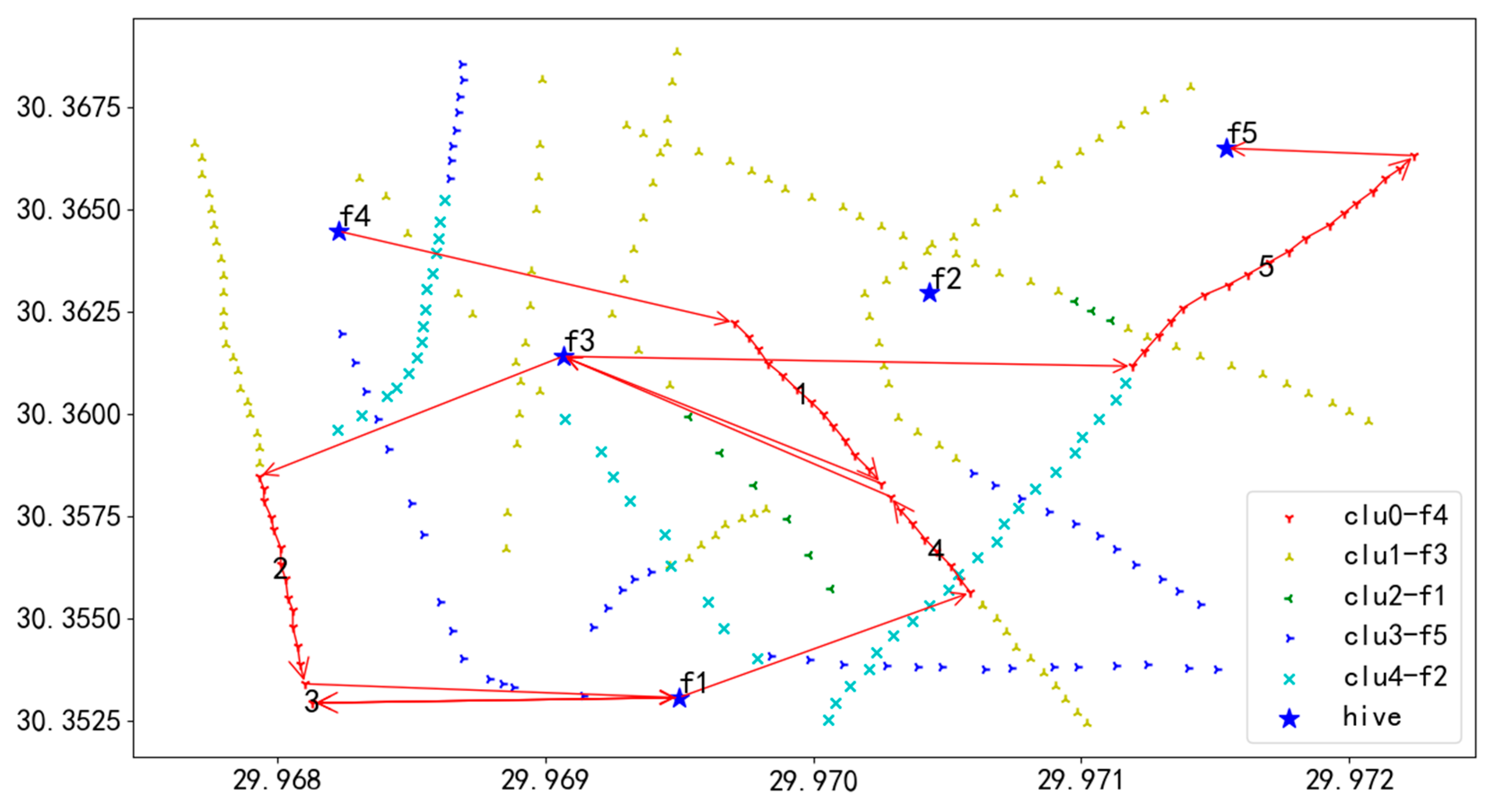
Step 1: Population coding: The length of the chromosome is equal to the number of unit tasks, with the first half used to mark the sequence numbers of the tasks and the second half representing the UAV’s serial number that directly constitutes the chromosome. To ensure the effectiveness and rationality of task assignment, we introduce three constraints: Constraint (9) ensures that each UAV is assigned at least one task; Constraint (10) ensures that each task is executed by only one UAV; Constraint (11) maintains the flow balance throughout the entire task assignment process, ensuring that the amount of tasks assigned to each UAV matches its execution capability. As illustrated in Figure 4, in the case of 12 unit tasks being carried out by 3 UAVs, each UAV will perform tasks, and each unit task can only be assigned to one UAV. Specifically, UAV number 1 is responsible for unit tasks numbered 3, 4, and 11; UAV number 2 is responsible for unit tasks numbered 1, 2, 5, 7, and 10; UAV number 3 is responsible for unit tasks numbered 6, 8, 9, and 12.

Figure 4.
Outer chromosome encoding.
Step 2: Population initialization: Firstly, a numerical sequence is generated based on the number of unit tasks to form the first layer of the chromosome encoding. Subsequently, a UAV is randomly assigned to each unit task to form the second layer of the chromosome encoding. This process ensures that each UAV is assigned at least once. The process is repeated until the population size reaches the preset value.
Step 3: Pre-processing optimization: In order to meet the requirements of the location of the hives, this paper discusses the optimization strategies of the initial and landing hives. In addition, considering that the power consumption caused by the takeoff and landing process affects task execution, this paper analyzes how to reasonably divide the task under the comprehensive consideration of the takeoff and landing loss, thereby ensuring that the UAV can efficiently complete all inspection tasks before the power is exhausted. The above strategies can be found in Section 3.2.2.
Step 4: ENS_SS is used for non-dominated sorting. The ENS_SS function was used to perform non-dominated ranking of population results. The function classifies the individuals in the population to determine the level and critical level of each individual. The ENS_SS function ranks the individuals of the population through a non-dominant relationship, where the lowest layer is marked as 1, indicating that these individuals are not dominated by any other individuals in the population.
Step 5: Calculate the crowding distance: The individual crowding distance for individuals within each class is calculated. Crowding distance is an index to measure the distribution density of individuals in the solution space, which plays an important role in maintaining the diversity of solution sets.
Step 6: Select operation: The selection operator of binary tournament method is used to select the individuals with better performances according to their non-dominant ranking and crowding degree distance, and the selected individuals will be included in the next generation population.
Step 7: Crossover and variation: An analog binary crossover operator is used to perform the crossover operation. The binary crossover operator simulates the single-point crossover process of binary coding to realize the gene recombination of individuals in a population, which is suitable for real coding individuals. The basic idea is to cross-operate between parent individuals in order to produce new offspring individuals while maintaining the diversity of the population. In addition, polynomial variation is used for variation operation. Polynomial variation increases the diversity of the population by introducing random perturbations to individual genes, thus improving the global search ability of the algorithm.
Step 8: Generative progeny: The selected individuals, the offspring individuals produced by crossing, and the mutated individuals were combined, and the optimal n individuals were selected to form a new generation population according to the criteria of non-dominance ordering and crowding degree distance.
Repeat Steps 6–8 until the preset number of iterations is met or the termination condition is reached.
3.2.2. Path Optimization Based on the Enhanced Elite Retention Genetic Algorithm
Aiming at the dependence of UAVs on specific hives, this section focuses on the optimization strategies of takeoff and landing hives. In addition, in view of the limitations that power consumption may pose to mission execution during takeoff and landing, this section will also discuss the scheme of task re-segmentation by taking into account the takeoff and landing energy consumption to ensure the completion of UAV mission execution. The detailed steps are as follows:
Step 1: Takeoff hive optimization: To ensure that each hive is served by at least one UAV, we take the following steps to determine the starting hive for the UAVs: First, calculate the distances from the starting and ending transmission towers of the UAV’s task to each candidate hive. Next, sum up the total distances from the starting and ending towers to the assigned hives for each UAV. Finally, select the solution with the minimum total distance as the final result.
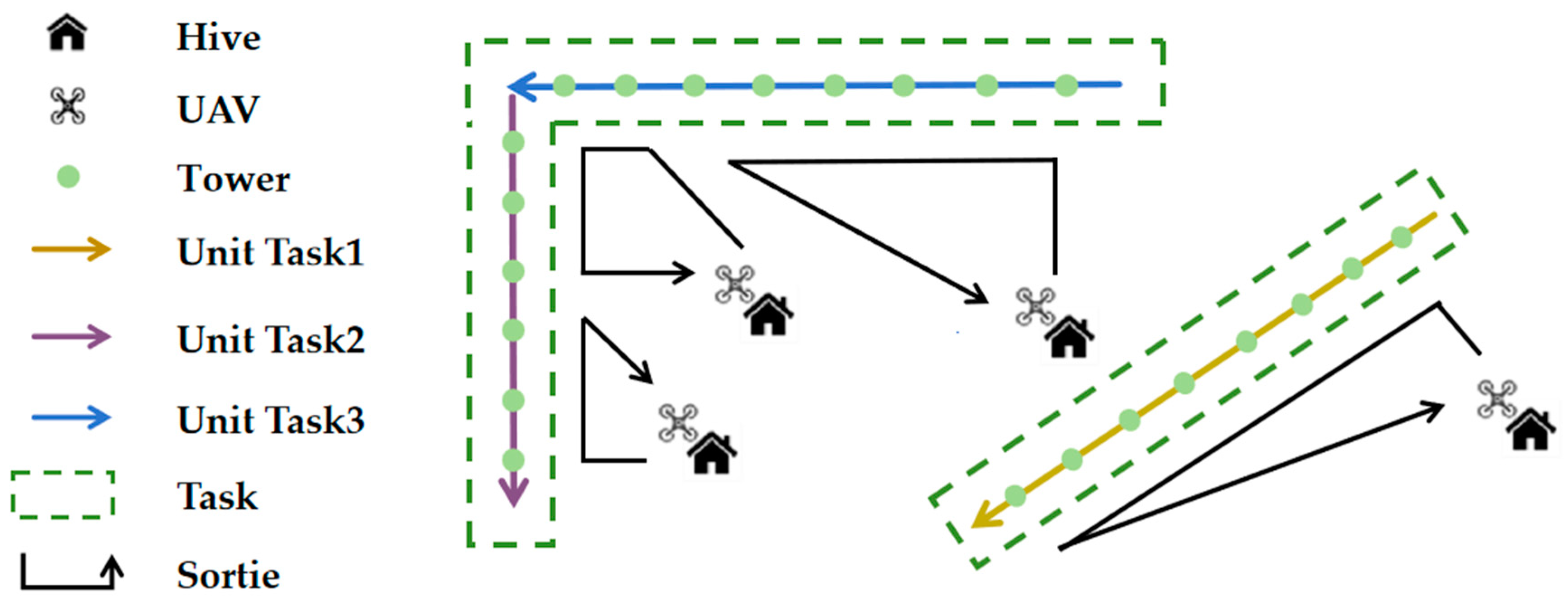
Step 2: Hive insertion within unit tasks: During task execution, UAVs may experience reduced endurance due to the need to transfer between towers and hives. To avoid this risk, the algorithm evaluates the total energy consumption of unit tasks before optimizing UAV routes. If the total energy consumption is less than the UAV’s safe flight range, the task segment is considered continuously executable. Conversely, if the total energy consumption exceeds the UAV’s safe flight range, additional hives are introduced as waypoints, and the unit tasks are further divided to ensure feasibility. The specific process of task segmentation is shown in Figure 5.
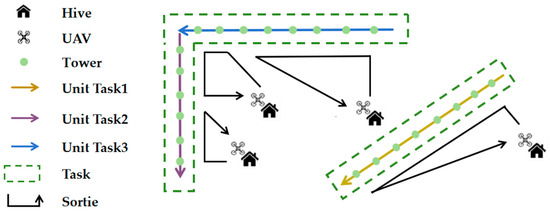
Figure 5.
Transit hive insertion.
Step 3: Sorting and fusion of unit tasks: After the endurance is verified, each UAV is given a final unit task to perform. This section uses the genetic algorithm to enhance the elite retention policy to improve inspection efficiency and path optimization. The steps of the algorithm are as follows:
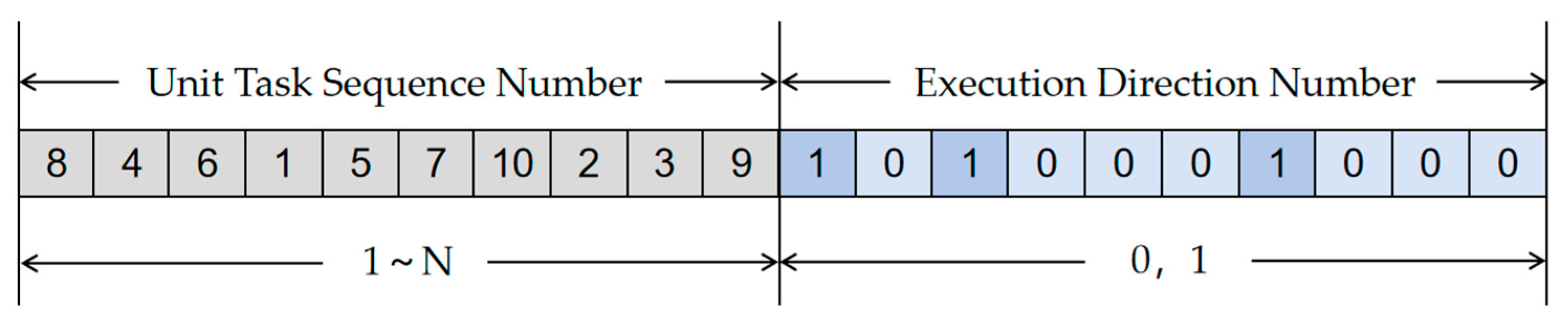
1. Population coding: The chromosome uses a two-part integer encoding strategy, and its length is set to twice the number of tasks assigned by the UAV. The first half of the code consists of a sequential sequence of natural numbers that define the execution order of the task unit in the flight table. The second half of the code adopts an independent 0, 1 binary format, which is used to specify the execution direction of the unit task, and the chromosome structure is shown in Figure 6.
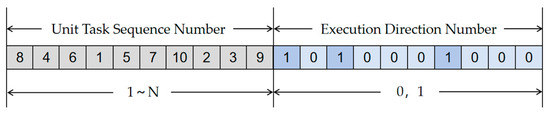
Figure 6.
Inner chromosome encoding.
2. Population initialization: In the initialization phase, the task units assigned to each UAV are first renumbered. The sequence number of the task unit is generated by a random algorithm to ensure that the probability of each unit task being assigned the execution direction is equal. The above arrangement is fused with the code of the patrol direction to form a chromosome. This process is repeated until an initial population that meets the preset size is built.
3. Decoding and fitness calculation: Individual encodings are parsed, and the unit task list according to sort encoding is rearranged. The execution direction of the tasks according to the direction code is determined: If the direction code is 0, the tasks are arranged in ascending order of the tower number. If the direction code is 1, it is sorted in descending order. The value of the objective function is calculated according to the optimized flight list to evaluate the individual fitness of the task, thereby ensuring the minimization of the flight distance of each UAV. The fitness function is as follows:
4. Selection operator: The binary tournament method is used to randomly select two individuals and compare their fitness, and the individuals with better fitness are put into the next generation population. This process is repeated until a sufficient number of individuals are selected.
5. Population crossover: Since the chromosomes contain two types of encodings, crossover operations must be performed accordingly for each type. First, the maternal population is sorted by fitness and then evenly divided into two sublists. Next, individuals at corresponding positions from the two sublists are selected for crossover pairing to effectively recombine genetic information.
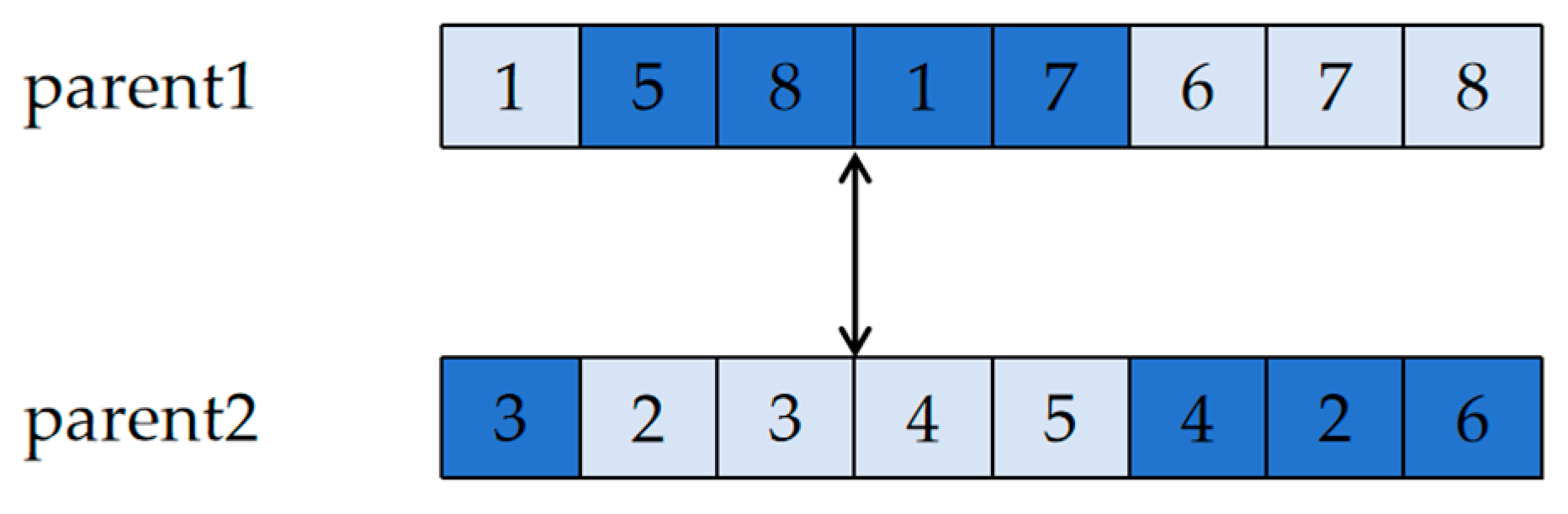
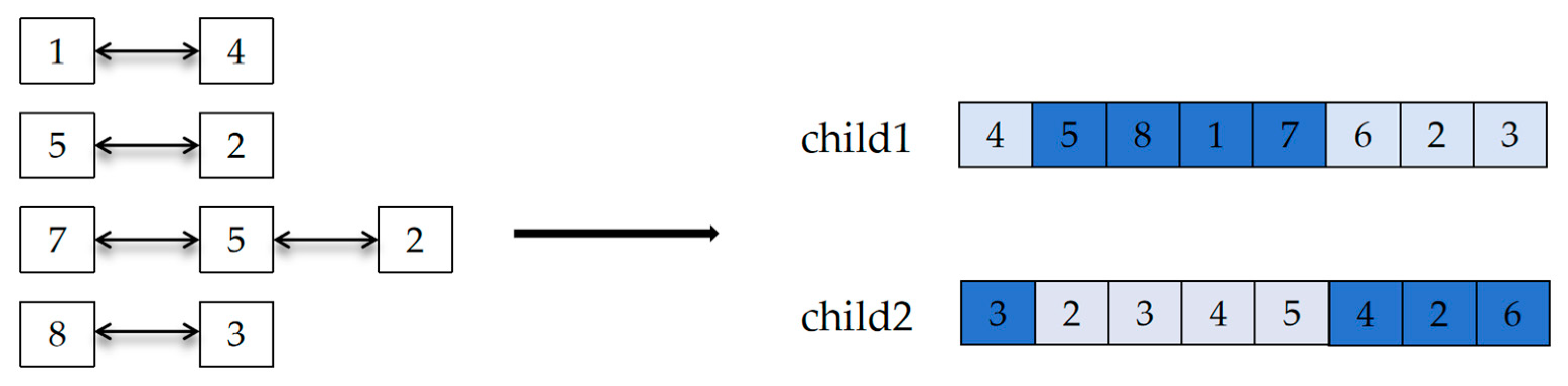
(1) Sequencing coding: For sorted encoding, partial-matched crossing is used. The crossing regions are identified, and the positions of the two sets of genes are swapped, as shown in Figure 7.
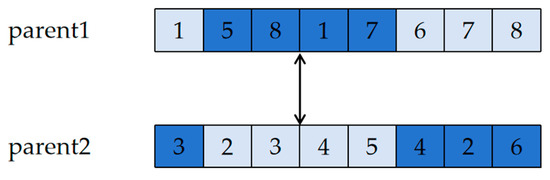
Figure 7.
Swap gene positions.
After the initial crossover operation, systematic conflict detection is performed to identify potential conflicts in the coding bits. By analyzing the exchanged genomes, the mapping relationship is constructed; then, the chromosome is repaired, as shown in Figure 8.

Figure 8.
Gene conflict detection.
Finally, the results of the sort encoding are shown in Figure 9.
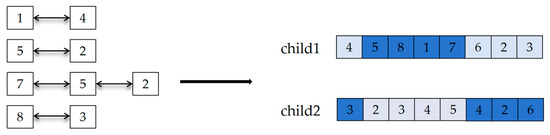
Figure 9.
Sorting encoding crossover.
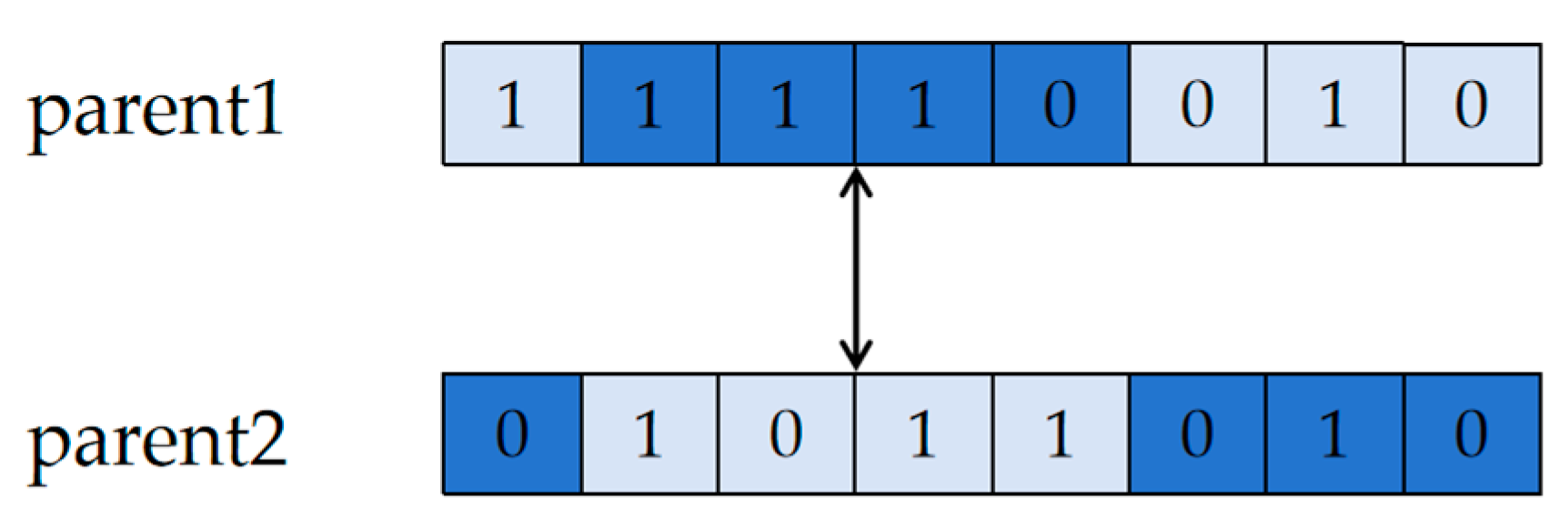
(2) Directional coding: Two points are randomly selected in two coding strings, and the gene fragments between these two points are exchanged, as shown in Figure 10. The method is direct and effective, aiming to explore the solution space and enhance genetic diversity through the recombination of gene fragments.
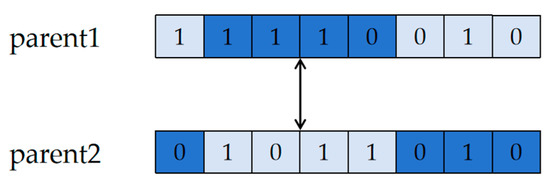
Figure 10.
Directional encoding crossover(c).
Finally, the results of the sort encoding are shown in Figure 11.

Figure 11.
Directional encoding crossover.
6. Population variation: In the variation process of ordering encoding, the inversion mutation operator is applied. Two encoding positions are randomly selected based on a preset probability, and their positions are swapped, as shown in Figure 12. For directional encoding, each encoding position undergoes possible mutations independently and with the same probability, as shown in Figure 13.
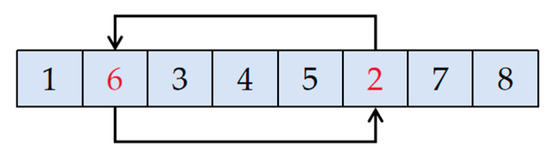
Figure 12.
Sorting encoding variation.

Figure 13.
Directional encoding variation.
7. Generate progeny: The parent population is combined with the population obtained in Step 6 to form a merged population that is twice the size of the initial population. Subsequently, the merged population is sorted based on the fitness of individuals, and the top m individuals with the highest fitness are selected to form the next generation population.
Step 4: UAV landing hive optimization based on the enhanced elite retention genetic algorithm: To ensure that only one UAV resides in each hive at the beginning and end of the mission, this study introduces Constraint (13) and employs genetic algorithms with enhanced elitist retention to optimize UAV landing in the hive. Transfer between cells is achieved by adding UAVs to the mission list while reducing air loss under endurance constraints. In addition, the mission sequence is reviewed; eligible air flights are merged, and the objective function values are updated to optimize landing assignments and avoid UAV collisions.
After completing the above four steps, the pre-processing optimization phase is over. This phase aims to optimize the order and direction of each UAV’s mission to minimize the distance flown. Finally, the total flight distance and the individual flight distance of each UAV are obtained. These optimization results are presented in the form of populations and serve as input to the ENS_SS function for non-dominated sorting, which is used to classify population individuals hierarchically based on non-dominated relationships and provide a basis for subsequent genetic algorithm operations.
4. Experimental Verification
4.1. Experimental Environment and Data Set
The UAVs listed in this article are M300 RTK and have an endurance of 3000 s. The algorithm was implemented using the Python language. All experiments were based on Intel(R) Core(TM) i5-13500 CPU (3.60 GHz) and 16 GB RAM. The experimental environment was PyCharm 2023 of 64-bit Windows 11 operating system.
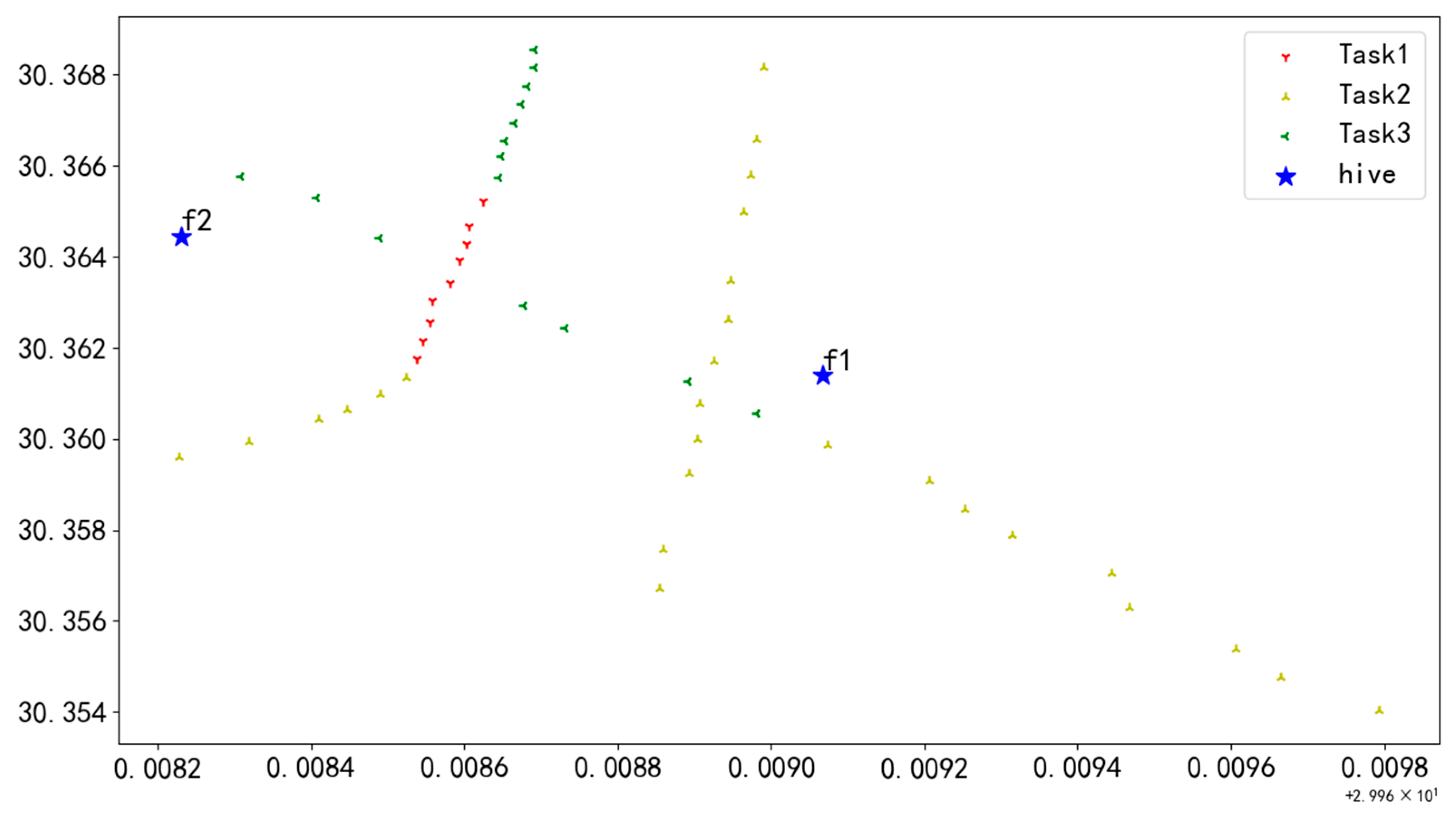
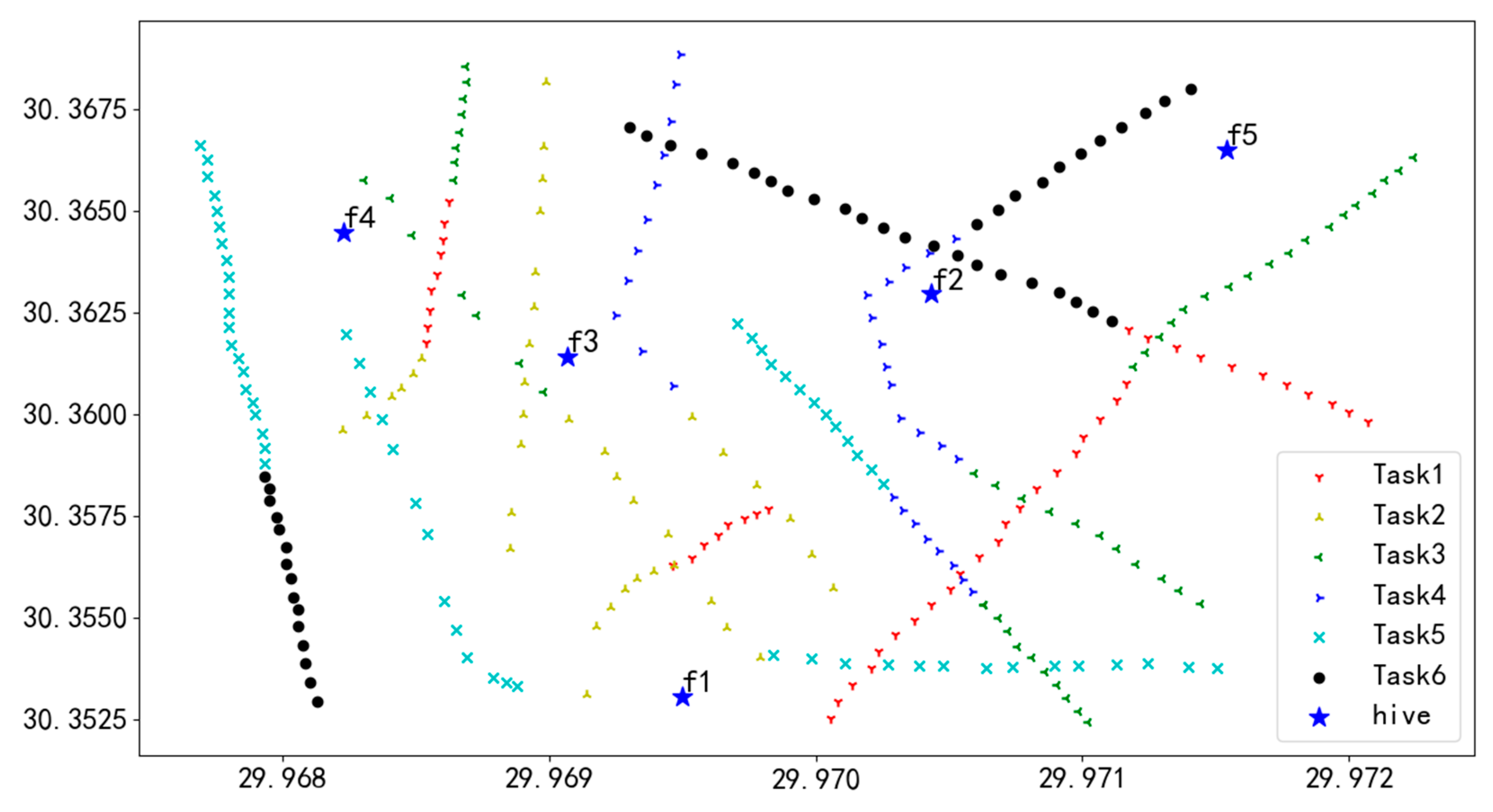
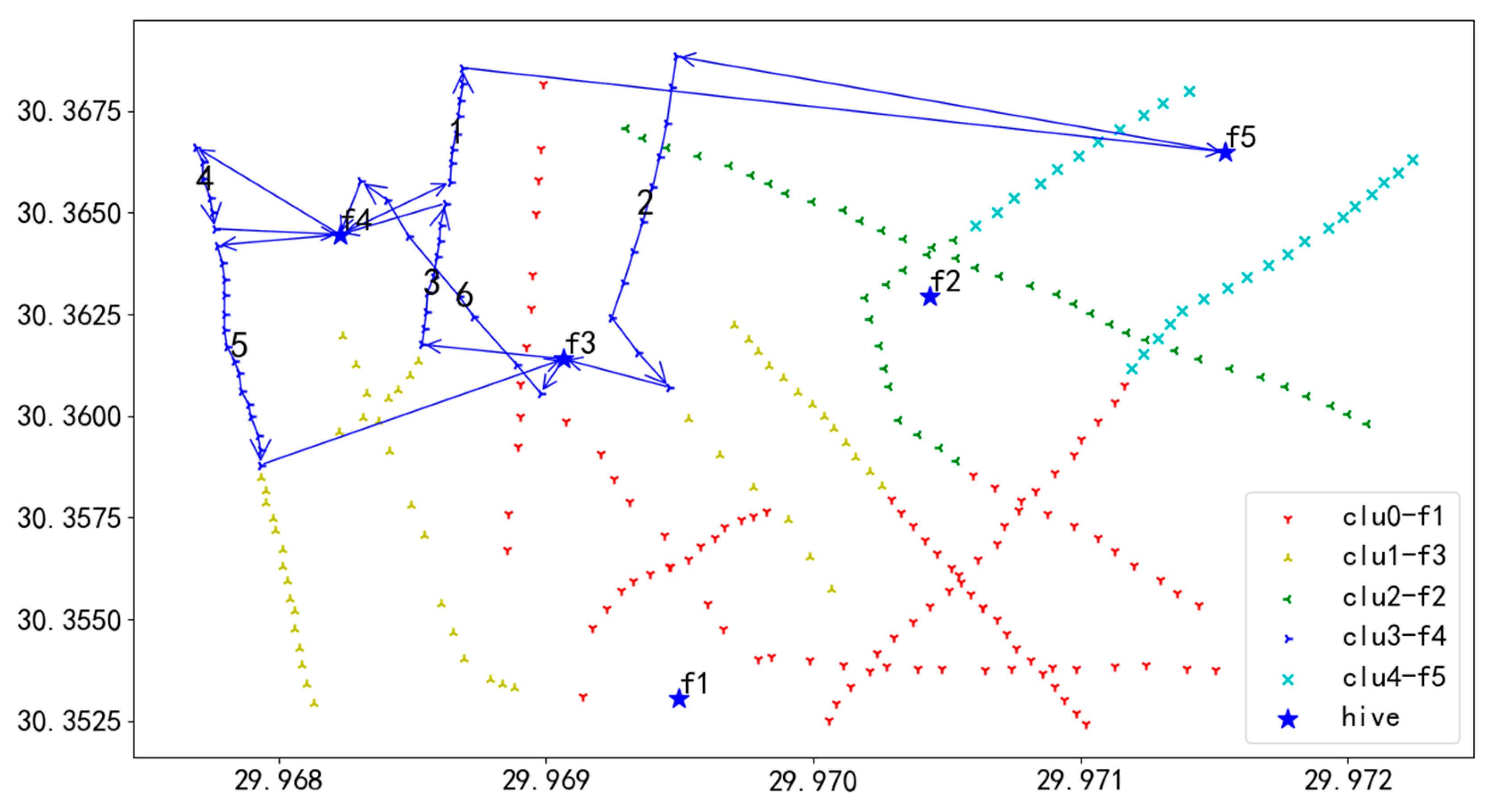
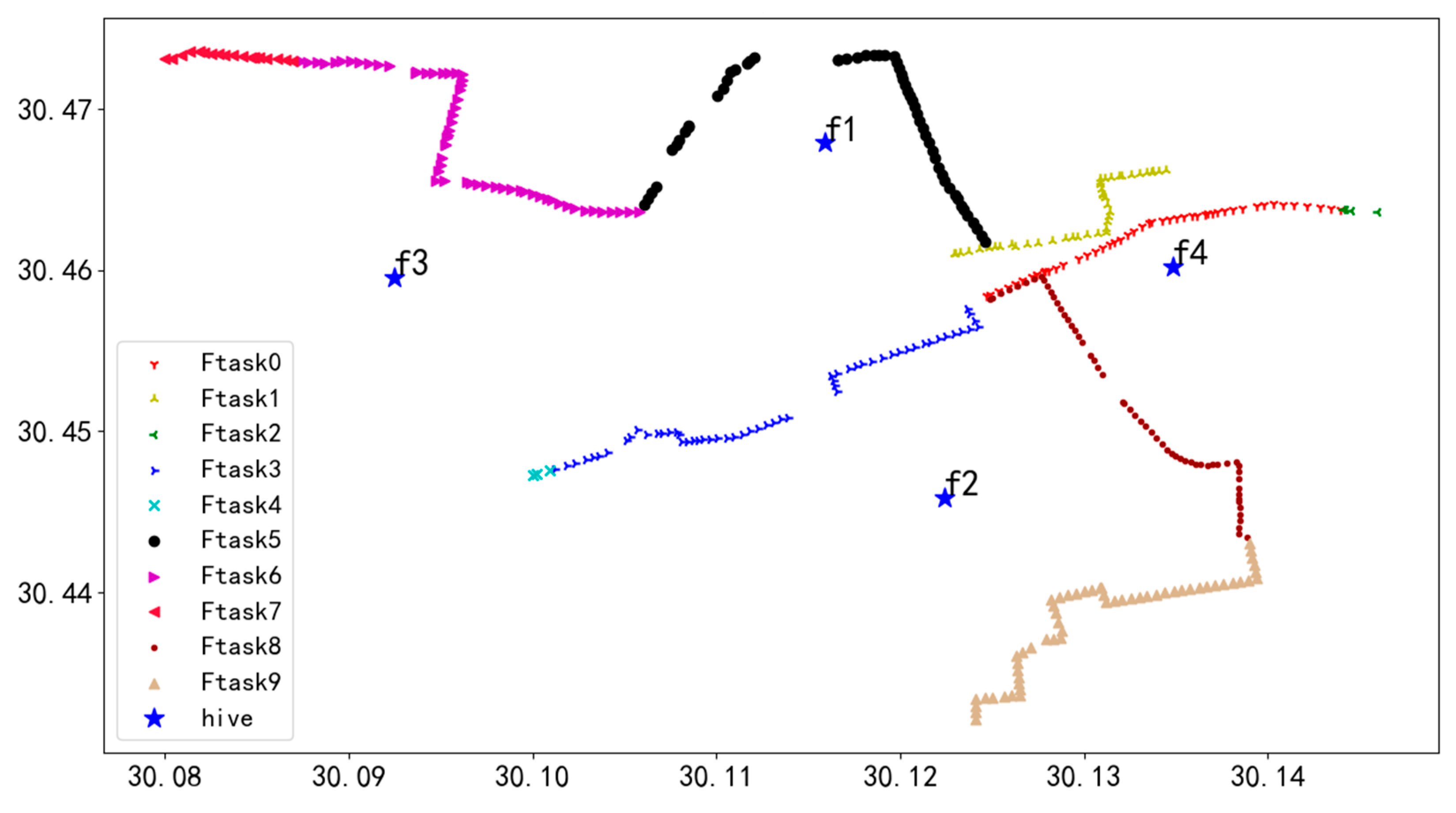
The experimental data were collected from a power grid scene in Zhejiang Province, China, whose geographical location was 30.3525–30.3675° N and 119.967–119.973° E. As shown in Figure 14, the grid scenario includes 11 transmission lines, 284 transmission towers, five UAV power-changing hives, and six task packages from different clients. Each node in the diagram corresponds to a tower or a power-changing hive with a clear latitude and longitude identifier, and the different colors of the nodes map the specific tasks covered by each task package.
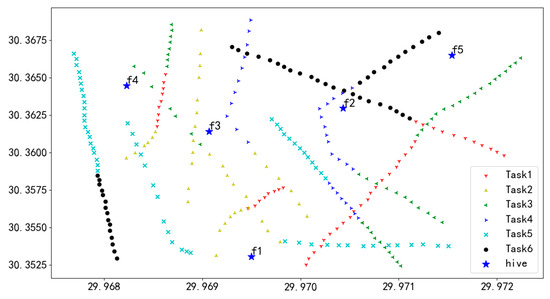
Figure 14.
Top view of the realistic power grid scene with 284 task points.
4.2. Parameter Settings

Table 3.
Parameter settings of the NSGA-II algorithm.

Table 4.
Parameter settings of unit task ordering and direction optimization.

Table 5.
Parameter settings for the optimization of the final landing hive of UAVs.
4.3. Experimental Results
4.3.1. The Result of Unit Task Segmentation
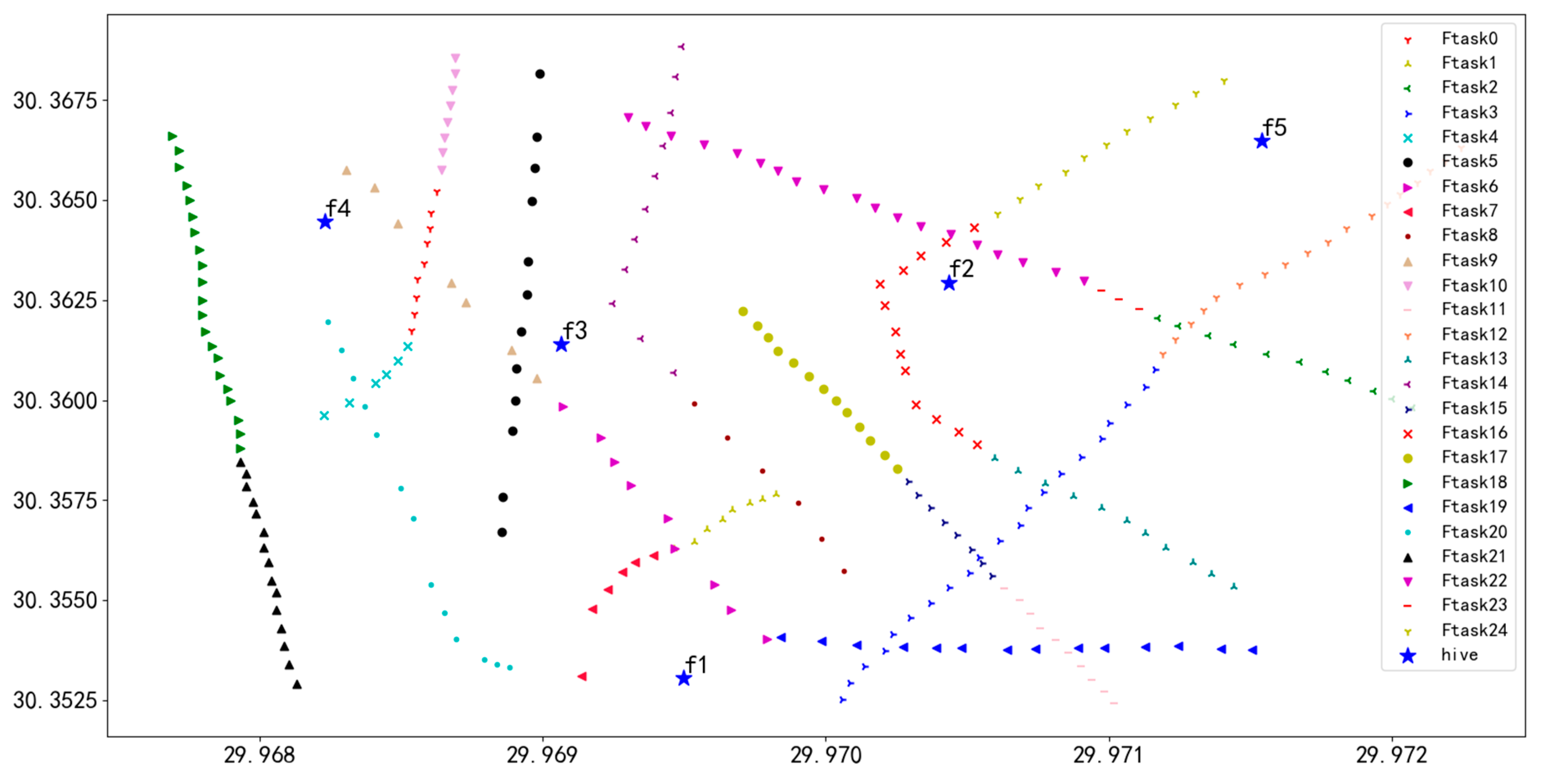
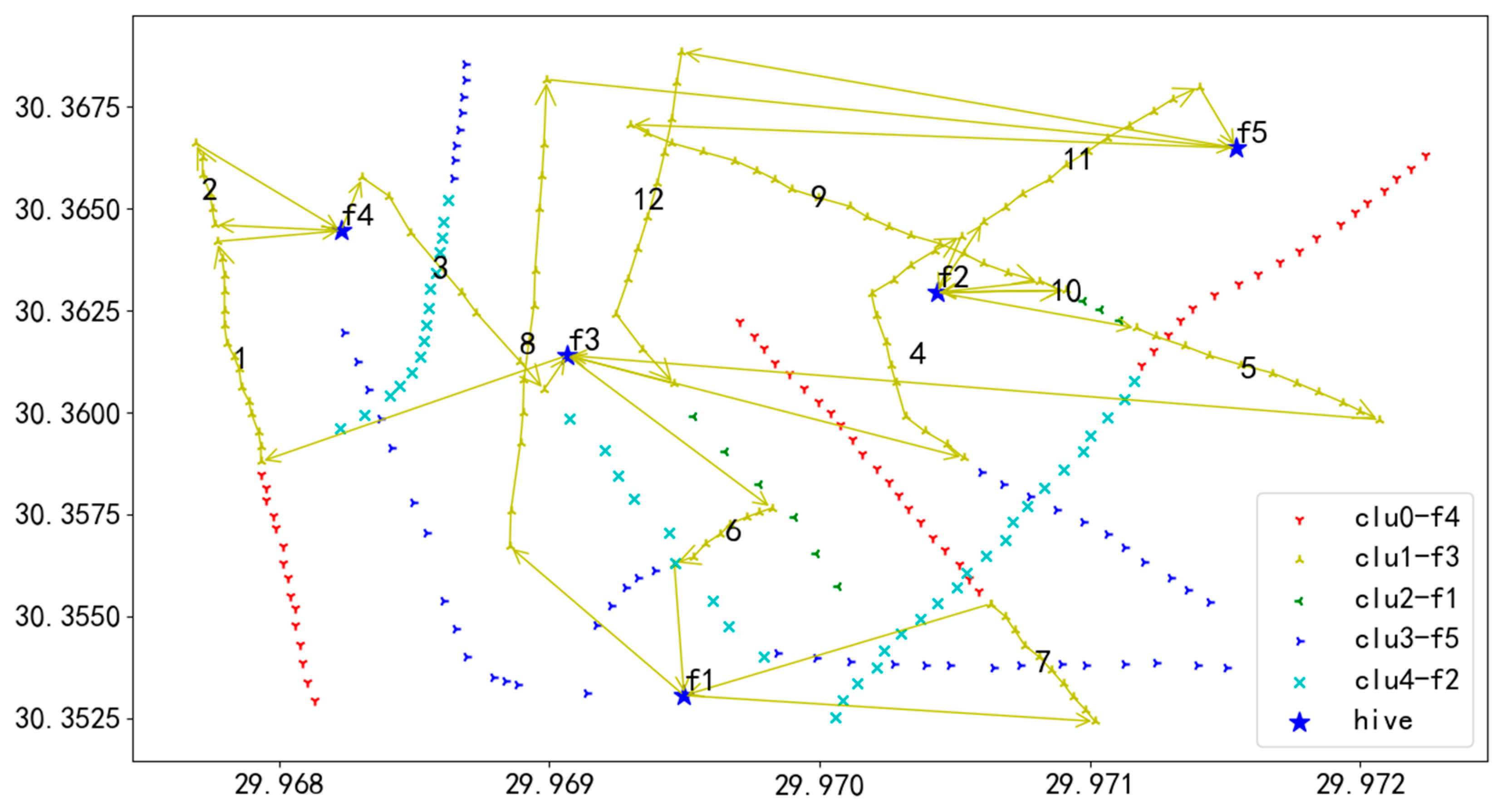
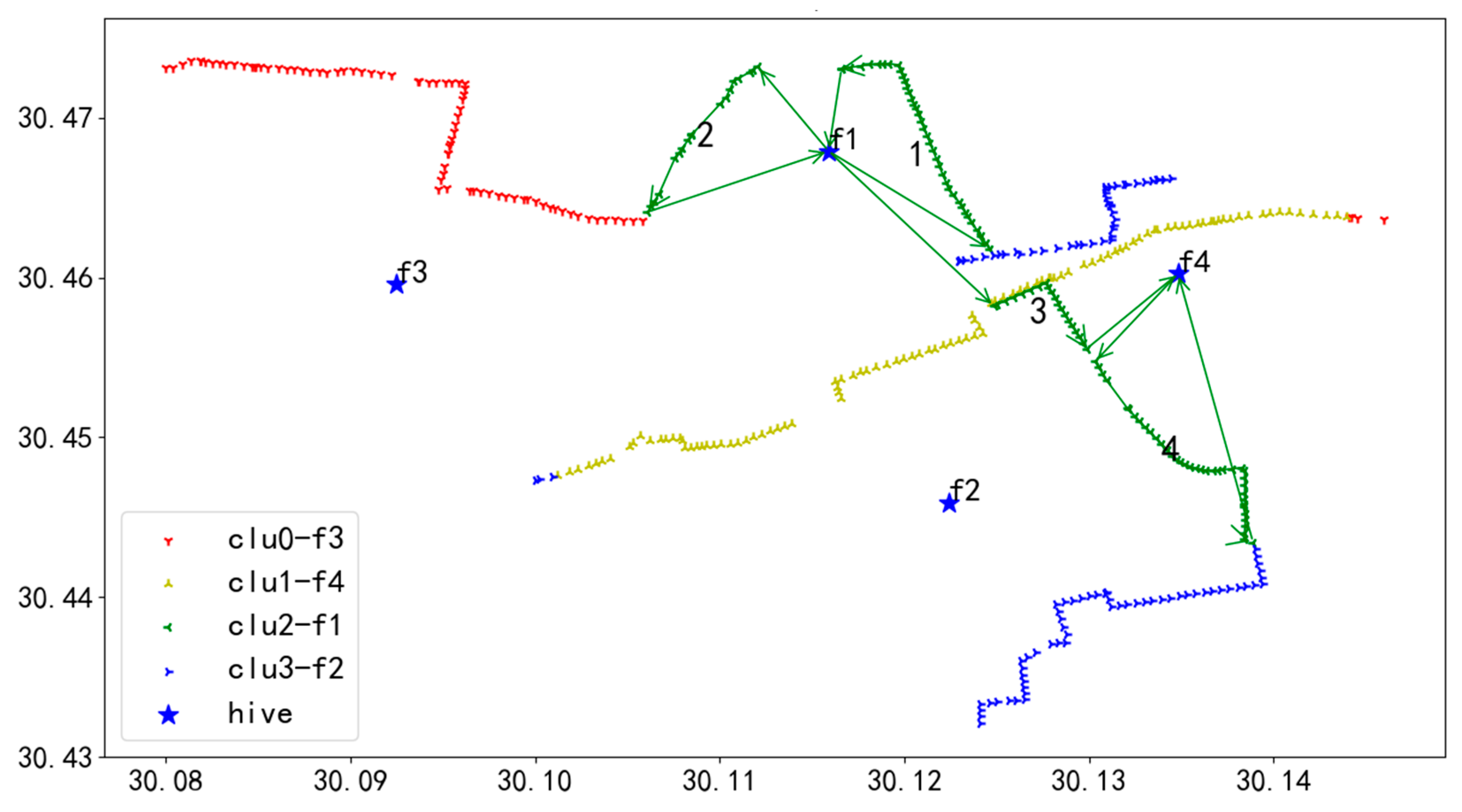
Following the algorithm’s procedure, we performed unit task segmentation in the power grid scenario, resulting in 25 task fragments, as illustrated in Figure 15. In the figure, each unit task (ftask) is denoted by a unique color and symbol and is numbered from 0 to 24.
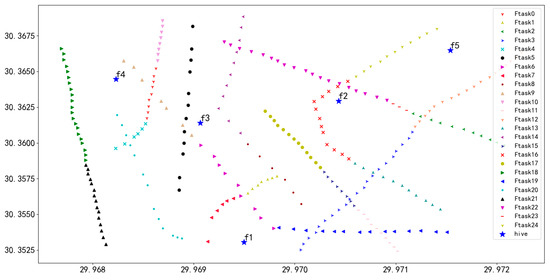
Figure 15.
Unit task segmentation in 284 task point scenarios.
4.3.2. The Results of the Bilevel Optimization Algorithm
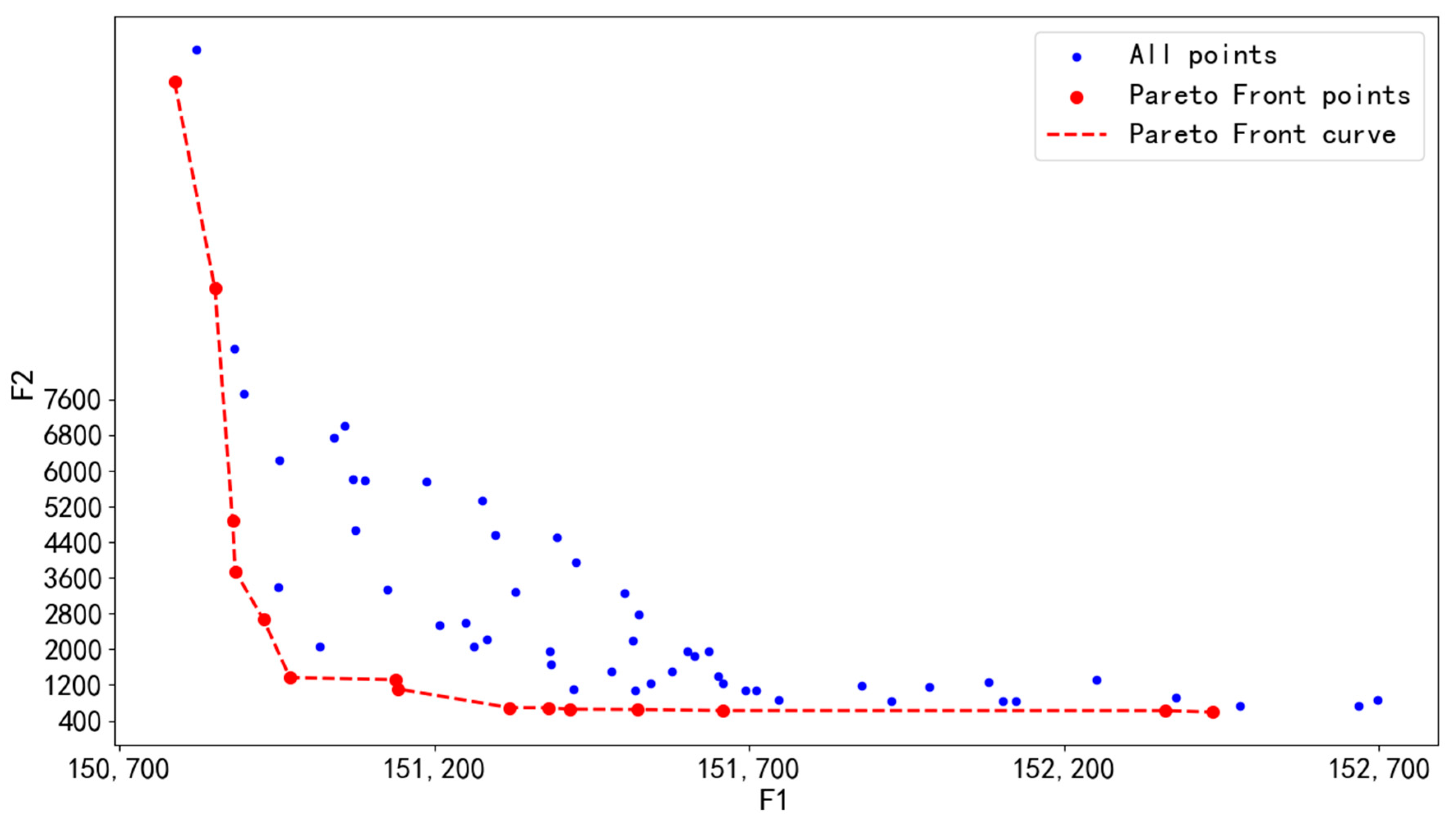
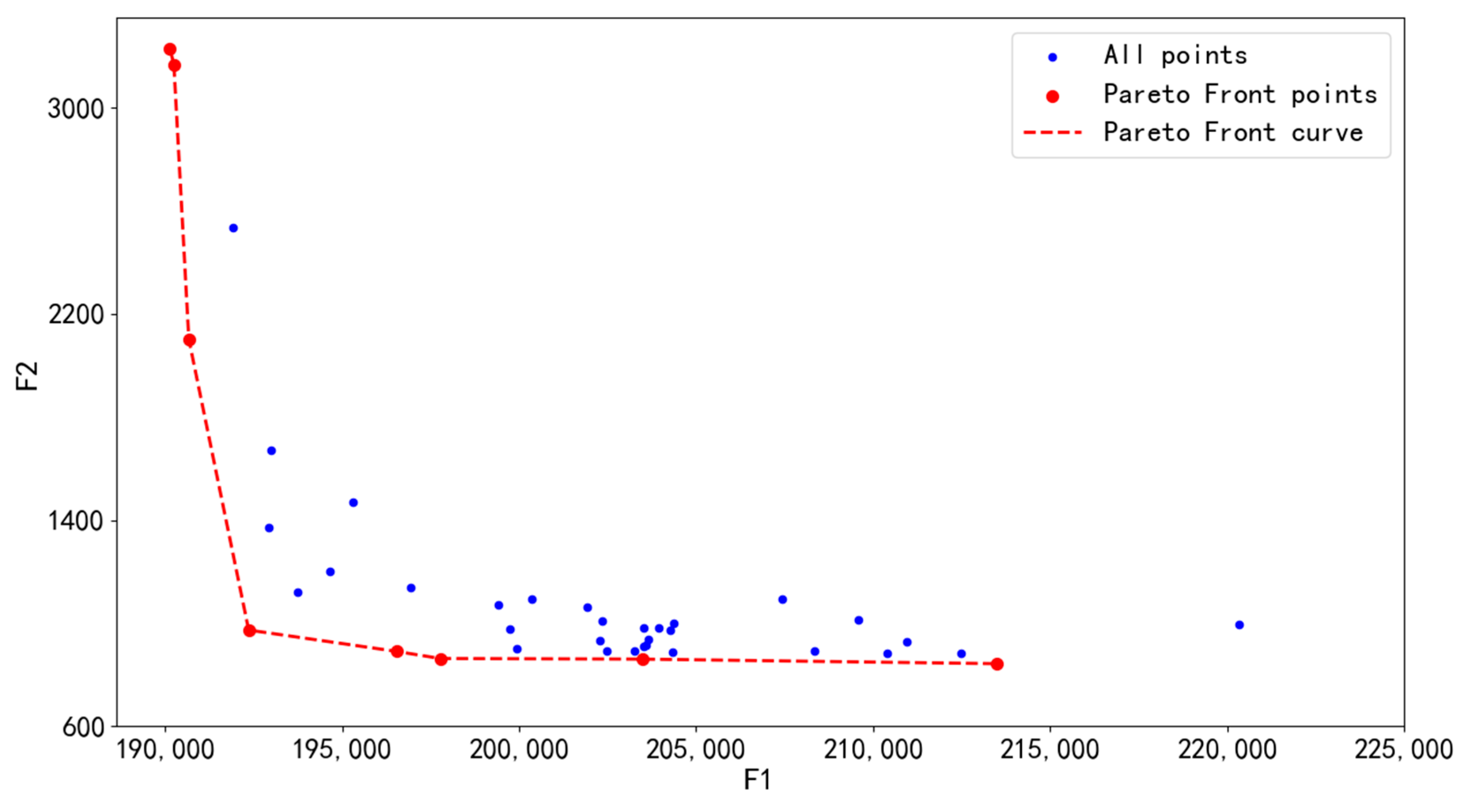
Using the bilevel optimization algorithm proposed in this paper, task assignment and path planning were performed for the task units in Section 4.3.1. A Pareto front was established between the two optimization objectives, revealing the trade-off between the total flight distance and the balance of flight distances among individual UAVs. This Pareto front was constructed by combining the Pareto solution sets from ten runs of the algorithm, forming a new and more comprehensive Pareto front, as shown in Figure 16.
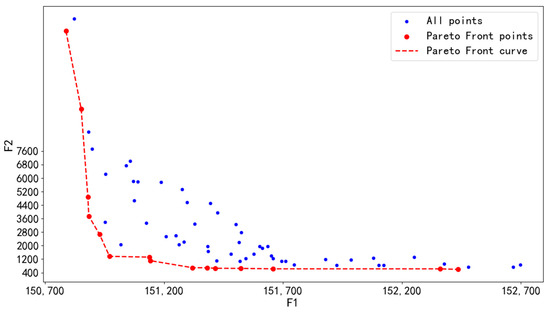
Figure 16.
Pareto front obtained by GA-NSGA-II algorithm in 284 task points.
In the figure, the blue dots represent all potential solutions generated by the algorithm, the solid red dots identify the Pareto front points recognized by the algorithm, and the dashed red line indicates the Pareto front curve constructed by these Pareto front points. From the figure, it can be observed that as the iteration process progresses, the Pareto front points (solid red dots) gradually approach and stabilize near a certain curve, indicating that the algorithm can effectively approximate the true Pareto front. Furthermore, the Pareto front curve represented by the dashed red line exhibits smooth and continuous characteristics, further confirming the convergence trend of the solution set of the algorithm.
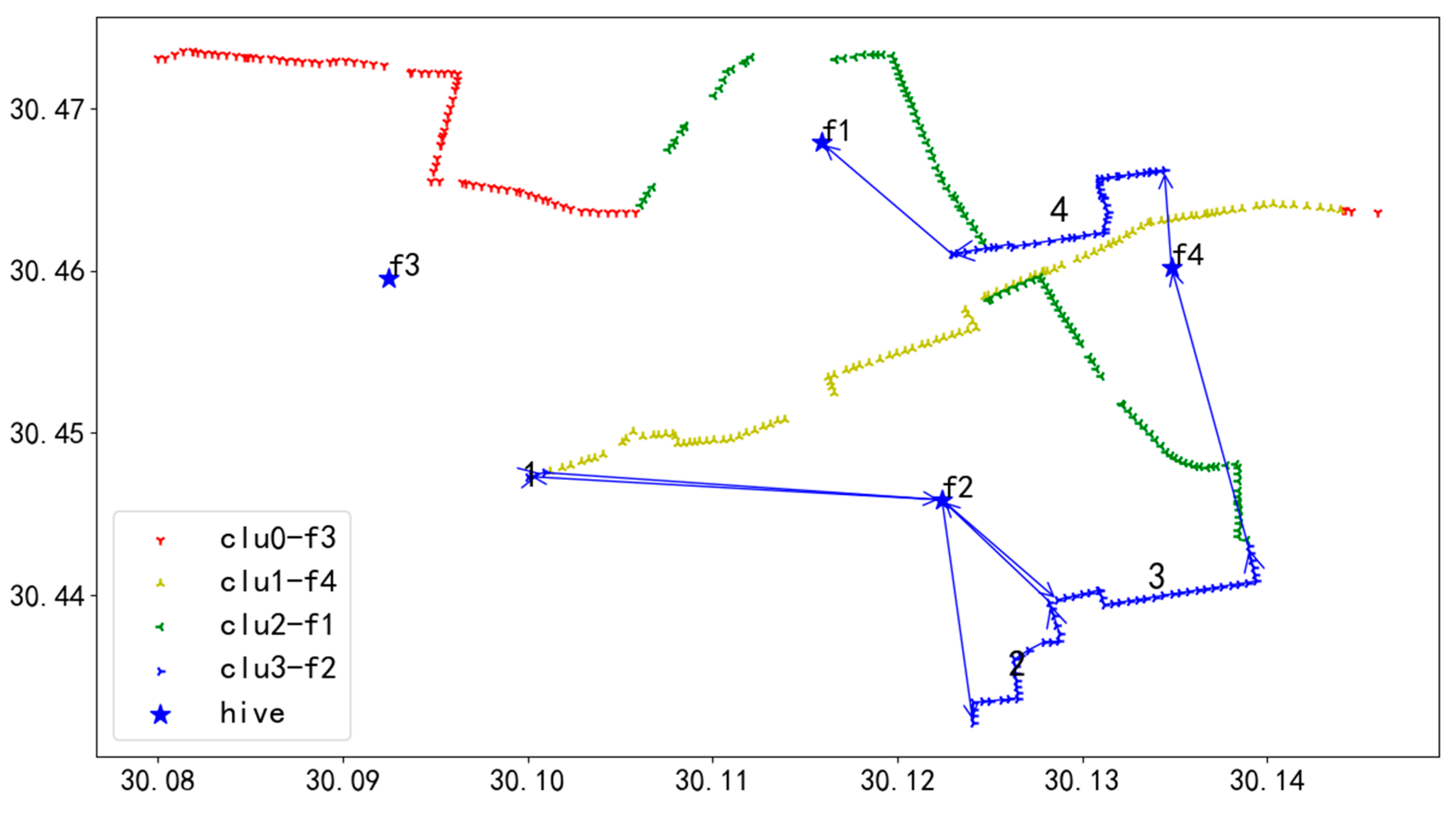
Among the Pareto-optimal solutions, the solution with the minimum F2 value was selected, and the corresponding flight sequence diagrams for this particular solution were generated (as shown in Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20).
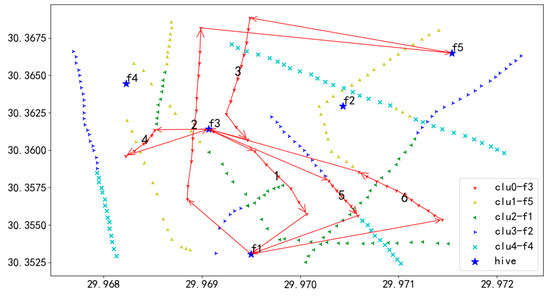
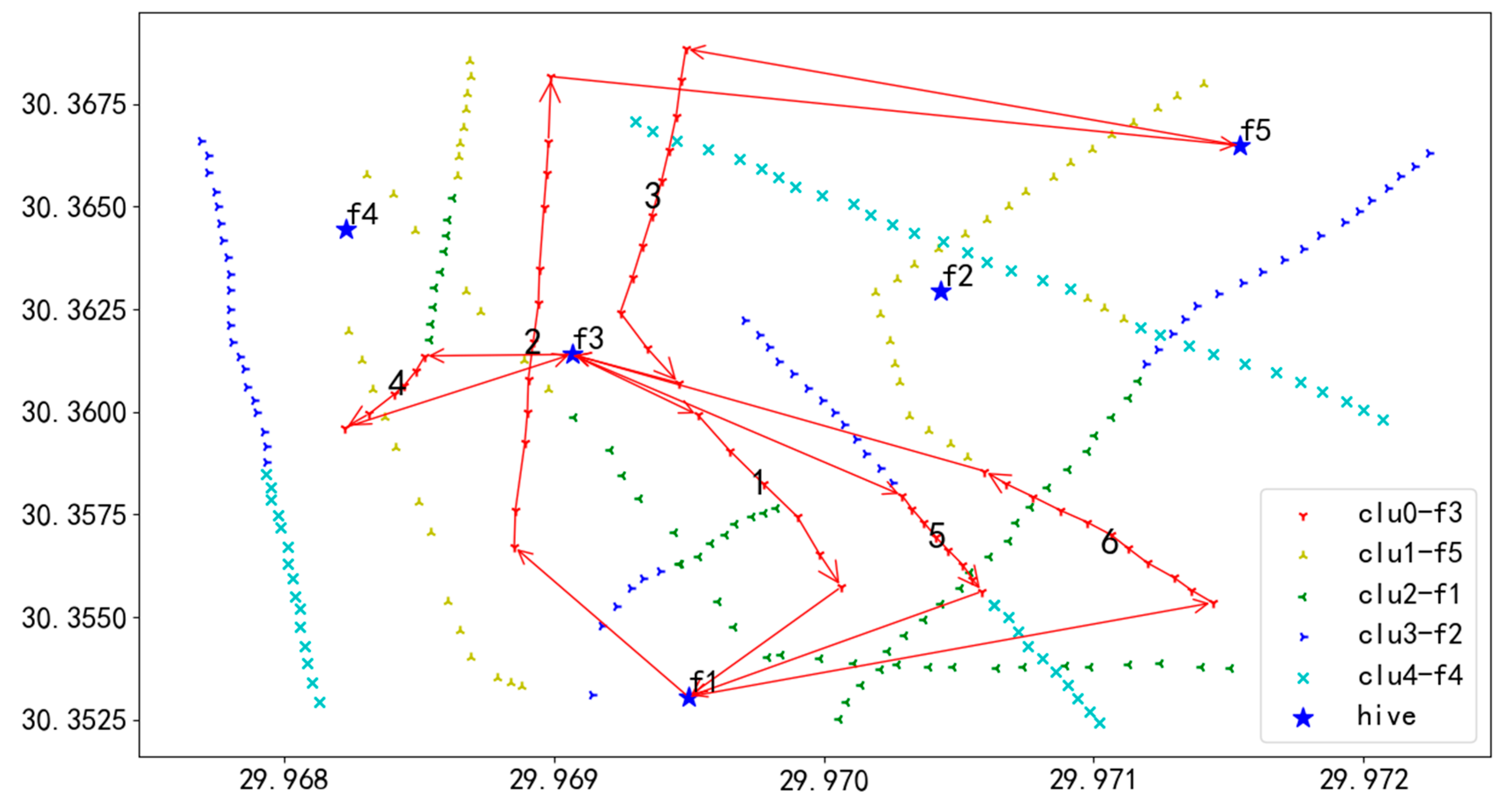
Figure 17.
U1 flight sequence obtained by GA-NSGA-II algorithm in 284 task points.
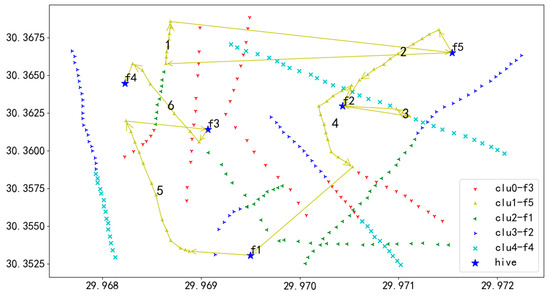
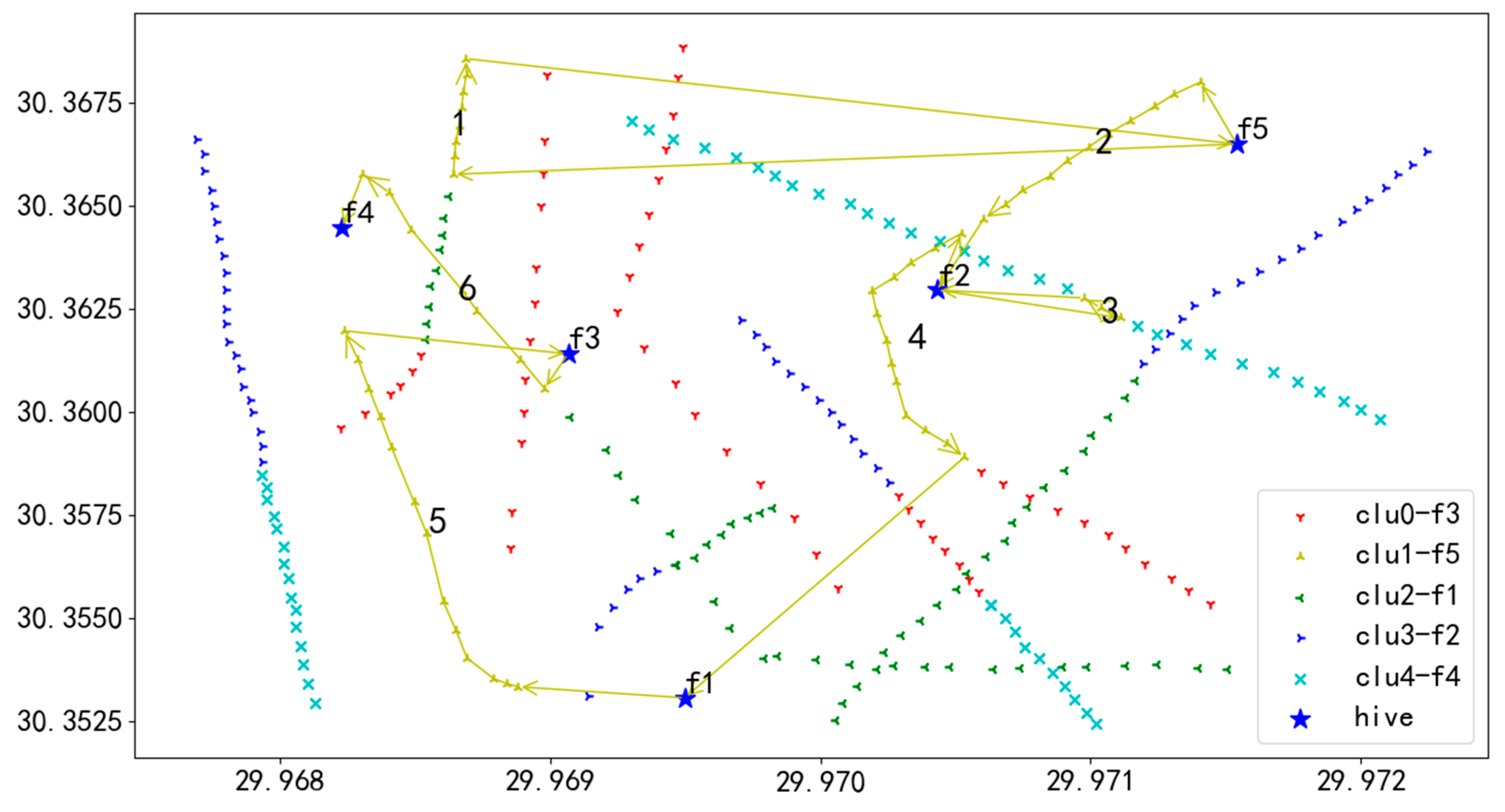
Figure 18.
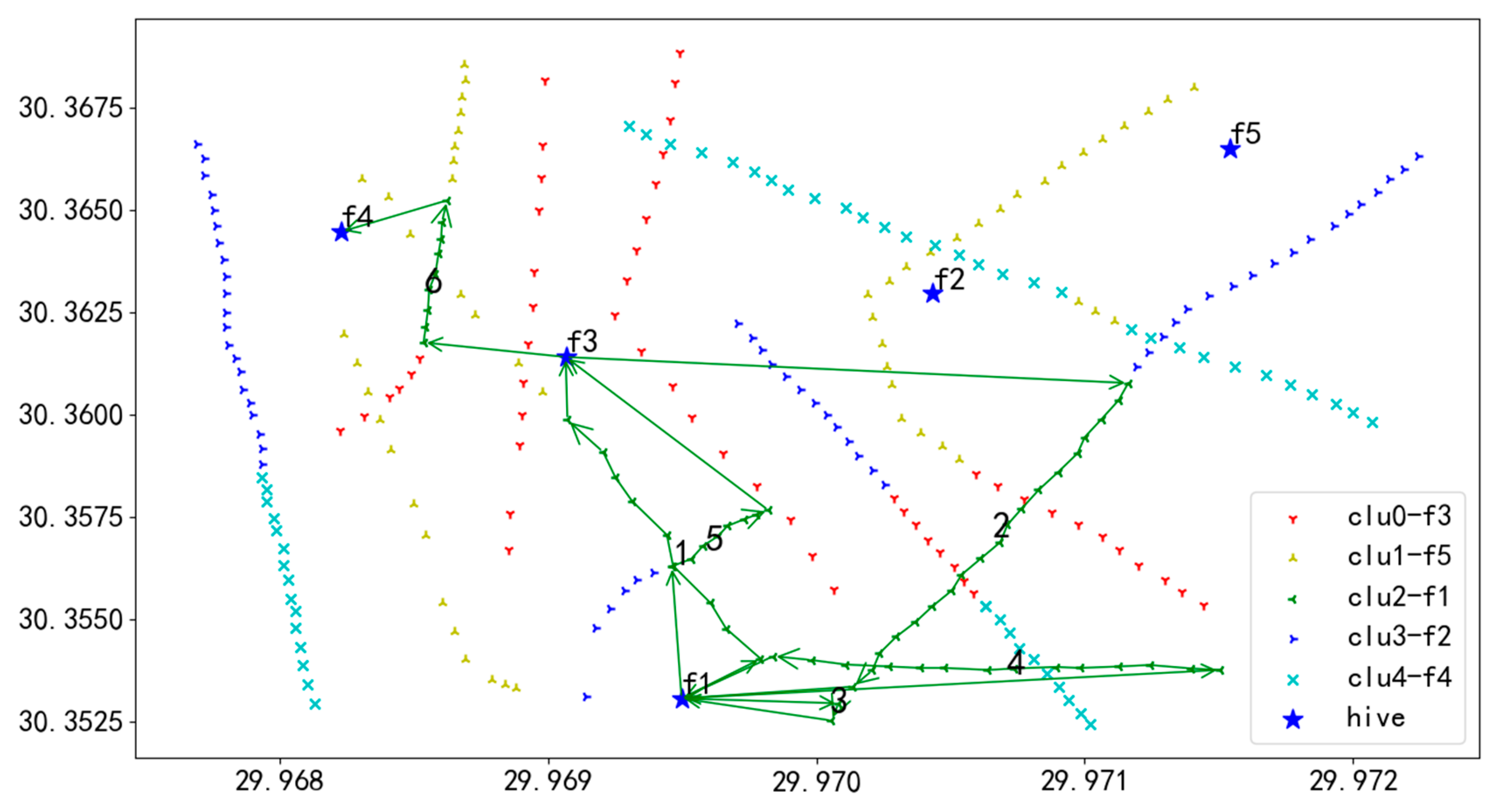
U2 flight sequence obtained by GA-NSGA-II algorithm in 284 task points.
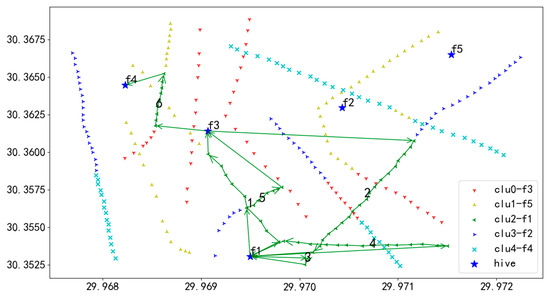
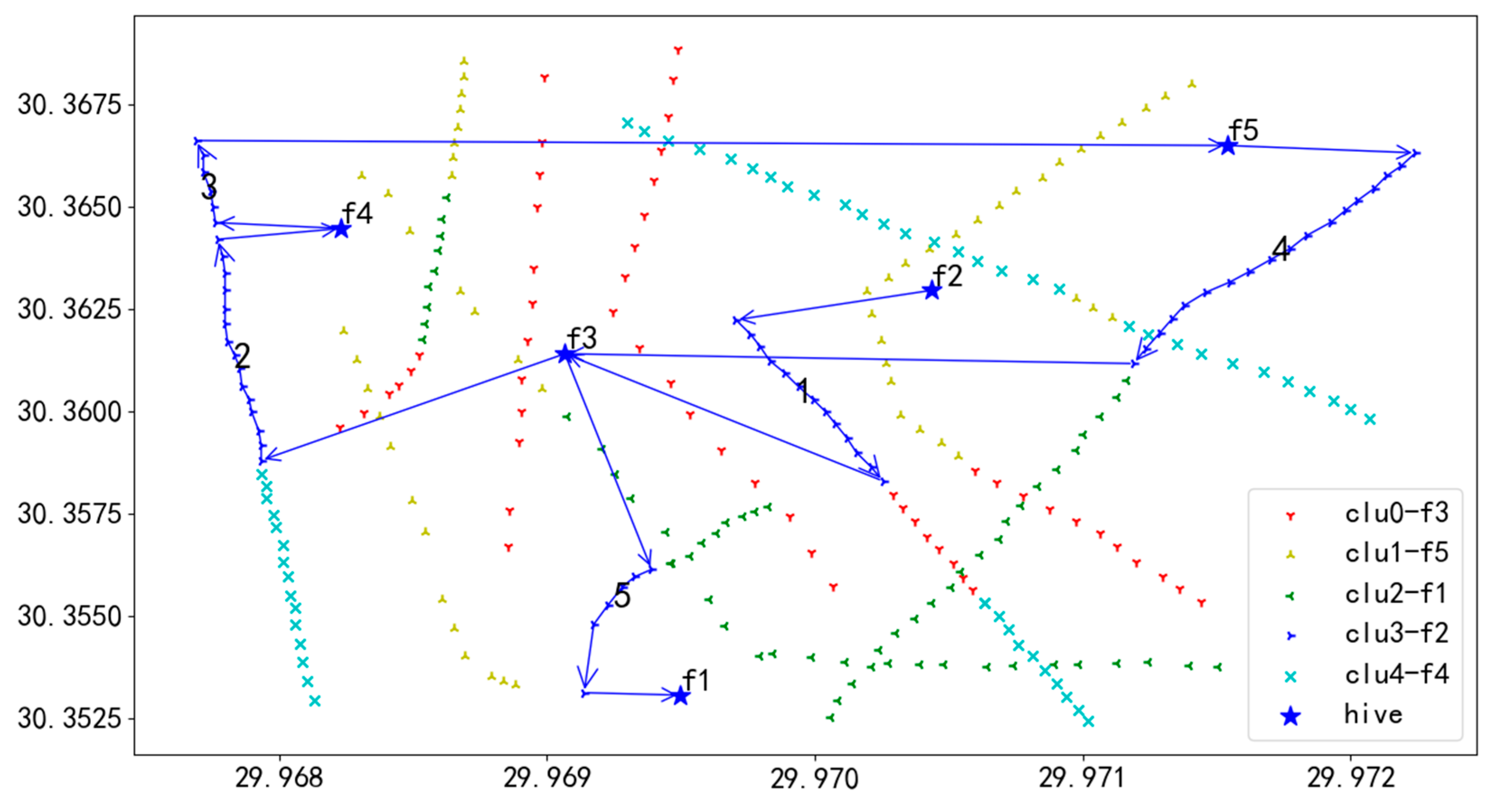
Figure 19.
U3 flight sequence obtained by GA-NSGA-II algorithm in 284 task points.
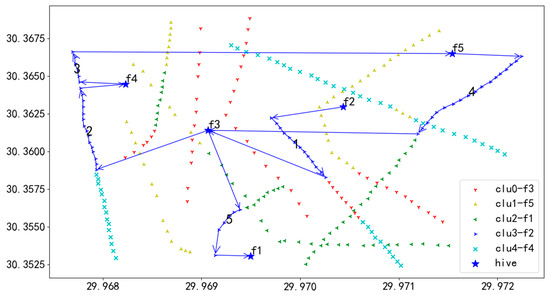
Figure 20.
U4 flight sequence obtained by GA-NSGA-II algorithm in 284 task points.
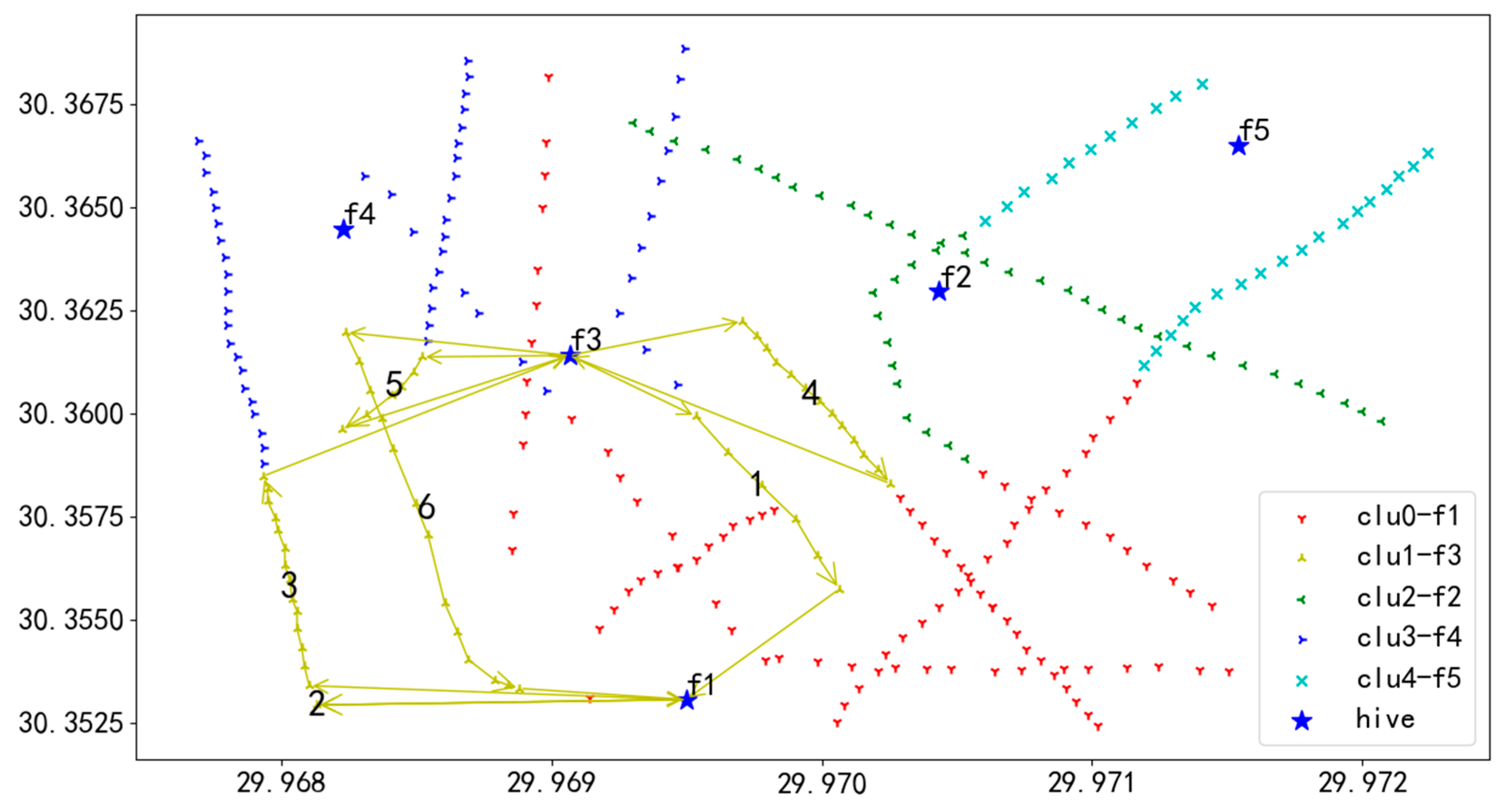
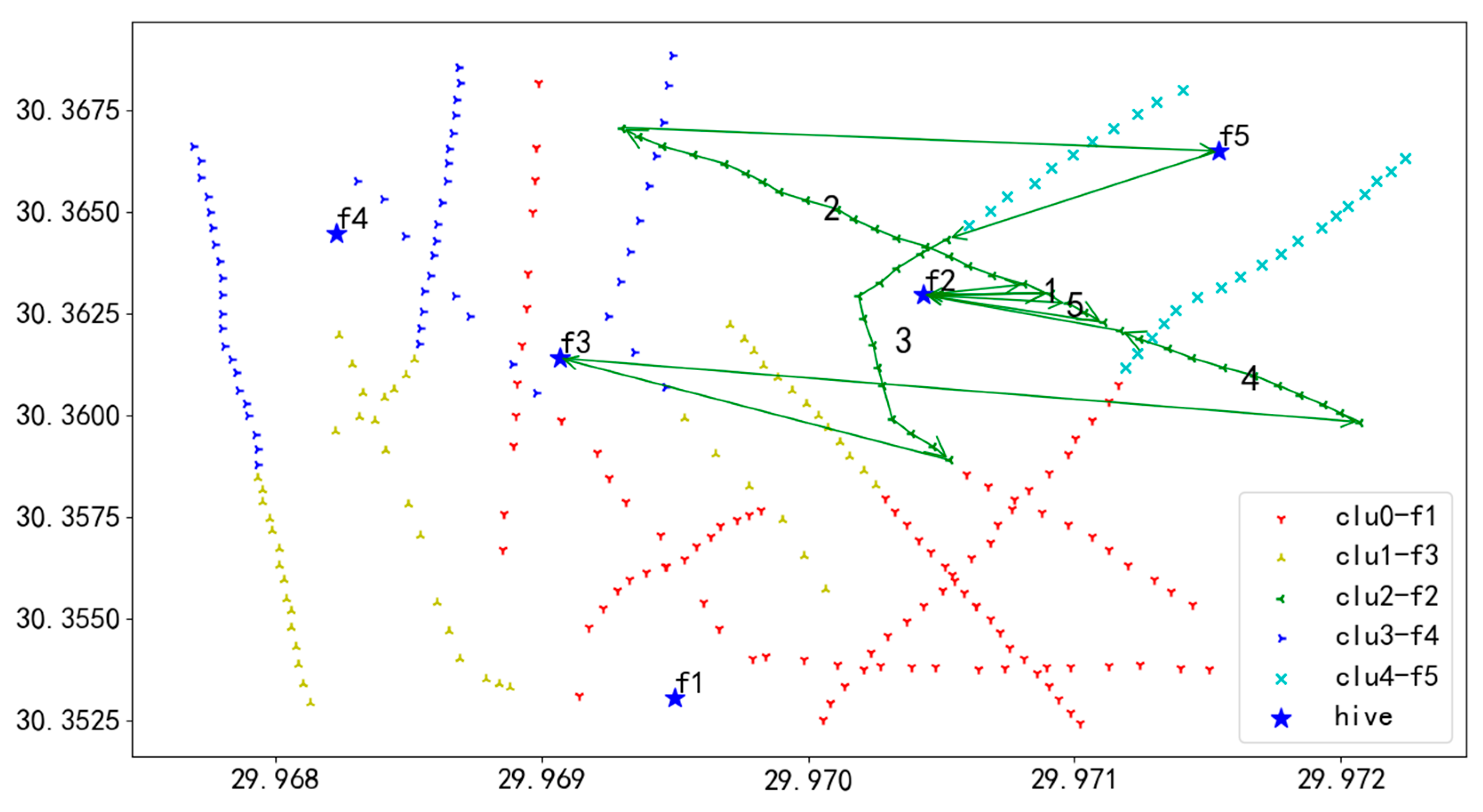
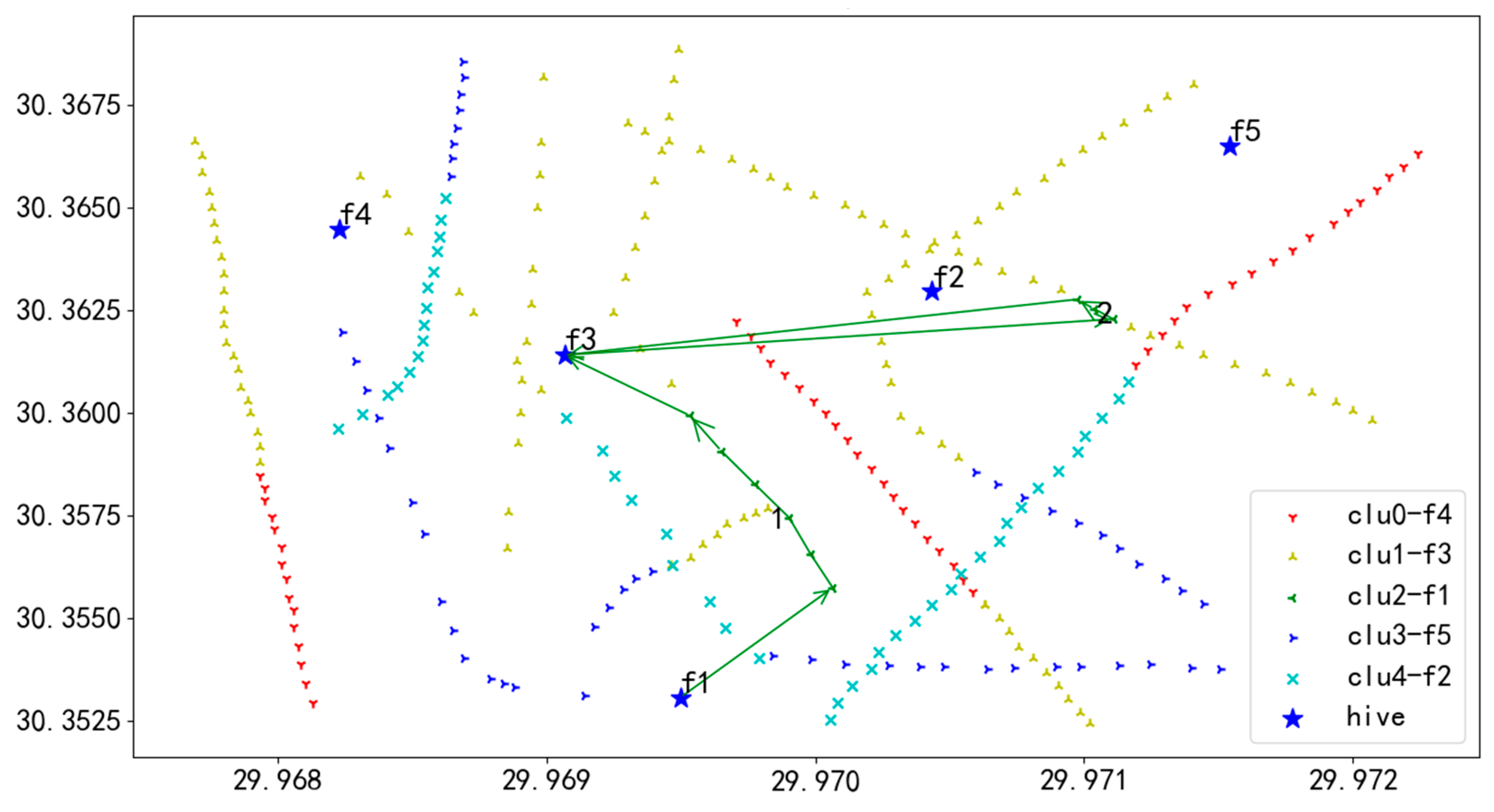
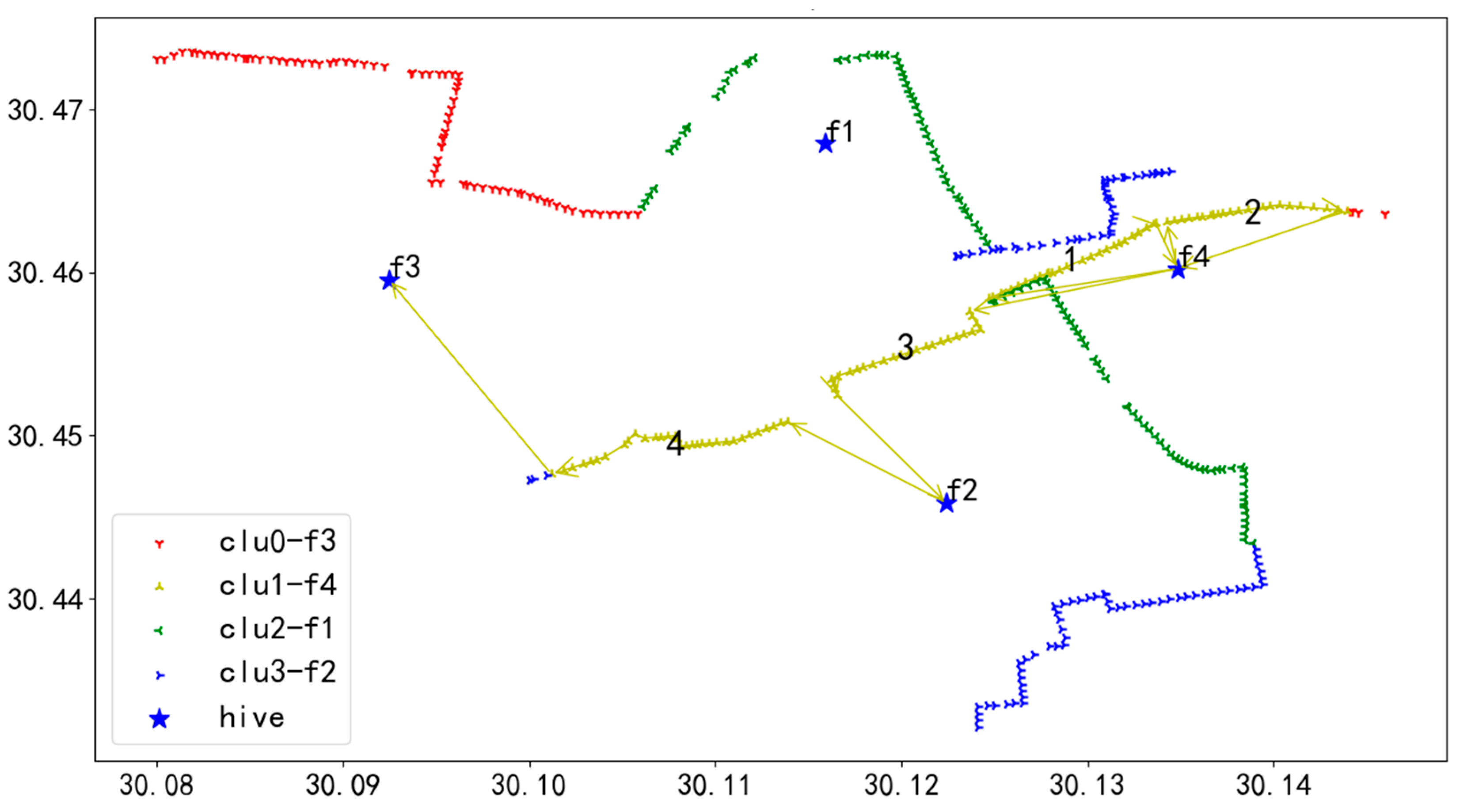
In Figure 17, the red line delineates the flight route of UAV U1. Departing from the initial hive f3, UAV U1 navigates to the first task on Route 1, successively inspecting each task on this route until completion. After finishing Route 1, U1 flies to hive f1 for a battery swap. Post-replacement, U1 moves to the initial task of Route 2 and continues inspections following the sequence of tasks numbered 1 through 6. Upon completing inspections of all tasks across the routes, U1 lands at hive f3, marking the end of the flight mission.
In Figure 18, the yellow line depicts the flight path of UAV U2. Starting from the initial hive f5, UAV U2 heads to the first task on Route 1 and successively inspects each task on this route until the tasks are completed. After finishing Route 1, U2 flies to hive f5 for a battery replacement. Once the battery replacement is completed, U2 proceeds to the starting task of Route 2 and continues with the inspection tasks in the order of tasks numbered 1 through 6. Ultimately, after completing the inspection of all tasks on all routes, U2 lands at hive f4, concluding the entire flight mission.
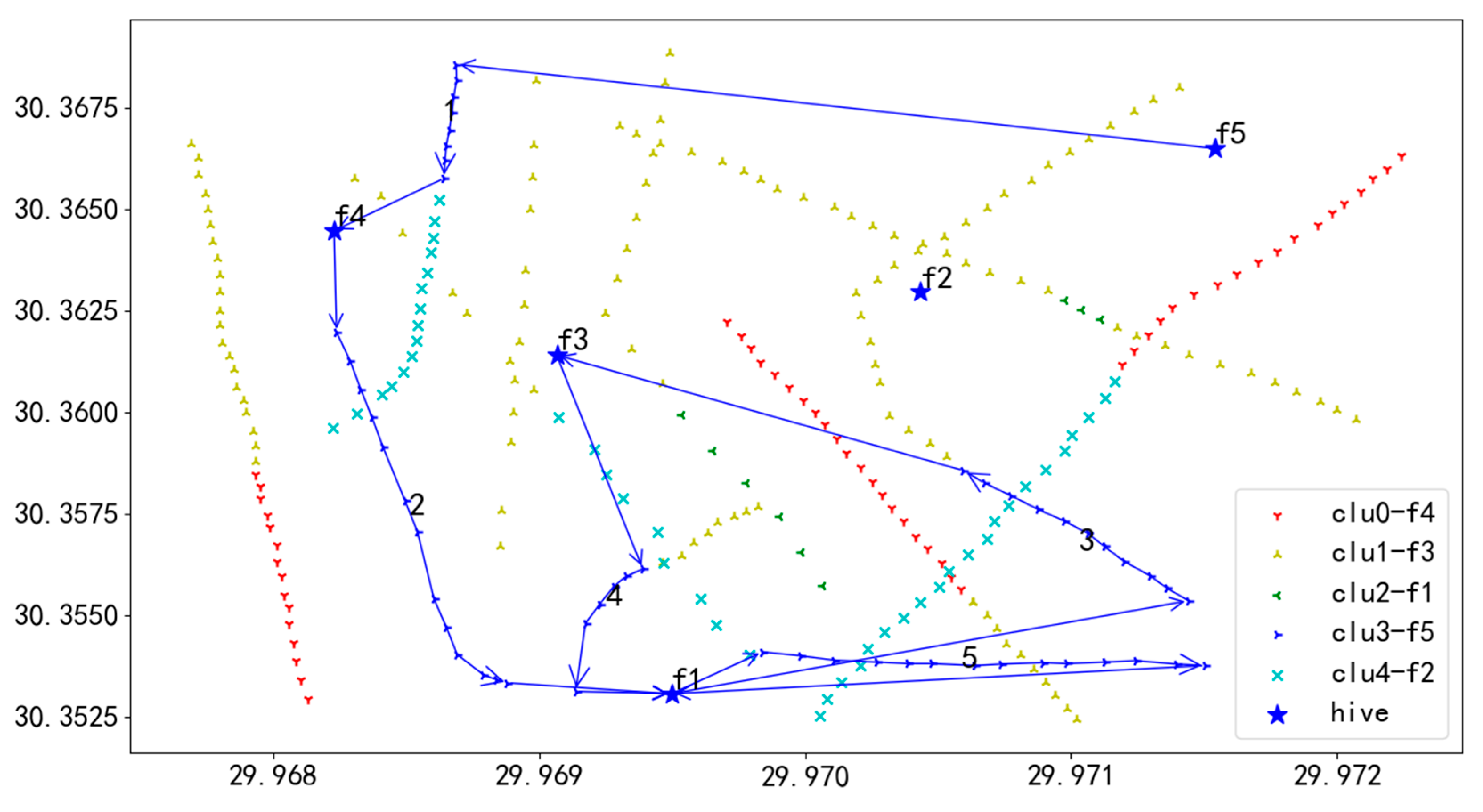
In Figure 19, the green line represents the flight path of UAV U3. UAV U3 departs from the starting hive f1 and proceeds to the first task on Route 1, conducting inspections of each task on this route in sequence until the tasks are completed. After finishing Route 1, U3 returns to hive f3 for a battery replacement. Following the battery replacement, U3 flies to the starting task of Route 2 to continue inspections, executing the tasks in the order of numbers 1 through 6. Ultimately, after completing the inspection of all tasks on all routes, U3 lands back at hive f4, marking the end of the entire flight mission.
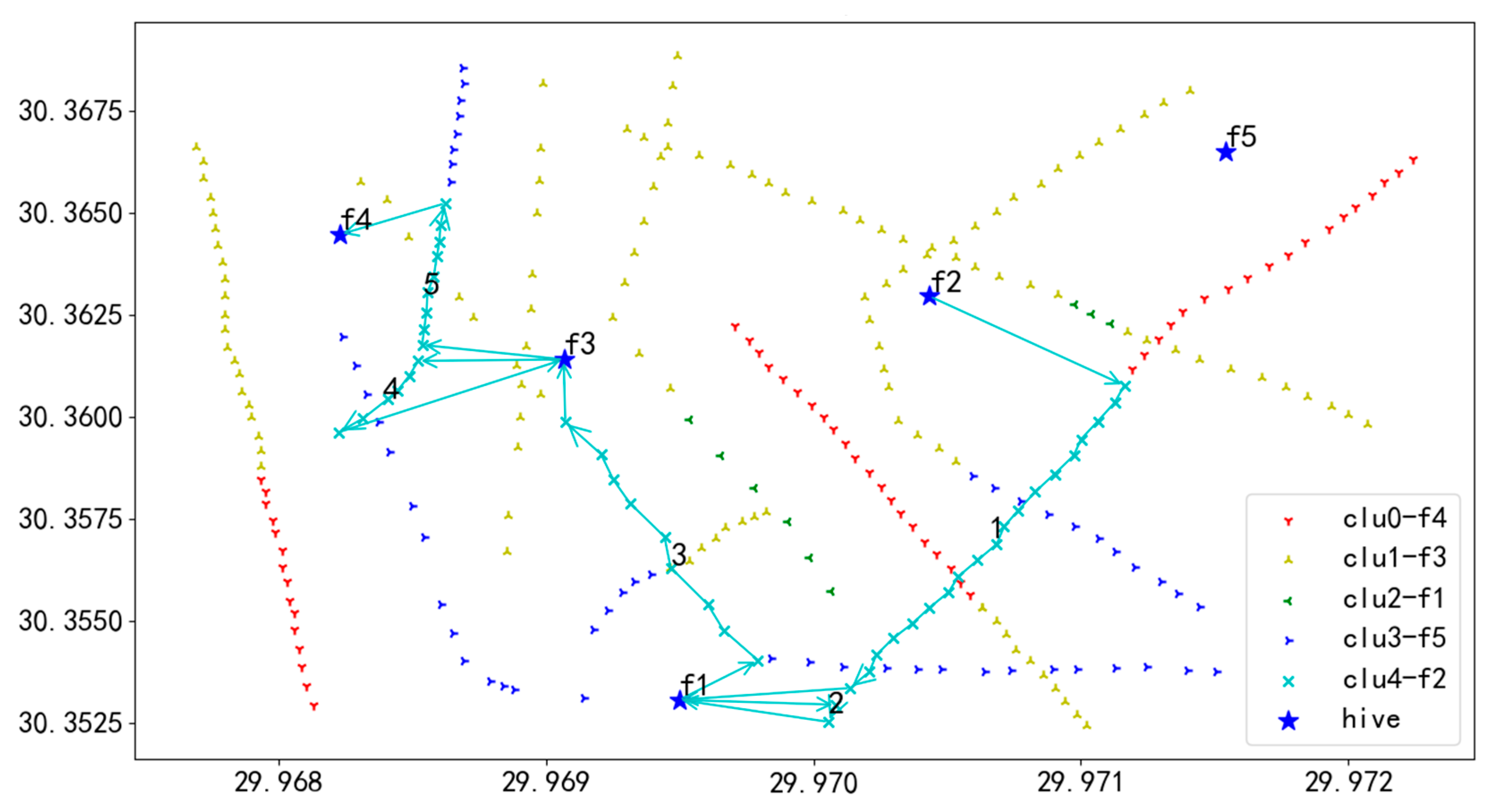
In Figure 20, the blue line illustrates the flight route of UAV U4. UAV U4 takes off from the starting hive f2 and heads to the first task on Route 1, inspecting each task on this route in sequence until the tasks are completed. After finishing Route 1, U4 flies to hive f3 for a battery swap. Following the battery replacement, U4 proceeds to the starting task of Route 2 and continues with inspections, executing tasks in the order of numbers 1 through 5. Ultimately, after completing the inspection of all tasks on all routes, U4 lands at hive f1, concluding the entire flight mission.
In Figure 21, the Tiffany blue line shows the flight path of UAV U5. UAV U5 departs from the starting hive f4 and proceeds to the first task on Route 1, successively inspecting each task on this route until the tasks are completed. After finishing Route 1, U5 flies to hive f2 for a battery replacement. Once the battery replacement is complete, U5 moves to the starting task of Route 2 to continue inspections, following the sequence of tasks numbered 1 through 6. Ultimately, after completing the inspection of all tasks on all routes, U5 lands at hive f2, concluding the entire flight mission.
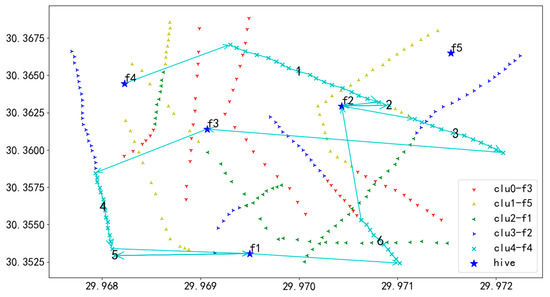
Figure 21.
U5 flight sequence obtained by GA-NSGA-II algorithm in 284 task points.
4.4. Comparison of Experimental Results
This research is a brand new problem, and there is no algorithm that can be used for comparison, so two different methods are designed for comparison according to the condition requirements. By comparing the balance between the inspection distance and total inspection distance, the advantages of this algorithm and other algorithms in power grid inspection are verified.
4.4.1. Comparison with Other Algorithms
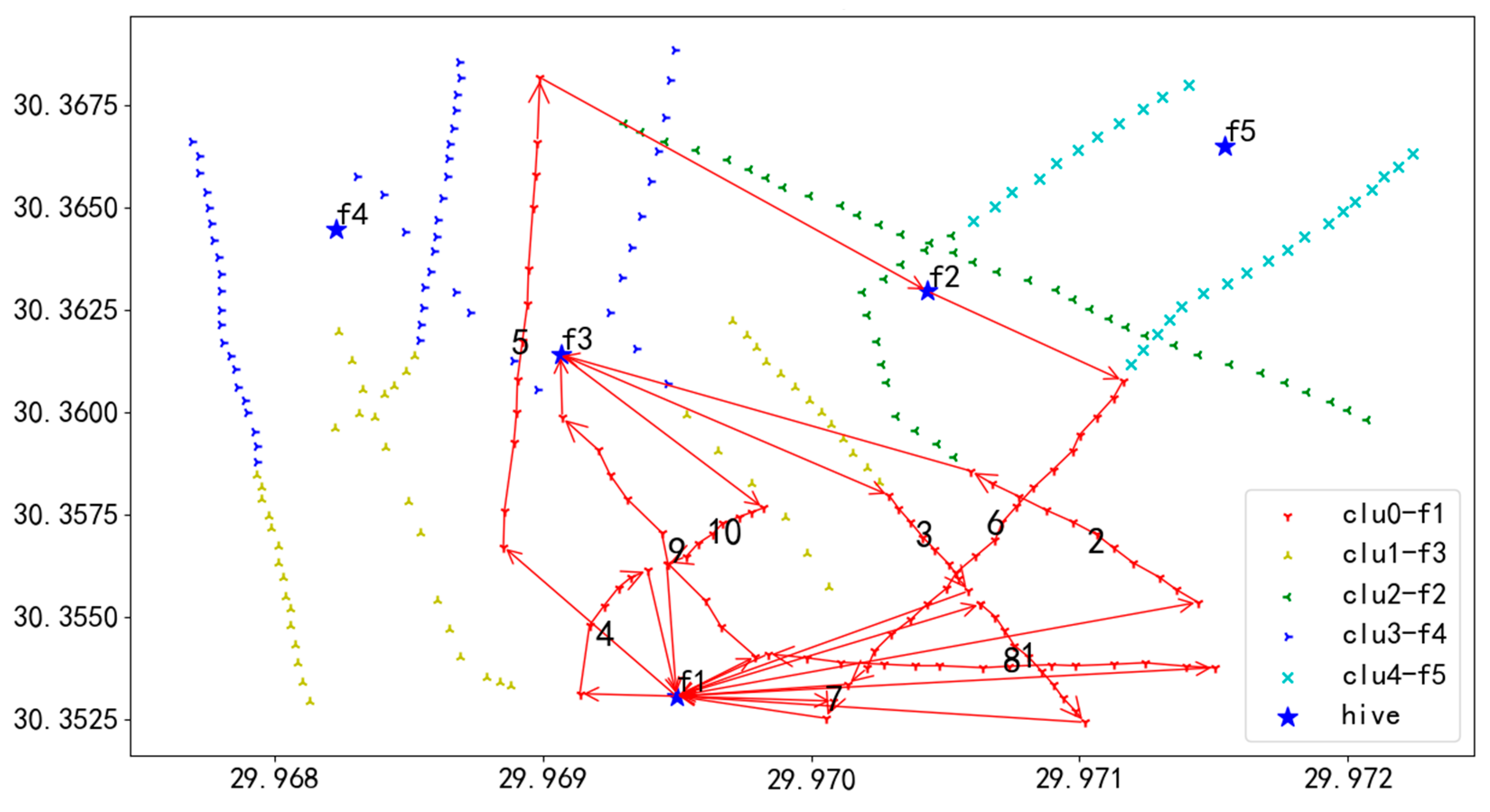
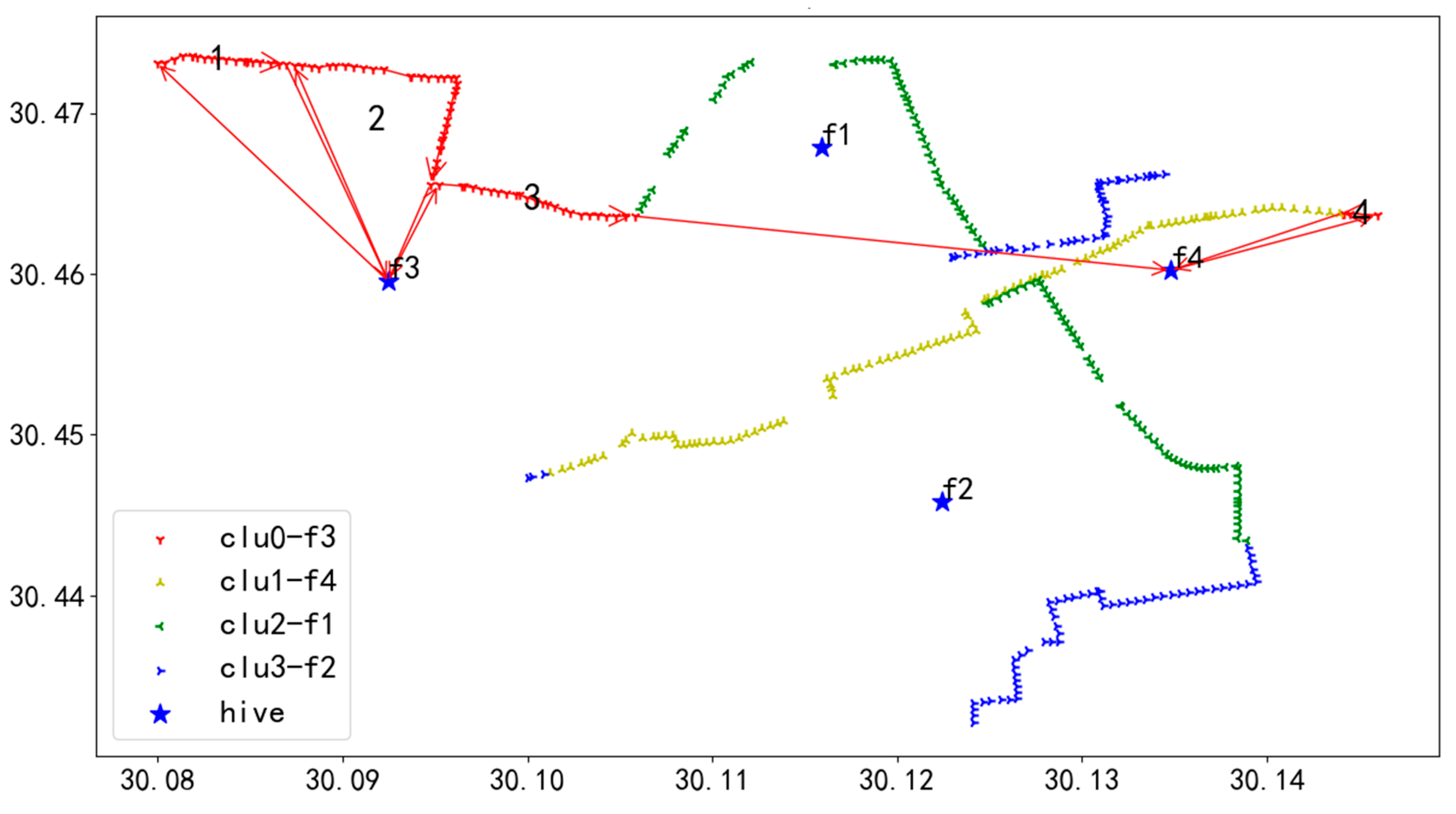
1. Task-adaptive clustering optimization algorithm: The task-adaptive clustering optimization algorithm firstly distributes the tasks of the cut grid line units by clustering the algorithm and then optimizes the order and direction of the UAV inspection unit tasks using the adaptive genetic algorithm based on the elite retention strategy. Although the algorithm can quickly generate inspection schemes, it is difficult to balance the tasks assigned by cluster, resulting in a large difference in inspection distances between UAVs; the flight routes are shown in Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26.
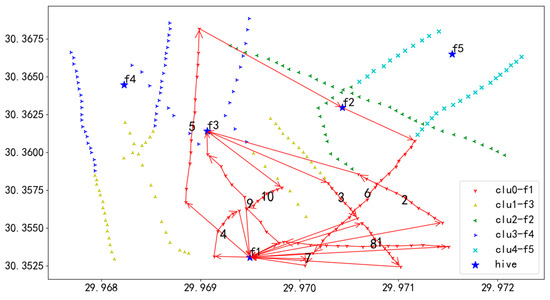
Figure 22.
U1 flight sequence obtained by adaptive clustering algorithm in 284 task points.
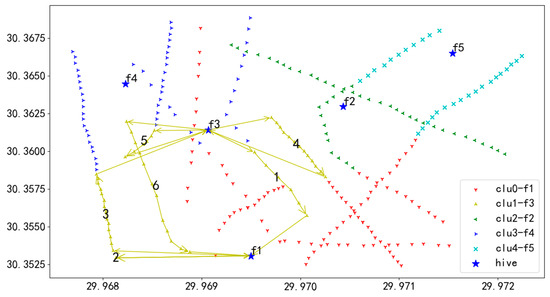
Figure 23.
U2 flight sequence obtained by adaptive clustering algorithm in 284 task points.
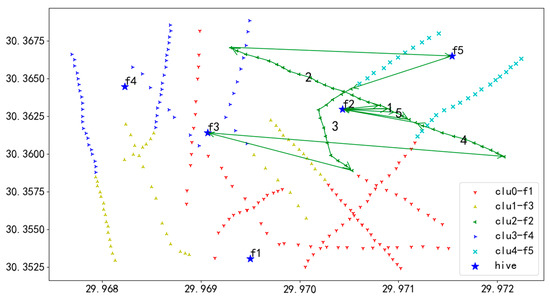
Figure 24.
U3 flight sequence obtained by adaptive clustering algorithm in 284 task points.
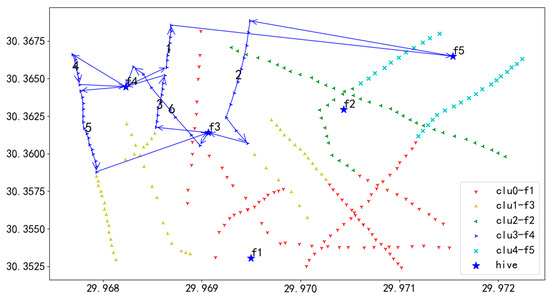
Figure 25.
U4 flight sequence obtained by adaptive clustering algorithm in 284 task points.
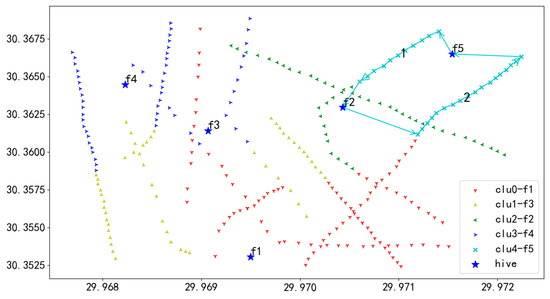
Figure 26.
U5 flight sequence obtained by adaptive clustering algorithm in 284 task points.
In Figure 22, UAV U1 takes off from hive f1, first inspects the towers on the route marked as 1, then returns to f1 for battery swapping, and continues the inspection in the order of 1 to 10, finally landing at hive f1.
In Figure 23, UAV U2 takes off from hive f3, first inspects the towers on the route marked as 1, then returns to f1 for battery swapping, and continues the inspection in the order of 1 to 6, finally landing at hive f1.
In Figure 24, UAV U3 takes off from hive f2, first inspects the towers on the route marked as 1, then returns to f1 for battery swapping, and continues the inspection in the order of 1 to 5, finally landing at hive f1.
In Figure 25, UAV U4 takes off from hive f4, first inspects the towers on the route marked as 1, then returns to f5 for battery swapping, and continues the inspection in the order of 1 to 6, finally landing at hive f4.
In Figure 26, UAV U5 takes off from hive f5, first inspects the towers on the route marked as 1, then returns to f2 for battery swapping, and continues the inspection in the order of 1 to 2, finally landing at hive f5.
The flight routes of the UAVs clearly illustrate a significant imbalance in mission execution. UAV U1 needs to take off and land from the hive 10 times to complete the inspection of the assigned power poles, whereas UAV U5 only requires two takeoffs and landings. This substantial disparity in flight distances leads to a considerable difference in the time each UAV spends on its mission. Consequently, the overall efficiency of the inspection process is severely compromised, and the potential advantages of multi-UAV inspections are not fully realized.
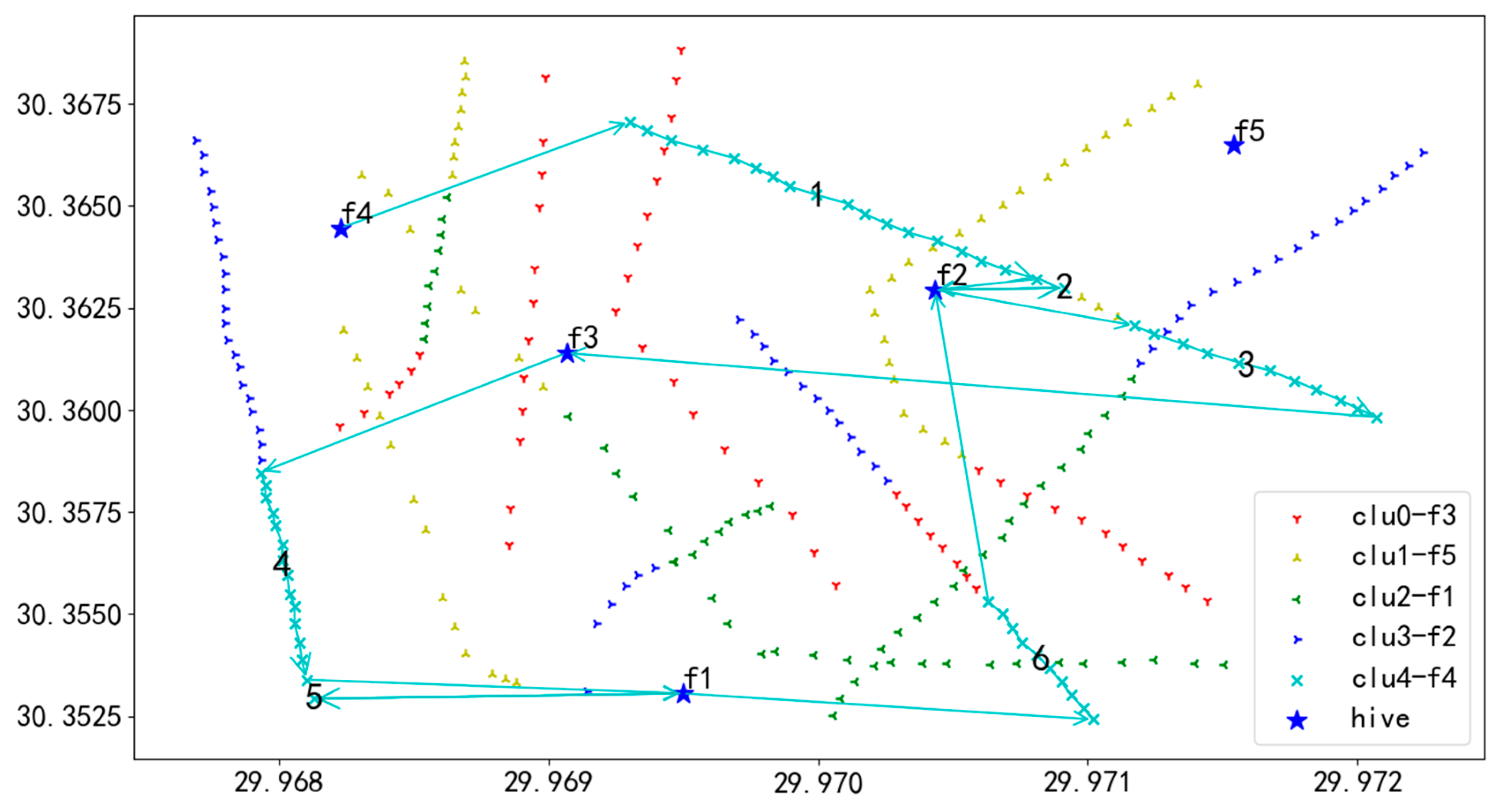
2. GA-GA bilevel optimization algorithm: The GA-GA algorithm aims to minimize the total inspection distance of UAVs. The GA algorithm is used to optimize task assignment in the outer layer, and the adaptive genetic algorithm based on the elite retention strategy is used to optimize the inspection order and direction of UAVs in the inner layer. However, the algorithm only focuses on single-objective optimization and fails to achieve the balanced distribution of the inspection distance among the UAVs, resulting in a large difference in flight distance between UAVs; the flight routes are shown in Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31.
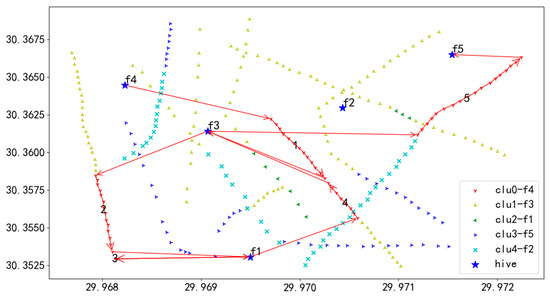
Figure 27.
U1 flight sequence obtained by GA-GA algorithm in 284 task points.
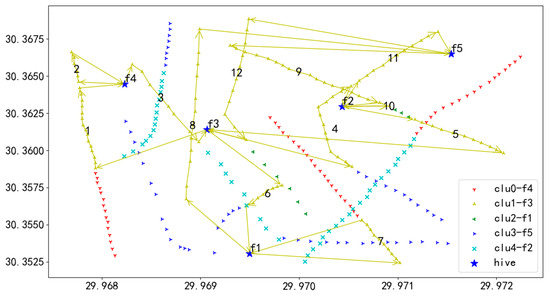
Figure 28.
U2 flight sequence obtained by GA-GA algorithm in 284 task points.
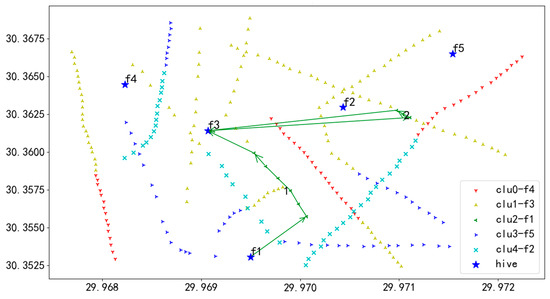
Figure 29.
U3 flight sequence obtained by GA-GA algorithm in 284 task points.
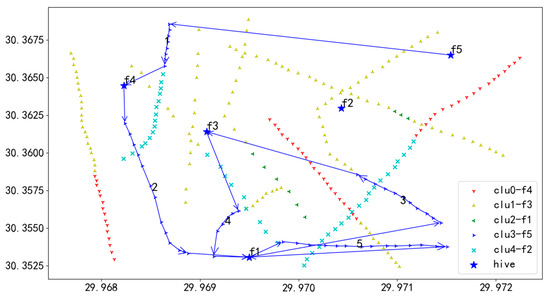
Figure 30.
U4 flight sequence obtained by GA-GA algorithm in 284 task points.
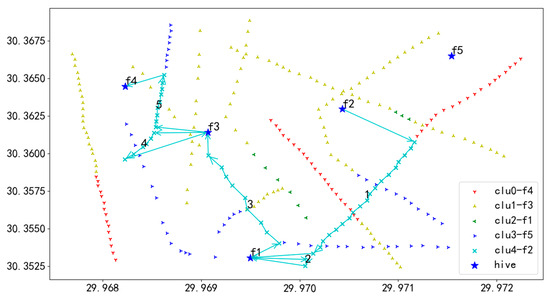
Figure 31.
U5 flight sequence obtained by GA-GA algorithm in 284 task points.
In Figure 27, UAV U1 takes off from hive f4, first inspects the towers on the route marked as 1, then returns to f3 for battery swapping, and continues the inspection in the order of 1 to 5, finally landing at hive f5.
In Figure 28, UAV U2 takes off from hive f3, first inspects the towers on the route marked as 1, then returns to f4 for battery swapping, and continues the inspection in the order of 1 to 11, finally landing at hive f5.
In Figure 29, UAV U3 takes off from hive f1, first inspects the towers on the route marked as 1, then returns to f3 for battery swapping, and continues the inspection in the order of 1 to 2, finally landing at hive f3.
In Figure 30, UAV U4 takes off from hive f5, first inspects the towers on the route marked as 1, then returns to f4 for battery swapping, and continues the inspection in the order of 1 to 5, finally landing at hive f1.
In Figure 31, UAV U5 takes off from hive f2, first inspects the towers on the route marked as 1, then returns to f1 for battery swapping, and continues the inspection in the order of 1 to 5, finally landing at hive f4.
The GA-GA algorithm and the adaptive clustering optimization algorithm exhibit similar issues in their results. As shown in Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31, there is a significant disparity in flight distances among UAVs, which similarly leads to a large difference in the time required for each UAV to complete its mission. This imbalanced task assignment severely reduces the overall efficiency of the inspection process and fails to fully leverage the advantages of multi-UAV inspections.
In order to further compare the performance of the task-adaptive clustering optimization algorithm, the GA-GA algorithm, and the GA-NSGA-II algorithm, we recorded the total flight distance, the flight distance of each UAV, and the corresponding runtime for all three algorithms. For the mission-adaptive clustering optimization algorithm and the GA-GA algorithm, we select the shortest flight distance from the 10 flight results and take it as the final representative result of the algorithm. Then, the results of the GA-NSGA-II algorithm which are superior to the task-adaptive clustering optimization algorithm and the GA-GA algorithm are selected for comparison. The specific data of the comparison are shown in Table 6.

Table 6.
Comparison of results from three algorithms.
The results from Table 6 indicate that the GA-NSGA-II bilevel optimization algorithm demonstrates significant advantages in two key optimization objectives: the total flight distance and the balance of the UAV workload. Specifically, this algorithm is capable of identifying solutions that not only reduce the overall flight distance but also distribute the workload among UAVs more evenly. Compared with the task-adaptive clustering optimization algorithm and the GA-GA bilevel optimization algorithm, the GA-NSGA-II algorithm not only effectively decreases the total flight distance of the UAVs but also performs better in terms of workload distribution balance.
In our comparative analysis, we selected results from the GA-NSGA-II algorithm that outperformed both the GA-GA bilevel optimization algorithm and the adaptive clustering optimization algorithm in terms of total flight distance and standard deviation. The results show that, compared to the GA-GA bilevel optimization algorithm, the GA-NSGA-II algorithm reduces the standard deviation of flight distances among UAVs by 41.91% to 84.63% and the flight distance of the longest UAV flight by 29.41% to 43.98%. When compared to the adaptive clustering optimization algorithm, the standard deviation of flight distances among UAVs is reduced by 18.25% to 94.93%, and the flight distance of the longest UAV flight is reduced by 15.97% to 37.33%.
However, it can also be seen from the table that, compared to the running time of the task-adaptive clustering optimization algorithm, the GA-NSGA-II bilevel optimization algorithm takes a longer time, which is an obvious drawback of the GA-NSGA-II bilevel optimization algorithm. Nevertheless, since this study focuses on optimizing offline tasks in large-scale power grid scenarios, the impact of the running time is not significant.
These results suggest that the GA-NSGA-II algorithm offers a significant performance improvement in optimizing UAV task assignment and path planning. It effectively balances the workload of UAVs while significantly reducing the total flight distance, providing an efficient and balanced solution for UAV mission planning.
4.4.2. Comparison with Other Power Grid Scenarios
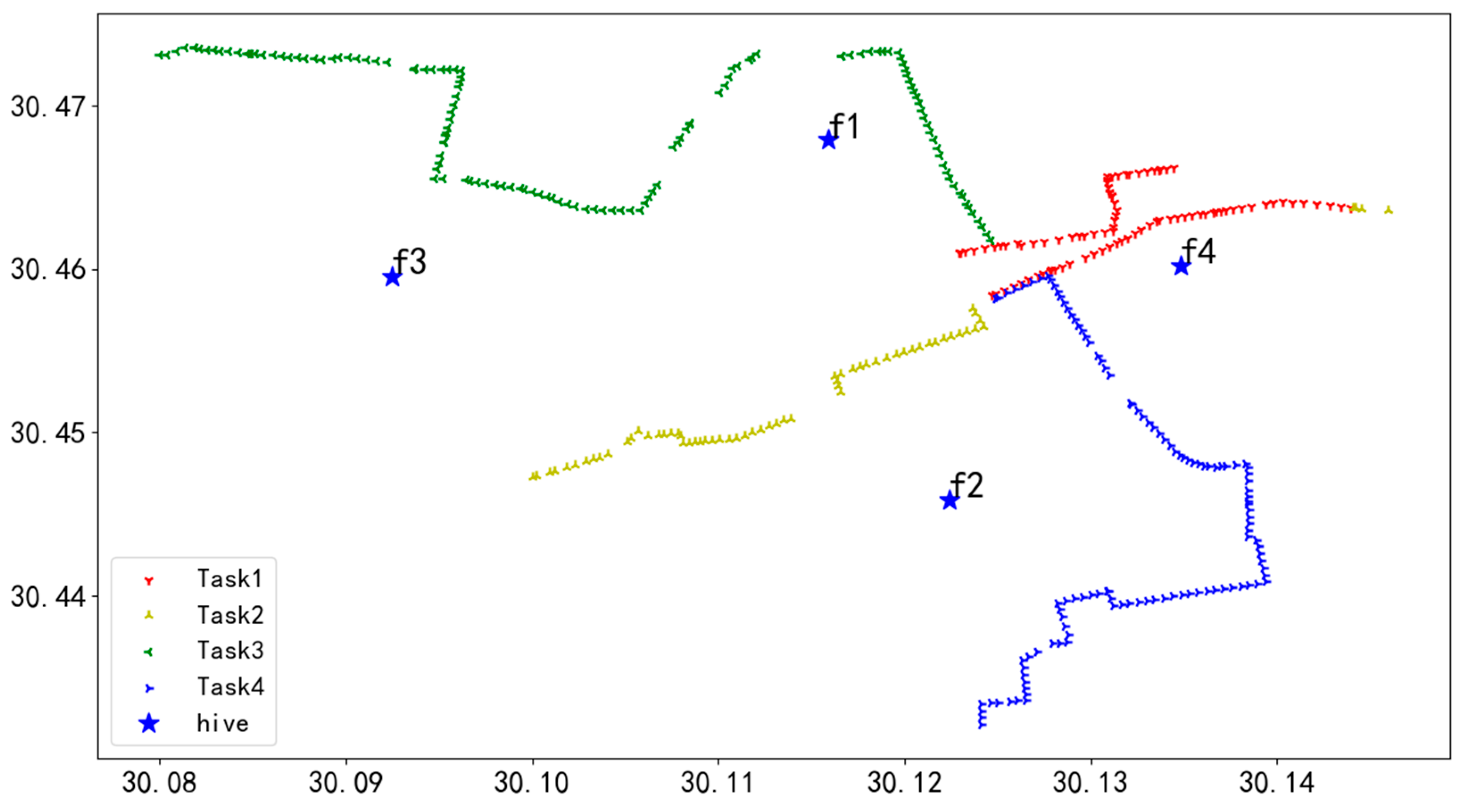
To verify the effectiveness of the GA-NSGA-II bilevel optimization algorithm, we selected a new scenario with sparsely distributed transmission towers for validation, in contrast to the previously dense scenario. The new scenario is also located in Zhejiang Province, geographically situated between 30.34° N and 30.47° N latitude and between 119.75° E and 120.15° E longitude. It consists of five transmission lines, 406 towers, and four UAV battery swap hives from four different task packages, as shown in Figure 32.
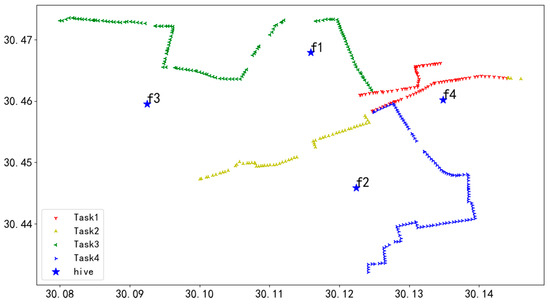
Figure 32.
Top view of the realistic power grid scene with 406 task points.
Following the algorithm’s procedure, after performing unit task segmentation in the power grid scenario, we obtained 10 task fragments, as shown in Figure 33. In the figure, each unit task (ftask) is represented by a unique color and symbol and is numbered from 0 to 9.
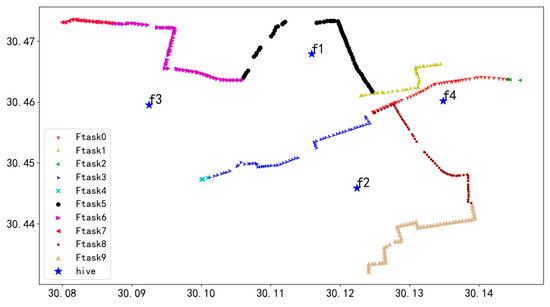
Figure 33.
Unit task segmentation in 406 task point scenarios.
Subsequently, we obtained the Pareto front of the total flight distance and the equilibrium of flight distances among individual UAVs through multiple runs, as shown in Figure 34.
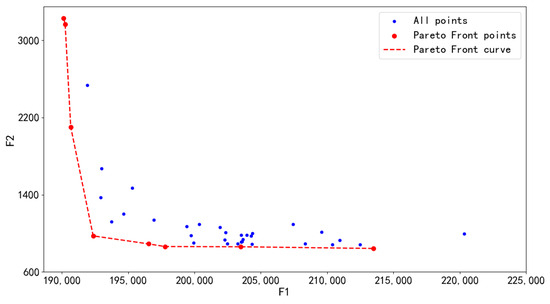
Figure 34.
Pareto front obtained by GA-NSGA-II algorithm in 406 task points.
Among the Pareto-optimal solutions generated from the new scenario data, the solution with the minimum F2 value was still selected. For this particular solution, the corresponding flight sequence diagrams were generated (as shown in Figure 35, Figure 36, Figure 37 and Figure 38).
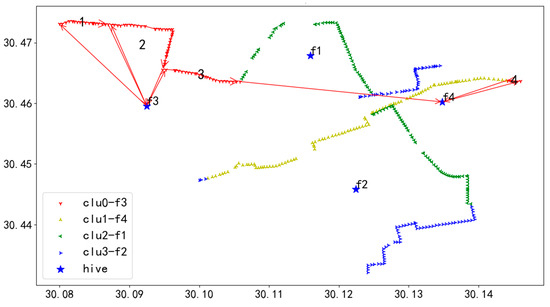
Figure 35.
U1 flight sequence obtained by GA-NSGA-II algorithm in 406 task points.
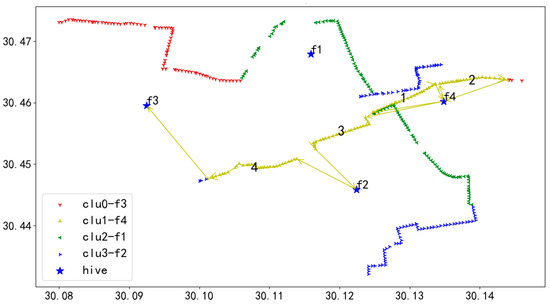
Figure 36.
U2 flight sequence obtained by GA-NSGA-II algorithm in 406 task points.
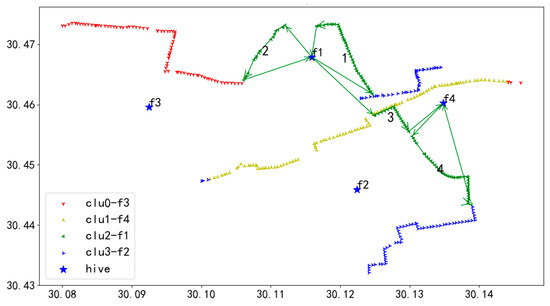
Figure 37.
U3 flight sequence obtained by GA-NSGA-II algorithm in 406 task points.
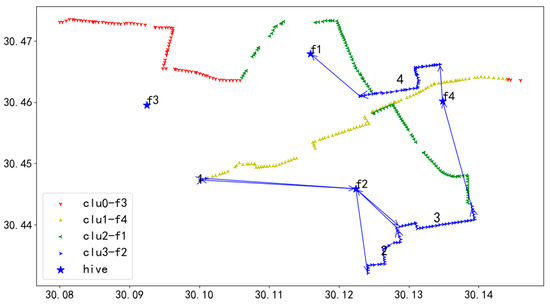
Figure 38.
U4 flight sequence obtained by GA-NSGA-II algorithm in 406 task points.
In Figure 35, UAV U1 takes off from hive f3, first inspects the towers on the route marked as 1, then returns to f3 for battery swapping, and continues the inspection in the order of 1 to 4, finally landing at hive f4.
In Figure 36, UAV U2 takes off from hive f4, first inspects the towers on the route marked as 1, then returns to f4 for battery swapping, and continues the inspection in the order of 1 to 4, finally landing at hive f3.
In Figure 37, UAV U3 takes off from hive f1, first inspects the towers on the route marked as 1, then returns to f1 for battery swapping, and continues the inspection in the order of 1 to 4, finally landing at hive f4.
In Figure 38, UAV U4 takes off from hive f2, first inspects the towers on the route marked as 1, then returns to f2 for battery swapping, and continues the inspection in the order of 1 to 4, finally landing at hive f1.
From the results shown in Figure 35, Figure 36, Figure 37 and Figure 38, we can observe that the flight routes of UAVs U1 to U4 are very close in distance.
The total flight distance of UAVs and the individual flight distances obtained by selecting the minimum F2 value are shown in Table 7.

Table 7.
The result table for 406 task points.
From the table, it can be seen that the GA-NSGA-II bilevel optimization algorithm still achieves a balanced assignment result for the sparse scenario with 406 tower task points. Therefore, it can be concluded that the GA-NSGA-II bilevel optimization algorithm has a very wide range of applicability.
5. Conclusions
To address the challenges of task assignment and path planning in multi-UAV power grid inspections, we propose a GA-NSGA-II bilevel optimization algorithm based on task segmentation. By segmenting the total task into smaller unit tasks according to the UAV flight endurance, this approach avoids excessive search dimensions and solution failures. The proposed bilevel framework aims to balance inspection distances among UAVs while minimizing the overall inspection distance. In the outer loop, the NSGA-II algorithm optimizes task assignments across UAVs, while in the inner loop, an adaptive genetic algorithm with elitist retention optimizes the inspection sequence and direction within each UAV domain. They together yield a Pareto-optimal solution set, thereby satisfying all constraints and objectives. In scenarios featuring 284 tower inspection task points, our proposed algorithm has demonstrated significant improvements over the GA-GA bilevel optimization approach. Specifically, it has reduced the standard deviation of UAV flight distances by 41.91% to 84.63% and the longest individual flight distance by 29.41% to 43.98%. When compared to the task-adaptive clustering optimization method, the algorithm achieved a decrease in the standard deviation of flight distances ranging from 18.25% to 94.93% and a reduction in the maximum flight distance from 15.97% to 37.33%. Furthermore, the effectiveness of our algorithm was also validated in an environment with 406 tower task points. The results confirmed the superiority of the GA-NSGA-II bilevel optimization algorithm in minimizing the total inspection distance and achieving a more balanced distribution of workloads among UAVs. This highlights the algorithm’s potential to enhance operational efficiency and fairness in UAV-assisted inspection tasks.
Author Contributions
Conceptualization, Y.L. and S.M.; methodology, Y.L. and C.C.; software, Y.L.; validation, Y.L. and Y.S.; formal analysis, Y.L., Y.S. and S.M.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L.; visualization, Y.L.; supervision, S.M. and Y.S.; project administration, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rave, A.; Fontaine, P.; Kuhn, H. Drone location and vehicle fleet planning with trucks and aerial drones. Eur. J. Oper. Res. 2023, 308, 113–130. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. Coop. Robot. Sens. Netw. 2015, 2015, 31–51. [Google Scholar]
- Duan, X.; Liu, H.; Tang, H.; Cai, Q.; Zhang, F.; Han, X. A novel hybrid auction algorithm for multi-UAVs dynamic task assignment. IEEE Access 2019, 8, 86207–86222. [Google Scholar] [CrossRef]
- Song, J.; Zhao, K.; Liu, Y. Survey on mission planning of multiple unmanned aerial vehicles. Aerospace 2023, 10, 208. [Google Scholar] [CrossRef]
- Peng, Q.; Wu, H.; Xue, R. Review of dynamic task allocation methods for UAV swarms oriented to ground targets. Complex Syst. Model. Simul. 2021, 1, 163–175. [Google Scholar] [CrossRef]
- Katrasnik, J.; Pernus, F.; Likar, B. A survey of mobile robots for distribution power line inspection. IEEE Trans. Power Deliv. 2010, 25, 485–493. [Google Scholar]
- Yang, L.; Fan, J.F.; Liu, Y.H. A review on state-of-the-art power line inspection techniques. IEEE Trans. Instrum. Meas. 2020, 69, 9350–9365. [Google Scholar] [CrossRef]
- Luo, Y.H.; Yu, X.; Yang, D.S. A survey of intelligent transmission line inspection based on unmanned aerial vehicle. Artif. Intell. Rev. 2023, 56, 173–201. [Google Scholar]
- Foudeh, H.A.; Luk, P.C.K.; Whidborne, J.F. An advanced unmanned aerial vehicle (UAV) approach via learning-based control for overhead power line monitoring: A comprehensive review. IEEE Access 2021, 9, 130410–130433. [Google Scholar]
- Liu, H.; Wu, G. A Dynamic Task Scheduling Method for Multiple UAVs Based on Contract Net Protocol. Sensors 2022, 22, 4486. [Google Scholar] [CrossRef]
- Seenu, N.; RM, K.C.; Ramya, M.; Janardhanan, M.N. Review on state-of-the-art dynamic task allocation strategies for multiple robot systems. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 47, 929–942. [Google Scholar]
- Bethke, B.; Valenti, M.; How, J.P. UAV task assignment. IEEE Robot. Autom. Mag. 2008, 15, 39–44. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Y.; Vashisth, A.; Fan, H.; Sartoretti, G.A. CAtNIPP: Context-aware attention-based network for informative path planning. In Proceedings of the Conference on Robot Learning, Atlanta, GA, USA, 6–9 November 2023; pp. 1928–1937. [Google Scholar]
- Asadzadeh, S. UAV-based remote sensing for the petroleum industry and environmental monitoring: State-of-the-art and perspectives. J. Pet. Sci. Eng. 2022, 208, 109633. [Google Scholar] [CrossRef]
- Kim, K.S.; Kim, H.Y.; Choi, H.L. A bid-based grouping method for communication-efficient decentralized multi-UAV task allocation. Int. J. Aeronaut. Space Sci. 2020, 21, 290–302. [Google Scholar] [CrossRef]
- Chen, J.; Du, C.; Han, P.; Zhang, Y. Sensitivity analysis of strictly periodic tasks in multi-core real-time systems. IEEE Access 2019, 7, 135005–135022. [Google Scholar] [CrossRef]
- Cattrysse, D.G.; Van Wassenhove, L.N. A survey of algorithms for the generalized assignment problem. Eur. J. Oper. Res. 1992, 60, 260–272. [Google Scholar] [CrossRef]
- Poudel, S.; Moh, S. Task assignment algorithms for unmanned aerial vehicle networks: A comprehensive survey. Veh. Commun. 2022, 35, 100469. [Google Scholar] [CrossRef]
- Li, K.; Yan, X.; Han, Y. Multi-mechanism swarm optimization for multi-UAV task assignment and path planning in transmission line inspection under multi-wind field. Appl. Soft Comput. 2024, 150, 111033. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, H.; Zhang, Y. Coordinated optimization algorithm combining GA with cluster for multi-UAVs to multi-tasks task assignment and path planning. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; pp. 1026–1031. [Google Scholar]
- Huo, L.; Zhu, J.; Wu, G. A novel simulated annealing based strategy for balanced UAV task assignment and path planning. Sensors 2020, 20, 4769. [Google Scholar] [CrossRef] [PubMed]
- Torreno, A.; Onaindia, E.; Komenda, A.; Štolba, M. Cooperative multi-agent planning: A survey. ACM Comput. Surv. (CSUR) 2017, 50, 1–32. [Google Scholar] [CrossRef]
- Wu, H.S.; Li, H.; Xiao, R.B. Modeling and simulation of dynamic ant colony’s labor division for task allocation of UAV swarm. Phys. A Stat. Mech. Its Appl. 2018, 8, 127–141. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Yang, Q. Dynamic task allocation of multiple UAVs based on improved A-QCDPSO. Electronics 2022, 11, 1028. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Zhang, L. Mixed inspection mission based multi-depot UAV swarm routing problem in transmission line: MILP formulation and efficient metaheuristic. J. Intell. Syst. 2025, 20, 123–145. [Google Scholar]
- Rubens, J.M.; Afonso; Marcos, R.O.A. Task allocation and trajectory planning for multiple agents in the presence of obstacle and connectivity constraints with mixed-integer linear programming. Int. J. Robust Nonlinear Control 2020, 30, 5464–5491. [Google Scholar]
- Wang, X.; Liu, Z.; Li, X. Optimal delivery route planning for a fleet of heterogeneous drones: A rescheduling-based genetic algorithm approach. Comput. Ind. Eng. 2023, 179, 109179. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, K. Multi-UAV cooperative task allocation based on IDACLD. In Proceedings of the First Aerospace Frontiers Conference (AFC 2024), Xi’an, China, 12–15 April 2024; Volume 13218, p. 132181V. [Google Scholar]
- Hu, C.; Qu, G.; Zhang, Y. Pigeon-inspired fuzzy multi-objective task allocation of unmanned aerial vehicles for multi-target tracking. Appl. Soft Comput. 2022, 126, 109310. [Google Scholar] [CrossRef]
- Ermağan, U.; Yıldız, B.; Salman, F.S. A learning based algorithm for drone routing. Optimization Online 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).