Development of a Laser Surgical Device with Vibration Compensation: Mechanical Design and Validation of Its Compliant Mechanism
Abstract
Featured Application
Abstract
1. Introduction
- (1)
- Resting tremor, which occurs when the hands are relaxed, without any intentional movement. It is the most common type of tremor and is often associated with medical conditions such as essential tremor or Parkinson’s disease.
- (2)
- Action tremor, which occurs during voluntary movements, such as holding surgical instruments or performing (delicate) procedures. It can be exacerbated by factors such as fatigue, stress, and anxiety, all of which are often present in surgical environments.
- Reduced precision and accuracy: hand tremors can cause surgeons to perform inaccurate incisions. This leads to tissue damage and potential complications.
- Increased procedural time: trying to compensate for hand tremors can make surgical procedures longer. This can be detrimental to the patient’s safety.
- Emotional distress: surgeons with hand tremors may experience anxiety and self-doubt. This can further impair their performance and increase the risk of errors.
- Inaccurate tissue removal: uncontrolled hand tremors can lead to uneven or imprecise tissue removal. This potentially affects the effectiveness of the procedure.
- Targeted tissue damage: hand tremors can cause an unwanted deviation from the intended target. This results in unintentional tissue damage or collateral injury.
- Excessive procedural complexity: compensating for hand tremors can make surgery more challenging and time-consuming.
- Increased risk of complications: imprecise surgery can increase the risk of complications such as bleeding, infection, and scarring.
2. Design of the Laser Scalpel
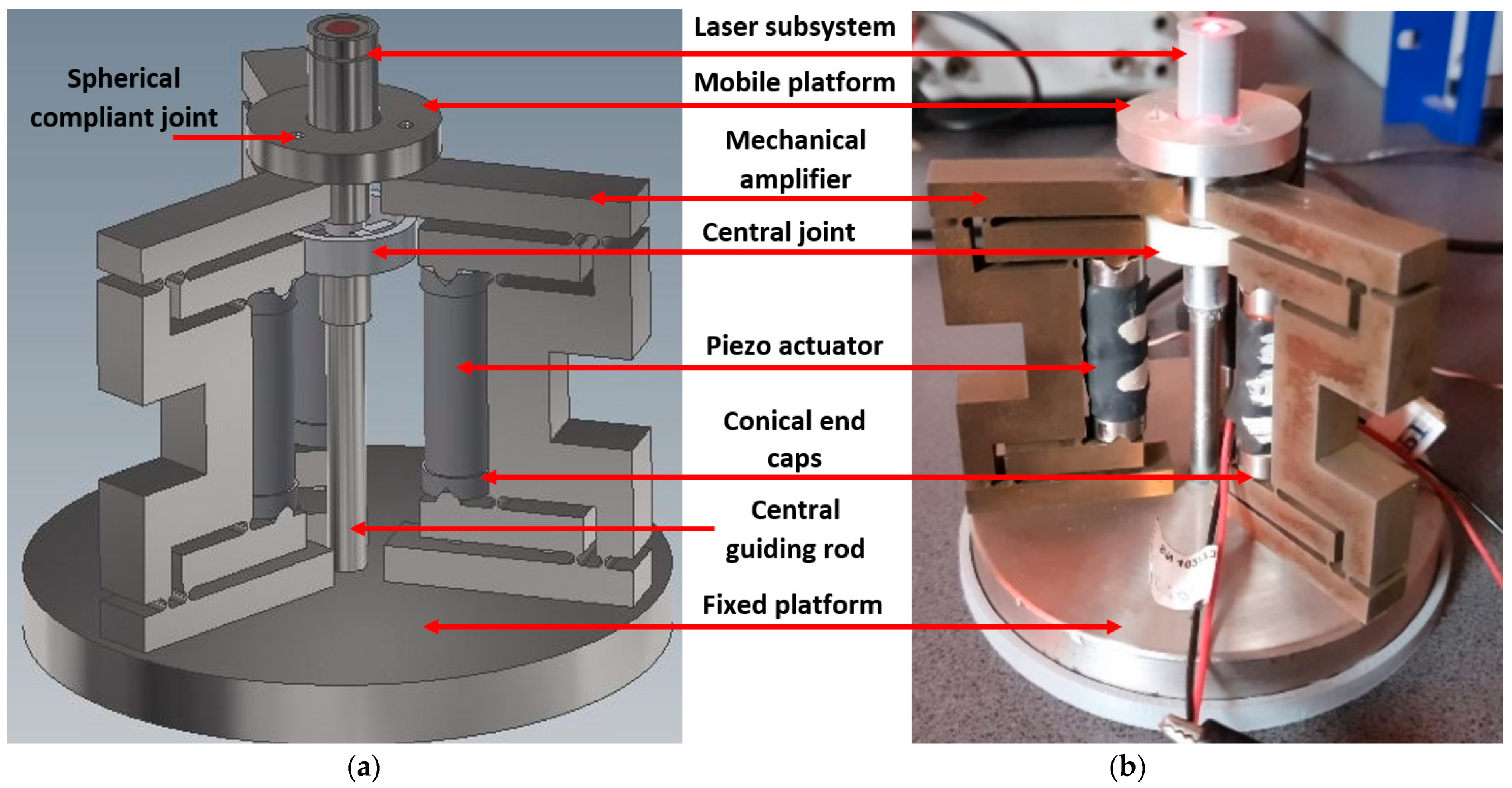
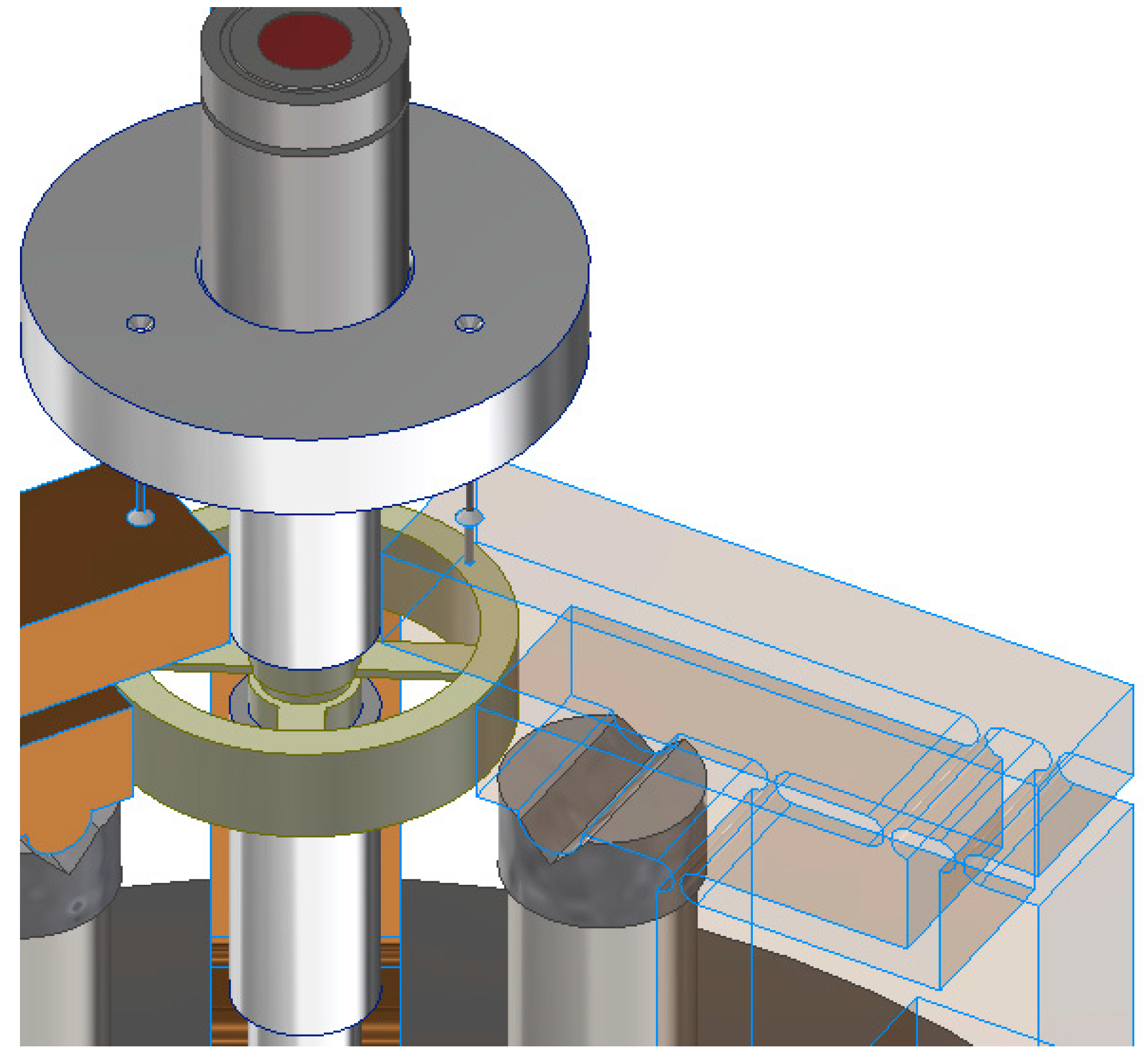
2.1. General Structure and Components
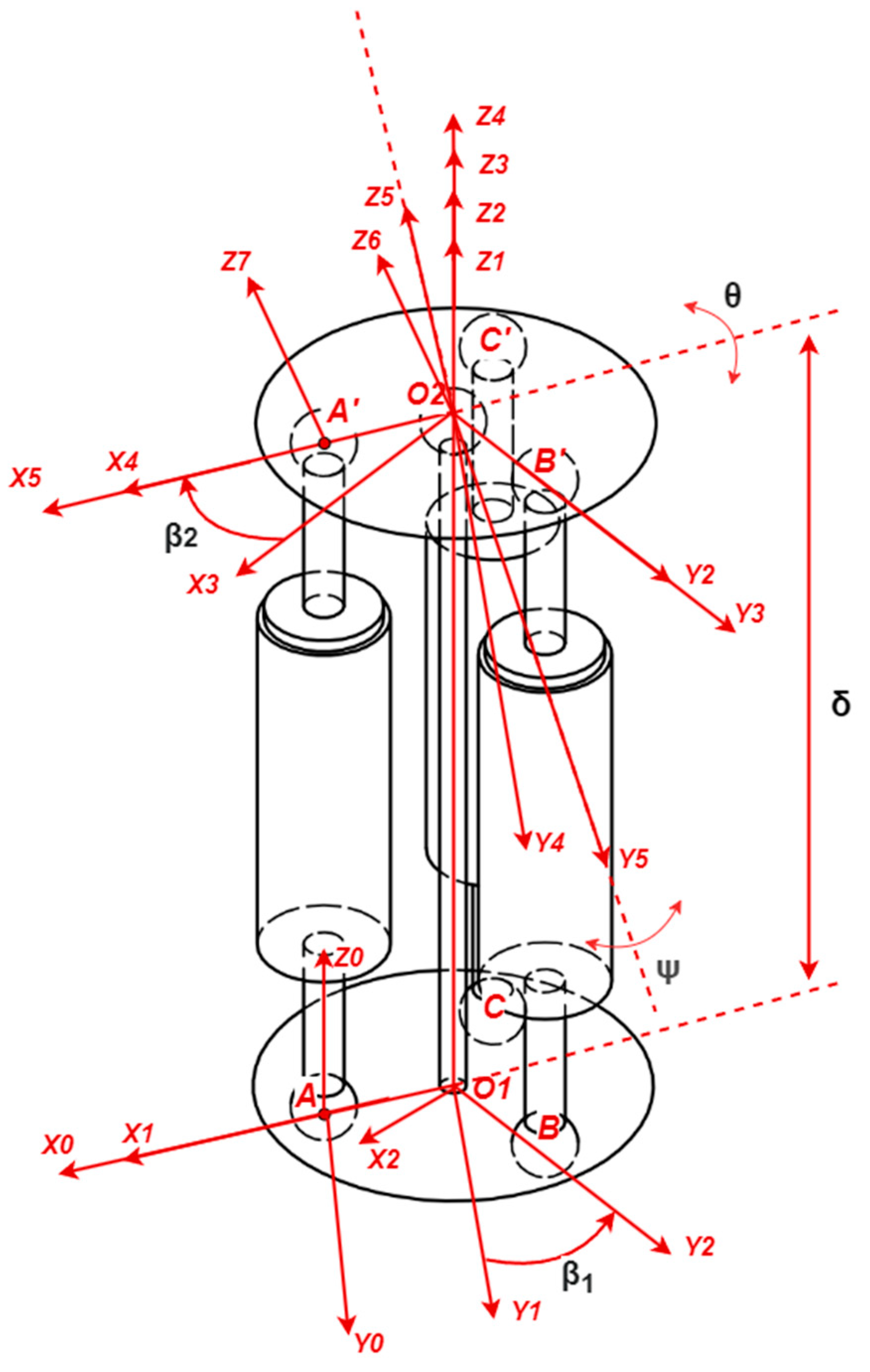
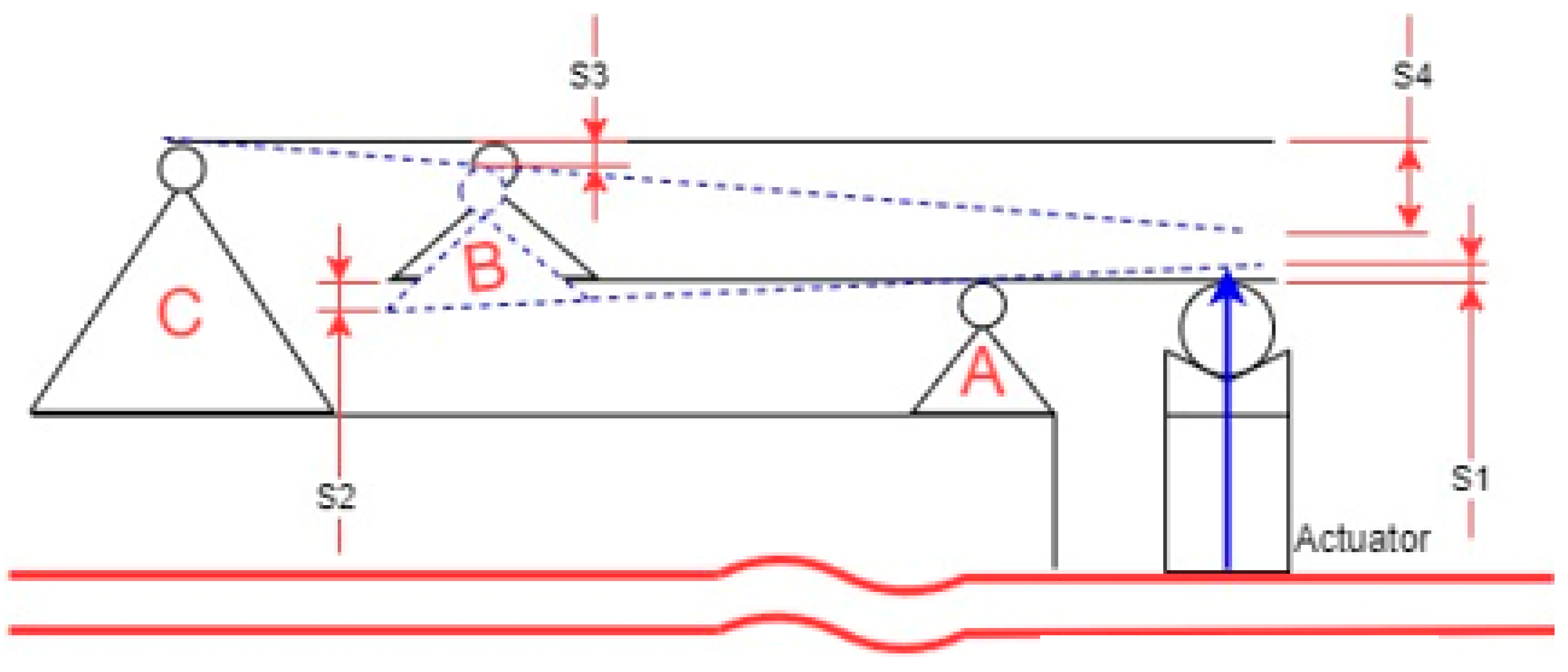
2.2. Schematic Diagram for a Modified Stewart Platform
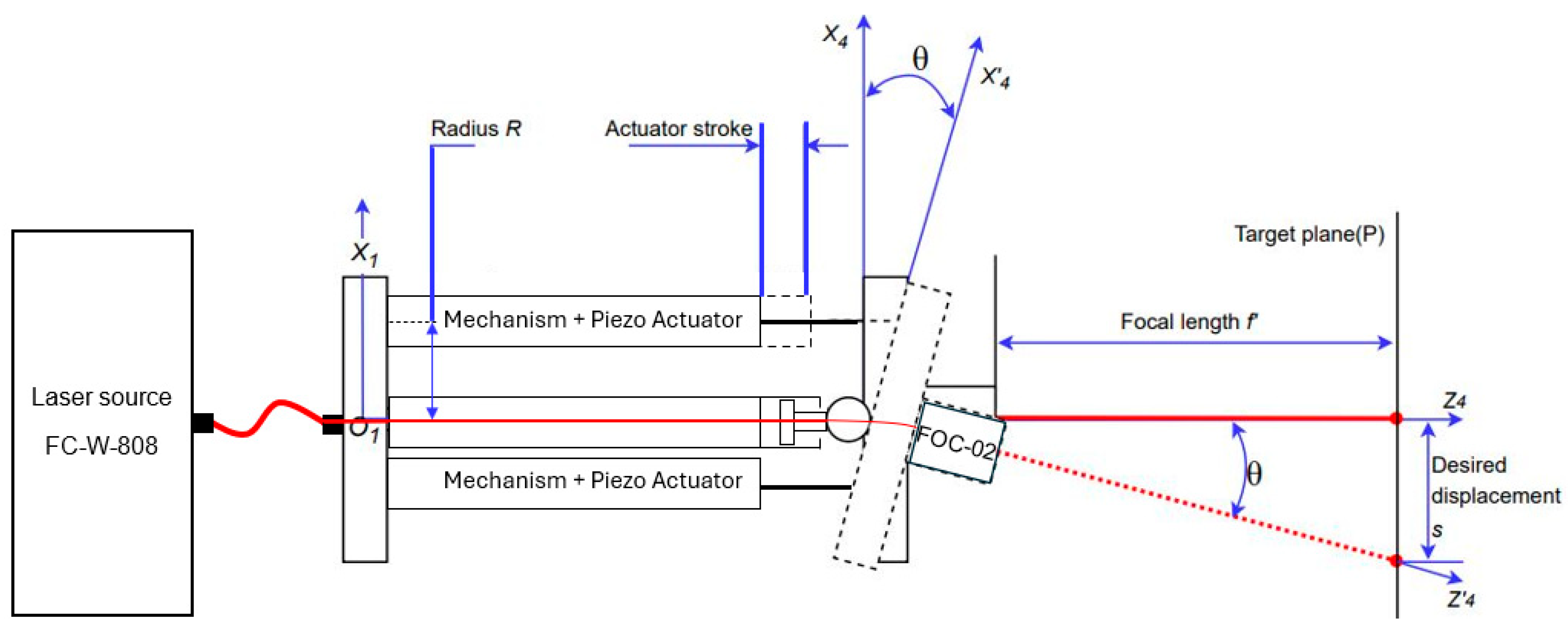
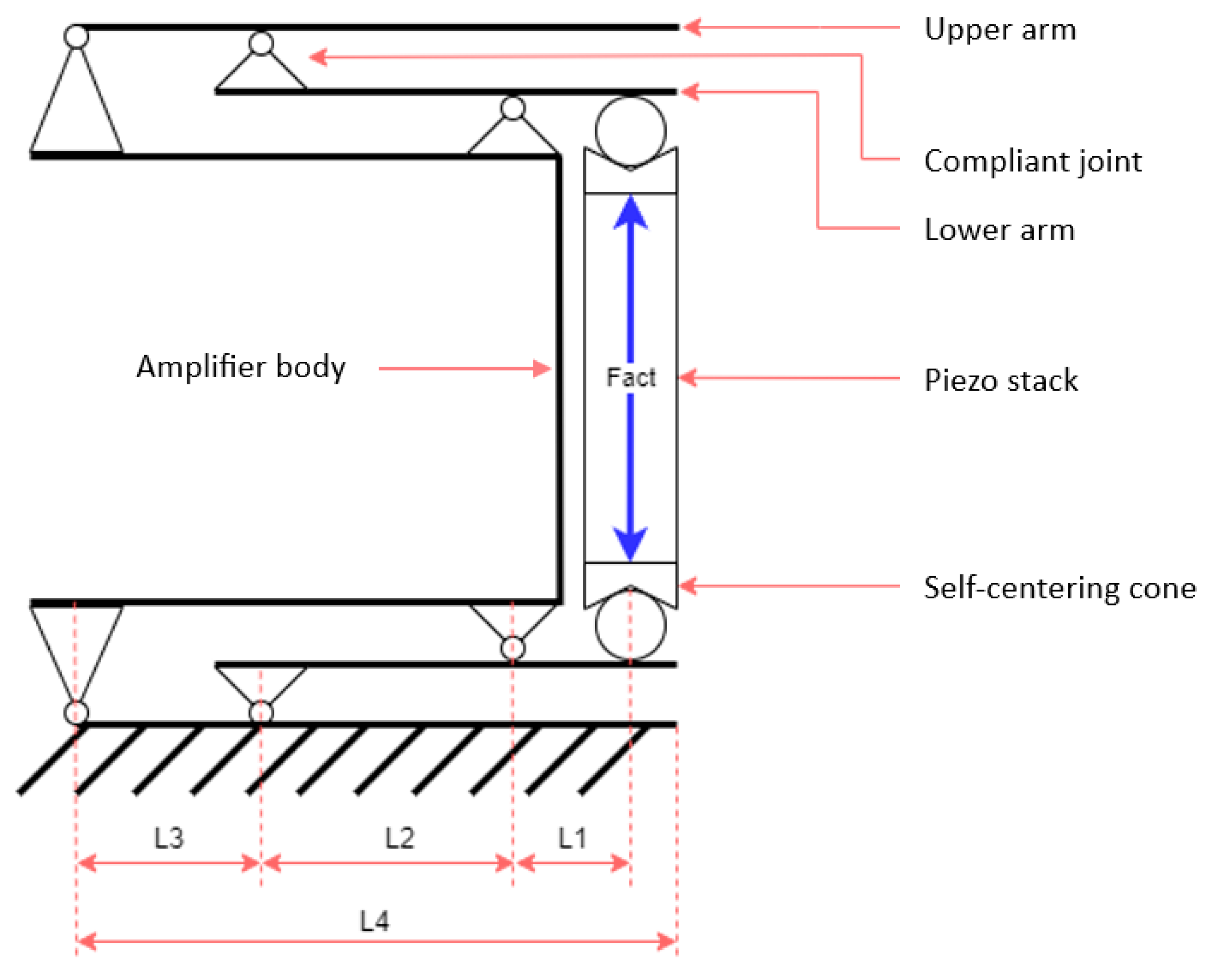
2.3. Schematics of the Mechanical Amplifier
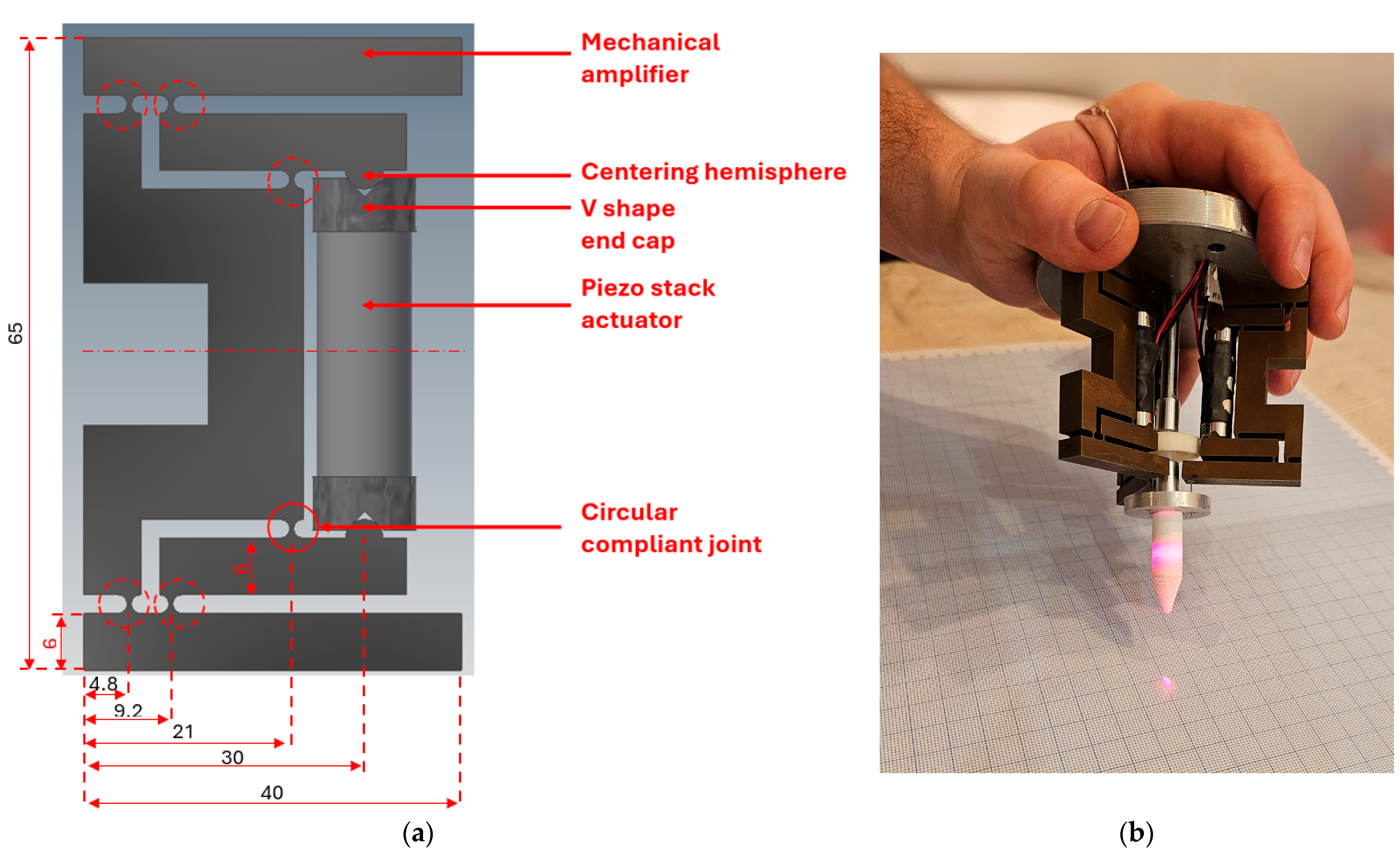
2.4. Three-Dimensional Model of the Mechanical Amplifier
3. Experimental Validation of the Mechanical Amplifier
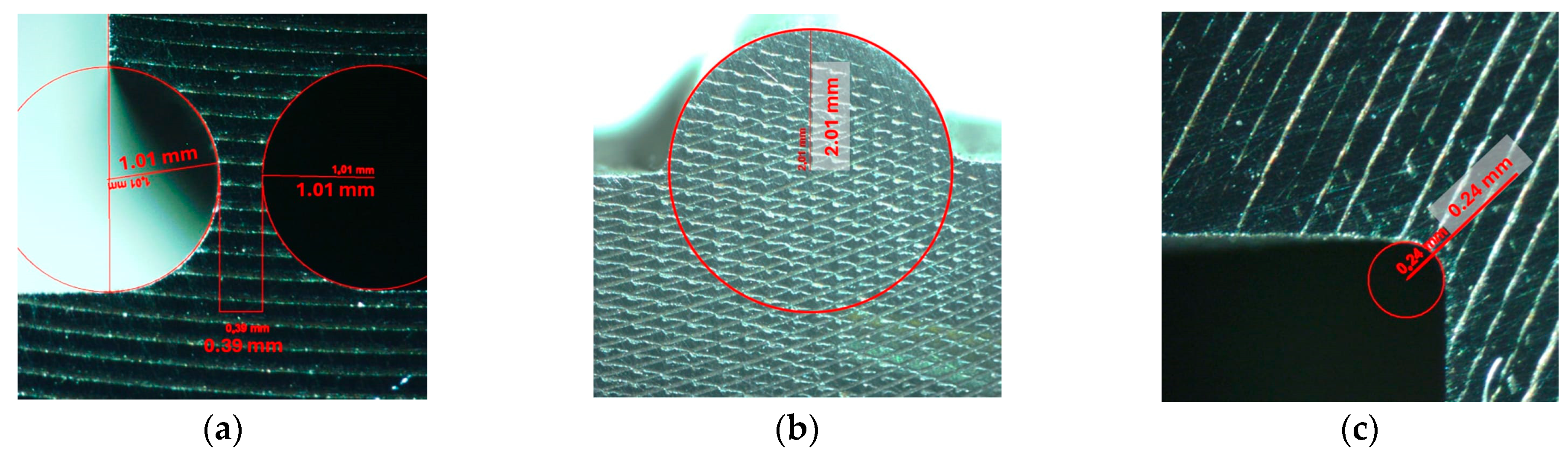
3.1. Manufacturing of the Mechanical Amplifier
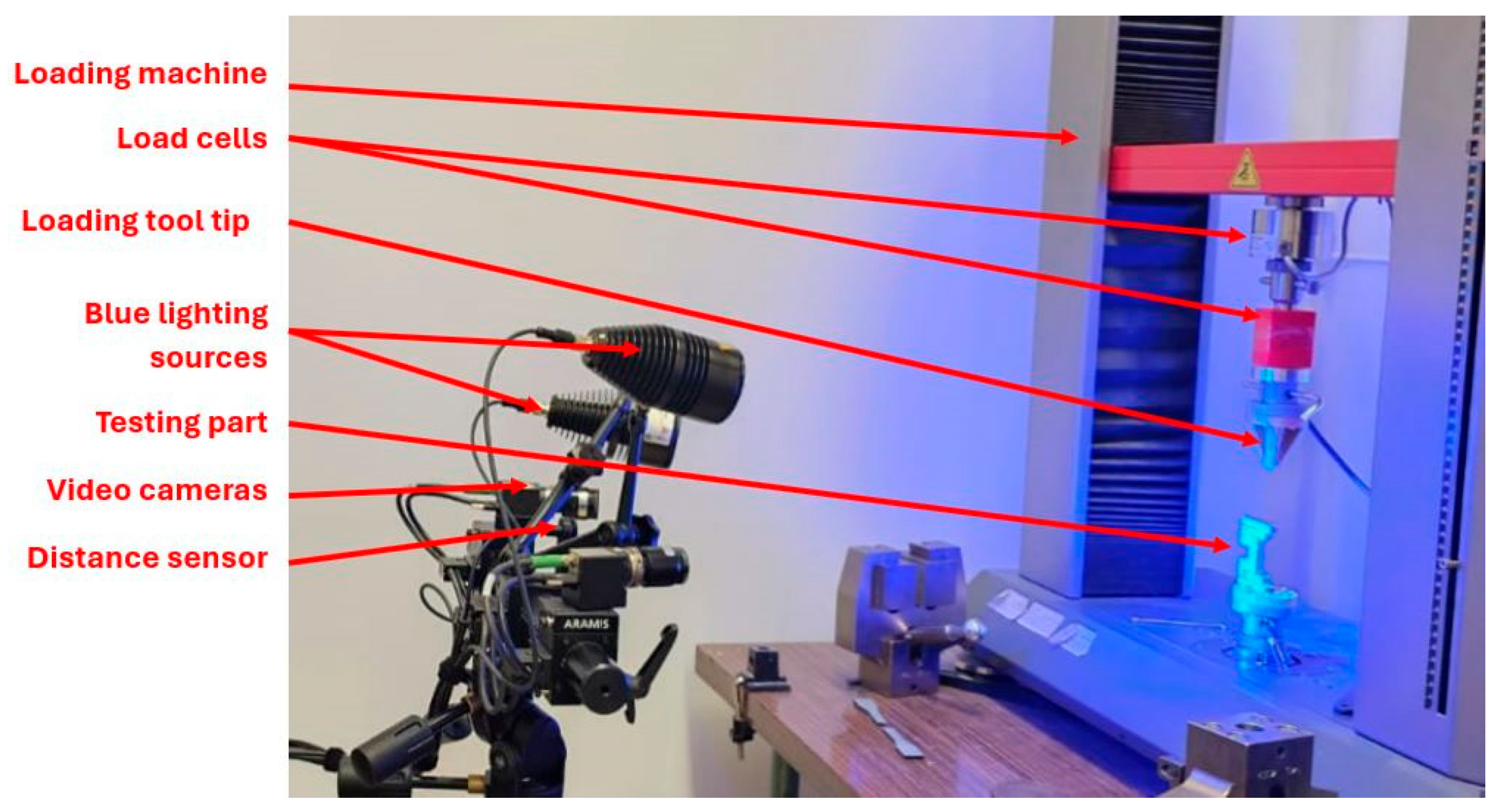
3.2. Setup for the Experimental Static Analysis
- (i)
- The setup of the 3D system requires two cameras that are positioned at different angles to capture stereoscopic images of the speckle pattern on the specimen. These cameras create a 3D reconstruction of the surface using triangulation.
- (ii)
- A precise calibration process using a known pattern, such as the checkerboard presented in Figure 11a. This phase is essential to determine the orientation of the camera and the spatial relationships. The calibration defines the transformation from 2D image coordinates to 3D world coordinates.
- (iii)
- Speckle pattern tracking. The specimen is coated with a random speckle pattern, as shown in Figure 11b. As the sample is deformed, the Aramis DIC Zeiss Correlate software tracks the movement of these speckles in both images. The displacement fields are calculated in 3D (i.e., along the coordinates X, Y, and Z).
- (iv)
- Calculus of the strain. The strain is derived from the gradients of the displacement field. In practice, because the DIC measures surface data, the Z-strain often refers to out-of-plane surface deformation gradients rather than through-thickness strain.
- (v)
- Data analysis with ZEISS Correlate, where one can visualize displacement and strain components, including out-of-plane (i.e., along the Z axis) deformations.
3.3. Comparison of the Experimental and FEA Results
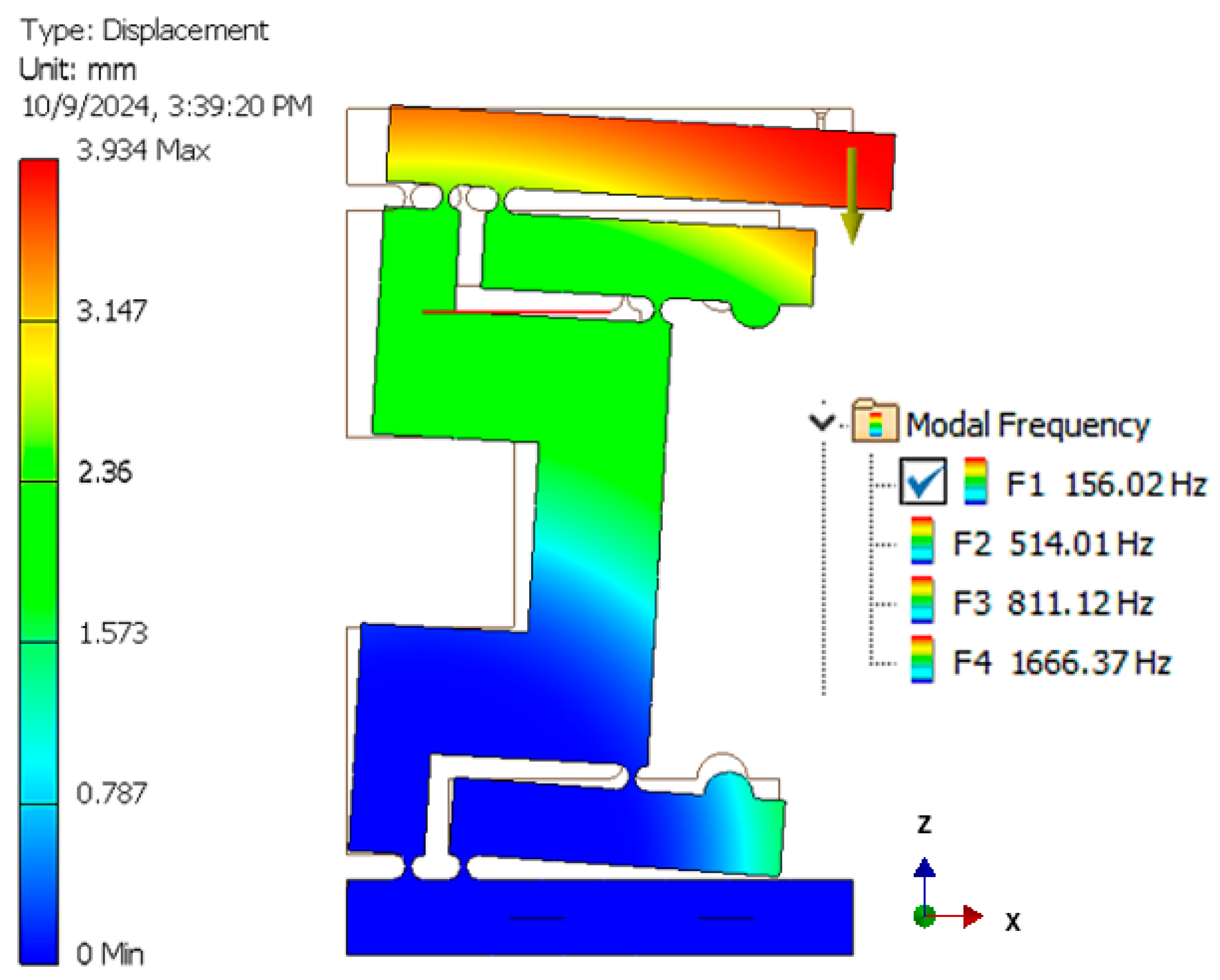
3.4. Preliminary Dynamic Simulations
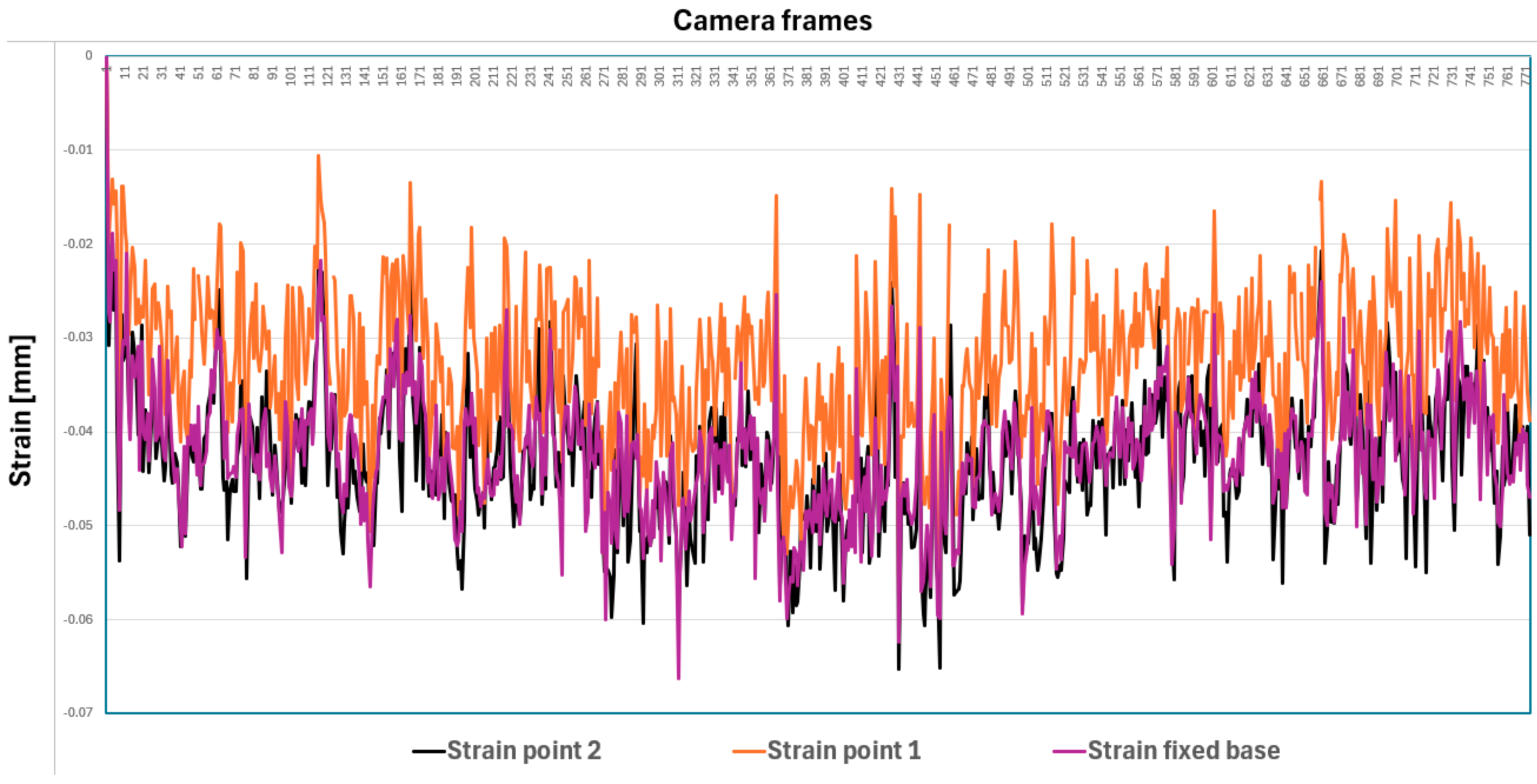
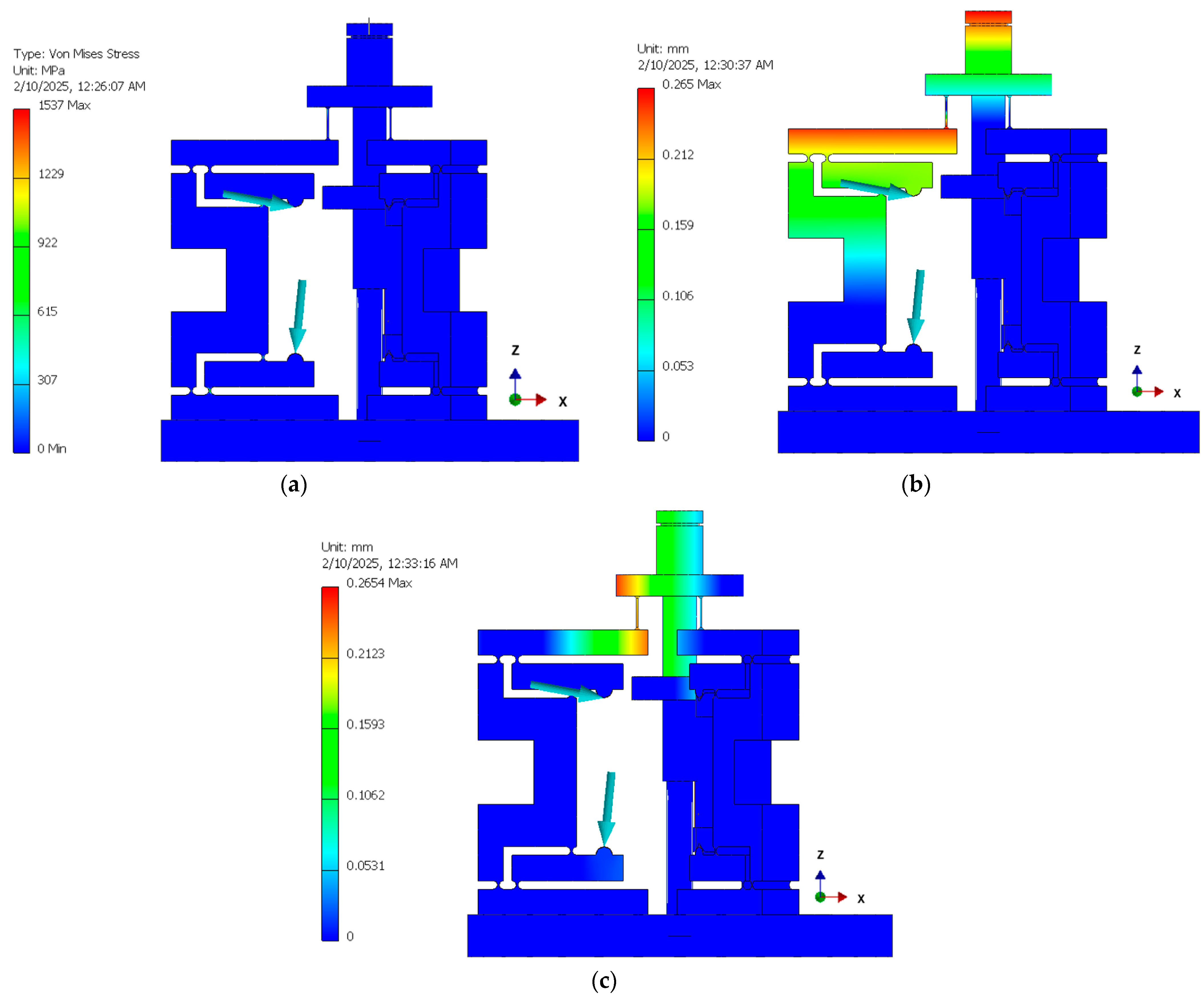
3.5. Mechanical Subassembly Testing
- Point 3 (upper arm tip) shows an X displacement of 0.159 mm and a Z displacement of −0.218 mm.
- Point 2 (middle arm) shows an X displacement of 0.145 mm and a Z displacement of −0.068 mm.
- Point 1 (lower arm) shows an X displacement of 0.035 mm and a Z displacement of −0.088 mm.
3.6. Three DOF FEA
- Passive piezoelectric actuators (that were not involved in the actuation) were replaced with solid steel blocks in order to simplify the model.
- The actuator responsible for the system displacement was removed, and previously determined dimensional constraints were applied to calculate the reaction forces at the corresponding points.
- The diode component was modeled as an aluminum block to represent its structural impact.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Bhatia, K.P.; Bain, P.; Bajaj, N.; Elble, R.J.; Hallett, M.; Louis, E.D.; Raethjen, J.; Stamelou, M.; Testa, C.M.; Deuschl, G.; et al. Consensus Statement on the Classification of Tremors. from the Task Force on Tremor of the International Parkinson and Movement Disorder Society. Mov. Disord. 2018, 33, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Bain, P.A. Combined Clinical and Neurophysiological Approach to the Study of Patients with Tremor. J. Neurol. Neurosurg. Psychiatry 1993, 56, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Ang, W.T.; Pradeep, P.K.; Riviere, C.N. Active Tremor Compensation in Microsurgery. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 3, pp. 2738–2741. [Google Scholar]
- Brown, W.J.; Buckland, E.L.; Izatt, J.A. Portable Optical Coherence Tomography (OCT) Devices and Related Systems. U.S. Patent Application 0081166, 2007. [Google Scholar]
- Erickson, S.J.; Godavarty, A. Hand-Held Based near-Infrared Optical Imaging Devices: A Review. Med. Eng. Phys. 2009, 31, 495–509. [Google Scholar] [CrossRef]
- Capitán-Vallvey, L.F.; Palma, A.J. Recent Developments in Handheld and Portable Optosensing—A Review. Anal. Chim. Acta 2011, 696, 27–46. [Google Scholar] [CrossRef]
- Demian, D.; Duma, V.-F.; Sinescu, C.; Negrutiu, M.L.; Cernat, R.; Topala, F.I.; Hutiu, G.; Bradu, A.; Podoleanu, A.G. Design and Testing of Prototype Handheld Scanning Probes for Optical Coherence Tomography. Proc. Inst. Mech. Eng. H 2014, 228, 743–753. [Google Scholar] [CrossRef]
- Monroy, G.L.; Won, J. Clinical Translation of Handheld Optical Coherence Tomography: Practical Considerations and Recent Advancements. J. Biomed. Opt. 2017, 22, 1–30. [Google Scholar] [CrossRef]
- Lu, C.D.; Kraus, M.F.; Potsaid, B.; Liu, J.J.; Choi, W.; Jayaraman, V.; Cable, A.E.; Hornegger, J.; Duker, J.S.; Fujimoto, J.G. Handheld Ultrahigh Speed Swept Source Optical Coherence Tomography Instrument Using a MEMS Scanning Mirror. Biomed. Opt. Express 2014, 5, 293. [Google Scholar] [CrossRef]
- Roizenblatt, M.; Edwards, T.; Gehlbach, P.L. Robot-Assisted Vitreoretinal Surgery: Current Perspectives. Robot. Surg. Res. Rev. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Ida, Y.; Sugita, N.; Ueta, T.; Tamaki, Y.; Tanimoto, K.; Mitsuishi, M. Microsurgical Robotic System for Vitreoretinal Surgery. Int. J. Comput. Assist. Radiol. Surg. 2012, 7, 27–34. [Google Scholar] [CrossRef]
- Rusch, M.; Hoffmann, G.; Wieker, H.; Bürger, M.; Kapahnke, S.; Berndt, R.; Rusch, R. Evaluation of the MMI Symani® Robotic Microsurgical System for Coronary-Bypass Anastomoses in a Cadaveric Porcine Model. J. Robot. Surg. 2024, 18, 168. [Google Scholar] [CrossRef]
- Kwoh, Y.S.; Hou, J.; Jonckheere, E.A.; Hayati, S.A. Robot with Improved Absolute Positioning Accuracy for CT Guided Stereotactic Brain Surgery. IEEE Trans. Biomed. Eng. 1988, 35, 153–160. [Google Scholar] [CrossRef]
- Taylor, R.; Jensen, P.; Whitcomb, L.; Barnes, A.; Kumar, R.; Stoianovici, D.; Gupta, P.; Wang, Z.; deJuan, E.; Kavoussi, L. A Steady-Hand Robotic System for Microsurgical Augmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI’99, Cambridge, UK, 19–22 September 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1031–1041. [Google Scholar] [CrossRef]
- Probst, P. A Review of the Role of Robotics in Surgery: To DaVinci and Beyond! Mo Med. 2023, 120, 389–396. [Google Scholar]
- Lanfranco, A.R.; Castellanos, A.E.; Desai, J.P.; Meyers, W.C. Robotic Surgery: A Current Perspective. Ann. Surg. 2004, 239, 14–21. [Google Scholar] [CrossRef]
- Veluvolu, K.C.; Ang, W.T. Estimation of Physiological Tremor from Accelerometers for Real-Time Applications. Sensors 2011, 11, 3020–3036. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, R.; MacLachlan, R.A.; Oh, M.Y.; Riviere, C.N. Positioning Accuracy of Neurosurgeons. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 206–209. [Google Scholar]
- Riviere, C.N.; Rader, R.S.; Khosla, P.K. Characteristics of Hand Motion of Eye Surgeons. In Proceedings of the 19th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 30 October–2 November 1997; Volume 4, pp. 1690–1693. [Google Scholar]
- Lin, Z.; Deng, A.; Hou, N.; Gao, L.; Zhi, X. Advances in Targeted Retinal Photocoagulation in the Treatment of Diabetic Retinopathy. Front. Endocrinol. 2023, 14, 1108394. [Google Scholar] [CrossRef]
- Reddy, S.V.; Husain, D. Panretinal Photocoagulation: A Review of Complications. Semin. Ophthalmol. 2018, 33, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Becker, B.C.; MacLachlan, R.A.; Lobes, L.A.; Riviere, C.N. Semiautomated Intraocular Laser Surgery Using Handheld Instruments. Lasers Surg. Med. 2010, 42, 264–273. [Google Scholar] [CrossRef]
- Channa, R.; Iordachita, I.; Handa, J.T. Robotic Eye Surgery. Retina 2017, 37, 1220–1228. [Google Scholar] [CrossRef]
- Olds, K.C.; Taylor, R.H. Steady Hand Micromanipulation Robot. U.S. Patent 8,911,429 B2, 2017. [Google Scholar]
- Becker, B.C.; Valdivieso, C.R.; Biswas, J.; Lobes, L.A.; Riviere, C.N. Active Guidance for Laser Retinal Surgery with a Handheld Instrument. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 5587–5590. [Google Scholar] [CrossRef]
- Riviere, C.N.; Khosla, P.K. Microscale Tracking of Surgical Instrument Motion. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI’99, Cambridge, UK, 19–22 September 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1080–1087. [Google Scholar]
- Routray, A.; MacLachlan, R.A.; Martel, J.N.; Riviere, C.N. Real-Time Incremental Estimation of Retinal Surface Using Laser Aiming Beam. In Proceedings of the 2019 International Symposium on Medical Robotics (ISMR), Atlanta, GA, USA, 3–5 April 2019; pp. 1–5. [Google Scholar]
- Verrelli, D.I.; Qian, Y.; Wilson, M.K.; Wood, J.; Savage, C. Intraoperative Tremor in Surgeons and Trainees. Interact. Cardiovasc. Thorac. Surg. 2016, 23, 410–415. [Google Scholar] [CrossRef]
- Csókay, A. A Novel Microsurgical Technique Reduces Hand Tremor in the Course of Lateral Suboccipital Approach. Surg. Neurol. 2007, 67, 392–393. [Google Scholar] [CrossRef]
- Nica, D.F.; Gabor, A.G.; Duma, V.-F.; Tudericiu, V.G.; Tudor, A.; Sinescu, C. Sinus Lift and Implant Insertion on 3D Printed Polymeric Maxillary Models: Ex vivo training for in vivo surgical procedures. J. Clin. Med. 2021, 10, 4718. [Google Scholar] [CrossRef]
- Singh, G.; Jie, W.W.J.; Sun, M.T.; Casson, R.; Selva, D.; Chan, W. Overcoming the Impact of Physiologic Tremors in Ophthalmology. Graefes Arch. Clin. Exp. Ophthalmol. 2022, 260, 3723–3736. [Google Scholar] [CrossRef]
- Lora-Millan, J.S.; Delgado-Oleas, G.; Benito-León, J.; Rocon, E. A Review on Wearable Technologies for Tremor Suppression. Front. Neurol. 2021, 12, 700600. [Google Scholar] [CrossRef]
- Kim, J.; Wichmann, T.; Inan, O.T.; Deweerth, S.P. A Wearable System for Attenuating Essential Tremor Based on Peripheral Nerve Stimulation. IEEE J. Transl. Eng. Health Med. 2020, 8, 2000111. [Google Scholar] [CrossRef]
- Huen, D.; Liu, J.; Lo, B. An Integrated Wearable Robot for Tremor Suppression with Context Aware Sensing. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; pp. 312–317. [Google Scholar]
- Tan, U.-X.; Latt, W.T.; Shee, C.Y.; Ang, W.T. Design and Development of a Low-Cost Flexure-Based Hand-Held Mechanism for Micromanipulation. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4350–4355. [Google Scholar]
- Zhao, S.; Aye, Y.N.; Shee, C.Y.; Chen, I.-M.; Ang, W.T. A Compact 3-DOF Compliant Serial Mechanism for Trajectory Tracking with Flexures Made by Rapid Prototyping. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4475–4480. [Google Scholar]
- Yang, S.; MacLachlan, R.A.; Riviere, C.N. Manipulator Design and Operation of a Six-Degree-of-Freedom Handheld Tremor-Canceling Microsurgical Instrument. IEEE/ASME Trans. Mechatron. 2015, 20, 761–772. [Google Scholar] [CrossRef]
- MacLachlan, R.A.; Becker, B.C.; Tabarés, J.C.; Podnar, G.W.; Lobes, L.A.; Riviere, C.N. Micron: An Actively Stabilized Handheld Tool for Microsurgery. IEEE Trans. Robot. Publ. IEEE Robot. Autom. Soc. 2012, 28, 195–212. [Google Scholar] [CrossRef]
- Song, C.; Gehlbach, P.L.; Kang, J.U. Active Tremor Cancellation by a “Smart” Handheld Vitreoretinal Microsurgical Tool Using Swept Source Optical Coherence Tomography. Opt. Express 2012, 20, 23414–23421. [Google Scholar] [CrossRef] [PubMed]
- Riviere, C.N.; Rader, R.S.; Thakor, N.V. Adaptive Canceling of Physiological Tremor for Improved Precision in Microsurgery. IEEE Trans. Biomed. Eng. 1998, 45, 839–846. [Google Scholar]
- Yang, S.; MacLachlan, R.A.; Martel, J.N.; Lobes, L.A.; Riviere, C.N. Comparative Evaluation of Handheld Robot-Aided Intraocular Laser Surgery. IEEE Trans. Robot. 2016, 32, 246–251. [Google Scholar] [CrossRef]
- Iordachita, I.I.; de Smet, M.D.; Naus, G.; Mitsuishi, M.; Riviere, C.N. Robotic Assistance for Intraocular Microsurgery: Challenges and Perspectives. Proc. IEEE Inst. Electr. Electron. Eng. 2022, 110, 893–908. [Google Scholar] [CrossRef]
- Riviere, C.N.; Ang, W.T.; Khosla, P.K. Toward Active Tremor Canceling in Handheld Microsurgical Instruments. IEEE Trans. Robot. Autom. 2003, 19, 793–800. [Google Scholar] [CrossRef]
- Comeaga, C.D.; Nita, E.I.; Gramescu, B. Tremor Orientation and Compensation System in Laser Medical Equipment—Part 1. In Proceedings of the 2021 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25–27 March 2021; pp. 1–6. [Google Scholar]
- Comeaga, C.D.; Nita, E.I.; Coanda, P. Tremor Orientation and Compensation System in Laser Medical Equipment—Part II. In Proceedings of the 2021 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25–27 March 2021; pp. 1–6. [Google Scholar]
- Nita, E.I.; Coanda, P.; Comeaga, D.C. Laser Surgical Devices with Optical Solution for Damping Physiological Tremor. In Proceedings of the SPIE of the Advances in 3OM: Opto-Mechatronics, Opto-Mechanics, and Optical Metrology, Timisoara, Romania, 13–16 December 2021; p. 52. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: Hoboken, NJ, USA, 2001; ISBN 978-0-471-38478-6. [Google Scholar]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges; CRC Press: Boca Raton, FL, USA, 2003; ISBN 978-0-8493-1367-7. [Google Scholar]
- Farhadi, D.; Tolou, N.; Herder, J. A Review on Compliant Joints and Rigid-Body Constant Velocity Universal Joints Toward the Design of Compliant Homokinetic Couplings. J. Mech. Des. 2015, 137, 032301. [Google Scholar] [CrossRef]


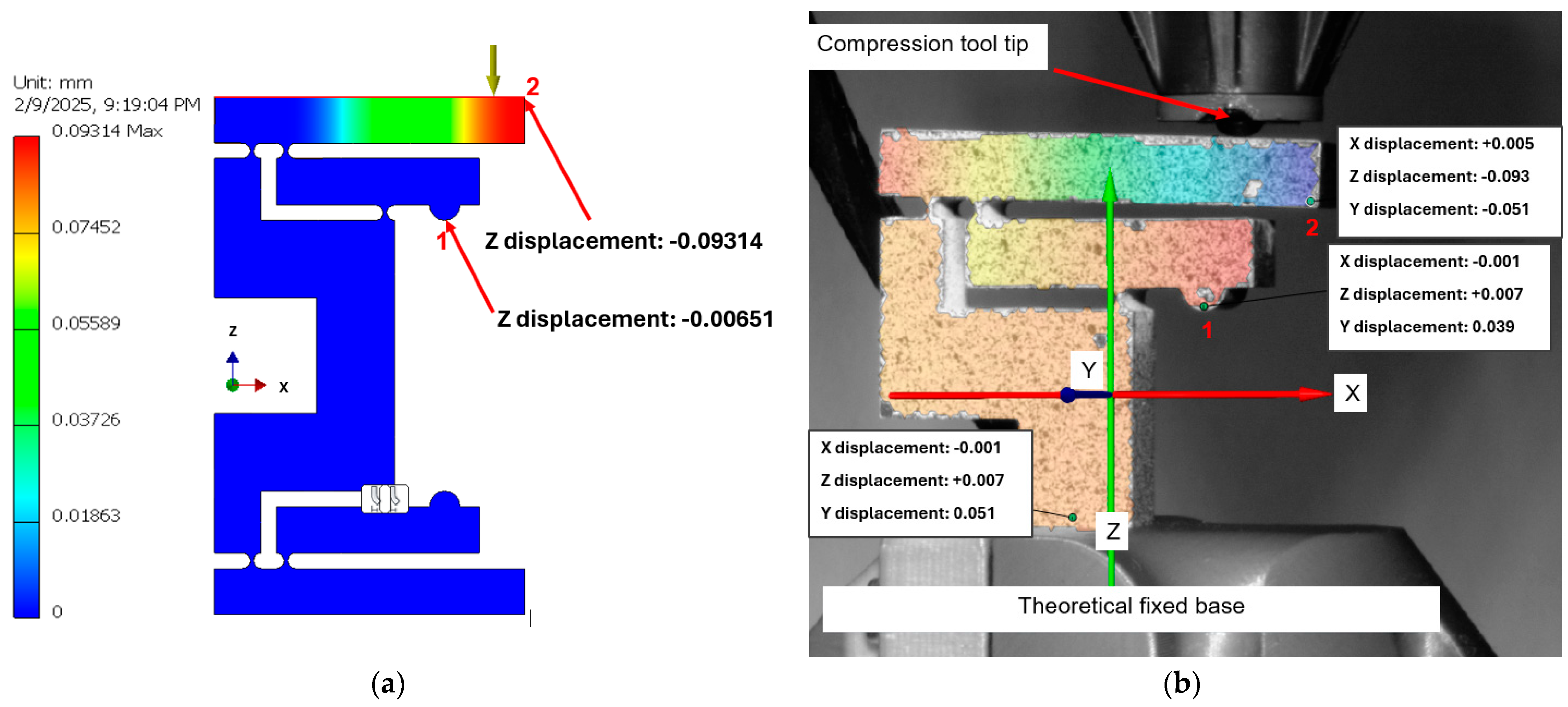


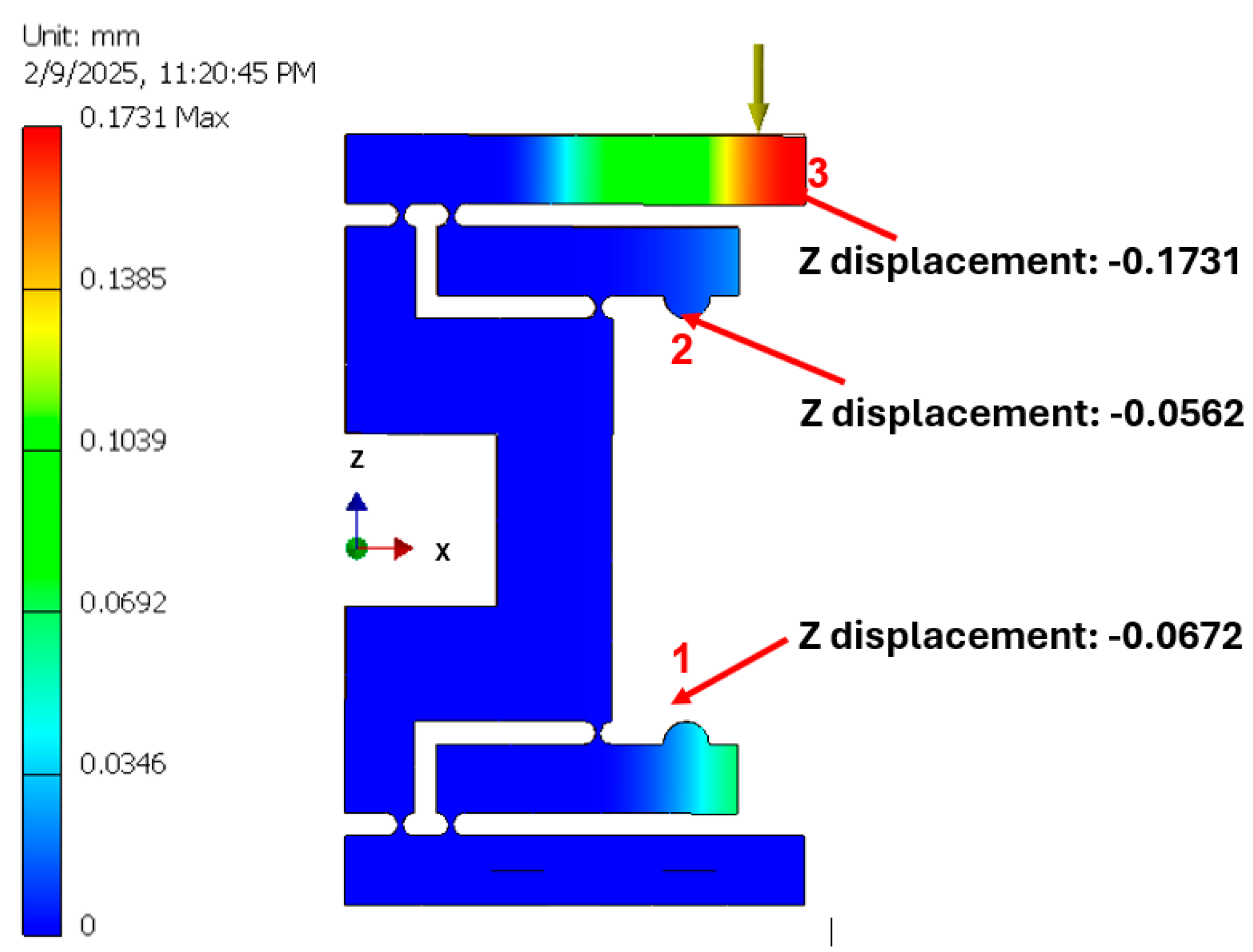


| Test No. | Measured Points | FEA Displacement [mm] | Absolute Experimental Displacement [mm] | Error [%] | Pass/Fail |
|---|---|---|---|---|---|
| 1 | Point 1 (Z axis) | 0.0065 | 0.007 | −7.52% | Pass |
| Point 2 (Z axis) | 0.0931 | 0.091 | 0.15% | Pass | |
| 2 | Point 1 (Z axis) | 0.0672 | 0.048 | 22.78% | Fail |
| Point 2 (Z axis) | 0.0562 | 0.035 | −32.35% | Fail | |
| Point 3 (Z axis) | 0.1731 | 0.193 | 11.49% | Fail | |
| 3 | Point 1 (Z axis) | 0.0672 | 0.063 | 6.25% | Pass |
| Point 2 (Z axis) | 0.0562 | 0.053 | 5.69% | Pass | |
| Point 3 (Z axis) | 0.1731 | 0.163 | 5.83% | Pass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niță, E.I.; Comeagă, D.C.; Apostol, D.A.; Duma, V.-F. Development of a Laser Surgical Device with Vibration Compensation: Mechanical Design and Validation of Its Compliant Mechanism. Appl. Sci. 2025, 15, 3686. https://doi.org/10.3390/app15073686
Niță EI, Comeagă DC, Apostol DA, Duma V-F. Development of a Laser Surgical Device with Vibration Compensation: Mechanical Design and Validation of Its Compliant Mechanism. Applied Sciences. 2025; 15(7):3686. https://doi.org/10.3390/app15073686
Chicago/Turabian StyleNiță, Emil Ionuț, Daniel C. Comeagă, Dragos A. Apostol, and Virgil-Florin Duma. 2025. "Development of a Laser Surgical Device with Vibration Compensation: Mechanical Design and Validation of Its Compliant Mechanism" Applied Sciences 15, no. 7: 3686. https://doi.org/10.3390/app15073686
APA StyleNiță, E. I., Comeagă, D. C., Apostol, D. A., & Duma, V.-F. (2025). Development of a Laser Surgical Device with Vibration Compensation: Mechanical Design and Validation of Its Compliant Mechanism. Applied Sciences, 15(7), 3686. https://doi.org/10.3390/app15073686








