Low-Frequency Sound Absorption in Air Pipelines and Water-Filled Pipelines Based on Metamaterials
Abstract
1. Introduction
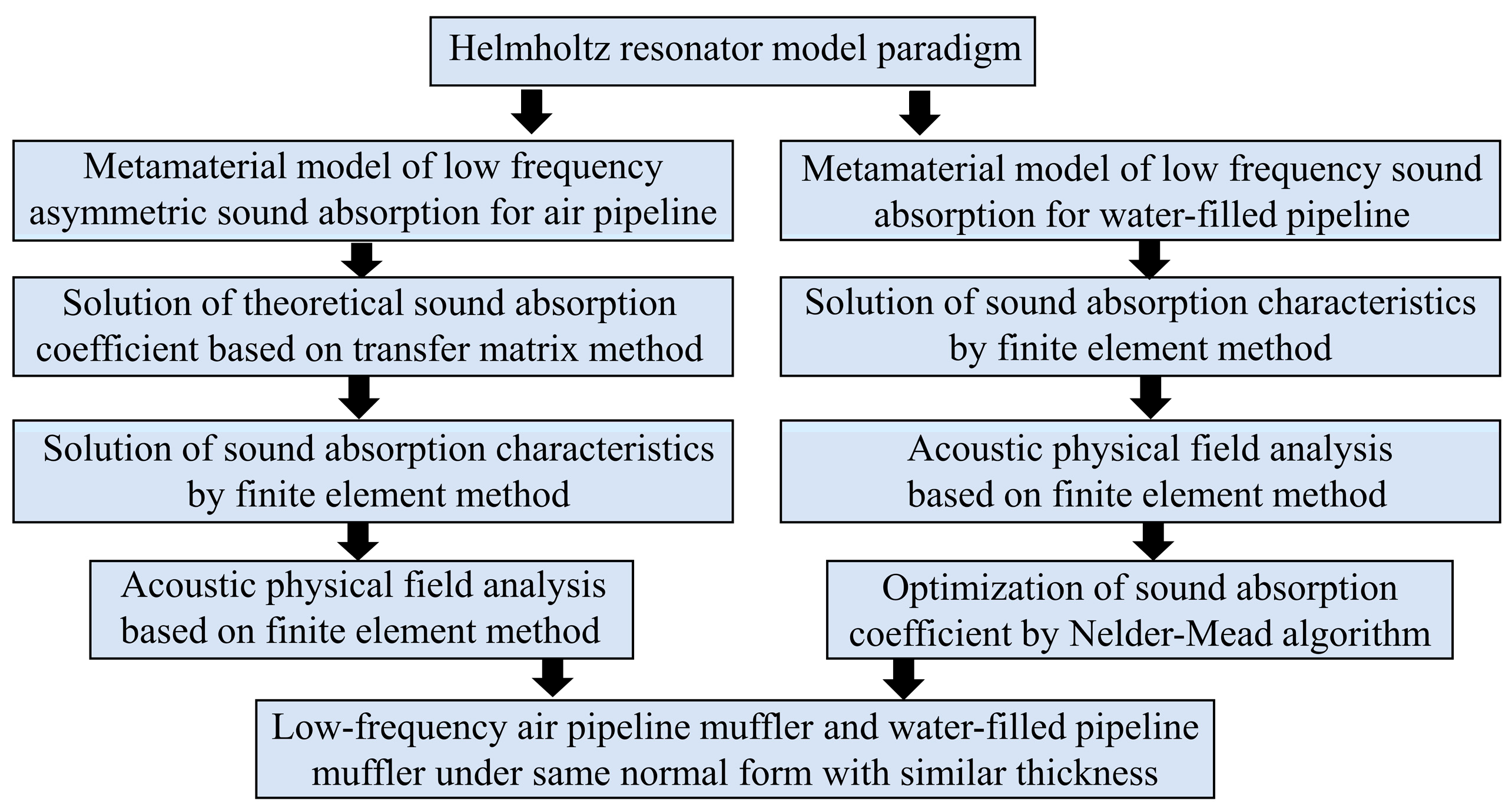
2. Design Paradigm and Theoretical Method
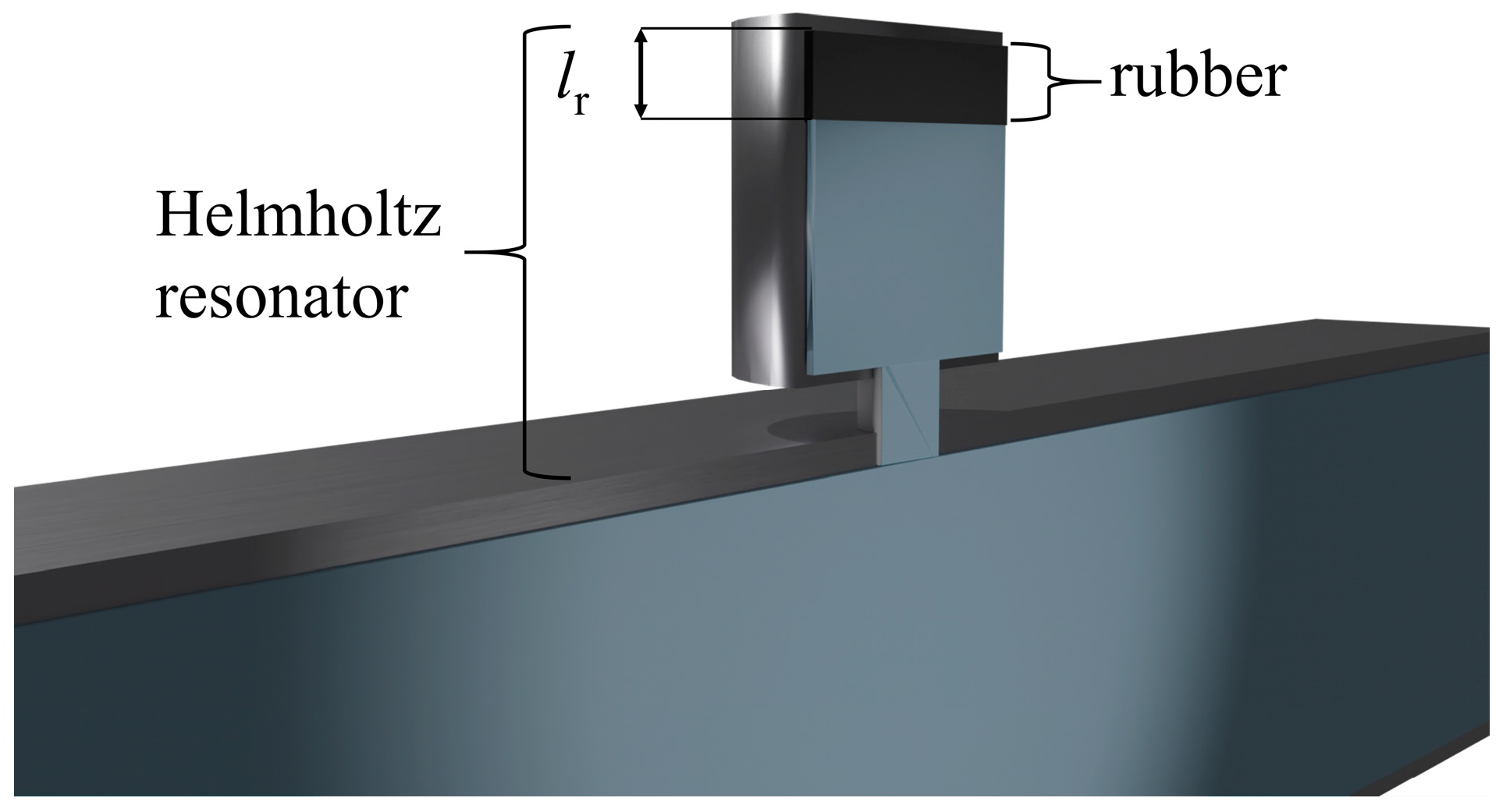
2.1. Structure of the Low-Frequency Asymmetric Absorption Metamaterials for Air Pipeline
2.2. Theory of the Asymmetric Absorption Metamaterials
2.3. Structure of the Low-Frequency Composite Absorption Metamaterials for Water-Filled Pipeline
2.4. Construction of Metamaterial Finite Element Model and Nelder–Mead Optimization Algorithm
3. Results
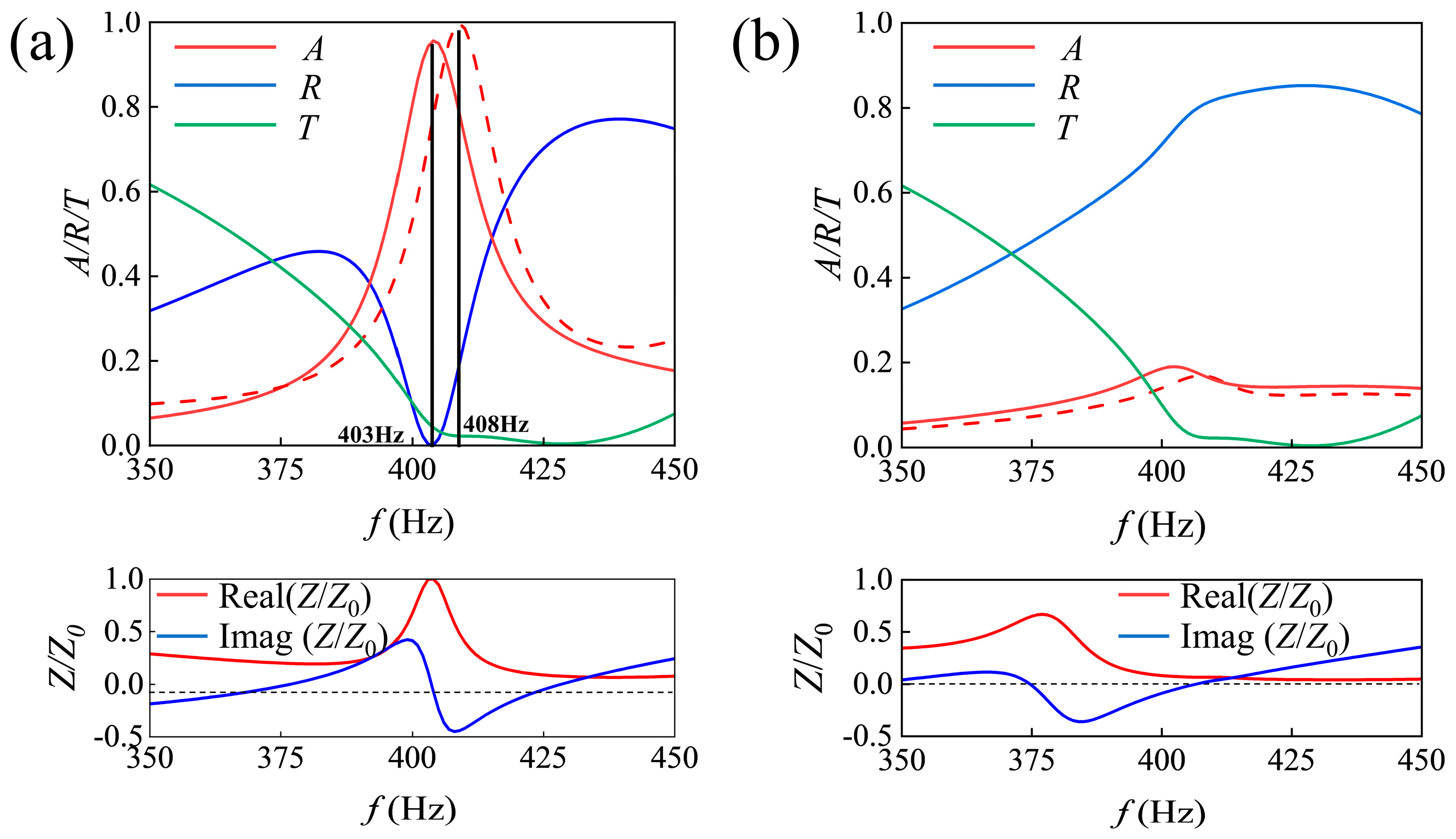
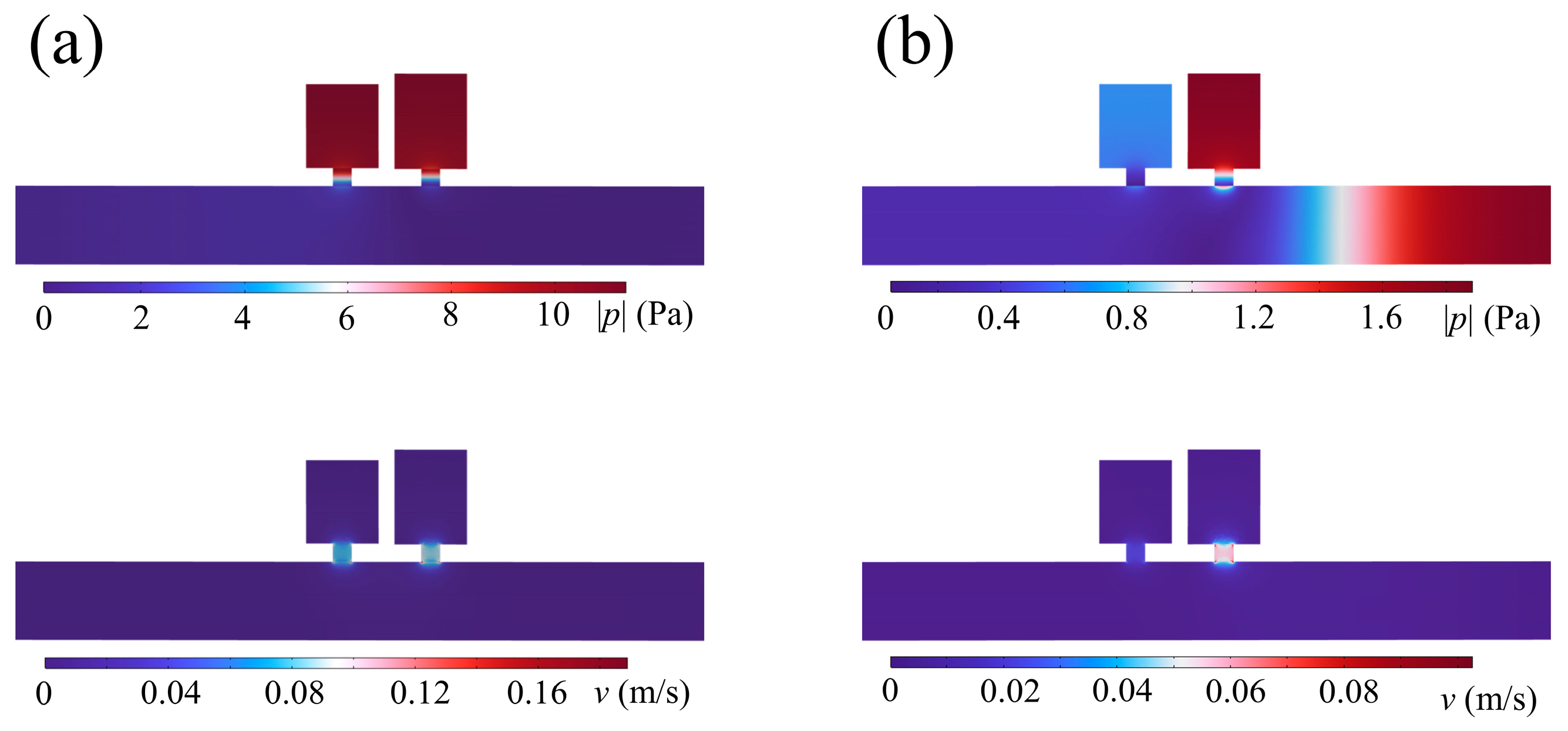
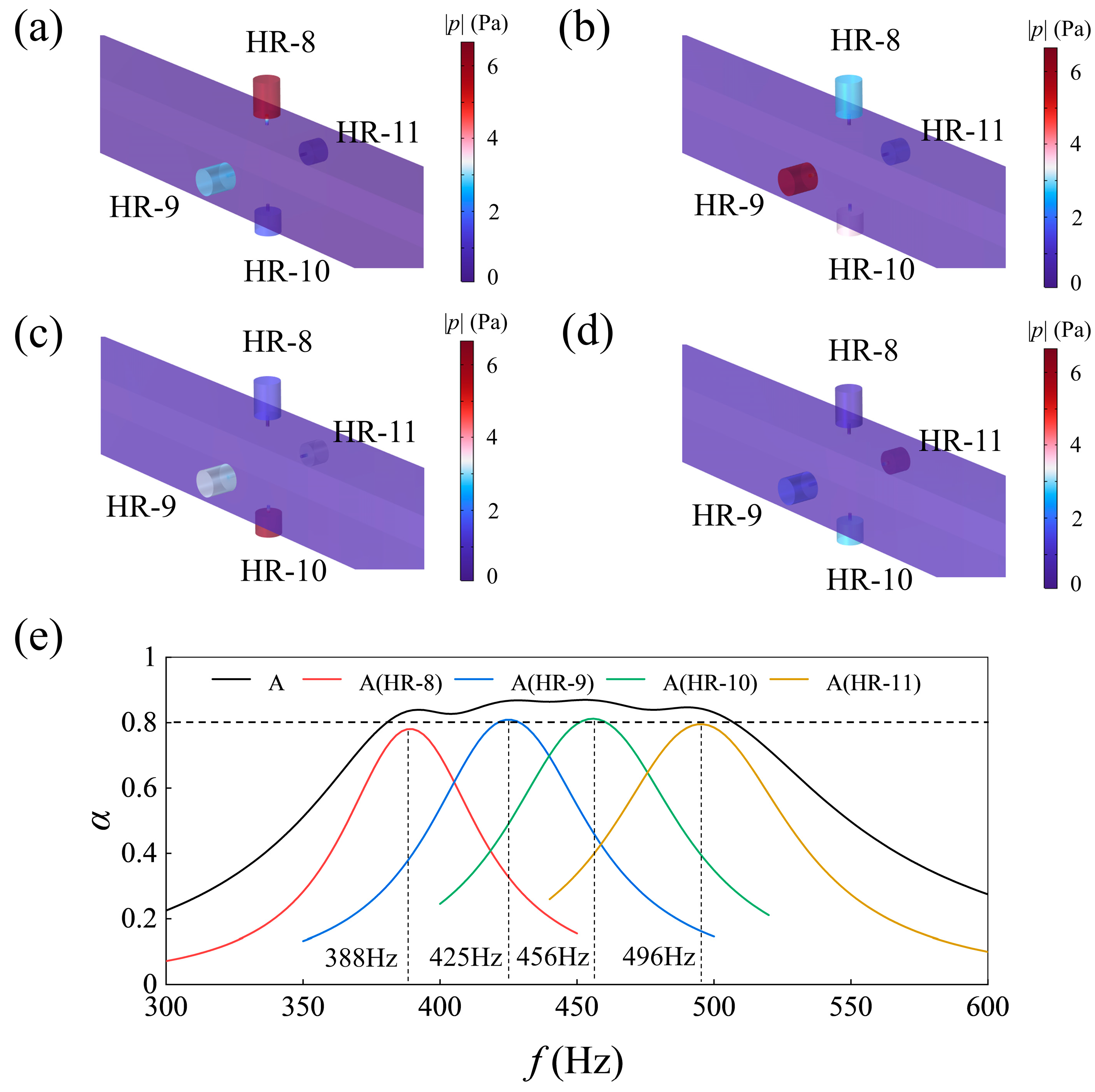
3.1. Asymmetric Sound Absorption in Air Piplines
3.2. Low-Frequency and Broadband Composite Absorbing Metamaterial in Water-Filled Piplines
3.3. Final Closure of the Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, D.L.; Du, C.Y.; Shen, H.J.; Liu, J.W.; Wen, J.H. An analysis of structural-acoustic coupling band gaps in a fluid-filled periodic pipe. Chin. Phys. Lett. 2017, 34, 076202. [Google Scholar] [CrossRef]
- Catron, F.; Fagerlund, A. Noise generation and propagation effects on piping system components. Noise Control Eng. J. 2009, 57, 570–577. [Google Scholar] [CrossRef]
- Celik, S.; Nsofor, E.C. Studies on the flow-induced noise at the evaporator of a refrigerating system. Appl. Therm. Eng. 2011, 31, 2485–2493. [Google Scholar]
- Ye, L.; Wang, X.; Wu, W.; Ma, H.; Li, N. Study on acoustic characteristics of air pipeline with guide vane and bionic guide vane. Ocean Eng. 2023, 284, 115197. [Google Scholar]
- Gong, F.L.; Li, Q.; Sun, X.M.; Kong, Y.; Liu, S. Theoretical and experimental study of a two-dimensional circular stealth acoustic lens. Phys. Scr. 2024, 99, 115945. [Google Scholar]
- Zheng, B.; Liu, Z.; Liu, B.; Chen, X.; An, D.; Cao, G.; Liu, S. High-Throughput Superresolved Focal Imaging Based on a Phase-Modulated Acoustic Superoscillatory Lens. Phys. Rev. Appl. 2022, 18, 014048. [Google Scholar] [CrossRef]
- Kim, J.W.; Hwang, G.; Lee, S.J.; Kim, S.H.; Wang, S. Three-dimensional acoustic metamaterial Luneburg lenses for broadband and wide-angle underwater ultrasound imaging. Mech. Syst. Signal Process 2022, 179, 109374. [Google Scholar]
- Zaremanesh, M.; Bahrami, A. Two-dimensional honeycomb lattice structure for underwater acoustic cloaking using pentamode materials. Phys. Scr. 2023, 99, 015946. [Google Scholar] [CrossRef]
- Raza, M.; Ahsan, M.; Alonazi, W.B.; Naqvi, S.A.; Braaten, B. Design and analysis of arbitrary shaped bifunctional cloaks for multifunctional material composites. Phys. Scr. 2023, 98, 115020. [Google Scholar]
- Wang, Y.; Ge, Y.; Zhou, Z.; Chen, Z.D. Transmissive invisibility cloak using phase gradient metasurfaces. Phys. Scr. 2024, 99, 085527. [Google Scholar]
- Yang, R.; Zhang, X.; Wang, G. A hybrid acoustic cloaking based on binary splitting metasurfaces and near-zero-index metamaterials. Appl. Phys. Lett. 2022, 120, 021603. [Google Scholar]
- Xue, Y.; Zhao, J.; Zhang, X.; Sessler, G.M.; Kupnik, M. Acoustic energy harvesting with irradiated cross-linked polypropylene piezoelectret films. Phys. Scr. 2019, 94, 095002. [Google Scholar]
- Ma, K.J.; Tan, T.; Liu, F.R.; Zhao, L.C.; Liao, W.H.; Zhang, W.M. Acoustic energy harvesting enhanced by locally resonant metamaterials. Smart Mater. Struct. 2020, 29, 075025. [Google Scholar]
- Ma, K.; Tan, T.; Yan, Z.; Liu, F.; Liao, W.H.; Zhang, W. Metamaterial and Helmholtz coupled resonator for high-density acoustic energy harvesting. Nano Energy 2021, 82, 105693. [Google Scholar]
- Bok, E.; Park, J.J.; Choi, H.; Han, C.K.; Wright, O.B.; Lee, S.H. Metasurface for water-to-air sound transmission. Phys. Rev. Lett. 2018, 120, 044302. [Google Scholar]
- Huang, Z.; Zhao, Z.; Zhao, S.; Cai, X.; Zhang, Y.; Cai, Z.; Yang, J. Lotus metasurface for wide-angle intermediate-frequency water–air acoustic transmission. ACS Appl. Mater. Interfaces 2021, 13, 53242–53251. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.T.; Zhang, S.C.; Zhu, T.; Tian, Y.Z.; Wang, Y.F.; Wang, Y.S. Hybrid metasurfaces for perfect transmission and customized manipulation of sound across water–air interface. Adv. Sci. 2023, 10, 2207181. [Google Scholar]
- Liu, J.; Li, Z.; Liang, B.; Cheng, J.C.; Alù, A. Remote Water-to-Air Eavesdropping with a Phase-Engineered Impedance Matching Metasurface. Adv. Mater. 2023, 35, 2301799. [Google Scholar]
- Zhou, P.; Jia, H.; Bi, Y.; Yang, Y.; Yang, Y.; Zhang, P.; Yang, J. Water–air acoustic communication based on broadband impedance matching. Appl. Phys. Lett. 2023, 123, 191701. [Google Scholar]
- Ma, G.; Yang, M.; Xiao, S.; Yang, Z.; Sheng, P. Acoustic metasurface with hybrid resonances. Nat. Mater. 2014, 13, 873–878. [Google Scholar]
- Duan, M.; Yu, C.; Xu, Z.; Xin, F.; Lu, T. Acoustic impedance regulation of Helmholtz resonators for perfect sound absorption via roughened embedded necks. Appl. Phys. Lett. 2020, 117, 151904. [Google Scholar] [CrossRef]
- Dannemann, M.; Kucher, M.; Kunze, E.; Modler, N.; Knobloch, K.; Enghardt, L.; Sarradj, E.; Höschler, K. Experimental Study of Advanced Helmholtz Resonator Liners with Increased Acoustic Performance by Utilising Material Damping Effects. Appl. Sci. 2018, 8, 1923. [Google Scholar] [CrossRef]
- Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 2019, 145, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, N.M.; Stavroulakis, G.E. FEM Investigation of a Multi-Neck Helmholtz Resonator. Appl. Sci. 2023, 13, 10610. [Google Scholar] [CrossRef]
- Qu, S.; Gao, N.; Tinel, A.; Morvan, B.; Romero-García, V.; Groby, J.P.; Sheng, P. Underwater metamaterial absorber with impedance-matched composite. Sci. Adv. 2022, 8, eabm4206. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.Q.; Liu, S.L.; Yu, S.Y.; Lu, M.H.; Zhu, J.; Chen, Y.F. Broadband gradient impedance matching using an acoustic metamaterial for ultrasonic transducers. Sci. Rep. 2017, 7, 42863. [Google Scholar] [CrossRef]
- Gan, Z.; Mo, Y.; Fan, H.; Zhu, Y.; Zhang, H. Ultra-broadband underwater meta-absorber with gradient impedance-matched composite material. Smart. Mater. Struct. 2024, 33, 115018. [Google Scholar] [CrossRef]
- Wu, B.; Chen, B.; Ma, S.; Zhang, D.; Zu, H.R. An Ultra-Broadband and Highly-Efficient Metamaterial Absorber with Stand-Up Gradient Impedance Graphene Films. Materials 2023, 16, 1617. [Google Scholar] [CrossRef]
- Mo, J.; Peng, Z.; Wang, X. Achieving Enhanced Sound Insulation through Micromembranes-Type Acoustic Metamaterials. Appl. Sci. 2022, 12, 1950. [Google Scholar] [CrossRef]
- Pan, L.; Martellotta, F. A Parametric Study of the Acoustic Performance of Resonant Absorbers Made of Micro-perforated Membranes and Perforated Panels. Appl. Sci. 2020, 10, 1581. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Wang, Y.; Wang, W.; Zhang, B.; Gai, X. Membrane acoustic metamaterial absorbers with magnetic negative stiffness. J. Acoust. Soc. Am. 2017, 141, 840–846. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhang, X.; Fang, Y.; Jiang, Z. A compact low-frequency sound-absorbing metasurface constructed by resonator with embedded spiral neck. Appl. Sci. 2020, 117, 221902. [Google Scholar] [CrossRef]
- Kong, D.Q.; Huang, S.B.; Li, D.; Cai, C.; Zhou, Z.; Liu, B.T.; Cao, G.X.; Chen, X.F.; Li, Y.; Liu, S.C. Low-frequency multi-order acoustic absorber based on spiral metasurface. J. Acoust. Soc. Am. 2021, 151, 12–18. [Google Scholar] [CrossRef]
- Almeida, G.D.N.; Vergara, E.F.; Barbosa, L.R.; Brum, R. Low-frequency sound absorption of a metamaterial with symmetrical-coiled-up spaces. Appl. Acoust. 2021, 172, 107593. [Google Scholar] [CrossRef]
- Hong, Z.; Wu, F.; Bai, C.; An, K.; Wang, J.; Yang, B. Two-port network spiral type asymmetric absorption system. Appl. Acoust. 2022, 192, 108730. [Google Scholar] [CrossRef]
- Ma, P.S.; Kim, H.S.; Lee, S.H.; Seo, Y.H. Quasi-perfect absorption of broadband low-frequency sound in a two-port system based on a micro-perforated panel resonator. Appl. Acoust. 2022, 186, 108449. [Google Scholar] [CrossRef]
- Meng, D.; Li, L.; Wu, Z. Helmholtz resonator-based acoustic metamaterials enabling broadband asymmetric sound absorption and ventilation. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1242–1250. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, X.; Yang, M.; Xiao, S.; Yang, Z. Hybrid membrane resonators for multiple frequency asymmetric absorption and reflection in large waveguide. Appl. Phys. Lett. 2017, 110, 021901. [Google Scholar] [CrossRef]
- Qi, H.B.; Fan, S.W.; Jiang, M.; Tang, X.L.; Wang, Y.S. Low-frequency ultra-broadband ventilated muffler based on a resonance-labyrinthine metamaterial. Extrem. Mech. Lett. 2024, 67, 102120. [Google Scholar] [CrossRef]
- Liu, B.; Yang, L. Transmission of low-frequency acoustic waves in seawater piping systems with periodical and adjustable helmholtz resonator. J. Mar. Sci. Eng. 2017, 5, 56. [Google Scholar] [CrossRef]
- Long, H.; Cheng, Y.; Liu, X. Asymmetric absorber with multiband and broadband for low-frequency sound. Appl. Phys. Lett. 2017, 111, 143502. [Google Scholar]


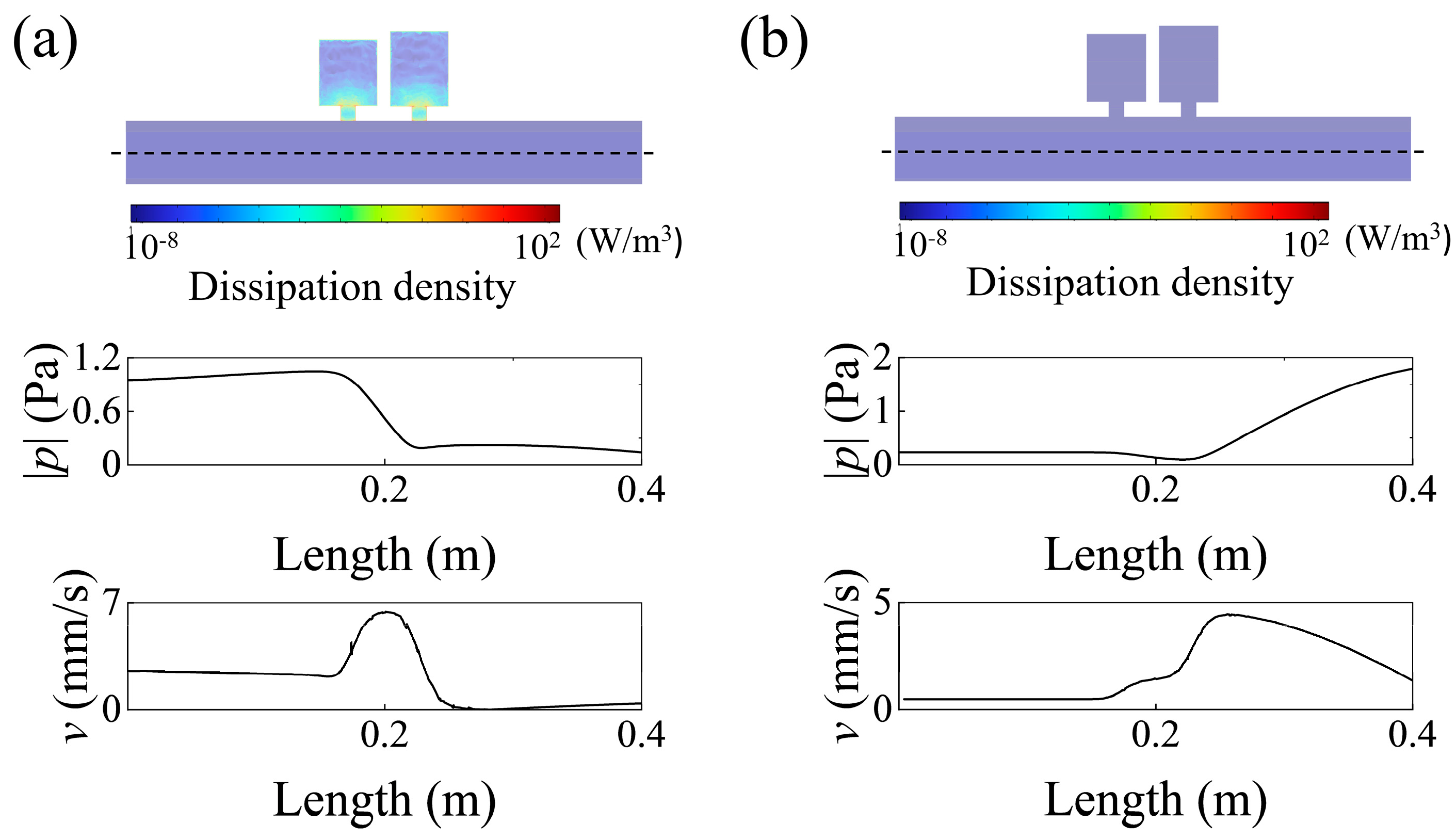
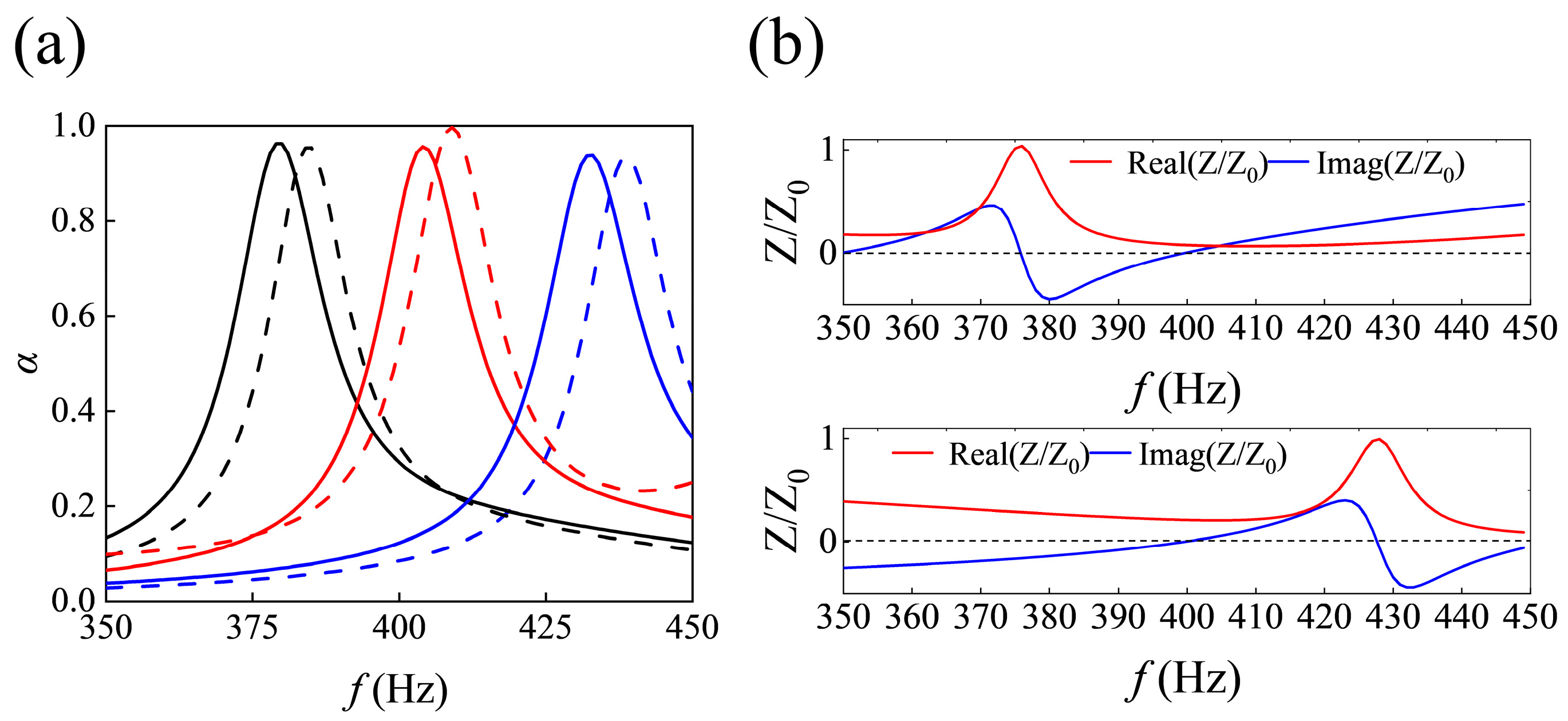
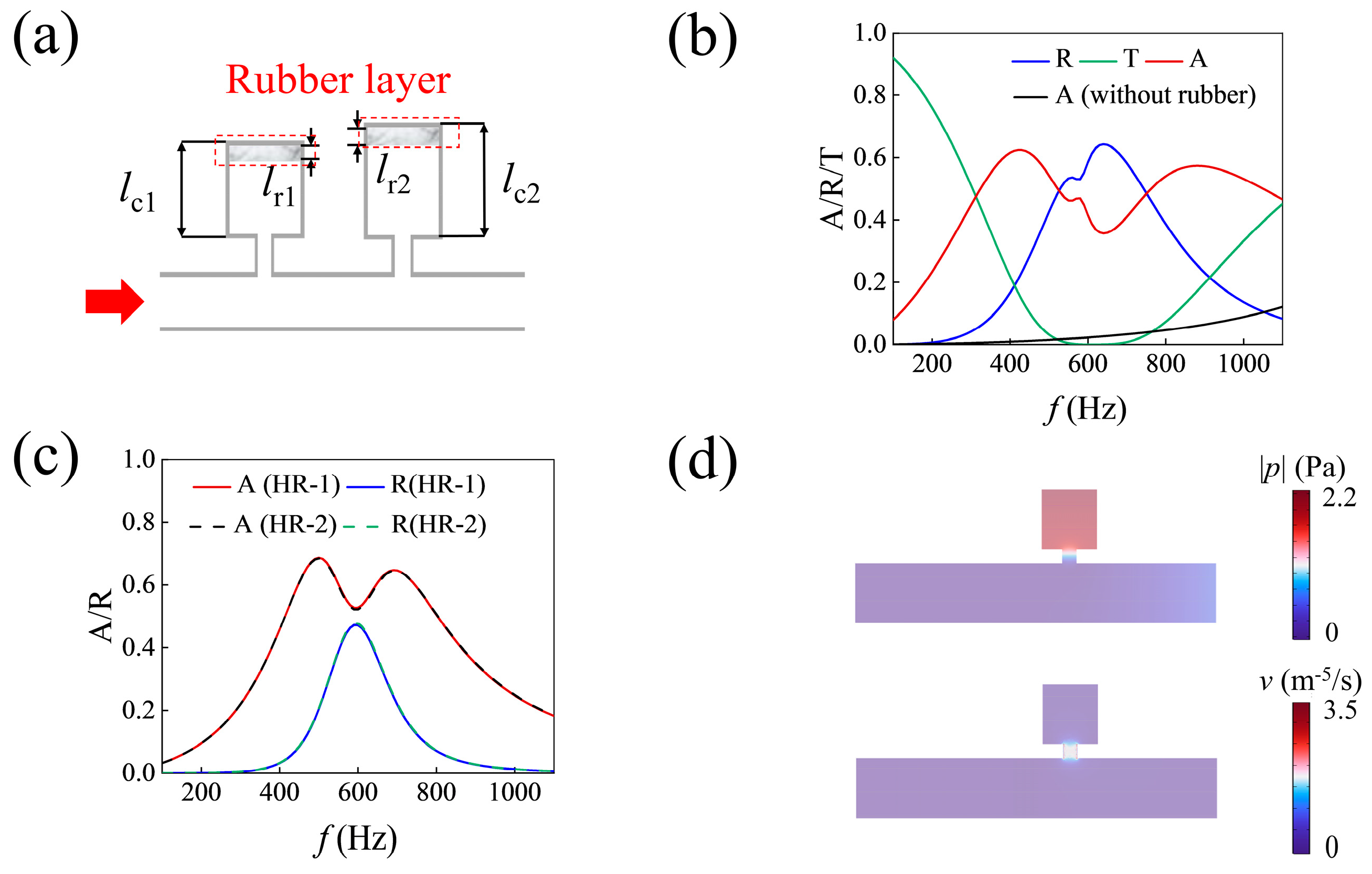
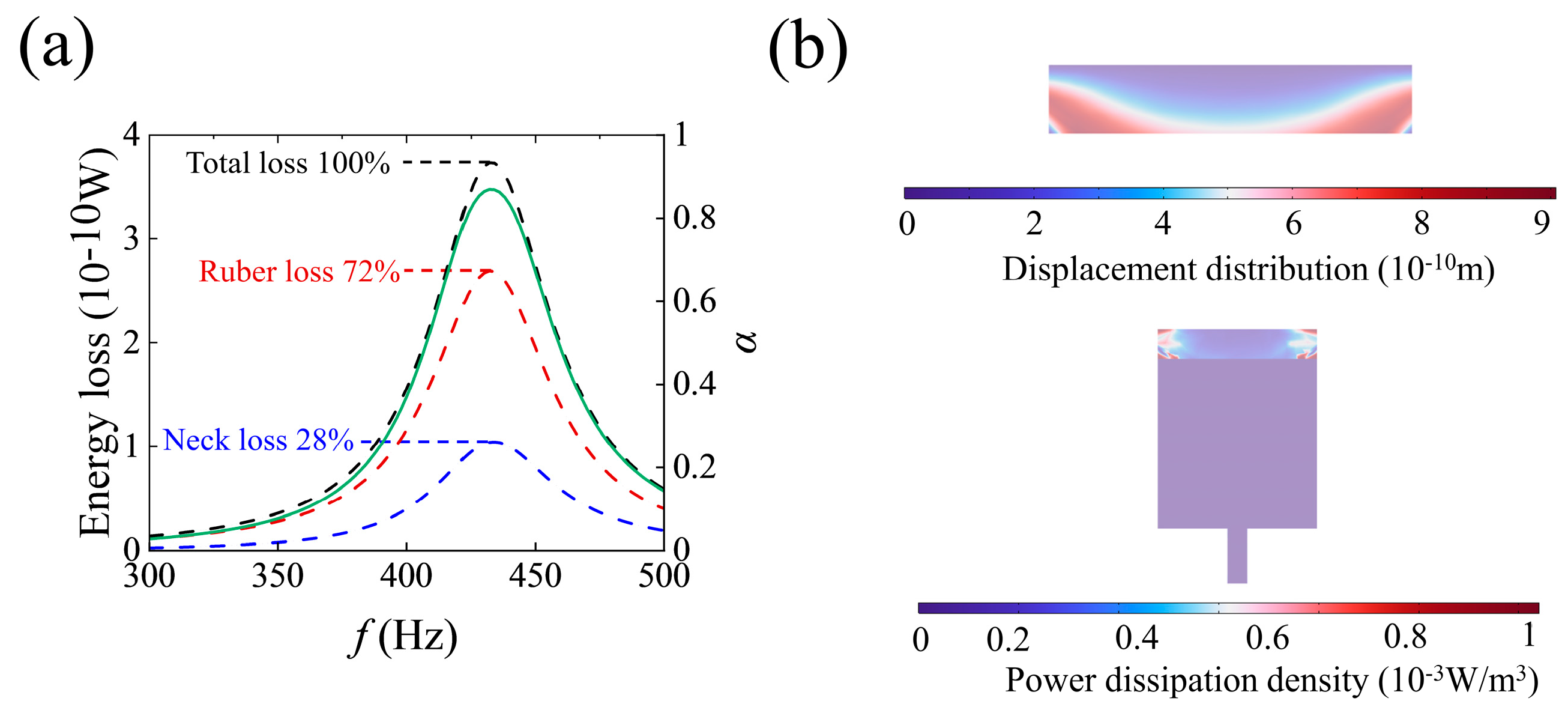
| lni (mm) | ri (mm) | lci (mm) | Di (mm) | |
|---|---|---|---|---|
| HR-1 | 11.5 | 6 | 53 | 46 |
| HR-2 | 11 | 6 | 60 | 46 |
| HR-3 | 12 | 6 | 58 | 46 |
| HR-4 | 11 | 6 | 68 | 46 |
| HR-5 | 11 | 6 | 48 | 46 |
| HR-6 | 10 | 6 | 55 | 46 |
| HR-7 | 5.5 | 1 | 20 | 16 |
| HR-8 | 6.5 | 1 | 25 | 16 |
| HR-9 | 5 | 1 | 20 | 16.5 |
| HR-10 | 4.5 | 1 | 16 | 16 |
| HR-11 | 4.5 | 1 | 14 | 14.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Liu, Z.; Li, A.; Zheng, B.; Liu, S. Low-Frequency Sound Absorption in Air Pipelines and Water-Filled Pipelines Based on Metamaterials. Appl. Sci. 2025, 15, 3820. https://doi.org/10.3390/app15073820
Liu B, Liu Z, Li A, Zheng B, Liu S. Low-Frequency Sound Absorption in Air Pipelines and Water-Filled Pipelines Based on Metamaterials. Applied Sciences. 2025; 15(7):3820. https://doi.org/10.3390/app15073820
Chicago/Turabian StyleLiu, Botao, Zigeng Liu, Ang Li, Bo Zheng, and Shengchun Liu. 2025. "Low-Frequency Sound Absorption in Air Pipelines and Water-Filled Pipelines Based on Metamaterials" Applied Sciences 15, no. 7: 3820. https://doi.org/10.3390/app15073820
APA StyleLiu, B., Liu, Z., Li, A., Zheng, B., & Liu, S. (2025). Low-Frequency Sound Absorption in Air Pipelines and Water-Filled Pipelines Based on Metamaterials. Applied Sciences, 15(7), 3820. https://doi.org/10.3390/app15073820





