Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
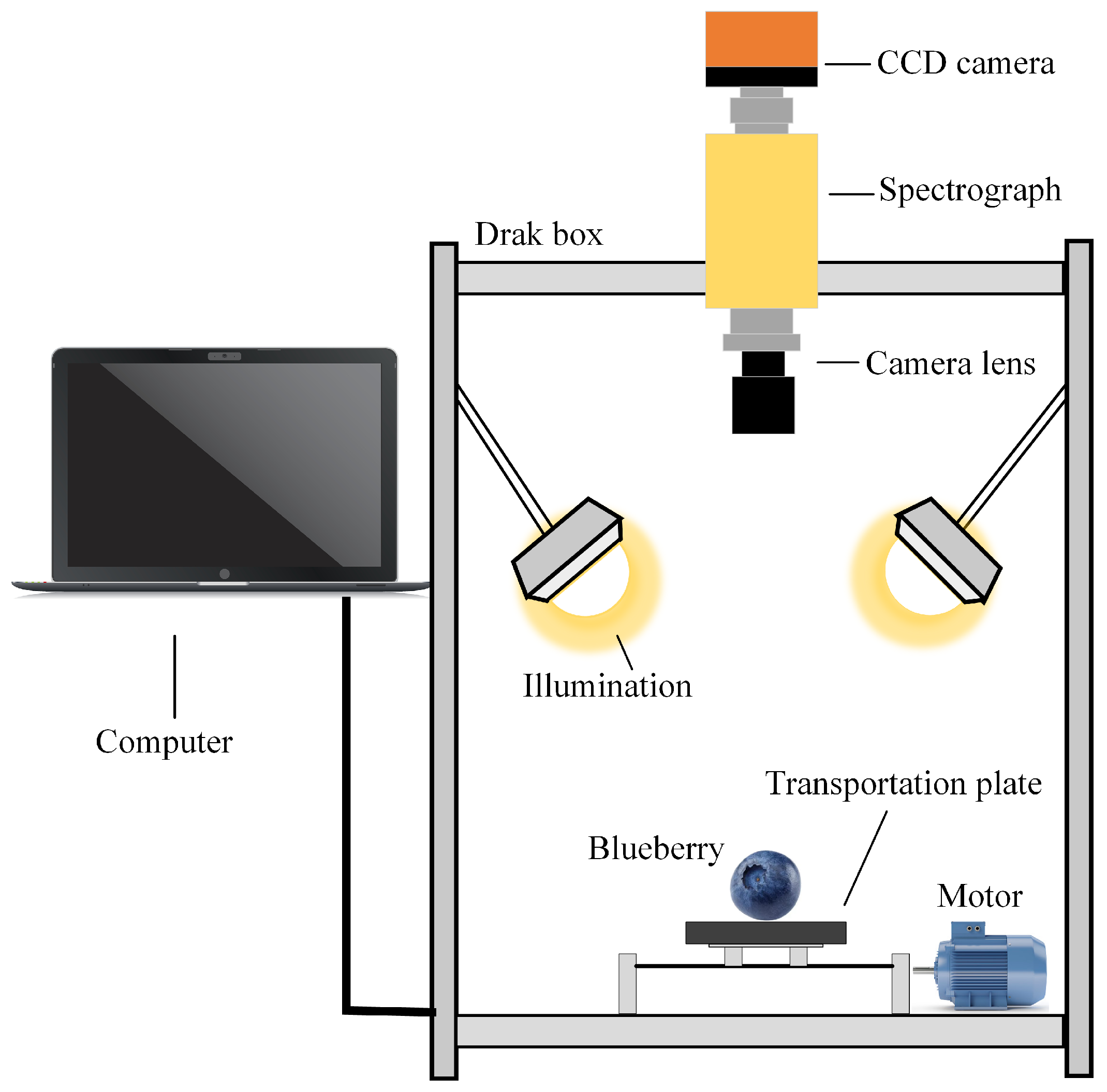
2.2. Hyperspectral Image Acquisition
2.3. Soluble Solids Content Measurement
2.4. Spectral Preprocessing Methods
2.5. Principal Component Analysis Algorithm
2.6. Feature Wavebands Selection Algorithms
2.6.1. Uninformative Variables Elimination
2.6.2. Successive Projections Algorithm
2.7. Partial Least Squares Regression Modeling Algorithm
2.8. Model Performance Evaluation
3. Results
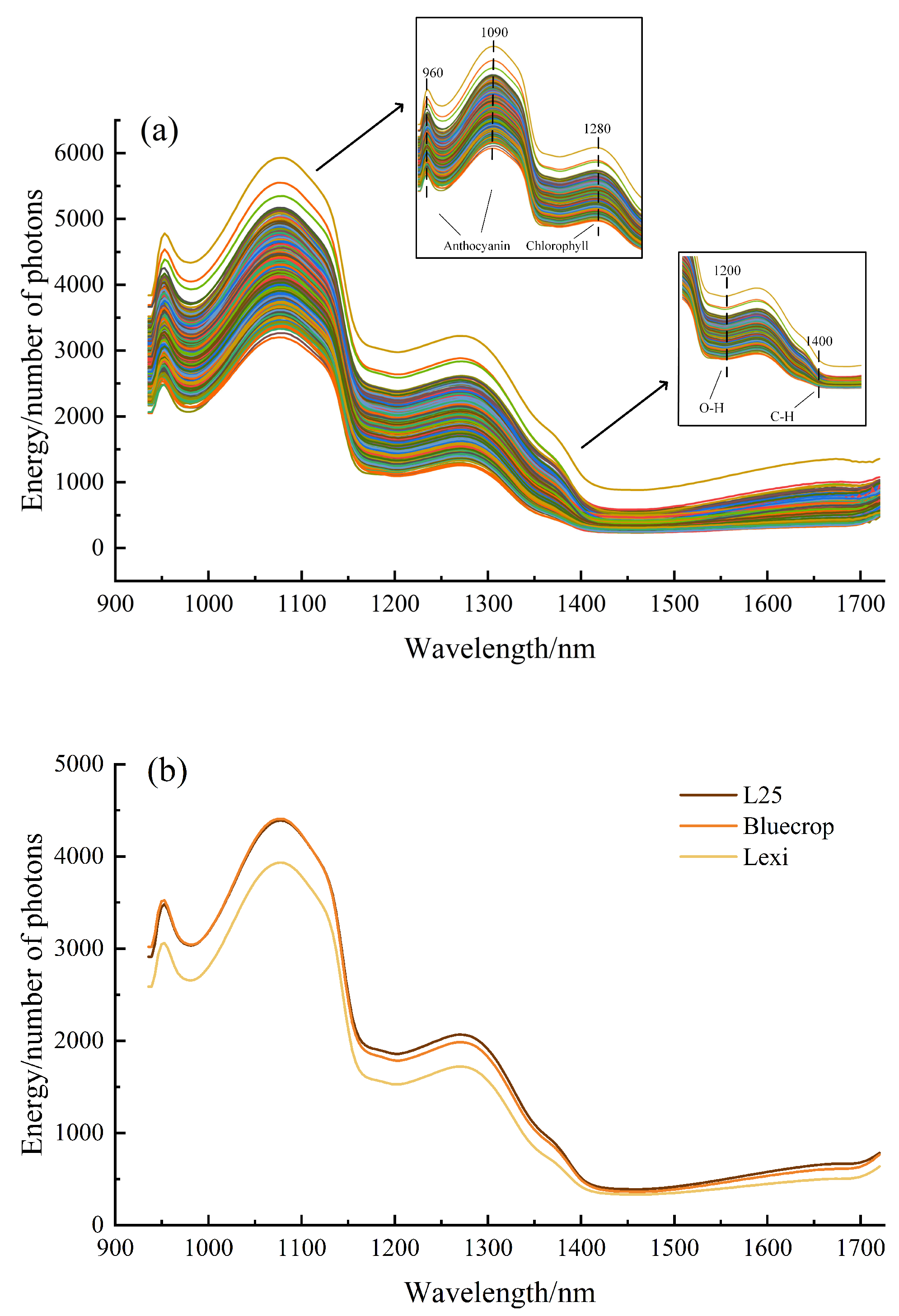
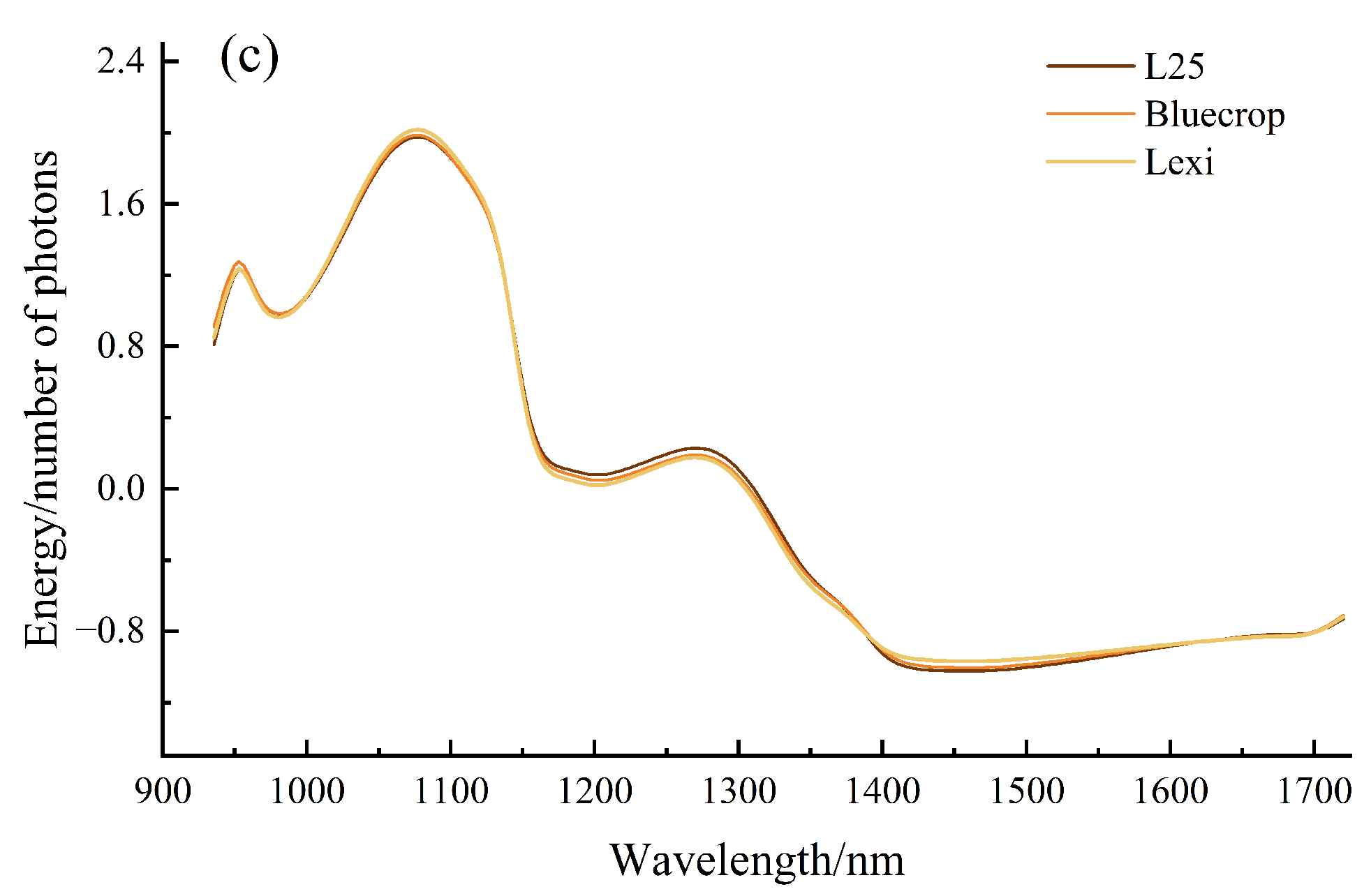
3.1. Spectral Analysis
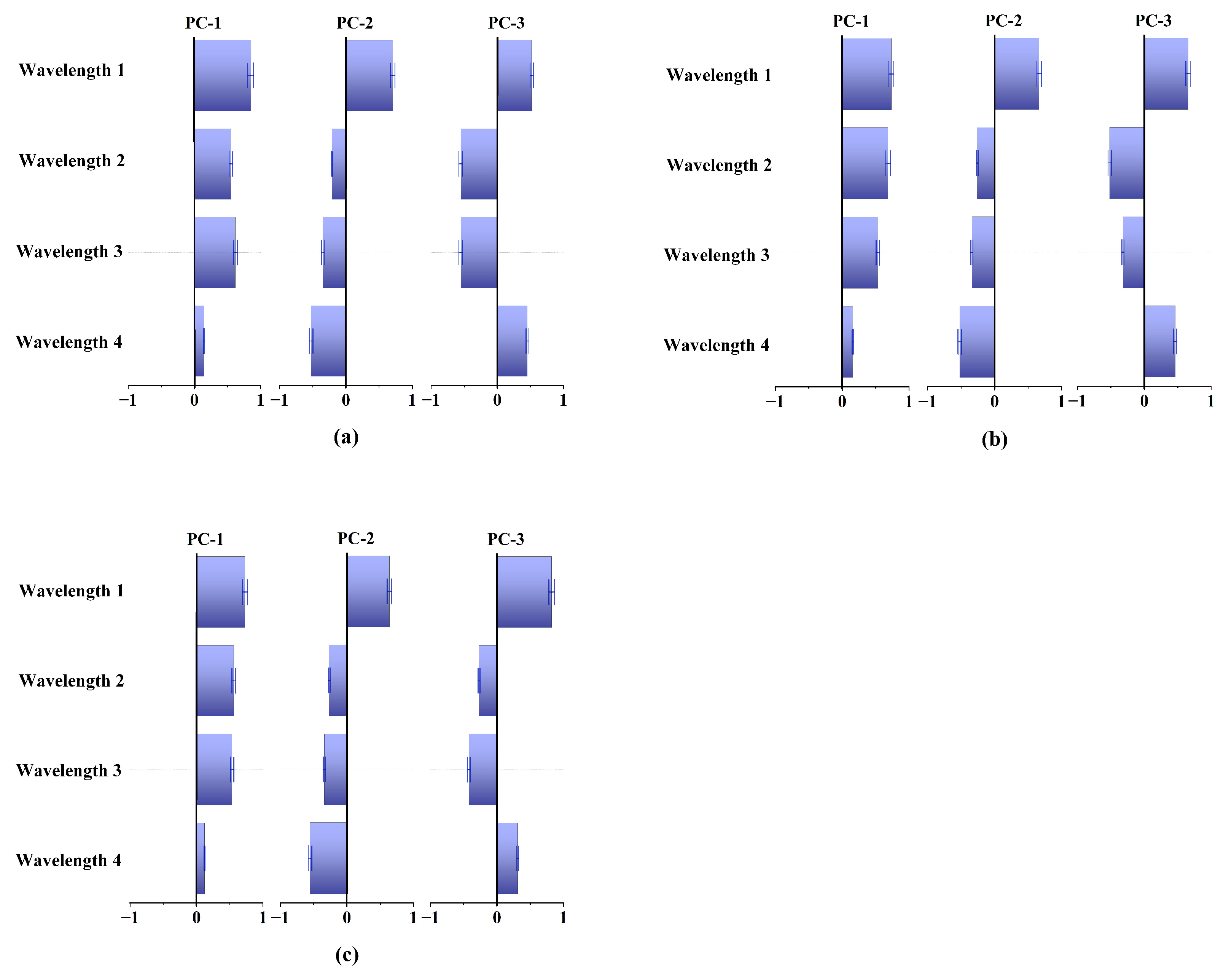
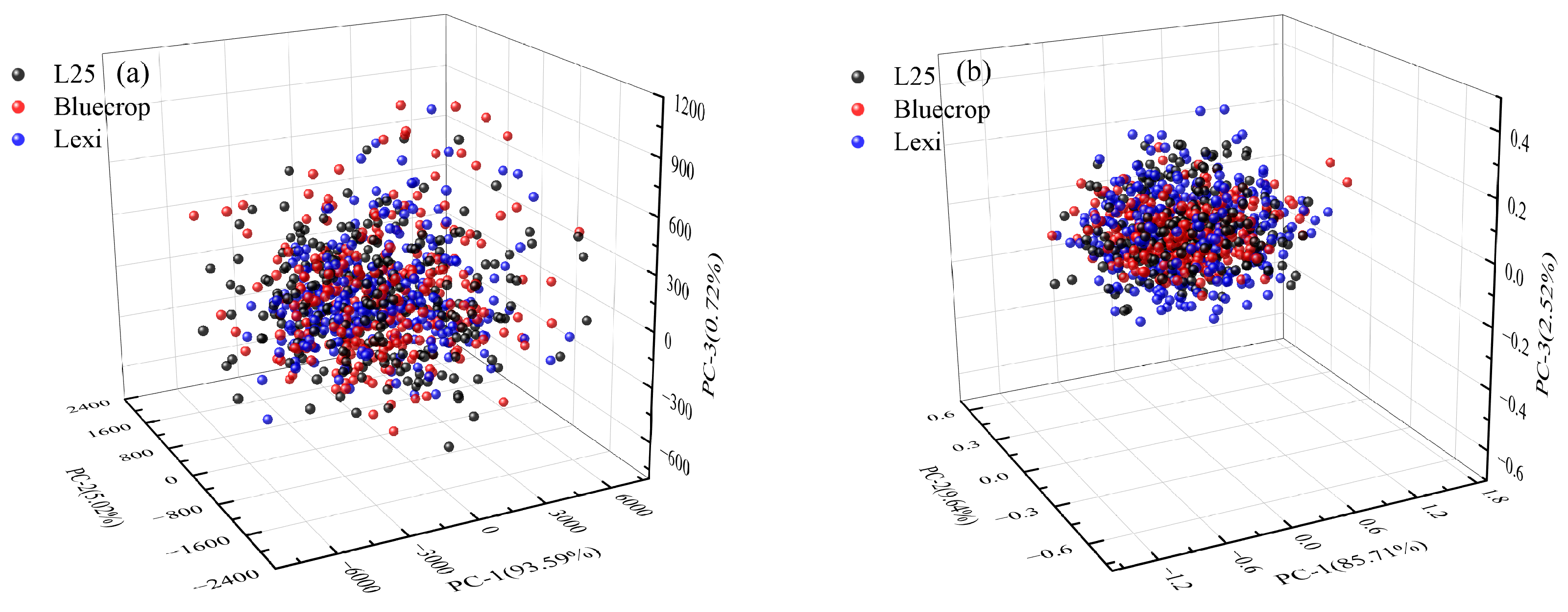
3.2. Principal Component Analysis
3.3. Outlier Elimination
3.4. Dataset Split
3.5. A Universal Prediction Model for SSC of Multiple Blueberry Varieties
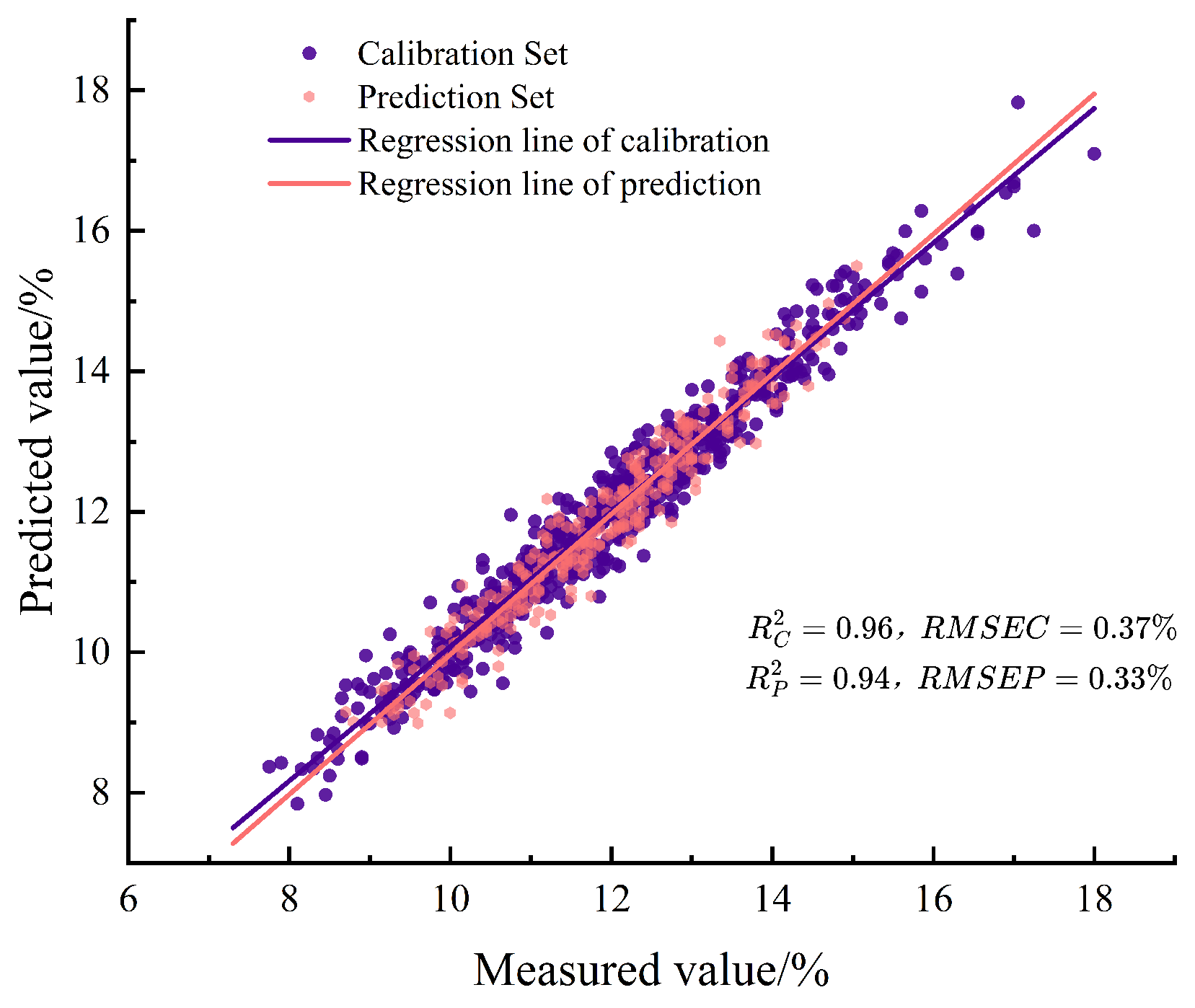
3.5.1. PLSR Model Based on Full-Wavelength Spectra with Different Pretreatments
3.5.2. PLSR Model Based on UVE Algorithm
3.6. Simplified Model
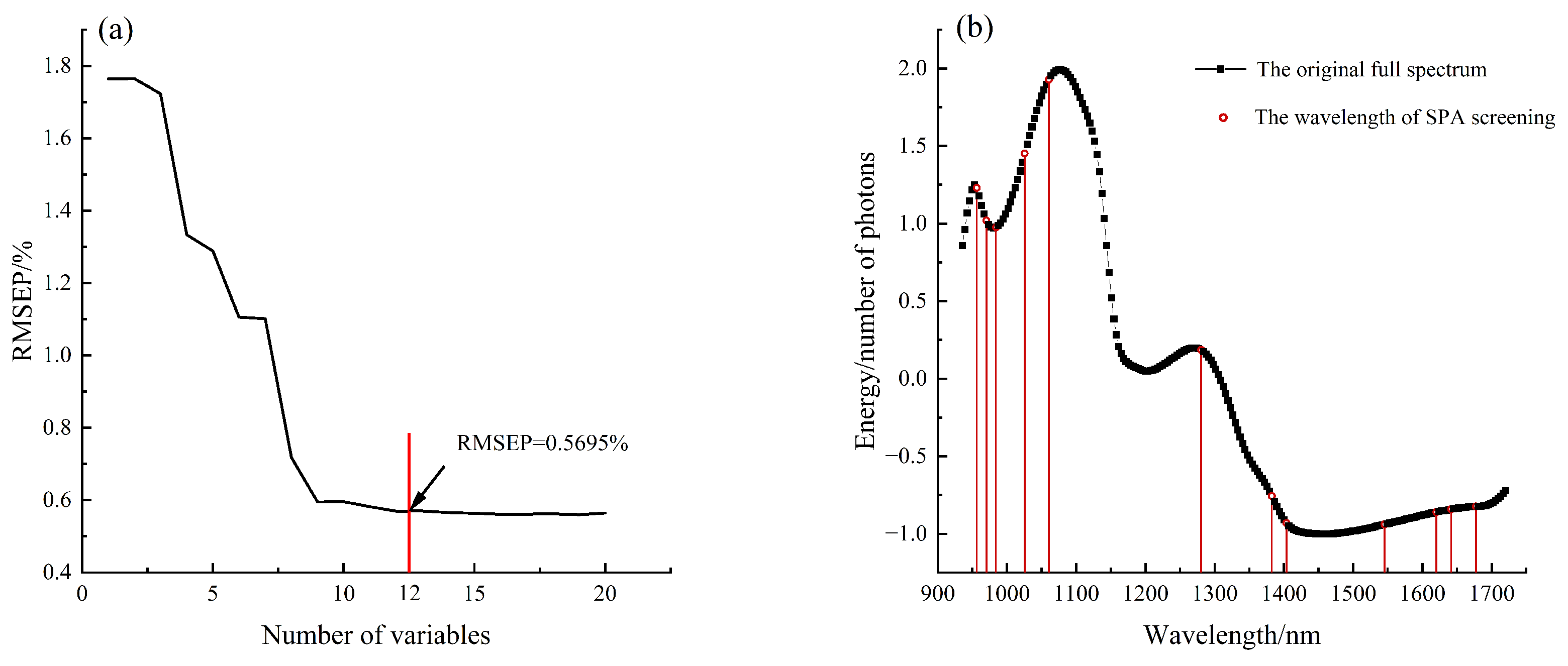
3.6.1. SPA for Further Variable Screening
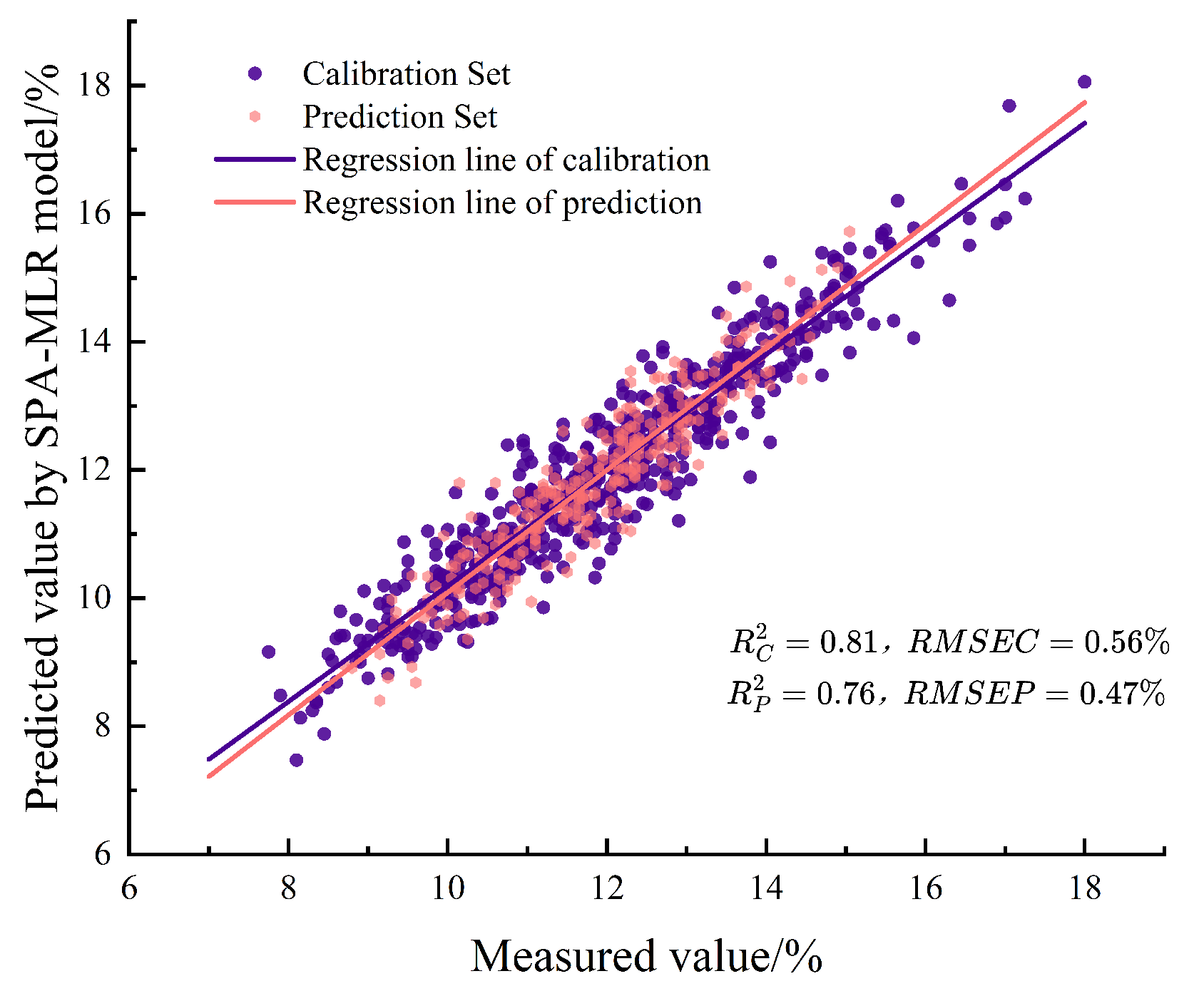
3.6.2. Simplified Prediction Model of UVE-SPA-MLR
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Hung, Y.-C.; Chen, M.; Lin, M.; Lin, H. Enhanced storability of blueberries by acidic electrolyzed oxidizing water application may be mediated by regulating ROS metabolism. Food Chem. 2019, 270, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Felgus-Lavefve, L.; Howard, L.; Adams, S.H.; Baum, J.I. The effects of blueberry phytochemicals on cell models of inflammation and oxidative stress. Adv. Nutr. 2022, 13, 1279–1309. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, B.; Ma, Y.; Sun, X.; Lin, Y.; Meng, X. Polyphenols, anthocyanins, and flavonoids contents and the antioxidant capacity of various cultivars of highbush and half-high blueberries. J. Food Compos. Anal. 2017, 62, 84–93. [Google Scholar] [CrossRef]
- Totad, M.G.; Sharma, R.R.; Sethi, S.; Joshi, A.; Verma, M.K.; Sharma, V.K.; Singh, S.; Dhiman, M.R.; Jaiswal, S. Genotypic variability in nutritional and functional attributes of blueberry varieties grown in northern-western Himalayas. J. Food Sci. Technol. 2020, 57, 2251–2258. [Google Scholar] [CrossRef]
- Duan, Y.; Tarafdar, A.; Chaurasia, D.; Singh, A.; Bhargava, P.C.; Yang, J.; Li, Z.; Ni, X.; Tian, Y.; Li, H.; et al. Blueberry fruit valorization and valuable constituents: A review. Int. J. Food Microbiol. 2022, 381, 109890. [Google Scholar] [CrossRef]
- ElMasry, G.; Wang, N.; ElSayed, A.; Ngadi, M. Hyperspectral imaging for nondestructive determination of some quality attributes for strawberry. J. Food Eng. 2007, 81, 98–107. [Google Scholar] [CrossRef]
- Te, M.; Xia, Y.; Inagaki, T.; Tsuchikawa, S. Rapid and nondestructive evaluation of soluble solids content (SSC) and firmness in apple using Vis–NIR spatially resolved spectroscopy. Postharvest Biol. Technol. 2021, 173, 111417. [Google Scholar] [CrossRef]
- Zheng, W.; Bai, Y.; Luo, H.; Li, Y.; Yang, X.; Zhang, B. Self-adaptive models for predicting soluble solid content of blueberries with biological variability by using near-infrared spectroscopy and chemometrics. Postharvest Biol. Technol. 2020, 169, 111286. [Google Scholar] [CrossRef]
- Lan, W.; Jaillais, B.; Renard, C.M.G.C.; Leca, A.; Chen, S.; Le Bourvellec, C.; Bureau, S. A method using near infrared hyperspectral imaging to highlight the internal quality of apple fruit slices. Postharvest Biol. Technol. 2021, 175, 111497. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, C.; Yang, H.; Jiang, H.; Li, L.; Yang, G. Non-destructive and in-site estimation of apple quality and maturity by hyperspectral imaging. Comput. Electron. Agric. 2022, 195, 106843. [Google Scholar] [CrossRef]
- Mo, C.; Kim, M.S.; Kim, G.; Lim, J.; Delwiche, S.R.; Chao, K.; Lee, H.; Cho, B.-K. Spatial assessment of soluble solid contents on apple slices using hyperspectral imaging. Biosyst. Eng. 2017, 159, 10–21. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, W.; Li, J.; Zhao, C.; Liu, C.; Huang, D.; Gong, L. Detection of slight bruises on apples based on hyperspectral imaging and MNF transform. Spectrosc. Spectr. Anal. 2014, 5, 1367–1372. [Google Scholar]
- Qiao, S.; Tian, Y.; Wang, Q.; Song, S.; Song, P. Nondestructive detection of decayed blueberry based on information fusion of hyperspectral imaging (HSI) and low-field nuclear magnetic resonance (LF-NMR). Comput. Electron. Agric. 2021, 184, 106100. [Google Scholar] [CrossRef]
- Bu, Y.; Luo, J.; Li, J.; Chi, Q.; Guo, W. Detection of hidden bruises on kiwifruit using hyperspectral imaging combined with deep learning. Int. J. Food Sci. Technol. 2024, 59, 5975–5984. [Google Scholar] [CrossRef]
- Weng, S.; Pan, M.; Tan, Y.; Zhang, Q.; Zheng, L. Prediction of soluble solid content in apple using image spectral super-resolution. Spectrosc. Spectr. Anal. 2024, 44, 3095–3100. [Google Scholar]
- Leiva-Valenzuela, G.A.; Lu, R.; Aguilera, J.M. Prediction of firmness and soluble solids content of blueberries using hyperspectral reflectance imaging. J. Food Eng. 2013, 115, 91–98. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, B.; Li, J.; Liu, C.; Huang, W.; Tian, X. Prediction of soluble solids content of apple using the combination of spectra and textural features of hyperspectral reflectance imaging data. Postharvest Biol. Technol. 2016, 121, 51–61. [Google Scholar] [CrossRef]
- Zhang, Z.; Shang, H.; Wang, H.; Zhang, Q.; Yu, S.; Wu, Q.; Tian, J. Hyperspectral imaging for the nondestructive quality assessment of the firmness of Nanguo pears under different freezing/thawing conditions. Sensors 2019, 19, 3124. [Google Scholar] [CrossRef]
- Haghbin, N.; Bakhshipour, A.; Zareiforoush, H.; Mousanejad, S. Non-destructive pre-symptomatic detection of gray mold infection in kiwifruit using hyperspectral data and chemometrics. Plant Methods 2023, 19, 53. [Google Scholar] [CrossRef]
- Qi, H.; Shen, C.; Chen, G.; Zhang, J.; Chen, F.; Li, H.; Zhang, C. Rapid and non-destructive determination of soluble solid content of crown pear by visible/near-infrared spectroscopy with deep learning regression. J. Food Compos. Anal. 2023, 123, 105585. [Google Scholar] [CrossRef]
- Wu, D.; Wan, G.; Jing, Y.; Liu, G.; He, J.; Li, X.; Yang, S.; Ma, P.; Sun, Y. Hyperspectral imaging combined with deep learning for discrimination of Lingwu long jujube in terms of the time after bruising. Microchem. J. 2023, 194, 109238. [Google Scholar] [CrossRef]
- Fan, S.; Huang, W.; Guo, Z.; Zhang, B. Prediction of soluble solids content and firmness of pears using hyperspectral reflectance imaging. Food Anal. Methods 2015, 8, 1936–1946. [Google Scholar] [CrossRef]
- Qiao, S.; Tian, Y.; Gu, W.; He, K.; Yao, P.; Song, S.; Wang, J.; Wang, H.; Zhang, F. Research on simultaneous detection of SSC and FI of blueberry based on hyperspectral imaging combined MS-SPA. Eng. Agric. Environ. Food 2019, 12, 540–547. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, B.; Li, J.; Huang, W.; Wang, C. Effect of spectrum measurement position variation on the robustness of NIR spectroscopy models for soluble solids content of apple. Biosyst. Eng. 2016, 143, 9–19. [Google Scholar] [CrossRef]
- Silalahi, D.D.; Midi, H.; Arasan, J.; Mustafa, M.S.; Caliman, J.-P. Robust generalized multiplicative scatter correction algorithm on pretreatment of near infrared spectral data. Vib. Spectrosc. 2018, 97, 55–65. [Google Scholar] [CrossRef]
- Syvilay, D.; Detalle, V.; Wilkie-Chancellier, N.; Texier, A.; Martinez, L.; Serfaty, S. Novel approach of signal normalization for depth profile of cultural heritage materials. Spectrochim. Acta Spectrosc. 2017, 127, 28–33. [Google Scholar] [CrossRef]
- Mishra, P.; Woltering, E.; Brouwer, B.; Hogeveen-van Echtelt, E. Improving moisture and soluble solids content prediction in pear fruit using near-infrared spectroscopy with variable selection and model updating approach. Postharvest Biol. Technol. 2021, 171, 111348. [Google Scholar] [CrossRef]
- Femenias, A.; Gatius, F.; Ramos, A.J.; Sanchis, V.; Marín, S. Standardisation of near infrared hyperspectral imaging for quantification and classification of DON contaminated wheat samples. Food Control 2020, 111, 107074. [Google Scholar] [CrossRef]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Huang, M.; Tang, J.; Yang, B.; Zhu, Q. Classification of maize seeds of different years based on hyperspectral imaging and model updating. Comput. Electron. Agric. 2016, 122, 139–145. [Google Scholar] [CrossRef]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Wu, J.; Bernacchi, C. Estimating photosynthetic traits from reflectance spectra: A synthesis of spectral indices, numerical inversion, and partial least square regression. Plant Cell Environ. 2020, 43, 1241–1258. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Huang, W.; Zhao, C.; Zhang, B. A comparative study for the quantitative determination of soluble solids content, pH, and firmness of pears by Vis/NIR spectroscopy. J. Food Eng. 2013, 116, 324–332. [Google Scholar] [CrossRef]
- Li, J.; Huang, W.; Chen, L.; Zhang, B. Variable selection in visible and near-infrared spectral analysis for noninvasive determination of soluble solids content of ‘Ya’ pear. Food Anal. Methods 2014, 7, 1891–1902. [Google Scholar] [CrossRef]
- Wu, D.; Sun, D.-W. Potential of time series-hyperspectral imaging (TS-HSI) for non-invasive determination of microbial spoilage of salmon flesh. Talanta 2013, 111, 39–46. [Google Scholar] [CrossRef]
- Lleó, L.; Roger, J.M.; Herrero-Langreo, A.; Diezma-Iglesias, B.; Barreiro, P. Comparison of multispectral indexes extracted from hyperspectral images for the assessment of fruit ripening. J. Food Eng. 2011, 104, 612–620. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, C.; Liu, F.; Kong, W.; He, Y.; Lou, B. Hyperspectral imaging analysis for ripeness evaluation of strawberry with support vector machine. J. Food Eng. 2016, 179, 11–18. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, H.; Sun, X.; Jiang, X.; Rao, Y.; Zhang, Y. Development of multi-cultivar universal model for soluble solid content of apple online using near infrared spectroscopy. Spectrosc. Spectr. Anal. 2020, 40, 922–928. [Google Scholar]
- Pan, T.; Chyngyz, E.; Sun, D.-W.; Paliwal, J.; Pu, H. Pathogenetic process monitoring and early detection of pear black spot disease caused by Alternaria alternata using hyperspectral imaging. Postharvest Biol. Technol. 2019, 154, 96–104. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, K.; Zhao, N.; Yang, J.; Zhang, Y.; Ma, C.; Pan, L.; Tu, K. Information fusion of hyperspectral imaging and electronic nose for evaluation of fungal contamination in strawberries during decay. Postharvest Biol. Technol. 2019, 153, 152–160. [Google Scholar] [CrossRef]
- Song, A.; Wang, C.; Wen, W.; Zhao, Y.; Guo, X.; Zhao, C. Predicting the oil content of individual corn kernels combining NIR-HSI and multi-stage parameter optimization techniques. Food Chem. 2024, 461, 140932. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, W.; Che, T.; Hu, J.; Cao, S.; Liu, W.; Kang, J.; Tang, W.; Li, H. Comparison of diffuse reflectance and diffuse transmittance Vis/NIR spectroscopy for assessing soluble solids content in kiwifruit coupled with chemometrics. Appl. Sci. 2024, 14, 10001. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, Y.; Feng, G.; Zeng, M.; Liu, S. Optimization of near-infrared detection model of blueberry sugar content based on deep belief network and hybrid wavelength selection method. Spectrosc. Spectr. Anal. 2022, 42, 3775–3782. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Z.; Zou, C.; Jiang, S.; El-Seedi, H.R.; Zou, X. General model of multi-quality detection for apple from different origins by Vis/NIR transmittance spectroscopy. Food Biophys. 2022, 16, 2582–2595. [Google Scholar] [CrossRef]


| Sample Type | Sample Set | Quantities | Range | Mean Value | Standard Deviation |
|---|---|---|---|---|---|
| L25 | Calibration Set | 225 | 7.90∼ 17.05 | 11.71 | 1.87 |
| Prediction Set | 74 | 8.55∼15.65 | 11.62 | 1.48 | |
| Bluecrop | Calibration Set | 225 | 8.10∼15.90 | 11.64 | 1.56 |
| Prediction Set | 73 | 9.15∼14.30 | 11.62 | 1.22 | |
| Lexi | Calibration Set | 225 | 7.75∼18.00 | 12.54 | 1.72 |
| Prediction Set | 73 | 9.30∼15.10 | 12.46 | 1.19 | |
| Total | Calibration Set | 675 | 7.75∼18.00 | 11.96 | 1.77 |
| Prediction Set | 220 | 8.55∼15.65 | 11.90 | 1.36 |
| Sample Set | Pre-Processing | The Number of LVs | RMSEC/% | RMSEP/% | RPD | ||
|---|---|---|---|---|---|---|---|
| Multi-variety blueberry mixed dataset | Raw | 21 | 0.95 | 0.38 | 0.89 | 0.40 | 2.98 |
| S-G | 23 | 0.95 | 0.39 | 0.90 | 0.39 | 3.13 | |
| MSC | 23 | 0.95 | 0.32 | 0.93 | 0.34 | 3.90 | |
| SNV | 24 | 0.96 | 0.32 | 0.93 | 0.34 | 3.89 | |
| S-G+MSC | 24 | 0.96 | 0.36 | 0.93 | 0.33 | 3.89 | |
| S-G+SNV | 21 | 0.96 | 0.37 | 0.93 | 0.33 | 3.92 | |
| S-G+MSC+SNV | 21 | 0.96 | 0.37 | 0.94 | 0.33 | 3.94 |
| Spectral Band | Number of Spectral Variables | LVs | RMSEC/% | RMSEP/% | RPD | ||
|---|---|---|---|---|---|---|---|
| The original full spectrum | 224 | 21 | 0.95 | 0.38 | 0.89 | 0.40 | 2.98 |
| The full spectrum after pretreatment | 224 | 21 | 0.96 | 0.37 | 0.94 | 0.33 | 3.94 |
| Spectral region after UVE method | 117 | 20 | 0.96 | 0.38 | 0.93 | 0.35 | 3.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Chen, G.; Liu, D.; Tian, N. Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology. Appl. Sci. 2025, 15, 3888. https://doi.org/10.3390/app15073888
Meng L, Chen G, Liu D, Tian N. Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology. Applied Sciences. 2025; 15(7):3888. https://doi.org/10.3390/app15073888
Chicago/Turabian StyleMeng, Lingqi, Guoliang Chen, Dayang Liu, and Ning Tian. 2025. "Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology" Applied Sciences 15, no. 7: 3888. https://doi.org/10.3390/app15073888
APA StyleMeng, L., Chen, G., Liu, D., & Tian, N. (2025). Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology. Applied Sciences, 15(7), 3888. https://doi.org/10.3390/app15073888





