Application of Hybrid MCDA Tools for Constructability Review in Infrastructure Projects: A Bridge Case Study
Abstract
:1. Introduction
- Application of the CRP at the feasibility stage of infrastructure projects, addressing a gap in current practices and contributing to early-stage decision-making.
- The introduction of a hybrid DSS model that integrates the most suitable MCDA tools with innovative strategies to evaluate constructability criteria comprehensively.
- Validation of the proposed DSS through application to a real-world case study, representing how to customize the decision matrix and also demonstrating its practicality and effectiveness in optimizing decision-making processes for large-scale infrastructure projects.
2. Related Work
2.1. Constructability Review Process
2.2. Decision Support System
3. Proposed Methodology
3.1. Outline of the Proposed Method
3.2. Design and Conducting Survey
- Regulations (prerequisite project set-up such as sustainability);
- Engineering design and construction;
- Logistics, such as procurement;
- Project management,
3.3. Identification of Key Criteria
3.4. Hybrid Multi-Criteria Decision Analysis (MCDA)
3.4.1. Definition of Decision Matrix
- Decision Matrix
3.4.2. MCDA Ranking
- TOPSIS:
- SAW:
- VIKOR:
- PROMETHEE II
- Step 1:
- Normalize the decision matrix
- Step 2:
- Assess the evaluative variances of option i compared with the remaining alternatives.
- Step 3:
- A preference function is a function of the contrast between evaluations of two criteria (a and b), indicated as . There are six types of preference functions; Type 1 has been used in this research, which is .
- Step 4:
- The multi-criteria preference index is subsequently characterized as the weighted mean of the preference functions.
- Step 5:
- Establish the leaving and entering outranking flows, in which m is the of alternatives while each alternative has to deal with (m − 1) number of other options as below.
- Step 6:
- Compute the gross outranking flow for each option, as shown below belongs to the alternative a:
- Step 7:
- Seeking the best alternative by looking at the value as the highest one will best interpret the variance of leaving flow with entering flow as the most significant [42].
- COPRAS:
- Step 1:
- A decision matrix () is formed and normalized.
- Step 2:
- The sum total of the weighted normalized values is specified using for profit criteria and for cost criteria:where k is the number of profit/benefit criteria, and the rest of the criteria from k + 1 to n are the number of cost criteria. The and values show the degree of accomplishment of the objective for alternatives. A higher value for and a lower value for points to better alternatives.
- Step 3:
- Determine the comparative importance of alternatives.
- Step 4:
- The ultimate ranking is carried out based on the computed values as outlined below.where is the maximum value of the relative significance of alternatives. Alternatives (tie points) with higher values of will have a higher rank.
- CODAS:
- Step 1:
- Build the decision matrix as a first step, like all MCDA methods.
- Step 2:
- Normalize the decision matrix to the range of 0 to 1 ().
- Step 3:
- Weight calculation of the normalized matrix.
- Step 4:
- Verify the negative solution (ns) by the equation below:
- Step 5:
- Measure the Euclidean and Taxi distance of each alternative from the negative ideal solution by calculating the below equations:
- Step 6:
- Assessment matrix will be developed by:
- Step 7:
- Conclude the evaluation rank for each alternative.
- Step 8:
- Sort the scores by descending and select the best option.
3.4.3. Borda Count Method
4. Bridge Case Study for CRP Assessment
4.1. Summary of Existing Bridge
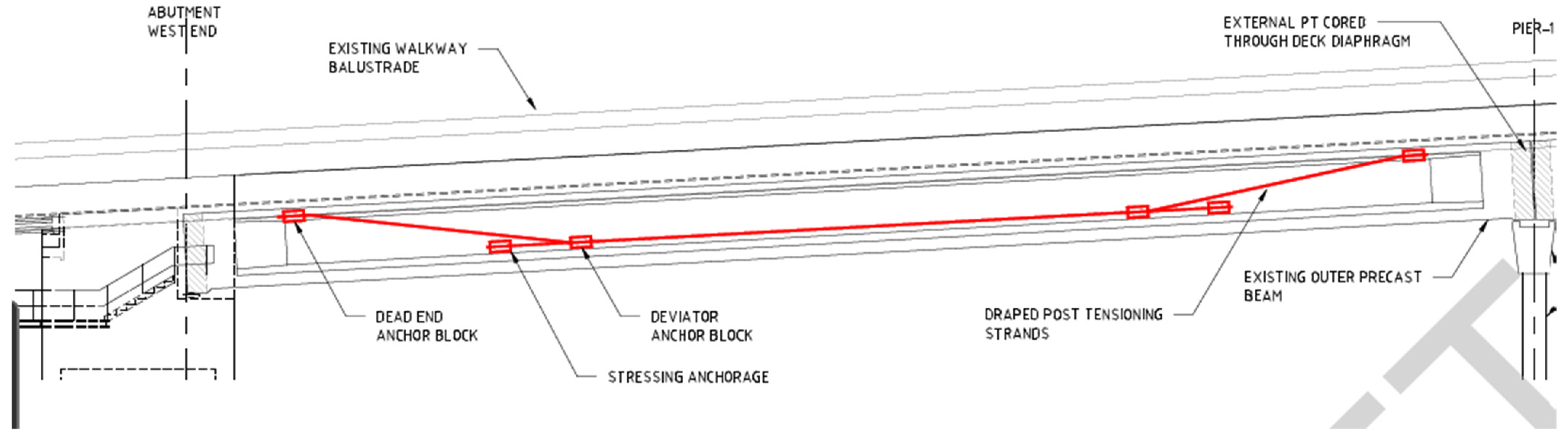
4.2. Description of Upgrading Scenario
- The provision of a 3.5 m shared path on each side of the bridge with improvements to connection to the existing path network on the eastern and western sides of the river, as shown in Figure 5b.
- Safety railings on each side of the pathways that adopt all suicide prevention measures.
- Improvements to path lighting.
- Upgrades to the bridge feature lighting.
- Upgrades to the bridge maintenance and inspection gantry.
- Bridge strengthening to carry current traffic loadings.
4.3. Customize a Decision Matrix for a Case Study: Upgrade and Strengthening of an Existing Bridge
- The benefit-based scale ranges from 1 to 10, where higher values indicate a more favorable outcome.
- The minimum-based scale ranges from 1 to 10, where lower values signify a more desirable result.
- The binary solution, with options represented as 0 or 1, where the preferred choice is assigned a value of 1.
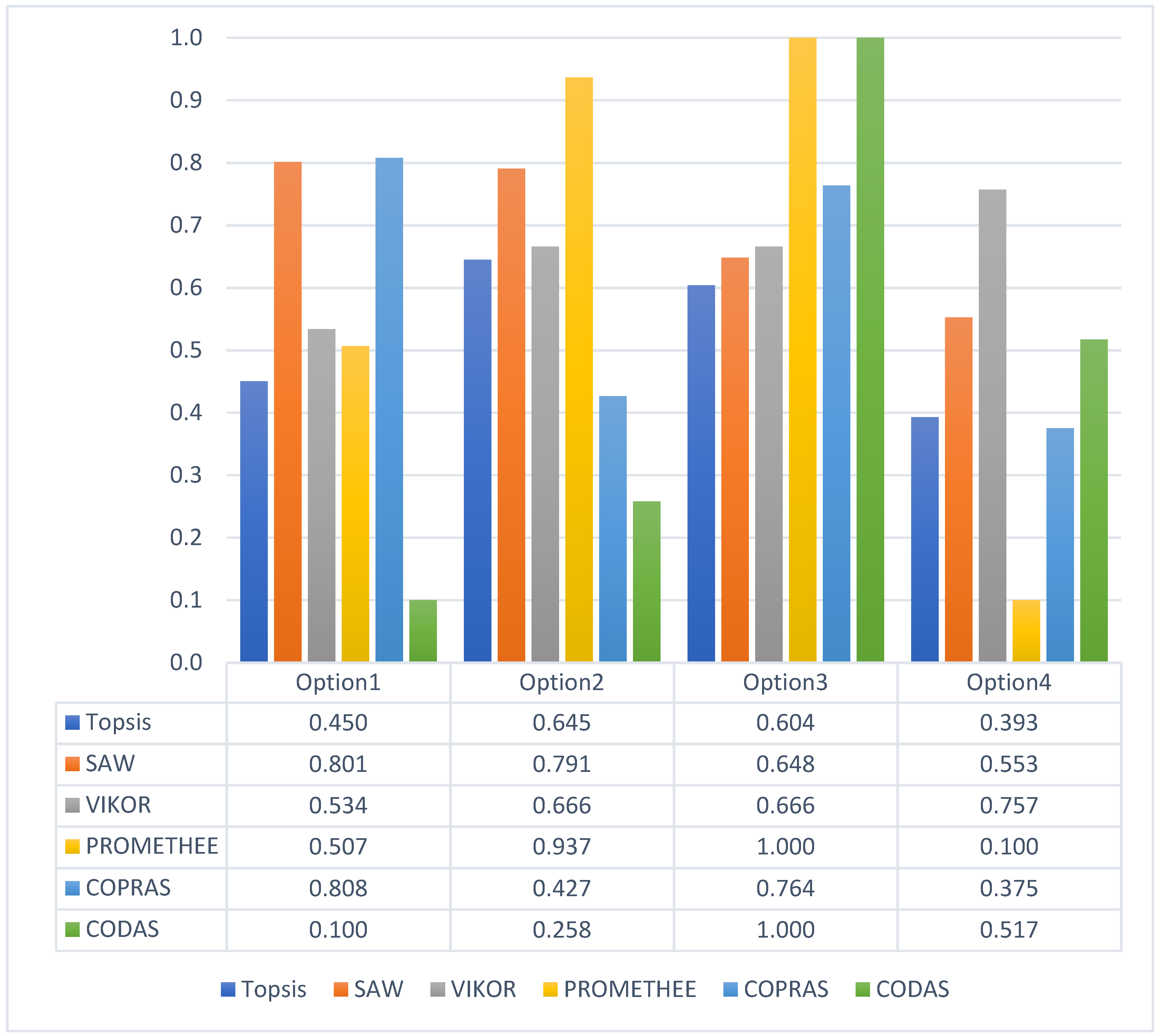
4.4. Bridge Case Study Results
4.5. Comparative Results to Single MCDM Methods
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jadidoleslami, S.; Saghatforoush, E.; Zare Ravasan, A. Constructability obstacles: An exploratory factor analysis approach. Int. J. Constr. Manag. 2021, 21, 312–325. [Google Scholar] [CrossRef]
- Griffith, A.; Sidwell, T. Constructability Concepts and Principles. In Constructability in Building and Engineering Projects; Macmillan Education UK: London, UK, 1995; pp. 1–30. [Google Scholar]
- Wong, W.H.; Lam, P.T.I.; Chan, E.H.W.; Shen, L.Y. A study of measures to improve constructability. Int. J. Qual. Reliab. Manag. 2007, 24, 586–601. [Google Scholar] [CrossRef]
- Rahman, S.; Odeyinka, H.; Perera, S.; Bi, Y. Product-cost modelling approach for the development of a decision support system for optimal roofing material selection. Expert Syst. Appl. 2012, 39, 6857–6871. [Google Scholar]
- Ogbu, C.; Ebiminor, V. Influence of Project Setting on the Constructability Practices of Indigenous Road Construction Firms in Nigeria. FUTY J. Environ. 2021, 15, 49–64. [Google Scholar]
- Ighodaro, C.A. Transport infrastructure and economic growth in Nigeria. J. Res. Natl. Dev. 2009, 7. [Google Scholar]
- Marcher, C.; Giusti, A.; Matt, D.T. Decision support in building construction: A systematic review of methods and application areas. Buildings 2020, 10, 170. [Google Scholar] [CrossRef]
- Kumari, A.; Acherjee, B. A novel hybrid multi-criteria decision methodology for assessing tool materials in friction stir welding process. Int. J. Interact. Des. Manuf. IJIDeM 2024, 18, 4963–4986. [Google Scholar]
- Rashidi, M.; Ghodrat, M.; Samali, B.; Kendall, B.; Zhang, C. Remedial Modelling of Steel Bridges through Application of Analytical Hierarchy Process (AHP). Appl. Sci. 2017, 7, 168. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, X.; Zhou, L.; Qin, J.; Rezaei, J. An analytical framework for the best–worst method. Omega 2024, 123, 102974. [Google Scholar] [CrossRef]
- Thakkar, J.J. Stepwise weight assessment ratio analysis (SWARA). In Multi-Criteria Decision Making; Springer: Berlin/Heidelberg, Germany, 2021; pp. 281–289. [Google Scholar]
- Yazdani, M.; Zarate, P.; Kazimieras Zavadskas, E.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar]
- Kifokeris, D.; Xenidis, Y. Constructability: Outline of Past, Present, and Future Research. J. Constr. Eng. Manag. 2017, 143, 04017035. [Google Scholar] [CrossRef]
- Getuli, V.; Giusti, T.; Capone, P. A Decision Support System (DSS) for constructability assessment in seismic retrofit of complex buildings. In Proceedings of the ISARC International Symposium on Automation and Robotics in Construction, Oulu, Finland, 15–18 June 2015; p. 1. [Google Scholar]
- Fadoul, A.; Tizani, W.; Koch, C. Constructability assessment model for buildings design. In Proceedings of the 24th EG-ICE International Workshop on Intelligent Computing in Engineering 2017, Nottingham, UK, 10–12 July 2017; pp. 86–95. [Google Scholar]
- Bonilla, M.; Rasdorf, W.; Akhnoukh, A.; Norboge, N.; Findley, D.; Fullerton, C. Critical Constructability Review Indicators for Construction of Transportation Infrastructure. In Construction Research Congress 2022; ASCE: Reston, VA, USA, 2022; pp. 544–552. [Google Scholar]
- Taherdoost, H.; Madanchian, M. Multi-Criteria Decision Making (MCDM) Methods and Concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Rashidi, M.; Ghodrat, M.; Samali, B.; Mohammadi, M. Decision Support Systems; InTech: London, UK, 2018. [Google Scholar]
- Lemass, B. Structured Conceptual Design: The New Frontier; Pearson Education Australia: Frenchs Forest, Australia, 2004. [Google Scholar]
- Jato-Espino, D.; Castillo-Lopez, E.; Rodriguez-Hernandez, J.; Canteras-Jordana, J.C. A review of application of multi-criteria decision making methods in construction. Autom. Constr. 2014, 45, 151–162. [Google Scholar]
- Khairul, M.S.; Siahaan, A.P.U. Decision support system in selecting the appropriate laptop using simple additive weighting. Int. J. Recent Trends Eng. Res. 2016, 2, 215–222. [Google Scholar]
- Mousavi, V.; Varshosaz, M.; Rashidi, M.; Li, W. A New Multi-Criteria Tie Point Filtering Approach to Increase the Accuracy of UAV Photogrammetry Models. Drones 2022, 6, 413. [Google Scholar] [CrossRef]
- Rashidi, M.; Samali, B.; Sharafi, P. A new model for bridge management: Part B: Decision support system for remediation planning. Aust. J. Civ. Eng. 2016, 14, 46–53. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rashidi, M.; Yu, Y.; Samali, B. Integration of TLS-derived Bridge Information Modeling (BrIM) with a Decision Support System (DSS) for digital twinning and asset management of bridge infrastructures. Comput. Ind. 2023, 147, 103881. [Google Scholar]
- Sharafi, P.; Rashidi, M.; Samali, B.; Ronagh, H.; Mortazavi, M. Identification of factors and decision analysis of the level of modularization in building construction. J. Archit. Eng. 2018, 24, 04018010. [Google Scholar]
- Sadeghi, H.; Zhang, X. Towards safer tower crane operations: An innovative knowledge-based decision support system for automated safety risk assessment. J. Saf. Res. 2024, 90, 272–294. [Google Scholar]
- Mousavi, V.; Rashidi, M.; Mohammadi, M.; Samali, B. Evolution of Digital Twin Frameworks in Bridge Management: Review and Future Directions. Remote Sens. 2024, 16, 1887. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar]
- Keršuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar]
- Hwang, C.-L.; Yoon, K.; Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Abdullah, L.; Adawiyah, C.R. Simple additive weighting methods of multi criteria decision making and applications: A decade review. Int. J. Inf. Process. Manag. 2014, 5, 39. [Google Scholar]
- Brans, J.-P.; Vincke, P.; Mareschal, B. How to select and how to rank projects: The PROMETHEE method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar]
- Albadvi, A.; Chaharsooghi, S.K.; Esfahanipour, A. Decision making in stock trading: An application of PROMETHEE. Eur. J. Oper. Res. 2007, 177, 673–683. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Šarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comput. Econ. Cybern. Stud. Res. 2016, 50, 25–44. [Google Scholar]
- Dominguez, L.A.P.; Borroel, E.Z.; Quezada, O.E.I.; Ortiz-Munoz, D.; Najera-Acosta, A. CODAS, TOPSIS, and AHP Methods Application for Machine Selection. J. Comput. Cogn. Eng. 2023, 2, 322–330. [Google Scholar]
- Opricovic, S. Multicriteria optimization of civil engineering systems. Fac. Civ.Eng. Belgrade 1998, 2, 5–21. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar]
- Kibira, D.; Morris, K.C.; Kumaraguru, S. Methods and tools for performance assurance of smart manufacturing systems. J. Res. Natl. Inst. Stand. Technol. 2016, 121, 282. [Google Scholar] [CrossRef] [PubMed]
- Zionts, S.; Wallenius, J. An interactive multiple objective linear programming method for a class of underlying nonlinear utility functions. Manag. Sci. 1983, 29, 519–529. [Google Scholar] [CrossRef]
- Podvezko, V. The comparative analysis of MCDA methods SAW and COPRAS. Eng. Econ. 2011, 22, 134–146. [Google Scholar] [CrossRef]
- Agrawal, N. Multi-criteria decision-making toward supplier selection: Exploration of PROMETHEE II method. Benchmarking Int. J. 2022, 29, 2122–2146. [Google Scholar] [CrossRef]
- Baydaş, M.; Yılmaz, M.; Jović, Ž.; Stević, Ž.; Özuyar, S.E.G.; Özçil, A. A comprehensive MCDM assessment for economic data: Success analysis of maximum normalization, CODAS, and fuzzy approaches. Financ. Innov. 2024, 10, 105. [Google Scholar]
- Radulescu, C.Z.; Radulescu, M. A hybrid group multi-criteria approach based on SAW, TOPSIS, VIKOR, and COPRAS methods for complex IoT selection problems. Electronics 2024, 13, 789. [Google Scholar] [CrossRef]
- Wei, J.; Lin, X. The multiple attribute decision-making VIKOR method and its application. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar]
- Roozbahani, A.; Ebrahimi, E.; Banihabib, M.E. A Framework for Ground Water Management Based on Bayesian Network and MCDM Techniques. Water Resour. Manag. 2018, 32, 4985–5005. [Google Scholar] [CrossRef]
- Samimpey, R.; Saghatforoush, E. Practical Framework to Facilitate Constructability Implementation Using Building Information Modeling Approach: A Case Study. Int. J. Innov. Technol. Manag. IJITM 2024, 21, 1–30. [Google Scholar]








| Tool | Developer | Advantage | Disadvantage |
|---|---|---|---|
| AHP | Thomas L. Saaty [38] 1970s | Consistency factor can give the decision maker the idea of any essential reassessment [18] | If a new option is introduced after completing the calculation, the entire evaluation process must be restarted, making it time-consuming [18] |
| SMART | George T. Doran [39] 1981 | High level of accuracy in certain tasks | Because of its simplicity, it may not be suitable in consideration of complicated circumstances [18] |
| TOPSIS | Hwang et al. [30] 1981 | Can compare each alternative with the ideal solution [8] | The subjectivity of weighting criteria and the difficulty to create the decision matrix and judging the criteria value [18] |
| SAW | Zionts and Wallenius [40] 1968 | Straight forward method [8] | Considers only maximizing evaluation criteria, requiring minimizing criteria to be transformed into maximizing ones using appropriate formulas before application. This limitation is overcome by the COPRAS [41] |
| COPRAS | Zavadkas et al. [34] 1994 | An interdependent solution between criteria and alternatives [8] | Less stable than other methods in the case of data variation [41] |
| PROMETHEE | Brans et al. [32] 1986 | An appropriate solution even when simple and efficient information is available [35]. | Fails to offer a clear method for assigning weights [42]. |
| CODAS | Keshavarz Ghorbaee et al. [35] 2016 | A relatively recent approach measures the overall performance of an alternative based on its distance from the negative ideal point [43]. | Sensitivity to the normalization approach [43]. |
| VIKOR | Opricovic [37] 1998 | A comparison solution once there are conflicting factors while considering both the worst and best solution [8] | Can be sensitive to changes in weights and thresholds. And, complexity increases with the number of criteria and alternatives [44]. |
| Tool | Summary |
|---|---|
| TOPSIS | The preferred option will be the closet to the ideal solution and the extreme away from the negative solution |
| SAW | The core concept involves calculating the weighted total of performance ratings for each option across all relevant characteristics |
| COPRAS | Alternatives will be ranked sequentially according to their importance |
| PROMETHEE | An interactive tool that is able to be quantitative and qualitative |
| CODAS | Assessment with the Euclidean and Taxicab distance measurements |
| VIKOR | Its result will be the closest option to the ideal solution |
| Engineering Design and Construction | Logistics | Project Management | Regulations |
|---|---|---|---|
| Aesthetics and Innovation | Effective Communication and Teamwork | Operation and Maintenance | Sustainability |
| Construction Type | Legal and Political Changes | Profitability | Health and Safety |
| Construction Duration | Supply Chain | Project Duration and Scheduling | Urban Planning |
| Design and Complexity | Site Maneuverability | Quality | Contract Type and Form |
| Material Selection | Procurement and Contract Type |
| Integer Weight Associated with the Level of Importance | |||||
|---|---|---|---|---|---|
| Integer Weight = | 0 | 1 | 2 | 3 | 4 |
| Importance level = | 1 | 3 | 5 | 7 | 9 |
| Criteria Percentage = | |||||||
|---|---|---|---|---|---|---|---|
| Importance Level = | 1 | 3 | 5 | 7 | 9 | Sub-criteria Importance | Overall Importance |
| Sub-criteria percentage | % | ||||||
| Importance Level | Sub-Criteria Importance | Overall Importance |
|---|---|---|
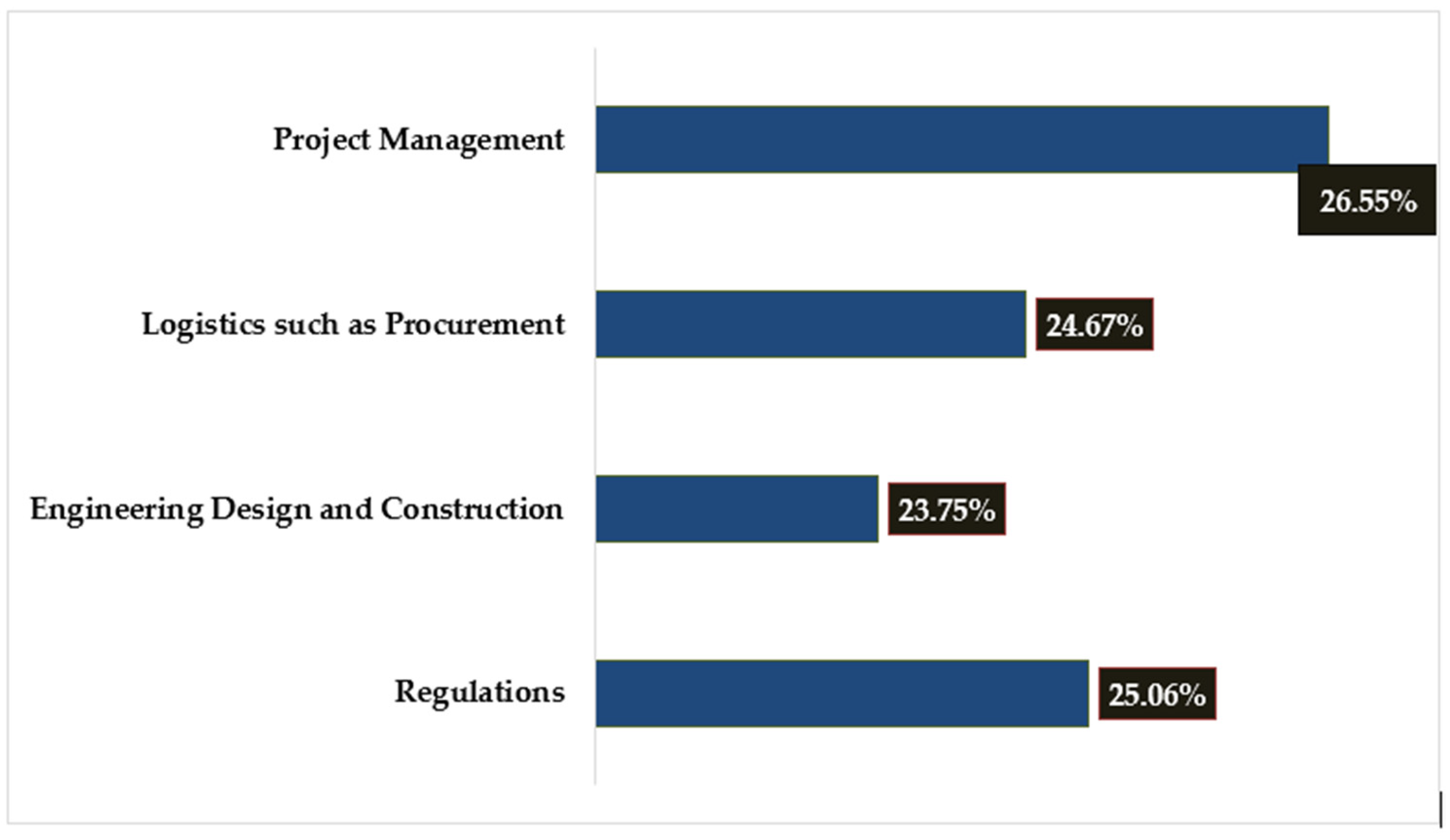
| Sustainability | 23.00 | 5.77% |
| Health and Safety | 30.70 | 7.70% |
| Urban planning | 23.40 | 5.86% |
| Contract type and form | 22.90 | 5.73% |
| Sum | 100.00 | 25.06% |
| Importance Level | Sub-Criteria Importance | Overall Importance |
|---|---|---|
| Aesthetics and Innovation | 16.10 | 3.83% |
| Construction type | 19.40 | 4.61% |
| Construction duration | 21.10 | 5.01% |
| Design and Complexity | 23.30 | 5.54% |
| Material selection | 20.10 | 4.77% |
| Sum | 100.00 | 23.75% |
| Importance Level | Sub-Criteria Importance | Overall Importance |
|---|---|---|
| Procurement and Contract type | 19.60 | 4.83% |
| Effective communication and Teamwork | 21.00 | 5.18% |
| Legal and Political changes | 18.50 | 4.56% |
| Supply chain | 21.70 | 5.36% |
| Site maneuverability | 19.20 | 4.73% |
| Sum | 100.00 | 24.67% |
| Importance Level | Sub-Criteria Importance | Overall Importance |
|---|---|---|
| Operation and Maintenance cost | 19.70 | 5.22% |
| Profitability | 20.10 | 5.35% |
| Project duration and Scheduling | 20.10 | 5.34% |
| Quality | 19.90 | 5.28% |
| Productivity and efficiency | 20.10 | 5.34% |
| Sum | 100.00 | 26.54% |
| Alternatives | Strengthening Type | Pathway | Civil Works (Western and Eastern Approaches) |
|---|---|---|---|
| Option 1 | Post-tensioning | Double pathway with cantilever below | Eastern approach |
| Option 2 | Post-tensioning | Single pathway with cantilever below | Western approach |
| Option 3 | Post-tensioning | Single pathway without cantilever below | Eastern approach |
| Option 4 | Addition of piling and piers | Single pathway without cantilever below | Western approach |
| Main Groups | Criteria | Sub-Criteria Weight | Option 1 | Option 2 | Option 3 | Option 4 |
|---|---|---|---|---|---|---|
| Regulations | Sustainability | 7.51% | 6 | 4 | 3 | 8 |
| Health and Safety | 9.99% | 4 | 8 | 5 | 6 | |
| Urban Planning | 7.57% | 9 | 6 | 4 | 4 | |
| Engineering Design and Construction | Aesthetics and Innovation | 3.83% | 9 | 6 | 8 | 3 |
| Construction Type | 4.61% | 9 | 9 | 9 | 5 | |
| Construction Duration | 5.01% | 6 | 3 | 4 | 9 | |
| Design and Complexity | 5.54% | 1 | 1 | 1 | 0.001 | |
| Material Selection | 4.77% | 3 | 6 | 8 | 8 | |
| Project Management | Operation and Maintenance Cost | 5.22% | 4 | 2 | 7 | 5 |
| Profitability | 5.35% | 3 | 5 | 7 | 8 | |
| Project Duration and Scheduling | 5.34% | 8 | 4 | 2 | 6 | |
| Quality | 5.28% | 9 | 9 | 9 | 6 | |
| Productivity and Efficiency in Resource Management | 5.34% | 5 | 7 | 8 | 3 | |
| Logistics | Legal and Political Changes | 7.68% | 6 | 8 | 9 | 3 |
| Supply Chain | 9.03% | 4 | 5 | 7 | 9 | |
| Site Maneuverability | 7.96% | 4 | 6 | 8 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorasani Nejad, M.; Rashidi, M.; Mousavi, V. Application of Hybrid MCDA Tools for Constructability Review in Infrastructure Projects: A Bridge Case Study. Appl. Sci. 2025, 15, 3923. https://doi.org/10.3390/app15073923
Khorasani Nejad M, Rashidi M, Mousavi V. Application of Hybrid MCDA Tools for Constructability Review in Infrastructure Projects: A Bridge Case Study. Applied Sciences. 2025; 15(7):3923. https://doi.org/10.3390/app15073923
Chicago/Turabian StyleKhorasani Nejad, Mansoureh, Maria Rashidi, and Vahid Mousavi. 2025. "Application of Hybrid MCDA Tools for Constructability Review in Infrastructure Projects: A Bridge Case Study" Applied Sciences 15, no. 7: 3923. https://doi.org/10.3390/app15073923
APA StyleKhorasani Nejad, M., Rashidi, M., & Mousavi, V. (2025). Application of Hybrid MCDA Tools for Constructability Review in Infrastructure Projects: A Bridge Case Study. Applied Sciences, 15(7), 3923. https://doi.org/10.3390/app15073923









