Six Sigma-Based Frequency Response Analysis for Power Transformer Winding Deformation
Abstract
:1. Introduction
1.1. Literature Survey
1.2. Contribution
1.3. Research Gap and Novelty of the Proposed FRA6σ Framework
1.4. Paper Organization
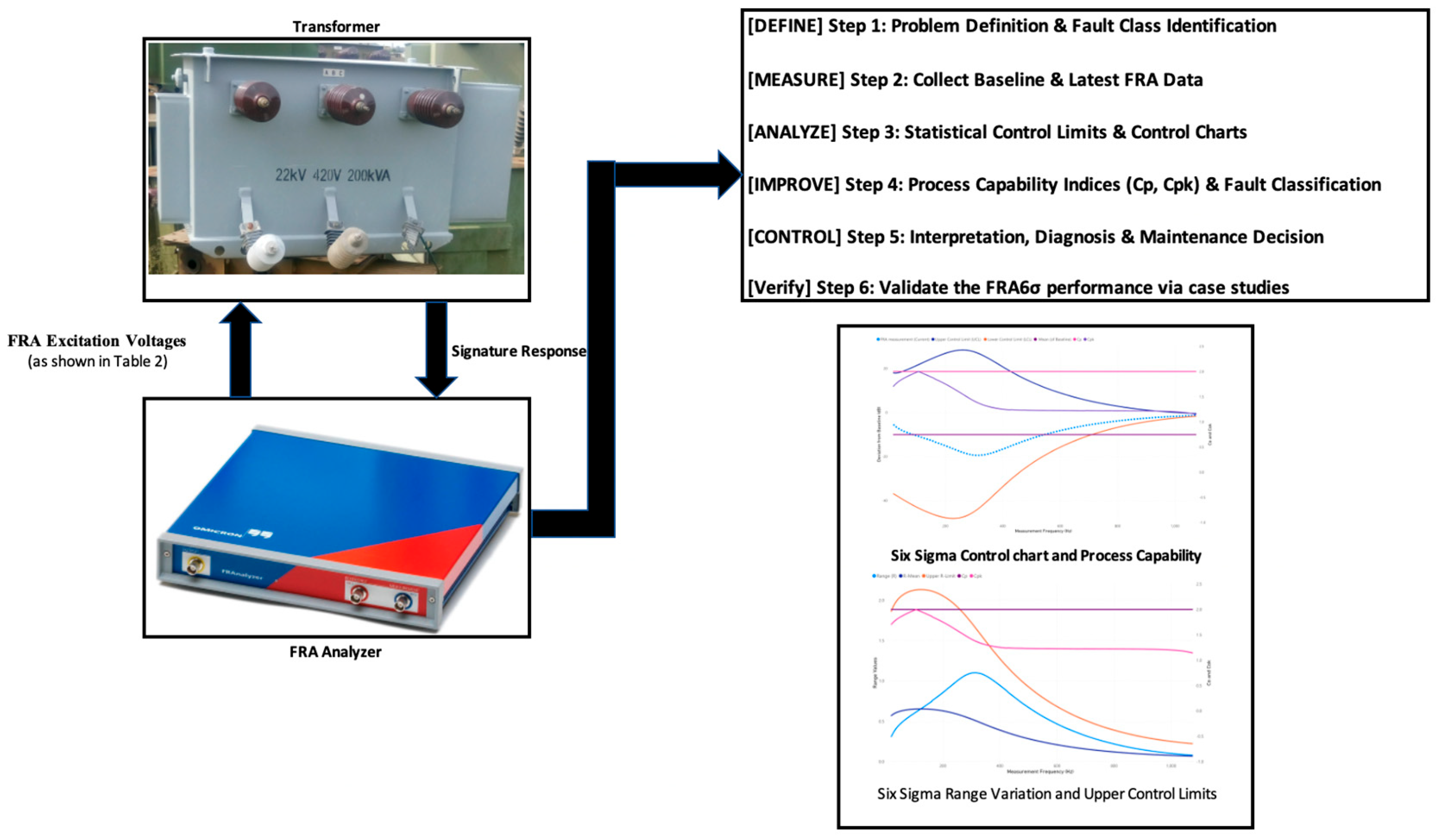
2. Materials and Methods
2.1. Proposed FRA6σ Approach—Define Phase
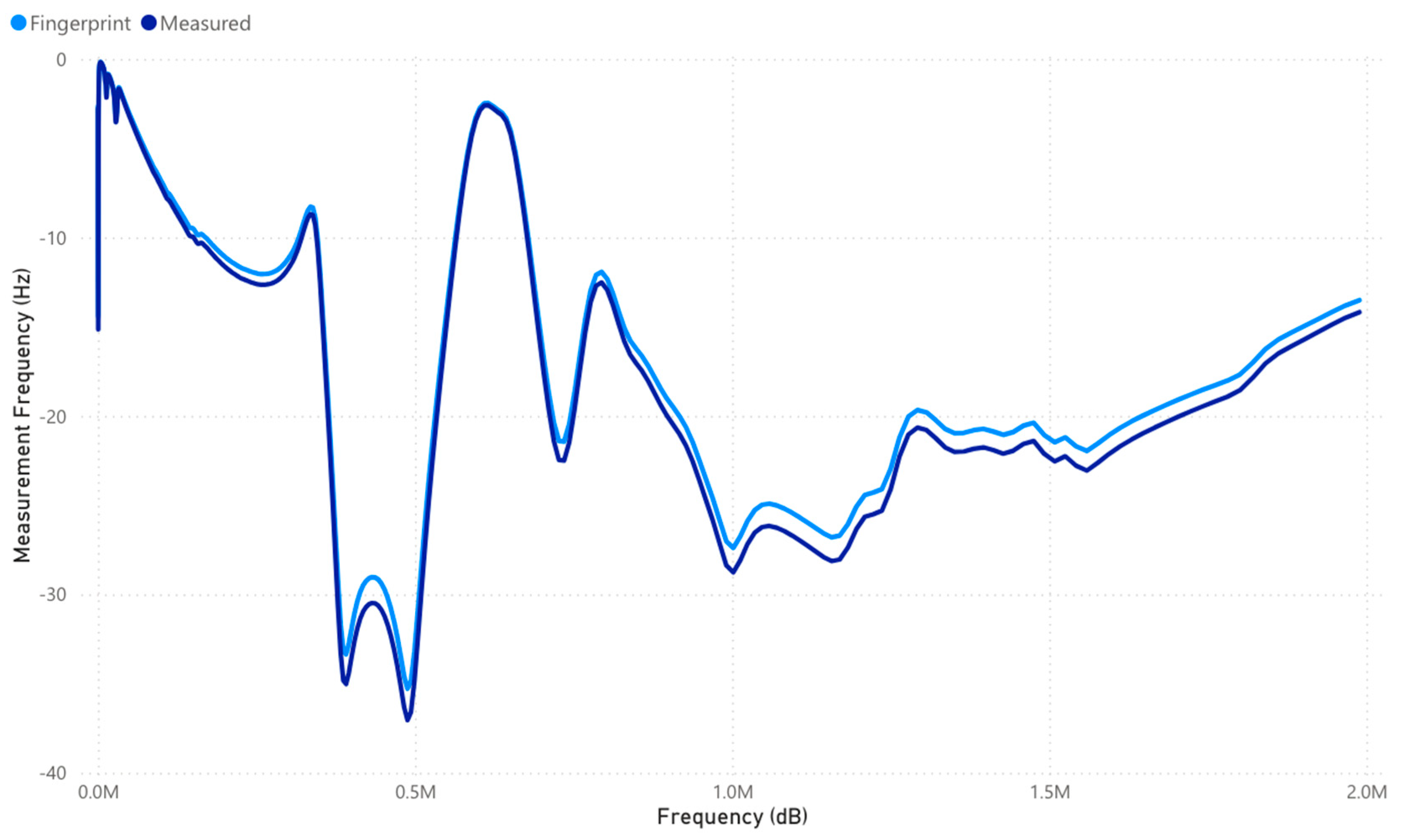
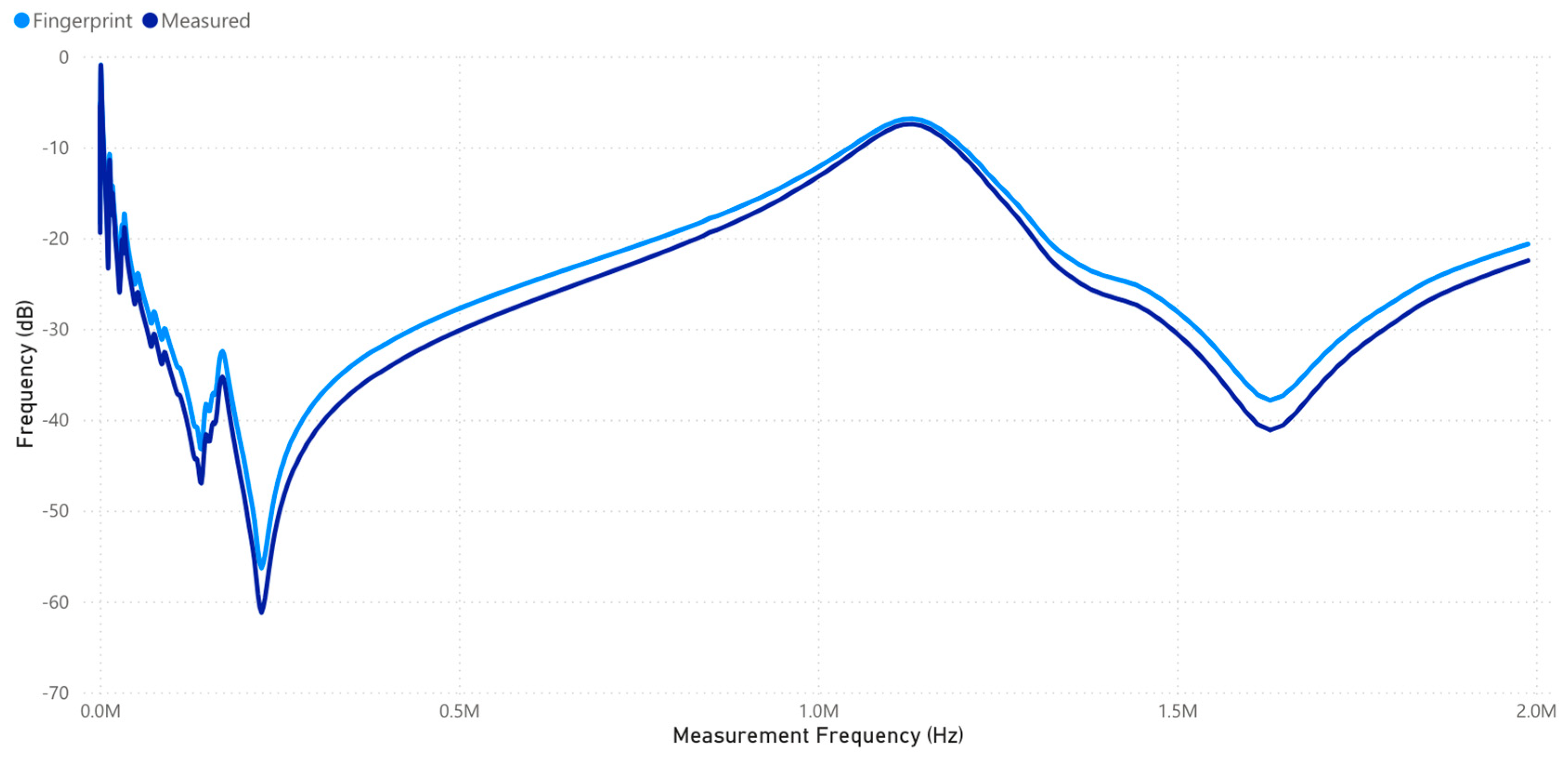
2.1.1. Step 1: Collect FRA Data—Measure Phase
2.1.2. Step 2: Computing Statistical Control Limits—Analyze Phase
- Mean Response () Calculation
- 2.
- Standard Deviation () Calculation
- 3.
- Control Limits Calculation
2.1.3. Step 3: Control Chart Plot—Analyze Phase
- Fingerprint Mean Response () Plot
- 2.
- UCL and LCL Plot as Boundary Lines
- 3.
- Latest FRA Measurement Overlay
2.1.4. Step 4: Sigma Level and Process Capability Determination
- Process Capability Index () Computation
- 2.
- Process Capability Index Relative to the Mean () Computation
2.1.5. Step 5: Interpreting the Six Sigma Analysis—Control Phase
2.2. Outlier Detection and Treatment in FRA-Six Sigma
3. Results—Verify Phase
3.1. Case 1
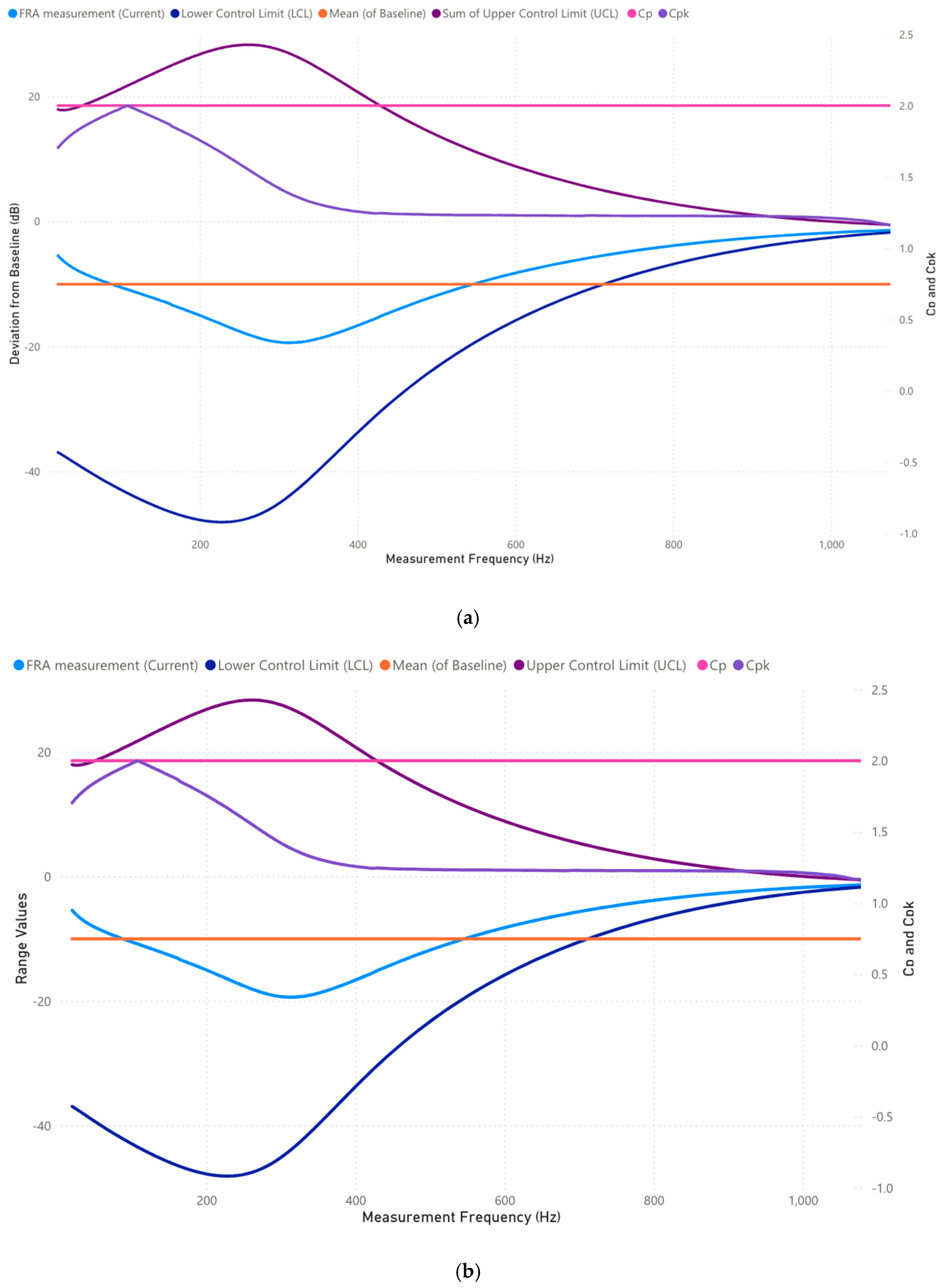
3.1.1. Case 1: Analysis of 10–1000 Frequency Range (Hz)
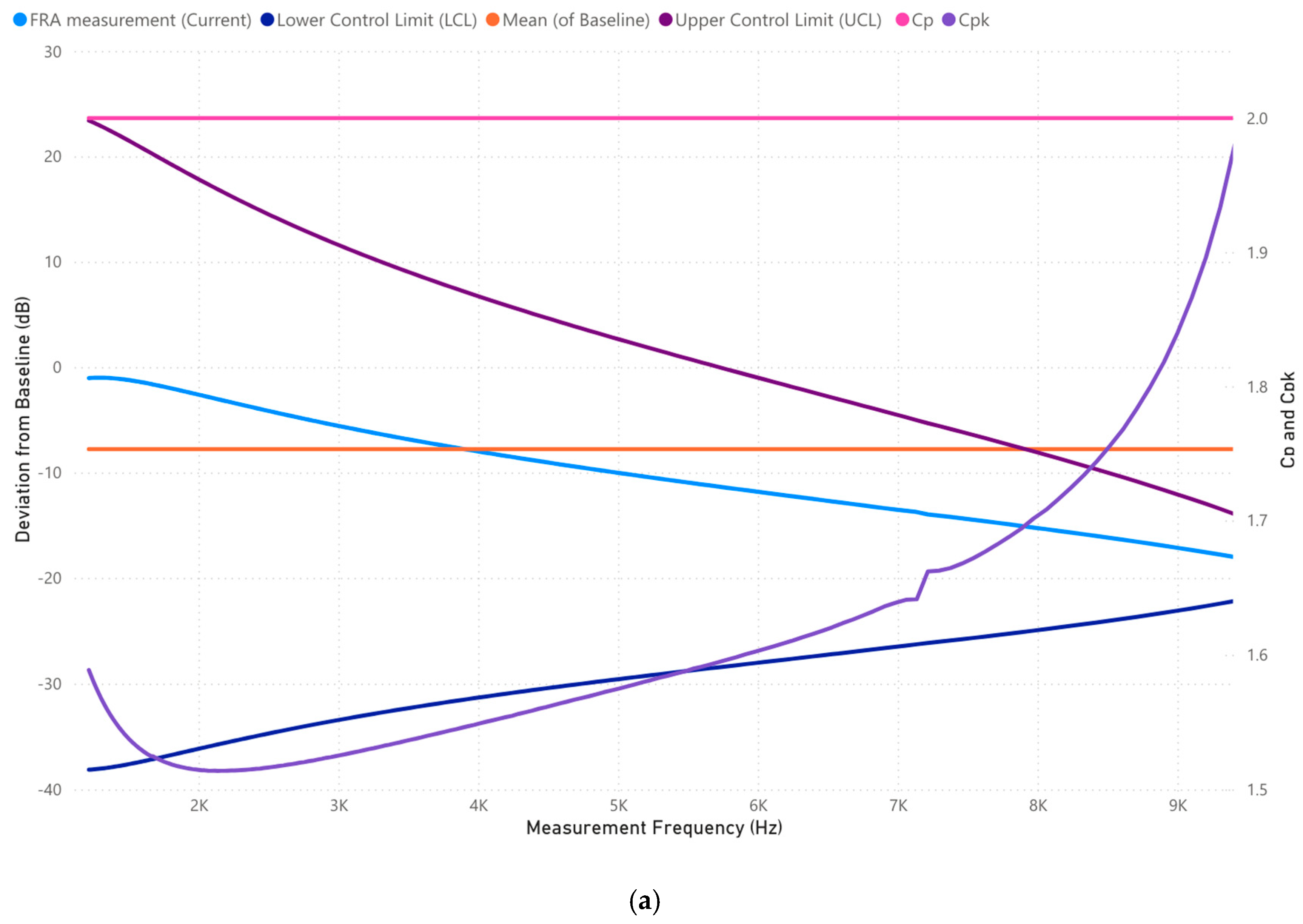
3.1.2. Case 1: Analysis of 1000–10,000 Frequency Range (Hz)
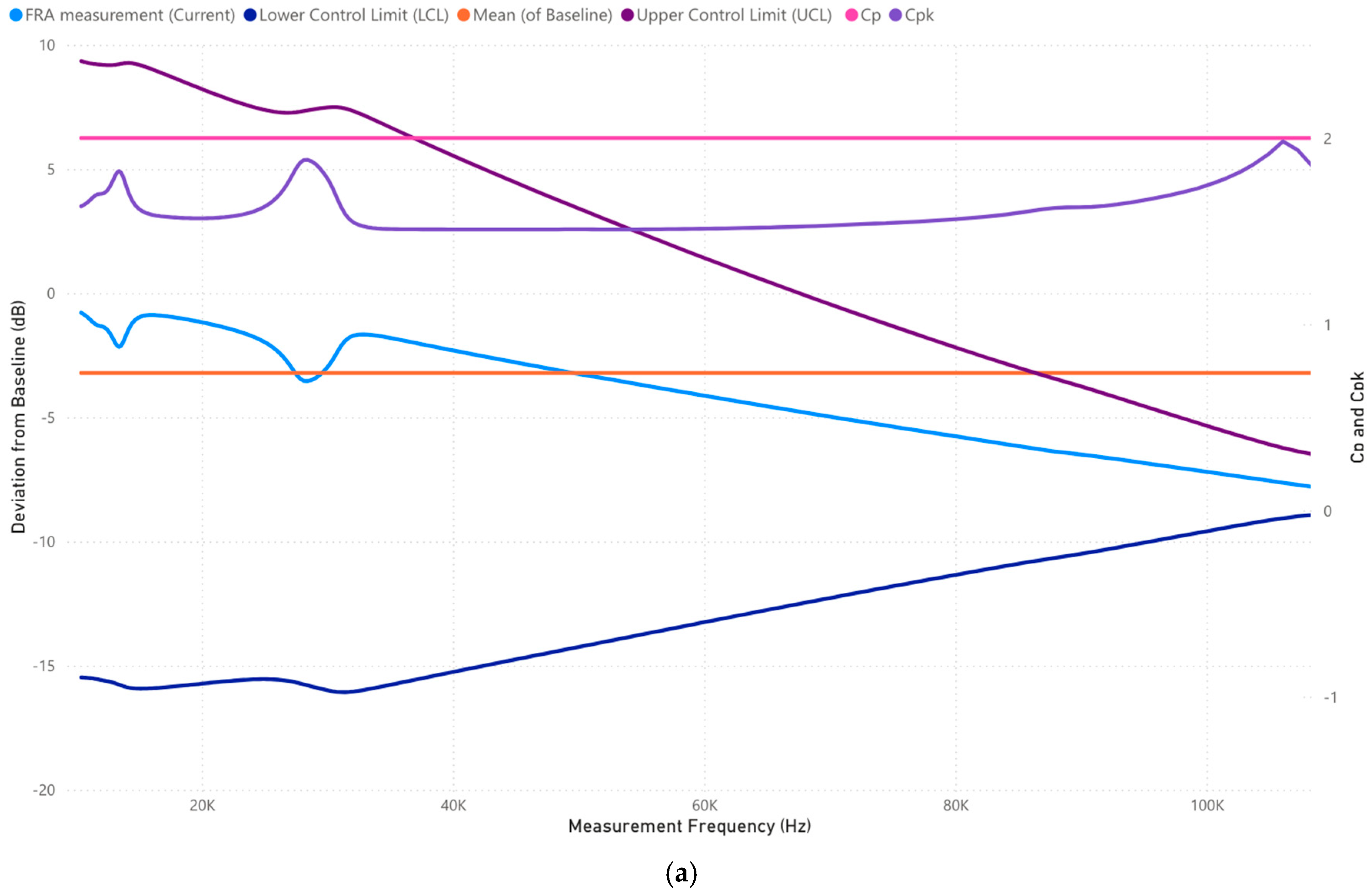
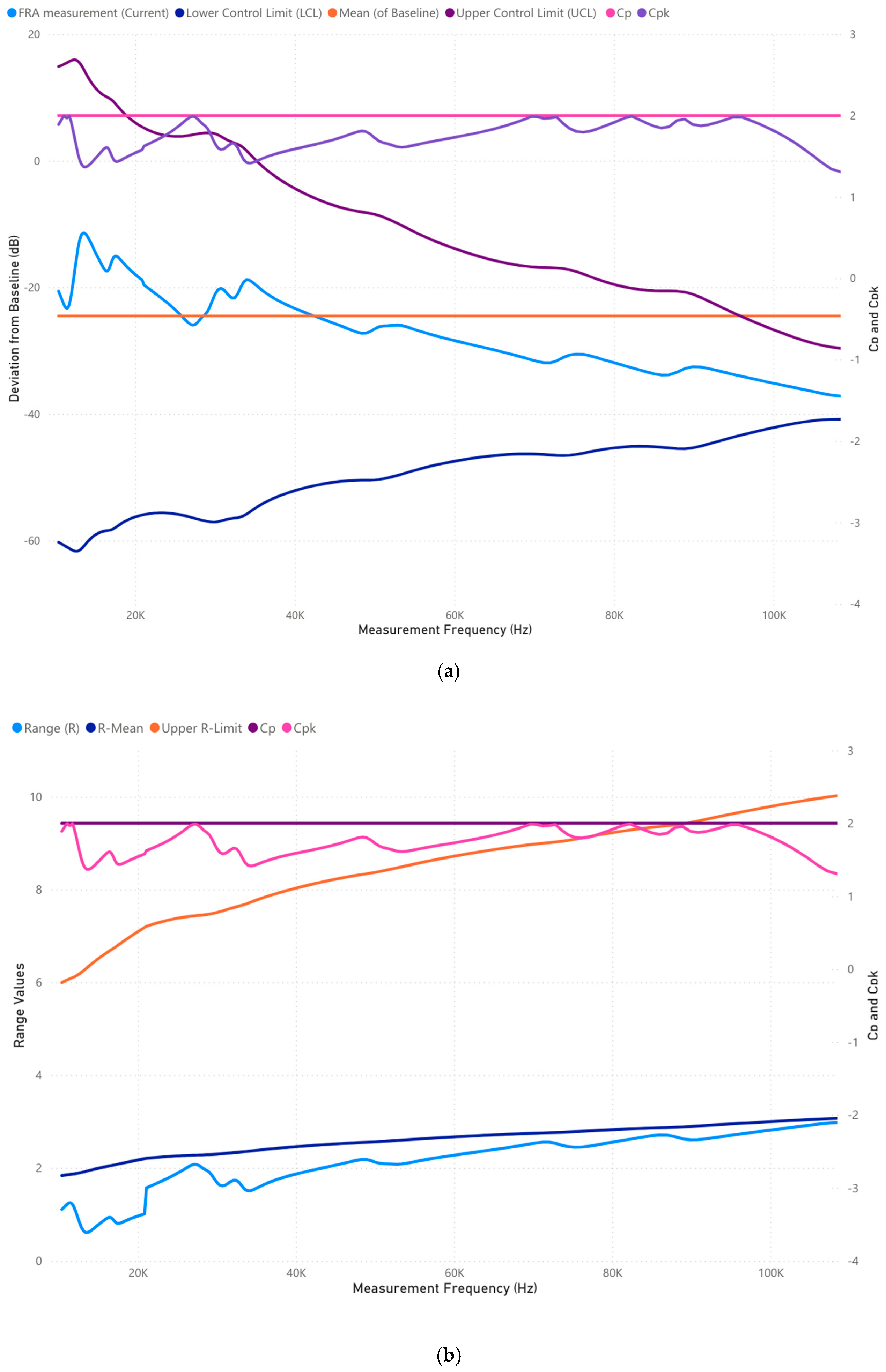
3.1.3. Case 1: Analysis of 10,000–100,000 Frequency Range (Hz)
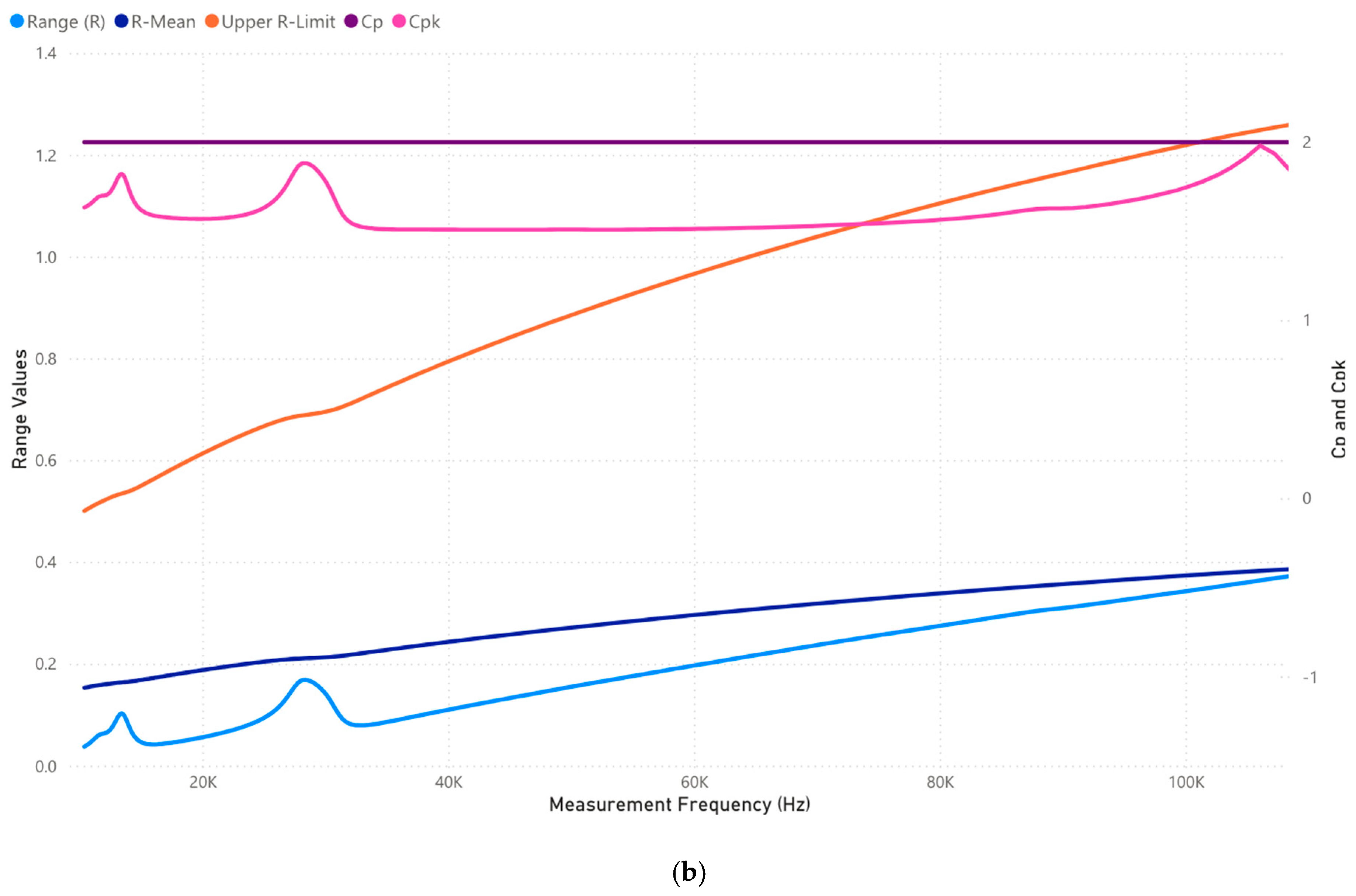
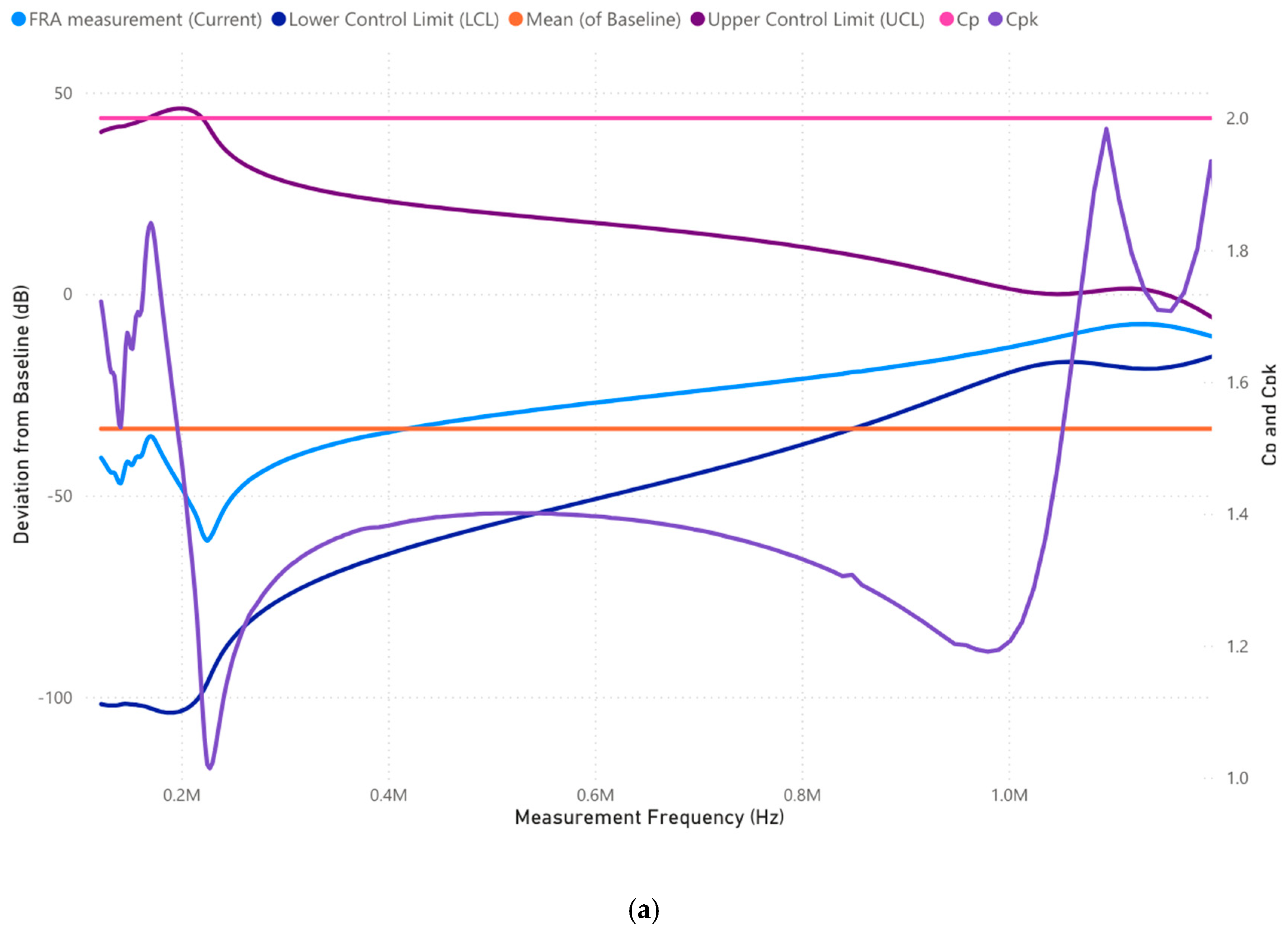
3.1.4. Case 1: Analysis of 100,000–1,000,000 Frequency Range (Hz)
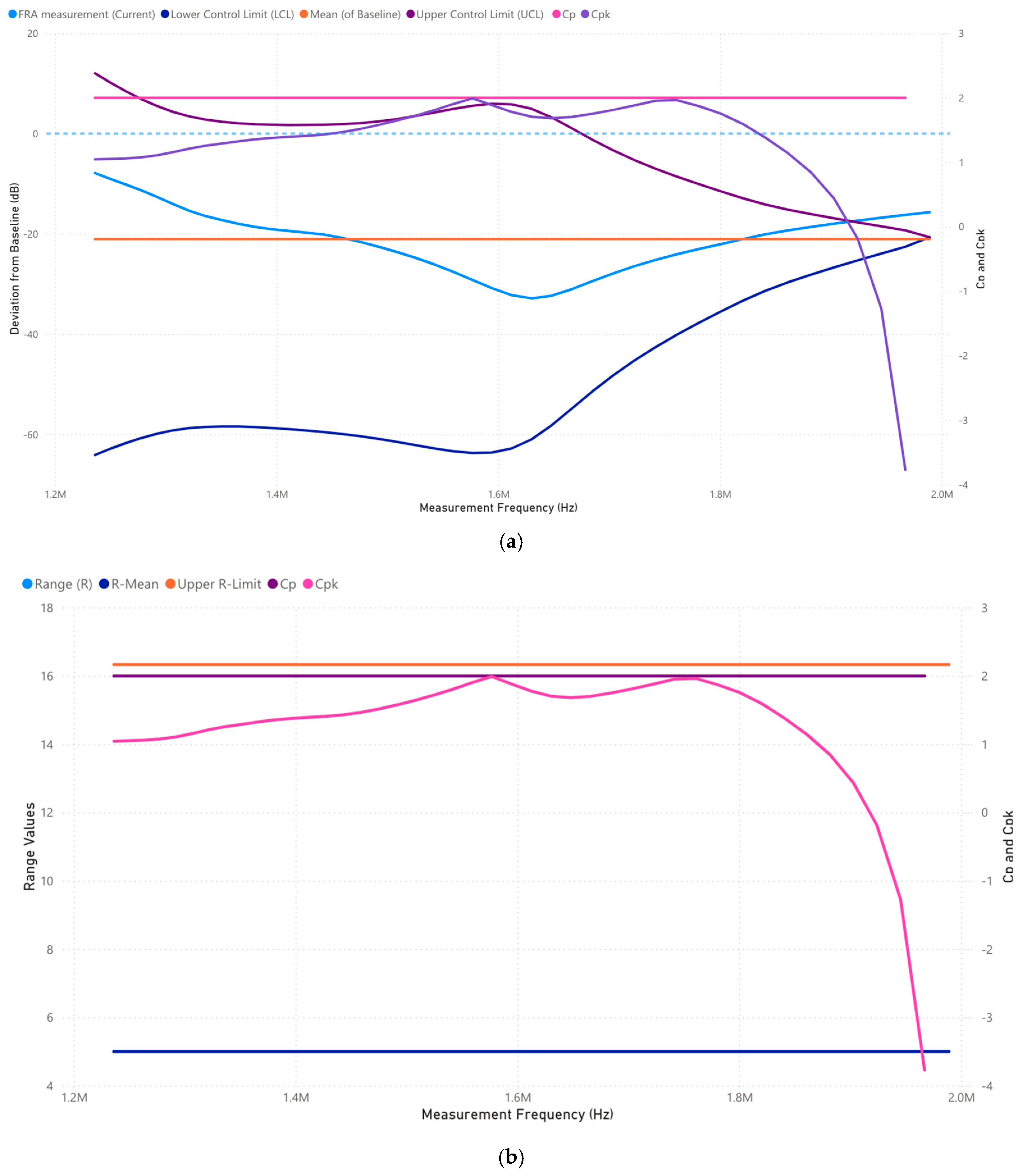
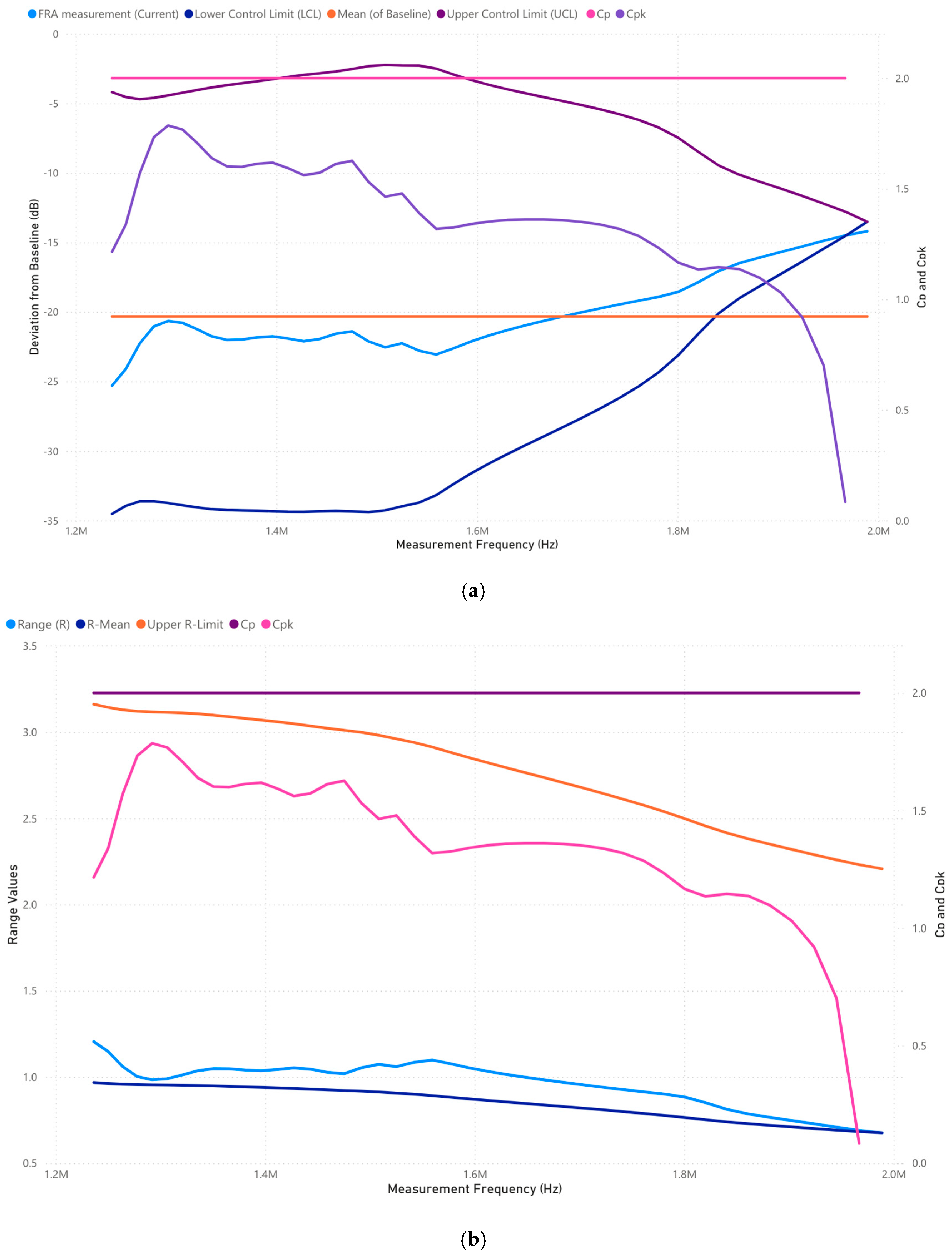
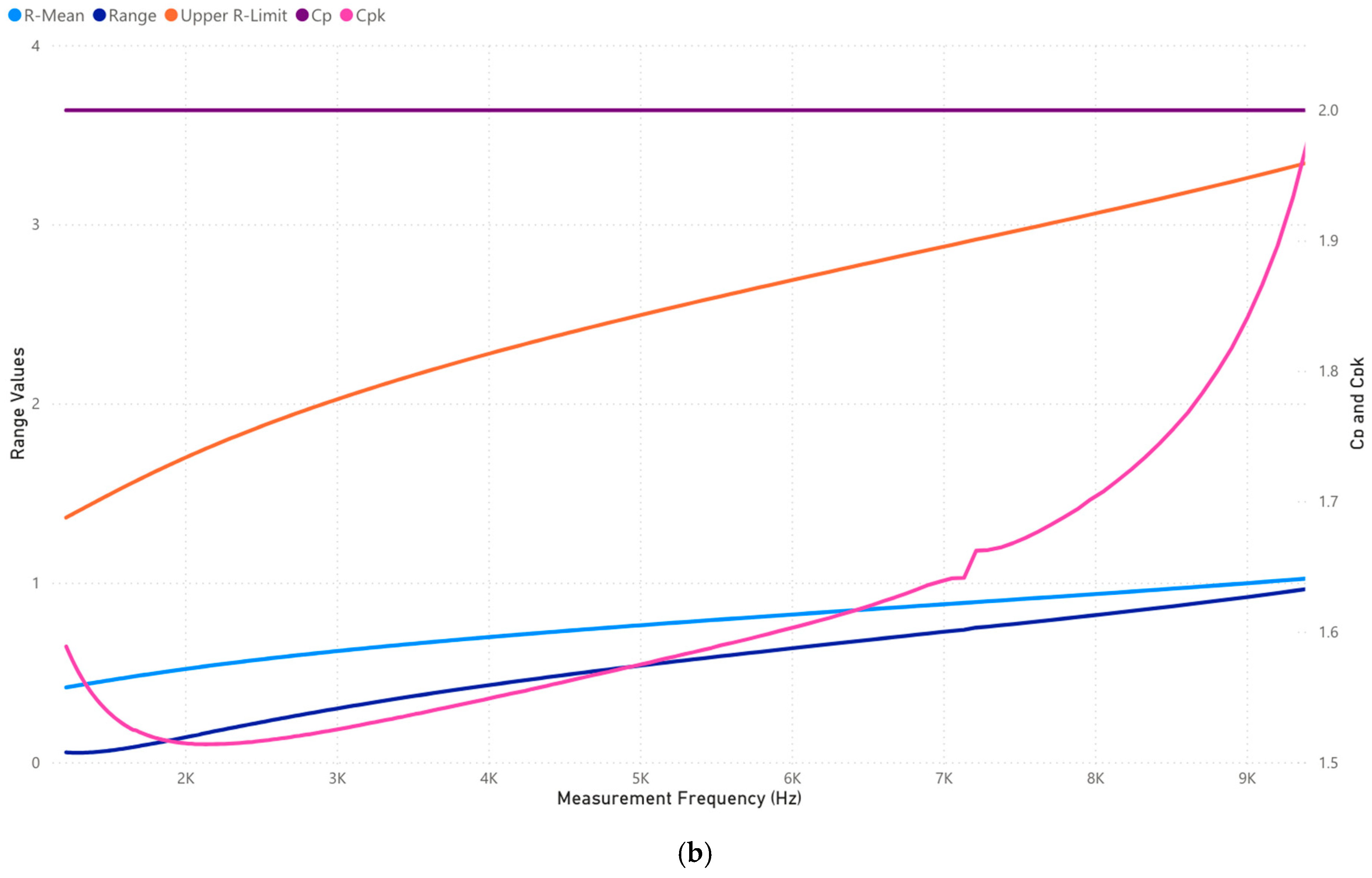
3.1.5. Case 1: Analysis of 1,000,000–2,000,000 Frequency Range (Hz)
3.2. Case 2
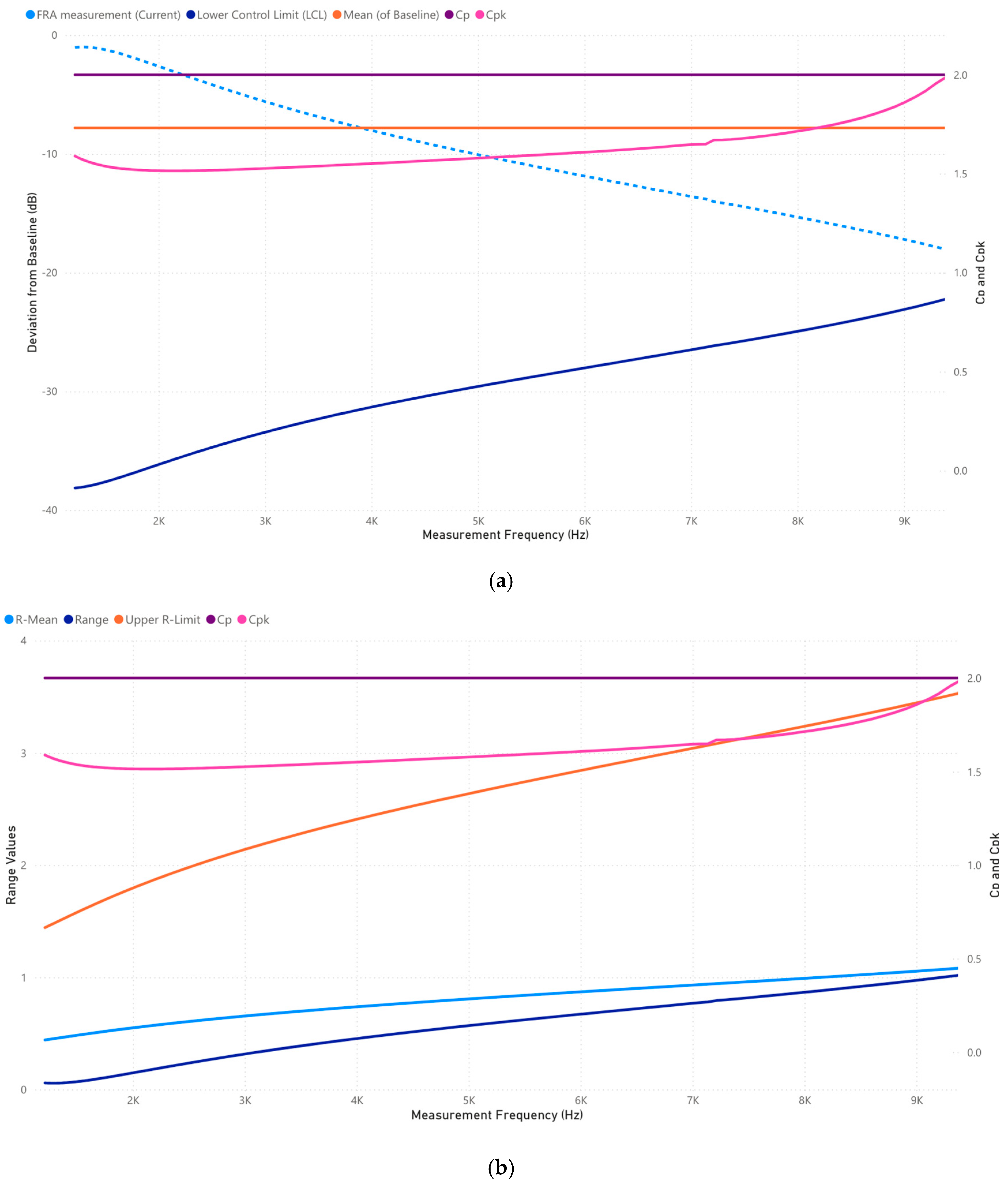
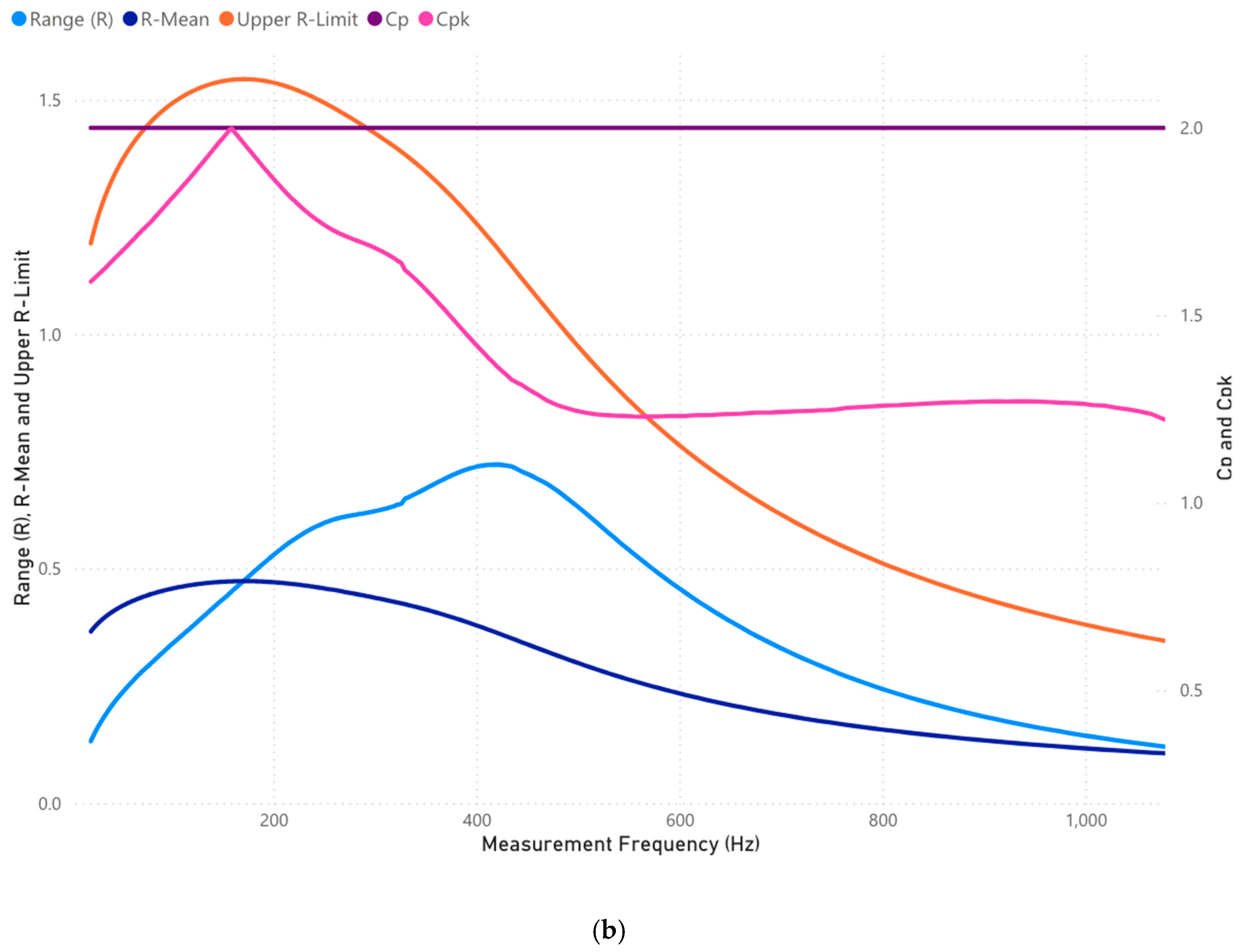
3.2.1. Case 2: Analysis of 10–1000 Frequency Range (Hz)
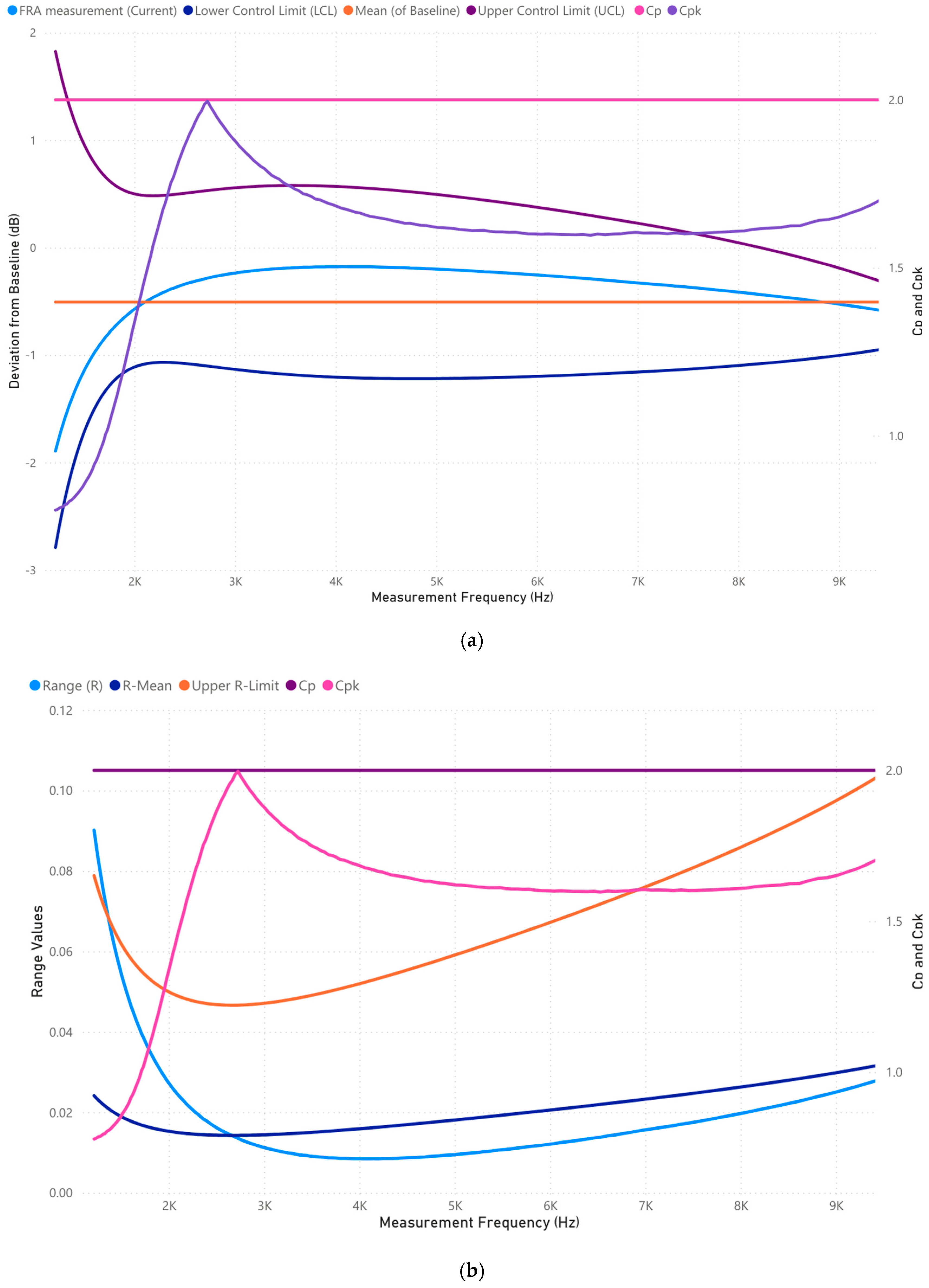
3.2.2. Case 2: Analysis of 1000–10,000 Frequency Range (Hz)
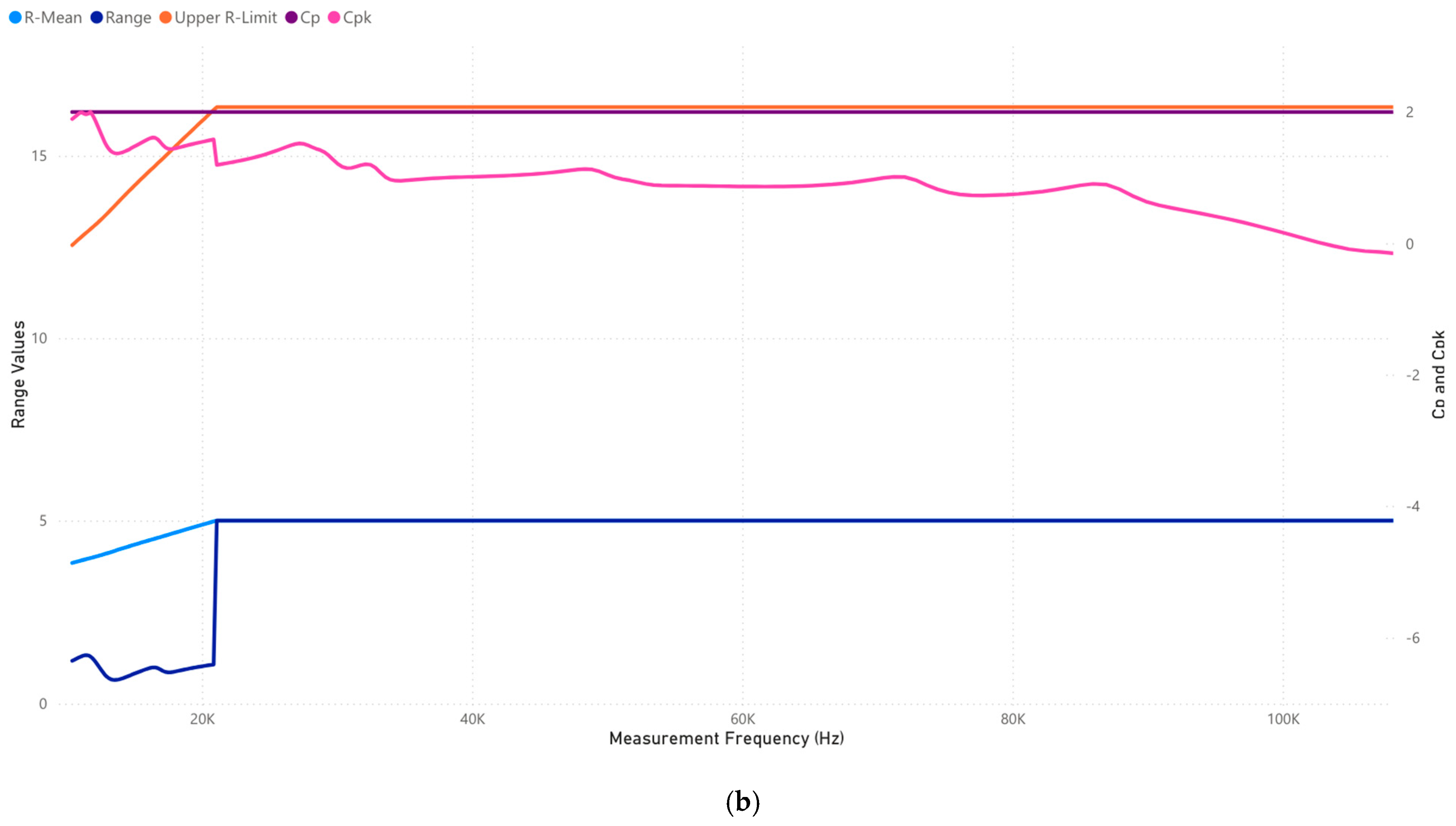
3.2.3. Case 2: Analysis of 10,000–100,000 Frequency Range (Hz)
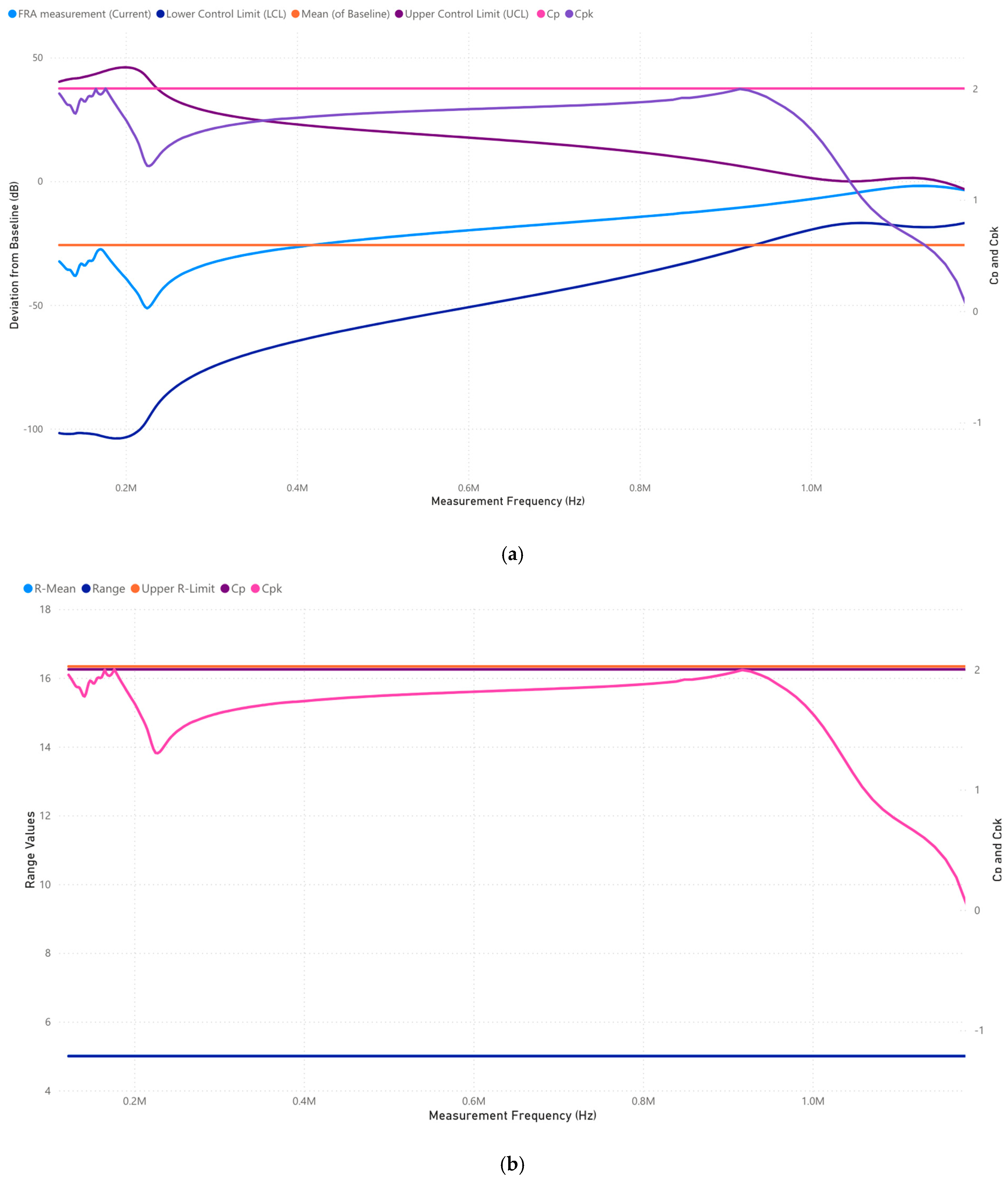
3.2.4. Case 2: Analysis of 100,000–1,000,000 Frequency Range (Hz)
3.2.5. Case 2: Analysis of 1,000,000–2,000,000 Frequency Range (Hz)
3.3. Case 3
3.3.1. Case 3: Analysis of 10–1000 Frequency Range (Hz)
3.3.2. Case 3: Analysis of 1000–10,000 Frequency Range (Hz)
3.3.3. Case 3: Analysis of 10,000–100,000 Frequency Range (Hz)
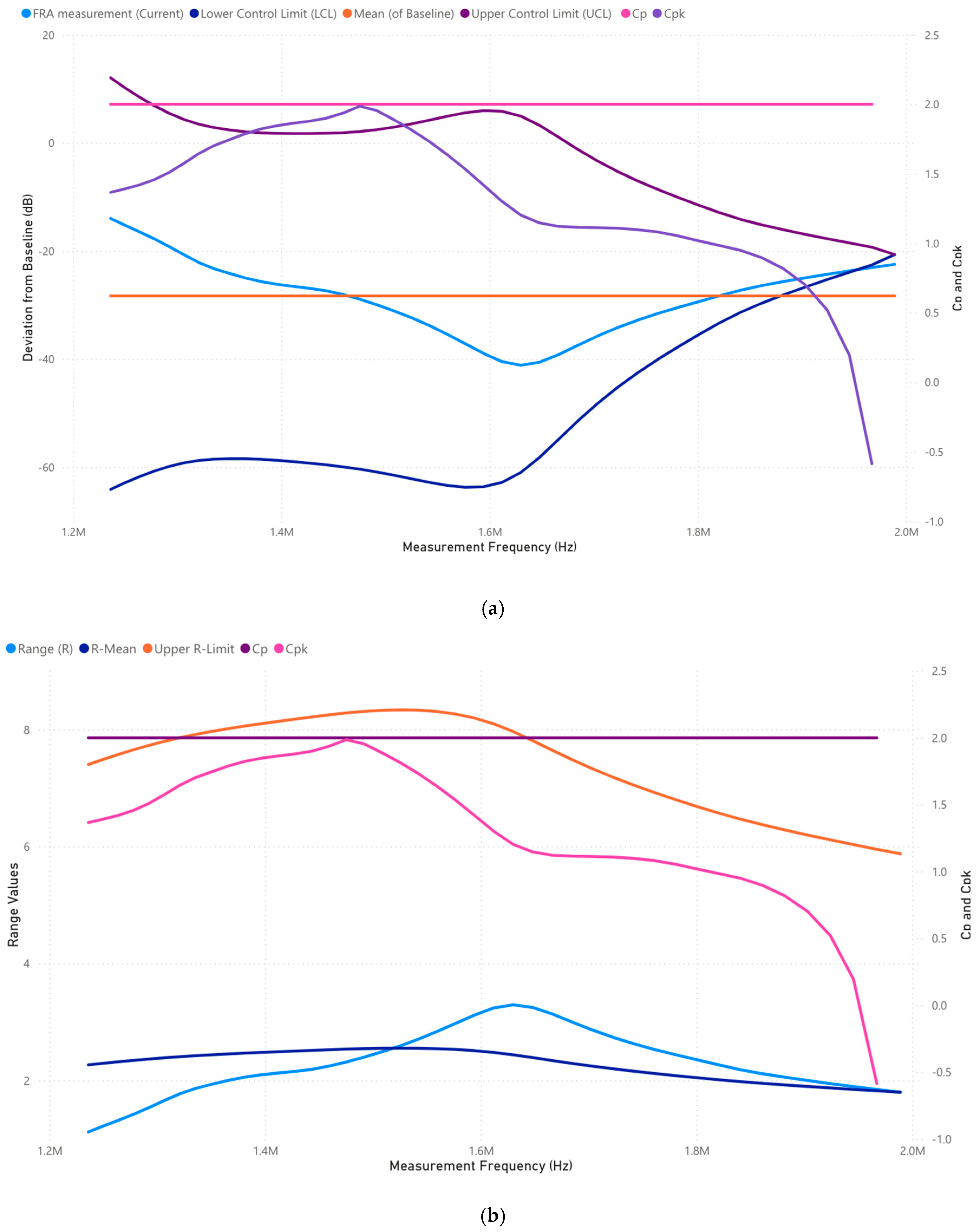
3.3.4. Case 3: Analysis of 100,000–1,000,000 Frequency Range (Hz)
- A strong drop-off at ~250 kHz, suggesting potential winding-to-ground insulation degradation.
- An additional divergence at ~800 kHz, which may indicate tap changer degradation or internal grounding anomalies.
3.3.5. Case 3: Analysis of 1,000,000–2,000,000 Frequency Range (Hz)
4. Discussion
- FRA6σ successfully detects faults at an early stage, particularly in core deformation, clamping pressure relaxation, winding displacement, and insulation degradation—even when these are not yet physically observable.
- The approach outperforms conventional FRA by leveraging statistical control limits (UCL, LCL) and process capability indices (,), making fault detection more quantifiable and repeatable.
- The methodology is particularly effective in the mid-to-high-frequency ranges, where insulation weaknesses and partial discharges are challenging to identify using standard FRA or physical assessment alone.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 6σ | Six Sigma |
| Cp | Process capability index |
| Cpk | Process capability performance index |
| FRA | Frequency response analysis |
| FRA6σ | Frequency response analysis with Six Sigma |
| LCL | Lower control limit |
| UCL | Upper control limit |
| PD | Partial discharge |
| X-chart | |
| -chart | Range chart |
References
- Aleissaee, A.A.; Kumar, A.; Anwer, R.M.; Khan, S.; Cholakkal, H.; Xia, G.-S.; Khan, F.S. Transformers in Remote Sensing: A Survey. Remote Sens. 2023, 15, 1860. [Google Scholar] [CrossRef]
- Maurício, J.; Domingues, I.; Bernardino, J. Comparing Vision Transformers and Convolutional Neural Networks for Image Classification: A Literature Review. Appl. Sci. 2023, 13, 5521. [Google Scholar] [CrossRef]
- Patwardhan, N.; Marrone, S.; Sansone, C. Transformers in the Real World: A Survey on NLP Applications. Information 2023, 14, 242. [Google Scholar] [CrossRef]
- Kim, H.-C.; Kim, J.-S. Development and Validation of Reliability Testing Methods for Insulation Systems in High-Voltage Rotating Electrical Machinery on Ships. J. Mar. Sci. Eng. 2025, 13, 186. [Google Scholar] [CrossRef]
- Pei, T.; Zhang, H.; Hua, W.; Zhang, F. Comprehensive Review of Bearing Currents in Electrical Machines: Mechanisms, Impacts, and Mitigation Techniques. Energies 2025, 18, 517. [Google Scholar] [CrossRef]
- Oh, Y.-H.; Hong, D.-K.; Park, J.-K.; Ahn, H.-M.; Song, K.-D. Optimum Design of Transformers for Offshore Wind Power Generators Considering Their Behavior. Electronics 2025, 14, 233. [Google Scholar] [CrossRef]
- Arı, İ.; Mamiş, M.S. Voltage Distribution on Transformer Windings Subjected to Lightning Strike Using State-Space Method. Appl. Sci. 2025, 15, 1569. [Google Scholar] [CrossRef]
- Cao, C.; Li, Z.; Wang, J.; Zhang, J.; Li, Y.; Wang, Q. Research on Simulation Analysis and Joint Diagnosis Algorithm of Transformer Core-Loosening Faults Based on Vibration Characteristics. Energies 2025, 18, 914. [Google Scholar] [CrossRef]
- Hu, H.; Xu, K.; Zhang, X.; Li, F.; Zhu, L.; Xu, R.; Li, D. Research on Predictive Maintenance Methods for Current Transformers with Iron Core Structures. Electronics 2025, 14, 625. [Google Scholar] [CrossRef]
- Rugthaicharoencheep, N.; Nedphokaew, S. Simulation and Analysis of the Optimal Electric Field from Modifications to the Winding Design for the Tesla Transformer. Energies 2025, 18, 339. [Google Scholar] [CrossRef]
- Zhou, Q.; Mao, Y.; Guo, F.; Liu, Y. Seismic Response Prediction of Porcelain Transformer Bushing Using Hybrid Metaheuristic and Machine Learning Techniques: A Comparative Study. Mathematics 2024, 12, 2084. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Chen, J.; Bie, Y.; Jiang, J.; Yang, X. Oil Pressure Monitoring for Sealing Failure Detection and Diagnosis of Power Transformer Bushing. Energies 2021, 14, 7908. [Google Scholar] [CrossRef]
- de Castro, B.A.; Lucas, G.B.; Fernandes, G.S.; Fraga, J.R.C.P.; Riehl, R.R.; Andreoli, A.L. Assessment of Partial Discharges Evolution in Bushing by Infrared Analysis. Eng. Proc. 2021, 10, 18. [Google Scholar] [CrossRef]
- Zemouri, R. Power Transformer Prognostics and Health Management Using Machine Learning: A Review and Future Directions. Machines 2025, 13, 125. [Google Scholar] [CrossRef]
- Ko, S.; Lee, S. Multi-Patch Time Series Transformer for Robust Bearing Fault Detection with Varying Noise. Appl. Sci. 2025, 15, 1257. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, J.; Xu, P.; Liang, Y.; Dai, Y.; Gao, T.; Bai, Y. Bearing Fault Diagnosis for Cross-Condition Scenarios Under Data Scarcity Based on Transformer Transfer Learning Network. Electronics 2025, 14, 515. [Google Scholar] [CrossRef]
- Trela, K.; Gawrylczyk, K.M. Modeling of Axial Displacements of Transformer Windings for Frequency Response Analysis Diagnosis. Energies 2024, 17, 3274. [Google Scholar] [CrossRef]
- Kornatowski, E.; Banaszak, S.; Molenda, P. Quality Index for Assessment of the Mechanical Condition of Transformers’ Active Part with Frequency Response and Vibroacoustic Measurements. Energies 2024, 17, 1431. [Google Scholar] [CrossRef]
- Al-Ameri, S.M.; Kamarudin, M.S.; Yousof, M.F.M.; Salem, A.A.; Siada, A.A.; Mosaad, M.I. Interpretation of Frequency Response Analysis for Fault Detection in Power Transformers. Appl. Sci. 2021, 11, 2923. [Google Scholar] [CrossRef]
- Al-Ameri, S.M.; Almutairi, A.; Kamarudin, M.S.; Yousof, M.F.M.; Abu-Siada, A.; Mosaad, M.I.; Alyami, S. Application of Frequency Response Analysis Technique to Detect Transformer Tap Changer Faults. Appl. Sci. 2021, 11, 3128. [Google Scholar] [CrossRef]
- Tahir, M.; Tenbohlen, S. Transformer Winding Condition Assessment Using Feedforward Artificial Neural Network and Frequency Response Measurements. Energies 2021, 14, 3227. [Google Scholar] [CrossRef]
- Al-Ameri, S.M.; Alawady, A.A.; Abdul-Malek, Z.; Noorden, Z.A.; Yousof, M.F.M.; Salem, A.A.; Mosaad, M.I.; Abu-Siada, A. Frequency Response Analysis: An Enabling Technology to Detect Internal Faults within Critical Electric Assets. Appl. Sci. 2022, 12, 9201. [Google Scholar] [CrossRef]
- Ding, H.; Zhao, W.; Diao, C.; Li, M. Electromagnetic Vibration Characteristics of Inter-Turn Short Circuits in High Frequency Transformer. Electronics 2023, 12, 1884. [Google Scholar] [CrossRef]
- Al-Ameri, S.M.; Alawady, A.A.; Yousof, M.F.M.; Kamarudin, M.S.; Salem, A.A.; Abu-Siada, A.; Mosaad, M.I. Application of Frequency Response Analysis Method to Detect Short-Circuit Faults in Three-Phase Induction Motors. Appl. Sci. 2022, 12, 2046. [Google Scholar] [CrossRef]
- Hu, C.; Zhu, X.; Lu, Y.; Liu, Z.; Wang, Z.; Liu, Z.; Yin, K. Localization and Diagnosis of Short-Circuit Faults in Transformer Windings Injected by Damped Oscillatory Wave. Energies 2024, 17, 6259. [Google Scholar] [CrossRef]
- Tabrez, M.; Sadhu, P.K.; Hossain Lipu, M.S.; Iqbal, A.; Husain, M.A.; Ansari, S. Power Conversion Techniques Using Multi-Phase Transformer: Configurations, Applications, Issues and Recommendations. Machines 2022, 10, 13. [Google Scholar] [CrossRef]
- Luo, X.; Xiao, Q.; Wang, Q.; Gan, W.; Deng, B.; Sheng, Z. Research on short-circuit force of transformer winding with single-phase short-circuit and three-phase short-circuit. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; pp. 219–223. [Google Scholar]
- Tang, Y.; Chang, Y.; Tang, J.; Xu, B.; Ye, M.; Yang, H. A Novel Faulty Phase Selection Method for Single-Phase-to-Ground Fault in Distribution System Based on Transient Current Similarity Measurement. Energies 2021, 14, 4695. [Google Scholar] [CrossRef]
- Tahir, M.; Tenbohlen, S. A Comprehensive Analysis of Windings Electrical and Mechanical Faults Using a High-Frequency Model. Energies 2020, 13, 105. [Google Scholar] [CrossRef]
- Mynarek, P.; Kołodziej, J.; Młot, A.; Kowol, M.; Łukaniszyn, M. Influence of a Winding Short-Circuit Fault on Demagnetization Risk and Local Magnetic Forces in V-Shaped Interior PMSM with Distributed and Concentrated Winding. Energies 2021, 14, 5125. [Google Scholar] [CrossRef]
- Shi, X.; Wei, R.; Zhang, W. Research on Online Detection Method of Transformer Winding Deformation Based on VFTO Characteristics. Energies 2023, 16, 3496. [Google Scholar] [CrossRef]
- Sanchez-Gonzalez, A.; Medrano, N.; Calvo, B.; Martinez, P.A. A Multichannel FRA-Based Impedance Spectrometry Analyzer Based on a Low-Cost Multicore Microcontroller. Electronics 2019, 8, 38. [Google Scholar] [CrossRef]
- Banaszak, S.; Kornatowski, E.; Szoka, W. The Influence of the Window Width on FRA Assessment with Numerical Indices. Energies 2021, 14, 362. [Google Scholar] [CrossRef]
- Banaszak, S.; Gawrylczyk, K.M.; Trela, K.; Bohatyrewicz, P. The Influence of Capacitance and Inductance Changes on Frequency Response of Transformer Windings. Appl. Sci. 2019, 9, 1024. [Google Scholar] [CrossRef]
- Kornatowski, E.; Banaszak, S. Frequency Response Quality Index for Assessing the Mechanical Condition of Transformer Windings. Energies 2020, 13, 29. [Google Scholar] [CrossRef]
- Phillip, M.; Singh, A.; Ramlal, C.J. Narrow Band Frequency Response Analysis of Power Transformers with Deep Learning. Energies 2023, 16, 6347. [Google Scholar] [CrossRef]
- Tahir, M.; Tenbohlen, S. Transformer Winding Fault Classification and Condition Assessment Based on Random Forest Using FRA. Energies 2023, 16, 3714. [Google Scholar] [CrossRef]
- Huerta-Rosales, J.R.; Granados-Lieberman, D.; Garcia-Perez, A.; Camarena-Martinez, D.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M. Short-Circuited Turn Fault Diagnosis in Transformers by Using Vibration Signals, Statistical Time Features, and Support Vector Machines on FPGA. Sensors 2021, 21, 3598. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, C.; Zhou, Q.; Xu, L.; Gui, Y.; Yao, C. Identification of Power Transformer Winding Mechanical Fault Types Based on Online IFRA by Support Vector Machine. Energies 2017, 10, 2022. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Abu-Siada, A.; Chen, X.; Li, Z.; Xu, Y.; Zhang, L.; Tong, Y. Fault Diagnosis of Transformer Windings Based on Decision Tree and Fully Connected Neural Network. Energies 2021, 14, 1531. [Google Scholar] [CrossRef]
- Suassuna de Andrade Ferreira, R.; Picher, P.; Ezzaidi, H.; Fofana, I. A Machine-Learning Approach to Identify the Influence of Temperature on FRA Measurements. Energies 2021, 14, 5718. [Google Scholar] [CrossRef]
- Ismail, F.B.; Mazwan, M.; Al-Faiz, H.; Marsadek, M.; Hasini, H.; Al-Bazi, A.; Yang Ghazali, Y.Z. An Offline and Online Approach to the OLTC Condition Monitoring: A Review. Energies 2022, 15, 6435. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, X.; Cai, Y.; Tian, X. Robust collaborative optimization design of plug-in hybrid electric bus based on 6 Sigma theory. IEEE Trans. Transp. Electrif. 2024, 10, 10253–10261. [Google Scholar]
- Niemann, J.; Reich, B.; Stöhr, C. Lean six sigma. In Lean Six Sigma: Methoden zur Produktionsoptimierung; Springer: Berlin/Heidelberg, Germany, 2021; pp. 11–61. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Six Sigma. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Six_Sigma (accessed on 24 February 2025).
- IEEE. PC57.149/D9.2 Jun 2012—IEEE Draft Guide for the Application and Interpretation of Frequency Response Analysis for Oil Immersed Transformers; IEEE: Piscataway, NJ, USA, 2012; pp. 1–68. Available online: https://ieeexplore.ieee.org/document/6239540 (accessed on 10 March 2025).
- CIGRE WG A2.53. Advances in the Interpretation of Transformer Frequency Response Analysis (FRA); Technical Brochure 812; CIGRE: Paris, France, 2020; Available online: https://electra.cigre.org/312-october-2020/technical-brochures/advances-in-the-interpretation-of-transformer-frequency-response-analysis-fra.html (accessed on 10 March 2025).
- Liu, Y.; Chen, G.; Xu, F.; Zhao, T.; Liu, H. Low-frequency noise removal and acoustic spectral distribution assessment method for high-voltage power transformers with varying service lifetimes. IET Electr. Power Appl. 2025, 19, e12545. [Google Scholar] [CrossRef]
- Babak, V.; Babak, S.; Zaporozhets, A. Tasks and Main Methods of Statistical Diagnostics of Electric Power Equipment. In Statistical Diagnostics of Electric Power Equipment; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2025; Volume 573. [Google Scholar] [CrossRef]
- Bagheri, M.; Lu, M.; Naderi, M.S.; Phung, B.T. Transformer frequency response: A new technique to analyze and distinguish the low-frequency band in the frequency response analysis spectrum. IEEE Electr. Insul. Mag. 2018, 34, 39–49. [Google Scholar] [CrossRef]
- Kornatowski, E.; Banaszak, S. Diagnostics of a transformer’s active part with complementary FRA and VM measurements. IEEE Trans. Power Deliv. 2013, 29, 1398–1406. [Google Scholar] [CrossRef]
- Munir, B.S.; Smit, J.J.; Rinaldi, I.G. Diagnosing winding and core condition of power transformer by vibration signal analysis. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23 September 2012; pp. 429–432. [Google Scholar] [CrossRef]
- Dastous, J.B.; Picher, P. Transformer and Reactor Mechanical Condition Assessment. In Transformer and Reactor Life Management; Springer Nature: Cham, Switzerland, 2024; pp. 619–664. Available online: https://link.springer.com/content/pdf/10.1007/978-3-031-77219-1_21.pdf (accessed on 10 March 2025).
- Hashemnia, N.; Abu-Siada, A.; Masoum, M.A.; Islam, S.M. Characterization of transformer FRA signature under various winding faults. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23 September 2012; pp. 446–449. Available online: https://ieeexplore.ieee.org/abstract/document/6416174/ (accessed on 10 March 2025).
- Tang, W.H.; Wu, Q.H.; Tang, W.H.; Wu, Q.H. Winding frequency response analysis for power transformers. In Condition Monitoring and Assessment of Power Transformers Using Computational Intelligence; Springer: London, UK, 2011; pp. 163–175. Available online: https://link.springer.com/chapter/10.1007/978-0-85729-052-6_9 (accessed on 10 March 2025).
- Hashemnia, N.; Abu-Siada, A.; Islam, S. Impact of axial displacement on power transformer FRA signature. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21 July 2013; pp. 1–4. Available online: https://ieeexplore.ieee.org/abstract/document/6672949/ (accessed on 10 March 2025).
- Mitchell, S.D.; Welsh, J.S. Methodology to locate and quantify radial winding deformation in power transformers. High Volt. 2017, 2, 17–24. [Google Scholar]
- Tahir, M.; Tenbohlen, S. FRA lookup charts for the quantitative determination of winding axial displacement fault in power transformers. IET Electr. Power Appl. 2020, 14, 2370–2377. [Google Scholar]
- Abu-Siada, A.; Aljohani, O. Detecting incipient radial deformations of power transformer windings using polar plot and digital image processing. IET Sci. Meas. Technol. 2018, 12, 492–499. [Google Scholar]
- Nasser Al-Ameri, S.M. Improvement of Distribution Transformer Fault Analysis Using FRA Method. Doctoral Dissertation, Universiti Tun Hussein Onn Malaysia, Parit Raja, Malaysia, 2021. Available online: http://eprints.uthm.edu.my/id/eprint/942 (accessed on 10 March 2025).
- Fofana, I.; Hadjadj, Y. Electrical-Based Diagnostic Techniques for Assessing Insulation Condition in Aged Transformers. Energies 2016, 9, 679. [Google Scholar] [CrossRef]
- Ahmed Al-subari, M.M. Investigating the Application of Frequency Response Analysis for Diagnosing Tap Changer on Power Transformer. Doctoral Dissertation, Universiti Tun Hussein Onn Malaysia, Parit Raja, Malaysia, 2021. Available online: http://eprints.uthm.edu.my/id/eprint/433 (accessed on 10 March 2025).
- Abd Rahman, M.S. Identification of Partial Discharge Sources and Their Location Within High Voltage Transformer Windings. Doctoral Dissertation, University of Southampton, Southampton, UK, 2014. Available online: https://eprints.soton.ac.uk/369418/ (accessed on 10 March 2025).
- Sikorski, W.; Walczak, K.; Gil, W.; Szymczak, C. On-Line partial discharge monitoring system for power transformers based on the simultaneous detection of high frequency, ultra-high frequency, and acoustic emission signals. Energies 2020, 13, 3271. [Google Scholar] [CrossRef]








| Ref. | Fault Type | Category | Cause | Effect on Transformer |
|---|---|---|---|---|
| [23,24] | Inter-Turn Short Circuit | Electrical Fault | Insulation breakdown between adjacent winding turns. | Increased winding currents, localized overheating, and accelerated insulation degradation. |
| [25,26,27] | Phase-to-Phase Short Circuit | Electrical Fault | Breakdown of insulation between phases. | High-circulating currents, increased loss, and potential failure of windings. |
| [28] | Phase-to-Ground Fault | Electrical Fault | Breakdown of winding insulation to transformer core or tank. | Large fault currents, overheating, risk of catastrophic failure. |
| [29,30,31] | Radial Deformation of Windings | Mechanical Fault | Electromagnetic forces cause outward/inward movement of windings. | Reduced mechanical strength, increased stress on insulation, and possible turn-to-turn faults. |
| Axial Displacement of Windings | Mechanical Fault | Short circuit forces push windings up/down along the core. | Potential loosening of clamping structure, increased mechanical stress. | |
| Winding Looseness | Mechanical Fault | Mechanical vibrations, insufficient clamping force, or thermal expansion. | Higher noise, excessive vibration, and risk of progressive deformation. |
| Excitation Voltage (V) | Method | Application |
|---|---|---|
| 0.2–2 V | FRA | Common for standard FRA testing to avoid saturation and maintain linearity. |
| 1 V RMS | FRA Setup | Most used voltage for FRA across a wide frequency range (20 Hz–2 MHz). |
| 5–20 V | Impulse FRA (IFRA) | Higher voltage is used in some impulse-based FRA methods but is less common in industry practice. |
| k Value | Confidence Interval (%) | Sensitivity Level |
|---|---|---|
| 3 | 99.73% | More strict |
| 2 | 95.45% | Moderate |
| 1.5 | 86.64% | Sensitive |
| Cp | Sigma Level (σ-Level) | Process Stability | Action Required |
|---|---|---|---|
| 2.00 | ≥6σ | Highly stable | No action required |
| 1.75 | 4σ–5σ | Acceptable but monitor trends | Routine monitoring |
| 1.50 | 4σ–5σ | Acceptable but monitor trends | Routine monitoring |
| 1.25 | 3σ–4σ | Marginal stability | Investigate for early-stage faults |
| 1.00 | 3σ–4σ | Marginal stability | Investigate for early-stage faults |
| 0.75 | <3σ | Process out of control | High probability of transformer failure |
| 0.50 | <3σ | Process out of control | High probability of transformer failure |
| Sample Size (n) | D4 Constant |
|---|---|
| 2 | 3.267 |
| 3 | 2.574 |
| 4 | 2.282 |
| 5 | 2.114 |
| 6 | 2.004 |
| Condition | Observation in -Chart | Conclusion |
|---|---|---|
| Stable process | (1) Transformer process is stable. (2) Variations are within acceptable limits. (3) No significant mechanical changes detected. | |
| Potential faults detected | (1) Excessive mechanical variation or an emerging defect is indicated. (2) Possible faults include winding displacement, insulation failure, core movement, or clamping pressure loss. |
| Ref. | Frequency Range (Hz) | Category/Region | Likely Transformer Faults | Physical Interpretation |
|---|---|---|---|---|
| [46,47,48,49,50] | 10–1000 | Low frequency | Core deformation, core movement, core looseness, magnetostriction effects | (1) Magnetic properties dominate. (2) Deviation in this range indicates core structure faults. |
| [51,52,53,54,55] | 1000–10,000 | Mid–low frequency | Clamping pressure loss, bulk winding movement, mechanical displacement | (1) Related to overall winding movement and mechanical stress. (2) Affected by winding shifting, clamping pressure loss, and bulk displacement. |
| [46,47,56,57,58,59] | 10,000–100,000 | Mid frequency | Axial and radial winding deformation, disc space variation, insulation compression failure | (1) Influenced by inter-winding and intra-winding capacitance. (2) Significant for radial and axial deformation in the windings. |
| [46,47,60,61,62] | 100,000–1,000,000 | High frequency | Insulation breakdown between winding turns, tap changer defects, grounding issues | (1) Small, localized defects in conductor insulation. (2) Sensitive to changes in grounding and inter-turn short circuits. |
| [46,47,63,64] | 1,000,000–2,000,000 | Upper high frequency | Partial discharges, floating metal parts, loose clamps and connections | (1) Dominated by parasitic capacitance and localized insulation breakdown. (2) Detects floating conductive parts, loose clamps, and insulation failure. |
| Condition | Observation | Conclusion |
|---|---|---|
| Case 1: Transformer is stable | FRA data remains within 6σ control limits. Cp and Cpk > 1.33. | No significant mechanical changes detected. Transformer is in good condition. |
| Case 2: Gradual degradation | FRA response approaches UCL/LCL but remains within limits. Cp and Cpk = 1.0–1.33. | Early signs of mechanical drift. Requires monitoring. |
| Case 3: Potential defects | FRA data crosses UCL/LCL in specific frequency bands. Cp or Cpk < 1. | Possible transformer defects (e.g., winding deformation, insulation failure). Immediate action required. |
| Case | Frequency Range (Hz) | FRA6σ Results (Proposed Approach) | Physical Inspection Findings | Remarks on Fault Detection |
|---|---|---|---|---|
| Case 1 | 10–1000 (Low frequency) | Minor core movement detected; slight deviation but within acceptable range | No visible core deformation | FRA6σ shows slight mechanical stress not yet detectable physically |
| 1000–10,000 (Mid–low frequency) | Clamping pressure loss suspected; FRA response shifts towards LCL | No looseness detected during inspection | Early detection of clamping pressure relaxation before full loosening | |
| 10,000–100,000 (Mid frequency) | Radial winding deformation developing; deviation approaches UCL | No visible deformation | Incipient issue identified before physical manifestation | |
| 100,000–1,000,000 (High frequency) | No major insulation breakdown, FRA response stable | No visible insulation failure | No immediate concern; both methods align | |
| 1,000,000–2,000,000 (Upper high frequency) | No signs of floating metal parts or PDs | No loose conductive parts detected | FRA6σ confirms no high-risk failure modes | |
| Case 2 | 10–1000 (Low frequency) | Significant core deformation detected | Minor signs of core displacement | FRA6σ detects early signs before they become severe |
| 1000–10,000 (Mid–low frequency) | Bulk winding movement identified; response near UCL | Slight shifting of winding observed | FRA6σ is more sensitive to mechanical shifts | |
| 10,000–100,000 (Mid frequency) | Disc spacing variation suspected; response fluctuation in this range | No visible disc compression | FRA6σ detects early winding structure changes before compression is visible | |
| 100,000–1,000,000 (High frequency) | Insulation degradation detected; Cpk drops below 1 | No immediate insulation failure detected | FRA6σ captures insulation weakening before failure | |
| 1,000,000–2,000,000 (Upper high frequency) | Potential partial discharge activity detected | No floating metal parts found | Incipient PD activity flagged early by FRA6σ | |
| Case 3 | 10–1000 (Low frequency) | Core movement minimal; response within expected limits | No core issues found | No significant deviation detected |
| 1000–10,000 (Mid–low frequency) | No major clamping loss; response remains stable | No visible mechanical issues | FRA6σ confirms stability | |
| 10,000–100,000 (Mid frequency) | Minor winding displacement; Cpk remains above 1.33 | No winding displacement observed | FRA6σ detects marginal deviations that might evolve later | |
| 100,000–1,000,000 (High frequency) | No insulation issues found; minor response variations | No insulation failure | FRA6σ confirms expected aging but no critical defects | |
| 1,000,000–2,000,000 (Upper high frequency) | No floating parts or PDs detected | No defects found | FRA6σ aligns with physical inspection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thango, B.A. Six Sigma-Based Frequency Response Analysis for Power Transformer Winding Deformation. Appl. Sci. 2025, 15, 3951. https://doi.org/10.3390/app15073951
Thango BA. Six Sigma-Based Frequency Response Analysis for Power Transformer Winding Deformation. Applied Sciences. 2025; 15(7):3951. https://doi.org/10.3390/app15073951
Chicago/Turabian StyleThango, Bonginkosi A. 2025. "Six Sigma-Based Frequency Response Analysis for Power Transformer Winding Deformation" Applied Sciences 15, no. 7: 3951. https://doi.org/10.3390/app15073951
APA StyleThango, B. A. (2025). Six Sigma-Based Frequency Response Analysis for Power Transformer Winding Deformation. Applied Sciences, 15(7), 3951. https://doi.org/10.3390/app15073951






