Next Article in Journal
Prediction Model for Compaction Quality of Earth-Rock Dams Based on IFA-RF Model
Previous Article in Journal
Analysis of Tribological Properties of Expanded Graphite—Alloy Steel Pair Under High Loads in Dry and Humid Conditions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 7
10.3390/app15074023
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study on Single-Event Transient Hardness of Semi-Enclosed Gate NMOS

by
Zhuoxiang Wang
,
Gang Li
and
Minghua Tang
*
School of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(7), 4023; https://doi.org/10.3390/app15074023
Submission received: 11 March 2025 / Revised: 31 March 2025 / Accepted: 3 April 2025 / Published: 5 April 2025
Browse Figures
Versions Notes

Abstract

:
Based on the simulation software, single-event transient (SET) simulations were conducted on semi-enclosed gate NMOS devices. The simulation involved bombarding the semi-enclosed gate NMOS devices with heavy ions under specific conditions. A comparative analysis was conducted to evaluate the single-event transient tolerance of traditional NMOS and semi-enclosed gate NMOS. Simulation curves from transient to steady-state states under different Linear Energy Transfer (LET) values, as well as potential distribution and current density distribution maps following heavy ion bombardment, were analyzed. Furthermore, single-event transient simulations were carried out on inverters composed of both NMOS types, with subsequent analysis. The results ultimately demonstrate that the semi-enclosed gate NMOS exhibits superior single-event transient tolerance compared to conventional NMOS.
Keywords:
TCAD; semi-enclosed; NMOS; SET

1. Introduction

As spacecraft electronic systems advance towards higher integration, the reliability issues induced by the space radiation environment have become increasingly prominent. Among these issues, single-event effects (SEEs), which are transient fault phenomena triggered by high-energy particles, have emerged as a critical technical bottleneck limiting the long-term operation of onboard equipment [1,2,3,4,5,6]. When high-energy charged particles (including protons, electrons, and heavy ions) penetrate semiconductor devices, the transient plasma generated by their ionization can induce abnormal charge transport at sensitive nodes of the device. This may lead to severe consequences such as logic state errors, memory cell upsets, and even functional module failures [7]. Notably, as CMOS technology advances into the nanoscale, the reduction in critical charge and sensitive volume due to device miniaturization has resulted in an increased susceptibility to SEEs [8,9,10,11,12]. This heightened sensitivity underscores the growing challenge of ensuring the reliability of nanoscale electronic devices in radiation-prone environments. To enhance the level of radiation-hardened design, the enclosed gate NMOS achieves effective management of radiation-induced charge through its unique gate topology. This device employs a fully enclosed gate structure, which reconstructs the electric field distribution near the drain–body junction, significantly improving the directional collection capability of ionized charge. As a result, the enclosed-gate NMOS demonstrates remarkable advantages in radiation resistance, making it a promising solution for applications in radiation-prone environments [13,14,15,16,17,18,19]. To further balance the requirements of radiation hardness and integration density, the academic community has proposed a variant of the semi-enclosed gate structure. This design adopts a partially enclosed gate layout, achieving approximately 40% optimization in the layout area while maintaining electric field control capabilities. This is of significant importance for enhancing the radiation resistance of high-speed circuits. Currently, academic research on semi-enclosed gate structures has mainly focused on their protective mechanisms against Total Ionizing Dose (TID) effects (TID is a performance degradation phenomenon in electronic devices caused by cumulative radiation dose during prolonged exposure to ionizing radiation environments, which can ultimately lead to failure of electronic devices [20].), while analysis of mechanisms related to single-event effects (SEEs) has been relatively scarce [21,22]. Therefore, this study systematically constructs comprehensive physical process models for a Single Event Transient (SET) based on TCAD three-dimensional (3D) device(TCAD 2017) simulation software and Virtuoso simulation software(the version number is 6.1.7). TCAD simulation is used to investigate the behavior of a single device under single-event transient conditions, while Virtuoso simulation is employed to study the single-event transient effects of a semi-annular gate NMOS transistor in a digital inverter circuit. The purpose is to investigate, through simulation analysis, the superiority of enclosed gate NMOS over traditional NMOS in resisting SET effects, and to study the SET performance of semi-enclosed gate NMOS transistors under different radiation conditions, including current transient pulses, internal electric fields, and changes in the internal potential of the device. This work demonstrates the advantages of the semi-enclosed gate structure in mitigating SET. SET is a phenomenon in integrated circuits where heavy particles from cosmic rays penetrate semiconductor materials (such as silicon) and cause ionization, generating electron–hole pairs that lead to transient voltage or current disturbances [23,24,25,26,27,28,29]. These findings provide significant theoretical guidance for the design of radiation-hardened integrated circuits in deep sub-micron technology and hold certain engineering value for the development of highly reliable aerospace electronic systems.

2. Simulation Setup

In this simulation, the Sentaurus TCAD simulation software(TCAD 2017) was employed, utilizing a three-dimensional numerical simulation approach to investigate the SEE in a semi-enclosed gate NMOS transistor based on a 55 nm bulk silicon process. The device modeling diagram and material doping data are shown in Figure 1 and Table 1, respectively. This method allows for the acquisition of the electrical response of the device under particle incidence conditions, thereby enabling the analysis of the sensitivity and mechanisms of SET. By simulating the impact of heavy ions on the semi-enclosed gate NMOS transistor, this study aims to provide detailed insights into the internal electric field and potential changes along the particle trajectory, as well as the variations in charge collection efficiency and pulse width. These results will contribute to a deeper understanding of the SET mechanisms in semi-enclosed gate structures and offer valuable guidance for the design of radiation-hardened integrated circuits in advanced technology nodes. After modeling the semi-enclosed gate NMOS transistor, calibration of the I–V (current-voltage) characteristic curve is required. During the calibration, the Vg-Id curve of a conventional NMOS transistor is used as a reference. Due to structural differences between the devices, the calibration is considered successful as long as the increasing trends of their current-voltage (I–V) characteristics exhibit similarity. Differences in the slopes can be tolerated. The calibration curve is illustrated in Figure 2. The calibrated model is capable of more precisely predicting the impact of single event effects on the performance of the semi-enclosed gate NMOS device.
Research has found that the morphology and distribution density of the ionization track directly affect the charge collection efficiency and the severity of SEEs [30,31,32,33]. This study aims to conduct s analysis with traditional NMOS transistors and, by simulating ionization tracks under different incident conditions, focuses on investigating how the physical effects generated after particle incidence influence the transient response of the device. The findings are expected to contribute to formulating more effective strategies for mitigating SEE in advanced semiconductor devices, particularly in radiation-prone environments. In the SET simulation, the carrier concentration is modeled using the Fermi distribution. The physical model for carrier concentration comprehensively considers the bandgap narrowing effect in highly doped semiconductors. The non-equilibrium carrier generation-recombination model encompasses Shockley indirect recombination, radiative recombination, and Auger recombination mechanisms, whose dependence on carrier concentration directly influences carrier lifetime. The carrier mobility model incorporates ionized impurity scattering, surface scattering, and carrier–carrier scattering. The impact ionization model adopts the Selberherr impact ionization model, which characterizes carrier multiplication phenomena through electric field-dependent impact ionization coefficients.
This simulation study first conducted heavy ion bombardment simulations on semi-enclosed gate NMOS and conventional NMOS under identical conditions, analyzing transient differences in drain current and temporal variation of drain charge. Subsequently, SET responses of semi-enclosed gate NMOS were analyzed under different Linear Energy Transfer (LET) values: 20 MeV·cm2/mg, 30 MeV·cm2/mg, 40 MeV·cm2/mg, 50 MeV·cm2/mg, 60 MeV·cm2/mg, and 70 MeV·cm2/mg. This range corresponds to ions commonly encountered in space environments. For instance, Fe ions with LET values around 20 MeV·cm2/mg–30 MeV·cm2/mg in silicon are typical components of Galactic Cosmic Rays (GCRs). Heavier ions, such as Xe, with LET values as high as 60 MeV·cm2/mg–70 MeV·cm2/mg, are also present in GCR and solar particle events. The incident positions of the particles are illustrated in Figure 3, and all undefined simulation conditions adhere to Table 2. After TCAD simulations and analysis of individual devices, the semi-enclosed gate NMOS and conventional NMOS were configured as inverter structures using Virtuoso simulation software (the version number is 6.1.7). A double-exponential current source was then employed to perform SET simulations on both types of inverters, analyzing pulse voltage variations at the output.

3. Analysis of Simulation Results

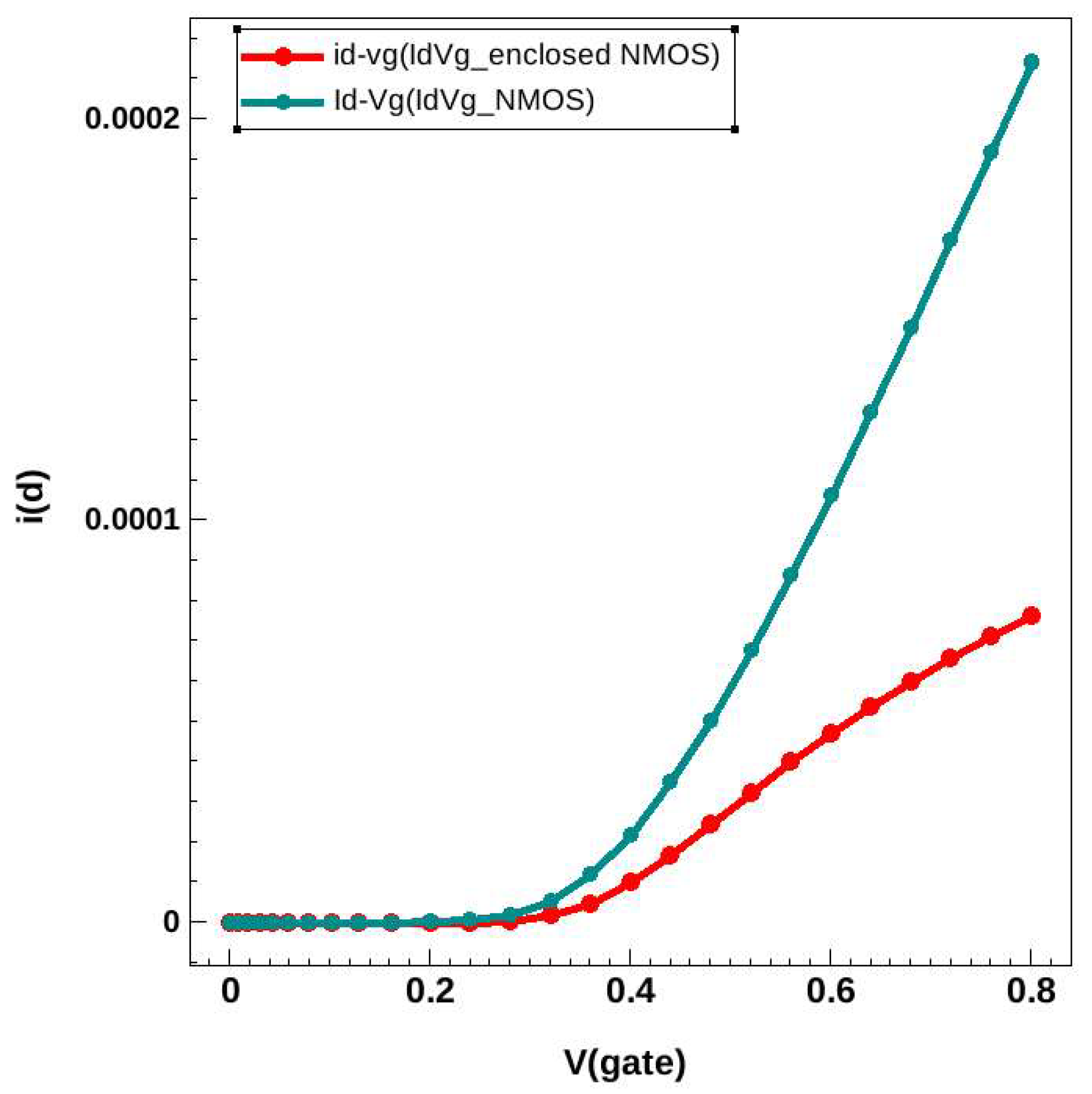
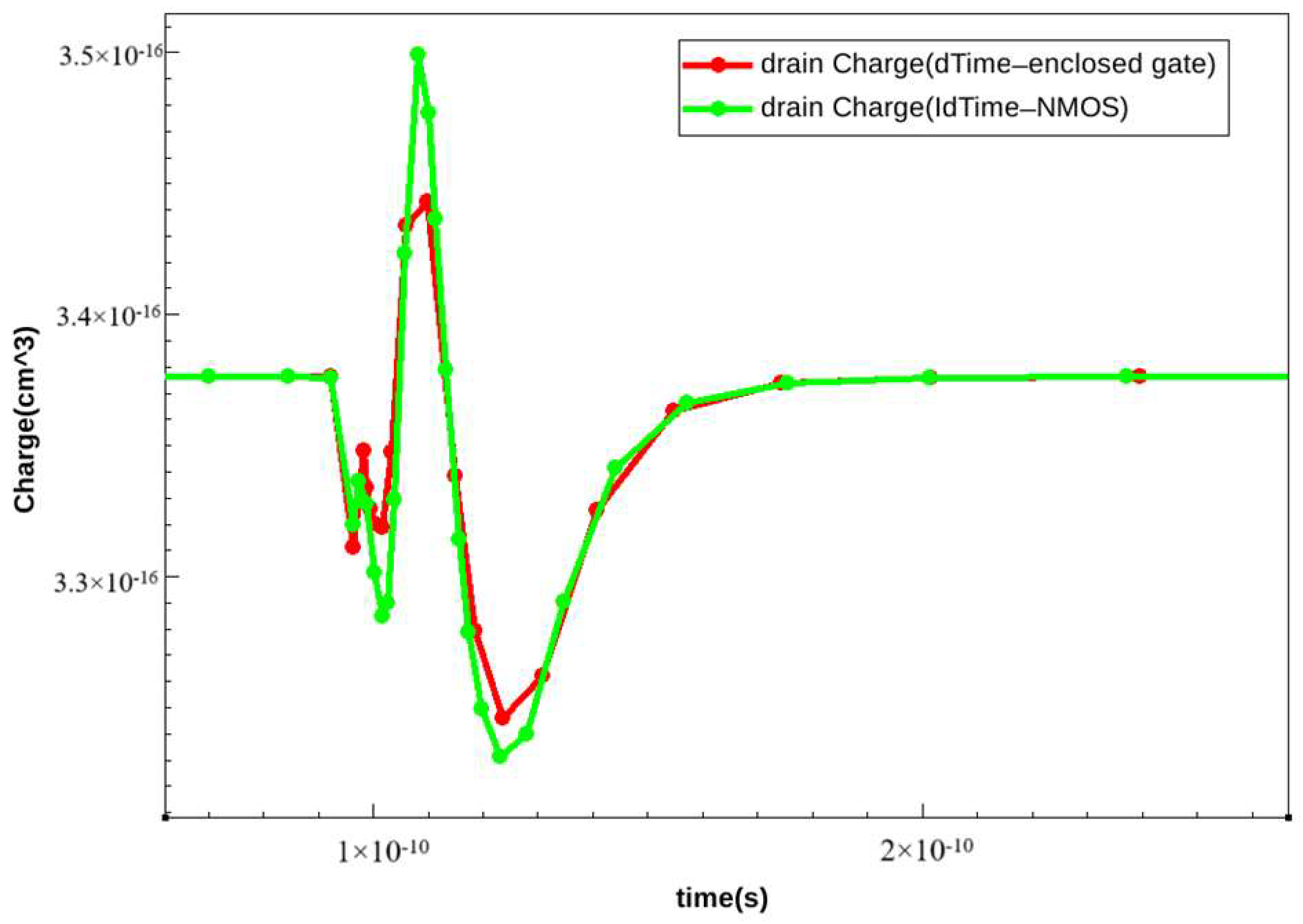
3.1. Simulation and Analysis of Single-Event Transients in Conventional NMOS vs. Semi-Enclosed NMOS

From the current transient curve in Figure 4, it can be concluded that the pulse width of the traditional NMOS is 72 ps, while that of the semi-enclosed gate NMOS is 70 ps. The peak transient drain current of the traditional NMOS is 2.206 mA, compared to 2.102 mA for the semi-enclosed gate NMOS. This clearly demonstrates that both the pulse width and peak current of the semi-enclosed gate NMOS are smaller than those of the traditional NMOS, indicating that the semi-enclosed gate NMOS exhibits superior suppression effectiveness against SET compared to the traditional NMOS.
Further analysis of the drain charge characteristics of both NMOS types, as shown in Figure 5, reveals that, at 100 ps, the traditional NMOS loses a significantly larger amount of drain charge than the semi-enclosed gate NMOS. By 110 ps, as the devices recover to their steady states, the traditional NMOS also gains substantially more charge than the semi-enclosed gate NMOS. Since current arises from the movement of charges, which alters the charge quantity, a larger and more rapid change in charge quantity results in a higher current. Consequently, the current in the traditional NMOS is greater than that in the semi-enclosed gate NMOS.

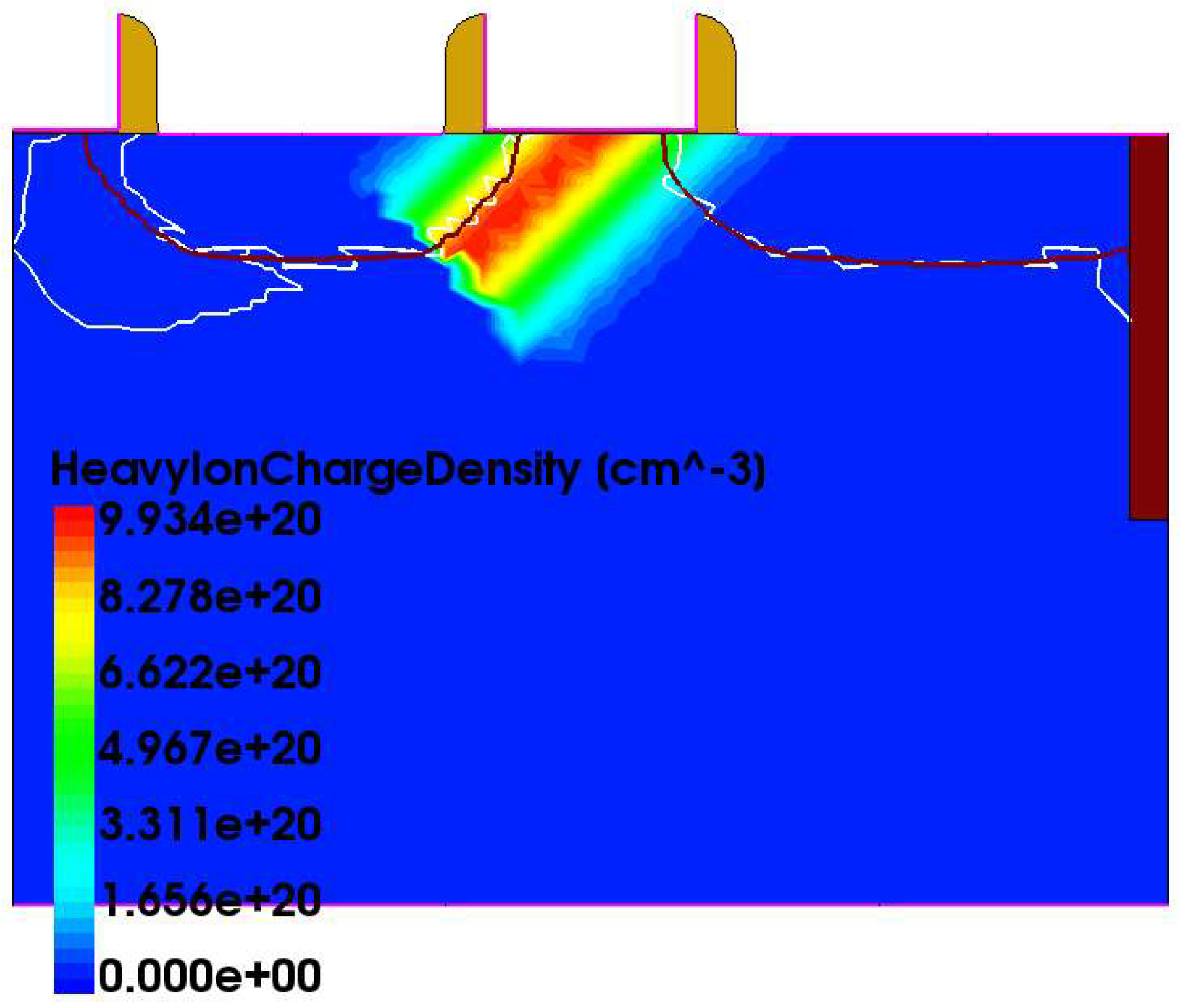
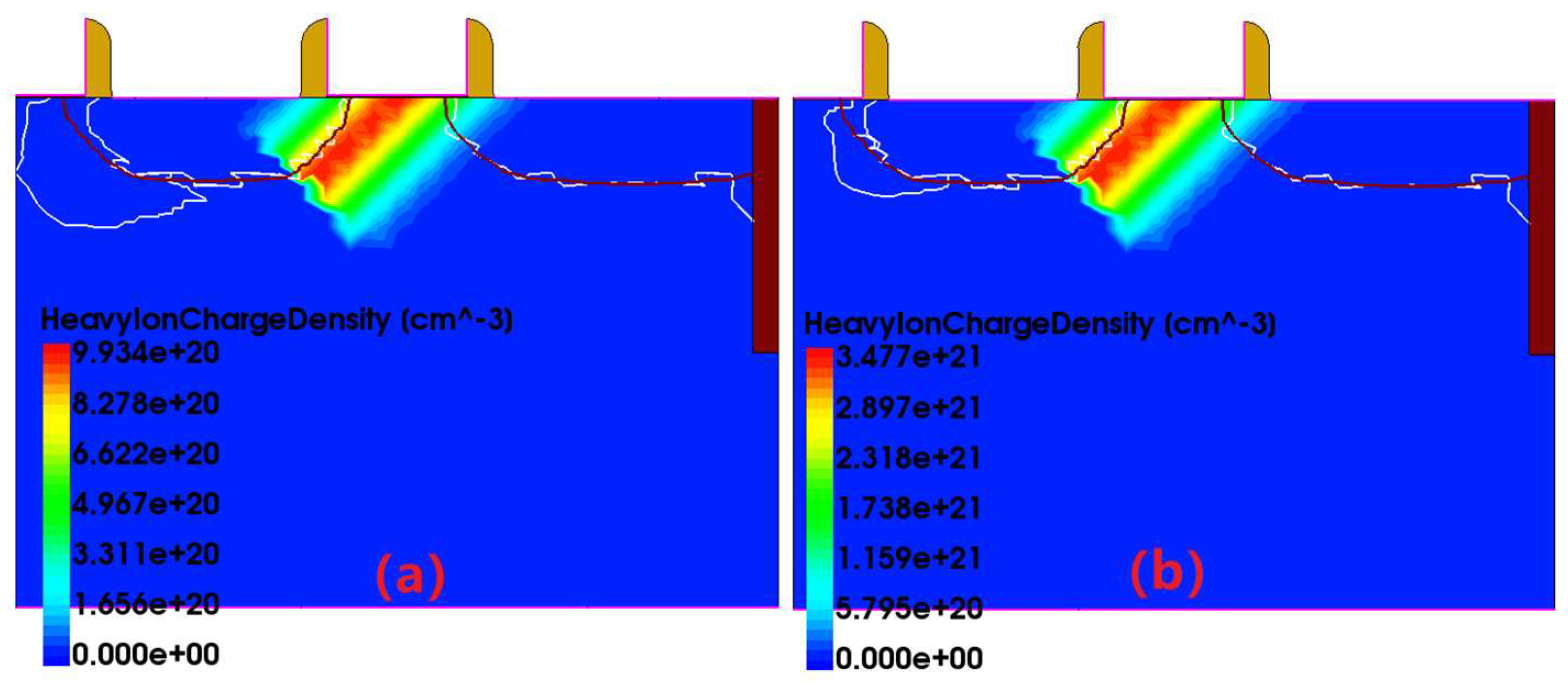
3.2. Analysis of Heavy Particle Irradiation with Different LETs and Internal Mechanisms

From Figure 6, it can be observed that when heavy particles are incident at an angle of 150°, with the direction of incidence parallel to the channel, the transient current peaks reach their maximum at around 100 ps for LET values ranging from 20 to 70. The peak transient currents for LET values of 20 MeV·cm2/mg, 30 MeV·cm2/mg, 40 MeV·cm2/mg, 50 MeV·cm2/mg, 60 MeV·cm2/mg, and 70 MeV·cm2/mg are 2.1959 mA, 3.1112 mA, 4.2419 mA, 5.3875 mA, 6.3796 mA, and 7.3675 mA, respectively. This clearly indicates that the peak transient current increases with the LET value of the incident energy. Additionally, the time required for the semi-enclosed gate NMOS device to recover to a stable state after a single event transient also increases with higher LET values.
To further analyze the underlying mechanisms of the semi-enclosed gate NMOS device, we examine the heavy ion-induced charge density gradient (Heavyion charge density) in Figure 7. The figure shows that the heavy particle enters from the center of the gate and diagonally penetrates towards the drain, with its energy center almost entirely covering the conductive channel. Due to the obstruction by the gate, the energy of the 20 MeV·cm2/mg particle slightly diminishes as it enters the conductive channel region, with a small portion covering the drain and an even smaller portion dispersing towards the source. The ionization density is uniformly distributed along the incident trajectory in a cylindrically symmetric form, with its concentration decreasing gradually from 9.934 × 1020 cm−3 to zero. The region of maximum energy gradient diffusion occurs within the range of from 6.622 × 1020 cm−3 to 3.311 × 1020 cm−3. When heavy ions pass through the sensitive region, their ionization density exhibits a positive correlation with the Linear Energy Transfer rate (LET), and electron-hole pairs are continuously generated along their motion trajectory. The total charge generated, Qtotal, is proportional to LET:
Qtotal = k ⋅ LET ⋅ D
k is a proportionality constant, D is the thickness of the sensitive region traversed by the ion, LET is in MeV·cm2/mg, and we assume a constant LET along the path for simplicity. This assumes the ion travels a fixed distance D through the device, depositing energy uniformly in a cylindrical region around its trajectory. The drain collects these carriers with a characteristic collection time constant τc, leading to a current that rises as follows:
I(t) = I0 ⋅ (1 − e−t/τc)   0 < t < T
After the ion exits at t = T, no further charge is generated, and the current decays as the collected carriers deplete:
I(t) = I0 ⋅ [e−(t − T)/τc − e−t/τc]   t > T
Based on this, it can be inferred that, when the particle first strikes, the device has not yet undergone ionization, and no current is generated, resulting in the drain current being at its minimum. As the heavy particle penetrates, the energy deposition gradually spreads, increasing the affected area and causing the internal ionization range within the semi-enclosed gate NMOS device to expand. This leads to a gradual rise in the drain current until the ionization region reaches its maximum extent, corresponding to the peak drain current. Subsequently, after the heavy particle has fully penetrated, its impact on the semi-enclosed gate NMOS device gradually diminishes. During this period, the internal ionization range progressively shrinks until it eventually returns to zero, resulting in the drain current gradually decreasing back to its minimum value.

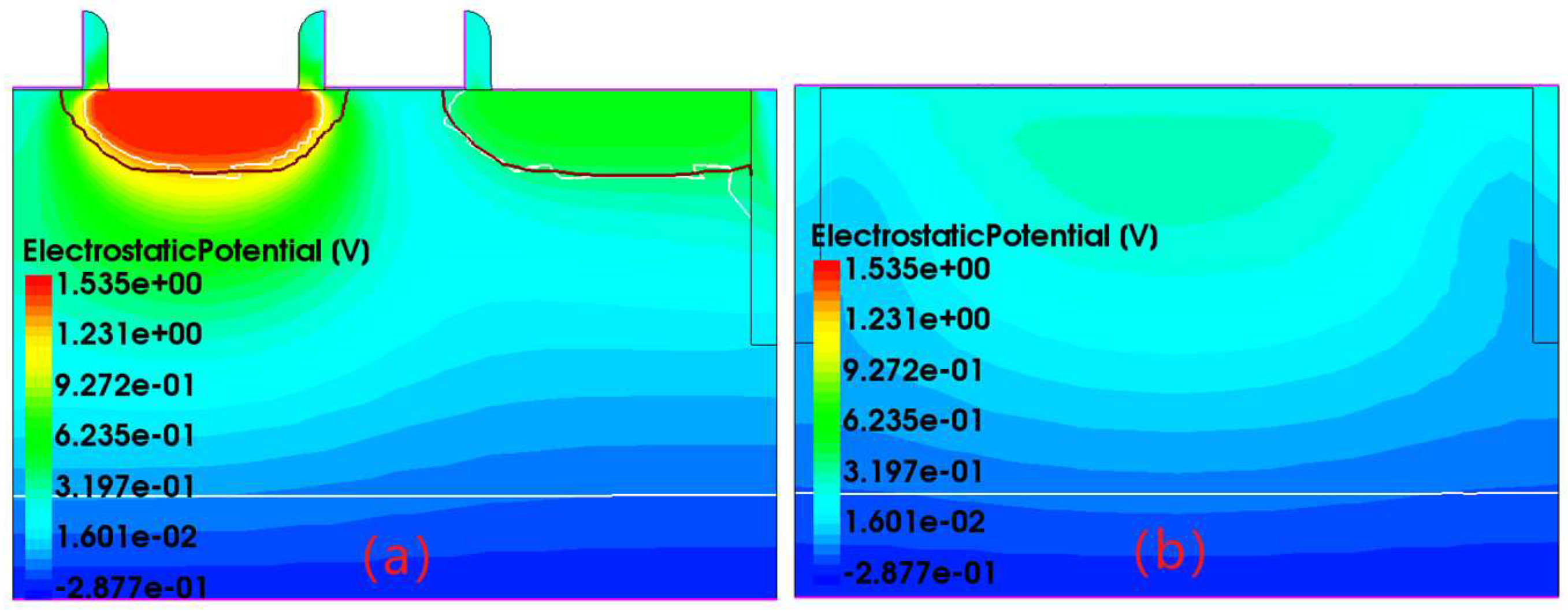
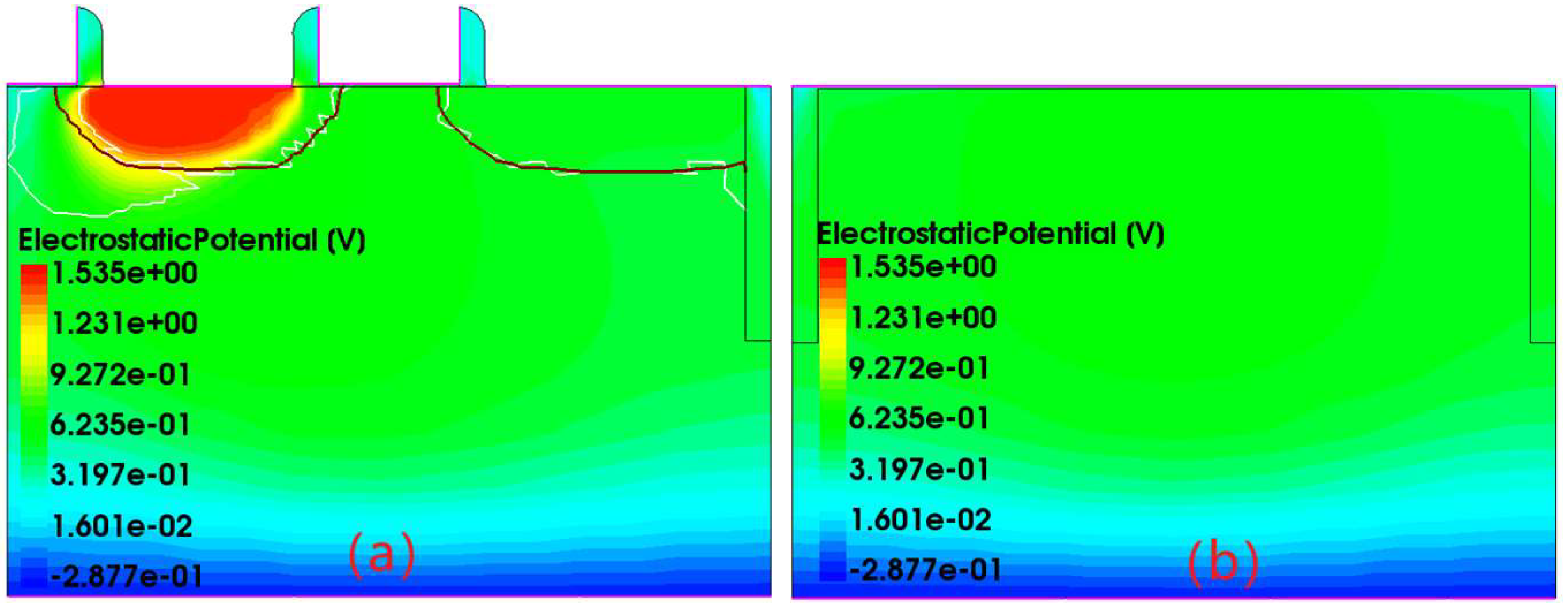
3.3. Analysis of Electric Potential Gradient Distribution at Different Times

To further analyze the mechanism of the semi-enclosed gate NMOS device transitioning from a non-steady state to a steady state after heavy ion incidence and to interpret the changes in the simulation curve, the simulation captured three time periods: the moment of incidence, the moment when the drain current approached its peak, and the moment when the device returned to a steady state. The svisual tool was used to analyze the potential distribution of the device at these three time nodes.
From Figure 8a, it can be observed that, at the moment of incidence, the drain exhibits a very high potential due to the application of a 1 V driving voltage, while the source has a low potential. The source and drain are separated by an even lower potential in the conductive channel region, effectively blocking current flow. Figure 8b shows that, except for a weak potential distribution at the very top, there is almost no potential distribution in the lower regions, resulting in almost no current generation at this stage.
Subsequently, Figure 9a, which depicts the cross-sectional view of the device during the mid-incidence period, reveals the most significant impact of the heavy ion incidence. The drain remains at a high potential, and the source remains at a low potential. However, the potential in the conductive channel region connecting the two terminals is at the same gradient as the source, effectively linking the drain and source. This causes the potential to decrease from the drain to the source, creating a gradient. Compared to Figure 8, the potential gradient in Figure 9, ranging from 9.272 × 10−1 V to 3.197 × 10−1 V, spreads across 80% of the plane. This condition leads to significant current generation, reaching the peak current value.
Finally, Figure 10 shows that the potential gradient returns to a state similar to that in Figure 8, interrupting the current and restoring the device to its pre-incidence steady state. In summary, the simulated drain current output curve exhibits a sudden rise from a very low current state to a peak, followed by a rapid decline back to a very low drain current state, forming the single-event transient current. This behavior is consistent with the observed transient response of the device under heavy ion incidence.

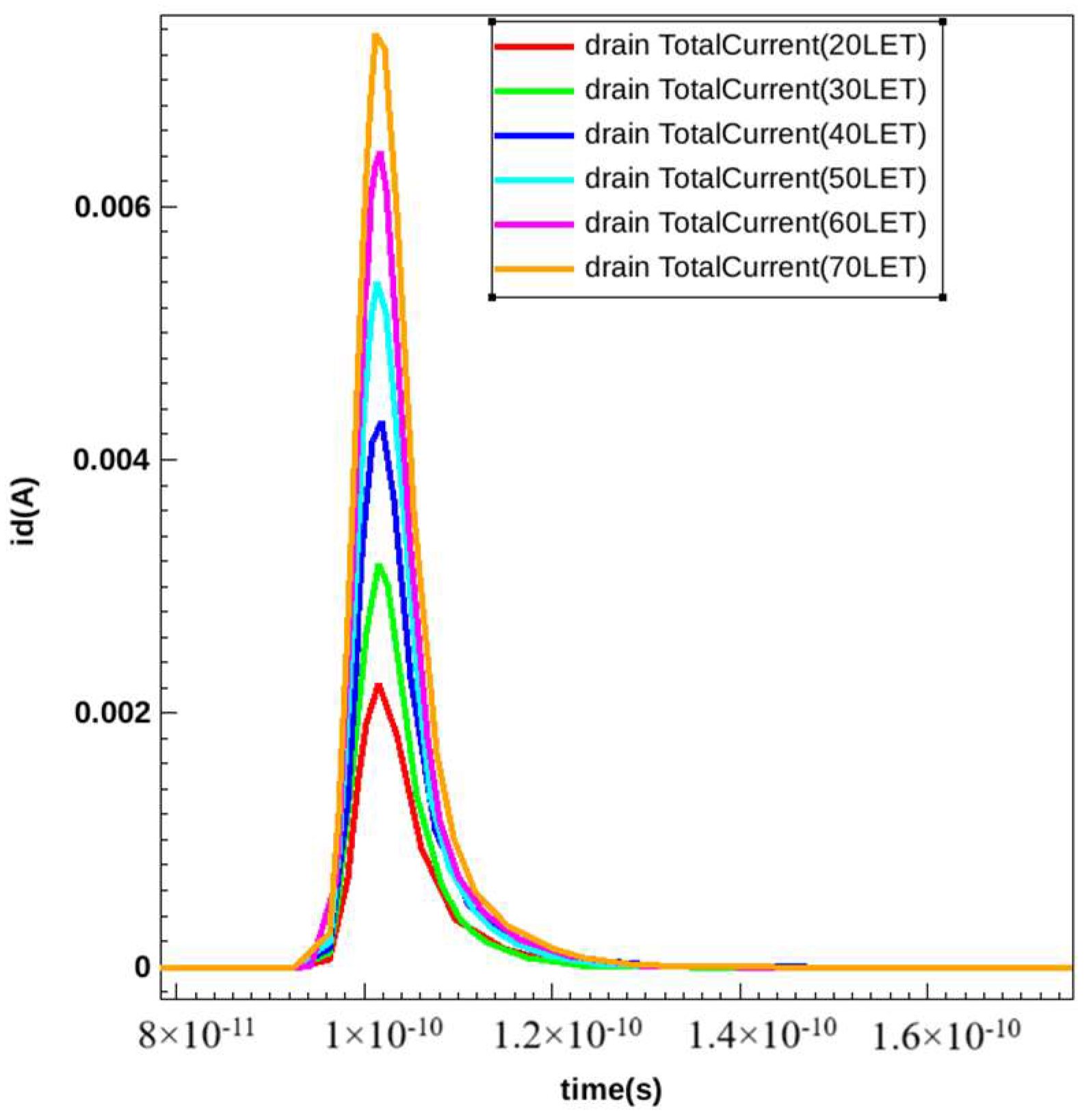
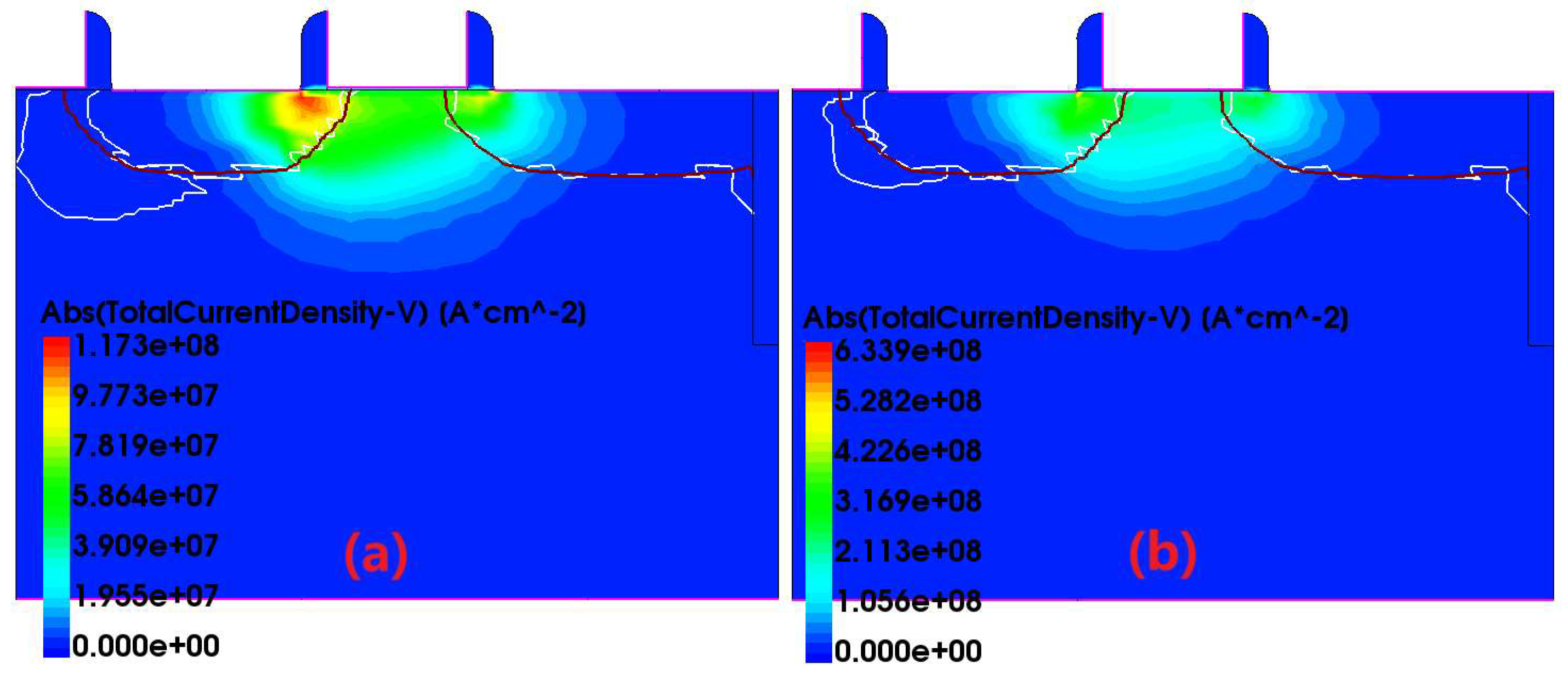
3.4. Analysis of the Change of Current Peak Value Caused by Different LET Incidence

To delve deeper into the analysis of the drain current simulation output results caused by heavy ions with different LET values incident on the semi-enclosed gate NMOS device, it is essential to examine the internal physical changes within the device post-incidence. The simulation primarily compares and analyzes the mechanisms of device changes following the incidence of particles with LET values of 20 MeV·cm2/mg and 70 MeV·cm2/mg.
From Figure 11, it can be inferred that after heavy ions enter the semi-enclosed gate NMOS device, the radiation range of particles with a 20 MeV·cm2/mg LET value is roughly similar to that of particles with a 70 MeV·cm2/mg LET value. However, the average energy density of the 70 MeV·cm2/mg LET particles within the device is nearly an order of magnitude higher than that of the 20 MeV·cm2/mg LET particles. Consequently, the ionization density in the semi-enclosed gate NMOS device is also an order of magnitude higher for the 70 MeV·cm2/mg LET particles. This results in the generation of more electron–hole pairs in the channel, enabling the drain to collect more electrons. This leads to the situation depicted in Figure 12, where Figure 12a represents the 20 MeV·cm2/mg LET case and Figure 12b represents the 70 MeV·cm2/mg LET case.
From Figure 12, it is evident that, compared to the potential distribution caused by the 20 MeV·cm2/mg LET particles, the high-potential region at the drain for the 70 MeV·cm2/mg LET particles is smaller and shifted to the left. This configuration increases the distance between the high-potential drain and the low-potential source, resulting in a longer current path. This facilitates the flow of more electrons, allowing the drain to detect a higher current.
Further supporting this analysis, Figure 13 provides a clearer conclusion. By comparing the current density maps in Figure 13a for the 20 MeV·cm2/mg LET case and Figure 13b for the 70 MeV·cm2/mg LET case, it is observed that, regardless of the LET value, the current density is highest in the channel, indicating that the channel is conducting. However, the average current density in the semi-enclosed gate NMOS device for the 70 MeV·cm2/mg LET case is an order of magnitude higher than that for the 20 MeV·cm2/mg LET case, generating more current. This explains why the simulation results show an increase in the peak drain current as the LET value increases.
In summary, a higher LET value leads to an increased ionization density within the device, which subsequently causes an elevation in the average current density, thereby generating more pronounced transient current responses. This analysis provides a comprehensive understanding of how different LET values affect the single-event transient behavior of semi-enclosed-gate NMOS devices. It reveals that this influence mechanism is essentially consistent with that observed in conventional NMOS transistors. It can be concluded that, from the perspective of single-event transient mechanisms, there is no need to overly consider potential incompatibility caused by differences in single-event transient mechanisms when replacing traditional NMOS with enclosed-gate NMOS. This finding offers valuable insights for the design of radiation-hardened integrated circuits.

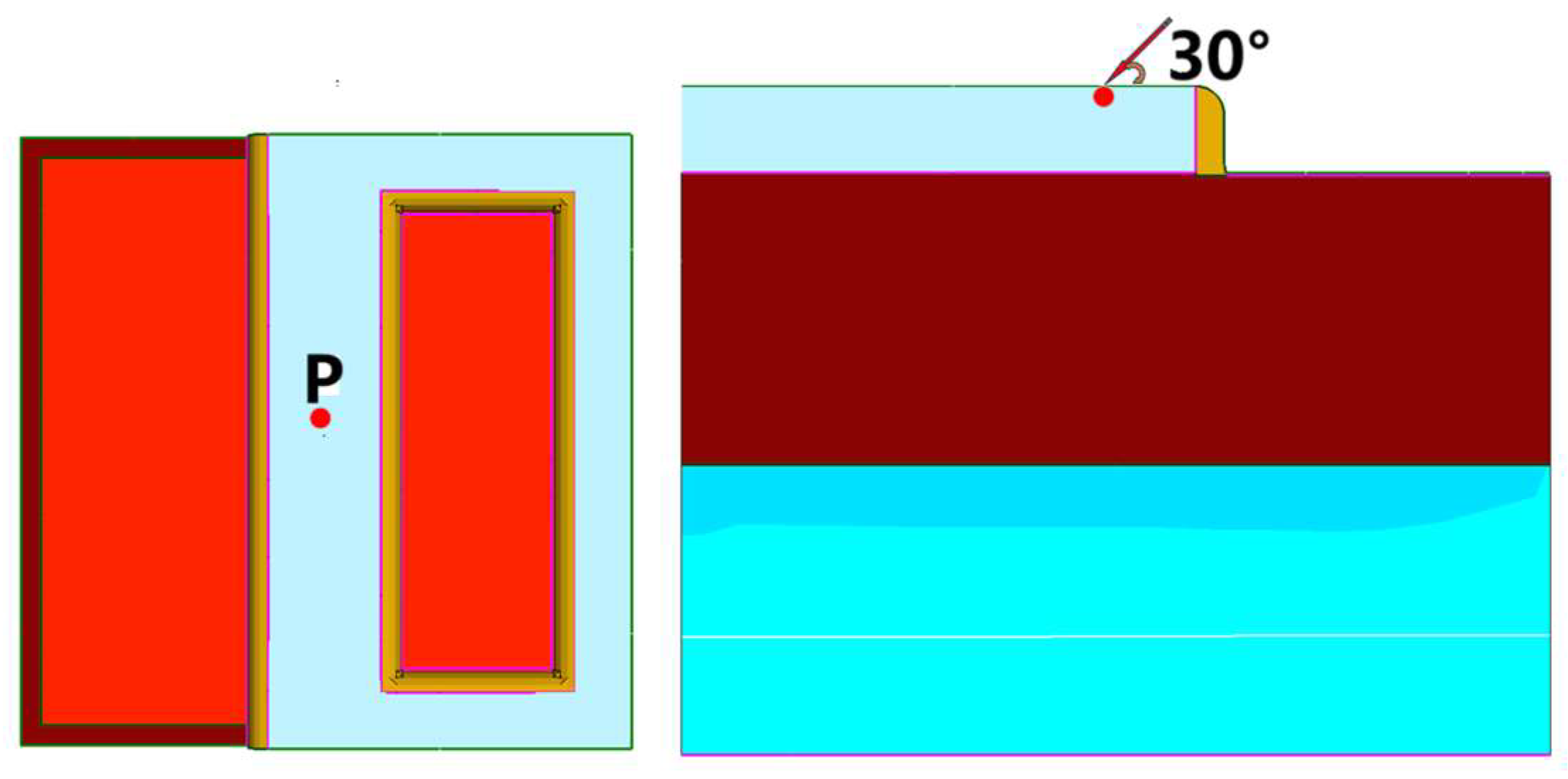
4. Analysis of the Impact Mechanism of Different Incident Positions on Single-Event Transients

To thoroughly validate the improved resistance to Single-Event Transients (SETs) of semi-enclosed gate NMOS compared to conventional NMOS, we employed Cadence Virtuoso layout design software(the version number is 6.1.7) to model both conventional NMOS and semi-enclosed gate NMOS devices [34]. Relevant parasitic parameters were extracted, and SET simulation analysis was conducted using the double-exponential current source method. As shown in Figure 14, (a) represents an inverter composed of conventional NMOS, while (b) illustrates the semi-enclosed-gate NMOS inverter structure; all modeling parameters were adopted from the minimum-size parameters in the SMIC 55 nm process library [35].
From the simulated voltage pulse curves shown in Figure 15, it can be analyzed that the semi-enclosed gate NMOS inverter exhibits an output voltage pulse width of 100 ps under single-event transient effects, while the traditional NMOS inverter shows 112 ps. The voltage peak of the semi-enclosed gate is −5.968 mV compared to −6.812 mV for the traditional NMOS. Additionally, the voltage recovery time to steady state for the semi-enclosed gate inverter is 1.224 ns, whereas the traditional NMOS requires 1.414 ns. These results demonstrate that using semi-enclosed gate NMOS as the fundamental circuit unit provides superior performance in terms of voltage peak suppression, pulse width reduction, and stabilization time mitigation caused by single-event transients when compared to conventional NMOS structures.

5. Conclusions

Based on the simulation results summarized above, it can be concluded that semi-enclosed gate NMOS demonstrates superior suppression of SET effects compared to conventional NMOS when tested as individual devices. Furthermore, its internal mechanisms under particle bombardment are fundamentally similar to those of other NMOS structures. Therefore, when employing semi-enclosed gate NMOS in radiation-hardened circuit design, there is no need to account for unexpected impacts arising from divergent internal mechanisms relative to other NMOS configurations. This structural compatibility allows its direct implementation in circuit design frameworks. Subsequent inverter architecture simulation analyses further validate the reliability of semi-enclosed gate NMOS for radiation-hardened circuit applications. These advantages position semi-enclosed gate NMOS as a practical and scalable solution for enhancing the radiation tolerance of critical electronic systems in aerospace, medical, and high-energy physics applications.

Author Contributions

Writing—original draft, Z.W.; Writing—review and editing, G.L.; Project administration, M.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (2023YFF0719600), the National Natural Science Foundation of China (U23A20322), and Hunan Provincial Natural Science Foundation (2023JJ50009, 2023JJ30599).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

https://drive.google.com/drive/folders/1D78GUXID4pHnQpBF6j2hkFIaJEb1Js6c?usp=drive_link.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, C. The influence with reliability of motional satellite by the single-event phenomena. Semicond. Intell. 1998, 35, 1–8. [Google Scholar]
  2. Chen, P. Radiation Effects on Semiconductor Devices and Integrated Circuits; National Defense Industry Press: Beijing, China, 2005. [Google Scholar]
  3. Johnston, A.H. Space radiation effects and reliability considerations for micro- and optoelectronic devices. IEEE Trans. Device Mater. Reliab. 2010, 10, 449–459. [Google Scholar] [CrossRef]
  4. Koons, H.C. The impact of the space environment on space systems. In Proceedings of the 6th Space Charging Technology Conference, Como, Italy, 5–9 October 1998. [Google Scholar]
  5. Tribble, A.C. The space environment and its impact on spacecraft design. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit 31st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
  6. Darrin, M.A.G. The impact of the space radiation environment on micro electro mechanical systems (MEMS) and microstructures. In Proceedings of the European Conference on Radiation & Its Effects on Components & Systems, Cap d’Agde, France, 23 September 2005. [Google Scholar] [CrossRef]
  7. Schott, J.U. Particle radiation effects in charge coupled devices (CCDs) with applications in single event experiments. In Proceedings of the RADECS 91 First European Conference on Radiation and its Effects on Devices and Systems, Montpellier, France, 9–12 September 1991; pp. 353–356. [Google Scholar] [CrossRef]
  8. Massengill, L.W.; Bhuva, B.L.; Holman, W.T.; Alles, M.L.; Loveless, T.D. Technology scaling and soft error reliability. In Proceedings of the 2012 IEEE International Reliability Physics Symposium (IRPS), Anaheim, CA, USA, 15–19 April 2012. [Google Scholar] [CrossRef]
  9. Huard, V. Technology scaling and reliability: Challenges and opportunities. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015. [Google Scholar] [CrossRef]
  10. DasGupta, S. Effect of well and substrate potential modulation on single event pulse shape in deep submicron CMOS. IEEE Trans. Nucl. Sci. 2007, 54, 2407–2412. [Google Scholar] [CrossRef]
  11. Gadlage, B.M. Comparison of heavy ion and proton induced combinatorial and sequential logic error rates in a deep submicron process. IEEE Trans. Nucl. Sci. 2005, 52, 2120. [Google Scholar] [CrossRef]
  12. Mahatme, N.N. Comparison of combinational and sequential error rates for a deep submicron process. IEEE Trans. Nucl. Sci. 2011, 58, 2719. [Google Scholar] [CrossRef]
  13. Li, D.M. Study of total ionizing dose radiation effects on enclosed gate transistors in a commercial CMOS technology. Chin. Phys. 2007, 16, 3760–3765. [Google Scholar]
  14. Vinogradov, S.M.; Atkin, E.V.; Ivanov, P.Y. Creating a parameterized model of a CMOS transistor with a gate of enclosed layout. J. Phys. Conf. Ser. 2016, 675, 042043. [Google Scholar]
  15. Kumar, A.; Shilla, P.; Kamal, Y. Study and Analysis of Enclosed Gate FET’s. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1033, 012024. [Google Scholar] [CrossRef]
  16. Masalskii, N.V. Simulation of Silicon FETs with a Fully Enclosed Gate with a High-k Gate Dielectric. Russ. Microelectron. 2023, 52, 228–232. [Google Scholar] [CrossRef]
  17. Masalsky, N.V. CVC Simulation of Ultrathin Soi-Cmos Nanotransistors with a Fully Enclosed Gate. Russ. Microelectron. 2021, 50, 387–393. [Google Scholar] [CrossRef]
  18. SIilvestrl, M.; Gerardin, S.; Paccagnella, A. Degradation Induced by X-Ray Irradiation and Channel Hot Carrier Stresses in 130-nm NMOSFETs With Enclosed Layout. IEEE Trans. Nucl. Sci. 2008, 55, 3216–3223. [Google Scholar]
  19. Beznenova, V.; Michalowska-Forsyth, A. Aspect ratio of radiation-hardened MOS transistors Modelling of the equivalent channel dimensions of integrated MOS transistors in radiation-hardened enclosed layout. Elektrotechnik Informationstechnik 2018, 135, 61–68. [Google Scholar] [CrossRef]
  20. Lantz, M.D.; Galloway, K.F. Total Dose Effects on Circuit Speed Measurements. IEEE Trans. Nucl. Sci. 1983, 30, 4264–4269. [Google Scholar] [CrossRef]
  21. Platcheck, G.P.; Cardoso, G.S.; Balen, T.R. Pseudosymmetric Enclosed Layout Transistors for Radiation Hardened Analog Applications. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2072–2076. [Google Scholar] [CrossRef]
  22. Platcheck, P.; Cardoso, G.S.; Balen, T.R. Behavioral and Variability Analysis of Enclosed Layout Transistors for Radiation Hardened Analog Circuits. In Proceedings of the 2024 IEEE 25th Latin American Test Symposium (LATS), Maceio, Brazil, 9–12 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
  23. Adell, P. Analysis of single-event transients in analog circuits. IEEE Trans. Nucl. Sci. 2000, 47, 2616–2623. [Google Scholar] [CrossRef]
  24. Poivey, C. Development of a test methodology for single-event transients (SETs) in linear devices. IEEE Trans. Nucl. Sci. 2001, 48, 2180–2186. [Google Scholar] [CrossRef]
  25. Hirao, T. Studies of single-event transient current induced in GaAs and Si diodes by energetic heavy ions. Radiat. Phys. Chem. 2001, 60, 269–272. [Google Scholar] [CrossRef]
  26. Sternberg, A.L. Effect of amplifier parameters on single-event transients in an inverting operational amplifier. IEEE Trans. Nucl. Sci. 2002, 49, 1496–1501. [Google Scholar] [CrossRef]
  27. Adell, P.C. Single event transient effects in a voltage reference. Microelectron. Reliab. 2004, 45, 355–359. [Google Scholar] [CrossRef]
  28. Buchner, S.; Mcmorrow, D. Single-Event Transients in Bipolar Linear Integrated Circuits. IEEE Trans. Nucl. Sci. 2006, 53, 3079–3102. [Google Scholar]
  29. Nichols, D.K.; Coss, J.R. Heavy ion and proton induced single event transients in comparators. IEEE Trans. Nucl. Sci. 1996, 43, 2960–2967. [Google Scholar]
  30. Pimingstorfer, H.; Halama, S.; Selberherr, S. A TCAD Environment for Process and Process and Device Engineering. ICVC: International Conference on VLSI and CAD 2. 1991. Available online: https://www.iue.tuwien.ac.at/pdf/ib_1991/CP1991_Pimingstorfer_1.pdf (accessed on 2 April 2025).
  31. Odanaka, S. TCAD: CHALLENGED TO VIRTUAL PROCESS. ICVC Int. Conf. VLSI CAD 1995, 4, 197–202. [Google Scholar]
  32. Walton, A.J. Total TCAD strategy for DFM in IC technology development. IEE Proc. Sci. Meas. Technol. 1997, 144, 63–68. [Google Scholar]
  33. Biegel, B.A. Accuracy counts in modeling TCAD’s future. IEEE Potentials 2000, 19, 19–22. [Google Scholar]
  34. Dai, L. CMOS Integrated Circuit EDA Technology, 2nd ed.; China Machine Press: Beijing, China, 2022; p. 469. [Google Scholar]
  35. 55 nm Logic Low Leakage 1.2 V/1.8 V/2.5 V and Ultra Low Power 0.9 V/1.8 V/2.5 V RF Calibre LVS Release Note 2016.
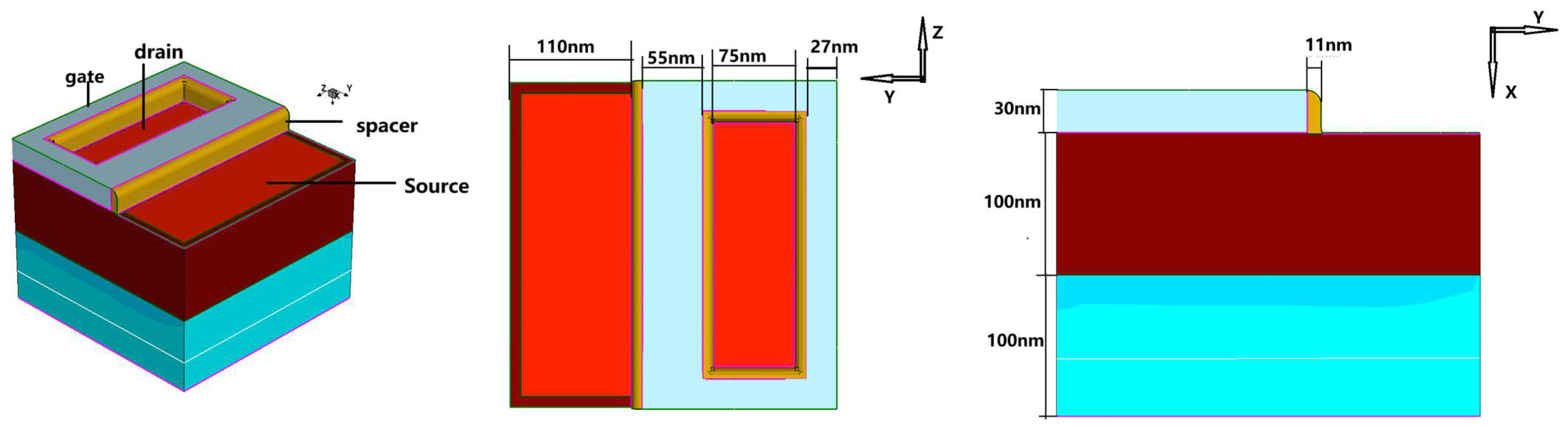
Applsci 15 04023 g001
Figure 1. Three-dimensional diagram of a semi-enclosed gate NMOS device.
Figure 1. Three-dimensional diagram of a semi-enclosed gate NMOS device.
Applsci 15 04023 g001
Applsci 15 04023 g002
Figure 2. Calibration of Id-Vg characteristics for conventional NMOS and semi-enclosed gate NMOS.
Figure 2. Calibration of Id-Vg characteristics for conventional NMOS and semi-enclosed gate NMOS.
Applsci 15 04023 g002
Applsci 15 04023 g003
Figure 3. Schematic diagram of heavy particle incidence position.
Figure 3. Schematic diagram of heavy particle incidence position.
Applsci 15 04023 g003
Applsci 15 04023 g004
Figure 4. Drain transient characteristics between semi-enclosed gate NMOS and conventional NMOS under identical simulation conditions.
Figure 4. Drain transient characteristics between semi-enclosed gate NMOS and conventional NMOS under identical simulation conditions.
Applsci 15 04023 g004
Applsci 15 04023 g005
Figure 5. The comparison of the charge quantity at the drain between semi-enclosed-gate NMOS and conventional NMOS over time.
Figure 5. The comparison of the charge quantity at the drain between semi-enclosed-gate NMOS and conventional NMOS over time.
Applsci 15 04023 g005
Applsci 15 04023 g006
Figure 6. Output waveforms of drain transient current induced by heavy-ion bombardment with different LETs.
Figure 6. Output waveforms of drain transient current induced by heavy-ion bombardment with different LETs.
Applsci 15 04023 g006
Applsci 15 04023 g007
Figure 7. Heavy ion charge density gradient distribution.
Figure 7. Heavy ion charge density gradient distribution.
Applsci 15 04023 g007
Applsci 15 04023 g008
Figure 8. Electric potential gradient distribution at 0 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Figure 8. Electric potential gradient distribution at 0 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Applsci 15 04023 g008
Applsci 15 04023 g009
Figure 9. Electric potential gradient distribution at 10−10 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Figure 9. Electric potential gradient distribution at 10−10 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Applsci 15 04023 g009
Applsci 15 04023 g010
Figure 10. Electric potential gradient distribution at 10−9 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Figure 10. Electric potential gradient distribution at 10−9 s time. (a) Sectional view parallel to the conductive channel. (b) Sectional view perpendicular to the conductive channel.
Applsci 15 04023 g010
Applsci 15 04023 g011
Figure 11. Heavy ion charge densities after incidence of different LET heavy particles. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Figure 11. Heavy ion charge densities after incidence of different LET heavy particles. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Applsci 15 04023 g011
Applsci 15 04023 g012
Figure 12. Electrostatic potential of peak current moment. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Figure 12. Electrostatic potential of peak current moment. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Applsci 15 04023 g012
Applsci 15 04023 g013
Figure 13. Current density of peak current moment. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Figure 13. Current density of peak current moment. (a) Image at LET = 20 MeV·cm2/mg; (b) image at LET = 70 MeV·cm2/mg.
Applsci 15 04023 g013
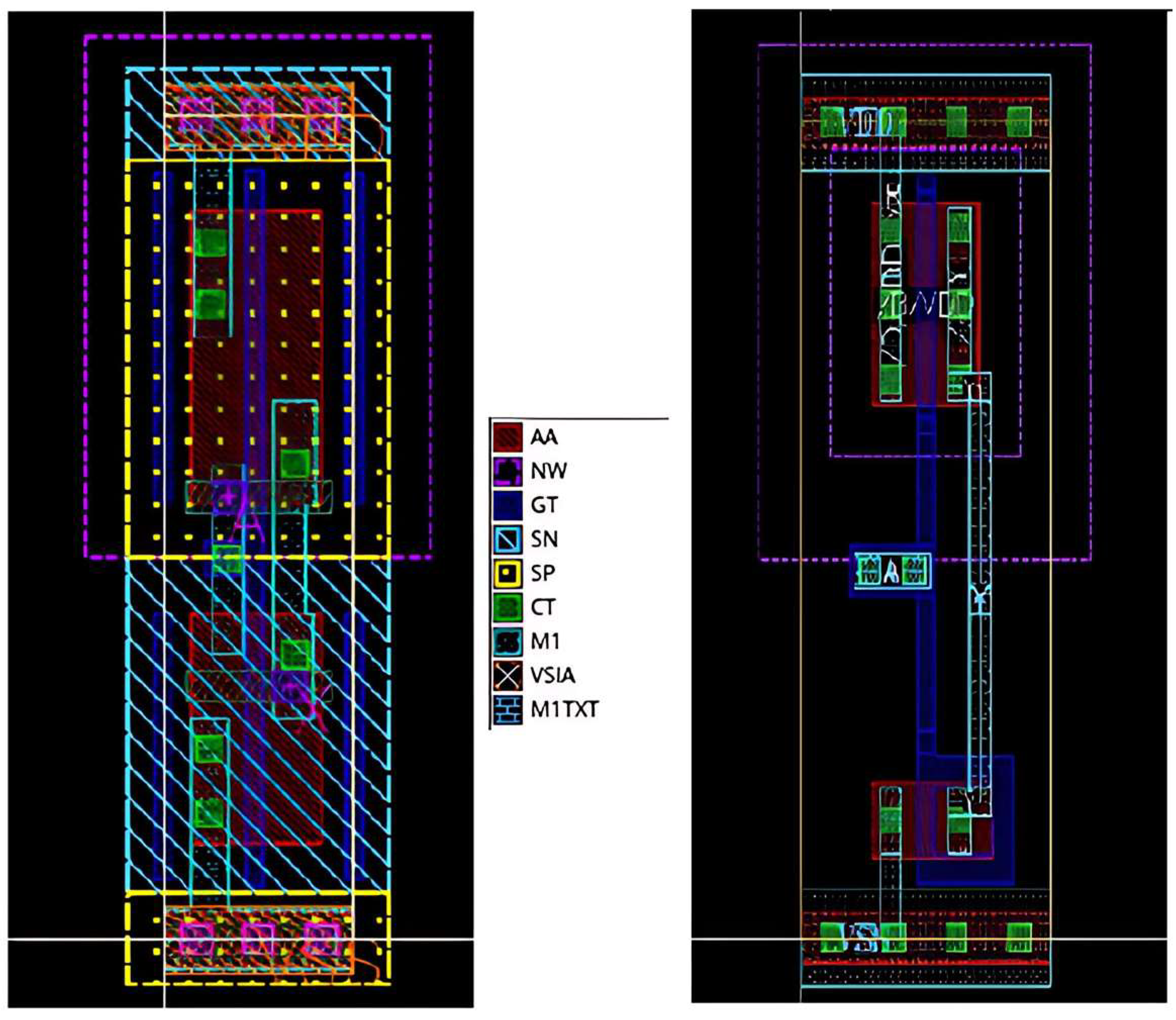
Applsci 15 04023 g014
Figure 14. Structural diagrams of semi-enclosed gate NMOS inverters and conventional NMOS inverters.
Figure 14. Structural diagrams of semi-enclosed gate NMOS inverters and conventional NMOS inverters.
Applsci 15 04023 g014
Applsci 15 04023 g015
Figure 15. Simulation diagram of the pulse waveform for single-event transient voltage in semi-enclosed gate NMOS inverters and conventional NMOS inverters.
Figure 15. Simulation diagram of the pulse waveform for single-event transient voltage in semi-enclosed gate NMOS inverters and conventional NMOS inverters.
Applsci 15 04023 g015
Table 1. Modeling parameters of the semi-enclosed gate NMOS device.
Table 1. Modeling parameters of the semi-enclosed gate NMOS device.
PartMaterial (or Element)Size (or Concentration)
GatePolysilicon55 nm
Source/Drain DopingAs2 × 1020 cm−3
SpacerSi3N410 nm
Gate OxideSiO21 nm
Channel DopingB8.5 × 1017 cm−3
Table 2. Simulation conditions.
Table 2. Simulation conditions.
ParameterValue
Gate Bias Voltage (V)0
Drain Bias Voltage (V)1
LET(MeV·cm2/mg)20
Heavy Particle Incident Angle (°)30
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, Z.; Li, G.; Tang, M. Study on Single-Event Transient Hardness of Semi-Enclosed Gate NMOS. Appl. Sci. 2025, 15, 4023. https://doi.org/10.3390/app15074023

AMA Style

Wang Z, Li G, Tang M. Study on Single-Event Transient Hardness of Semi-Enclosed Gate NMOS. Applied Sciences. 2025; 15(7):4023. https://doi.org/10.3390/app15074023

Chicago/Turabian Style

Wang, Zhuoxiang, Gang Li, and Minghua Tang. 2025. "Study on Single-Event Transient Hardness of Semi-Enclosed Gate NMOS" Applied Sciences 15, no. 7: 4023. https://doi.org/10.3390/app15074023

APA Style

Wang, Z., Li, G., & Tang, M. (2025). Study on Single-Event Transient Hardness of Semi-Enclosed Gate NMOS. Applied Sciences, 15(7), 4023. https://doi.org/10.3390/app15074023

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop