Prediction Model for Compaction Quality of Earth-Rock Dams Based on IFA-RF Model

Abstract

The current evaluation models for earth-rock dam compaction quality seldom incorporate parameter uncertainty considerations. Additionally, the existing models frequently demonstrate constrained prediction accuracy and generalization capabilities. To resolve these issues, we present an intelligent evaluation method for the compaction quality of earth-rock dams that explicitly accounts for parameter uncertainty. The method utilizes a dynamic inertia weight, an adaptive factor, and a differential evolution strategy to enhance the search capability of the firefly algorithm. Furthermore, the random forest (RF) algorithm’s Ntree and Mtry parameters are adaptively optimized through the improved firefly algorithm (IFA) to develop a dam compaction quality prediction model. This model aims to reveal the complex nonlinear mapping relationship between input influencing factors, such as compaction parameters, material source parameters, and meteorological factors, and the compaction quality. The proposed model improves the prediction accuracy, generalization ability, and robustness. The improved firefly optimization-based random forest (IFA-RF) is applied in practical engineering projects, and the results validate that this method can reliably and accurately predict the compaction quality of earth-rock dam construction in real time (R = 0.90107, MSE = 0.0000602, p = 0.000) and thereby guide remedial measures to ensure engineering safety and quality compliance.

1. Introduction

In the construction quality management of earth-rock dams, compaction quality control is a critical factor in ensuring the stability and disaster resistance of the dam structure. However, traditional compaction quality control methods primarily rely on test pit experiments to determine the dry density. These methods are subject to limitations such as insufficient sampling points, being time-consuming, and retrospective evaluation, which hinder real-time monitoring and consequently compromise both the timeliness and accuracy of construction efficiency evaluations and quality assessments [1]. Therefore, developing a method that can evaluate the compaction quality of earth-rock dams accurately and comprehensively in real time holds significant engineering value.

Extensive research has been conducted on this topic, focusing on the development of quality evaluation models based on real-time monitoring technology and the application of intelligent optimization algorithms. Domestically, a real-time monitoring system based on GPS, GPRS, and PDA technology was proposed by Zhong et al. [2] and Cui et al. [3], successfully realizing full-process online monitoring of the compaction process, including parameters such as vehicle speed, number of passes, and compaction thickness. Liu et al. [4] introduced the compaction value (CV) as a real-time indicator of compaction quality, verifying the significant correlation between CV and compaction degree. Other studies, such as those by Ran et al. [5], applied multiple linear regression analysis to assess factors affecting the shear strength of earth-rock dams, while Wang et al. [6] developed a nonlinear model for compaction degree using BP neural networks. Wang et al. [7] and Liu et al. [8] proposed compaction quality evaluation methods based on chaotic firefly algorithm (FA)-enhanced support vector regression (SVR) and adaptive differential evolution algorithm-improved extreme learning machine (ELM), respectively. Wang et al. [9] established a real-time evaluation model for compaction quality using a kernel method combined with an adaptive chaotic bacterial foraging algorithm. Hao et al. [10] developed a full-section compaction quality evaluation method for subgrades based on PSO-BPNN-AdaBoost (PBA). These studies have made significant progress in compaction quality evaluation. Internationally, Roland Anderegg et al. [11] built an intelligent feedback control system based on GPS for the real-time evaluation of roadbed compaction quality. Rinehart et al. [12] developed a 3D vibration monitoring system for continuous compaction quality detection and feedback control. Kassem et al. [13] introduced a compaction monitoring system (CMS) for monitoring and documenting the compaction process of asphalt mixtures. Sivagnanasuntharam et al. [14] proposed a practical method to maximize the benefits of the current intelligent compaction (IC) technology for quality control (QC). Although these studies have made notable advancements, limitations such as small sample sizes and data uncertainty in the parameters influencing compaction quality hinder the ability to fully reflect the spatial distribution of compaction quality.

Currently, scholars widely employ linear and nonlinear regression models for compaction quality evaluation. However, traditional methods frequently neglect parameter uncertainty, and their fitting accuracy requires enhancement with compromised generalization ability. To overcome these limitations, intelligent algorithms have been increasingly applied in the analysis and prediction of compaction quality. Techniques such as artificial neural networks, genetic algorithms, and RF have demonstrated effectiveness. The RF algorithm [15], recognized for its strong nonlinear modeling capability and high noise resistance, is particularly suitable for small sample datasets and has demonstrated good performance in predicting uncertain engineering parameters, garnering attention from both academia and industry [16,17,18]. Nevertheless, the parameter selection process in RF still depends on manual tuning, which may result in unstable model performance and limit its precision and generalization ability [19,20]. To address this issue, researchers have recently introduced intelligent optimization algorithms to improve the RF. Zhang et al. [21] proposed a dam deformation prediction model based on an improved particle swarm optimization algorithm, which enhanced the model’s prediction performance by optimizing the RF parameters.

This study proposes IFA, which introduces dynamic inertia weight, sine function adaptive factors, and differential evolution strategies to strengthen the algorithm’s search capability while avoiding local optima entrapment. By hybridizing IFA with the RF algorithm, an IFA-RF model is developed to adaptively optimize the RF parameters, thereby systematically improving the prediction accuracy, robustness, and generalization ability. Ultimately, this study integrates real-time compaction monitoring systems, test pit experiment data, and meteorological data to propose an IFA-RF compaction quality evaluation model, providing a new technical approach and theoretical support for the construction quality control of earth-rock dams.

2. Materials and Methods

2.1. Method for Collecting Compaction Quality Influence Parameters

Relevant studies [16] have indicated that material source parameters, compaction parameters, and meteorological parameters significantly affect the compaction quality of earth-rock dams. In this study, material source parameters, compaction parameters, and meteorological parameters serve as input parameters for the prediction model, while compaction dry density is considered as the output parameter. The compaction parameters are collected using the real-time monitoring method for dam compaction quality proposed by Zhong et al. [2] and Cui et al. [3], which comprehensively and continuously monitors the compaction parameters (compaction speed, compaction thickness, number of compaction passes, and excitation force). The material source parameters are obtained through on-site test pit experiments (including moisture content tests, density tests, and particle size analysis tests). Meteorological parameters are acquired in real-time through a small meteorological station located at the construction site [19].

2.2. Uncertainty Analysis of Parameters

Uncertainty theory is the science that examines the unpredictability and fuzziness in systems, processes, or models. The core idea is that many real-world problems lack a clearly defined solution path and are characterized by varying degrees of fuzziness and uncertainty. Entropy, originally introduced as a thermodynamic measure of molecular disorder, was later incorporated into information theory by mathematician Claude Shannon in 1948. In this context, entropy quantifies the uncertainty of information and has since been widely applied across various fields. A higher value of information entropy indicates greater uncertainty within the system. Jaynes established entropy’s pivotal role as “a measure of uncertainty”, thereby creating a universal paradigm for cross-disciplinary uncertainty quantification [22]. Recent years have witnessed a surge in the scholarly adoption of information entropy as a metric for parametric uncertainty quantification [23]. While entropy-based methods provide a robust and computationally efficient framework for uncertainty quantification, it is important to contextualize their use within the broader landscape of uncertainty quantification techniques. Monte Carlo methods, for example, rely on repeated random sampling to estimate outcome distributions, offering high accuracy but often at significant computational cost. Bayesian inference incorporates prior knowledge and updates probabilities with new data, making it suitable for problems with well-defined priors but requiring substantial computational resources and expertise. In contrast, entropy-based methods balance computational efficiency and interpretability, making them ideal for real-time decision-making and large-scale data analysis. By leveraging entropy’s inherent properties, our approach offers a practical and scalable solution for quantifying uncertainty in material source parameters, avoiding the need for extensive computational resources or complex probabilistic models.

In this study, information entropy is employed to quantify the uncertainty of material source parameters. The calculation procedure is as follows.

The value range of the parameter is divided into equal intervals, and the frequency of occurrence for each interval is recorded as n.

The frequency of each interval is calculated using Formula (1):

$$P={\displaystyle \frac{n}{101}}\times 100\%$$

(1)

where P is the frequency of the i-th interval, n is the occurrence count of the values in the interval, and 106 is the total number of samples.

The entropy value of the parameter is then calculated using Formula (2):

$$E=-k{\displaystyle \sum _{j=1}^m{P}_j\ln P_j}$$

(2)

where E is the entropy value, m is the number of intervals, $k=1/\ln (m)$, and $P_j$ is the frequency of the j-th interval.

This process is repeated for all material source parameters. The resulting entropy values are used to assess the degree of uncertainty associated with each parameter. Higher entropy values correspond to higher levels of uncertainty.

2.3. Traditional Evaluation Methods for Compaction Quality

2.3.1. Evaluation of Rolling Quality Based on BP Neural Network

Artificial neural networks (ANNs) are computational models that simulate the behavior of human brain neurons, characterized by core features such as nonlinear mapping, self-learning, and adaptability. They are widely used in various research fields. The backpropagation (BP) neural network is a multi-layer feedforward network based on error backpropagation. It minimizes prediction error by adjusting network weights and thresholds and is commonly implemented in three-layer structures. This study constructs a BPNN model to evaluate the compaction quality of earth-rock dams based on the principles of BPNNs and incorporating data from real-time compaction monitoring systems, test pit experiments, and meteorological parameters collected from small weather stations.

2.3.2. Evaluation of Rolling Quality Based on Regression Analysis

Regression analysis is a statistical method used to explore the relationship between a dependent variable and multiple independent variables, thereby enabling the construction of interpretable regression models to predict future values. Based on the theory of linear regression and incorporating real-time compaction monitoring system data, field test data, and meteorological parameters, this study constructs a multiple linear regression model to assess the dry density of compacted concrete dams. The specific steps are as follows: (a) collect the compaction parameters (such as the number of passes and thickness); meteorological parameters (such as temperature and humidity); and test pit data (such as the uniformity coefficient, P5 content, curvature coefficient, and total material moisture content) to establish a basic database for a compaction quality evaluation; (b) select significant influencing parameters through a correlation analysis and apply five-fold cross-validation to divide the data into training and testing sets; (c) based on the principles of linear regression, fit the dry density prediction model using the training set data; and (d) use the model to predict the test set and analyze the correlation and errors in the predicted results.

2.4. Improving Firefly Optimization Algorithm

The firefly algorithm (FA) is a population-based optimization technique inspired by the bioluminescent communication patterns of fireflies in nature. By simulating the mutual attraction among individual fireflies, the algorithm iteratively converges towards the optimal solution of a given optimization problem. The FA exhibits notable efficacy in tackling global optimization challenges, particularly those involving multimodal functions. However, the traditional FA is prone to entrapment in local optima when addressing complex, high-dimensional problems, which can adversely affect both the efficiency of the search process and the quality of the resulting solutions. To enhance the search capabilities of the FA, this study proposes an improved strategy that integrates dynamic inertia weights, adaptive factors, and the differential evolution algorithm. The introduction of dynamic inertia weights enables fireflies to adjust the balance between exploration and exploitation throughout the search process, thereby reducing the likelihood of premature convergence. The adaptive factor dynamically adjusts the step size of the fireflies’ movements based on the current search state, enhancing the algorithm’s adaptability to complex search spaces. Additionally, the incorporation of the differential evolution algorithm utilizes differences between individuals to guide the population towards the global optimum, thereby improving both the global search capability and the solution quality of the FA. With these enhancements, the improved FA demonstrates superior search performance and greater stability in resolving complex optimization problems.

2.4.1. Firefly Algorithm

In the FA algorithm, each firefly represents a candidate solution to the optimization problem, with its brightness serving as an indicator of solution quality—greater brightness denotes a superior solution. The FA operates by simulating mutual attraction among fireflies, enabling the swarm to progressively converge toward the optimal solution. Specifically, the attractiveness of a firefly is proportional to its brightness and diminishes with increasing distance, reflecting the natural attenuation of light. During each iteration, fireflies adjust their positions by moving toward individuals exhibiting higher brightness, with the movement’s direction and magnitude governed by both the brightness differential and their spatial proximity. The formula is as follows:

$$x=x_i+\beta e^{-\gamma r^2}(x_j-x_i)+\alpha \epsilon$$

(3)

where $x_i$ and $x_j$ represent the positions of fireflies i and j, respectively, $\beta$ is the attraction coefficient, $\gamma$ is the light intensity decay factor, r is the distance between fireflies, $\alpha$ is the random disturbance coefficient, and $\epsilon$ is a random variable that follows a normal distribution. The firefly algorithm (FA) demonstrates robust global search capabilities; however, it is susceptible to becoming trapped in local optima, particularly within complex, high-dimensional search spaces. This limitation is intensified when the light intensity decay factor is substantial, as it significantly impedes the algorithm’s convergence speed. To address these challenges, this study proposes three enhancements to the classical FA.

2.4.2. Dynamic Inertia Weight

In the firefly algorithm, the concept of inertia weight is employed to balance the exploration and exploitation phases of the search process. Dynamic inertia weight (DIW) serves as an enhancement strategy that adaptively adjusts the inertia weight throughout the algorithm’s iterations. Initially, a higher inertia weight encourages the fireflies to explore the search space more extensively, thereby reducing the likelihood of premature convergence to local optima. As the iterations proceed, the inertia weight is progressively decreased, enabling the fireflies to concentrate on exploiting the most promising regions, which enhances the precision of convergence. The dynamic inertia weight decreases linearly from 0.9 to 0.4. The inertia weight $\omega$ can be dynamically adjusted according to the following formula:

$$w=w_{\max }-(w_{\max }-w_{\min })\cdot t/T$$

(4)

where w_max and w_min represent, respectively, the maximum and minimum values of the inertia weight, t is the current iteration number, and T is the total number of iterations.

Through the dynamic adjustment of inertia weight, the algorithm initially emphasizes extensive exploration and subsequently accelerates convergence. This strategy enhances the firefly algorithm’s adaptability in managing the trade-off between exploration and exploitation throughout the optimization process.

2.4.3. Adaptive Factor

The adaptive factor in the improved firefly algorithm (FA) dynamically adjusts key parameters based on the algorithm’s current state. Specifically, it modulates the attraction coefficient, which controls the interaction between fireflies. When fireflies cluster around a local optimum, the adaptive factor reduces the attraction coefficient, weakening their mutual attraction. This adjustment enables the fireflies to escape the local optimum, thereby enhancing the algorithm’s exploratory capability. Conversely, in regions likely to yield superior solutions, the adaptive factor increases the attraction coefficient, strengthening the attraction and accelerating convergence toward these promising areas. The initial value of the adaptive factor is set to 2.0. The formula for the adaptive factor is as follows:

$$a=\sin (\pi \cdot t/(2\cdot t_{\max }))$$

(5)

where t and t_max are the current and maximum iteration numbers, respectively, and a is the adaptive factor, t_max = 200. By incorporating the adaptive factor, the algorithm can automatically adjust the individual search steps during the search process, thereby improving both convergence and global search capabilities.

2.4.4. Differential Evolution Strategy

Differential evolution strategy (DES) is a population-based optimization algorithm that generates new solutions through mutation, crossover, and selection operations. In this study, the DES is embedded into the FA to enhance the algorithm’s ability to escape local optima. Specifically, by applying differential mutation to the positions of some fireflies in each iteration, the algorithm is able to escape local optima. Additionally, crossover operations are used to generate new solutions, which further enhances the global search ability.

2.4.5. Improved Firefly Algorithm

To enhance the global search capability of the FA and avoid entrapment in local optima, this study integrates three components: DIW, an adaptive factor, and DES. Specifically, DIW balances global and local searches by promoting broader exploration during the initial stages while concentrating on refining the optimal solution in later stages. The adaptive factor enables dynamic adjustments in the search strategy across different phases, thereby improving the algorithm’s ability to escape local optima. Additionally, incorporating DES further augments the FA’s exploration capabilities in complex search spaces. The workflow of the IFA is as follows: Step 1: Initialize the firefly population and related parameters. Step 2: Compute the brightness of each firefly based on the objective function and rank them accordingly. Step 3: Update the positions of the fireflies using DIW to enhance the global search capability. Step 4: Adjust the movement step size of each firefly according to the adaptive factor. Step 5: Apply DES by performing mutation and crossover operations on a subset of individuals. Step 6: Check the convergence condition. If it is met, output the optimal solution; otherwise, return to Step 2 for further iterations.

2.4.6. Algorithm Performance Comparison

To validate the effectiveness, superiority, and efficiency of the proposed algorithm, the FA and the IFA were tested using benchmark functions. The four benchmark functions used in this study are the Sphere function (f₁), Rastrigin function (f₂), Ackley function (f₃), and Griewank function (f₄). These functions can be accessed at http://www.sfu.ca/~ssurjano/index.html, (accessed on 9 October 2024).

$$f_1={\displaystyle {\sum }_{i=1}^n{x}_i^2}$$

(6)

$$f_2=10n+{\displaystyle {\sum }_{i=1}^n(x_i^2-10}\cos (2\pi x_i)$$

(7)

$$f_3=1+{\displaystyle \frac{1}{4000}}{\displaystyle {\sum }_{i=1}^n\left(x_i^2\right)-{\displaystyle {\prod }_{i=1}^n\cos (\frac{x_i}{\sqrt{i}})}}$$

(8)

$$f_4=-20\exp (-0.2\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\left(x_i^2\right)}})-\exp ({\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\cos \left(2\pi x_i\right)})+20+\exp (1)$$

(9)

For both the FA and IFA algorithms, the following parameters were set: number of fireflies: 50, maximum iterations (Max_iteration): 300, search space boundaries: ±5, and dimension (dim): 5. The optimization results for the FA and IFA on these benchmark functions are presented in

Table 1. Test results of benchmark functions on the FA algorithm and IFA algorithm.

Functions	Optimal Solution	FA		IFA
		Optimal Solution	Execution Time (s)	Optimal Solution	Execution Time (s)
f1	f(0,0,0,0,0) = 0	0.005622466	1.47	2.04 × 10−15	1.52
f2	f(0,0,0,0,0) = 0	4.093030513	2.03	0.996754151	2.11
f3	f(0,0,0,0,0) = 0	0.167418872	2.51	4.23 × 10−8	2.58
f4	f(0,0,0,0,0) = 0	0.001441134	2.08	0.001130785	2.15

. It can be observed that, compared to the FA, the IFA—by incorporating dynamic adjustment factors, inertia weight, and differential evolution strategies—demonstrates an improved ability to escape local optima and enhance the global search capability. For benchmark functions f₁ to f₃, the optimization results for IFA are significantly better than those for FA. For the f₄ benchmark function, the IFA’s results are slightly better than the FA’s, though the improvement is not as pronounced. The IFA exhibits a slight increase in computation time compared to the standard FA. However, it achieves a significant enhancement in optimization performance. Given the practical requirements of hydraulic engineering construction sites, obtaining more precise results is of paramount importance. In light of the substantial improvement in optimization effectiveness, the marginal increase in computation time is entirely justified and worthwhile. In conclusion, the proposed IFA demonstrates excellent accuracy, effectiveness, and superiority in optimization performance. Therefore, this algorithm is employed to optimize the parameters of RF.

2.5. Compression Quality Evaluation Model Based on an Improved Firefly Algorithm Optimizing Random Forest

To enhance the precision and reliability of the compaction quality evaluation for earth-rock dams, this study proposes a model that integrates swarm intelligence optimization algorithms with machine learning. The compaction process involves multiple operational parameters (e.g., compaction cycles, moisture content, and compaction thickness), which exhibit high nonlinearity and complex interrelationships. Therefore, to effectively evaluate the compaction quality of earth-rock dams, the IFA is employed to adaptively optimize the parameters of the RF model, thereby enhancing its predictive capabilities.

2.5.1. Random Forest

For the compaction quality evaluation in the core wall region of earth-rock dams, the RF proposed by Breiman [16] is used to predict the dry density. This algorithm utilizes the Bootstrap resampling method to generate multiple samples from the original compaction data, each of which is used to construct decision trees. These trees are then aggregated, and the final dry density prediction is obtained by averaging the predictions of the individual trees. The law of large numbers ensures that random forests do not overfit as the number of trees increases, although they do exhibit a finite error value. Extensive research [16,17,18] has demonstrated that RF is one of the best algorithms currently available, known for its resistance to overfitting, robustness in handling noise and outliers, low generalization error, and superior prediction accuracy, even in the presence of multicollinearity.

It is important to note that, if the value of “Mtry” is too small, overfitting may occur, leading to increased classification error and reduced accuracy. Conversely, if “Mtry” is too large, the RF construction time increases, which slows down the process. A small “Ntree” may result in insufficient training, reducing the randomness of RF, while a large value may overly randomize the model, increasing the computation time and reducing the classification precision. However, RF lacks the ability to autonomously determine the optimal “Mtry” and “Ntree”. To ensure both generalization capability and accuracy, an optimization algorithm is necessary to fine-tune these parameters.

2.5.2. Improved Firefly Optimized Random Forest Algorithm

The core concept of the IFA optimized RF algorithm is to utilize the RF hyperparameters as the initial positions of the fireflies. The fitness of each firefly is computed, and through the movement and updating of the fireflies, the one with the lowest fitness is selected to determine the optimal RF hyperparameters. The pseudocode of the IFA-RF algorithm is presented in Algorithm 1. The procedure is as follows:

Step 1: Initialization of the FA: Set the Parameters: Initialize the FA parameters, including population size, maximum iterations, initial brightness, attraction coefficient, and step size factor. Generate the initial population: Randomly generate a set of firefly individuals, each representing a solution (i.e., a combination of the RF’s Ntree and Mtry parameters).

Step 2: Introduction of dynamic Inertia Weight and Adaptive Factors: Introduce a dynamic inertia weight to regulate the search range of solutions during firefly movement. As iterations proceed, the inertia weight gradually decreases, improving the local search capability in the later stages of convergence. Dynamically adjust the movement step size and attraction coefficient based on the relative brightness and fitness differences between fireflies. The attraction between superior individuals is increased to accelerate convergence, while the attraction between inferior individuals is decreased to avoid local optima.

Step 3: Introduction of DES: Apply the differential evolution strategy to each firefly. Select three individuals from the current population, compute the difference vector, and generate a new candidate solution. Compare the fitness of the candidate solution with that of the current solution, selecting the superior one to advance to the next generation.

Step 4: Firefly Movement and Updates: Based on the objective function (the error between predicted and actual compaction quality), compute the brightness of each firefly. Calculate the movement vector of each firefly based on brightness differences and the introduced dynamic inertia weight and adaptive factor, then update the individual positions. Update the positions and brightness values for each firefly.

Step 5: Adaptive Optimization of RF Hyperparameters: Upon convergence or reaching the maximum iteration, extract the Ntree and Mtry parameter combination corresponding to the optimal firefly. Use this optimal parameter combination to train the RF and apply it to compaction quality prediction.

Step 6: Model Evaluation and Validation: Evaluate the RF model optimized by the IFA by calculating the prediction accuracy, error rates, and other performance indicators. Apply the model to real-world data to validate its generalization capability and robustness.

Algorithm 1: The pseudo-code of the IFA-RF algorithm

Input: Rolling parameters, material characteristic parameters, meteorological factors 1: Initialize IFA-RF parameters, such as the number of fireflies, maximum iteration count (max_gen), Mtry, Ntree, lower bounds for parameters, upper bounds for parameters, and dim. 2: Initialize the firefly population and fitness values. 3: Compute the initial fitness of each firefly’s position in the random forest model and identify the initial optimal solution. 4: For gen = 1:max_gen % Loop through the number of iterations 5:  Dynamically adjust the differential evolution parameter (F) using a sine-function-based adaptive factor. 6:  For i = 1:n  % Iterate over each firefly 7:    For j = 1:n  % Compare each firefly 8:       If  Check each firefly’s fitness and compute the distance between two fireflies, then update the position using the dynamically adjusted inertia weight. 9:       Verify if the search position exceeds the search space. If so, reposition the firefly within the bounds; otherwise, leave the position unchanged. 10:       End if 11:   End For 12:      Randomly select two fireflies and perform differential mutation to generate a new solution, ensuring that the mutated solution stays within the search space. 13:      Perform crossover based on a defined crossover probability to randomly select genes and generate a trial solution. 14:      Calculate the fitness of the new solution using random forest. 15:       If 16:      the fitness of the trial solution is better than the current one, update the firefly’s position and fitness. 17:      End If 18:      If 19:      the fitness of the current optimal solution is better, update the optimal solution and its fitness. 20:      End If 21:   End For 22: End For 23: Output the optimal random forest parameters. 24: Use the optimized parameters to train the random forest model and predict dry density. Output: Prediction results of dry density

3. Results

This study uses the compaction process of a specific earth-rock dam in Southwestern China as a case study. The power station controls a watershed area of approximately 65,700 km², with a total reservoir capacity of 10.154 billion m³ and an active storage capacity of 6.56 billion m³, thereby providing multi-year regulation capability. The main structures of the project consist of a rockfill dam with a gravel-core wall, a spillway, a flood discharge tunnel, a draw-off tunnel, an underground powerhouse, and other related facilities. The proposed compaction quality prediction model for the earth-rock dam, based on the IFA-RF model, is applied to predict the actual compaction process. A comparative analysis is conducted between the proposed model and traditional compaction quality prediction models, such as RF, BPNN, and multiple linear regression (MLR), to validate the consistency, superiority, and robustness of the proposed model.

3.1. Data Acquisition and Preprocessing

The data for this study were obtained from multiple sources: material source testing data, real-time compaction monitoring system reports, meteorological data from an intelligent weather monitoring system, and test pit experimental data. These data provide the material parameters, compaction parameters, meteorological parameters, and dry density values. Following the data collection and preprocessing methods discussed in the previous section, the collected data were integrated into a single dataset, which includes 106 sets of data. The partial statistical summary of the sample set is shown in

Table 2. The partial statistical summary of the sample set.

	Moisture Content (%)	P5 Content (%)	Rolling Thickness	Humidity	Total Passes	Dry Density
Number of cases	106	106	106	106	106	106
average	8.526	42.38486	0.2556	44.75280	19.7	2.2104
median	8.5	42.75	0.26	49.66935	19	2.21
standard deviation	0.2756	4.54036	0.03186	17.28726	5.667	0.01702
minimum value	8	2.35559	0.16	11.058	9	2.17
Maximum value	9.4	48.2	0.31	72.42679	36	2.25

.

3.2. Construction of the Driving Model and Correlation Analysis

This study employs a multiple linear regression (MLR) method to construct data-driven models that relate the compaction parameters, material source parameters, and meteorological parameters to the compaction quality indicator (dry density). These models help determine the influence of each parameter on the compaction quality, providing a scientific and rational theoretical foundation for controlling the compaction quality during earth-rock dam construction.

To improve the accuracy of the MLR model, the 106 sets of data related to the influencing parameters and the dry density evaluation were normalized. Considering both the correlation coefficient (R) and the significance analysis results, only the parameters with significant correlation were selected for the regression models relating the response parameters to the overall dry density. Subsequently, MLR analysis was performed using SPSS software (www.ibm.com/legal/copytrade.shtml, accessed on 5 January 2025) to establish the dry density driving model, which is outlined as follows:

$${\widehat{y}}_i^c=0.58-0.05x_i^{c1}+0.069x_i^{c2}-0.178x_i^{c3}$$

(10)

$${\widehat{y}}_i^l=0.554-0.311x_i^{l1}-0.062x_i^{l2}+0.246x_i^{l3}-0.069x_i^{l4}$$

(11)

$${\widehat{y}}_i^w=0.539+0.029x_i^{w1}-0.079x_i^{w2}$$

(12)

where ${\widehat{y}}_i^c$, ${\widehat{y}}_i^l$, and ${\widehat{y}}_i^w$ represent the linear regression evaluation values of the dry density-driven models for the compaction parameters, material source parameters, and meteorological parameters, respectively. $x_i^{c1}$, $x_i^{c2}$, and $x_i^{c3}$ refer to the compaction thickness, static compaction cycles, and total cycles, respectively. $x_i^{l1}$, $x_i^{l2}$, $x_i^{l3}$, and $x_i^{l4}$ include the full material moisture content, curvature coefficient, P5 content, and uniformity coefficient, respectively. $x_i^{w1}$ and $x_i^{w2}$ refer to temperature and humidity.

By constructing the driving model for the compaction parameters and their correlation with the dry density, it was found that, under conditions where the basic parameters cannot be guaranteed to remain constant, the number of static compaction cycles still shows a strong correlation with the dry density. Additionally, full material moisture content and P5 content are strongly correlated with compaction dry density, while temperature and humidity show weak correlations. Among these, humidity has a greater impact on compaction quality than temperature. Therefore, the input parameters for the model, such as the number of static compaction cycles from the compaction parameters, full material moisture content and P5 content from the material source parameters, and humidity from the meteorological parameters, all significantly influence the compaction dry density. These parameters provide a scientifically sound theoretical basis for controlling compaction quality at the earth-rock dam construction site.

3.3. Quantitative Results of Uncertainty in Parameters

Based on information entropy theory and following the steps outlined in Section 3.1 for entropy calculation, the uncertainty of the P5 content was quantified using 106 data points as an example. The result, as shown in

Table 3. Frequency distribution table of the P5 content.

Group (%)	38.2–40.2	40.2–42.2	42.2–44.2	43.42–46.2	46.2–48.2
Count (n)	9	34	37	11	9
Frequency	0.09	0.34	0.37	0.11	0.09

, reveals that the entropy value for P5 content is 0.8766. The final entropy values for the material source parameters are presented in

Table 4. Entropy values of the compaction quality influence parameters.

Parameter	Material Source Parameters				Compaction Parameters				Meteorological Parameters
	P5 Content	Moisture Content	Curvature Coefficient	Uniformity Coefficient	Compaction Thickness	Static Compaction Cycles	Total Compaction Cycles	Total Compaction Cycles	Temperature	Humidity
Entropy value	0.8766	0.7760	0.7109	0.6755	0.5082	0.5915	0.3093	0.6409	0.8569	0.9093

. From the table, it can be seen that all material source parameters have entropy values greater than 0.5, indicating considerable uncertainty in these parameters. Among them, the uncertainty of the P5 content and moisture content is notably higher than that of the curvature coefficient and the uniformity coefficient. The geological variability of the material source parameters primarily stems from two aspects. On the one hand, it arises from the variability of uncontrollable factors, such as the inability to precisely control the moisture content, which leads to significant spatial variability in the moisture content of dam materials across the entire slab. On the other hand, it results from the randomness of the material source parameters, which is introduced by the limited number of test pit experiments used to obtain these parameters, thereby causing inherent randomness. The entropy values for the compaction parameters are shown in Table 4. It can be observed that the entropy values for compaction thickness, static compaction cycles, and total cycles are all greater than 0.5, although relatively small, indicating a certain level of uncertainty in these parameters. Among them, the uncertainty for static compaction cycles is lower than 0.5, suggesting that the static compaction cycles are well controlled within the specified range. The entropy values for the meteorological parameters are presented in Table 4. It can be observed that the entropy values for all meteorological parameters exceed 0.5, indicating significant uncertainty. The uncertainty of the meteorological parameters is notably higher than that of the material source parameters. This is because meteorological data exhibit large variations throughout the day, resulting in greater uncertainty.

The aforementioned study reveals that the influencing parameters exhibit uncertainty. Specifically, the probability distribution function of the material source parameters was obtained through statistical analysis of historical material source data. Based on this probability distribution function, the material source parameters at unmeasured points on the slab were randomly simulated using simulation software. Finally, the dry density evaluation results for the entire slab, obtained through the IFA-RF method, demonstrated a certain degree of randomness. This randomness inevitably introduces random errors into the compaction quality evaluation results, and the magnitude of these errors determines the accuracy of the evaluation. Therefore, by conducting 100 random simulations and selecting evaluation results with a confidence level above 95% as the final evaluation values, the results are more closely aligned with actual conditions, ensuring the data’s research value.

3.4. IFA-RF Algorithm Model Optimization and Learning

In this study, the number of static compaction cycles, P5 content, moisture content, humidity, and curvature coefficient were chosen as input variables, with dry density as the output variable. The IFA-RF algorithm was employed to construct the prediction model. To evaluate the prediction stability and generalizability of the proposed algorithm, this study adopted a five-fold cross-validation method, dividing the dataset into five parts, with four parts as the training set and one part as the testing set. This study specifically employed an RF algorithm designed for small-sample datasets, and several scholars have demonstrated the feasibility of predictions using small sample sizes [24,25]. These datasets were input into the IFA-RF algorithm, and the IFA was used to optimize the parameters of the RF model. The optimal values for the Ntree and Mtry parameters were found to be 132 and 2, respectively. Subsequently, the RF model was trained using these optimal parameters, achieving high-accuracy predictions of the dry density.

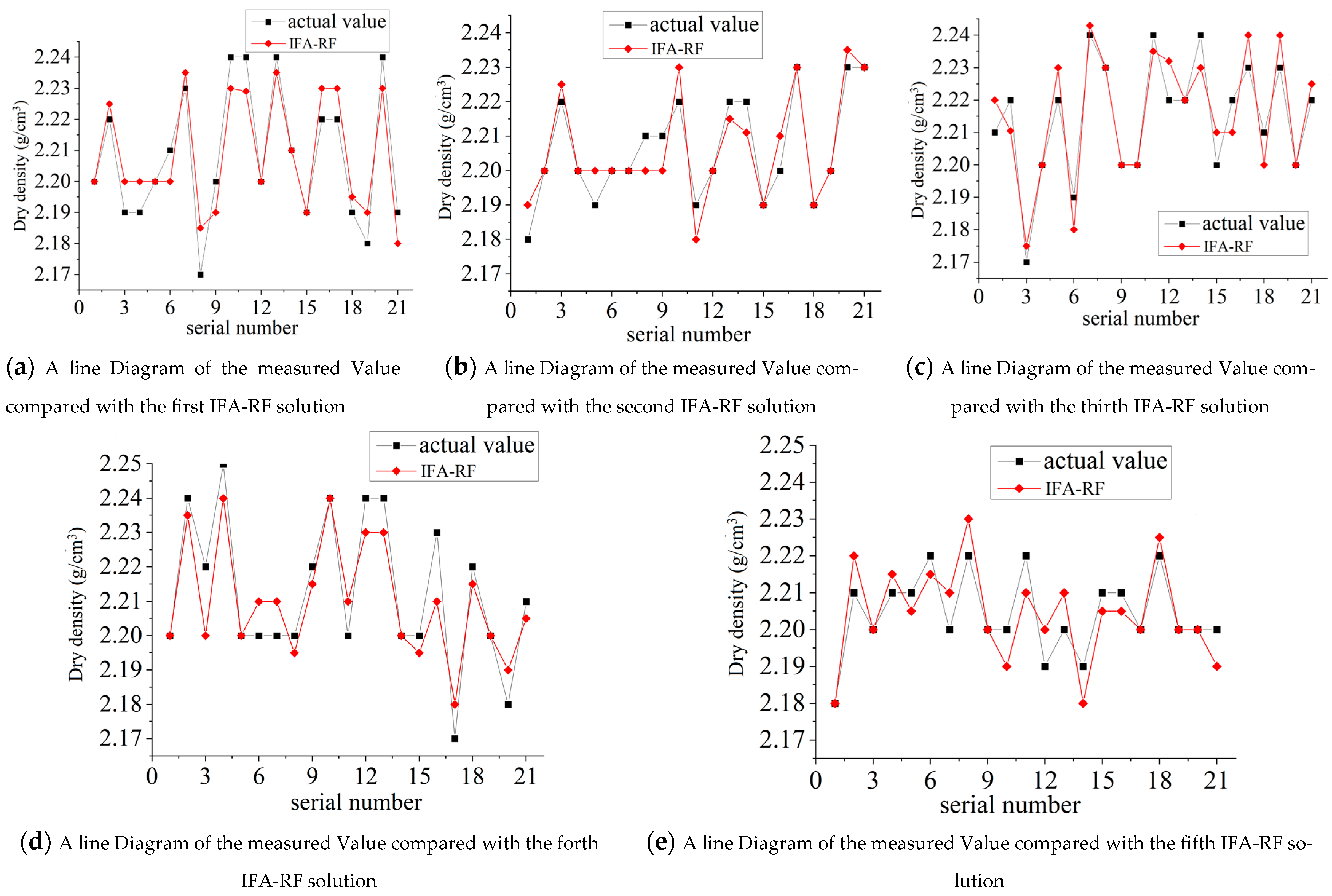
3.5. Prediction Results Analysis

The measured values of dry density were compared with the prediction results from the IFA-RF model. The line chart depicting the results of the five-fold cross-validation is presented in Figure 1, which visually illustrates the relationship between the measured values and the predicted values from the model.

3.6. Comparison and Discussion of Compaction Quality Prediction Models

In the comparison and discussion of compaction quality prediction models, error metrics are commonly used as indicators to assess the fitting performance of the model. The mean squared error (MSE) and normalized mean squared error (NMSE) are used as average error metrics, reflecting the overall deviation of the model’s predicted values from the observed values. Smaller values of these metrics indicate better model performance. Additionally, the mean absolute error (MAE) measures the average absolute deviation between individual observations and the arithmetic mean, while the Pearson correlation coefficient (R) is used to assess the linear relationship between two random variables.

In this study, the evaluation of the compaction quality prediction method not only considers the error analysis and comparison among the IFA-RF, RF, BPNN, and MLR models but also incorporates the mean values and standard deviations, thereby providing a more comprehensive comparison of model performance.

Through error analysis, the MSE, MAE, and R for the IFA-RF model’s predicted dry density values were calculated and compared with the observed values. This evaluation assesses the effectiveness of the IFA-RF algorithm in predicting the compaction quality of earth-rock dams. The results indicate that the significance test was below the 0.05 significance level, and the correlation coefficient between the actual and predicted values was 0.90107, suggesting a significant correlation. This implies that the predicted results effectively reflect the actual values, confirming that the proposed model is suitable for predicting compaction quality in earth-rock dams.

Furthermore, the MAE for the IFA-RF model’s predictions was 0.00609 and the MSE was 6.02 × 10⁻⁵, indicating high prediction accuracy. To validate the consistency and superiority of the proposed IFA-RF algorithm, a comparative analysis was conducted of the performance of the IFA-RF, RF, BP neural network (BPNN), and multiple linear regression (MLR) models in practical engineering applications. The prediction results of the four models were compared and analyzed (see Figure 2). In the BPNN configuration, the hidden layer comprised 10 neurons. The training process was configured to run for a maximum of 10,000 iterations with a learning rate of 0.00001, and training could be terminated early once the target error fell below 0.000004. In the RF model, the number of trees was fixed at 500, and at each split, the optimal division was selected from only two candidate features.

The analysis of Figure 2 leads to the following conclusions.

Accuracy Analysis: The analysis reveals that the relative error and mean squared error (MSE) of the four compaction quality prediction models are consistent in terms of accuracy levels, while the accuracy levels for the mean absolute error (MAE) are nearly identical. In terms of correlation coefficients, the correlation between the prediction results and the measured values exceeds 0.7 for all four models, indicating a strong correlation between the predicted and actual values. The 95% confidence interval for IFA-RF is [0.862, 1.041], which does not include zero and has a relatively narrow range. The t-value of 21.087 is significantly greater than the critical value of 2, further supporting the significant positive impact of IFA-RF on the dependent variable and validating its statistical significance. The statistical results further confirm the significance of all the models: RF ([0.461, 0.837], p = 0.000), MLR ([0.098, 0.622], p = 0.007), and BPNN ([0.090, 0.356], p = 0.001). Significance testing reveals that the results of all four models are statistically significant at the 0.01 level. Based on these findings, the IFA-RF algorithm model and traditional compaction quality prediction models show consistency in predicting the compaction quality.

Superior Performance: In terms of prediction accuracy, the IFA-RF model yields prediction results with average values closest to the measured average, followed by the BPNN, RF, and MLR models, in decreasing order of similarity. Regarding standard deviation, the BPNN’s prediction results are closest to the measured values. This is due to the higher uncertainty inherent in BPNN as a “black box” fitting model, which results in a larger standard deviation, despite its poor prediction accuracy. In contrast, the linear regression method, which computes prediction results using formulae, exhibits low dispersion and, consequently, the smallest standard deviation. However, the IFA-RF model not only matches the measured values well in terms of trend but also achieves the highest accuracy. Additionally, the IFA-RF model outperforms the RF, BPNN, and MLR models in terms of MSE and MAE, and it attains a higher correlation coefficient than all three. Overall, the IFA-RF-based compaction quality prediction model demonstrates superior performance, exhibiting the closest trend to the measured values, minimal error, and the best correlation.

Additionally, the robustness of the proposed IFA-RF model was tested using noisy data. The model’s robustness is characterized by the decline in accuracy as noise is added to the data. Random noise values following a normal distribution were added to the training dataset, and the noise variance was adjusted to control its magnitude. The decline in model accuracy with increasing noise intensity was then evaluated to assess the model’s noise resistance. The noise levels were calibrated based on preliminary field data, so that the variance and distribution of the noise approximate the measurement errors and environmental fluctuations typically observed in operational conditions. Although the noise model is relatively simplistic—employing independent random perturbations—it is intended to mimic the typical uncertainties encountered in practice. The complexity of the construction environment for hydraulic engineering core–wall rockfill dams inevitably introduces noisy data into the compaction operation information. Therefore, the stronger the model’s robustness, the more effective it is for accurately predicting the spatial compaction quality of the dam.

Figure 3 illustrates the decrease in the Pearson correlation coefficient (R) of different models as the noise intensity ($\mathsf{\sigma }$) increases. As shown in Figure 3, the BPNN model exhibits the poorest noise resistance, with its accuracy rapidly declining as the noise intensity increases. The RF and MLR models, while more resistant to noise than the BPNN model, also show a significant decline in accuracy, especially the MLR model, which experiences a sharp drop in accuracy when the noise intensity reaches 0.9. In contrast, the accuracy of the IFA-RF model decreases gradually with noise increases, without any sharp drop, indicating that the proposed model has strong noise resistance. Therefore, in terms of robustness, the IFA-RF model is well suited for establishing a dynamic evaluation model for the compaction quality of earth-rock dams. However, since IFA-RF is also a black box fitting model, the predicted values inherently exhibit a degree of uncertainty. The authors intend to investigate this further in future research. Furthermore, we plan to proactively collect additional independent datasets in future studies to conduct comprehensive external validation of the IFA-RF model, thereby rigorously assessing its generalizability and strengthening the reliability of its application in diverse real-world scenarios.

4. Conclusions

To address the issues of ignoring parameter uncertainty in earth-rock dam compaction quality evaluation and the limitations in prediction accuracy and generalization of traditional compaction quality evaluation models, a prediction model for the compaction quality of earth-rock dams based on IFA-RF is proposed. A predictive analysis and performance comparison study was conducted using actual compaction data from a southwestern earth-rock dam project. The following conclusions were drawn:

(1)

Uncertainty Analysis: An uncertainty analysis method was applied to scientifically and rationally analyze the influencing parameters of compaction quality. The uncertainty was quantified, and by considering the parameter uncertainty, the evaluation results for the earth-rock dam compaction quality were made more comprehensive and precise.

(2)

IFA: An improved firefly algorithm, coupled with DIW, adaptive factors, and DES, was proposed. DIW allowed the search process to gradually shift from broad exploration to local optimization. A sine function was used to adjust the F parameter in the differential evolution strategy, enhancing the algorithm’s adaptability. Additionally, differential mutation and crossover strategies were introduced in each iteration to improve the population diversity and enhance the global search capability. Compared to the traditional FA, the proposed IFA demonstrated superior accuracy, effectiveness, and robustness when optimizing four benchmark functions.

(3)

Compaction Quality Prediction Model: A compaction quality prediction model based on the IFA-RF was developed. The algorithm adaptively optimized the Ntree and Mtry parameters of the RF, creating a model that revealed the complex nonlinear relationships between input factors, such as compaction parameters, material source parameters, and meteorological parameters, and the compaction quality. The model’s predictive performance was further improved. Verification through an engineering case study showed that, compared to prediction models based on traditional RF, BPNNs, and MLR, the proposed model exhibited superior accuracy.